Pressure and Temperature Effects on the Activity and Structure of the Catalytic Domain of Human MT1-MMP

Abstract

Membrane type 1-matrix metalloproteinase (MT1-MMP or MMP-14) is a zinc-transmembrane metalloprotease involved in the degradation of extracellular matrix and tumor invasion. While changes in solvation of MT1-MMP have been recently studied, little is known about the structural and energetic changes associated with MT1-MMP while interacting with substrates. Steady-state kinetic and thermodynamic data (including activation energies and activation volumes) were measured over a wide range of temperatures and pressures by means of a stopped-flow fluorescence technique. Complementary temperature- and pressure-dependent Fourier-transform infrared measurements provided corresponding structural information of the protein. MT1-MMP is stable and active over a wide range of temperatures (10–55°C). A small conformational change was detected at 37°C, which is responsible for the change in activity observed at the same temperature. Pressure decreases the enzymatic activity until complete inactivation occurs at 2 kbar. The inactivation is associated with changes in the rate-limiting step of the reaction caused by additional hydration of the active site upon compression and/or minor conformational changes in the active site region. Based on these data, an energy and volume diagram could be established for the various steps of the enzymatic reaction.

Introduction

Membrane-type 1 matrix metalloproteinase (MT1-MMP or MMP-14) is a calcium- and zinc-dependent transmembrane endopeptidase. It belongs to the family of Matrix Metalloproteinases (MMPs) with at least 23 members expressed in the human organism (1). MT1-MMP is involved in the mediation of pericellular proteolysis of extracellular matrix components, essential for the physiological remodeling processes such as tissue repair, development, and morphogenesis. However, the biological role of MT1-MMP and its full spectrum of in vivo substrates is still largely unknown (2). In recent years, >60 different substrates of MT1-MMP were identified: peptide substrates like extracellular matrix components and serum proteins, growth factors, cytokines, chemokines, and several other cell surface biomolecules (2, 3). Despite their role in several physiological processes like wound healing, bone resorption, organogenesis, and uterine involution, MMPs are especially studied because they are associated with pathologic conditions including inflammatory, autoimmune, or vascular disorders and oncogenesis. In particular, MT1-MMP is overexpressed in many cancer types and increases tumor cell growth, invasion, and metastasis by degrading extracellular matrix components and making paths through surrounding tissues (4, 5, 6). Recent investigations have also implicated MT1-MMP activity in myocardial infarctions and dysfunctions (7, 8). For these reasons, shedding light on the mechanism and function of MT1-MMP is fundamental to prevent pathologic conditions, and inhibition of its activity is an obvious therapeutic approach to limit cancer progression and other severe diseases. The catalytic domain of MT1-MMP can be effectively (but not selectively) inhibited by the protein inhibitors N-TIMP-2 and N-TIMP-3 (9). In the last decades, carboxyl, thiol, and hydroxamic acid-based inhibitors have been developed without being successful in clinical trials against single MMPs (e.g., MT1-MMP) because of their tendency to chelate the catalytic zinc in a nonselective way (10).

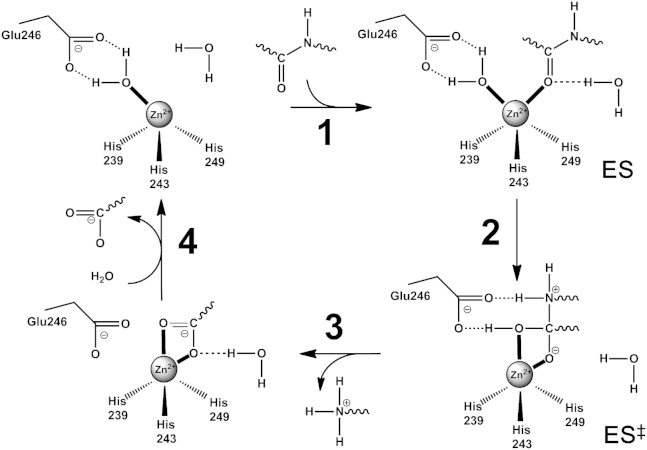
Recently, the study of the role of water dynamics on the substrate-enzyme interaction of the catalytic domain of MT1-MMP revealed a strong coupling between water and protein dynamics being crucial for catalysis, suggesting its potential key role for molecular recognition (11, 12, 13). All the MMP family members share a similar monomeric and globular catalytic domain of ∼165 amino acids with three α-helices, five stranded β-sheets, two zinc and at least two calcium binding sites. The first zinc site has structural function while the second catalytic zinc is located in the active site. The active site architecture is almost identical and superimposable among all the MMP members, suggesting a shared catalytic mechanism (14). Even if the noninhibited structure of MT1-MMP is not available as of this writing (15), a comparative study of other noninhibited MMPs reveals that usually the substrate binding site is characterized by a hydrophobic pocket called S1′, which determines substrate specificity and a solvent-exposed catalytic Zn²⁺ ion coordinating the Nϵ2 atoms of a histidines tripod of the conserved sequence HEXXHXXGXXH and a weakly bound water molecule in a distorted tetrahedral coordination with binding distances of ∼2.1 Å (16, 17). Mechanistic studies at close-to-neutral pH revealed that a water molecule is extremely polarized between the conserved glutamate base and the zinc Lewis acid in a Glu-H₂O-Zn bridge (Fig. 1, 1) (18, 19). A single-step catalytic mechanism of peptide hydrolysis is usually suggested for MMPs, which involves the formation of a Michaelis complex (17). Upon peptide docking (ES, 1), the nucleophilic attack of the water oxygen on the peptide carbon is performed and the glutamate polarized proton water is shuttled toward the nitrogen of the scissile amide, forming a metal penta-coordinated intermediate (2). The transition complex (ES^‡) is dominated by the formation of the C-O bond through nucleophilic attack. The second water proton is then transferred to the amine group by the conserved glutamate and the breakdown of the C-N bond occurs (3). An auxiliary water molecule is suggested to act as an electrophilic agent to the carbonyl oxygen of the substrate. The last step corresponds to the release of the carboxylate product and the reuptake of a water molecule (4). Despite the large number of theoretical studies on MMPs, experimental evidences of their reactions are still incomplete and the molecular mechanisms remain disputable (16, 17). Even if it is known that enzymes fluctuate between different conformational states and that enzymatic reactions may involve several substates (20), the classical transition state theory is still the only formalism generally used to reveal thermodynamic data of the reactions (21). In this study we set out to modulate the kinetics of the enzymatic reaction of MT1-MMP using both temperature and pressure perturbation, thereby allowing alteration of the underlying rate and equilibrium constants and yielding additional information on the structural dynamics, energetics, and transition state of the reaction (22, 23, 24). Moreover, the results obtained broaden our understanding of the MT1-MMP’s catalytic activity over a wide range of temperatures and pressures, i.e., they also include extreme environmental conditions.

Figure 1.

Model of the catalytic mechanism of hydrolysis of MMPs (17).

It is well known that pressure-dependent studies can reveal new routes in the pathway of enzymatic reactions and allow characterizing volume changes associated with substrate binding and transition state formation. Pressure has also proven to be an important tool to probe conformational states as it can shift the population among different substates based on their volumetric properties, thereby giving new insights into the reaction dynamics and mechanism of biochemical conversions (22), or revealing equilibria between otherwise unresolved substates (25). Generally, pressures below 10 kbar reversibly affect weak chemical bonding within the protein itself and with the surrounding water, such as hydrogen bonds and hydrophobic and van der Waals interactions (26). These weak interactions are important to maintain the native protein conformation. Breakage of covalent bonds are very rare in this pressure range. Pressure modulation has also been shown to stabilize and help identify folding intermediates and is a useful tool to characterize aggregation and fibrillation pathways of amyloidogenic proteins, such as those involved in diseases such as Parkinson’s, Alzheimer’s, and tumors (27).

Moreover, pressure-jump relaxation techniques can be used to trigger biochemical reactions, with significant advantages compared to temperature-jump techniques, as pressure propagates and equilibrates rapidly. High pressure is generally a rather mild perturbating agent, and can hence be used to modulate enzymatic reactions by affecting changes in volumetric properties, which are also known to be sensitive to changes in hydration and conformation of the reactants (21, 28). In this work, standard reaction (ΔG°, ΔH°, ΔS°) and activation (ΔG^‡, ΔH^‡, ΔS^‡) values for the thermodynamic functions of the MT1-MMP enzymatic reaction were determined from temperature-dependent studies of the reaction rate during catalysis of a collagen-like peptide. A similar pressure-dependent analysis allowed having access to the activation volume, ΔV^‡, which corresponds to the volume difference between the transition-state and enzyme-substate complex. By this combined study, a full description of the thermodynamics and kinetics of the MT1-MMP reaction is obtained in an unprecedented way, similar to a recent study on urease (22). To reveal corresponding information about the structural stability of the enzyme and secondary structural changes of the enzyme upon changes in temperature and pressure, temperature- and pressure-dependent Fourier-transform infrared (FTIR) spectroscopy measurements were carried out as well.

Materials and Methods

Materials and sample preparation

The catalytic domain of human membrane-type 1 matrix metalloproteinase was expressed into Escherichia coli BL21(DE) (Novagen, Madison, WI) and subsequently purified using the inclusion bodies method as described in a previous work (15). The fluorogenic collagen-like peptide Mca-Lys-Pro-Leu-Gly∼Leu-Lys(Dnp)-Ala-Arg-NH₂ (MCA, methoxy-coumarin-4-acetyl; DNP, 2,4-dinitrophenyl) was synthesized by standard solid phase synthesis (SPS; Rink amide ChemMatrix, Sigma-Aldrich, St. Louis, MO) using Fmoc chemistry and n-methylpyrrolidon as solvent (29). All other chemicals were of analytical grade and obtained from various commercial sources. Protein quantification was spectrophotometrically determined by using the calculated molar extinction coefficient at 280 nm (35,410 M⁻¹ cm⁻¹) and the purity of the enzyme was determined by sodium dodecyl sulfate polyacrylamide gel electrophoresis.

Temperature- and pressure-dependent activity profile

Enzymatic assays at different temperatures were performed by monitoring the increase in fluorescence intensity of MCA due to the decrease of FRET quenching by DNP upon cleavage of the fluorogenic peptide (λ_ex: 340 nm; λ_em: 400 nm) (29). Initial rates of hydrolysis of MT1-MMP were determined with a rapid mixing stopped-flow unit (RX2000; Applied Photophysics Ltd., Leatherhead, Surrey, UK) combined with a fluorescence spectrophotometer (Cary Eclipse, Varian, Cary, NC). Temperature was controlled with a refrigerated/heating circulator system (model No. F12, Julabo USA, Allentown, PA). A quartz cuvette was used because of its heat-retaining capacity and quick temperature equilibration. Measurements were performed adding the enzyme to the reaction mixture in 50 mM Tris/HCl (pH 7.4), 100 mM NaCl, and 5 mM CaCl₂, and varying concentrations of fluorescent peptide (1–4 μM). Temperature was varied from 10 to 55°C and buffers were adjusted to the appropriate pH value at the assay temperature. A calibration curve was measured where the maximal fluorescent signal upon complete hydrolysis corresponds to the total substrate concentration. The experiment was repeated at least twice and error bars were calculated from the standard deviation. Initial rates of hydrolysis were calculated by linear regression of the first data points during the initial 10 s of the reaction (fluorescence intensity versus time curve). Steady-state parameters (K_M, k_cat) for the hydrolysis of the substrate were estimated by fitting of the reaction rates in the Michaelis-Menten plots (v_i = v_max[S]/(K_M+[S])) using OriginLab 8.6 software (OriginLab, Northampton, MA), where v_i is the initial rate (s⁻¹), [S] is the substrate concentration (M), v_max the maximum reaction rate (s⁻¹) attained at the saturating substrate concentration, and K_M is the Michaelis-Menten constant.

High-pressure kinetic experiments up to 2 kbar were performed with a Hi-Tech Scientific high-pressure stopped-flow spectrophotometer HPSF-56 (TgK Scientific, Bradford on Avon, UK) constructed based on a previously developed apparatus (30). The two reagents and a collection syringe assembly were mounted inside the high-pressure vessel with pressure-stable sapphire windows for spectroscopic detection. After mixing 0.1 μM MT1-MMP protein and 250 μM peptide substrate (final concentrations), the reaction was monitored by a photomultiplier using a 400-nm-cutoff long-pass filter to eliminate detection of excitation light at 340 nm. The dead time of the system was <10 ms. The activation volume, ΔV^‡, was obtained from the pressure dependence of the natural logarithm of the ratio of rate constants, k_cat/k_cat,0, according to Eq. 1, where k_cat is the rate at pressure p, and k_cat,0 is the corresponding value at ambient pressure (1 bar) (31):

$$\text{d}\text{ln}\left(k_{\text{cat}}/k_{\text{cat},0}\right)/\text{d}p=-\Delta V^{‡}/RT.$$ (1)

Temperature- and pressure-dependent FTIR spectroscopy

Temperature-dependent FTIR experiments were carried out by measuring the amide I′ band of 25 mg/mL MT1-MMP in 50 mM BisTris in D₂O pH 7.4, 100 mM NaCl, 5 mM CaCl₂ and by varying temperature (20–90°C) and pressure (1–14 kbar). The contribution of a blank sample of buffer solution was measured separately and subtracted. Measurements were performed using a Nicolet 5700 instrument (Thermo Fisher Scientific, Waltham, MA) equipped with a liquid-nitrogen cooled MCT-detector (HgCdTe) in the wavenumber range from 4000 to 1100 cm⁻¹. A sample volume of ∼20 μL was placed between two CaF₂ windows separated by a Mylar spacer (thickness 50 μm, effective sample volume 3.9 μL) and assembled in a temperature cell. To make sure that the sample is equilibrated, each temperature was maintained for 12 min before collecting spectra.

Pressure-dependent FTIR spectra were collected in a MAGNA 550 (Thermo Fisher Scientific) equipped with a liquid-nitrogen cooled MCT-detector (HgCdTe) within 4000–650 cm⁻¹. To achieve pressures up to 16 kbar, a membrane-driven diamond anvil cell (Diacell VivoDAC; Almax easyLab, Diksmuide, Belgium), equipped with an automated pneumatic pressure controller (Diacell iGM Controller; Almax easyLab), was used. For the high-pressure FTIR experiments, a 50-μm-thick gasket made of brass with a 0.5 mm drilled opening (effective sample volume 9.8 nL) was placed onto a 730-μm-thick Type IIa diamond window (Almax easyLab). For accurate determination of the pressure in the sample, the pressure dependence of the SO₄²⁻ stretching mode of BaSO₄ was used as internal pressure gauge. The temperature was controlled via an external water bath, measuring the temperature with a digital thermometer placed in the sample cell (accuracy ± 0.5°C), offering a controllable temperature range of 1–98°C, and the sample chamber was continuously purged with CO₂-free and dry air. For each temperature or pressure, a single spectrum was obtained by collecting and averaging 256 spectra in a row by using OMNIC 7.2 spectral processing software (Thermo Electron, Thermo Fisher Scientific, Waltham, MA), and was apodized by a Happ-Genzel function. Spectra were processed and analyzed with Thermo Grams 9.1 software (Thermo Fisher Scientific) as follows: after buffer subtraction and smoothing, the area of amide I′ band (1700–1600 cm⁻¹) was normalized. To reveal the number of subbands and detect conformational changes, second derivative spectra and Fourier self-deconvoluted spectra were analyzed. The amide I′ band region of MT1-MMP could be decomposed into nine underlying subbands, and the underlying secondary structure element could be determined using mixed Gaussian-Lorentzian lineshape functions in the fitting procedure (see the Supporting Material).

Results and Discussion

In this work it was assumed that the hydrolysis of the peptide by MT1-MMP proceeds in two steps according to the simplest model that accounts for the kinetic properties of many enzymes and correspondingly to the general scheme of Michaelis-Menten kinetics,

$$\text{E}+\text{S}\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}\text{ES}\stackrel{k_2}{\to }\text{E}+\text{P},$$

where k₁ and k₋₁ are the rate constants for the formation and dissociation of the enzyme-substrate complex ES, respectively; k₂ is the rate constant for the breakdown of the ES complex to the formation of free enzyme, E; and product, P. In this model the enzyme-substrate interaction (E + S $\rightleftarrows$ ES) is fast compared to the chemical reaction that accounts for the product formation (ES → E + P) (32). The latter represents the reaction-limiting step, thus k₂ corresponds to the first-order catalytic rate constant k_cat (turnover number) in the steady-state approximation. Because k₋₁ >> k_cat, the Michaelis-Menten constant can be approximated by the dissociation constant (K_M = K_D = k_-1/k₁) for the ES complex (22). Here, we determined the effect of temperature and pressure on these two parameters. The results are discussed in the following.

Temperature activity profile

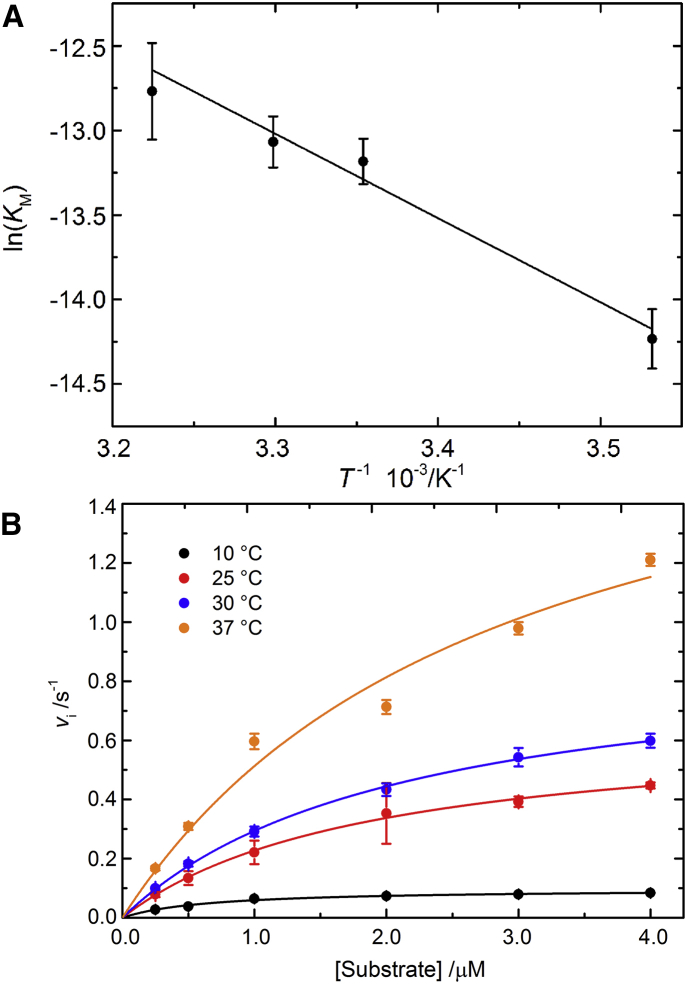
The effect of temperature on the rate of hydrolysis of the peptide by the catalytic domain of MT1-MMP was studied at temperatures between 10 and 55°C at atmospheric pressure. The steady-state kinetic parameters were determined by Michaelis-Menten plots for different temperatures (Fig. 2 B). Over the temperature range of 10–37°C, the kinetic parameters K_M, k_cat, and the ratio k_cat/K_M, i.e., the enzymatic efficiency, are consistent with those reported in the literature (29, 33, 34) and exhibit a significant (reversible) temperature dependence as shown in Table 1.

Figure 2.

(A) Effect of temperature on the equilibrium constant K_M for the formation of the MT1-MMP-substrate complex in the range 10–37°C, at atmospheric pressure in 50 mM Tris, 100 mM NaCl, and 5 mM CaCl₂, at pH 7.4. The linear correlation coefficient is r = 0.953. (B) Michaelis-Menten plots for the determination of the steady-state kinetic parameters between 10 and 37°C.

Table 1.

Kinetic parameters for the hydrolysis of a fluorescent peptide by the catalytic domain of MT1-MMP

T / K	KM/μM	kcat/s−1	kcat/KM 106/M−1 s−1
283 (10°C)	0.6 ± 0.1	0.33 ± 0.04	0.55
298 (25°C)	1.8 ± 0.3	2.1 ± 0.6	1.17
303 (30°C)	2.1 ± 0.3	3.4 ± 0.4	1.62
310 (37°C)	2.8 ± 0.8	6.8 ± 0.8	2.43

The values were obtained at different temperatures in 50 mM Tris, 100 mM NaCl, and 5 mM CaCl₂ at pH 7 and with 1 bar of atmospheric pressure.

The turnover number, k_cat, increases with increasing temperature as expected for an enzymatic reaction, up to 20-fold at 37°C compared to the value at 10°C. The Michaelis constant, K_M, shows a weaker temperature dependence, corresponding to an approximately fourfold increase in the range from 10 to 37°C. Hence, the ratio k_cat/K_m increases moderately only as a function of temperature. Such behavior indicates that the thermally induced reduction of the affinity (increase of K_M) is more than compensated by an increase in turnover number (k_cat) (32).

Temperature effect on the equilibrium constant

The Michaelis constant, K_M, represents the equilibrium constant for the reaction E + S $\rightleftarrows$ ES, hence it is possible to derive thermodynamic parameters associated with the formation of the ES complex such as the standard enthalpy, entropy, and free energy change of the reaction (ΔH°, ΔS°, ΔG°) from its temperature-dependent behavior using the thermodynamic relationship ΔG° = −RT ln(K_M) and invoking the van ’t Hoff equation, which relates the temperature dependence of K_M to the standard enthalpy change, ΔH° and entropy change, ΔS°. The calculated values are displayed in Table 2 and were determined from fits of the –ln(K_M) versus T⁻¹ plots (Fig. 2 A) (22)

$$-\text{ln}\left(K_M\right)=\Delta H°/RT-\Delta S°/R,$$ (2)

where R is the gas constant, T is the absolute temperature, and K_M is the Michaelis constant in M. The enthalpy change associated with the interaction between the enzyme and substrate is mainly constituted of two contributions: a favorable enthalpic contribution due to the establishment of optimal electrostatic interactions and formation of hydrogen bonds, and an unfavorable contribution from desolvation of polar groups (35). The favorable total enthalpy contribution to the binding (= ΔH°(1/K_M) = −ΔH°(K_M)) amounts to −41 ± 5 kJ mol⁻¹, indicating that the desolvation effect is more than compensated by well-placed hydrogen bonds and optimal van der Waals contacts upon substrate binding. On the other hand, the entropy change can be considered as the sum of a conformational and a desolvational term. The negative value of the overall measured entropy change (ΔS°(1/K_M) = −28 ± 3 J mol⁻¹ K⁻¹) indicates that the loss of conformational degrees of freedom resulting from the enzyme-substrate complex formation accounts more than the release of water molecules from the substrate and desolvation of the cavity upon binding. Overall, the association of MT1-MMP with the substrate peptide is exothermic and enthalpically driven, accompanied by an unfavorable but relatively small entropic contributions, rendering the enzyme-substrate association spontaneous in the whole covered range of temperatures (e.g., ΔG°₂₉₈(1/K_M) = −33 ± 5 kJ/mol).

Table 2.

Thermodynamic parameters determined from the temperature-dependent measurements of the MT1-MMP enzymatic reaction

Parameter	kJ mol−1
ΔH°(1/KM)	−41 ± 5
ΔS°(1/KM)	(−0.028 ± 0.003) K−1
ΔG°298(1/KM)	−33 ± 5
Ea(kcat)37–55°C	30 ± 2
Ea(kcat)10–37°C	82 ± 2
ΔH‡ (kcat)	80 ± 2
ΔS‡ (kcat)	(0.085 ± 0.007) K−1
ΔG‡298 (kcat)	55 ± 4
ΔHT‡	42 ± 7
ΔST‡	(0.06 ± 0.01) K−1
ΔGT‡298	22 ± 9

The binding values of the thermodynamic functions (ΔH°, ΔS°, ΔG°) were determined from the van ’t Hoff analysis of the temperature dependence of K_M. Activation values (ΔH^‡, ΔS^‡, ΔG^‡) and the apparent activation energy, E_a, were derived from the temperature dependence of k_cat and the Eyring plot. Thermodynamic quantities associated with the catalytic specificity (ΔH_T^‡, ΔS_T^‡, ΔG_T^‡) were calculated from the corresponding binding and activation parameters.

Temperature effect on the rate constant

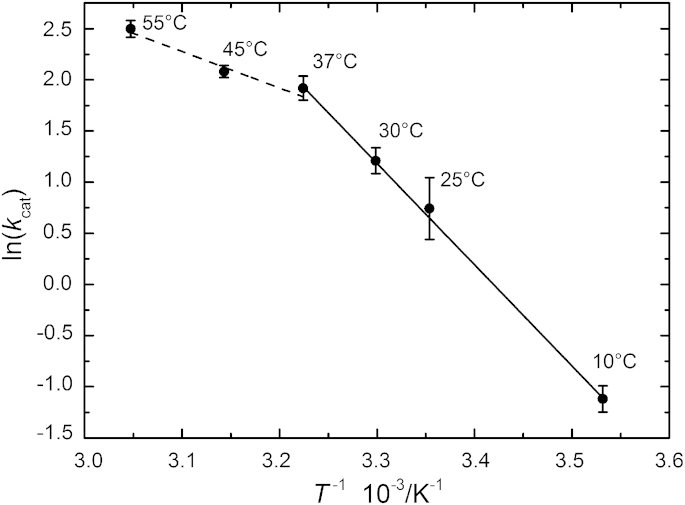
The temperature dependence of the rate constant k_cat is of fundamental importance to characterize the underlying driving forces associated with the energy barriers associated with the MT1-MMP-catalyzed hydrolysis reaction, providing insights into the energetic characteristics of the process of bond-breaking and/or bond-making that leads to the formation of the products (22). Thus, the Arrhenius plot for the cleavage of the fluorescent peptide was determined (Fig. 3) and the apparent activation energy, E_a, for the catalytic step of the enzymatic reaction was derived by fitting the data in the range 10–37°C using

$$\text{ln}\left(k_{\text{cat}}\right)=\text{ln}\left(A\right)-E_a/RT,$$ (3)

where k_cat is the rate constant (expressed in s⁻¹) at the absolute temperature T, and A is the preexponential factor that is proportional to the collision frequency.

Figure 3.

Arrhenius plot for the hydrolysis of the collagen-like peptide by the catalytic domain of MT1-MMP. The determined apparent activation energy, E_a amounts to 82 ± 2 kJ mol⁻¹ in the temperature range 10–37°C (where the protein is in its native state) and 30 ± 2 kJ mol⁻¹ in the range 37–50°C. Linear correlation coefficients correspond to r = 0.999 and r = 0.974, respectively.

A biphasic temperature-dependent behavior of the MT1-MMP’s turnover rate constant was observed with deviation from linearity starting at ∼37°C, reflecting partial inactivation and denaturation of the enzyme (see below for corresponding structural data). The activation energy calculated between 10 and 37°C corresponds to E_a = 82 ± 2 kJ mol⁻¹ for the natively folded protein, a value typical for enzymatic catalysis of peptide substrates by MMPs (16, 17, 33, 36), and decreases to 30 ± 6 kJ mol⁻¹ between 37 and 55°C. The entropy and enthalpy changes of the catalytic step were determined by using the absolute rate theory for the analysis of the rate constant k_cat, where the temperature dependence on the rate constant is expressed by the Eyring equation (assuming a transmission coefficient of 1) (22):

$$\text{ln}\left(k_{\text{cat}}/T\right)=-\Delta H^{‡}/RT+\text{ln}\left(k_{\text{B}}/h\right)+\Delta S^{‡}/R.$$ (4)

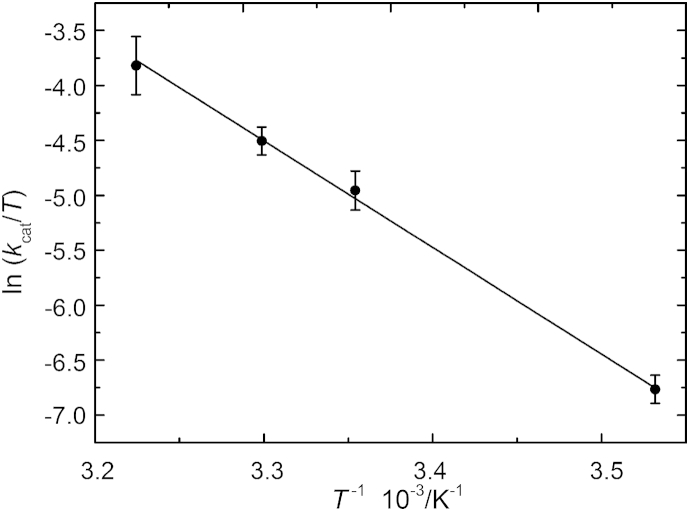
From the linear fits of the Eyring plot (Fig. 4), the thermodynamic activation functions ΔH^‡ and ΔS^‡ were determined from the slope and the intercept values, respectively. The activation free energy, ΔG^‡, associated with k_cat was estimated by using the relationship ΔG^‡ = ΔH^‡ − TΔS^‡. All thermodynamic values associated with the catalytic step reaction are displayed in Table 2. The contribution to the activation barrier to catalysis is predominantly enthalpic in nature (ΔH^‡ = 80 ± 2 kJ mol⁻¹) and penalized by a substantial increase of the activation entropy (ΔS^‡ = 85 ± 7 J K⁻¹ mol⁻¹), where −TΔS^‡ compensates up to one-third of the enthalpic contribution (−TΔS^‡ ≈ −25 kJ mol⁻¹ at 298 K), resulting in ΔG^‡ = 55 ± 4 kJ mol⁻¹. The large positive and favorable value of ΔS^‡ most likely indicates that the transition state involves the release of protein-bound waters into the bulk, i.e., significant dehydration of the reactants. Studies on MMP-2 and MMP-3 in the presence of organic solvents demonstrated that more than one water molecule per enzyme is needed for optimal catalysis: in particular, three water molecules are required for MMP-3 catalytic activity and six waters for MMP-2 (37). The entropy cost of transferring a water molecule from the protein to the liquid is up to 8.4 kJ mol⁻¹ (38). Thus, the experimentally observed 25 kJ mol⁻¹ for the entropy term would be consistent with the release of three weakly bound water molecules from the protein upon formation of the ES^‡ complex.

Figure 4.

Effect of temperature on k_cat/T (Eyring plot) for the peptide hydrolysis by the catalytic domain of MT1-MMP in the temperature range 10–37°C, at atmospheric pressure. The linear correlation coefficient is r = 0.998.

At least one molecule close to the catalytic zinc of MMPs is displaced during catalysis. This finding is further supported by theoretical studies (16, 17, 39) and by a recent experimental study on MT1-MMP suggesting that a water molecule bound to the catalytic zinc in a tetracoordinated fashion is displaced by the peptide substrate forming a pentacovalent complex during hydrolysis (11). The other water molecules could occupy any sites of the enzyme but their binding within the catalytic cavity is more likely (37). The gain in free energy due to the release of water molecules might be important for the stabilization of the transition state by formation of favorable electrostatic interactions for the bond breakage (40). The Arrhenius activation energy, E_a, and the activation enthalpy, ΔH^‡, are not distinguishable within the experimental error. As a matter of fact, these two thermodynamic values are often interchangeably used to define the activation barrier of a reaction because the difference between these two energies is generally small and close to the accuracy of the experiment (E_a = ΔH^‡ + RT, where RT = 2.5 kJ/mol at 298 K) (41).

Temperature effect on the secondary structure of MT1-MMP

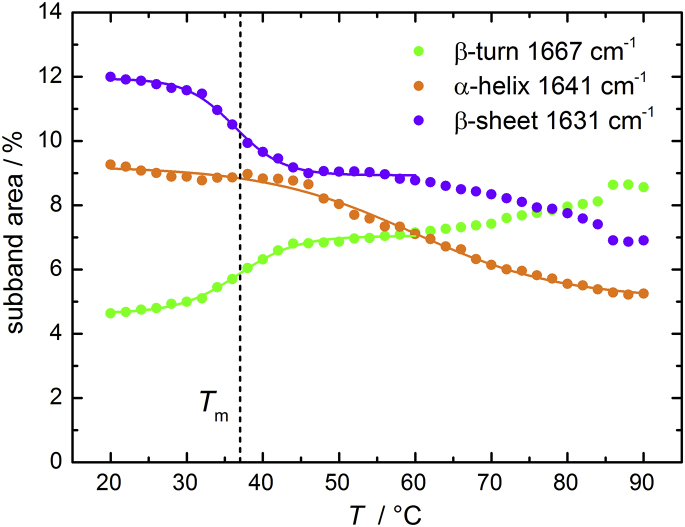
Information about the effect of temperature on the protein’s secondary structure was obtained from the study of temperature-induced changes of the most characteristic vibrational band, the amide I′, in the IR region, for which 85% of the vibration energy comes from C=O stretching. This band covers wavenumbers in the range of 1600–1700 cm⁻¹ in D₂O, and its component subbands strongly depend on the secondary structure as summarized in Table 3 (42, 43, 44). Deconvoluted FTIR absorption spectra were obtained as function of temperature in the range between 20 and 90°C at ambient pressure (see the Supporting Material). When the temperature is increased, the mainly affected bands are intramolecular β-sheets (∼1631 cm⁻¹), helices (∼1641 cm⁻¹), and β-turns (∼1667 cm⁻¹) (Fig. 5). The temperature-dependent equilibrium constant, K = K(T), for the (partial) unfolding transition of the protein has been determined from fitting the temperature-dependent FTIR data with a two-state model using (43)

$$K=\left|A^{\text{obs}}-A^U\right|/\left|A^F-A^{\text{obs}}\right|,$$ (5)

where A^obs corresponds to the experimentally observed subband area at the wavenumber of interest and temperature T; and A^F, A^U are the values for the fitted starting and endpoints of the transition, respectively (low-temperature folded form A^F at 20°C and high-temperature unfolded form A^U at 60°C).

Table 3.

Amide I′ band wavenumbers and assignments to secondary structure elements for proteins in D₂O as solvent (44)

Amide I′ Band Region (cm−1)	Secondary Structural Element
<1615	side chains
∼1615, ∼1684	intermolecular β-sheets
∼1627, ∼1635	intramolecular β-sheets
∼1641	310 helix
∼1643	disordered structures
∼1655 (∼1641)	α-helix (exposed)
∼1660–1670	loops/turns

Figure 5.

Temperature-dependence of the relative intensities of secondary structure elements of MT1-MMP obtained from the subband analysis of the amide I′ band. Data were fitted with a two-state transition model as described in the text.

The crystal structure of monomeric human MT1-MMP bound to the natural inhibitor TIMP-2 exhibits a content of 14% β-sheet and 21% α-helix (PDB: 1BUV) (45). Our FTIR data shows a similar amount of β-sheets (12%) but a lower content of α-helices compared with the crystal structure. Differences from crystal structure and FTIR data are often observed and can be explained in terms of different extinction coefficients of secondary structure elements (44). As we discuss relative structural changes here only, such differences are not important. As shown in Fig. 5, MT1-MMP is stable over a wide range of temperatures. The overall changes in secondary structural elements are rather small, amounting to ∼4–6% over the whole temperature range from 20 to 90°C. What is still clearly seen is a structural transition taking place at ∼37°C, i.e., the temperature at which a breakpoint in the Arrhenius plot of the enzymatic activity is observed (Fig. 3). The transition is accompanied by a decrease of the subband area at 1631 cm⁻¹ from 12 to 9%, corresponding to a partial loss of intramolecular β-sheets. Concomitantly, we observe an increase of the subband at 1667 cm⁻¹ from 4 to 7%, which is characteristic for β-turn formation. The absorption band peaked at 1641 cm⁻¹ may be assigned to an (exposed) α-helix. The amount of the observed α-helix secondary structure remains constant up to 50°C, i.e., in the temperature range where the enzyme is still active, and decreases slightly beyond that temperature, from ∼9 to 5% at 90°C. From the van ’t Hoff plot, the standard van ’t Hoff enthalpy (ΔH°_vH), entropy (ΔS°_vH), and Gibbs energy (ΔG°_vH) changes at the midpoint temperature (T_m) associated with the conformational transition (representing partial unfolding) at 37°C can be obtained (see the Supporting Material). An averaged enthalpy change of ΔH°_vH = 190 ± 25 kJ mol⁻¹ and an entropy change of ΔS°_vH = 0.6 ± 0.1 kJ mol⁻¹ K⁻¹ is obtained, i.e., it is an entropy-driven process, which leads to ΔG°_vH = 7.2 ± 0.2 kJ mol⁻¹ at 298 K.

Pressure activity profile

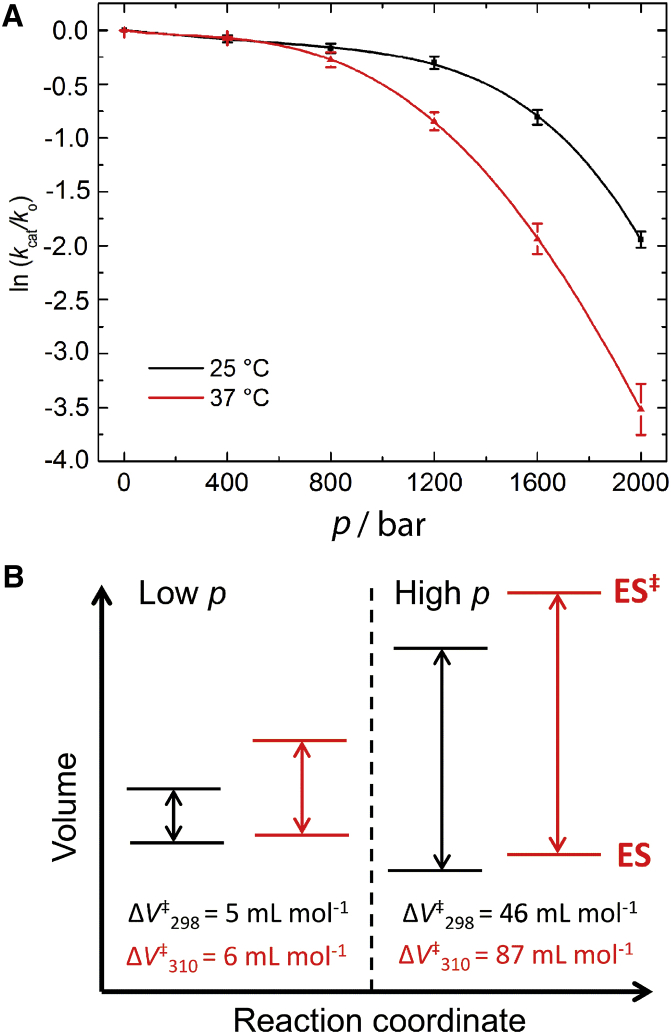
The pressure-dependent activity of MT1-MMP was studied by measuring the steady-state kinetics at pressures up to 2000 bar for two temperatures, 25 and 37°C (Fig. 6). Reaction slopes exhibited nearly linear behavior, implying saturating of the enzyme with substrate (see the Supporting Material). In this case, the volumetric contribution of the binding process is negligible and the activation volume is given by the catalytic step, i.e., ΔV^‡ = ΔV^‡_cat (22). Within the formalism of transition-state theory, the pressure dependence of the rate constant, k_cat, can be fitted to the integrated Eq. 1, where ΔV^‡ is the activation volume, corresponding to the volume difference between the transition-state and the ES complex of the catalytic step, i.e., ES → ES^‡ (46). Whereas the activation energy is always positive, the activation volume can have either a negative or a positive value, depending on the changes in the specific molecular interactions occurring, which are accompanied by solvational changes (e.g., rearrangement or release of water molecules) and packing effects (e.g., via changes in protein conformation during ligand binding and the catalytic step) (21, 47). Fig. 6 A reveals that the enzymatic activity decreases over the whole pressure range studied. The effect may be described as biphasic, with two different pressure regimes. At low pressures, between 1 bar and 0.8 kbar, the activity decreases only very slightly: a 20% decrease of the initial k_cat is observed at 0.8 kbar for both temperatures (25 and 37°C). At higher pressures, between 1 and 2 kbar, k_cat decreases dramatically with increasing pressure. At 2 kbar, the decrease of the initial rate amounts to 86% at 25°C and to 99% at 37°C. To better understand the reason of the deviation from linearity in the ln(k_cat/k_o) versus p plots, a pressure-dependent FTIR study of the secondary structure of MT1-MMP was performed (see below). The activation volumes, ΔV^‡_cat at 25 and 37°C, as determined by Eq. 1, are displayed in the scheme shown in Fig. 6 B.

Figure 6.

(A) Pressure dependence of the enzymatic activity of MT1-MMP at 25°C (298 K) and 37°C (310 K). The value k_cat/k₀ corresponds the ratio between the rate constant at pressure p and the rate constant at atmospheric pressure (1 bar). The data points have been fitted to a fourth polynomial function to calculate the pressure-dependent changes in activation volume, ΔV^‡_cat. (B) Schematic representation of the activation volumes of the catalytic step at 25 and 37°C, respectively, displaying the difference between the volume of the transition state (ES^‡) and that of the enzyme-substrate complex (ES). Each diagram represents data for the low (e.g., 400 bar, left) and the high (e.g., 1600 bar, right) pressure regime.

We found activation volumes of ΔV^‡_cat = 5 ± 0.6 mL mol⁻¹ for T = 25°C (298 K) and ΔV^‡_cat = 6 ± 1 mL mol⁻¹ for T = 37°C (310 K) in the low-pressure regime, and ∼10-fold higher values at high pressures, ΔV^‡_cat = 46 × 4 mL mol⁻¹ at 25°C and ΔV^‡_cat = 87 ± 9 mL mol⁻¹ at 37°C. The ΔV^‡ values are positive, indicating that the volume of the activated complex is larger than the volume of the enzyme-substrate complex, i.e., pressure reduces the rate of hydrolysis by favoring a lower volume reactant state. Generally, pressure-induced changes in the rate of enzyme-catalyzed reactions can be due to changes in the protein structure and hydration, the reaction mechanism (in the rate-limiting step), the conformation and hydration of the substrate, or the physical properties of the solvent. For example, the inwards withdrawal of water-exposed substrate groups at the enzyme-water interface during catalysis often requires the release of a large quantity of electrostricted water, leading to a volume increase of the system (48). Here, ΔV^‡_cat is given by the volume difference between ES^‡ and ES. The value of ΔV^‡_cat at low pressures (<1 kbar) observed here, is relatively small (5–6 mL mol⁻¹), indicating a rather compact transition state. The small volume increase may be explained by the release of water from the active site upon ES^‡ formation and consequently creation of some void volume within the active site. In addition, in the low pressure range, ΔV^‡_cat is essentially temperature independent, i.e., the activation volume is not affected by the structural transition observed at 37°C, indicating that the compact transition state remains essentially unchanged. This scenario would be consistent with this model of the catalytic mechanism of MMPs (Fig. 1) and the results obtained from the temperature-dependent study. With increasing pressure (>0.8 kbar), ΔV^‡_cat increases steadily. Such higher pressures may induce expansion by additional hydration of the active site. Pressure-induced penetration of water molecules into the protein interior is a phenomenon generally observed upon compression of proteins in the multi-kbar range (49, 50) and can heterogeneously affect the protein structure (51).

Minor conformational changes may also occur, which are clearly observed in the FTIR data above ∼2 kbar, and could lead to an increase of ΔV^‡_cat as well. In this pressure range, the temperature significantly affects the activation volume by almost a factor of two from 25 to 37°C. This effect may be explained in terms of an additional increase in hydration capacity of the catalytic cleft and a change in solvent-exposed groups due to the β-sheet/β-turn conformational change taking place at 37°C. Concurrent to this interpretation, the pressure-induced displacement of a conformational equilibrium between two states of the enzyme (A$\rightleftarrows$B) with different activities cannot be excluded. It has been shown that minor changes upon pressurization, e.g., the electrostriction of a broken salt bridge or the penetration of a water molecule, can cause a nonlinearity of the plot of the logarithm of the equilibrium constant versus pressure (52). Thus, by fitting our data with the integral form of the equation for the pressure dependence of the equilibrium constant, K_eq = [A]/[B] = exp[(p_1/2−p)ΔV^o/(RT)] (with ΔV^o standard molar volume change, p_1/2 transition pressure for which K_eq = 1; for details, see the Supporting Material) (53, 54), it is possible to interpret the pressure-induced changes of k_cat in terms of concentration changes of the more active MT1-MMP species (A) and reveal the parameters ΔV° and p_1/2. We obtained for the pressure-induced conformational changes values of ΔV° = −93 ± 6 mL mol⁻¹ and p_1/2 = 1080 ± 25 bar (r² = 0.9998) for T = 37°C, and ΔV° = −85 ± 10 mL mol⁻¹ and p_1/2 = 1475 ± 60 bar (r² = 0.997) for T = 25°C. The transition is characterized by a considerable negative volume change, which is likely to involve a significant decrease in protein hydration or release of void volume.

Pressure effect on the secondary structure of MT1-MMP

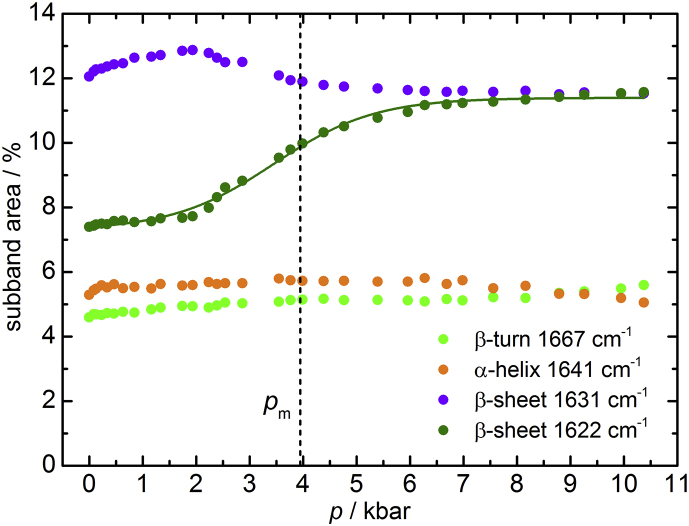
Different effects may account for the biphasic pressure-dependent activity of MT1-MMP, including changes in compressibility and conformational changes of the system (e.g., partial unfolding, which can lead to loss of enzyme functional properties) or changes in the rate-determining step (21). Changes in quaternary structure, such as dissociation of the subunits, are probably not relevant because the catalytic domain of MT1-MMP is also active as a monomer in solution. To shed more light on the possible origin of the activity changes at higher pressures, pressure-dependent FTIR spectroscopy data were additionally recorded. The secondary structure of MT1-MMP was analyzed over a pressure range between 1 bar and 11 kbar at 20°C (Fig. 7). Remarkably, no significant contributions from unfolded conformations are detected even at 7 kbar. Upon pressurization, no marked changes are observed for most of the underlying subbands, including α-helices, while intramolecular β-sheets are mostly affected by increasing the pressure up to 7 kbar, showing an increase of ∼4% of the initial amount, starting at ∼2 kbar, with a transition pressure, p_m, of ∼3.5 kbar. According to the band assignment, another, nonnative β-sheet structure (at 1622 cm⁻¹) is formed. The accompanying volume change of this conformational transition, ΔV, upon pressure-induced unfolding amounts to −23.4 mL mol⁻¹. At high pressure, protein unfolding is generally characterized by negative and small volume changes ranging from −50 to −100 mL mol⁻¹ (49). The small volume change observed here is most likely due to a decrease of the void volume and/or changes in hydration (e.g., the hydration of cavities previously devoid of water) in the course of this conformational transition (50). What is also clear from these studies is that the MT1-MMP is very pressure-stable, indicating dense packing of the amino acids in the tertiary structure of the protein, including the active site, and the absence of a large cavity volume. The small value of the pressure-induced volume change is comparable with the volume of a water molecule (18 mL mol⁻¹), only. The absence of a significant change in secondary structure below 2 kbar supports the idea that the activity change is due to change of the rate-limiting step of the reaction (the various steps of the reaction are expected to invoke different volume changes) or due to minor conformational changes induced by pressure, possibly between the native state and a less catalytically active higher-energy conformer (see previous section).

Figure 7.

Pressure dependence of the relative amount of secondary structure elements of MT1-MMP at T = 20°C obtained from the subband analysis of the amide I′ band. Data were fitted with a two-state transition model as well.

Conclusions

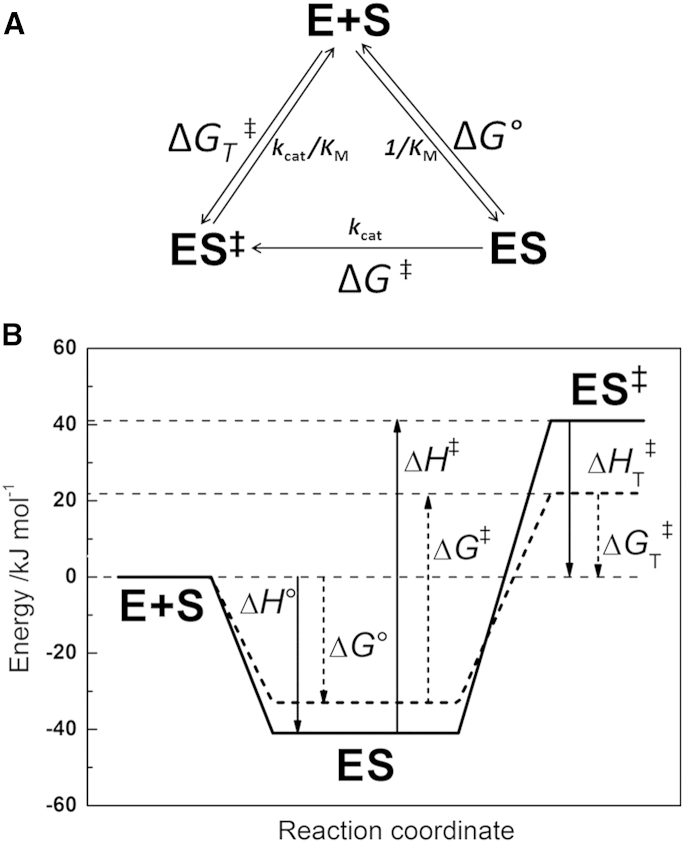
In this work, temperature and pressure were used as physical parameters for studying the energetics, stability, and kinetics of the catalytic domain of human MT1-MMP and to explore the temperature and pressure limits of its activity. Temperature can affect enzyme systems due to two major effects: that on the enzyme-catalyzed reaction and that on the inactivation of the enzyme. Being able to independently describe these two contributions is not an easy task because they are often strongly interrelated and take place simultaneously. Hence, complementary structural measurements using FTIR spectroscopy were employed next to the activity measurements. Although temperature is a much more widely used parameter to probe biological systems, pressure plays an equivalent important role as thermodynamic variable. In particular, changing the temperature of a biochemical system at atmospheric pressure produces simultaneous effects on volume and thermal energy, which can be separated by applying additional pressure-dependent measurements. In this work, the temperature-dependent study of the enzymatic activity of MT1-MMP yielded both kinetic and thermodynamic parameters for the hydrolysis reaction of a collagen-like peptide substrate, thereby expanding our knowledge of the forces and energetic contributions that dictate and control the enzymatic catalysis. We propose that the MT1-MMP-catalyzed hydrolysis of the collagen-like peptide follows the scheme illustrated in Fig. 8 B, which represents the free energies and their corresponding enthalpic components in the form of an energy diagram. Fig. 8 A represents the scheme of the MT1-MMP catalyzed peptide hydrolysis in terms of the free energies derived from the transition theory. The activation energy ΔG^‡ = 55 ± 4 kJ mol⁻¹, associated with k_cat, is counteracted by a favorable binding energy ΔG° = −33 ± 5 kJ mol⁻¹ of the ES complex defined by 1/K_M at 298 K. The net activation free-energy for the transformation from E+S to ES^‡ related to the specificity constant k_cat/K_M was calculated from the relation ΔG_T^‡ = ΔG^‡ + ΔG° = 22 ± 9 kJ mol⁻¹ and corresponds to the free energy difference between the activated transition state complex (ES^‡) and free substrate and enzyme (E+S) (32).

Figure 8.

(A) Thermodynamic and kinetic parameters associated with the enzyme-substrate formation and catalysis (32). (B) Schematic energy diagram for the MT1-MMP-catalyzed hydrolysis reaction of a collagen-like peptide. The free energy ΔG°(1/K_m) and enthalpy ΔH°(1/K_m) change are associated with MT1-MMP-substrate formation. The activation free energy ΔG^‡(k_cat) and activation enthalpy ΔH^‡(k_cat) change correspond to the catalytic step of the enzymatic reaction. The resultant ΔG^‡_T(k_cat/k_M) and ΔH^‡_T(k_cat/k_M) are the net activation free energy and enthalpy difference for the E+S to ES^‡ transformation.

The activity of MT1-MMP is affected by temperature and pressure, but their effects on the enzymatic activity largely differ in magnitude and origin. Our conformational studies using FTIR spectroscopy suggest that the structural changes induced by pressure are different from those induced by temperature. MT1-MMP is quite stable and active over a wide range of temperatures, from 10 to 55°C, where partial unfolding of the protein sets in, which is reflected by a small decrease of the α-helix content (∼4%). Interestingly, a modest conformational change is observed at ∼37°C, corresponding to a 4% decrease of intramolecular β-sheets with concomitant formation of β-turns. This small conformational change is reflected in a change of the slope of the Arrhenius plot at the same transition temperature, leading to a decrease of the activation energy, E_a, from 82 to 30 kJ mol⁻¹ at the higher temperatures. Assuming the temperature-induced structural changes to occur as a two-state process, analysis of the FTIR temperature profiles allowed assessing the thermodynamic values (ΔH°_vH, ΔS°_vH, ΔG°_vH) of this conformational transition (Table 4), which is driven by a gain in conformational entropy. Interestingly, the pressure dependence of the catalytic activity of MT1-MMP exhibits a more-phasic behavior. A marked pressure effect is observed above a pressure of ∼1 kbar and k_cat decreases rapidly until almost complete deactivation of the enzyme at ∼2 kbar. The corresponding activation volumes, ΔV^‡_cat, were determined for 25 and 37°C over the whole pressure range. The ΔV^‡_cat values are positive, and range from 5 to 6 mL mol⁻¹ below 1 kbar to 46 and 86 mL mol⁻¹ at 2 kbar for 25 and 37°C, respectively, i.e., it increases ∼10-fold with respect to the low-pressure range at the same temperature. The corresponding pressure-dependent FTIR data revealed minor conformational changes taking place at ∼3.5 kbar (Fig. 7), which are accompanied by a small volume decrease of ∼−23.4 mL mol⁻¹.

Table 4.

Thermodynamic values associated with the conformational transitions occurring at ∼310 and ∼329 K

	β-sheet (kJ mol−1)	β-turn (kJ mol−1)	α-helix (kJ mol−1)
ΔH°vH	213 ± 10	165 ± 6	92 ± 4
ΔS°vH	(0.69 ± 0.03) K−1	(0.53 ± 0.02) K−1	(0.28 ± 0.02) K−1
ΔG°298	7.4 ± 3.6	7.0 ± 3.3	8.6 ± 3.9
ΔG°310	−0.9 ± 0.3	0.7 ± 0.3	5.2 ± 2.9
ΔG°323	−9.8 ± 4.6	−6.2 ± 3.0	1.6 ± 0.9
Tm/K	309 ± 3	311 ± 3	329 ± 7
ν /cm−1	1631	1667	1641

Values were obtained by fitting the experimental data with a two-state model to the temperature course of different secondary structure elements.

Because no significant structural changes were observed below 2 kbar, the pressure-induced decrease in the enzyme activity is probably associated with changes in the rate-limiting step of the reaction. The small value of ΔV^‡ below 1 kbar is more likely associated with the release of water molecules from the active site upon formation of the transition state and before the bond breakage, resulting in void volumes formation. The release of at least one weakly bound water molecule is also suggested by our temperature-dependent measurements and would be consistent with our model of hydrolysis of MMPs. On the other hand, the high hydrostatic pressures (beyond 1 kbar) likely increase the level of hydration due to minor conformational changes. At these high pressures, further deceleration of the enzymatic activity is observed at 37°C, the temperature where the β-sheet/β-turn transition occurs. An alternative to this model corresponds to the pressure-induced displacement of a conformational equilibrium between two states of MT1-MMP with different activity, with ΔV° = −85 mL mol⁻¹ and p_1/2 = 1475 bar at 25°C and ΔV° = −93 mL mol⁻¹ and p_1/2 = 1080 bar at 37°C, respectively.

Based on these temperature- and pressure-dependent studies, an energy and volume diagram could be established for the various steps of the enzymatic reaction (Figs. 6 and 8). To conclude, the stability and function of enzymes can be described as a multidimensional surface as function of temperature, pressure, and solution conditions, including the presence of cosolutes and cosolvents. Here we show that already the additional parameter pressure next to temperature allows modulation of the enzyme’s stability and function in a complex way. Exploration of the combined temperature-pressure-cosolvent phase space on enzyme stability and function remains a formidable task still to be undertaken, but will be highly rewarding in the light of pharmaceutical and biotechnological applications, next to understanding enzymatic activity of proteins operating in organisms thriving under extreme environmental conditions.

Author Contributions

E.D., S.S., and C.R. carried out all the experiments and contributed equally to the experimental work; E.D. and R.W. designed the research and analyzed results; and all the authors contributed to discussing the results and writing the article.

Editor: Catherine Royer.