Tests for Gene-Environment Interactions and Joint Effects With Exposure Misclassification

Abstract

The number of methods for genome-wide testing of gene-environment (G-E) interactions continues to increase, with the aim of discovering new genetic risk factors and obtaining insight into the disease-gene-environment relationship. The relative performance of these methods, assessed on the basis of family-wise type I error rate and power, depends on underlying disease-gene-environment associations, estimates of which may be biased in the presence of exposure misclassification. This simulation study expands on a previously published simulation study of methods for detecting G-E interactions by evaluating the impact of exposure misclassification. We consider 7 single-step and modular screening methods for identifying G-E interaction at a genome-wide level and 7 joint tests for genetic association and G-E interaction, for which the goal is to discover new genetic susceptibility loci by leveraging G-E interaction when present. In terms of statistical power, modular methods that screen on the basis of the marginal disease-gene relationship are more robust to exposure misclassification. Joint tests that include main/marginal effects of a gene display a similar robustness, which confirms results from earlier studies. Our results offer an increased understanding of the strengths and limitations of methods for genome-wide searches for G-E interaction and joint tests in the presence of exposure misclassification.

Many complex diseases (D) have a multifactorial etiology resulting from the interplay of genetic factors (G) and environmental exposures (E). Numerous statistical and epidemiologic papers have considered the discovery and characterization of G-E interaction (1–16), including discussions about efficiently testing G-E interactions (17) and conducting gene-environment-wide interaction studies (GEWIS) (18, 19). These have examined the effect of violations to G-E independence in great detail.

In this paper, we build upon the work of Mukherjee et al. (12), who compared via simulation study the false positive rate and empirical power of several G-E interaction search methods. We extend the simulation study in 2 ways. First, we augment the catalog of G-E interaction search strategies with recently introduced methods. Our catalog contains single-step and modular G-E interaction search strategies, the latter of which screen for G-E and/or marginal D-G association before subsequent G-E interaction testing. Beyond these, we also evaluate “gene-discovery” tests for the joint effect of G and G-E interaction (20–22). These 2-degrees-of-freedom (DF) methods are less powerful than a pure marginal D-G test when there is no multiplicative G-E interaction and are empirically noted to be more powerful given modest-to-strong G-E interaction. Power for testing the G-E interaction component may be further increased relative to the standard 2-DF likelihood ratio test (20) through data-adaptive use of the G-E independence assumption (2, 21). In all, we evaluate 14 G-E interaction and gene-discovery methods.

The second extension of this paper relative to Mukherjee et al. (12) is an evaluation of the effects of exposure misclassification on all methods. Previous studies have investigated exposure misclassification (20, 23–26), but no systematic published comparison under uniform simulation settings is available. Exposure misclassification / measurement error may arise in case-control studies because of recall bias, with the extent of misclassification possibly differing between cases and controls (25–27). This can be particularly challenging in meta-analyses of G-E interaction, in which the degree of measurement error in exposure data may differ across studies, leading to spurious null and non-null findings.

Misclassification in E introduces bias in the estimation of main effects and G-E interactions (28–30), and nondifferential misclassification typically reduces power (31, 32). Lindström et al. (24) studied the effects of nondifferential misclassification on 4 tests for G or G-E interaction and found that tests with a marginal D-G association component were more robust to exposure misclassification. In recent workshops initiated by the National Institutes of Health, the detrimental effects of exposure misclassification, both in increased type I error and decreased power, were discussed (33, 34). Zhang et al. (23) corrected the maximum likelihood estimate of odds ratios under misclassification, using an estimate of the misclassification error rate from separate validation data. In many GEWIS, no validation data are available to implement regression calibration or other methods of adjustment from the measurement error literature (35, 36). Stenzel et al. (37) compared several single-step procedures for G-E interaction under the dual scenario of exposure-biased sampling and exposure misclassification. Others have studied the effect of model violations on estimation of G-E interaction, including misspecification of the main effects in characterizing the outcome-exposure relationship (38) and the impact of unmeasured exposure confounders on G-E interaction (22). However, limited literature is available on studying G-E correlation and exposure misclassification simultaneously.

The present report is organized as follows. In “Methods,” we describe the testing procedures evaluated, divided into single-step or modular G-E interaction methods and gene-discovery methods. In “Simulation Settings,” we describe our simulation design to evaluate each method, including our approach for generating misclassified exposure data. We present operating characteristics of the methods under correctly classified and misclassified exposure scenarios in the “Results” section, and we conclude the paper with the “Discussion” section.

METHODS

We consider a case-control study with n₁ cases and n₀ controls evaluating a set of M binary genetic markers, G, and a single environmental exposure, E. Let E = 1 (E = 0) denote an exposed (unexposed) individual and, for each genetic marker, G = 1 (G = 0) denote whether an individual is a carrier (noncarrier). Let D denote disease status, where D = 1(D = 0) indicates an affected (unaffected) individual. The population parameters for a given marker are p_dge ≡ Pr(G = g, E = e|D = d), d, g, e ∈ {0, 1}. Because of the sampling mechanism, $\sum _{g,e}{p}_{0ge}=\sum _{g,e}{p}_{1ge}=1,$ and thus the corresponding frequencies follow a multinomial distribution. Table 1 defines 7 log-odds ratios pertaining to these probabilities. The quantities θ_GE and γ_GE give G-E association in the control and case populations, respectively; α_G and α_E give marginal D-G and D-E association, respectively; and β_G and β_E give the respective main effects of G and E (D-G association in the subgroup E = 0 and D-E association in the subgroup G = 0). A nonzero value of β_GE, in the final row of Table 1, defines a multiplicative G-E interaction. In its simplest form, a GEWIS tests M potential G-E interactions, namely β_GE = 0 corresponding to each marker.

Table 1.

Seven Key Log-Odds Ratios Defined by the Case-Control Probabilities, p_dge, d, g, e ∈ {0,1}, for a Given Marker^a

Log-Odds Ratio	Value	Description
θGE	log(p011p000/p001p010)	G-E given D = 0
γGE	log(p111p100/p101p110)	G-E given D = 1
αG	log([p111 + p110][p001 + p000]/[p101 + p100][p011 + p010])	D-G (marginal)
αE	log([p111 + p101][p010 + p000]/[p110 + p100][p011 + p001])	D-E (marginal)
βG	log(p000p110/p010p100)	D-G given E = 0 (main)
βE	log(p000p101/p001p100)	D-E given G = 0 (main)
βGE	log(p001p010p100p111/p000p011p101p110)	Multiplicative G-E interaction

^a p_dge ≡ Pr(G = g, E = e|D = d).

Single-step exhaustive methods

The methods herein test all M markers for G-E interaction, with no initial screening or prioritizing. A common adjustment to the significance threshold α_test is the Bonferroni correction. Each marker is tested at significance threshold α_test/M, controlling the family-wise error rate (FWER) at level α_test.

Case-control

The standard approach, case-control (CC) calculates ${\hat{\beta }}_{GE},$ the maximum likelihood estimate of β_GE, and tests H₀:β_GE = 0 via Wald or likelihood ratio tests using logistic regression for P(D = 1|G, E).

Case-only

Proposed by Piegorsch et al. (1), case-only (CO) tests for G-E association among cases (D = 1)—namely, H₀:γ_GE = 0. This can be achieved through modeling P(G =1|E, D = 1) via logistic regression. If a rare disease approximation is made and G-E independence is assumed in the entire population, the likelihood ratio test for H₀:γ_GE = 0 is also a valid test for H₀:β_GE = 0. This does not estimate main effects of G or E (β_G or β_E).

Empirical Bayes

To trade off between the more efficient but potentially biased CO analysis and the always unbiased but less efficient CC analysis, Mukherjee and Chatterjee (2) proposed a shrinkage estimator based on the retrospective likelihood framework of Chatterjee and Carroll (39). The estimator is given by $(\hat{w}){\hat{\gamma }}_{GE}+(1-\hat{w}){\hat{\beta }}_{GE},$ where the weight $\hat{w}=\widehat{\mathrm{Var}}\hspace{0.17em}({\hat{\beta }}_{GE})/[\widehat{\mathrm{Var}}({\hat{\beta }}_{GE})+({\hat{\beta }}_{GE}-{\hat{\gamma }}_{GE}{)}^2]$ adaptively controls the contribution from ${\hat{\gamma }}_{GE}.$ The delta method approximates the variance of this shrinkage estimator, and Wald tests based on asymptotic normality allow for inference. Regression versions of CO and empirical Bayes (EB) using the retrospective likelihood framework (39) based on case-control data that provide estimates of all model parameters—not just β_GE—are implemented in the R package CGEN (40, 41).

Modular methods

These methods introduce a screening or prioritizing step based on G-E or marginal D-G association before proceeding to the final G-E interaction test. In contrast to single-step exhaustive methods, these either test only a subset of markers or vary the significance threshold for each marker on the basis of the screening results. Statistical independence of the screening step and the final G-E interaction test underlies these modular methods, thereby maintaining overall type I error.

Two-step G-E screening

Murcray et al. (4) proposed this 2-step procedure to leverage the efficiency of CO while maintaining robustness to G-E association:

1. Screening step: Conduct a likelihood ratio test of G-E association in the combined sample of cases and controls. The subset of m markers exceeding a screening significance threshold with marker-level error rate α_scr proceeds to the next testing step.

2. Testing step: For these m markers, conduct a CC analysis of H₀:β_GE = 0 using significance threshold α_test/m.

Under G-E independence in the underlying population, G-E correlation in the case-enriched case-control sample indicates the presence of G-E interaction. Screening based on γ_GE alone (i.e., CO) would not be asymptotically independent of the second-step test statistic given by CC. The power of 2-step G-E screening (TS) is increased when many null markers are screened out—i.e., $m\ll M,$ with the magnitude of increase depending on the choice of α_scr. Murcray et al. (4) used α_scr = 0.05, but follow-up empirical studies showed that the power increase is maximized when α_scr is chosen on the basis of the case-control ratio, number of markers, and disease prevalence (11, 18). A more recent approach from Wason and Dudbridge (13) screens on the basis of a linear combination of the observed G-E associations resembling EB: ${\hat{\gamma }}_{GE}+(\hat{k}){\hat{\theta }}_{GE},$ where $\hat{k}=\widehat{\mathrm{Var}}({\hat{\gamma }}_{GE})/\widehat{\mathrm{Var}}({\hat{\theta }}_{GE})$ ensures asymptotic independence with the subsequent testing step. Like Wason and Dudbridge, we find this method to have very similar performance to TS and thus refrain from presenting the results.

Hybrid 2-step screening

Murcray et al. (11) later extended TS to 2 screening steps, one for G-E association, as in TS, and the other for marginal D-G association using α_G—the rationale being that the presence of G-E interactions will lead to G-E or D-G association in the case-control sample. Given a significance threshold α_scr, m_assc and m_marg markers, respectively, will pass each screening step, and only these are eligible for the final-step G-E interaction test. As with TS, many markers will fail both screenings, and so a less restrictive Bonferroni correction is needed at the second-step CC test for G-E interaction. The desired FWER, α_test, is spent between the markers from each screening step on the basis of a preselected weight ρ ∈ (0,1). For those markers that pass both screening steps, the significance threshold is max{ρα_test/m_marg, (1 − ρ)α_test/m_assc}. For the D-G–only markers, the significance level is ρα_test/m_marg, and for the G-E–only markers, it is (1 − ρ)α_test/m_assc. Using ρ = 0 makes hybrid 2-step screening (H2) and TS equivalent. The G-E and D-G screening components are asymptotically independent of the testing step (4, 42), implying that the hybrid screening and G-E interaction testing steps are independent. Thus, a FWER of α_test is maintained.

Cocktail

Hsu et al. (14) characterized TS and H2 as special cases of a class of modular methods for GEWIS testing, consisting of separate choices of 1) screening, 2) G-E interaction test, and 3) type I error control modules, and proposed the comprehensive class of “cocktail” (CT) procedures. In the screening step (the first module), CT adaptively tests for G-E association or marginal D-G association, as in H2. In the second module, if marginal D-G association is declared statistically significant, then EB, which is independent of the D-G test, is used to test for G-E interaction. Otherwise, CC is used, being independent of a test for G-E association in the combined case-control sample. In the third module, and in contrast to TS and H2, no markers “fail” the screening step in CT. Rather, following the weighted hypothesis testing approach of Ionita-Laza et al. (43), α_test is spent differentially between all markers: Those that are more significant at the screening step are given a lower significance threshold to pass at the final interaction test, as explained below.

For each marker, p^GE and p^DG denote, respectively, the p values corresponding to the G-E and D-G screening steps. The screening module p value is $p_{\mathrm{scr}}^{CT}=p^{DG}I(p^{DG}\le t)+p^{GE}I(p^{DG}>t),$ where t is a prespecified threshold, e.g., t = 0.001, and I(·) is the indicator function. The G-E interaction test p value is $p_{\mathrm{test}}^{CT}=p^{EB}I(p^{DG}\le t)+p^{CC}I(p^{DG}>t),$ where p^EB and p^CC are the p values from EB and CC, respectively. To combine these modules, CT spends α_test between markers, comparing each $p_{\mathrm{test}}^{CT}$ to a potentially different significance threshold. The 5 markers with the smallest values of $p_{\mathrm{scr}}^{CT}$ have the most liberal significance threshold for testing for interaction: α_test/(2 × 5). The next 10 markers have a stricter threshold, α_test/(2² × 10), and so forth. Each time, the size of the group doubles (5, 10, 20, …), and half of the remaining significance level (α_test/2, α_test/2², α_test/2³, …) is equally distributed to all markers in the group. The p values $p_{\mathrm{scr}}^{CT}$ and $p_{\mathrm{test}}^{CT}$ are independent (14) but depend on a subjective threshold t. Hsu et al. (14) proposed a modified version not requiring a threshold but for which the screening and test p values may be correlated. Because the modified CT did not appreciably differ from CT in our simulation studies, we do not consider it further.

Joint marginal/association screening

Gauderman et al. (16) proposed adding the asymptotically independent likelihood ratio test statistics from the G-E and D-G screening steps and comparing to a ${\chi }_2^2$ distribution as a single screening statistic. This screening step can remove markers from the G-E interaction step, as in TS or H2, or preferentially rank markers, as in CT. We consider the latter, which had better performance in Gauderman et al. Ege and Strachan (15) proposed a similar extension: G-E and D-G associations are separately estimated for each exposure group, and the likelihood ratio statistics are averaged between exposure groups. Because of its similarity, we do not evaluate this approach.

Joint tests for discovering new loci by leveraging G-E interaction

Even though some previously described methods leverage information on G-E or marginal D-G association to screen markers, the final underlying null hypothesis tested is H₀:β_GE =0, and the search is one for pure G-E interactions. In contrast, the proceeding 4 strategies expand this null hypothesis and represent an agnostic search for discovery of loci, identifying those for which α_G ≠ 0, β_G ≠ 0, or β_GE ≠ 0. This modifies the definition of type I error and power relative to the standard G-E interaction null hypothesis and results in increased rejection rates.

Marginal association

This is the standard genome-wide association study test of H₀:α_G = 0, the marginal D-G association test H2, CT, and joint marginal/association screening (EDG×E) use for screening/prioritizing candidate markers. Although counterintuitive, it is possible that α_G ≠ 0 and β_G = β_GE = 0—i.e., there is a marginal effect of G but no effect in either of the exposure subgroups. This will hold if β_E ≠ 0 and θ_GE ≠ 0 (Equation W1, Web Appendix 1, available at http://aje.oxfordjournals.org/). Thus, because of nonlinearity of the odds ratio measures, marginal association (MA) may identify markers that are not associated with D in either exposure subgroup.

Two-DF joint tests: JOINT(CC) and JOINT(EB)

Kraft et al. (20) suggested a joint test of H₀:β_G = β_GE = 0, which tests for an effect of G in either exposure subgroup by using standard prospective logistic regression and case-control data. We call this test JOINT(CC). A likelihood ratio test statistic is compared with a ${\chi }_2^2$ distribution. Rejection of H₀ does not indicate in which subgroup D-G association holds. In contrast, CC tests for a difference in association between exposure groups: H₀:β_GE = (β_G + β_GE) − β_G = 0. When estimates of β_G and β_GE are negatively correlated, JOINT(CC) may have a larger rejection rate than CC, even when β_G = 0 (cf. page 114, (20)). We may also use the retrospective likelihood framework (39) to derive 2-DF tests for H₀:β_G = β_GE = 0. When based on the constrained maximum likelihood, it is susceptible to bias and type I error inflation, like CO. Thus, we consider the EB version of this joint test that adaptively leverages G-E independence. Implemented in CGEN, this is denoted by JOINT(EB).

Two-DF marginal + G-E interaction tests: MA+CC and MA+EB

Dai et al. (42) proved that the maximum likelihood estimate of α_G is asymptotically independent of that of both β_GE (CC) and γ_GE (CO), and, consequently, of any weighted average of the two (EB). On the basis of this, in a contemporaneous paper by the same authors, Dai et al. (21) proposed a simultaneous test of H₀:α_G = β_GE = 0. The marginal effect, α_G, is estimated via maximum likelihood, and CC, CO, or EB can estimate β_GE. Denoted MA+CC or MA+EB, this leverages the G-E independence assumption, leading to a more powerful test for the G-E interaction component β_GE than JOINT. As with MA, these 2-DF tests may have larger rejection rates than either CC or JOINT, because α_G may be nonzero, even if β_G = β_GE = 0.

The difference between JOINT(CC)/JOINT(EB) and MA+CC/MA+EB is whether one is testing the main or marginal effect of G (β_G or α_G, respectively). In the case of crossover interactions with opposite effects of G in each exposure subgroup, JOINT(CC) and JOINT(EB) are likely to be more powerful than MA+CC and MA+EB.

Subgroup tests in the exposed group: CC(EXP) and EB(EXP)

We propose a novel test of D-G association in the exposed group (E = 1) alone—namely, H₀:β_G + β_GE = 0. This is equivalently a test of $H_0:{\beta }_{GE}^{\ast }=0$ from the constrained prospective model $\text{logit}(P(D|G,E))={\beta }_0+{\beta }_{E}E+{\beta }_{GE}^{\ast }G\times E,$ which assumes β_G = 0. The resultant χ² test statistic will have 1 DF and be more powerful for testing pure interactions in which the genetic effect is present only in the exposed group. Asymptotically, CC(EXP) is more powerful than CC if β_G = 0 (44) (i.e., if the constraint is satisfied) but will lead to type I error when β_G ≠ 0. We also use the general retrospective likelihood framework to derive a Wald test for the above hypothesis, H₀:β_G + β_GE = 0. We consider the EB version of this subgroup test in the exposed group, again using CGEN. This test, denoted by EB(EXP), adaptively leverages the G-E independence assumption.

SIMULATION SETTINGS

To quantitatively evaluate these G-E interaction methods, we modified the simulation study of Mukherjee et al. (12), focusing on modest but plausible effect sizes for β_GE and α_G, on the basis of recent published analysis findings (45–47). We simulated M = 100,000 genetic markers with n₀ = n₁ =20,000 cases and controls. Given the control prevalence of a marker G and the environmental factor E (respectively P_G and P_E) and θ_GE, the control probability vector p₀ = {p₀₀₀, p₀₀₁, p₀₁₀, p₀₁₁} is obtained by solving the following system of equations:

$$\begin{array}{cc}& \exp \{{\theta }_{GE}\}=\frac{p_{000}(p_{000}-(1-P_G-P_E))}{(1-P_G-p_{000})(1-P_E-p_{000})},\hfill \\ & p_{001}=1-P_G-p_{000},p_{010}=1-P_E-p_{000}.\hfill \end{array}$$

We set P_G = f² + 2f(1 − f), where the minor allele frequency f is 0.2 for the causal marker and f ∼ Unif[0.1, 0.3] for null markers, and P_E = 0.3. For the causal marker, we used θ_GE ∈ {log(0.8), log(1), log(1.1)}, and, for the null markers, we sampled θ_GE from a mixture of Normal(0, log(1.5)/2), and point-mass, δ₀(0), distributions, with the proportion of zeros given by p_ind ∈ {0.95, 0.995, 1}. This is a key parameter controlling the fraction of markers correlated with E.

Choices of β_E, β_G, and β_GE, together with p₀, define the case probability vector p₁ = {p₁₀₀, p₁₀₁, p₁₁₀, p₁₁₁} (48): p₁₀₀ ∝ p₀₀₀, p₁₀₁ ∝ exp{β_E}p₀₀₁, p₁₁₀ ∝ exp{β_G}p₀₁₀, and p₁₁₁ ∝ exp{β_E + β_G + β_GE}p₀₁₁. Equation W1 in Web Appendix 1 expresses the marginal log-odds ratios α_G and α_E as functions of p₀, β_G, β_E, and β_GE, demonstrating that, given p₀, there are 3 free parameters between α_G, α_E, β_G, β_E, and β_GE. By definition, α_E is constant across all genetic markers (i.e., for any given set of p₀, β_G, β_E, and β_GE). However, when θ_GE and P_G randomly vary across markers, the strategy used by Mukherjee et al. (12) and others, which specifies β_E, β_G, and β_GE, will not satisfy this invariance of α_E across all markers. This incoherence is avoided by fixing α_E = 1.35, β_G, and β_GE, the latter 2 of which are specific to each marker, and then solving for each marker-specific β_E. For the causal marker, we used β_G ∈ {log(1), log(1.2)} and β_GE < log(1.35). For all other markers, we set β_G = log(1). Fixing α_E, β_G, and β_GE induces a value of α_G, the marginal genetic log-odds ratio.

For each marker, we generated the case and control data independently from multinomial distributions by using p₀ and p₁, respectively. To simulate exposure misclassification, we varied the sensitivity and specificity parameters. For a given marker, let r₁ = {r₁₀₀, r₁₀₁, r₁₁₀, r₁₁₁} be the cell frequency vector for the cases. Each subject in r₁₁₁ or r₁₀₁, corresponding to those for whom E = 1 in truth, was independently moved to r₁₁₀ or r₁₀₀, respectively, with probability of 1 − sensitivity. Simultaneously, each subject in r₁₁₀ or r₁₀₀, corresponding to E = 0, was moved to r₁₁₁ or r₁₀₁, respectively, with probability of 1 − specificity. An analogous strategy was used for the control vector, r₀. Perfect classification corresponds to sensitivity =specificity = 1. We also considered nondifferential misclassification (sensitivity = specificity = 0.8) and differential misclassification (sensitivity = 1.0 and specificity = 0.8 for cases, and sensitivity = specificity = 0.8 for controls).

Web Table 1 describes additional settings: different effect or sample sizes, a rare exposure with more severe misclassification, or some null markers having non-null genetic main effects, with the results plotted in Web Figures 1–9. We generated 5,000 case-control data sets for each setting, calculating FWER (nominally 0.05), expected number of false positives, and power. We used α_scr = 5 × 10⁻⁴ (TS and H2), ρ = 0.5 (H2), and t = 10⁻³ (CT).

RESULTS

Methods for G-E interaction search

Table 2 presents FWER and expected number of false positives for all G-E interaction methods. Because of differences in the null hypotheses, no such table can be meaningfully extracted for the gene-discovery methods. All methods have inflated error rates under differential misclassification when p_ind = 0.95 (i.e., when 5% of markers are associated with exposure), including the robust CC, identifying 3 null markers per data set. In contrast, when all markers are independent of E (p_ind = 1), FWER is generally controlled. Under nondifferential misclassification, FWER is less inflated, with the exception of CO: When p_ind = 0.995, FWER is 0.06–0.08 for EB, TS, and H2 and 0.13 for EDG×E and CT. Under perfect classification, the expected number of false positives is 2,234 for CO when p_ind = 0.95. However, misclassification attenuates both G-E association and the observed G-E interaction, and the expected number of false positives correspondingly decreases (e.g., to 1,039). For EB, the adaptive linear combination of CC and CO, FWER is as large as 0.49 under differential misclassification and p_ind = 0.95.

Table 2.

Family-Wise Error Rate (Expected Number of False Positives) for the G-E Interaction Testing Procedures as P_E, p_ind, and Misclassification of the Exposure E in the Cases and Controls Vary^a

Cases {SE, SP}	Controls {SE, SP}	pind	PE	Method
				CC	MA	CO	EB	TS	H2	EDG×E	CT
{1,1}	{1,1}	0.950	0.3	0.05 (0.05)	0.55 (0.80)	1.00 (2234)	0.23 (0.26)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)
{1,1}	{1,1}	0.995	0.3	0.05 (0.05)	0.12 (0.12)	1.00 (223)	0.04 (0.04)	0.04 (0.05)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)
{1,1}	{1,1}	1.000	0.3	0.05 (0.05)	0.06 (0.06)	0.05 (0.05)	0.02 (0.02)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.03 (0.03)
{0.8,0.8}	{0.8,0.8}	0.950	0.3	0.06 (0.06)	0.54 (0.78)	1.00 (1039)	0.39 (0.49)	0.09 (0.10)	0.09 (0.10)	0.19 (0.21)	0.18 (0.19)
{0.8,0.8}	{0.8,0.8}	0.995	0.3	0.04 (0.05)	0.12 (0.13)	1.00 (104)	0.06 (0.07)	0.08 (0.08)	0.06 (0.06)	0.13 (0.14)	0.13 (0.13)
{0.8,0.8}	{0.8,0.8}	1.000	0.3	0.04 (0.05)	0.05 (0.05)	0.05 (0.05)	0.02 (0.02)	0.05 (0.05)	0.05 (0.05)	0.05 (0.06)	0.04 (0.04)
{1,0.8}	{0.8,0.8}	0.950	0.3	0.95 (3)	0.55 (0.80)	1.00 (1670)	1.00 (7)	1.00 (17)	1.00 (16)	1.00 (24)	1.00 (21)
{1,0.8}	{0.8,0.8}	0.995	0.3	0.30 (0.35)	0.11 (0.12)	1.00 (167)	0.53 (0.75)	0.99 (5)	0.97 (4)	1.00 (7)	1.00 (7)
{1,0.8}	{0.8,0.8}	1.000	0.3	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.02 (0.02)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.04 (0.04)
{1,1}	{1,1}	0.950	0.1	0.05 (0.05)	0.13 (0.14)	1.00 (1591)	0.49 (0.68)	0.05 (0.05)	0.05 (0.05)	0.04 (0.05)	0.04 (0.05)
{1,1}	{1,1}	0.995	0.1	0.05 (0.05)	0.06 (0.06)	1.00 (159)	0.08 (0.08)	0.04 (0.04)	0.05 (0.05)	0.04 (0.04)	0.05 (0.05)
{1,1}	{1,1}	1.000	0.1	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.02 (0.02)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.04 (0.04)
{0.6,0.6}	{0.6,0.6}	0.950	0.1	0.05 (0.05)	0.12 (0.13)	0.27 (0.32)	0.06 (0.06)	0.07 (0.07)	0.06 (0.06)	0.09 (0.10)	0.13 (0.13)
{0.6,0.6}	{0.6,0.6}	0.995	0.1	0.05 (0.05)	0.06 (0.06)	0.07 (0.08)	0.03 (0.03)	0.05 (0.05)	0.05 (0.06)	0.05 (0.06)	0.05 (0.05)
{0.6,0.6}	{0.6,0.6}	1.000	0.1	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.02 (0.02)	0.05 (0.05)	0.05 (0.05)	0.05 (0.05)	0.04 (0.04)

Abbreviations: CC, case-control; CO, case-only; CT, cocktail; EB, empirical Bayes; EDG×E, joint marginal/association screening; H2, hybrid 2-step; p_ind, proportion of markers in which the genetic marker (G) and exposure (E) are independent; P_E, probability that E = 1; SE, sensitivity, or the probability that E is correctly classified when E = 1 in truth; SP, specificity, or the probability that E is correctly classified when E = 0 in truth; TS, 2-step G-E screening.

^a We simulated 5,000 data sets with n = 20,000 each of cases and controls and M = 100,000 genetic markers, with exactly 1 having multiplicative G-E interaction (β_GE ≠ 0). The family-wise error rate is the proportion of simulated data sets with at least 1 significant (null) finding, with nominal value 0.05 and standard deviation due to simulation variability of 0.003, and the expected number of false positives is the average number of significant findings per simulated data set. The marginal exposure log-odds ratio was α_E = log(1.5) (P_E = 0.3) or log(1.75) (P_E = 0.1). For each null marker, the main genetic log-odds ratio was β_G = 0 and the carrier prevalence was P_G = f² + 2f(1 − f), where f ∼ Unif[0.1, 0.3] is the minor allele frequency. The extent of exposure misclassification increases as either sensitivity or specificity decreases.

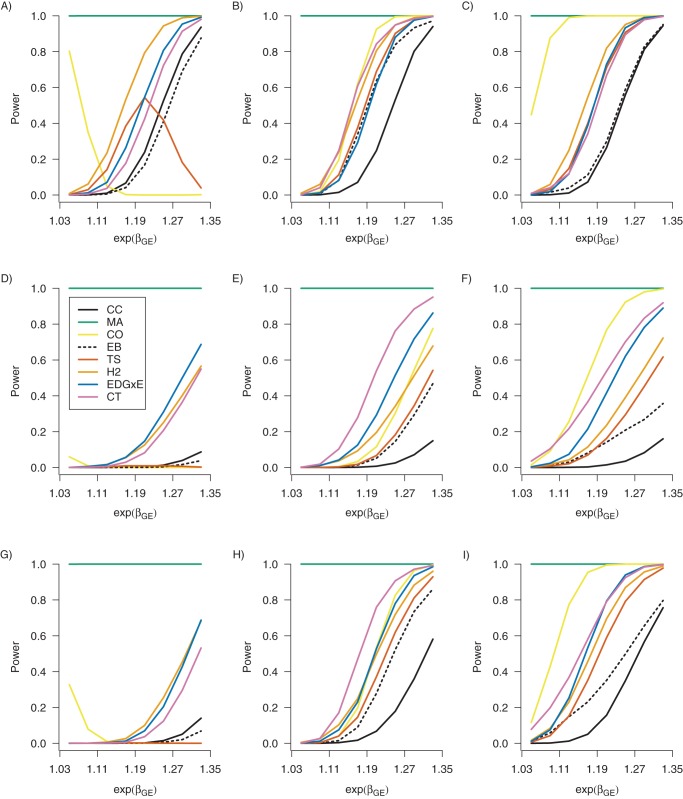
Figure 1 plots power for the G-E interaction methods and, for comparison, MA, against exp{β_GE} for β_G = log(1.2), P_E =0.3 and p_ind = 0.995. Web Figures 1–6 plot power under additional settings. The gene-discovery method MA is considerably more powerful than the G-E interaction methods because α_G is typically much larger than β_GE in this parameterization (Equation W1 in Web Appendix 1). Screening for D-G association confers robustness to misclassification, which is most evident when θ_GE = log(0.8) (left column of Figure 1), but no single method dominates in all settings. Most robust to misclassification are CT and EDG×E, which use a weighted p value screening step; H2, for which screening is a dichotomous step, also has high power but is more susceptible to misclassification. When θ_GE = log(1) (middle column of Figure 1) and exp{β_GE} =1.25, the relative power loss of CT, EDG×E, and H2 between correct classification and nondifferential misclassification is 20%, 42%, and 64%, respectively. Finally, the rejection rate of CO, which is nonmonotonic with β_GE when θ_GE = log(0.8), is explained by noting that γ_GE = β_GE + θ_GE (Table 1).

Figure 1.

Empirical power to detect gene-environment (G-E) interaction in 1 marker for 7 G-E interaction methods (CC, case-control; CO, case-only; CT, cocktail; EB, empirical Bayes; EDG×E, joint marginal/association screening; H2, hybrid 2-step; TS, 2-step G-E screening) and the marginal (MA) method from 5,000 data sets with n = 20,000 each of cases and controls and M = 100,000 − 1 null genetic markers. From top to bottom, each row corresponds to perfect classification, nondifferential misclassification (sensitivity and specificity of 0.8), and differential misclassification (sensitivity of 1 and specificity of 0.8 for cases, and sensitivity and specificity of 0.8 for controls) of the exposure variable. From left to right, each column corresponds to θ_GE = log(0.8), θ_GE = 0, and θ_GE = log(1.1). The exposure prevalence was P_E = 0.3, and the marginal exposure log-odds ratio was α_E = log(1.5). For the non-null marker, the main genetic log-odds ratio was β_G = log(1.2), and the carrier prevalence was P_G = 0.36. For each null marker, β_G = 0 and P_G = f² + 2f(1 − f), where f ∼ Unif[0.1, 0.3] is the minor allele frequency.

Joint tests for discovery of new loci

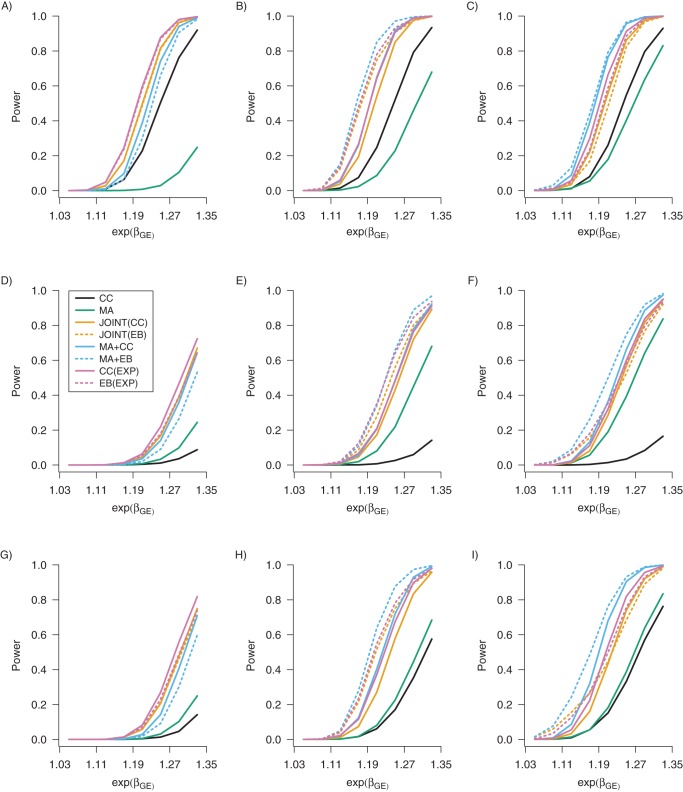
Figure 2 presents the empirical rejection rates of the gene-discovery methods and, for comparison, CC, against exp{β_GE} for β_G = log(1), and Web Figures 7–9 plot rejection rates under several additional settings. The rejection rate of MA is smaller than others but invariant to misclassification, as it does not depend on E; this robustness translates in part to the joint tests MA+CC and MA+EB. The data-adaptive EB methods, JOINT(EB), MA+EB, and EB(EXP), are more powerful than those maximizing the prospective likelihood alone, JOINT(CC), MA+CC, and CC(EXP) when θ_GE = 0 or, on occasion, when misclassification attenuates the empirical θ_GE sufficiently to zero (bottom right panel, Figure 2). Finally, we note that if β_G ≠ log(1), CC(EXP) and EB(EXP), which assume this equality constraint, would be less powerful. In general, the expanded null hypothesis of the gene-discovery methods is more robust to exposure misclassification, as expected. A large marginal D-G association will increase the rejection rate substantially (Web Figure 8, which differs from Figure 2 by β_G = log(1.2)). Conversely, a small marginal D-G association, in conjunction with misclassification, will decrease the rejection rate substantially (Web Figure 9).

Figure 2.

Empirical power for discovery of 1 marker for the case-control method (CC) and 7 gene-discovery methods (CC(EXP), CC applied to exposed subgroup; EB(EXP), empirical Bayes applied to exposed subgroup; JOINT(CC), 2-DF joint test; JOINT(EB), empirical Bayes 2-DF joint test; MA, marginal; MA+CC, marginal + case-control; MA+EB, marginal + empirical Bayes) from 5,000 data sets with n = 20,000 each of cases and controls. From top to bottom, each row corresponds to perfect classification, nondifferential misclassification (sensitivity and specificity of 0.8), and differential misclassification (sensitivity of 1 and specificity of 0.8 for cases, and sensitivity and specificity of 0.8 for controls) of the exposure variable. From left to right, each column corresponds to θ_GE = log(0.8), θ_GE = 0, and θ_GE = log(1.1). The exposure prevalence was P_E = 0.3, and the marginal exposure log-odds ratio was α_E = log(1.5). The main genetic log-odds ratio was β_G = 0, and the carrier prevalence was P_G = 0.36.

DISCUSSION

Nondifferential misclassification may reduce power to detect true interactions in a GEWIS setting; however, differential misclassification may increase or decrease type I error and power. Relative to testing all markers, modular procedures that leverage empirical G-E and/or D-G associations to first screen or prioritize markers may have more power to detect G-E interactions. In the first such 2-stage procedure, which uses only G-E association (4), the power gain depends on choosing the optimal value of screening significance level, which in turn depends on the case-control ratio, number of markers, and disease prevalence (11, 18). A suboptimal choice may result in an empirical power curve that is nonmonotonic with β_GE, seen here and previously (12). Later 2-step procedures that also account for D-G association (H2, EDG×E, CT) do not exhibit this undesirable property.

Because D-G association is unaffected by exposure misclassification, modular methods for G-E interaction that use D-G association for screening or prioritization were found to be more robust to exposure misclassification. That joint tests making use of D-G association are more robust to misclassified exposure has been noted previously (24), but we document and quantify this for modern modular methods for G-E interaction. However, even for these methods, FWER inflation under the dual challenge of differential misclassification and G-E association still remains. A limitation of all modular methods is a dependence on the choice of multiple tuning parameters: α_scr (TS, H2), size of weighted p value groups (CT, EDG×E), ρ (H2), and t (CT).

Gene-discovery methods using joint tests for genetic association and G-E interaction fundamentally differ and may identify genetic markers with marginal effects (α_G ≠ 0) or joint effects (β_G ≠ 0, β_GE ≠ 0). An implication of this expanded null hypothesis is that, in realistic scenarios in which more genetic markers will have detectable non-null effects for a given sample size, the number of markers identified will be considerably larger than those obtained from G-E interaction methods. One must then investigate which markers are implicated in G-E interaction. Any metric to evaluate gene-discovery methods must take into account the context of the study—specifically, what types of markers are of greater importance to identify. If discovery of new loci by leveraging G-E interaction is the goal and marginal D-G association is anticipated, then the joint tests, particularly MA+EB and JOINT(EB), are robust to modest levels of misclassification (which confirms and expands on the results of Lindström et al. (24)) and are able to leverage G-E independence for even greater power for testing the G-E interaction component of a joint test.

Several limitations and possible extensions of this study exist. First, we do not consider nonparametric tree-based (49) or Boolean combinatorial methods (50) or tests for additive interaction (51). Second, we examine the impact of exposure misclassification but do not propose any remedy. Regression calibration and imputation methods accounting for measurement error are possible solutions (35). Most require estimation of the misclassification probabilities or existence of validation data. One might incorporate exposure quality into the construction of weights in meta-analyses of multiple studies. Third, there are many possible reasons beyond exposure misclassification that GEWIS studies lack power to detect G-E interactions, including small sample size (52), misclassification of the genetic markers (53), or more complex multimarker interactions (9). A key challenge for this and previous similar simulation studies is to realistically generate the underlying genetic architecture of a trait and magnitude and number of non-null G-E interactions. Some specific limitations include between-marker independence, the generation of G-E associations from a mixture distribution, a lack of null markers having only main genetic effects, and consideration of just one causal marker for empirical power estimation (in the case of G-E interaction). Using readily available single-nucleotide polymorphism simulation routines that generate realistic linkage disequilibrium structure (54, 55) and simulating effect size parameters randomly from published estimates of genetic effect size distributions (56, 57) would make our simulation study more realistic, moving away from a fixed single-parameter null/causal scenario toward a continuum of plausible genetic effect sizes. This would present challenges in terms of defining alternative metrics of average performance rather than simple type I error and power. Incorporating these into simulation studies remains an important extension of our work.