Gene-based Association Analysis for Censored Traits Via Fixed Effect Functional Regressions

Summary

Genetic studies of survival outcomes have been proposed and conducted recently, but statistical methods for identifying genetic variants that affect disease progression are rarely developed. Motivated by our ongoing real studies, we develop here Cox proportional hazard models using functional regression (FR) to perform gene-based association analysis of survival traits while adjusting for covariates. The proposed Cox models are fixed effect models where the genetic effects of multiple genetic variants are assumed to be fixed. We introduce likelihood ratio test (LRT) statistics to test for associations between the survival traits and multiple genetic variants in a genetic region. Extensive simulation studies demonstrate that the proposed Cox RF LRT statistics have well-controlled type I error rates. To evaluate power, we compare the Cox FR LRT with the previously developed burden test (BT) in a Cox model and sequence kernel association test (SKAT) which is based on mixed effect Cox models. The Cox FR LRT statistics have higher power than or similar power as Cox SKAT LRT except when 50%/50% causal variants had negative/positive effects and all causal variants are rare. In addition, the Cox FR LRT statistics have higher power than Cox BT LRT. The models and related test statistics can be useful in the whole genome and whole exome association studies. An age-related macular degeneration dataset was analyzed as an example.

1 Introduction

Using modern genotyping and sequencing technology, large numbers of genetic variants can be assayed in a chromosomal region of interest or a gene region. The high dimensional nature of the data raises challenges in gene-based statistical analysis of disease gene mapping. Ordinary fixed effect regression models may not be able to estimate the genetic effects of all genetic variants due to a large number of genetic terms in the regression model. To analyze high-density genetic variant data, two methods among many others have been developed in recent years to model the contribution of the genetic variants in a gene region: (1) mixed models which treat the genetic contribution of genetic variants as random, and (2) fixed effect functional regression (FR) models which model the genetic contribution of genetic variants as an unknown function of physical position.

In mixed models, the regression coefficients of multiple genetic variants in a major genetic region are assumed to be random with means of zero and constant variance. The association between phenotypic traits and genetic variants is tested by testing a null hypothesis of zero variance by a sequence kernel association test (SKAT). For quantitative and dichotomous traits, Lee et al. (2012) found that the SKAT and its optimal unified test (SKAT-O) have higher power than burden test (BT). Here the burden test is one class of rare variant tests and the rare variants may have minor allele frequencies (MAFs) of less than 0.01 ~ 0.05. The burden tests collapse the genotypes of multiple rare variants into a summary variable to test for association between the trait of interest and the genetic variants [Li and Leal, 2008; Madsen and Browning, 2009; Morris and Zeggini, 2010]. Kernel-based tests and burden tests were extended to analyze time-to-event outcomes [Cai et al., 2011; Chen et al., 2014; Lin et al., 2011]. Chen et al. (2014) developed a Cox SKAT likelihood ratio test (LRT) and Cox BT LRT to analyze rare variants and found that Cox SKAT LRT had accurate type I error rates and good power performance.

Fixed effect FR models are based on traditional theory of population genetics. The FR models treat the contribution of genetic variants as an unknown function of physical position [Fan et al., 2013, 2014; Luo et al., 2011, 2012, 2013; Vsevolozhskaya et al., 2014; Wang et al., 2015; Zhang et al., 2014; Zhao et al., 2015]. For quantitative traits, functional linear models lead to both F-distributed and χ²-distributed test statistics which are almost always more powerful than SKAT and SKAT-O [Fan et al., 2013; Luo et al., 2012; Wang et al., 2015]. For dichotomous traits, FR models lead to test statistics which are more powerful than SKAT and SKAT-O except in some cases when the causal variants are all rare [Fan et al., 2014; Luo et al., 2011, 2013; Vsevolozhskaya et al., 2014]. Therefore, FR models usually outperform other methods and hold promise for use in gene-based association analysis of complex diseases. This stimulates us to develop fixed effect FR based models to analyze survival traits.

Here we develop FR based Cox proportional hazard models for a gene-based association analysis of survival traits adjusting for covariates. The genetic effects of multiple genetic variants are assumed to be fixed. The proposed Cox models can analyze rare variants or common variants or a combination of the two. LRT statistics are introduced to test for an association between the survival traits and multiple genetic variants in a genetic region. Extensive simulations are performed to evaluate type I error rates and power. The proposed methods were applied to analyze an age-related macular degeneration dataset.

2 Methods

Consider n individuals who are sequenced in a genomic region that has m variants. We assume that the m variants are located in a region with ordered physical positions 0 ≤ u₁ < ⋯ < u_m, and that each variant’s physical position u_j is known, e.g., in terms of base pair positions. To make the notation simpler, we normalize the region [u₁, u_m] to be [0, 1]. For the i-th individual, let T_i denote the survival time, and C_i denote the respective right-censoring time. Let y_i = min(T_i,C_i) be the observed time-to-event and censoring indicator δ_i = 1_(yi=Ti). In addition, let G_i = (g_i(u₁), ⋯, g_i(u_m))′ denote the genotype of the m variants, and Z_i = (z_i1, ⋯, z_ip)′ denote a p × 1 vector of fixed effect covariates. For the genotypes, we assume that g_i(u_j) (= 0, 1, 2) is the number of minor alleles of the individual at the j-th variant located at the position u_j.

2.1 Functional Regression Based Cox Proportional Hazard Models

In addition to the time-to-event observation y_i and covariates, we denote the i-th individual’s genetic variant function (GVF) as X_i(u), u ∈ [0, 1]. Notice that the data set includes n discrete realizations or observations G_i of the genotypes, one for each individual. By using the genetic variant information G_i, we may estimate the related genetic variant function X_i(u), which will be discussed below. To relate the genetic variant function to the time-to-event observation adjusting for covariates, we consider the following fixed effect FR based Cox proportional hazard model

$${\lambda }_i(s)={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +{\int }_0^1{X}_i(u)\beta (u)du),$$ (1)

where λ₀(s) is the baseline hazard function, α is a p × 1 vector of fixed regression coefficients of covariates, and β(u) is the genetic effect of genetic variant function X_i(u) at the position u.

In the Cox model (1), the genetic variant functions X_i(u) are assumed to be smooth. This assumption can be relaxed by considering the following fixed effect beta-smooth only Cox model

$${\lambda }_i(s)={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +\sum _{j=1}^m{g}_i(u_j)\beta (u_j)),$$ (2)

where the genetic effect function β(u) is assumed to be continuous/smooth and so it is called beta-smooth only Cox model. In the above model (2), the integration term ${\int }_0^1{X}_i(u)\beta (u)du$ in Cox model (1) is replaced by a summation term ${\sum }_{j=1}^m{g}_i(u_j)\beta (u_j)$, and we make no assumption about smoothness of the genetic variant functions X_i(u). We use the raw genotype data G_i = (g_i(u₁), ⋯, g_i(u_m))′ directly in the beta-smooth only Cox model (2).

The genetic effect function β(u) in the Cox models (1) and (2) is assumed to be smooth, i.e., β(u) is a continuous function of physical position u. One may expand it by B-spline or Fourier basis functions. Formally, let us expand the genetic effect function β(u) by a series of K_β basis functions ψ₁(u), ⋯, ψ_Kβ (u) as β(u) = (ψ₁(u), ⋯, ψ_Kβ(u))(β₁, ⋯, β_Kβ)′ = ψ(u)′β, where β = (β₁, ⋯, β_Kβ)′ is a K_β × 1 vector of coefficients and ψ(u) = (ψ₁(u), ⋯, ψ_Kβ(u))′. We consider two types of basis functions: (1) the B-spline basis: ψ_k(u) = B_k(u), k = 1, ⋯, K_β; and (2) the Fourier basis: ψ₁(u) = 1, ψ_2r+1(u) = sin(2πru), and ψ_2r(u) = cos(2πru), r = 1, ⋯, (K_β − 1)/2. Here for Fourier basis, K_β is taken as a positive odd integer [de Boor, 2001; Ferraty and Romain, 2010; Horváth and Kokoszka, 2012; Ramsay et al., 2009; Ramsay and Silverman, 2005].

To estimate the genetic variant functions X_i(u) from the genotypes G_i, we use an ordinary linear square smoother [Fan et al., 2013, 2014; Ramsay et al., 2009; Ramsay and Silverman, 2005; Vsevolozhskaya et al., 2014; Wang et al., 2015]. Let ψ_k(u), k = 1, ⋯, K, be a series of K basis functions, such as the B-spline basis and Fourier basis functions. Let Φ denote the m × K matrix containing the values ψ_k(u_j), and we let ϕ(u) = (ϕ₁(u), ⋯, ϕ_K(u))′. Using the discrete realizations G_i = (g_i(u₁), ⋯, g_i(u_m))′, we estimate the genetic variant function X_i(u) using an ordinary linear square smoother as follows [Ramsay and Silverman, 2005, Chapter 4]

$${\hat{X}}_i(u)=(g_i(u_1),\cdots ,g_i(u_m))\mathrm{\Phi }{[\mathrm{\Phi }\prime \mathrm{\Phi }]}^{-1}\varphi (u).$$ (3)

Assume that the genetic effect β(u) is expanded by a series of basis functions ψ_k(u), k = 1, ⋯, K_β, as β(u) = ψ(u)′β. Replacing X_i(u) in the Cox proportional hazard model (1) by X̂_i(u) in (3) and β(u) by the expansion, we have a revised Cox hazard model

$${\lambda }_i(s)={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +(g_i(u_1),\cdots ,g_i(u_m))\mathrm{\Phi }{[\mathrm{\Phi }\prime \mathrm{\Phi }]}^{-1}{\int }_0^1\varphi (u)\psi \prime (u)du\beta )={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +W_i^{\prime }\beta ),$$ (4)

where $W_i^{\prime }=(g_i(u_1),\cdots ,g_i(u_m))\mathrm{\Phi }{[\mathrm{\Phi }\prime \mathrm{\Phi }]}^{-1}{\int }_0^1\varphi (u)\psi \prime (u)du$. In the statistical packages R or Matlab, codes to calculate Φ[Φ′Φ]⁻¹ and ${\int }_0^1\varphi (u)\psi \prime (u)du$ are readily available [Ramsay et al., 2009].

For the beta-smooth only Cox proportional hazard model (2), β(u_j) is introduced as the genetic effect at the position u_j. In this article, we assume that the genetic effect function β(u) is a continuous function of the physical position u. Therefore, β(u_j), j = 1, 2, ⋯, m, are the values of function β(u) at the m physical positions. Expanding β(u_j) by B-spline or Fourier basis functions as above, the Cox model (2) can be revised as

$${\lambda }_i(s)={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +[\sum _{j=1}^m{g}_i(u_j)({\psi }_1(u_j),\cdots ,{\psi }_{K_{\beta }}(u_j))\left]{({\beta }_1,\cdots ,{\beta }_{K_{\beta }})}^{\prime }\right)={\lambda }_0(s)\text{exp}(Z_i^{\prime }\alpha +W_i^{\prime }\beta ),$$ (5)

where $W_i^{\prime }={\sum }_{j=1}^m{g}_i(u_j)({\psi }_1(u_j),\cdots ,{\psi }_{K_{\beta }}(u_j))$.

To test for association between the m genetic variants and the survival trait, the null hypothesis is H₀ : β = (β₁, ⋯, β_Kβ)′ = 0. By fitting the Cox models, we may test the null H₀ : β = 0 by a χ²-distributed LRT (Cox FR LRT) statistic with K_β degrees of freedom [Cox, 1972; Cox and Oakes, 1984]. In the data analysis and simulations, we used functions in the fda R package to create the basis functions. The order of the B-spline basis was 4, the number of B-spline basis functions was K = K_β = 10, and the number of Fourier basis functions was K = K_β = 11. To make sure that the results are valid and stable, we examined a wide range of parameters: 6 ≤ K = K_β ≤ 13 for B-spline and Fourier basis functions.

2.2 Simulation Studies

Extensive simulations were performed to evaluate the performance of the proposed Cox FR LRT statistics. The sequence data are of European ancestry from 10,000 chromosomes covering 1 Mb regions, simulated by Yun Li at the University of North Carolina, Chapel Hill using the calibrated coalescent model as programmed in COSI. The sequence data were generated using COSI’s calibrated best-fit models, and the generated European haplotypes mimick CEPH Utah individuals with ancestry from northern and western Europe in terms of site frequency spectrum and LD patterns [Figure 4 in Schaffner et al., 2005; The International HapMap Consortium 2007]. Genetic regions of 6 kb length were randomly selected for empirical type I error and power calculations.

In our simulations, we define rare variants to be the genetic variants whose MAFs are less than or equal to 0.03. Two scenarios were considered: (1) some causal variants are rare and some are common; (2) all causal variants are rare. We reported the results of Cox SKAT LRT and Cox BT LRT proposed by Chen et al. (2014) for comparison by using R package SeqMeta. To make the comparison valid, we used the same strategy as Chen et al. (2014) to generate phenotype data, as described next.

Type I Error Simulations

For a constant a > 0, let U ~ U(0, a) denote a uniform random variable on (0, a). To evaluate the type I error rates of the proposed LRT statistics, we generated baseline survival time from a Weibull (2, 2) using this formula [Bender et al., 2005]

$$T(z_1,z_2)=\sqrt{-\frac{4\text{log}U}{\text{exp}(0.005(z_1-50)+0.05z_2)}},$$ (6)

where z₁ is a continuous covariate from a normal distribution N(50, 5²), z₂ is a dichotomous covariate taking values 0 and 1 with a probability of 0.5, and U was uniformly distributed random variable U(0, 1). As explained in Chen et al. (2014), z₁ is a covariate to simulate age, and z₂ is a covariate to simulate sex. Four censoring schemes were considered: (1) C = ∞, no censoring, (2) C ~ U(0, 10), (3) C ~ U(0, 5), and (4) C ~ U(0, 3). The time-to-event time is calculated by y_i = min(T_i,C_i) and the censoring indicator is calculated by δ_i = 1_(Ti≤Ci) for a random sample T_i,C_i, i = 1, 2 ⋯, n. The proportions of censored observations in 4 censoring schemes are 0, 17.5%, 35.0%, and 56.5%, respectively.

Genotypes were selected from variants in 6 kb subregions which were randomly selected from the 1 Mb region. Notice that the trait values are not related to the genotypes, and so the null hypothesis holds. The sample sizes of the datasets were 1,000, 2,000, 3,000, and 4,000. For each combination of a sample size and a censoring scheme, 36 independent randomly seeded simulations were implemented: 10⁵ phenotype-genotype datasets in each simulation were generated. For each data set, we fit the proposed Cox models and calculated the Cox FR LRT statistics and related p-values. However, the statistics could not be computed on some replicates due to failure to converge. Thus, the total number of analyzable replicates ranges from 0 to 3.6 × 10⁶. After the simulations were complete, an empirical type I error rate was calculated as the proportion of the total p-values which were smaller than a given α level. If the total number of simulations is 0, no type I error rate is available.

Empirical Power Simulations

To evaluate the power of the proposed Cox FR LRT statistics and the Cox SKAT LRT and Cox BT LRT proposed by Chen et al. (2014), we simulated data sets under the alternative hypothesis by randomly selecting 6 kb subregions to obtain causal genetic variants. For each sample dataset, a subset of q causal variants located in the selected 6 kb subregion was then randomly selected, yielding genotypes G = (g(u₁), ⋯, g(u_q))′. Then, we generated the survival time by

$$T(z_1,z_2,G)=\sqrt{-\frac{4\text{log}U}{\text{exp}(0.005(z_1-50)+0.05z_2+{\beta }_{1}g(u_1)+\cdots +{\beta }_{q}g(u_q))}},$$ (7)

where z₁ and z₂ were the same as in the type I error model (6), G = (g_i(u₁), ⋯, g_i(u_q))′ were genotypes of the i-th individual at the causal variants, and the βs are additive effects for the causal variants defined as follows. We used |β_j| = c| log₁₀(MAF_j)|/2, where MAF_j was the MAF of the jth variant. Three different settings were considered: 5%, 10%, and 15% of variants in the 6 kb subregion are chosen as causal variants in the main text and Supplementary Materials, Appendix A. When some causal variants are rare and some are common, c = log(9.0), log(4.5), and log(3.5) if 5%, 10%, and 15% of the variants were causal, respectively. When all causal variants are rare, c = log(18.0), log(9.0), and log(4.5) if 5%, 10%, and 15% of the variants were causal, respectively. For each setting, 1,000 datasets were simulated to calculate the empirical power as the proportion of p-values which are smaller than a given α level.

In the Supplementary Materials, Appendix B, three more settings were considered: 30%, 40%, and 50% of variants were causal in the 6 kb subregion. When some causal variants are rare and some are common, c = log(1.75), log(1.50), and log(1.25) if 30%, 40%, and 50% of the variants were causal, respectively. When all causal variants are rare, c = log(2.5), log(2.0), and log(1.5) if 30%, 40%, and 50% of the variants were causal, respectively.

For each dataset, the causal variants are the same for all the individuals in the dataset, but we allow the causal variants to be different from dataset to dataset.

2.3 Real Data Analysis

We applied the proposed Cox models to analyze age-related eye disease study (AREDS) data [Age-Related Eye Disease Study Research Group, 1999]. AREDS is a clinical trial to learn about the risk factors for macular degeneration and cataract, two leading causes of vision loss in older adults. A total of 2,914 individuals were included in our analysis. Each individual has long-term phenotypic data and was genotyped using a customized exome chip. We tested two gene regions, CFH and ARMS2. In both gene regions, single variant analysis showed that some SNPs are associated with the risk of macular degeneration and its progression [Seddon et al., 2007; Fritsche et al., 2013]. In our analysis, we included all genetic variants in a gene region if they were located within 10 kb of either gene boundary by using ANNOVAR [Wang et al., 2010]. We tested the association between the time to advanced age-related macular degeneration of left eye and each of the two genes using the Cox FR LRT statistics of the proposed Cox models adjusted for age and gender. We also compared with the results of Cox SKAT LRT and Cox BT LRT [Chen et al., 2014].

3 Results

3.1 Empirical Type I Error Rates

The empirical type I error rates for the proposed Cox FR LRT statistics and the Cox SKAT LRT statistic are reported in Tables 1 and 2 at four nominal significance levels α = 0.05, 10⁻³, 10⁻⁴, and 10⁻⁵. In Table 1, all variants in 6 kb regions were used to generate genotype data but none of them relates to the trait. In Table 2, only rare variants in 6 kb regions were used to generate genotype data. The results of the “Basis of both GVF and β(u)” statistics were based on Cox model (4) by smoothing both the GVF and the genetic effect function β(u) by either B-spline or Fourier basis functions, and the results of the “Basis of beta-Smooth Only” statistics were based on Cox model (5) by smoothing the genetic effect function β(u) only.

Table 1. Empirical Type I Error Rates of the Cox FR LRT Statistics and Cox SKAT LRT, When All Variants in 6 kb Regions Were Used to Generate Genotype Data.

The order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 10; the number of Fourier basis functions was K = K_β = 11. The results of Cox SKAT LRT were from R SeqMeta package by Chen et al. (2014).

Sample Size n	The Censoring Scheme	Number of Simulations	Nominal Level α	Cox FR LRT Statistics				Cox SKAT LRT
				Basis of both GVF and β (u)		Basis of beta-Smooth Only
				B-sp Basis	Fourier Basis	B-sp Basis	Fourier Basis
1,000	∞	2,600,000	0.05	0.05608	0.05576	0.05608	0.05576	0.06944
			10−3	0.00123	0.00120	0.00123	0.00120	0.00184
			10−4	0.00014	0.00013	0.00014	0.00013	0.00021
			10−5	1.42 × 10−5	1.19 × 10−5	1.42 × 10−5	1.19 × 10−5	2.38 × 10−5
	U(0, 10)	2,100,000	0.05	0.05634	0.05604	0.0564	0.05604	0.07244
			10−3	0.00127	0.00123	0.00127	0.00123	0.00188
			10−4	0.00012	0.00013	0.00012	0.00013	0.00020
			10−5	1.19 × 10−5	1.29 × 10−5	1.19 × 10−5	1.29 × 10−5	1.67 × 10−5
	U(0, 5)	1,600,000	0.05	0.05805	0.057089	0.05810	0.05709	0.07739
			10−3	0.00134	0.00129	0.00134	0.00129	0.00203
			10−4	0.00015	0.00013	0.00015	0.00013	0.00021
			10−5	1.31 × 10−5	9.38 × 10−6	1.31 × 10−5	9.38 × 10−6	1.63 × 10−5
	U(0, 3)	1,400,000	0.05	0.06139	0.05963	0.06156	0.05963	0.08189
			10−3	0.00145	0.00138	0.00146	0.00138	0.00198
			10−4	0.00017	0.00017	0.00018	0.00017	0.00021
			10−5	1.43 × 10−5	1.57 × 10−5	1.50 × 10−5	1.57 × 10−5	2.00 × 10−5
2,000	∞	3,500,000	0.05	0.05318	0.05288	0.05318	0.05288	0.06207
			10−3	0.00115	0.00111	0.00115	0.00111	0.00145
			10−4	0.00012	0.00012	0.00012	0.00012	0.00016
			10−5	1.51 × 10−5	1.37 × 10−5	1.51 × 10−5	1.37 × 10−5	1.97 × 10−5
	U(0, 10)	3,400,000	0.05	0.05331	0.05318	0.05331	0.05318	0.06411
			10−3	0.00116	0.00113	0.00116	0.00113	0.00155
			10−4	0.00011	0.00011	0.00011	0.00011	0.00017
			10−5	1.29 × 10−5	1.35 × 10−5	1.29 × 10−5	1.35 × 10−5	1.91 × 10−5
	U(0, 5)	2,900,000	0.05	0.05418	0.05354	0.05418	0.05354	0.06782
			10−3	0.00118	0.00111	0.00118	0.00111	0.00162
			10−4	0.00013	0.00011	0.00013	0.00011	0.00018
			10−5	1.66 × 10−5	1.00 × 10−5	1.66 × 10−5	1.00 × 10−5	2.76 × 10−5
	U(0, 3)	1,400,000	0.05	0.05605	0.05438	0.05610	0.05438	0.07248
			10−3	0.00127	0.00116	0.00128	0.00116	0.00166
			10−4	0.00014	0.00012	0.00014	0.00012	0.00017
			10−5	1.43 × 10−5	1.50 × 10−5	1.43 × 10−5	1.50 × 10−5	1.57 × 10−5
3,000	∞	3,400,000	0.05	0.05200	0.05176	0.05200	0.05176	0.05927
			10−3	0.00109	0.00106	0.00109	0.00106	0.00137
			10−4	0.00012	0.00010	0.00012	0.00010	0.00014
			10−5	1.29 × 10−5	1.18 × 10−5	1.29 × 10−5	1.18 × 10−5	1.71 × 10−5
	U(0, 10)	3,500,000	0.05	0.05207	0.05196	0.05207	0.05196	0.06041
			10−3	0.00109	0.00110	0.00109	0.00110	0.00136
			10−4	0.00012	0.00011	0.00012	0.00011	0.00014
			10−5	9.14 × 10−6	1.20 × 10−5	9.14 × 10−6	1.20 × 10−5	1.69 × 10−5
	U(0, 5)	3,400,000	0.05	0.05275	0.05232	0.05276	0.05232	0.06303
			10−3	0.00109	0.00108	0.00109	0.00108	0.00144
			10−4	0.00012	0.00012	0.00012	0.00012	0.00015
			10−5	1.18 × 10−5	1.44 × 10−5	1.18 × 10−5	1.44 × 10−5	1.23 × 10−5
	U(0, 3)	2,500,000	0.05	0.05422	0.05295	0.05422	0.05295	0.06736
			10−3	0.00114	0.00114	0.00114	0.00114	0.00147
			10−4	0.00012	0.00011	0.00012	0.00011	0.00015
			10−5	1.36 × 10−5	6.80 × 10−6	1.40 × 10−5	6.80 × 10−6	1.44 × 10−5
4,000	∞	3,500,000	0.05	0.05131	0.05125	0.05131	0.05125	0.05750
			10−3	0.00107	0.00104	0.00107	0.00104	0.00127
			10−4	0.00011	0.00012	0.00011	0.00012	0.00015
			10−5	1.14 × 10−5	1.40 × 10−5	1.14 × 10−5	1.40 × 10−5	1.34 × 10−5
	U(0, 10)	3,400,000	0.05	0.05153	0.05142	0.05153	0.05142	0.05855
			10−3	0.00110	0.00108	0.00110	0.00108	0.00129
			10−4	0.00011	0.00011	0.00011	0.00011	0.00014
			10−5	1.09 × 10−5	1.00 × 10−5	1.09 × 10−5	1.00 × 10−5	1.56 × 10−5
	U(0, 5)	3,300,000	0.05	0.05201	0.05166	0.05201	0.05166	0.06081
			10−3	0.00105	0.00107	0.00105	0.00107	0.00134
			10−4	0.00011	0.00011	0.00011	0.00011	0.00014
			10−5	7.58 × 10−6	1.03 × 10−5	7.58 × 10−6	1.03 × 10−5	1.48 × 10−5
			0.05	0.05304	0.05220	0.05305	0.05220	0.06466
			103	0.00112	0.00108	0.00112	0.00108	0.00137

Table 2. Empirical Type I Error Rates of the Cox FR LRT Statistics and Cox SKAT LRT, When Only Rare Variants in 6 kb Regions Were Used to Generate Genotype Data.

The order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 10; the number of Fourier basis functions was K = K_β = 11. The results of Cox SKAT LRT were from R SeqMeta package by Chen et al. (2014).

Sample Size n	The Censoring Scheme	Number of Simulations	Nominal Level α	Cox FR LRT Statistics				Cox SKAT LRT
				Basis of both GVF and β(u)		Basis of beta-Smooth Only
				B-sp Basis	Fourier Basis	B-sp Basis	Fourier Basis
1,000	∞	600,000	0.05	0.05870	0.05779	0.05871	0.05779	0.07172
			10−3	0.00137	0.00139	0.00137	0.00139	0.00191
			10−4	0.00013	0.00012	0.00013	0.00012	0.00023
			10−5	5.00 × 10−6	1.00 × 10−5	5.00 × 10−6	1.00 × 10−5	2.67 × 10−5
	U(0, 10)	800,000	0.05	0.05981	0.05938	0.05984	0.05938	0.07504
			10−3	0.00140	0.00140	0.00141	0.00140	0.00200
			10−4	0.00016	0.00012	0.00016	0.00012	0.00018
			10−5	1.38 × 10−5	1.00 × 10−5	1.50 × 10−5	1.00 × 10−5	2.00 × 10−5
	U(0, 5)	300,000	0.05	0.06344	0.06180	0.06357	0.06180	0.08164
			10−3	0.00160	0.00156	0.00161	0.00156	0.00230
			10−4	0.00016	0.00016	0.00016	0.00016	0.00021
			10−5	1.33 × 10−5	1.33 × 10−5	1.33 × 10−5	1.33 × 10−5	1.00 × 10−5
2,000	∞	3,000,000	0.05	0.05427	0.05392	0.05427	0.05392	0.06327
			10−3	0.00116	0.00113	0.00116	0.00113	0.00153
			10−4	0.00011	0.00011	0.00011	0.00011	0.00015
			10−5	1.20 × 10−5	1.40 × 10−5	1.20 × 10−5	1.40 × 10−5	1.67 × 10−5
	U(0, 10)	2,400,000	0.05	0.05489	0.05443	0.05489	0.05443	0.06553
			10−3	0.00122	0.00119	0.00122	0.00119	0.00161
			10−4	0.00013	0.00013	0.00013	0.00013	0.00016
			10−5	1.67 × 10−5	8.75 × 10−6	1.67 × 10−5	8.75 × 10−6	2.00 × 10−5
	U(0, 5)	200,000	0.05	0.05629	0.05556	0.05630	0.05556	0.06960
			10−3	0.00128	0.00119	0.00128	0.00119	0.00166
			10−4	0.00014	0.00014	0.00014	0.00014	0.00026
			10−5	1.50 × 10−5	1.00 × 10−5	1.50 × 10−5	1.00 × 10−5	3.50 × 10−5
3,000	∞	3,300,000	0.05	0.05297	0.05262	0.05297	0.05262	0.06016
			10−3	0.00111	0.00108	0.00111	0.00108	0.00140
			10−4	0.00011	0.00011	0.00011	0.00011	0.00015
			10−5	1.06 × 10−5	1.18 × 10−5	1.06 × 10−5	1.18 × 10−5	1.61 × 10−5
	U(0, 10)	3,000,000	0.05	0.05302	0.05253	0.05302	0.05253	0.06134
			10−3	0.00112	0.00110	0.00112	0.00110	0.00142
			10−4	0.00013	0.00011	0.00013	0.00011	0.00015
			10−5	1.20 × 10−5	1.40 × 10−5	1.20 × 10−5	1.40 × 10−5	1.77 × 10−5
	U(0, 5)	2,100,000	0.05	0.05437	0.05365	0.05437	0.05365	0.06436
			10−3	0.00116	0.00115	0.00116	0.00115	0.00145
			10−4	0.00012	0.00012	0.00012	0.00012	0.00015
			10−5	1.38 × 10−5	1.33 × 10−5	1.38 × 10−5	1.33 × 10−5	1.43 × 10−5
	U(0, 3)	300,000	0.05	0.05792	0.05516	0.05795	0.05516	0.06883
			10−3	0.00126	0.00115	0.00126	0.00115	0.00169
			10−4	0.00014	0.00010	0.00014	0.00010	0.00017
			10−5	2.00 × 10−5	1.00 × 10−5	2.00 × 10−5	1.00 × 10−5	2.00 × 10−5
4,000	∞	3,600,000	0.05	0.05212	0.05196	0.05212	0.05196	0.05807
			10−3	0.00109	0.00105	0.00109	0.00105	0.00130
			10−4	0.00011	0.00011	0.00011	0.00011	0.00015
			10−5	1.17 × 10−5	1.33 × 10−5	1.17 × 10−5	1.33 × 10−5	1.53 × 10−5
	U(0, 10)	3,200,000	0.05	0.05233	0.05205	0.05233	0.05205	0.05937
			10−3	0.00111	0.00110	0.00111	0.00110	0.00132
			10−4	0.00011	0.00012	0.00011	0.00012	0.00015
			10−5	1.28 × 10−5	1.56 × 10−5	1.28 × 10−5	1.56 × 10−5	1.59 × 10−5
	U(0, 5)	3,200,000	0.05	0.05351	0.05291	0.05351	0.05291	0.06177
			10−3	0.00115	0.00112	0.00115	0.00112	0.00139
			10−4	0.00011	0.00012	0.00011	0.00012	0.00014
			10−5	1.16 × 10−5	1.56 × 10−5	1.16 × 10−5	1.56 × 10−5	1.28 × 10−5
	U(0, 3)	1,800,000	0.05	0.05552	0.05411	0.05553	0.05411	0.06591
			10−3	0.00118	0.00114	0.00118	0.00114	0.00140
			10−4	0.00013	0.00013	0.00013	0.00013	0.00014
			10−5	1.17 × 10−5	1.00 × 10−5	1.17 × 10−5	1.00 × 10−5	1.28 × 10−5

Tables 1 and 2 show that the Cox FR LRT statistics of the proposed Cox models control the type I error correctly, no matter whether the genotype data are smoothed or not and which basis functions are used to smooth the GVF and β(u). In addition, the results of “Basis of both GVF and β(u)” are very similar to those of “Basis of beta-Smooth Only” in Tables 1 and 2; and actually, many of them are identical. We also note that the empirical type I error rates of Cox SKAT LRT are inflated compared to those of the Cox FR LRT as well as the nominal levels. In Table 2, the computation of type I error rates failed due to convergence issues for censoring U(0, 3) for sample sizes 1,000 and 2,000 when the causal variants are all rare.

3.2 Statistical Power Evaluation

Based on the simulated sequence data, the power of the proposed Cox FR LRT statistics was compared with Cox SKAT LRT and Cox BT LRT by Chen et al. (2014). The Cox FR LRT statistics are those considered in the type I error simulations, i.e., the LRT statistics of Cox models (4) and (5). The results are reported in Figures 1 and 2. In Figure 1, some causal variants are rare and some are common. In Figure 2, all causal variants are rare. In the legend of the Figures, “GVF&Beta, B-sp” (or “GVF&Beta, F-sp”) means that both genetic variant functions and genetic effect function β(u) were smoothed by B-spline (or Fourier) basis functions, “Beta, B-sp” (or “Beta, F-sp”) means that only the genetic effect function β(u) was smoothed by B-spline (or Fourier) basis functions (i.e., beta-smooth only), “B-sp” means a B-spline basis was used, and “F-sp” means a Fourier basis was used.

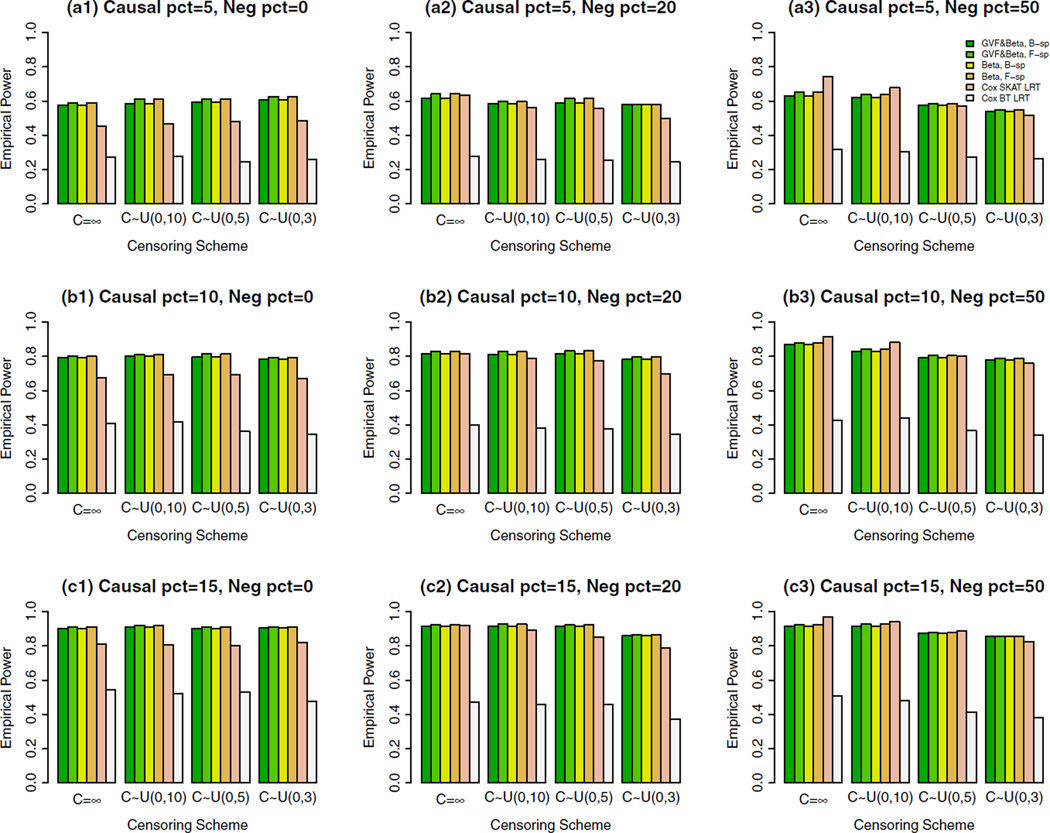
Figure 1. The Empirical Power of the Cox FR LRT Statistics of the Cox Models (4) and (5) and Cox SKAT LRT and Cox BT LRT by Chen et al. (2014) at α = 0.001, When Some Causal Variants are Rare and Some are Common and a Sample Size of 2,000.

When Neg pct = 0, All Causal Variants Had Positive Effects; When Neg pct = 20, 20%/80% Causal Variants Had Negative/Positive Effects; When Neg pct = 50, 50%/50% Causal Variants Had Negative/Positive Effects.

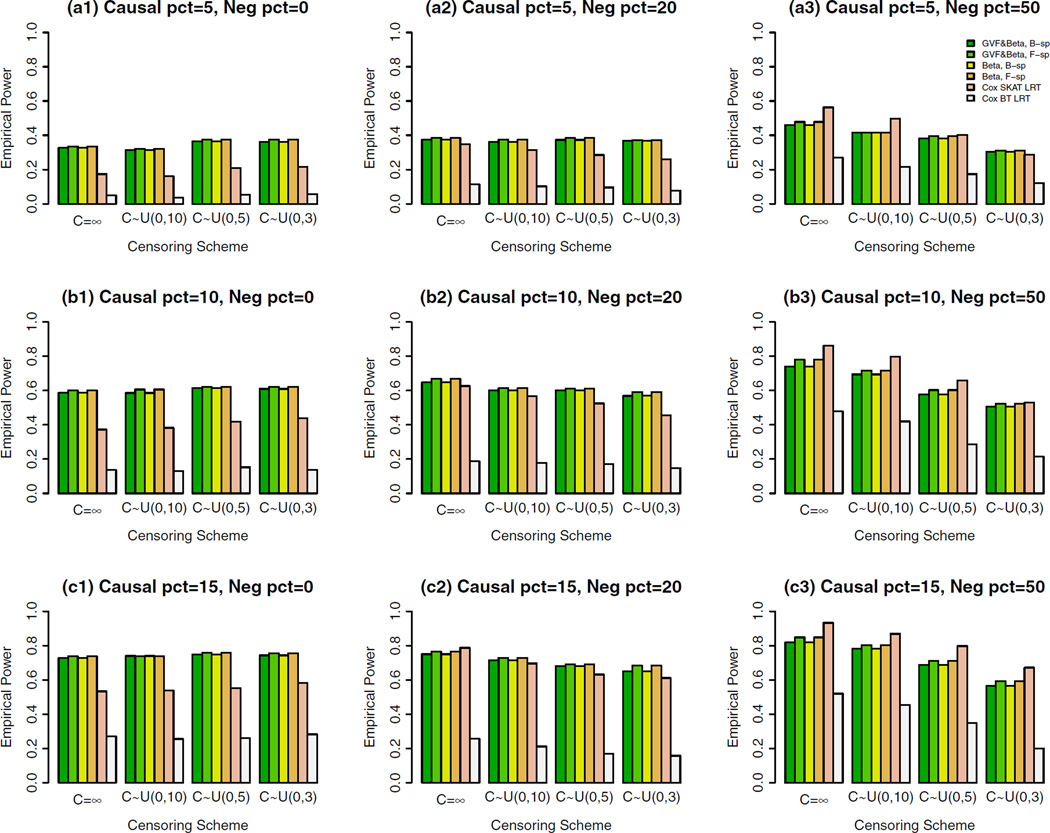
Figure 2. The Empirical Power of the Cox FR LRT Statistics of the Cox Models (4) and (5) and Cox SKAT LRT and Cox BT LRT by Chen et al. (2014) at α = 0.001, When All Causal Variants are Rare and a Sample Size of 2,000.

When Neg pct = 0, All Causal Variants Had Positive Effects; When Neg pct = 20, Causal Variants Had Negative/Positive Effects; When Neg pct = 50, 50%/50% Causal Variants Had Negative/Positive Effects.

When some causal variants are rare and some are common as shown in Figure 1, the Cox FR LRT statistics of the proposed Cox models have higher power than that of Cox SKAT LRT when all causal variants had positive effects [graphs (a1), (b1), and (c1) in Figure 1]; When 20%/80% causal variants had negative/positive effects in graphs (a2), (b2), and (c2) in Figure 1, the Cox FR LRT statistics have slightly higher or higher power than that of Cox SKAT LRT; When 50%/50% causal variants had negative/positive effects, in graphs (a3), (b3), and (c3) in Figure 1, the Cox FR LRT statistics have similar power as that of Cox SKAT LRT.

When all causal variants are rare as shown in Figure 2, the Cox FR LRT statistics of the proposed Cox models have higher power than that of Cox SKAT LRT when all causal variants had positive effects [graphs (a1), (b1), and (c1) in Figure 2]; When 20%/80% causal variants had negative/positive effects in graphs (a2), (b2), and Figure 2, the Cox FR LRT statistics have similar power as that of Cox SKAT LRT; When 50%/50% causal variants had negative/positive effects, in graphs (a3), (b3), and (c3) in Figure 2, the Cox FR LRT statistics have lower power than that of Cox SKAT LRT.

In total, we compared the power of four Cox FR LRT statistics of the fixed effect models: two are based on B-spline basis functions, and two are based on Fourier basis functions. In the two Cox FR LRT statistics to use B-spline (or Fourier) basis functions, one is to smooth both the genetic variant functions and the genetic effect function β(u), and the other is only to genetic effect function β(u) (i.e., beta-smooth only). Generally, the four Cox FR LRT statistics of the proposed Cox models have similar power. The power levels of beta-smooth only are almost identical to those of smoothing both the genetic variant functions and genetic effect function β(u) by B-spline basis (or Fourier basis). Therefore, the Cox FR LRT statistics do not strongly depend on whether the genotype data are smoothed or not, or which basis functions are used. Hence, they are very stable in terms of power performance.

3.3 Additional Simulation Results

In the Supplementary Materials, Appendix A, more simulation results are presented for three sets of parameters:

1. In Tables A.1 and A.2 and Figures A.1 and A.2, the order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 6; the number of Fourier basis functions was K = K_β = 7.

2. In Tables A.3 and A.4 and Figures A.3 and A.4, the order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 8; the number of Fourier basis functions was K = K_β = 9.

3. In Tables A.5 and A.6 and Figures A.5 and A.6, the order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 12; the number of Fourier basis functions was K = K_β = 13.

For the first set of parameters, the computation of all simulations of type I error rates succeed. For the second set of parameters, the computation of most simulations of type I error rates succeed. However, the computation of more simulations of type I error rates failed for the third set of parameters. The type I error rate results of Supplementary Materials are similar to those of the main text, i.e., the Cox FR LRT statistics control the type I error rates correctly.

The empirical power levels in Figures A.1 and A.2 are slightly lower than those of Figures 1 and 2. On the other hand, the empirical power levels in Figures Figures A.3, A.4, A.5, and A.6 are similar to those of Figures 1 and 2. Therefore, the range of parameters 8 ≤ K = K_β ≤ 13 should be fine to use in fitting the proposed Cox models, in terms of controlling type I error rates well and good power.

In the Supplementary Materials, Appendix B, three more settings were considered: 30%, 40%, and 50% of variants were causal in the 6 kb subregion. In Figures B.1 – B.8, the range of parameters K and K_β are from 6 to 13 as those in the main text and Supplementary Materials, Appendix A. If some causal variants are rare and some are common, the Cox FR LRT statistics have higher or similar power as Cox SKAT LRT. If all causal variants are rare, the Cox FR LRT statistics have higher or similar power as Cox SKAT LRT except when 50%/50% causal variants had negative/positive effects.

The Cox FR LRT statistics have higher power than Cox BT LRT in all the Figures 1, 2, A.1 – A.6 and B.1 – B.8. In addition, the power levels of Cox SKAT LRT are higher than those of Cox BT LRT in all the Figures B.1 – B.8 except when 50% variants are causal and all causal variants had positive effects [graph (c1) in Figures B.1 – B.8]. This is consistent with the results of Chen et al. (2014).

3.4 Application to AREDS Data

Table 3 shows the results of association analysis of AREDS data for the two genes, CFH and ARMS2, using the proposed Cox FR LRT, Cox SKAT LRT, and Cox BT LRT. We analyze the data three times in each gene region: (1) all genetic variants, (2) common variants only, and (3) rare variants only. Here the rare variants are defined as those that the MAF ≤ 0.05, and common variants are defined as those that the MAF > 0.05.

Table 3. Association Analysis of Age-Related Eye Disease Study (AREDS) Data.

The results of “Basis of both GVF and β(u)” were based on the Cox model (4) by smoothing both the GVF and the genetic effect function β(u), and the results of “Basis of beta-Smooth Only” were based on the Cox model (5) by smoothing the genetic effect function β(u) only. The order of B-spline basis was 4, and the number of B-spline basis functions was K = K_β = 10; the number of Fourier basis functions was K = K_β = 11. The results of Cox SKAT LRT and Cox BT LRT were from R SeqMeta package by Chen et al. (2014). The rare variants are defined as those that the MAF ≤ 0.05, and common variants are defined as those that the MAF > 0.05.

The Type of Variant	The Name of Gene	The Number of SNPs	P-values
			Cox FR LRT Statistics				Cox SKAT LRT	Cox BT LRT
			Basis of both GVF and β(u)		Basis of beta-Smooth Only
			B-sp Basis	Fourier Basis	B-sp Basis	Fourier Basis
All	CFH ARMS2	162 25	4.95 × 10−51 4.28 × 10−43	7.19 × 10−49 4.37 × 10−43	4.95 × 10−51 4.28 × 10−43	7.19 × 10 −49 4.37 × 10−43			4.03 × 10−15 9.65 × 10−7	9.74 × 10−53 2.56 × 10−37
Common	CFH ARMS2	59 18	5.74 × 10−53 1.32 × 10−42	1.46 × 10−49 7.72 × 10−42	5.74 × 10−53 1.32 × 10−42	1.46 × 10−49 7.72 × 10−42	1.58 × 10−8 3.60 × 10−6	1.68 × 10−46 6.39 × 10−39
Rare	CFH ARMS2	103 7	2.71 × 10−11 NA	5.71 × 10−8 0.017543	2.71 × 10−11 0.001922	5.71 × 10−8 NA	4.56 × 10−9 0.000607	1.28 × 10−7 0.000202

By analyzing all genetic variants, both genes are significant since all the p-values are small, suggesting that gene-based method can be used in the genome-wide association study of survival outcome and is complimentary to single marker test analysis. For the ARMS2 gene, the p-values of the Cox FR LRT, 4.28 × 10⁻⁴³ and 4.37 × 10⁻⁴³, are much smaller than 9.65 × 10⁻⁷ of Cox SKAT LRT and 2.56×10⁻³⁷ of Cox BT LRT. For the CFH gene, the p-values of the Cox FR LRT, 4.95 × 10⁻⁵¹ and 7.19 × 10⁻⁴⁹, are much smaller than 4.03 × 10⁻¹⁵ of Cox SKAT LRT, but slightly larger than 9.74 × 10⁻⁵³ of Cox BT LRT.

The results of analyzing common variants only are similar to those of analyzing all genetic variants by the Cox FR LRT and Cox BT LRT. The p-values of Cox SKAT LRT of analyzing common variants only are bigger than those of analyzing all genetic variants. For the CFH gene, there are 103 rare variants in the gene region and the results of analyzing rare variants only are less significant than those of analyzing all genetic variants or common variants only. For the ARMS2 gene, there are only 7 rare variants and the results of analyzing rare variants only are not reliable by FR based Cox models.

From the analysis of AREDS data, we may see that it is a good strategy to analyze all genetic data instead of only analyzing rare or common variants. In the analysis of rare variants, the FR based Cox models can not converge for the ARMS2 gene since there are only 7 variants. Note the cutoff is 0.05 to define the rare variants and the cutoff is artificial. By using different cutoffs, one will get different results. Therefore, it is better to analyze all variants to get a uniform result.

In the Table 3, the results of the Cox FR LRT statistics of beta-smooth only are identical to those of smoothing both the genetic variant functions X_i(u) and the genetic effect function β(u) except for ARMS2 gene of analyzing rare variants only. Thus, whether the genetic variant functions are smoothed or not does not have much impact on the results. We observed this for quantitative and dichotomous traits in Fan et al. (2013, 2014) and Wang et al. (2015).

4 Discussion

In this article, we developed FR based Cox proportional hazard models for gene-based association analysis of survival traits adjusting for covariates. By fitting the proposed Cox models, Cox FR LRT statistics are introduced to test for an association between the survival traits and multiple genetic variants. Extensive simulations are performed to evaluate empirical type I error rates and power of the Cox FR LRT statistics. We show that the Cox FR LRT statistics control the type I error very well. The Cox FR LRT statistics have higher power than Cox SKAT LRT when all causal variants had positive effects no matter some causal variants are rare and some are common or all causal variants are rare. If 20%/80% causal variants had negative/positive effects, the Cox FR LRT statistics have higher power than (or similar power as) that of Cox SKAT LRT, when some causal variants are rare and some are common (or all causal variants are rare). If 50%/50% causal variants had negative/positive effects, the Cox FR LRT statistics have similar power as (or lower power than) that of Cox SKAT LRT, when some causal variants are rare and some are common (or all causal variants are rare).

In our simulation studies on our linux system, it takes about 24, 40, 90, and 120 hours to analyze 10⁵ phenotype-genotype datasets to calculate the four Cox FR LRT statistics and Cox SKAT LRT in Tables 1 and 2 for sample sizes of 1,000, 2,000, 3,000, and 4,000, respectively. The models and related test statistics can be useful in the whole genome and whole exome association studies.

The proposed methods were applied to analyze an age-related macular degeneration dataset. For both CFH and ARMS2, the results of the Cox FR LRT statistics are much more significant than Cox SKAT LRT and are similar to Cox BT LRT if all or only common variants were used in the analysis. For the CFH gene, the results of the Cox FR LRT statistics are similar to Cox SKAT LRT but more significant than Cox BT LRT if only rare variants were used in the analysis. For the ARMS2 gene, there are only 7 rare variants and the results are not reliable by the FR Cox models. In practice, one can perform analysis by the Cox FR LRT statistics and Cox SKAT LRT and Cox BT LRT to make a comparison, and this can be readily done using our R codes and the R SeqMeta package.

It is noteworthy that SKAT and Cox SKAT LRT were constructed as score tests on the variance component parameter for the genetic random variations in linear/logistic or Cox mixed effects models. The test statistic is a weighted sum of single-marker score test statistics when using the linear kernel [Chen et al., 2014; Lee et al., 2012]. Therefore, the test statistics of SKAT and Cox SKAT LRT only model pair-wise linkage disequilibrium (LD) between each individual marker and the trait locus, while the LD among genetic markers are not modeled.

In the proposed FR based Cox models, the genetic effects are treated as a function of the physical position and the genetic variant data are viewed as stochastic functions of the physical position and so any orders of LD are taken care of in the models [Ross, 1996]. The regression coefficients of genetic terms in the models of SKAT and Cox SKAT LRT do not depend on the physical position, while our genetic effect function is actually a function of physical position. Hence, the proposed Cox models can fully utilize LD and physical position information.

Chen et al. (2014) reported that the score test shows inflated type I error rates when the effective sample size is small (e.g., in finite samples with a high proportion of censoring), and the Cox SKAT LRT has better finite-sample performance than the score test. However, it is worth noting that the LRT follows a chi-square distribution asymptotically under the null hypothesis, thus for variants with very low minor allele counts (e.g., singletons), LRT asymptotics may not work well either. In practice, such variants are usually filtered out or collapsed together. Therefore, it would be necessary for Cox SKAT LRT to go through genotype quality control or filtering procedures prior to analysis. However, we do not need to remove any variants before running the proposed FR based Cox models. Note that the number of B-spline or Fourier basis functions is fixed in our Cox models and does not depend on the number of genetic variants. Therefore, one may keep all variants for a uniform analysis. Actually, with more genetic variants, we estimate more accurate genetic variant functions.

The Cox FR LRT statistics could not be computed in some simulation replicates due to failure of convergence. The failure of the convergence is due to a number of parameters, i.e., the number of B-spline or Fourier basis functions. When the number of B-spline or Fourier basis functions is 6 or 7, all simulation of 1,200,000 datasets were successfully done in Tables A.1 and A.2. When the number of B-spline or Fourier basis functions increase, not all models can be successfully fit. Once the calculation can be done, the type I error rates are around the nominal levels. However, when the number of B-spline or Fourier basis functions is 6 or 7, the empirical power levels in Figures A.1 and A.2 are slightly lower than those of Figures 1 and 2 when the number of B-spline or Fourier basis functions is 10 or 11. Therefore, we report the results of the number of B-spline or Fourier basis functions of 10 and 11 in the main text.