New approach to develop ultra-high inhibitory drug using the power function of the stoichiometry of the targeted nanomachine or biocomplex

Abstract

Aims:

To find methods for potent drug development by targeting to biocomplex with high copy number.

Methods:

Phi29 DNA packaging motor components with different stoichiometries were used as model to assay virion assembly with Yang Hui's Triangle 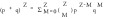, where Z = stoichiometry, M = drugged subunits per biocomplex, p and q are the fraction of drugged and undrugged subunits in the population.

Results:

Inhibition efficiency follows a power function. When number of drugged subunits to block the function of the complex K = 1, the uninhibited biocomplex equals q^z, demonstrating the multiplicative effect of stoichiometry on inhibition with stoichiometry 1000 > 6 > 1. Complete inhibition of virus replication was found when Z = 6.

Conclusion:

Drug inhibition potency depends on the stoichiometry of the targeted components of the biocomplex or nanomachine. The inhibition effect follows a power function of the stoichiometry of the target biocomplex.

Bacteria, viruses and cells contain biocomplexes and nanomachines composed of multiple subunits, such as biomotors [1–4], pumps [5], exosomes [6–8], valves [9–11], membrane pores [12–15], chaperonins [16], PCNA [17], ATPase [18,19] and tubes [20]. From a nanobiotechnological standpoint, these nanomachines can be used and converted to build sophisticated nanodevices including molecular sensors [21–23], patterned arrays, actuators [24], chips, microelectromechanical systems [25], molecular sorters [26], single pore DNA sequencing apparatus [12–13,21,27] or other revolutionary electronic and optical devices [28,29]. From a pharmaceutical standpoint, these multisubunit biocomplexes or nanomachines have a potential for use as drug targets for therapeutics, as well as diagnostic applications such as pathogen detection, disease diagnosis, drug delivery and treatment of diseases [22–23,30–31]. In the Additional Strand Catalytic E family including the ATPases Associated with diverse cellular Activities (AAA+) and the FtsK-HerA superfamily in bacteria, viruses and cells, there are nanomotors that perform a wide range of functions [19,32–33] critical to chromosome segregation, bacterial binary fission, DNA/RNA and cell component transportation, membrane sorting, cellular reorganization, cell division, RNA transcription, as well as DNA replication, riding, repair and recombination [1,34–36]. One of the directions of NIH Roadmap is to utilize these cellular nanomachines and biocomplexes for biomedical applications.

Acquired drug resistance has become a major reason for failure treatment of a range of diseases, that is, the chemotherapy for cancer, bacterial or viral infections. Drug resistance of cancer has escalated and has partially contributed to the approximate 600,000 deaths in the USA in 2012 [37]. HIV drug resistance has also become a major issue [38]. Many common pathogens have become resistant to current drug treatments with new infectious diseases on the rise. The use of multidrug-resistant agents in biological weapons has created a previously unrealized challenge [39]. Thus, there is a need to develop new treatment strategies to combat drug resistance with new drug development methods.

The first USA FDA-approved drug to treat multidrug-resistant tuberculosis, bedaquiline, follows a novel mechanism of inhibiting the bacterial ATP synthase of Mycobacterium tuberculosis and other mycobacterial species, but had little activity against other bacteria [40]. To combat multidrug resistance in cancer, several approaches have been explored. One method is to target components that are highly important for the growth of the biological entity [41,42]. Another approach uses nanodrug delivery carriers that are expected to enhance the binding efficiency of drugs to cancer cells [43–46] or cocktail therapy [47]. A third approach is to develop new combinational drugs with higher potency by acting on multiple targets [48,49]. This involves identifying multiple targets that when treated leads to a synergetic effect and optimizing the design of multitarget ligands [50].

The approach of developing highly potent drugs through targeting of protein or RNA complexes with high stoichiometry has never been reported due to challenges in comparing efficacies of two drugs that can be confused by target essentiality with binding affinity. For instance, if two drugs target two stoichiometrically different targets, it becomes extremely difficult to prove whether the difference in drug efficiency is due to differences in their target binding affinity or essential level in the growth of the biological organism. In order to quantify effects from targeting biocomplexes of different stoichiometry, a well-studied multicomponent system is required that allows empirical comparison of functional inhibition of individual components that are composed of different number of subunits.

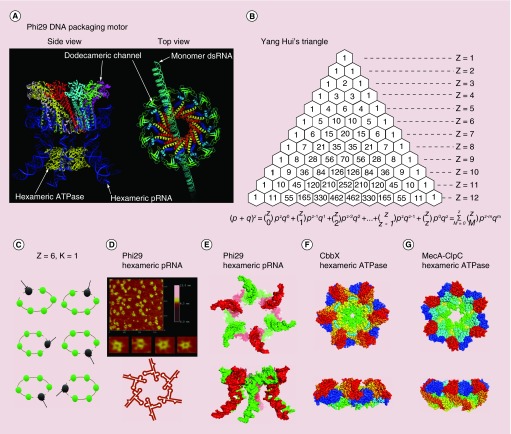
An example of one nanobiomachine is the dsDNA translocation motor, for which the ATPase protein is a pivotal component that assembles into a hexameric ring structure and translates the action of ATP binding and hydrolysis into mechanical motion to translocate DNA physically. The DNA packaging motor of bacteriophage phi29 (Figure 1A) [9,51–53] is composed of three essential co-axial rings: a dodecameric connector ring located at the vertex of the viral procapsid, a hexameric packaging RNA (pRNA) ring [52] bound to the N-terminus of the connector [54] and a hexameric ring of ATPase gp16 attached to the helical region of pRNA [10,19,55], powered through the hydrolysis of ATP resulting in DNA packaging. The use of Yang Hui's Triangle (Figure 1B) or binomial distribution to determine the stoichiometry of the pRNA was first reported in 1997 [56]. The use of similar mathematical methods to determine the stoichiometry of the protein subunits has also been reported more recently [51]. The copy number of ATP molecules required to package one full phi29 genomic dsDNA was predicted to be 10,000 [57]. It has recently been shown that this hexameric motor uses a revolution mechanism without rotation to translocate its genomic DNA [10,19,33,35–36,58].

Figure 1. . Stoichiometry of viral DNA packaging motor.

(A) Illustration of Phi29 DNA packaging motor composed of one copy of genomic DNA that revolves through the channel wall (left panel), six copies of pRNA, six copies of ATPase gp16 and a connector channel. (B) Yang Hui Triangle. (C) Illustration of Z = 6 and K = 1, drug targeting anyone subunit of the complex will block its activity. (D) Atomic force microscopy image of hexameric re-engineered pRNA rings. (E) 3D structure of hexameric pRNA ring top view and side view from the crystal structure of 3WJ (PDB ID: pRNA 3WJ, 4KZ2). (F) A crystal hexameric structure of AAA+ Protein CbbX withtop view and side view [59] (PDB ID: CbbX, 3Zuh [60]). (G) Structure of the hexameric AAA+ molecular machine ClpC with adaptor protein MecA [61] (PDB ID: MecA-ClpC, 3PXG).

AAA+: ATPases associated with diverse cellular activities.

In this report, we hypothesize that the inhibitory efficiency of a drug is related to the stoichiometry of its targeted biocomplex; the higher the stoichiometry of the target complex, the more efficient the drug. This can lead to the development of potent therapeutics against high-stoichiometric biomachines or biocomplexes as drug targets. We proved this hypothesis by using a mutant subunit as the drugged inactive target to calculate the theoretical inhibition efficiency via binomial distribution, and compared with experimental data from a defined in vitro viral assembly system. Since biomotors share certain common structures and operation mechanisms [1,36,62–63], the approach in drug development reported here should have general applications especially in developing new generations of drugs for combating the rising acquired drug resistance in viruses, bacteria and cancers [38,64–65].

Methods

Preparation of mutant genomic dsDNA

Phi29 genomic DNA-gp3 was purified from Bacillus subtilis SpoA12 cells by CsCl gradient ultracentrifugation as described previously [66]. Mutant dsDNA was prepared by digesting the phi29 genomic dsDNA with EcoR1 restriction enzyme in fast digest buffer (Fermentas, USA) at 37°C for 1 h followed by ethanol precipitation. The mutant DNA was tested by 1% agarose gel electrophoresis, stained by ethidium bromide (Sigma, USA) and imaged by Typhoon (GE Healthcare, USA).

Preparation of mutant pRNA

Wild-type phi29 pRNA and inactive mutant as drugged pRNA were prepared by in vitro transcription. In the inactive mutant pRNA, the first four bases ‘UUCA’ located at the 5′ end were mutated to ‘GGGG.’ BglII-digested plasmid pRT71 was used as DNA template [67] in the PCR reaction for both RNAs. Oligonucleotide 5′-TAA TAC GAC TCA CTA TAG GGG TGG TAC-3′ and 5′-TTA TCA AAG TAG CGT GCA C-3′ were used as primers for mutant pRNA. RNAs were then transcribed by T7 RNA polymerase using double-stranded DNA generated from PCR, as described before [68]. The RNA from in vitro transcription was further purified by 8 M urea 8% polyacrylamide gel electrophoresis as described previously [67].

Preparation of mutant ATPase gp16

The purification of wild-type gp16 has been described previously [66]. The walker B mutant gp16 was constructed by introducing mutations in the gp16 gene. The amino acid residues D255 and E256 in walker B motif of gp16 were mutated to E255 and D256, respectively. The mutation was introduced with the Quick Change site-directed mutagenesis kit (Stratagene, USA) using appropriate primers. The expression and purification of protein were carried out followed a published procedure [51].

Antisense oligonucleotides

Antisense oligonucleotides P3 and P15 were designed to be reversely complementary to different regions on the pRNA molecule and chemically synthesized by IDT (IOWA, USA). P3 oligo (5′-TTGCCATGATTGACAAC-3′) targets the region of 83–99 nucleotides at the 3′end of pRNA, P15 oligo (5′-AAGTACCGTACCATTGA-3′) targets the region of 1–17 nucleotides at the 5′end of pRNA. P8 oligo (5′-TAATACGACTCACTATAGGGGTGGTAC-3′) was designed as a nontargeting control in the test. 1 μl of individual oligos at 100 μM were mixed with 1 μl of pRNA at 4 μM and dialyzed on a 0.025 μm mixed cellulose esters VSWP filter membrane (Millipore Corp, Darmstadt, Germany) against TBE buffer (89 mM Tris-HCl, pH 8.3, 89 mM boric acid and 2.5 mM EDTA) at room temperature for 15 min. The purified RNA complex was used for in vitro phi29 assembly assay.

In vitro phi29 assembly assay

Purified components were subjected to in vitro viral assembly assay as described previously [69]. Briefly, 10 μg of purified procapsids were mixed with 100 ng of pRNA in 5 μl of reaction buffer (10 mM ATP, 6 mM 2-mercaptoethanol and 3 mM spermidine in TMS buffer) at room temperature for 30 min. Purified DNA-gp3 and gp16 were then added and the reaction mixture was incubated at room temperature for 1 h to initiate DNA packaging. Finally, the DNA filled procapsids were incubated with 10 μl of gp8.5–9 extract from Escherichia coli containing plasmid pARgp8.5–9 and 20 μl of gp11–14 extract from E. coli to complete the infectious phage assembly.

The newly assembled infectious viruses were plated with inoculated B. subtilis bacteria Su⁺⁴⁴ cells onto a half LB plate covered with top agar. After 12-h incubation at 37°C, the viral assembly efficiency (plaque-forming unit [PFU]) was calculated by counting the formed plaque numbers. Mixing different ratios of mutant with wild-type components, while keeping all other components the same, the viral assembly efficiency (PFU) versus ratio of mutant components gave an empirical curve for vial assembly inhibition assay, and it was compared with theoretical curves from the binomial distribution equation.

In vivo viral assembly assay

Plasmid pRBwtRNA containing the pRNA coding sequence under T7 promoter was constructed by ligating the fragment coding pRNA sequence and T7 promoter into pRB381-L550 vector (modified and kindly provided by M Wang and H Zalkin) following a previously described method [70]. Plasmid pRBmutRNA contained mutant pRNA under its natural promoter PE1 sequence, and the mutation was changing sequence 5′UUGA-3′ at its 3′end to 5′GGGG-3′. The DNA fragments coding mutant pRNA sequence and PE1 sequence were prepared by PCR as described previously [70]; and digested with HindIII-BglII restriction enzyme. The mutant pRNA sequence coding fragment was further ligated with a 6.0kb fragment from pRB381-L550 that was digested with HindIII and partially digested with BglII.

The plasmids pRBmutRNA, pRBwtRNA and pRB381-L550 were transformed into B. subtilis cells following methods described previously [70]. The B. subtilis cells harboring transformed plasmids were incubated in 416 medium with 10 mg/ml of neomycin for 3 h at 37°C and then plated onto LB-neomycin (10 mg/ml) plates for plaque formation analysis.

Results

The definition of ‘stoichiometry’

The definition of the stoichiometry in this report is different from conventional definition of stoichiometry used to evaluate drug efficiency. Conventionally the concept of stoichiometry refers to the number of a drug binding to each target molecule, which is also known as B_max. In this study, the definition of stoichiometry refers to the copy number of subunit within a biocomplex or the nanomachine that serves as drug target.

The definition of ‘K value,’ & K = 1 is one key for ultra-high inhibition efficacy

Suppose a biocomplex drug target contains Z copies of subunits, then K is the copy number (K ≤ Z) of drugged subunits required to inhibit the function of the complex or the nanomachine. As an analogy to the difference between the parallel circuit and the serial circuit, when the Christmas lights are arranged in a parallel circuit, any light bulbs that are burnt out will not affect other bulbs. But in a serial circuit, any one light bulb that is broken will stop the entire lighting system, which is K = 1. Thus, the K value is the key to the probability of inactive nanomachines or biocomplexes by combination and permutation of all subunits. K = 1 is critical for such ultra-high inhibition effect. The foundation of the approach in this report is the difference in probability of inhibited biocomplexes in systems of different K values with combination and permutation algorithms. Biological systems display complicated reactions. Many reactions involve multiple subunits to work cooperatively sequentially or precessively to accomplish one essential biological function [33,71–78]. Single assembly pathways have been reported in the viral assembly system [79,80]. In most cases of the sequential, cooperative and precessive reaction, inactivation of any one, not necessary all, of the subunits will result in inhibition of its function, thus K = 1. Drug synergism was utilized in multitarget drug therapy; in short, a drug combination can simultaneously act on multiple targets in disease networks to produce a synergistic effect [50,81]. However, our design reported here is unique from the conventional synergistic approach. We suggest that using multisubunit biocomplexes as drug target could lead to development of ultra-high potent drugs. In a conventional six-component system, for example one drug is designed to target component 3 to stop the entire system, since the drug can only target component 3, the condition fits the model of Z = 1 and K = 1. Thus, the inhibition efficiency and substrate targeting efficiency (p) of drug will be in linear relationship. However, in the system in this report, the entire system will be blocked when drug targets any subunit of a hexamer, which is Z = 6 and K = 1. Thus the probability of remaining undrugged targets will be q⁶, where q represents the fraction of untargeted hexamer subunits; in other words, the drug inhibition efficiency will be 1-q⁶, which increases following a power function compared with the linear for conventional mono-subunit approaches.

Assuming that at least K copies of drugged subunits were needed to deactivate the nanomachine or biocomplex, the probability of functional biocomplexes in the presence of various ratios of inhibited and wild-type subunits could be predicted from Equation 2. When K = 1, it implies that drug binding to one subunit will inactivate the subunit, and one drugged subunit per multisubunit complex is sufficient to inhibit the overall function of the complex. The inhibition efficiency by drugs targeting multisubunit biocomplexes with stoichiometry of Z will equal 1-q^z, as shown in Table 1. An example for such a probability calculation when Z = 6 and K = 1 is as follows: since it was assumed that six (Z = 6) copies of subunits per element were required for function and one drugged subunit (K = 1) was sufficient to block its activity, all elements possessing one to five copies of drugged subunits would be nonfunctional (Figure 1C). Only those complexes possessing six copies of normal subunits will be functional. The chance for a complex containing six copies of unaffected subunits in a population is q⁶ and the inhibition efficiency will be 1-q⁶.

Table 1. . Probability of the complex containing M copies of drugged subunits and n copies of undrugged subunits.

Inhibited subunits (p)	Z = 3				Z = 12
	M = 0, n=3	M = 1, n = 2	M = 2, n = 1	M = 3, n = 0	M = 0, n = 12	M = 1, n = 11	M = 2, n = 10	M = 3, n = 9	M = 4, n = 8	M = 5, n = 7	M = 6, n = 6	M = 7, n = 5	M = 8, n = 4	M = 9, n = 3	M = 10, n = 2	M = 11, n = 1	M = 12, n = 0
0	1.0000	0.0000	0.0000	0.0000	1.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
0.1	0.7290	0.2430	0.0270	0.0010	0.2824	0.3766	0.2301	0.0852	0.0213	0.0038	0.0005	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
0.2	0.5120	0.3840	0.0960	0.0080	0.0687	0.2062	0.2835	0.2362	0.1329	0.0532	0.0155	0.0033	0.0005	0.0001	0.0000	0.0000	0.0000
0.3	0.3430	0.4410	0.1890	0.0270	0.0138	0.0712	0.1678	0.2397	0.2311	0.1585	0.0792	0.0291	0.0078	0.0015	0.0002	0.0000	0.0000
0.4	0.2160	0.4320	0.2880	0.0640	0.0022	0.0174	0.0639	0.1419	0.2128	0.2270	0.1766	0.1009	0.0420	0.0125	0.0025	0.0003	0.0000
0.5	0.1250	0.3750	0.3750	0.1250	0.0002	0.0029	0.0161	0.0537	0.1208	0.1934	0.2256	0.1934	0.1208	0.0537	0.0161	0.0029	0.0002
0.6	0.0640	0.2880	0.4320	0.2160	0.0000	0.0003	0.0025	0.0125	0.0420	0.1009	0.1766	0.2270	0.2128	0.1419	0.0639	0.0174	0.0022
0.7	0.0270	0.1890	0.4410	0.3430	0.0000	0.0000	0.0002	0.0015	0.0078	0.0291	0.0792	0.1585	0.2311	0.2397	0.1678	0.0712	0.0138
0.8	0.0080	0.0960	0.3840	0.5120	0.0000	0.0000	0.0000	0.0001	0.0005	0.0033	0.0155	0.0532	0.1329	0.2362	0.2835	0.2062	0.0687
0.9	0.0010	0.0270	0.2430	0.7290	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0005	0.0038	0.0213	0.0852	0.2301	0.3766	0.2824
1	0.0000	0.0000	0.0000	1.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	1.0000

Rationale behind selection of multisubunit biocomplexes as efficient drug targets

Mechanisms for drug inhibition of organism growth are to block or stop an essential biological element from functioning. When a drug is designed to target the subunit of a complex with targeting efficiency p, a fraction of subunits will not interact with the drug (a percentile given as q, p + q = 1) and will remain active and exert their function properly. Some biological elements are monomers containing only one subunit, while other biological elements, such as the biomotors of hexameric AAA+ family, consist of multiple subunits [19,34]. Conventional drugs are designed to inhibit pathogenesis through targeting of a single subunit molecule, such as an enzyme or a structural protein of a virus. In this situation, the inhibition efficiency is proportional to the substrate targeting efficiency p and the effect is proportional to the first order of p. As described above, in most cases of sequential action or cooperatives in multiple subunit complexes, inactivation of one, not all, of the subunits will result in inhibition of its function. Thus, if complexes containing Z copies of subunits exercise their function in a sequential and cooperative way, then K = 1, and the fraction of the uninhibited active biocomplex will be q^z, a higher order with regards to the stoichiometry. The inhibition proportion will equal 1-q^z.

In this investigation, a well-defined in vitro phi29 viral assembly system was used to represent a multisubunit nanomachine target, with the mutant component representing a target component that has been inactivated by an effective drug. Then, the inhibition efficiencies by targeting different elements of the phi29 DNA packaging motor with different stoichiometry were compared. The viral assembly competition assays combined with binomial distribution analysis illustrated the concept that drug targeting functional biological complexes of a higher stoichiometry has a higher efficiency than drug acting on a single subunit target.

When the target element is a monomer containing only one subunit, the inhibition efficiency can be calculated through a binomial distribution (Equation 1), where p and q are the fractions of drugged (substrate targeting efficiency) and undrugged (normal active elements) subunits, respectively (p+q = 1).

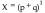Equation 1

However, when the target element contains multiple subunits, a high-order binomial distribution (Equation 2) is applied to calculate the drug inhibition effect by finding the ratio of resulted active and inactive complexes, where Z represents the total number of subunits (the stoichiometry) in one biocomplex and M represents the number of drugged subunits in one biocomplex.

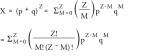Equation 2

For example, if Z is 3, the probability of all combinations of drugged subunits (M) and undrugged subunits (N; M + N = Z) in a given biocomplex entity can be determined by the expansion of Equation 2: (p+q)³ = p³+3p²q+3pq²+q³ = 1. That is, the probability of a complex element possessing three copies of drugged subunits in the population is p³, two copies of drugged and one copy of undrugged or wild-type subunit is 3p²q, one copy of drugged and two copies of undrugged subunits is 3pq², and three copies of undrugged subunits is q³. Assuming there were 70% (p = 0.7) of subunits inactivated by bound drugs, and 30% (q = 0.3) unaffected subunits in the population, then the percentage of elements possessing at least two copies of normal subunits would be the sum of those possessing one copy of drugged and two copies of undrugged wild-type subunits, 3pq², and those possessing three copies of native subunits is q³. That is 3pq² + q³ = 3(0.7)(0.3)² + (0.3)³ = 0.216 = 21.6%. In another example, if one complex contains six subunits, and five out of the six subunits need to remain uninhibited in order to be biologically functional, the active complex ratio in the population will be the sum of: the probability of each element containing five undrugged subunits and the probability of each element containing six undrugged subunits.

The probability X in the population displaying a certain combination of undrugged versus drugged subunits can be predicted by a binomial distribution, as shown in Equation 2. Table 2 shows the probability of a given element with M drugged and N undrugged subunits at increasing percentages of drugged subunits in the population, considering that the total subunits in one element (Z) is 3 or 12. The formula, 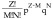(from Equation 2) was used to calculate each combination probability value, the coefficient 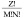in this equation can also be calculated using Yang Hui Triangle, which is also called Pascal's Triangle, or binomial distribution (Figure 1B) [82].

Table 2. . Predicted inhibition efficiency of drugs targeting biocomplexes, K = 1.

Drugged subunit (p)	Inhibition efficiency of the multisubunit complex with
	Z = 1	Z = 2	Z = 3	Z = 6	Z = 10	Z = 100	Z = 1000
0	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
0.1	0.1000	0.1900	0.2710	0.4686	0.6513	1.0000	1.0000
0.2	0.2000	0.3600	0.4880	0.7379	0.8926	1.0000	1.0000
0.3	0.3000	0.5100	0.6570	0.8824	0.9718	1.0000	1.0000
0.4	0.4000	0.6400	0.7840	0.9533	0.9940	1.0000	1.0000
0.5	0.5000	0.7500	0.8750	0.9844	0.9990	1.0000	1.0000
0.6	0.6000	0.8400	0.9360	0.9959	0.9999	1.0000	1.0000
0.7	0.7000	0.9100	0.9730	0.9993	1.0000	1.0000	1.0000
0.8	0.8000	0.9600	0.9920	0.9999	1.0000	1.0000	1.0000
0.9	0.9000	0.9900	0.9990	1.0000	1.0000	1.0000	1.0000
1	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

In vitro virus assembly system used for testing the hypothesis

The highly sensitive in vitro phi29 assembly system was used to determine the inhibition efficiency of drugs targeting multisubunit complexes [56,69,79,83]. Bacteriophage phi29 DNA packaging motor contains 1 copy of genomic dsDNA, 6 copies of packaging RNA, 6 copies of ATPase protein gp16 and more than 10,000 copies of ATP. The stoichiometry of RNA in phi29 has been proven by extensive studies including single-molecule studies [84] Atomic force microscopy images (Figure 1D) [85,86], pRNA crystal structure determination (Figure 1E) [87] and mathematical studies [56]. The stoichiometry of gp16 in phi29 has been proven by multiple approaches including native gel binding, capillary electrophoresis assays, Hill constant determination and by titration of mutant subunits using binomial distribution [19,33]. Many other AAA+ superfamily members have been found to be hexamers as well [59,61,88–92], such as a red type rubisco activase AAA+ protein CbbX (Figure 1F) [59] and MecA-ClpC molecular machine (Figure 1G) [61]. The copy number of ATP molecules was calculated based on the fact that six ATP molecules are required to package one pitch of dsDNA with 10.5 basepairs (bp) [93], thus one ATP is used to package 1.7 bp. The entire phi29 genome is composed of 19.4 kbp, thus, it is expected that more than 10,000 ATP molecules are required to package the entire phi29 genome. The phi29 DNA nanomotor which packages an entire genomic DNA into the procapsid can be treated as a disease model for drug inhibition efficiency analysis.

In vitro testing of the hypothesis using DNA element with stoichiometry of 1

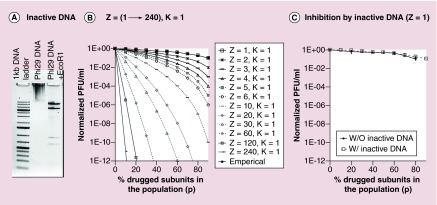
The inhibition efficiency of drugs targeting a single subunit substrate was tested by in vitro phi29 assembly inhibition by mutating the genomic dsDNA (Figure 2A). Various ratios of mutant DNA were mixed with wild-type DNA in in vitro viral assembly assays. The empirical curve of viral assembly efficiency against drugged mutant DNA ratio fits well with the theoretical curve from binomial distribution for Z = 1 and K = 1 (Figure 2B). This suggests that when designing drug targeting the genomic DNA in phi29 nanomotor, it is expected to be a first-order inhibition response. Comparing the in vitro phi29 assembly inhibition, by adding drugged mutant DNA, with simply diluting wild-type DNA concentration as a control, revealed that the drugged mutant DNA did not cause much difference (Figure 2C). The results showed that the inhibition effect of drugs targeting the substrate with stoichiometry of 1 is minimal.

Figure 2. . Theoretical plot (with variable Z) and empirical data to illustrate inhibition efficiency with drug targeting to genomic DNA (Z-1).

(A) Gel showing the phi29 genome DNA treated with endonuclease EcoR1. (B) Plot of virion assembly derived from binomial distribution Equation 2, which showed that the DNA has stoichiometry of 1. (C) Viral assembly inhibition effect of mutant DNA as model of drugged component with Z = 1, showing the linear relationship to p with low slope.

W: With; W/O: Without.

In vitro testing of the hypothesis using RNA elements with stoichiometry of 6

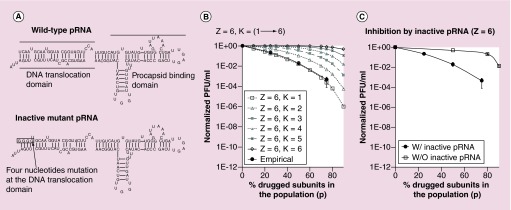
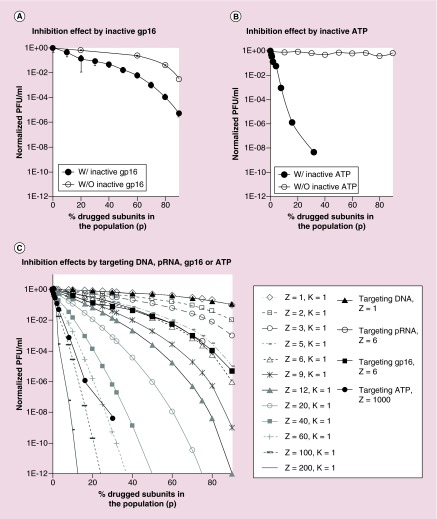
The pRNA of phi29 contains two domains: a head–loop domain essential for procapsid binding and a helix domain essential for DNA translocation (Figure 3A, upper panel) [30,94–95]. The right-hand loop and left-hand loop of two pairing pRNA molecules can interact with each other by complementary base pairing. Extensive studies have led to the conclusion that six copies of pRNA form a hexameric ring which binds to the procapsid for virus activity [84–87]. Drugged mutant pRNA was constructed by mutating four nucleotide sequences at the 5′end region of pRNA (Figure 3A, lower panel), which has been shown to compete with wild-type pRNA for procapsid binding, but was found to be deficient in allowing DNA packaging to occur [70]. The theoretical curves generated using the expansion of binomial distribution equation while total subunit number Z is 6 and varying K number from 1 to 6 are shown in Figure 3B. Fitting the empirical data from phage assembly efficiency at different ratios of drugged mutant pRNAs into the theoretical curves, the empirical data fit into the theoretical curve of Z = 6 and K = 1. It suggested that the pRNA oligomer ring is composed of six copies of pRNA subunits and one subunit of the pRNA multimer blockage is sufficient to block the phage assembly activity. Comparing the empirical curve for viral assembly efficiency against different ratios of drugged mutant pRNAs with the wild-type pRNA concentration dilution control, addition of drugged mutant pRNA showed a much stronger inhibition effect (Figure 3C).

Figure 3. . Theoretical plot (K = 1 to 6) and empirical data to illustrate inhibition efficiency with drug targeting pRNA (Z = 6).

(A) The sequence and secondary structure of wild-type pRNA of phi29 DNA packaging motor (upper panel) and inactive mutant pRNA with four bases mutation at 5′end of the DNA translocation domain serving as a model of drugged inactive pRNA (lower panel). (B) Fitting the phage assembly inhibition result by inactive mutant pRNA with the theoretical plots derived from Equation 2 matched with Z = 6 and K = 1. (C) Comparing the viral assembly inhibition effect by drugged pRNA at different concentration with the undrugged pRNA with same dilution factor.

W: With; W/O: Without.

To further prove the concept that drugs targeting biocomplex with high stoichiometry causes stronger inhibition effect, antisense oligonucleotides which can bind to pRNA molecules were designed as mock drugs in the viral assembly assay. The oligonucleotides P15, and P3 were designed to target the 5′-end and 3′-end regions on pRNA, respectively. It was confirmed that the antisense oligonucleotides can be hybridized to pRNA by gel shift assay (data not shown). When mixing the antisense oligonucleotides with wild-type pRNA for in vitro phi29 assembly assay, complete inhibition effects were shown by antisense oligonucleotides P15, and P3, but not with the nontargeting control oligonucleotide P8 [96]. By mixing the nontargeting oligo P8 with pRNA, it generated plaques with 4.4 × 10⁶ PFU on the plate.

In vivo testing of the hypothesis using RNA elements with stoichiometry of 6

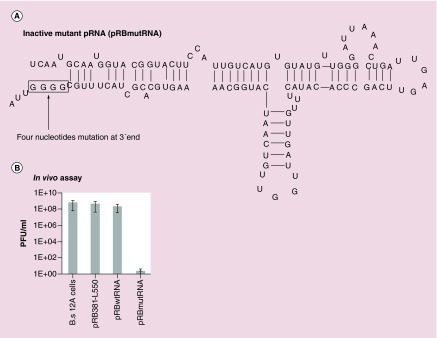
Formation of the hexameric ring of pRNA in the phi29 dsDNA packaging motor has been discovered through biochemical and structural studies [52,84,87,97–104] and activity assays [95,105]. The observed high inhibition efficiency by drugged mutant pRNA on phi29 assembly in vitro was striking [70,106]. To test whether such a high level of inhibition was attainable in vivo, pRBmutRNA plasmid expressing a pRNA with four-base mutation at the 3′ end (Figure 4A) was transformed into B. subtilis DE1 cells. Plasmid pRBwtRNA contained the pRNA coding sequence but do not express pRNA in B. subtilis DE1 cells, and vector pRB381-L550 was introduced as well as a negative control. The results showed that only cells harboring pRBmutRNA plasmid were completely resistant to plaque formation by wild-type phi29 virus infection. Control cells, including B. subtilis 12A cells alone, B. subtilis DE1 cells carrying vector pRB381-L550 alone and cells carrying a wild-type pRNA coding sequence but no expression plasmid pRBwtRNA were all positive for plaque formation (Figure 4B). The ability of mutant pRNAs generated in cells by plasmid pRBmutRNA completely inhibited plaque formation indicated that hexameric pRNA in DNA packaging nanomotor may be a potential target for developing potent antiviral agents [70].

Figure 4. . Complete inhibition of viral assembly in vivo by mutant pRNA as a model of drugged complex (Z = 6).

(A) Inactivation of pRNA by introducing a 4-nucleotide mutation at the 3′end. (B) Virion production by wild-type phi29 infection using host cell B. subtilis harboring plasmid expressing mutant pRNA, wildtype pRNA or plasmid only.

In vitro testing of the hypothesis using the ATPase with stoichiometry of 6

Hexameric folding of ATPase gp16 protein in the phi29 dsDNA packaging motor has been discovered [1,19,33,35]. The hexameric gp16 protein complex functions as ATPase like many other AAA+ superfamily members. ATP binding to one subunit of gp16 stimulates the ATPase to change its conformation from having a lower affinity to one having a higher affinity for dsDNA.

Determination of gp16 stoichiometry was carried out by in vitro phage assembly assay and based on the binomial distribution of wild-type and Walker B mutant gp16 [51]. Different ratios of drugged Walker B mutant gp16 were mixed with undrugged gp16 to test the inhibition efficiency of gp16 mutation on phi29 DNA packaging motor. Assuming K = 1 and the total copy number of gp16 (Z) is between 1–12, theoretical curves for the production of phi29 virion against the ratio of the Walker B mutant corresponding to the stoichiometry (Z) of 1–12 were generated according to Equation 2. The empirical data nearly perfectly overlapped the theoretical curve of Z = 6, K = 1 [51]. This data suggested that phi29 DNA packaging motor has six copies of ATPase gp16 components, and only one copy of the drugged gp16 can block the phi29 motor function. Comparing the inhibition effect of adding mutant gp16 with wild-type gp16 at different concentrations, adding mutant gp16 had a much stronger inhibition effect than the wild-type gp16 concentration dilution control (Figure 5A). Comparing the inhibition effect of mutation on hexameric gp16 to the effect of mutation on single subunit target DNA, the gp16 mutation displayed a much stronger inhibition effect on virus assembly than the same ratio of DNA mutation, indicating the hexameric ATPase protein complex of virus assembly system should be an efficient target for generating new antivirus drugs with high potency.

Figure 5. . Comparision of inhibition efficiency using targets with different Z values.

(A) Virion production inhibition effect of mutant gp16 (Z = 6) at different concentration. (B) Inhibition efficiency by γ-s-ATP with ATP with high Z value. (C) Comparing the virus assembly inhibition effect by drugged components of DNA, pRNA, gp16 and ATP with stoichiometry of 1, 6, 6 and 10,000, respectively.

W: With; W/O: Without.

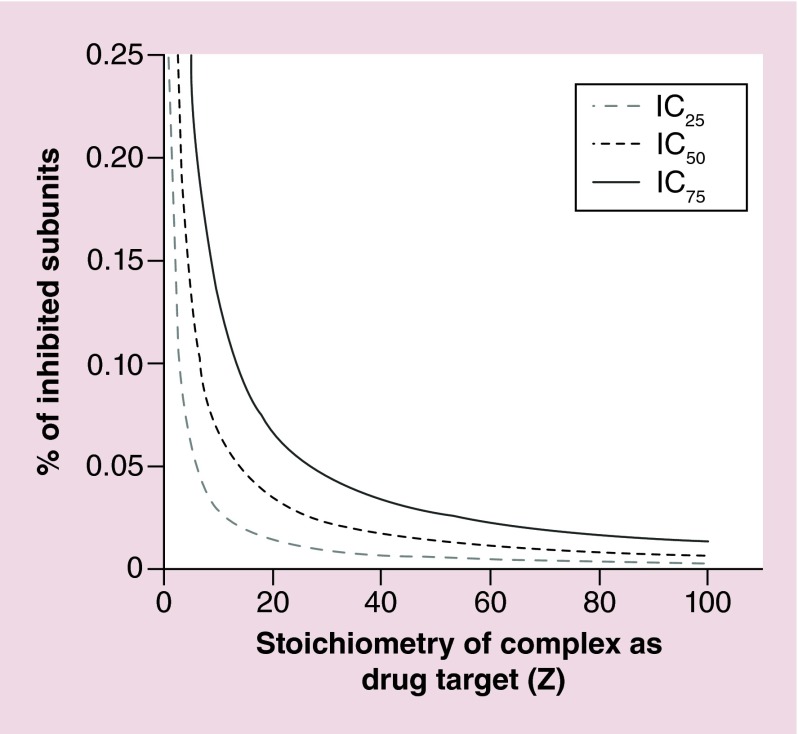
In vitro testing of the hypothesis using ATP with stoichiometry of more than 10,000

It has been reported that six ATP molecules are required to package one pitch of dsDNA with 10.5 bp [91], thus 1 ATP is used to package 1.7 bp. As the entire phi29 genomic DNA has 19,000 base pairs, it is expected that more than 10,000 ATP molecules are required to package the entire phi29 genome. The functional viral production unit displayed in Figure 5 is expressed as PFU, and production of one functional unit of PFU require 10,000 ATP subunits to package one genomic DNA. Thus, the ATP in one phi29 nanomotor can be regarded as a stoichiometry of 10,000. One nonhydrolysable ATP analog γ-S-ATP was treated as the drugged subunit that mixed with ATP at different ratios to test the inhibition effect of γ-S-ATP on phi29 assembly efficiency. It was found that the inhibition curve of mutant ATP fits into the theoretical curve between Z = 100, K = 1 and Z = 60, K = 1 (Figure 5B). The empirical ATP value derived from binomial distribution assay was different from real condition, since the binomial distribution equation was based on a condition that each subunit has the same binding affinity to the biocomplex in the targeted nanomotor, but due to the change of the γ-S-ATP structure, it has a ATPase gp16 binding affinity lower than the normal ATP. Furthermore, the affinity difference in each subunit has a multiplicative effect in the nanomotor's activity. Thus, there is a big discrepancy between the curves with predicted Z value and the empirical Z value.

Comparing virus assembly inhibition effect using different components, the γ-S-ATP showed a severe inhibition effect (Figure 5C). Adding 20% of γ-s-ATP nearly completely inhibited the viral assembly. Comparing the inhibition effect targeting to ATP, pRNA, ATPase gp16 and DNA with stoichiometry of 10,000, 6, 6 and 1, respectively, γ-S-ATP showed the strongest inhibition effect, while drugged mutant pRNA and mutant gp16 showed stronger inhibitory effect than mutant DNA (Figure 5C). For example, adding 20% mutant DNA caused 20% inhibition effect in viral assembly, while 20% of drugged mutant pRNA exerted 74% of inhibition effect on viral assembly and 20% of γ-S-ATP almost completely inhibited the viral assembly, indicating the higher the stoichiometry, the stronger the inhibition efficacy.

Mathematical reasoning for the increase of inhibition efficacy

Using a biological complex with higher stoichiometry as drug target will substantially reduce the proportion of noninhibited complex. For K = 1, the proportion of noninhibited complex is q^Z. Table 3 compares the proportion of noninhibited complex from two populations with Z = 6 and Z = 1, respectively, with varied substrate targeting efficiency (p) when K = 1. For example, when q = 0.4, the proportion of noninhibited complex is q^Z = 0.4¹ = 0.4 for Z = 1, K = 1. Therefore, only 1–0.4 = 60% of complex is inhibited. In contrast, for Z = 6, K = 1, the proportion of noninhibited complex is q^Z = 0.4⁶ = 0.0041. Therefore, 1–0.0041 = 99.59% of complex is inhibited. The ratio of the proportions of noninhibited complex equals 0.0041/0.4 = 0.0102, indicating a 1/0.0102 = 98-fold decrease in the proportion of noninhibited complex. One more example is to use the drug targeting efficiency p = 0.9 to compare the inhibition efficiency between two groups with Z = 6 and Z = 1. For Z = 6, K = 1, the proportion of inhibited complex is 1-q^Z = 1–0.1⁶ = 0.999999. The proportion of noninhibited complex is q^Z = 0.1⁶ = 1E-6. For Z = 1, K = 1, the proportion of inhibited complex is 1-q^Z = 1–0.1 = 0.9. The proportion of noninhibited complex is q^Z = 0.1. The ratio of inhibition efficiency equals to 1E-6/0.1 = 1E-5, indicating a 10,000-fold increase in inhibition efficiency (Table 3).

Table 3. . Comparison of proportion of noninhibited complex between Z = 6 and Z = 1 when K = 1 but having equal drug targeting efficacy.

Substrate targeting efficacy (p)	Proportion of noninhibited complex from the population with Z = 6	Proportion of noninhibited complex from the population with Z = 1	Ratio of the proportions of noninhibited complex from the two populations with Z = 6 and Z = 1	Reduction (fold) in proportion of noninhibited complex comparing Z = 6 and Z = 1
0	1	1	1	1
0.1	0.5314	0.9	0.5905	1.7
0.2	0.2621	0.8	0.3277	3.1
0.3	0.1176	0.7	0.1681	5.9
0.4	0.0467	0.6	0.0778	12.9
0.5	0.0156	0.5	0.0312	32
0.6	0.0041	0.4	0.0102	98
0.7	7E-04	0.3	0.0024	416
0.8	1E-04	0.2	0.0003	3333
0.9	1E-06	0.1	1E-05	10,000

The equation displays inhibitory effect with a power function of stoichiometry since when K = 1, the percentage of uninhibited biocomplexes in the population equal to q^z. Since (P + q) = 1, thus q ≤ 1, thus the larger the Z, the smaller the value of q^z. That is to say, the higher the stoichiometry, the smaller number of the uninhibited background will display. With the same substrate targeting efficacy, p, the inhibition efficiency is determined by z, the power of the component. The inhibitory effect is a power function concerning the stoichiometry. Thus, the higher the stoichiometry, the more efficient the inhibition comparing the drugs with same binding affinity.

The half maximal inhibitory concentration (IC₅₀) is commonly used to evaluate drug effect, which quantitatively indicates how much of a particular drug is needed to inhibit a given biological process by half. If we denote p_IC150 as the percentage of drugged subunit needed to reach to 50% inhibition in the in vitro assay in the defined system, thus 1-(1-p_IC150)^Z = 50%. Solving this equation, p_IC150 = 1-0.5^1/Z. Figure 6 shows the relationship between stoichiometry (Z) and drug targeting level p to reach the inhibition effect (IC), where p is the combined result of drug binding efficacy and drug concentration (dosage). When biocomplexes with stoichiometry of Z are used as drug targets, the dosage of drug or the drug binding affinity presented by percentage of drugged subunits to reach IC₅₀, IC₂₅ or IC₇₅ decreases. This clearly shows that as Z increases, p_IC150 decreases (Figure 6) and hence the drug is more potent.

Figure 6. . Relationship between stoichiometry (Z) and drug targeting level (p, a combined result of drug binding efficacy and drug concentration) to reach the inhibition effect (IC).

Discussion

Aiming to find a method for developing drugs with ultra-high potency, we proposed that the inhibition efficiency of a given drug depends on stoichiometry of the biocomplex or biomachine that was used as drug target. Here the definition of the stoichiometry is different from conventional definition of stoichiometry used to evaluate drug efficiency. Conventional thinking in drug development emphasizes stoichiometry which refers to the number of drug binding per target molecule, which is also known as B_max. In this study the definition of stoichiometry refers to the copy number of subunit within a biocomplex that serves as drug target. We used phi29 viral components with a series of variable but known stoichiometry as mock drug targets to test the hypothesis. Both in vitro and in vivo virion assembly assays were employed to compare the inhibition efficiency targeting to components with different numbers of subunit stoichiometry. Viral inhibition efficiency was analyzed with Yang Hui's (Pascal's) Triangle (or known as binomial distribution). It was found that inhibition efficiency on virus replication correlates to the component stoichiometry of nanomachine as drug target. It displayed power law inhibitory effect since when K = 1, the percentage of uninhibited biocomplexes in the population equal to q^z. With the same q and same K value, the inhibition efficiency is determined by z, the number of subunits within the biocomplex or the bio-machine as drug target. Here z serves as the power in the equation, thus, the inhibitory effect is the power of the stoichiometry. Empirical data demonstrated that the target with thousand subunits shows higher inhibition effect than the targets with six subunits and in turn higher than the target with single subunit.

In evaluation of drug effect, two parameters were commonly used. One is the half maximal inhibitory concentration (IC₅₀), which quantitatively indicates how much of a particular drug is needed to inhibit a given biological process by half. It is universally used as a measure of drug potency in pharmacological research. Another important parameter is the median lethal dose (LD₅₀), which is also known as 50% of lethal concentration (LC₅₀). LD₅₀ is frequently used to indicate a substance's acute toxicity. Obviously, the usefulness of a drug will dependent on the ratio of LD₅₀ to IC_50. The larger this ratio, the safer the drug. By ways of increasing the inhibition efficiency through targeting to the components with high stoichiometry, the IC₅₀ of a drug will decrease. As a result, lower concentration of drug will be required for reaching a desired effect, resulting in a reduced toxicity of the drug.

Most of current anticancer, antivirus or antibacteria drugs target single enzymes or single proteins. Our data showed that drugs selected to target components, biocomplexes or nanomachines with high copy numbers could lead to a much higher efficacy, and it could potentially solve the problem of low drug effect and multidrug resistance.

Conclusion

Targeting the functional biological units with higher stoichiometries will have a higher efficiency of inhibition. The inhibition effect is power, other than proportional, to the copy number of the drug-targeted element of the machine. The new theory developed herein suggests that potent drugs can be developed by targeting biocomplex with high stoichiometry, and a complete inhibition of virus, bacterium or cancer is possible if a biomachine with high stoichiometry is identified. Since biomotors share certain common structure and operation mechanism in viruses, bacteria and cells, this approach should have general application in drug development.

Future perspective

Living systems contain many elegant arrays, motors and nanomachines that are multisubunit complex. As reported here, these biocomplex with high copy number of components can serve as potent drug targets. For example, most members of the AAA+ family are hexamer [19,88–89,107–109]. However, these machines are common in living systems therefore the specificity and toxicity is an issue. For bacteria and virus, since our goal is to kill them nonexclusively, the specificity and toxicity is not an issue as long as the target biocomplex is not identical to that in human body. For cancers drugs, as long as a mutation is found in the multiple-subunit biocomplex, it will be an ideal target for potent drug.

Executive summary.

Aim

• A method for developing potent drugs is sought.

Hypothesis

• Drug inhibition potency depends on the stoichiometry of the targeted biocomplex.

Approach

• Phi29 viral components with variable stoichiometry were used as model to prove the hypothesis

• Virion assembly efficiency was assayed and analyzed with Yang Hui's Triangle:

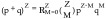
Results

• Inhibition efficiency displayed a power function of the stoichiometry of the target biocomplexes. The uninhibited biocomplex in population can equals to q^z. Thus, the inhibitory effect is a power of the stoichiometry.

• Targets with thousand subunit showed higher inhibition effect than with six subunits, and in turn higher than target with single subunit.

• A complete inhibition of virus, bacterium or cancer was demonstrated when targets with high stoichiometry was used as target.

Conclusion

• Drug inhibition potency depends on the stoichiometry of the targeted components of the biocomplex or nanomachine.

• The inhibition effect displayed a power function of the stoichiometry of the target biocomplex.

• Since biomotors share certain common structure and operation mechanism in viruses, bacteria and cells, this approach should have general application in drug development.