A continuous linear optimal transport approach for pattern analysis in image datasets

Abstract

We present a new approach to facilitate the application of the optimal transport metric to pattern recognition on image databases. The method is based on a linearized version of the optimal transport metric, which provides a linear embedding for the images. Hence, it enables shape and appearance modeling using linear geometric analysis techniques in the embedded space. In contrast to previous work, we use Monge's formulation of the optimal transport problem, which allows for reasonably fast computation of the linearized optimal transport embedding for large images. We demonstrate the application of the method to recover and visualize meaningful variations in a supervised-learning setting on several image datasets, including chromatin distribution in the nuclei of cells, galaxy morphologies, facial expressions, and bird species identification. We show that the new approach allows for high-resolution construction of modes of variations and discrimination and can enhance classification accuracy in a variety of image discrimination problems.

1. Introduction

Automated pattern learning from image databases is important for numerous applications in science and technology. In the health sciences arena, biomedical scientists wish to understand patterns of variation in white and gray matter distributions in the brains of normal versus diseased volunteers from magnetic resonance images (MRI) [26,27]. Pathologists wish to understand patterns of morphological variations between benign versus malignant cancer cell populations through a variety of microscopy techniques [28,30]. Other applications include morphometrics [31], the analysis of facial images [32,17], and the analysis of mass distributions in telescopic images of galaxies [14]. The goal is usually related to discovery and understanding any discriminant pattern among different classes. More specifically, the objective in many morphometry-related applications is to determine whether statistically significant discriminating information between two or more classes (e.g. benign vs. malignant cancer cells) exists. If so, it is also often desirable to determine through visualization the nature (e.g. biological interpretation) of the found differences.

Numerous image analysis methods have been described to facilitate discrimination and understanding from image databases. A critical step in this process is the choice of an image similarity (or distance) criterion, based on which image clustering, classification and related analysis can be performed. While the Euclidean distance between pixel intensities (after images are appropriately normalized for rotation and other uninteresting variations) remains a viable alternative in many cases [45], typically employed distances involve the extraction of numerical descriptors or features for the images at hand. In many applications [14,33], feature-based distances lead to high performance and accurate image classification. Feature-based methods commonly incorporate shape-related features [34], texture-related features [44], such as Haralick and Gabor features, derived based on the adaptations of Fourier and Wavelet transforms [46,35], and others [47]. Most feature-based approaches, however, are not ‘generative’ and thus any statistical modeling performed in feature space is not easily visualized. This can be readily understood by noting that the transformation (from the ambient image space to feature space) is not invertible: one can extract features from images, though it is not generally possible to obtain an image from an arbitrary point in feature space.

In analyzing shape distributions obtained from image data, numerous approaches based on differential geometry have been employed. Grenander et al. [37], for example, have described methods for comparing the shape of two brains (or brain structures) by minimizing the amount of incremental ‘effort’ required to deform one structure onto another. Likewise, Joshi et al. [38], and Klassen et al. [39] have described similar approaches for determining the distance between two shapes as encoded by medial axis models and contours, respectively. Such approaches are not only capable of measuring differences between shapes without loss of information, but are also generative and thus allow for interpolating between shape exemplars, thus giving researchers access to geometrical properties of shape distributions from image databases. It is worthwhile noting that the approaches described in these references, however, do not allow for one to encode information regarding intensity variations, or texture. Moreover, such approaches can be computationally expensive to employ in pattern recognition tasks on large datasets.

Active appearance models [7,8] and Morphable Models [48] are another class of approaches that can be used for modeling shape and intensity variations in a set of images. Such methods are parametric, nonlinear, and generative. However, these methods require the definition of characteristic landmarks, as well as the correspondence between the landmarks of all images in the set.

Finally, we also mention that several graph-based techniques have also been developed for interpreting variations in image databases. The idea in such methods is to obtain an understanding of the geometric structure of such variations by applying manifold and graph connectivity learning algorithms [40,41]. These methods find a linear embedding for the images, which preserve the local structure of the data in the image space. Such approaches have been often employed in studying variations in image databases [40]. We note that, generally speaking, such methods are not generative. As with the numerical feature approach above, it is generally not possible to reconstruct an image corresponding to any arbitrary point in feature space (other than images present in the same dataset).

1.1. Previous work on linear optimal transport (LOT)

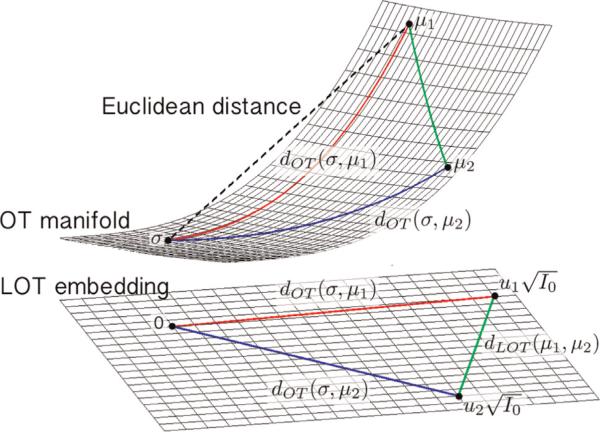
In [21,22] we have recently introduced a new approach based on the mathematics of optimal transport (OT) for performing discrimination and visualizing meaningful variations in image databases. Interpreting images as nonnegative measures one can employ the Kantorovich–Wasserstein distance to measure the similarity between pairs of images. The metric space is formally a Riemannian manifold [42] where at each point one can define a tangent space endowed with an inner product. The OT distance is then the length of the shortest curve (geodesic) connecting two images (see Fig. 1). The linear optimal transport (LOT) idea presented in [21] involves computing a modified version of the OT metric between images by first computing the necessary optimal transport plans between each image and a reference point, and then quantifying the similarity between the two images as a functional of computed transport plans. The idea is depicted in Fig. 1.

Fig. 1.

The geometry of the OT manifold and the LOT embedding.

In short, the LOT framework initially proposed in [21], and refined in [22] for the analysis of cell images can be viewed as a new nonlinear image transformation method. The ‘analysis’ portion of the transform consists of computing a linear embedding for given images by finding the transport plans from images to a reference image. In this manner, each point in the embedding corresponds to a transport plan that maps an image to the reference image. The ‘synthesis’ operation relates to computing the image corresponding to a point in the embedding.

One of the major benefits of this signal transformation framework is that it facilitates the application of the OT metric to pattern recognition on image databases. If a given pattern recognition task (e.g. clustering or classification) requires all pairwise distances for a given database of N images to be computed, one can compute the LOT distance between them with only N optimal transport problems, as opposed to the usual N(N – 1)/2 computations that would be required in the standard approach [20]. Beyond just an improvement in computation time, the LOT image transformation framework also allows for the unification of the discrimination and visualization tasks. Discrimination using Euclidean distances in the LOT space are akin to a modified (linearized) version of the transport metric, described as a generalized geodesic by Ambrosio et al. [43], and have been shown to be very sensitive in capturing the necessary information in a variety of discrimination tasks [21,22]. In addition, given that the new transformation framework is invertible, the framework also allows for the direct visualization of any statistical modeling (e.g. principal component analysis and linear discriminant analysis) in the embedding. This enables direct visualization of important variations in a given database.

1.2. Contribution highlights

The work described in [21,22] utilizes Kantorovich's formulation of the OT problem in a discrete setting (particle-based). That is, images are viewed as mass distributions and modeled as sums of discrete delta ‘functions’ placed throughout the image domain. The underlying OT problem then simplifies to a linear programming problem and is solved using existing approaches. The method in [21,22] is, however, computationally expensive as the computational complexity of linear programming solvers is generally of polynomial order (w.r.t. number of particles) and in addition it requires an initial particle approximation step.

Here we improve the work in [21,22] by utilizing Monge's formulation of the underlying OT problem. In particular, we highlight the following contributions:

• We describe a continuous version of the LOT framework that bypasses many of the difficulties associated with the discrete formulation. In this respect, we define a forward and inverse transform operation based on continuous transport maps, define an improved reference estimation algorithm, as well as describe the range within which points in LOT space are invertible according to the continuous formulation.

• We show experimentally that the new formulation significantly speeds up the computation of the LOT embedding for a set of images.

• We demonstrate that (in contrast to the previous method), the new method allows for reliable information extraction from high resolution, non-sparse, images.

• We demonstrate that the method performs well in comparison to other methods in several discrimination tasks, while at the same time allowing for meaningful generative modeling and visualization.

We start by reviewing the LOT framework, and then describe the nonlinear minimization technique we use, in Sections 2 and 3. Section 4 describes our approach for computing the LOT embedding using the continuous OT maps between each image and a template in a given dataset. In Section 5 we describe how to combine the LOT embedded images together with PCA and penalized LDA to visualize meaningful information in different datasets. We describe the datasets used in this paper and demonstrate the output of our LOT framework by showing modes of variations, discrimination modes, and classification results for all the datasets, in Section 6. Finally, the paper is summarized and our contributions are highlighted in Section 7.

2. Linearized optimal transport

Optimal transport methods have long been used to mine information in digital image data (see for example [36]). The idea is to minimize the total amount of mass times the distance that it must be transported to match one exemplar to another. Let μ₁ and μ₂ be two nonnegative probability measures defined over a 2D domain Ω such that μ₁(Ω) = μ₂(Ω) = 1. Let Π(μ₁, μ₂) be the set of all couplings between the two measures. That is, let A and B be measurable subsets of Ω, and let π ∈ Π(μ₁, μ₂). Then π(A × B) describes, how ‘mass’ originally in set A in measure μ₁ is transported to set B in measure μ₂ so that all mass in μ₁ can be transported to the same configuration as the mass in μ₂. The optimal transport plan, with quadratic cost, between μ₁ and μ₂ is given as the minimizer of

$$d_{OT}^2({\mu }_1,{\mu }_2)=\underset{\pi \in \prod ({\mu }_1,{\mu }_2)}{\inf }{\int }_{\Omega \times \Omega }{\mid {\overrightarrow{x}}_1-{\overrightarrow{x}}_2\mid }^{2}d\pi .$$ (1)

where ${\overrightarrow{x}}_1$ and ${\overrightarrow{x}}_2$ are coordinates in domains of μ₁ and μ₂, respectively, and | · | denotes the Euclidean norm. In Wang et al. [21] a linearized version of the OT metric is described, which is denoted as the linear optimal transportation (LOT), based on the idea of utilizing a reference measure σ. Let π_μi denote a transport plan between σ and μ_i. In addition, let Π(σ,μ₁,μ₂) be the set of measures such that if π ∈ Π(σ,μ₁,μ₂), π(A × B × Ω) = π_μ1 (A × B), and π(A × Ω × C) = π_μ2 (A × C). Then, in the most general setting, the LOT can be defined as

$$\underset{\pi \in \prod (\sigma ,{\mu }_1,{\mu }_2)}{\inf }{\int }_{\Omega \times \Omega \times \Omega }{\mid {\overrightarrow{x}}_1-{\overrightarrow{x}}_2\mid }^{2}d\pi .$$ (2)

In [21] a ‘particle’-based approach is utilized for computing (2). The idea is to first approximate the measures μ₁, μ₂ and σ using a weighted linear combination of masses and compute (2) by solving the associated linear program [21]. Because linear programs are expensive to compute (generally scale as O(n³), where n is the number of particles used to approximate the image), Wang et al. proposed a particle approximation algorithm to reduce the number of pixels in each image prior to computation.

Instead, here we describe an extension of the LOT computation to the set of smooth densities, together with a few additional modifications required by the continuous formulation, that can significantly reduce the computational complexity while at the same time allowing transport maps to be computed at full image resolution. Let μ₁, μ₂, and σ be smooth measures on Ω with $d\sigma =I_{0}d\overrightarrow{x}$, $d{\mu }_1=I_{1}d\overrightarrow{x}$ and $d{\mu }_2=I_{2}d\overrightarrow{x}$, where I₀, I₁ and I₂ are the corresponding densities. Monge's formulation of the OT problem between σ and μ₁, for example, is to find a spatial transformation (a map) $f_1\left(\overrightarrow{x}\right)=\overrightarrow{x}-u_1\left(\overrightarrow{x}\right)$ that minimizes

$$d_{OT}^2(\sigma ,{\mu }_1)=\underset{f_1}{\inf }{\int }_{\Omega }{\mid f_1\left(\overrightarrow{x}\right)-\overrightarrow{x}\mid }^2{I}_0\left(\overrightarrow{x}\right)d\overrightarrow{x}$$ (3)

subject to the constraint that the map f₁ pushes measure μ₁ into measure σ. When the mapping is smooth, this requirement can be written in differential form as

$$\det \left(D_{f_1}\left(\overrightarrow{x}\right)\right)I_1\left(f_1\left(\overrightarrow{x}\right)\right)=I_0\left(\overrightarrow{x}\right),$$ (4)

where D_f1 is the Jacobian matrix of f₁. Eq. (4) specifies the mass preserving property that the mapping must have. In addition, we note that f₁ is a 2D map: $f_1\left(\overrightarrow{x}\right)={[f_1^x\left(\overrightarrow{x}\right),f_1^y\left(\overrightarrow{x}\right)]}^T$, with f₁^x and f₁^y denoting the x and y components of the map, respectively. Similarly, we note that $u_1\left(\overrightarrow{x}\right)={[u_1^x\left(\overrightarrow{x}\right),u_1^y\left(\overrightarrow{x}\right)]}^T$, where u₁^x and u₁^y are displacement fields in the x and y directions, respectively. Now let us similarly define $f_2\left(\overrightarrow{x}\right)=\overrightarrow{x}-u_2\left(\overrightarrow{x}\right)$ as the continuous OT mapping between σ and μ₂.

Using $f_1\left(\overrightarrow{x}\right)$ and $f_2\left(\overrightarrow{x}\right)$ in Eq. (2), the LOT distance between measures μ₁ and μ₂ with respect to the reference measure σ can be written as

$$d_{LOT}^2({\mu }_1,{\mu }_2)={\int }_{\Omega }{\mid f_1\left(\overrightarrow{x}\right)-f_2\left(\overrightarrow{x}\right)\mid }^2{I}_0\left(\overrightarrow{x}\right)d\overrightarrow{x}={\int }_{\Omega }{\mid u_1\left(\overrightarrow{x}\right)-u_2\left(\overrightarrow{x}\right)\mid }^2{I}_0\left(\overrightarrow{x}\right)d\overrightarrow{x}={\int }_{\Omega }{\mid u_1\left(\overrightarrow{x}\right)\sqrt{I_0\left(\overrightarrow{x}\right)}-u_2\left(\overrightarrow{x}\right)\sqrt{I_0\left(\overrightarrow{x}\right)}\mid }^{2}d\overrightarrow{x}={\Vert u_1-u_2\Vert }_{\sigma }^2$$ (5)

where ${\Vert g\Vert }_{\sigma }={\left({\int }_{\Omega }{\mid g\left(x\right)\mid }^2{I}_0\left(x\right)dx\right)}^{1∕2}$. Thus the functions $\sqrt{I_0}$ and $\sqrt{I_0}$ are natural isometric linear embeddings (with respect to the LOT) for I₁ and I₂, respectively.

From the geometric point of view, the LOT transform can be viewed as the identification (projection), P, of the OT manifold on the tangent space at σ. Hence, given a measure μ_i with the optimal transport map f_i (with respect to σ) we have

$$P\left({\mu }_i\left(\overrightarrow{x}\right)\right)=u_i\left(\overrightarrow{x}\right)\sqrt{I_0\left(\overrightarrow{x}\right)}$$ (6)

where $u_i\left(\overrightarrow{x}\right)=\overrightarrow{x}-f_i\left(\overrightarrow{x}\right)$. See Fig. 1 for a visualization. From (6) we have $P\left(\sigma \right)=0$ and we can write

$$d_{LOT}({\mu }_i,\sigma )={\Vert P\left({\mu }_i\right)-P\left(\sigma \right)\Vert }_{\sigma }={\Vert P\left({\mu }_i\right)\Vert }_{\sigma }={\left({\int }_{\Omega }{\mid f_i\left(\overrightarrow{x}\right)-\overrightarrow{x}\mid }^2{I}_0\left(\overrightarrow{x}\right)d\overrightarrow{x}\right)}^{1∕2}=d_{OT}({\mu }_i,\sigma )$$ (7)

therefore, P preserves the OT distance between μ_i and σ.

3. Optimal transport minimization

There exist several algorithms for finding an estimate of the solution to the OT problem. Haker et al. [11] utilized a variational approach for computing a transport map by minimizing the problem in (3), while Wang et al. [20,21], for example, made use of Kantorovich's formulation of the problem in a discrete setting (2) to achieve a solution based on linear programming. Benamou et al. [3] solved the OT problem by resetting the problem into a continuum mechanics framework. More recently, Chartrand et al. [5] introduced a gradient descent solution to the Monge–Kantorovich problem, which solves the dual problem. In another interesting approach toward solving the OT problem, Haber et al. [10] reformulated the problem as a penalized projection of an arbitrary mapping onto the set of mass preserving mappings. In this paper, we show that the LOT approach, introduced in [21], can be extended to use the continuous formulation in (3), thus allowing for the use of full resolution images hitherto impossible with the state of the art methods. We employ the generic approach as described in [11]. Given densities I₀ and I₁, the method works by first finding an initial measure preserving ‘guess’, that is det$\left(D_{f_0}\left(\overrightarrow{x}\right)\right)I_1\left(f_0\left(\overrightarrow{x}\right)\right)=I_0\left(\overrightarrow{x}\right)$, and then minimizing (3) based on a partial differential equation approach.

3.1. Finding an initial measure preserving (MP) map

We follow the approach described in [11], originally proposed in [13], for finding an initial measure preserving map. Briefly, the initial measure preserving map can be found by solving a series of 1D problems. In 1D, the OT solution can be found by simply computing the points along the line where the integrals of the two functions coincide. In 2D, the initial mapping can be found by solving a series of 1D problems as described below.

Let Ω = [0,1]² and I₀ and I₁ be the two density maps (images) one wishes to compare through the OT approach. In order to find an initial MP map, $f_0\left(\overrightarrow{x}\right)=\overrightarrow{x}-u_0\left(\overrightarrow{x}\right)$ we first find the transportation map parallel to the x-axis, a(x):

$${\int }_0^{a\left(x\right)}{\int }_0^1{l}_1(\eta ,\rho )d\eta d\rho ={\int }_0^x{\int }_0^1{I}_0(\eta ,\rho )d\eta d\rho ,$$ (8)

Then the transport map along the y-axis, b(x,y), is calculated by differentiating the equation above with respect to η and solving for b(a(x),y):

$$\frac{\partial a\left(x\right)}{\partial x}{\int }_0^{b(a\left(x\right),y)}{I}_1(a\left(x\right),\rho )d\rho ={\int }_0^y{I}_0(x,\rho )d\rho ,$$ (9)

and hence $f_0\left(\overrightarrow{x}\right)=[a\left(\overrightarrow{x}\right),b\left(\overrightarrow{x}\right)]$. In practice, $a\left(\overrightarrow{x}\right)$ and $b\left(\overrightarrow{x}\right)$ cab be found with simple numerical integration techniques.

3.2. Optimal transport minimization

We employ a fundamental theoretical result [4,9] which states that there is a unique optimal MP mapping f* that minimizes Eq. (3), and it can be written as the gradient of a convex function $p:\Omega \to \mathbb{R},f^{\ast }=\nabla p$, and hence it is curl free. Once an initial mapping f₀ is found, we follow a gradient descent process [11] to make f₀ curl free. We use the closure under composition and closure under inversion properties of the MP mappings [11] and define $f≔f_0\left(s^{-1}\left(\overrightarrow{x}\right)\right)$. Note that f is a MP mapping from I₀ to I₁, if and only if s is a MP mapping from I₀ to itself, meaning that

$$\det \left(D_s\left(\overrightarrow{x}\right)\right)I_0\left(s\left(\overrightarrow{x}\right)\right)=I_0\left(\overrightarrow{x}\right).$$ (10)

Now we update $s(\overrightarrow{x},t)$, starting from $s(\overrightarrow{x},0)=\overrightarrow{x}$, such that $f_0\left(s^{-1}(\overrightarrow{x},t)\right)$ converges to a curl free mapping from I₀ to I₁. For $s(\overrightarrow{x},t)$ to be a MP mapping from I₀ to itself, $\partial s∕\partial t$ should have the following form:

$$\frac{\partial s}{\partial t}=\left(\frac{1}{I_0}\xi \right)\circ s,$$ (11)

for some vector field ξ on Ω with div(ξ) = 0 and $\langle \xi ,\overrightarrow{n}\rangle =0$ on $\partial \Omega$, where $\overrightarrow{n}$ is normal to the boundary of Ω. From (11), it follows that for $f(\overrightarrow{x},t)=f_0\left(s^{-1}(\overrightarrow{x},t)\right)$ to be a MP mapping from I₀ to I₁ we need

$$\frac{\partial f}{\partial t}=-\frac{1}{I_0}{D}_f\xi .$$ (12)

Differentiating the OT objective function,

$$M={\int }_{\Omega }{\Vert f(\overrightarrow{x},t)-\overrightarrow{x})\Vert }^2{I}_0\left(\overrightarrow{x}\right)d\overrightarrow{x}.$$ (13)

with respect to t and after rearranging we have

$$\frac{\partial M}{\partial t}=-2{\int }_{\Omega }\langle f(\overrightarrow{x},t),I_0\left(\overrightarrow{x}\right)\left(\frac{\partial s}{\partial t}\circ s^{-1}(\overrightarrow{x},t)\right)\rangle d\overrightarrow{x}.$$ (14)

Substituting (11) into the above equation we get

$$\frac{\partial M}{\partial t}=-2{\int }_{\Omega }\langle f(\overrightarrow{x},t),\xi (\overrightarrow{x},t)\rangle d\overrightarrow{x}.$$ (15)

Writing the Helmholtz decomposition of f as $f=\nabla \varphi +\chi$ and using the divergence theorem we get

$$\frac{\partial M}{\partial t}=-2{\int }_{\Omega }\langle \chi (\overrightarrow{x},t),\xi (\overrightarrow{x},t)\rangle d\overrightarrow{x},$$ (16)

thus, ξ = χ decreases M the most. But to find χ we first need to find ϕ. Given that div(χ) = 0 and $\langle \chi ,\overrightarrow{n}\rangle =0$, we take the divergence of the Helmholtz decomposition of f and we find ϕ from

$$\{\begin{array}{c}\Delta \left(\varphi \right)=\mathrm{div}\left(f\right)\hfill \\ \langle \nabla \varphi ,\overrightarrow{n}\rangle =\langle f,\overrightarrow{n}\rangle \mathrm{on}\partial \Omega .\hfill \end{array}\phantom{\}}$$ (17)

Hence, $\xi =f-\nabla \left({\Delta }^{-1}\mathrm{div}\left(f\right)\right)$ where Δ⁻¹ div(f) is the solution to (17). Substituting ξ back into (12) we have

$$\frac{\partial f}{\partial t}=-\frac{1}{I_0}{D}_f(f-\nabla \left({\Delta }^{-1}\mathrm{div}\left(f\right)\right)),$$ (18)

which for $f\in {\mathbb{R}}^2$ can be even simplified further:

$$\frac{\partial f}{\partial t}=-\frac{1}{I_0}{D}_f{\nabla }^{\perp }{\Delta }^{-1}\mathrm{di}v\left(f^{\perp }\right).$$ (19)

where $\perp$ indicates rotation by 90°. Finally, the MP mapping is updated using the gradient descent approach as follows:

$$f(\overrightarrow{x},t+1)=f(\overrightarrow{x},t)+\alpha \frac{1}{I_0\left(\overrightarrow{x}\right)}{D}_f{\nabla }^{\perp }{\Delta }^{-1}\mathrm{div}\left(f^{\perp }(\overrightarrow{x},t)\right)$$ (20)

where α is the gradient descent step. In our implementation α is found based on a backtracking line search approach. The gradient descent method described above is shown to converge to the global optimum [1]. This method can be thought of as a gradient descent approach on the manifold of the MP mappings from I₀ to I₁.

4. Calculating LOT embedding from optimal transport maps

The linear embedding, as explained in Section 2, is calculated with respect to the template image I₀. Given a set of images I₁,...,I_N, I₀ is initially set to the average image via $I_0=1∕N{\sum }_{i=1}^N{I}_k$. The set of OT maps that transform each image I_k into I₀ is computed via the OT minimization procedure described above. Having the mappings $f_k\left(\overrightarrow{x}\right)$ for k = 1 ··· N, the reference (template) image is updated iteratively using the mean optimal transport map. This iterative approach helps ‘sharpen’ the estimated template as well as have it be a more representative intrinsic ‘mean’ image for the given dataset. Fig. 2shows the calculated mean using the mentioned approach as well as the average image for a set of images including 40 faces with neutral expressions. The increase in sharpness is clearly evident.

Fig. 2.

Calculated mean image (a) and the average image (b) for the 40 neutral faces.

The outcome of this procedure is used as the ‘reference’ template I₀, and the corresponding mappings f_k, k = 1, ..., N such that det$\left(D_{f_k}\left(\overrightarrow{x}\right)\right)I_k\left(f_k\left(\overrightarrow{x}\right)\right)=I_0\left(\overrightarrow{x}\right)$ are calculated for the I₀. The LOT embedding for an image I_k, as described in Section 2, is given by $u_k\left(\overrightarrow{x}\right)\sqrt{I_0\left(\overrightarrow{x}\right)}$. This linear embedding can now be used for a variety of purposes, including clustering and classification, as well as visualization of main modes of variation, as we show below.

We emphasize that in contrast to other ‘data driven’ methods [16,2] for computing a linear embedding of a nonlinear dataset, the LOT embedding is generative. Meaning that, one is not only able to visualize any original image, but also able to visualize any point in the LOT space (subject to the constraint described in the next section) to obtain a synthetic image, which lays on the OT manifold in the image space. Let $v\left(\overrightarrow{x}\right)$ correspond to the displacement field of an arbitrary point in LOT space. Its corresponding image is computed by setting $f_v\left(\overrightarrow{x}\right)=\overrightarrow{x}-v\left(\overrightarrow{x}\right)$, and then computing the corresponding image I_v by

$$I_v\left(\overrightarrow{x}\right)=\det {\left(D_{f_v}\left(f_v^{-1}\left(\overrightarrow{x}\right)\right)\right)}^{-1}{I}_0\left(f_v^{-1}\left(\overrightarrow{x}\right)\right)=\det \left(D_{f_v^{-1}}\left(\overrightarrow{x}\right)\right)I_0\left(f_v^{-1}\left(\overrightarrow{x}\right)\right)$$ (21)

where $f_v^{-1}$ refers to the inverse transformation of f_v, such that $f_v^{-1}\left(f_v\left(\overrightarrow{x}\right)\right)=\overrightarrow{x}$. Eq. (21) shows that, any arbitrary point in LOT space, with corresponding displacement field $v\left(\overrightarrow{x}\right)$, is visualizable if and only if D_fv is not singular, and hence f⁻¹ exists. Next, we devise an approach which gives us the visualizable range in the LOT space.

4.1. Visualizable range in the LOT space

We utilize an orthogonal expansion in order to describe a visualizable range for the LOT embedding computed with respect to a chosen reference. Let the mean displacement field for the embedded images be $\overline{u}\left(\overrightarrow{x}\right)=(1∕N){\sum }_k{u}_k\left(\overrightarrow{x}\right)$. Now let [v₁,...,v_M] be an orthonormal basis for the zero mean displacement fields, $[u_1-\overline{u},\dots ,u_N-\overline{u}]$. Such a basis can be obtained using PCA or a Gramschmidt orthogonalization process, for example. Hence, the displacement field of an arbitrary point in LOT space can always be written as follows:

$$v\left(\overrightarrow{x}\right)=\overline{u}\left(\overrightarrow{x}\right)+\beta \sum _k{c}_k{v}_k\left(\overrightarrow{x}\right)$$ (22)

where c_ks are coefficients of linear combination with $\sqrt{{\sum }_k{c}_k^2}=1$, and β is a constant which corresponds to the range of change in the direction of ${\sum }_k{c}_k{v}_k$. Therefore we can rewrite the mapping as below:

$$f_v\left(\overrightarrow{x}\right)=\overline{f}+\beta \sum _k{c}_k{f}_k$$ (23)

where $\overline{f}=\overrightarrow{x}-\overline{u}\left(\overrightarrow{x}\right)$ and $f_k=\overrightarrow{x}-v_k\left(\overrightarrow{x}\right)$. The goal is to find the maximum β, for the D_fv remains nonsingular, or in other words, det$\left(D_{f_v}\left(\overrightarrow{x}\right)\right)\ne 0$ for all x ∈ Ω. Expanding det(D_fv) and after rearranging one can write

$$\det \left(D_{f_v}\right)=\frac{\partial f_v^d}{\partial x}\frac{\partial f_v^y}{\partial y}-\frac{\partial f_v^x}{\partial y}\frac{\partial f_v^y}{\partial x}=\det \left(D_{\overline{u}}\right)+\beta \sum _k{c}_k(\det \left(D_{h_k}\right)+\det \left(D_{g_k}\right))+{\beta }^2\sum _k\sum _l{c}_k{c}_l\det \left(D_{w_{k,l}}\right)$$ (24)

where $h_k\left(\overrightarrow{x}\right)=[v_k^x\left(\overrightarrow{x}\right),{\overline{u}}^y\left(\overrightarrow{x}\right)],g_k\left(\overrightarrow{x}\right)=[{\overline{u}}^x\left(\overrightarrow{x}\right),v_k^y\left(\overrightarrow{x}\right)]$, and $w_{k,l}\left(\overrightarrow{x}\right)=[v_k^x\left(\overrightarrow{x}\right),v_l^y\left(\overrightarrow{x}\right)]$. In order to find the visualizable range, the above equation is set to zero and is solved for $\beta \left(\overrightarrow{x}\right)$ for each $\overrightarrow{x}\in \Omega$. Finally we choose ${\beta }^{\ast }-{\min }_{\overrightarrow{x}}\mid \beta \left(\overrightarrow{x}\right)\mid$ to denote the range in ${\sum }_k{c}_k{v}_k\left(\overrightarrow{x}\right)$ direction. Although the process above leads to a very conservative bound for β, |β| <β*, it enables one to find the visualizable range for any linear combination of the orthonormal basis displacement fields. In all of the computational experiments shown in the following sections ${\beta }^{\ast }\gg 4\sigma$, where σ is the standard deviation of the projected images on the given direction in LOT space.

5. Modeling shape and appearance

Having the linearly embedded images with respect to the reference image, I₀, enables one to visualize any point in the embedded space (subject to the restrictions described above). Hence, linear data analysis techniques such as principal component analysis (PCA) and linear discriminant analysis (LDA) provide visualizable modes of variations in the embedded space.

5.1. Visualizing variations within a single class

We utilize PCA (in kernel space) to visualize the main modes of variation in texture and shape within the dataset. Briefly, let S be the inner product matrix of the LOT embeddings of the images:

$${\mathbf{S}}_{k,l}=\frac{1}{N}{\int }_{\Omega }(u_k\left(\overrightarrow{x}\right)-\overline{u}\left(\overrightarrow{x}\right))\cdot (u_l\left(\overrightarrow{x}\right)-\overline{u}\left(\overrightarrow{x}\right))I_0\left(\overrightarrow{x}\right)d\overrightarrow{x},$$ (25)

Let the corresponding eigenvalues γ_i be

$${\mathbf{Se}}_i={\gamma }_i{\mathbf{e}}_i.$$ (26)

where i = 1...N and e_i s are the eigenvectors. The PCA directions are then given by

$$v_i\left(\overrightarrow{x}\right)=\frac{1}{\sqrt{{\gamma }_{i}N}}\sum _{k=1}^N{\mathbf{e}}_i\left[k\right]u_k\left(\overrightarrow{x}\right),$$ (27)

with corresponding eigenvalues γ_i. The variations in the dataset along the ith prominent variation direction can then be computed about the mean:

$$f_{\beta ,i}\left(\overrightarrow{x}\right)=\overrightarrow{x}-(\overline{u}\left(\overrightarrow{x}\right)+\beta v_i\left(\overrightarrow{x}\right)),$$ (28)

with the corresponding image computed by $\det \left(D_{f_{\beta ,i}^{-1}}\left(\overrightarrow{x}\right)\right))I_0\left(f_{\beta ,i}^{-1}\left(\overrightarrow{x}\right)\right)$, as mentioned earlier, and with β being a coefficient computed in units of standard deviations σ_i computed over the projection of data on v_i. Note that for each direction β is chosen such that |β| <β*.

5.2. Visualizing discriminant information between different classes

In order to find the most discriminant variation in a dataset containing two classes we apply the methodology we described in [19], which is a penalized version of the well-known Fisher linear discriminant analysis (FLDA), to the PCA-space of the LOT embeddings. The reason behind applying FLDA in the PCA-space is that the number of data samples is usually much smaller than the dimensionality of the embedded space. Therefore, the data can be presented in a lower dimensional space of the size equal to the number of sample points. In the PCA-space of the LOT embeddings, the kth image is represented by

$${\mathbf{z}}_k\left[i\right]={\int }_{\Omega }{v}_i\left(\overrightarrow{x}\right)u_k\left(\overrightarrow{x}\right)d\overrightarrow{x}$$ (29)

with i = 1...N. The discriminant directions are then calculated in the PCA-space using

$${\mathbf{w}}^{\ast }=\underset{\mathbf{w}}{\mathrm{argmax}}\frac{{\mathbf{w}}^T{S}_T\mathbf{w}}{{\mathbf{w}}^T(S_w+∊I)\mathbf{w}}$$ (30)

where $S_T={\sum }_{k=1}^N({\mathbf{z}}_k-\overline{\mathbf{z}}){({\mathbf{z}}_k-\overline{\mathbf{z}})}^T$ is the total scatter matrix, $S_w={\sum }_c{\sum }_{k\in c}({\mathbf{z}}_k-{\overline{\mathbf{z}}}_c){({\mathbf{z}}_k-{\overline{\mathbf{z}}}_c)}^T$ represents the ‘within class’ scatter matrix, and ${\overline{\mathbf{z}}}_c$ is the center of class c. Note that, ε is a constant and we use the approach described in [22] to compute the appropriate value for ε in each case. Finally, the discriminant directions in the LOT embedding space are given by

$$v_{pLDA}\left(\overrightarrow{x}\right)=\sum _{k=1}^N{\mathbf{w}}^{\ast }\left[k\right]u_k\left(\overrightarrow{x}\right)$$ (31)

The variations along v_pLDA and around the mean are then visualized using the same scheme explained in the previous section.

6. Computational experiments

Here we describe results obtained in analyzing 4 different datasets using the proposed method. These datasets contain images of chromatin distribution in two types of cancerous thyroid cells, spiral and elliptical galaxies, human facial expressions, and part of the Caltech-UCSD Birds 200 dataset. These datasets are chosen to cover a broad spectrum of applications, in order to demonstrate versatility and the limitations of the proposed approach.

6.1. Datasets

The human facial expression dataset used below is part of the Carnegie Mellon University Face Images database, and is described in detail in [15]. Each image contains 276 × 276 grayscale pixels of 40 subjects under two classes of expressions, namely neutral and smiling. The light variation in these images is relatively minor and facial area, gender, and expression differences are the major variations in the dataset. The second dataset we used consists of segmented thyroid nuclei from patients with two types of follicular lesions, namely follicular adenoma (FA) of the thyroid and follicular carcinoma (FTC) of the thyroid. Tissue blocks, belonging to 27 patients with FA and 20 patients with FTC, were obtained from the archives of the University of Pittsburgh Medical Center. The study was approved as an exempt protocol by the Institutional Review Board of the University of Pittsburgh.

All images were acquired using an Olympus BX51 microscope equipped with a 100× UIS2 UPlanFl oil immersion objective (numerical aperture 1.30; Olympus America, Central Valley, PA) and 2 megapixel SPOT Insight camera (Diagnostic Instruments, Sterling Heights, MI). Image specifications were 24 bit RGB channels and 0.074 μm/pixel, 118 × 89 μm field of view. Slides were chosen that contained both lesion and adjacent normal appearing thyroid tissue (NL) where possible. The pathologist (J.A.O.) took 10–30 random images from non-overlapping fields of view of lesion and/or normal thyroid to guarantee that the data for each patient contained numerous nuclei for subsequent analysis. Nuclei were segmented semi-automatically utilizing the approach described in [6]. The segmented cells are visually inspected by the pathologist (J.A.O.) and on average 27 cells were taken from each patient leading to 756 nuclei for FA and 509 for FTC cases. The third dataset we employed contains two classes of galaxy images, including 225 elliptical galaxies and 223 spiral galaxies [14]. Finally, the last dataset is part of the Caltech-UCSD Bird 200 dataset, and it contains 30 images of two similar bird species, namely Gadwall and Mallard. Finally, we note that prior to the analysis shown below, each dataset was pre-processed so as to remove translations, rotations, and image flips as described in [21,22]. In addition, each grayscale image containing one segmented morphological exemplar was normalized so that the sum of its pixels was set to 1.

6.2. Visualizing modes of variation

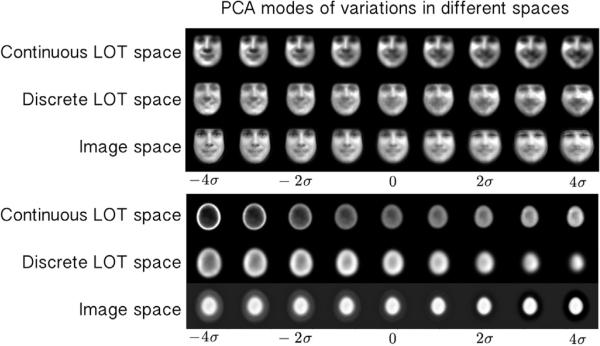
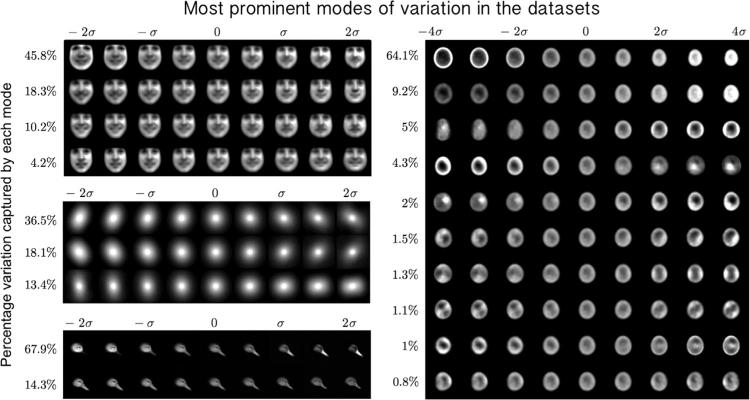
One of the most important contributions of the LOT framework is to provide a visual image exploration tool which automatically captures and visualizes the modes of variations/discrimination in a set of images. We applied the proposed continuous LOT framework to model and visualize modes of variation in the datasets described above. Fig. 3 shows a comparison between the PCA modes obtained using image space (utilizing the L₂ metric) [18], the discrete LOT-space as proposed by [21], and the continuous LOT-space obtained from the approach presented in this work. The photo-realistic improvement is self-evident. Fig. 4 (a), (b), (c), and (d) also shows the top 4 PCA modes for the human facial expression dataset, 3 PCA modes for the galaxy image dataset, 2 PCA modes for the bird image dataset, and the first 10 PCA modes for the nuclear chromatin distribution dataset, respectively. Several variations are visible: illumination changes, large vs. small, hairy vs. smooth, elongated vs. round, neutral vs. smiling, etc.

Fig. 3.

PCA modes in the continuous LOT space, discrete LOT space, and image space for the facial expression and the nuclei datasets.

Fig. 4.

The first 4 PCA modes for the facial expression dataset, capturing 78.5% of the variations in the dataset (a), the first 3 modes of variations for the galaxy dataset, capturing 68.1% of variations in the dataset (b), the first 2 modes of variations for the bird image dataset capturing 82.2% of the variations in the dataset (c), and the first 10 PCA modes for nuclei dataset, capturing 90.39% of the variations in the dataset (d). For visualization purposes, the images are contrast stretched.

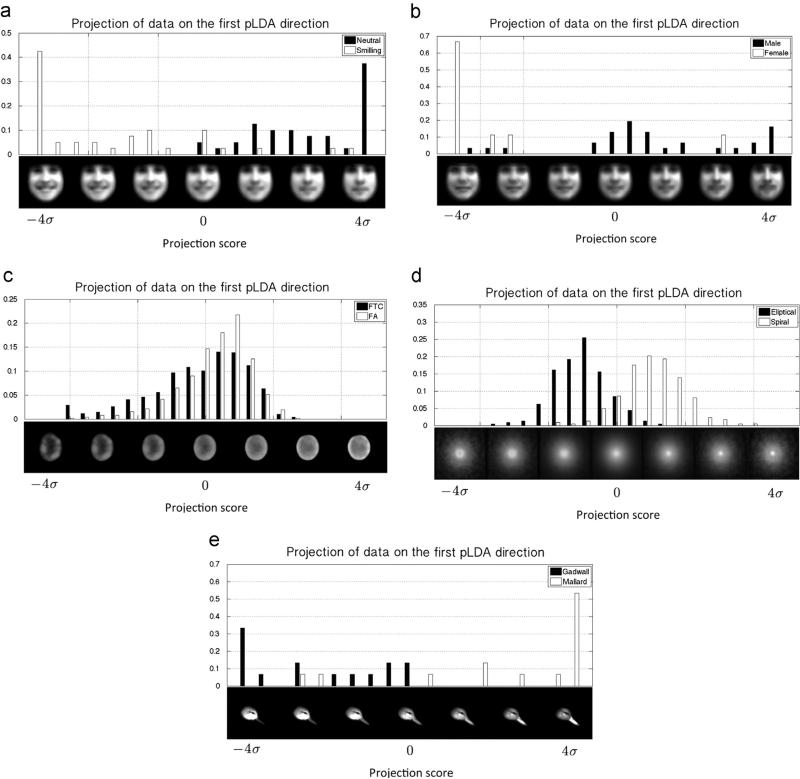
Fig. 5 shows discriminant directions between smiling vs. neutral faces, women vs. men, cancerous vs. normal nuclei images, eliptical vs. spiral galaxy images, and Mallard vs. Gadwall bird images. The histograms in Fig. 5 show the distribution of the projected LOT embeddings onto the corresponding v_pLDA direction. The variations along v_pLDA are computed about the mean as described above. It can be seen that the LOT framework represented in this paper is capable of capturing the visual differences of the images. We note that, in order to avoid over fitting, 20% of the dataset is kept out as the test data and v_pLDA is calculated based on the remaining 80%, training data for each experiment. Fig. 5 shows the projection of the test data on the v_pLDA calculated from the training dataset. The p-value (computed using only held out test data) for all experiments in Fig. 5, calculated from the Kolmogorov–Smirnov test (computed using held out data only), is zero to numerical precision. The visualization on the face image datasets confirm that the LOT approach captures the expected morphology changes between smiling and neutral faces, as well as female vs. male faces (e.g. appearance of facial hair). Differences between the FA and FTC nuclei can be summarized by the amount of relative chromatin that is present at the center of the nucleus, as opposed to its periphery. A similar statement can be made for summarizing differences in mass distributions between elliptical versus spiral galaxies. Spiral galaxies tend to have more mass, in relative terms, concentrated further away from the center of the galaxy. Finally, differences between the Gadwall and Mallard bird species can be summarized by the fact that the Gadwall species, on average, have thinner beaks, rounder heads, and brighter feather coloration in the head region. These examples are meant to highlight the type of information that the LOT and penalized LDA approaches, when combined, can capture, as well as to demonstrate some of its limitations (described below).

Fig. 5.

The histogram of the distribution of the projected LOT embeddings on the corresponding discriminant direction, and the visualized −4σ to 4σ variation of points around this direction about the mean for smiling and neutral faces: (a) male versus female faces (just neutral faces); (b) normal and cancerous cells; and (c) elliptical and spiral galaxies. The x-axis of the histograms is in the units of standard deviation.

6.3. Computation time analysis

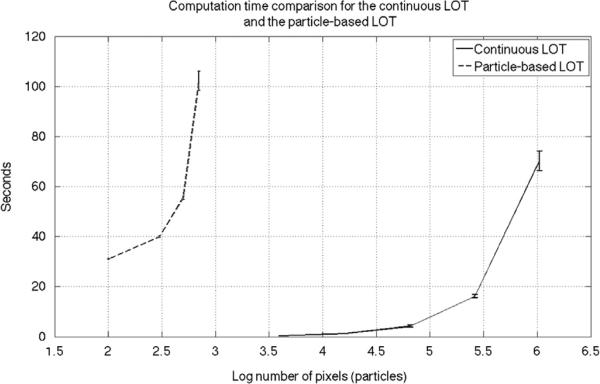
In order to compare the computation time for calculating the LOT embedding with particle-based and continuous LOT implementations we devised the following experiment. First we ran the particle-based code on the facial expression dataset images with 100, 300, 500, and 700 particles. The average computational time is reported in Fig. 6 (note the x-axis is in log scale). We note that the reported computational time includes the particle approximation step we described in [21,22]. For the continuous LOT code, on the other hand, we resized the images in the dataset to 64 × 64, 128 × 128, 256 × 256, 512 × 512 and 1024 × 1024 and ran the code. The average run time for the continuous LOT is also reported in Fig. 6. In order to make a fair comparison one can think of the total number of pixels as the number of particles and compare the results in that manner. It is clear that the continuous LOT code is significantly faster than the particle-based LOT code. We note that the computational complexity of each iteration of the continuous LOT code is of the order of O(n log (n)), where n is the total number of pixels in the image. The algorithm usually converges in less than 100 iterations. The codes were executed on a MacBook pro, with 2.9 GHz Intel Core i7 and 8 GB 1600 MHz DDR3.

Fig. 6.

Computation time comparison for the continuous LOT and the particle-based LOT. The x-axis shows the number of pixels in log scale for the continuous LOT and the number of particles in log scale for the particle-based LOT.

6.4. Classification results

Here we have tested the ability of the continuous LOT approach described above for classification tasks in the aforementioned image datasets. We have also compared the approach to our previous, particle-based method [21]. In doing so, we have limited the number of particles used in this method to 300. This is so that the average computation times between the continuous and particle-based versions are comparable while the visualizations are still acceptable. For 300 particles and images of size 256 × 256, the particle-based method is on average 10 times slower than the proposed method. In addition, we also compare the method described above to the tangent distance method described in [45], also used in face classification [12], and the truncated PCA coefficients (capturing 90% of variations). In all but one of the classification tasks, we have used a 10-fold cross validation technique, where a linear support vector machine classifier is computed on the training set, and tested on the held out test image. All classification results are shown in Table 1.

Table 1.

Accuracy table for classification of facial expressions, gender in facial expression dataset, galaxy dataset, and bird type (Mallard vs. Gadwall) using a linear SVM classifier with 10-fold cross validation in image space, truncated PCA coefficients, particle based LOT-space, and continuous LOT-space.

Embedded space	Accuracy%
	Neutral vs. smiling	Spiral vs. elliptical	Male vs. female	Mallard vs. Gadwall
Tangent metric	77.35 ± 0.74	77.64 ± 0.51	81.04 ± 1.43	77.71 ± 2.3
PCA coefficients	69.05 ± 1.14	78.4 ± 0.54	79.42 ± 1.57	76.59 ± 1.6
Particle-based LOT	74.27 ± 1.28	72.5 ± 0.6	77.7 ± 1.4	81.76 ± 1.74
Continuous LOT	83.04 ± 0.8	77.82 ± 0.35	82.45 ± 0.8	85.26 ± 1.35

The classification strategy used for the nuclear dataset is different given the slightly different nature of the problem. Here labels are available only for sets of nuclei (not individual nuclei) and the task is to test whether a patient (not an individual nucleus) can be classified as FA or FTC. This leads to a need for estimating a low dimensional density for each class in the training set. To that end, we designed a classifier based on computing the K-nearest neighbors (K-NN) method on the LDA direction together with a majority voting step. A ‘leave one patient out’ scheme is used for cross validation, in which all nuclei corresponding to one patient are held out for testing and the nuclei from rest of the patients are used as the training data (to find the LDA direction as well as the optimum K in K-NN). The results are summarized in Table 2.

Table 2.

Accuracy table for patient classification in the thyroid nuclei dataset using K-NN on the first LDA direction in (a) image space, (b) truncated PCA coefficients, (c) particle based LOT-space, and (d) continuous LOT-space.

Tangent metric		Label		PCA Coefficients		Label
		FA	FTC			FA	FTC
Test	FA	21	6	Test	FA	21	6
	FTC	2	18		FTC	12	8
(a)	Accuracy	82.98%		(b)	Accuracy	61.70%
Particle-based LOT		Label		Continous LOT		Label
		FA	FTC			FA	FTC
Test	FA	27	0	Test	FA	27	0
	FTC	0	20		FTC	0	20
(c)	Accuracy	100%		(d)	Accuracy	100%

It can be seen that in all the experiments, the continuous LOT approach described above significantly outperforms our earlier particle-based version of the LOT. We also note that in all attempted classification tasks, the proposed LOT approach provides better or comparable accuracies in comparison to the tangent metric and the truncated PCA coefficients. We note that the p-values calculated from Welch's t-test between different methods on each dataset show that the improvement in accuracy for the proposed method compared to the particle-based LOT is statistically significant (p-value <0:01) for all datasets.

7. Summary and discussion

We described a new method for information extraction from image databases utilizing the mathematics of optimal transport. The approach can be viewed as a new invertible transformation method that computes the relative placement of intensities in an image dataset relative to a ‘reference’ point. Distances computed in the so-called linear optimal transport (LOT) space are akin to a linearized version of the well-known optimal transport (OT), also known as the earth mover's distance. Moreover, the transformation is invertible, thus allowing for direct visualization of any statistical model constructed in LOT space. In short, the framework thus enables exploratory visual interpretation of image databases, as well as supervised learning (classification), in a unified manner.

In practice, we envision this approach to be most useful in information discovery settings where optimal feature sets have yet to be discovered, as well as in tasks where a visual interpretation of any information is necessary. One such well-suited application is the detection of cancer from cell morphology. We have recently shown that the discrete LOT technique can be used to classify certain types of thyroid cancers with near perfect sensitivity and specificity [25] on a cohort of 94 patients. At the same time the technique can be utilized to provide biological information regarding chromatin reorganization differences in different cancer types. In contrast, the classification accuracy utilizing state of the art feature sets [33] is significantly lower. Similarly, we have recently shown that the discrete LOT approach also allows one to detect mesothelioma, a type of lung cancer usually associated with exposure to asbestos, directly from effusion cytology specimens [24], thus obviating the need for invasive biopsies which are often necessary for diagnosis. The advances discussed in this paper could be used to improve accuracy while at the same time significantly reduce the computation time involved in such diagnostic tests from a few hours on a Beowulf-type cluster [25] to minutes on a modern standard desktop workstation. We have shown that the approach can also produce visualizations of significantly higher resolution.

The work presented here builds on our own earlier work on this topic [21,22]. Relative to this work, the main innovation described here is an adaptation of the LOT framework to utilizing a continuous formulation for the underlying optimal transport problem, rather than a discrete formulation as done in [21,22]. In the process, we described a modification of the reference estimation algorithm based on estimating the intrinsic mean in the dataset, as well as described how to utilize deformation fields in order to compute the necessary LOT embedding. In this paper we utilized the algorithm described in [11] to solve the underlying OT problem, though other approaches can be used as well [23]. We have also described a method for calculating regions in LOT space where the transform, computed using deformation fields as described here, is invertible. Finally, we have also described how to utilize the continuous formulation of the LOT for tasks related to visualization using PCA and LDA.

We compared the performance of the ‘continuous’ LOT approach described here to the ‘discrete’ version we described earlier [21,22] in visualization and discrimination tasks using several image databases. The approach described here is much faster to compute than our previously described version, given that it relies on a gradient descent-estimate for transport maps, rather than discrete transport plans obtained via linear programming minimization. As a result, it is now possible to utilize images at their full resolution for visualization and discrimination tasks. Consequently, visualizations computed using PCA and penalized LDA look significantly more photo-realistic, classification accuracies are improved, in addition to the computation time being decreased. In addition, we compared the LOT distances computed using both continuous and discrete approaches to other distances often employed in visualization and discrimination tasks. We have shown that using the same classifier (linear SVM) the classification accuracy of the proposed LOT metric computed utilizing a continuous formulation for the underlying OT problem outperforms that of the tangent metric for images, the PCA subspace of the image space, and our earlier particle-based LOT approach.

While the approach is effective in mining information from image databases, it is worthwhile to point out a few of its limitations. We note that the convergence speed of the optimal transport solver depends on the smoothness of the input images. This effect is also demonstrated by Chartrand et al. [5], for example. Therefore, in order to ensure the smoothness of the input images, the images are filtered with a Gaussian filter of small standard deviation (1–2 pixels) as a preprocessing step. This process leads to the loss of high frequency content in the images being analyzed. Results reported in this paper, however, have found that this effect is not significant for the datasets we tested. In addition, we note that the ‘linearization’ afforded by the LOT approach we described here, while seemingly effective for many applications, does not provide for a perfect representation model for certain image datasets. We note, for example, that the models produced by our method in regions near the mouth (see Fig. 3), though visually superior to the other alternatives we tested, are not visually sharp. We postulate that this is due to the large intensity variations that are possible near this region (e.g. open versus closed mouth and visibility of teeth). Techniques for overcoming these and other issues will be subject of future work.

Biography

Soheil Kolouri received his B.S. degree in Electrical Engineering from Sharif University of Technology, Tehran, Iran, in 2010, and his M.S. degree in Electrical Engineering, in 2012, from Colorado State University, Fort Collins, Colorado. He received his doctorate degree in biomedical engineering from Carnegie Mellon University, in 2015, where his research was focused on applications of the optimal transport in image modeling, computer vision, and pattern recognition. His thesis, titled, “Transportbased pattern recognition and image modeling”, won the best thesis award from the Biomedical Engineering Department at Carnegie Mellon University.

Akif B. Tosun received his B.S. degree in computer engineering from Hacettepe University, Turkey, in 2006, and his Ph.D. degree in computer engineering at Bilkent University, Turkey, in 2012. He is currently a Post-Doctoral Research Scholar and his work includes the development of novel approaches for cancer diagnosis using image analysis techniques and machine learning algorithms at Carnegie Mellon University, USA.

John A. Ozolek graduated from the University of Pittsburgh School of Medicine with the M.D. degree, in 1989. He completed residency in Pediatrics and Fellowship in Neonatal-Perinatal Medicine at the University of Pittsburgh before practicing in the United States Air Force and private practice. He returned to train in Anatomic Pathology and completed a Fellowship in Pediatric Pathology at Children's Hospital of Pittsburgh where he remains on staff. He has extensive collaborations with the Center for Bioimage Informatics and Department of Mathematics at Carnegie Mellon University to develop algorithms and computational approaches for automating tissue recognition in research and clinical applications.

Gustavo K. Rohde earned B.S. degree in Physics and Mathematics, in 1999, and the M.S. degree in Electrical Engineering, in 2001, from Vanderbilt University. He received a doctorate in Applied Mathematics and Scientific Computation, in 2005, from the University of Maryland. He is currently an Associate Professor of Biomedical Engineering, and Electrical and Computer Engineering at Carnegie Mellon University.