Disease and Polygenic Architecture: Avoid Trio Design and Appropriately Account for Unscreened Control Subjects for Common Disease

Abstract

Genome-wide association studies (GWASs) are an optimal design for discovery of disease risk loci for diseases whose underlying genetic architecture includes many common causal loci of small effect (a polygenic architecture). We consider two designs that deserve careful consideration if the true underlying genetic architecture of the trait is polygenic: parent-offspring trios and unscreened control subjects. We assess these designs in terms of quantification of the total contribution of genome-wide genetic markers to disease risk (SNP heritability) and power to detect an associated risk allele. First, we show that trio designs should be avoided when: (1) the disease has a lifetime risk > 1%; (2) trio probands are ascertained from families with more than one affected sibling under which scenario the SNP heritability can drop by more than 50% and power can drop as much as from 0.9 to 0.15 for a sample of 20,000 subjects; or (3) assortative mating occurs (spouse correlation of the underlying liability to the disorder), which decreases the SNP heritability but not the power to detect a single locus in the trio design. Some studies use unscreened rather than screened control subjects because these can be easier to collect; we show that the estimated SNP heritability should then be scaled by dividing by (1 − K × u)² for disorders with population prevalence K and proportion of unscreened control subjects u. When omitting to scale appropriately, the SNP heritability of, for example, major depressive disorder (K = 0.15) would be underestimated by 28% when none of the control subjects are screened.

Main Text

Optimal experimental design of genetic studies of disease for discovery of associated loci depends on the underlying genetic architecture of the trait. Although the true genetic architecture of the trait is usually not known, different experimental designs aim at exposing causal loci of differing population frequencies. For example, the optimal experimental design to detect de novo mutations is a trio design in which affected probands and their parents are genotyped.¹ In contrast, genome-wide association studies (GWASs) are an optimal design for a genetic architecture that includes many common causal loci of small effect (a polygenic architecture). Here, we consider two designs of GWASs, which we show deserve careful consideration: designs based on parent-offspring trios and designs based on unscreened control subjects. We assess these designs in terms of quantification of the total contribution to disease risk of genome-wide genetic markers, via estimation of so-called SNP heritability,² and the power to detect an associated risk allele.

Our study is motivated by experiences with GWAS designs for psychiatric disorders, but our results are parameterized based on baseline disease risk and heritability, and are, therefore, applicable to the full range of diseases and disorders with a polygenic genetic architecture of underlying risk. For psychiatric disorders, GWASs have had variable success in detecting genome-wide significant common SNPs. On the one hand, 108 significant loci were recently found for schizophrenia (SCZ [MIM: 181500]) in a sample comprising 36,989 case subjects,³ whereas only two loci were found in one study on major depressive disorder (MDD [MIM: 608516])⁴ but none in another,⁵ no loci for attention-deficit/hyperactivity disorder (ADHD [MIM: 143465]),⁶ and only single-study genome-wide significant loci for autism spectrum disorder (ASD [MIM: 209850]).^{7, 8, 9} Sample size is pivotal in explaining this discrepancy, because much smaller numbers of cases were included for MDD (5,303 and 9,240, respectively), ADHD (2,960), and ASD (2,705, 1,984, and 1,553, respectively) than for SCZ. Other contributing factors have, nevertheless, been proposed, such as the impact of de novo mutations in ASD^{10, 11} (although these are expected to explain only a small proportion of variation),¹² lower family-based heritability of MDD (∼0.4 versus ∼0.8 for SCZ, ASD, and ADHD, assuming a similar genetic architecture between disorders),¹³ and higher prevalence and greater heterogeneity of MDD.¹⁴ Here, we show that the trio design, which is regularly applied in ASD and ADHD, and use of unscreened control subjects deserves careful consideration in the context of an underlying polygenic architecture, which is an important consideration for design of future studies that strive to increase sample size.¹⁵

The impact of trio design and the use of unscreened control subjects on the SNP heritability have, to the best of our knowledge, not yet been described, probably because the methods for estimation of SNP heritability were developed only in recent years.^{16, 17} The impact on the power to detect a single locus has, on the other hand, been studied in the pre-GWAS era of candidate genes,^{18, 19, 20, 21} but we could find no clear-cut comparison of the power to detect an associated risk allele with trio studies versus screened control studies, and we will therefore also give an overview of these differences. We investigate the trio design and the use of unscreened control subjects by analytical derivation followed by simulation studies to validate theory. Assortative mating (correlation in liability between spouses) is included in our trio design analyses, because this has been reported for a range of psychiatric disorders.^{22, 23, 24, 25} For example, a spouse correlation on the social responsiveness scale (a quantitative measure of autistic traits) of 0.29 has been reported in a population sample²³ and of 0.26 in parents of ASD probands.²² For ADHD a spouse correlation of 0.11 on the ADHD index in population samples has been reported.²⁵ In trio designs, genotypes of proband cases are compared to genotypes of pseudocontrol subjects (the non-transmitted parental alleles).

SNP Heritability Calculations

The SNP heritability estimates the total proportion of variance tagged by common SNPs from a genome-wide association study.^{2, 16} If samples with GWAS data are population samples, then the variance estimated on the observed scale $\left({\hat{h}}_o^2\right)$ is expressed with the Robertson’s transformation on the liability scale $\left({\hat{h}}_l^2\right)$ as²⁶

$${\hat{h}}_l^2={\hat{h}}_o^2\frac{K\left(1-K\right)}{z^2},$$ (Equation 1)

where z denotes the height of the standard normal density function at the threshold corresponding to a baseline disease risk K. Quantification on the liability scale is most interpretable because it allows direct comparisons of estimates of heritability from family data that are reported on this scale to estimates of variance explained by individual genome-wide significant loci. However, usually GWAS samples are oversampled for case subjects compared to population samples and the transformation of proportion of variance attributable to SNPs estimated from case-control data $\left({\hat{h}}_{occ}^2\right)$ must also account for the proportion of cases in the sample P by^{2, 27}

$${\hat{h}}_l^2={\hat{h}}_{occ}^2\frac{K^2{\left(1-K\right)}^2}{P\left(1-P\right)z^2},$$ (Equation 2)

which reduces to Equation 1 when the sample is a population sample and P = K. However, these transformations assume that control subjects are screened. To account for control subjects being unscreened, we define F as the proportion of falsely classified control subjects, $F=N_{falsecontrols}/(N_{falsecontrols}+N_{truecontrols})=N_{falsecontrols}/N_{controls}$. We closely followed the derivations of Golan et al. (paragraphs 1.2 and 1.3 of their Supplemental Materials)²⁷ to derive an updated equation (Table S1) validated by simulation (Table S2),

$${\hat{h}}_l^2={\hat{h}}_{occ}^2\frac{K^2{\left(1-K\right)}^2}{P\left(1-P\right){\left(1-F\right)}^2{z}^2},$$ (Equation 3)

which reduces to Equation 2 when F = 0 and control subjects are screened. If a proportion $u$ of the control subjects are a random sample from the population, then one can assume that F ≈ Ku. Therefore, if it is unknown whether control subjects are screened or not, the potential underestimation when all control subjects are unscreened (u = 1) of the SNP heritability ${\hat{h}}_l^2$ estimated from the standard Equation 2 can be assessed as ${\hat{h}}_l^2{\left(1-K\right)}^2$ and thus depends on baseline risk K. In trio designs where probands are ascertained randomly, the pseudocontrol subjects are equivalent to unscreened control subjects under a polygenic model (Figure S1).

For the trio design, the SNP heritability was derived for a disease parameterized with normally distributed phenotypic (l) and genetic (G) liabilities with means E(l) = E(G) = 0 and variances V_l = 1 and $V_G=h_l^2$, the true heritability on the liability scale in the parental generation.²⁸ Under the liability-threshold model, individuals are deemed affected when their liability (l) is larger than threshold (T) such that $P\left(l>T|l\sim N\left(\mathrm{0,1}\right)\right)=K$. Parental assortative mating was taken into account by parameterizing a spouse liability correlation of ρ_l and genetic correlation of ${\rho }_G=h_l^2{\rho }_l$.²⁸ The E(G) of proband case subjects and pseudocontrol subjects were derived by considering the variance-covariance matrix of l and G of individuals that could contribute to a trio design (proband, sibling, mother, father, pseudocontrol). To account for the affected proband, the variance-covariance matrix of random families was conditioned on the proband being affected by accounting for the reduction in variance as a result of the Bulmer effect²⁹ in related individuals described by Tallis.³⁰ To account for a second affected sibling, the variance-covariance matrix was further conditioned on the sibling also being affected. Details of these derivations are provided in the Supplemental Methods and were validated with a simulation study in R (Tables S3 and S4).

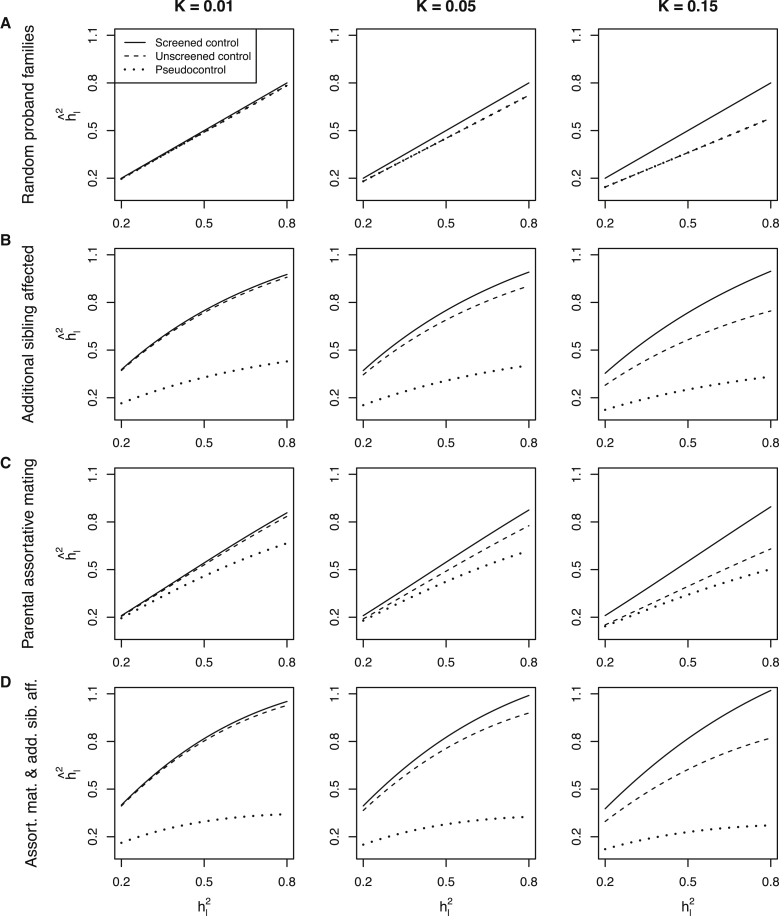
Figure 1A displays the SNP heritability assessed from unscreened control subjects (Figure 1A, dashed line), which is equivalent to estimates from pseudocontrol subjects from random families with at least one affected proband (Figure 1A, dotted line) and screened control subjects (Figure 1, solid lines). Although the standard transformation (Equation 2) applied to derive estimates of SNP heritability on the liability scale $\left({\hat{h}}_l^2\right)$ is expected to give unbiased estimates of the true SNP heritability when case subjects are randomly ascertained and control subjects are screened (Figure 1A, solid line), the transformation underestimates $h_l^2$ by a factor (1 − K)² when diseases are common (high K) and control subjects are unscreened or are pseudocontrol subjects (Figure 1A, dashed and dotted line). The estimated heritability from the Equation 2 transformation ${\hat{h}}_l^2$ severely underestimates $h_l^2$ when data result from a trio design with probands ascertained from multiplex families (Figure 1B, dotted line), for example, ${\hat{h}}_l^2=0.31$ for K = 0.05 and $h_l^2=0.5$, because the mean liability of pseudocontrol subjects is greater than the average in the population and so the contrast in genetic values between case subjects and pseudocontrol subjects is less than between case subjects and screened control subjects (Table 1, additional sibling affected), which is not fully compensated by the fact that case subjects from multiplex families have higher mean liability than randomly selected case subjects (Table 1, random proband families). In contrast, when case subjects are selected from multiplex families and control subjects are screened, the estimated SNP heritability based on the standard transformation is an overestimate of $h_l^2$ (for example, ${\hat{h}}_l^2=0.75$ for K = 0.05 and $h_l^2=0.5$). When control subjects are unscreened, the SNP heritability is found between the SNP heritabilities from screened and pseudocontrol subjects (Figure 1, dashed lines), when SNP heritabilities are estimated by Equation 2. In the context of assortative mating, a trio design comparison of probands to pseudocontrol subjects yields decreased ${\hat{h}}_l^2$ (Figure 1C; Table 1, parental assortative mating; spouse correlation ρ_l = 0.3). Again, comparing the probands to screened control subjects (from the offspring generation) does in fact overestimate the heritability in the parent generation $h_l^2$; this is, however, a well-known consequence of assortative mating and is not restricted to the trio design $\left(V_{G,offspring}=V_{G,parents}+\left(1/2\right){\rho }_{G,parents}{V}_{G,parents}\right)$.²⁹ The most pronounced difference between screened and pseudocontrol control subjects is found for probands with an additional affected sibling in the context of parental assortative mating (Figure 1D; Table 1, additional sibling affected and parental assortative mating).

Figure 1.

Relationship between the True SNP Heritability and Its Estimates Based on the Standard Transformation with Equation 2 from Trio Data, Screened Controls, and Unscreened Controls

The SNP heritability ${\hat{h}}_l^2$ that would be estimated based on the standard liability transformation equation (Equation 2) for GWASs using pseudocontrol subjects (dotted lines), unscreened control subjects (dashed lines), and screened control subjects (solid lines) compared to the true parental SNP heritability $h_l^2$ for designs based on randomly ascertained proband families (A), families with an additional affected sibling (B), in the context of parental assortative mating with a correlation on the liability scale of ρ_l = 0.3 (C), and families with an additional affected sibling in the context of parental assortative mating (D) for disorders with lifetime risk K = 0.01, 0.05, and 0.15. The pseudocontrol subjects of random proband families are equivalent to unscreened control subjects (dashed and dotted lines overlap in A), and the slope of these lines are defined by (1 − K)², i.e., the underestimation of ${\hat{h}}_l^2$ when mistakenly applying Equation 2 rather than Equation 3 to transform the heritability on the observed scale to the liability scale when none of the control subjects are screened.

Table 1.

Mean Genetic Liabilities and SNP Heritability Estimated from the Standard Transformation with Equation 2 from GWAS using Trio Design, Screened Control Subjects, or Unscreened Control Subjects for Actual Parental Heritability 0.5

K	$h_l^2$Parents	Mean Genetic Liability (E(G))				${\hat{h}}_l^2$Assessed from Proband
Case	Control
Screened	Unscreened	Pseudo	Screened	Unscreened	Pseudo
Random Proband Families
0.01	0.5	1.333	−0.013	0.000	0.000	0.500	0.490	0.490
0.05	0.5	1.031	−0.054	0.000	0.000	0.500	0.451	0.451
0.15	0.5	0.777	−0.137	0.000	0.000	0.500	0.361	0.361
Additional Sibling Affected
0.01	0.5	1.634	−0.013	0.000	0.543	0.749	0.736	0.328
0.05	0.5	1.275	−0.054	0.000	0.424	0.750	0.690	0.307
0.15	0.5	0.972	−0.137	0.000	0.323	0.735	0.565	0.251
Parental Assortative Mating
0.01	0.5	1.386	−0.016	0.000	0.097	0.542	0.530	0.459
0.05	0.5	1.075	−0.060	0.000	0.075	0.547	0.490	0.424
0.15	0.5	0.812	−0.148	0.000	0.057	0.552	0.395	0.341
Additional Sibling Affected and Parental Assortative Mating
0.01	0.5	1.706	−0.016	0.000	0.670	0.818	0.803	0.296
0.05	0.5	1.335	−0.060	0.000	0.525	0.826	0.756	0.278
0.15	0.5	1.021	−0.148	0.000	0.402	0.818	0.624	0.230

The mean genetic liabilities E(G) are displayed for probands, unrelated screened control subjects, unrelated unscreened control subjects, and their pseudocontrol subjects as well as the SNP heritability ${\hat{h}}_l^2$ estimated from Equation 2 from comparing case subjects to these three sets of control subjects, for different parameterization of baseline disease risk K and a fixed underlying heritability of $h_l^2=0.5$. The probands are parameterized in line with Figure 1 to be selected from random proband families (Figure 1A), families with an additional affected sibling (Figure 1B), families in the context of parental assortative mating (Figure 1C), and families with an additional affected sibling in the context of assortative mating (Figure 1D), respectively.

Power Calculations

The power to detect an associated risk allele in a case-control association test follows from the non-centrality parameter NCP of the χ² test statistic. This NCP is expressed in terms of sample size N, proportion of case subjects in the study v, the allele frequency in case subjects p_case, the allele frequency in control subjects p_control, and the mean allele frequency in the sample $\overline{p}=v{p}_{case}+\left(1-v\right)p_{control}$ as

$$NCP=\frac{{\left(p_{case}-p_{control}\right)}^2}{\overline{p}\left(1-\overline{p}\right)\left(\frac{1}{2N\text{∗}v}+\frac{1}{2N\text{∗}\left(1-v\right)}\right)}$$ (Equation 4)

and the power as $P\left(x>\sqrt{NCP}+x_T|z\sim N\left(\mathrm{0,1}\right)\right)$, where x_T is the $z$ -value quantile-function of the standard normal distribution for the desired significance threshold, here set at α = 5 × 10⁻⁸ (x_T = −5.45). The power of different experimental designs is reflected in the appropriate expressions of p_case and p_control. We parameterize a disease with a baseline lifetime disease risk $K$, a di-allelic locus with risk allele frequency P(B) = p, non-risk allele frequency P(b) = q = 1 − p, relative risk of heterozygotes $R{R}_{Bb}=P\left(Disease|Bb\right)/P\left(Disease|bb\right)$, and relative risk of the homozygotes $R{R}_{BB}=P\left(Disease|BB\right)/P\left(Disease|bb\right)$.^{31, 32} When control subjects are screened, power follows from p_case = k_bbRR_Bbp(1 + p(RR_Bb − 1))/K, where $k_{bb}=P\left(Disease|\text{bb}\right)=K/\left(q^2+2pqR{R}_{Bb}+p^{2}R{R}_{BB}\right)$ and p_control = ((1 − k_bbRR_Bb)p(1 − p) + (1 − k_bbRR_BB)p²)/(1 − K),³² which agrees with the genetic power calculator of Purcell et al.³³ When control subjects are unscreened, the power of an association study is expressed by Equation 4 with p_control = p. For the trio design, power was assessed by substituting in Equation 4 the allele frequency in probands and pseudocontrol subjects (the non-transmitted alleles of the parents). When trios are ascertained from families with an additional affected sibling or when there is assortative mating, the risk allele frequency in control subjects can be derived from combined and conditional genotype frequencies of an individual, the affected sibling, and the parents. Under assortative mating, expressions are dependent on spouse liability correlation ρ_liability, which results in the correlation between the parental genotypes as ${\rho }_{locus}={\rho }_{liability}{h}_{locus}^2$.²⁸ It follows that assortative mating (for example, ρ_liability = 0.3) has no impact on the power to detect a single locus for loci typical of polygenic architecture that explain less than 1% of variation (ρ_locus = 0.3 × 0.01 = 0.003).²⁸ When assuming a small RR_Bb typical of complex genetic disease and a multiplicative model on the disease scale ($R{R}_{BB}=R{R}_{Bb}^2$, implying additively on the underlying risk scale), the variance attributable to the risk locus can be approximated by $h_{locus}^2\approx 2pq{\left(R{R}_{Bb}-1\right)}^2/i^2$ with i = z/K the mean liability of case subjects and z the height of the standard normal density function at the threshold corresponding to a baseline disease risk K.³² The expressions to derive allele frequencies in trios are closed but complex (Supplemental Methods) and were validated by simulation (Table S5).

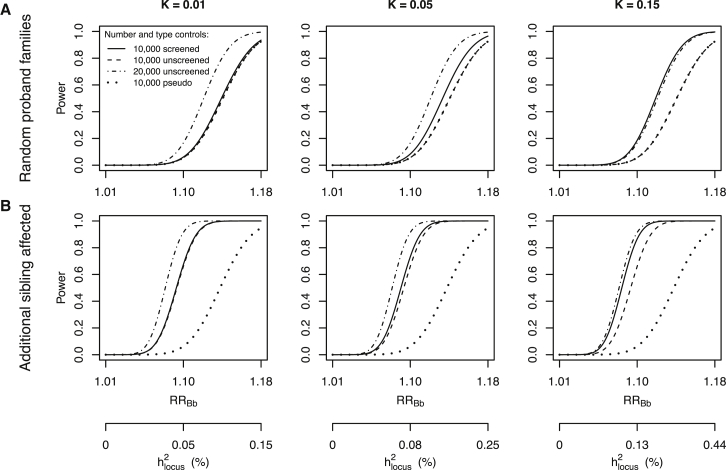
Figure 2 displays the power to detect an associated risk allele for probands from random trios with an affected proband (Figure 2A) and multiplex trios with an additional affected sibling (Figure 2B), when the risk allele has a frequency of P(B) = p = 0.2 for disorders with baseline risk K = 0.01, 0.05, and 0.15 in a sample of n = 10,000 trios (probands versus pseudcontrol subjects) against RR_Bb given an underlying additive effect $\left(R{R}_{BB}=R{R}_{Bb}^2\right)$ (dotted line). Note that pseudocontrol subjects from random families are equivalent to unscreened control subjects (Figure S1), which are displayed in Figure 2 for 10,000 unscreened control subjects (dashed line) and 20,000 unscreened control subjects (dot-dashed line) compared to 10,000 probands. The solid line on each graph is the power for 10,000 probands compared to 10,000 unrelated screened control subjects. Figure 2A shows that there is little to be gained in screening control subjects for diseases of lifetime morbid risk < 1%, but for more common disorders (such as ADHD and MDD), there is an important gain in power, which can also be gained by increasing the number of unscreened control subjects. When trios come from families with an additional affected sibling, the case subjects have an increased probability of carrying the risk allele and so when matched with screened control subjects, there is a gain in power compared to random ascertainment of case subjects (solid line in Figure 2B versus solid line in Figure 2A). For example, when p = 0.2, RR_Bb = 1.2, then p_{proband B} = 0.248 and p_{proband A} = 0.231, respectively (these frequencies do not depend on K). However, when the association study is of case subjects from multiplex families compared to pseudocontrol subjects, there is little gain in power compared to trios based on randomly selected case subjects (dotted line in Figure 2B versus dotted line in Figure 2A), because the pseudocontrol subjects also have increased probability of carrying the risk allele (p_{pseudocontrol B} = 0.215 and p_{pseudocontrol A} = 0.2). The maximum power difference between using screened and pseudocontrol subjects depends on RR_Bb, K, sample size, and whether probands are ascertained randomly or from families with an additional affected sibling (Table 2), but is found for a sample comprising 20,000 subjects at RR_Bb = 1.11 and K = 0.15 for probands with additional affected siblings, under which scenario a total sample size of n = 15,945 is needed when control subjects are screened versus n = 44,574 for the pseudocontrol trio design, respectively, to obtain a power of 0.8. For unscreened control subjects (equivalent to pseudocontrol subjects from random families), the most pronounced decrease in power in a sample of 20,000 subjects is found for a locus with RR_Bb = 1.14 in disease with K = 0.15 where unscreened control subjects yield a power of 0.39 and screened control subjects a power of 0.74. As expected, the impact of using screened control subjects is higher for more common disorders. Allele frequencies in probands, pseudocontrol subjects, and screened control subjects for all Figure 2 scenarios are presented in Figure S2. Furthermore, the power differences between pseudocontrol and screened control studies are consistent for other risk allele frequencies, e.g., p = 0.6 (Figure S3) underlying actual recessive (RR_Bb = 1; Figure S4) and dominant (RR_Bb = RR_BB; Figure S5) effects. In addition, to select only trios with unaffected parents has no impact on power of pseudocontrol studies, because although the risk allele frequency in pseudocontrol subjects decreases, the frequency in case subjects decreases proportionally (Figure S6). When unscreened control subjects are much easier to obtain then screened control subjects, the loss of power due to not screening can be balanced by increasing the number of unscreened control subjects, which is illustrated for different numbers of unscreened control subjects in Figure S7. Note that Equation 4 defines a limit to the power-gain from increasing the number of unscreened control subjects, but that when increasing number of unscreened control subjects from 10,000 to 20,000, the loss of power due to not screening is balanced for all scenarios under consideration here. In Figure 2, the additional x axis is variance explained by the locus, and therefore the results generalize to many combinations of p and RR_Bb that together explain the same locus variance.³¹ Although association studies have similar power to detect a locus based on RR_Bb regardless of baseline disease risk K, the variance explained by a locus is much larger for high K. Therefore, to detect a risk allele that explains the same proportion of genetic variance, a much larger sample size is needed for larger K (Figure 3).

Figure 2.

Power to Detect a Single Risk Variant in Association Studies of 10,000 Case Subjects that Use a Trio Design, Screened Control Subjects, or Unscreened Control Subjects

Power of association analysis comparing 10,000 probands to 10,000 screened control subjects (solid line), 10,000 unscreened control subjects (dashed), 20,000 unscreened control subjects (dot-dashed), and 10,000 pseudocontrol subjects (dotted) to detect a single associated risk variant for a risk allele with frequency p = 0.2, for a baseline disease risk K = 0.01, 0.05, and 0.15. Power was estimated for risk variants with underlying additive effect $\left(R{R}_{BB}=R{R}_{Bb}^2\right)$ for random ascertainment of probands (A) and probands from families with an additional affected sibling (B). Note that pseudocontrol subjects from random families are equivalent to unscreened control subjects and that the dotted and dashed lines in (A) overlap. The variation explained on the liability scale was approximated by $h_{locus}^2\approx 2p\left(1-p\right){\left(R{R}_{Bb}-1\right)}^2/i^2$, where i equals z/K the mean liability of probands, and z the height of the standard normal density function at the threshold corresponding with disease of lifetime risk K.

Table 2.

Maximum Power Difference between Trio Design and Screened Control Subject Studies with 20,000 Subjects

K	RRBb	Allele Frequencies			Power (n = 20,000)		n (Power = 0.8)
Proband	Pseudo	Screened	Pseudo	Screened	Pseudo	Screened
Proband from Random Proband Families
0.01	1.147	0.223	0.200	0.200	0.56	0.58	25,226	24,714
0.05	1.144	0.222	0.200	0.199	0.51	0.63	26,327	23,712
0.15	1.135	0.221	0.200	0.196	0.39	0.74	29,670	21,297
Proband from Families with an Additional Affected Sibling
0.01	1.115	0.228	0.209	0.200	0.17	0.91	39,201	17,307
0.05	1.113	0.227	0.209	0.199	0.15	0.92	40,533	16,923
0.15	1.108	0.226	0.208	0.197	0.11	0.94	44,574	15,945

The loci with allele frequency p = 0.2 from Figure 2 that result in most pronounced decrease in power for pseudocontrol compared to screened control studies for a sample of 10,000 case subjects and 10,000 control subjects are displayed in detail. The power difference depends on the baseline disease risk K, its effect size RR_Bb, and whether the probands are from random proband families or families with an additional affected sibling (compare to solid and dotted lines, respectively, in Figure 2). For these loci, the allele frequencies in probands, pseudocontrol subjects, and screened control subjects is displayed, as well as the power given a sample size of n = 20,000 (50% case subjects) and the required sample size to obtain a power of 0.8. Note that pseudocontrol subjects from random families are equivalent to unscreened population control subjects.

Figure 3.

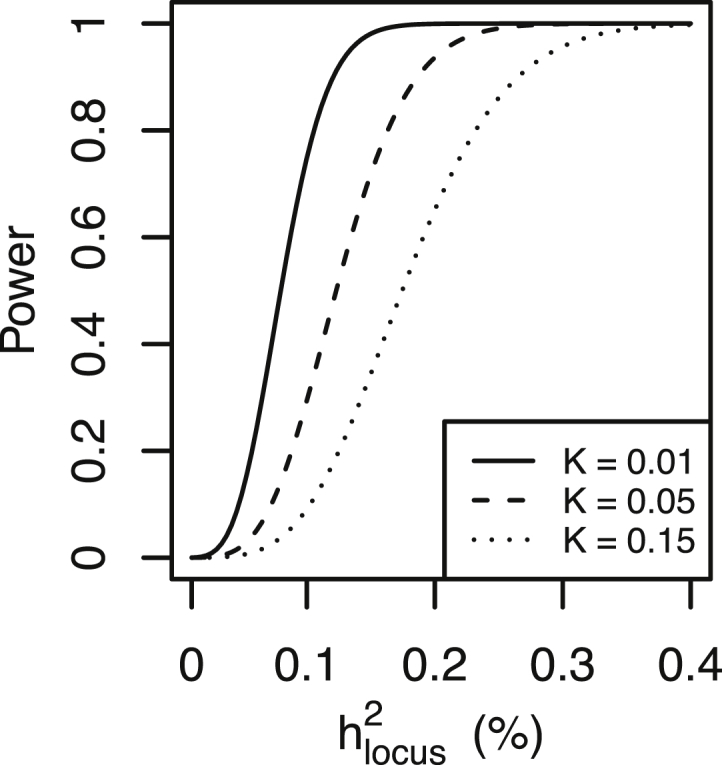
Power to Detect an Associated Locus by the Proportion of Variation It Explains

The power to detect an associated locus depends on the proportion of variation it explains on the liability scale $h_{locus}^2$, the baseline disease risk K, and is displayed for random case versus screened control. For a locus with the same $h_{locus}^2$, larger sample sizes are required for larger K. $h_{locus}^2$ can be approximated by 2p(1 − p)(RR_Bb − 1)²/i², where i equals z/K the mean liability of probands, and z the height of the standard normal density function at the threshold corresponding with disease of lifetime risk K. The (complex) relation between allele frequency p, $R{R}_{Bb}$, and the non-centrality parameter NCP given $h_{locus}^2$ results in an identical relation between power and $h_{locus}^2$ for varying p.

To summarize our findings, our results generate two important conclusions that trio-based samples and unscreened control subjects for common diseases deserve careful consideration when the underlying genetic architecture is highly polygenic. We have quantified this in two ways, first by the underestimation of SNP heritability through application of the inappropriate transformation equation, and second by power calculations of association analysis. We derived a transformation equation for the SNP heritability that is appropriate for unscreened control samples (Equation 3).

The use of trio designs most commonly occurs for pediatric diseases and disorders in which it is relatively easy to obtain blood samples from parents. Trio designs are needed to detect de novo causal mutations,³⁴ to determine accurately phased haplotypes,³⁴ and to undertake parent-of-origin analyses implied by a hypothesis of parental imprinting.³⁵ Trio designs have also been considered for detection of gene-environment interaction.^{36, 37} In the pre-GWAS era, trio designs were recommended to protect against potential bias from population stratification,¹ and although this quality is also sometimes promoted for trio GWAS, with genome-wide SNP data, other strategies, such as genomic principal components³⁸ or mixed model association analysis,³⁹ appropriately account for population stratification without the need to incur 50% higher costs by genotyping three samples to generate two genomes. While acknowledging the benefits of parent-offspring trios under some experimental paradigms, trio-design GWASs have been undertaken without full regard of the implications to power under the genetic architecture implicated by the GWAS paradigm. We draw the following conclusions.

• (1)If the case probands of trios are ascertained randomly, then the resulting case-pseudocontrol study is equivalent to a case-unscreened control design under a polygenic genetic architecture and has little impact on the SNP heritability and power for disorders that are less common, but for more common disorders there is important decrease in SNP heritability (Figure 1A) and loss of power (Figure 2A), inadvertently contributing to the missing heritability problem. For example, in a study on MDD (lifetime risk K ∼ 0.15)^{13, 40} where all control subjects are unscreened, the SNP heritability (say 0.3) would reduce by a factor of 0.72 (0.72 × 0.3 = 0.22) (hence underestimated by 28%) when not accounting for the unscreened control subjects (i.e., applying Equation 2 rather than Equation 3). For disorders such as MDD, even when control subjects have been screened, it is likely that some control subjects remain misclassified, because onset can occur throughout the lifetime. Naturally, it should also be noted that when super-control subjects are used (control subjects screened to be at the lower end of the liability distribution, for example based on low scores for the personality trait neuroticism in the context of MDD), SNP heritability estimates based on the standard transformation equation would be biased upward. The loss of power due to including unscreened control subjects can be compensated by increasing the number of control subjects (Figures 2 and S7), in particular in the context of the continuously decreasing costs for genotyping, but this requires caution when estimating the SNP heritability, because Equation 3 should then be applied rather than the standard Equation 2.
• (2)If case probands are ascertained from multiplex families, then the SNP heritability and power of GWASs are substantially reduced when using pseudocontrol subjects even for less-common disorders (see Figures 1B and 2B, respectively; modeled on families with two affected siblings). Even in the absence of deliberate ascertainment of multiplex families, studies are likely to be biased by self-ascertainment because parents from multiplex families might be more concerned with the genetic origins of the disorder. In fact, 43.6% of the 1,369 families included in the Autism Genome Project (AGP) had two or more children affected with ASD while counting up to third-degree relatives.⁷ However, the proportion of multiplex families is often not reported, as is the case for the family-based studies,^{41, 42, 43} contributing to the most recent ADHD meta-analysis,⁶ which leaves the loss in power due to included multiplex families unknown, but likely. In addition, in a number of families with a first affected child, parents will stop having children, so that a second affected child is never observed. Our results are consistent with the simplex versus multiplex and simulation results of Klei et al. in analyses of ASD samples.⁴⁴
• (3)Assortative mating considerably decreases the SNP heritability assessed from trio design compared to screened control subjects also for small K (Figure 1C), but it does not impact the power to detect a single locus under a polygenic model, because of the small proportions of variation explained by single loci (<1%). Assortative mating is possibly common for psychiatric disorders^{22, 23, 24, 25} and needs to be considered when interpreting SNP heritability in general and for trio design in particular. These results and point (2) could explain why lower SNP-based heritabilities were found in the ADHD pseudocontrol samples from the Psychiatric Genomics Consortium compared to case-control samples (see Table S5 of Lee et al.).¹⁴

We also take the opportunity to re-emphasize that parameterization of power in terms of genotype relative risk can be misleading because the same RR_Bb operating in common disease implies a much higher proportion of variance explained by the locus compared to a locus operating in a less common disease. For example, when the risk allele has frequency p = 0.2 and effect size RR_Bb = 1.1, the locus explains 0.05%, 0.08%, and 0.13% of the variance in disease liability for a disorder of frequency K = 0.01, 0.05, and 0.15, respectively. Hence, to detect a locus that explains the same proportion of variance in liability, much larger samples are needed for common disorders (Figure 3). For example, samples of n = 4,059 (50% case subjects, 50% screened control subjects) are needed to detect a locus that explains 0.5% of the variance in liability for a disorder lifetime risk K = 0.01 (RR_Bb = 1.39), compared to samples of n = 9,181 when the disorder risk is K = 0.15 (RR_Bb = 1.21). Similar arguments have been used to explain that much larger GWAS samples are needed for MDD compared to schizophrenia.⁴⁵

To the best of our knowledge, the impact of the trio design and use of unscreened control subjects on the SNP heritability has not yet been addressed, but our power analyses build upon a rich literature exploring the characteristics of family-based association studies in the pre-GWAS era. Ferreira et al. showed that the trio-based transmission disequilibrium test (TDT) has less power when an additional (non-genotyped) sibling is affected compared to random families with one affected sibling.¹⁸ Li et al.,¹⁹ Risch and Teng,⁴⁶ and Risch⁴⁷ showed that case-control studies are generally more powerful when case subjects are from families with an additional affected sibling, which is in line with our results (Figure 2B compared to Figure 2A). Teng and Risch found that family-based approaches have less power than case-unrelated control strategies for families with multiple affected siblings.²⁰ Of note, our paper focuses on the pseudocontrol trio design, because this is how the trio design is typically applied in GWASs; however, the TDT has often been applied for candidate genes and could yield more power for rare disorders as has been indicated by Laird et al.²¹ The power to detect a locus with the use of unscreened control subjects can readily be calculated with the online power calculator of Purcell et al.³³ or the Quanto software from Gauderman.⁴⁸ Nevertheless, our study adds also to the current literature on the power to detect a single locus, because we directly compare pseudocontrol studies to screened control studies for multiplex families and assortative mating. As expected, there is overall similarity between consequences of design for the power to detect a single risk variant and expected SNP heritability, but in this study we have formalized these expectations and also shown that such similarity does not hold when considering assortative mating that impacts the estimated SNP heritability but not in power to detect a single risk variant.

To conclude, we advise against the use of trio designs for disorders with a polygenic genetic architecture, such as psychiatric disorders, and we advise careful consideration when using unscreened control subjects for prevalent disorders, because these designs can result in an underestimated SNP heritability and decreased power to detect an associated risk allele.

Published: February 4, 2016

Web Resources

The URLs for data presented herein are as follows:

• OMIM, http://www.omim.org/

• R statistical software, http://www.r-project.org/