Component-wise gradient boosting and false discovery control in survival analysis with high-dimensional covariates

Abstract

Motivation: Technological advances that allow routine identification of high-dimensional risk factors have led to high demand for statistical techniques that enable full utilization of these rich sources of information for genetics studies. Variable selection for censored outcome data as well as control of false discoveries (i.e. inclusion of irrelevant variables) in the presence of high-dimensional predictors present serious challenges. This article develops a computationally feasible method based on boosting and stability selection. Specifically, we modified the component-wise gradient boosting to improve the computational feasibility and introduced random permutation in stability selection for controlling false discoveries.

Results: We have proposed a high-dimensional variable selection method by incorporating stability selection to control false discovery. Comparisons between the proposed method and the commonly used univariate and Lasso approaches for variable selection reveal that the proposed method yields fewer false discoveries. The proposed method is applied to study the associations of 2339 common single-nucleotide polymorphisms (SNPs) with overall survival among cutaneous melanoma (CM) patients. The results have confirmed that BRCA2 pathway SNPs are likely to be associated with overall survival, as reported by previous literature. Moreover, we have identified several new Fanconi anemia (FA) pathway SNPs that are likely to modulate survival of CM patients.

Availability and implementation: The related source code and documents are freely available at https://sites.google.com/site/bestumich/issues.

Contact: yili@umich.edu

1 Introduction

Rapid advances in technology that have generated vast amounts of data from genetic or genome studies have led to a high demand for developing powerful statistical learning methods for extracting information effectively. For instance, understanding clinical and pathophysiologic heterogeneities among subjects at risk and designing effective treatment for appropriate subgroups is one of the most active areas in genetic studies. Wide heterogeneities present in patients’ response to treatments or therapies. Understanding such heterogeneities is crucial in personalized medicine, and discovery of genetic variants offers a feasible approach. However, serious statistical challenges arise when identifying real predictors among hundreds of thousands of candidates, and an urgent need has emerged for the development of effective algorithms for model building and variable selection.

The last three decades have given rise to many new statistical learning methods, including CART (Breiman et al., 1984), random forest (Breiman, 2001), neural networks (Bishop, 1995), SVMs (Boser et al., 1992) and high dimensional regression (Fan and Li, 2001, 2002; Gui and Li, 2005; Tibshirani, 1996, 1997). Boosting has emerged as a powerful framework for statistical learning. It was originally introduced in the field of machine learning for classifying binary outcomes (Freund and Schapire, 1996), and later its connection with statistical estimation was established by Friedman et al. (2000). Friedman (2001) proposed a gradient boosting framework for regression settings. Bühlmann and Yu (2003) proposed a component-wise boosting procedure based on cubic smoothing splines for L2 loss functions. Bühlmann (2006) demonstrated that the boosting procedure works well in high-dimensional settings. For censored outcome data, Ridgeway (1999) applied boosting to fit proportional hazards models, and Li and Luan (2005) developed a boosting procedure for modeling potentially non-linear functional forms in proportional hazards models.

Despite the popularity of aforementioned methods, issues such as false discovery (e.g. seletion of irrelevant SNPs) and difficulty in identifying weak signals present further barriers. Simultaneous inference procedure, including the Bonferroni correction, has been widely used in large-scale testing literature. However, in many high-dimensional settings, such as in genetic studies, variable selection is serving as a screening tool to identify a set of genetic variants for further investigation. Hence, a small number of false discoveries would be tolerable and simultaneous inference would be too conservative. In contrast, the false discovery rate (FDR), defined as the expected proportion of false positives among significant tests (Benjamini and Hochberg, 1995), is a more relevant metric for false discovery control under the framework of variable selection. However, few existing variable selection algorithms control false discoveries. This has brought an urgent need of developing computationally feasible methods that tackle both variable selection and false discovery control.

We propose a novel high-dimensional variable selection method for survival analysis by improving the existing variable selection methods in several aspects. First, we have developed a computationally feasible variable selection approach for high-dimensional survival analysis. Second, we have designed a random sampling scheme to improve the control of the false discovery rate. Finally, the proposed framework is flexible to accommodate complex data structures.

The rest of the article is organized as follows. In Section 2 we introduce notation and briefly review the L₁ penalized estimation and gradient boosting method that are of direct relevance to our proposal. In Section 3 we develop the proposed approach, and in Section 4 we evaluate the practical utility of the proposal via intensive simulation studies. In Section 5 we apply the proposal to analyze a genome-wide association study of cutaneous melanoma. We conclude the article with a brief discussion in Section 6.

2 Model

2.1 Notation

Let D_i denote the time from onset of cutaneous melanoma to death and C_i be the potential censoring time for patient i, $i=1,\dots ,n$. The observed survival time is $T_i=\min \{D_i,C_i\}$, and the death indicator is given by ${\delta }_i=I(D_i\le C_i)$. Let ${\mathbf{X}}_i={(X_{i1},\cdots ,X_{ip})}^T$ be a p-dimensional covariate vector (contains all the SNP information) for the ith patient. We assume that, conditional on ${\mathbf{X}}_i$, D_i is independently censored by C_i. To model the death hazard, consider

$${\lambda }_i(t|{\mathbf{X}}_i)=\underset{dt\to 0}{\lim }\frac{1}{dt}Pr(t\le D_i<t+dt|D_i\ge t,{\mathbf{X}}_i)={\lambda }_0(t)\exp ({\mathbf{X}}_i^T\mathit{\beta }),$$

where ${\lambda }_0(t)$ is the baseline hazard function and $\mathit{\beta }=({\beta }_1,\cdots ,{\beta }_p)$ is a vector of parameters. The corresponding log-partial likelihood is given by

$$l_n(\mathit{\beta })={\displaystyle \sum _{i=1}^n{\delta }_i}\left[{\mathbf{X}}_i^T\mathit{\beta }-\log \left\{{\displaystyle \sum _{\ell \in R_i}\exp }\left({\mathbf{X}}_{\ell }^T\mathit{\beta }\right)\right\}\right],$$

where $R_i=\{\ell :T_{\ell }\ge T_i\}$ is the at-risk set. The goal of variable selection is to identify $S_0=\{j:{\beta }_j\ne 0\}$, which contains all the variables that are associated with the risk of death.

2.2 L₁ penalized estimation

Tibshirani (1997) proposed a Lasso procedure in the Cox model, e.g. estimate $\mathit{\beta }$ via the penalized partial likelihood optimization

$$\widehat{\mathit{\beta }}={\displaystyle \underset{\mathit{\beta }}{\text{argmax}}}\{l_n(\mathit{\beta })-\lambda ||\mathit{\beta }|{|}_1\},$$ (1)

where $\parallel ·{\parallel }_1$ is the L₁ norm. To solve (1), Tibshirani (1997) considered a penalized reweighted least squares approach. Let $\mathbf{X}=({\mathbf{X}}_1,\dots ,{\mathbf{X}}_n)$ be the p × n covariate matrix and define $\eta ={\mathbf{X}}^T\mathit{\beta }$. Let $l_n^{\prime }(\eta )$ and $l_n^{″}(\eta )$ be the gradient and Hessian of the log-partial likelihood with respect to $\eta$ respectively. Given the current estimator $\widehat{\eta }={\mathbf{X}}^T\widehat{\mathit{\beta }}$, a two-term Taylor expansion of the log-partial likelihood leads to

$$l_n(\mathit{\beta })\approx \frac{1}{2}{(z(\widehat{\eta })-{\mathbf{X}}^T\mathit{\beta })}^T{l}_n^{″}(\widehat{\eta })(z(\widehat{\eta })-{\mathbf{X}}^T\mathit{\beta }),$$

where $z(\widehat{\eta })=\widehat{\eta }-l_n^{″}{(\widehat{\eta })}^{-1}{l}_n^{\prime }(\widehat{\eta })$. Similar to the problem of conditional likelihood (Hastie and Tibshirani, 1990), the matrix $l_n^{″}(\widehat{\eta })$ is non-diagonal, and solving (1) may require $O(n^3)$ computations. To avoid this difficulty, Tibshirani (1997) used some heuristic arguments to approximate the Hessian matrix with a diagonal one, e.g. treated off-diagonal elements as zero. An iteratively procedure is then conducted based on the penalized reweighed least squares

$$\frac{1}{n}{\displaystyle \sum _{i=1}^{n}w}{(\widehat{\eta })}_i{(z{(\widehat{\eta })}_i-{\mathbf{X}}_i^T\mathit{\beta })}^2+\lambda ||\mathit{\beta }|{|}_1,$$ (2)

where the weight $w{(\widehat{\eta })}_i$ for subject i is the ith diagonal entry of $l_n^{″}(\widehat{\eta })$.

To obtain a more accurate estimation, Gui and Li (2005) used a Cholesky decomposition to obtain $A={(l_n^{″}(\widehat{\eta }))}^{1/2}$ such that ${\mathbf{A}}^T\mathbf{A}=l_n^{″}(\widehat{\eta })$. The iterative procedure in (2) is then revised as

$$\frac{1}{n}{\displaystyle \sum _{i=1}^N(z^{*}(}\widehat{\eta }{)}_i-{\mathbf{X}}_i^{*}{}^T\mathit{\beta }{)}^2+\lambda ||\mathit{\beta }|{|}_1,$$

where $z^{*}(\widehat{\eta })=Az(\widehat{\eta })$ and ${\mathbf{X}}^{*}=AX$. Alternatively, Geoman (2010) combined gradient descent with Newton’s method and implemented his algorithm in an R package penalized.

2.3 Gradient boosting

Gradient boosting has emerged as a powerful tool for building predictive models; its application in the Cox proportional hazards models can be found in Ridgeway (1999) and Li and Luan (2005). The idea is to pursue iterative steepest ascent of the log likelihood function. At each step, given the current estimate of $\mathit{\beta }$, say $\widehat{\mathit{\beta }}$, let $\widehat{\eta }={\mathbf{X}}^T\widehat{\mathit{\beta }}$. The algorithm computes the gradient of the log-partial likelihood with respect to ${\eta }_i$, the ith component of $\eta$,

$$U_i=\frac{\partial }{\partial {\eta }_i}{l}_n(\eta ){|}_{\eta =\widehat{\eta }}={\delta }_i-{\displaystyle \sum _{\ell =1}^n\frac{{\delta }_{\ell }I(T_i\ge T_{\ell })\exp ({\widehat{\eta }}_i)}{{\displaystyle \sum _{k=1}^{n}I}(T_k\ge T_{\ell })\exp ({\widehat{\eta }}_k)}},$$

for $i=1,\cdots ,n$, and then fits this gradient (also called working response or pseudo response) to $\mathbf{X}$ by a so-called base procedure (e.g. least squares estimation). Specifically, to facilitate variable selection, a component-wise algorithm can be implemented by restricting the search direction to be component-wise (Bühlmann and Yu, 2003; Li and Luan, 2005). For instance, fit component-wise model

$${\tilde{\beta }}_j=\underset{{\beta }_j}{\text{argmin}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{(U_i-X_{ij}{\beta }_j)}^2},$$

for $j=1,\dots ,p$. Compute

$$j^{\star }=\underset{1\le j\le p}{\text{argmin}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{(U_i-X_{ij}{\tilde{\beta }}_j)}^2}.$$

and update ${\widehat{\beta }}_{j^{\star }}={\widehat{\beta }}_{j^{\star }}+v {\tilde{\beta }}_{j^{\star }}$, where v is a positive small constant (say 0.01) controlling the learning rate (Friedman, 2001). For least squares estimation, the gradient boosting is is exactly the usual forward stagewise procedure (termed as linear-regression version of the forward-stagewise boosting in Algorithm 16.1 of Hastie et al., 2009). Bühlmann and Hothorn (2007) refer to the same procedure as “L2boost”.

This approach is to detect a component-wise direction along which the partial likelihood would ascend most rapidly. At each boosting iteration only one component of $\mathit{\beta }$ is selected and updated. The variable selection can be achieved if boosting stops at an optimal number of iterations. This optimal number works as the regularization parameter and it can be determined by cross-validation (Simon et al., 2011). However, as we will show in simulation, the cross-validated choice still includes certain amount of false positive selections. A computationally feasible method is needed to control false discoveries.

2.4 Control of the false discovery rate (FDR)

Benjamini and Hochberg’s FDR-controlling procedure (Benjamini and Hochberg, 1995), or BH’s procedure for short, is a recent innovation for controlling the FDR. Consider a setting where we test a large number of tests simultaneously. Let R be the number of total discoveries (selection of SNPs) and let V be the number of false discoveries (selection of irrelevant SNPs). If we denote the False Discovery Proportion by

$$\text{FDP}=V/R,$$

then FDR is simply the expectation of false discovery proportion (FDP). In the simplest setting (i.e. P-values associated all component tests are independent), BH’s procedure is able to control the FDR at any preselect level $0<q<1$ (called the FDR-control parameter).

In the past 20 years, BH’s procedure has inspired a great deal of research: many variants of the procedure have been proposed, and many insights and connections have been discovered. For instance, Efron (2008, 2012) and Storey (2003) have pointed out an interesting connection between the BH’s procedure and the popular Empirical Bayes method. In particular, they proposed a Bayesian version of the FDR which they call the Local FDR (Lfdr) and showed that two versions of FDR are intimately connected to each other. Another useful variant of BH’s procedure is the Significance Analysis of Microarrays (SAM; Tusher et al., 2001), a method that was originally designed to identify genes in microarray experiments. While the success of the BH’s procedure hinges on an accurate approximation of the P-values associated with individual tests, SAM is comparably more flexible for it is able to handle more general experimental layouts and summary statistics, where the P-values may be hard to obtain or to approximate. See Efron (2012) for a nice review on FDR-controlling methods, Lfdr and SAM.

3 Proposed methods

3.1 Component-wise gradient boosting procedure

To introduce the proposed method, we first consider a variant of component-wise gradient boosting method that is computationally efficient in high-dimensional settings.

Algorithm 1 (Componentwise Gradient Boosting)

Initialize ${\widehat{\mathit{\beta }}}^{(0)}=0$. For $m=1,\cdots ,M_{stop}$, iterate the following steps:

1. For $j=1,\dots ,p$, compute the componentwise gradient

   $$G_j=\frac{\partial }{\partial {\beta }_j}{l}_n(\mathit{\beta }){|}_{\mathit{\beta }={\widehat{\mathit{\beta }}}^{(m-1)}}.$$ (3)

2. Compute $j^{\star }={\text{argmax}}_{1\le j\le p}|G_j|.$

3. Update ${\widehat{\beta }}_{j^{\star }}^{(m)}={\widehat{\beta }}_{j^{\star }}^{(m-1)}+v {\tilde{\beta }}_{j^{\star }}$, where ${\tilde{\beta }}_{j^{\star }}$ can be estimated by one-step Newton’s update

   $${\tilde{\beta }}_{j^{\star }}={\{\frac{{\partial }^2}{\partial {\beta }_{j^{\star }}^2}{l}_n(\mathit{\beta }){|}_{\mathit{\beta }={\widehat{\mathit{\beta }}}^{(m-1)}}\}}^{-1} \frac{\partial }{\partial {\beta }_{j^{\star }}}{l}_n(\mathit{\beta }){|}_{\mathit{\beta }={\widehat{\mathit{\beta }}}^{(m-1)}}.$$

4. Iterate until $m=M_{stop}$ for some stopping iteration M_stop.

Algorithm 1 is closely connected to the traditional boosting procedure we described in Section 2.3, which first computes the working response, U_i, and then fits the working response to each covariate by least squares. For instance, under the chain rule of differentiation,

$$\underset{1\le j\le p}{\text{argmin}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{(U_i-X_{ij}{\tilde{\beta }}_j)}^2}=\underset{1\le j\le p}{\text{argmax}}|{\displaystyle \sum _{i=1}^n{U}_i}{X}_{ij}|=\underset{1\le j\le p}{\text{argmax}}|G_j|,$$

where G_j was defined in (3).

In contrast, Algorithm 1 is based on gradient with respect to $\mathit{\beta }$ and it avoids the calculation of working response. Such a component-wise update is connected with a minimization-maximization (MM) algorithm (Hunter and Lange, 2004; Lange, 2013). For instance, in a minorization step, given the mth step estimate ${\widehat{\mathit{\beta }}}^{(m-1)}$, an application of Jensen’s inequality leads to the following minority surrogate function

$$\begin{array}{l}{l}_n(\mathit{\beta })\ge {\displaystyle \sum _{j=1}^p{\displaystyle \sum _{i=1}^n{\alpha }_j}}{\delta }_i[\frac{X_{ij}}{{\alpha }_j}({\beta }_j-{\widehat{\beta }}_j^{(m-1)})+{\mathbf{X}}_i^T{\widehat{\mathit{\beta }}}^{(m-1)}\\ \hspace{1em}-\log \left\{{\displaystyle \sum _{\ell \in R_i}\exp }\left(\frac{X_{\ell j}}{{\alpha }_j}({\beta }_j-{\widehat{\beta }}_j^{(m-1)})+{\mathbf{X}}_{\ell }^T{\widehat{\mathit{\beta }}}^{(m-1)}\right)\right\}]\\ =g(\mathit{\beta }|{\widehat{\mathit{\beta }}}^{(m-1)})={\displaystyle \sum _{j=1}^{p}g}({\beta }_j|{\widehat{\mathit{\beta }}}^{(m-1)}),\end{array}$$

where $g({\beta }_j|{\widehat{\mathit{\beta }}}^{(m-1)})$ is defined implicitly, all ${\alpha }_j\ge 0,\hspace{0.17em}{\sum }_j{\alpha }_j=1$ and ${\alpha }_j>0$ whenever $X_{ij}\ne 0$. In the maximization step, we maximize (or monotonically increase) the selected component of the surrogate function to produce the next iteration estimators, e.g. consider $g({\beta }_{j^{\star }}|{\widehat{\mathit{\beta }}}^{(m-1)})$ and update ${\beta }_{j^{\star }}$. Then the boosting algorithm monotonically increase the original log-partial likelihood by increasing the surrogate functions. Note that as long as the ascent property is achieved, the choice of α_j is not crucial, e.g. it can be considered as part of a control for step size. Moreover, as one only needs to increase the surrogate function instead of maximizing it, one-step Newton iterations (with step-size control) shall provide sufficient and rapid updates at each boosting step. The parameter v can be regarded as controlling the step size of the one-step Newton procedure. This may explain the reason that in practice the best strategy for learning rate of a boosting procedure is to set v to be very small (v < 0.1).

Instead of using ${\tilde{\beta }}_{j^{\star }}$, an alternative approach is to use the normalized updates with norm normalized to be 1, e.g. ${\widehat{\beta }}_{j^{\star }}^{(m)}={\widehat{\beta }}_{j^{\star }}^{(m-1)}+v\times \text{sign}(G_j)$. Its main disadvantage is that its performance is sensitive to the choice of learning rate. Although $\text{sign}(G_j)$ provides an ascent direction, a sufficiently small step length may be needed. Empirically we found that the procedure with fitted ${\tilde{\beta }}_{j^{\star }}$ provides better performance.

3.2 Boosting with stability selection for false discovery control

Stability Selection was recently introduced by Meinshausen and Bühlmann (2010) as a general technique designed to improve the performance of a variable selection algorithm. The idea is to identify variables that are included in the model with high probabilities when a variable selection procedure is performed on randomly sampled of the observations. For completeness of exposure, we summarize the procedure of stability selection as follows. Let I be a random subsample of $\{1,\cdots ,n\}$ of size $\lfloor n/2\rfloor$, draw without replacement. Here $\lfloor n/2\rfloor$ is defined as the largest integer not greater than $n/2$. For variable $j\in \{1,\cdots ,p\}$, the random sampling probability that the jth variable is selected by the stability selection is

$${\widehat{\Pi }}_j=P{r}^{*}[j\in \widehat{S}(\mathbf{I})],$$

where $\widehat{S}(\mathbf{I})=\{j:{\widehat{\beta }}_j^{(\mathbf{I})}\ne 0\}$ denotes the variable selected by the variable selection procedure based on the subsample I, and the empirical probability $P{r}^{*}$ is with respect to the random sampling. For a threshold ${\Pi }_{\text{thres}}\in (0,1)$, the set of variables selected by stability selection is then defined as

$${\widehat{S}}_{\text{stable}}=\{j:{\widehat{\Pi }}_j\ge {\Pi }_{\text{thres}}\}.$$

A particularly attractive feature of stability selection is that its relatively insensitive to the tuning parameter (e.g. M_stop for boosting) and hence cross-validation can be avoided. However, a new regularization parameter needs to be determined is the threshold Π_thres. To address this question, an error control was provided by an upper bound on the expected number of falsely selected variables (Meinshausen and Bühlmann, 2010; Theorem 1). More formally, let $E|\widehat{S}(I)|$ be the expected number of selected variables and define V to be the number of falsely selected variables. Assume an exchangeable condition, then the expected number V of falsely selected variables is bounded for ${\Pi }_{\text{thres}}\in (0.5,1)$ by

$$E[V]\le \frac{1}{2{\Pi }_{\text{thres}}-1}\frac{{(E|\widehat{S}(I)|)}^2}{p}.$$

Based on such a bound, the tuning parameter Π_thres can be chosen such that $E[V]$ is controlled at the desired level, e.g. for $E[V]<1$, if $E|\widehat{S}(I)|<p^{\frac{1}{2}}$,

$${\Pi }_{\text{thres}}=\left(1+\frac{{(E|\widehat{S}(I)|)}^2}{p}\right)/2.$$ (4)

The property of the above procedure relies on restricted assumptions such as exchangeability condition (e.g. the joint distribution of outcomes and covariates is invariant under permutations of non-informative variables), which, as noted by Meinshausen and van de Geer (2011), are not likely to hold for real data. In genetic studies with extensive correlation structure among SNP markers, the exchangeability condition fails and using threshold in (4) has been shown to suffer a loss of power (Alexander and Lange, 2011). Moreover, in computing the threshold in (4), we face a tradeoff. Commonly used variable selection procedures will select certain amount of false positives. On one hand, we want $E|\widehat{S}(I)|$ to be large to select the true informative predictors, but on the other hand, a large $E|\widehat{S}(I)|$ also can render Π_thres large (which leads to too conservative threshold). If $E|\widehat{S}(I)|>p^{\frac{1}{2}}$, we cannot control the error $E[V]$ with the formula in (4).

To improve the performance of stability selection and determine a data-driven threshold for the selection frequency, we adopt the idea of SAM (Tusher et al., 2001) and propose a random permutation based stability selection boosting procedure.

Algorithm 2 (Boosting with Stability Selection and Permutation)

1. For $s=1,\cdots ,100$, we draw random subsample of the data of size $\lfloor n/2\rfloor$. On the sth subsample, implement the proposed boosting approach (e.g. Algorithm 1). Record the set of selected predictors at the sth subsampling, ${\widehat{S}}^{(s)}=\{j:{\widehat{\beta }}_j^{(s)}\ne 0\}$, and compute ${\widehat{\Pi }}_j=\frac{1}{S}{\sum }_{s=1}^{S}I(j\in {\widehat{S}}^{(s)})$, where I(A) is an indicator function taking the value 1 when condition A holds and 0 otherwise.

2. For $b=1,\cdots ,B$, randomly permute the outcomes so that the relation between covariates and outcomes is decoupled. Repeat the stability-based boosting described in step (a) on the permuted sample and record the set of selected predictors ${\tilde{S}}^{(b)}$, and compute ${\tilde{\Pi }}_j^b=\frac{1}{S}{\sum }_{s=1}^{S}I(j\in {\tilde{S}}^{(b)})$.

3. Order the values of ${\widehat{\Pi }}_j$ for $1,\cdots ,p$, and let ${\widehat{\Pi }}_{(j)}$ be the jth largest value. Likewise let ${\tilde{\Pi }}_{(j)}^{(b)}$ be the jth largest value of ${\tilde{\Pi }}^{(b)}=({\tilde{\Pi }}_1^{(b)},\cdots ,{\tilde{\Pi }}_p^{(b)})$.

4. Define the estimated empirical Bayes false discovery rate (Efron, 2012) corresponding to the jth largest ${\widehat{\Pi }}_{(j)}$ as

   $${\overline{Fdr}}_{(j)}=\min \left\{\frac{1}{B}\frac{{\displaystyle \sum _{b=1}^B{\displaystyle \sum _{j\prime =1}^{p}I}}({\tilde{\Pi }}_{j\prime }^{(b)}\ge {\widehat{\Pi }}_{(j)})}{{\displaystyle \sum _{j\prime =1}^{p}I}({\widehat{\Pi }}_{j\prime }\ge {\widehat{\Pi }}_{(j)})},1\right\}.$$
5. For a pre-specified value $q\in (0,1)$, calculate a data-driven threshold

   $${\widehat{\Pi }}_{\text{thres}}(q)=\min \{{\widehat{\Pi }}_{(j)}:{\overline{Fdr}}_{(j)}\le q\}.$$

   Then this ${\widehat{\Pi }}_{\text{thres}}(q)$ can be used to determine the selected variables. If q = 0.2 and 5 variables are selected with selection frequency greater than ${\widehat{\Pi }}_{\text{thres}}(0.2)$, then 1 of these 5 variables would be expected to be false positive.

4 Simulations

Finite-sample properties of the proposed method were evaluated through a series of simulation studies. Death times were generated from the exponential model, $\lambda (t|{\mathbf{X}}_i)=0.5\exp ({\mathbf{X}}_i^T\mathit{\beta })$ for $i=1,\dots ,n$, where n = 1000 and ${\mathbf{X}}_i={(X_{i1},\cdots ,X_{i2000})}^T$ came from multivariate normal distributions. These 2000 predictors were in 10 blocks with equal numbers of predictors within each block. We considered three simulation schemes with within-block correlation coefficients varying between 0.2, 0.5 and 0.8. For all three schemes, the between-block correlation coefficients were 0 (i.e. independent between blocks). We chose 10 true signals; one from each block, with true β in $\pm 0.5,\pm 1,\pm 1.5,\pm 2,\pm 2.5$. All other covariate effects are zero. Censoring times were generated from uniform distributions, with the percentage of censored subjects then being approximately 20–30%. Each data configuration was replicated 100 times.

We first assess the speed of our algorithm. Table 1 compares the computation time for the proposed approach with Lasso for proportional hazard models (implemented with R package penalized). These timings were taken on an Dell laptop (model XPS 15) with quad-core 2.1-GHz Intel Core i7-3612QM processor and 8 GB RAM. Numerically, we find the proposed approach is faster than R package penalized. As a gradient based method, at each iteration the computational speed of the proposed approach is faster than those approaches that require inverting the Hessian matrix. It is known that finding the proper regularization parameter is difficult for the Lasso procedure, especially for survival settings for which piece-wise linear solution path (LARS; Efron et al., 2004) is not available and a grid search (Simon et al., 2011) or bisection method (Geoman, 2010) is required (e.g. multiple Lasso procedures are needed for a series of tuning parameters). In contrast, in boosting procedure, the number of iteration works as tuning parameter and the selection of optimal tuning parameter can be implemented in a single boosting procedure. Moreover, the optimal choice is less critical as boosting is more robust to overfitting (Hastie et al., 2009).

Table 1.

Comparisons of computation time: 1 simulation loops; n = 1000 and p = 2000

Lasso	Boosting
7.49 min	4.16 min

The boosting procedure is described in Sections 3.1; The Lasso is implemented using R package penalized; 10-fold cross-validation was implemented to determine the optimal tuning parameters.

We compared the proposed methods, Lasso for proportional hazard models, univariate approaches with either Bonferroni correction (termed Univariate Bonferroni in Table 2) or Benjamini and Hochberg’s (1995) procedure for FDR control (below a threshold 0.2; termed Univariate FDR in Table 2). For Lasso and the boosting approach without stability control (Algorithm 1), 10-fold cross-validation was implemented to determine the optimal tuning parameters (e.g. Simon et al., 2011). For the boosting approach with stability selection, we repeatedly drew 100 random subsamples of the data of size $\lfloor n/2\rfloor$. Both the thresholds defined in formula (4) and Algorithm 2 with q = 0.2 (termed S-Boosting-1 and S-Boosting-2 respectively) were used for variable selection. Table 2 shows that the boosting without stability selection (termed Boosting in Table 2) outperform the univariate approaches in the average number of false positives (FP), average FDP, average number of false negative (FN) and the empirical probabilities to identify the true signal (Power). Though the Lasso has comparable performances in terms of FN and Power, the FPs of the boosting methods are substantially fewer than the Lasso. Finally, the proposed boosting method with stability selection and permutation (S-Boosting-2) further reduces the FPs and it outperforms S-Boosting-1.

Table 2.

Summary of simulation results

Correlation	Methods	FP	FDP	FN	Power
0	Univariate Bonferroni	0.01	0	2.28	0.77
	Univariate FDR	1.94	0.18	1.49	0.85
	Lasso	185.22	0.95	0	1
	Boosting	15.76	0.61	0	1
	S-Boosting-1	0.01	0	0	1
	S-Boosting-2	0	0	0	1
0.5	Univariate Bonferroni	85.29	0.92	2.32	0.77
	Univariate FDR	172.32	0.95	0.81	0.92
	Lasso	186.17	0.95	0	1
	Boosting	22.31	0.69	0	1
	S-Boosting-1	0.08	0.01	0	1
	S-Boosting-2	0.01	0	0	1
0.8	Univariate Bonferroni	131.42	0.94	2.17	0.78
	Univariate FDR	207.52	0.96	0.68	0.93
	Lasso	185.14	0.95	0	1
	Boosting	29.25	0.75	0	1
	S-Boosting-1	0.36	0.03	0.1	0.99
	S-Boosting-2	0.03	0.01	0	1

FP: the average number of false positives; FDP: false discovery proportion; FN: average number of false negative; Power: the empirical probabilities to identify the true signal

5 Application of cutaneous melanoma data

Cutaneous melanoma (CM) is one of the most aggressive skin cancers, causing the greatest number of skin cancer related deaths worldwide. Among the CM patients, wide heterogeneities are present. The commonly used clinicopathological variables, such as tumor stage and Breslow thickness (Balch et al., 2009), may have insufficient discriminative ability (Schramm and Mann, 2011). Discovery of genetic variants would offer a feasible approach to understanding mechanisms that may affect clinical outcomes and the sensitivity of individual cancer to therapy (Liu et al., 2012, 2013; Rendleman et al., 2013). We applied our proposed procedures to a genome-wide association study reported by Yin et al. (2015) to analyze the association of 2339 common single-nucleotide polymorphisms (SNPs) with overall survival in CM patients. Our goal was to identify SNPS that are relevant to overall survival among the patients.

The dataset contains a total of 858 CM patients, with 133 deaths observed during the follow-up, where the median follow-up time was 81.1 months. The overall survival time was calculated from the date of diagnosis to the date of death or the date of the last follow-up. Genotyped or imputed common SNPs (minor allele frequency $\ge 0.05$, genotyping rate $\ge 95\%$, Hardy-Weinberg equilibrium P-value $\ge 0.00001$ and imputation r${}^2\ge 0.8$) within 14 autosomal FA genes or their $\pm 20$-kb flanking regions were selected for association analysis (Yin et al., 2015). As a result, 321 genotyped SNPs and 2018 imputed SNPs in the FA pathway were selected for further analysis. Other covariates to adjust for included age at diagnosis, Clark level, tumor stage, Breslow thickness, sentinel lymph node biopsy and the mitotic rate.

The proposed boosting procedure with stability selection was implemented to select informative SNPs (coded as 0, 1; without or with minor alleles). The importance of predictors is evaluated by the proportion of times that the predictor is selected in the model among the 100 subsamples. We also compared the proposed methods with the Lasso, the boosting procedure without stability selection and univariate approaches. The results are summarized in Table 3. The Lasso procedure selected 25 SNPs. Among them, 12 SNPs with absolute coefficients larger than 0.01 are listed in Table 3. None of these predictors pass the univariate approaches with Bonferroni correction or Benjamini and Hochberg’s (1995) procedure for FDR control (with a threshold 0.2). As we found in Section 4, these results argue that the univariate approaches may have more false negatives than other methods. In contrast, the boosting procedure selected 7 predictors, which were a subset of top 12 SNPs selected by the Lasso. To further control the false selections, the estimated false discovery rate, $\overline{Fdr}$, were also calculated to determine a data-driven threshold for the selection frequency such that $\overline{Fdr}\le 0.2$. Three of the SNPs selected by both Lasso and boosting pass the threshold ${\widehat{\Pi }}_{thres}(0.2)=72\%$. The remaining variables find insignificant support from stability selection. Table 4 summarizes the numbers of selected variables from the Lasso and the boosting without or with stability selection. These results are consistent with those from simulation section. The Lasso tends to select too many variables. The boosting selects substantially fewer variables than the Lasso. The boosting procedure with stability selection provides a control for false positives.

Table 3.

Summary of selected SNPs by Lasso (sorted by the magnitude of coefficients; only predictors with absolute coefficients larger than 0.01 are included), their estimated coefficients by boosting without stability selection, P-values based on univariate approach, selection frequencies based on stability selection

SNPs	Chromosome	Gene	${\widehat{\beta }}_{\text{Lasso}}$	${\widehat{\beta }}_{\text{Boosting}}$	P-value	Frequency (%)
rs74189161	13	BRCA2	−0.11	−0.10	0.002	72*
rs356665	9	FANCC	−0.09	−0.04	0.03	88*
rs11649642	16	FANCA	−0.08	−0.05	0.01	27
rs9567670	13	BRCA2	−0.07	−0.03	0.01	51
rs8081200	17	BRIP1	−0.06	−0.02	0.05	38
rs3087374	15	FANC1	−0.06	−0.01	0.02	73*
rs35322368	9	FANCC	0.06	0	0.03	65
rs57119673	16	FANCA	−0.04	−0.01	0.03	54
rs8061528	16	BTBD12	−0.03	0	0.12	36
rs2247233	15	FANC1	0.02	0	0.15	39
rs848286	2	FANCL	0.02	0	0.02	23
rs62032982	16	PALB2	0.01	0	0.04	34

${\widehat{\beta }}_{\text{Lasso}}$: coefficients from Lasso; ${\widehat{\beta }}_{\text{Boosting}}$: coefficients from boosting; P-value: calculated from univariate approach; Frequency $(\%)$: selection frequencies across 100 subsampling; $\overline{Fdr}$: estimated empirical Bayes false discovery rate (based 500 permuted samples); the false discovery control of the predictors under stability selection are coded by (*) to indicate that the selection frequencies pass the $\overline{Fdr}$ threshold.

Table 4.

Numbers of selected variables

Lasso	Boosting	Stability selection
25	7	3

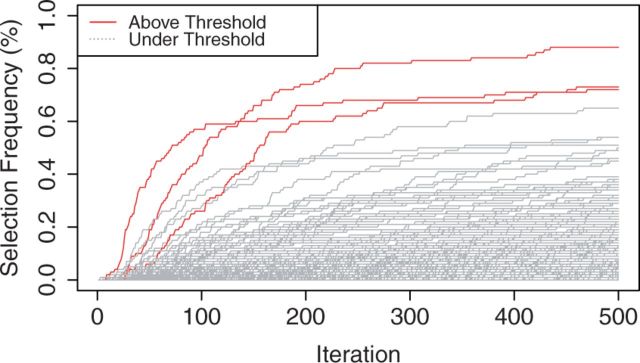
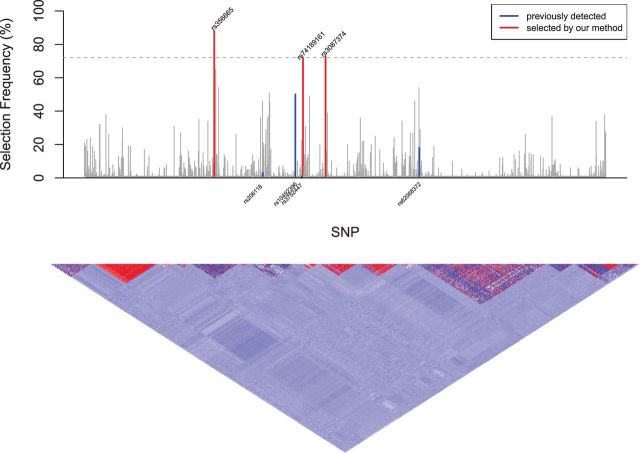
Figure 1 shows the stability path (selection frequencies across boosting iterations). The variables with selection frequencies larger than the threshold (estimated empirical Bayes false discovery rate $\overline{Fdr}\le 0.2$; based 500 permuted samples) are plotted as solid lines, while the path of the remaining variables are shown as broken lines. The top 3 variables stand out clearly and the number of boosting iteration is less critical. A Manhattan plot was given in Figure 2 with the dashed horizontal line corresponding to the estimated threshold ${\widehat{\Pi }}_{thres}(0.2)=72\%$. Three variables have selection frequencies larger than this dashed horizontal line. The vertical blue lines highlight the selection frequencies of the four previously-detected SNPs that are associated with overall survival of CM patients by Yin et al. (2015). The red vertical lines highlight the SNPs whose selection frequencies pass the estimated threshold. The lower panel of Figure 2 illustrates pairwise correlations across the 2339 SNPs with the strength of the correlation, from positive to negative, indicated by the color spectrum from red to dark blue. One of the top SNPs in our finding, rs74189161 (with selection frequency = 72% and $\overline{Fdr}=0.16$) is strongly correlated with rs3752447 identified by Yin et al. (2015), with correlation coefficients $r^2=1$ (calculated with plink v1.07; Purcell et al., 2007). Besides confirming the previously reported SNP, we also found some novel signals. For example, we identified a cluster of signals around SNP rs356665 in gene FANCC and a SNP rs3087374 in gene FANC1. Both two genes have previously been reported having regulation effects with the FA pathway (Thompson et al., 2012; Jenkins et al., 2012; Kao et al., 2011). Mutations in the FA pathway are identified in diverse cancer types (Hucl and Gallmeier, 2011) and therefore are likely to modulate the survival of CM patients.

Fig. 1.

Selection Path: selection frequencies across 500 boosting iterations; Threshold: estimated empirical Bayes false discovery rate $\overline{Fdr}\le 0.2$ (based 500 permuted samples)

Fig. 2.

Manhattarn Plot for Selection Frequency (%); dashed horizontal line: estimated threshold ${\widehat{\Pi }}_{\text{thres}}(0.2)=72\%$; vertical blue lines: selection frequencies of the four previously-detected SNPs that are associated with overall survival of CM patients by Yin et al. (2015); red vertical lines: the SNPs whose selection frequencies pass the estimated threshold; the lower panel: pairwise correlations across the 2339 SNPs with the strength of the correlation, from positive to negative, indicated by the color spectrum from red to dark blue

6 Discussion

Reducing the number of false discoveries is often very desirable in biological applications since follow-up experiments can be costly and laborious. We have proposed a boosting method with stability selection to analyze high-dimensional data. We demonstrated and compared performances of the proposed method and the commonly used univariate approaches or Lasso for variable selection. The proposed method outperformed other methods in terms of substantially reduced false positives and low false negatives.

Finally, it is worth mentioning that the traditional gradient boosting approach described in Section 2.3 cannot accommodate some important models, including survival models with time-varying effects wherein the generic function eta not only depends on X, but also on time. In contrast, the proposed modification of gradient boosting works in flexible parameter spaces, even including infinite-dimensional functional spaces. In the latter case, as the search space is typically a functional space, one needs to calculate the Gâteaux derivative of the functional in order to determine the optimal descent direction. We will report the work elsewhere.

Funding

Drs Li and Lin’s research is partly supported by the Chinese Natural Science Foundation (11528102). Dr Wei’s research is partly supported by NIH grants R01CA100264 and R01CA133996. Dr Hyslop’s research is partly supported by a NIH grant P30CA014236. Dr Lee’s research is partly supported by NCI SPORE P50 CA093459, and philanthropic contributions to The University of Texas M.D. Anderson Cancer Center Moon Shots Program, the Miriam and Jim Mulva Research Fund, the Patrick M. McCarthy Foundation and the Marit Peterson Fund for Melanoma Research.

Conflict of Interest: none declared.