Bayesian Analysis of Ambulatory Blood Pressure Dynamics with Application to Irregularly Spaced Sparse Data

Abstract

Ambulatory cardiovascular (CV) measurements provide valuable insights into individuals' health conditions in “real-life,” everyday settings. Current methods of modeling ambulatory CV data do not consider the dynamic characteristics of the full data set and their relationships with covariates such as caffeine use and stress. We propose a stochastic differential equation (SDE) in the form of a dual nonlinear Ornstein-Uhlenbeck (OU) model with person-specific covariates to capture the morning surge and nighttime dipping dynamics of ambulatory CV data. To circumvent the data analytic constraint that empirical measurements are typically collected at irregular and much larger time intervals than those evaluated in simulation studies of SDEs, we adopt a Bayesian approach with a regularized Brownian Bridge sampler (RBBS) and an efficient multiresolution (MR) algorithm to fit the proposed SDE. The MR algorithm can produce more efficient MCMC samples that is crucial for valid parameter estimation and inference. Using this model and algorithm to data from the Duke Behavioral Investigation of Hypertension Study, results indicate that age, caffeine intake, gender and race have effects on distinct dynamic characteristics of the participants' CV trajectories.

1. Introduction

Coronary heart disease (CHD) is the leading cause of morbidity and mortality in older adults, and instances of deaths due to CHD and stroke are estimated by the Centers for Disease Control and Prevention (CDC) as “nearly twice the number of lives claimed by cancer or collectively by World War II, and the Korean and Vietnam conflicts” (Centers for Disease Control and Prevention, 1999). There has been increasing evidence that cardiovascular (CV) measures such as ambulatory blood pressure (ABP) taken in everyday, non-laboratory settings provide better diagnostic and prognostic value than multiple clinic blood pressure (BP) readings (Clement et al., 2003; Dolan et al., 2009), and are indicative of the occurrence of multiple CV events (Beckham et al., 2009; Willich et al., 1992; Muller, Tofler and Stone, 1989).

ABP and related CV activities (CA) have well established circadian patterns, characterized by rises in early morning, culminating in a plateau around noon, and followed by nocturnal (nighttime) dipping. While nighttime BP has been found to be a stronger predictor of cardiovascular risk than clinic or daytime ABP (Hansen et al., 2011), increasing evidence has pointed to the importance of also considering morning surges in ABP in addition to nighttime BP (Kario et al., 2003; Verdecchia et al., 2012). The importance of studying the dynamics of ABP is further reflected in the inclusion of trend reports in popular ABP measurement tools such as the dabl system (O'Brien, 2011), which provide indices such as time-weighted measures of variability, measures of nocturnal dip, morning surge, peak as well as trough levels, and smoothness of BP curves, among many other indices of CV events (Dolan et al., 2006; Rothwell et al., 2010). Despite the richness of the dynamic information in ABP data, diagnosis/prognosis involving ABP is typically performed on levels of ABP obtained from isolated segments of the data. As an example, morning surge is typically defined as a rise in BP > 55mmHg from the lowest nighttime reading (for a review see O'Brien, 2011). In a similar vein, individuals are identified as exhibiting BP non-dipping—a commonly used prognostic indicator of CV morbidity and mortality for both hypertensive and non-hypertensive individuals—when they show < 10% fall in systolic BP (SBP) from day to night (Ingelsson et al., 2006; Fagard et al., 2008). Such conventional approaches of analyzing ABP rely solely on levels of BP during selected time windows, and utilize levels of BP at a single time point (e.g., the lowest nighttime reading), which are less than ideal given the noisy nature of BP and other CV measures. In addition, some of the more subtle individual differences in dynamic characteristics of CV measures, such as the surge and dipping rates of CV measures, are completely bypassed.

One possible way to extract more dynamic information from individuals' full time series of CV measures is to analyze such data in the context of a stochastic differential equation (SDE) model. The SDE of choice has to capture critical aspects of CV dynamics while providing a platform to relate these dynamic attributes to individual difference characteristics such as stress levels, age, and so on. To enable SDE modeling of multiple measures of population CV activities (e.g., systolic BP, diastolic BP and heart rate), we propose a latent SDE in the form of a dual nonlinear Orstein-Uhlenbeck (OU) model with person-specific dynamic effects. This modeling framework provides a direct way to (i) represent the unobserved dynamics of CV activities based on noisy multivariate measurements from multiple subjects; (ii) accommodate subject-specific, irregularly spaced discrete time points, particularly the sparse measurements at night to minimize disruptions to the participants' sleep schedules; and (iii) allow the evaluation of questions pertaining to the dynamics of ambulatory CV data, including individual differences in morning surge and nighttime dipping patterns.

Estimation and inference of SDE models using ambulatory CV data are challenging. Due to the intractability of the proposed SDE, we employ discretization approximation (Pedersen, 1995). Unfortunately, real-life ambulatory CV data are characterized by much sparser and irregularly spaced time intervals than those investigated in most simulation studies involving nonlinear SDE models (Kou et al., 2012; Lindström, 2012). Achieving reasonable estimation properties necessitates the use of a large number of imputations between subsequent observed intervals, a procedure that quickly becomes inefficient for the kind of data considered. We develop an efficient regularized Brownian bridge sampler (RBBS) and multiresolution (MR) algorithm to fit the proposed SDE model.

2. Data Analytic and Methodological Issues

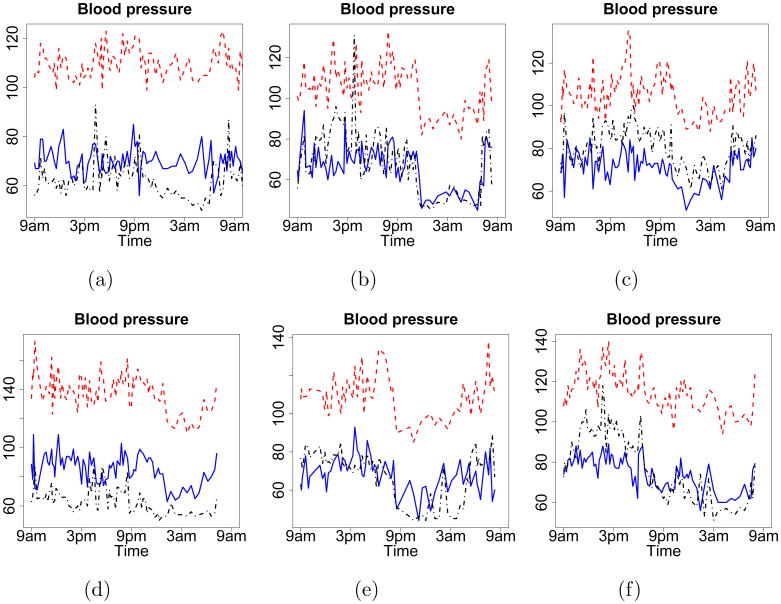
The empirical data in our study consist of CV measures from multiple subjects. Figure 1 shows the data from six subjects from the study. The red dashed, blue solid, and black dot-dashed curves are SBP, DBP, and heart rate, respectively. All three measures are characterized by relatively systematic circadian rhythms and yet, some subject-specific characteristics.

Fig 1.

Trajectories of SBP, DBP and heart rate of six subjects in the case study, which are the red dashed, blue solid, and black dot-dashed curves, respectively.

Over a 24-hour period, all three measures typically decrease to their lowest points during nighttime sleep and increase rapidly upon rising in the morning. However, the circadian patterns and magnitudes of change, which are related to cardiovascular risk, show considerable between-subject heterogeneities. Consider the baseline levels around which the trajectories fluctuate at daytime and nighttime as two equilibria. First, the differences between two equilibria may be different for different subjects. For instance, the subject in Figure 1a shows less difference in his/her daytime and nocturnal equilibria than the subject depicted in 1b, thus signaling less dipping (or poorer recovery). Second, even if the differences between two equilibria are similar, the magnitudes of the equilibria can be different (e.g., Figures 1c and 1d). Such cases demonstrate that using the differences between the equilibria alone to analyze BP data may obscure important dynamic features of the data. Third, the rates of change during dipping and surge may be different and also show various degrees of asymmetry across subjects. Both the morning surge rate and nocturnal dipping rate in Figure 1b are large; the nocturnal equilibrium, in particular, is attained very quickly and efficiently. In comparison, the subject in Figure 1e shows quick dipping and slower surge than the subject in Figure 1b, while Figure 1f shows the reverse change patterns. Lastly, SBP, DBP and HR often share common features/circadian trends within subjects, thus motivating us to use a latent process to characterize their common dynamics.

We formulate a Latent Stochastic Differential Equation Model (LSDEM) to capture subject-specific (i.e., covariate-dependent): i) daytime and nighttime CV equilibria, ii) nighttime dipping rate and morning surge rate, and iii) dipping and surge patterns. The Ornstein-Uhlenbeck (OU) process is widely used to model a stochastic process that fluctuates around an equilibrium (Uhlenbeck and Ornstein, 1930; Ricciardi and Sacerdote, 1979; Beaulieu et al., 2012). The CV patterns observed in Figures 1 motivated us to employ a modified dual-OU process model expressed as:

$$d{x}_i(t)=[I(t\in M_i){\beta }_{i1}^{\ast }{({\beta }_{i2}^{\ast }-x_i(t))}^{{\beta }_{i3}^{\ast }}+I(t\notin M_i){\beta }_{i4}^{\ast }{({\beta }_{i5}^{\ast }-x_i(t))}^{{\beta }_{i6}^{\ast }}]dt+\sqrt{\psi }d{B}_t,$$ (2.1)

where x_i(t) is the ith subject's latent CV activity at time t, M_i is subject i's daytime period, determined based on commonly used time windows and subject-specific data cues (which include e.g., the preawakening window during which participants have not started engaging in their everyday routines but may have started to show rises in CV activities), and ψ is the variance of the Wiener process, commonly referred to as the diffusion parameter. The ${\beta }_{ij}^{\ast }={\mathbf{w}}_i^T{\mathit{\beta }}_j$ for j = 1, …, 6 are subject-specific dynamic parameters, where w_i and β_j are vectors of covariates and slope parameters, respectively. Moreover, ${\beta }_{i1}^{\ast }$, ${\beta }_{i3}^{\ast }$, ${\beta }_{i4}^{\ast }$, and ${\beta }_{i6}^{\ast }$ are assumed to be positive.

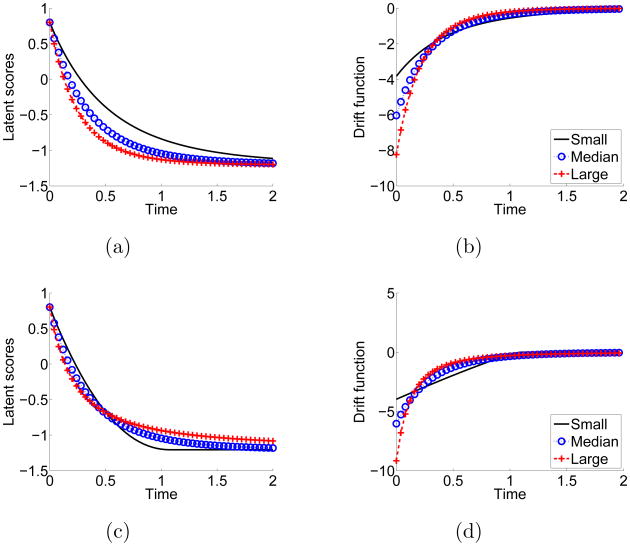
The conventional OU process is a special case of (2.1) with ${\beta }_{i1}^{\ast }={\beta }_{i4}^{\ast }$, ${\beta }_{i2}^{\ast }={\beta }_{i5}^{\ast }$, and ${\beta }_{i3}^{\ast }={\beta }_{i6}^{\ast }=1$. The drift function in (2.1) quantifies the absolute rates of change. The ${\beta }_{i2}^{\ast }$ and ${\beta }_{i5}^{\ast }$ are used to represent the daytime and nighttime equilibria, respectively, around which the CV trajectories fluctuate. It is assumed that the rate of change of CV activities is proportional to the difference between the current CV activities and the equilibrium, and the relative rates of change in daytime and nighttime are modeled by ${\beta }_{i1}^{\ast }$ and ${\beta }_{i4}^{\ast }$, respectively. The first row of plots in Figure 2 illustrates the effect of ${\beta }_{i4}^{\ast }$ during dipping. The left plots show the trajectories simulated from (2.1) with 3 levels of ${\beta }_{i4}^{\ast }$ and ψ = 0. The right plots show the corresponding values of the drift function, where a value of zero on the ordinate represents no change in the value of x_i(t) for a specific value of dt. The larger ${\beta }_{i4}^{\ast }$ is, the faster CV activities go to the night equilibrium. The ${\beta }_{i3}^{\ast }$ and ${\beta }_{i6}^{\ast }$ affect the shape of the drift function. We interpret them as the change instability parameters. The second row of Figure 2 illustrates the effect of ${\beta }_{i6}^{\ast }$ during dipping. Larger ${\beta }_{i6}^{\ast }$ leads to quicker dipping at the beginning. However, the rate of change decreases more quickly as CV activities approach the equilibrium. Hence, the rate of change is less stable. In comparison, the rate of change decreases more slowly for smaller ${\beta }_{i6}^{\ast }$ values. The interpretations of ${\beta }_{i1}^{\ast }$ and ${\beta }_{i3}^{\ast }$ are similar for morning surge.

Fig 2.

The latent scores and corresponding drift functions given different parameter values in (2.1). The first row of plots features the expected trajectories and the drift function with different relative change rates, while the second row is those with different change instabilities. The red cross, blue circle, and black solid curves are generated from large, medium, and small relative change rates or change instabilities, respectively.

We assume the diffusion parameter, ψ, to be constant in (2.1). Substantively, it is reasonable to assume that the main variations of CV activities among subjects stem from differences in mean levels of CV activities during daytime and nighttime, as well as the transitions in between, which are mainly characterized by the drift function in (2.1). Consequently, the diffusion function only characterizes the fluctuation around the equilibriums of CV activities, the scale of which is comparatively small and the differences across subjects are comparatively insignificant. Thus, we only consider a constant diffusion function in the current analysis.

Methodological challenges associated with fitting SDE models such as that shown in (2.1) can become formidable in the presence of sparse and wide-ranging time intervals. Among methods for estimating parameters in SDEs (for a review see Sørensen, 2004), likelihood-based methods have received much attention, but they require solutions of transition density functions of SDEs that are analytically available for only a very limited class of SDEs. Methods to circumvent this difficulty include closed-form expansion of the transition density (Ait-Sahalia, 2008), exact simulation method (Beskos et al., 2006; Sermaidis et al., 2013), and discrete Euler-Maruyama approximation with data augmentation between observed time points (Pedersen, 1995; Durham and Gallant, 2002; Zhu, Taylor and Song, 2011). The last approach is popular due to its general applicability, but the time intervals in studies involving ambulatory measures are usually too large to enable accurate estimation. Specifically, to achieve reasonable approximation accuracy, the time points between successive observations need to be augmented with missing data (Elerian, Chib and Shephard, 2001). Increasing the number of the augmented time points leads to better approximation, but also increases the dependency among modeling parameters and the diffusion paths (Elerian, Chib and Shephard, 2001), leading to slower convergence of the data augmentation algorithms for estimation and inference. In situations involving irregularly spaced time points, this problem is exacerbated because large time intervals require more imputed time points to insure approximation accuracy. Block updating algorithms have been proposed to alleviate the dependency among missing data at augmented time points, but the dependency between parameters in the diffusion function and the diffusion paths remains problematic in most SDEs (Roberts and Stramer, 2001). To handle these problems, we adopt a Bayesian approach for parameter estimation and inference, and utilize two efficient MCMC algorithms, namely, block updating with regularized Brownian bridge sampler (RBBS) and a multiresolution (MR) algorithm, derived and adapted respectively from Lindström (2012), and Kou et al. (2012), to fit the proposed SDE model.

Bayesian approaches have served as promising tools for the estimation and inference for SDEs (Elerian, Chib and Shephard, 2001; Roberts and Stramer, 2001; Durham and Gallant, 2002; Golightly and Wilkinson, 2008). Recently, Stramer et al. (2011) proposed the use of two different simulation-based approximations to achieve better approximation of the likelihood with fewer imputations. Golightly and Wilkinson (2011) developed particle MCMC algorithms to update the processes globally and sequentially, avoiding the dependency problem as the processes and parameters are sampled jointly.

3. Latent Stochastic Differential Equation Models (LSDEMs)

While the SDE model shown in (2.1) is designed specifically to capture ambulatory CV dynamics, our estimation algorithms are applicable to a broader class of models that includes other linear and nonlinear latent stochastic models (LSDEMs) as special cases. The general model is a hierarchical model consisting of two parts: (i) a factor analysis model that relates a vector of latent variables to their noisy, observed counterparts, and (ii) a SDE model for describing the changes in the latent variables.

3.1. Factor Analysis Model

Let x_i(t) be a q × 1 vector of latent processes of interest, where the indices i and t, respectively, denote individuals and time; y_i(t) is a p × 1 vector of observed processes (e.g., SBP, DBP, and heart rate in our study). The latent variables in x_i(t) are measured indirectly through y_i(t) based on the measurement model:

$${\mathbf{y}}_i(t)=\mathit{\mu }+\mathbf{\Lambda }{\mathbf{x}}_i(t)+{\mathit{\epsilon }}_i(t),$$ (3.1)

where μ is a p × 1 vector of intercepts, Λ is a p × q loading matrix, and ε_i(t) denotes a p × 1 vector of measurement error processes that is independent of x_i(t). In most human dynamics studies, however, we only measure y_i(t) at irregularly spaced time points t_ij for j = 1, …, T_i and i = 0, …, n, where t_ij is the jth time point for the ith individual. The measurement model (3.1) at t_ij is given by y_ij = μ + Λx_ij + ε_ij, 1 ≤ j ≤ T_i, 1 ≤ i ≤ n, where x_ij = x_i(t_ij), ε_ij = ε_i(t_ij) and y_ij = y_i(t_ij). The ε_ij is independent of x_ij and follows N(0, Σ_ε), in which Σ_ε is a diagonal matrix with diagonal elements ( ${\sigma }_{\epsilon 1}^2,\dots ,{\sigma }_{\epsilon p}^2$).

3.2. SDE Model for Latent Change Processes

We consider SDEs for delineating the dynamics of latent variables. Let d be the differential operator. The SDE model of interest is given by

$$d{\mathbf{x}}_i(t)=\mathbf{f}({\mathbf{x}}_i(t),{\mathit{\theta }}_{xi})dt+\mathbf{S}({\mathbf{x}}_i(t),{\mathit{\theta }}_{xi})d{\mathbf{B}}_i(t),$$ (3.2)

where f(·) = (f₁(·), …, f_q(·)) is a q × 1 vector of drift functions, S is a q × q matrix of diffusion functions, and B_i(t) is a q × 1 vector of standard Wiener processes, whose increments, dB_i(t), are Gaussian distributed with zero means and variances that increase with the length of time interval, dt. Moreover, θ_xi = g(w_i, b), where g(·) is a known function with a vector of parameters b and covariates w_i. One important question of our study is to identify predictors that can explain the heterogeneities in dynamics across subjects. The θ_xi is used to characterize subject-specific differences in change as related to known, person-specific covariates. A heuristic interpretation of f and S is that f governs that local changes (i.e., drift rates) in x_i(t) over dt, whereas S governs the variance of local changes, or in other words, the diffusion rates.

Since most SDEs in (3.2) do not have analytical solutions, it is common to employ a discretized approximation, such as Euler-Maruyama, at selected time points to form an approximate likelihood for model (3.2):

$$\mathrm{\Delta }{\mathbf{x}}_{ij}=\mathbf{f}({\mathbf{x}}_{ij},{\mathit{\theta }}_{xi})\mathrm{\Delta }{t}_{ij}+\mathrm{\Delta }{t}_{ij}^{1/2}\mathbf{S}({\mathbf{x}}_{ij},{\mathit{\theta }}_{xi}){\mathbf{Z}}_{ij}$$ (3.3)

for 0 ≤ j < T_i and 1 ≤ i ≤ n, where Δx_ij = x_i,j+1 − x_ij, Δt_ij = t_i,j+1 − t_ij, and Z_ij follows a multivariate Gaussian distribution N(0, I_q), in which I_q is a q × q identity matrix. When j = 0, the initial observations of the processes x_i0 are assumed to be known for all i.

Empirical data are usually sampled at relatively sparse intervals, so the Euler-Maruyama approximation (3.3) performed only at empirically observed time points usually leads to poor likelihood approximation (Elerian, Chib and Shephard, 2001). To increase the accuracy of the approximation (3.3), we impute x_i(t) at additional unobserved time points between t_ij's as missing data. In practice, the number of imputed missing data between two observed time points determines the resolution and accuracy of the approximation (3.3). Let ${\mathbf{X}}^{(0)}=({\mathbf{X}}_1^{(0)},\dots ,{\mathbf{X}}_n^{(0)})$ and ${\mathbf{X}}_i^{(0)}=({\mathbf{x}}_{i1},\dots ,{\mathbf{x}}_{i{T}_i})$ be the processes at the observed time points for the ith individual. More time points are imputed between two adjacent time points with larger Δt_ij. The time intervals after imputation are close to the minimal time interval before imputation. Denote $t_{ij}^{(1)}$ be the ith subject's jth time point after imputation, $\mathrm{\Delta }{t}_{ij}^{(1)}=t_{i,j+1}^{(1)}-t_{ij}^{(1)}$, and $x_{ij}^{(1)}=x_i(t_{ij}^{(1)})$ for $0\le j<T_i^{(1)}$ and 1 ≤ i ≤ n. Let this imputation be the 1st resolution. The accuracy of the Euler-Maruyama approximation can be refined by increasing the number of imputed time points, i.e., increasing the resolution. The kth resolution is constructed by imputing one time point between two adjacent time points at the (k − 1)th resolution. For notational simplicity, we assume that only 1 time point is imputed between each pair of adjacent observed time points to construct the 1st resolution. However, the algorithm is applicable to general situations with heterogeneous imputation at the 1st resolution. Let k* = 2^k. At the kth resolution, let ${\mathbf{x}}_{ij}^{(k)}={\mathbf{x}}_i(t_{ij}^{(k)})$, and $t_{ij}^{(k)}=t_{is}^{(k-1)}+(t_{i,s+1}^{(k-1)}-t_{is}^{(k-1)})\frac{j-2s}{2}$ for 2s ≤ j ≤ 2(s+1) and $s=0,\dots ,T_i^{(k-1)}$.

Consequently, ${\mathbf{x}}_{i,sk\ast }^{(k)}={\mathbf{x}}_{is}$. Let $\mathrm{\Delta }{t}_{ij}^{(k)}=t_{i,j+1}^{(k)}-t_{ij}^{(k)}$, ${\mathbf{X}}_i^{(k)}=({\mathbf{x}}_{i1}^{(k)},\dots ,{\mathbf{x}}_{i,T_i^{(k)}}^{(k)})$, and ${\mathbf{X}}^{(k)}=({\mathbf{X}}_1^{(k)},\dots ,{\mathbf{x}}_n^{(k)})$. The approximated transition density is

$$P_k({\mathbf{x}}_{i,j+1}^{(k)}|{\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})={\varphi }_q({\mathbf{x}}_{ij}^{(k)}+\mathbf{f}({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})\mathrm{\Delta }{t}_{ij}^{(k)},\mathrm{\Delta }{t}_{ij}^{(k)}\sum ({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})),$$ (3.4)

where $\sum ({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})=\mathbf{S}({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})\mathbf{S}{({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})}^T$ and φ_q(μ, Σ) denotes the density of a q–dimensional Gaussian random vector with mean vector μ and covariance matrix Σ.

4. Bayesian estimation and inference with MCMC algorithms

Let Y_i = (y_i1, …, y_iTi), Y = (Y₁, …, Y_n), and θ = {b, μ, Λ, Σ_ε}. We augment X^(k) to the observed data Y, and then use MCMC algorithms (Hastings, 1970; Geman and Geman, 1984) to sample P_k(θ, X^(k)|Y) ∝ P_k(Y, X^(k)|θ)P(θ). Generally, any distributions representing the prior information could be used. We assume that P(θ) = P(μ)P(Λ, Σ_ε)P(b), and use the prior distributions leading to standard full conditional distributions:

$$P({\mu }_r)={\varphi }_1({\mu }_{r0},{\sigma }_{\mu 0}^2),P({\mathbf{\Lambda }}_r)={\varphi }_p({\mathbf{\Lambda }}_{0r},{\sigma }_{\epsilon r}^2{\sum }_{\mathbf{\Lambda }r}),P({\sigma }_{\epsilon r}^2)=IG(a_{1r},a_{2r}),$$ (4.1)

where r = 1, …, p, μ_r is the rth row of μ, and ${\mathbf{\Lambda }}_r^T$ is the rth row of Λ. The μ_r0, ${\sigma }_{\mu 0}^2$, Λ_0r, a_1r, a_2r and positive definite matrix Σ_Λr are hyperparameters, the values of which are assumed to be given by prior information. The IG(·, ·) stands for the inverse gamma distribution. The μ_r estimate is more robust with different signal strengths, e.g., scale of ${\sigma }_{\epsilon r}^2$. Hence, its prior distribution is assumed to be independent of ${\sigma }_{\epsilon r}^2$. As b includes parameters that are involved in the functions f(···) and S(···), the corresponding prior distributions have to be tailored specifically to the dynamic model considered.

For sparsely spaced data, efficient sampling X^(k) is very challenging. Most approaches based on the Euler-Maruyama approximation only use one resolution k. Larger k results in better approximation, but it increases computational costs from two aspects. First, the dimension of X^(k) increases with k. Second, the MCMC efficiency decreases dramatically because smaller $\mathrm{\Delta }{t}_{ij}^{(k)1/2}\mathbf{S}({\mathbf{x}}_{ij}^{(k)},{\mathit{\theta }}_{xi})$ leads to high correlations among ${\mathbf{x}}_{ij}^{(k)}$. Consequently, more iterations of Gibbs sampler are required to obtain ‘good’ MCMC samples that cover the entire parameter/unobserved components space. Choosing k to strike an effective balance between approximation accuracy and sampling efficiency is challenging, especially for nonlinear processes, where a large k is usually required. We develop an efficient multiresolution MCMC algorithm (Kou et al., 2012) to address such challenging issue.

4.1. Multiresolution (MR) Algorithm

The MR algorithm (Kou et al., 2012) provides one way to circumvent the inadequacies of using one specific resolution scheme by consolidating samples obtained at multiple resolutions. They proposed the MR algorithm for stochastic processes observed at discrete time points for a single subject. We will extend the MR algorithm for latent processes for population data.

The MR approach is a mixture of a series of local samplers and a global sampler, and generates samples for every resolution sequentially. In each iteration, the local samplers and the global sampler are chosen with certain probabilities. The MR algorithm begins with the first resolution with the least imputation. At each resolution, any MCMC algorithms designed for a single resolution can be used as local samplers, which explore the local features of P_k(θ, X^(k)|Y). Starting from the second resolution, a global sampler called “cross-resolution sampler” is also used, which essentially performs independent Metropolis-Hastings (MH) update of X^(k) and θ jointly. Let ${\mathbf{T}}^{(k)}=\{t_{ij}^{(k)}|0\le j\le T_i^{(k)},1\le i\le n\}$ and X^(k)\(k−1) be the processes at T^(k) but not at T^(k−1). The proposal distribution q(X^(k), θ) = q(X^(k)\(k−1)|X^(k−1), θ)q(X^(k−1), θ), where q(X^(k−1), θ) = P_k−1(θ, X^(k−1)|Y). Practically, (X^(k−1), θ) are empirically sampled from the MCMC samples for P_k−1(θ, X^(k−1)|Y). The proposal samples are weighted in order that the target distribution follows P_k(θ, X^(k)|Y). The cross-resolution sampler is independent of the current state of X^(k) and θ and overcomes the degeneracy caused by increasing dependency among ${\mathbf{x}}_{ij}^{(k)}$ as k increases. Moreover, the empirical samples from a coarser resolution P_k−1(θ, X^(k−1)|Y) have lower autocorrelation. Hence, cross-resolution sampler could move across the space of X^(k) and θ faster. It is worth noting that even though the cross-resolution sampler for (X^(k), θ) is based on the MCMC samples of X^(k−1), the MCMC samples of X^(k) at T^(k−1) are partially different from those of X^(k−1) because local samplers are also used with nonzero probability. More details of the MR algorithm and cross-resolution sampler can be found in Supplement S1.2 and S1.3, and Kou et al. (2012).

4.1.1. Local Updating Algorithms

Let k̃ = k* − 1. We use two local samplers to generate posterior samples of X^(k) including (i) a 1-step RBBS that samples ${\mathbf{x}}_{ij}^{(k)}$ at each time point; and (ii) a block updating scheme for X_is = (x_i,sk*, …, x_i,(s+1)k*) based on a (k̃ + 2)-step RBBS. Related samplers were proposed for univariate and multivariate nonlinear SDEs for a single subject with observed processes, respectively, in Kou et al. (2012) and Lindström (2012). We extend these samplers to handle latent SDEs for population data. The general idea of the RBBSs is to construct a multivariate normal proposal distribution for ${\mathbf{x}}_{ij}^{(k)}$ and ${\mathbf{X}}_{is}^{(k)}$ sequentially, and use MH algorithm. Lindström (2012) is an extension of Durham and Gallant (2002)'s results on nonlinear processes, in which the drift functions dominate the diffusion functions. Users should adjust the tuning parameter α according to specific problems, for which Lindström (2012) provided intuitive suggestions. More information regarding these extensions is described in Supplement S1.4.

5. Case Study

We analyzed a set of 24-hour ambulatory CV data from the Duke Biobehavioral Investigation of Hypertension study (Sherwood et al., 2002). The dataset consists of 179 men and women whose ages range from 25 to 45 years. Ambulatory BP and other CV measures were monitored using the noninvasive AccuTracker II ABP Monitor (Suntech AccuTracker II, Raleigh, NC) from around 9 AM until the same time in the following morning. The monitors were programmed to measure four times an hour at random intervals ranging from 12 to 28 minutes apart during waking hours. During sleeping hours, the monitors were programmed to record only two readings hourly, customized to fit the participants' sleep habits. The study maintained participants' normal schedules and documented a diary entry indicating posture, activity, location, positive affect and negative affect at each reading. Mood states were scored by circling a number on a 5-point Likert Scale, with 1 representing “not at all” and 5 representing “very much”.

Covariates of interest used in x_i in model (2.1) are i) mean caffeine consumption during daytime and nighttime; ii) overall negative emotion score calculated as the mean of “Stress”, “Anger” and “Tense” ratings throughout the entire day; iii) overall positive emotion score calculated as the mean of “Happy” and “In control”ratings throughout the day; iv) gender; v) race; and vi) age. In addition, it is assumed that the effects of caffeine consumption during daytime (nighttime) only affect the CV activities in the daytime (nighttime) through ${\beta }_{i1}^{\ast }$, ${\beta }_{i2}^{\ast }$, and ${\beta }_{i3}^{\ast }$( ${\beta }_{i4}^{\ast }$, ${\beta }_{i5}^{\ast }$, and ${\beta }_{i6}^{\ast }$).

Time was rescaled such that 1 unit represents 12 hours. The resulting lengths of time intervals between two adjacent observed time points range from 0.01 to 0.48, corresponding to a range of .72 minutes to 5.76 hours in time. To form the 1st resolution, imputed time points are placed evenly between two observed time points. The time intervals between the imputed time points are around 0.07 (corresponding to 5 minutes). To obtain the daytime and nighttime windows in (2.1), we used manual coding to extract subject-specific time windows for each subject. Specifically, the daytime window for each subject was defined to end when systematic dipping of BP and heart rate were observed, while the nighttime window was defined to end when systematic rise in BP and heart rate were observed.

The measurement model for the latent process x_ij at j = sk* is given by

$${(y_{is1},y_{is2},y_{is3})}^T={(1,{\lambda }_1,{\lambda }_2)}^T{x}_{ij}+{({\epsilon }_{is1},{\epsilon }_{is2},{\epsilon }_{is3})}^T,$$ (5.1)

where y_is1, y_is2, and y_is3 are, respectively, SBP, DBP, and heart rate at the sth observed time for the ith subject. Each y_isj, j = 1, 2, 3, was standardized by the mean and standard deviation calculated using all i and s. Moreover, ${({\epsilon }_{is1},{\epsilon }_{is2},{\epsilon }_{is3})}^T~N[\mathbf{0},\mathit{\text{diag}}({\sigma }_{\epsilon 1}^2,{\sigma }_{\epsilon 2}^2,{\sigma }_{\epsilon 3}^2)]$, and the 1 in the loading matrix is fixed for identification. The initial conditions of the latent SDEs were fixed to the estimated factor scores of the subjects using the values of SBP, DBP, and heart rate at the first observed time point. Without any prior information, vague prior distributions β_j ∼ N(b_0j, Σ_0bj)I(S_j) and ψ ∼ IG(a_ψ1, a_ψ2) were assumed for the parameters in model (2.1), where b_0j = 0, Σ_0bj = 10⁶I, for j = 1, …, 6; a_ψ1 = 0.01, and a_ψ2 = 0.01. $S_j=\{{\mathbf{\beta }}_j|{\mathbf{w}}_i^T{\mathbf{\beta }}_j>0,i=1,\dots ,n\}$ for j = 1, 3, 4, 6, and S₂ = S₅ = R⁷. We also set Λ_0r = 0, Σ_Λr = 10⁶, a_1r = 3, and a_2r = 1 in (4.1).

5.1. Results

Four resolutions were used in the MR algorithm described in Section 4.1. For each resolution in the MR algorithm, 2000 burnin samples were discarded and another 4000 MCMC samples were acquired for estimation and inference. The MR algorithm improves the efficiency of the MCMC algorithm by dramatically reducing the autocorrelations of the MCMC samples of most parameters (see Supplement S2 for further details). In this study, the selection of tuning parameter α in RBBS does not affect the sampling algorithm much because the drift function does not dominate the diffusion function. Estimated posterior means (Est), standard errors (SE) and their quotient (Z) based on the finest resolution are shown in Table 1. The Z values that pass the false positive rate threshold (Benjamini and Hochberg, 1995) q=0.05 are highlighted in bold font, while those between q=0.05 and q=0.10 are highlighted in bold and italic font.

Table 1.

The estimates (Est), standard errors (SE) and Est/SE (Z) in the case study.

		Intercept	Caffeine	Negative	Positive	Gender	Race	Age
Relative	Est	2.568	0.606	0.026	0.214	0.458	0.242	-0.083
surge	SE	0.188	0.189	0.149	0.121	0.173	0.179	0.149
rate ${\beta }_1^{\ast }$	Z	13.669	3.203	0.176	1.773	2.649	1.349	-0.557
Daytime	Est	0.377	0.025	0.106	-0.014	0.206	-0.163	0.110
equilibrium	SE	0.049	0.030	0.058	0.044	0.043	0.056	0.045
${\beta }_2^{\ast }$	Z	7.624	0.827	1.839	-0.324	4.777	-2.944	2.414
Daytime	Est	1.621	-0.203	-0.196	-0.181	-0.238	-0.034	0.157
instability	SE	0.142	0.082	0.126	0.126	0.135	0.159	0.130
${\beta }_3^{\ast }$	Z	11.445	-2.480	-1.555	-1.438	-1.758	-0.212	1.212
Relative	Est	2.737	0.326	0.002	0.236	0.269	0.632	0.184
dipping	SE	0.262	0.342	0.193	0.156	0.224	0.258	0.220
rate ${\beta }_4^{\ast }$	Z	10.448	0.954	0.010	1.518	1.200	2.447	0.837
Nighttime	Est	-1.206	0.168	0.067	-0.013	0.298	-0.109	0.147
equilibrium	SE	0.115	0.063	0.075	0.084	0.073	0.106	0.072
${\beta }_5^{\ast }$	Z	-10.459	2.678	0.886	-0.159	4.081	-1.024	2.027
Nighttime	Est	1.135	0.702	0.286	-0.030	0.060	-0.113	-0.001
instability	SE	0.214	0.477	0.182	0.101	0.134	0.146	0.133
${\beta }_6^{\ast }$	Z	5.299	1.473	1.573	-0.295	0.448	-0.772	-0.006
ψ	Est	2.992	SE	0.114

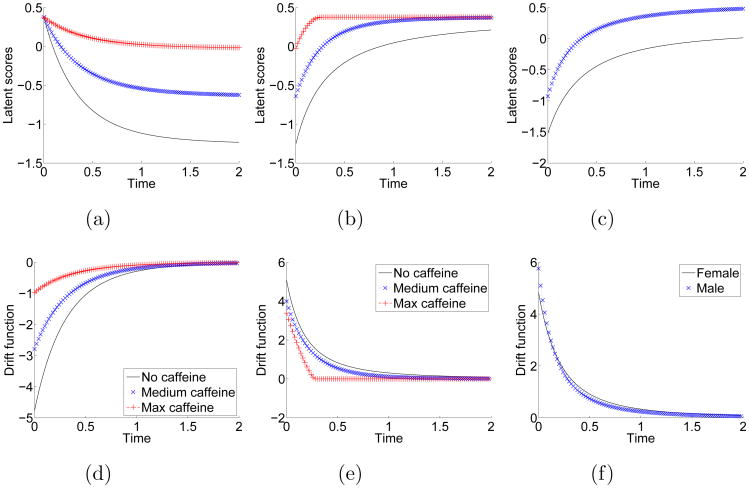
Some covariates were found to be significantly correlated with one or more aspects of the participants' CV trajectories. Based on the estimated coefficients, we numerically simulated the mean trajectories of subjects with different levels of certain covariates from (2.1), which are plotted in Figure 3. For continuous covariates, three levels of covariates were used, namely, the minimum, median, and maximum of the covariates. Table 2 shows the estimated equilibriums of SBP, DBP, and HR at daytime and nighttime for different levels of covariates.

Fig 3.

The first and second columns are the estimated mean trajectories and drift functions of CV trajectories, respectively. The first and second columns show the night dipping and morning surge given different levels of caffeine consumption, respectively. The third column displays the gender differences during morning surge.

Table 2.

Estimated equilibriums of SBP, DBP, and HR at daytime and nighttime for different levels of covariates. For continuous covariates, the first and second rows are equilibriums at the minimum and maximum of the covariates. For gender, the first row is female's equilibriums. For race, the first row is black subjects' equilibriums.

	Night Equilibrium		Morning Equilibrium
	Caffeine	Gender	Gender	Race	Age
SBP	100	95.2	125.1	131.9	126.2
	121.9	105.8	132.5	123.9	132.5
DBP	58.7	55.2	77.4	82.4	78.1
	71.7	63.1	82.8	76.4	82.8
HR	68	66.4	76.5	78.7	76.8
	75.4	70	78.9	76	78.9

We calculated the posterior predictive p-value (Gelman, Meng and Stern, 1996) of the χ² goodness of fit measure:

$$D(\mathbf{Y},\mathbf{X},\mathbf{\Lambda },{\sum }_{\mathit{\epsilon }})=\sum _{i=1}^n\sum _{j=1}^{T_i}{({\mathbf{y}}_{ij}-\mathbf{\Lambda }{\mathbf{x}}_{ij})}^T{\sum }_{\mathit{\epsilon }}^{-1}({\mathbf{y}}_{ij}-\mathbf{\Lambda }{\mathbf{x}}_{ij}).$$

Let X_k, Λ_k, and Σ_εk be the kth MCMC sample of X, Λ, and Σ_ε, respectively. Y_k was generated based on (5.1) with X_k, Λ_k, and Σ_εk. The estimated posterior predictive p-value is the proportion of D(Y_k, X_k, Λ_k, Σ_εk) that are greater than D(Y, X_k, Λ_k, Σ_εk) for all MCMC samples (0.485), indicating a reasonable fit of the model to the data. We also checked the predictive performance of our model. The pointwise estimated median and 95% credible intervals formed by all Y_k for three randomly selected subjects are displayed in Figure S3. The prediction is reasonably good even in the presence of sparsely spaced observations.

The acceptance rates of the cross-resolution move are 0.04, 0.14, and 0.27 at the 2nd, 3rd and 4th resolution, respectively. The increasing acceptance rates agree with Kou et al. (2012). As k increases, the empirical distribution for P_k−1(θ, X^(k−1)|Y) becomes a better proposal distribution because the difference between P_k−1(θ, X^(k−1)|Y) and P_k(θ, X^(k)|Y) decreases.

The estimation is not very sensitive to the specification of the hyperparameters in (4.1). Specifically, we set the covariance matrices of the multivariate normal prior distributions to 10I, which represents moderate prior covariances, and changed the prior mean to two times or half of the estimated parameters. The estimation results were similar to Table 1.

5.2. Substantive Findings

One interesting finding is that the estimated intercept of ${\beta }_3^{\ast }$ is significantly greater than 1. From a modeling aspect, this contradicts the common assumption of the linear OU process and demonstrates the added value of the nonlinear model considered. Practically, compared to the dipping at night, the daytime surge is much faster at the beginning and slower at the end, resulting in a less stable change.

The covariates were found to play discrepant roles in affecting the subjects' daytime and nighttime CV dynamics. To further shed light on the substantive implications of such differences, we compared two aspects of the modeling results thought to be important from a CV standpoint: i) daytime and nighttime equilibrium levels of CV activities (modeled by ${\beta }_2^{\ast }$ and ${\beta }_5^{\ast }$); ii) relative rates and the instability of the surge and dipping of CV activities.

Caffeine and gender were related to the CV activities equilibrium at night, while gender, race and age are related to the daytime equilibrium. i) The effects of caffeine intake in the literature remain mixed. For instance, Eggertsen et al. (1993) reported that “habitual coffee drinking did not influence the 24-hour blood pressure profiles.” However, Green and Suls (1996) found that caffeine intake affected daytime SBP as well as DBP, and night time BP. Lane et al. (2002) showed increased levels of ABP persisting for a few hours following caffeine consumption. In this study, we found that caffeine significant increased the CV activities equilibrium at night (β₅₁), which is shown in Figure 3a. In contrast, caffeine intake in the daytime did not affect the CV activities equilibrium in the morning (Figure 3b). ii) Carels, Blumenthal and Sherwood (2000) showed that effect of negative emotion increases the whole day CV activities. However, the daytime and nighttime CV activities were not studied separately. In our study, the daytime equilibrium was not related to negative emotion. iii) We found that male subjects have higher equilibrium in both day and night. Studies using 24-hour ABP have shown that BP is higher in men than in women at similar ages (Reckelhoff, 2001). iv) Elder subjects have higher daytime equilibrium. In the US population, SBP increases progressively with age, and DBP peaks at around age 55 years. Central arterial stiffening with age is considered to account for this phenomenon (Franklin et al., 1997). v) Minority subjects exhibit higher daytime equilibrium. However, black and white subjects do not show much difference in the nighttime equilibrium. Hinderliter et al. (2004) reported that African Americans have a smaller nocturnal decline in BP than white subjects.

The disagreement between Hinderliter et al. (2004) and our result regarding race difference in nighttime equilibrium may be explained by the relative rate of change found to be smaller for black subjects in our model. In Hinderliter et al. (2004), the daytime and nighttime BP were defined to be the average BP when subjects are awake or asleep. As illustrated in Figure 2a, the average score is larger for subjects with smaller rate of change even when the daytime and nighttime equilibriums are identical. In this aspect, our result agrees with Hinderliter et al. (2004), which may shed light on the advantage of our data analysis by considering the change of CV activities in addition to equilibriums.

The rate of change of CV activities was seldom studied in the literature. i) We found that white subjects have faster nighttime relative dipping rate. The pattern of latent scores and drift functions are similar to those shown in Figures 2a and 2b. ii) The daytime surge rate and stabilization parameter are affected by daytime caffeine intake. Although the absolute rates of change of caffeine users are relative small due to the smaller difference between the two equilibriums, relative morning surge rates are larger and the surge rates are more stable. The patterns of latent scores and drift functions for subjects with different levels of caffeine consumption are shown in Figures 3b and 3e. iii) Male subjects have higher relative surge rate. The latent scores and drift functions for male and female are shown in Figures 3c and 3f.

6. Conclusion

We have presented a latent SDE framework for population dynamic data with covariates measured at irregularly spaced time points. Using the Euler-Maruyama approximation to generate numerical solutions of the SDEs, several local and global samplers for sampling the latent processes have been developed based on modifications of existing samplers in the literature. The proposed model has been applied to the Duke Biobehavioral Investigation of Hypertension study. Significant covariate effects have been identified. Risk factors of Coronary heart disease (CHD) in different scenarios have been discussed. Several scientific findings in our analysis were not evident from previous studies. First, more information of the population dynamic data is revealed in our study. Instead of studying the difference between daytime and nighttime CV activities, we investigate several dynamic characteristics of CV activities, including the daytime and nighttime equilibriums, rates of change and change stability during the night dipping and morning surge, respectively. Second, we explain the variation among the population dynamic data with the effects of covariates. We identify covariates that are correlated with these dynamic characteristics. Third, the covariates effects for the characteristics in daytime and nighttime are found to be asymmetric.

There are still some limitations of the proposed model, and further developments are needed. First, the processes between different subjects are assumed to be independent in our model. One possible alternative is to consider random effects variations of the proposed modeling framework to allow for information borrowing among subjects. Second, the time windows for capturing BP surges and dipping were constructed based on subjective information. It would be more appealing to develop data-driven methods to extract daytime and nighttime windows, or estimate the transition/change points empirically (e.g., Barry and Hartigan, 1993). Finally, the initial conditions of the SDEs were fixed to the estimated latent scores for each subject at the first observed time point. Other methods for approximating the unknown initial conditions (e.g., as mixed effects to be estimated as other modeling parameters; Chow et al., 2015) can, in principle, be used with the proposed MR algorithm. The effects of using different approaches to estimate the initial conditions of latent SDE models warrant further investigation.

The MR algorithm can produce efficient MCMC chains as the resolution increases. However, careful design and implementation are still required for the MR algorithm to work properly and efficiently. The proposal distribution consists of two parts, i.e., the posterior distribution at the previous resolution and the proposal distribution of the processes at additional time points at the new resolution. The posterior distribution depends recursively on the local updating algorithm at the first resolution. Thus, the performance of the local updating algorithms should be reasonably satisfactory at the first resolution in order to provide good building blocks for the MR algorithm. Otherwise, the empirical distribution of the MCMC samples may not approximate the posterior distribution well, and may not serve as a good proposal distribution in the cross-resolution sampler, resulting in low acceptance rate of the cross resolution move and offsetting any potential advantages of the MR algorithm. We use the sampler in Lindström (2012) as the second part, which contains a tuning parameter accounting for the nonlinearity of the processes. We suggest using the same tuning parameter in the local sampler with high acceptance rate.

The efficiency of the MR algorithm may be reduced when the number of subjects is large. The MR algorithm is essentially a MH algorithm, which updates the processes for all subjects at observed and imputed time points and all parameters simultaneously. Maintaining the acceptance ratio of a large number of random variables is challenging for the MH algorithm. Algorithms to update the processes subject by subject may be helpful. In addition, other MCMC algorithms (e.g., Andrieu, Doucet and Holenstein, 2010; Golightly and Wilkinson, 2011; Stramer et al., 2011) that sample the stochastic processes globally and do not lead to convergence problem when the number of imputation increases are worthy of further research.

Another caveat is that even though the block updating scheme can overcome the dependence between the latent states, the dependence between the latent states and the parameters in the diffusion function remains, as discussed by Roberts and Stramer (2001)¹. In our studies, the MCMC algorithms work satisfactorily at the first resolution, and the MR algorithm keeps improving the MCMC algorithms as the number of imputation increased. However, when the 1-step and block updating algorithm fail at the first resolution, other alternative MCMC algorithms should be considered as the building block for the MR resolution to work properly.