Abstract
Biomarkers associated with heterogeneity in subject responses to treatment hold potential for treatment selection. In practice, the decision regarding whether to adopt a treatment-selection marker depends on the effect of using the marker on the rate of targeted disease and on the cost associated with treatment. We propose an expected benefit measure that incorporates both effects to quantify a marker's treatment-selection capacity. This measure builds upon an existing decision-theoretic framework, but is expanded to account for the fact that optimal treatment absent marker information varies with the cost of treatment. In addition, we establish upper and lower bounds on the expected benefit for a perfect treatment-selection rule which provides the basis for a standardized expected benefit measure. We develop model-based estimators for these measures in a randomized trial setting and evaluate their asymptotic properties. An adaptive bootstrap confidence interval is proposed for inference in the presence of non-regularity. Alternative estimators robust to risk model misspecification are also investigated. We illustrate our methods using the Diabetes Control and Complications Trial where we evaluate the expected benefit of baseline hemoglobin A1C in selecting diabetes treatment.
Keywords: Adaptive bootstrap, Biomarker, Expected benefit, Potential outcomes, Treatment selection
1. Introduction
In many clinical settings for disease prevention and treatment, there is significant heterogeneity in subject response to the same treatment. Biomarkers associated with this heterogeneity, such as demographic or genetic characteristics, can be used to help subjects select treatment to ensure that a therapy is only delivered to subjects who are likely to benefit from it.
Statistical measures for quantifying the performance of candidate treatment-selection markers are essential for developing these markers and evaluating their clinical impact. Testing for a marker by treatment interaction is a common strategy for identifying treatment-selection markers. However, there is a growing emphasis on developing measures of treatment-selection ability that are directly linked to clinical outcomes. Much of this work focuses on the effect of using the marker on the targeted disease. For example, the reduction in population disease rate as a result of treatment selection (Song and Pepe, 2004; Zhang, Tsiatis, Laber, and others, 2012); the accuracy for classifying a subject into treatment-effective or ineffective categories (Huang and others, 2012); the distribution of the disease risk difference conditional on a marker in the population or in the marker-positive group (Cai and others, 2011; Foster and others, 2011; Huang and others, 2012; Zhao and others, 2013), all quantify, in some fashion, the impact of using the marker to select treatment on the rate of disease. In practice, a treatment may affect the population through not only its effect on the targeted disease but also other costs such as side effect burden or monetary cost. Thus, another important consideration in assessing a treatment-selection rule is the proportion of subjects selected for treatment (Janes and others, 2014). One way to incorporate both disease risk and proportion treated is to adopt a decision-theoretic framework that puts the marker's effect on disease and the proportion treated on the same scale by means of a treatment-disease cost ratio. An example is the net benefit measure characterizing the reduction in the sum of disease and treatment cost comparing a marker-based treatment strategy with the strategy of treating no one (Vickers and others, 2007, Rapsomaniki and others, 2012).
In this paper, we develop a new measure named expected benefit that extends the net benefit measure to quantify the reduction in the sum of disease and treatment cost by using the marker. This measure is based on the comparison between a marker-based treatment-selection rule and the optimal treatment strategy absent the marker information, where the latter is allowed to vary with the treatment–disease cost ratio. In addition, we propose a novel method to standardize the expected benefit of a treatment-selection strategy relative to the benefit that can potentially be achieved using a perfect treatment-selection rule. While the latter is not identifiable in general, we show that upper and lower bounds can be established through a potential outcomes framework. We develop a model-based strategy for deriving the treatment-selection rule and for estimating the corresponding (standardized) expected benefit using data from a randomized trial, and develop asymptotic theory for the estimators. The expected benefit is not a smooth function of the generative model which can cause the standard bootstrap to fail; therefore, we develop a novel adaptive bootstrap confidence interval that provides consistent inference. We also investigate alternative strategies for deriving the treatment-selection rule and estimators of expected benefit that are robust to model misspecification.
In Section 2, we introduce the concept of expected benefit, derive bounds on the expected benefit of a perfect treatment-selection rule, and define the standardized expected benefit. We develop estimation methods and theoretical results in Section 3. Simulation studies are presented in Section 4 where we investigate finite sample performance of the estimators. Application of the methodology to the Diabetes Control and Complications Trial is presented in Section 5. We then conclude the paper with a summary and discussion.
2. Methods
We consider the setting of a randomized trial with two arms, 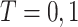 indicating the untreated and treated groups, respectively. Let
indicating the untreated and treated groups, respectively. Let 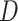 be a binary outcome that the treatment is intended to prevent, which we call “targeted disease,” with
be a binary outcome that the treatment is intended to prevent, which we call “targeted disease,” with 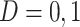 indicating control and case status, respectively, and
indicating control and case status, respectively, and 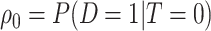 and
and 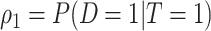 indicating disease prevalence in untreated and treated groups. Let
indicating disease prevalence in untreated and treated groups. Let 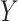 denote the biomarker of interest, which may be univariate or multivariate. Let
denote the biomarker of interest, which may be univariate or multivariate. Let 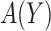 be a treatment-selection rule based on the marker, which takes values 1 and 0 corresponding to the recommendation for or against the treatment, respectively. Let
be a treatment-selection rule based on the marker, which takes values 1 and 0 corresponding to the recommendation for or against the treatment, respectively. Let 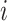 be subject indicator. With
be subject indicator. With 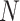 participants in the trial, we observe i.i.d. data
participants in the trial, we observe i.i.d. data  .
.
As in Vickers and others (2007), we assume the cost of the treatment due to side effects, subject burden, and/or monetary cost can be quantified as 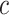 times the cost per disease outcome, where
times the cost per disease outcome, where 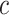 is a non-negative utility parameter indicating the ratio of treatment cost relative to disease cost. For example, in Vickers and others (2007), based on a patient survey,
is a non-negative utility parameter indicating the ratio of treatment cost relative to disease cost. For example, in Vickers and others (2007), based on a patient survey, 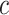 was chosen to be 5% for treating breast cancer with adjuvant chemotherapy, which corresponds to assuming that the cost of death is 20 times the cost of chemotherapy. Without loss of generality, let the cost per disease outcome be 1 such that disease and treatment cost will be represented in units of the burden per disease outcome. The total cost of a treatment-selection strategy
was chosen to be 5% for treating breast cancer with adjuvant chemotherapy, which corresponds to assuming that the cost of death is 20 times the cost of chemotherapy. Without loss of generality, let the cost per disease outcome be 1 such that disease and treatment cost will be represented in units of the burden per disease outcome. The total cost of a treatment-selection strategy 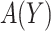 and of the optimal treatment strategy absent the marker information can thus be computed as follows.
and of the optimal treatment strategy absent the marker information can thus be computed as follows.
At cost ratio  , the total cost of a treatment-selection rule
, the total cost of a treatment-selection rule 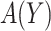 , i.e. the sum of disease and treatment cost, is equal to
, i.e. the sum of disease and treatment cost, is equal to 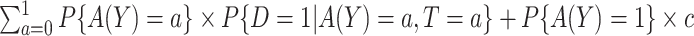 . As shown in supplementary material available at Biostatistics online, Appendix A, this equals
. As shown in supplementary material available at Biostatistics online, Appendix A, this equals
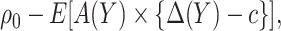 |
(2.1) |
where 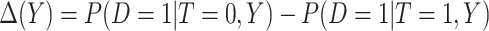 is the absolute risk difference conditional on
is the absolute risk difference conditional on 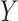 between untreated and treated. Without the biomarker, treatment will be applied either to all subjects or to no one. If treating all, the total cost is
between untreated and treated. Without the biomarker, treatment will be applied either to all subjects or to no one. If treating all, the total cost is 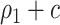 , and if treating none, the total cost is
, and if treating none, the total cost is 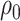 . Therefore, absent the marker, the optimal treatment-selection rule that minimizes the total cost is to treat everyone if
. Therefore, absent the marker, the optimal treatment-selection rule that minimizes the total cost is to treat everyone if 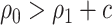 , and to treat no one otherwise (Vickers and others, 2007). The total cost of the optimal marker-independent rule is therefore
, and to treat no one otherwise (Vickers and others, 2007). The total cost of the optimal marker-independent rule is therefore
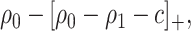 |
(2.2) |
where 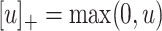 is the positive-part function.
is the positive-part function.
We define the expected benefit for a rule  and cost ratio
and cost ratio 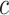 as the difference between (2.2) and (2.1), i.e.
as the difference between (2.2) and (2.1), i.e. 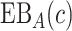 is the reduction in the total cost using
is the reduction in the total cost using 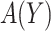 relative to the optimal rule absent the marker:
relative to the optimal rule absent the marker:
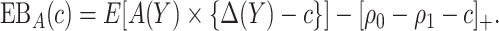 |
(2.3) |
Note that the first component of (2.3) is exactly the net benefit measure of 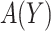 (Vickers and others, 2007); the second component of (2.3) is the net benefit of an optimal treatment-selection rule absent any marker information. Thus, the expected benefit of a marker-based treatment-selection rule can be interpreted as the incremental value in net benefit compared with the optimal treatment strategy without the biomarker. If
(Vickers and others, 2007); the second component of (2.3) is the net benefit of an optimal treatment-selection rule absent any marker information. Thus, the expected benefit of a marker-based treatment-selection rule can be interpreted as the incremental value in net benefit compared with the optimal treatment strategy without the biomarker. If 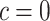 and
and 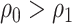 , this reduces to the decrease in the disease rate, a measure advocated by Janes and others (2014). Hereafter, to simplify notation we write
, this reduces to the decrease in the disease rate, a measure advocated by Janes and others (2014). Hereafter, to simplify notation we write 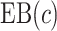 with the understanding that the underlying strategy
with the understanding that the underlying strategy 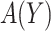 is implicit.
is implicit.
The incremental value in net benefit by using the marker is informative for several reasons. Net benefit itself is useful for comparing treatment-selection strategies because the difference in net benefit between two models is equal to the difference in their expected benefits, as the second component of (2.3) does not depend on the marker. However, the net benefit of a marker-based strategy does not always properly quantify the absolute benefit gained by the marker for different choices of the treatment–disease cost ratio because the default strategy of no treatment may not be the optimal strategy absent the marker information. The expected benefit measure, in contrast, takes into account the optimal treatment choice absent the marker. Moreover, when we evaluate whether a new model improves over an existing marker/model, the expected benefit of the existing marker can serve as a useful reference for gauging whether the difference in expected benefit between models is meaningful.
In practice, it is difficult to agree upon one single parameter 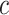 . An expected benefit curve, which plots
. An expected benefit curve, which plots 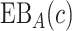 versus
versus 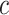 , can be used to gauge marker value at multiple values of
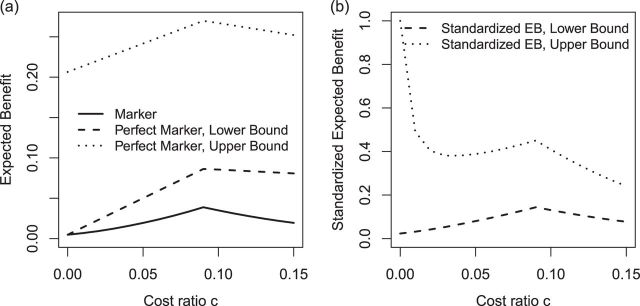
, can be used to gauge marker value at multiple values of 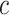 . Examples of EB curves are shown in Figure 1 in Section 5.
. Examples of EB curves are shown in Figure 1 in Section 5.
Fig. 1.
Expected benefit curves of HBA1C and the bounds for perfect biomarker for guiding the prevention of microalbuminuria in the DCCT example.
2.1. Perfect treatment-selection capacity and standardized expected benefit
In this section, we derive the expected benefit of a perfect treatment-selection rule which can be used to standardize the expected benefit of a marker-based rule. This type of standardization puts the expected benefit measure on a scale between 0 and 1 and makes it invariant to the choice of disease cost. Standardization has been used when measuring a biomarker's capacity for risk prediction, e.g. in Bura and Gastwirth (2001) and Baker and others (2009), but not yet for treatment selection.
We define a perfect treatment-selection rule using a potential outcomes framework. Let 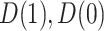 denote the pair of potential outcomes under treatment or no treatment, respectively. The four possible values of
denote the pair of potential outcomes under treatment or no treatment, respectively. The four possible values of 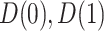 are shown below with
are shown below with 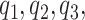 and
and 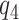 denoting the unobserved population proportion of subjects falling into each category, where benefits and harms are with respect to the targeted disease of interest.
denoting the unobserved population proportion of subjects falling into each category, where benefits and harms are with respect to the targeted disease of interest.
 |
Given cost ratio 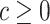 , a perfect treatment-selection rule will recommend treatment for all treatment-benefited subjects and recommend against treatment for all others. This will lead to a population-averaged total disease and treatment cost of
, a perfect treatment-selection rule will recommend treatment for all treatment-benefited subjects and recommend against treatment for all others. This will lead to a population-averaged total disease and treatment cost of 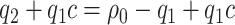 . Thus, the expected benefit of a perfect treatment-selection rule, i.e. the “perfect expected benefit” (PEB), is
. Thus, the expected benefit of a perfect treatment-selection rule, i.e. the “perfect expected benefit” (PEB), is 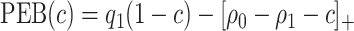 .
.
While in general 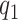 is not identifiable given the observed data, upper and lower bounds can be identified using a disease risk model, i.e. the model of the risk of
is not identifiable given the observed data, upper and lower bounds can be identified using a disease risk model, i.e. the model of the risk of 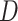 conditional on
conditional on 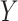 and
and 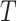 . Let
. Let 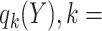 1, 2, 3, and 4 indicate the probability that a subject with marker
1, 2, 3, and 4 indicate the probability that a subject with marker 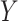 falls into the
falls into the 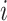 th potential outcome category. Let
th potential outcome category. Let 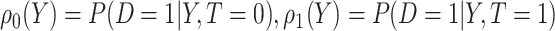 . Then
. Then
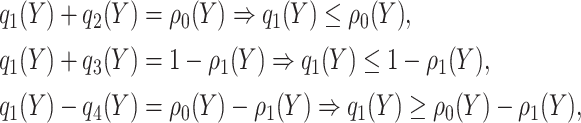 |
which implies 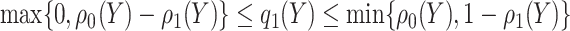 . Taking an expectation over
. Taking an expectation over 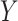 , we have
, we have 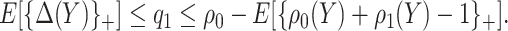 Note that alternative nonparametric bounds for
Note that alternative nonparametric bounds for 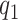 can be derived without relying on any biomarker model:
can be derived without relying on any biomarker model: 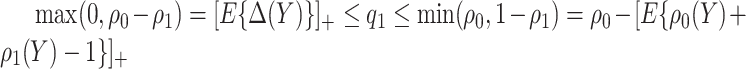 . The bounds constructed based on the disease risk model are narrower since
. The bounds constructed based on the disease risk model are narrower since 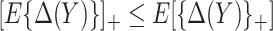 and
and 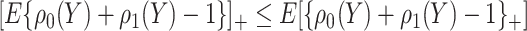 , and will be the focus of this paper. These types of restrictions on the probability of potential outcome category have also been recognized by others, e.g. Gadbury and others (2004), Huang and others (2012), and Zhang and others (2013).
, and will be the focus of this paper. These types of restrictions on the probability of potential outcome category have also been recognized by others, e.g. Gadbury and others (2004), Huang and others (2012), and Zhang and others (2013).
Using disease risk model, we obtain lower and upper bounds for the perfect expected benefit
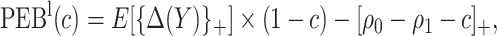 |
(2.4) |
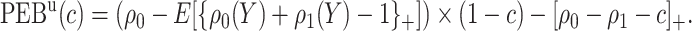 |
(2.5) |
Finally, dividing the expected benefit of a marker-based treatment-selection strategy by the bounds of expected benefit from perfect treatment selection, we obtain bounds for the standardized expected benefit: 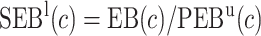 and
and 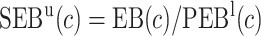 .
.
In summary, the expected benefit of a perfect treatment-selection rule can be derived but is non-identifiable due to the non-identifiability of the percent of “benefited” individuals (or equivalently, the percent of “harmed” or “unbenefited” since 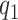 can be determined when any of
can be determined when any of 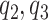 , or
, or 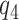 is fixed). An alternative to constructing bounds on
is fixed). An alternative to constructing bounds on 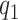 using a risk model is to conduct a sensitivity analysis treating the percent harmed (
using a risk model is to conduct a sensitivity analysis treating the percent harmed (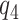 ) as a sensitivity parameter, and to compute PEB for each fixed
) as a sensitivity parameter, and to compute PEB for each fixed 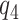 value. A narrower bound for PEB might be achieved when a narrow range of
value. A narrower bound for PEB might be achieved when a narrow range of 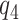 is plausible based on biological assumptions. In the special case where the treatment has a monotone effect on the targeted disease and will not cause any harm (so
is plausible based on biological assumptions. In the special case where the treatment has a monotone effect on the targeted disease and will not cause any harm (so 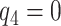 ), we have
), we have 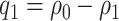 , and PEB can be uniquely identified as
, and PEB can be uniquely identified as 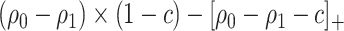 , which is equal to its lower bound in (2.4) since
, which is equal to its lower bound in (2.4) since 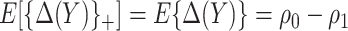 under monotonicity.
under monotonicity.
The expected benefit from perfect treatment selection sets a reference for gauging the benefit of a particular treatment-selection rule or the difference in benefit between two rules. A demonstration of the comparison between two markers is presented in supplementary material available at Biostatistics online, Figure 1.
3. Derivation of treatment-selection rules and estimation of expected benefit
In this section, we consider methods for deriving marker-based treatment-selection rules in order to maximize expected benefit and to estimate their (standardized) expected benefit. We consider the class of selection rules 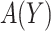 which depends on the sign of a smooth function of
which depends on the sign of a smooth function of 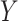 , namely
, namely 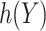 , i.e.
, i.e. 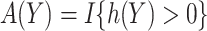 . We propose two strategies for optimizing the selection rule
. We propose two strategies for optimizing the selection rule 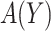 and estimating (standardized) expected benefit. The first requires correct modeling of the risk difference
and estimating (standardized) expected benefit. The first requires correct modeling of the risk difference 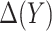 , whereas the second does not and is thus more robust to model misspecification. However, the first strategy is more efficient under a correctly specified model.
, whereas the second does not and is thus more robust to model misspecification. However, the first strategy is more efficient under a correctly specified model.
3.1. Model-based approach
Based on (2.3), it can be seen that a marker-based rule 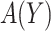 that optimizes expected benefit at cost ratio
that optimizes expected benefit at cost ratio 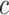 is equal to
is equal to 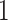 whenever
whenever 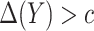 and
and 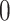 otherwise. That is,
otherwise. That is, 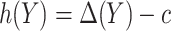 . For details, see, e.g. Vickers and others (2007). We model the disease risk with a generalized linear model (GLM):
. For details, see, e.g. Vickers and others (2007). We model the disease risk with a generalized linear model (GLM): 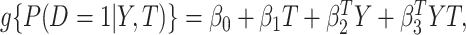 where
where 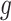 is a known link function, e.g. the logit or inverse normal CDF. Let
is a known link function, e.g. the logit or inverse normal CDF. Let 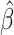 denote the maximum likelihood estimator (MLE) of
denote the maximum likelihood estimator (MLE) of 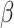 , and let
, and let 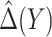 denote the MLE of
denote the MLE of 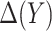 . A model-based treatment-selection rule can be constructed as
. A model-based treatment-selection rule can be constructed as 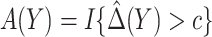 . Assuming that the model for
. Assuming that the model for 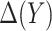 is correctly specified, a model-based estimator of expected benefit can be constructed based on (2.3):
is correctly specified, a model-based estimator of expected benefit can be constructed based on (2.3): 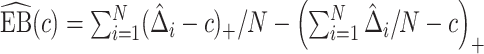 , where
, where 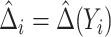 is the estimate of
is the estimate of 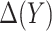 for subject
for subject 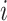 . Note that a good fit of the risk model itself is sufficient for the good fit of the model for
. Note that a good fit of the risk model itself is sufficient for the good fit of the model for 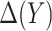 , but not necessary. Hosmer–Lemeshow type techniques can be used to evaluate both types of calibration (Huang and Pepe, 2010; Janes and others, 2014).
, but not necessary. Hosmer–Lemeshow type techniques can be used to evaluate both types of calibration (Huang and Pepe, 2010; Janes and others, 2014).
We estimate the lower bound on PEB with 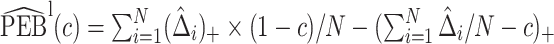 and the upper bound with
and the upper bound with 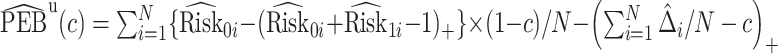 , where
, where 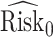 and
and 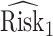 are model-based estimates of
are model-based estimates of 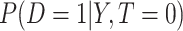 and
and 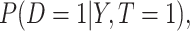 respectively. Corresponding lower and upper bounds on
respectively. Corresponding lower and upper bounds on 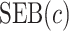 can be estimated as
can be estimated as 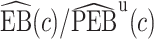 and
and 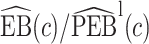 .
.
3.2. Robust approaches
Optimality of a model-based treatment-selection rule 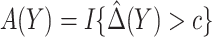 and validity of the model-based estimator for corresponding expected benefit rely critically on correct specification of the model for
and validity of the model-based estimator for corresponding expected benefit rely critically on correct specification of the model for 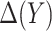 . Here we describe alternative approaches for characterizing the optimal treatment-selection rule and for estimating expected benefit that are more robust to model misspecification, in the sense that good performance of the derived rule and unbiasedness of the estimates of EB do not require correct specification of
. Here we describe alternative approaches for characterizing the optimal treatment-selection rule and for estimating expected benefit that are more robust to model misspecification, in the sense that good performance of the derived rule and unbiasedness of the estimates of EB do not require correct specification of 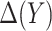 .
.
Suppose that we are interested in picking the best rule among all rules of the form 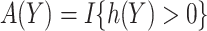 with
with 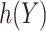 belonging to a pre-specified class, e.g.
belonging to a pre-specified class, e.g. 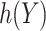 can be a linear function of
can be a linear function of 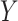 . The optimal rule can be estimated by maximizing an estimate of the expected benefit. Following the notations in Section 2.1, let
. The optimal rule can be estimated by maximizing an estimate of the expected benefit. Following the notations in Section 2.1, let 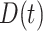 indicate the potential disease outcome if a subject were to receive treatment
indicate the potential disease outcome if a subject were to receive treatment 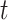 ,
, 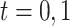 . Let
. Let 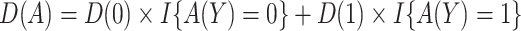 be the potential outcome that would be observed if a randomly chosen subject from the population were to be assigned treatment according to rule
be the potential outcome that would be observed if a randomly chosen subject from the population were to be assigned treatment according to rule 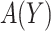 . The expected benefit under
. The expected benefit under 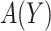 can be represented as
can be represented as 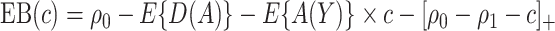 . Let
. Let 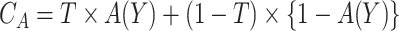 be the indicator of observing
be the indicator of observing 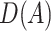 , i.e.
, i.e. 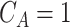 if
if 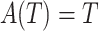 . Then to estimate
. Then to estimate 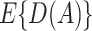 , one can use the inverse-probability weighted estimator (IPWE)
, one can use the inverse-probability weighted estimator (IPWE)
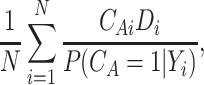 |
(3.1) |
or a doubly robust augmented IPWE
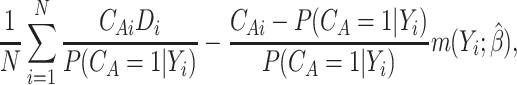 |
(3.2) |
where 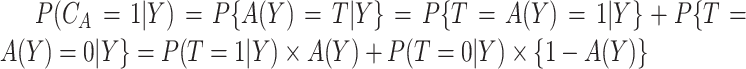 ;
; 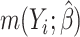 , an estimate of
, an estimate of 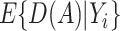 equals
equals  based on some working risk model. The doubly robust estimator augments the IPWE of
based on some working risk model. The doubly robust estimator augments the IPWE of 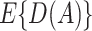 with a term that involves the risk of
with a term that involves the risk of 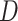 given
given 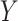 and
and 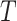 . It has the double-robustness property in that it is consistent for
. It has the double-robustness property in that it is consistent for 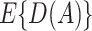 if either
if either  or the risk model is correctly specified. In a randomized trial,
or the risk model is correctly specified. In a randomized trial,  is known, so consistency of the estimator is always achievable; the second term in (3.2) “augments” the empirical estimate so as to increase asymptotic efficiency as shown in Zhang, Tsiatis, Laber, and others (2012).
is known, so consistency of the estimator is always achievable; the second term in (3.2) “augments” the empirical estimate so as to increase asymptotic efficiency as shown in Zhang, Tsiatis, Laber, and others (2012).
Based on the IPWE and the augmented estimator of 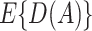 in (3.1) and (3.2), corresponding empirical and augmented estimators for
in (3.1) and (3.2), corresponding empirical and augmented estimators for 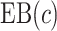 are
are
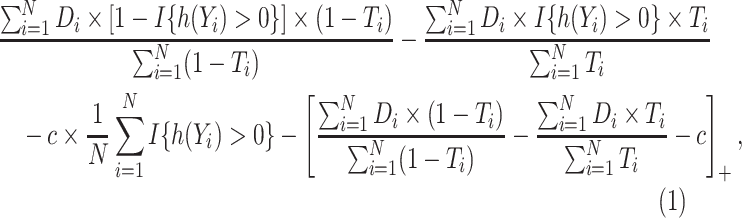 |
(3.3) |
and
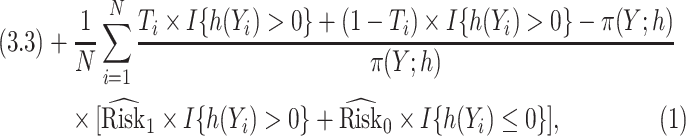 |
(3.4) |
respectively, with 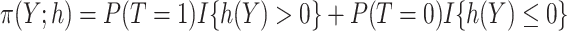 .
.
As in Zhang, Tsiatis, and others (2012) and Zhao and others (2012), the problem of maximizing the expected benefit estimators in (3.3) and (3.4) can be transformed into a weighted classification problem. Consider deriving a rule based on a linear marker combination 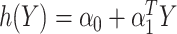 . As shown in supplementary material available at Biostatistics online, Appendix C, the values
. As shown in supplementary material available at Biostatistics online, Appendix C, the values 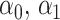 that maximize these expect benefit estimates can be shown to be the minimizers of
that maximize these expect benefit estimates can be shown to be the minimizers of
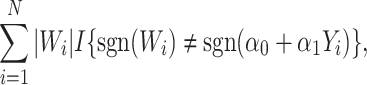 |
(3.5) |
with 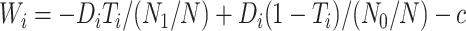 for maximizing (3.3) and
for maximizing (3.3) and 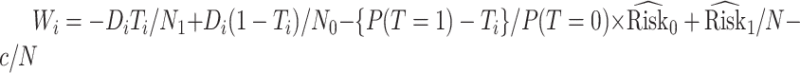 for maximizing (3.4), where
for maximizing (3.4), where 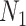 and
and 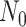 are sample sizes in treated and untreated groups. We consider two algorithms in the simulation studies to derive
are sample sizes in treated and untreated groups. We consider two algorithms in the simulation studies to derive 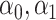 for minimizing (3.5), one fitting a weighted linear logistic regression model regressing binary outcome
for minimizing (3.5), one fitting a weighted linear logistic regression model regressing binary outcome 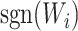 versus
versus 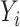 with individual weight
with individual weight 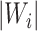 , the other directly solving for
, the other directly solving for 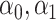 by minimizing (3.5) through a grid search.
by minimizing (3.5) through a grid search.
Finally, we consider an alternative robust approach for deriving 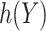 that is computationally simpler. We adopt a working model
that is computationally simpler. We adopt a working model 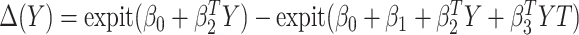 for risk difference based on a GLM. Let
for risk difference based on a GLM. Let 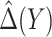 be the MLE of
be the MLE of 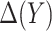 , and
, and 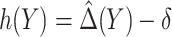 . An optimal
. An optimal 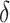 can be identified by maximizing the empirical (3.3) or doubly robust (3.4) estimator of EB using this
can be identified by maximizing the empirical (3.3) or doubly robust (3.4) estimator of EB using this 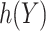 and a grid search. Note
and a grid search. Note 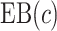 in a randomized trial can be represented as
in a randomized trial can be represented as
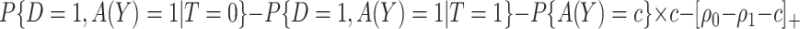 |
(3.6) |
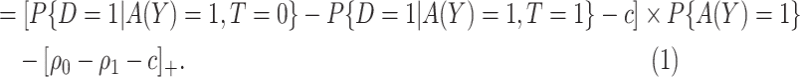 |
(3.7) |
The IPWE estimator (3.3) is an empirical estimator for estimating EB as represented in (3.6), whereas an alternative empirical estimator for estimating EB as represented in (3.7) can be constructed by maximizing 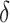 over
over
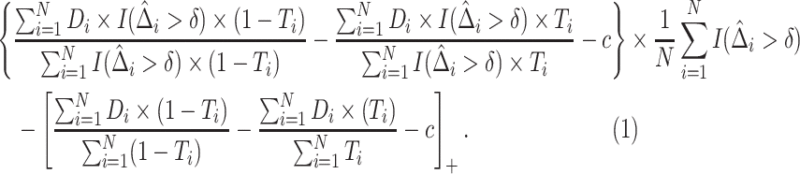 |
(3.8) |
The empirical estimator (3.8) uses data more efficiently compared with the IPWE estimator (3.3) by taking into account the condition: 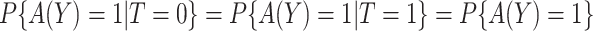 , ensured by randomization. We use this estimator together with the augmented estimator in our simulation study and data example for identifying
, ensured by randomization. We use this estimator together with the augmented estimator in our simulation study and data example for identifying 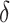 based on
based on 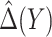 .
.
Expected benefits of these “robust treatment rules” can be estimated using cross-validation. These robust methods target scenarios where the model for risk and/or risk difference is prone to misspecification. The bounds for PEB in (2.4) and (2.5) rely heavily on correct specification of the risk model. Therefore, we do not consider robust estimation techniques for the bounds.
3.3. Asymptotic theory for the model-based estimator of expected benefit
When 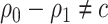 , the following theorem holds as proved in supplementary material available at Biostatistics online, Appendix D.
, the following theorem holds as proved in supplementary material available at Biostatistics online, Appendix D.
Theorem 1 —
Under the regularity conditions specified in supplementary material available at Biostatistics online, Appendix D,
,
,
,
, and
as defined in Section 3.1 are asymptotically normal as
for
.
When 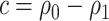 ,
, 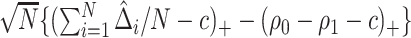 converges to a mixture of 0 and a truncated normal distribution (supplementary material available at Biostatistics online, Appendix E). As a result, asymptotic normality of
converges to a mixture of 0 and a truncated normal distribution (supplementary material available at Biostatistics online, Appendix E). As a result, asymptotic normality of 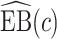 ,
, 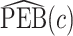 , or
, or 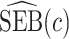 does not hold. Even when asymptotic normality of these estimators does hold, we recommend the bootstrap for constructing confidence intervals since computation of the asymptotic variance of these estimators requires numerical differentiation. When
does not hold. Even when asymptotic normality of these estimators does hold, we recommend the bootstrap for constructing confidence intervals since computation of the asymptotic variance of these estimators requires numerical differentiation. When 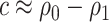 , the standard bootstrap percentile confidence interval (CI) can lead to undercoverage. Therefore, we adopt an adaptive bootstrap CI following the ideas of Berger and Boos (1994), Laber and Murphy (2011), and Robins (2004). Specifically, the proposed interval is equivalent to the standard bootstrap percentile CI when
, the standard bootstrap percentile confidence interval (CI) can lead to undercoverage. Therefore, we adopt an adaptive bootstrap CI following the ideas of Berger and Boos (1994), Laber and Murphy (2011), and Robins (2004). Specifically, the proposed interval is equivalent to the standard bootstrap percentile CI when 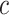 is far from
is far from  and is equivalent to a projection interval otherwise, which is the union of bootstrap intervals as described below. Because the behavior of the CI is automatically dictated by the data, we term it “adaptive.”
and is equivalent to a projection interval otherwise, which is the union of bootstrap intervals as described below. Because the behavior of the CI is automatically dictated by the data, we term it “adaptive.”
Let 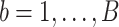 index bootstrap samples drawn from the original data with replacement. We add a superscript
index bootstrap samples drawn from the original data with replacement. We add a superscript 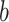 , to indicate that a statistic has been computed using a bootstrap sample. For any
, to indicate that a statistic has been computed using a bootstrap sample. For any 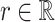 defines
defines 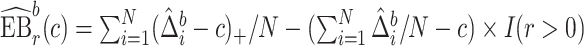 ,
, 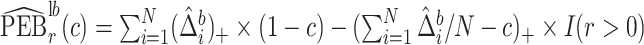 , and
, and 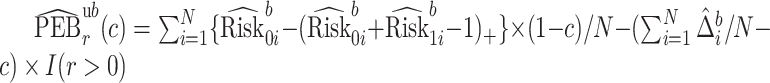 . Let
. Let 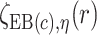 ,
, 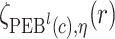 , and
, and 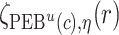 denote
denote 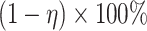 percentile bootstrap CIs formed by taking empirical percentiles of
percentile bootstrap CIs formed by taking empirical percentiles of 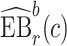 ,
, 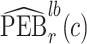 , and
, and 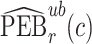 over bootstrap samples, respectively. Let
over bootstrap samples, respectively. Let 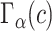 denote an asymptotically valid
denote an asymptotically valid  CI for
CI for 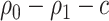 . The
. The 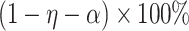 projection intervals for
projection intervals for 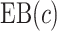 ,
, 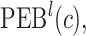 and
and 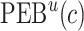 are given by
are given by 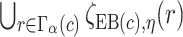 ,
, 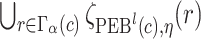 , and
, and 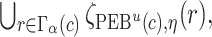 respectively. Let
respectively. Let 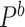 denotes probability taken with respect to the bootstrap sampling algorithm, conditional on the observed data. The following Theorem 2 is proved in supplementary material available at Biostatistics online, Appendix F.
denotes probability taken with respect to the bootstrap sampling algorithm, conditional on the observed data. The following Theorem 2 is proved in supplementary material available at Biostatistics online, Appendix F.
Theorem 2 —
Let
be a sequence of positive random variables satisfying
and
almost surely as
. Define
if
and
otherwise. The
adaptive bootstrap CIs for
,
and
based on pre-specified
are given by
,
, and
, respectively. Assume
has a continuous and bounded density function. For
, we have
;
;
.
If
then the right-hand side of the foregoing inequalities can be replaced with equalities.
Remark 1 —
Berger and Boos (1994) recommend choosing
to quite small in which case
. Consequently, the proposed projection CI is nearly exact in large samples provided
, but potentially conservative otherwise. However, Theorem 2 suggests a procedure which provides exact coverage when
and is thus both adaptive and less conservative than the projection interval. For these reasons, it is recommended in practice.
Remark 2 —
The conditions of the preceding theorem can be relaxed at the expense of a possibly more conservative confidence interval. In supplementary material available at Biostatistics online, Appendix G, we provide a locally consistent projection confidence interval that does not require
to have smooth bounded density. However, this interval requires taking a union over a larger set and is thus potentially more conservative in some settings. We defer the detailed investigation of this CI to future work.
4. Simulation studies
Consider a two-arm 1 : 1 randomized trial where a biomarker 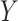 following a standard normal distribution is measured. Suppose the risk of a binary disease
following a standard normal distribution is measured. Suppose the risk of a binary disease 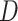 conditional on
conditional on 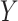 and
and 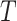 follows a linear logistic model:
follows a linear logistic model: 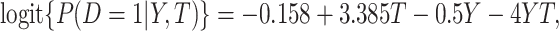 with disease prevalences
with disease prevalences 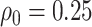 and
and 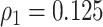 . We consider cost ratios
. We consider cost ratios 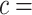 0, 0.105, 0.125, 0.145, and 0.175, which correspond to expected benefit values of 0.043, 0.059, 0.063, 0.048, and 0.029. The pairs of lower and upper bounds for expected benefit from perfect treatment selection are
0, 0.105, 0.125, 0.145, and 0.175, which correspond to expected benefit values of 0.043, 0.059, 0.063, 0.048, and 0.029. The pairs of lower and upper bounds for expected benefit from perfect treatment selection are 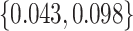 ,
, 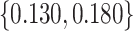 ,
, 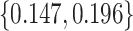 ,
, 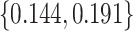 , and
, and 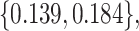 respectively.
respectively.
Tables 1 and 2 show performance of the model-based estimators for 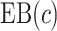 ,
, 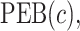 and
and 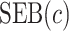 for sample sizes 200, 500, and 2000 based on 5000 simulations and 1000 bootstrap samples. At
for sample sizes 200, 500, and 2000 based on 5000 simulations and 1000 bootstrap samples. At 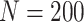 , model-based estimators have minimal bias for each measure. Coverage of 95% percentile bootstrap CI is close to the nominal level when
, model-based estimators have minimal bias for each measure. Coverage of 95% percentile bootstrap CI is close to the nominal level when 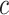 is away from
is away from  , whereas undercoverage is observed when
, whereas undercoverage is observed when 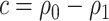 , which is not alleviated with an increase in sample size. The adaptive bootstrap CI fixes the undercoverage where we adopt the projection interval (with
, which is not alleviated with an increase in sample size. The adaptive bootstrap CI fixes the undercoverage where we adopt the projection interval (with 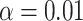 ) when
) when  is close to
is close to 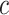 (defined as
(defined as 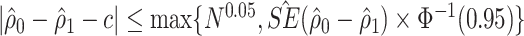 in the simulation study and data example).
in the simulation study and data example).
Table 1.
Performance of the model-based estimator of EB with 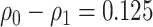
Cost ratio 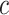
|
0.000 | 0.105 | 0.125 | 0.145 | 0.175 |
|---|---|---|---|---|---|
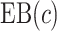 |
0.043 | 0.059 | 0.063 | 0.048 | 0.029 |
|
Bias
|
||||
| 200 | 2.02 |
 7.90 7.90 |
 15.55 15.55 |
 6.33 6.33 |
2.17 |
| 500 | 1.22 |
 3.26 3.26 |
 10.72 10.72 |
 3.00 3.00 |
1.50 |
| 2000 | 0.24 |
 0.33 0.33 |
 5.62 5.62 |
 0.15 0.15 |
0.66 |
SD
|
|||||
| 200 | 0.29 | 0.27 | 0.27 | 0.29 | 0.29 |
| 500 | 0.29 | 0.28 | 0.29 | 0.33 | 0.35 |
| 2000 | 0.29 | 0.31 | 0.31 | 0.40 | 0.38 |
SE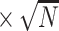
|
|||||
| 200 | 0.28 | 0.27 | 0.27 | 0.27 | 0.26 |
| 500 | 0.29 | 0.29 | 0.30 | 0.32 | 0.32 |
| 2000 | 0.29 | 0.31 | 0.32 | 0.39 | 0.38 |
| Coverage of 95% percentile bootstrap CI | |||||
| 200 | 95.10 | 91.80 | 83.80 | 95.20 | 96.90 |
| 500 | 95.10 | 94.90 | 84.60 | 96.30 | 95.80 |
| 2000 | 94.50 | 96.40 | 85.10 | 96.80 | 95.50 |
| Coverage of 95% adaptive bootstrap CI | |||||
| 200 | 95.22 | 97.04 | 95.56 | 96.48 | 97.02 |
| 500 | 95.12 | 97.42 | 95.88 | 96.82 | 95.98 |
| 2000 | 94.62 | 96.68 | 95.88 | 96.72 | 95.78 |
Table 2.
Performance of the model-based estimator for bounds of PEB(c) and SEB(c)
Cost ratio 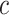
|
0.000 | 0.105 | 0.125 | 0.145 | 0.175 | 0.000 | 0.105 | 0.125 | 0.145 | 0.175 |
|---|---|---|---|---|---|---|---|---|---|---|
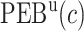 |
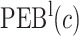 |
|||||||||
| 0.098 | 0.180 | 0.196 | 0.191 | 0.184 | 0.043 | 0.130 | 0.147 | 0.144 | 0.139 | |
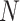 |
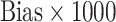 |
|||||||||
| 200 |
 0.10 0.10 |
 11.73 11.73 |
 20.31 20.31 |
 12.08 12.08 |
 4.93 4.93 |
2.02 |
 9.82 9.82 |
 18.45 18.45 |
 10.27 10.27 |
 3.18 3.18 |
| 500 |
 0.53 0.53 |
 5.53 5.53 |
 13.37 13.37 |
 6.04 6.04 |
 2.00 2.00 |
1.22 |
 3.97 3.97 |
 11.84 11.84 |
 4.55 4.55 |
 0.56 0.56 |
| 2000 |
 0.28 0.28 |
 0.98 0.98 |
 6.38 6.38 |
 1.02 1.02 |
 0.32 0.32 |
0.24 |
 0.51 0.51 |
 5.92 5.92 |
 0.57 0.57 |
0.11 |
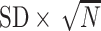 |
||||||||||
| 200 | 0.33 | 0.29 | 0.31 | 0.34 | 0.39 | 0.29 | 0.25 | 0.28 | 0.32 | 0.38 |
| 500 | 0.33 | 0.30 | 0.32 | 0.37 | 0.44 | 0.29 | 0.26 | 0.29 | 0.36 | 0.43 |
| 2000 | 0.34 | 0.32 | 0.32 | 0.43 | 0.45 | 0.29 | 0.28 | 0.30 | 0.42 | 0.45 |
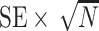 |
||||||||||
| 200 | 0.32 | 0.31 | 0.32 | 0.34 | 0.38 | 0.28 | 0.27 | 0.29 | 0.32 | 0.37 |
| 500 | 0.33 | 0.31 | 0.32 | 0.37 | 0.42 | 0.29 | 0.28 | 0.29 | 0.36 | 0.42 |
| 2000 | 0.33 | 0.32 | 0.33 | 0.43 | 0.45 | 0.29 | 0.29 | 0.30 | 0.42 | 0.45 |
| Coverage of 95% percentile bootstrap CI | ||||||||||
| 200 | 94.90 | 88.20 | 77.80 | 90.70 | 95.90 | 95.10 | 89.60 | 78.70 | 92.70 | 96.70 |
| 500 | 94.50 | 91.50 | 77.70 | 93.80 | 95.50 | 95.10 | 94.20 | 80.70 | 96.10 | 95.50 |
| 2000 | 94.50 | 95.80 | 80.10 | 96.50 | 95.00 | 94.50 | 96.40 | 82.20 | 96.70 | 95.20 |
| Coverage of 95% adaptive bootstrap CI | ||||||||||
| 200 | 94.94 | 95.98 | 94.54 | 94.98 | 95.86 | 95.22 | 96.26 | 94.22 | 95.72 | 96.62 |
| 500 | 94.52 | 96.08 | 94.34 | 95.42 | 95.50 | 95.12 | 97.04 | 94.86 | 96.56 | 95.64 |
| 2000 | 94.82 | 96.64 | 95.06 | 96.42 | 95.18 | 94.62 | 96.74 | 95.14 | 96.72 | 95.58 |
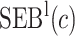 |
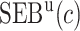 |
|||||||||
| 0.436 | 0.327 | 0.323 | 0.253 | 0.156 | 1.000 | 0.452 | 0.429 | 0.336 | 0.207 | |
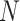 |
 |
|||||||||
| 200 | 9.12 |
 30.47 30.47 |
 58.66 58.66 |
 27.63 27.63 |
4.30 | 0.00 |
 42.79 42.79 |
 74.27 74.27 |
 39.34 39.34 |
 0.86 0.86 |
| 500 | 10.19 |
 10.73 10.73 |
 38.06 38.06 |
 12.60 12.60 |
3.42 | 0.00 |
 17.01 17.01 |
 47.53 47.53 |
 19.03 19.03 |
0.24 |
| 2000 | 2.66 |
 0.74 0.74 |
 19.51 19.51 |
 0.96 0.96 |
2.05 | 0.00 |
 2.30 2.30 |
 23.24 23.24 |
 2.43 2.43 |
1.36 |
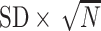 |
||||||||||
| 200 | 2.02 | 1.23 | 1.24 | 1.31 | 1.36 | 0.00 | 1.41 | 1.46 | 1.57 | 1.65 |
| 500 | 2.12 | 1.25 | 1.27 | 1.45 | 1.60 | 0.00 | 1.38 | 1.44 | 1.71 | 1.94 |
| 2000 | 2.21 | 1.35 | 1.29 | 1.66 | 1.70 | 0.00 | 1.45 | 1.39 | 1.89 | 2.06 |
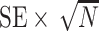 |
||||||||||
| 200 | 1.92 | 1.26 | 1.25 | 1.25 | 1.22 | 0.00 | 1.50 | 1.51 | 1.53 | 1.49 |
| 500 | 2.06 | 1.31 | 1.31 | 1.45 | 1.49 | 0.00 | 1.48 | 1.50 | 1.70 | 1.82 |
| 2000 | 2.15 | 1.34 | 1.31 | 1.66 | 1.70 | 0.00 | 1.45 | 1.44 | 1.90 | 2.06 |
| Coverage of 95% percentile bootstrap CI | ||||||||||
| 200 | 95.10 | 95.80 | 91.40 | 96.80 | 97.30 | 100.00 | 94.10 | 88.80 | 96.50 | 97.40 |
| 500 | 95.10 | 96.70 | 90.80 | 96.90 | 95.60 | 100.00 | 95.50 | 87.80 | 96.60 | 95.80 |
| 2000 | 94.20 | 96.20 | 89.40 | 96.80 | 95.60 | 100.00 | 96.40 | 87.20 | 97.00 | 95.40 |
| Coverage of 95% adaptive bootstrap CI | ||||||||||
| 200 | 95.12 | 97.82 | 95.88 | 97.24 | 97.20 | 100.00 | 97.02 | 94.86 | 97.02 | 97.40 |
| 500 | 95.10 | 97.94 | 95.72 | 97.28 | 95.74 | 100.00 | 97.04 | 94.80 | 96.88 | 95.86 |
| 2000 | 94.16 | 96.18 | 97.82 | 96.68 | 95.58 | 100.00 | 96.44 | 97.28 | 96.84 | 95.42 |
Table 3 presents performance of various robust estimators of treatment-selection rules and robust estimators of expected benefit. These simulations explore performance of various treatment-selection rules under the correctly specified risk model, so that one can examine the penalty associated with the use of the robust methods in terms of increased variability and suboptimal expected benefit. For each rule derived from a simulated dataset, expected benefit in the population is computed through numerical integration. With 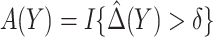 , estimating the optimal
, estimating the optimal 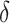 rather than using
rather than using 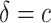 leads to smaller expected benefit and larger variability for the small sample size of 200, but the difference is minimal when the sample size is as large as 2000. Performance of the treatment-selection rule derived by minimizing weighted classification errors through a grid search is comparable with that based on
leads to smaller expected benefit and larger variability for the small sample size of 200, but the difference is minimal when the sample size is as large as 2000. Performance of the treatment-selection rule derived by minimizing weighted classification errors through a grid search is comparable with that based on 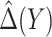 and estimated
and estimated 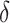 . In general, using the augmented version for
. In general, using the augmented version for 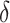 estimation or for weight computation leads to a small increase in expected benefit and decreased variability. Between the two algorithms for weighted classification, the grid search in general does better than weighted logistic regression, especially for large cost ratio; the latter has performance worse than the optimal strategy absent the marker at cost ratio 0.175. Note that the advantage of the robust approaches is expected to become apparent when the model of risk difference is misspecified (an example is presented in supplementary material available at Biostatistics online, Table S3).
estimation or for weight computation leads to a small increase in expected benefit and decreased variability. Between the two algorithms for weighted classification, the grid search in general does better than weighted logistic regression, especially for large cost ratio; the latter has performance worse than the optimal strategy absent the marker at cost ratio 0.175. Note that the advantage of the robust approaches is expected to become apparent when the model of risk difference is misspecified (an example is presented in supplementary material available at Biostatistics online, Table S3).
Table 3.
MEAN (SD) of expected benefit of a derived treatment-selection rule in the population and MEAN(SD) of naive and cross-validated estimate of corresponding expected benefit
 |
TYPE | PAR
|
NPAR1
|
NPAR2
|
WLOGIS1
|
WLOGIS2
|
WCLASS1
|
WCLASS2
|
|---|---|---|---|---|---|---|---|---|
Cost ratio 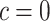
| ||||||||
| 200 | True | 0.0406 (0.0035) | 0.0337 (0.011) | 0.0363 (0.0084) | 0.0329 (0.0105) | 0.0362 (0.0085) | 0.0335 (0.0122) | 0.0377 (0.0072) |
| Naive | 0.0454 (0.0208) | 0.0586 (0.0299) | 0.0552 (0.0298) | 0.0404 (0.0368) | 0.0432 (0.0339) | 0.0602 (0.0331) | 0.0559 (0.033) | |
| CV | 0.0391 (0.0325) | 0.0303 (0.0329) | 0.0328 (0.031) | 0.0316 (0.036) | 0.0336 (0.0336) | 0.0307 (0.0381) | 0.0358 (0.0351) | |
| 500 | True | 0.042 (0.0012) | 0.0385 (0.006) | 0.0398 (0.004) | 0.0345 (0.0069) | 0.0401 (0.004) | 0.038 (0.0071) | 0.04 (0.0038) |
| Naive | 0.0439 (0.0133) | 0.0513 (0.0198) | 0.0499 (0.019) | 0.0374 (0.0244) | 0.0426 (0.0218) | 0.0524 (0.0218) | 0.0499 (0.0211) | |
| CV | 0.041 (0.0209) | 0.0364 (0.022) | 0.0381 (0.0198) | 0.0336 (0.0239) | 0.0382 (0.0217) | 0.0357 (0.0251) | 0.0383 (0.0222) | |
| 2000 | True | 0.0427 (3e 04) 04) |
0.0415 (0.002) | 0.0418 (0.0015) | 0.0359 (0.0034) | 0.0422 (0.001) | 0.0412 (0.0025) | 0.0417 (0.0016) |
| Naive | 0.0433 (0.0065) | 0.0468 (0.0102) | 0.0463 (0.0095) | 0.0368 (0.0125) | 0.0432 (0.0109) | 0.0472 (0.0114) | 0.0462 (0.0106) | |
| CV | 0.0428 (0.0105) | 0.0413 (0.0108) | 0.0417 (0.0099) | 0.0359 (0.0124) | 0.0421 (0.0109) | 0.0409 (0.0123) | 0.0416 (0.0111) | |
Cost ratio 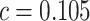
| ||||||||
| 200 | True | 0.0542 (0.0067) | 0.0474 (0.0136) | 0.049 (0.0119) | 0.0366 (0.0221) | 0.0403 (0.0173) | 0.0472 (0.0181) | 0.0515 (0.0119) |
| Naive | 0.0518 (0.0194) | 0.0653 (0.0273) | 0.0629 (0.0262) | 0.0398 (0.0322) | 0.0374 (0.0298) | 0.064 (0.0294) | 0.0598 (0.0287) | |
| CV | 0.0379 (0.0306) | 0.0299 (0.031) | 0.0318 (0.0287) | 0.0178 (0.0344) | 0.0217 (0.0314) | 0.0287 (0.0383) | 0.0343 (0.0333) | |
| 500 | True | 0.0572 (0.002) | 0.0536 (0.0066) | 0.0543 (0.0055) | 0.0477 (0.0127) | 0.0471 (0.0092) | 0.0538 (0.007) | 0.0553 (0.0045) |
| Naive | 0.0559 (0.0127) | 0.0633 (0.0185) | 0.0623 (0.0175) | 0.0474 (0.0224) | 0.0442 (0.0188) | 0.0627 (0.0202) | 0.0606 (0.019) | |
| CV | 0.0501 (0.0197) | 0.0454 (0.0206) | 0.0464 (0.0186) | 0.0373 (0.0241) | 0.0387 (0.0193) | 0.0455 (0.0238) | 0.0478 (0.0205) | |
| 2000 | True | 0.0585 (5e 04) 04) |
0.0571 (0.0022) | 0.0573 (0.002) | 0.0543 (0.0044) | 0.0487 (0.0049) | 0.0569 (0.0024) | 0.0573 (0.0017) |
| Naive | 0.0588 (0.0069) | 0.0622 (0.0103) | 0.0619 (0.0096) | 0.0547 (0.0106) | 0.0488 (0.0097) | 0.0618 (0.0114) | 0.061 (0.0104) | |
| CV | 0.0575 (0.0106) | 0.0557 (0.0109) | 0.056 (0.0099) | 0.0524 (0.0111) | 0.0478 (0.0096) | 0.0555 (0.0122) | 0.0561 (0.0109) | |
Cost ratio 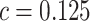
| ||||||||
| 200 | True | 0.0577 (0.0072) | 0.0514 (0.0136) | 0.0529 (0.0119) | 0.0356 (0.0233) | 0.0397 (0.0185) | 0.0489 (0.0203) | 0.0535 (0.0143) |
| Naive | 0.0485 (0.0197) | 0.0625 (0.0265) | 0.0605 (0.0255) | 0.0318 (0.0309) | 0.0293 (0.0294) | 0.0595 (0.0284) | 0.0552 (0.0278) | |
| CV | 0.0327 (0.0298) | 0.0257 (0.0302) | 0.0275 (0.0282) | 0.009 (0.0328) | 0.0131 (0.0306) | 0.0214 (0.0379) | 0.0275 (0.0334) | |
| 500 | True | 0.0611 (0.0022) | 0.0577 (0.0067) | 0.0583 (0.0056) | 0.0465 (0.0148) | 0.0457 (0.011) | 0.0569 (0.0079) | 0.0584 (0.0051) |
| Naive | 0.0531 (0.013) | 0.0608 (0.0177) | 0.06 (0.0169) | 0.0389 (0.0224) | 0.0355 (0.02) | 0.0587 (0.0194) | 0.0567 (0.0183) | |
| CV | 0.0463 (0.0191) | 0.0419 (0.0199) | 0.0428 (0.0186) | 0.0285 (0.0238) | 0.03 (0.0201) | 0.0406 (0.0235) | 0.0432 (0.0204) | |
| 2000 | True | 0.0626 (6e 04) 04) |
0.0611 (0.0024) | 0.0613 (0.0021) | 0.052 (0.0069) | 0.047 (0.0057) | 0.0602 (0.0024) | 0.0606 (0.0018) |
| Naive | 0.0575 (0.0068) | 0.0607 (0.0094) | 0.0604 (0.0089) | 0.0464 (0.0114) | 0.0411 (0.0105) | 0.0592 (0.0102) | 0.0585 (0.0095) | |
| CV | 0.0555 (0.0096) | 0.0537 (0.01) | 0.0539 (0.0094) | 0.0445 (0.0114) | 0.0401 (0.0104) | 0.0528 (0.011) | 0.0534 (0.01) | |
Cost ratio 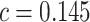
| ||||||||
| 200 | True | 0.042 (0.008) | 0.0368 (0.0127) | 0.038 (0.0111) | 0.0164 (0.0221) | 0.0205 (0.0171) | 0.0309 (0.021) | 0.0356 (0.0152) |
| Naive | 0.0429 (0.0205) | 0.058 (0.0261) | 0.0562 (0.0254) | 0.0227 (0.0293) | 0.0199 (0.0287) | 0.0529 (0.0277) | 0.0484 (0.0272) | |
| CV | 0.0255 (0.0293) | 0.0199 (0.0294) | 0.0217 (0.028) |
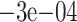 (0.0301) (0.0301) |
0.0038 (0.0286) | 0.0121 (0.0372) | 0.018 (0.0337) | |
| 500 | True | 0.0459 (0.0025) | 0.0426 (0.0071) | 0.0432 (0.0061) | 0.0246 (0.0151) | 0.0245 (0.0113) | 0.0399 (0.0092) | 0.0415 (0.0063) |
| Naive | 0.0462 (0.0148) | 0.0549 (0.018) | 0.0542 (0.0176) | 0.0253 (0.0236) | 0.0227 (0.0218) | 0.0504 (0.0199) | 0.0485 (0.019) | |
| CV | 0.0389 (0.0195) | 0.0348 (0.0202) | 0.0357 (0.0194) | 0.0155 (0.0235) | 0.0174 (0.0211) | 0.0307 (0.0248) | 0.0336 (0.0221) | |
| 2000 | True | 0.0476 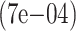
|
0.0463 (0.0024) | 0.0464 (0.0022) | 0.0275 (0.0081) | 0.0251 (0.0059) | 0.0437 (0.0024) | 0.0441 (0.0019) |
| Naive | 0.048 (0.009) | 0.0519 (0.0104) | 0.0516 (0.0104) | 0.0277 (0.0147) | 0.025 (0.0128) | 0.0485 (0.0112) | 0.0477 (0.0109) | |
| CV | 0.0462 (0.0107) | 0.0444 (0.011) | 0.0446 (0.011) | 0.0262 (0.0144) | 0.024 (0.0127) | 0.042 (0.0119) | 0.0425 (0.0114) | |
Cost ratio 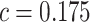
| ||||||||
| 200 | True | 0.0214 (0.0075) | 0.0179 (0.0106) | 0.0191 (0.009) |
 0.0044 (0.0183) 0.0044 (0.0183) |
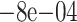 (0.012) (0.012) |
0.0054 (0.0194) | 0.01 (0.0139) |
| Naive | 0.0318 (0.0209) | 0.0489 (0.0257) | 0.0474 (0.0254) | 0.0094 (0.0247) | 0.007 (0.0242) | 0.0404 (0.0261) | 0.0354 (0.0259) | |
| CV | 0.013 (0.0274) | 0.0097 (0.0275) | 0.0113 (0.0272) |
 0.0117 (0.0242) 0.0117 (0.0242) |
 0.0079 (0.0231) 0.0079 (0.0231) |
 0.004 (0.0341) 0.004 (0.0341) |
0.0014 (0.0318) | |
| 500 | True | 0.0257 (0.0035) | 0.0227 (0.007) | 0.023 (0.0067) |
 0.0011 (0.0094) 0.0011 (0.0094) |
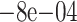 (0.0065) (0.0065) |
0.0135 (0.0107) | 0.0154 (0.0077) |
| Naive | 0.0313 (0.0158) | 0.0417 (0.0184) | 0.0412 (0.0184) | 0.0052 (0.0191) | 0.0032 (0.0183) | 0.0326 (0.0201) | 0.0305 (0.0197) | |
| CV | 0.0234 (0.0198) | 0.0204 (0.0202) | 0.0211 (0.0201) |
 0.0029 (0.0177) 0.0029 (0.0177) |
 0.0015 (0.0172) 0.0015 (0.0172) |
0.0093 (0.0254) | 0.0124 (0.0237) | |
| 2000 | True | 0.028 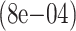
|
0.0266 (0.0032) | 0.0266 (0.0031) |
 0.003 (0.0041) 0.003 (0.0041) |
 0.0024 (0.0035) 0.0024 (0.0035) |
0.0189 (0.0038) | 0.0193 (0.0034) |
| Naive | 0.0293 (0.0085) | 0.0339 (0.0103) | 0.0337 (0.0104) |
 0.0014 (0.0107) 0.0014 (0.0107) |
 0.0012 (0.0103) 0.0012 (0.0103) |
0.0254 (0.0116) | 0.0246 (0.0114) | |
| CV | 0.0274 (0.0106) | 0.0257 (0.0111) | 0.0258 (0.0112) |
 0.0025 (0.0101) 0.0025 (0.0101) |
 0.0022 (0.01) 0.0022 (0.01) |
0.0177 (0.0133) | 0.0183 (0.0129) | |
PAR : corresponds to the rule
: corresponds to the rule 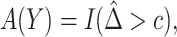 where
where 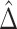 is the estimated risk difference based on the GLM risk model NPAR1
is the estimated risk difference based on the GLM risk model NPAR1 , NPAR2
, NPAR2 : correspond to
: correspond to 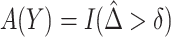 with
with 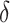 chosen to maximize the empirical or augmented estimate of EB; WLOGIS1
chosen to maximize the empirical or augmented estimate of EB; WLOGIS1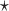 , WLOGIS2
, WLOGIS2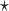 : correspond to rule
: correspond to rule 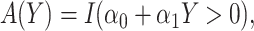 where
where 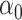 and
and 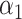 are estimated based on converting the problem to a weighted classification problem, which is solved using weighted logistic regression with empirical weight or augmented weight, respectively; WCLASS1
are estimated based on converting the problem to a weighted classification problem, which is solved using weighted logistic regression with empirical weight or augmented weight, respectively; WCLASS1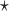 , WCLASS2
, WCLASS2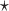 : correspond to rule
: correspond to rule 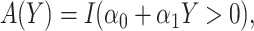 where
where 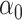 and
and 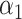 are estimated based on converting the problem to a weighted classification problem, which is solved using a grid search with empirical weight or augmented weight, respectively;True
are estimated based on converting the problem to a weighted classification problem, which is solved using a grid search with empirical weight or augmented weight, respectively;True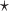 : indicates population performance of a treatment-selection rule derived from a training data.
: indicates population performance of a treatment-selection rule derived from a training data.
In Table 3, we also compare naive estimates of expected benefit using the same data where a treatment-selection rule is derived, and estimates based on random cross-validation. For the latter, we randomly split the data into 2/3 training and 1/3 test, estimate a treatment-selection rule from the training set, then compute the expected benefit for this rule using the test set; an average of expected benefit estimates is computed over 500 splits. From Table 3, we see that naive estimates of expected benefit can have severe overestimation even with a sample size as large as 2000, for all estimators. An exception is the model-based estimator whose overfitting bias is minimal for sample sizes >500. The overfitting bias is corrected by cross-validation.
Bootstrap standard errors and CI coverage for robust estimates of EB are presented in supplementary material available at Biostatistics online, Table 1. Undercoverage of ordinary bootstrap CIs happens in some cases when the cost ratio equals  ; the adaptive bootstrap CI alleviates the problem.
; the adaptive bootstrap CI alleviates the problem.
5. Data example
In this section, we illustrate the approaches using the Diabetes Control and Complications Trial (DCCT) 5, a large-scale randomized controlled trial designed to compare intensive and conventional diabetes therapy with respect to their effects on the development and progression of early vascular and neurologic complications of diabetes. Overall, 1441 patients with insulin-dependent diabetes mellitus were enrolled beginning in 1983 and followed through 1999. One outcome significantly impacted by intensive therapy in DCCT is microalbuminuria, a sign of kidney damage, defined as albumin excretion rate >40 mg/24 h. Our analysis here consists of 579 subjects in the secondary prevention cohort of DCCT, defined as patients with mild preexisting retinopathy or other complications, who did not have microalbuminuria and neuropathy at baseline. We consider baseline hemoglobin A1C (HBA1C) as a biomarker for selecting treatment: a linear logistic regression model of microalbuminuria developed during the study versus treatment and baseline HBA1C and their interaction shows a significant interaction between treatment and HBA1C.
We estimate the (standardized) expected benefit of HBA1C. The curve of model-based estimator of 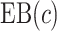 versus
versus 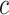 is presented in Figure 1(a), together with estimated lower and upper bounds of PEB. Corresponding bounds for standardized expected benefit of HBA1C are displayed in Figure 1(b). For a set of chosen cost ratios, the model-based estimates and their 95% CI are shown in Table 4. For example, at cost ratio
is presented in Figure 1(a), together with estimated lower and upper bounds of PEB. Corresponding bounds for standardized expected benefit of HBA1C are displayed in Figure 1(b). For a set of chosen cost ratios, the model-based estimates and their 95% CI are shown in Table 4. For example, at cost ratio 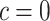 , i.e. equal treatment cost between the two diabetes therapies, HBA1C has an EB of 0.005, while the PEB can range from 0.005 to 0.206, implying that standardized EB of HBA1C is >2.3%. If
, i.e. equal treatment cost between the two diabetes therapies, HBA1C has an EB of 0.005, while the PEB can range from 0.005 to 0.206, implying that standardized EB of HBA1C is >2.3%. If 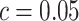 , i.e. the additional cost by intensive therapy compared with conventional therapy is 5% the cost of developing microalbuminuria, HB1AC has an EB of 0.019, which corresponds to 8–38.8% of PEB. Supplementary material available at Biostatistics online, Table 2 presents cross-validated EB for the model-based estimator and robust estimators. In general, we see a reduction in EB resulted from CV. Treatment-selection rules based on
, i.e. the additional cost by intensive therapy compared with conventional therapy is 5% the cost of developing microalbuminuria, HB1AC has an EB of 0.019, which corresponds to 8–38.8% of PEB. Supplementary material available at Biostatistics online, Table 2 presents cross-validated EB for the model-based estimator and robust estimators. In general, we see a reduction in EB resulted from CV. Treatment-selection rules based on 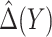 and the estimated threshold
and the estimated threshold 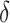 or based on linear marker combinations that minimize weighted classification errors using augmented weights have slightly better CV estimates of EB compared with the model-based estimator.
or based on linear marker combinations that minimize weighted classification errors using augmented weights have slightly better CV estimates of EB compared with the model-based estimator.
Table 4.
Estimate and 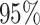 adaptive CI of model-based estimator of expected benefit in DCCT example
adaptive CI of model-based estimator of expected benefit in DCCT example
Cost ratio 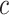
|
0 | 0.05 | 0.10 | 0.12 |
|---|---|---|---|---|
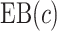 |
0.005 (0, 0.166) | 0.019 (0, 0.123) | 0.035 (0.001, 0.102) | 0.028 (0, 0.119) |
 |
0.005 (0, 0.166) | 0.05 (0.031, 0.157) | 0.086 (0.029, 0.149) | 0.084 (0.029, 0.149) |
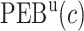 |
0.206 (0.157, 0.352) | 0.242 (0.192, 0.335) | 0.267 (0.216, 0.329) | 0.261 (0.211, 0.343) |
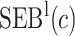 |
0.023 (0, 0.498) | 0.08 (0, 0.382) | 0.131 (0.003, 0.334) | 0.107 (0.001, 0.366) |
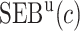 |
1 (1, 1) | 0.388 (0, 0.802) | 0.408 (0.026, 0.809) | 0.333 (0.005, 0.823) |
Note: the adaptive CI was constructed using 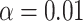 ; the optimal treatment-selection rule at cost ratio
; the optimal treatment-selection rule at cost ratio 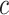 is to recommend intensive treatment if
is to recommend intensive treatment if  .
.
6. Discussion
We developed an expected benefit measure for characterizing the capacity of biomarkers for treatment selection, and developed the concept of a perfect treatment-selection rule that correctly identifies subjects who will benefit from treatment. Expected benefit of the latter is in general not identifiable and we developed bounds for it based on disease risk model. The idea of generating bounds can be readily applied to other summary measures such as the reduction in the population disease rate under marker-based treatment (Song and Pepe, 2004). An interesting observation regarding the model-based bounds is that their width depends on how well the risk model used to construct the bounds can identify the percent of subjects “benefited” by treatment. A model that better predicts heterogeneity in treatment benefit in terms of larger variability in 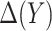 tends to move up the lower bound for PEB by increasing
tends to move up the lower bound for PEB by increasing 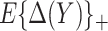 . When we have several risk models in a population, e.g. risk given
. When we have several risk models in a population, e.g. risk given 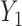 and risk given
and risk given 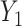 and
and  , tighter bounds can be constructed combining bounds derived from individual risk models. Specifically, at a given cost ratio, the lower bound of PEB can be constructed as the maximum among individual lower bounds, and the upper bound can be constructed as the minimum among individual upper bounds. However, the variance may be difficult to calculate in this case and will require further investigation.
, tighter bounds can be constructed combining bounds derived from individual risk models. Specifically, at a given cost ratio, the lower bound of PEB can be constructed as the maximum among individual lower bounds, and the upper bound can be constructed as the minimum among individual upper bounds. However, the variance may be difficult to calculate in this case and will require further investigation.
We developed a GLM model-based approach for deriving treatment-selection rules to maximize the expected benefit. In addition, we considered robust approaches that combine the risk difference from the GLM model and an estimated threshold, or that find marker combinations that directly maximize the estimate of expected benefit. The latter can be computationally intensive if a grid search is used to identify model parameters; the GLM model, in contrast, can be easily implemented with standard statistical software. The model-based approach can lead to treatment-selection rules with better performance as well as increased efficiency in estimating the expected benefit when the risk model is correctly specified, while the robust approaches are less affected by misspecification of the working risk model and can be used for sensitivity analysis.
For inference about expected benefit, we proposed an adaptive bootstrap procedure to handle non-regularity when the cost ratio is close to the average treatment effect. This idea of using data to adaptively construct a bootstrap CI has great potential to be used in other types of biomarker evaluation and comparison problems where non-regularity can occur at some point in the parameter space.
In this paper, we consider the treatment–disease cost ratio 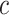 to be constant in the population, and vary
to be constant in the population, and vary 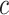 using a sensitivity analysis. In practice, one needs to put the burdens of disease and treatment on the same scale to determine the value of
using a sensitivity analysis. In practice, one needs to put the burdens of disease and treatment on the same scale to determine the value of 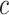 . For example, Gail (2009) evaluated the benefit of using the Gail model for recommending tamoxifen for breast cancer prevention. Tamoxifen has been shown to increase the risk of “secondary” events such as stroke and endometrial cancer. Gail (2009) assumed that burden per secondary event is the same as the burden per breast cancer event, and chose
. For example, Gail (2009) evaluated the benefit of using the Gail model for recommending tamoxifen for breast cancer prevention. Tamoxifen has been shown to increase the risk of “secondary” events such as stroke and endometrial cancer. Gail (2009) assumed that burden per secondary event is the same as the burden per breast cancer event, and chose 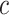 to be the increased rate of having any secondary event due to tamoxifen. Alternatively, if one can associate a monetary cost with each disease event, and a monetary cost with treatment (potentially including the cost of the treatment itself and the cost due to secondary events), then
to be the increased rate of having any secondary event due to tamoxifen. Alternatively, if one can associate a monetary cost with each disease event, and a monetary cost with treatment (potentially including the cost of the treatment itself and the cost due to secondary events), then  can be computed as the rate of the latter relative to that of the former. In some settings, the cost ratio might be a function of the biomarker. For example, the cost of mammography use for breast cancer prevention might depend on women's age (Gail, 2009). It is straightforward to extend the concept of expected benefit to allow
can be computed as the rate of the latter relative to that of the former. In some settings, the cost ratio might be a function of the biomarker. For example, the cost of mammography use for breast cancer prevention might depend on women's age (Gail, 2009). It is straightforward to extend the concept of expected benefit to allow 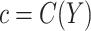 to be a function of the biomarker in scenarios where information is available for modeling
to be a function of the biomarker in scenarios where information is available for modeling 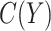 as proposed in Janes and others (2013).
as proposed in Janes and others (2013).
Finally, while the concepts of perfect and/or standardized expected benefits are restricted to binary disease outcomes, the concept of expect benefit itself and the estimation and inference methods developed here can be readily generalized to handle continuous outcomes.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org
Funding
This work was supported by NIH grant R01 GM106177-01, P01 CA142538, R01 CA152089 and U01 CA086368.
Supplementary Material
Acknowledgements
Conflict of Interest: None declared.
References
- Baker S. G., Cook N. R., Vickers A., Kramer B. S. Using relative utility curves to evaluate risk prediction. Journal of the Royal Statistical Society. 2009;172((4)):729–748. doi: 10.1111/j.1467-985X.2009.00592.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger R. L., Boos D. D. P values maximized over a confidence set for the nuisance parameter. Journal of the American Statistical Association. 1994;89((427)):1012–1016. [Google Scholar]
- Bura E., Gastwirth J. L. The binary regression quantile plot: assessing the importance of predictors in binary regression visually. Biometrical Journal. 2001;43((1)):5–21. [Google Scholar]
- Cai T., Tian L., Wong P. H., Wei L. J. Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics. 2011;12((2)):270–282. doi: 10.1093/biostatistics/kxq060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DCCTRG. The effect of intensive treatment of diabetes on the development and progression of long-term complications in insulin-dependent diabetes mellitus. New England Journal of Medicine. 1993;329((14)):977–986. doi: 10.1056/NEJM199309303291401. [DOI] [PubMed] [Google Scholar]
- Foster J. C., Taylor J. M. G., Ruberg S. J. Subgroup identification from randomized clinical trial data. Statistics in Medicine. 2011;30((24)):2867–2880. doi: 10.1002/sim.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadbury G. L., Iyer H. K., Albert J. M. Individual treatment effects in randomized trials with binary outcomes. Journal of Statistical Planning and Inference. 2004;121((2)):163–174. [Google Scholar]
- Gail M. H. Value of adding single-nucleotide polymorphism genotypes to a breast cancer risk model. Journal of the National Cancer Institute. 2009;101((13)):959–963. doi: 10.1093/jnci/djp130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Gilbert P. B., Janes H. Assessing treatment-selection markers using a potential outcomes framework. Biometrics. 2012;68((3)):687–696. doi: 10.1111/j.1541-0420.2011.01722.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Pepe M. S. Assessing risk prediction models in case–control studies using semiparametric and nonparametric methods. Statistics in medicine. 2010;29((13)):1391–1410. doi: 10.1002/sim.3876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes H., Brown M. D., Pepe M. S., Huang Y. Statistical methods for evaluating and comparing biomarkers for patient treatment selection. International Journal of Biostatistics. 2014 doi: 10.1515/ijb-2012-0052. in Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janes H., Pepe M. S., Huang Y. A framework for evaluating markers used to select patient treatment. Medical Decision Making. 2013;34((2)):159–167. doi: 10.1177/0272989X13493147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laber E. B., Murphy S. A. Adaptive confidence intervals for the test error in classification. Journal of the American Statistical Association. 2011;106((495)):904–913. doi: 10.1198/jasa.2010.tm10053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapsomaniki E., White I. R., Wood A. M., Thompson S. G. A framework for quantifying net benefits of alternative prognostic models. Statistics in Medicine. 2012;31((2)):114–130. doi: 10.1002/sim.4362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J. M. In Proceedings of the Second Seattle Symposium in Biostatistics. New York: Springer; 2004. Optimal structural nested models for optimal sequential decisions; pp. 189–326. [Google Scholar]
- Song X., Pepe M. S. Evaluating markers for selecting a patient's treatment. Biometrics. 2004;60((4)):874–883. doi: 10.1111/j.0006-341X.2004.00242.x. [DOI] [PubMed] [Google Scholar]
- Vickers A. J., Kattan M. W., Sargent D. J. Method for evaluating prediction models that apply the results of randomized trials to individual patients. Trials. 2007;8((1)):14. doi: 10.1186/1745-6215-8-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B., Tsiatis A. A., Davidian M., Zhang M., Laber E. B. Estimating optimal treatment regimes from a classification perspective. Stat. 2012;1((1)):103–114. doi: 10.1002/sta.411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B., Tsiatis A. A., Laber E. B., Davidian M. A robust method for estimating optimal treatment regimes. Biometrics. 2012;68((4)):1010–1018. doi: 10.1111/j.1541-0420.2012.01763.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Wang C., Nie L., Soon G. Assessing the heterogeneity of treatment effects via potential outcomes of individual patients. Journal of the Royal Statistical Society. 2013;62((5)):687–704. doi: 10.1111/rssc.12012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao L., Tian L., Cai T., Claggett B., Wei L. J. Effectively selecting a target population for a future comparative study. Journal of the American Statistical Association. 2013;108((502)):527–539. doi: 10.1080/01621459.2013.770705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Zeng D., Rush A. J., Kosorok M. R. Estimating individualized treatment rules using outcome weighted learning. Journal of the American Statistical Association. 2012;107((499)):1106–1118. doi: 10.1080/01621459.2012.695674. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.