Mechanical Folding and Unfolding of Protein Barnase at the Single-Molecule Level

Abstract

The unfolding and folding of protein barnase has been extensively investigated in bulk conditions under the effect of denaturant and temperature. These experiments provided information about structural and kinetic features of both the native and the unfolded states of the protein, and debates about the possible existence of an intermediate state in the folding pathway have arisen. Here, we investigate the folding/unfolding reaction of protein barnase under the action of mechanical force at the single-molecule level using optical tweezers. We measure unfolding and folding force-dependent kinetic rates from pulling and passive experiments, respectively, and using Kramers-based theories (e.g., Bell-Evans and Dudko-Hummer-Szabo models), we extract the position of the transition state and the height of the kinetic barrier mediating unfolding and folding transitions, finding good agreement with previous bulk measurements. Measurements of the force-dependent kinetic barrier using the continuous effective barrier analysis show that protein barnase verifies the Leffler-Hammond postulate under applied force and allow us to extract its free energy of folding, ΔG₀. The estimated value of ΔG₀ is in agreement with our predictions obtained using fluctuation relations and previous bulk studies. To address the possible existence of an intermediate state on the folding pathway, we measure the power spectrum of force fluctuations at high temporal resolution (50 kHz) when the protein is either folded or unfolded and, additionally, we study the folding transition-path time at different forces. The finite bandwidth of our experimental setup sets the lifetime of potential intermediate states upon barnase folding/unfolding in the submillisecond timescale.

Introduction

In recent years, the advent of single-molecule techniques has expanded the horizons of molecular biophysics. They offer the possibility to observe and manipulate one molecule at a time with unprecedented spatial and temporal resolution, such that transient molecular states and rare trajectories become experimentally accessible (1). One goal of single-molecule experiments is the full characterization of the molecular free energy landscape (mFEL) in nucleic acids and proteins. The mFEL describes the free energy changes along one or more reaction coordinates between the folded and unfolded molecular states (2, 3). A full knowledge of the mFEL for a given protein would allow us to characterize its folding pathway under different conditions (such as a temperature variation, the addition of a chemical denaturant, or the application of mechanical forces).

Atomic force microscopy (AFM) and optical tweezers (OT) are experimental techniques particularly well-suited to study the dynamic behavior of single proteins under the action of mechanical force. Such techniques offer the possibility to observe individual folding and unfolding events, thereby providing new tools to experimentally investigate the folding reaction (4, 5, 6). By applying forces at the ends of the molecule, invaluable information about thermodynamics and kinetics of folding can be obtained and used to reconstruct main features of the mFEL. In this work, we use OT to mechanically fold and unfold barnase, a 110-amino-acids-long bacterial ribonuclease protein secreted by Bacillus amyloliquefaciens that degrades RNA in the absence of its inhibitor barstar. This protein has been extensively studied in bulk experiments using protein engineering with Φ-value analysis, fluorescence, and x-ray crystallography (7, 8, 9, 10). Some controversial results suggested the possible existence of a high-energy intermediate state along the folding pathway, and this debate is nowadays still open (11, 12, 13). Here we combine pulling and passive experiments to characterize the folding and the unfolding reaction pathway of barnase with a time resolution of milliseconds. This requires the accurate knowledge of the elastic response of the peptide chain that we measured in our experiments using a recently developed method (14). Then, by applying the continuous effective barrier analysis (CEBA), we estimate the free energy of folding of barnase and the position of the transition state in unfolding and folding reactions along the molecular extension, which we assume to be a suitable reaction coordinate in these experiments. The CEBA method is based on the purely diffusive one-dimensional Kramers theory for activated transitions, and was originally introduced in force-spectroscopy studies of nucleic acid hairpins (15, 16). We validate our estimation for the free energy of folding of barnase by using fluctuation relations, which allow us to recover free energy differences from irreversible work measurements (17, 18). We also extract the power spectrum of the fluctuations of barnase in both the folded and the unfolded states. Our results show that barnase is a two-state folder under force, although we cannot exclude the presence of short-lived intermediate states of lifetime in the submillisecond scale.

The mechanical unfolding of barnase has been previously investigated using AFM and molecular dynamic simulations (19). In that case, no regular pattern was observed in the mechanical unfolding of barnase, probably because unfolding events <30 pN are smeared out by background noise due to the limited force resolution of the AFM instrument used in those experiments. These studies suggest that the TS upon mechanical unfolding is close to the native state, in agreement with the results we present in this article. Our results thus complement previous studies and provide a clearer description of the force-dependent thermodynamics and kinetics of the folding of barnase.

Materials and Methods

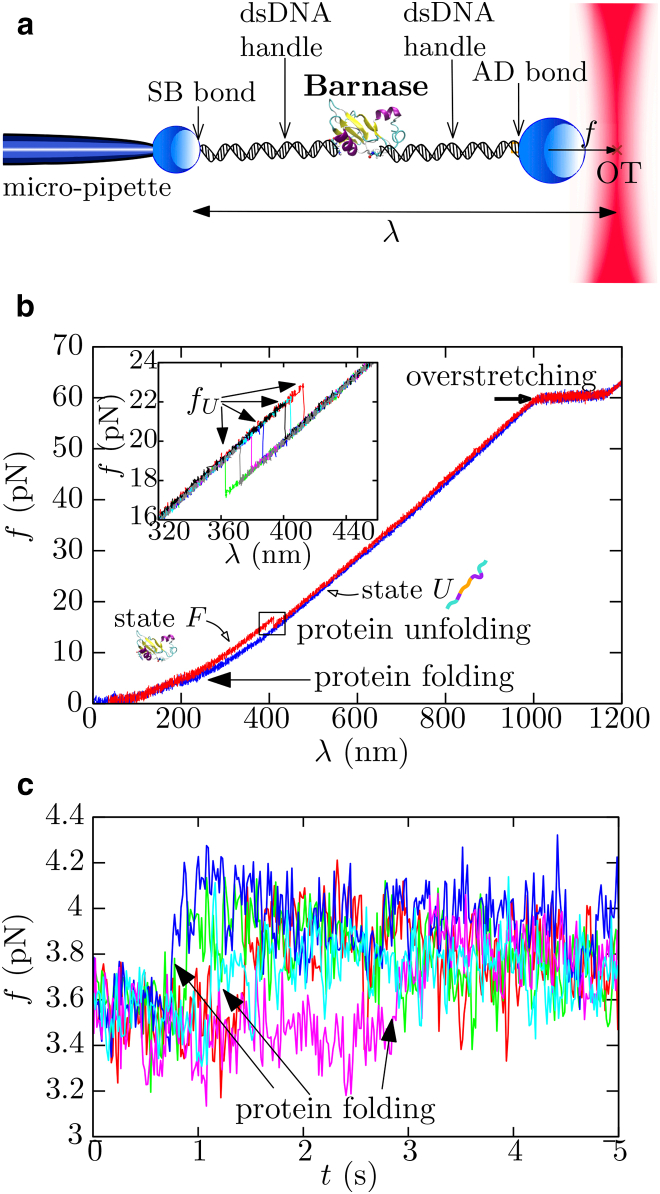
In our OT setup (Fig. 1 a), the N- and C-terminals of barnase are tethered via Cys residues to two double-stranded DNA (dsDNA) handles made of 500 basepairs, as described in Section S1 in the Supporting Material (3, 20, 21, 22, 23, 24, 25, 26). Each end of the molecular construct is tethered to a polystyrene micron-sized bead using streptavidin-biotin (2.0–2.9-μm-diameter bead; G. Kisker Biotech, Steinfurt, Germany) or antidigoxigenin-digoxigenin bonds (3.0–3.4-μm diameter bead; Spherotech, Libertyville, IL). One bead is then immobilized at the tip of the micropipette by air suction, whereas the other is captured in the optical trap. The optical trap has a force-dependent stiffness equal to k(f) = 0.062 + 0.00059f, as previously reported in Forns et al. (27). Our OT instrument allows us to externally control the distance λ between the tip of the micropipette and the center of the optical trap (28). The larger we set this distance, the larger the force applied to the molecular system. If not stated otherwise, the standard temporal acquisition rate in our experiments is 4 kHz, meaning that signals collected in the photodetectors are averaged out by the electronic processors to four data points per millisecond. Experiments were performed at room temperature (T ∼ 298 K) and in a buffer containing 10 mM Na₂HPO₄, 10 mM NaH₂PO₄ and at pH 7.0. Throughout the article, energies will be given in k_BT units (1 k_BT = 0.6 kcal/mol at room temperature).

Figure 1.

Force-spectroscopy experiments with OT on barnase. (a) Not-to-scale scheme of the molecular experimental setup: barnase is linked to two dsDNA handles and the whole construct is inserted between two polystyrene beads. One bead is immobilized at the tip of a micropipette by air suction whereas the other is captured in the optical trap. Force is exerted to the captured bead and translated to the molecular system. (b) Example of FDC measured in pulling experiments performed at 60 nm/s. Under the stretching protocol (red), the molecule abruptly unfolds at ∼20 pN, whereas in the releasing protocol (blue), the molecule folds back at ∼4 pN (arrow). At ∼60 pN, we observe the overstretching transition of the handles. (Inset) Collection of stretching traces acquired in independent experiments, where it can be seen that unfolding forces f_U vary in each experiment. (c) Example of FTTs measured in passive experiments (i.e., at λ-constant). Each color is an independent experiment where barnase was initially set in state U at f_p = 3.6 pN. To see this figure in color, go online.

Pulling experiments consist of sequentially stretching and releasing the molecular construct between 0.5 and 70 pN. In the stretching (releasing) process, the trap-pipette distance λ increases (decreases) at a constant pulling speed v. As a consequence, the force applied to the molecular system also increases (decreases), as can be appreciated in the measured force-versus-distance curves (FDC) (Fig. 1 b). The loading rate r, defined as the speed at which force increases (decreases), can be extracted from r = k_effv, where k_eff is the effective stiffness of the trap-handles system (equal to the slope of the FDC). At a given value of the applied force, f_U, an abrupt drop in force is observed (square box in Fig. 1 b), which signals the unfolding of the molecule (23, 29). The unfolding force f_U changes upon independent repetitions of pulling experiments, as can be seen in the inset of Fig. 1 b, which reports several stretching curves. At ∼60 pN, the overstretching transition of the 500-basepairs-long dsDNA handles is observed (30, 31). Therefore, the FDC measured during the stretching part of the pulling cycle shows a single jump followed by the overstretching (red curve in Fig. 1 b). This signature corresponds to a single protein tethered between the two polystyrene beads (Fig. 1 a). The folding of barnase along the releasing process usually occurs at forces <5 pN (blue curve in Fig. 1 b), much below the typical unfolding forces. Therefore, the protein exhibits large hysteresis effects. The folding transition is not clearly visible in the FDC as it is masked by thermal fluctuations. Occasionally, the protein does not fold as revealed by the absence of a force rip in the next pull. To ensure folding, we stop and hold the pulling experiment at the minimum force value of 0.5 pN for 2 s to increase the probability of folding at the end of the releasing process.

We also carried out passive experiments (32, 33, 34): starting from the unfolded state, the force was relaxed until a preset force value (f_p) between 3 and 6 pN was reached. At that point, the release process stops and the distance λ is kept constant during a time interval of ∼15 s. A collection of force-versus-time traces (FTTs) measured in such passive mode at f_p = 3.6 pN is shown in Fig. 1 c, where folding is revealed as an abrupt jump in force (arrows). Once barnase folds in passive experiments, it is never observed to unfold again in the experimentally accessed timescales.

Results and Discussion

Elastic properties of the peptide chain

Two branches of force are observed in the experimental FDCs obtained in pulling experiments (Fig. 1 b): the upper branch shows the elastic response of the molecular construct when barnase is folded in its native globular conformation (state F), and the lower branch shows it when the protein is unfolded (state U). As shown in Alemany and Ritort (14), the effective stiffness of each branch, $k_{\text{eff}}^F$ and $k_{\text{eff}}^U$, respectively, satisfies

$$\frac{1}{k_{\text{eff}}^F}=\frac{1}{k_{\text{b}}}+\frac{1}{k_{\text{h}}}+\frac{1}{k_{\text{d}}},$$ (1a)

$$\frac{1}{k_{\text{eff}}^U}=\frac{1}{k_{\text{b}}}+\frac{1}{k_{\text{h}}}+\frac{1}{k_{\text{p}}},$$ (1b)

where k_b is the stiffness of the optical trap, k_h is the stiffness of the dsDNA handles, k_d is the stiffness of the protein in state F, and k_p is the stiffness of barnase in state U (i.e., it is the stiffness of the polypeptide chain).

Both $k_{\text{eff}}^F\left(f\right)$ and $k_{\text{eff}}^U\left(f\right)$ can be estimated from the slopes of the FDC along the folded and unfolded force-branches measured in pulling experiments (Fig. 2 a). The subtraction of their inverse values at a given force f gives

$$\frac{1}{k_{\text{eff}}^U\left(f\right)}-\frac{1}{k_{\text{eff}}^F\left(f\right)}=\frac{1}{k_{\text{p}}\left(f\right)}-\frac{1}{k_{\text{d}}\left(f\right)}.$$ (2)

Therefore, by fitting the experimental measurement of ${\left(k_{\text{eff}}^U\right)}^{-1}-{\left(k_{\text{eff}}^F\right)}^{-1}$ to an analytical expression for k_p⁻¹ – k_d⁻¹, we can extract the elastic properties of the polypeptide chain (14). Here, the elastic rigidity of the polypeptide chain k_p(f) is assumed to satisfy the wormlike-chain (WLC) elastic model. To model it we use the interpolation formula derived in Bustamante et al. (35) and also the more accurate numerical expression presented in Bouchiat et al. (36) (Eq. S1 in Section S2). The folded protein is modeled as a single bond that is oriented under mechanical force as a single dipole does under the action of a magnetic field (14, 27) (Eq. S2). The result of the fit allows us to estimate the persistence length P and the inter-amino-acid distance d_aa of the polypeptide chain (Fig. 2 b). Values recovered for P and d_aa using the WLC interpolation formula proposed by Bouchiat et al. (36) are in very good agreement with values proposed in previous single-molecule studies (21, 23) (Table 1). Thus, barnase apparently behaves as a two state system in pulling experiments: each force branch corresponds to a given protein state (F or U) that contains the elastic response of the full molecular construct.

Figure 2.

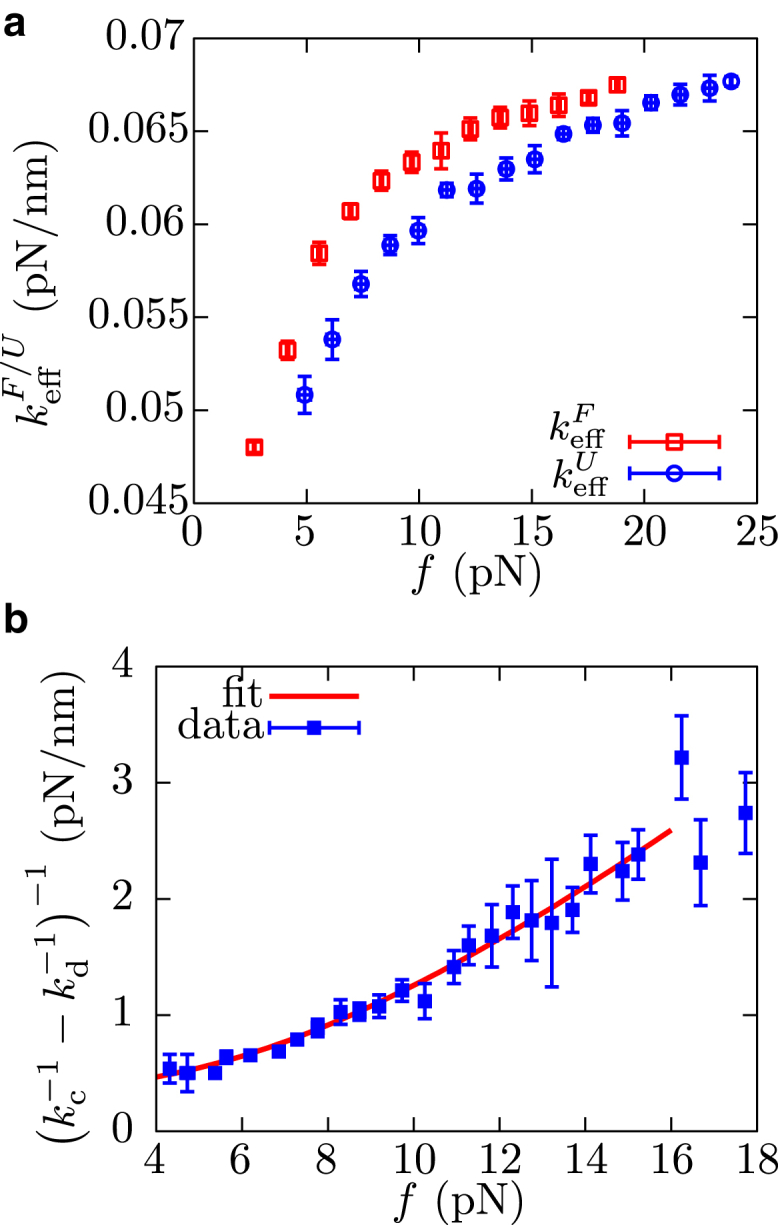
Elastic response of the peptide chain. (a) Effective stiffnesses along the folded and unfolded force branches, $k_{\text{eff}}^F$ (red open squares) and $k_{\text{eff}}^U$ (blue solid circles), respectively, obtained for one molecule. (b) Experimental measurement of ${\left({\left(k_{\text{eff}}^U\right)}^{-1}-{\left(k_{\text{eff}}^F\right)}^{-1}\right)}^{-1}$ and fit to Eq. 2 using the WLC elastic model (Eqs. S1 and S2). The resulting values for P and d_aa are given in Table 1. Data is obtained by averaging over 11 molecules. Error bars are standard statistical errors. To see this figure in color, go online.

Table 1.

Elastic Parameters for the Peptide Chain

WLC Model (Reference)	P (nm)	daa (nm/aa)
(35)	0.85 ± 0.05	0.36 ± 0.01
(36)	0.60 ± 0.05	0.34 ± 0.01

Results of the fit of ${\left({\left(k_{\text{eff}}^U\right)}^{-1}-{\left(k_{\text{eff}}^F\right)}^{-1}\right)}^{-1}$ to the interpolation formula for the WLC elastic model proposed in Bustamante et al. (35) (top) and Bouchiat et al. (36) (bottom) (Eqs. 2, S1, and S2). Error bars are standard errors from the fit.

The unfolding pathway of barnase

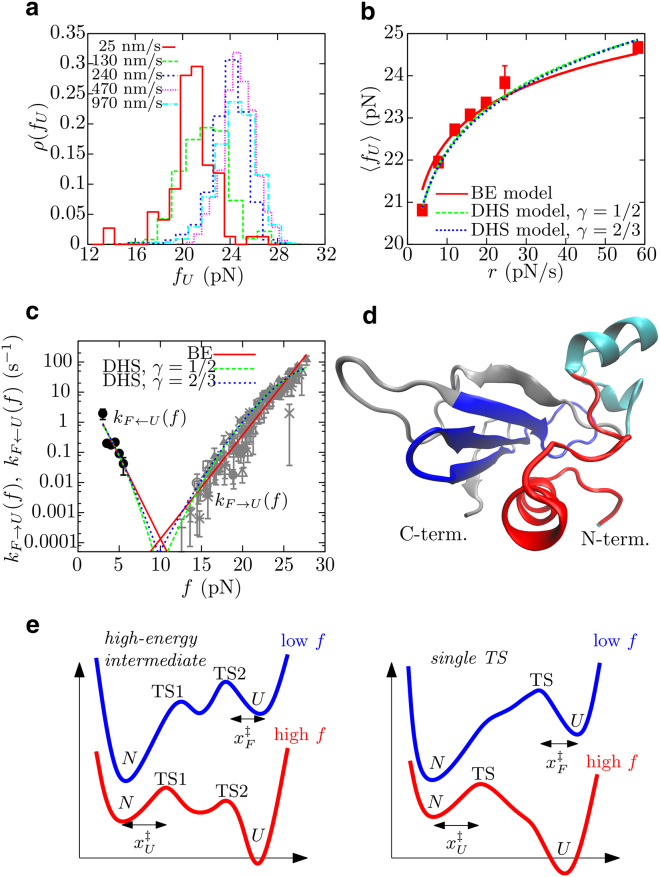
Fig. 3 a shows the histograms of unfolding forces, ρ(f_U), obtained in pulling experiments performed at different pulling speeds. The unfolding force distributions shift to higher force values as the pulling speed increases due to hysteresis effects. This is also observed in the plot of the average unfolding force 〈f_U〉 against the loading rate r (Fig. 3 b). Finally, the force-dependent unfolding kinetic rate k_F→U(f) can be measured from unfolding forces by modeling the mechanical unfolding of barnase as a first-order Markov process (Section S3). Results obtained at different loading rates are shown in Fig. 3 c (gray symbols), where it is observed that all experimental points fall into the same master curve within error bars.

Figure 3.

Mechanical unfolding, folding, and TS of barnase. (a) Unfolding force histograms obtained at different pulling speeds. (b) Dependence of average unfolding forces 〈f_U〉 with loading rate r (r = $v{k}_{\text{eff}}^F$, where $k_{\text{eff}}^F$ ∼ 0.069 pN/nm). Fits to the analytical expressions provided by the BE (red line; Eq. S6) and DHS (green and blue lines for γ = 1/2 and 2/3, respectively; Eq. S8) models are shown. (c) Unfolding and folding kinetic rates, k_F→U(f) (gray, each symbol is associated to a different pulling speed in the range 25–960 nm/s) and k_F←U(f) (black), respectively, as a function of force. Fits to the analytical expressions provided by the BE and DHS models are shown (Eqs. S5 and S7, respectively). Color code as in (b). (d) Structure of barnase in the folded state. (Red) The first 25 amino acids to unfold in the mechanical unfolding process; (cyan) helices 2 and 3, which first unfold in chemical denaturation. (Blue) The hydrophobic core of the protein, dominated by β-sheets (made of a total of 29 amino acids); its formation corresponds to the TS-mediating mechanical folding from state U. (e) Two possible scenarios explain our experimental results for the mFEL of the protein barnase. (Left) There is a high-energy intermediate state surrounded by TS1, that is located close to state N and mediates unfolding at high forces, and TS2, that is located close to state U and mediates folding at low forces. (Right) The mFEL has a single TS that changes its position along the reaction coordinate as a function of force. To see this figure in color, go online.

The force-induced unfolding of barnase can be modeled using the widely accepted Bell-Evans (BE) and Dudko-Hummer-Szabo (DHS) models (37, 38, 39, 40, 41, 42, 43) (Section S4), which assume the existence of a single kinetic barrier in the mFEL that the protein needs to energetically overcome to unfold. The BE model assumes that the position of the transition state relative to the native state, $x_U^{‡}$, does not depend on force, whereas the height of the kinetic barrier decreases by the amount $-f{x}_U^{‡}$. The DHS model considers either a parabolic or a linear-cubic-like shape of the mFEL (labeled by γ = 1/3 and 2/3, respectively) and assumes that the force decreases the energy of a given molecular configuration of extension x_m by the amount −fx_m. Both models provide analytical expressions for the rate-dependent average force, 〈f_U〉(r), and the force-dependent unfolding kinetic rate, k_F→U(f) (see Eqs. S6 and S8, respectively, for 〈f_U〉(r); and Eqs. S5 and S7, respectively, for k_F→U(f)), which are simultaneously fitted to the experimental data to extract the kinetic rate of unfolding at zero force, $k_m^u$, the distance $x_U^{‡}$, and the height of the kinetic barrier, $\Delta G_U^{‡}$. Results are shown in Fig. 3, b and c (red for the BE model; green and blue lines for the DHS model with γ = 1/3 or 2/3, respectively), and numerical values are summarized in Table 2. Estimations for $k_m^u$ and $x_U^{‡}$ obtained using the BE or the DHS model are different. This is probably due to the fact that the range of forces covered in our measurements span ∼10 pN, which is large enough for corrections to the BE model to be relevant. In contrast, the two fits to the DHS model provide similar values within error bars suggesting that it is a more accurate model to describe our experimental data.

Table 2.

Results from the Simultaneous Fit of 〈f_U〉(r) and k_F→U(f) to the BE and DHS Model

Model	$k_m^u$ (s−1)	$x_U^{‡}$ (nm)	$\Delta G_U^{‡}$ (kBT)
BE	3.3 × 10−6.0 ± 0.1	2.64 ± 0.06	—
DHS, γ = 1/2	4.7 × 10−12 ± 1	7 ± 1	34 ± 1
DHS, γ = 2/3	1.6 × 10−10.0 ± 0.6	6.0 ± 0.5	29 ± 1

Numerical values for $k_m^u$, $x_U^{‡}$, and $\Delta G_U^{‡}$ obtained by simultaneously fitting the average unfolding force 〈f_U〉 versus the pulling speed and the force-dependent unfolding kinetic rate k_F→U(f) to analytical expressions provided by the BE model and the DHS model, with γ = 1/2 or 2/3 (Eqs. S5–S8, respectively).

According to the DHS model, $x_U^{‡}$ ∼ 6.5 nm (obtained by averaging results for γ = 1/3 and 2/3 in Table 2), which at 20 pN corresponds to the release of ∼25 amino acids of a total of 110. The molecular structure of the transition state of protein barnase has been previously determined combining protein-engineering with Φ-value studies and molecular dynamic simulations (9, 10, 19). There, it is suggested that such TS is close to state F, with most of the native contacts essentially formed except for the first five amino acids plus the ∼20 amino-acids-long region containing α-helices 2 and 3 (cyan region in Fig. 3 d), which are unfolded. It is remarkable that the estimated number of amino acids that separate states N and the TS are similar in both chemical and mechanical denaturation experiments. This result does not necessarily imply that the unfolding pathway in the two different denaturation processes is the same, but rather that the properties of the kinetic barriers are similar. Indeed, from the DHS model we get $\Delta G_U^{‡}$ ∼ 31 k_BT, which is also in good agreement with previous bulk experimental estimates. In Matouschek et al. (7), the authors obtain that $\Delta G_U^{‡}$ ∼ 20 kcal/mol ∼34 k_BT, using the transition state Eyring theory (44) and the value $k_m^u$ of unfolding kinetic rate at zero denaturant concentration (1.1 × 10⁻⁴ s⁻¹) determined in urea-denaturation experiments (7, 45). The latter value for $k_m^u$ is too high compared to our zero-force estimates (see Table 2), suggesting the inapplicability of Eyring theory to a complex reaction such as protein folding. However, we cannot exclude also the possibility that the unfolding pathway at the probed forces (i.e., >10 pN) is different from that probed in urea denaturation experiments. In fact, the release of 25 amino acids to reach the transition state along mechanical unfolding experiments probably implies the unfolding of helix 1 (found between amino acids 7 and 17) and the stretching of unstructured regions found in the native structure of barnase (red region in Fig. 3 d). To clarify this aspect and fully characterize the mechanical unfolding pathway of barnase, experiments with circular permutations pulled from different internal residues along the sequence should be performed (23).

Finally, several attempts have been performed to characterize the unfolding kinetic rate of barnase, and values ranging between $k_m^u$ ∼ 10⁻⁴ s⁻¹ and $k_m^u$ ∼ 10⁻⁷ s⁻¹ have been proposed at zero concentration of denaturant (8, 19). Here, we extract the unfolding kinetic rate at zero force by fitting both the BE and the DHS model to our experimental results. Even though the order of magnitude of the value of $k_m^u$ found using the BE model appears to be in reasonable agreement with previous estimations obtained in urea denaturation experiments, it has been already discussed how this is not a proper model to describe the mechanical unfolding of barnase with our data, less the extrapolation of the unfolding rate to zero force. On the other hand, results obtained with the DHS model are up to five orders-of-magnitude lower than previously reported estimations for $k_m^u$. Such discrepancy might indicate that neither the BE nor the DHS model provide meaningful extrapolations of the kinetic properties of the protein at zero force because both fits are performed using forces >10 pN (which are far from 0 pN). It is important to keep in mind that the values of the rates extrapolated to zero force, $k_m^u$, should be taken with caution, at most they are upper bounds to the true zero force rates.

According to the Leffler-Hammond postulate (46, 47), the distance $x_U^{‡}$ increases as the force or the concentration of denaturant decreases. An examination of the first two columns in Table 2 shows that a large value of $x_U^{‡}$ is correlated with a low value of $k_m^u$, the constraint being the experimentally measured unfolding rates that are essentially proportional to $k_m^u$exp(f$x_U^{‡}$/k_BT) in the BE and DHS models. Therefore, if it were possible to measure the unfolding kinetic rate of barnase at low values of force (f < 10 pN) we could expect to obtain, for the slopes of log(k_F→U(f)) versus f, values for $x_U^{‡}$(f) falling in the range of the estimates reported from the DHS model (6–7 nm) and, consequently, lower values for $k_m^u$ (10⁻¹¹–10⁻¹⁰ s⁻¹). This would not necessarily improve the agreement between urea and mechanical denaturation experiments as both types of experiments are just providing upper bounds (with the estimate from Eyring theory, $k_m^u$ ∼ 10⁻⁴ s⁻¹, providing the largest upper bound as it assumes no recrossing events). Ultimately, the quantitative disagreement found between experimental estimates in urea and force might be also taken as indication of different unfolding pathways below and above 10 pN.

The folding pathway of barnase

In passive experiments, the folding of barnase is identified as an abrupt increase of force (arrows in Fig. 1 c). From the survival probability of state U at different preset forces f_p, we measure the force-dependent folding kinetic rate k_F←U(f) (see Section S5). Results are shown in Fig. 3 c (solid black circles). Additionally, fits corresponding to both the BE and the DHS models are shown, which allow us to estimate the relative distance between state U and the TS, $x_F^{‡}$, the height of the kinetic barrier relative to state U, $\Delta G_F^{‡}$, and the kinetic rate of folding at zero force, $k_m^f$. Numerical results are summarized in Table 3.

Table 3.

Results from Fit of k_F←U(f) to the BE and DHS Models

Model	$k_m^f$ (s−1)	$x_F^{‡}$ (nm)	$\Delta G_F^{‡}$ (kBT)
BE	40 ± 20	5 ± 1	—
DHS, γ = 1/2	2 ± 1	2.8 ± 0.6	5 ± 1
DHS, γ = 2/3	7 ± 3	3.6 ± 0.8	5 ± 1

Numerical values for $k_m^f$, $x_F^{‡}$, and $\Delta G_F^{‡}$ obtained by fitting the force-dependent folding kinetic rate to the analytical expressions provided by the BE model and the DHS model with γ = 1/2 or 2/3 (Eqs. S5 and S7, respectively).

Previous protein engineering-based experiments reported values for $k_m^f$ and $\Delta G_F^{‡}$ at ∼10 s⁻¹ and 9.6 kcal/mol ∼6 k_BT, respectively (7). As it can be seen in Table 3, our results obtained by fitting the BE or the DHS to the force-dependent folding kinetic rate are in reasonable agreement. In the study of the mechanical folding transition of barnase, our data was measured at low forces (∼4 pN) and therefore there is not much extrapolation at zero force for the folding kinetic rate. This explains the good agreement found between urea and mechanical denaturation experiments. Additionally, for the BE model we find $x_F^{‡}$ = 5 nm, which at 4 pN implies that the difference in extension between the TS and state U is of ∼35 amino acids. In the case of the DHS, $x_F^{‡}$ = 3.2 nm (obtained by averaging results using γ = 1/2 and 2/3), which at 4 pN corresponds to ∼34 amino acids. Again, results are in agreement with former protein engineering studies and molecular dynamic simulations (7, 10), where a second TS close to state U is determined with only the three central β-strands of the native state formed (blue region in Fig. 3 d). Remarkably, the TS mediating barnase folding and unfolding differ in position along the reaction coordinate, as can be inferred from the estimated distances $x_U^{‡}$ and $x_F^{‡}$ and the corresponding number of amino acids, whose sum (between 48 and 60) does not add up to the total number of amino acids (i.e., 110). Our results show that the TS at large forces is close to state F, whereas at low forces it is close to state U. Hence, the TS approaches state F as force increases, in agreement with the Leffler-Hammond postulate (46, 47). However, the measured unfolding and folding rates span nonoverlapping ranges of forces, so the different positions of the TS measured from F and U cannot be taken as direct evidence of the existence of two distinct TS. In fact, a single TS with a position that shifts with force might be in accordance with the observations too. Therefore, the question remains whether the mFEL of barnase contains two TS with a high-energy intermediate state of short lifetime in between (Fig. 3 e, left), or it has a single TS that moves along the reaction coordinate (Fig. 3 e, right). Remarkably, the scenario inferred from our force measurements with the molecular extension as reaction coordinate agree well with that derived from kinetic rate measurements in bulk upon changing temperature or denaturant, where Chevron-like plots similar to that shown in Fig. 3 c have been observed (7, 48, 49).

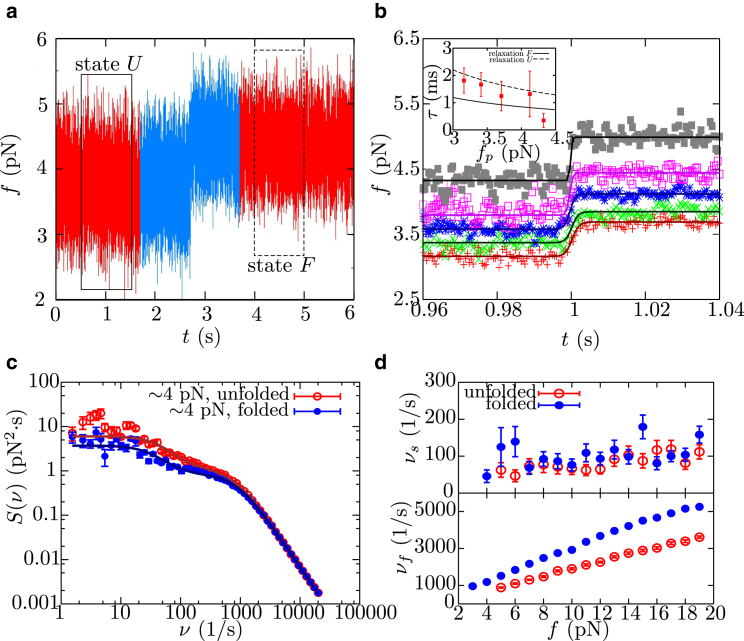
To study whether a fast intermediate state is present in the folding pathway of barnase, passive experiments were performed at high temporal resolution at different preset forces f_p (50 kHz, Fig. 4 a). No fast conformational transitions (hopping) between states F or U and a possible intermediate were observed at the single trajectory level. To check whether deviation of a two-state behavior takes place, folding trajectories obtained at a given f_p were shifted in time and aligned at the center of the transition (taken arbitrarily as t₀ = 0 s), using the 1-s data trace before and after the transition (Fig. 4 a, blue). Then, they were averaged on temporal windows of 0.5 ms, as described in Neupane et al. (50) and Woodside et al. (51). Results of such alignment performed at different values of f_p are shown in Fig. 4 b, where a zoom around the transition is shown. To check for deviations from the two-state behavior, aligned curves are fitted to the sigmoid function

$$f\left(t\right)=\frac{f_{\text{max}}+f_{\text{min}}}{2}+\frac{f_{\text{max}}-f_{\text{min}}}{2}\text{tanh}\left(\frac{t-t_0}{{\tau }_{\text{TP}}}\right),$$ (3)

where f_min and f_max are the average forces corresponding to the force level of states U and F along the FTT, respectively, and τ_TP is the measured folding path time (50, 52, 53, 54). Deviations of the experimental data to the sigmoidal behavior would hint at the presence of intermediates. Fits to Eq. 3 are shown in Fig. 4 b (solid lines), and no evidence of intermediate states was found for all measured values of f_p. In addition, for all cases the value of Δf = f_max − f_min corresponds to the release of ∼110 amino acids, which is the total number of amino acids of barnase (14). This result suggests that barnase behaves as a two-state folder in the millisecond timescale under the action of mechanical force. Our results so far cannot exclude the existence of a high-energy intermediate of submillisecond lifetime. This temporal upper bound is compatible with previous estimations of the submillisecond or thousands of picoseconds lifetime of the intermediate determined using nuclear magnetic resonance and molecular dynamic simulations, respectively (55, 56).

Figure 4.

Folding of barnase measured at high temporal resolution. (a) Example of FTTs recorded at a 50 kHz sampling rate that shows the folding of barnase as a sudden rise in force. (Red) Data for complete trajectory. (Blue) Data used for the alignment with other folding trajectories. (Boxed regions) Data used to compute the power spectrum of fluctuations when barnase is in state F (f_min = 3.8 pN, solid box) or U (f_max = 4.1 pN, dashed box). (b) Force-time trace obtained by aligning and averaging different folding trajectories (obtained at the same value of f_p) at the center of the force jump along a folding event and fits to a sigmoid function (Eq. 3). (Inset) The value τ_TP extracted from fit as a function of f_p, and relaxation time of the experimental setup (made by the bead in the optical trap, the handles, and the protein) as a function of force when barnase is at state F (solid line) or U (dashed line). (c) Power spectrum of the fluctuations of barnase recorded in passive mode experiments at 50 kHz for state F (blue circles) and U (red circles) at 4 pN. In each case, the fit to a double Lorentzian function (solid lines; Eq. S11) is shown, which allows us to determine the values of ν_f and ν_s, characteristic of the fast and slow relaxation modes. (d) Force-dependence of slow and fast frequency modes, ν_s and ν_f, respectively, obtained from the power spectrum of fluctuations measured in passive mode for the folded and unfolded states of barnase. To see this figure in color, go online.

As a second test to detect intermediate states along the folding pathway, we measured the power spectrum of force fluctuations at different f_p values when barnase is in state F or U (Fig. 4 c, at 4 pN) (57, 58, 59). These were obtained using 1-s-long selected passive traces measured at different f_p values and at 50 kHz (dashed and solid boxes in Fig. 4 a), where no evident transitions between states F and U are observed, but masked conformational transitions between F or U and a possible transition state might occur. In all cases, the resulting power spectra show two characteristic frequencies (ν_f and ν_s for the fast and slow modes, respectively) and can be fitted to the sum of two Lorentzian functions (solid lines in Fig. 4 c and Section S6). It can be seen in Fig. 4 d (top) that the slow component ν_s does not depend on the configuration of barnase (F or U), and from its linear force-dependent behavior we can infer that it is due to the universal axial fluctuations that take place along the optical axis of the OT setup, as it was already shown in Ribezzi-Crivellari et al. (59). If ν_s were related to conformational transitions involving the intermediate state, the force-dependence behavior for branches F and U would be different, increasing and decreasing with force, respectively. In contrast, the fast component ν_f (Fig. 4 d, bottom), which also increases with force, indeed depends on the state of barnase and is due to the longitudinal elastic fluctuations of the whole molecular construct that are larger along the U branch (Section S6). Moreover, the force-dependence of the amplitudes of the two frequency modes does not reveal (neither discard) the presence of an intermediate state in between states F and U, as it is the case in Žoldák et al. (58) (Section S6). We conclude that, in the temporal resolution of 50 kHz, fluctuations measured in passive FTTs do not reveal conformational transitions between states F or U and an intermediate state.

Another possible manifestation of the existence of the transition state in the mechanical folding pathway of barnase would be the measurement of a large transition path-time. This could indicate that traces in Fig. 4 b were time-averaged with a too low pass filter (relative to the lifetime of the intermediate), so conformational transitions are averaged out. To check that this is not the case, we compare the measurement of the transition path time and the time resolution of our experimental setup, given by the inverse of ν_f when barnase is either folded or unfolded (equal to $k_{\text{eff}}^F/\eta$ or $k_{\text{eff}}^U/\eta$, respectively, where η is the friction coefficient due to the bead and dsDNA handles; Section S6). In Fig. 4 b (inset), we find that the transition path time τ_TP decreases with f_p and falls, within error bars, between the relaxation time of the molecular system when barnase is folded and unfolded. Hence, τ_TP cannot be resolved in our measurements. This suggests that any potential observation of fast intermediate states in the submillisecond scale in the folding of barnase is limited by the time resolution of our mini-tweezers instrument through the corner frequency of the bead in the optical trap and the molecular construct. The improvement of such resolution would make it possible to accurately measure the transition path time of the protein free from instrumental effects (50, 51, 52, 53, 54), and therefore to observe fast high-energy intermediates, if any exist.

Free energy of formation

The free energy of formation of barnase can be determined from the study of the force-dependent kinetic barrier B(f) that mediates its folding/unfolding transitions. B(f) can be measured from the unfolding and folding kinetic rates, which satisfy

$$k_{F\to U}\left(f\right)=k_0\text{exp}\left(-\frac{B\left(f\right)}{k_{\text{B}}T}\right),$$ (4a)

$$k_{F\leftarrow U}\left(f\right)=k_0\text{exp}\left(-\frac{B\left(f\right)-\text{Δ}G\left(f\right)}{k_{\text{B}}T}\right),$$ (4b)

where k₀ is the attempt frequency at zero force, and ΔG(f) is the free energy difference between states U and F at force f. The latter term is equal to ΔG₀ (free energy of formation) plus a force-dependent elastic term that can be estimated from elastic models and that contains the stretching of the released polypeptide chain in state U and the orientation of the molten globule in state F (Eq. S13). To study the behavior of B(f), we use the CEBA (Section S7). As it was already shown in Manosas et al. (15) and Bizarro et al. (16), the CEBA consists in matching by continuity the profile of the effective barrier B(f) estimated from unfolding and folding measurements of logk_F→U(f) and logk_F←U(f) (Eq. 4; see red squares and blue circles in Fig. 4 a, respectively), which gives an estimate of the molecular free energy of formation, ΔG₀. The matching is done by vertically shifting the profile of the kinetic barrier measured from folding data by the quantity ΔG₀. We get ΔG₀ = 20 ± 5 k_BT = 12 ± 3 kcal/mol. Additionally, using the CEBA we can also get a lower bound estimate for the attempt frequency at zero force which here equals k₀ > 150 s⁻¹ by assuming that at large forces (∼25 pN) the kinetic barrier vanishes (Fig. 5 a). This must be a lower bound as barnase has been shown to have a kinetic barrier at much larger forces at ∼70 pN (19). We can also determine k₀ by averaging the results obtained from the expressions $k_m^u$exp($\Delta G_U^{‡}$) and $k_m^f$exp($\Delta G_F^{‡}$) by taking the values of $k_m^u$, $\Delta G_U^{‡}$, $k_m^f$, and $\Delta G_F^{‡}$ determined by fitting the DHS model to our force-spectroscopy data (Tables 2 and 3). We get k₀ = 1610 s⁻¹ for γ = 1/2 and k₀ = 670 s⁻¹ for γ = 2/2, both in agreement with the lower bound value determined by CEBA.

Figure 5.

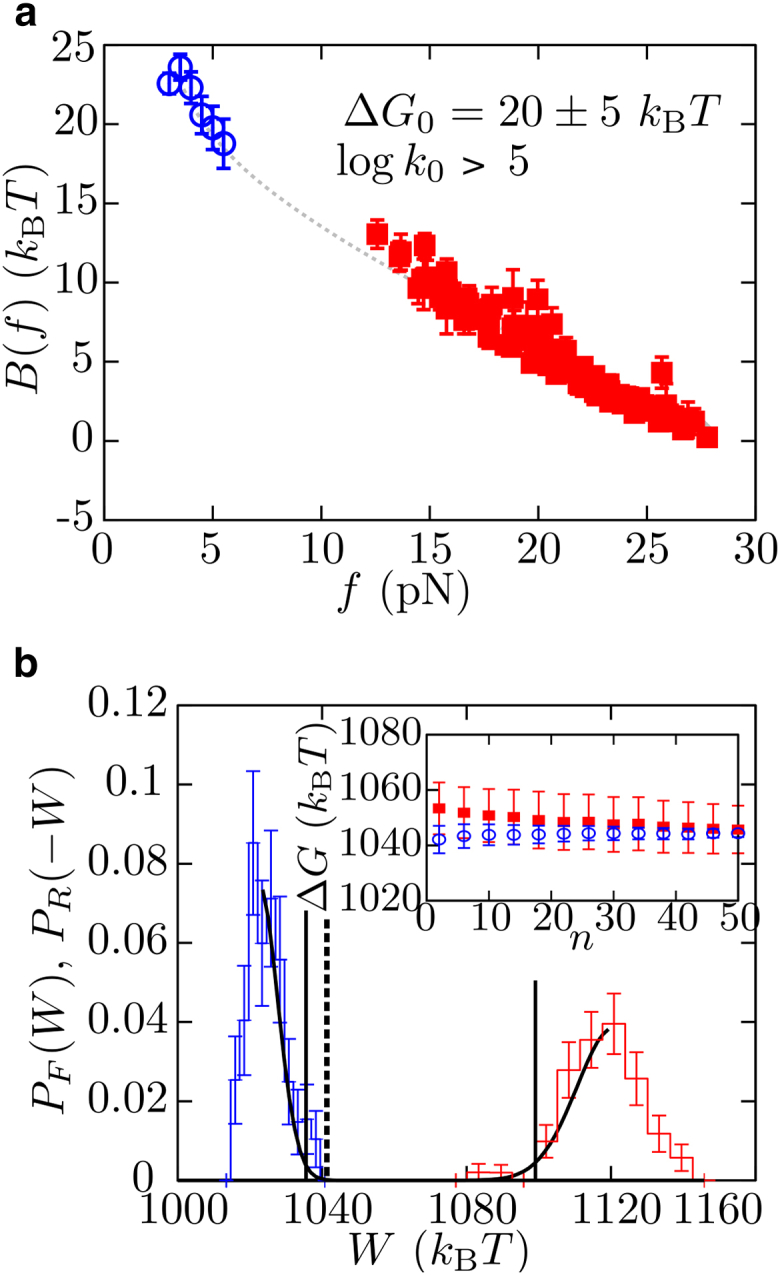
Reconstruction of the kinetic barrier and free-energy recovery of barnase. (a) Profile of the kinetic barrier B(f) determined using the CEBA method. (Red squares are obtained from logk_F→U(f) (Eq. S14a), and blue squares are obtained from logk_F←U(f) (Eq. S14c).) By imposing the continuity of B(f) from extrapolation (gray-dashed curve), we estimate the free energy of formation of barnase, ΔG₀ = 20 ± 5 k_BT. Additionally, assuming that at large forces the kinetic barrier goes to zero, gives a lower bound for logk₀ ∼ 5 (hence, k₀ ∼ 150 s⁻¹). Error bars are computed using the bootstrap method and by propagation of the errors of the elastic parameters. (b) Stretching (red) and releasing (blue) work histograms, and results of the fit to Eq. S18 of the respective leftmost tails (black). Error bars are obtained using the bootstrap method. (Solid vertical lines) Free energy values obtained using the Jarzynski estimator with stretching and releasing work values independently. (Dashed vertical line) Free energy estimation obtained by correcting the effect of bias using the random energy model. (Inset) Convergence of the Jarzynski estimated corrected by the bias using the random energy model as a function with the number of work measurements n. To see this figure in color, go online.

The free energy of formation ΔG₀ can also be determined from irreversible work measurements using fluctuation relations (18, 60, 61). The Crooks fluctuation relation and Jarzynski equality have been previously applied to pulling experiments to extract the free energy of formation of nucleic-acid hairpins (62, 63) and proteins (22). However, due to the large hysteresis effects reported in our experiments, the Crooks fluctuation relation cannot be applied and the bias of the Jarzynski estimator must be determined to extract a reliable value for ΔG₀.

We proceed as described in Palassini and Ritort (64) (Section S8), where the bias problem was mapped to the random energy model (65). First, we obtain the histograms of work values (defined as the area below the FDC) measured along independent repetitions of stretching and releasing experiments, P_F(W) and P_R(W), and fit the leftmost tails to Eq. S18; and in Fig. 5 b (note the minus sign for the work in P_R(−W)). Next, we determine the free energy difference of the whole molecular system between the initial and the final states, ΔG, from the Jarzynski estimator ΔG = −log〈exp(−W/k_BT)〉 (where the average 〈…〉 is performed over a finite number n of work measurements; Eq. S16). Two different Jarzynski estimators are obtained from unfolding and folding work values, which differ by ∼40 k_BT (vertical solid lines in Fig. 5 b). The dependences of the two Jarzynski estimators for ΔG as a function of n are fitted to the corresponding theoretical prediction of the bias, as given in Eq. S20 (64) (inset of Fig. 5 b). We observe that the two predictions obtained for stretching and releasing work measurements converge to ΔG = 1048 ± 6 k_BT (dashed vertical line in Fig. 5 b), proving the reliability of the approach. Finally, we subtract from ΔG the different stretching contributions (coming from the optical trap, handles, and polypeptide chain) to extract the free energy of folding of barnase at zero force. We get ΔG = 14 ± 5 k_BT = 8 ± 3 kcal/mol (Table 4; Section S9).

Table 4.

Fluctuation Theorem Applied to Barnase

ΔG (kBT)	$\text{Δ}{W}_{NU}^{\text{st}}$ (kBT)	$\text{Δ}{W}_{NU}^{\text{handles}}$ (kBT)	$\text{Δ}{W}_{NU}^{\text{bead}}$ (kBT)	ΔG0 (kBT)
1048 ± 5	40.0 ± 0.5	80 ± 3	915	14 ± 5

The free energy ΔG is obtained from the application of Jarzynski equality and corrected by an estimation of the bias (Eqs. S16 and S17, respectively). Once the different energetic contributions from the experimental setup are removed (Eq. S21 and Section S9), the free energy of formation of barnase is obtained.

The values recovered for ΔG₀ (12 ± 3 kcal/mol from CEBA method; 8 ± 3 kcal/mol from fluctuation relations) agree within error bars between themselves and with previous estimations obtained from bulk (10.2 ± 0.4 kcal/mol and 9.8 ± 1.3 kcal/mol) (8, 19).

Conclusions

In this article, we have investigated the mechanical folding/unfolding of the protein barnase. Our results provide a full picture of the elastic response and the mechanical unfolding and folding pathways of barnase and allow us to characterize main features of the mFEL.

First, we extract the elastic properties of the polypeptide chain in the force interval from 4 to 25 pN from pulling experiments by directly measuring the stiffness of the molecular setup, as it was done for short ssDNA molecules in Alemany and Ritort (14). Fits to different analytical expressions of the ideal wormlike-chain elastic model give a persistence length value in the range 0.60–0.85 nm, and an inter-amino-acid distance of 0.34–0.36 nm/aa (Table 1). These results are in very good agreement with the widely accepted values used to characterize protein folding in previous force spectroscopy studies (23, 34, 35, 66, 67).

Next we characterize the unfolding pathway of barnase under applied force from pulling experiments performed at different loading rates ranging from 3 to 60 pN/s. In these experiments, an unfolding event is detected through an abrupt jump in force in the measured FDC corresponding to the release of the 110 amino acids of the protein. We use the BE and the DHS Kramers-based models, which allow us to fit the rate-dependent average unfolding forces 〈f_U〉(r) and the force-dependent unfolding kinetic rate k_F→U(f) to get estimates for the distance $x_U^{‡}$ between the native state and the TS; the height of the kinetic barrier to unfold, $\Delta G_U^{‡}$; and the kinetic rate of unfolding at zero force, $k_m^u$ (Table 2). The distance $x_U^{‡}$ can be converted to the number of amino acids released in the TS upon unfolding, which equals ∼17 or 25 out of 110 (15 and 22% of the protein length, respectively) if we use the BE or the DHS models, respectively. Hence, we hypothesize that the TS mediating unfolding lies closer to state F than to state U of the protein, in agreement with previous measurements carried out combining techniques such as protein engineering with Φ-value analysis, urea denaturation, and molecular dynamic simulations. This result does not necessarily imply that the unfolding pathway of barnase is the same, but rather that the kinetic barrier has similar properties. In fact, the value for $\Delta G_U^{‡}$ as predicted by the DHS model is in remarkable agreement with values obtained using bulk techniques (7, 9). Noticeably, the mechanical unfolding of barnase has been previously investigated using AFM in a range of pulling speeds between 3000 and 150,000 nm/s, at least two orders-of-magnitude faster than the ones reported here (19). There, the average unfolding force is found at 70 pN and the value estimated for $x_U^{‡}$ is 0.3 nm. This is a further confirmation of the Leffler-Hammond postulate (46, 47): the position of the transition state upon mechanical denaturation is expected to approach the folded state as the force applied to the ends of the molecule increases. Our optical tweezers experiments and the AFM ones in Best et al. (19) are probing pretty different force regimes.

To study the folding pathway of the protein, we performed passive experiments where the folding of barnase is detected through a sudden force jump corresponding to the collapse of 110 amino acids toward the native structure. By fitting the BE and the DHS models to the force-dependent kinetic rate k_F←U(f), we get estimates for the distance between the TS and U, $x_F^{‡}$; the height of the kinetic barrier to fold, $\Delta G_F^{‡}$; and the kinetic rate of folding at zero force, $k_m^f$ (Table 3). Again, the distance $x_F^{‡}$ can be converted into the number of amino acids collapsed in the TS upon folding, which equals 35 or 23 if we use the BE or the DHS models, respectively. We hypothesize that the TS mediating folding is close to state U, with the main hydrophobic core of the protein (mostly made of β-sheets) folded.

Two decades ago, the folding pathway of barnase was studied in great detail using protein engineering, nuclear magnetic resonance, calorimetry, and urea denaturation experiments (7, 8, 68). In these studies, an observed nonlinearity of the logarithm of unfolding and folding kinetic rates under the action of urea was attributed to the possible presence of a submillisecond intermediate (55, 56). However, later hydrogen-exchange and denaturant-dependent unfolding experiments questioned the interpretation of former results (12). Remarkably enough, our results support a similar nonlinear scenario but using a different reaction coordinate (molecular extension versus urea or temperature). Our experimental observations can be explained either in terms of an mFEL with one or two TS mediating the native and unfolded states (Fig. 3 e). Both situations would agree with the Leffler-Hammond postulate, but for the latter case one might expect the presence of an intermediate state limited by the two distinct TS. Such an intermediate is not observed in pulling experiments or in passive traces, suggesting that it should be a high-energy state of short lifetime. To check this, we increased the temporal resolution of our equilibrium experiments up to 50 kHz. An accurate study of the elastic fluctuations and the behavior of the molecule during the folding transition did not reveal the presence of such an intermediate state. We find that the folding transition (i.e., the jump in force in our FTTs) is dominated by the relaxation time of the experimental system, made of the protein, the handles, and the bead captured in the optical trap. Hence, to test the hypothesis of the existence of a submillisecond intermediate state in the mechanical folding of barnase with force-spectroscopy experiments, the experimental time resolution of the OT instrument should be improved or the relaxation time of the experimental setup must be reduced. Alternatively, one might consider future strategies aiming to isolate the intermediate by pulling from different positions in circular permutants of barnase.

In this article, we also considered two different methods to recover the folding free energy of barnase at zero force. The first method (CEBA) consists in imposing the continuity in the profile of the force-dependent kinetic barrier B(f) measured from unfolding and folding kinetic rates, from which we obtain ΔG₀ = 20 ± 5 k_BT. In the second method, we apply the Jarzynski equality to recover the free energy from irreversible work measurements in pulling experiments. However, due to hysteresis effects, it is important to correct the bias of the Jarzynski estimator to get reliable values for ΔG₀. Here we proceed as described in Palassini and Ritort (64), where the bias problem is mapped to the random energy model. We get ΔG₀ = 14 ± 5 k_BT. Both results, which, when averaged, give the value of 10 ± 7 k_BT ∼ 10 ± 4 kcal/mol, are in good agreement within error bars with previous estimations from bulk (8, 19).

The CEBA method also provides a lower bound for the attempt frequency at zero force, k₀, which can be estimated by assuming that at large forces, the effective barrier vanishes. We get k₀ > 150 s⁻¹. Remarkably, k₀ > 150 s⁻¹ is consistent with the estimations of $k_m^u$, $k_m^f$, $\Delta G_U^{‡}$, and $\Delta G_F^{‡}$ (Tables 2 and 3) determined from the DHS model by taking k₀ = $k_m^u$exp($\Delta G_U^{‡}$/k_BT) and k₀ = $k_m^f$exp($\Delta G_F^{‡}$/k_BT). By averaging over the two estimations (BE and DHS), we obtain k₀ ∼ 1610 s⁻¹ for the DHS with γ = 1/2 and k₀ ∼ 670 s⁻¹ for the DHS with γ = 2/3. Additionally, the profile of B(f) is observed to satisfy the Leffler-Hammond postulate (46, 47), because its slope decreases as force increases. This trend is also predicted by the DHS model, which in fact reproduces the observed force-dependence of the effective barrier (Fig. 5 a) using the parameters from Table 2. Because the absolute value of such slope is equal to the relative distance between the TS and state F, the TS is located close to state U at low values of the force and approaches state F as force increases. This is in agreement with the structures proposed for the TS mediating mechanical unfolding and folding from bulk and present OT experiments.

Future work should focus on the direct measurement of the transition path time, which requires an improvement of the instrumental time resolution. This would reveal the existence of fast intermediates along the folding pathway. A first approach should involve the decreasing of the relaxation time of the different elements of the experimental setup. For instance, by performing experiments with a stiffer optical trap, stiffer molecular handles or smaller polystyrene beads would decrease the relaxation time of beads and handles, and hence the total relaxation time of the system would be dominated by the intrinsic folding time of barnase. One should also try combining OT investigations with protein engineering studies based on circular permutants as has been done for other proteins (23). This should help to elucidate whether such an intermediate does indeed exist, and to estimate its lifetime.

Author Contributions

A.A. performed research, analyzed data, and wrote the article; B.R.-S. performed research, expressed the protein, and wrote the article; S.F. expressed the protein and wrote the article; C.C. designed research and wrote the article; and F.R. designed research and wrote the article.

Editor: Matthias Rief.