Short Hydrogen Bonds and Proton Delocalization in Green Fluorescent Protein (GFP)

Abstract

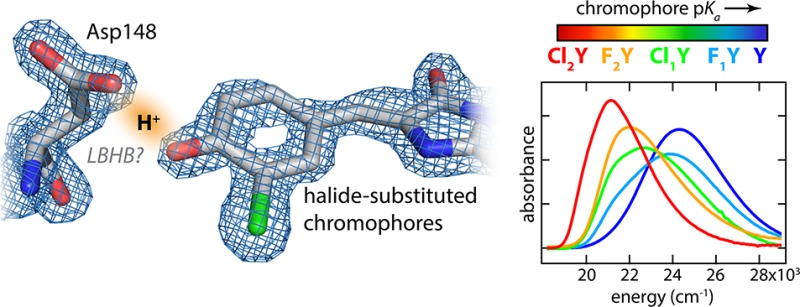
Short hydrogen bonds and specifically low-barrier hydrogen bonds (LBHBs) have been the focus of much attention and controversy for their possible role in enzymatic catalysis. The green fluorescent protein (GFP) mutant S65T, H148D has been found to form a very short hydrogen bond between Asp148 and the chromophore resulting in significant spectral perturbations. Leveraging the unique autocatalytically formed chromophore and its sensitivity to this interaction we explore the consequences of proton affinity matching across this putative LBHB. Through the use of noncanonical amino acids introduced through nonsense suppression or global incorporation, we systematically modify the acidity of the GFP chromophore with halogen substituents. X-ray crystal structures indicated that the length of the interaction with Asp148 is unchanged at ∼2.45 Å while the absorbance spectra demonstrate an unprecedented degree of color tuning with increasing acidity. We utilized spectral isotope effects, isotope fractionation factors, and a simple 1D model of the hydrogen bond coordinate in order to gain insight into the potential energy surface and particularly the role that proton delocalization may play in this putative short hydrogen bond. The data and model suggest that even with the short donor–acceptor distance (∼2.45 Å) and near perfect affinity matching there is not a LBHB, that is, the barrier to proton transfer exceeds the H zero-point energy.

Short abstract

Halogenated tyrosines are introduced into GFP to modify the chromophore acidity and probe the effect of pK_a matching across a putative low-barrier hydrogen bond.

Introduction

Hydrogen bonds play a critical role in the structure and function of biological macromolecules. In this capacity they exist in a wide range of geometries (i.e., lengths and angles) and strengths. Of particular interest are the mechanisms whereby H-bonds facilitate enzymatic catalysis.^1,2 Many examples are known in which the removal of even a single H-bond can slow down reactions by several orders of magnitude.^3,4 Structural surveys of enzymes with transition state analogues bound have revealed an unusual prevalence of abnormally short H-bonds (<2.5 Å), and this has led to much speculation about the possible role of these interactions.⁵⁻⁷ Low-barrier hydrogen bonds (LBHBs)—those in which the barrier to proton transfer is of the same order as the zero-point energy—have been proposed to stabilize transition states through quantum resonance.^5,8,9 However, comparisons to normal H-bonding in the uncatalyzed reactions in solution and considerations of charge solvation inside proteins have cast doubt on the original premise.¹⁰⁻¹² Nonetheless, the abundance of short H-bonds, whether low-barrier or otherwise, in enzyme active sites is probably not coincidental.

Definitive identification of LBHBs in proteins through experimental means has proven to be challenging. Most putative protein LBHBs are identified indirectly either by particularly short H-bond donor–acceptor distances or by the appearance of far downfield proton resonances in ¹H NMR. In several cases more quantitative metrics such as isotope fractionation factors have been measured,¹³ and there is at least one example of a direct observation of a LBHB with neutron diffraction crystallography.¹⁴

Many studies in small molecules have convincingly identified LBHBs in crystals and in the gas phase;^15,16 however solution studies—in some cases of the very same molecules—have revealed protons predominantly localized to either heteroatom.¹⁷⁻¹⁹ This effect has been attributed to the inherently asymmetric solvation microenvironment experienced by each molecule in solution that tends to result in pK_a mismatches which bias the proton to one side or the other.¹⁸ This is an illustration of the delicate balancing act between proton binding sites mediated by the intrinsic pK_a’s and their interplay with the environment necessary to sustain a true LBHB. These considerations have led some to conclude that most inferred LBHBs are instead short ionic H-bonds absent very precise proton affinity matching.¹²

A short donor–acceptor distance is a necessary but not sufficient condition to form a LBHB. The other critical requirement, as mentioned above, is that there be close “pK_a matching” between the two proton binding sites. Protein environments will, in general, perturb the pK_a’s of buried ionizable groups. To avoid confusion with the solution pK_a’s we favor the term differential acidity (ΔpK_α , where we use the subscript α to distinguish this from the conventional pK_a) as a metric of the in situ mismatch of donor and acceptor proton binding energies in pK_a units.²⁰ (We adopt the convention that ΔpK_α = pK_α(Cro) – pK_α(Asp148), where Cro denotes Chromophore. This means that ΔpK_α > 0 implies greater proton stabilization on the chromophore while ΔpK_α < 0 implies greater stabilization on Asp148.) Thus, it is of interest to empirically vary ΔpK_α —ideally at fixed geometry—in order to answer two questions: (i) How much must the acidity of one site be altered to match that of the other (i.e., until ΔpK_α = 0)? (ii) When ΔpK_α is close to zero, is the interaction a LBHB? In pursuit of this goal we focus on a green fluorescent protein (GFP) mutant thought to contain a LBHB and take advantage of the unique sensitivity and specificity of the chromophore absorption to access a range of measurable (and in principle calculable) properties diagnostic of the underlying H-bond energetics.

GFP has long been an indispensable tool in cellular imaging due to its autocatalytically formed fluorescent chromophore. The single most important determinant of its visible absorbance spectrum is the protonation state of the phenolate portion of the chromophore. The neutral chromophore, so-called A-state, has an absorbance peaked near 400 nm (25,000 cm^–1) while the anion, the B-state, is peaked around 470 nm (21,200 cm^–1).²¹ Wild-type GFP features an ultrafast excited-state proton transfer (ESPT) reaction in which excitation of the A-state results in fluorescence emission characteristic of the B-state in a matter of picoseconds.²² The mutation S65T abrogates this process and dramatically increases the chromophore’s sensitivity to solution pH having an in situ pK_a of ∼5.7.^23,24 A second mutation, H148D, rescues ESPT by positioning an alternative terminal proton acceptor with an extremely short H-bond to the phenolic oxygen of <2.4 Ų⁵ and has a rate of ESPT less than 100 fs.^26,27 Furthermore, the A-state absorbance band was significantly red-shifted to 415 nm and, uniquely among GFPs, demonstrated an absorbance band shift upon exchange to D₂O.²⁶ All of these factors led to the proposal that the Asp148–chromophore interaction is a LBHB. In the present work we critically analyze this claim by incrementally increasing the chromophore acidity and investigating the spectral and structural consequences of these perturbations.

A key enabling technology for this undertaking is the introduction of noncanonical amino acids through the technique of nonsense suppression. This method utilizes a tRNA complementary to the Amber stop codon (UAG) which is charged with an exogenously added synthetic amino acid by an engineered aminoacyl-tRNA synthetase. In recent years as this technology has matured, large libraries of available noncanonical amino acids have been created and the production of proteins containing these has become increasingly commonplace.²⁸ Whereas conventional mutagenesis is limited to rather large structural and functional jumps among the 20 naturally occurring amino acids, nonsense suppression presents opportunities to introduce perturbations which are far more subtle. Thus, we incrementally modify the acidity of the GFP chromophore through the introduction of halide substituted tyrosines at position 66. This residue together with Thr65 and Gly67 participates in the autocatalytic chromophore maturation reaction in the folded protein. Once maturation is complete, the halide-substituted tyrosyl group comprises the phenolic portion of the chromophore (Figure 1).

Figure 1.

(Left) Structure of the GFP chromophore with the phenolic portion highlighted. (Right) Introduced halogen substituents with their corresponding shorthand names, intrinsic denatured pK_a values (see Figure S.3), and their differential acidities with respect to Asp148 in the folded protein deduced from the model described below.

Methods

The halogen substituted tyrosines were prepared via chemical or enzymatic synthesis and introduced into recombinantly expressed GFP with nonsense suppression or global incorporation. All constructs are based on a circularly permuted Superfolder GFP and, unless otherwise indicated, contain the mutations S65T and H148D. The naming shorthand for proteins with modified chromophores is Y, Tyr66; F₁Y, Y66(3-fluoro-Tyr); Cl₁Y, Y66(3-chloro-Tyr); F₂Y, Y66(3,5-difluoro-Tyr); and Cl₂Y, Y66(3,5-dichloro-Tyr).

For detailed methods see Supporting Information (SI) S.2.

Results and Discussion

Structural Evidence for Short Hydrogen Bonds

When evaluating the role of ΔpK_α it is necessary that the geometry of the interaction, particularly the O–O distances, be unchanged in order to isolate the effect. To this end we obtained X-ray crystal structures of Y, Cl₁Y, and Cl₂Y with PDB IDs 4ZF3, 4ZF4, and 4ZF5, respectively (see SI S.3).

The most important conclusion to draw from these structures is that r_O–O is indeed maintained very closely across this series at approximately 2.45 Å (Figure 2 and Table S.2). (Note that in Cl₁Y the chlorine atom could in principle occupy either position due to the free rotation of the tyrosine phenol group prior to chromophore maturation. However, we observe 100% occupancy of the shown isomer.) This result is assumed to hold also for F₁Y and F₂Y, for which we do not have structures, because fluorine is sterically smaller and exerts a lesser effect on the acidity than chlorine. The structures for Y, Cl₁Y, and Cl₂Y adopt a different conformation of Asp148 than in the original structure of S65T, H148D from Shu et al. (PDB ID: 2DUF),²⁵ which was in an otherwise WT background and not circularly permuted. However, the phenomenology of Y in comparison to the original protein is nearly indistinguishable including the perturbed absorbance band, rapid ESPT, and the spectral isotope effect, providing strong evidence of functional similarity. Another difference is that Cl₁Y and Cl₂Y demonstrate a noticeable twist in the chromophore geometry relative to Y (Figure 2). The concern is that this twist, rather than the degree of proton sharing, may dominate the absorbance. This is likely not the case, however, because Cl₁Y and Cl₂Y have almost identical A- and B-state spectra under denaturing conditions (Figure S.1) and nearly the same twist in the structure. Yet, the natured proteins at low pH show dramatically different peak positions correlated with the chromophore acidity (Figure 3).

Figure 2.

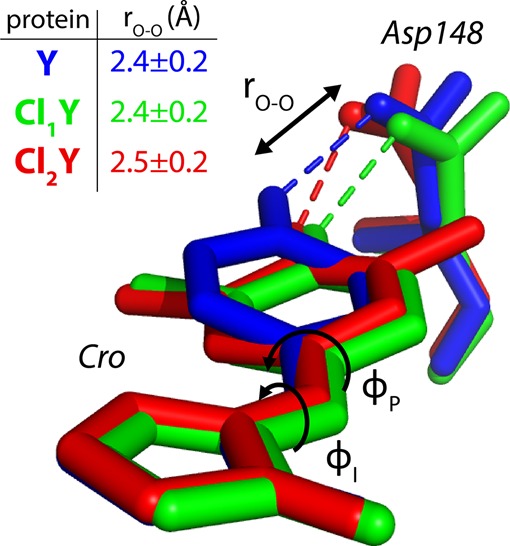
Overlay of the chromophore (Cro) and Asp148 for the aligned structures of Y, Cl₁Y, and Cl₂Y with tabulated r_O–O distances. Y and Cl₁Y are from the A chains which had lower B-factors. Cl₂Y is from chain B because chain A had an alternate deprotonated conformation (see SI S.6).

Figure 3.

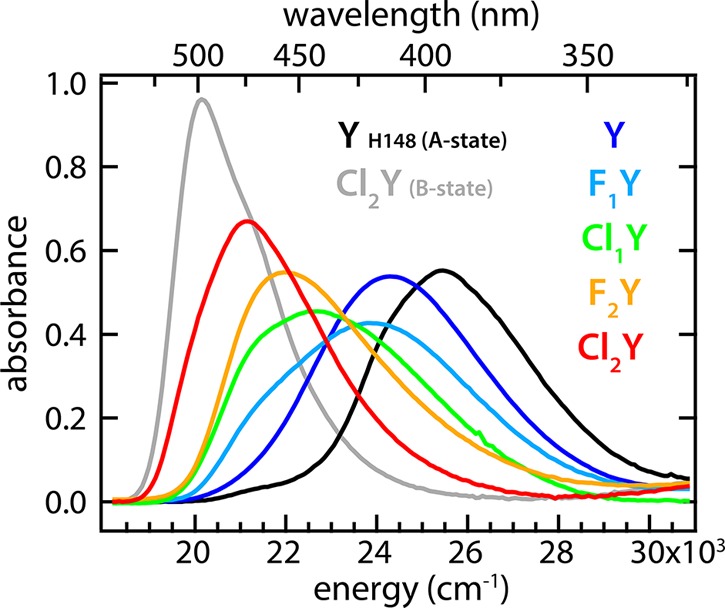
Spectra of natured substituted GFP protein in the limit of low pH (colored traces) shown with spectra for pure A- and B-states for comparison. All spectra are scaled by their associated B-state oscillator strength.

All three structures were obtained at pH 5.0 in order to favor the protonated form (Figure S.3). While the X-ray resolution is insufficient to visualize protons, we can infer the existence of a single proton between Asp148 and the chromophore on the basis of both the prohibitive energetic penalty a doubly deprotonated species would incur and the presence in all species of only two optical states as a function of pH (Figures S.2 and S.3). Unexpectedly, we observed in one of two chains of the Cl₂Y asymmetric unit an apparently deprotonated structure in which the ionized Asp148 was relocated away from the chromophore (Figure S.6). This is, to our knowledge, the first example of an alternative backbone geometry of β-strand 7 (Figure S.7). Strand 7 has been the object of considerable attention for its dynamical role in proton transfer,²⁹ FP sensor mechanisms,³⁰ and peptide photodissociation.³¹ This new data may facilitate the development of specific structural models of these transitions in the future. The interested reader is referred to SI S.6.

pK_a Titration and Spectral Response

In order to assess the effects of the halogen substitutions on the absorbance bands and the intrinsic pK_a’s of the chromophore, pH titrations were performed on protein denatured in 6 M guanidinium HCl to expose the chromophore to solution. As expected the chromophore pK_a’s changed in response to halogen substitution ultimately spanning a range of 3.5 pK_a units (Figure S.3). Furthermore, the absorbance bands due to the protonated and deprotonated forms of all species were largely unaffected by the presence of the substituents (Figure S.1).

pH titrations of the natured protein were also measured and found to have clean isosbestic points. Like the denatured protein, the B-state absorbance bands showed only small shifts among the halogen substituted species (Figure S.2). In contrast, the A-state bands were massively perturbed by the halogen substituents causing the peaks to shift across the entire spectral range, with those with high intrinsic pK_a’s resembling the usual A-state and those with lower intrinsic pK_a’s resembling the B-state (Figure 3). This result is particularly striking when viewed in light of the exceptional consistency of the A-state absorbance band energy across the enormous variety of GFP mutants all peaked near 397 nm (25,200 cm^–1).

The series of halogen substituted chromophores can be considered as internally titrating against Asp148. In other words, progressively increasing the acidity of the chromophore with respect to Asp148 decreases ΔpK_α until matched (ΔpK_α = 0) and beyond (ΔpK_α < 0), at which point the proton is more stable on Asp148. Depending on the distance—which we know to be ∼2.45 Å—and the degree of coupling, the potential energy surface along this bond will dictate the character of this proton “tug-of-war” between these sites.

Before undertaking a semiquantitative approach toward this interaction, it is important to clearly define what a LBHB is in unambiguous energetic terms.¹² We define a LBHB as an H-bonding interaction in which the barrier to proton transfer between the donor and acceptor atoms is equal to or lower than the proton zero-point energy (H-ZPE). This definition implicitly contains the requirement of ΔpK_α near to zero. A further consequence is that the proton probability density of a LBHB thus defined will have a single broad peak at or near the bond midpoint.

Physical Model

In the analysis of this short H-bond we have utilized the coupled Morse potential model put forward by Ross McKenzie.^32,33 This model has the advantage of using only two fit parameters and retaining physical transparency while describing experimental H-bond properties with reasonable accuracy. We have adapted the linear bond model in order to calculate approximate protein absorbance spectra as a function of chromophore acidity and can additionally make predictions for the trends in spectral isotope effects and isotope fractionation factors. The basic method is described below, and additional information can be found in SI S.5.

The model takes as input two Morse potential diabatic states for the proton donor and acceptor sites. These potential energy functions, representing the respective proton-bound states at infinite separation, serve as the diagonal of a 2 × 2 Hamiltonian matrix with the scalar coupling energy (Δ_DA) on the off-diagonal. Matrix diagonalization yields as eigenvalues the ground- and excited-state adiabatic potential energy surfaces (PESs). The associated eigenvectors describe the relative contribution of the two input diabats at each point along the bond. These are used to calculate the mapping between a particular proton position and the corresponding excitation energy. For example, if at some location there is 50% contribution from both A- and B-state diabats, then the excitation energy would be halfway between the A- and B-state basis states. Next, the proton (or deuteron) probability distribution functions on this PES are determined using a finite difference solution to the 1D Schrödinger equation. The resulting eigenstates are thermally populated according to Maxwell–Boltzmann statistics. The final step is to convert these probability densities into a spectrum using the mapping described above. This was accomplished by performing a probability-weighted histogram of excitation energies and then convolving the result with normalized Gaussians with width characteristic of the pure A-/B-state absorbance bands to approximate the homogeneous and inhomogeneous broadening. The process was repeated for each of the substituted chromophores where the input diabat for Asp148 remained the same while the chromophore diabats have proton binding energies scaled appropriately for their intrinsic pK_a differences. [The differences in proton binding free energy are calculated by ΔΔG° = ln 10 × RTΔpK_a. Due to the chemical similarities among the substituted chromophores, we make the assumption that ΔΔG° is dominated by the enthalpic portion (ΔΔH°). Thus, the input chromophore Morse potential binding energies are shifted by ΔΔG° directly. Furthermore, when transferred to the protein environment, the chromophore’s ΔH° of proton binding will surely change, however, we assume that the relative enthalpy (ΔΔH°) among the substituted chromophores will remain the same.] Apart from these energy shifts, the input diabats are all identical. The final model fixes the O–O distance to 2.45 Å and varies global parameters for (i) the energy offset between Asp148 and the set of chromophore diabats and (ii) the magnitude of the coupling parameter between the sites (Δ_DA) to output simulated absorbance spectra. Lastly, the parameters giving the best overlap to energy-normalized experimental spectra were obtained using global nonlinear least-squares optimization in Matlab.

Figure 4 illustrates the results of applying this model with a range of coupling energies (Δ_DA). The best fit was obtained with the coupling parameter Δ_DA = 30.1 kcal/mol. For comparison the parameters fit by McKenzie for the distance dependence of the coupling predict Δ_DA = 38.9 kcal/mol at 2.45 Å. The offset energy parameter was such that ΔpK_α = 0 was found to occur between Cl₁Y and F₂Y. More specifically, a hypothetical substituted chromophore with an intrinsic denatured pK_a of 7.0 would be expected to share the proton equally with Asp148 (Figure 1). One might be tempted to directly compare the intrinsic pK_a of aspartic acid (∼3.9) with that of the substituted chromophores in solution or to conclude that Asp148 has a pK_a of 7.0 in the protein. These comparisons, however, are not correct because they neglect the protein solvation environment which will, in general, affect the two sites differently. Consequently, when referring to this interaction within the protein we can speak only of differential acidities (ΔpK_α).

Figure 4.

Comparison of the model results for the PESs, thermal probability densities, and simulated absorbance spectra among coupling energies (Δ_DA) for high-barrier, best fit, and low-barrier proton transfer. Note that while the PESs show only the ground state, the effect of low lying excited states are taken into account for both the thermal probability densities and simulated spectra.

The simulated spectra with the best-fit value of Δ_DA accurately capture the shift in energy as well as the changes in width of the “A state” absorbance band among the substituted chromophores (Figure 4F). This shift in peak position would seem to suggest a low-barrier or single-welled potential, however, the best-fit PESs indicate that there is a barrier between the sites with a height exceeding the H-ZPEs (Figure 4D; see also Figure 7A). Consequently, the proton probability density appears as two distinct peaks (Figure 4E). To critically assess the uniqueness of the coupling energy fit (Δ_DAfit) and to better understand the relationship between the barrier height and resulting spectra, we performed simulations for 0.5Δ_DAfit, Δ_DAfit, and 2Δ_DAfit (Figure 4). For small coupling energy (0.5Δ_DAfit, Figure 4A,B,C), and thus large barriers, the spectra present two distinct bands of fixed position and width which are essentially the A- and B-state basis spectra. With large coupling energy (2Δ_DAfit, Figure 4G,H,I) the H-ZPE exceeds the barrier height, thus representing the LBHB case, and the absorbance bands shift position over a relatively small energy range. However, the bandwidth is similar to that of the A- or B-state basis spectra. At the best fit coupling energy (Δ_DAfit, Figure 4D,E,F) the peak position shifts over a greater energy range and is accompanied by a dramatic change in the peak width with the greatest width occurring for matched affinities (Cl₁Y, Figure 4E). This behavior is most consistent with the experimental data (Figure 3). The spectral isotope effects (SIEs)—the changes in the spectrum upon H to D exchange—are also quite distinct between the different coupling energies and will be discussed further below.

Figure 7.

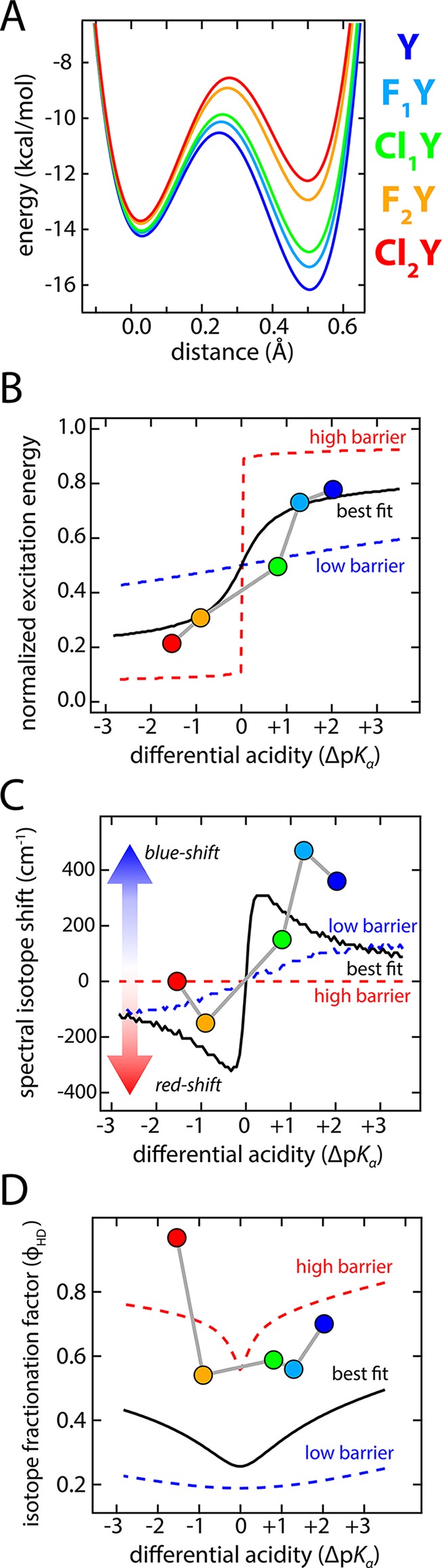
Results of modeling and comparisons of trends with experimental observations. The solid black curves in B, C, D, and E are calculated from the best fit parameters while the dashed red and blue curves correspond to high (0.5Δ_DA) and low (2Δ_DA) barrier predictions, respectively. We note that the calculated fractionation factors are certainly underestimates since they are derived from a 1D model and neglect the bending mode contributions.³⁴

Isotope Effects

Equilibrium isotope effects are a powerful tool to probe potential energy surfaces. We utilize two equilibrium isotope phenomena in this study in order to obtain additional information and constraints on the nature of the Asp148-chromophore H-bond: spectral isotope effects (SIEs)—the spectral change induced by isotopic substitution—and isotope fractionation factors—the energetic isotope preference. We consider each of these in comparison to the model results across the substituted chromophore series. It should be emphasized that the global parameter fitting was performed only against the absorbance spectra in H₂O and that all the isotope effects emerged naturally from this fit.

In the model above we have described a method for mapping the hydron probability density to a predicted absorbance spectrum. Hydrogen to deuterium substitution, insofar as it alters this probability density, will lead to changes in the resulting spectra. Generally electronic absorbance spectra of molecules in water are insensitive to the mole fraction of deuterium even when possessing a titratable site. wtGFP’s spectrum, for instance, has no detectable change. This can be understood through the fact that the chromophore participates only in “normal” H-bonds. In these longer interactions the hydron potential well is deep and is reasonably approximated as a harmonic oscillator. Thus, even though H to D substitution changes the ZPE, the position expectation value remains unchanged and so also the spectrum. In contrast, S65T H148D GFP has a short ionic H-bond, and the coupling between the proton binding sites can strongly perturb the PES. In particular, by introducing a much greater degree of anharmonicity, H may spread out toward the H-bond acceptor while D, by virtue of its lower ZPE, will remain more localized to the donor. With this qualitative picture we can evaluate the experimental SIEs and the model predictions.

Each of the halogen substituted proteins was exchanged into solutions of identical hydron activity (i.e., pH or pD) with varying mole fractions of deuterium, and the absorbance spectra were measured (Figure 5). The peak spectral isotope shifts (H to D) change sign through the acidity progression and decrease in magnitude out on the extrema to make an S-shaped curve (Figure 7C). (We note that there may also be secondary geometric isotope effects which would add some complication to the interpretation by subtly altering the bond length.³³ Due to the approximate nature of the model we neglect this in the present work.) This is broadly consistent with the logic described above if we assume the proton affinity of Asp148 to be constant while titrating it against the series of chromophores with variable proton affinities. For large |ΔpK_α| the shift tends toward zero because the PES is only weakly perturbed. As ΔpK_α approaches zero, the magnitude of the shift increases as the anharmonicity becomes more pronounced. However, once ΔpK_α changes sign, so also does the spectral isotope shift since H to D exchange leads to greater localization in the opposite well.

Figure 5.

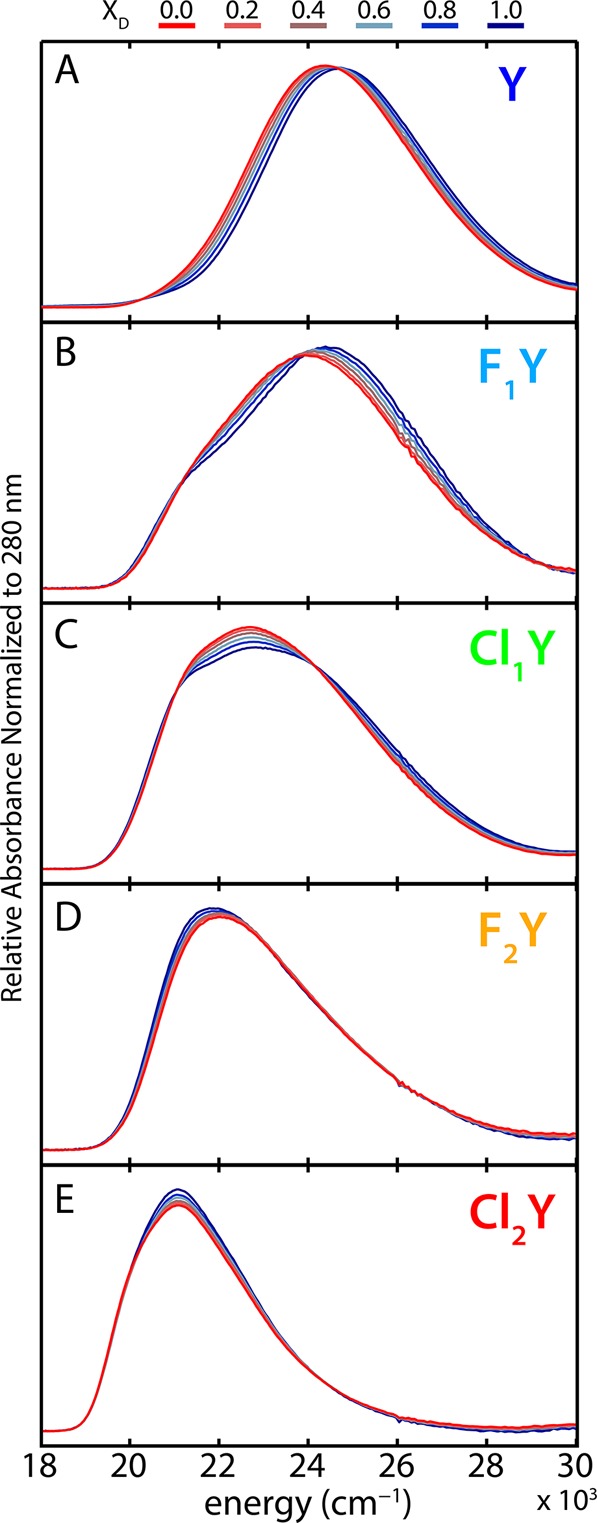
Spectral isotope effects (SIEs) for all proteins at pH(D) 5.0. 100% H₂O is shown in red transitioning to 100% D₂O in blue. Organic acids typically exhibit slightly higher pK_a’s in D₂O, however, since most of these species are dominated by the protonated form at pH(D) 5.0, this effect should be negligible. Cl₂Y is 86% protonated at pH 5.0 and thus may have slight error.

In addition to the spectral isotope shift there is also useful information in the changes in peak shapes. This is particularly true of Cl₁Y, the protein with the closest Asp148-chromophore proton affinity matching. The experimental data show a significant decrease in peak intensity along with some broadening to both red and blue edges (Figure 5C). This same effect is captured in the best-fit spectra (solid and dashed green in Figure 4F). When the ZPE is slightly above the barrier there is very little SIE (solid and dashed green in Figure 4I) even though significant shifts are obtained for affinity mismatched species. In the event of an extremely strongly coupled single-welled potential one would actually anticipate the opposite effect, that is, an affinity matched D-bound species would have a sharper peak.

Further information about the energetics of the H-bond comes from the isotope fractionation factor (ϕ_HD). ϕ_HD is defined as the equilibrium constant for the exchange reaction in which an H in a bond or complex is swapped for a D from the solvent. Strongly coupled H-bonds energetically favor H over D and lead to H enrichment beyond the solvent composition (Figure 6). This effect is due to a reduction in the H/D ZPE difference in the perturbed PES relative to water thus creating a thermodynamic preference for H. Theoretical considerations suggest that ϕ_HD should be minimized for LBHBs, and, indeed, the lowest experimental values (∼0.3) have been measured in putative LBHB-containing complexes.^13,34

Figure 6.

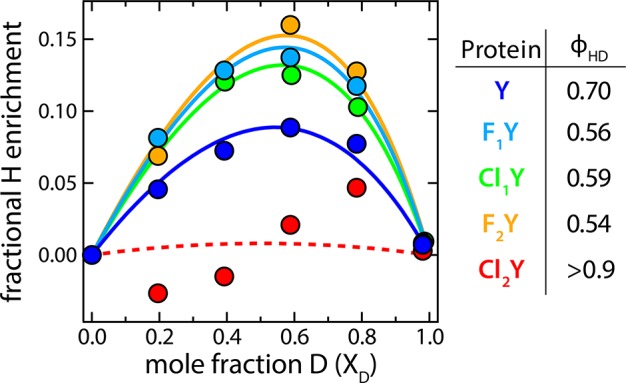
Fits to the isotope enrichment as a function of mole fraction deuterium with the calculated ϕ_HD’s tabulated on the right. Cl₂Y had only small differences in the H and D basis spectra, which led to considerably more uncertainty in the calculated enrichment. Thus, we indicate the fit with a dashed line and can only say that ϕ_HD is greater than 0.9.

The existence of an SIE was critical to the determination of ϕ_HD since it allowed us to accurately decompose the absorbance spectrum into a linear combination of H- and D-bound basis spectra. We observed a U-shaped trend for ϕ_HD with a stronger effect for those species with ΔpK_α closer to zero. This trend is consistent with that calculated from the best-fit model but not the LBHB results, which depend only weakly on ΔpK_α (Figure 7D). The calculation of ϕ_HD from our 1D model, described in SI S.5, is known to significantly underestimate the value of ϕ_HD because it neglects the bending degrees of freedom,³⁴ however the trends with respect to ΔpK_α should remain robust. The differences in magnitude between the data and best fit may be ascribed to this underestimation tendency. Kreevoy and Liang estimated that the true ϕ_HD for a LBHB should be greater than that derived from a 1D model by a factor of ∼1.7,³⁴ which would put the model into closer quantitative agreement with the data.

Absence of Low-Barrier Hydrogen Bonds

In summary, this very simple model with only two global fit parameters makes surprisingly accurate predictions of trends in absorbance spectra, spectral isotope effects, and isotope fractionation factors. The very fact that the model can successfully capture these properties appears to justify the most important assumption in which the substituted chromophore proteins were all modeled identically save the proton binding energy offsets calculated from pK_a values for the chromophores in the denatured protein. The results strongly suggest against a LBHB interaction even though the prerequisite donor–acceptor distance and affinity matching conditions are met. This conclusion is drawn from several lines of evidence. First, the trends in the absorbance spectra with changing acidities conform most closely to those calculated from the best-fit coupling energy (Δ_DA) in detail of peak top and width (Figure 4F and Figure 7B). Likewise this Δ_DA also captures the trends in the spectral isotope effects and isotope fractionation factors which have poor correspondence to the predicted LBHB results (Figure 7C,D). Second, upon H to D exchange the SIE of the most closely affinity-matched species, Cl₁Y, shows a significant decrease in absorbance near the middle of the band (compare Figure 5C to Figure 4F solid and dashed green). This effect is anticipated by the best fit model but is absent for the LBHB case and emphasizes how D pulls away from the central barrier. Lastly, the magnitude of ϕ_HD at ∼0.6 while suggesting a perturbed H-bond does not reach the low values, ∼0.3, expected for a true LBHB (Figure 6).

The model presented above is entirely static. Another interpretation of the data is possible in which fluctuations in the protein and nearby solvent bias a low-barrier or barrierless PES toward one site or another even with perfect affinity matching on average. In this case one might view the model results presented as a time-averaged effective potential. Such a scenario, though beyond the scope of this paper, would also likely result in similar predictions for changes in spectra, spectral isotope effects, and isotope fractionation factors with respect to chromophore acidities and cannot be ruled out. This idea would be consistent with the many observations of Perrin et al. in which molecules forming symmetric H-bonds in crystallo are not symmetric in solution.^17,18 Furthermore, the immediate environment of the GFP chromophore is quite polar and contains numerous water molecules inside the β-barrel. A priori such surroundings would be expected to better stabilize a concentrated charge than the more diffuse charge associated with a LBHB.^11,12 Thus, the microscopic conditions for a largely symmetric LBHB may be only rarely encountered.

The lack of a LBHB in this poised model system may hold general implications for the existence and/or function of such interactions in proteins. The catalytic LBHB proposal posits that, in the course of an enzymatic reaction, the transition state transiently matches proton affinity with a protein H-bond partner and via a LBHB affords differential stabilization of 10–20 kcal/mol relative to the bound substrate.⁸ Were such a large energetic preference present, one would expect LBHB character to dominate short protein H-bonds with affinity matched partners. Our inability to create such an interaction even while finely tuning the chromophore acidity suggests that there is no particular stabilization associated with a LBHB relative to a short ionic H-bond. The generality of this conclusion could be tested in the future in a number of proteins which share a common H-bonding motif—that is, a phenolate based chromophore engaged in a short H-bond. Among these are photoactive yellow protein (PYP) and ketosteroid isomerase (KSI). PYP has been shown by neutron diffraction crystallography to possess singly peaked deuteron density equidistant between Glu46 and the p-coumaric acid chromophore.¹⁴ Moreover, it also features a significant SIE³⁵ and thus represents one of the best candidates for a genuine protein LBHB. KSI, despite sharing a similar interaction between Tyr16 and phenolate or naptholate transition state analogues, displays electronic³⁶ and vibrational³⁷ spectroscopic data which quite clearly indicate well resolved protonation states suggestive of a double-welled potential. Systematic acidity perturbation of these systems and comparison to the results presented herein may help to clarify how the environmental context leads to diverse behavior among these otherwise geometrically similar situations.

Conclusions

We have successfully utilized methods of nonsense suppression and global incorporation to introduce a series of synthetic halide-substituted tyrosines into GFP that go on to make up the phenolic portion of the autocatalytically formed chromophore. Through inductive effects the substituents decreased the chromophore pK_a in the order Y > F₁Y > Cl₁Y > F₂Y > Cl₂Y for a total span of 3.5 pK_a units. This enabled us to test the effect of proton affinity matching on a short protein H-bond by expressing these species in an S65T, H148D GFP mutant thought to harbor a LBHB between the chromophore and Asp148. X-ray crystal structures of the unmodified and the two chloro-substituted species revealed a largely conserved bond geometry with an O–O distance of ∼2.45 Å, thus suggesting that the origins of the spectral shifts are largely isolated to the variation in chromophore acidities. The electronic absorbance spectra of the natured proteins were all found to titrate between a clearly deprotonated state at high pH and a highly unusual seemingly mixed state at low pH. This low pH mixed state contained the putative LBHB and gave rise to absorbance bands smoothly shifting between the protonated and deprotonated basis states with increasing acidity.

A 1D coupled Morse potential model provided a simple framework through which to interpret the experimental results and, with only two global fit parameters, was able to robustly model trends in the spectra, spectral isotope effects, and isotope fractionation factors. From the modeling results we draw two major conclusions. First, we predict that a modified chromophore having a solution pK_a of ∼7.0 would, in the folded protein, be perfectly affinity matched to Asp148. Second, even under conditions of minimal differential acidity the predicted barrier to proton transfer exceeds the H-ZPE. The experimental observations most directly supporting this second claim are a marked decrease in intensity in the middle of the spectrum for near affinity matched sites upon H to D exchange, and higher isotope fractionation factors than expected for a LBHB. This evidence, however, cannot rule out an alternative model in which the dynamic solvation environment leads to bond asymmetry. In either case the fact remains that, relative to short ionic H-bonds, there appears to be no particular stabilization due to LBHBs and the accompanying proton delocalization across the bond. In fact, the absence of LBHBs suggests that the protein may actively avoid such a configuration. Distinguishing between these hypotheses will be the work of more sophisticated calculations. Regardless, our results suggest that even under seemingly ideal conditions for symmetric LBHB formation (i.e., O–O distances <2.5 Å and near perfect proton affinity matching) they are not observed.

Supporting Information Available

The following file is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.5b00160.

• Additional information on the synthesis and incorporation of unnatural amino acids, X-ray crystallography statistics, the details of the 1D potential energy model, and ionization state dependent structural changes

  (PDF)

This work was funded in part by a grant from the NIH (GM27738). L.M.O. acknowledges the financial support of an NSF Graduate Research Program Fellowship.

The authors declare no competing financial interest.