Abstract
Blebs are pressure-driven cell protrusions implicated in cellular functions such as cell division, apoptosis, and cell motility, including motility of protease-inhibited cancer cells. Because of their mechanical nature, blebs inform us about general cell-surface mechanics, including membrane dynamics, pressure propagation throughout the cytoplasm, and the architecture and dynamics of the actin cortex. Mathematical models including detailed fluid dynamics have previously been used to understand bleb expansion. Here, we develop mathematical models in two and three dimensions on longer timescales that recapitulate the full bleb life cycle, including both expansion and healing by cortex reformation, in terms of experimentally accessible biophysical parameters such as myosin contractility, osmotic pressure, and turnover of actin and ezrin. The model provides conditions under which blebbing occurs, and naturally gives rise to traveling blebs. The model predicts conditions under which blebs travel or remain stationary, as well as the bleb traveling velocity, a quantity that has remained elusive in previous models. As previous studies have used blebs as reporters of membrane tension and pressure dynamics within the cell, we have used our system to investigate various pressure equilibration models and dynamic, nonuniform membrane tension to account for the shape of a traveling bleb. We also find that traveling blebs tend to expand in all directions unless otherwise constrained. One possible constraint could be provided by spatial heterogeneity in, for example, adhesion density.
Introduction
The eukaryotic cell surface is the site of cell-cell communication (1), cell-environment interactions including motility and mechanosensing (2), and cell morphogenesis (3), among other processes. Many of these processes involve mechanical forces and deformation, making mechanics of the cell surface an increasingly important topic of investigation.
The study of cell-surface mechanics is complicated by dynamic interactions among its multiple constituents with distinct material properties. The plasma membrane is fluid (4); it resists deformation and experiences surface tension on the order of 10–100 pN/nm (5, 6) that is spatially and temporally nonuniform (7). Below the membrane is an layer of F-actin with microarchitecture distinct from that of the cytoplasmic F-actin farther into the cell (8), termed the cortex. The cortex is anisotropic poroviscoelastic material (9, 10) that generates internal active contractile stresses by association with myosin (6). The membrane and cortex are decorated with a myriad of molecules, some of which interact with both of them, thereby facilitating dynamic adhesion between them (11). This complexity obscures fundamental questions such as, how quickly is hydrostatic pressure propagated through the cortex (12, 13, 14), or surface tension across the membrane (4, 7, 15)? These questions have functional consequences, since membrane bending and tension are implicated in, for example, endocytosis (5), motility (15, 16), and cell polarization (17), and the cortex is implicated in cell division, initiation of filopodia and other cellular protrusions (18), both facilitation and prevention of vesicle export (19), and wound healing (9).
An example of a cell process that involves all the above components is offered by cellular blebbing, pressure-driven protrusions that occur in many cell types and conditions (20, 21, 22). An individual bleb begins with an initiation phase during which the membrane separates from the cortex, either spontaneously or under experimental triggering such as laser ablation (8, 20). Initiation is followed by a rapid expansion phase, which, unlike other cellular protrusion, is not actively driven by cytoskeletal polymerization (23). After expansion, blebs can exhibit a range of dynamic behaviors: Stationary blebs heal in place with a slower timescale (on the order of minutes). Other classes of bleb that have been experimentally observed travel around the periphery of the cell—a phenomenon termed circus movement (24, 25, 26)—or repeatedly bleb on top of an existing bleb (20). The complete life cycle is determined by a complex interplay between flow of cytosol into the bleb, contractive forces in the cortex, and the formation and maintenance of membrane-cortex adhesions. Blebs are implicated in nonlamellipodial cell motility (27, 28) (for example, in protease-inhibited cancer cells (29)), as well as in maintaining homeostasis during division (30), and it is speculated that they have a role in the origin of eukaryotic life (31).
Traveling waves of protrusion are increasingly reported in different cell types (17, 32), but these protrusions are typically F-actin-enriched (although see (33)), whereas blebs represent regions with reduced F-actin. A fundamental question in the understanding of any traveling-wave phenomenon (3) is what determines the traveling velocity of a traveling bleb. And, in the case of blebs which may be stationary or travel, even simultaneously at different locations on the same cell, what determines whether a bleb will travel or heal in place?
Several theoretical models of blebbing have been developed to capture various aspects of the process. Computational fluid dynamics models (12, 34, 35) have been developed to understand the initial expansion phase during which cytosolic fluid follows the protruding membrane. Due to the computational cost of solving the fluid equations, along with their mechanical interaction with immersed structures (which typically have subsecond dynamics (12, 34)), simulations of these models are typically limited to two-dimensional (2D) approximation and timescales of seconds. Other researchers (26) have used force-balance models (33, 36) to obtain computationally tractable models describing the full life cycle. These models are in 2D and must assume an a priori bleb-healing velocity to generate traveling blebs. Continuum analytical models (37, 38, 39) have also been developed that move beyond the typical small-deformation approximations typically used to describe membrane geometry. These models capture details of the shape of stationary blebs that have, among other findings, implicated lipid flow in determining bleb behavior.
A full, 3D description of the full life cycle of traveling blebs is therefore lacking. In this work, we develop a model of local cell-surface mechanics on timescales of seconds to minutes, thereby including cortex turnover and bleb healing. We exploit two simplifying assumptions: First, we assume that hydrodynamic equilibrium is reached rapidly. We thus avoid computationally taxing fluid dynamic simulation, albeit at the expense of losing information about the expansion phase. Second, our model contains a single, “effective” cortex corresponding to the weighted average of cortical actin, allowing us to include implicitly the cytoskeleton further inside the cell.
An emerging feature of this model is that transient detachment between membrane and cortex can lead to 1) rapid healing, 2) stationary bleb formation, and 3) spontaneous bleb travel, depending on model parameters. Our model makes two main contributions: First, since traveling blebs arise naturally, we can elucidate the determinants of bleb travel. In particular, several simplifying assumptions allow us to obtain an analytic expression for bleb travel velocity that provides experimentally accessible perturbations predicted to accelerate or decelerate travel. Our second finding is that the biophysical ingredients hypothesized to account for blebbing produce traveling blebs with unrealistic geometry. This suggests a yet-to-be-identified mechanism that plays a role in cell integrity and the localization of morphological perturbations. We explore the influence of dynamic, nonuniform membrane tension; hydrostatic pressure equilibration occurring at multiple length scales (i.e., global versus local (34)); and spatial heterogeneity. We find the latter sufficient to maintain bleb compactness during travel.
Materials and Methods
Our minimal model, summarized schematically in Fig. 1, consists of four fundamental dynamic variables, as functions of time, t, and location on the 2D cell surface, parametrized by . The actin cortex has local height described by measured normal to the mean cell surface from its steady-state configuration, , and thickness . The cortical-cytoplasmic actin cytoskeleton can in principle have complicated morphologies that cannot be accounted for by a single location, , so we think of as the weighted average position of maximal cortical actin. Membrane-cortex adhesions are described by density in molecules/nm2. Finally, the membrane has local height . Note that our model is agnostic about the molecular constituents of the membrane, and it could include the plasma membrane and permanently membrane-associated proteins and cytoskeletal networks (33). Our approach is similar to previous descriptions of membrane mechanics (1, 7, 26, 36).
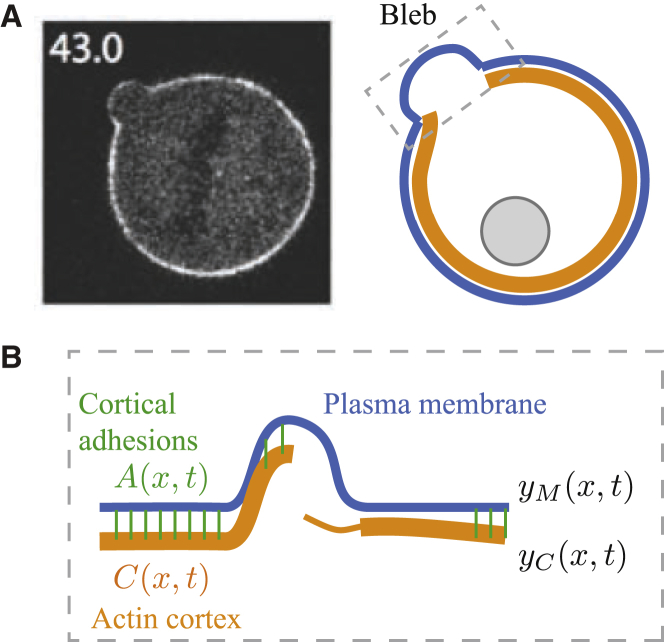
Figure 1.
(A) Micrograph of a single bleb induced by laser ablation on the surface of a HeLa cell 43 s after initial formation, taken from (64). (B) Model components. At each location on the surface of the cell, x, four quantities are represented: the height of the membrane, ; the height and thickness of the actin cortex, and respectively; and the local density of membrane-cortex anchoring proteins, . Note that the schematic shows the range of possible model states (e.g., thick or thin cortex, protruding or proximal membrane), whereas specific predicted dynamics will be determined by simulation. To see this figure in color, go online.
Assembly and turnover
The cortex is an active, anisotropic poroviscoelastic material (9, 10). Since the molecular details of cortex assembly are still under investigation (40), we assume simple first-order kinetics,
| (1) |
The first parameter, ω, governs cortex assembly, and assumes that new cortex requires adhesion to a nearby membrane (although existing cortex can exist anywhere), consistent with the observation that cortical actin has different architecture than cytoplasmic F-actin (8). The second term describes cortex turnover with rate (11). Although we use the term thickness, we interpret c as a combination of density and spatial thickness, with the fluorescence intensity of labeled F-actin serving as its experimental proxy. Therefore, c has arbitrary units.
In stereotypical prebleb conditions, the cortex is attached to the membrane via membrane-cortex adhesion molecules, including ezrin-radixin-moesin family proteins (11), as well as any other membrane proteins that interact with F-actin (41). Therefore, we use the generic term “adhesion” to describe the combined effect of these proteins. We use similar first-order kinetics for adhesion assembly and turnover, with three additional assumptions: 1) adhesion assembly saturates at high cortex thickness; 2) adhesion attachment requires proximity between cortex and membrane, with characteristic distance δ, that describes the “reach” of adhesion molecules, which may be as large as (8); and 3) adhesion detachment is force-dependent, with characteristic breaking force . These assumptions lead to
| (2) |
where and have units of and , respectively, and is the cortex thickness at which adhesion assembly is half-maximal. The numerator follows from the assumption that adhesions collectively behave like springs with Hookean stiffness κ. Note that adhesion turnover, (11), is significantly faster than cortex turnover, leading to a separation of timescales that we exploit.
Mechanics
The above equations describing assembly and disassembly kinetics are coupled to a mechanical description of the membrane and cortex via mechanical energy,
| (3) |
where
| (4) |
The first term corresponds to tension on the adhesions. Since these adhesions break at moderate tension, we model them as linear springs. The second term is hydrostatic pressure, , specified below. Membrane mechanics are described by
| (5) |
which corresponds to the standard Canham-Helfrich energy with membrane tension and bending rigidity (26, 36, 38, 42). These functional forms represent a small-deformation approximation and comprise a simplifying assumption to make the model more easily amenable to the analysis. We therefore do not expect our model to capture the shape of a fully expanded bleb with high accuracy. More geometrically complex models have been developed for that purpose (39). Finally, the mechanics of the actin-myosin cytoskeleton is included in
| (6) |
accounting for activity of the cortex, which generates contraction stress , assumed to be proportional to cortex thickness. The first term in Eq. 6 accounts for inward contractility, as the cortical cytoskeleton pulls against the cytoplasmic cytoskeleton, generating a normal (inward) force, as shown in Fig. S1 in the Supporting Material. Note that this term has been neglected in previous work (26). The second term accounts for tangential stress in the plane of the cortex, where is the cortex dimension that translates the 3D contractile stress to a tangential planar contractile tension. Importantly, we find that in traveling blebs, where the cortex is discontinuous, the tangential term does not generate sufficient inward force to heal the tail of the bleb as it travels, highlighting the importance of the normal contractility term. Cortex elasticity terms describing how the cortex resists deformation are straightforward to add, but we find that omitting them does not detract from our key results.
The mechanical features included in the energy equation (Eq. 3) can also be understood by their equivalent force-balance form, expressed in Eqs. 8 and 9 below.
Pressure propagation inside the complex rheology of the cytoplasm is under intense investigation (12, 30, 43). To address the nature of pressure dynamics, we investigate several pressure model variants. As a base model, we assume that pressure is locally relaxed when the membrane is allowed to relax:
| (7) |
where sets the characteristic distance at which pressure is significantly reduced. The pressure drop would be lessened if the membrane is locally water-permeable (44), which would have the effect of reducing the coefficient relating pressure to membrane extrusion. Other model variants explore the possibility of rapidly equilibrated pressure across the whole cell surface and a mixture of global and local pressure relaxation.
The dynamics of membrane tension are also under investigation (3, 6, 15, 17, 45). Under the simplest assumption, membrane tension, , is spatially uniform and constant in time. We use this as our base model, but we also explore membrane tension that is spatially nonuniform and dynamically responds to local stretching/unruffling and cortex attachment (see Results).
Preliminary analysis
Taking the variational derivative of Eq. 3 leads to force-balance equations for the cortex and membrane:
| (8) |
| (9) |
Physical parameters are summarized in Table 1.
Table 1.
Model Parameters
| Symbol | Dimensions | Meaning |
|---|---|---|
| ω | (A.U.) | cortex assembly rate constant |
| r | cortex turnover rate constant | |
| adhesion assembly rate | ||
| adhesion turnover rate | ||
| (A.U.) | cortex thickness at adhesion saturation | |
| δ | adhesion length between cortex and membrane | |
| κ | adhesion spring constant | |
| adhesion breaking strength | ||
| membrane tension | ||
| membrane bending modulus | ||
| Pa/(A.U.) | actin-myosin contractility (per unit of c) | |
| Pa/nm | hydrostatic pressure scale |
A.U., arbitrary unit.
Values for many of these parameters have been estimated (see the Supporting Material). The spatial terms significantly complicate both numerical solution and analysis of the model, and we find that their omission does not significantly influence blebbing dynamics. This is expected for membrane bending, since bending forces are expected to be negligible on length scales above (1). Therefore, unless otherwise noted below, we neglect the tangential cortex stress, and membrane bending, terms. However, see the Supporting Material for solutions with full terms.
We achieve nondimensionality by choosing a characteristic actin cortex thickness, , a characteristic density of adhesions, , a characteristic time, (11), a characteristic position, , and a characteristic length, , resulting in a nondimensional model,
| (10) |
| (11) |
| (12) |
| (13) |
with six nondimensional parameters defined in Table 2.
Table 2.
Nondimensional Parameters
| Symbol | Definition | Interpretation |
|---|---|---|
| Cortex intensity | ||
| ε | ratio of adhesion and cortex turnover times | |
| D | adhesion reach | |
| adhesion bond strength | ||
| M | myosin contractility relative to adhesion strength | |
| P | pressure relative to adhesion strength |
Here, we provide an overview of the roles of each term in Eqs. 10–13. The first and second terms in the C equation (Eq. 10) describe cortex formation and turnover, respectively. The first and second terms in the A equation (Eq. 11) describe attachment and detachment of cortex-membrane adhesions. The first exponential in Eq. 11 arises because the membrane and cortex must be in proximity for an adhesion to form. The second exponential in Eq. 11 describes the accelerated breaking of adhesions under force. Equations 12 and 13 describe five forces acting on the membrane and cortex. The terms, in order of appearance, describe adhesion force on the cortex; myosin contractility of the cortex; adhesion force on the membrane; pressure; and membrane tension.
Note that our choice of nondimensionalization means that only relative changes in and are physically meaningful. We numerically solve these equations as described in the Supporting Material (46).
Results
Model exhibits blebbing and nonblebbing behaviors
The quantitative model combines five mechanisms of the membrane-cortex interaction: force-sensitive adhesions, local hydrostatic pressure, cortex contractility, membrane tension and cortex turnover. We numerically simulate the model and find that three classes of dynamics arise from the same model at different parameters: stable nonblebbing states, stationary blebbing, and traveling blebs. We discuss these in turn.
At equilibrium, the membrane and cortex are locally approximately flat. We apply an initial perturbation corresponding to local ablation by locally reducing the adhesion density by 99%. In blebbing states, the membrane will detach from the cortex and protrude locally. The membrane then continues to move away from the thinning cortex as the detached region grows in both lateral size (along the surface) and height (i.e., normal to the cell surface) until it reaches a maximum size around . The adhesions subsequently accumulate under the protruding membrane and the cortex is able to reattach and thicken. Under the influence of cortex contraction, the bleb heals and the membrane returns to its equilibrium. This bleb-like behavior is observed in 2D (Fig. 2 A, left) and 3D (Fig. 2 B) simulations. In contrast, at different biophysical parameters, the detached region of membrane may not grow after perturbation, but instead may directly and rapidly return to equilibrium, as shown in Fig. 2 A, right. This stable behavior is observed in both 2D (Fig. 2 A, right) and 3D (not shown).
Figure 2.
Model exhibits stationary blebs and nonblebbing states in 2D and 3D. (A) Profile of stationary solution of the 2D system. (Left) Excitable state, in which an initial perturbation (cyan dashed line) expands both in height (normal to the cell surface) and laterally (along the cell surface) before retracting. (Right) Nonexcitable state, in which the initial perturbation rapidly and directly returns to equilibrium. Parameter values are , , , , for the excitable state, and for the nonexcitable state. (B) Profile of the stationary solution of the 3D system in an excitable state. Parameter values are , , , , and . Note that our choice of nondimensionalization means that only relative changes in and are physically meaningful. To see this figure in color, go online.
Blebs as excitable phenomena
Although numerical simulation of the full model reveals a range of blebbing behavior, we seek to elucidate how biophysical parameters determine the class of dynamics, specifically whether or not a bleb forms. To this end, we simplify the model by neglecting the tension term in Eq. 13. Heuristically, we model an (unrealistic) system in which a patch of cell surface has been cut off from its neighbors (as in Fig. S1 E). This transforms the force-balance equations (Eqs. 12 and 13) into a pair of algebraic equations,
| (14) |
| (15) |
shown in Fig. 3 A as a function of A and C. These are then substituted into the assembly/disassembly equations, yielding
| (16) |
| (17) |
The model is now a system of two ordinary differential equations (ODEs) amenable to phase-plane analysis (47). We plot nullclines in which (Fig. 3, B and D, green) or (Fig. 3, B and D, orange). Four regimes of behavior are observed in this system: In one (Fig. 3, B, top left), there is a single stable equilibrium with no threshold behavior. In this regime, perturbations rapidly return to their steady state. We identify this with the stable nonblebbing behavior of the full model.
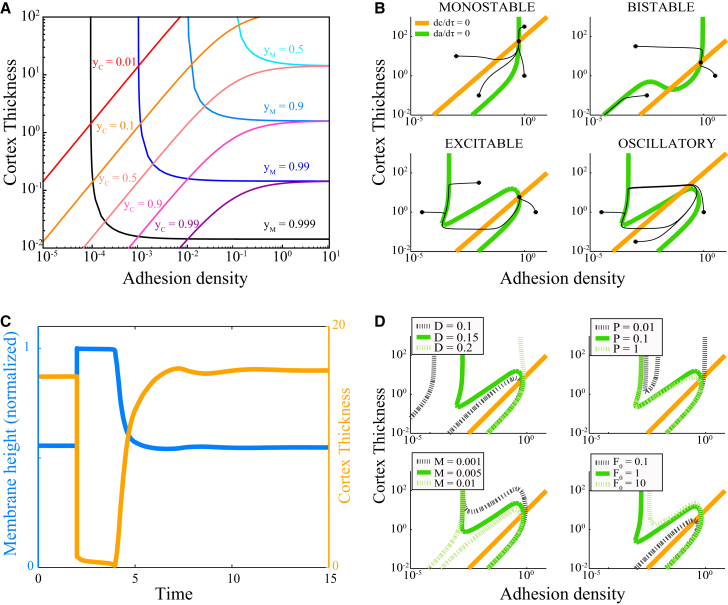
Figure 3.
Emergence of blebbing states can be understood in terms of the local A–C phase plane. (A) Since the model assumed force-balance between adhesions, cortex, and membrane, particular values of A and C determine the current positions of the membrane and cortex, and via Eqs. 14 and 15. (B) Range of behaviors of the system of equations given different parameter sets visualized by the nullclines (C, orange; A, green) of the nondimensionalized system of equations (Eqs. 16 and 17). Sample trajectories are shown in black. The monostable parameters are , , , , and . The bistable parameters are , , , , and . The oscillatory parameters are , , , , and . The excitable parameters are , , , , and . (C) A time series plot of membrane position (blue) and cortex thickness (orange) beginning in the steady state, with a perturbation at time . (D) The effect of parameter variation on the nullclines. Parameters that are not being varied, as indicted in the legend, are fixed at , , , , and . To see this figure in color, go online.
The stable equilibrium can exhibit excitability (Fig. 3, B and D, bottom left), a threshold phenomenon in which small perturbations rapidly return to the equilibrium, but a sufficiently large perturbation results in a large, slow excursion in parameter space that eventually returns to the equilibrium. We identify this with blebbing behavior in the full model and it is characterized by a fold in the nullcline.
One such excitation trajectory is shown in Fig. 3 C. Before the initial perturbation, , the flat surface is stable to small perturbations but susceptible to large perturbations such as the decrease in adhesion density applied here at . The membrane rapidly finds a new mechanical equilibrium, pushed out by hydrostatic pressure, which is no longer in competition with cortical contraction. The comparatively slow timescale of cortical turnover (Fig. 3, B and D, orange line) leads to a delay before cortex begins to reform , after which the cortex accumulates, pulling in the membrane. Note that many excitable trajectories exhibit low-amplitude oscillations in the cortex as it heals, corresponding to a slight “overshooting” of the equilibrium . Interestingly, such overshooting has been observed experimentally (8).
The minimum threshold to initiate an excitation can be extracted from Fig. 3 as follows: The stable equilibrium is at the intersection of the two nullclines. From this point, removing adhesions corresponds to moving horizontally to the left. When adhesion removal is sufficient to cross the nullcline, an excitation is initiated. Since the nullcline determines this threshold, it is independent of membrane tension. This is in disagreement with previous estimates of the threshold, where membrane tension was predicted to be a strong determinant of the size of initial ablation required for bleb initiation (21). In contrast, our model predicts that membrane tension determines how big a bleb grows (laterally), but not whether it initially grows. This tension independence arises heuristically because, once a patch of membrane has been deadhered, membrane tension promotes bleb growth by pulling neighboring adhesions and inhibits bleb growth by pulling in the deadhered region. By the force-balance condition (Eq. 9), these forces are equal.
We also observe oscillations (Fig. 3, B and D, bottom right), which could represent continually blebbing cells (20). At yet other parameters, the same model exhibits bistable states (Fig. 3, B and D, top right) in which the flat, unperturbed equilibrium is stable but is accompanied by a second state in which all adhesions are broken, and hydrostatic pressure is too great for the actin cortex to overcome, so that healing does not spontaneously occur. We expect this permanently damaged state to not be observed experimentally as other cellular processes adjust to heal the cortex.
Thus, by observing the nullclines for different parameters, our model makes predictions about the emergence of blebbing after changes in biophysical parameters (Fig. 3 D). We summarize these predictions here and in Table S1. Increasing the effective reach of adhesion molecules corresponds to increasing D and abolishes excitability, whereas decreasing D is predicted to not abolish blebbing but extends the excitable trajectory, therefore predicting a slower healing period. Increasing hydrostatic pressure, e.g., by decreasing extracellular pressure by modulating osmolites, leads to emergence of blebbing from nonblebbing states, in agreement with experiment (6) and intuition. Decreasing myosin contractility abolishes excitability, whereas increasing it delays healing.
Biophysical determinants of travel and travel velocity
The previous section’s analysis predicts when the cell surface will be excitable and how the bleb evolves in height, but not its dynamics along the cell surface. To understand bleb travel, we return to the full, spatially extended model, first in 2D, then in 3D.
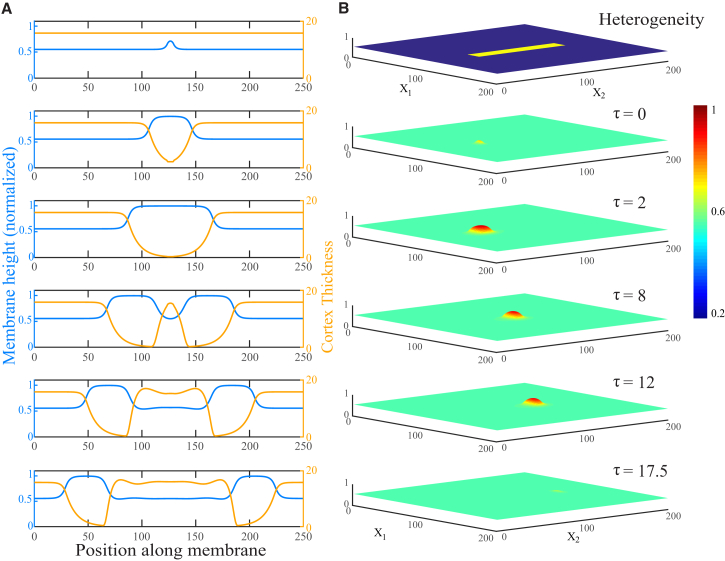
Excitable parameter sets all spread laterally. However, some parameter sets expand in a limited manner, which we identify as stationary blebs, whereas others trigger traveling pulses that persist, as shown in Fig. 4 A. We identify these as traveling blebs. In 2D, they move in both directions from the site of initial triggering. The time interval from triggering and expansion to healing is equal to the healing time in the local analysis and is determined by the cortex turnover time, . The width of the traveling bleb, w, is thus determined by its travel velocity, .
Figure 4.
Traveling blebs in 2D and 3D. (A) Profile of a traveling bleb in 2D after a perturbation at time . The membrane height is indicated by the blue line and cortex thickness by the orange line. Parameter values are , , , , and . (B) Profile of a traveling bleb in 3D after a perturbation at time in the spatial-heterogeneity hypothesis model, shown at the top (see Results). To see this figure in color, go online.
Traveling pulses are a generic feature of spatially extended excitable systems (48, 49, 50). In many cases, neighboring regions are coupled with the diffusion of a molecular participant. In these reaction-diffusion systems, a simple mathematical condition, sometimes called the Maxwell condition (51, 52), exists for determining whether an excitation will induce a traveling pulse or remain localized. Since our system is not a reaction-diffusion system, the Maxwell condition fails to predict whether the blebs travel or not.
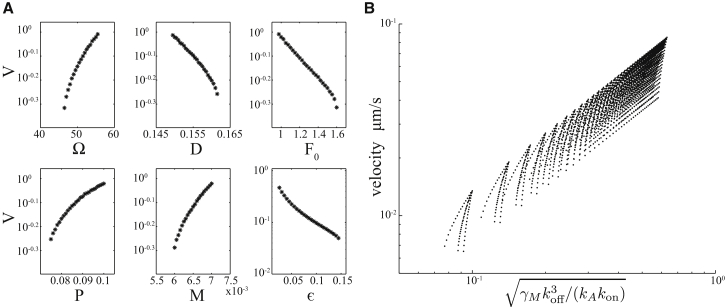
A major goal of this work is to elucidate the determinants of the traveling velocity, which is known for reaction-diffusion waves and mechanical linear waves (3). Parameter variations, shown in Fig. 5, reveal that the parameter regime that allows traveling blebs is narrow in all nondimensional parameters except ε. Indeed, its relative range is < , corresponding to a twofold change. The model therefore predicts a nondimensional velocity, , yielding the following dimensional velocity, the principle result of this work:
| (18) |
| (19) |
where the function h expresses to a weak dependence. We confirm this prediction in Fig. 5 B by performing a large panparametric search through parameter space. Eq. 19 predicts that travel will accelerate with increasing membrane tension, with a specifically square-root dependence, and will decelerate with adhesion formation rate , a parameter that could be varied by increasing the abundance of total adhesion molecules. The affinity of adhesions for the cortex, , is also predicted to have a decelerating influence on bleb travel. Interestingly, all other parameters, including hydrostatic pressure and myosin contractility, are predicted to have only a minor influence on travel velocity. Note, however, that these parameters strongly determine whether or not a bleb can form, and whether or not the bleb travels laterally. This model prediction is distinct from a previous prediction (26), which posited that cortex healing has an intrinsic velocity, and that this velocity determines bleb travel velocity.
Figure 5.
Velocity of traveling blebs. (A) Plot of each of the six nondimensional parameters, , D, , P, M, and E, versus nondimensional velocity. Parameter ranges show the full extent of the parameter regime exhibiting traveling solutions. The fixed parameters in each plot are , , , , and . (B) Plot of the hypothesized relationship between velocity (Eq. 19) and velocity observed in the numerical simulation.
Hypotheses for compact traveling blebs
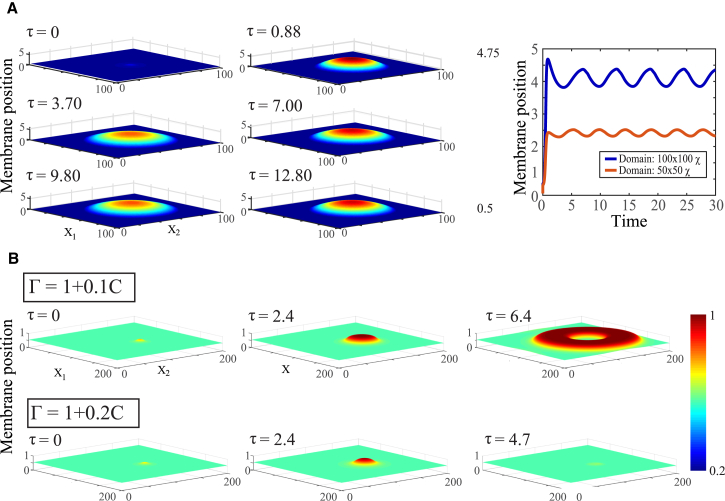
In 3D, the base model also exhibits excitations that either travel or heal in place, in agreement with the local analysis and 2D model. Parameter conditions for excitability and travel are the same as for the 2D model, as is travel velocity. However, we find that a localized initial perturbation spreads radially in all directions, leading to an expanding bull’s-eye or target pattern (Fig. 6 B and Movie S3). This is a generic feature of excitable systems and arises because of inherent symmetry: a protruding region of membrane will pull neighboring regions of membrane, without directional bias.
Figure 6.
Alternative hypotheses for hydrostatic pressure and membrane tension dynamics. (A) Profile of a 3D bleb using the global pressure model (Eq. 20), which assumes that pressure equilibrates instantaneously across the domain. The bleb expands and contracts in oscillatory cycles (right). (B) Profile of a 3D bleb using a nonuniform tension model (Eq. 21), which assumes that membrane tension depends on the cortex thickness at a given point on the membrane. As the strength of this dependence increases (bottom row), the bleb no longer travels across the membrane. Here, is the nondimensionalized membrane tension. To see this figure in color, go online.
Since traveling blebs are not experimentally observed to expand in bull’s-eye patterns, we are led to investigate the question of what gives rise to spatially compact traveling blebs. That is, what breaks the symmetry, inducing travel in a single direction?
We introduce three hypotheses. The first is that hydrostatic pressure may be reduced globally fast enough that, once the excited region enlarges past a certain size, there is no longer sufficient pressure to drive further excitation, thus limiting the target pattern to a compact region. In our model, we modify the membrane force-balance equation, Eq. 9, by including the pressure term:
| (20) |
This equation corresponds to a shared, global pressure that responds to pressure release (via membrane protrusion) instantly anywhere in the domain. We variously simulated purely global pressure, purely local pressure, and pressure with both local and global equilibration, based on recent theoretical evidence (53).
We find that global pressure dynamics can limit the bleb’s outward growth when is sufficiently large. However, we do not see symmetry breaking, even upon introduction of parametric noise (Fig. 6 A). Interestingly, at intermediate global pressures, the bleb does not heal and instead undergoes slow oscillations (Fig. 6 A, right). These oscillations reveal an inherent negative feedback between cortical formation, which builds pressure, which in turn breaks adhesions, weakening the cortex.
The second hypothesis is that bleb compactness and asymmetry is due to a dynamic, nonuniform membrane tension. Based on recent evidence (45), we introduce the assumption that tension increases with increasing local cortical actin contractility,
| (21) |
We find that this is sufficient to terminate the protrusion (Fig. 6 B), but again do not observe symmetry breaking.
Our third hypothesis is that large-length-scale heterogeneity, specifically on the approximately micron length scale of blebs, exists in the local density of proteins such as adhesion molecules and cortical actin nucleators. These manifest as spatial heterogeneity in model parameters such as D and . Since these parameters sensitively determine whether the bleb can travel, such heterogeneity might create specific paths, forcing traveling blebs to spread only in specific directions. We simulate the model on a surface in which a small rectangular region has parameters distinct from those of the surrounding region, as shown in Fig. 4 B, top. Since the parameter region allowing traveling blebs is fairly narrow (Fig. 5), it is straightforward to find parameter sets with less than twofold variation for which the equilibrium is the same but only one set allows travel. As expected, blebs initiated in the excitable-travel region remain compact and move with velocity v from Eq. 19, and with front-to-back width .
We conclude that small differences across large length scales in the underlying biophysical properties of the cell surface are sufficient to explain compact traveling blebs. This hypothesis makes the prediction that subsequent traveling blebs will tend to occur in the same location on the cell surface, provided that the heterogeneity’s own timescale of variation is longer than the bleb lifetime.
Discussion
Excitability is a recurrent theme in cell biology (50, 54, 55, 56). We find that the conditions for excitability emerge naturally from the mechanical properties of the cell surface, specifically, the combination of a contractile cortex, a membrane exposed to internal hydrostatic pressure, and force-sensitive adhesions connecting them. In addition, membrane mechanical properties (i.e., surface tension) are sufficient for this excitability to lead to either limited-growth stationary blebs that heal in place or traveling blebs reminiscent of circus movement. Notably, three classes of dynamics arise from the same model at different parameters: stable, nonblebbing states (Fig. 2 B), stationary blebs (Fig. 2 A and C), and traveling blebs (Fig. 4, A and B). Thus, our model provides quantitative conditions for bleb growth and whether the bleb heals locally or travels.
The model makes two main contributions. First, it allows elucidation of the determinants of the travel velocity in terms of biophysical parameters such as membrane tension and adhesion kinetics (Eq. 19). Surprisingly, we find that hydrostatic pressure and myosin contractility only weakly determine velocity, whereas they strongly determine other features, such as whether the bleb forms and bleb height. This is in contrast to previous assumptions (26) and other traveling waves in biology (3).
Our second finding is that known biophysical mechanisms are insufficient to account for the compactness of traveling blebs in 3D. The excitability inherent in the system leads to traveling waves. However, a striking distinction from other excitable waves in a 2D domain is that other waves create bull’s-eye patterns or spiral patterns. Since local membrane-cortex detachment promotes nearby detachment symmetrically, why do blebs travel in a compact shape rather than spreading in all directions? Generically, for a shape to remain approximately constant as it travels, the normal velocity on its perimeter must vary from maximal at its front to zero at its sides. This observation, termed the graded-radial-extension condition (57), was made for steady cell motility but holds in general and therefore must be true for compact traveling blebs. One hypothesis we find sufficient to maintain compact travel is heterogeneity in the biophysical properties of the cell surface, such as adhesion density. There is no direct evidence that such heterogeneity is responsible for determining bleb travel paths, and it is likely that other mechanisms can explain compact travel. Since membrane tension is a strong determinant of local expansion velocity, it is possible that a model including different nonuniform membrane tension can recover a compact bleb in the absence of parametric heterogeneity. Other alternatives are constraints set by lipid flow through the neck of the bleb (4), or nematic ordering in the cortex (33), which would break isotropic symmetry. For cells adhered to a rigid surface, the curvature is higher at the cell perimeter. This higher curvature could also potentially bias bleb formation and travel. We anticipate that this will be a future direction of research.
A crucial feature of our model is the presence of a normal stress generated by the cortex, in addition to tangential stresses. We find that this normal stress is necessary for the dynamic healing and retraction of a traveling bleb. If myosin in the cortex generates an isotropic contractile stress, then it will induce stress in any direction in which there is F-actin. There is significant F-actin beneath the cortex (∼60% of the density in the cortex (8)), which is referred to as the cytoplasmic actin network and which plays a role in cell integrity (58). Our results suggest that it also plays a role in retracting cellular protrusions.
Increasingly, mechanics is included in theoretical models of cellular processes (7, 41, 59, 60, 61). In these cases and others, subcellular mechanics equilibrates on subsecond timescales but drives processes that play out over seconds or more slowly; therefore, mechanics is included via instantaneous force-balance or, equivalently, minimization of an energy functional, as in Eq. 3, at every moment in time. Instead of reaction-transport (diffusion or advection) partial differential equations, these models can be expressed as a boundary value problem at each moment in time coupled to local time-dependent governing equations. This distinct class of models presents new opportunities for mathematical development. For excitable reaction-diffusion systems, a straightforward condition termed the Maxwell condition (51, 52, 62) can be computed that determines whether the excitation will generate traveling waves. Analogous conditions for the new class of mechanical models may exist, and they will be the subject of future research.
Our model makes several testable predictions about how bleb behavior will be modulated by experimental perturbations. The specific predictions about bleb formation and travel velocity, in Results, correspond to changes in hydrostatic pressure, which can be modulated via the extracellular pressure by, e.g., osmolites; cortical turnover, which can be promoted or slowed by jasplakinolide or cytochalasin D (8, 30); and myosin contractility, which in blebs has been demonstrated to be susceptible to blebbistatin and indirectly to Y-compound (6). In addition to these experiments, our model predicts that the “reach” of the adhesion molecules, δ, influences bleb characteristics via the (nondimensional) parameter D. It might be possible to modulate this parameter by mutagenically elongating or truncating cortex-membrane adhesion molecules.
In addition to the model variants we explored here, this model is readily extendible to different surface geometries and assumptions about stresses below and above the cell surface. An intriguing direction of research is the coupling of this model of surface mechanochemistry with different rheological models of how stress evolves inside the cell (13, 53). Another direction is the coupling to extracellular fluid dynamics, which have recently been proposed to play a role in determining membrane dynamics, even on slow timescales (63).
Author Contributions
K.M. and J.F.A. designed the research, developed and analyzed the model and wrote the article. K.M., H.Y., and J.L. wrote numerical solvers and performed numerical simulations.
Acknowledgments
We thank Robert Guy for valuable discussion.
This work was supported in part by National Science Foundation CAREER grant DMS-1454739 to J.A.
Editor: Sean Sun.
Footnotes
A detailed description of the model, two figures, two tables, and five movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30057-1.
Supporting Material
This movie corresponds to the parameters in Fig. 4 A.
This movie corresponds to Fig 2 B
Travel is unrestricted and the excitation spreads in all directions.
This movie corresponds to Fig. 4 B.
This movie corresponds to Fig. 6 A.
References
- 1.Allard J.F., Dushek O., van der Merwe P.A. Mechanical modulation of receptor-ligand interactions at cell-cell interfaces. Biophys. J. 2012;102:1265–1273. doi: 10.1016/j.bpj.2012.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhu C. Mechanochemistry: a molecular biomechanics view of mechanosensing. Ann. Biomed. Eng. 2014;42:388–404. doi: 10.1007/s10439-013-0904-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Allard J., Mogilner A. Traveling waves in actin dynamics and cell motility. Curr. Opin. Cell Biol. 2013;25:107–115. doi: 10.1016/j.ceb.2012.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rangamani P., Benjamini A., Oster G. Small scale membrane mechanics. Biomech. Model. Mechanobiol. 2014;13:697–711. doi: 10.1007/s10237-013-0528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu J., Sun Y., Drubin D.G. Mechanochemical crosstalk during endocytic vesicle formation. Curr. Opin. Cell Biol. 2010;22:36–43. doi: 10.1016/j.ceb.2009.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tinevez J.-Y., Schulze U., Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Peleg B., Disanza A., Gov N. Propagating cell-membrane waves driven by curved activators of actin polymerization. PLoS One. 2011;6:e18635. doi: 10.1371/journal.pone.0018635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Clark A.G., Dierkes K., Paluch E.K. Monitoring actin cortex thickness in live cells. Biophys. J. 2013;105:570–580. doi: 10.1016/j.bpj.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Salbreux G., Prost J., Joanny J.F. Hydrodynamics of cellular cortical flows and the formation of contractile rings. Phys. Rev. Lett. 2009;103:058102. doi: 10.1103/PhysRevLett.103.058102. [DOI] [PubMed] [Google Scholar]
- 10.Hannezo E., Dong B., Hayashi S. Cortical instability drives periodic supracellular actin pattern formation in epithelial tubes. Proc. Natl. Acad. Sci. USA. 2015;112:8620–8625. doi: 10.1073/pnas.1504762112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fritzsche M., Thorogate R., Charras G. Quantitative analysis of ezrin turnover dynamics in the actin cortex. Biophys. J. 2014;106:343–353. doi: 10.1016/j.bpj.2013.11.4499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Strychalski W., Guy R.D. A computational model of bleb formation. Math. Med. Biol. 2013;30:115–130. doi: 10.1093/imammb/dqr030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Charras G.T., Mitchison T.J., Mahadevan L. Animal cell hydraulics. J. Cell Sci. 2009;122:3233–3241. doi: 10.1242/jcs.049262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Clark A.G., Wartlick O., Paluch E.K. Stresses at the cell surface during animal cell morphogenesis. Curr. Biol. 2014;24:R484–R494. doi: 10.1016/j.cub.2014.03.059. [DOI] [PubMed] [Google Scholar]
- 15.Fogelson B., Mogilner A. Computational estimates of membrane flow and tension gradient in motile cells. PLoS One. 2014;9:e84524. doi: 10.1371/journal.pone.0084524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yip A.K., Chiam K.H., Matsudaira P. Traction stress analysis and modeling reveal that amoeboid migration in confined spaces is accompanied by expansive forces and requires the structural integrity of the membrane-cortex interactions. Integr Biol (Camb) 2015;7:1196–1211. doi: 10.1039/c4ib00245h. [DOI] [PubMed] [Google Scholar]
- 17.Weiner O.D., Marganski W.A., Kirschner M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leijnse N., Oddershede L.B., Bendix P.M. An updated look at actin dynamics in filopodia. Cytoskeleton (Hoboken) 2015;72:71–79. doi: 10.1002/cm.21216. [DOI] [PubMed] [Google Scholar]
- 19.Wollman R., Meyer T. Coordinated oscillations in cortical actin and Ca2+ correlate with cycles of vesicle secretion. Nat. Cell Biol. 2012;14:1261–1269. doi: 10.1038/ncb2614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Charras G.T. A short history of blebbing. J. Microsc. 2008;231:466–478. doi: 10.1111/j.1365-2818.2008.02059.x. [DOI] [PubMed] [Google Scholar]
- 21.Charras G.T., Coughlin M., Mahadevan L. Life and times of a cellular bleb. Biophys. J. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Paluch E.K., Raz E. The role and regulation of blebs in cell migration. Curr. Opin. Cell Biol. 2013;25:582–590. doi: 10.1016/j.ceb.2013.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Danuser G., Allard J., Mogilner A. Mathematical modeling of rukaryotic cell migration: insights beyond experiments. Annu. Rev. Cell Dev. Biol. 2012;29:501–528. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fujinami N., Kageyama T. Circus movement in dissociated embryonic cells of a teleost, Oryzias latipes. J. Cell Sci. 1975;19:169–182. doi: 10.1242/jcs.19.1.169. [DOI] [PubMed] [Google Scholar]
- 25.Olson E.C. Onset of electrical excitability during a period of circus plasma membrane movements in differentiating Xenopus neurons. J. Neurosci. 1996;16:5117–5129. doi: 10.1523/JNEUROSCI.16-16-05117.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lim F.Y., Chiam K.-H., Mahadevan L. The size, shape, and dynamics of cellular blebs. Europhys. Lett. 2012;100:28004. [Google Scholar]
- 27.Logue J.S., Cartagena-Rivera A.X., Waterman C.M. Erk regulation of actin capping and bundling by Eps8 promotes cortex tension and leader bleb-based migration. eLife. 2015;4:e08314. doi: 10.7554/eLife.08314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Charras G., Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat. Rev. Mol. Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 29.Friedl P., Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- 30.Sedzinski J., Biro M., Paluch E. Polar actomyosin contractility destabilizes the position of the cytokinetic furrow. Nature. 2011;476:462–466. doi: 10.1038/nature10286. [DOI] [PubMed] [Google Scholar]
- 31.Baum D.A., Baum B. An inside-out origin for the eukaryotic cell. BMC Biol. 2014;12:76. doi: 10.1186/s12915-014-0076-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ryan G.L., Watanabe N., Vavylonis D. A review of models of fluctuating protrusion and retraction patterns at the leading edge of motile cells. Cytoskeleton (Hoboken) 2012;69:195–206. doi: 10.1002/cm.21017. [DOI] [PubMed] [Google Scholar]
- 33.Kapustina M., Elston T.C., Jacobson K. Compression and dilation of the membrane-cortex layer generates rapid changes in cell shape. J. Cell Biol. 2013;200:95–108. doi: 10.1083/jcb.201204157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Strychalski W., Copos C.A., Guy R.D. A poroelastic immersed boundary method with applications to cell biology. J. Comput. Phys. 2015;282:77–97. [Google Scholar]
- 35.Young J., Mitran S. A numerical model of cellular blebbing: a volume-conserving, fluid-structure interaction model of the entire cell. J. Biomech. 2010;43:210–220. doi: 10.1016/j.jbiomech.2009.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Alert R., Casademunt J., Sens P. Model for probing membrane-cortex adhesion by micropipette aspiration and fluctuation spectroscopy. Biophys. J. 2015;108:1878–1886. doi: 10.1016/j.bpj.2015.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Woolley T.E., Gaffney E.A., Goriely A. Cellular blebs: pressure-driven, axisymmetric, membrane protrusions. Biomech. Model. Mechanobiol. 2014;13:463–476. doi: 10.1007/s10237-013-0509-9. [DOI] [PubMed] [Google Scholar]
- 38.Woolley T.E., Gaffney E.A., Goriely A. Three mechanical models for blebbing and multi-blebbing. IMA J. Appl. Math. 2014;79:636–660. [Google Scholar]
- 39.Woolley T.E., Gaffney E.A., Goriely A. Membrane shrinkage and cortex remodelling are predicted to work in harmony to retract blebs. R. Soc. Open Sci. 2015;2:150184. doi: 10.1098/rsos.150184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bovellan M., Romeo Y., Charras G. Cellular control of cortical actin nucleation. Curr. Biol. 2014;24:1628–1635. doi: 10.1016/j.cub.2014.05.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Paszek M.J., DuFort C.C., Weaver V.M. The cancer glycocalyx mechanically primes integrin-mediated growth and survival. Nature. 2014;511:319–325. doi: 10.1038/nature13535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 43.Charras G.T., Yarrow J.C., Mitchison T.J. Non-equilibration of hydrostatic pressure in blebbing cells. Nature. 2005;435:365–369. doi: 10.1038/nature03550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Taloni A., Kardash E., La Porta C.A. Volume changes during active shape fluctuations in cells. Phys. Rev. Lett. 2015;114:208101. doi: 10.1103/PhysRevLett.114.208101. [DOI] [PubMed] [Google Scholar]
- 45.Peukes J., Betz T. Direct measurement of the cortical tension during the growth of membrane blebs. Biophys. J. 2014;107:1810–1820. doi: 10.1016/j.bpj.2014.07.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wise S.M., Kim J., Lowengrub J.S. Solving the regularized, strongly anisotropic Cahn-Hilliard equation by an adaptive nonlinear multigrid method. J. Comput. Phys. 2007;226:414–416. [Google Scholar]
- 47.Edelstein-Keshet L. SIAM; Philadelphia, PA: 1988. Mathematical Models in Biology. [Google Scholar]
- 48.Idema T., Dubuis J.O., Liu A.J. The syncytial Drosophila embryo as a mechanically excitable medium. PLoS One. 2013;8:e77216. doi: 10.1371/journal.pone.0077216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ryan G.L., Petroccia H.M., Vavylonis D. Excitable actin dynamics in lamellipodial protrusion and retraction. Biophys. J. 2012;102:1493–1502. doi: 10.1016/j.bpj.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bement W.M., Leda M., von Dassow G. Activator-inhibitor coupling between Rho signalling and actin assembly makes the cell cortex an excitable medium. Nat. Cell Biol. 2015;17:1471–1483. doi: 10.1038/ncb3251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Britton N.F. Threshold phenomena and solitary traveling waves in a class of reaction-diffusion systems. SIAM J. Appl. Math. 1982;42:188–217. [Google Scholar]
- 52.Mori Y., Jilkine A., Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Strychalski W., Guy R.D. Intracellular pressure dynamics in blebbing cells. Biophys. J. 2016;110:1168–1179. doi: 10.1016/j.bpj.2016.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang C.-H., Tang M., Devreotes P.N. An excitable signal integrator couples to an idling cytoskeletal oscillator to drive cell migration. Nat. Cell Biol. 2013;15:1307–1316. doi: 10.1038/ncb2859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Xiong Y., Huang C.-H., Devreotes P.N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl. Acad. Sci. USA. 2010;107:17079–17086. doi: 10.1073/pnas.1011271107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Fitzhugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1961;1:445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lee J., Ishihara A., Jacobson K. Principles of locomotion for simple-shaped cells. Nature. 1993;362:167–171. doi: 10.1038/362167a0. [DOI] [PubMed] [Google Scholar]
- 58.Luo W., Yu C.H., Bershadsky A.D. Analysis of the local organization and dynamics of cellular actin networks. J. Cell Biol. 2013;202:1057–1073. doi: 10.1083/jcb.201210123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Thon J.N., Macleod H., Italiano J.E., Jr. Microtubule and cortical forces determine platelet size during vascular platelet production. Nat. Commun. 2012;3:852–859. doi: 10.1038/ncomms1838. [DOI] [PubMed] [Google Scholar]
- 60.Dobrowsky T.M., Daniels B.R., Wirtz D. Organization of cellular receptors into a nanoscale junction during HIV-1 adhesion. PLOS Comput. Biol. 2010;6:e1000855. doi: 10.1371/journal.pcbi.1000855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Qi S., Krogsgaard M., Chakraborty A.K. Molecular flexibility can influence the stimulatory ability of receptor-ligand interactions at cell-cell junctions. Proc. Natl. Acad. Sci. USA. 2006;103:4416–4421. doi: 10.1073/pnas.0510991103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Murray J.D. Springer; Berlin, Germany: 1989. Mathematical Biology: I. An Introduction. [Google Scholar]
- 63.Carlson A., Mahadevan L. Elastohydrodynamics and kinetics of protein patterning in the immunological synapse. PLOS Comput. Biol. 2015;11:e1004481. doi: 10.1371/journal.pcbi.1004481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Biro M., Romeo Y., Paluch E.K. Cell cortex composition and homeostasis resolved by integrating proteomics and quantitative imaging. Cytoskeleton (Hoboken) 2013;70:741–754. doi: 10.1002/cm.21142. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
This movie corresponds to the parameters in Fig. 4 A.
This movie corresponds to Fig 2 B
Travel is unrestricted and the excitation spreads in all directions.
This movie corresponds to Fig. 4 B.
This movie corresponds to Fig. 6 A.