Low-dimensionality in gene expression data enables the accurate extraction of transcriptional programs from shallow sequencing

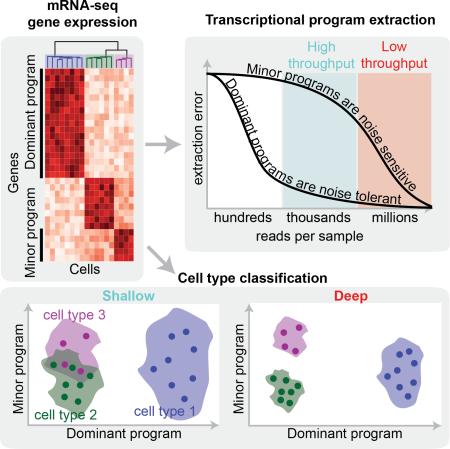
Summary

A tradeoff between precision and throughput constrains all biological measurements, including sequencing-based technologies. Here, we develop a mathematical framework that defines this tradeoff between mRNA-sequencing depth and error in the extraction of biological information. We find that transcriptional programs can be reproducibly identified at 1% of conventional read depths. We demonstrate that this resilience to noise of “shallow” sequencing derives from a natural property, low-dimensionality, that is a fundamental feature of gene expression data. Accordingly, our conclusions hold for ~350 single cell and bulk gene expression datasets across yeast, mouse and human. In total, our approach provides quantitative guidelines for the choice of sequencing depth necessary to achieve a desired level of analytical resolution; we codify these guidelines in an open source “Read Depth Calculator.” This work demonstrates that the structure inherent in biological networks can be productively exploited to increase measurement throughput, an idea that is now common in many branches of science such as image processing.

Graphical Abstract

Introduction

All measurements, including biological measurements, contain a trade-off between precision and throughput. In sequencing based measurements like mRNA-seq, measurement precision is determined largely by the sequencing depth applied to individual samples. At high sequencing depth, mRNA-seq can detect subtle changes in gene expression including the expression of rare splice variants or quantitative modulations in transcript abundance. However, such precision comes at a cost, and sequencing transcripts from 10,000 single cells at deep sequencing coverage (10⁶ reads per cell) currently requires two weeks of sequencing on a HiSeq 4000.

Not all biological questions require such extreme technical sensitivity. For example, a catalog of human cell types and the transcriptional programs that define them can potentially be generated by querying the general transcriptional state of single cells (Trapnell, 2015). In principle, theoretical and computational methods could elucidate the tradeoff between sequencing depth and granularity of the information that can be accurately extracted from samples. Accordingly, optimizing this tradeoff based on the granularity required by the biological question at hand would yield significant increases in the scale at which mRNA-seq can be applied, facilitating applications such as drug screening and whole organ or tumor profiling.

The modern engineering discipline of signal processing has demonstrated that structural properties of natural signals can often be exploited to enable new classes of low cost measurements. The central insight is that many natural signals are effectively “low dimensional”. Geometrically, this means that these signals lie on a noisy, low-dimensional manifold embedded in the observed, high-dimensional measurement space. Equivalently, this property indicates that there is a basis representation in which these signals can be accurately captured by a small number of basis vectors relative to the original measurement dimension (Donoho, 2006; Candès et al., 2006; Hinton et al., 2006). Modern algorithms exploit the fact that the number of measurements required to reconstruct a low dimensional signal can be far fewer than the apparent number of degrees of freedom. For example, in images of natural scenes, correlations between neighboring pixels induce an effective low dimensionality such that most images are dominated by low frequency content. This allows high accuracy image reconstruction even in the presence of considerable measurement noise such as point defects in many camera pixels (Duarte et al. 2008). For example, in images of natural scenes, correlations between neighboring pixels induce an effective low dimensionality that allows high accuracy image reconstruction even in the presence of considerable measurement noise such as point defects in many camera pixels (Duarte et al., 2008).

Like natural images, it has long been appreciated that biological systems contain structural features that can lead to an effective low dimensionality in data. Most notably, genes are commonly co-regulated within transcriptional modules; this produces covariation in the expression of many genes (Eisen et al., 1998; Segal et al., 2003; Bergmann, et al., 2003). The widespread presence of such modules indicates that the natural dimensionality of gene expression is not determined by the number of genes in the genome, but rather by the number of regulatory modules. By analogy to signal processing, this natural structure suggests that the lower effective dimensionality present in gene expression data can be exploited to make accurate, “inexpensive” measurements that are not degraded by noise. But when, and at what error tradeoff, can low dimensionality be leveraged to enable low cost, high information-content biological measurements?

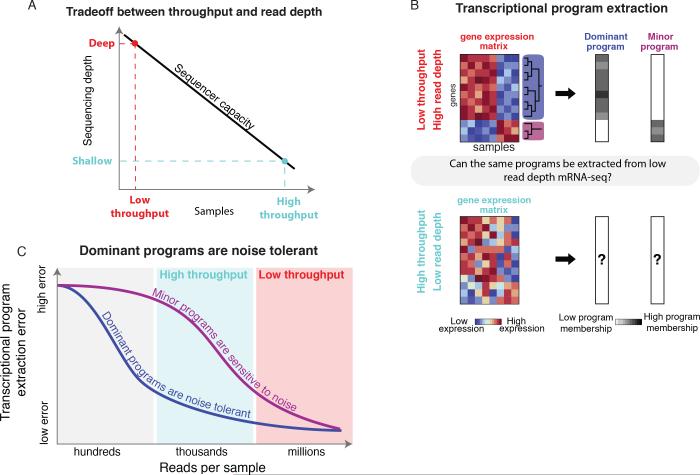
Here, inspired by these developments in signal processing, we establish a mathematical framework that addresses the impact of reducing coverage depth, and hence increasing measurement noise, on the reconstruction of transcriptional regulatory programs from mRNA-seq data. Our framework reveals that “shallow mRNA-seq”, which has been proposed to increase mRNA-seq throughput by reducing sequencing depth in individual samples (Jaitin et al., 2014; Pollen et al., 2014; Kliebenstein, 2012) (Figure 1A), can be applied generally to many bulk and single cell mRNA-seq experiments. By investigating the fundamental limits of shallow mRNA-seq, we define the conditions under which it has utility and complements deep sequencing.

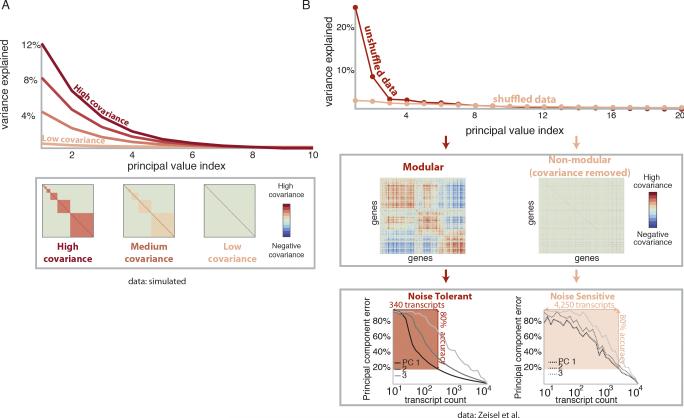
Figure 1. A mathematical model reveals factors determining the performance of shallow mRNA-seq.

(A) mRNA-seq throughput as a function of sequencing depth per sample for a typical sequencing capacity of 200 million reads.

(B) Unsupervised learning techniques are used to identify transcriptional programs. We ask when and why shallow mRNA-seq can accurately identify transcriptional programs.

(C) Decreasing sequencing depth adds measurement noise to the transcriptional programs identified by principal component analysis. Our approach reveals that dominant programs, defined as those that explain relatively large variances in the data, are tolerant to measurement noise.

Our analysis reveals that the dominance of a transcriptional program, quantified by the fraction of the variance it explains in the dataset, determines the read depth required to accurately extract it. We demonstrate that common bioinformatic analyses can be performed at 1% of traditional sequencing depths with little loss in inferred biological information at the level of transcriptional programs. We also introduce a simple “Read Depth Calculator” that determines optimal experimental parameters to achieve a desired analytical accuracy. Our framework and computational results highlight the effective low dimensionality of gene expression, commonly caused by co-regulation of genes, as both a fundamental feature of biological data and a major underpinning of biological signals’ tolerance to measurement noise (Figure 1B, 1C). Understanding the fundamental limits and tradeoffs involved in extracting information from mRNA-seq data will guide researchers in designing large-scale bulk mRNA-seq experiments and analyzing single-cell data where transcript coverage is inherently low.

Results

Statistical properties of gene expression data determine the accuracy of Principal Component Analysis at low read depth

To delineate the impact of sequencing depth on the analysis of mRNA-seq data, we developed a mathematical framework that models the performance of a common bioinformatics technique, transcriptional program identification, at low sequencing depth. We focus on transcriptional program identification as it is central in many analyses including gene set analysis, network reconstruction (Holter et al., 2001; Bonneau, 2008), and cancer classification (Alon et al., 1999; Shai et al., 2003; Patel et al., 2014), as well as the analysis of single cell mRNA-seq data. Our model defines exactly how reductions in read-depth corrupt the extracted transcriptional programs and determines the precise depth required to recover them with a desired accuracy.

Our analysis focuses on the identification of transcriptional programs from mRNA-seq data through Principal Components Analysis (PCA), because of its prevalence in gene expression analysis (Alter et al., 2000; Ringner, 2008) and its fundamental similarities to other commonly used methods. A recent review called PCA the most widely used method for unsupervised clustering and noted that it has already been successfully applied in many single-cell genomics contexts (Trapnell, 2015). Additionally, research in the computer science community over the last decade has shown that many other unsupervised learning methods, including k-means, spectral clustering, and locally linear embedding, are naturally related to PCA or its generalization, Kernel PCA (Ding et al., 2004; Ng et al., 2001; Ham et al., 2004; Bengio et al., 2004). Because of the deep connection between PCA and other unsupervised learning techniques, we expect that our conclusions in this section will extend to other methods of analysis (and we provide such parallel analysis in the supplementary information). Here, we focus on PCA because the well-defined theory behind it provides a unique opportunity to understand, analytically, the factors that determine the robustness of program identification to low coverage sequencing noise.

PCA identifies transcriptional programs by extracting groups of genes that co-vary across a set of samples. Co-varying genes are grouped into a gene expression vector known as a principal component. Principal components are weighted by their relative importance in capturing the gene expression variation that occurs in the underlying data. Decreasing sequencing depth introduces measurement noise into the gene expression data and corrupts the extracted principal components.

If the transcriptional programs obtained from shallow mRNA-seq data and deep mRNA-seq data are similar, then we can accurately perform many gene expression analyses at low depth while collecting data in much higher throughput (Figure 1). We therefore developed a mathematical model that quantifies how the principal components computed at low and high sequencing depths differ. The model reveals that performance of transcriptional program extraction at low read depth is specific to the dataset and even the program itself. It is the dominant transcriptional programs, which capture most variance, that are the most stable.

Formally, the principal components are defined as the eigenvectors of the gene expression covariance matrix, and the principal values λ_i are the associated eigenvalues that equal the variance of the data projected onto the component (Alter et al., 2000; Holter et al., 2001). We use perturbation theory to model how the eigenvectors of the gene expression covariance matrix change when measurement noise is added (Stewart et al., 1990; Shankar, 2012). We perform our analysis in units of normalized read counts for conceptual clarity (or normalized transcript counts where appropriate), but an identical analysis and error equation can be derived in FPKM units through a simple rescaling. The principal component error is defined as the deviation between the deep (pc_i) and shallow $\left(p{\widehat{c}}_i\right)$ principal components.

$$\mathrm{Principal}\mathrm{component}\mathrm{error}:\Vert {\mathit{pc}}_{\mathit{i}}-\mathit{p}{\widehat{\mathit{c}}}_{\mathit{i}}\Vert \approx \sqrt{{\sum }_{\mathit{j}\ne \mathit{i}}{\left(\frac{{\mathit{pc}}_{\mathit{i}}^{\mathit{T}}(\widehat{\mathit{C}}-\mathit{C}){\mathit{pc}}_{\mathit{j}}}{{\lambda }_{\mathit{i}}-{\lambda }_{\mathit{j}}}\right)}^2}$$ (1)

where C and Ĉ are the covariance matrices obtained from deep and shallow mRNA-seq data respectively. Equation 1 can be used to model the impact of shallow sequencing on any given mRNA-seq dataset. Moreover, qualitative analysis of the equation reveals the key factors that determine whether low depth profiling will accurately identify transcriptional programs. As expected, this equation indicates that the principal component error depends on generic features including read depth and sample number as these affect the difference between the shallow and deep covariance matrices in the numerator of Equation 1 (see Supplemental Information Section 2.1). However, Equation 1 also reveals that the principal component error depends on a system-specific property, the relative magnitude of the principal values (captured by λ_i - λ_j). Since the principal values correspond to the variance in the data along a principal component, this term quantifies whether the information in the gene expression data is concentrated among a few transcriptional programs. When genes covary along a small number of principal axes, the dataset has an effective low-dimensionality i.e. the data is concentrated on a low-dimensional sub-space, and transcriptional programs can be extracted even in the presence of sequencing noise.

Mouse tissues can be distinguished at low depth in bulk mRNA-seq samples

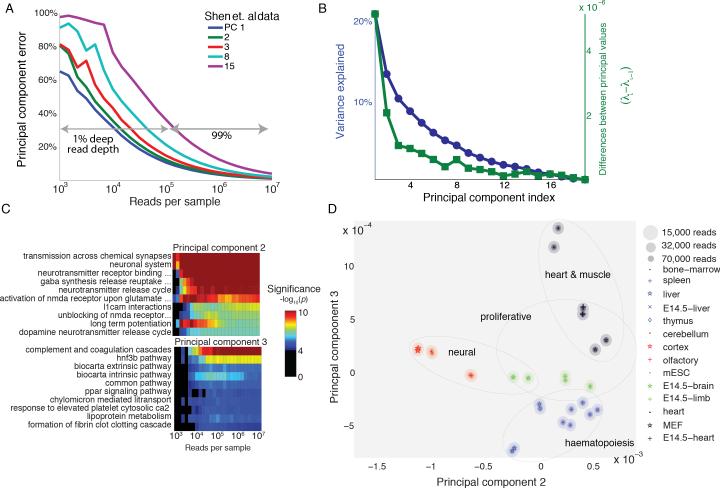
To understand the implications of this result in the context of an established mRNA-seq data set, we applied Equation 1 to a subset of the mouse ENCODE data that uses deep mRNA-seq (>10⁷ reads per sample) to profile gene expression of 19 different mouse tissues with a biological replicate (Shen et al. 2012) (see Experimental Procedures). The analysis revealed that the leading, dominant transcriptional programs could be extracted with less than 1% of the studies original read depth. Specifically, the first three principal components could be recovered with more than 80% accuracy (i.e. an error of 1−.8=20%) with just 55,000 reads per experiment (Figures 2A and S1A). To reach 80% accuracy for all of the first nine principal components, only 145,000 reads were needed (Figure S1B). Increasing read depth further had diminishing returns for principal component accuracy. To increase the accuracy of the first three principal components an additional 5% (from 80% to 85%), 55% more reads were required. We confirmed these analytical results by simulating shallow mRNA-seq through direct sub-sampling of reads from the raw data set (see Experimental Procedures).

Figure 2. Transcriptional states of mouse tissues are distinguishable at low read coverage.

(A) Principal component error as a function of read depth for selected principal components for the Shen et al. data. For first three principal components, 1% of the traditional read depth is sufficient for achieving >80% accuracy. Improvements in error exhibit diminishing returns as read depth is increased. Less dominant transcription programs (principal components 8 and 15 shown) are more sensitive to sequencing noise.

(B) Variance explained by transcriptional program (blue) and differences between principal values (green) of the Shen et al. data. The leading, dominant transcriptional programs have principal values that are well-separated from later principal values suggesting that these should be more robust to measurement noise.

(C) Gene Set Enrichment significance for the top ten terms of principal component two (top) and three (bottom) as a function of read depth. 32,000 reads are sufficient to recover all top ten terms in the first three principal components. (Analysis for first principal component shown in Figure S1D and S1E.)

(D) Projection of a subset of the Shen et al. tissue data onto principal components two and three. The ellipses represent uncertainty at specific reads depths. Similar tissues lie close together. Transcriptional program two separates neural tissues from non-neural tissues while transcriptional program three distinguishes tissues involved in haematopoiesis from other tissues. This is consistent with the GSEA of these transcriptional programs in (C).

Further, as predicted by Equation 1, the dominant principal components were more robust to shallow sequencing noise than the trailing, minor principal components. This is a direct consequence of the fact that the leading principal values are well-separated from other principal values, while the trailing values are spaced closely together. For instance, λ₁ is separated from other principal values by at least λ₁-λ₂≈5×10⁻⁶, more than two orders of magnitude greater than the minimum separation of λ₂₅ from other principal values, 1.5×10⁻⁸ (Figure 2B). Therefore the 25^th principal component requires almost four million reads, 140 times more than the first principal component, to be recovered with the same 80% accuracy.

To explore whether the shallow principal components also retained the same biological information as the programs computed from deep mRNA-seq data, we compared results from Gene Set Enrichment Analysis applied to shallow and deep mRNA-seq data. At a read depth of ~10⁷ reads per sample, the first three principal components have many significant functional enrichments with the second and third principal components enriched for neural and haematopoietic processes respectively (Figure 2C; see Figure S1C for first principal component). These functional enrichments corroborate the separation seen when the gene expression profiles from each tissue are projected onto the second and third principal components (see Experimental Procedures). Neural tissues (cerebellum, cortex, olfactory, and E-14.5 brain) project along the second principal component while the haematopoietic tissues (spleen, liver, thymus, bone marrow, and E-14.5 liver) project along the third principal component (Figure 2D).

The statistically significant enrichments of the first three principal components persisted at low sequencing depths. At less than 32,000 reads per sample, only 0.37% of the total reads, all ten of the top gene sets for these principal components passed our significance threshold of p<10⁻⁴ (negative predictive value and positive predictive value in Figures S1D,E). To put this result in perspective, using only 32,000 reads per sample (corresponding to PCA accuracies of 81%, 79% and 75% for the first three principal components respectively) would allow a faithful recapitulation of functional enrichments while still multiplexing thousands of samples, rather than dozens, in a single Illumina HiSeq sequencing lane. Additionally, this low number of reads was still sufficient to separate the different cell types (Figure 2D). We obtained similar results when working in FPKM units, suggesting that the broad conclusions of our analysis are insensitive to gene expression units (Figures S1F, S1G, S1H).

Transcriptional states in single cells are distinguishable with less than 1,000 transcripts per cell

We wanted to explore whether shallow mRNA-seq could also capture gene expression differences between individual single cells within a heterogeneous tissue, arguably a more challenging problem than distinguishing different bulk tissue samples. In addition to the biological importance of quantifying variability at the single cell level, single cell mRNA-seq data provides necessary context for analyzing the performance of shallow sequencing for two reasons. First, single cell mRNA-seq experiments are inherently “low depth” measurements as current methods can capture only a small fraction (~20%) (Shalek et al., 2014) of the ~300K transcripts (Velculescu et al., 1999) typically contained in individual cells. Second, since advances in microfluidics (Macosko et al., 2015) now facilitate the automated preparation of tens of thousands of individual cells for single cell mRNA-seq, sequencing requirements impose a key bottleneck on the further scaling of single-cell throughput.

To probe the impact of sequencing depth reductions on single cell mRNA-seq data, we analyzed a dataset characterizing 3,005 single cells from the mouse cerebral cortex and hippocampus (Zeisel et al., 2015) which were classified bioinformatically at full sequencing depth (average of ~15,000 unique transcripts per cell) into nine different neural and non-neural cell types. In addition to providing a rich biological context for analysis, this dataset allows for a quantitative analysis of low-depth transcriptional profiling as it incorporates molecular barcodes known as unique molecular identifiers (UMIs) that enable the precise counting of transcripts from each single cell. The Zeisel et al. data therefore allowed us to analyze the impact of sequencing depth reductions quantitatively in units of transcript counts rather than in the less precise unit of raw sequencing reads.

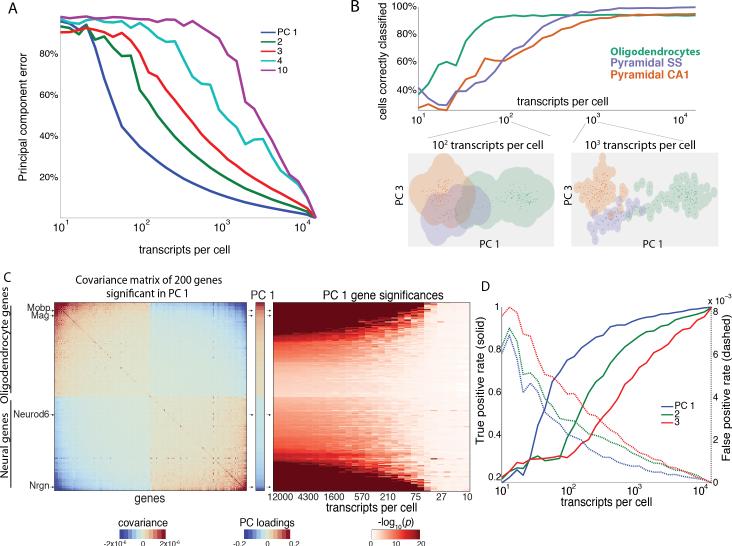
Similarly to the bulk tissue data, we found that leading principal components in single cells could be reconstructed with a small fraction of the total transcripts collected in the raw data set. We focused our analysis on three classes of cell types, two classes of pyramidal neurons with similar gene expression profiles, and oligodendrocytes, which are transcriptionally distinct. As the first three principal values were well-separated from the others (Figure S2A), Equation 1 estimated that the first three principal components could be reconstructed with 11%, 22%, and 38% error respectively with just 1000 transcripts per cell (Figure 3A).

Figure 3. Transcriptional states of single cells in the mouse brain are distinguishable at low transcript coverage.

(A) Principal component error as a function of read depth for selected principal components for the Zeisel et al. data.

(B) Accuracy of cell type classification as a function of transcripts per cell. Accuracy plateaus with increasing transcript coverage. At 1000 transcripts per cell, all three cell types can be distinguished with low error. At 100 transcripts per cell, pyramidal cells cannot be distinguished from each other, while oligodendrocytes remain distinct.

(C Left) Covariance matrix of genes with high absolute loadings in the first principal component. The genes with the 100 highest positive and 100 lowest negative loadings are displayed.

(C Middle) First principal component is enriched for genes indicative of oligodendrocytes and neurons.

(C Right) Genes significance as a function of transcript count for the first principal component.

(D) True and false detection rates as a function of transcript count for genes significantly associated with the first three principal components. Below 100 transcripts per cell, false positives are common.

We confirmed this result computationally. With just 100 unique transcripts, we were able to separate oligodendrocytes from the two classes of pyramidal neurons with >90% accuracy. With 1000 unique transcripts per cell, we were able to distinguish pyramidal neurons of the hippocampus from those of cortex with the same >90% accuracy (Figure 3B). The different depths required to distinguish these subclasses of neural and non-neural cell-types reflect the differing robustness of the corresponding principal components. The first principal component captures a broad distinction between oligodendrocytes and pyramidal cell types (Figure 3C Left) and is the most robust to low read depths. The third principal component captures a more fine-grained distinction between pyramidal neurons, but is less robust than the first principal component at low read depth, and hence requires more coverage. This is consistent with biological intuition: more depth is required to distinguish between pyramidal neural subtypes than between oligodendrocytes and pyramidal neurons.

We next asked how contributions of individual genes to a principal component change as a function of read depth. For every principal component, we derived a null model consisting of the distribution of the individual gene weightings, called loadings, from a shuffled version of the data (see Experimental Procedures). Comparing the data to the null model, we found that at a depth of ~340 transcripts, >80% of genes significantly associated with the first principal component could still be detected (Figure 3C, 3D and Experimental Procedures). At just 100 transcripts per cell, we were still able to identify oligodendroycte markers, such as myelin-associated oligodendrocyte basic protein (Mobp) and myelin-associated glycoprotein (Mag), as well as neural markers, such as Neuronal differentiation 6 (Neurod6) and Neurogranin (Nrgn), as statistically significant, and reliably classify these distinct cell types. However, below 100 transcripts per cell, cell type classification becomes inaccurate, and this is correlated with markers such as Neurod6 being no longer statistically associated with the first principal component.

We were able to reach similar conclusions with three other single cell mRNA-seq datasets (Shalek et al., 2013; Treutlein et al., 2014; Kumar et al., 2014). With similarly low sequencing depths, we were able to distinguish transcriptional states of single cells collected across stages of the developing mouse lung (Figure S2B-D), wild type mouse embryonic stem cells from stem cells with a single gene knockout (Figure S2E-G), and heterogeneity within a population of bone-marrow-derived dendritic cells (Figure S2H-J). These results were also not PCA specific. We additionally examined two of these datasets with t-SNE and LLE, two nonlinear alternatives to PCA, and achieved successful classification of transcriptional states (Figure S2K-L), in each case recapitulating the results of the original studies with fewer than 5000 reads per cell. These results suggest that low-dimensionality enables high accuracy classification at low-read depth across many methods.

Gene expression covariance induces tolerance to shallow sequencing noise

In the datasets we consider, the dominant noise-robust principal components corresponded directly to large modules of co-varying genes. Such modules are common in gene expression data (Eisen et al., 1998; Alter et al., 2000; Bergmann et al., 2003; Segal et al., 2003). We therefore studied the contribution of modularity to principal component robustness in a simple, mathematical model of gene expression (Supplemental Information Section 2.2). Our analysis showed that the variance explained by a principal component, and hence its noise tolerance, increases with the covariance of genes within the associated module (Figure 4A) and also the number of genes in the module (Figure S3A-C). While highly expressed genes also contribute to noise tolerance, in the Shen et al. data set we found little correlation between the expression level of a gene and its contribution to the error of the first principal component (R²=0.13, Figure S3D).

Figure 4. Modularity of gene expression enables accurate, low depth transcriptional program identification.

(A) Variance explained and covariance matrix for increasing gene expression covariance in a model.

(B) Variance explained by different principal components for the Zeisel et al. data set. (Middle) Covariance matrix shows large modules of covarying genes. (Bottom) Dominant transcriptional programs are robust to low-coverage profiling as predicted by model. Shuffling the dataset destroys the modular structure, resulting in noise-sensitive transcriptional programs. For the shuffled data, 4250 transcripts are required for 80% accuracy of the first three principal components, whereas 340 transcripts suffices for the original dataset.

This analysis predicts that the large groups of tightly co-varying genes observed in the Shen et al. and Zeisel et al. datasets will contribute significantly to principal value separation and noise tolerance. To directly quantify the contribution of covariance to principal value separation in these data, we randomly shuffled the sample labels for each gene. In the shuffled data, genes vary independently which eliminates gene-gene covariance, raising the effective dimensionality of the data. In contrast to the natural, low dimensional data, the principal values of the resulting data were nearly uniform in magnitude. This significantly diminished the differences between the leading principal values within the shuffled data (Figure 4B, top panel).

Consequently, reconstruction of the principal components became more read depth intensive. For instance to recover the first principal component with 80% accuracy from the shuffled Zeisel et al. data, 12.5 times more transcripts are required than for the unshuffled data (Figure 4B, bottom panels). We reached a similar conclusion for the mouse ENCODE data, where shuffling also decreased the differences between the leading principal values and the rest, causing a 23-fold increase in sequencing depth required to recover the first principal component with 90% accuracy (Figure S4).

Large-scale survey reveals that shallow mRNA-seq is widely applicable due to gene-gene covariance

Both our analysis of Equation 1 and our computational investigations of mRNA-seq datasets suggest that high gene-gene covariances increase the distance of leading principal values from the rest, thereby enabling the recovery of dominant principal components at low mRNA-seq read depths. This finding, if a common phenomenon, suggests that shallow mRNA-seq may be rigorously employed when answering many biological questions. To assess whether our findings are broadly applicable, we performed a broad computational survey of available gene expression data.

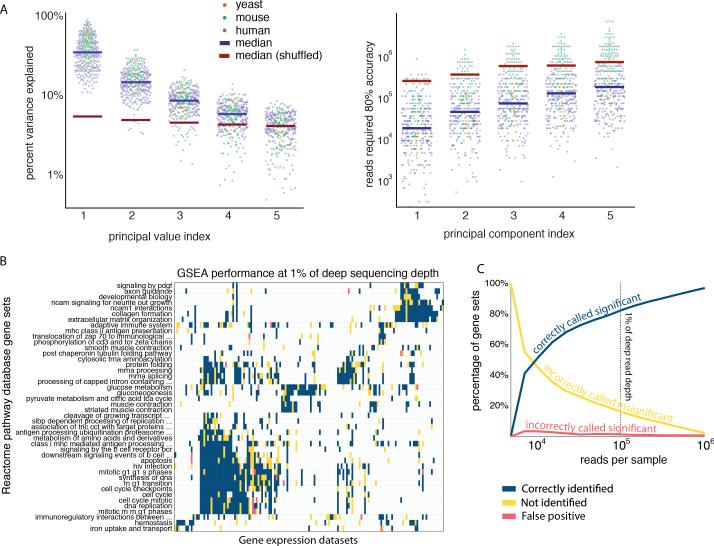
Since both gene covariances and principal values are fundamental properties of the biological systems under study, these quantities may be analyzed using the wealth of microarray datasets available, leveraging a larger collection of gene expression datasets as compared to mRNA-seq (see Figure S5A for analyses of several mRNA-seq datasets). We selected 352 gene expression datasets from the Gene Expression Omnibus (Edgar, et al., 2002) spanning three species (yeast: 20 datasets, mouse: 106 datasets, and human: 226 datasets) that each contained at least 20 samples and were performed on the Affymetrix platform.

Despite the differences between these datasets in terms of species and collection conditions, they all possessed favorable principal value distributions reflecting an effective low dimensionality. For instance, on average the first principal value was roughly twice as large as the second principal value, and together the first five principal values explained a significant majority of the variance, suggesting that these datasets contain a few, dominant principal components (Figure 5A, left panel). By shuffling these datasets to reorder the sample labels for each gene, we again found that these principal components emerge from gene-gene covariance.

Figure 5. Gene expression survey of 352 public datasets reveals broad tolerance of bioinformatics analysis to shallow profiling.

(A, left) Variance explained by the first five transcriptional programs of 352 published yeast, mouse, and human microarray datasets. Shuffling microarray datasets removes gene-gene covariance and destroys the relative dominance of the leading transcriptional programs.

(A, right) Read depth required to recover with 80% accuracy the first five principal components of the 352 datasets. Removing gene expression covariance from the data requires a median of ~10 times more reads to achieve the same accuracy.

(B) Accuracy of Gene Set Enrichment Analysis of the human microarray datasets at low read depth (100,000 reads, i.e. 1% deep depth). Reactome pathway database gene sets are correctly identified (blue) or not identified (yellow) at low read depth (false positives in red). ~80% of gene sets can be correctly recovered at 100,000 reads.

(C) Accuracy of Gene Set Enrichment Analysis as a function of read-depth.

We related this pattern of dominant principal components to the ability to recover biological information with shallow mRNA-seq in these datasets. To generate synthetic mRNA-seq data from these microarray datasets, we applied a probabilistic model to simulate mRNA-seq at a given read depth (see Experimental Procedures). We found that with only 60,000 reads per sample, 84% of the 352 datasets have ≤20% error in their first principal component. This translates into an average of almost 1000% read depth savings to recover the first principal component with an acceptable PCA error tolerance of 20% (Figure 5A right panel). By applying GSEA to the first principal component of each of the 352 datasets at low (100,000 reads per sample) and high-read depths (10 million reads per sample), we found that >60% of gene set enrichments were retained with only 1% of the reads (Figure 5B and 5C). This analysis demonstrates that biological information was also retained at low depth.

Collectively, our analyses demonstrate that the success of low-coverage sequencing relies on a few dominant transcriptional programs. We also show that many gene expression datasets contain such noise-resistant programs as determined by PCA and identified them with dominant dimensions in the dataset. Futhermore, low-dimensionality and noise-robustness are properties of the gene expression datasets themselves and exist independent of the choice of analysis technique. Therefore, unsupervised learning methods other than PCA would reach similar conclusions, an expectation we verified using Non-negative Matrix Factorization (Figure S5B).

The Read Depth Calculator: A quantitative framework for selecting optimal mRNA-seq read depth and number of biological samples

The optimal choice of read depth in an mRNA-seq experiment is of widespread practical relevance, therefore we developed a Read Depth Calculator that can provide quantitative guidelines for shallow mRNA-seq experimental design. Having pinpointed the factors that determine the applicability of shallow mRNA-seq, we applied this understanding to determine the read depth and number of biological samples to profile when designing an experiment. To do so, we simplified the principal component error described by Equation 1 by assuming that the principal values of mRNA-seq data are “well-separated”, i.e. that ratio between consecutive principal values λ_i+1/λ_i is small (as defined in Supplemental Information Section 2.1), an assumption justified by our large-scale microarray survey (See Figures S5C,D). These assumptions enable us to provide simple guidelines for making important experimental decisions, for example choosing read depth, N:

$$\mathit{N}\approx \frac{{\kappa }^2}{\mathit{n}{\lambda }_{\mathit{i}}{\Vert {\mathit{pc}}_{\mathit{i}}-\mathit{p}{\widehat{\mathit{c}}}_{\mathit{i}}\Vert }^2}$$ (2)

where n is the number of biological samples, κ is a constant that can be estimated from existing data. (See Supplemental Information Section 2.1 for a derivation of this equation and its limitations). This relationship can be understood intuitively. First, Equation 2 states that the principal component error decreases with read depth, a consequence of the well-known fact that the Signal-to-Noise ratio of a Poisson random variable is proportional to $\sqrt{N}$. The read depth also depends on λ_i which comes from the λ_i-λ_j term of Equation 1. Finally, the influence of the sample number n on read depth follows from the definition of covariance as an average over samples. (Figure S5E shows that n is approximately statistically uncorrelated with principal values across the microarray datasets.)

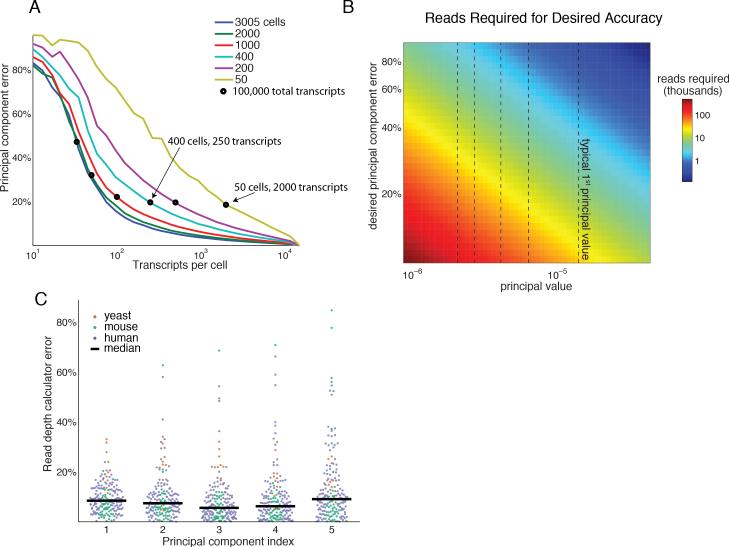
Equation 2 has implications for optimizing the tradeoff between read depth and sample number in single cell mRNA-seq experiments. As principal component error depends on the product of read depth and number of samples, error in mRNA-seq analyses can be reduced equivalently in two ways, by either increasing the total number of profiled cells or the transcript coverage. To illustrate this point, we computationally determined the error in the first principal component of the single cell mouse brain data from Zeisel et al. as a function of cell number. Consistent with Equation 2, our calculations show that increasing the number of profiled cells reduces error in the first principal component (Figure 6A). Furthermore, we show that with the Zeisel et al data, multiple different experimental configurations with the same total number of transcripts can yield the same principal component error. For example, 100,000 transcripts divided between either 50 or 400 cells both yield approximately a 20% principal component error. This result is of particular relevance in single cell experiments because transcript depth per cell is currently limited by a ~20% mRNA capture efficiency, and so cannot be easily increased (Shalek, et al., 2014). In such cases, limited sequencing resources might be best used to sequence more cells at low depth rather than allocating sequencing resources to oversampling a few thousand unique transcripts.

Figure 6. Mathematical framework provides a Read Depth Calculator and guidelines for shallow mRNA-seq experimental design.

(A) Error in the first principal component of the Zeisel et al. dataset for varying cell number and read-depth. Black circles denote a fixed number of total transcripts (100,000). Error can be reduced by either increasing transcript coverage or the number of cells profiled.

(B) Number of reads required (color) to achieve a desired error (y-axis) for a given principal value (x-axis). Typical principal values (dashed black vertical lines) are the medians across the 352 gene expression datasets.

(C) Error of the Read Depth Calculator (Equation 2) across 176 gene expression datasets used for validation (out of 352 total). The calculator predicts the number of reads to achieve 80% PCA accuracy in each dataset (colored dots). The predicted values closely agree with simulated results, with the median error <10% for the first five transcriptional programs.

Experimentalists can use the Read Depth Calculator to predict requirements for read depth or sample number in high throughput transcriptional profiling given their desired accuracy based on the statistics of principal value separation in our global survey. Figure 6B shows the reads required for desired accuracies and an assumed principal value for a human transcriptional experiment with 100 samples (typical values for the first five principal values for human are indicated in dashed lines). As an illustration, a hypothetical experiment with a typical first principal value of 1.4×10⁻⁵ (median principal value from the 226 human microarray datasets) and 100 samples where 80% PCA accuracy is tolerable requires less than 5,000 reads per experiment or less than 500,000 reads in total, occupying less than 0.125% of a single sequencing lane in the Illumina HiSeq 4000.

The predictions from this analytically derived Read Depth Calculator are demonstrably accurate. We compared the analytically predicted number of reads required for 80% PCA accuracy in the first five transcriptional programs to the value determined through simulated shallow mRNA-seq for 226 microarray and 4 mRNA-seq human datasets. We determined κ empirically by fitting 50% of the datasets. Cross-validation with the remaining 50% of the datasets showed remarkable agreement between the analytical predictions and computationally determined values. In these calculations, the analytically predicted number of reads required to reach 80% accuracy deviates from the depth required in simulation by less than 10% (Figure 6C). The Read Depth Calculator is available online (http://thomsonlab.github.io/html/formula.html).

Finally, while we use the first principal component for illustration, Equation 2 can be applied to any principal component, including the trailing principal components. Recent work discusses a statistical method to identify those principal components that are likely to be informative, and this work can be used in conjunction with Equation 2 to pinpoint the relevant principal components and the sequencing parameters needed to estimate them satisfactorily (Klein et al., 2015).

Discussion

Single cell transcriptional profiling is a technology that holds the promise of unlocking the inner workings of cells and uncovering the roots of their individuality (Klein et al. 2015; Macosko et al. 2015). We show that for many applications that rely on the determination of transcriptional programs, biological insights can be recapitulated at a fraction of the widely proposed high read depths. Our results are based on a rigorous mathematical framework that quantifies the tradeoff between read depth and accuracy of transcriptional program identification. Our analytical results pinpoint gene-gene covariance, a ubiquitous biological properties, as the key feature that enables uncompromised performance of unsupervised gene expression analysis at low read depth. The same mathematical framework also leads to practical methods to determine the optimal read depth and sample number for the design of mRNA-seq experiments.

Given the principal values that we observe in the human microarray datasets, our analysis suggests that one can profile tens of thousands of samples, as opposed to dozens, while still being able to accurately identify transcriptional programs. At this scale, researchers can perform entire chemical or genetic knockout screens or profile all ~1,000 cells in an entire C. elegans, 40 times over, in a single 400,000,000 read lane on the Illumina HiSeq 4000. Because shallow mRNA-based screens would provide information at the level of transcriptional programs and not individual genes, complementing these experiments by careful profiling of specific genes with targeted mRNA-seq (Fan, et al., 2015) or samples of interest with conventional deep sequencing would provide a more complete picture of the relevant biology.

Fundamentally, our results rely on a natural property of gene expression data: its effective “low-dimensionality.” We observed that gene expression datasets often have principal values that span orders of magnitude independently of the measurement platform, and that this property is responsible for the noise tolerance of early principal components. These leading, noise-robust principal components are effectively a small number of “dimensions” that dominate the biological phenomena under investigation. These insights are consistent with previous observations that were made following the advent of microarray technology (Eisen et al., 1998; Segal et al., 2003; Bergmann, et al., 2003), proposing that low dimensionality arises from extensive covariation in gene expression. We suggest that the covariances and principal values in gene expression are determined by the architectural properties of the underlying transcriptional networks, such as the co-regulation of genes, and therefore it is the biological system itself that confers noise tolerance in shallow mRNA-seq measurements. Related work in neuroscience has explored the implications of hierarchical network architecture for learning the dominant dimensions of data (Saxe, et al., 2013; Hinton et al., 2006).

Discovering and exploiting low-dimensionality to reduce uncertainty in measurements is at the heart of modern signal processing techniques (Donoho 2006; Candès, et al., 2006). These methods first found success in imaging applications, where low dimensionality arises from the statistics and redundancies of natural images, enabling most images to be accurately represented by a small number of wavelets or other basis functions. Our results suggest that shallow mRNA-seq is similarly enabled by an inherent low-dimensionality in gene expression datasets that emerges from groups of covarying genes. Just as only a few wavelets are needed to represent most images, only a few groups of transcriptional programs seem to be necessary to produce a coarse-grained representation of transcriptional state.

We believe that the measurement of many diverse biological systems could benefit from the identification and analysis of hidden low-dimensional representations. For instance, proteome quantification, protein-protein interactions, and human genetic variant data all contain high levels of correlations, suggesting these datasets may all be effectively low dimensional. We anticipate new modes of biological inquiry as advances from signal processing are integrated into biological data analysis and as the underlying structural features of biological networks are exploited for large scale measurements.

Experimental Procedures

Simulated shallow sequencing through down-sampling of reads

Transcriptional data sets were obtained from the Gene Expression Omnibus (Zeisel et al. was from www.linnarssonlab.org). mRNA_seq read counts were normalized by the total number of reads in the sample. For each read depth, we model the sequencing noise with a multinomial distribution. The Zeisel et al. data was sampled without replacement because of the unique molecular identifiers (See Supplemental Experimental Procedures).

Finding genes significantly associated with a principal component

We first generated a null-distribution of gene loadings from the principal components of a shuffled, transcript-count matrix. p-values were computed with respect to this distribution; averages over 15 replicates are reported.

Gene Set Enrichment Analysis

Gene Set Enrichment Analysis was performed with 1370 gene lists from MSigDB (Subramanian et al. 2005). The loadings of each principal component were collected in a distribution and loadings within 2 standard deviations from the mean of this distribution were considered for analysis. We applied a hypergeometric test with significance p-values cutoff of 10⁻⁴.