Conformational Heterogeneity Within the LID Domain Mediates Substrate Binding to Escherichia coli Adenylate Kinase: Function Follows Fluctuations

Abstract

Proteins exist as dynamic ensembles of molecules, implying that protein amino acid sequences evolved to code for both the ground state structure as well as the entire energy landscape of excited states. Accumulating theoretical and experimental evidence suggests that enzymes use such conformational fluctuations to facilitate allosteric processes important for substrate binding and possibly catalysis. This phenomenon can be clearly demonstrated in Escherichia coli adenylate kinase, where experimentally observed local unfolding of the LID subdomain, as opposed to a more commonly postulated rigid-body opening motion, is related to substrate binding. Because “entropy promoting” glycine mutations designed to increase specifically the local unfolding of the LID domain also affect substrate binding, changes in the excited energy landscape effectively tune the function of this enzyme without changing the ground state structure or the catalytic site. Thus, additional thermodynamic information, above and beyond the single folded structure of an enzyme–substrate complex, is likely required for a full and quantitative understanding of how enzymes work.

1 Introduction: The Invisible Excited State Energy Landscape Is Generally Important for Enzyme Allostery and Function: Is This Knowledge Relevant to Understanding Escherichia coli Adenylate Kinase?

1.1 An Emerging Relationship Between Protein Conformational Fluctuations and Enzymatic Function

Enzymes are ubiquitous catalysts for the chemical reactions of life [1–3]. In disease states resulting from altered chemistry, enzymes are often the targets of bioactive compounds and commercially available pharmaceuticals. As such, the fundamental importance of detailed and predictive understanding of enzymatic function is generally critical to the effectiveness of medicine as well as increased knowledge of the underlying biology. Much progress has been made in understanding the structure and mechanism of some enzymes, currently culminating in the ability to alter rationally function in limited favorable cases [2–4]. One outstandingly unique example of the successful application of understanding is the fully computational design of a novel enzyme [5].

Such progress has been incrementally achieved, building on more than a century of studies focused on enzyme reaction kinetics and the thermodynamic properties of enzyme–substrate interactions [6]. However, a predictive chemical and physical understanding of such parameters is limited, with insights being gained mostly from biological investigations of enzymatic adaptation [7, 8]. The present inability to modulate consistently and rationally classical enzymological observables by mutation highlights the true dearth of our collective understanding of such basic phenomena.

An emerging consensus in the field is that the lack of understanding of native state conformational fluctuations (i.e., dynamics) is at least one of the critical barriers to the physical understanding of enzymatic function [9]. Of late, numerous investigations have taken up this challenge [10–14]. Accepting this consensus, however, much remains unknown concerning the nature of the ensemble of interconverting functionally relevant conformations and the transition states governing the kinetics of these interconversions [15, 16].

1.2 Insights into Proteins from Investigating Conformational Fluctuations in the Native State Ensemble

One approach to addressing this issue (and the one adopted by our laboratory) has been to consider the functionally relevant native state of an enzyme to be approximated by the set of all possible equilibrium microstates generated by local unfolding of the protein [17–19]. The approach has proved to be successful in recapitulating, and in several cases quantitatively predicting diverse and seemingly unrelated properties of protein native states, including hydrogen exchange protection factors [20], allosteric communication between domains [21, 22], and global stability effects of pH [23] and denaturant [24].

Importantly, these investigations have given credence to the non-intuitive possibility that an ensemble of mostly folded (but containing segments that are highly disordered) states, experimentally indistinguishable from the equilibrium local unfolding model used in our theoretical approach, may indeed be critical for enzyme function and adaptation. The importance of these observations is twofold. First, important processes such as allostery can occur in the absence of a pathway of intraprotein communication that can be gleaned from analysis of the high resolution structure [21, 22, 25, 26], a strategy that dominates the biophysical analysis of function. Second, and equally important, changes in function can be modulated by changing the stability in different parts of the molecule, independent of the nature of the change, a phenomenon that is exemplified by the ability of surface mutations, for example, to modulate activity [27, 28]. As a consequence, the susceptibility of functional changes will be heterogeneously distributed throughout the protein in a way that may stand counter to intuitive notions of work being propagated in a mechanical way through the protein [29].

With regard to fluctuations and enzyme function, a still rich set of studies by Somero and colleagues [8, 30] has demonstrated the importance of enzyme conformational fluctuations through purely evolutionary considerations. In general, these studies have illuminated the amazing ability of enzymatic adaptation to recapitulate precisely the homeostatic K_m and k_cat at a wide variety of physiological temperatures. Intuitively, this process of adaptation may be imagined to involve point mutations that preserve similar active site structure in order to preserve the chemical function. Somero’s seminal contribution was the discovery of glycine (Gly) point mutations in lactate dehydrogenase that served to adapt the enzyme to psychrophilic conditions [8]. Indeed, these mutations were located outside the active site, suggesting conserved ground state structure and chemistry. Such mutants were hypothesized to function by adding more conformational entropy to the native state ensemble, implying that conformational states other than the ground state structure conferred the temperature adaptation. Given these observations, the natural questions then become: which conformational states besides the ground state are functionally relevant, and how can these invisible excited states be studied without affecting the catalytic activity of the ground state?

Inspired by such questions, our group has been working towards a comprehensive understanding of the native state of enzymes, and proteins in general, as the Boltzmann statistically weighted set of all possible conformational states of local unfolding. In the extreme cases, local unfolding of all residues within all states is equivalent to global unfolding of the molecule, and no local unfolding within any state is equivalent to a single ground state conformation, such as the X-ray crystal structure. In our view, quantitation of the populations of conformational states that exist between these two extremes, which have been largely ignored in most other work, turn out to be crucial for understanding how enzymes may function, adapt, and evolve [31]. In the following chapter we elaborate on experimental results [27] that document local unfolding in the native state ensemble of adenylate kinase (AK) and the implications thereof for biological function (substrate binding and possibly catalysis) and evolutionary adaptation [28].

1.3 Domain Structure of Adenylate Kinase: How Relevant Is the LID Domain to Structure and Function?

AK has been studied in detail for decades by many groups, and much is known about its structure, function, chemical kinetics, and taxonomy [11, 32–38]. AK catalyzes the reversible Mg²⁺ dependent phosphoryl transfer reaction ATP + AMP ↔ 2ADP [39], and consequently plays a primary role in maintaining proper cellular energy balance.

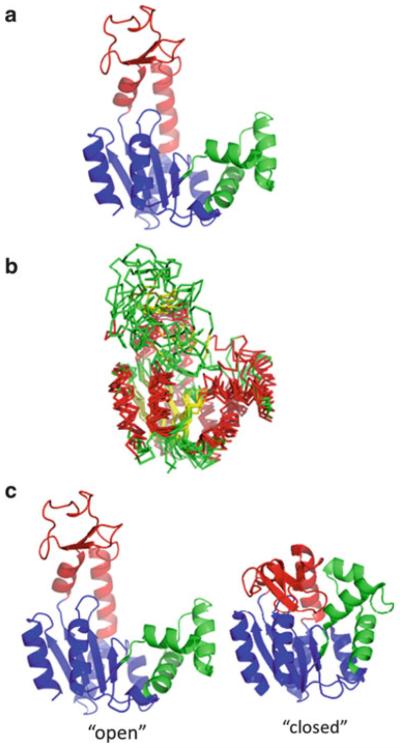
The enzyme has a structure composed of up to three domains: a “CORE” domain important for overall stability, which also contains the catalytic residues critical to phosphoryl-transfer, an “AMPbd” domain containing the AMP and ATP substrate binding sites, and an optional “LID” domain that increases catalytic efficiency by covering the binding sites (Fig. 1a). Although the known structures document conformational heterogeneity of the LID domain (Fig. 1b), central to most experimental interpretations [11, 12, 32] and computational simulations [40–46] are X-ray crystal structures of an “open” state [33] where the LID domain is away from the AMPbd domain and a “closed” state [34] where the LID domain closely contacts the AMPbd and CORE domains, enclosing substrate (Fig. 1c). In particular, most computational work treats the reaction coordinate of AK as a hinged rigid-body movement between the open and closed states. As will become clear in the following analysis, our experimental data [27, 28] directly challenge this popular interpretation for the Escherichia coli form of the enzyme, AK(e).

Fig. 1.

Domain structure and conformational heterogeneity in E. coli adenylate kinase [AK(e)]. (a) The enzyme is composed of three domains: a CORE domain (blue, residues 1–28, 73–112, 177–214, PDB ID 4AKE), a AMPbd domain (green, residues 28–72), and a LID domain (red, residues 113–176). (b) Multiple superposition of various known apo structures of AK demonstrating conformational heterogeneity of the LID. PDB structures 1AK2, 1E4V, 2AR7, 2RH5, 2XB4, 3GMT, 3NDP, each pairwise superimposed on 4AKE, the AK(e) structure are displayed. Helices are colored red, strands yellow, and loops green. Optimal pairwise superpositions of each structure with apo AK(e) (PDB ID 4AKE) were performed with TM-align [70] and displayed with pyMOL (Schrödinger, Inc., New York). (c) Commonly assumed “open” and “closed” structures of AK(e), based on PDB structures 4AKE and 1AKE, respectively. Coloring is identical to (a)

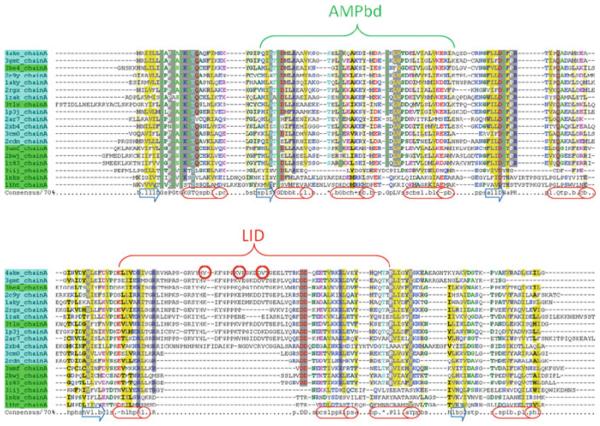
While not frequently addressed, taxonomic evidence also calls into question the importance of rigid-body LID movement for the reaction proper. Comparison of amino acid sequences and crystal structures for AK from many species demonstrates that the LID domain is not essential for a functional enzyme [38, 47]. Although there are exceptions, notably for mitochondrial AK [37], an organizing trend in these data is that eukaryotic AKs lack some or the entire LID, while prokaryotic forms contain the LID (Fig. 2). Thus, an interesting speculation is that an optional LID domain is an evolutionary innovation, of marginal importance for catalytic function per se but of great importance for regulation or “fine-tuning” of the existing function. In other words, the rigid opening and closing of a catalytically non-essential LID, the focus of so much computational attention, may not necessarily be investigating the most biologically important adaptation. This proposal is firmly supported by the experimental evidence for functionally relevant local unfolding in AK(e), described below.

Fig. 2.

Well known diversity of homologous AK amino acid sequences: “short” and “long” forms. All adenylate kinase structures were retrieved from the Protein Data Bank (PDB) [71]. Amino acid sequences corresponding to each structure were extracted and clustered at 60% identity using the CD-HIT webserver [72]. Representatives from each cluster were aligned using PROMALS3D [73] and colored with CHROMA [74]. Locations of structural helices are marked with red cylinders and strands by blue arrows. Prokaryotic or eukaryotic mitochondrial and chloroplast sequences are indicated by cyan and eukaryotic cytosolic sequences by green. Domain structure referred to in Fig. 1a is labeled. Sites of three “entropy-promoting” valine to glycine mutations in the LID domain of AK(e), discussed in detail later in the text, are indicated by red circles

2 Revealing an Enzyme’s Invisible Excited State Energy Landscape: Deploying Surface Glycine Mutations as Selective Probes Decoupling the Ground State from Temperature-Dependent Fluctuations

2.1 A Creative Mutation Strategy Based on Entropic Stabilization of Excited Conformational States

In order to investigate how similar native state conformational fluctuations are to unfolding reactions, and to uncover the functional significance of such local unfolding for binding or catalysis, consider the following set of experiments designed to amplify and examine fluctuations in AK(e). The goal of this mutation strategy was to probe selectively the conformational manifold of states that comprise various states of the LID domain, in search of states that both resemble local unfolding and are relevant to substrate binding. To accomplish this goal, point mutations were carefully chosen to promote excited states without disturbing the structural or catalytic properties of the fully folded ground state. As discussed above, this mutation strategy could be considered an in vitro reflection of a natural strategy observed in the functional adaptation of lactate dehydrogenase [8].

In principle, the energetic promotion of unfolded or excited states could be affected purely by changes in the denatured state itself, with no energetic or structural perturbation to the folded conformation. A good example of this principle is the thermodynamic mechanism by which denaturants destabilize protein folds [48]. Urea, for example, stabilizes both the native and denatured states of proteins in water. The apparent destabilization of the folded conformation results from the greater stabilization of the denatured state, due to the much larger amount of surface area exposed therein [48]. To effect such a change by point mutation, the specific properties of amino acids that are greatly expressed in the denatured state and weakly expressed in the folded state must be considered. In the denatured state, peptides quasi-randomly search through available conformational degrees of freedom because of the presence of many rotatable bonds. The restriction of this conformational freedom is manifest as the large unfavorable entropy of protein folding [49]. The beta-branched amino acids valine (Val) and isoleucine (Ile) are known to have a relatively small decrease in conformational entropy upon unfolding, due to steric collisions of their bulky side chains in the denatured state [49, 50]. The absence of a side chain in Gly, on the other hand, results in a comparatively large increase in the conformational entropy of unfolding [49]. Therefore, Val to Gly point mutations should, in principle, decrease the stability of a protein’s folded structure by increasing the conformational entropy of the denatured state.

Unlike structure-based mutagenesis that stabilizes or destabilizes multiple interactions within the folded state of a protein, one advantage of this selective denatured state approach is that the expected stability change can be quantitatively estimated. Moreover, as the change is entirely due to conformational entropy, the stability change can actually be accurately simulated using a conceptually simple algorithm based on hard-sphere collision of atomic radii and well known geometric features of polypeptides such as bond lengths and angles [28, 51, 52]. Such a simulation was performed for pairs of unstructured host pentamers in which the central residue was either Gly or not-Gly (e.g., Ala or Val). An ensemble of denatured state conformations was constructed for each pentamer by sampling a uniform distribution of φ and ϕ torsions n_test times and retaining only those n_allowed conformations that did not sterically clash [28]. Then, the ratio of available conformational space for each pentamer was calculated as described previously [53]:

$${\Omega }_{\text{Ala}-\text{Gly}}=\frac{[n_{\text{allowed},\text{Ala}}∕n_{\text{test},\text{Ala}}]}{[n_{\text{allowed},\text{Gly}}∕n_{\text{test},\text{Gly}}]}$$ (1)

The expected change in entropy could then be estimated through the expression [53]

$$\Delta \Delta S_{\text{Ala}-\text{Gly}}=-R\ln \left[{\Omega }_{\text{Ala}-\text{Gly}}\right]$$ (2)

According to this analysis, the conformational entropy difference obtained when Ala is mutated to Gly is 2.2 cal/(mol K) (Table 1), a value similar to that measured from calorimetric protein unfolding experiments (2.3–2.7 cal/(mol K) [49]). Simulations involving Val result in an even larger gain of entropy (Table 1). For this latter mutation, the difference is approximately 0.9 kcal/mol at 25°C. In short, these studies reveal that mutations either from Ala or Val to Gly can affect the conformational entropy of a disordered state by almost 1.0 kcal/mol, even if the change does not affect the stabilizing non-covalent interactions in either state. This observation can be put to use in the search for locally unfolded states in AK(e).

Table 1.

Simulation of the relative conformational space available upon glycine mutation in a disordered peptide

Host–guest pentapeptide pair	Ω X-Gly	ΔΔSX-Gly (cal/(mol K))
[AAAAA]–[AAGAA]	3.03	2.20
[AAVAA]–[AAGAA]	4.28	2.89

All simulations were performed using MPMOD software [28, 51, 52]. Equal probabilities were assumed for all valine rotamers. Atomic radii were taken from published values [76–78]

Having a substantial expected entropy change, Val to Gly mutations at various surface exposed positions in the AK(e) LID domain were selected for experimental test. As discussed, this type of mutation would be expected to increase the conformational entropy associated with unfolding this region of the protein, if indeed locally unfolded states were already significantly populated in the native state ensemble. Several objective criteria were defined for selecting mutation positions, such that the expected energetic effects would exclusively perturb the denatured state conformational entropy rather than the folded protein structure. These criteria were (1) the side chains of the mutated residues were highly surface exposed, involving no or few intermolecular contacts, (2) the side chains did not contain charged or polar groups that might contribute to important hydrogen bonds or longrange electrostatics, and (3) the mutated residues were at least 8 Ådisant from the active site, thus ensuring no contact with ligand. Ideally, such a strategy would be expected not to disturb any stabilizing contacts in the folded structure, not to disturb any contacts between enzyme and ligand, and not to disturb essential catalytic chemistry. Thus, it was also expected that little or no perturbation would occur to the structure of the bound complex. Although other positions in the AK(e) LID domain could potentially satisfy these requirements, three positions were selected for further study: Val 135, Val 142, and Val 148 (Fig. 3). These three surface exposed valines were experimentally mutated to Gly.

Fig. 3.

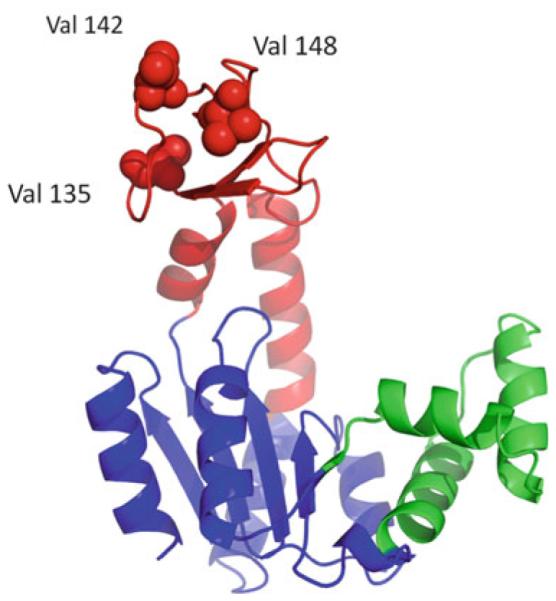
Three surface exposed valine to glycine entropy promoting mutations in the AK(e) LID domain. Domain colors are as given in Fig. 1a. The locations of the mutations, not expected to affect the folded ground state structure of the enzyme, are shown as space filling spheres

2.2 Entropy Promoting Mutations Do Not Perturb the Enzyme Ground State Structure of AK(e)

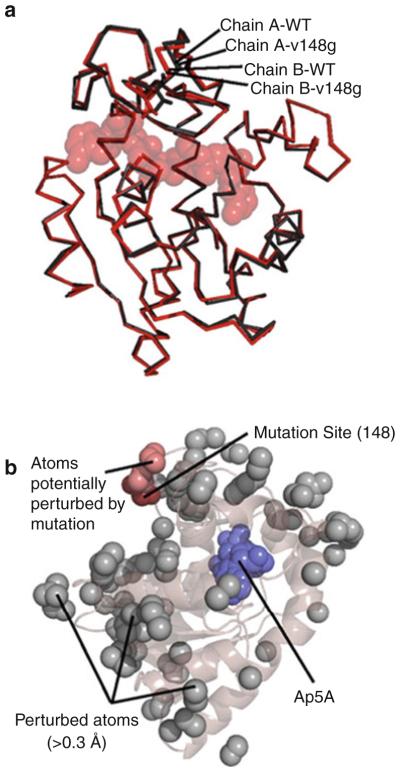
Did the entropy-promoting mutations actually preserve the ground state structure of AK(e)? Careful comparison of X-ray structures of the wild-type enzyme bound complex with the mutant V148G bound complex, demonstrates an affirmative answer to this question. Such a detailed comparison was possible due to the fortunate crystallization of both systems in the same (P2,2,2) space group and asymmetric unit. The all-atom RMSD between wild-type and mutant structures is quite small, approximately 0.2 Å. This value was, surprisingly, less than the approximately 0.4 ÅRMSD obtained between the two distinct molecular copies in the respective asymmetric units (Fig. 4a). Crystal packing effects on each structure could be quantitatively assessed and were also found to be minimal (Fig. 4a). Excluding such artifacts, atomic positions that were potentially different (>0.3 Å) between the optimally aligned structures of V148G and wild-type are highlighted in Fig. 4b. According to the figure, the mutation site clearly did not exhibit increased structural differences relative to the rest of the molecule. In particular, the active site region around the Ap5A was not disproportionally affected by structural changes. Also, most of the atoms that did show small structure differences were localized to surface exposed side chains (Fig. 4b), where increased mobility likely resulted in a poorer determination of electron density. Within the experimental resolution, it appeared that the mutation strategy was indeed successful at preserving the ground state structure.

Fig. 4.

The ground state structure of AK(e) is unaffected by entropy-promoting LID mutations. (a) Structural alignment of the experimentally determined crystal structures of wild-type (PDB ID 3HPQ) and mutant V148G (PDB ID 3HPR). Shown in red are chains of each protein from positions A of their respective asymmetric units, and shown in black are chains from positions B. Substrate analog Ap5A is shown in spacefill. (b) Analysis of possible structural perturbations due to mutation. The gray spheres represent all atoms that move >0.3 Åfrom the wild-type to the mutant structure in both copies within the asymmetric unit. The dark red spheres show the mutation site V148G. The light red spheres show all perturbed atoms (gray) that can be connected to the mutation site by a continuous chain of no more than 6 Åper step of other perturbed atoms. Ap5A is shown in blue spacefill

Global unfolding experiments monitored by circular dichroism (CD) also corroborated that the ground state structure was preserved for these mutants. Two state thermodynamic analysis of the data revealed that the apparent melting temperatures (T_m) of all mutants were decreased by less than 1.5°C relative to wild-type (Fig. 5). These results are consistent with the expected effects of the entropy promoting mutations in two ways. First, the global stability, as estimated by the T_m, was minimally affected by mutations (Fig. 5, inset), suggesting that the ground state structures of all mutants were minimally affected. Second, all mutants slightly destabilized the structure relative to wild-type, as predicted if the conformational entropy of the denatured states were actually increased, as described above.

Fig. 5.

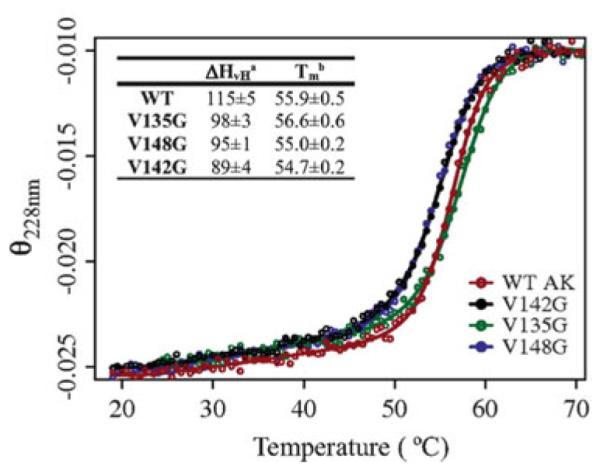
Thermal unfolding monitored by circular dichroism for wild-type AK(e) and mutants, global stability was minimally affected. Signal was monitored at 228 nm and is given in units of (degrees cm²)/(dmol res). Denatured state signals are normalized to a common value to aid interpretation. Smooth lines result from fits of the data points to a two-state thermodynamic model. The inset table shows thermodynamic parameters obtained from the two-state fits: superscript a is the van’t Hoff enthalpy in kcal/mol at the transition midpoint temperature T_m (superscript b)

3 The AK(e) Energy Landscape: Experimental Evidence for Local Unfolding of the LID Domain

3.1 Exchange Broadening Observed in 2D NMR Spectrum of the Mutant LID Domain

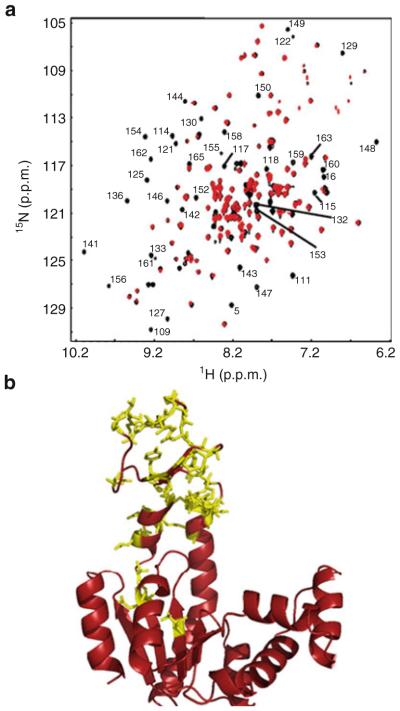
If indeed these mutations minimally perturbed the ground state of AK(e), how could their effects on excited states be described and quantified? One clue came from comparison of the NMR ¹H–¹⁵N HSQC spectra of wild-type and the mutant V142G, both in the absence of ligand. These data provided a site-resolved view of possible structural or dynamic changes caused by the mutation. In agreement with the crystallographic results, most amide resonances throughout the wild-type and mutant proteins exhibited respective peaks with similar location and intensity (Fig. 6a), suggesting overall similarity of the ground state conformation. However, closer inspection of these data indicated that a number of peaks essentially disappeared in the mutant spectrum (Fig. 6a). Interestingly, no new resonances appeared in the mutant, and the missing resonances reappeared at lower temperature (data not shown), suggesting both that the ground state structure was not altered and that no new structure, such as a “closed” LID domain, was substantially populated as a result of the mutation. The most probable explanation for these observations was that a chemical exchange process had broadened the peaks beyond detection. All except two of the broadened and assignable residues were consecutive in sequence from position 109 to 165 (Fig. 6b). This suggested that the mutation was affecting a large region of the protein, encompassing the LID domain. We also observed that the HSQC spectra of the other two mutants, V135G and V148G, were qualitatively similar in terms of peak broadening in the LID domain (data not shown). This last result might also be expected if all three mutants were involved in the same physical process, in other words all promoting the same gain of denatured state conformational entropy in the LID domain.

Fig. 6.

NMR results implicating LID domain effects due to entropy promoting mutations. (a) ¹H–¹⁵N HSQC spectra of wild-type (black) and mutant V142G AK(e) at 33°C. Labels indicate those residues that were assignable from published values [75] and also exhibited measurable intensity in the wild-type spectrum but no measurable intensity in V142G. (b) The same residues labeled in Fig. 6a are shown as yellow sticks, projected onto the “open” conformation of AK(e) (PDB ID 4AKE)

3.2 NMR Relaxation Dispersion Is Not Consistent with Rigid-Body Opening and Closing of the LID Domain

To explore the possibility that the entropy promoting mutants affect a conformational exchange process, NMR relaxation dispersion experiments (¹⁵N Carr-Purcell-Meiboom-Gill, CPMG [54–56]) were performed on the V142G protein. Under the assumption of a two state conformational exchange process on the microsecond to millisecond time scale, CPMG profiles can estimate the chemical shifts of the two conformations, the populations of each conformation, and the rates of interconversion between them. (It is noted in passing that these experiments have been used with good effect to measure other properties of AK(e), such as the conformational change under saturation of ligand, and the conformational transition relevant to product release [11].)

In general, conformational transitions between two kinetically distinct substates A and B in a protein’s energy landscape result from changes in atomic motions. If these transitions are both fast relative to the NMR timescale and occur between different magnetic environments such that a chemical shift difference Δω can be detected, populations of the states p_A and p_B can be estimated from the following basic equations [57]:

$$R_{2,\text{eff}}=R_{20}+R_{\text{ex}}$$ (3)

In these equations, R₂₀ is the intrinsic relaxation in the absence of chemical exchange, R_ex is the chemical exchange contribution to R_2,eff, the observed transverse relaxation rate, and k_ex is the sum of the forward (k_AB) and reverse (k_BA) rate constants.

Variables p_A, p_B, k_AB, and k_BA were extracted from relaxation–dispersion experiments using the procedure described by Vallurupalli and Kay [58] as summarized in the following. First, R_2,eff was measured for each resonance from the difference in intensities between spectra collected in the absence (I_reference) and presence (I_vCPMG) of a constant time relaxation element of duration T:

$$R_{\text{ex}}~\frac{p_{\text{A}}{p}_{\text{B}}\Delta {\omega }^2}{k_{\text{ex}}}$$ (4)

Next, the individual contributions to R_2,eff, as expressed in the Bloch–McConnell equations [59] were obtained by minimizing the chi-squared value (χ²) of the following equation:

$$R_{2,\text{eff}}=\frac{1}{T}\ln \left(\frac{I_{\text{vCPMG}}}{I_{\text{reference}}}\right)$$ (5)

In (6), R_2,eff is the measured value from (5) and σ_R2,eff is the error in said value, estimated by propagating through (5) the standard deviation of the average noise observed in the spectra. $R_{2,\text{eff}}^{\text{calc}}$ was calculated by numerical solution of the Bloch–McConnell equations, assuming ideal CPMG refocusing pulses, with the summation over all increments of vCPMG. Finally, values of k_AB and k_BA were calculated from the values of k_ex and p_B obtained from the fitting results of (6) according to the relations k_AB = k_ex/p_B, k_ex = k_AB + k_BA, and k_BA = k_ex/p_A. In this analysis, states A and B corresponded to conformational states of the LID domain such that state A was folded and state B was unfolded, as noted in Table 2.

Table 2.

CPMG results for LID domain residues of apo V142G AK(e)

Residue	kunfolding (S−1)a	kfolding (S−1)a	Punfolded (%)b	Δω (ppm)c	(χ2)/Nd
125	18 ± 1	570 ± 100	3.0 ± 0.6	3.29	1.4 ± 0.4
130	31 ± 3	670 ± 46	4.4 ± 0.4	1.70	1.9 ± 0.0
141	28 ± 5	600 ± 120	4.5 ± 0.1	2.35	1.2 ± 0.3
142	13 ± 1	140 ± 36	8.5 ± 0.2	2.08	2.8 ± 0.3
143	24 ± 1	660 ± 22	3.5 ± 0.1	2.86	3.0 ± 1.7
146	12 ± 4	200 ± 150	5.7 ± 4.5	1.30	1.1 ± 0.7
148	20 ± 1	290 ± 72	6.5 ± 0.1	4.60	1.4 ± 0.4
159	19 ± 6	530 ± 430	3.5 ± 0.3	4.10	0.7 ± 0.1
Global fit	19 ± 0	420 ± 27	4.3 ± 0.3	N/A	2.0 ± 0.4

^aAverage rate constants and standard error from three direct repeats of complete experimental and fitting procedure (TP Schrank, A Majumbar, unpublished results). Experimental conditions were 19°C in the absence of substrate

^bCalculated from the presumed rate constants, with propagated standard error

^cThe expected change in chemical shift upon unfolding this residue, based on random coil values [60, 79]

^dAverage and standard deviation of the reduced chi-squared value for the three individual fits

Under apo conditions, the CPMG data for V142G revealed two interesting findings. First, all of the residues in the LID domain could be well fitted (either individually or globally) to a common two state process (Fig. 7, Table 2). Importantly, the Δω used in these fits assumed a transition between the chemical shifts for the folded AK(e) and random coil chemical shifts for all residues [60]. This observed common process was therefore consistent with an equilibrium between the wild-type folded structure and a random-coil-like unfolded structure. Second, the unfolded LID domain was significantly populated to a level of approximately 3–9% in the V142G mutant at 19°C (Table 2). These results are particularly striking because they suggested that the LID domain could independently unfold to a random-coil-like state, in stark contrast to the usual depiction of AK(e) LID motion as a rigid-body open and closing.

Fig. 7.

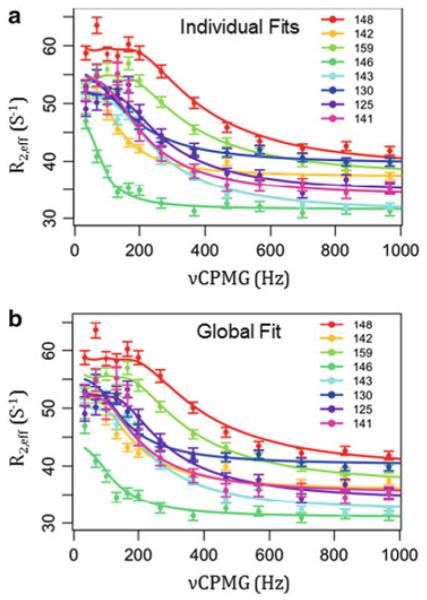
CPMG results for apo V142G are consistent with all-or-none local unfolding of the LID domain. (a) Individual fits of the data, i.e., data points for each residue are fitted to (6) to obtain many sets of fitted parameters. These fitted parameters are individually listed in Table 2. (b) Global fit of all data points from all residues to a hypothetical two state transition between folded AK(e) and random coil chemical shifts. This one set of fitted parameters is given in Table 2 in the row labeled “Global”. Relaxation dispersion data was collected for apo V142G AK(e) at 19°C in 50 mM MOPS, 50 mM NaCl, 20 mM MgCl₂, 5% glycerol, 8 mM DTT, 8 mM TCEP, pH 7.85. Data were collected at both 800 and 600 MHz field strength; 800 MHz results are displayed

3.3 Local Unfolding of the AK(e) LID Domain Is Essential for Substrate Binding

The “closed” conformation of AK(e) (Fig. 8) suggests that access of substrate to the binding site is sterically blocked relative to the “open” conformation. Could a local unfolding event like that observed (and apparently affected by the surface exposed mutations) be important for substrate binding and possibly catalytic function?

Fig. 8.

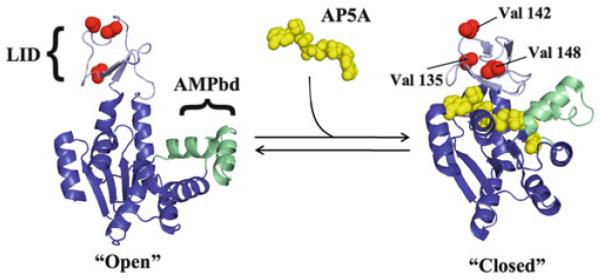
Schematic equilibrium of binding Ap5A to structurally open and closed AK(e). Global conformations, domain structure, and locations of entropy-promoting LID domain mutations are displayed. Bisubstrate analog P¹,P⁵-di(adenosine-5′) pentaphosphate (Ap5A) is shown in yellow. Note that even in the global “closed” conformation the locations of all three valines are solvent exposed

To ascertain the impact of the mutations on substrate binding, isothermal titration calorimetry (ITC) experiments were used to measure the binding between AK(e) and the bisubstrate analog P¹,P⁵-di(adenosine-5′) pentaphosphate (Ap5A, Fig. 8).

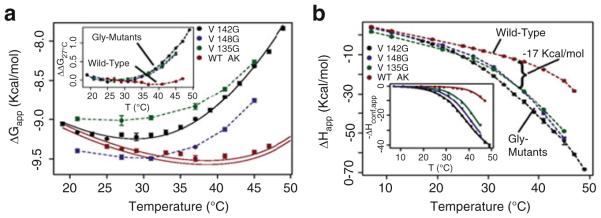
All three mutants resulted in substantial changes in the thermodynamics of binding. At 37°C and above, all mutations decreased binding affinity of the substrate analog (Fig. 9a), while simultaneously effecting large increases in the favorable enthalpy of binding (Fig. 9b). The observed temperature dependencies of the binding affinities were similar among all the mutants but different from wild-type AK(e) (Fig. 9a, inset). The binding enthalpies were also similar among the mutants but different from wild-type (Fig. 9b). Taken together with the global stability and local unfolding results described in previous sections, all three mutants were likely manifesting these functional changes by a similar mechanism.

Fig. 9.

Surface mutations affect the thermodynamics of binding. (a) Apparent free energy (ΔG_app) of binding substrate analog Ap5A. Solid black line shows the fitted curve for V142G data. Solid red lines represent the prediction of wild-type data based on the fitting of ΔH_conf,app. Error bars show the average standard error of the prediction. The inset displays the change in ΔG_app for each protein referenced with respect to 27°C: ΔΔG^27°C(T) = ΔG(T) – ΔG(27°C), clearly demonstrating the similar effects of each mutant on binding. (b) Apparent enthalpy of binding (ΔH_app) Ap5A; similar changes are evident for all mutants. The inset shows corrected data and fits for ΔH_conf,app (6)

The most straightforward interpretation of the ITC results is to postulate that the binding reaction is coupled to a conformational equilibrium that could be modulated by the entropy-promoting mutations. An expression articulating this idea is an association reaction where a “binding incompetent” (BI) state, having little or no affinity for substrate, is in equilibrium with a “binding competent” (BC) high-affinity state. The addition of substrate promotes the population of the BC state through mass action [61]. The apparent free energy would thus consist of two terms [27]:

$${\chi }^2=\sum _{\text{vCPMG}}\frac{{[R_{2,\text{eff}}\left(\text{vCPMG}\right)-R_{2,\text{eff}}^{\text{calc}}\left(\text{vCPMG}\right)]}^2}{{\left[{\sigma }_{R_{2,\text{eff}}}\left(\text{vCPMG}\right)\right]}^2}$$ (6)

In (7) the first term represents the intrinsic free energy of interaction between the BC state and the substrate and the second term accounts for the apparent contribution of the conformational equilibrium between the BI and BC states to the free energy.

Similarly, the binding enthalpy of the equilibrium also has two terms [27]:

$$\begin{array}{cc}\hfill \Delta G_{\text{app}}\left(T\right)& =\Delta G_0\left(T\right)-\Delta G_{\text{conf},\text{app}}\left(T\right)\hfill \\ \hfill & =-RT\ln K_0\left(T\right)+RT\ln (1+K_{\text{conf}}\left(T\right))\hfill \end{array}$$ (7)

The conformational term in (8) can be used to fit directly the ITC data (Fig. 9b, inset) for the thermodynamic parameters governing the conformational equilibrium (T_m,conf, ΔC_p,conf, and ΔH_conf [27]). This was done for the V142G mutant and its experimental parameters were used to obtain fitted estimates for the other mutants, under the strong assumption that the conformational process was identical for all species.

Two important findings emerged from the calorimetric data. First, the enthalpy difference between the BI and BC states is significant: ΔH_conf = 33 ± 1 kcal/mol at 35.1°C (Table 3). As described below, this value is almost exactly what would be expected for the enthalpy of unfolding of the entire LID domain. Second, the calorimetric data obtained for all Val to Gly mutants and wild-type could be reasonably fit with this common ΔH_conf, a common ΔC_p,conf of 660 ± 70 cal/ (mol K), and an individual T_m,conf (the midpoint temperature of the BC to BI transition). As can be seen in Table 3, the mutation effects on the local unfolding transition can be large, shifting from the T_m,conf = 52°C of wild-type to 35°C for V142G.

Table 3.

Thermodynamic parameter estimates for AK(e) and mutants BI to BC conformational transitions obtained from mathematical fitting of ITC data

	ΔHm,conf (kcal/mol)a	ΔCp,conf (cal/(mol K))b	Tm,conf (°C)c
V142G	33 ± 1	660 ± 60	35.1 ± 0.3
V148G	Unchanged from V142Gd	Unchanged from V142G	37.9 ± 0.3
V135G	Unchanged from V142G	Unchanged from V142G	41.1 ± 0.2
Wild-type	Unchanged from V142G	Unchanged from V142G	52.3 ± 0.1

^aExperimentally observed transition enthalpy at T_m,conf of V142G

^bExperimentally observed heat capacity of V142G

^cTransition midpoint temperature, error is 95% confidence interval estimated from the fitted model

^d“Unchanged from V142G” means that the V142G value was used in the fitting routine for this mutant. The fitting routine has been described in detail [27]

The importance of these calorimetric results is threefold. First, the fact that only the T_m,conf differs between each mutant suggests that the mutations have indeed selectively increased the conformational entropy of the BI state, which might be thermodynamically considered a locally unfolded state. Second, the conformational and thermodynamic character of the BI state appears common to the wild-type AK(e) and all three mutants. Third, the transition between the BI and BC states is consistent with a cooperative two-state process [27].

What is the relation between the binding reaction and the local unfolding event in the LID domain? The most reasonable answer is that they are thermodynamically indistinguishable: the BI state demonstrated by ITC could be the random coil state of the LID domain demonstrated by the globally fit CPMG results.

A quantitative link between the two states is provided by the COREX algorithm [17], which uses the high resolution structure as a template in conjunction with a long-standing surface area based parameterization [62] of protein energetics to predict the ΔH and ΔC_p of unfolding of different regions of the protein. If the BI state were indeed a locally unfolded state, a reasonable model based on the NMR data would be to assume that residues 110–164 are unfolded in the BI state (c.f. Fig. 6b). Using the COREX energy function, the predicted thermodynamics of unfolding this region in wild-type were compared with the experimentally determined values. The agreement between calculation and experiment is excellent (Table 4). The calculation for global unfolding of V142G also matches the experimental value, indicating that a two state approximation for global unfolding of the entire molecule, as used for the CD data in Fig. 5, was appropriate.

Table 4.

Experimental and predicted thermodynamics of local and global unfolding

		Locala		Globala		Suma
Parameter	T (°C)	Isothermal titration calorimetryc	COREXd,e	Circular dichroismc	COREXe,f	Experimentally determinedg	COREXe,h
ΔH (kcal/   mol)	35.1	33 ± 1b	32.7	34 ± 9i	40.6	67 ± 10	73.3
	54.7	46 ± 2j	46.5	89 ± 4	88.2	135 ± 6k	134.6
ΔCp (kcal/   (mol K))		0.66 ± 0.6	0.7	2.8 ± 0.2	2.4	3.5 ± 0.3	3.1

^aPaired experimental and computational measures of possible two state unfolding reactions

^bErrors represent experimental 95% confidence intervals

^cExperimental parameter estimates from ITC (Fig. 9a, inset) and CD of V142G (Fig. 5), respectively

^dResidues 110–164 of AK(e)

^eValues computed using the COREX energy function and the PDB 4AKE structure, errors are assumed to be within ±10%.

^fResidues 1–109 and 165–214 of AK(e)

^gSum of enthalpy and heat capacity for the BI to BC reaction (ITC) and the native to denatured transition (CD)

^hResidues 1–214 of AK(e)

ⁱCalculated as ΔH_global (54.7) + ΔC_p,global (35.1–54.7).

^jCalculated as ΔH_local (35.1) + ΔC_p,local (54.7–35.1)

^kPropagated 95% Confidence Interval.

3.4 Estimating the Populations in a Three State Model of AK(e) Conformational Equilibrium

In summary, multiple lines of experimental (ITC, HSQC, CPMG, CD, crystallographic), computational (equilibrium simulation, COREX), and theoretical (gain-of-entropy) evidence are converging on the notion that the conformational change in the AK(e) LID domain is more complex than a simple rigid-body opening and closing. Specifically, the data demonstrate that the LID domain can transiently unfold from a binding competent (BC) state to a binding incompetent state (BI), in equilibrium with a fully unfolded (U) state:

$$\Delta H_{\text{app}}\left(T\right)=\Delta H_0\left(T\right)-\Delta H_{\text{conf},\text{app}}\left(T\right)=\Delta H_0\left(T\right)-\frac{K_{\text{conf}}\left(T\right)}{1+K_{\text{conf}}\left(T\right)}\Delta H_{\text{conf}}\left(T\right)$$ (8)

According to this formalism, the populations of all three states can be simulated [27] given K_conf (the equilibrium between BC and BI in (9), estimated from ITC data in Table 4) and K_unf (the equilibrium between globally folded and unfolded states, estimated from CD data in Table 4). The results indicate that the locally unfolded BI state is substantially populated for the wild-type enzyme to a level of about 5% at 37°C (Fig. 10, orange bar). For the V142G mutant, a similar population exists at a lower temperature, approximately 20°C (Fig. 10). Importantly, this latter value quantitatively agrees with the 3–9% populations obtained by the CPMG experiments as described above in Sect. 3.2. The fact that two independent biophysical techniques (calorimetry and NMR), which are each sensitive to different properties of the protein, yielded similar results strongly suggests that the model whereby the crystallographic “open” and “closed” conformations are in equilibrium is simply incorrect (or at best, incomplete).

Fig. 10.

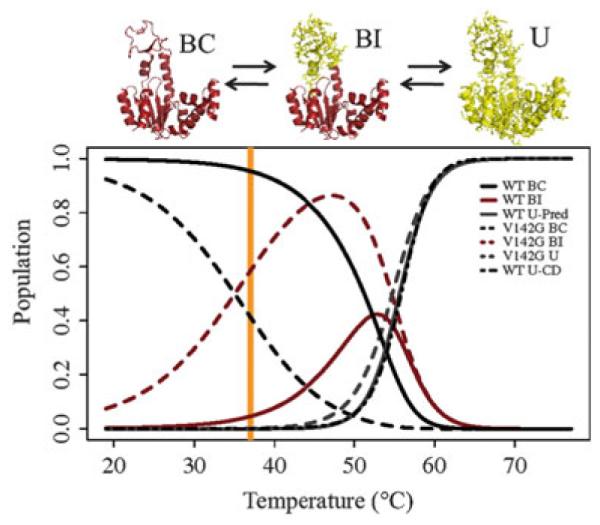
Population simulations for wild-type AK(e) and V142G agree with experimentally determined CPMG population. In the molecular figures, red indicates folded conformation and yellow indicated unfolded (U) conformation. Populations are calculated from the BI–BC (K_conf) equilibrium estimated from the ITC experimental data, and from the U–BI (K_unfolded) equilibrium estimated from the CD unfolding experiments on V142G. (The validity of this approach can be appreciated in this figure from the high probability of the BI state at 47°C, before the global unfolding transition.) Thus, the partition function Q for this system is Q = 1 + K_conf + (K_conf × K_unfolded). In this model, the probability of BC, BI, and U states are given by 1/Q, K_conf/Q, and K_conf × K_unfolded/Q, respectively. The black dot-dashed line for wild-type shows the population of the U state calculated directly from the CD unfolding data (Fig. 5, inset table). Orange line marks the optimal growth temperature of E. coli, 37°C

4 The AK(e) Functional Landscape: The Biologically Adaptive Potential of Local Unfolding of the LID Domain

4.1 The Population of the Unfolded LID Domain Regulates the K_m of the Enzyme

The data reviewed here require construction of an equilibrium model for the conformational states of the LID domain that is more complex than the interconversion between two ostensibly folded “open” and “closed” states. Is this new model, which predicts local unfolding of the LID, relevant to the function of AK (e)? The answer is of course yes. Because the population of BI state is 5% under physiological conditions, the equilibrium between the BI and BC states tunes the K_m of the enzyme, as an increased population of states that do not bind substrate will decrease the apparent affinity of enzyme for substrate. What are the implications for biological adaptation of AK and possibly other enzymes?

To adapt to a new environment an enzyme must alter its kinetic parameters such as K_m and k_cat, while simultaneously maintaining the structural properties of the catalytic site, which permit the functional chemistry and the molecular recognition of the substrate. Numerous studies have demonstrated that one common adaptive strategy that achieves this goal is to allow changes in regions of the protein distant to the active site, with the architecture and functional groups of the active site proper remaining highly conserved [12, 30, 63–65]. In the specific case of cold temperature adaptation, the main target of adaptive mutations appears to be increased conformational flexibility [8, 10]. Somero and colleagues have previously hypothesized that, in cold-adapted enzymes, decreased substrate affinity is a consequence of a more flexible native state exploring nonbinding conformations.

The experimental results presented in this chapter support that hypothesis and demonstrate how changes to the populations of low affinity or binding incompetent (BI) excited states, rather than perturbing the structure of the fully folded ground state, can effect adaptive change. Such potential adaptation can be visualized by plotting the temperature dependence of the fitted apparent association constant (K_app) of inhibitor binding for the wild-type AK(e) and V142G enzymes (Fig. 11). Considering K_app as a surrogate adaptive endpoint and 37°C as the original homeostatic temperature, the V142G mutation reduces the surrogate homeostatic temperature [i.e., K_app,mutant(T_adaptive) = K_{app,wild-type} (37°C)] by approximately 10°C [27]. Thus, a single adaptive functional change can be mediated by a single point mutation. Of course, this phenomenon could apply to any protein–ligand binding reaction with similar thermodynamic features.

Fig. 11.

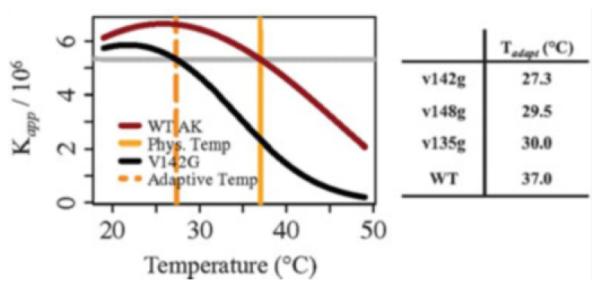
Temperature adaptation of K_m arising from surface exposed glycine mutations that redistribute the ensemble populations of binding incompetent (BI) conformational states. Plot of the apparent binding affinity (K_app) for Ap5A, computed from fitted ITC data (Fig. 9). The dashed orange line marks the temperature where K_app of V142G is equivalent to K_app of wild-type AK(e) at 37°C. The dashed orange line can therefore be considered as a surrogate homeostatic temperature for V142G. In other words, V142G could be a cold-adapted enzyme due to the single glycine mutation. The table indicates the new surrogate homeostatic temperatures computed for the remaining mutants

4.2 The Biological Importance of Enzyme Functional Adaptability Through Local Unfolding

The importance of this adaptation strategy is twofold. First, the change in binding occurs in the absence of active site changes or core structural deformation of the protein. Instead, the affinity is modulated by changing the conformational fluctuations around the protein’s average structure. To date, structure-based protein design strategies have been largely based on static representations of the protein and ligand [5, 66]. In contrast, these experimental results reveal an alternative strategy for evolutionary adaptation or rational design that targets fluctuations rather than structure. The fact that all three valine to glycine mutations produced similar effects suggests that this approach is robust. Second, the increased population of binding incompetent states among the members of the native state ensemble, as proposed by Somero and colleagues [8], is directly confirmed to be an effective strategy for the adaptive modulation of binding affinity.

Somero and colleagues hypothesized that k_cat could also be affected by flexibility-altering mutations. Preliminary results suggest that, under substrate saturating conditions, the equilibrium between BC and BI forms of AK is biased towards the substrate-bound conformation. Under such conditions, the rate of interconversion between BC and BI, as measured by CPMG, is equivalent for both wild-type AK(e) and the V142G mutant (Table 2). Moreover, this rate of interconversion is quantitatively indistinguishable from (not faster than) k_cat [67]. This last result implies that the BC to BI local unfolding equilibrium is relevant not only to K_m but also to product release, a conclusion in agreement with previously published results from other investigators [11, 67]. If true, local unfolding of the lid domain, mediated by single surface exposed glycine mutations, would dominate the evolutionary adaptability of both the binding and catalytic function of this essential enzyme.

4.3 Perturbation of the Ensemble, in Addition to Inspection of Static Structure, Is Necessary to Understand the Functional Landscape

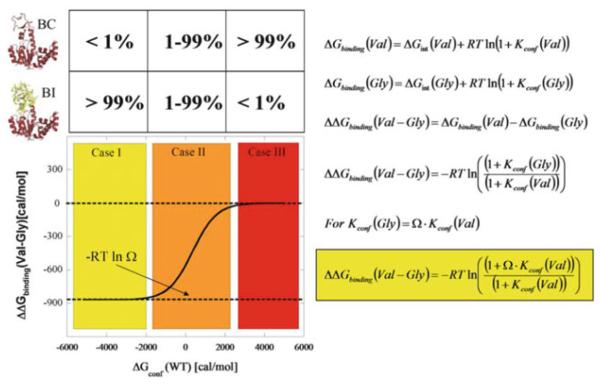
It cannot be overemphasized that the functional adaptability conferred by the local unfolding of the LID domain is a consequence of the ensemble nature of AK(e). In general, the ensemble nature of proteins means that the phenotypic impact of mutation on function or stability will depend on how the ensemble is distributed, or “poised”, prior to the mutation [25, 26]. Of crucial importance is the realization that such insight is impossible to obtain from analysis of a single structure, such as a ground state X-ray structure. This can be conceptually demonstrated with a highly simplified protein ensemble consisting of only two states (Fig. 12). One state in this ensemble consists of the entire protein folded (i.e., a binding competent (BC) ground state structure), and the second state partially unfolds a subdomain (i.e., a binding incompetent (BI) excited state structure). For this thermodynamic system, the effect of a valine to glycine mutation (e.g., the surface exposed mutants discussed in this chapter) on the ability to bind ligand will depend on where the equilibrium between the two states is poised. Generally, the range of responses can be divided into three categories (red, yellow, and orange regions in Fig. 12); a detailed discussion has been previously published [68]. Briefly, in the red region, where the BC state is favored, the mutation will have no effect. In contrast, in the yellow region, where the BI state is favored, the mutation will have a maximum effect. When both states are populated, the effect will be intermediate.

Fig. 12.

Expected outcomes for Val to Gly mutation effects on ligand binding. The simplest case of a two-state ensemble is displayed. In the molecular picture, red indicates folded parts of the protein and yellow indicates unfolded parts. Note that the diagrams and equations are general and may apply to many enzyme–ligand systems, although they describe the specific case of AK(e) and its LID domain as discussed in the text. The equations are restatements and syntheses of equations previously discussed in the text: symbol Ω, denoting conformational degrees of freedom, was introduced in (1) and (2), K_conf and ΔG_conf in (7) and (8). Case II (orange) is the energetic region where the greatest experimentally observed changes would occur, and the approximately 5% unfolded LID domain for wild-type AK(e) places it in this region

Closer analysis of these different cases reveals an important point. For any ensemble involving two or more states, there will always be linkage effects and thus a range of values (y-axis of Fig. 12) possible for ΔΔG_binding (Val-Gly), depending on where the equilibrium is poised prior to the mutation. Consequently, a difference (or lack of a difference) in ΔΔG_binding (Val-Gly) does not by itself give insight into either the nature of the fluctuations (i.e., whether they are rigid-body hinge motions or local unfolding) or any possible coupling that exists between different parts of the molecule. Insight can be gained, however, by perturbing the equilibrium and observing how the binding is affected (as was done for AK(e) in Fig. 9). Thus, a strategy to determine for any enzyme where the equilibrium is poised is mutational perturbation and observation of the amplification or suppression of functional effects. For AK(e), the model depicted in Fig. 12 is precisely the case for the three LID domain valine to glycine entropy promoting mutations. By changing the temperature, the BC to BI equilibrium, and thus the ΔΔG_binding (Val-Gly), is shifted in a manner proscribed by the expressions in Fig. 12.

5 Conclusion: An Emerging Correspondence Between the Energetic and Functional Landscapes of AK(e) Mediated by Excited State Conformational Fluctuations of Local Unfolding

By employing a mutation strategy that affected the conformational entropy of local unfolding without affecting the average folded structure, insight has been gained into the energetic and functional landscapes of AK(e). Multiple experimental techniques, including X-ray crystallography (Fig. 4), NMR spectroscopy (Figs. 6 and 7), circular dichroism spectroscopy (Fig. 5), and isothermal titration calorimetry (Fig. 9) have been brought to bear on the question. All experimental results, supported by thermodynamic simulation (Figs. 10 and 11, Table 4) agree on two major conclusions: (1) the LID domain of AK(e) undergoes an all-or-none local unfolding reaction that affects substrate binding to the enzyme and (2) this locally infolded state of the LID domain is populated to a level of approximately 5% in the apo form of the enzyme.

The previously unappreciated experimental fact is that the unfolded LID domain is a dominant influence on the energetic and functional landscapes of AK(e). This holds important, possibly paradigm-changing, implications for the investigation and understanding of how the enzyme works. In particular, these results force a revision of the intuitively appealing canonical picture of the molecule undergoing rigid-body opening and closing hinge motions during its catalytic cycle. This canonical picture has been the most common framework for molecular dynamics simulation, as the assumption of two well-defined conformational end-states permits the most efficient use of limited computational sampling resources. However, the results presented here reveal a need for computational approaches that can thoroughly sample disorder (i.e., quantify conformational entropy on large systems), such as state of the art methods that can lengthen the timescales of atomic simulation [69].

Perhaps the most intriguing implications arise regarding the evolution of enzyme function and the adaptability of enzymes to different biological environments. As proposed many years ago by Somero [8] and others, flexibility can be key to temperature adaptation. The fact that single point mutants to glycine, in surface exposed locations of the enzyme distant from the active site, can conserve relative function at substantially different temperatures experimentally demonstrates a remarkably efficient mechanism for enzyme evolution. This mechanism may well be immediately applicable to the rational design of amino acid substitutions affecting function in other therapeutic or industrially important enzymes.

It is likely that detailed investigation of the amino acid substitution patterns in the LID domains of other AK homologs (Fig. 2) will permit rationalization of those patterns in energetic terms that cannot presently be explained by the general physico-chemical rules summarized within amino acid substitution matrices. Especially interesting would be a functional explanation of why the LID domain seems to be “binary”: either present or absent in the biological record (Fig. 2). Perhaps the LID domain was an evolutionary innovation, biophysically rooted in the energetic linkage described in Fig. 12, which allowed greater catalytic control over this metabolically indispensable enzyme.

Abbreviations

AK

Adenylate kinase

AK(e)

E. coli adenylate kinase

Ala

Alanine

AMP

Adenosine monophosphate

AMPbd

AMP binding domain of adenylate kinase

Ap5A

P¹,P⁵-di(adenosine-5′) pentaphosphate

ATP

Adenosine triphosphate

BC

Binding competent

BI

Binding incompetent

CD

Circular dichroism spectroscopy

CORE

Core domain of adenylate kinase

CPMG

Carr-Purcell-Meiboom-Gill

Gly

Glycine

HSQC

Heteronuclear single quantum coherence

Ile

Isoleucine

ITC

Isothermal titration calorimetry

K

Equilibrium constant

LID

LID domain of adenylate kinase

NMR

Nuclear magnetic resonance spectroscopy

U

Unfolded

Val

Valine

ΔG

Gibbs free energy

ΔS

Entropy change