comets (Constrained Optimization of Multistate Energies by Tree Search): A Provable and Efficient Protein Design Algorithm to Optimize Binding Affinity and Specificity with Respect to Sequence

Abstract

Practical protein design problems require designing sequences with a combination of affinity, stability, and specificity requirements. Multistate protein design algorithms model multiple structural or binding “states” of a protein to address these requirements. comets provides a new level of versatile, efficient, and provable multistate design. It provably returns the minimum with respect to sequence of any desired linear combination of the energies of multiple protein states, subject to constraints on other linear combinations. Thus, it can target nearly any combination of affinity (to one or multiple ligands), specificity, and stability (for multiple states if needed). Empirical calculations on 52 protein design problems showed comets is far more efficient than the previous state of the art for provable multistate design (exhaustive search over sequences). comets can handle a very wide range of protein flexibility and can enumerate a gap-free list of the best constraint-satisfying sequences in order of objective function value.

1. Introduction

Protein design requires the prediction and selection of protein sequences with desired properties, generally some combination of structure stability, binding to desired ligands, and lack of binding to undesired ligands. The gold standard for protein design is natural evolution, in which protein mutations confer fitness advantages only if several desired properties are all present: mutants must be sufficiently stable, effective at binding or catalysis, and selective for their fitness-conferring function (Frey et al., 2010). Researchers have tried to emulate this process by directed evolution experiments (Arnold, 1998). But methods to optimize these properties computationally (Donald, 2011) allow enormous sequence spaces to be searched without enormous resource expenditures and thus greatly expand the space of possible designs. Such searches require algorithms that do not analyze each candidate sequence separately: Large sequence spaces are too expensive to analyze one by one. Computational protein designers have used three different strategies to achieve the desired properties with their new sequences: energy minimization of a single desired protein or complex structure (“single-state design”); heuristic minimization of some function combining multiple desired properties (“traditional multistate design methods”); and analysis of one sequence at a time in detail (“single-sequence analysis”).

Single-state design is the most developed class of dedicated protein design algorithms. It is commonly used to improve fold stability by selecting mutants that minimize the protein's total energy (Donald, 2011; Kuhlman and Baker, 2000; Desmet et al., 1992; Gainza et al., 2012; Georgiev et al., 2014), and to increase binding affinity by selecting mutants that minimize the energy of a complex (Karanicolas and Kuhlman, 2009; Georgiev et al., 2008; Floudas et al., 1999). Some of these methods are provable: Given a sequence space to search, a model of the protein's conformational space, and an energy function, they are guaranteed to return the lowest-energy sequence and conformation (the global minimum-energy conformation, or GMEC). The dead-end elimination (DEE) (Desmet et al., 1992) and A* (Leach and Lemon, 1998) algorithms have this guarantee. In their original form, they assume a discrete conformational space, but they have been extended to include both continuous sidechain (Georgiev et al., 2008; Gainza et al., 2012) and backbone (Georgiev and Donald, 2007; Hallen et al., 2013) flexibility. Provable single-state methods can also enumerate either a gap-free list of the lowest-energy sequences and conformations (Leach and Lemon, 1998; Gainza et al., 2012; Hallen et al., 2013), or of the sequences with the lowest-energy optimal conformations (Roberts, 2014). Other single-state methods are not provable, most prominently Metropolis Monte Carlo–based methods (Lee and Levitt, 1991; Kuhlman and Baker, 2000), but are popular for reasons of computational speed. All these methods use some simplified model of protein conformational flexibility. A popular but highly approximate model is to allow the conformation of each amino acid to be selected from a discrete set, referred to as rotamers. This model can be made substantially more accurate by allowing small, continuous conformational adjustments around the rotameric conformations, which can be incorporated while maintaining provable accuracy (Georgiev et al., 2008; Gainza et al., 2012; Hallen et al., 2013).

Single-state design can be thought of as the stabilization of a desired “state” of a protein—essentially, its fold, overall conformation, and ligand-binding mode. This paradigm can be extended to include multiple states, possibly with different ligands, in order to specify multiple desired properties for the designed sequence. This strategy is known as multistate protein design (Davey and Chica, 2012). DEE has been extended to multistate design in the type-dependent DEE algorithm (Yanover et al., 2007). This algorithm prunes rotamers that are guaranteed not to be part of the optimal conformation of a state of the protein. It offers a significant advantage in efficiency, but does not reduce the number of sequences that must be considered in multistate design, because it only eliminates rotamers in comparison to more favorable rotamers of the same amino-acid type.

On the other hand, nonprovable methods have also been developed to try to optimize objective functions based on the energies of multiple states, without considering each sequence separately. Genetic algorithms have been used to optimize differences in energy between states (Lewis et al., 2014) as well as other objective functions (Leaver-Fay et al., 2011), and belief propagation has been used to optimize sums of energies of different states, in order to design a binding partner appropriate for multiple ligands (Fromer et al., 2010b,a,b; Fromer, 2010). Type-dependent DEE can also be combined with such techniques, to reduce the conformational space that is searched heuristically (Yanover et al., 2007; Fromer et al., 2010a). In addition, some design systems can be described fairly accurately by an energy function whose terms depend only on the amino acid types of one or a few residues (Grigoryan et al., 2006); the CLASSY method (Grigoryan et al., 2009) derives such energy functions by least-squares fitting, and then uses them to perform efficient multistate designs that bypass conformational search entirely and use integer linear programming algorithms to find the optimum of the sequence-based energy function with a provable guarantee of optimality. However, for design systems that are not well described by a cluster expansion (i.e., that exhibit significant higher-order interactions between conformational changes at different residues), previous multistate design algorithms cannot provide any guarantees about the optimality of their designed sequences without an exhaustive search over sequence space.

Methods that consider each candidate sequence explicitly are another important and highly versatile category of computational protein design methods. However, the computational costs can be very high—linear in the number of sequences, and thus exponential in the number of simultaneously mutable positions. Molecular dynamics can be applied for single-sequence analysis in protein design (Leech et al., 1996; Zheng et al., 2008), using simulations over time to investigate the properties of a candidate sequence. Molecular dynamics readily models all types of protein flexibility with many different energy functions, including effects like solvent polarization (Sitkoff et al., 1994) or explicit solvent. It also allows the user to account for entropic contributions to binding energies. More recent algorithms account for entropy without the steep costs of simulation over time. The K* algorithm in osprey (Lilien et al., 2005; Georgiev et al., 2008; Gainza et al., 2012; Gainza et al., 2013) predicts the binding of a mutant protein sequence to a ligand by computing an ensemble of low-energy protein states to provably approximate the binding constant K_a within a desired relative error for the user-specified flexibility model and energy function. Though it provides a vast speedup relative to exhaustive search over all conformations at each sequence, it does require explicit consideration of each sequence sufficient to bound the energies in its ensemble. K* in osprey (Gainza et al., 2013) has yielded several multistate protein designs that were successful experimentally. The calculations have involved both comparisons of the bound and unbound states of a single complex (Rudicell et al., 2014; Roberts et al., 2012; Gorczynski et al., 2007) and of multiple complexes (Chen et al., 2009; Frey et al., 2010; Stevens et al., 2006; Georgiev et al., 2012), and the osprey-designed proteins have performed well in vitro (Rudicell et al., 2014; Roberts et al., 2012; Gorczynski et al., 2007; Chen et al., 2009; Frey et al., 2010; Stevens et al., 2006; Georgiev et al., 2012) and in vivo (Rudicell et al., 2014; Roberts et al., 2012; Gorczynski et al., 2007; Frey et al., 2010) as well as in nonhuman primates (Rudicell et al., 2014).

We now present an algorithm distinct from these three traditional strategies that combines advantages from all three: comets. Like other multistate methods, it optimizes an energy measure that considers multiple states: for example, it can directly optimize the binding energy (the difference in energy between the bound and unbound states), or the difference in binding energy between two different ligands. Like single-sequence analysis, it allows consideration of a wide variety of stability, affinity, and specificity requirements during sequence selection. This is facilitated by its accommodation of optimization constraints: for example, it can optimize binding to one ligand while constraining binding energy for other ligands. It provably returns the best sequence for its specified optimization problem, without performing an exhaustive search over the possible sequences. Some previous methods can do this for single-state design problems, but before comets it was impossible for most multistate problems. As a result, comets provides a vast performance improvement over the previous state-of-the-art for provable multistate design, which is exhaustive search over sequence space.

By presenting comets, this article makes the following contributions:

• 1. A novel and versatile framework for multistate protein design, allowing constrained optimization of any linear combinations of state energies.

• 2. An algorithm to solve problems in this framework that provably obtains the same results as exhaustive search over sequences but is combinatorially faster than this exhaustive search, as shown by empirical measurements on 52 protein design problems.

• 3. Support for continuous sidechain and backbone flexibility in comets.

• 4. The ability to enumerate as many constraint-satisfying sequences as desired, in a gap-free list in ascending order of the desired objective function.

• 5. An implementation of comets in our laboratory's open-source osprey protein-design software package (Frey et al., 2010; Chen et al., 2009; Georgiev et al., 2008), available for download at our website (Georgiev et al., 2009) as free software.

2. Methods

2.1. Problem formulation

Let us consider a protein design problem where we wish to consider mutating n residues. The output of our calculation will be a sequence s: an ordered list of n amino acid types. We have a set A of states. Each state is a protein structure containing our n mutable residues, along with a (possibly continuous) conformation space for each sequence assignment, which we call the flexibility model for the state. We consider functions of the form

where the c_a are real coefficients. We call these functions linear multistate energies (LMEs). comets is an algorithm to minimize any LME f (s) with respect to sequence s, under constraints of the form c_i(s) < 0, where each c_i is also an LME. LMEs are suitable for representing stability, affinity, and selectivity requirements in protein design. For example, to optimize a binding energy, we set A = {b, u} to consist of the bound state b and the unbound state u, and optimize f (s) = E_b – E_u. That is, we set c_b = 1, c_u = −1 and c₀ = 0 for our objective function. A highly simplified, “toy” example of this setup is in Supplementary Material A (available online at www.liebertpub.lcom/cmb).

The choice of objective function and constraints defines the physical problem we wish to solve. We require a computational model of proteins to convert this into a computational problem. To model protein flexibility, we use the very general model of the DEEPer algorithm (Hallen et al., 2013) in osprey. The protein in each state is allowed to have any number of degrees of freedom, which can be either continuous or discrete, and which fully specify both the sequence and conformation of the protein. Each residue in each state has a set of “residue conformations” (RCs) (Hallen et al., 2013). An RC is a portion of conformational space defined by bounds on every conformational degree of freedom available to the residue. These bounds must be tight enough that once a residue conformation is assigned to every residue, the energy minimum over this limited conformational space can be found by local minimization. Thus, RCs define a partitioning of conformational space that allows local minimization to be used as a subroutine in our global search. A residue conformation is associated with a specific amino acid type. This framework is suitable for accommodating both continuous sidechain and backbone flexibility, but it reduces to the model of continuous sidechain flexibility of Georgiev et al. (2008) and Gainza et al. (2012) if only sidechain dihedrals are used as continuous degrees of freedom. If each sidechain dihedral is confined to a single value within each residue conformation, then this special case is just the commonly used rigid-rotamer approximation (Desmet et al., 1992; Leach and Lemon, 1998). In both of these special cases, each residue conformation represents a single sidechain rotamer.

The model of flexibility may differ between states; in fact, different residues may be made flexible. For example, in a calculation with a bound and an unbound state of a protein, the ligand will have flexibility in the bound state, but will be absent from the unbound state (Fig. 1). But all states have the same set of mutable residues, and the same set of allowed amino-acid types at each mutable residue. This way, comets outputs a sequence applicable to all states.

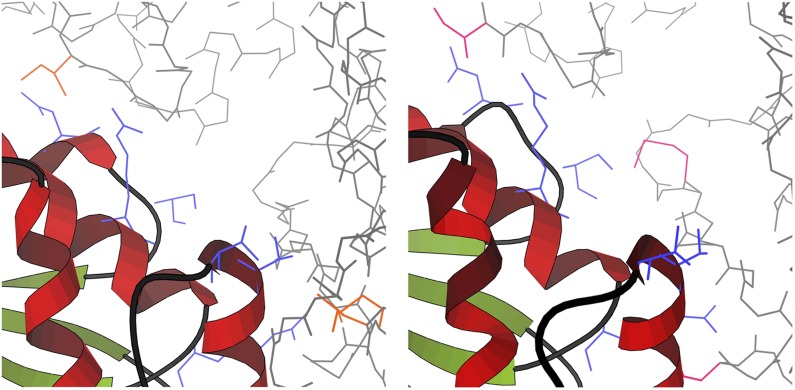
FIG. 1.

Flexible and mutable residues in a design for specificity. The apoptotic regulator CED4 forms two different dimers, one to block apoptosis (left; PDB id 2a5y [Yan et al., 2005]) and one to induce it (right; PDB id 3lqr [Qi et al., 2010]). We want to design for specificity (to block apoptosis), so we allow mutations to some residues in the binding site (blue). To accurately model the conformational changes induced by the mutations, we also model as flexible the residues on the opposite side of each interface that interact with the mutable residues (orange, pink). Analysis of this calculation and others is described in section 3.

To model energy, we must have an “energy function” that estimates the energy of a given sequence and conformation. Our implementation of comets uses a pairwise additive energy function, i.e., a sum of energy terms that each depend on the conformations of at most two residues. This property is only used in the computation of lower bounds for LMEs over subsets of the sequence space and state conformational spaces (section 2.2.2; Supplementary Material B), so a non-pairwise energy function that admits such lower-bound computations would also be compatible with comets. comets will return optimal results for the given model of flexibility and energy function.

2.2. A* over sequences

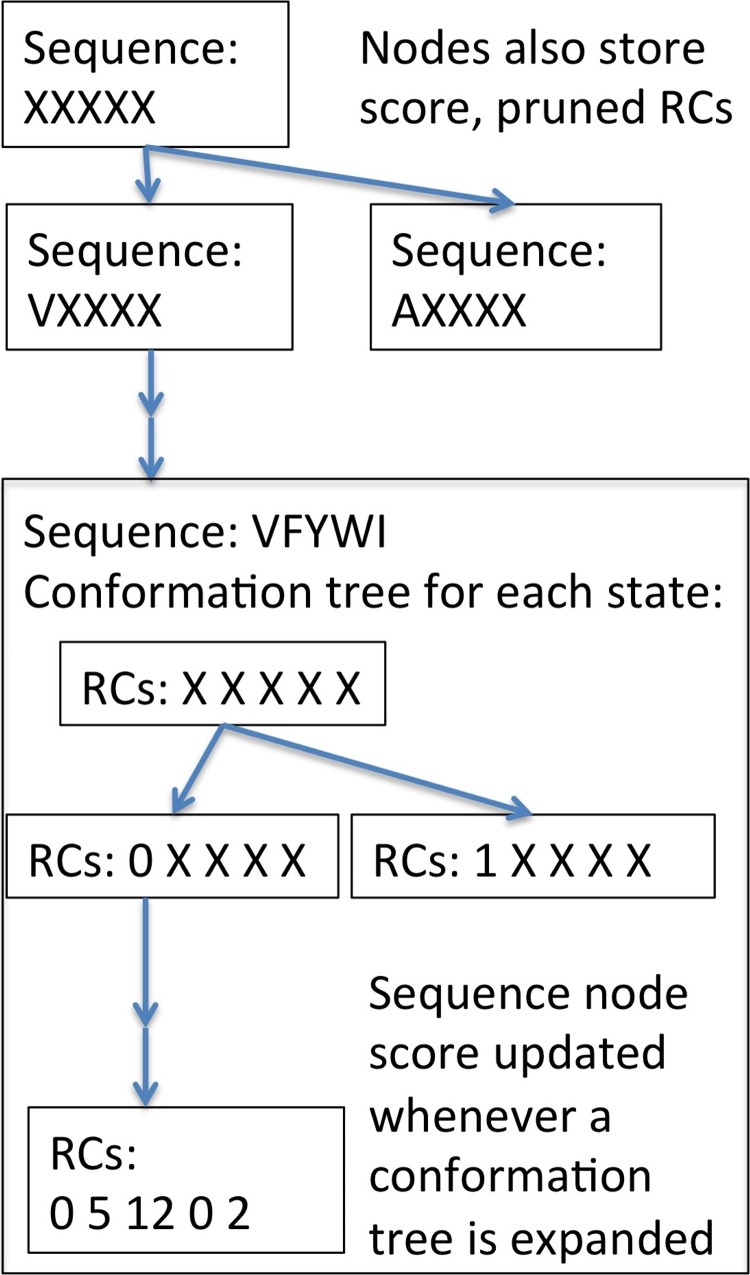
comets uses the A* (Hart et al., 1968) search algorithm to search sequence space. In most previous applications of A* to protein design (Leach and Lemon, 1998; Georgiev et al., 2008), nodes of the tree correspond to partially defined conformations. Each partially defined conformation is specified by RC assignments for one or more residues. Thus, each node corresponds to the conformational space made up of all conformations consistent with the partial definition. A node's score is a lower bound on all the conformational energies in this space. comets is similar, but nodes correspond to partially defined sequences and thus to a sequence space. A node's score is a lower bound on the objective function for all sequences in the node's sequence space (Fig. 2).

FIG. 2.

Expansion steps during node processing generate nodes with partially (e.g., VXXXX or AXXXX) and then fully (e.g., VFYWI) defined sequences. Once a node has a fully defined sequence, conformational trees are built for it for all states. Then conformational tree expansions lead to fully processed nodes. X, unassigned amino acid or RC; V, Val; A, Ala; F, Phe; Y, Tyr; W, Trp; I, Ile.

In A*, we repeatedly process the lowest-scoring node in the tree. Processing a node means either splitting it into several nodes that partition its sequence space, or computing a higher score (i.e., tighter bound) for it (that is still a valid lower bound). Score computation may involve conformational search (Fig. 2), and some nodes will be processed until their sequence is fully defined and the optimal conformation for each state is fully determined. These nodes are termed fully processed, and their objective function and constraint LMEs can be evaluated exactly. When the lowest-scoring node is fully processed, we can return its sequence as optimal, because its objective function value (at optimal conformations for each state) is better than any sequence in any of the sequence spaces of the other nodes in the tree. This is because the other nodes' scores are lower bounds on their optimal objective function values.

2.2.1. Types of nodes

We will store two types of nodes in our tree (Fig. 2). Examples of each type of node in the toy example are given in Supplementary Material A.

The first type has a sequence that is not fully defined: Not all mutable residues have an assigned amino-acid type. At these nodes, we store information on which RCs are pruned at each residue in each state (for the assigned amino-acid types if assigned; for all amino acid types if not assigned). The pruned RCs are those that cannot be part of the optimal conformation for that state for any sequence in the sequence space of the node. We store pruned pairs of RCs as well as individual pruned RCs.

The second type of node has a fully defined sequence: an amino-acid type assigned for each mutable residue. At each such node, for each state, we store an A* tree expanding the conformational space for that sequence. These trees are identical to those used in DEEPer in osprey (Hallen et al., 2013): Their nodes each represent a subset of conformational space, defined by RC assignments to some of the residues, which restrict the values of the proteins' degrees of freedom to the bounds associated with the assigned RCs. The score of each node is a lower bound on the energy of all conformations in its allowed conformational space.

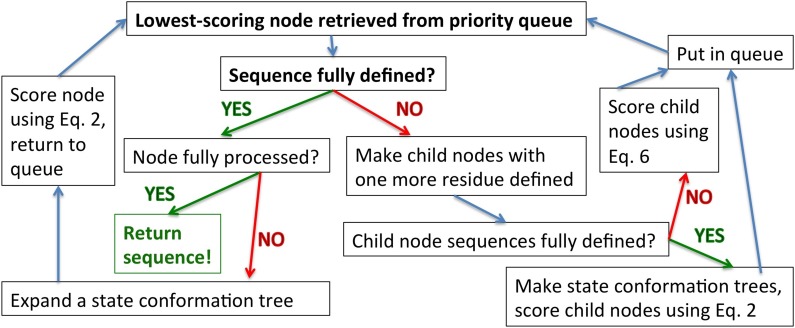
2.2.2. Node-processing operations

For either type of node, node processing consists of two steps: an “expansion” step and a “bounding” step (Fig. 3). Every time we extract a node from the priority queue, meaning it is the lowest score in the tree, we choose the appropriate processing operation and perform it (Fig. 3).

FIG. 3.

comets is a sequence of node-processing operations.

Expansion step. For a node without a fully defined sequence, the expansion step splits the node n into several nodes whose sequence spaces partition the sequence space of n. If the first mutable residue without an amino acid type assigned in n is residue r, then this partition can be performed by creating a node for each amino acid type a allowed at r. These child nodes will each have a sequence space identical to that of n, except with the amino acid a assigned to residue r. For a node n with a fully defined sequence, we split the lowest-scoring node in one of n's conformational trees: Each child node has a different RC assignment for a residue whose RC is not assigned at the parent node. This is the same type of split used in DEEPer (Hallen et al., 2013), and essentially as in previous protein design applications of A*.

Bounding step. In the bounding step, a lower bound is computed for the objective function and for each of the constraint LMEs. If the lower bound for any of the constraint LMEs c_i is greater than 0, then we know all sequences at the node violate that constraint, and we eliminate the node. Otherwise, the node score is set to be the lower bound on the objective function. Details of the method for computing lower bounds are provided in Supplementary Material B.

For nodes without fully defined sequences, we update the list of pruned RCs for the child node before computing bounds. Pruning is performed by type-dependent DEE (Yanover et al., 2007)—in our implementation, the various pruning algorithms available in osprey (Georgiev et al., 2008; Gainza et al., 2013; Georgiev et al., 2006) are used.

2.3. Starting and finishing the calculation

Hence, to perform comets, we create a priority queue of A* tree nodes and initialize it with a node representing the entire sequence space we are searching. We then repeatedly extract the lowest-scoring node from the priority queue and process it with the appropriate node-processing operation.

Each operation will define either the sequence or the conformation in one of the states at a residue where it was previously not defined, so in a finite number of steps, we will achieve a node whose sequence and optimal state conformations are fully defined, that is, a fully processed node. If our lower-bounding techniques are adequate, very few sequences will need to be fully processed, so this sequence A* tree will return the optimal sequence with great efficiency compared to exhaustive search over sequences. Running comets until n sequences have been returned will yield the n sequences that have the lowest objective function values among all sequences satisfying the constraints.

3. Results

Protein design calculations were performed in order to measure the efficiency of comets and its ability to design proteins with properties undesignable by single-state methods. Systems of four types were used: designs for specificity on a protein that can form two or more different complexes; optimization of the binding energy for a single complex; stabilization of a single protein robust to choice of force field; and stabilization of the reduced form of angiotensinogen relative to the oxidized form or vice versa. Details of these test cases are in Supplementary Material C.

3.1. Measurement of efficiency

comets was run on 52 protein design test cases to measure its efficiency advantages across a range of different objective functions and constraints. The test cases used 44 protein structures, and 25 modeled flexibility using rigid rotamers while the other 27 used continuous flexibility.

Exhaustive search, the only other provable algorithm for multistate design, must calculate the GMEC for each sequence in each state. For an s-state design space with N sequences, this means that N sequences must be considered explicitly and sN state GMECs must be calculated—a formidable proposition, since N grows exponentially with the number of mutable residues and each state GMEC calculation is NP-hard (Pierce and Winfree, 2002). To measure the ability of comets to avoid these calculations, the number g of state GMECs calculated by each run of comets was measured and compared to sN. Also, comets provably need not even consider each sequence explicitly, even briefly. To determine if this reduced consideration of sequences provides a significant advantage in efficiency, the number m of sequence tree nodes created in each comets run was measured and compared to N. Hence, m is the number of partial sequences explicitly considered in a comets run.

Many provable algorithms, including A* (Leach and Lemon, 1998) and integer linear programming (Kingsford et al., 2005), and non-provable methods like Monte Carlo (Kuhlman and Baker, 2000) can minimize an LME using (a) an exhaustive search over sequences without (b) also exhaustively searching over conformations. So even without comets there is no need for an exhaustive search over conformational space. However, all previous provable methods for typical (non-sequence-based) energy functions must still compute the GMEC of each state for every sequence when performing multistate design, because they are intended to calculate the minimum of an energy function (with respect to sequence and conformation). In contrast, comets calculates the constrained minimum (over all sequences) of a linear combination of minima (over all conformations) of energy functions. Hence, in this article, we measure the ability of comets to avoid computing GMECs for most of the sequences, and sometimes even to avoid any explicit consideration of most of the remaining sequences. These are the main novel abilities of comets.

3.1.1. Reduction in number of state GMECs calculated

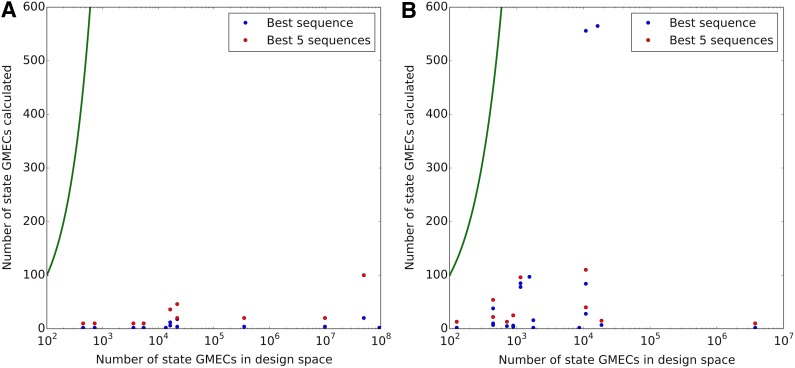
comets calculates only a very small portion of state GMECs (Fig. 4)—often only the state GMECs for the sequences being returned as optimal. To calculate the best sequence in rigid designs, the average run needed to calculate only 0.05% of the state GMECs in the design space. This portion increased to 0.1% for enumeration of the best five sequences. For continuous designs (Gainza et al., 2012; Hallen et al., 2013), 2% of the state GMECs were calculated for runs finding only the best sequence, and 4% were calculated for runs enumerating the best five sequences.

FIG. 4.

Number g of state GMECs calculated in comets runs with (A) rigid or (B) continuous flexibility, compared to the number sN of state GMECs in the entire design space (sN is the number of sequences in the design space times the number of states). Results are shown both for calculation of the best sequence and for enumeration of the best five, when possible under the design constraints. Exhaustive search would have to calculate all state GMECs (green curve).

3.1.2. Reduction in number of sequences considered explicitly

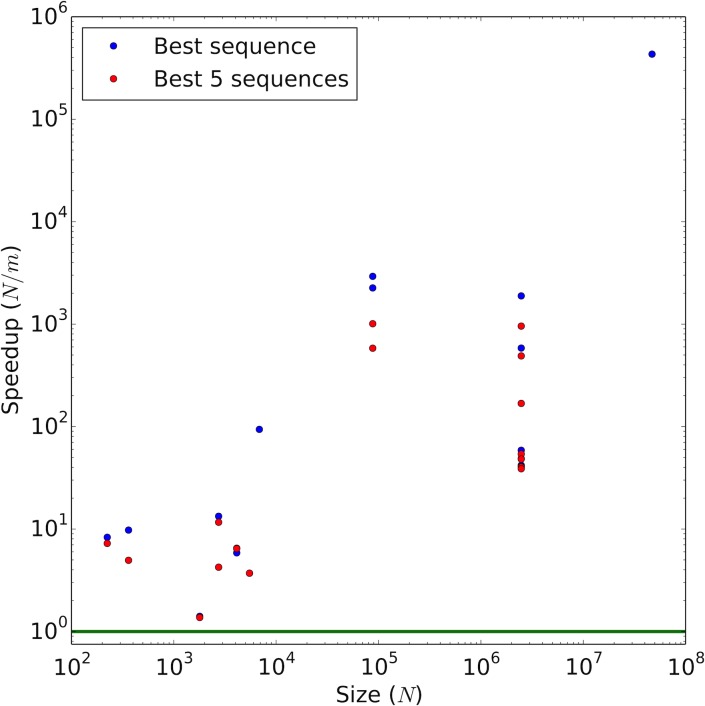
Reduced explicit consideration of sequences was found to provide a significant combinatorial speedup in comets runs without continuous flexibility. For calculation of the best sequence in these rigid designs, the median m/N was 0.02, and many runs with larger design spaces generated significantly fewer sequence tree nodes relative to the design space size (Fig. 5)—the largest sequence space to return a constraint-satisfying sequence had 47 million sequences with m/N = 2 × 10⁻⁶ (i.e., a 5 × 10⁵-fold speedup). The median increased to 0.03 for enumeration of the best five sequences. For continuous designs, the median m/N values were 0.63 for the best sequence and 0.69 for the best five.

FIG. 5.

Speedup due to reduced explicit consideration of sequences in comets, compared to exhaustive search (green line), for designs with rigid rotamers. m: number of sequence tree nodes created in comets; N: number of sequences in the design space. Magnifying this speedup, comets handles sequences that it considers explicitly very efficiently (Fig. 4).

3.1.3. Provably finding unsatisfiable constraints

The statistics above exclude runs for which no sequences can satisfy the constraints. comets can provably verify when no satisfying sequences exist and did so for 8 of the 27 continuous runs and 5 of the 25 rigid runs.

3.2. Differences in sequences returned by multistate designs and single-state proxies

Single-state design is often used as a proxy or a “first step” in multistate design. To test whether this approximation yields sequences similar to the optimal ones from multistate design, sequence divergences were calculated between optimal sequences from multistate design and optimal sequences from corresponding proxy single-state designs.

Our results indicate that single-state approaches are likely to yield sequences far from the optimal one. For specificity design problems favoring a complex P:A over a complex P:B, mutable-residue sequence divergence between the single-state optimal sequence for complex P:A and the multistate optimal sequence was 33% (averaged over 13 designs). Similarly, for multispecificity designs (optimizing the sum of binding energies for complexes P:A and P:B), the best sequence averaged 36% sequence divergence from the single-state optimum for complex P:A (10 designs). These divergences are nearly as high as the 39% (8 design pairs) average sequence divergence between comparable specificity and multispecificity designs—that is, between a protein optimally designed to bind A while not binding B, and a protein optimally designed to bind both A and B. So the difference is quite functionally significant.

Further details on the test cases are provided in Supplementary Material C.

These results show that explicit, provable multistate design provides significant advantages in the calculation of optimal sequences for a wide range of problems, and that comets provides an efficient way to perform such designs. The number of sequences and of state GMECs considered could likely be reduced substantially further using improved energy bounds. Thus, comets liberates provable multistate protein design from the efficiency barrier imposed by exhaustive search.

4. Conclusions

comets fills an important lacuna in protein design. A designer can now optimize any linear combination of optimal state energies, using constraints to ensure the desired combination of stability, affinity, and specificity. This can all be done with provable guarantees of optimality, both for the output sequence and for the state conformational energies of each candidate sequence. A wide range of conformational flexibility, both continuous and discrete, can be accommodated. Thus, comets offers a wide range of advantages to the molecular design community.

Acknowledgments

We would like to thank Dr. Ivelin Georgiev for helpful discussions and for providing useful multistate protein design problems; Dr. Kyle Roberts for helpful discussions and advice on the algorithms; Dr. Kyle Roberts and Pablo Gainza for providing PDB files and scripts for testing; all members of the Donald lab for helpful comments; and the PhRMA foundation (M.A.H.) and NIH (grant 2R01-GM-78031-05 to B.R.D.) for funding.

Author Disclosure Statement

No competing financial interests exist.