Abstract

The integration of local heat sources with solid-state nanopores offers new means for controlling the transmembrane transport of charged biomacromolecules. In the case of electrophoretic transport of DNA, recent experimental studies revealed unexpected temperature dependences of the DNA capture rate, the DNA translocation velocity, and the ionic current blockades produced by the presence of DNA in the nanopore. Here, we report the results of all-atom molecular dynamics simulations that elucidated the effect of temperature on the key microscopic processes governing electric field-driven transport of DNA through nanopores. Mimicking the experimental setup, we simulated the capture and subsequent translocation of short DNA duplexes through a locally heated nanopore at several temperatures and electrolyte conditions. The temperature dependence of ion mobility at the DNA surface was found to cause the dependence of the relative conductance blockades on temperature. To the first order, the effective force on DNA in the nanopore was found to be independent of temperature, despite a considerable reduction of solution viscosity. The temperature dependence of the solution viscosity was found to make DNA translocations faster for a uniformly heated system but not in the case of local heating that does not affect viscosity of solution surrounding the untranslocated part of the molecule. Increasing solution temperature was also found to reduce the lifetime of bonds formed between cations and DNA. Using a flow suppression algorithm, we were able to separate the effects of electro-osmotic flow and direct ion binding, finding the reduced durations of DNA–ion bonds to increase, albeit weakly, the effective force experienced by DNA in an electric field. Unexpectedly, our simulations revealed a considerable temperature dependence of solvent velocity at the DNA surface—slip velocity, an effect that can alter hydrodynamic coupling between the motion of DNA and the surrounding fluid.
Keywords: plasmonic heating, nanopore transport, DNA sequencing, electrophoresis, ionic current, electro-osmosis
Introduction
Electrophoretic transport of biomolecules through a nanopore in a thin solid-state membrane is a process that has many potential applications in bionanotechnology.1−4 Ionic current signatures produced by translocating biomolecules have been used for single molecule sensing and analysis,5−8 including efforts directed toward realizing nanopore sequencing of DNA.9−11 Incorporation of “active” components, such as as electrodes12−15 or light-responsive elements,16−19 offers new routes for controlling the nanopore translocation process and new means for detection and identification of the passing biomolecules.
Recently, laser-induced plasmon heating emerged as a novel approach to affecting the nanopore transport. In a typical experimental setup, small metallic nanoparticles are placed in the vicinity of a nanopore. Illumination of the particles with a laser beam rapidly (in tens of nanoseconds or less) heats up the nanopore volume; switching the laser off rapidly cools the nanopore volume back to the ambient temperature. Such plasmon-induced local heating has already been used for modulation of local temperature in a biological nanopore alpha-hemolysin,20 subdiffraction limit profiling of optical field intensity,21 control over nanopore electrical resistance,22 stretching of DNA in a nanopore,23 inducing defects in lipid bilayer membranes,24 and parallel fabrication of nanopores in graphene.25 Local heating may also play a role in application of plasmonic nanopores to DNA sequencing, whereby the optical field produced by the plasmonic nanostructure is used to both control the translocation of DNA and read out the DNA sequence by means of Raman scattering.26
Local heating of solid-state nanopores was found to have perplexing effects on nanopore transport of ions and DNA.28 The local heating not only increased the ionic current through an open pore in accord with the expectations, but also altered the ratio of the blockade to open-pore currents. While having no effect on the duration of the ionic current blockades, local heating considerably affected the frequency of the blockade events, i.e., the process of DNA capture. The capture rate dependence was sensitive to the electrolyte conditions: as the temperature of the nanopore volume increased, the capture rate decreased in KCl solution but increased in LiCl. The susceptibillity to the electrolyte type was attributed to the differential thermophoretic effect on DNA, which is positive in KCl but negative in LiCl buffers.28 Further experiments elucidated the effects of global heating on DNA translocation.29
Here, we report an all-atom, explicit solvent molecular dynamics (MD) study of the effect of temperature on DNA capture and translocation processes. Reproducing experimental conditions, we investigate how local or global modulations of temperature affect the ionic current blockades, the DNA capture rate, and the effective force on DNA. We show that changes in local ion mobility near DNA are responsible for the observed dependence of relative blockade amplitude on temperature, whereas a temperature dependence of ion binding to DNA alters its effective charge. The results of our study provide further insights into the behavior of DNA subject to local temperature gradients, which is important for the development of biomedical applications that incorporate local heating sources.27,30
Results and Discussion
The primary objective of this work was elucidation of temperature effects on DNA translocation through plasmonic nanopores. Figure 1 illustrates the experimental system considered. The key element of the plasmonic nanopore system is a gold bow tie structure placed on top of a solid-state membrane.21,28 A nanopore is drilled through the gap of the bow tie structure, connecting the two solution-filled compartments with a water-filled passage. A DNA molecule introduced at one side of the nanopore can be electrophoretically driven through the nanopore. The temperature of the system in the vicinity of the nanopore is modulated by illuminating the bow tie structure with a laser beam; the higher the power of the beam the higher the temperature of the bow tie and the surrounding solution.
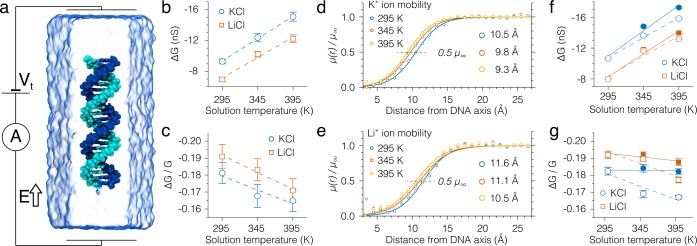
Figure 1.

Plasmonic nanopores. (a) Schematic illustration of the experimental setup used for the measurements of the effect of plasmonic heating on DNA and ion transport through a solid-state nanopore. Two gold triangular prisms (yellow) rest on top of a solid-state membrane (gray) in a bow tie arrangement. In the geometrical center of the bow tie structure, a nanopore in the membrane connects the two solution-filled compartments. A transmembrane bias is induced across the membrane, driving the passage of charged solutes (ions and DNA) from one compartment to the other, through the nanopore. The translocation of DNA through the nanopore is detected as a transient reduction of the nanopore ionic current. The temperature of the bow tie is controlled by a laser-induced plasmon excitations (not shown). The background image shows the distribution of temperature within the symmetry plane of the bow tie indicated by a dashed line in the inset. The temperature map was obtained using the COMSOL Multiphysics software as described in ref (27); the temperature of the bow tie was set to 395 K. The dashed rectangle indicates the approximate location of the all-atom system used for MD simulations. (Inset) Top view of the plasmonic nanopore system detailing the arrangement of the bow tie near the nanopore. (b) Cut-away view of the all-atom model featuring a SiO2 membrane (gray) with an hourglass nanopore in it (3.5 nm in diameter in the middle, 5 nm at the pore entrances), a gold bow tie nanoantenna (yellow), a 20-bp piece of a double-stranded DNA (teal and blue), and electrolyte solution (small spheres). The DNA is initially placed ∼10 nm above the pore entrance and oriented along the z axis, the axis of the nanopore. During MD simulations, a set of constraints allows the molecule to move along and rotate about the z axis. The temperature of the bow tie Tbt is independently controlled from the temperature of bulk solution (295 K). All simulations are performed at a transmembrane bias Vt = 350 mV.
To determine the effect of temperature on nanopore transport of DNA, we built several atomic-scale models of the experimental plasmonic nanopore system. Due to its relatively large size, only a part of the bow tie structure immediately adjacent to the nanopore was explicitly modeled, Figure 1b. Even smaller systems were used to investigate the effect of temperature on ion mobility and binding kinetics. In the remainder of our study, we consider only the temperature effects on DNA transport through plasmonic nanopores, neglecting the possibility of high-intensity optical fields acting directly on DNA.26,31 In doing so, we limit our investigation to the cases where the outcome of the experimental observations does not depend on the polarization of the incident laser beam, which was the experimental situation realized thus far.28 The possibility of direct optical trapping of DNA in the absence of local heating effects has been investigated in ref (26).
All-Atom MD Simulations of DNA Capture and Translocation
To determine the effect of local heating and electrolyte conditions on electrophoretic transport of DNA through solid-state plasmonic nanopores, we built several all-atom models containing the key elements of the experimental system. Each model, Figure 1b, featured two tips of the gold bow tie, a SiO2 membrane containing an hourglass nanopore, a 20-basepair (bp) double-stranded (ds) DNA molecule, water, and ions. In this work, we used a shell of amorphous SiO2 to model an oxidized surface of a Si3N4 membrane;32 the membrane and the gold bow tie were made hollow to reduce the total number of atoms in the simulation system. Two systems containing either 2 M KCl or 2 M LiCl were built. Each system was simulated either at uniform room temperature (295 K) or under a local heating condition, whereby the temperature of the bow tie was maintained at 395 K and the temperature of the solution away from the bow tie was set to 295 K. The local heating was realized by the dual temperature control method27 as described in SI. Figure S1 shows a steady state distribution of temperature in the simulations performed under the local heating conditions.
Each simulation of the electrophoretic transport began having the DNA molecule aligned with the nanopore axis (z-axis); the DNA’s center of mass (CoM) was located ∼9 nm away from the nanopore entrance, Figure 1b. Prior to the application of the electric field, each system was equilibrated for 1 ns having the DNA molecule restrained to its initial location. A uniform external electric field was then applied to produce a transmembrane bias of 350 mV;33,34 the polarity of the bias was chosen to produce translocation of negatively charged DNA through the nanopore. To increase our chances of observing spontaneous capture of DNA by the nanopore, we used custom restraints to limit the translational and rotational degrees of freedom of the DNA molecules to translation along the pore axis and rotation about the pore axis. Doing so also considerably reduced the number of conformations that a DNA molecule could adopt in the nanopore, which increased the accuracy of the ionic current blockade determination. Although the DNA capture rates obtained from such simulations could not be directly compared to experimental capture rates, the simulations, nevertheless, allowed for comparative study of nanopore transport under different electrolyte and temperature conditions.
Figure 2a–d shows the outcome of 16 DNA transport simulations: four independent simulations for each of the four electrolyte and temperature conditions. To characterize the translocation process, we plot in the top panels of Figure 2a–d the location of the DNA’s CoM. Starting from the same initial condition, the molecules first undergo stochastic displacement along the pore axis driven by random forces from the solution. As the molecules approach the nanopore entrance, the electrophoretic force on the DNA increases, making the molecule’s motion more deterministic and unidirectional. Inside the nanopore, the electrophoretic force dominates over random forces from the environement, producing rapid DNA translocation and exit from the nanopore. As DNA molecules translocate through the nanopore, the nanopore ionic current exhibits transient reductions, bottom panels of Figure 2a–d. In fact, the simulated ionic current traces are remarkably similar to experimental ionic current traces obtained for longer DNA molecules.35
Figure 2.
Molecular dynamics simulations of DNA capture and translocation through plasmonic nanopores. (a–d) The z-coordinate of the DNA’s CoM (top) and the ionic current flowing through the nanopore (bottom) in MD simulations of DNA capture. The outcomes of four independent simulations (indicated by color) are shown for each temperature and electrolyte condition. The z axis is defined in Figure 1b; dashed lines indicate the location of the top and bottom membrane surfaces. The ionic current traces (bottom panels) were obtained by applying a 1.9 ns moving average filter to 9.6 ps sampled instantaneous currents. The DNA’s CoM coordinates were recorded every 9.6 ps. (e) The average capture rate versus the bow tie temperature for two electrolyte conditions. For each trajectory, the capture rate was computed as inverse of the time elapsed from the beginning of the simulations to the first moment the molecule’s center of mass passed through the nanopore entrance—the plane of the top surface of the membrane. (f) The average translocation time versus the bow tie temperature for two electrolyte conditions. For each trajectory, the translocation time (shown as a color filled bar) was computed as the time elapsed from the last moment the DNA’s CoM passed through the nanopore entrance and the first moment the DNA reached the nanopore exit—the plane of the bottom surface of the membrane. Open bars with a dashed-line outline show the DNA translocation times computed as a product of the simulated translocation time at 295 K and the ratio of the solvent viscosity at 332 K (average temperature in the nanopore in our simulations) and 295 K, η332 K, C/η295 K, C, Figure 4g, where C denotes either KCl or LiCl. Open bars with a solid-line outline show the DNA translocation times computed as a product of the DNA translocation time at 295 K in 2 M KCl and (η/η295 K, 2 M KCl) (F295 K, 2 M KCl/F), where F and η are the simulated effective force, Figure 4b, and viscosity for the specified solvent and temperature condition. (g, h) The absolute, ΔG = (Ib – I0)/Vt, and relative, ΔG/G = (Ib – I0)/I0, conductance blockades produced by the translocation of a 20-bp DNA. The open-pore, I0, ionic current was computed by averaging the ionic current prior to DNA capture. The blockade current, Ib, was chosen as the minimum value of the 1.9 ns-averaged ionic current traces, panels a–d, during the DNA translocation. In panels e–h, each data point indicates an average of the four independent simulations performed at the same temperature and electrolyte conditions; the error bars show the standard error of the mean.
Analysis of the simulation trajectories characterized the DNA transport process in terms of the average capture rate, Figure 2e; the average translocation time, Figure 2f; and the absolute, Figure 2g, and relative, Figure 2h, conductance blockades. For each simulation, we computed a capture rate as a multiplicative inverse of the time elapsed from the beginning of the simulation and the moment the DNA’s CoM passed through the nanopore entrance—the plane of the top membrane surface. In the simulations performed under identical heating and ionic solution conditions, the DNA capture time varied considerably from one simulation to the other. Typically, capture events were observed within 30 to 100 ns, which correspond to 10–33 capture events in 1 μs. Such very high capture rates were, of course, a consequence of the simulations setup. Nevertheless, the simulated capture events clearly exhibited the expected stochastic features of the DNA capture process. Unfortunately, the high statistical error in the determination of the average capture rate caused by the limited number of independent MD runs did not allow us to determine the effect of the electrolyte and temperature conditions.
The simulated movement of DNA molecules through the nanopore was more deterministic than the DNA capture. Hence, the statistical error in determining the average DNA translocation time was considerably less than in determining the average capture rate. In our analysis, we defined the translocation time as the time it took the DNA’s CoM to pass from the top surface to the bottom surface of the membrane, a distance of ∼10 nm. When simulated at uniform room temperature, DNA translocation was about 2 times faster in KCl than in LiCl solution, Figure 2f. Heating reduced the translocation time for both KCl and LiCl, but the reduction was more pronounced for LiCl than for KCl. In experiment, local heating had no measurable effect on DNA translocation time, whereas global heating resulted in DNA moving faster through the pore.28 The results of our simulations and experiment could be reconciled assuming the DNA translocation time in experiment is determined by the untranslocated part of the DNA molecule (DNA blob), which was not modeled in our simulations. MD simulations of the effective force in heated nanopores (described below) provide further support to this hypothesis.
The ionic current traces shown in Figure 2a–d were used to compute the conductance blockades produced by the passage of the DNA molecules through the nanopore. The instantaneous values of the ionic current were determined by computing the ion displacements between consecutive frames of the MD trajectories.33,34 For each electrolyte and heating condition, we determined an open-pore current value, I0, as the mean ionic current flowing through the nanopore before the moment the DNA entered the nanopore. Previous MD studies36 found the open-pore current to increase with temperature at the rate prescribed by the bulk conductivity dependence on temperature. In our simulations, the open-pore conductance increased with the bow tie temperature less rapidly than the bulk electrolyte conductivity with the bulk solution temperature, Figure S2, because the temperature of the electrolyte in the nanopore volume was considerably smaller than the temperature of the bow tie, Figure S1. Each ionic current trace characterizing a single DNA translocation event was averaged by applying a moving average filter with the 1.9 ns window; the minimum value of the ionic current was chosen as the blockade current Ib. The absolute and relative conductance blockades were obtained according to their definitions, i.e., as ΔG = (Ib – I0)/Vt and ΔG/G = (Ib – I0)/I0, correspondingly, where Vt = 350 mV was the transmembrane bias. The simulated conductance blockades and their dependence on temperature are shown in Figure 2g–h. Despite the approximations made during the setup of the simulations, the obtained conductance blockades closely resemble experimentally reported ones.28
Microscopic Mechanism of Relative Conductance Blockade Dependence on Temperature
To elucidate the microscopic processes that give rise to the observed temperature effects, we built several additional all-atom models containing a short fragment of a dsDNA (22-bp) in an evenly heated 2 M KCl or LiCl electrolyte solution, Figure 3a. The use of uniform heating is justified by the fact that, although the heating of a plasmonic nanopore device is local at the length scale of the device, it is nearly uniform at the length scale of a short DNA fragment confined to the constriction of the nanopore.26 Furthermore, because the electric field across the membrane is highly inhomogeneous and is focused at the pore constriction, modeling the constriction region of the nanopore is expected to provide insights into the temperature dependence of the ionic current blockade and the effective electrophoretic force of a full-scale system. In our simulations of the bulk systems, the DNA fragment was restrained to align with the z-axis through a set of harmonic constraints that also reported on the effective force applied to DNA by the electric field. An electric field corresponding to a potential drop of 350 mV over 10 nm distance was applied parallel to the DNA (z-axis). Each of the two systems (2 M KCl or 2 M LiCl) was simulated at a uniform temperature of 295, 345, and 395 K.
Figure 3.
Bulk electrolyte simulations of the temperature effect
on ionic
current blockade. (a) A typical simulation system containing a 22-bp
dsDNA molecule (teal and blue) submerged in an electrolyte solution
(semitransparent surface). The system is subject to a constant electric
field of 35 mV/nm. A set of harmonic
restraints prevents DNA from drifting in the electric field, reporting
on the value of the effective force. The temperature of the system
is uniformly set to a prescribed value. (b, c) The temperature dependence
of the absolute, ΔG = (Ib – I0)/Vt, and relative, ΔG/G = (Ib – I0)/I0, conductance
blockades. Here, I0 is obtained as the
bulk ionic current density j0 multiplied
by the cross-sectional area of
the simulation unit cell within the plane perpendicular to the molecule’s
axis; Ib is the actual current flowing
through the simulations system and Vt =
35 (mV/nm)·Lz (nm),
where Lz is the size
of the system along the z axis. (d, e) Normalized
mobility of ions as a function of the radial distance from the central
axis of the DNA helix. Each radial profile was normalized by the corresponding
average value of mobility in the bulk electrolyte region r > R*, where R* = 2.2 nm for all solutions and temperatures. Solid lines
are fit
to data of a smooth-step function 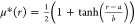 , where the fitting parameters a and b characterize the location and the steepness,
respectively, of the smooth step. (f, g) Absolute (panel f) and relative
(panel g) conductance blockades computed using the normalized number
density and mobility of ions, eqs 1 and 2 (see SI for details). As before, R* was set to 2.2 nm, and the value of R0 was set to 2.7 nm in order to compare the results to those shown
in panels b–c. Open symbols show the conductance blockades
computed using the number density and mobility dependences observed
in the MD simulations. Filled symbols indicate the conductance blockade
values that would be observed if the normalized ion mobility, μ(r)/μ∞, were independent of solution
temperature. Dashed and solid lines in both panels show linear fits
to the data.
, where the fitting parameters a and b characterize the location and the steepness,
respectively, of the smooth step. (f, g) Absolute (panel f) and relative
(panel g) conductance blockades computed using the normalized number
density and mobility of ions, eqs 1 and 2 (see SI for details). As before, R* was set to 2.2 nm, and the value of R0 was set to 2.7 nm in order to compare the results to those shown
in panels b–c. Open symbols show the conductance blockades
computed using the number density and mobility dependences observed
in the MD simulations. Filled symbols indicate the conductance blockade
values that would be observed if the normalized ion mobility, μ(r)/μ∞, were independent of solution
temperature. Dashed and solid lines in both panels show linear fits
to the data.
Flow of ions pass biomolecules in bulk electrolyte solutions cannot be described via open-pore or blockade currents per se. Yet, one can quantify the suppression of the ionic flow caused by the molecule in its vicinity. Previous MD simulations have found the ion mobility near DNA to be suppressed in comparison to the bulk value.37,38 The distance (from the molecule) at which the ions regain their bulk mobility can depend on various factors, including temperature. The plots of the radial profiles of ionic current density indicate that this distance in our simulations is ∼1.2 nm from the DNA surface or R* = 2.2 nm from the DNA axis, Figure S3. Hereafter, we refer to the region farther than 2.2 nm from the DNA axis as bulk solution.
Knowing the average current density in the bulk electrolyte region and the cross-sectional area of the simulation system, we can estimate the magnitude of the ionic current that would have flown in the absence of the molecule, i.e., the open-pore current I0. The blockade current Ib can be obtained directly form the simulations as the total current flowing in the direction of the applied field. Figure 3b–c plots the absolute and relative conductance blockades computed using the I0 and Ib values obtained from the simulations of a DNA fragment in uniform solution. Interestingly, the absolute conductance blockades have similar values to those observed in the simulations of the DNA capture, Figure 2g,h. This resemblance supports the conclusion about the major role of the ion mobility suppression in determining the absolute conductance blockade.38 Noticeable differences in the values of relative conductance blockades can be readily explained. First and foremost, the relative conductance blockade depends on the open-pore conductance value, which is considerably greater for the bulk electrolyte system, Figure 3a, in comparison to the plasmonic nanopore system, Figure 1b. Other factors that may contribute to the observed differences are the reduction of ion mobility by the nanopore walls, the hourglass shape of the nanopore, and the nonuniform distribution of temperature (Figure S1) in the plasmonic nanopore system. Overall, the dependence of the relative conductance blockades on the solution temperature is, however, captured correctly: the relative conductance blockade decreases in magnitude as temperature increases.
To explain the observed changes of the conductance blockades, we computed the radial profiles of ion mobility, μ(r), as a function of the distance from the DNA axis, r. The profiles of ion mobility were determined by first computing the radial profiles of ion and water velocities, vion(r) and vwater(r), Figure S4. The local ion mobility was then computed as μion(r) = (vion(r) – vwater(r))/E, where E was the magnitude of the applied electric field. As expected, ion mobility increases with the distance from the DNA and with the solution temperature, Figure S5. To quantitatively compare the changes in the ion mobility profiles, we normalized the ion mobility profiles by the corresponding bulk ion mobility values. The normalized mobility profiles, Figure 3d–e, clearly show that, as the temperature of the electrolyte solutions increases, the ion mobility reaches its bulk value (μ∞) faster. To highlight the change, we fitted the normalized mobility dependences with a smooth-step function (solid lines) and marked the level at which the ions gain 50% of their bulk mobility values (black dashed lines), Figure 3d–e. Clearly, the intersection of the fit with the 50%-level is closer to DNA at higher temperatures of the electrolyte solutions.
To directly show that the change of the ion mobility with temperature explains the dependence of the conductance blockades on temperature, we express the absolute and relative conductance blockades as (see SI for details):
| 1 |
 |
2 |
Here, Lz is the dimension of the simulation system along the direction of the applied electric field; q, n∞, and μ∞ are the charge, the number density, and the ion mobility in the bulk electrolyte solution, correspondingly; n*(r) (shown in Figure S6) and μ*(r) are the normalized (by the corresponding values in the bulk electrolyte region) profiles of the ion number density and ion mobility; r is the distance from the DNA axis; R* is the distance from the DNA axis at which ion mobility and number density return to their bulk values; R0 is the radius of the pore to which the comparison is being made (for the calculations of the relative conductance blockade). In both equations, the summation is performed over all ion types present in the solution (e.g., K+, Li+, Cl–). The conductance blockades computed using the above expressions, Figure 3f–g (open symbols), reproduce the results of our previous calculations based on direct determination of the ionic current, Figure 3b–c.
Using eqs 1 and 2, we can separate the dependence of the conductance blockades on bulk (μ∞) and normalized (μ*) mobilities of the ions. Thus, we can model an imaginary situation in which bulk mobilities retain their dependence on the temperature, but normalized ones remain unchanged, μ*(r,T) = μ*(r, 295 K). The results of calculations for such a situation are shown in Figure 3f–g (filled symbols): the temperature dependence of the relative conductance blockades is vanished. A similar outcome (no temperature dependence of the relative conductance blockade) could be expected from a model that does not take the reduction of ion mobility near DNA into account. Thus, our analysis indicates that the experimentally observed dependence of the relative conductance on temperature originates from the temperature dependence of ion mobility near DNA.
Temperature Dependence of the Effective Force in a Nanopore
To understand the origin of the dwell time dependence on local and global heating, we measured the effective force of the electric field on DNA in a plasmonic nanopore. For these simulations, we harmonically restrained a 77-bp fragment of random sequence dsDNA in a plasmonic nanopore. The DNA molecule was initially placed concentric with the nanopore, along the z-axis, Figure 4a. The average displacement of the DNA under a transmembrane bias of 350 mV reported on the effective force experienced by the DNA.39 The simulations of the effective force were carried out for three electrolyte solutions (2 M KCl, 2 M LiCl, and 1 M KCl) and two heating conditions (Tbt = 295 or 395 K). All other simulation conditions and protocols, including the dimensions of the nanopore and the bow tie and the local heating protocol, were identical to those used in our simulations of DNA capture, Figure 1b.
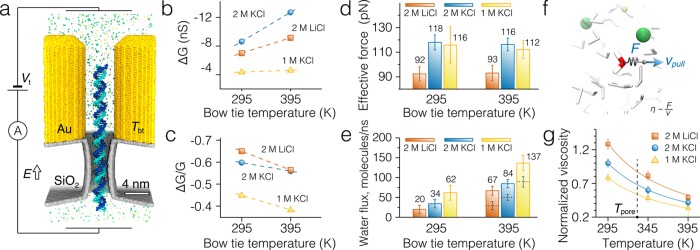
Figure 4.
Measurements of the effective force on DNA in a plasmonic nanopore. (a) Cut-away view of the simulation system. A 77-bp double-stranded DNA molecule is threaded through a 3.5 nm diameter nanopore in a solid-state membrane. The DNA’s phosphorus atoms are harmonically restrained to their initial coordinates. Displacement of the DNA from the initial coordinates in electric field E reports on the effective force.39 The temperature of the gold bow tie nanoantenna, Tbt, is maintained independently from the temperature of the solution using a dual thermostat method.27 The solid-state membrane and the gold bow tie have the same dimensions as in the simulations of the DNA capture, Figure 1b. (b, c) Absolute (panel b) and relative (panel c) conductance blockades produced by the double-stranded DNA molecule in plasmonic nanopores for two temperatures of the bow tie nanoantenna, Tbt, and several electrolyte solutions (2 M KCl, 2 M LiCl, and 1 M KCl). (d) The effective force experienced by the DNA molecule in a plasmonic nanopore at 2 M KCl, 2 M LiCl, or 1 M KCl electrolyte solutions at two bow tie temperatures. (e) The average flux of water flowing through the plasmonic nanopore blocked by DNA (filled bars). The flux is computed through the middle plane of the membrane perpendicular to the nanopore axis. The dashed lines show the water flux at Tbt = 395 K computed by multiplying the water flux values at 295 K and the ratio of solution viscosities at 295 and 332 K, the latter being the average temperature of the nanopore volume. (f) Setup of the all-atom MD simulations for measuring the relative solution viscosity. A single water molecule is pulled through a solution with a constant velocity vpull = 10 nm/ns. The average force required to maintain the constant velocity of the molecule is directly proportional to the solution viscosity. (g) Temperature dependence of electrolyte solutions’ viscosities normalized by the viscosity of 2 M KCl solution at 295 K. The procedure for obtaining the normalized viscosities is described in the text and is schematically shown in panel f. The vertical dashed line indicates the average temperature inside the nanopore at bow tie temperature of 395 K.
In addition to measuring the effective force (discussed in the next paragraph), the simulations provided a set of independent measurements of the blockade ionic current. Using the open-pore current data obtained from the DNA capture simulations, we computed the dependence of the absolute and relative conductance blockades on the bow tie temperature, Figure 4b–c (a separate open-pore simulation was performed for 1 M KCl). Interestingly, the conductance blockades measured for the 77-bp DNA fragment almost precisely matched the values obtained from the DNA capture simulations with the only noticeable deviation in the 2 M KCl solution at Tbt = 395 K.
More importantly, however, we find that the force experienced by the DNA in the plasmonic nanopore does not depend on the bow tie temperature within the accuracy of our measurement, Figure 4d, even though the same heating leads to a significant increase of the water flux through the pore, Figure 4e (filled bars). Whether local or global, heating reduces viscosity of the solvent in the nanopore, which increases the electro-osmotic flow that opposes the movement of the DNA in the electric field. To estimate the effect of temperature on the solution viscosity, we simulated the pulling of a single water molecule through a bulk electrolyte solution with a constant velocity vpull = 10 nm/ns, Figure 4f. In such simulations, viscosity of the solution is proportional to the quotient of the average force F required to pull the molecule divided by the target velocity, ηsolution ∼ F/vpull.40Figure 4g plots the simulated temperature dependence of the electrolytes’ viscosity normalized by the viscosity of a 2 M KCl solution at 295 K. Multiplication of the room temperature water flux values with the inverse ratio of the electrolyte viscosities at the average temperature of the nanopore volume (Tpore = 332 K) yields theoretical estimates (dashed lines in Figure 4e) that are only 56–62% of the flux values actually observed in the MD simulations. Thus, the water flux increases more strongly with temperature in our simulations than predicted by the continuum hydrodynamics model,41,42 which, as we show in the next section, can be explained by the temperature dependence of the slip velocity at the DNA surface.
Previous experimental,42−44 theoretical,41,45,46 and computational39,44,47,48 studies identified three mechanisms for the effective screening of the DNA charge in solid-state nanopores: direct binding of counterions to the molecule,41,43,44,47 binding of the DNA to the nanopore surface,48 and electro-osmotic screening due to the flow of solvent through the nanopore.39,41,42,45 Difficult to characterize experimentally, direct binding of ions was estimated to reduce the bare charge of DNA by ∼25% of its nominal value in 1 M KCl solution;42 the reduction could also depend on the cation type and concentration.44 In the next section, we evaluate the effect of temperature on the direct binding mechanism. Electro-osmotic screening was found to be independent of the solution’s viscosity but decrease with the pore diameter.39,41,42 Although we have previously shown that DNA binding to the pore walls can considerably reduce the effective force experienced by the DNA in a nanopore,48 we do not further consider this mechanism in this work as in all our simulations DNA does not come in contact with the nanopore surface.
It was previously suggested that the DNA translocation time τ is directly proportional to the viscosity of the solution η and inversely proportional to the effective force of the electric field on the DNA molecule, Feff.44−46 The simulated effective force on DNA did not show a temperature dependence within the accuracy of the force measurement (10–20% of the absolute values). In order to check if the relationship between the DNA translocation time and the solution viscosity holds in our DNA capture simulations, we first estimated the average viscosity of the solution inside the nanopore. Multiplication of the viscosity ratios at the average pore (332 K) and room (295 K) temperatures with the average DNA translocation times obtained at 295 K yields the DNA translocation times close to that obtained at Tbt = 395 K, Figure 2f. Thus, the simulated DNA translocation time is directly proportional to the average nanopore solution viscosity.
To test the relationship between the effective force experienced by the DNA in the nanopore and the DNA translocation time, we computed the DNA translocation times based on the normalized viscosity values, Figure 4g, the effective force experienced by the DNA in the pore, Figure 4d, and the DNA translocation time at 295 K in 2 M KCl as τ = (η/ηKCl, 295 K)(FKCl, 295 K/F)(τKCl, 295 K). The results of these predictive calculations accurately reproduce the simulated dependence of the DNA translocation times on the local heating of the bow tie within the simulation error, see open bars with solid outlines in Figure 2f.
The results of our DNA capture simulations and the force–viscosity scaling analysis indicate faster DNA translocations for locally heated bow tie structures, which appears to disagree with experiment.28 However, the key difference between our simulation and experiments is the length of the DNA molecule: 20-bp molecules were used in our DNA capture simulations whereas experiment was carried out using lambda-DNA (48.5 kbp). For DNA molecules much longer than the persistence length of DNA, the translocation velocity is determined by the balance of the effective force applied to DNA in the nanopore and the viscous drag of the polymer coil formed by the untranslocated part of the molecule.49 Our simulations have found the effective force in the nanopore to be insensitive to the changes in the nanopore temperature. Because the force of the applied electric field is localized to the volume of the nanopore, the above conclusion is valid for both global and local heating conditions. As local heating alters neither the effective force nor the viscous drag, it does not influence the translocation time of long DNA molecules. The global heating, however, lowers the viscous drag, leading to faster DNA translocations regardless of the length of the DNA molecule.
Temperature Dependence of DNA Charge Neutralization by Ion Binding and Slip Velocity
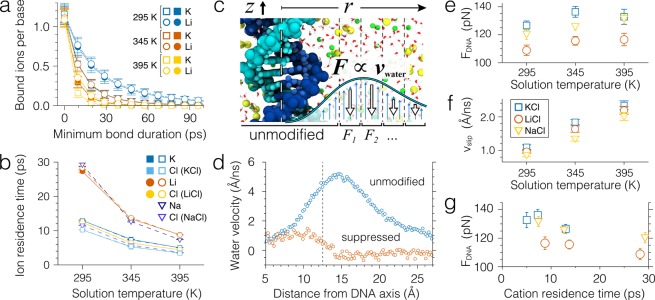
Transient binding of counterions to a DNA molecule can lower its effective charge and, thereby, the effective force that a DNA molecule experiences in a nanopore under a transmembrane bias.44,47 To elucidate the effect of temperature on DNA charge screening by ion binding, we computed the mean residence time of ions forming direct contacts with water molecules proximal to DNA atoms (ion binding to DNA takes place through an intermediate water molecule44,50), Figure 5a–b. For these calculations, we used 500 ns-long MD trajectories of the bulk electrolyte DNA systems, Figure 3a; the method used to compute ion binding times is described in ref (44) and summarized in the SI. The instantaneous number of ions bound to DNA (i.e., at zero minimum bond duration) is found to be independent of the ion type or temperature, Figure 5a. However, the number of ions that stay bound to DNA exponentially decreases with the duration of the bond. Consistent with our previous finding,44 lithium ions are more likely to form longer lasting bonds with DNA than potassium ions at the same temperature. To characterize ion binding onto DNA quantitatively, we fitted the plots of the number of bound ions versus their minimum bond duration by exponential functions, thus, obtaining the average binding time for each ion type and temperature, Figure 5b. The average binding time of cations is seen to decrease with temperature, the reduction being more prominent for lithium ions than for potassium ions.
Figure 5.
Effect of temperature on ion binding and its relation to the effective force on the DNA. (a) The average number of ions bound to a DNA nucleotide as a function of the minimum bond duration. Open and filled symbols show the results of analysis applied to simulations performed with and without the bulk flow suppression protocol, respectively. Lines show n = n0 e–t/t0 fits to the data, where n0 is the instantaneous number of ions (zero minimum bond duration) and t0 is the mean residence time. (b) Temperature dependence of the average residence time of ions near the DNA molecule in 2 M KCl and 2 M LiCl solutions. (c) Schematic illustration of the MD simulations of the DNA molecule in the bulk electrolyte solution in which the flow of water around the molecule is suppressed. Flow suppression forces applied 1.25 nm away from the DNA axis and thus do not affect ion binding to DNA (see panels a and b). The space around the molecule is split into 3 Å-wide cylindrical bins. Average velocity of water in each bin is computed every 1 ps and is used to calculate the friction forces that are applied to the water molecules in the direction opposite to the flow. The applied forces were computed according to a proportional-integral-derivative control mechanism, which is described in detail in SI. (d) Example profiles of water velocity near the DNA molecule in 2 M KCl solution at 295 K before and after the flow suppression is applied. Dashed line indicates the boundary (1.25 nm from the molecule’s axis) at which the flow suppression is enabled. (e–f) Temperature dependence of the average force acting on the 22-basepair DNA molecule (panel e) and of the water slip velocity near the molecule (panel f) in the electrolyte solution subject to a constant electric field of 35 mV/nm when the water flows are suppressed. Water slip velocity is defined as the mean water velocity in the region between 0.9 to 1.1 nm away from the molecule’s axis. Error bars show the standard error of the mean. (g) The same force plotted in panel e as a function of cation residence time near the molecule. Higher residence times correspond to lower solution temperatures (see panel b).
Using a theoretical model, we have previously shown that duration of ion-DNA bonds can affect the effective force that a DNA molecule experiences in an external electric field: longer lasting bonds produce a smaller-magnitude effective force.44 We were, however, not able to directly assess the magnitude of the effect in all-atom MD simulations because of the effect of the electro-osmotic flow. Similarly, in our simulation of bulk DNA systems (Figure 3a), temperature was found to not only change the ion binding time to DNA, Figure 5b, but also alter the profile of the solvent flow, Figure S4c,f.
To decouple the ion binding and electro-osmotic screening mechanisms, we carried out an additional set of MD simulations applying external friction forces to suppress the electro-osmotic flow around DNA without affecting ion binding to the molecule, Figure 5c. The flow suppression protocol employed a proportional-integral-derivative control mechanism described in detail in SI. Water molecules located within 1.25 nm from the DNA axis were not subject to the flow suppression forces, leaving the kinetics of ion binding to DNA unaffected, Figure 5a,b. Figure 5d illustrates the effect of the water flow suppression protocol: the electro-osmotic flow away from the DNA is substantially reduced. Furthermore, water flow away from the DNA was suppressed to the same degree at all temperature and electrolyte conditions, Figure S7, which allowed us to eliminate the effect of bulk electro-osmotic flow in comparative study of the systems.
Using the water suppression simulation protocol, we could obtain the dependence of the effective force on temperature for LiCl, NaCl, and KCl electrolytes in the absence of the electro-osmotic effect, Figure 5e. The measured forces were generally a factor of 2–3 higher than those obtained in the presence of the electro-osmotic flow and moderately increased with temperature. The forces remained considerably smaller than the maximum theoretical force (235 pN for our simulation systems), which we attribute to nonzero shear force of the water flow in immediate proximity to DNA (within 1.25 nm of the DNA central axis). The average velocity of water at the DNA surface—the water slip velocity, Figure 5f— is seen to increase with temperature; the increase being independent of the type of cations surrounding DNA. The observed increase of the slip velocity with temperature can explain stronger than expected increase of the water flux through a nanopore blocked by DNA, Figure 4e. The plot of the effective force versus ion binding time, Figure 5g, reveals a weak yet systematic dependence of the effective force on the lifetime of ion bond to DNA: the force decreases as the lifetime increases. The dependence, however, is weak enough to be concealed by the statistical error in our simulation of the effective force, Figure 4d.
Conclusions
Using the all-atom MD approach, we have systematically studied the effect of temperature on the process of DNA translocation through a solid-state nanopore. The results of our simulations have shown that, in addition to affecting bulk properties of electrolyte solutions such as viscosity and ionic conductivity, temperature can modify local interactions of ions and water with DNA. The temperature dependence of ion mobility near DNA surfaces causes the relative conductance blockade to depend on temperature,28 an effect that can not be explained by the temperature dependence of bulk ion conductivity alone. The temperature was also found to affect ion binding to DNA and the solvent velocity at the DNA surface, both of which can affect the effective force of an external electric field on DNA.
Although our simulations of DNA capture were designed to produce a substantial temperature gradient along the capture pathway, we did not observe any prominent thermophoretic effects that could explain the enhanced DNA capture in LiCl solutions reported in the experimental studies.28 The relatively high transmembrane bias used in our DNA capture simulations along with the high statistical uncertainty in determining the capture rate from all-atom MD simulations might have concealed the effect. Also, our simulations did not explore the possible effects of laser heating on the nanopore geometry and the charge of the nanopore walls,19 which could also modulate the nanopore conductance and the electro-osmotic flow. Our study highlights the unique capabilities of nanopore translocation experiments and atomistic MD simulations in probing thermal process in nanofluidic systems.
Acknowledgments
This work was supported by the grants from the National Institutes of Health (R01-HG007406 and P41-RR005969) and the National Science Foundation (DMR-0955959). The supercomputer time provided through XSEDE Allocation Grant MCA05S028 and the Blue Waters petascale supercomputer system (UIUC). The authors gladly acknowledge valuable discussions with Magnus Jonsson, Jim Wilson, and Cees Dekker.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.6b00463.
Detailed description of the simulation and analysis procedures; plots of temperature distribution in the locally heated nanopore; the simulated temperature dependence of bulk ion conductivity; profiles of ion mobility, current and ion densities, water and ion velocities (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Dekker C. Solid-State Nanopores. Nat. Nanotechnol. 2007, 2, 209–215. 10.1038/nnano.2007.27. [DOI] [PubMed] [Google Scholar]
- Kasianowicz J. J.; Robertson J. W. F.; Chan E. R.; Reiner J. E.; Stanford V. M. Nanoscopic Porous Sensors. Annu. Rev. Anal. Chem. 2008, 1, 737–766. 10.1146/annurev.anchem.1.031207.112818. [DOI] [PubMed] [Google Scholar]
- Zwolak M.; Di Ventra M. Colloquium: Physical Approaches to DNA Sequencing and Detection. Rev. Mod. Phys. 2008, 80, 141–165. 10.1103/RevModPhys.80.141. [DOI] [Google Scholar]
- Howorka S.; Siwy Z. S. Nanopore Analytics: Sensing of Single Molecules. Chem. Soc. Rev. 2009, 38, 2360–2384. 10.1039/b813796j. [DOI] [PubMed] [Google Scholar]
- Bezrukov S. M.; Vodyanoy I.; Parsegian V. A. Counting Polymers Moving through a Single Ion Channel. Nature 1994, 370, 279–281. 10.1038/370279a0. [DOI] [PubMed] [Google Scholar]
- Kasianowicz J. J.; Brandin E.; Branton D.; Deamer D. W. Characterization of Individual Polynucleotide Molecules Using a Membrane Channel. Proc. Natl. Acad. Sci. U. S. A. 1996, 93, 13770–13773. 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Q.; Braha O.; Conlan S.; Cheley S.; Bayley H. Stochastic Sensing of Organic Analytes by a Pore-Forming Protein Containing a Molecular Adapter. Nature 1999, 398, 686–690. 10.1038/19491. [DOI] [PubMed] [Google Scholar]
- Wanunu M.; Bhattacharya S.; Xie Y.; Tor Y.; Aksimentiev A.; Drndic M. Nanopore Analysis of Individual RNA/Antibiotic Complexes. ACS Nano 2011, 5, 9345–9353. 10.1021/nn203764j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke J.; Wu H.-C.; Jayasinghe L.; Patel A.; Reid S.; Bayley H. Continuous Base Identification for Single-Molecule Nanopore DNA Sequencing. Nat. Nanotechnol. 2009, 4, 265–270. 10.1038/nnano.2009.12. [DOI] [PubMed] [Google Scholar]
- Cherf G. M.; Lieberman K. R.; Rashid H.; Lam C. E.; Karplus K.; Akeson M. Automated Forward and Reverse Ratcheting of DNA in a Nanopore at 5-Å Precision. Nat. Biotechnol. 2012, 30, 344–348. 10.1038/nbt.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laszlo A. H.; Derrington I. M.; Ross B. C.; Brinkerhoff H.; Adey A.; Nova I. C.; Craig J. M.; Langford K. W.; Samson J. M.; Daza R.; Doering K.; Shendure J.; Gundlach J. H. Decoding Long Nanopore Sequencing Reads of Natural DNA. Nat. Biotechnol. 2014, 32, 829–833. 10.1038/nbt.2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gracheva M. E.; Xiong A.; Aksimentiev A.; Schulten K.; Timp G.; Leburton J.-P. Simulation of the Electric Response of DNA Translocation through a Semiconductor Nanopore-Capacitor. Nanotechnology 2006, 17, 622–633. 10.1088/0957-4484/17/3/002. [DOI] [Google Scholar]
- Luan B.; Peng H.; Polonsky S.; Rossnagel S.; Stolovitzky G.; Martyna G. Base-by-Base Ratcheting of Single Stranded DNA through a Solid-State Nanopore. Phys. Rev. Lett. 2010, 104, 238103. 10.1103/PhysRevLett.104.238103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traversi F.; Raillon C.; Benameur S. M.; Liu K.; Khlybov S.; Tosun M.; Krasnozhon D.; Kis A.; Radenovic A. Detecting the Translocation of DNA through a Nanopore Using Graphene Nanoribbons. Nat. Nanotechnol. 2013, 8, 939–945. 10.1038/nnano.2013.240. [DOI] [PubMed] [Google Scholar]
- Shankla M.; Aksimentiev A. Conformational Transitions and Stop-and-Go Nanopore Transport of Single-Stranded DNA on Charged Graphene. Nat. Commun. 2014, 5, 5171. 10.1038/ncomms6171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNally B.; Singer A.; Yu Z.; Sun Y.; Weng Z.; Meller A. Optical Recognition of Converted DNA Nucleotides for Single-Molecule DNA Sequencing Using Nanopore Arrays. Nano Lett. 2010, 10, 2237–2244. 10.1021/nl1012147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C.; Ye J.; Li Y.; Lagae L.; Stakenborg T.; Van Dorpe P. Detection of DNA Bases and Oligonucleotides in Plasmonic Nanoslits Using Fluidic SERS. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 4600707–4600707. 10.1109/JSTQE.2012.2226564. [DOI] [Google Scholar]
- Cecchini M. P.; Wiener A.; Turek V. A.; Chon H.; Lee S.; Ivanov A. P.; McComb D. W.; Choo J.; Albrecht T.; Maier S. A.; Edel J. B. Rapid Ultrasensitive Single Particle Surface-Enhanced Raman Spectroscopy Using Metallic Nanopores. Nano Lett. 2013, 13, 4602–4609. 10.1021/nl402108g. [DOI] [PubMed] [Google Scholar]
- Di Fiori N.; Squires A.; Bar D.; Gilboa T.; Moustakas T. D.; Meller A. Optoelectronic Control of Surface Charge and Translocation Dynamics in Solid-State Nanopores. Nat. Nanotechnol. 2013, 8, 946–951. 10.1038/nnano.2013.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiner J. E.; Robertson J. W. F.; Burden D. L.; Burden L. K.; Balijepalli A.; Kasianowicz J. J. Temperature Sculpting in Yoctoliter Volumes. J. Am. Chem. Soc. 2013, 135, 3087–3094. 10.1021/ja309892e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonsson M. P.; Dekker C. Plasmonic Nanopore for Electrical Profiling of Optical Intensity Landscapes. Nano Lett. 2013, 13, 1029–1033. 10.1021/nl304213s. [DOI] [PubMed] [Google Scholar]
- Li Y.; Nicoli F.; Chen C.; Lagae L.; Groeseneken G.; Stakenborg T.; Zandbergen H. W.; Dekker C.; Van Dorpe P.; Jonsson M. P. Photoresistance Switching of Plasmonic Nanopores. Nano Lett. 2015, 15, 776–782. 10.1021/nl504516d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belkin M.; Maffeo C.; Wells D. B.; Aksimentiev A. Stretching and Controlled Motion of Single-Stranded DNA in Locally Heated Solid-State Nanopores. ACS Nano 2013, 7, 6816–6824. 10.1021/nn403575n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palankar R.; Pinchasik B.-E.; Khlebtsov B. N.; Kolesnikova T. A.; Möhwald H.; Winterhalter M.; Skirtach A. G. Nanoplasmonically-Induced Defects in Lipid Membrane Monitored by Ion Current: Transient Nanopores versus Membrane Rupture. Nano Lett. 2014, 14, 4273–4279. 10.1021/nl500907k. [DOI] [PubMed] [Google Scholar]
- Nam S.; Choi I.; Fu C.; Kim K.; Hong S.; Choi Y.; Zettl A.; Lee L. P. Graphene Nanopore with a Self-Integrated Optical Antenna. Nano Lett. 2014, 14, 5584–5589. 10.1021/nl503159d. [DOI] [PubMed] [Google Scholar]
- Belkin M.; Chao S.-H.; Jonsson M. P.; Dekker C.; Aksimentiev A. Plasmonic Nanopores for Trapping, Controlling Displacement, and Sequencing of DNA. ACS Nano 2015, 9, 10598–10611. 10.1021/acsnano.5b04173. [DOI] [PMC free article] [PubMed] [Google Scholar]; PMID: 26401685.
- Belkin M.; Chao S.-H.; Giannetti G.; Aksimentiev A. Modeling Thermophoretic Effects in Solid-State Nanopores. J. Comput. Electron. 2014, 13, 826–838. 10.1007/s10825-014-0594-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicoli F.; Verschueren D.; Klein M.; Dekker C.; Jonsson M. P. DNA Translocations through Solid-State Plasmonic Nanopores. Nano Lett. 2014, 14, 6917–6925. 10.1021/nl503034j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verschueren D. V.; Jonsson M. P.; Dekker C. Temperature Dependence of DNA Translocations through Solid-State Nanopores. Nanotechnology 2015, 26, 234004. 10.1088/0957-4484/26/23/234004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duhr S.; Braun D. Why Molecules Move Along a Temperature Gradient. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 19678–19682. 10.1073/pnas.0603873103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pang Y.; Gordon R. Optical Trapping of a Single Protein. Nano Lett. 2012, 12, 402–406. 10.1021/nl203719v. [DOI] [PubMed] [Google Scholar]
- Raider S. I.; Flitsch R.; Aboaf J. A.; Pliskin W. A. Surface Oxidation of Silicon Nitride Films. J. Electrochem. Soc. 1976, 123, 560–565. 10.1149/1.2132877. [DOI] [Google Scholar]
- Aksimentiev A.; Heng J. B.; Timp G.; Schulten K. Microscopic Kinetics of DNA Translocation Through Synthetic Nanopores. Biophys. J. 2004, 87, 2086–2097. 10.1529/biophysj.104.042960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aksimentiev A.; Schulten K. Imaging α-Hemolysin with Molecular Dynamics: Ionic Conductance, Osmotic Permeability and the Electrostatic Potential Map. Biophys. J. 2005, 88, 3745–3761. 10.1529/biophysj.104.058727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenstein J. K.; Wanunu M.; Merchant C. A.; Drndic M.; Shepard K. L. Integrated Nanopore Sensing Platform with Sub-Microsecond Temporal Resolution. Nat. Methods 2012, 9, 487–492. 10.1038/nmeth.1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chimerel C.; Movileanu L.; Pezeshki S.; Winterhalter M.; Kleinekathofer U. Transport at the Nanoscale: Temperature Dependence of Ion Conductance. Eur. Biophys. J. 2008, 38, 121–125. 10.1007/s00249-008-0366-0. [DOI] [PubMed] [Google Scholar]
- Comer J.; Aksimentiev A. Predicting the DNA Sequence Dependence of Nanopore Ion Current Using Atomic-Resolution Brownian Dynamics. J. Phys. Chem. C 2012, 116, 3376–3393. 10.1021/jp210641j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesselheim S.; Müller W.; Holm C. Origin of Current Blockades in Nanopore Translocation Experiments. Phys. Rev. Lett. 2014, 112, 018101. 10.1103/PhysRevLett.112.018101. [DOI] [PubMed] [Google Scholar]
- Luan B.; Aksimentiev A. Electro-Osmotic Screening of the DNA Charge in a Nanopore. Phys. Rev. E 2008, 78, 021912. 10.1103/PhysRevE.78.021912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aksimentiev A.; Balabin I. A.; Fillingame R. H.; Schulten K. Insights into the Molecular Mechanism of Rotation in the Fo Sector of ATP Synthase. Biophys. J. 2004, 86, 1332–1344. 10.1016/S0006-3495(04)74205-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosal S. Electrokinetic-Flow-Induced Viscous Drag on a Tethered DNA Inside a Nanopore. Phys. Rev. E 2007, 76, 061916. 10.1103/PhysRevE.76.061916. [DOI] [PubMed] [Google Scholar]
- van Dorp S.; Keyser U. F.; Dekker N. H.; Dekker C.; Lemay S. G. Origin of the Electrophoretic Force on DNA in Solid-State Nanopores. Nat. Phys. 2009, 5, 347–351. 10.1038/nphys1230. [DOI] [Google Scholar]
- Keyser U. F.; Koeleman B. N.; van Dorp S.; Krapf D.; Smeets R. M. M.; Lemay S. G.; Dekker N. H.; Dekker C. Direct Force Measurements on DNA in a Solid-State Nanopore. Nat. Phys. 2006, 2, 473–477. 10.1038/nphys344. [DOI] [Google Scholar]
- Kowalczyk S. W.; Wells D. B.; Aksimentiev A.; Dekker C. Slowing Down DNA Translocation through a Nanopore in Lithium Chloride. Nano Lett. 2012, 12, 1038–44. 10.1021/nl204273h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosal S. Electrophoresis of a Polyelectrolyte through a Nanopore. Phys. Rev. E 2006, 74, 041901. 10.1103/PhysRevE.74.041901. [DOI] [PubMed] [Google Scholar]
- Ghosal S. Effect of Salt Concentration on the Electrophoretic Speed of a Polyelectrolyte through a Nanopore. Phys. Rev. Lett. 2007, 98, 238104. 10.1103/PhysRevLett.98.238104. [DOI] [PubMed] [Google Scholar]
- Luan B.; Aksimentiev A. Electric and Electrophoretic Inversion of the DNA Charge in Multivalent Electrolytes. Soft Matter 2010, 6, 243–246. 10.1039/B917973A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comer J.; Ho A.; Aksimentiev A. Toward Detection of DNA-Bound Proteins Using Solid-State Nanopores: Insights From Computer Simulations. Electrophoresis 2012, 33, 3466–3479. 10.1002/elps.201200164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storm A. J.; Storm C.; Chen J. H.; Zandbergen H. W.; Joanny J.-F.; Dekker C. Fast DNA Translocation through a Solid-State Nanopore. Nano Lett. 2005, 5, 1193–1197. 10.1021/nl048030d. [DOI] [PubMed] [Google Scholar]
- Yoo J.; Aksimentiev A. Improved Parametrization of Li+, Na+, K+, and Mg2+ Ions for All-Atom Molecular Dynamics Simulations of Nucleic Acid Systems. J. Phys. Chem. Lett. 2012, 3, 45–50. 10.1021/jz201501a. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.