Abstract
Populations of cells need to express proteins to survive the sudden appearance of stressors. However, these mechanisms may be taxing. Populations can introduce diversity, allowing individual cells to stochastically switch between fast-growing and stress-tolerant states. One way to achieve this is to use genetic networks coupled with noise to generate bimodal distributions with two distinct subpopulations, each adapted to a stress condition. Another survival strategy is to rely on random fluctuations in gene expression to produce continuous, unimodal distributions of the stress response protein. To quantify the environmental conditions where bimodal versus unimodal expression is beneficial, we used a differential evolution algorithm to evolve optimal distributions of stress response proteins given environments with sudden fluctuations between low and high stress. We found that bimodality evolved for a large range of environmental conditions. However, we asked whether these findings were an artifact of considering two well-defined stress environments (low and high stress). As noise in the environment increases, or when there is an intermediate environment (medium stress), the benefits of bimodality decrease. Our results indicate that under realistic conditions, a continuum of resistance phenotypes generated through a unimodal distribution is sufficient to ensure survival without a high cost to the population.
Introduction
Populations of cells that live in fluctuating environments must cope with a wide range of conditions and sudden changes in their surroundings. Cells can sense their environment and respond to changes. However, if the time required to initiate a response is longer than the time the stressor takes to act, cells need alternative strategies to ensure that the entire population is not killed off due to the sudden appearance of a stressor. Furthermore, initiating stress response mechanisms in all cells within a population may be costly. When sensing the environment is too slow or too costly, populations can rely on genetic and phenotypic variation to balance survival and growth. For example, they may sacrifice growth in low stress conditions to increase fitness in other environments (1, 2, 3). In the past decade, bet hedging, a type of nongenetic variation between individuals, has gained attention for its role in multiple biological processes (1, 3). For instance, the presence of subpopulations of nongrowing persister cells allows bacterial populations to survive high concentrations of antibiotics that target cell growth (4). This persistent population has been found in many pathogenic microbes, and has been shown to be an important contributor to antibiotic resistance (5). Similarly, under nutrient limitation, Bacillus subtilis generates phenotypic diversity resulting in normally growing cells, sporulating cells, and those that eventually become competent (6, 7). Maintaining different phenotypes within the same genotype allows populations of cells to ensure variability at every generation, reducing differences in the population growth rate across environments and ensuring survival under a variety of conditions (8).
In this article, we focus on how a population of cells grows in the presence of a time-varying stressor. Cells can express genes to tolerate high concentrations of a stressor, such as genes encoding efflux pumps, reductases, and DNA repair systems (9). However, these stress-response mechanisms can have a high metabolic cost (10). Thus, populations may use phenotypic diversity so that not all cells have the burden of expressing them. Two approaches are as follows. 1) The generation of two distinct phenotypic states optimized for each environment, which we refer to as a “bimodal distribution”. Establishing two well-defined phenotypes and stochastically switching between them can be advantageous in some conditions. For instance, in bacterial persistence, populations are bimodal, maintaining a small subpopulation of dormant cells in addition to normally growing cells (11). This type of bet-hedging has been evolved in Pseudomonas fluorescens in the presence of alternating stresses (12, 13). 2) An alternative approach is to generate a continuum of stress-resistance levels within a population, which we refer to as a “unimodal distribution”. In this case, cells have a similar phenotype with variations about the mean levels. In contrast to the bimodal case, there are not distinct phenotypic states. An example of unimodal distributions comes from TATA box-containing genes associated with stress response in Saccharomyces cerevisiae, which exhibit large levels of variability that protect against future environmental changes (14). Similarly, increased population heterogeneity has been shown to enhance survival of stress in S. cerevisiae (15). A broad, continuous distribution of phenotypes has also been evolved in Escherichia coli in a periodic selection and mutation experiment (16). Phenotypic diversity, in the form of bimodal or unimodal distributions of phenotypes, plays an important role in increasing fitness in uncertain environments.
The mathematical analysis of fluctuating environments dates back to work by Levins (17), who showed that environmental fluctuations hinder adaptation to a single phenotype. Since then, many studies have examined the relationship between time-varying environments and cellular phenotypes. Generally, cells are modeled as growing exponentially, with each phenotype having a distinct growth rate for each environment and a rate of switching to other phenotypes (18, 19, 20, 21, 22, 23). Given the large number of parameters present, numerical and analytical studies have primarily focused on the case with two environments and two phenotypes, with the following general conclusions: Two different optimal strategies can be found, where the optimum depends on the frequency at which the environment changes. A unimodal population is best for very rapid or very slow environmental changes, and a bimodal population where cells stochastically switch between two phenotypes is best for intermediate ranges of environmental switching (24). Furthermore, the unimodal population can be either adapted to this environment if the changes are slow, i.e., cells can sense and adapt to the extracellular conditions; or adapted to the mean environment if the changes are rapid (24). When cells do not explicitly sense their environment, bimodal strategies with stochastic switching between the two states are favored (20). Even in conditions where cells do sense their environment, bimodality can still be used to prevent complete extinction of the population if sensing is too slow (25, 26). In general, in a periodic environment, the optimal switching rate between phenotypes in a bimodal population is proportional to the asymmetry of the stress environment (25) and the transition rate between environmental states (18, 27). These results have provided insight into the cases where bimodal populations are favored, showing that bimodality coupled with stochastic switching between states is advantageous for a large range of conditions.
Although these studies have demonstrated the theoretical benefit of bimodality, >99% of E. coli genes show unimodal distributions in their protein levels (28). There are select examples of bimodal gene expression in E. coli, but relatively few cases exist; other bacterial species appear to be similar (29). Thus, we were motivated to understand the conditions where bimodal distributions of proteins increase the growth rate of a population with respect to a unimodal distribution. To achieve this, we developed a computational model and used a differential evolution algorithm (30) to evolve optimal or near-optimal distributions of phenotypes for a population growing in the presence of a time-varying stressor. When we restricted the concentration of the stressor to two levels (low and high), we were able to reproduce the benefits of bimodality previously reported. However, this benefit disappeared when variability in the concentration of the stressor was increased. This is the case when there is noise in the environment, or when there are more than two distinct environmental conditions. Given realistic conditions, unimodal distributions of proteins may be a straightforward bet-hedging approach for surviving in fluctuating environments.
Materials and Methods
Distribution of protein levels
In the context of general stress response, some proteins confer resistance to a broad range of chemicals, either by regulating expression of suites of genes or by directly providing stress resistance. Therefore, we represented the phenotype of a cell, P, as the concentration of a hypothetical protein involved in response to stress. To study populations of cells growing in fluctuating environments, we developed a model that assigns fitness values (growth rates) to a distribution of protein levels in a series of environments. We evolved the probability distribution of the protein under the basal conditions, where no stressor was present. This distribution is encoded by an n-dimensional vector, where the dimension corresponds to different protein levels in the population, and the n values correspond to the probability of expressing the phenotypes, p(P). The values of P were set to n bins: {0–100, 100–200,…, 9900–10000} molecules, to represent a typical range of protein numbers that can be found in both bacteria and yeast (31).
Gamma distributions
The n values in vector p(P) were extracted from a γ-distribution in the 1γ case, the weighted sum of two γ-distributions in the 2γ case, or evolved directly in the case with no restrictions.
A γ-distribution arises from a two-state model of gene expression, where the promoter can be ON or OFF and the protein is expressed in bursts (32). In this context, a corresponds to the number of bursts per cell cycle, while b is the average number of molecules produced per burst. For both the 1γ and 2γ cases, we restricted a to , and b to to maintain values in a biologically feasible range. This prevents the evolved distributions from being unrealistically sharp.
For the 1γ case,
| (1) |
where the values a (shape parameter) and b (rate parameter) define the distribution. The 1γ case has two parameters that are evolved in the differential evolution algorithm: a and b.
For the 2γ case,
| (2) |
where and set the relative weights of the two γ-distributions. The 2γ case has six parameters that are evolved: , , , , , and .
For the free case, p(P) is evolved directly, so there are n parameters evolved.
For each of the three cases, the distributions are normalized such that .
Environmental parameters
The concentration of the stressor, S, and the time spent in the different stress levels characterize the environment. For the case with two environmental states, the concentrations of the stressor were set to 0 mM (low stress) and 10 mM (high stress). The time spent in the two environments, measured in generations, is shown in Table 1.
Table 1.
Time Spent in Low and High Stress Conditions
| Environmental Transition Rate |
||||||
|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 30 | 100 | ||
| Ratio high:low | 1000:100 | 333:33 | 100:10 | 33:3 | 10:1 | |
| 1000:1000 | 333:333 | 100:100 | 33:33 | 10:10 | ||
| 1000:10,000 | 333:3333 | 100:1000 | 33:333 | 10:100 | ||
| 1000:100,000 | 333:33,333 | 100:10,000 | 33:3333 | 10:1000 | ||
| 1000:1,000,000 | 333:333,333 | 100:100,000 | 33:33,333 | 10:10,000 | ||
For each high to low stress ratio and environmental transition rate, the number of generations spent in each state is shown.
Cost and benefit
We used a cost-benefit function based on those from Wood and Cluzel (10), Dekel and Alon (33), and Garcia-Bernardo and Dunlop (34). The growth rate of a cell, , is defined in terms of c(P,S), the cost of growing when the concentration of stressor in the environment is S and the intracellular number of proteins is P. Briefly, the growth rate of a cell, , is defined in terms of c(P,S), where
| (3) |
Here, corresponds to the cost of expressing the stress resistance machinery at a level P, while is the cost of growing in the presence of a concentration of stressor S given a stress resistance level P:
| (4) |
| (5) |
| (6) |
| (7) |
where M = 15,000 molecules, n0 = 10−5, k = 1 mM, n = 2, bmax = 10, and kb = 15,000 molecules. See Garcia-Bernardo and Dunlop (34) for a complete description of the equations and parameters.
Using the cost, we defined the growth rate as
| (8) |
Note that is normalized to maintain growth rates between 0 and 1 when the cost is under the threshold . Cells with costs above are determined to be dead. The value is the maximal growth rate; positive values less than this indicate slow growth. The value corresponds to the cell dying in one generation. We set ; however, the results are not specific to the exact value used. Higher thresholds imply that cells need higher protein levels to survive, which increases the area in Fig. 3, where bimodality is favored, but not the qualitative results about where bimodality appears (Fig. S7 in the Supporting Material).
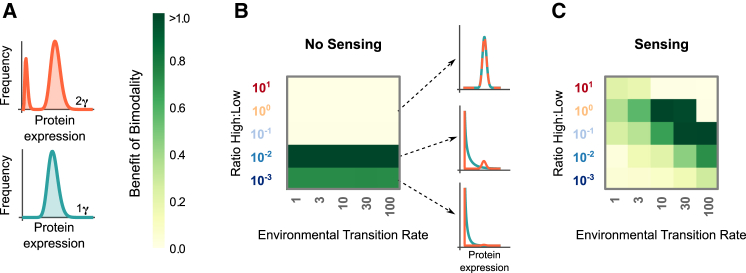
Figure 3.
Bimodality provides higher fitness than unimodality when the environment has two alternating states. (A) We compared conditions where we restricted protein levels to be either the weighted sum of two gamma distributions (2γ) or a single gamma distribution (1γ). (B and C) The benefit of bimodality is plotted as a function of the ratio of high to low stress and the environmental transition rate. (B) For populations with no sensing, there is a benefit to bimodality when the ratio of high to low stress is small, which is reflected in differences in the evolved distributions. (C) For populations with sensing, the benefit of bimodality depends on both the ratio of high to low stress and the environmental transition rate. The benefit is measured as the difference in growth rate between the strategies evolved with 2γ and 1γ restrictions (Fig. S1 and the Supporting Material). To see this figure in color, go online.
Fitness function
The fitness of a population with a distribution of protein levels is measured by the overall growth rate. As the fitness function, we use the geometric growth rate
| (9) |
where is the fraction of the population in the protein state P. The values and are the times spent in low and high stress conditions; and are the low and high stress conditions. The full derivation of this fitness function, including the modified fitness function for the sensing case, is provided in the Supporting Material.
Differential evolution algorithm
We used the differential evolution algorithm (30); further details are available in the Supporting Material.
Switching rates
In the no-sensing case, we assumed that switching between phenotypic states is fast in relation to the amount of time spent in each stress environment. Under this assumption, we do not explicitly model switching; instead, we assume that switching happens instantaneously and that the population of cells has identical protein distributions growing in the presence and absence of the stressor. In the sensing case, the transition from no-stress conditions to stress conditions is explicitly modeled as taking one generation (Supporting Material); however, we note this timescale is much shorter than the typical duration in each stress state (Table 1).
Bimodality metric
We do not explicitly calculate bimodality, rather we compare cells with the capacity to evolve a 2γ distribution with cells only able to evolve 1γ distributions. The benefit of bimodality is defined as the difference in fitness between these two cases. The 2γ distribution always performs better than or equal to 1γ, because the latter can always be obtained by zeroing the weight of one of the two γ-distributions, or by evolving two distributions with identical parameters. If the optimal distribution is a unimodal distribution, then the difference in fitness between the 2γ and 1γ distributions is zero. Conversely, a positive benefit of bimodality implies that a bimodal distribution has been obtained.
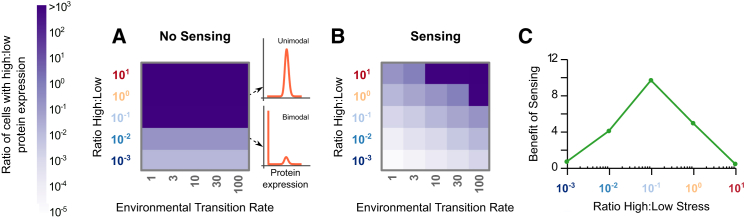
The ratio of cells with high to low protein expression (see Fig. 2) is defined as the ratio between the number of cells with above and below 5000 proteins. This threshold corresponds to the minimum protein level needed to survive in any studied environment (Fig. S7 B for ).
Figure 2.
Bimodality is evolved in many environmental conditions. (A and B) The ratio of cells with high to low protein expression is plotted as a function the ratio of high to low stress and the environmental transition rate. Representative protein histograms show unimodal (dark purple) and bimodal (light purple) distributions. (A) For populations with no sensing, bimodality is evolved when the ratio of high to low stress is small. The actual protein distributions for all ratios of high to low stress for a single environmental transition rate are shown in Fig. S6. (B) For populations with sensing, bimodality is evolved for a large region of environmental parameters and depends on both the ratio of stress conditions and the environmental transition rate. (C) The benefit of sensing is plotted as a function of the ratio of high to low stress, reaching its maximum for moderately asymmetric environments. The benefit is measured as the difference in growth rate between the sensing and no sensing populations (Fig. S1 and the Supporting Material). These simulations use an environmental transition rate of 10. Note that if the evolved distribution is unimodal, the difference in fitness between the 2γ and 1γ cases is zero. To see this figure in color, go online.
Addition of noise in the environment
We created exponential distributions of noise with mean noise levels between 0.025 and 0.5 mM. A random value from this distribution was added (subtracted) from the 0 (10 mM) environments. While the noise changes between generations of the algorithm, the noise was identical for all vectors encoding the distribution of protein levels (see the Supporting Material) within a generation. When the stress level is deterministic, the fitness can be calculated after visiting the high and low stress conditions once (Eq. 9). For the case with noise, the stress level changes with time. To reduce the variation in highest obtainable fitness between generations, the growth rate was calculated after 100 alternative visits to low and high stress conditions. To further reduce the differences between the simulations in the 1γ and 2γ cases, three independent simulations were run, and the simulation with the highest fitness was recorded. This was necessary because the differential evolution algorithm does not guarantee a globally optimal solution; therefore we ran three independent replicates and recorded the one with the highest fitness.
Intermediate environment
An intermediate environment was added, with a stressor concentration of 1.1 mM. We selected this value because the optimal concentration of protein in a fixed 1.1 mM environment is half-way between the optimal concentration for 0 and 10 mM due to the nonlinear nature of the growth rate function (Eq. 8; Fig. S7). The fitness of a population with a distribution of protein levels was calculated by cycling between the three stress conditions in this order: low; medium; low; and high stress.
Results and Discussion
Protein expression model and environmental variables
To study how populations of cells optimize growth in the presence of fluctuations in the concentration of a stressor in the environment, we developed a model where a protein controls the level of resistance to the stressor. For example, this could be a regulatory protein that controls expression of a suite of downstream genes involved in stress response, or it could provide stress resistance directly; examples include efflux pumps or proteins that induce growth arrest to evade antibiotics. In the model, increased protein expression allows for survival in high stress environments, but impacts growth in low stress environments because expression places a burden on the cell. We used a computational method (differential evolution algorithm) to find optimal or near-optimal distributions of protein levels in the population given a fluctuating environment as an input. Because we evolve the distributions directly, we do not explicitly model switching or specify the method by which the distributions are generated. Initially, we restricted the distribution of proteins to be the weighted sum of two gamma distributions, which can represent either unimodal or bimodal expression of proteins, depending on weighting values (Fig. 1 A). We later relaxed this restriction and obtained similar results, as discussed below. A gamma distribution arises from a two-state model of gene expression, where the promoter can be ON or OFF and the protein is expressed in bursts (32). We used the differential evolution algorithm to select the shape and rate parameters of the distributions (Materials and Methods). It is possible for the algorithm to evolve tight distributions, where there is little variation in protein levels, or broad distributions, where there is wide variation. We chose the upper and lower limits of the gamma distribution parameters to match in vivo values measured in bacteria (28). Importantly, we note that it is possible to evolve parameters such that the two gamma distributions collapse to a unimodal distribution. For example, if the weight of the second gamma distribution is zero, there will be only a single, unimodal population. Thus, the weighted sum of two gamma distributions allows a flexible representation where both unimodal and bimodal protein distributions with broad or narrow shapes can be evolved.
Figure 1.
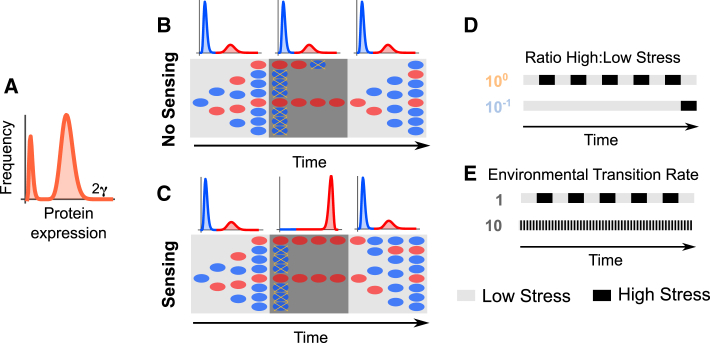
Population and environmental variables tested. (A) The distribution of protein levels in the population was initially restricted to be a weighted sum of two gamma distributions. (B) Environments vary between low and high stress. Without sensing, the population always maintains cells with low and high levels of protein expression (histograms), where cells switch stochastically between these two phenotypic states. Under low stress, cells with low protein expression (blue) grow well, while cells with high protein expression (red) grow slowly due to the burden of expressing the stress response protein. Under high stress, cells with low protein expression are killed (yellow “x” symbols), while cells with high protein expression survive. Note that the histograms are colored as blue and red to distinguish cells with low and high expression; however, all cells are part of the same bimodal distribution. While only a few cells are depicted for simplicity and to show relative growth rates, it is important to note that the distributions of cells remain constant within each environment. In the low stress region, the population grows at equilibrium. In the high stress region, red cells continuously switch to blue and die. (C) With sensing, populations maintain diversity as a bet-hedging strategy when stress levels are low. When stress levels are high, all surviving cells remain in the high protein state. (D) Cartoon showing ratio between the time spent in high and low stress. (E) Cartoon showing the environmental transition rate. Note that the ratio of high to low stress is identical for both transition rates shown. To see this figure in color, go online.
We also compared the ability of cells to sense environmental changes. In the case where cells cannot sense stress levels (Fig. 1 B), a bimodal population of cells grows well in the low stress environment, with cells in the low protein expression state growing faster than those in the high protein expression state. Individual cells within the population stochastically switch between the two states. When the environment changes and cells enter the high stress conditions, all the cells in the low expression state die off, but those with high expression survive. Because the cells do not sense their environment they continue to stochastically switch between phenotypic states. When this happens in the high stress environment, the cells that enter the low protein phenotype die. When conditions switch back to the low stress environment, the population can regrow, again with stochastic switching between the phenotypic states. Importantly, we assume fast switching rates, which results in identical distributions of phenotypes in low and high stress conditions (Materials and Methods). The sensing case is similar (Fig. 1 C), but once cells are in the high stress environment they do not switch to the low protein phenotype. The underlying protein distributions are shown in Fig. 1, B and C. In low stress conditions, the population exhibits a bimodal distribution with stochastic switching regardless of whether there is sensing or not. This is required, even with sensing, because we assume that the time required to sense and respond to a stress is long enough that any cells in the low protein phenotype will be killed by the stressor. The difference between the no sensing and sensing cases appears in the high stress conditions, where cells that can sense have no reason to switch to the low protein phenotype.
We also tested a broad range of environmental transition properties. We modified the ratio between the time spent in high and low stress (Fig. 1 D) and the environmental transition rate (Fig. 1 E). See Materials and Methods for a full description of the model and parameters.
Bimodality is evolved for a wide range of environmental conditions
Initially, we tested different environmental conditions, varying both the ratio of high to low stress and the rate of transition between environmental states. For each pair of values, we used the differential evolution algorithm to optimize the distribution of protein levels. We then recorded the relative sizes of the two evolved gamma distributions, comparing the ratio of cells exhibiting the high protein expression phenotype to the low protein phenotype. We found that two strategies were evolved: either the entire population was adapted to the high stress condition (darkest purple in Fig. 2, A and B) or a bimodal population with a resistant subpopulation appeared (light purple). A unimodal population with low protein expression (white) was never evolved, because resistant cells are required to survive the transition from low to high stress. With no sensing, bimodal distributions are evolved in the cases where the ratio of high to low stress is small because most of the time cells are in low stress conditions with rare excursions to the high stress environment (Fig. 2 A). The fraction of resistant cells depends only on the ratio of the stresses, and not on the environmental transition rate. This is because the growth rate of a population without sensing is constant for each stress condition, in contrast with the sensing case, where the growth rate changes during the time in high stress conditions as the cells adapt (Fig. 2 B). With sensing, the population can afford to lose a higher fraction of cells due to the sudden appearance of the stressor, because the remaining cells will adapt to the stress. Thus, with sensing, a higher fraction of the population can be devoted toward growing well in low stress, and bimodality is evolved under most environmental conditions.
To quantify the benefit of sensing, we measured the growth rate for populations of cells that were allowed to sense the environment, and for populations where sensing was prohibited. In all cases, sensing outperformed no sensing. However, the degree to which there was a benefit to sensing depended upon the ratio of high to low stress in the environment (Fig. 2 C). In the extreme cases where cells are mostly in stressed or unstressed environments, there is little advantage to sensing because conditions are well known. In contrast, when the time spent in each environment is symmetric, sensing has a distinct advantage. The highest benefit to sensing is achieved for moderately asymmetric environments, where the optimal strategy for the no-sensing population is a unimodal distribution with high protein levels, while the sensing population can rely on a bimodal distribution of phenotypes. Importantly, in our model the no-sensing case assumes fast switching rates. More generally, a nonsensing population could evolve an optimal switching rate to maximize its growth rate (19, 20). Thus, this value corresponds to an upper bound on the benefit of sensing. The metric we use here to measure the benefit of sensing can be translated into the amount of time it would take a population with sensing to overtake a population without sensing in a competitive growth experiment (Supporting Material and Fig. S1).
We next relaxed our requirement that the protein distribution be the weighted sum of two gamma distributions. We allowed the evolution of any type of distribution with no restrictions, finding equivalent results to the two gamma distribution case (Fig. S2). For the case of two well-defined environments, we found that bimodality is evolved for a large range of fluctuating environments.
In our initial tests, we assumed that the stressor was strong enough that it killed off all cells with low protein expression. We next asked whether our results were dependent on whether the stressor was weak or strong. We define a weak stressor as a toxin that inhibits growth for cells that do not have high levels of protein expression, in contrast to a strong stressor that kills these cells (Supporting Material). When they target bacteria, weak stressors are known as bacteriostatic, and strong stressors are bactericidal. Our results with weak stressors show that with no sensing, the evolved strategy is unimodal for nearly all environmental conditions (Fig. S3). Populations have low protein expression for all but the largest ratio of high to low stress. This corresponds to the case where the cells stay latent until the stressor has passed. A unimodal distribution with high protein expression is evolved only when the time spent in high stress conditions is large. Between these two survival strategies, i.e., unimodal adapted to low stress and unimodal adapted to high stress, bimodality is evolved for a very small region of the environmental parameter space. For the case with sensing, the optimal strategy is always to stay latent until the stressor is sensed. This is expected because the stressor only inhibits growth, and thus it is possible to adapt to it even if the toxin appears abruptly. Because the growth rate in high stress conditions is very small even when the population is perfectly adapted, staying latent is almost as good as adapting to the stress. Therefore the benefit of sensing is lower than in the case with a strong stressor, where cells die off if they do not adapt to the stress conditions. The evolved distributions with no restriction have equivalent results. Consistent with previous findings (35), our results show that bimodality is primarily beneficial when the strength of the stressor is strong.
Bimodality is beneficial for populations of cells growing in two well-defined stress conditions
We next asked under what environmental conditions bimodal populations outperform unimodal populations. To do this, we evolved distributions by restricting protein levels to follow either two weighted gamma distributions as before (we refer to this as 2γ ), or one gamma distribution (1γ ), as shown in Fig. 3 A. We evolved the optimal distributions for 1γ and 2γ given identical stress environments. Because it is possible for the 2γ distribution to recover a single gamma distribution, the 2γ case is always better than or equal to the 1γ case. We calculated the growth rate for the evolved strategies with the 1γ and 2γ restrictions as a function of the ratio of high to low stress and the environmental transition rate. For the no-sensing case, the optimal strategy depends only on the ratio of the stresses. When the ratio of high to low stress is large, the optimal strategy for both the 1γ and 2γ cases is a unimodal distribution adapted to high stress, so there is no benefit to bimodality. As the stress ratio decreases, there is a sudden transition where the 2γ distribution switches from a unimodal population to a bimodal population containing a subpopulation of cells with high protein expression while most cells have low expression. For the 1γ case to maintain a sufficient number of cells in the high protein phenotype under the same environmental conditions, many cells must express intermediate protein levels. Cells with intermediate protein expression provide no benefit to the population because they are not capable of surviving sudden stress, and also impose a modest burden on the growth of the population. As the stress ratio is further reduced, the difference between the two distributions diminishes as fewer cells need to maintain a high protein phenotype. This phenomenon is visible in the examples of evolved histograms (Fig. 3 B).
For the sensing case, bimodality is beneficial in environments with relatively symmetric levels of high and low stress (Fig. 3 C). Because the population is able to adapt to high stress conditions, the evolved distribution depends now on the time spent in low stress conditions and the number of transition events. Therefore, the benefit depends on both the ratio of stresses and the environmental transition rate. In Fig. 2, we show that sensing increases the parameter region where bimodality is evolved. However, when the population is able to sense the environment, the growth in high stress conditions is equal for both the unimodal and bimodal cases because they adapt to the stress in an identical way. Therefore, the benefit of bimodality is generally lower, though still positive, for sensing populations than for populations without sensing.
Increased variability in the environment decreases the benefit of bimodality
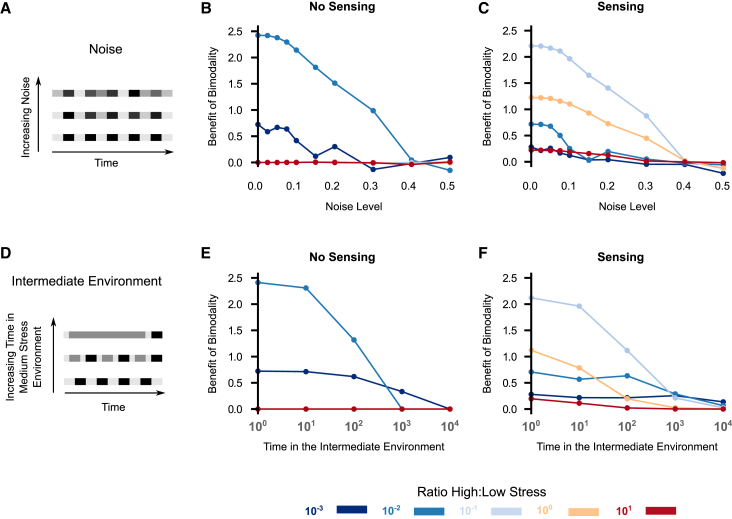
Although we found that bimodal distributions outperform unimodal distributions for a wide range of environmental conditions, we wondered whether this effect was due to the binary nature of the stresses (either low or high). We hypothesized that variability in the environment would decrease the benefit of bimodality. To test this, we introduced noise in the two stress levels (Materials and Methods, Fig. 4 A) and recalculated the benefit of bimodality, quantifying the difference in growth rates between the evolved distributions with the 2γ and 1γ restrictions. As noise increases, strategies with more cells in the elevated protein expression state are favored because less time is spent in the complete absence of a stressor. For the highest levels of noise, both 1γ and 2γ cases evolve unimodal distributions (Fig. S4). Consequently, we found that for both no-sensing and sensing populations (Fig. 4, B and C), the benefit of bimodality decreased as noise in the environment increased.
Figure 4.
The benefit of bimodality is reduced when environmental variation increases. (A) Cartoon showing increasing noise in the stress levels. (B and C) The benefit of bimodality is reduced for both (B) no sensing and (C) sensing populations as noise increases. Dots correspond to the replicate with highest evolved growth rate out of three independent simulations (Materials and Methods). (D) Cartoon showing the presence of an intermediate, medium stress environment. (E and F) The benefit of bimodality is reduced for both (E) no sensing and (F) sensing populations as the time in the intermediate environment increases. In (B) and (E), the benefit results for stress ratios 10−1 to 101 are all zero, and thus are hidden behind the 101 line. To see this figure in color, go online.
We also asked whether considering only two stress environments was leading to the observed benefits in bimodality. To test this, we increased the number of environmental states by adding an environment with medium stress and measured the benefit of bimodality as a function of the time spent in this intermediate environment (Fig. 4 D). Similar to simulations with increasing levels of noise, we found that for both no-sensing and sensing populations (Fig. 4, E and F), the benefit of bimodality decreased as the time in the intermediate environment increased. Two factors contribute to this decrease: First, if the cells are not able to sense their surroundings, both 1γ and 2γ cases evolve identical unimodal distributions when the time in the medium stress environment is large (Fig. S4). Second, if the cells are able to sense and adapt to the environment, the growth rate in medium stress conditions is identical for both the 1γ and 2γ cases because cells adapt perfectly to the medium stress condition, therefore the evolved distribution does not depend on the time spent in the medium stress environment. Thus, we find that under realistic scenarios, such as environments with noise or more than two discrete stress levels, unimodal distributions perform just as well as bimodal distributions.
We finally asked whether using the 2γ distribution was limiting how well the evolved strategies could perform in the intermediate environment. In principle, a trimodal distribution could provide the optimal conditions for three environments. To test this, we removed the 2γ restriction and allowed the distribution to evolve freely without any requirements on its shape. Even under these nonrestrictive conditions, the populations evolved only unimodal or bimodal distributions (Fig. S5). In fluctuating environments the advantage of bimodality comes from the ability to survive the sudden transition from low to high stress, which is not necessary for an intermediate stress state. Therefore, even with more than two distinct stress levels, it is only necessary to evolve two levels of protein expression: one that ensures survival in the highest level of stress, and a second that optimizes growth in low stress. We observe this in evolved distributions (Fig. S5) where cells either have protein levels sufficient to survive high stress or they have protein levels that are optimized for growth in the low and medium stress environments. The location of this latter peak depends upon the time spent in the intermediate environment. We note that in the presence of three mutually exclusive environments (as opposed to different levels of the same stressor), nonsensing populations would need to evolve trimodality to survive sudden environmental changes.
Conclusions
Populations of cells live in the presence of intermittent, time-varying stressors. Cells have mechanisms to survive the appearance of a stressor, but the cost associated with stress resistance can be high. Thus, cells need to balance high growth rates in the absence of the stressor with survival when a stressor appears abruptly in the environment. A possible strategy is to diversify the population, allowing some cells to grow well when no stress is present, while others have high enough protein expression that they can survive, hedging against the sudden appearance of a stressor. Phenotypic diversity within the population can be achieved through multimodal distributions of protein levels, or through a broad, continuous distribution of proteins.
Here, we compared bimodal and unimodal distributions that can result from diversity in gene expression, asking under what conditions bimodality is beneficial. We used a differential evolution algorithm to evolve optimal or near-optimal distributions of proteins for different environmental conditions. We varied the time spent in high and low stress, the environmental transition rate, the sensing capabilities of the cells, noise in the concentration of the stressor, and the number of stress levels. Because protein expression typically follows a gamma distribution in vivo, we initially restricted the evolved distributions to be either a single gamma distribution or the weighted sum of two gamma distributions. We used the difference in growth rate between the two alternatives to assess the benefit of bimodality, finding that while bimodality evolved for a wide range of conditions if the environment has only two well-defined states, this benefit disappears in the presence of noise or when the time spent in an intermediate environmental state increased.
A potential limitation of our model is the assumption of fast stochastic switching between phenotypes. This assumption results in the independence between the environment transition rate and the evolved distributions in the no-sensing case, as seen in Figs. 2 A and 3 B. Under more realistic conditions, populations can adapt their switching rates to the environment transition rates (19, 20). With adapted switching rates, the population will be enriched in the phenotypes that grow faster. Because populations of cells can further improve their fitness by tuning the switching rate, the benefit of sensing that we calculate corresponds to an upper bound. However, the expected effect of our assumption will be small, because the majority of the growth comes from the time in the low stress state. Here, we explore a large range of parameters, exploring optimal distributions without limiting ourselves to two environments and phenotypes. In the future, it will be interesting to explore the effect of including switching rates in the model.
Our results raise the question of what benefits are provided by bimodality, given realistic environmental conditions. One benefit may be longer autocorrelation times in the protein levels that bimodality can provide. Unimodal distributions in stress resistance levels can be the result of random fluctuations in gene expression (32). The half-life of these fluctuations is typically 1–3 generations (36, 37). On the contrary, the time spent in each phenotypic state with a bimodal system can be large, extending for many generations (38). An example of bimodal protein expression in E. coli is persistence, where fewer than 1% of cells in the population are in a resistant, nongrowing state that is tolerant to antibiotics (4). The switch between the growing and latent states is stochastic, and cells can stay in each state for many generations (39, 40). The advantage of bimodality in this case may come from the extended time the cells spend in the resistant state. One alternative to bimodality that could achieve longer stress resistance times would be to couple a unimodal distribution with sensing. In this case, cells could use noisy gene expression to survive a sudden stress shock, and then adapt to it. However, maintaining the sensing machinery may be costly if the stressor is only rarely encountered. In this study, we evolved distributions of protein levels, but our results do not specify how these distributions are achieved. Bimodality can be generated by genetic networks, such as through the use of positive feedback (38). The presence of these additional genetic control elements can add evolutionary and maintenance costs, which we have not included in our model. Unimodal distributions are more straightforward to generate, as noise in gene expression is sufficient to produce a continuum of resistance levels (38). In general, if the cost of maintaining the architecture required to generate bimodal distributions is higher than the benefit acquired, bimodality will not be evolved. In the future, it will be interesting to link the regulatory architecture required to generate protein distributions to the results presented here.
We conclude that bimodal protein expression patterns can be beneficial under certain conditions, such as when environmental states are well defined and the number of states is small. However, under realistic environmental conditions with noise and uncertainty in stress levels, unimodal protein distributions are often sufficient to provide diversity within the population that can ensure survival.
Author Contributions
J.G.-B. conceived and designed the experiments with input from M.J.D; J.G.-B. performed the experiments and analyzed the data; and J.G.-B. and M.J.D. wrote the article. All authors gave final approval for publication.
Acknowledgments
We thank Maggie Eppstein for helpful comments on the differential evolution algorithm. We also thank Nicholas Rossi and Imane El Meouche for their critical reading of the article.
This research was supported by the National Science Foundation (grant No. 1347635).
Editor: Reka Albert.
Footnotes
Supporting Materials and Methods and seven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30175-8.
Supporting Material
References
- 1.Simons A.M. Modes of response to environmental change and the elusive empirical evidence for bet hedging. Proc. Biol. Sci. 2011;278:1601–1609. doi: 10.1098/rspb.2011.0176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Leibler S., Kussell E. Individual histories and selection in heterogeneous populations. Proc. Natl. Acad. Sci. USA. 2010;107:13183–13188. doi: 10.1073/pnas.0912538107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Meyers L.A., Bull J.J. Fighting change with change: adaptive variation in an uncertain world. Trends Ecol. Evol. 2002;5347:551–557. [Google Scholar]
- 4.Keren I., Kaldalu N., Lewis K. Persister cells and tolerance to antimicrobials. FEMS Microbiol. Lett. 2004;230:13–18. doi: 10.1016/S0378-1097(03)00856-5. [DOI] [PubMed] [Google Scholar]
- 5.Fauvart M., De Groote V.N., Michiels J. Role of persister cells in chronic infections: clinical relevance and perspectives on anti-persister therapies. J. Med. Microbiol. 2011;60:699–709. doi: 10.1099/jmm.0.030932-0. [DOI] [PubMed] [Google Scholar]
- 6.Grossman A.D. Genetic networks controlling the initiation of sporulation and the development of genetic competence in Bacillus subtilis. Annu. Rev. Genet. 1995;29:477–508. doi: 10.1146/annurev.ge.29.120195.002401. [DOI] [PubMed] [Google Scholar]
- 7.Süel G.M., Garcia-Ojalvo J., Elowitz M.B. An excitable gene regulatory circuit induces transient cellular differentiation. Nature. 2006;440:545–550. doi: 10.1038/nature04588. [DOI] [PubMed] [Google Scholar]
- 8.Rainey P.B., Beaumont H.J.E., Zhang X.-X. The evolutionary emergence of stochastic phenotype switching in bacteria. Microb. Cell Fact. 2011;10(Suppl 1):S14. doi: 10.1186/1475-2859-10-S1-S14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Alekshun M.N., Levy S.B. Molecular mechanisms of antibacterial multidrug resistance. Cell. 2007;128:1037–1050. doi: 10.1016/j.cell.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 10.Wood K.B., Cluzel P. Trade-offs between drug toxicity and benefit in the multi-antibiotic resistance system underlie optimal growth of E. coli. BMC Syst. Biol. 2012;6:48. doi: 10.1186/1752-0509-6-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Balaban N.Q., Merrin J., Leibler S. Bacterial persistence as a phenotypic switch. Science. 2004;305:1622–1625. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- 12.Beaumont H.J.E., Gallie J., Rainey P.B. Experimental evolution of bet hedging. Nature. 2009;462:90–93. doi: 10.1038/nature08504. [DOI] [PubMed] [Google Scholar]
- 13.Rainey P.B., Travisano M. Adaptive radiation in a heterogeneous environment. Nature. 1998;394:69–72. doi: 10.1038/27900. [DOI] [PubMed] [Google Scholar]
- 14.Blake W.J., Balázsi G., Collins J.J. Phenotypic consequences of promoter-mediated transcriptional noise. Mol. Cell. 2006;24:853–865. doi: 10.1016/j.molcel.2006.11.003. [DOI] [PubMed] [Google Scholar]
- 15.Zhuravel D., Fraser D., Kærn M. Phenotypic impact of regulatory noise in cellular stress-response pathways. Syst. Synth. Biol. 2010;4:105–116. doi: 10.1007/s11693-010-9055-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ito Y., Toyota H., Yomo T. How selection affects phenotypic fluctuation. Mol. Syst. Biol. 2009;5:264. doi: 10.1038/msb.2009.23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Levins R. Princeton University Press; Princeton, NJ: 1968. Evolution in Changing Environments: Some Theoretical Explorations. Monographs in Population Biology. [Google Scholar]
- 18.Lachmann M., Jablonka E. The inheritance of phenotypes: an adaptation to fluctuating environments. J. Theor. Biol. 1996;181:1–9. doi: 10.1006/jtbi.1996.0109. [DOI] [PubMed] [Google Scholar]
- 19.Thattai M., van Oudenaarden A. Stochastic gene expression in fluctuating environments. Genetics. 2004;167:523–530. doi: 10.1534/genetics.167.1.523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kussell E., Leibler S. Phenotypic diversity, population growth, and information in fluctuating environments. Science. 2005;309:2075–2078. doi: 10.1126/science.1114383. [DOI] [PubMed] [Google Scholar]
- 21.Gander M.J., Mazza C., Rummler H. Stochastic gene expression in switching environments. J. Math. Biol. 2007;55:249–269. doi: 10.1007/s00285-007-0083-9. [DOI] [PubMed] [Google Scholar]
- 22.Gaál B., Pitchford J.W., Wood A.J. Exact results for the evolution of stochastic switching in variable asymmetric environments. Genetics. 2010;184:1113–1119. doi: 10.1534/genetics.109.113431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Visco P., Allen R.J., Evans M.R. Switching and growth for microbial populations in catastrophic responsive environments. Biophys. J. 2010;98:1099–1108. doi: 10.1016/j.bpj.2009.11.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Müller J., Hense B.A., Pötzsche Ch. Bet-hedging in stochastically switching environments. J. Theor. Biol. 2013;336:144–157. doi: 10.1016/j.jtbi.2013.07.017. [DOI] [PubMed] [Google Scholar]
- 25.Wolf D.M., Vazirani V.V., Arkin A.P. Diversity in times of adversity: probabilistic strategies in microbial survival games. J. Theor. Biol. 2005;234:227–253. doi: 10.1016/j.jtbi.2004.11.020. [DOI] [PubMed] [Google Scholar]
- 26.Solopova A., van Gestel J., Kuipers O.P. Bet-hedging during bacterial diauxic shift. Proc. Natl. Acad. Sci. USA. 2014;111:7427–7432. doi: 10.1073/pnas.1320063111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Acar M., Mettetal J.T., van Oudenaarden A. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 2008;40:471–475. doi: 10.1038/ng.110. [DOI] [PubMed] [Google Scholar]
- 28.Taniguchi Y., Choi P.J., Xie X.S. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science. 2010;329:533–538. doi: 10.1126/science.1188308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Smits W.K., Kuipers O.P., Veening J.-W. Phenotypic variation in bacteria: the role of feedback regulation. Nat. Rev. Microbiol. 2006;4:259–271. doi: 10.1038/nrmicro1381. [DOI] [PubMed] [Google Scholar]
- 30.Storn R., Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. [Google Scholar]
- 31.Futcher B., Latter G.I., Garrels J.I. A sampling of the yeast proteome. Mol. Cell. Biol. 1999;19:7357–7368. doi: 10.1128/mcb.19.11.7357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Friedman N., Cai L., Xie X.S. Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Phys. Rev. Lett. 2006;97:168302. doi: 10.1103/PhysRevLett.97.168302. [DOI] [PubMed] [Google Scholar]
- 33.Dekel E., Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature. 2005;436:588–592. doi: 10.1038/nature03842. [DOI] [PubMed] [Google Scholar]
- 34.Garcia-Bernardo J., Dunlop M.J. Noise and low-level dynamics can coordinate multicomponent bet hedging mechanisms. Biophys. J. 2015;108:184–193. doi: 10.1016/j.bpj.2014.11.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Salathé M., van Cleve J., Feldman M.W. Evolution of stochastic switching rates in asymmetric fitness landscapes. Genetics. 2009;182:1159–1164. doi: 10.1534/genetics.109.103333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rosenfeld N., Young J.W., Elowitz M.B. Gene regulation at the single-cell level. Science. 2005;307:1962–1965. doi: 10.1126/science.1106914. [DOI] [PubMed] [Google Scholar]
- 37.Charlebois D.A., Kaern M. What all the noise is about: the physical basis of cellular individuality. Can. J. Phys. 2012;923:919–923. [Google Scholar]
- 38.Kaern M., Elston T.C., Collins J.J. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 39.Rotem E., Loinger A., Balaban N.Q. Regulation of phenotypic variability by a threshold-based mechanism underlies bacterial persistence. Proc. Natl. Acad. Sci. USA. 2010;107:12541–12546. doi: 10.1073/pnas.1004333107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Jõers A., Kaldalu N., Tenson T. The frequency of persisters in Escherichia coli reflects the kinetics of awakening from dormancy. J. Bacteriol. 2010;192:3379–3384. doi: 10.1128/JB.00056-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.