A Mechanism for Cytoplasmic Streaming: Kinesin-Driven Alignment of Microtubules and Fast Fluid Flows

Abstract

The transport of cytoplasmic components can be profoundly affected by hydrodynamics. Cytoplasmic streaming in Drosophila oocytes offers a striking example. Forces on fluid from kinesin-1 are initially directed by a disordered meshwork of microtubules, generating minor slow cytoplasmic flows. Subsequently, to mix incoming nurse cell cytoplasm with ooplasm, a subcortical layer of microtubules forms parallel arrays that support long-range, fast flows. To analyze the streaming mechanism, we combined observations of microtubule and organelle motions with detailed mathematical modeling. In the fast state, microtubules tethered to the cortex form a thin subcortical layer and undergo correlated sinusoidal bending. Organelles moving in flows along the arrays show velocities that are slow near the cortex and fast on the inward side of the subcortical microtubule layer. Starting with fundamental physical principles suggested by qualitative hypotheses, and with published values for microtubule stiffness, kinesin velocity, and cytoplasmic viscosity, we developed a quantitative coupled hydrodynamic model for streaming. The fully detailed mathematical model and its simulations identify key variables that can shift the system between disordered (slow) and ordered (fast) states. Measurements of array curvature, wave period, and the effects of diminished kinesin velocity on flow rates, as well as prior observations on f-actin perturbation, support the model. This establishes a concrete mechanistic framework for the ooplasmic streaming process. The self-organizing fast phase is a result of viscous drag on kinesin-driven cargoes that mediates equal and opposite forces on cytoplasmic fluid and on microtubules whose minus ends are tethered to the cortex. Fluid moves toward plus ends and microtubules are forced backward toward their minus ends, resulting in buckling. Under certain conditions, the buckling microtubules self-organize into parallel bending arrays, guiding varying directions for fast plus-end directed fluid flows that facilitate mixing in a low Reynolds number regime.

Introduction

Transport processes that purposefully move organelles, chromosomes, and other objects from one place to another through cytoplasm are fundamental to the reproduction, growth, and development of eukaryotic cells. To drive transport, dimeric molecular motors couple alternating cycles of ATP-driven conformation change to cycles of filament binding and release to generate stepping forces that move motor-attached cargoes along cytoskeletal filaments (1). In many cases, the primary purpose of motor activity is to deliver individual cargoes to specific destinations. However, in other processes, the objective is to transfer force from motors to their filament tracks and/or to the cytoplasmic fluid that surrounds them. We report here a mathematical model for the mechanism of a microtubule-motor-driven process whose purpose is to drive fluid motion in a manner that accomplishes the mixing of two different masses of viscous cytoplasm. The process, cytoplasmic streaming in Drosophila oocytes, offers unique insights into how the responses of fluid and filament tracks to forces that are generated by motors can have long-range influences on cytoplasmic motion and organization. Our results provide a concrete quantitative framework for understanding the hydrodynamic underpinnings of transport processes, elucidate a general and hitherto unknown form of filament self-organization, and point out an intriguing mechanism for mixing fluids at low Reynolds number.

In the Drosophila ovary, a germline stem cell generates an egg chamber with 15 nurse cells that are connected by cytoplasmic channels to one another and to the anterior end of a developing oocyte. During the early and middle stages of oogenesis, mRNAs, protein complexes, and organelles synthesized in nurse cells are selectively transported into the oocyte (2). Disordered cytoplasmic flows (“slow streaming”) help disperse the new components after they enter the oocyte anterior. During this period, developmental determinants such as bicoid and oskar mRNA particles are transported toward particular regions of the oocyte margin and anchored to the cortex, thereby establishing the major body axes of the future organism (3, 4, 5, 6). Meanwhile, substantial amounts of material synthesized in somatic tissues, such as yolk, are transferred into the developing oocyte through follicle cells along its lateral membranes by endocytosis. In late oogenesis, at the beginning of stage 10B, nurse cells squeeze all their remaining cytoplasm into the oocyte anterior en masse. To mix this new material with the existing yolky ooplasm, cytoplasmic flows accelerate >10-fold and become coherent, following long, varying trajectories throughout the oocyte (“fast streaming”) (7). Mutations that allow premature fast streaming and its associated mixing prevent the localization of developmental determinants to their cortical target areas and thus disrupt the proper formation of body-axis polarity (8). Mutations that allow no fast streaming prevent the mixing of the oocyte with nurse-cell cytoplasm and can also cause embryonic lethality (9, 10, 11). Therefore, the biophysical mechanism that underlies fast streaming is important.

The force for streaming is generated by a plus-end-directed microtubule motor, kinesin-1 (10). In mid-oogenesis, before stage 10B, microtubules, many of which are nucleated at the oocyte cortex where γ-tubulin-based nucleation complexes are concentrated, extend their plus ends inward, forming a dynamic 3-D meshwork (11, 12, 13). Kinesin-1 is abundant and diffusely distributed (10, 14). The trajectories of slow cytoplasmic flows, as seen by observing the movements of yolk endosomes or other organelles, are short and randomly directed. At stage 10B, flows become fast, long-range, and ordered as a layer of subcortical microtubules organizes into parallel bending arrays (11, 13). This transition from slow to fast streaming coincides with a dispersal of cortical γ-tubulin and the loss of a diffuse f-actin meshwork that permeates the ooplasm (15, 16). It is particularly interesting that depolymerization of that f-actin meshwork, which should decrease cytoplasmic viscosity, allows premature fast streaming as early as stage 9 (8, 15).

From these and other observations, qualitative models have proposed that the normal slow-streaming process during mid-oogenesis reflects plus-end-directed kinesin-1 transport of cargoes that act as impellers to transfer force to cytoplasm that generates disordered fluid flows. Although the oocyte is capable of organizing subcortical microtubules into parallel arrays and driving fast, ordered flows, the process is restrained until stage 10B by certain factors, especially the cytoplasmic f-actin network (8, 10, 11, 15, 16). Weakening of that network at stage 10B allows a self-amplifying loop of kinesin-1-driven fast plus-end-directed fluid motion along with increasing microtubule alignment that helps generate long-range flows. In combination, these observations suggest that fast streaming is a self-organizing process with a relatively simple mechanism comprised of four principal components: a stationary cortical barrier, a population of microtubules whose minus ends are tethered to that barrier, kinesin-1 motor complexes, and cytoplasmic fluid.

To elucidate the streaming mechanism, we combined experimental observations with detailed mathematical modeling based on fundamental physical principles. Fluorescence microscopy of live oocytes examined relationships between the oocyte cortex, subcortical green-fluorescent-protein (GFP)-microtubule behavior, and streaming-driven motions of organelles. Based on those observations and the previous qualitative streaming hypotheses, a concrete quantitative model was developed using established estimates for microtubule stiffness, kinesin-1 velocity on microtubules, and cytoplasmic viscosity. The model defines size/spacing relationships for various kinesin cargoes that could generate enough viscous drag to drive the fast-streaming velocities that were observed. We then focused on a simple analysis of the effects of equal-opposite kinesin forces on the behavior of a single microtubule whose minus end is tethered in an imposed cytoplasmic flow field. Starting from any random configuration, kinesin forces along the length of the microtubule generate bending patterns that evolve into a stable helical wave that can become sinusoidal when adjacent to a nonmoving cortex-like barrier plane. To examine a more complex situation similar to that in an oocyte, we coupled the models for kinesin-driven cytoplasmic flow generation and filament bending to determine the behavior of a field of many microtubules with minus ends held stationary near a barrier plane in a self-generated flow field. Simulations show that microtubule behaviors evolve into the two states that are seen in oocytes; either noncorrelated helical bending, akin to slow streaming, or remarkably correlated parallel arrays that bend in a sinusoidal manner parallel to the cortical plane, akin to fast streaming. Key factors that determine evolution of the noncorrelated or correlated state are spacing between the cortex-like barrier and the level at which microtubules can become parallel to it, microtubule stiffness, and parameters that determine kinesin-derived force density along the microtubules: motor-cargo size/spacing, motor velocity, and cytoplasmic viscosity. The facts that the two simulation outcomes are analogous to the two states seen in oocytes and that they emerge over a full range of parameter variations suggest that the model is valid and that it provides a robust quantitative mechanism for kinesin-mediated cytoplasmic streaming.

Materials and Methods

Theoretical modeling and simulations

The central work here develops theoretical analyses and computer simulations of the mechanism of cytoplasmic streaming in Drosophila oocytes. Fully detailed mathematical analyses are presented in the Supporting Material. Three major parts to the modeling approach will be presented in Results.

• •Analysis of hydrodynamic flow induced by kinesin motion along microtubules. We employ theoretical calculations and numerical work to predict the magnitude of flow fields.
• •Waves created on a microtubule by kinesin motion. We develop and analyze a continuous model for this problem, leading to a detailed understanding of the steady-state nonlinear waves that are generated. Computer simulations are also employed to obtain quantitative estimates of frequency and wavelength based on parameters such as microtubule stiffness and ooplasmic viscosity.
• •Full hydrodynamic treatment of many microtubules and kinesin. We develop and implement a numerical model to describe this more complex situation, in which kinesin motors on different microtubules interact hydrodynamically, generating complex collective behavior. This leads to the investigation of a nonequilibrium disorder-order transition that takes place as model parameters are varied.

Genetics

To observe fluorescent microtubules in oocytes, a single copy of transgenic UASp-GFPS65c-α-tub84B was expressed in the female germline using P{w⁺ GAL4::VP16nos.UTR}MVD1 (nanos-Gal4) as a driver. To obtain egg chambers that were additionally homozygous for slow-Khc mutations, germline clones were induced in the GFP-tubulin background using an FLP/FRT mitotic recombination approach in females heterozygous for either Khc²³ or Khc¹⁷, as described previously (11). Egg chambers with a half dose of wild-type kinesin were obtained from females that were heterozygous for a small deletion that removes the Khc gene (Df(2R)BSC309/+). To observe lipid droplet motions, GFP-LD (P{UASp-GFP-LD}), which fuses the lipid-droplet-binding domain of Klar-β to GFP, was expressed in the female germline using the nanos-GAL4 driver (17).

Microscopy

Egg chambers were dissected from adult females and were mounted live in halocarbon oil on coverslips as described previously (11). They were imaged in time lapse with either a spinning-disk confocal fluorescence microscope (Fig. 1; Movies S1, S2, and S3) or an Olympus FV1000 two-photon fluorescence microscope (see Fig. 7; Movie S8). Fluorescence redistribution after photobleaching (FRAP) tests were performed using the Olympus FV1000 “bleach laser” function set to a wavelength of 880 nm at maximum intensity for a duration of 0.24 s.

Figure 1.

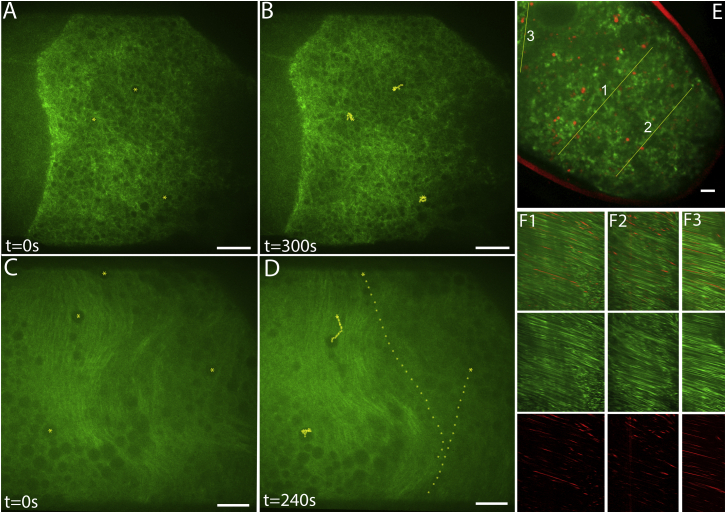
Microtubule organization and organelle motion in Drosophila oocytes. (A–D) Single optical sections from beneath the plasma membranes of live oocytes that contained GFP-α-tubulin (see other examples in Movies S1 and S2). (A) A stage 9 oocyte in which the centers of three yolk granules are marked with yellow dots. (B) The same oocyte 5 min later, with the positions of the three yolk granules marked at intervening 10 s intervals. The optical section is near the surface of the oocyte at the right side and is ∼10 μm deeper at the left side. Note at all depths the similarly disordered microtubules and slow granule movements. (C and D) A stage 10B oocyte with granules marked and tracked as in (A) and (B). In this case, the optical section is just beneath the oocyte surface at the lower left and is ∼10 μm deeper on the right. Note the parallel microtubule arrays at ∼5 μm depth. Organelle motion was negligible between the microtubule layer and the oocyte surface (left side), and was fast beneath the microtubule layer (right side). Only yolk endosomes that remained in the focal plane were used to mark streaming motions in this figure. (E) A single optical section from a time-lapse image series (Movie S3) showing a stage 10B oocyte with lipid droplets marked by GFP-LD (green) and endosomes carrying trypan blue (red). The yellow lines were used for generating the kymographs in (F). (F) Kymographs show the intensities of lipid-droplet and endosome signals along the lines marked in (E) (x axes) over time (y axis = 800 s). Scale bars, 10 μm.

Figure 7.

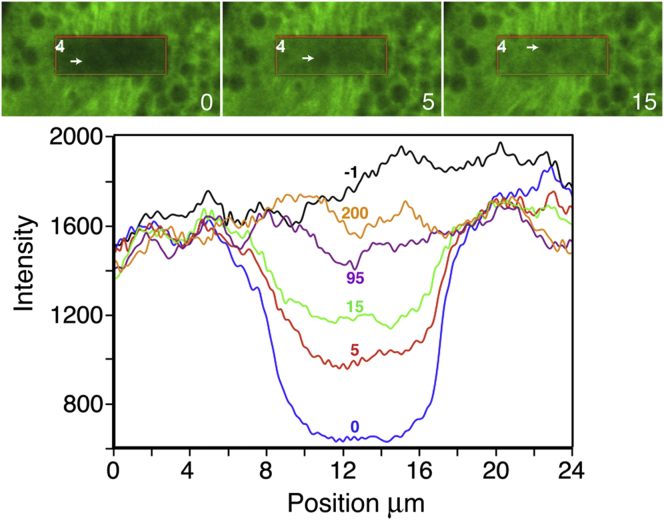
Subcortical arrays of microtubules are stationary during streaming. (Top) Subcortical GFP-tubulin in a stage 10B oocyte imaged by time-lapse two-photon fluorescence microscopy. Intense two-photon excitation was used to photobleach a 10 × 30 μm area (orange box) in a shallow optical section of well-aligned subcortical microtubules. White arrows mark the positions of a yolk granule carried by fast streaming at ∼300 nm/s. (Bottom) Fluorescence intensity was scanned from bottom (0 μm) to top (24 μm) of images at various time points (noted in seconds). The bleached zone did not move laterally, and fluorescence recovery was symmetrical, despite streaming of cytoplasm through the area (see Movie S8).

Organelle and microtubule motions

Curve radii for microtubule arrays were measured from time-lapse images of GFP-tubulin in fast-streaming oocytes. For clearly visible array waves, the radius was determined by fitting the most acute wave apex with a circle. Wave periods for arrays that remained visible in the optical section for sufficient duration were estimated from time-lapse videos by determining the time required for a complete wave cycle (peak to peak or front to front) to pass a fixed position. FRAP patterns were determined by plotting the average pixel intensity of a 15-μm-long line translated sideways along a 24 μm path following the long axis of the bleached rectangles.

To analyze streaming motions of organelles, three approaches were used. First, in spinning-disk images of oocytes that expressed GFP tubulin, organelles appeared dark by virtue of excluding the GFP. For each oocyte, the positions of the centers of 10 randomly selected dark organelles that were beneath the immobile oocyte cortical zone and that remained in the plane of focus for at least 50 s were marked in each frame using an MTrackJ version 1.5.0 plug-in for ImageJ version 1.42 (18). Velocity was determined by measuring the net distance traveled between the start and end points and dividing by time. This simple low-frequency sampling approach filtered out the influence of short-range multidirectional saltatory motions, thus focusing velocity values on bulk cytoplasmic flow (11). The second approach focused on yolk endosomes in egg chambers lacking GFP-tubulin. The abdomens of females were injected with 1 mg/mL trypan blue dye, which is coendocytosed with yolk from hemolymph by oocytes (11). After 2–4 h, ovaries were dissected and imaged using red fluorescent protein filters. Fluorescent endosomes were tracked and velocities were determined as for the GFP-tubulin-excluding organelles. In the third approach, females that expressed GFP-LD, which is targeted to lipid droplets, were injected with trypan blue and ovaries were imaged in two colors using GFP filters for GFP-LD and red fluorescent protein filters for trypan blue. To measure streaming velocities, three different areas within each of five oocytes were selected, in which endosomes and lipid droplets were free of the cortex and moved in the focal plane. In the center of each area, a line was drawn that followed the path of motion using ImageJ. A kymograph was then constructed (ImageJ, Velocity Measurement Tool Macro) that revealed pixel intensity changes along that line as a function of time. In each GFP-LD kymograph, slopes were measured for five randomly selected, well-defined GFP streaks and then averaged to reflect lipid-droplet velocity in that area. The three kymographs were then averaged to produce a velocity value for each oocyte.

Results

Streaming flows and microtubule bending

To gain insight into the behaviors of microtubules and cytoplasm during streaming, we used time-lapse fluorescence microscopy to image live oocytes dissected from female Drosophila that expressed GFP-tubulin in their germlines (Fig. 1; Movies S1 and S2). Comparison of stage 9 (slow-streaming) and stage 10B (fast-streaming) oocytes revealed striking differences. Fibrous fluorescence from microtubules in stage 9 was disordered. Motions of GFP-excluding organelles were also disordered and accomplished little net displacement over time (Fig. 1, A and B; Movie S1). The microtubule and organelle patterns did not vary substantially at different depths beneath the oocyte surface. In stage 10B, near the oocyte margin, microtubule fluorescence was dispersed among a layer of large organelles (∼5 μm in diameter) that moved little, presumably constrained by association with the cortex (Fig. 1, C and D, lower left). At ∼5 μm beneath that cortical layer and parallel to the plasma membrane, there was a dense zone of aligned microtubules that exhibited correlated wave-like bending behaviors. Organelles just inward from that microtubule layer moved fast over long distances, generally following the paths of the adjacent microtubule arrays. The average velocity determined by tracking of randomly selected GFP-excluding organelles, including slow ones associated with the cortex, was 217 ± 38 nm/s (n = 12 oocytes). To examine the streaming behaviors of specific organelles, females expressing GFP-LD, which tags lipid droplets that enter the oocyte anterior from nurse cells, were injected with trypan blue, which is taken up by the oocyte during endocytosis of yolk through lateral surfaces. Two-color time-lapse images (Fig. 1, E and F; Movie S3) showed that endosomes were relatively immobile in and near the cortex, but moved fast beneath it. Lipid droplets were excluded from the cortex and moved fast beneath it. The patterns of motion and the velocities of lipid droplets and endosomes that were free of the cortex were the same, reflecting bulk cytoplasmic flows. The average velocity of GFP-tagged lipid droplets determined from kymographs of oocyte regions that had relatively linear flow patterns (Fig. 1 F) was 313 ± 27 nm/s (mean ± SE of n = 5 oocytes).

A mechanism for kinesin-driven fluid flow and microtubule bending

Our findings, joined with past work described in the Introduction, support a self-organizing motility mechanism that is unique in its simplicity, relying primarily on a single filament type, microtubules, and a single motor protein species, kinesin-1. At the beginning of stage 10B, changes occur that allow robust movement of kinesin-1 along microtubules whose minus ends are thought to be tethered to the cortex. The kinesin-1 motors and their associated cargoes transfer force to adjacent cytoplasmic fluid by viscous drag, and hence, cytoplasm moves toward the plus ends. The force of each kinesin-1 on fluid is matched by an equal and opposite force on the microtubule that would displace it with the minus end leading, if it were free to move. However, because its minus end is tethered to the cortex, the microtubule responds to the kinesin force by buckling. In the fast-streaming state, hydrodynamic force transfer between neighboring microtubules, combined with drag on them from bulk cytoplasmic flow toward their plus ends, encourages parallel alignment and a correlation of bending behaviors. The correlated bending patterns vary over time, creating varying trajectories for fluid flows that facilitate nonlaminar motions and thus promote efficient mixing of cytoplasm, despite its high viscosity and the small scale.

Fluid flow caused by kinesin-driven motion

To elucidate the intuitive mechanism in quantitative terms, we considered three lines of inquiry. 1) How can bulk cytoplasmic fluid flows be driven by the movement of kinesin motors toward microtubule plus-ends? 2) How does microtubule bending occur in this situation? 3) How can the combination of these two effects lead to a self-organizing system of fast flows, aligned microtubules, and correlated bending behavior? To address these questions, a mathematical model was developed based on the physical principles of hydrodynamics. Simulations of the model with various parameters unexpectedly led to either disordered or aligned phases that resemble the slow- and fast-streaming states observed in oocytes.

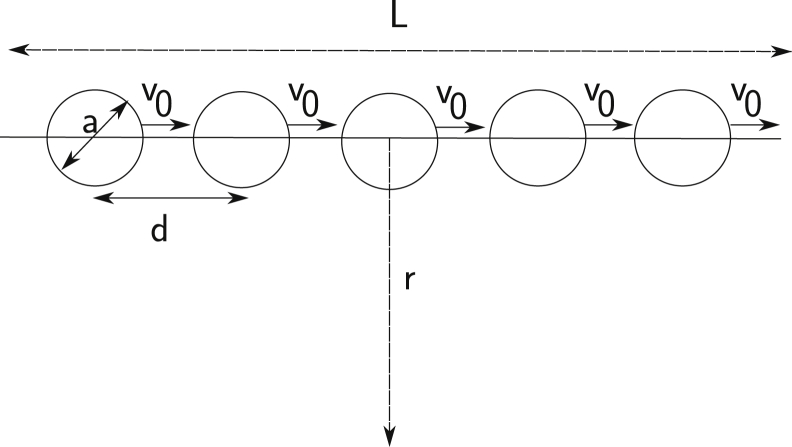
To begin, we developed a physical model for fluid flows based on known properties of microtubules, kinesin-1, and cytoplasm. A small moving object will interact with its surrounding cytoplasm by viscous drag (19, 20), moving the fluid such that flow velocity decreases with distance away from the object, r, as 1/r. Thus, a single kinesin-cargo complex traveling along a microtubule can move neighboring fluid, but the velocity of that movement becomes negligible at large distances. However, consider an in-vivo-like situation with many kinesin-cargoes traveling along a microtubule. As illustrated in Fig. 2, a linear array of spherical objects of diameter a, moving at velocity v₀, that are separated by distances d, will create drag similar to that of a long rod. As analyzed in detail in Section S2 in the Supporting Material, for distance scales ≫d, this train of objects is equivalent to a solid rod of diameter a, moving at a velocity of ∼(a/d)v₀. Because of its long length, a moving rod can generate a flow field with velocities that are substantial at large distances. In fact, the effect of a moving rod of length L is similar to the effect of a moving sphere of diameter L, up to slowly varying logarithmic corrections (19). Thus, fluid velocity will be comparable to that of the rod out to distances of order L. With kinesin-cargo complexes closely spaced all along a microtubule, L will be equivalent to the length of the microtubule, which in an oocyte could average tens of microns.

Figure 2.

Fluid movement by viscous drag on a train of motor-cargo complexes. A train of spherically shaped impellers of diameter a and separation d, all moving in a fluid with low Reynolds number at velocity v₀. The fluid velocity, v(r), is measured at a point distance r from the axis. Separated by small distances, the moving spheres should behave as a rod of length L.

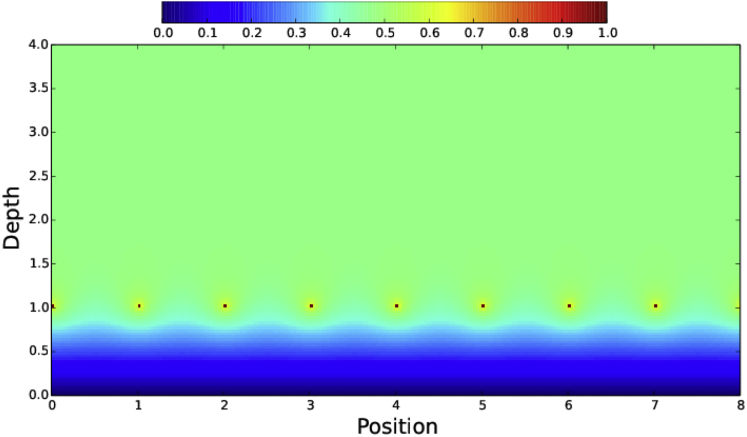
This analysis neglects the effect of the oocyte cortex, which will inhibit fluid flow next to its surface, since it is stationary. To analyze this cortical effect on a flow field generated by many aligned microtubules, similar to the situation during fast streaming, we considered an infinite array of parallel rods lying above a wall (Fig. 3). To simplify, instead of kinesin complexes moving along the rod surfaces, each rod (red) is modeled as moving along its length, which causes equivalent viscous drag and thus hydrodynamic flow. The cortex-like barrier below it imposes a fluid velocity of zero (dark blue) at its surface. The hydrodynamics of this situation can be understood by electrostatic analogy, because it maps onto the problem of an array of rods at constant potential above a grounded plane and can be solved by the method of images. In this case, fluid far from the wall and the array of rods moves at a constant intermediate velocity (Fig. 3, green). Therefore, a largely two-dimensional layer of microtubules near the cortex with closely spaced kinesin cargoes moving along them could cause mass fluid flow in an oocyte.

Figure 3.

Model of a fluid flow velocity field generated by kinesin-like motion. Shown is a cross-sectional view of an array of infinitely long microtubule-like rods (red dots) suspended in fluid at a depth of 1 (arbitrary units) above a nonmoving cortex-like barrier (y = 0). Coated evenly with kinesin-cargo complexes moving at a constant velocity into or out of the page, each rod generates fluid flow in that same direction. Relative fluid velocities are represented by colors as shown above in the color bar, with red being equivalent to the kinesin velocity, yellow and green to intermediate velocity, and blue to slow velocity. Velocity is fastest around each microtubule, goes linearly to zero at the cortical barrier plane, and asymptotes to a constant intermediate value (green) above.

Now we are in a position to determine the relationship between the velocity of kinesin and that of ooplasm during fast streaming. The velocity of ooplasm should be less than that of kinesin moving along cortical microtubules by a factor of ∼a/d. Kinesin-1-driven motions in metazoan cells vary from ∼100 to 1000 nm/s depending on which cargo type is being tracked, probably on regulatory influences, and perhaps also on how many kinesins are engaged in moving each cargo (21, 22, 23, 24). We elected to use the velocity of kinesin-1 itself measured directly in cells at v₀ = 780 nm/s (25). In our tests, the average velocity of fast-streaming lipid droplets beneath the microtubule layer is 313 ± 27 nm/s, suggesting that a/d is 0.4. With an average cargo diameter of a = 250 nm (e.g., lipid droplets), a spacing of d = 625 nm along microtubules should be sufficient to support the observed mass fluid velocity. Electron microscopy showing close association between lipid droplets and subcortical microtubules in stage 10B oocytes led originally to the suggestion that they are key streaming impellers (13). However, any kinesin-cargo complex should suffice if it is appropriately spaced along microtubules; e.g., filamentous kinesin cargoes such as microtubules with an average length of 5 μm would need to be spaced at only 3.13 μm and 40-nm-diameter small vesicles would need to be spaced closely at 100 nm. This logic leads to consideration of the possibility that kinesin-1 motors, each with its own rod-like geometry 30–80 nm long (26), could drive fast streaming if they were active without cargo bound and if they were closely spaced along microtubules. In summary, this fluid-flow analysis indicates that kinesin forces that are transferred to cytoplasmic fluid by viscous drag on any sort of cargo can indeed explain the magnitude and velocity of fluid motion in fast-streaming oocytes, even at substantial distances from the subcortical microtubule layer.

Dynamics of kinesin-driven microtubule bending

Can kinesin forces explain the correlated wave-like bending motions of microtubules seen during fast streaming? The general logic we used to analyze this considers the multiple forces that act on cortical microtubules. One is the force kinesins exert directly on a microtubule, a buckling force tangent to its long axis that is resisted by the elastic stiffness of the microtubule. Another force is exerted on the microtubule by the moving cytoplasmic fluid that surrounds it. Thus, the analysis must incorporate the determinants of fluid motion, which include drag from the moving kinesin complexes and from the buckling motions of the microtubules. It is consideration of these coupled effects that allows one to evolve the entire hydrodynamic system in time.

First, consider the magnitude of the force exerted by an individual kinesin motor on its point of attachment to a microtubule. This is equal and opposite to the viscous drag on the motor-cargo complex as it moves toward the plus end. With a motor complex of linear dimension a, the force due to Stokes drag is $3\pi \eta a\text{v}.$ Assuming a cytoplasmic viscosity, $\eta$, of 8 times that of water (27), and an in vivo kinesin velocity, v, of 780 nm/s, the drag force even from a large cargo (a = 2μm) would be only 0.12 pN; from a small cargo (a = 60 nm), it would be 0.007 pN. The force per unit of microtubule length, f_k, generated by a train of kinesin complexes walking along the microtubule can be estimated, because it is proportional to $\eta$, v, and, as discussed above, a/d, so that f_k$=\eta \text{v}a\text{/}d$. This force density is independent of microtubule length up to logarithmic corrections, and the load on a kinesin-cargo complex due to drag is far less than the stall force of kinesin-1 (>5 pN) (28).

We now use these observations to construct a model for the motion of a single minus-end-tethered microtubule interacting with many kinesins in fluid. Consider the multiple forces that act at any point on the microtubule (Fig. 4). As a kinesin steps toward the microtubule plus end, it applies force to the surrounding fluid, and it transfers an equal-opposite force (F_k) to the microtubule that is tangent to the microtubule’s long axis. Assuming that the microtubule is inextensible, the force on the microtubule creates a tension, T, acting on nearby subunits in opposing directions, giving a net force that we denote ΔT. The microtubule has an elastic bending constant, C, that will produce a force, F_e, perpendicular to the microtubule long axis. The total local force acting on an element of fluid next to a microtubule is the sum of the above forces,

$$\mathit{f}={\mathit{F}}_{\text{e}}+{\mathit{F}}_{\text{k}}+\Delta T.$$ (1)

This equation, supplemented with more detailed expressions for the terms on the righthand side (described below), gives the force acting on a point in the fluid, but this is not enough to determine the motion of the system. Hydrodynamic theory can be used to obtain that motion: The total force acting on an element of liquid has a long-range influence on velocities far from that point. The velocity of the fluid due to a force acting on a point is given by the Oseen tensor (Section S5 in the Supporting Material), which dictates that far from any surfaces, fluid velocity will diminish as the inverse of distance from the point of force, with an additional prefactor of order unity, depending on the force’s direction. Conversely, the velocity u(r) of fluid at an arbitrary point r, is the weighted sum over all forces. In more precise terms, this weight is the Oseen tensor, $\mathbf{J}(\mathbf{r},{\mathbf{r}}^{\prime })$, which connects the force density $\mathbf{f}\left({\mathbf{r}}^{\prime }\right)$ at point ${\mathbf{r}}^{\prime }$ in the fluid to the velocity at another location, r, so that

$$\mathbf{u}\left(\mathit{r}\right)=\int \mathbf{J}\left(\mathbf{r},{\mathbf{r}}^{\prime }\right)\mathbf{f}\left({\mathbf{r}}^{\prime }\right)d^3{r}^{\prime }.$$ (2)

The Oseen tensor can also take into account the presence of a wall (e.g., the oocyte cortex) where the velocity vanishes (Supporting Material; Eq. S42). These equations of motion for a microtubule are supplemented with the boundary conditions that the minus end is fixed in space, whereas the plus end is free to move. The implementation of this model is described in detail in Section S5.

Figure 4.

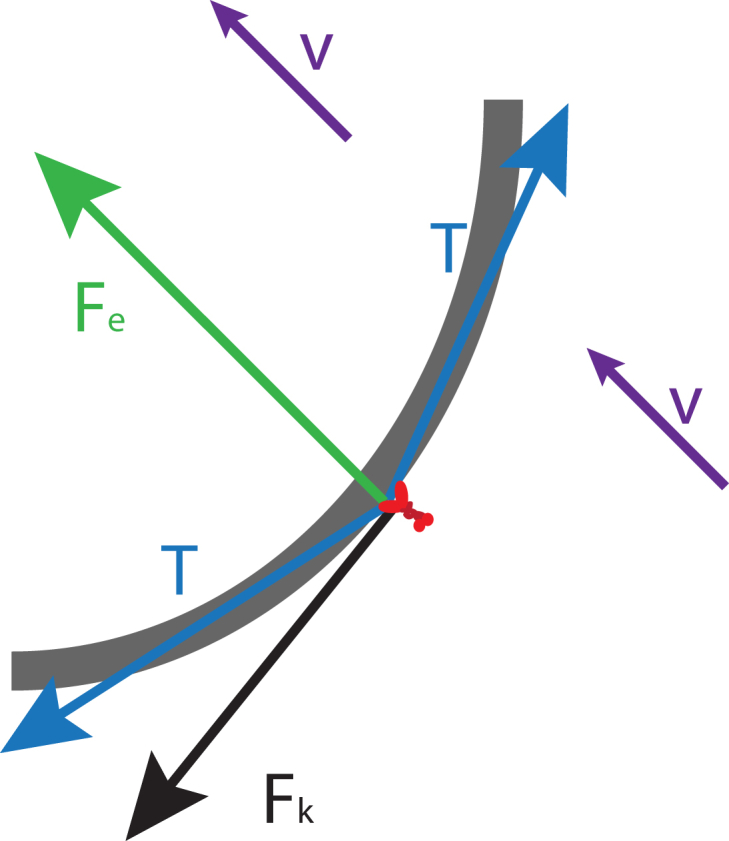
Force diagram for a microtubule-kinesin system. A small section of a microtubule (gray) is shown being acted on by kinesin forces all along its length that cause bending. A single kinesin (red) is shown to focus attention on multiple forces (arrows) that act at its point of attachment to the microtubule. A force tangent to the long axis of the microtubule is exerted by kinesins causing a total force along this section of F_k. The microtubule has an elastic bending constant that will produce a force (F_e) in this section that will oppose the microtubule bending. Tension (T) acts on neighboring elements of the microtubule in opposing directions tangent to the long axis. Force is transferred from the microtubule to the surrounding fluid, which will move at velocity v.

Before advancing to a more detailed mathematical analysis, we approximated microtubule motion under simplified physical conditions. Because the F_k kinesin forces are acting, on average, tangent to the microtubule all along its length, they will cause buckling if the microtubule is long enough. To understand this, we can make use of buckling theory for a rod with elastic constant C supporting a load. Consider a section of microtubule of length L. The critical buckling force the load must apply is f_B = π² C/L² if the directions of the end segments are not constrained. This will differ by a factor of order unity if there are such end constraints, or if the load is distributed evenly over the rod rather than being confined to its ends. The longitudinal force, f_L, due to kinesin, as discussed above, is f_L = f_k L. As L increases, f_L will increase and f_B will decrease. The point at which they are equal gives the value of L at which buckling will first occur. The radius of curvature, R, for buckling will be proportional to L and will occur at $R={\left(C/\beta f_{\text{k}}\right)}^{1/3},$ where β is a constant that will be determined by a more rigorous analysis outlined below that will allow comparison of theoretical predictions to measured microtubule curvatures in oocytes. We emphasize that this simplified buckling analysis is not precise, because it assumes a static load. With each kinesin force tangent to its local microtubule axis, as a microtubule bends over time, it redirects those forces, implying that the load on the filament is time dependent. We now present a more complete analysis of this dynamic situation.

To understand the motion of a single microtubule, one must consider that the surrounding fluid creates drag on it. We first consider a single microtubule with a local drag coefficient $\nu$, but with no long-range hydrodynamics. A full hydrodynamic treatment must include the motions of kinesins on many adjacent microtubules and the more complex flow field they generate. However, for a simple single-microtubule simulation, we will assume that the only effect of the other microtubules is to produce a constant fluid velocity field, v_s, which we will regard as a fixed external parameter. We show in Section S5.7 in the Supporting Material that this approximation of local drag is in good agreement with the full hydrodynamic treatment for a single microtubule system.

The single-microtubule dynamics model is developed in detail in Section S4 in the Supporting Material. It is similar to one developed previously for filament bending in gliding assays on glass surfaces coated with motors (29). However, our model is three-dimensional in an external fluid velocity field, rather than two-dimensional with no external velocity field. The configuration of the microtubule, r(s), is parameterized as a function of arclength, s. Assuming that drag is only local, and writing out the forces on the righthand side of Eq. 1 explicitly,

$$\nu \frac{\partial \mathbf{r}}{\partial t}=-C\frac{{\partial }^4\mathbf{r}}{\partial s^4}+\frac{\partial }{\partial s}\left(T\left(s\right)\frac{\partial \mathbf{r}}{\partial s}\right)-f_{\text{k}}\frac{\partial \mathbf{r}}{\partial s}+\nu {\text{v}}_{\text{s}}\hat{k},$$ (3)

where the position-dependent tension, T(s), enforces the inextensibility of the chain $\left|\partial \mathbf{r}/\partial s\right|=1$.

We can now use Eq. 3 to determine the three-dimensional motion of a microtubule subjected to kinesin forces while its minus end is tethered in free space. Mathematical analysis yields a set of traveling wave solutions for long chains (Sections S4.1–S4.4 in the Supporting Material). The equation for their shape can be mapped onto the equation for a spherical pendulum, and their form can be analyzed in several situations. For the case v_s = 0, there are circularly rotating solutions with angular velocity $f_{\text{k}}\text{/}\left(\nu R\right)$, where R is the radius of curvature (Supporting Material; Eq. S24). We have studied numerically how R depends on the fluid velocity field and found that it is quite insensitive over a wide range of v_s velocities. The precise value of R is determined by the boundary conditions, so we applied boundary conditions numerically that held the minus end at a fixed location but allowed it to pivot, whereas the plus end was completely free. Starting from random initial conditions, the equation rapidly goes to a steady state that typically is described by a curve that asymptotically becomes a helix that rotates uniformly at constant angular velocity ω (Fig. 5; Movie S4). The crumpled initial conditions are clearly not attainable with a real microtubule, but they are shown to demonstrate that even from such extreme starting configurations, the dynamics approach the same helical solution. The handedness that develops for the helix is random, but is stable once steady state is attained. A combination of this numerical work and our analytical results agrees with our much simpler buckling analysis, discussed above, that gives $R={\left(C/\beta f_{\text{k}}\right)}^{1/3}$; it also agrees with the power law found previously (29). However, now we can determine that β = 0.05 ± 0.0005. The asymptotic radius varies only slightly over a wide v_s flow field velocity range (Section S4.6 in the Supporting Material).

Figure 5.

Single-filament bending behavior generated by kinesin forces and an externally imposed fluid flow. Six time points from a 200 frame simulation of a microtubule-like filament with its minus-end (white ball) fixed in space but free to pivot (see Movie S4 and Section S4.6). Starting from initial random compressed configurations of the filament (left side), tangent forces from kinesins walking toward the free plus end, combined with an externally imposed fluid flow field (arrow) generates a stable rotating helical wave. Reasonable values for microtubule stiffness, kinesin force, and fluid viscosity produce a final radius of curvature between 25 and 54 μm. For viewing purposes, the diameter of the filament here is 2000-fold that of a real microtubule.

To move closer to the situation for a single microtubule in an oocyte, we studied variants of this model in which the boundary condition of the tethered minus end is altered such that it is no longer freely hinged about a fixed point, but is rigidly oriented in one direction, as if rooted in and projecting away from the cortex. Because of the stiffness of the microtubule, this shifts bending for the first circular turn away from the minus end. We also studied the influence of a barrier to motion that is similar to the oocyte cortex by adding a short-ranged repulsive wall potential that is positioned near the minus end and is parallel with the flow field (Section S4.6 in the Supporting Material). This still allows traveling waves, but for most values of the imposed fluid flow velocity, v_s, the waves evolve into flattened cycloidal or sinusoidal configurations parallel to the barrier (Movie S5). This behavior can also be understood in detail analytically, in excellent agreement with the simulations (Section S4.4 in the Supporting Material).

Self-organization of many microtubules using simulation

For a more complete model of microtubule behavior in oocytes, the same physical ingredients were considered, but with an array of 100 filaments tethered by their minus ends near a cortex-like barrier plane at which both fluid and filament velocities must be zero. Also, fluid flows were generated internally by kinesin motion toward plus ends, rather than being externally imposed. Thus, kinesin force and microtubule motion coupled to the surrounding cytoplasmic fluid should generate a complete hydrodynamic model as described by Eqs. 1 and 2. Constant kinesin velocity toward plus ends was combined with Eq. 2 to evolve the system in time. The added complexity of this system pushed solutions beyond the scope of current analytic treatments, but it could be modeled numerically (Section S5 in the Supporting Material). This model was unexpectedly predictive, giving rise to an order-disorder transition between two states similar to those observed in slow- and fast-streaming oocytes. To determine whether it is robust, repeated simulations with various parameter changes were used to focus on three general questions: 1) How can a collection of many noncorrelated microtubules that is being acted on by kinesin forces spontaneously self-organize into aligned arrays and undergo correlated bending as observed in fast streaming?, 2) Can parameter changes within the model explain the disorder-to-order transition?, and 3) If so, what parameters most directly influence that transition?

In simulations, microtubule-like filaments were modeled with free-rotating minus ends tethered at height H above the cortex-like barrier, representing a height at which microtubules that are constrained by minus-end segments rooted in the cortex could bend enough to lie parallel with it. The semiflexible nature of the filaments and their interactions with each other were ensured by modeling them as chains of balls with spring potentials between them and with next-nearest-neighbor repulsive potentials. The equilibrium distance between adjacent balls in a chain was 1 in the units used for the simulation. In Fig. 6, A and B, adjacent minus-end tether points are separated by 2 units, and chain lengths are 16 units. Two distinct behaviors of the system emerged in simulations. First, at intermediate kinesin force density on the filaments, and with filament tether points close to the cortical barrier (e.g., H = 1.0), bending dynamics did not become well ordered (Fig. 6 A; Movie S6). Small groups of filaments did correlate over short distances for brief times, creating patterns similar to those observed for microtubules in slow-streaming oocytes (Fig. 6 C; Movie S1), but long-range correlations did not develop. In the second behavior, increasing the distance between the filament tether points and the cortical barrier (H = 2.0) while holding all other parameters unchanged resulted in a striking self-organization into uniformly oriented bending arrays that lay parallel to the barrier (Fig. 6 B; Movie S7). Some filaments at the array edges, where there were few neighbors, exhibited independent helical behaviors akin to those of single filaments (Fig. 5; Movie S4), but those with a full set of neighbors exhibited strongly correlated bending dynamics similar to those of microtubules in fast-streaming oocytes (Fig. 6 D; Movie S2). When H was held at 2.0 while shifting other parameters to create much higher force density on microtubules, the first noncorrelated slow-streaming-like state was reproduced. Those parameter changes included increased kinesin velocity (v₀), larger kinesin-cargo diameter (a; increased drag), reduced spacing between kinesin-cargo complexes (d), or increased viscosity ($\eta$). This outcome could also result from decreased microtubule stiffness (C). Alternatively, parameter changes that resulted in much lower force density allowed evolution of correlated microtubule behavior, but substantially delayed its attainment and reduced the associated fluid velocity (v(r)). Those parameter changes included reduced kinesin velocity, smaller cargo diameter, increased cargo spacing, decreased viscosity, or increased microtubule stiffness. Repeated trials identified parameter values that favored correlated behavior and high fluid velocity: intermediate filament stiffness akin to that measured for microtubules (30, 31), intermediate kinesin force density along the filaments, and minus-end pivot points above the wall at a distance equivalent to the spacing between microtubule minus ends. At a spacing of 2 units between microtubule tether points combined with the intermediate values for stiffness and force density, the transition between weak and strong correlation occurred near a height of H = 1.5 units for chain lengths of 16 and 32, and for filament populations of 50 and 100. Thus, along with stiffness of microtubules and force density on them, the distance away from the cortex at which microtubules can form a parallel layer is a parameter that could control the transition from slow disordered to fast ordered streaming.

Figure 6.

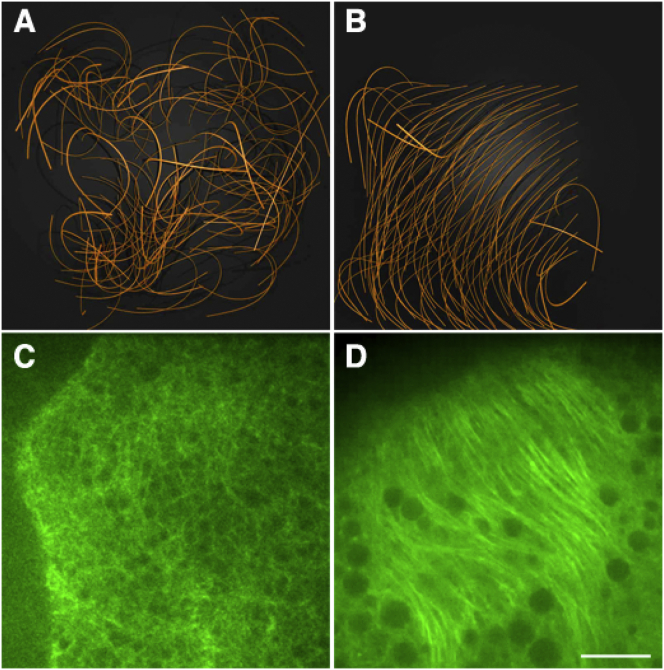
Correlated microtubule-array bending generated by kinesin shear force between fluid and filaments near a barrier plane. (A and B) Views from above of arrays of 100 microtubule-like filaments with minus-end pivot points at two distances from the cortical barrier, (A) H = 1.0 (see Movie S6) and (B) H = 2.0 (see Movie S7). These are outcomes after 200 iterations of simulations under conditions of 1) spacing between minus-end pivot points of 2 units; 2) initial randomized filament configurations; 3) kinesin-like fluid-filament shear forces tangent to each filament axis at all points; and 4) cytoplasmic fluid movements generated by the kinesin-filament shear forces. Note the largely noncorrelated bending behavior in (A) versus the correlated bending behavior in (B). (C and D) Shown are confocal images of GFP-α-tubulin at 0–10 μm depth beneath the oocyte membrane. Scale bar, 10 μm. (C) Stage 10A slow streaming (see Movie S1). (D) Stage 10B fast streaming (see Movie S2).

The subcortical microtubule layer is anchored

One key assumption for our model that is debatable is that the minus ends of microtubules that form the bending subcortical arrays are tethered to the cortex. Consistent with this, early studies showed that microtubule regrowth after depolymerization begins at the oocyte cortex (13). However, it was seen later that although γ-tubulin, which is a minus-end binding and nucleation factor, is concentrated in the cortex during slow streaming, it is not concentrated there during fast streaming, raising the possibility that microtubule minus ends are released from cortical anchors at the transition to fast streaming (15, 16, 32).

If the minus ends of oocyte microtubules are released from the cortex at the transition to fast streaming, they should be carried along by the fast cytoplasmic flows. To test this, we analyzed GFP-tubulin dynamics by FRAP in stage 10B oocytes using a two-photon microscope. Well-aligned bands of subcortical microtubules were marked by photobleaching within a shallow optical section; then, the positions of the bleached zone and streaming yolk granules were observed by time-lapse imaging. If minus ends are not tethered, such a bleached mark should move along with organelles in the cytoplasmic flow. The shallow bleached zones recovered fluorescence in a symmetrical fashion and they made no discernible shifts in position, despite fast flow of yolk granules through them (Fig. 7; Movie S8). This shows that subcortical microtubule arrays are not carried along by fast cytoplasmic streaming flows, indicating that they are indeed tethered to the cortex, consistent with the assumption used for our model.

Comparison to microtubule bending in oocytes

The fact that simulations with a full range of parameter variations led to two states of microtubule organization similar to those seen in oocytes suggests that the model represents the streaming mechanism well. To test the model further, the wave-like bending behaviors in model simulations were compared to real microtubule bending behavior in oocytes. We examined analytical solutions of single-microtubule bending using elastic constants for microtubules of C = 0.5 to 2 × 10⁻²³ Nm², as reported previously (30, 31) (Section S4.6 in the Supporting Material). With a kinesin velocity of 780 nm/s, a cargo diameter/spacing (a/d) between 0.4 and 1, and assuming a cytoplasmic viscosity in fast-streaming oocytes of 8 times that of water (27), the radius of curvature, R, is predicted to be 25–54 μm, and the wave period, τ, is predicted to be 203–1094 s. For comparison, we measured bending behaviors of GFP-tubulin microtubule arrays during fast streaming in stage 10B–11 oocytes. Array trajectories had varying degrees of curvature, and the curves oscillated in a sinusoidal fashion (Figs. 1 D and 6 D; Movie S2). Focusing on the most acute peaks, curve radii were estimated by fitting with circles of known diameter. The average minimum curvature radius was R = 16.3 ± 2.2 μm, mean ± SE of n = 6 oocytes (30 arrays), which is reasonably close to the 25 μm minimum predicted by the model. To estimate wave periods, τ, in oocytes, the amount of time for a complete wave form to pass a fixed point was determined for arrays that remained suitably in the optical section. The average was 370 ± 42s, mean ± SE of n = 6 oocytes (19 arrays). This is within the period range predicted, indicating that our model’s physical explanation for oocyte microtubule bending is valid.

Reducing kinesin-generated forces slows streaming flows and hinders microtubule alignment

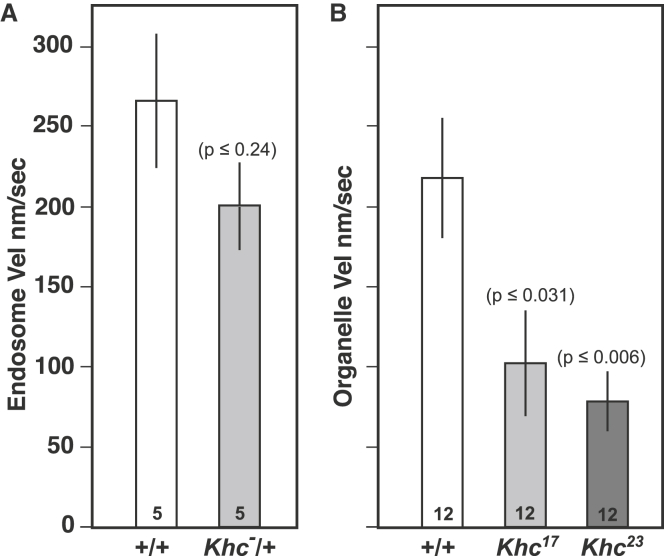
The many-filament model, which is based on fundamental physical principles, shows self-organizing fast streaming behavior similar to that seen in oocytes. For an additional test, we studied the effects of reducing kinesin-generated force density on cortical microtubules. As noted above, the prediction is that reduced force density will delay attainment of the correlated fast-streaming state and will result in reduced fluid velocity in that state. Considering the possibility that kinesin-1 concentration is a limiting factor, we attempted to reduce force density by eliminating one copy of the Khc gene, which is known to reduce the concentration of Khc protein (33). Stage 10B–11 oocytes heterozygous for a 60 kb deletion that removes the Khc gene (Df(2R)BSC309/+) did not show signs of delayed entry into fast streaming, and although the average velocity of fast-streaming endosomes was somewhat reduced, that change was not significant (Fig. 8 A). This suggests that even with half of the normal gene dosage in the female germline, Khc concentration in oocytes is not limiting for the fast-streaming pattern or velocity. This is consistent with prior observations that heterozygous Khc null mutations do not alter kinesin-1-driven transport processes, even in the long narrow confines of neuronal axons (21).

Figure 8.

Tests of reduced kinesin force density on microtubules in fast streaming. (A) The velocities of dye-loaded subcortical endosomes measured in stage 10B–11 oocytes from females with two copies (+/+) or one copy (Khc⁻/+) of the Khc gene. (B) Velocities of subcortical organelles in oocytes that were expressing GFP-tubulin. Organelles that exclude GFP-tubulin were tracked in stage 10B–11 oocytes that were wild-type (+/+) or that had been rendered homozygous for a Khc mutant allele (Khc¹⁷ or Khc²³), which are known to slow the movement of kinesin-1 on microtubules (33). Velocity analysis was done only in mutant oocytes that displayed correlated fast-streaming patterns of motion. Sample sizes (number of oocytes) are shown in each bar and variance is the standard error. p-Values reflect the comparison to +/+ using a two-tailed t-test with unequal variance.

Using another approach, we took advantage of two well-characterized recessive lethal alleles of Khc that cause 3.8-fold (Khc²³) and 1.6-fold (Khc¹⁷) slowing of motor velocity on microtubules in vitro (33) by changing single amino acids in the force-generating head domain of kinesin. To study their influences, females expressing GFP-tubulin and heterozygous for a mutant allele were induced to undergo mitotic recombination in their germline stem cells such that egg chambers descended from them were homozygous for the mutant allele (9, 11). In stage 10B–11 mutant oocytes, three different streaming behaviors were observed: 1) noncorrelated behavior and slow flow velocities for GFP-excluding organelles (Khc²³, 26 ± 5 nm/s, mean ± SE of n = 12 oocytes; Khc¹⁷, 38 ± 6 nm/s, mean ± SE of n = 12 oocytes); 2) faint patches of correlated microtubules with ordered streaming flows; and 3) more extensive, but still faint, subcortical microtubule arrays with uniform correlated streaming flows at velocities that were significantly less than those seen in controls (Fig. 8 B). These observations are consistent with the delayed self-organization and slowed fluid velocity predicted by the model for reduced force density on microtubules.

Discussion

In general, processes involving the transport of cargoes with a strong directional bias should be profoundly affected by hydrodynamic principles, because at low Reynolds number the motions of distant objects are coupled through viscous drag. Elegant studies by Hamaguchi and Hiramoto in sand dollar zygotes established that length-dependent pulling forces on astral microtubules emanating from the centrosome of the male pronucleus move it toward the cell center (34). They suggested that such forces are generated by drag on trains of organelles as they are carried by microtubule motors toward minus ends that are attached to the centrosome. It has since been shown that drag on dynein-cargo complexes indeed generates important length-dependent pulling forces on microtubules whose minus ends are attached to pronuclei (35, 36, 37). Our work has focused on what is in essence the reverse process: predominantly plus-end-directed transport driven by kinesin-1 along microtubules that are attached by their minus ends to the oocyte cortex. In contrast to the microtubule straightening-pulling effects of dynein cargoes walking toward anchored minus ends, drag on kinesin cargoes moving away from anchored minus ends causes microtubules to buckle and, under some conditions, to self-organize into parallel arrays that bend in a correlated fashion. The equal-opposite kinesin force transferred to cytoplasm drives long-range fluid flows in varying directions dictated by the bending arrays, which mixes the cytoplasm.

In developing oocytes, the timing of the switch from midstage slow streaming to late-stage fast streaming is crucial. If fast streaming occurs too early, the proper concentration and anchorage of key body-axis determinants at their cortical sites fails and subsequent embryo development proceeds without normal patterning (8, 38). On the other hand, if streaming-mediated mixing does not occur, embryos do not develop normally (11). Our hydrodynamic modeling shows that oocytes could control the slow- to fast-streaming transition by changing H, the distance between the cortical barrier plane and the level at which cortically tethered microtubules can align parallel to it. This is because fluid motion between the barrier plane and the microtubule layer makes an important contribution to hydrodynamic coupling of microtubules and thus to their correlated bending behavior. Since for fast streaming, the predicted optimum distance of microtubule arrays from the barrier is approximately twice the spacing between microtubule minus ends, if a shift away from the cortex is a trigger for correlation, it need not be large. High-resolution fluorescence images of stage 9 oocytes (12) suggest a spacing between cortical microtubules of ∼1 μm. Thus, a spacing increase between the cortex and the subcortical microtubule layer of just 1 μm could be sufficient to allow the switch to correlated fast streaming. Evidence consistent with a multimicron inward shift of microtubules during the transition from slow to fast streaming has been reported (16). How such a shift could be accomplished while keeping minus ends tethered is an interesting question. One possibility is that if the initial segments of microtubules are rigidly oriented at an average angle perpendicular to the cortex, changes in stiffness could increase the radius over which they could bend to form a subcortical layer. Alternatively, an increase in cortical microtubule density that reduces spacing between them could accomplish the transition without a subcortical shift. Future ultrastructural analysis of the organization of microtubules in and near the cortex before and after the transition should provide important insights into whether or not changes in H or cortical microtubule density contribute to the control mechanism.

Other model parameters could also influence the slow- to fast-streaming transition, including average kinesin-cargo size, spacing between cargoes along microtubules, kinesin velocity, cytoplasmic viscosity, or microtubule stiffness. We have shown that slow kinesin mutations hinder self-organization and reduce fast-streaming velocity, as predicted. Consistent with viscosity changes being important, destabilizing the cytoplasmic f-actin meshwork, which should decrease viscosity, stimulates premature fast streaming in stage 8–9 oocytes (8, 13, 15, 38) and hyperstabilizing the f-actin meshwork has been shown to prevent fast streaming in stage 11 oocytes (15).

Interestingly, model simulations show that increasing the separation distance between the subcortical microtubule layer and the cortical wall (beyond 2 units) facilitates rapid alignment into parallel arrays, but the amplitude of bending becomes less. Considering the purpose of fast streaming in oocytes, mixing of cytoplasm, this suggests that the transition from slow to fast states resets the system to the edge of a symmetry-breaking phase where there is sufficient order to align microtubules and generate robust cytoplasmic flow velocity, yet enough bending of the arrays to facilitate semichaotic variations in flow direction. In regard to a need for flow-pattern variation, rigorous analysis in two dimensions using the Thurston-Nielsen classification theorem has shown that topological chaos is crucial for efficient fluid mixing (39). This is particularly the case for the low-Reynolds-number regime (small scale and high viscosity) that exists in an oocyte. Thus, control of stage 10B parameters to encourage both fast flows and bending is likely an important element for successful mixing of nurse cell and oocyte cytoplasms. Another important consideration for mixing is that the hemispherical geometry of the oocyte cortex must introduce additional instabilities in microtubule array correlation and flow patterns. Simulations of streaming inside hemispheres will be computationally demanding but should produce additional insights into the biophysical mechanism of cytoplasmic-streaming-driven mixing.

Author Contributions

W.M.S. and J.M.D. conceived and designed the project. C.E.M., I.D., A.M.B., and W.M.S. planned, executed, and analyzed oocyte experiments. M.E.B. and J.M.D. developed the physical model and microtubule bending streaming simulations. C.E.M., W.M.S., and J.M.D. wrote the manuscript with input from I.D., M.E.B., and A.M.B.

Editor: David Sept.

Supporting Material

Movie S1. Weak Correlation of Microtubule Motion and Bending during Slow Cytoplasmic Streaming

Live stage 9 Drosophila oocytes containing GFP-α-tubulin expressed in the germline were dissected and mounted in halocarbon oil, and fluorescence was recorded at 5 s intervals using an inverted Ultraview spinning-disk confocal microscope. The image series is played back here at 30 frames/s. The optical section is 5−10 μm inward from the oocyte membrane (see Fig. 1, A and B).

Movie S2. Strong Correlation of Microtubule Motion and Bending Behavior during Fast Cytoplasmic Streaming

GFP-tubulin fluorescence images were recorded in stage 10B oocytes at 5 s intervals and are played back at 30 frames/s (see Fig. 1, C and D). The optical section, 5−10 μm inward from the oocyte membrane, cuts through subcortical cytoplasm in some areas, producing views of bright, ordered parallel arrays of undulating microtubules and of fast moving yolk endosomes (dark spheres). In other areas, where the section is shallower and cuts through the cortex, yolk endosomes associated with the cortex move slowly in the directions of overlying fast flows.

Movie S3. Endosome and Lipid Droplet Fast-Streaming Motion

Time-lapse confocal fluorescence images of a stage 10B oocyte showing endosomes containing trypan blue dye (red fluorescence) and lipid droplets tagged with GFP-LD (green fluorescence) expressed just in the germline. Images were collected in both channels at 2 s intervals, and are played back at 30 frames/s. The oocyte nucleus is seen as a dark sphere in the top left. Note the varying fast-streaming flow patterns.

Movie S4. A Simulation of Single-Filament Bending Behavior Induced by Kinesin Forces

The filament has microtubule-like stiffness and forces tangent to its axis at all points like those generated by kinesin-cargo complexes moving through cytoplasm toward the free plus end (see Fig. 5 and Section S4.6). Those plus-end directed walking forces, if unopposed, would propel the filament with its minus end leading, but its minus end (white sphere) is tethered in space. It can rotate, but not translate. A second force, representing a cytoplasmic streaming flow field is imposed on the system, moving constantly from the bottom to the top of the field of view. Repeated simulations consistently developed stable rotating helical wave forms, with handedness depending on the details of random initial filament configurations. Analytical solutions with reasonable values for microtubule stiffness, and kinesin force, predict a radius of curvature of 24−54 μm, which is roughly one-third the width of a stage 10B oocyte. To facilitate recognition of the bending behavior, the width of the filament here is scaled up to 2,000-fold that of a real microtubule.

Movie S5. A Simulation of Single-Filament Bending Behavior when Adjacent to an Impenetrable Wall

These parameters are the same as in Movie S4 but the system differs by the addition of a barrier that is parallel to the microtubule. This changes the travelling helical wave to a shape similar to a sinusoidal wave that is very well described by the mathematical analysis of Section S4.4. When the cytoplasmic streaming flow field is slower, the shape becomes similar to prolate cycloids that are also well described by the same analysis.

Movie S6. A Simulation of the Bending Behaviors of 100 Filaments with Minus Ends Tethered near a Barrier to Filament and Fluid Motions

The axis of each filament is initially in a random configuration (see Fig. 6 A and Section S5.11)) that changes due to interactions of microtubule-like stiffness, kinesin-like fluid-filament shear forces tangent to each filament at all points, and hydrodynamics as described in the Section S5 (parameters as in Fig. S16 d). Filament length is 16 (dimensionless units), at an elevation of H = 1 above a membrane-like wall. The velocity field at the wall vanishes, which suppresses hydrodynamic interactions between microtubules. In this case, the elevation of minus ends is too low to allow for long-range filament correlation and organized fast streaming.

Movie S7. A Simulation of the Bending Behaviors of 100 Filaments with Elevated Minus-End Tether Points

The parameters are as described for Movie S6, except that minus ends are tethered above the membrane barrier at H = 2 (see Fig. 6 B; parameters as in Fig. S16 c). In this case, fluid motion between the minus ends and the wall allow strong hydrodynamic interactions between microtubules that create long-range correlated behaviors and robust fast streaming. At higher minus-end tethering elevations, correlation becomes stronger and microtubule bending behavior is diminished, generating relatively straight stable arrays.

Movie S8. FRAP Evidence for Cortical Tethering of Microtubules

High-magnification GFP-tubulin images recorded with an Olympus 2-photon microscope in a stage 10B oocyte at 0.93 s intervals are played back here at 30 frames/s. High-intensity excitation was used to photobleach a shallow 10 × 30 μm area in subcortical arrays of microtubules. Note that the photobleached area remains stationary as fluorescence recovers, whereas organelles that exclude GFP tubulin stream past. Adjacent nonstreaming organelles are associated with the cortex. Quantification and other details of this experiment are presented in Fig. 7.