Genome-wide association of multiple complex traits in outbred mice by ultra low-coverage sequencing

Abstract

Two bottlenecks impeding the genetic analysis of complex traits in rodents are access to mapping populations able to deliver gene-level mapping resolution, and the need for population specific genotyping arrays and haplotype reference panels. Here we combine low coverage sequencing (0.15X) with a novel method to impute the ancestral haplotype space in 1,887 commercially available outbred mice. We mapped 156 unique quantitative trait loci for 92 phenotypes at 5% false discovery rate. Gene-level mapping resolution was achieved at about a fifth of loci, implicating Unc13c and Pgc1-alpha at loci for the quality of sleep, Adarb2 for home cage activity, Rtkn2 for intensity of reaction to startle, Bmp2 for wound healing, Il15 and Id2 for several T-cell measures and Prkca for bone mineral content. These findings have implications for diverse areas of mammalian biology and demonstrate how GWAS can be extended via low-coverage sequencing to species with highly recombinant outbred populations.

Introduction

Genome-wide association studies (GWAS) have delivered new insights into the biology and genetic architecture of complex traits but so far they have found application primarily in human genetics^1,2 and in plant species where naturally-occurring inbred lines exist ^3,4 . Two obstacles stand in the way of their routine application in other species: access to a mapping population able to deliver gene-level mapping resolution, and the deployment of a genotyping technology able to capture at least the majority of those sequence variants that contribute to phenotypic variation, in the absence of haplotype reference panels of the kind routinely employed in human populations to impute sequence variants.

In this study we exploit the properties of commercially available outbred mice for GWAS in the Crl:CFW(SW)-US_P08 stock. Compared to other mouse mapping populations, commercial outbred mice are maintained at relatively large effective population sizes and are descended from a relatively small number of founders, with mean minor allele frequencies and linkage disequilibrium (LD) resembling those found in genetically isolated human populations ⁵. Compared to a human GWAS, comparatively fewer markers are needed to tag the genome, thus requiring a lower significance threshold and a smaller sample size.

GWAS methodology typically uses arrays to genotype known single nucleotide polymorphisms (SNPs) and represents each individual’s genome as a haplotype mosaic of a reference panel of more densely typed or sequenced individuals (such as the 1000 Genomes Project ⁶), to impute genotypes at the majority of segregating sites in a population ⁷. However, in common with other populations that have not previously been subject to GWAS, commercial outbred mice lack accurate catalogs of sequence variants, allele frequencies and haplotypes, thus excluding the application of standard GWAS approaches.

We show here how low coverage sequencing overcomes these limitations. We apply a method that models each chromosome as a mosaic of unknown ancestral haplotypes that are jointly estimated as part of the analysis. Using this approach we map the genetic basis of multiple phenotypes in almost 2000 mice, in some cases at near single-gene resolution.

Results

Phenotypes

2,049 unrelated adult Crl:CFW(SW)-US_P08 outbred mice (CFW) from Charles River, Portage, USA ⁵ were subjected to a four-week phenotyping pipeline (see Methods and Supplementary Figure 1). We obtained measures for 200 phenotypes from 18 assays (Methods). Data are available on a mean of 1,578 animals (range 905 - 1,968) per phenotype. We assign each measure to one of the following three heuristic categories: behavior, physiological or tissue; physiological measures include those taken when the mice were alive such as body weight and cardiac function, while the tissue measures comprise those obtained after dissection such as blood clinical chemistry and neurogenesis. Supplementary Table 1 lists the phenotypes. We tested the effect of all potential covariates on the variance of each measure to regress them for the genetic analysis. The strongest effect is batch, affecting 190 measures with a mean effect of 15%.

Genotypes

In order to capture all common variants in the CFW mice, we employed a two-stage genotyping strategy using low coverage sequencing that makes use of, but does not require, prior knowledge of segregating sites. We first generated a list of candidate variant sites using GATK ⁸ and then imputed genotype probabilities at these sites.

We obtained a mean coverage of 0.15X sequence coverage per animal for 2,073 mice (range 0.06X to 0.51X). We identified 7,073,398 single-nucleotide polymorphisms (SNPs) in the ~370X pile-up of all sequence data that segregated in our sample and were either polymorphic in laboratory strains sequenced in the mouse genomes project (MGP) (3), or passed GATK’s variant quality score recalibration (VQSR) (Methods). We then imputed genotype dosages at these sites using our reference-panel free method, STITCH (Methods, and Davies et al 2016). After stringent post-imputation quality control we retained 5,766,828 high-quality imputed SNPs for subsequent analysis. Accuracy at these sites is very high: the mean SNP-wise correlation (r²) with 25 thousand sites polymorphic on a genotyping microarray⁹ using 44 samples was 0.974 before QC and 0.981 after QC. We annotated the high-quality imputed SNPs using the mouse reference mm10 assembly and identified 11,931 SNP positions in protein coding sequence causing amino acid changes in 3,938 individual genes (non-synonymous substitutions) and 25,669 that do not (synonymous substitutions). Supplementary Table 2 categorises the variants by chromosome and Supplementary Table 3 lists the numbers of variants obtained at each stage of the variant calling and imputation process.

Genetic architecture

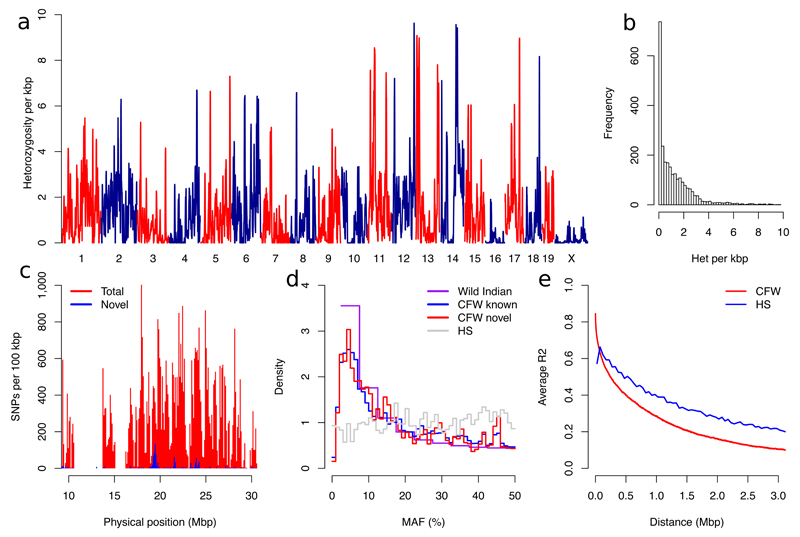
Inspection of the 5.7 million variants segregating in CFW mice revealed several notable characteristics. This total is about 1/3 fewer than the number segregating in heterogeneous stocks derived from classical laboratory inbred strains ^{10, 11,12} but far less than the 45 million segregating in the recently created Collaborative Cross (CC) and Diversity Outbred (DO) populations using wild-derived strains from different subspecies of mice ¹¹. Of the 5.7 million imputed variants, 97.6% were found in 36 sequenced inbred strains in the Sanger Mouse Genomes database Release 1505. The FVB/NJ strain alone contributes 38% of CFW alleles (Supplementary Table 4) and in combination with the progenitors of the mouse HS¹³ account for 76%. Wild-derived strains (LEWES/EiJ, ZALENDE/EiJ, WSB/EiJ, CAST/EiJ, MOLF/EiJ, PWK/PhJ, SPRET/EiJ) only account for about 5% of alternative alleles absent from other sequenced strains ^11,14. Both novel and known variants have very similar minor allele frequency distributions across the genome (Figures 1C and 1D).

Figure 1.

Sequence diversity of the CFW population. (a) Distribution of heterozygosity in 100kbp windows genome-wide. (b) Histogram of genome-wide heterozygosity. (c) Example of novel and total SNP density for a region of chromosome 19. Results are representative of those seen genome-wide. (d) Minor allele frequency (MAF) density for population of wild Indian (n=10, 44.9 M whole genome sequencing SNPs), CFW mice (n=2,073, 5.7M imputed SNPs) and HS mice (n=1,904, 11K SNPs from a genotyping array). Known CFW variation refers to those variants also segregating among 14 sequenced classical inbred strains. (e) The extent of linkage disequilibrium in CFW and HS mice. Values are mean r² between all pairs of SNPs binned by distance to the kbp.

The distribution of variants across the genome is highly non-uniform (Figure 1A). Chromosome 16 has only 20% of the variants found on chromosome 15, despite being almost the same size (Supplementary Table 2). This likely reflects an extreme bottleneck in the founding of the CFW, a view supported by the fact that only four ancestral haplotypes were required for the imputation procedure to work effectively. Further, just two haplotypes model the majority of samples: across chromosome 19, on average, 87.1% of samples are represented by only two haplotypes. Rates of heterozygosity are low (Figure 1B) with 22% of the genome close to fixation (Figures 1A and 1C). Average minor allele frequency (MAF) is 0.19. Figure 1E shows the decay of linkage disequilibrium with increasing distance (providing an indication of the expected mapping resolution obtainable with the CFW mice). Average pairwise r² falls to 0.28 at 1Mbp, 0.16 at 2 Mbp, and 0.10 at 3 Mbp.

We identified a subset of 359,559 SNPs, that tag all other SNPs with MAF >0.1% at LD r²>0.98. This subset was used for subsequent analyses except where stated otherwise. To investigate population structure and unequal relatedness between animals, we estimated identity by descent (IBD) from allele sharing between tagging SNPs. Supplementary Figure 2 plots the proportion of genome with IBD = 1 against IBD = 0. For GWAS, we removed 135 animals with higher relatedness than second-degree relatives, and 4 outliers identified from principal component analysis (PCA) on a genetic relatedness matrix (GRM). The population structure of the remaining 1934 animals was further assessed by performing another PCA on a GRM from only these mice. Supplementary Figure 3 plots the relationship between the first 5 principal components and shows no evidence of structure.

Genome-wide association

Genotypes and phenotypes were available for 1887 mice. We performed GWAS by testing association between the 359,559 tagging SNPs and all phenotypes. We transformed each phenotype by regression on relevant covariates (see Methods) and quantile-normalised the residuals. To test for association with SNPs on a given chromosome, we used a GRM based on those tagging SNPS on the other chromosomes ^15,16 to increase power ¹⁷. We calculated a genome-wide false discovery rate (FDR) separately for each phenotype to determine empirical trait-specific genome-wide significance thresholds (Methods).

At a 5% false discovery rate, we identified 255 QTLs in 92 out of 200 phenotypes (46%), as shown in Supplementary Table 5. Quantile-quantile plots for a representative selection of phenotypes are given in Supplementary Figure 4. It should be noted that due to the large number of SNPs used (in this case not pruned for LD) and the fact that LD extends over longer distances than exist in human populations, deviation from the expected values extends over a larger range of P-values than is commonly seen in human association studies.

Statistical power is expected to increase with MAF, and in our QTLs the MAF of significantly associated SNPs (range 1.7-50%, median 31%) was higher than expected (compared to all 5.7M SNPs) (Mann Whitney U test, P = 1.95e-28): at 133 QTLs (52%) MAF>30% and at only 11 (4%) is MAF <5% (Figure 2a).

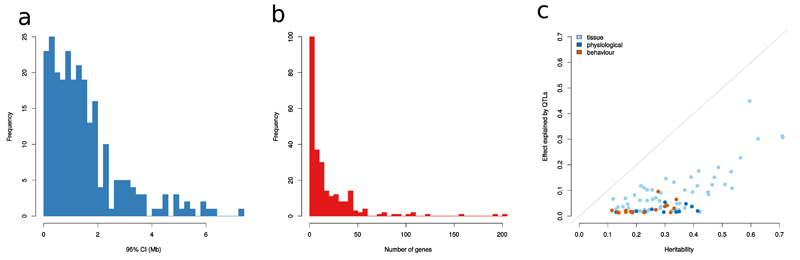
Figure 2.

Mapping resolution and effect size of QTLs. Frequency distribution of (a) the size and (b) the number of genes present in the 95% confidence intervals (CI) in 255 QTLs, (c) The sum of variance explained by the QTLs plotted against heritability in 92 measures where heritability could be estimated and at least one QTL was detected. Colour of dots indicates the type of measure: behaviour, physiological (body weight, respiratory, electrocardiography) or tissue (any measure obtained after dissection)

To aid gene identification, we estimated the 95% confidence intervals (CI) of every QTL using simulations based on the LOD-drop concept¹⁸. To do so, using the imputed dosages around each QTL we simulated causal SNPs that matched the QTL’s observed effect size. A local scan of the region using the mixed model but using a simulated phenotype was performed, and the location and LogP of the top SNP recorded. From 1,000 simulations, we derived the empirical distribution of the drop (Δ) in LogP between the most highly associated SNP and the causal SNP (Δ is zero when the top and causal SNPs coincide). After ranking the simulations at a given QTL by increasing value of Δ, the LOD-drop Δ(f) of the f% confidence interval was estimated by the maximum seen among the lowest f% simulations. The genomic interval spanning the LOD-drop Δ(f) determined the confidence interval of the QTL in the real phenotype data ¹⁸. Across all QTLs, the f = 95% CI widths ranged from 0.01-7.33Mb with a mean at 1.50Mb, 43% being less than 1Mb wide. On average each QTL covered 19 protein coding genes (0-205) with a median of 9 genes. Figure 2b shows the distribution of the number of genes at a QTL.

Heritability and variance attributable to QTLs

SNP-based heritability estimates exceeded 0 (at P<0.05) for 152 of 200 phenotypes, with a mean value of 26.3%, (range 9.1-71.1%), as reported in Supplementary Table 1. To assess how much of the heritability can be explained by detected QTLs (FDR<5%), we first estimated the effect size of each QTL by performing analysis of variance (ANOVA) at the most significantly associated SNP then summed the variance explained by all QTLs associated with every phenotype. On average, 21.1% of the heritability estimated for each trait with significant heritability can be explained in this way (Figure 2c). This indicates that missing heritability affects the CFW population, although to a lesser degree than most human GWAS.

Traits with higher heritabilities yielded proportionally more QTLs: the mean heritability of those traits for which at least one QTL was identified was 30.6%, compared to 20.6% for those without QTLs, a highly significant difference (t-test P-value = 8.9x10^-8). Mean heritabilities differed between the three categories of phenotypes: 14.5% for behavior, 18.2% for physiological and 24.2% for tissue phenotypes. We also noted the same pattern in the median locus effect size of the three categories: 1.37% for behavioural QTLs, 1.5% for physiological and 2.8% for tissue QTLs (Figure 2c).

Distribution of QTLs reflects genome-wide diversity

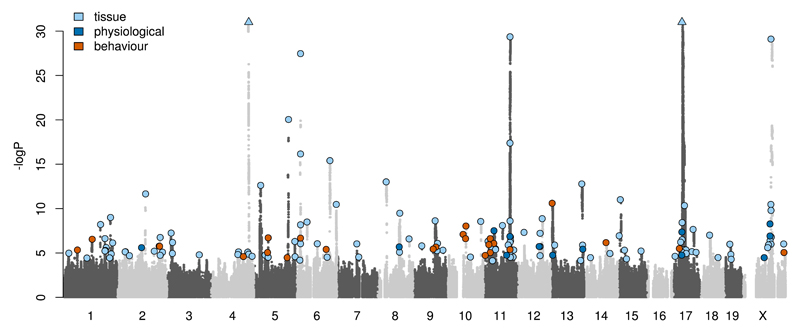
Many of the loci detected overlap, and are associated with, closely related phenotypic measures. Examples include the two QTLs for HDL and total cholesterol mapping over the Apoa2 gene on chromosome 1¹⁹, or the eight different bone mineral content measures mapping over Slc4a2 on chromosome 5²⁰. To avoid redundancy in our analysis we considered that if two overlapping QTLs (where the top SNP of the first QTL lies inside the 95% CI of the second QTL) were associated with measures of the same biological function they were representing a single locus. Using this approach we identified a reduced set of 156 unique loci, each associated with 1 to 12 measures. We report these 156 unique QTLs in Supplementary Table 6. A “Porcupine” plot on Figure 3 shows the superimposed Manhattan plots of all the measures where a least one QTL was detected and highlights the 156 unique loci. Some regions of the genome are devoid of any QTLs, reflecting the uneven genomic distribution of sequence variants, a prime example being the lack of any QTL detected on chromosome 16 (Figure 1A). Figure 3 also highlights the presence of clusters of QTLs, notably on chromosomes 6, 11, 17 and X. The chromosome 17 locus overlaps the major histocompatibility complex (MHC), a naturally highly polymorphic region in wild populations that remains highly variable in the CFW mice.

Figure 3.

Summary Manhattan plot of 92 phenotypes. Genome-wide representation of all unique QTLs (n=156, FDR<5%) identified in this study. Light and dark grey dots show association from the 92 measures where at least one QTL was detected at the tagging SNPs positions (n=359,559). Most significant SNPs at each QTL are marked with a colour dot, depending on the type of measure. Y-axis shows –log₁₀(P) of the imputed allele dosages with tested measures and is truncated at –log₁₀(P)=32. The position of the 2 strongest QTLs with –log₁₀(P) values of 133 (chr4) and 76 (chr17) is marked by triangles.

Identification of candidate genes in high-resolution QTLs

We focused on those QTLs containing small numbers of genes, since these loci provide a starting point for functional investigations. Of the 156 unique loci identified in this study, 56 contain three or fewer genes (36%) and 25 contain a single gene in the 95% confidence interval (6 QTLs do not overlap any gene).

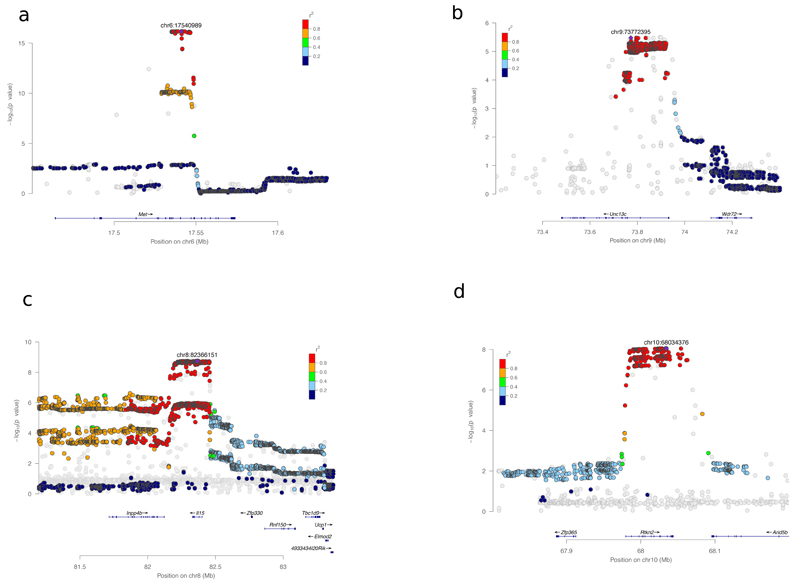
Table 1 lists the 25 QTLs containing a single gene. The table categorizes QTLs into three classes, according to prior evidence supporting the candidacy of the gene at the locus. (i) Phenotypes of knockouts support candidacy of three genes: Met, Fli1, and Grm7. The locus on chromosome 6 containing the Met gene contributes to all five muscles weight measures (Figure 4a). Met encodes a hepatocyte growth factor receptor and has a known function in embryonic development ^21,22 and regeneration²³ of adult limb skeletal muscle. Fli1 modulates B cells development ²⁴ and mice lacking Grm7 are more active when placed in a novel environment ²⁵ (ii) The genes at six loci are strongly corroborated by prior published evidence. These include the bone morphogenetic protein Bmp2 at a locus for wound healing ²⁶; PGC-1α, at a locus for sleep fragmentation, is involved in regulating inhibitory neurotransmission in the cerebral cortex associated with cortical hyperexcitability ²⁷; a protein kinase (PKCα) that promotes osteoblastic cell proliferation, at a locus for bone mineral content ^28,29; the pre B cell leukemia homeobox 1 (Pbx1) at a locus influencing NK cells population ³⁰ and finally an interleukin (Il15, Fig 4d) ³¹ and the transcription factor Id2 ³² at two independent loci affecting several T-cell measures. (iii) The remaining 16 QTLs contain single genes not previously associated with the trait, including five that concern behaviour. Notably, our mapping results implicate Unc13c in the quality of sleep (Fig 4b). UNC13C is involved in synaptic transmission ³³, but has never previously been associated with sleep. However, there is evidence for the differential expression of the human ortholog in individuals with poor sleep quality³⁴. Basal home cage activity is associated with Adarb2, a brain-specific adenosine deaminase acting on RNA ^35,36. Figure 4c shows that sequence variation affecting the interleukin 15 gene (Il15) is associated with the ratio of CD4+ to CD8+ T cells. Rtkn2, a member of the rhotekin family predominantly expressed in lymphoid cells ³⁷, influences intensity of reaction to startle (Fig 4d). CNVs for the human orthologue of Rtkn2 have been implicated in attention-deficit and hyperactivity disorder³⁸.

Table 1. QTLs mapping to a single gene.

Phenotype	Chr.	Position (Mb)	-logP	Gene	References
Knock-out mouse recapitulates the phenotype
Weight of soleus muscle (g)	6	17.5	16.2	Met	21–23
Total distance travelled in Elevated Plus Maze (cm)	6	110.2	5.6	Grm7	25
CD45+/CD3-/CD19+ cells (%)	9	32.6	5.8	Fli1	24
Association supported by literature
CD45+/CD3-/DX5+ cells (%)	1	168.2	4.7	Pbx1	30
Wound healing	2	134.2	5.5	Bmp2	26
Number of long (>1min) sleep episodes	5	51.8	6.8	Ppargc1a	27
Ratio of CD3+/CD4+ to CD3+/CD8+ cells	8	82.4	8.7	Il15	31
Bone mineral content	11	108.2	4.6	Prkca	28,29
CD3+/CD8+ cells (%)	12	25.5	5.4	Id2	32
No previous evidence
Length of tibia (mm)	5	51.7	4.5	Ppargc1a
Startle pulse reactivity	6	17.5	6.7	Met
Calcium (mmol/l)	6	17.5	8.3	Met
Total Cholesterol (mmol/l)	6	17.5	6.1	Met
Total Protein (g/l)	6	17.5	27.7	Met
CD45+/CD3-/CD19+ cells (%)	7	72.2	6.2	Mctp2
Number of long (>1min) sleep episodes	9	73.8	5.5	Unc13c
Startle pulse reactivity	10	68.0	8.0	Rtkn2
Weight of tibialis anterior muscle (g)	11	17.6	6.3	Etaa1
Length of tibia (mm)	12	83.6	7.1	Zfyve1
Basal activity	13	7.3	10.6	Adarb2
Respiratory rate during Hypoxic Ventilatory Decline	13	118.0	5.9	Hcn1
Total distance travelled in Elevated Plus Maze (cm)	14	82.1	6.2	Pcdh17
Measure of the size of tibia	15	26.6	5.3	Fbxl7
Percentage of Eosinophils (%)	17	70.4	5.2	Dlgap1
Percentage of Eosinophils (%)	X	155.6	6.0	Ptchd1

Figure 4.

Single-gene resolution mapping at 4 loci using the entire set of SNPs (7.1 M). (a) Weight of soleus muscle on chromosome 6 (n=1832), (b) Measure of the number of long sleep episodes on chromosome 9 (n=1577), (c) Ratio of CD4+ to CD8+ T cells (CD3+) on chromosome 8 (n=1324) and (d) Intensity of reaction to startle on chromosome 10 (n=1740). The plots were drawn using LocusZoom ⁴⁹. Strongest associated SNP is marked with a purple diamond, the other SNPs that passed post-imputation quality control (IMPUTE2-style INFO scores > 0.4 and HWE r²>1e^-6,) are coloured following LD r² with strongest SNP. The grey dots represent SNPs that failed post-imputation QC and therefore were not used for the analysis.

Discussion

Genome-wide association mapping for complex traits has been used extensively in human populations but less commonly in other organisms. We have shown here that mapping using commercially available outbred mice can identify individual genes involved in complex traits, some of which cannot easily be assayed in human subjects. Our results raise issues about the nature of mouse resources for mapping complex traits, and about the biological insights that can thereby be attained.

Several resources have been developed to provide GWAS tools to rodent genetics. These resources fall into two broad categories: (i) genetic reference populations, consisting of pre-existing inbred strains (Hybrid Mouse Diversity Panel, HMDP ¹²) or recombinant inbred strains (BxD³⁹ and Collaborative Cross⁴⁰), (ii) populations descended after multiple generations of pseudo-random breeding from inbred strains (diversity outcross (DO) mice ⁴¹ and heterogeneous stocks (HS)¹³). Each resource differs in its utility for GWAS, and no single population is ideal ¹.

Commercially available outbred mice are an alternative resource with a number of advantages, and the CFW stock has already been used to map skull shape QTLs ⁴². Compared to HMDP and HS animals, there was minimal evidence for population structure, and standard GWAS methods developed for human populations can be applied. LD decays fast enough to provide gene-level mapping resolution at about a fifth of loci, and although the resolution is still lower than in human populations, it is better than other mouse resources. The size of QTLs varied considerably, with the largest ones extending over several megabases, but half contained fewer than 10 genes, providing a relatively small list to investigate the biology at these sites.

Compared to other rodent mapping resources, our results also indicate that the CFW population delivers fewer loci for fewer phenotypes. We mapped loci for 92 out of 200 traits included in our phenotyping pipeline, yielding a mean number of 1.3 QTLs per trait, in 1,887 mice. One possible explanation for the low yield of QTLs is that the amount of genetic variation present in the CFW stock is relatively limited. Indeed, almost a quarter of the CFW genome is virtually devoid of variants. For comparison, the 5.7M variants in the CFW is less than the 7.2M segregating in the rat heterogeneous stock ¹⁰. However, a more important determinant for QTL detection in the CFW is likely to be allele frequencies (p), which are on average lower in the CFW than in the HS. Since the variance explained by a QTL is proportional to p(1 – p), effect sizes, and hence power, are systematically smaller in the CFW. Indeed, the median effect size is 1.6%, which, while dwarfing the effects found to underlie human quantitative traits, is still less than half that found in the rat HS (median estimate 5%) ¹⁰.

The inclusion of a large number of behavioural measures in our pipeline also contributed to the relatively low QTL detection rate. Almost a third of the traits (63/200) were collected from behavioral tests, yet the QTLs mapped with these measures accounted for less than 14% of the total. These phenotypes typically had lower heritabilities, with fully one quarter (16) having no significant genetic contribution. Note that these non-significant estimates (as well as those for non-behavioural phenotypes) do not necessarily mean the traits are not heritable: the standard errors on these estimates are large (Supplementary Table 1), so that no heritability less than 10% can be reliably estimated. Those loci we did detect had relatively lower effect sizes (mean for behavioural QTLs was 1.37, compared to 1.5 for physiological and 2.8 for tissue QTLs).

The heritability of the behavioural measures might also have been affected by the fact that mice were repeatedly tested over a 4 weeks period. Most behaviors are sensitive to repeated handling and exposure to different types of novel stimuli, as will happen during the extensive phenotypic battery deployed here. Habituation to these exposures makes it harder to detect alleles that affect baseline differences in behavior, especially anxiety-like behaviors for which three different assays were conducted over a relatively short time frame. A more focused assessment of a specific behavioral phenotype under tightly controlled environmental conditions could have yielded higher heritabilities for some traits.

These observations lead to two conclusions. First, finding more QTLs in the CFW will require thousands of mice. Supplementary Table 7 gives the power to detect QTLs in the CFW population as a function of effect size and sample size. For a typical QTL corresponding to the median effect size (1.6%) and sample size (1,732) in the current study, power is about 80% at a genome-wide significance level of 10%. Power falls off for smaller effects sizes: a 0.5% QTL is detectable with 6.6% power with 1,732 animals; increasing the sample size to 4,000 increases the power to 51%, and with 6,000 it is 85%. However, “winner’s curse” means that the true effects are likely to be lower than reported here, and given that our QTLs explain only 20% of the heritability it is reasonable to assume that the majority of loci will have effect sizes less than 1%. Second, additional loci can be found using different stocks. Not all commercial outbred mice populations are the same, as we previously documented in a survey of 66 stocks in which mean heterozygosity varied from 0.5% to 45% and mean minor allele frequencies from 0.03% to 0.5%⁵. The use of complementary populations will make additional alleles open to discovery.

Our study is the first to use extremely low coverage sequence to generate accurate genotypes without a reference panel. This strategy, and the associated STITCH algorithm⁴³, is generally applicable to any population, and any species, for which there is no information about segregating variation or haplotypes. It is competitive with arrays in terms of cost, although the optimal choice of strategy will depend on the reagents available for the population in question. An advantage of sequencing over array-based genotyping is that it does not require prior information about which variants are segregating in a population; nor does it require a pre-existing catalogue of variants or prior knowledge of the likely founders of the population. The only requirement is a high-quality reference genome.

One unexpected finding was that, only 25,000 SNPs in the standard megaMUGA mouse genotyping array are polymorphic in the CFW mice; many of the QTLs we mapped would likely have been overlooked by genotyping with this array. The CFW mice appear to be descended from four ancestral haplotypes, indicating this population was likely bottle-necked to two founding individuals. Our population is effectively biallelic at most loci, and there was little to be gained by considering haplotype-based tests of association (data not shown).

We could also test associations at candidate variants responsible for the effect. For example, the Met gene on chromosome 6 is associated with muscle phenotypes and our sequence data revealed two missense variants: I851M and R968C. The first variant is common amongst mouse strains and is not known to alter gene function. The second variant, confirmed by Sanger sequencing, is specific to the SWR/J strain⁴⁴. The human homolog (R988C) has been identified in two small cell lung cancer cell-lines and increases constitutive tyrosine phosphorylation activity in vitro ⁴⁵. The R968C missense variant is associated with the five muscle weight phenotypes but the direction of the effect of the alternative allele is positive in extensor digitorum longus (EDL) and gastrocnemius and negative in the others. This difference reflects differences in the muscle fiber composition (soleus is dominated by type 1 and 2A fibers, EDL is enriched in 2X and 2B fibers ⁴⁶) suggesting that R968C affects these fibers differently or shifts the composition in all muscles.

We have shown here how low-cost commercially available outbred mice can deliver novel biological insights. We found single genes at 16 loci where no prior evidence existed for their involvement (Table 1). Importantly, the loci include those from phenotypes that could not easily be assayed in human subjects, such as response to hypoxia and the sleep phenotypes. More than 50 QTLs contain documented candidate genes (Supplementary Table 5): Slc4a2, which leads to osteopetrosis when disrupted in mice ²⁰, is present at a QTL affecting bone mineral content; Apoa2 and Scarb1, both known to affect blood lipid homeostasis ^19,47 are detected at two distinct QTLs for cholesterol levels; Gdnf, a gene required for the neuronal colonization of the pancreas, at a locus for pancreatic amylase ⁴⁸. These examples demonstrate that the narrow QTLs detected in CFW mice can lead to the identification of the genes affecting the measured traits, emphasizing the potential of our results as a resource to identify new genes in those QTLs without documented candidates.

Online Methods

Study animals and phenotyping

A total of 2117 outbred mice (Crl:CFW(SW)-US_P08, 1065 males and 1052 females) were purchased from Charles River, Portage, USA at 4-7 weeks of age over a period of 2 years. Animals were selected from the breeding colony as to avoid siblings and half-siblings. Monthly shipments of approximately 130 mice were delivered, maintained and tested at the MRC Harwell in Harwell, Oxfordshire, UK following local regulations. Mice of the same age within each shipment were treated as a batch (approximately 30 animals, range 7 to 36, half males and half females, the total number of batch for the entire study is 69) and each animal randomly assigned a testing order. Mice were housed in IVC cages (3 per cage) on an ad lib diet for the duration of the study. At 16 weeks of age 2049 mice started a 4-weeks phenotyping pipeline in which we collected behavioral and physiological data (Suppl. Fig. 1 and full description of the phenotypes measured in the Supplementary Note). Mice within a batch performed each test during the same day following the assigned testing order. The sequencing of the animals was performed after completion of the study so experimenters were blind to the genotype of the mice during testing. Power calculations to estimate the sample size for the mapping experiment assumed effect sizes were similar to those identified in a previous analysis of outbred stocks ⁵. Every effort was made to minimize suffering by considerate housing and husbandry. All phenotyping procedures were examined for potential refinements. All animal work was carried out in accordance with UK Home Office regulations. The project was reviewed by the ethics committee at MRC-Harwell: Animal Welfare and Ethical Review Board, approval license PPL 30/2653.

Pre-processing of Phenotype Data

Analysis of the phenotypic data was performed using the R statistical analysis software ⁵⁰. Outliers, defined as observations more than 3 standard deviations from the mean, were excluded. The effect of covariates such as sex and batch on quantitative phenotypes were assessed with analysis of variance (ANOVA) and those explaining more than 1% of the variance at P<0.05 were included in a multiple linear regression model from which residual measures were obtained. Batch, defined here as mice of the same age in each individual shipment, was treated as a random effect. All tests with covariates and models used to generate the residuals for genetic mapping are shown in Supplementary Table 1. We then quantile-normalised the residuals to minimize the effects of non-normality.

Sequencing

Genomic DNA was extracted from tissue samples of 2,028 mice that began the pipeline using Nucleon BACC resin (Hologic) following the manufacturer’s instructions. DNA was obtained from an additional 45 mice from the same population where no phenotypic measures were available producing a total of 2073 samples for analysis. Each individual DNA sample was then sonicated and barcoded with an in house unique 8-mer oligonucleotide ⁵¹. Groups of 95 barcoded DNA samples were pooled and pair end 100bp sequenced on 1 lane Hi-Seq generating read groups of ~30 Gb sequence per lane/pool.

Alignment to mm10 reference and pre-processing of sequence data

BWA version 0.5.6 ⁵² was used to align the reads from each read group to the mouse mm10 reference genome. The BWA alignments were refined with Stampy v1.0.21 ⁵³ and converted into the bam format by samtools v0.1.18-dev⁵⁴. Library PCR duplicates were removed with samtools and sequence reads processed following the pipeline described ^11,14. All bam files were processed through the Indel Realignment and Base Quality Score Recalibration steps of the Genome Analysis Toolkit (GATK) ⁸ recommended Best Practices ⁵⁵. All pre-processing used GATK v2.4-9-g532efad. The option –rf BadCigar was applied to filter out reads that a) have hard/soft clips in the middle of the CIGAR string, b) start or end in deletions, c) fully hard/soft clipped, d) have consecutive INDELs in them. The option –rf BadMate was applied to filter out reads whose mate maps to a different contig. Previously discovered INDELs from all mouse strains in the Mouse Genome Project (MGP) ^11,56 were used as intervals for Indel Realignment in addition to those discovered in the 2073 mice, and SNPs from the Mus musculus domesticus strains in MGP were used as known sites masked for Base Quality Score Recalibration.

Variant calling from low coverage sequencing data

Variant calling was then performed using all 2073 bam files with GATK’s Unifed Genotyper with thresholds -stand_call_conf 30 and -stand_emit_conf 30, as well as options for building variant quality recalibration tables: -A QualByDepth -A HaplotypeScore -A BaseQualityRankSumTest -A ReadPosRankSumTest -A MappingQualityRankSumTest -A RMSMappingQuality -A DepthOfCoverage -A FisherStrand -A HardyWeinberg -A HomopolymerRun.

Raw vcf files from variant calling step for all chromosomes except chromosome Y were pooled together for variant quality score recalibration (VQSR) using GATK’s VariantRecalibrator under SNP mode. Training, known and true sets for building the positive model are the SNPs which segregate among the classical laboratory strains of the Mouse Genomes Project ¹¹ (2011 release REL-1211) on all chromosomes except chromosome Y. Transversion ratios (TsTv) and recalibration tables were generated at 14 sensitivities (100.0, 99.9, 99.0, 97.0, 95.0, 90.0, 85.0, 80.0, 75.0, 70.0, 65.0, 60.0, 55.0, 50.0) to training sets for runs of VQSR utilizing different sets of annotations. A final set of annotations for VQSR and sensitivities to known sites were chosen to maximize TsTv at both known and novel sites to reduce the rate of false positive calls. Sensitivity of 97% for known sites was selected for a total of 8,597,879 SNPs (6,430,809 known and 2,177,070 novel, TsTv of 2.13 at known sites and 1.56 at novel sites). We then further removed sites that were fixed alternative allele variants (hence non-polymorphic in our study) or were multi-allelic, leaving 7,073,398 (5,701,865 known, 1,371,533 novel, TsTv of 2.13 at known sites and 1.56 at novel sites) biallelic SNPs. The annotations used for VQSR were HaplotypeScore, BaseQualityRankSumTest, ReadPosRankSumTest, MappingQualityRankSumTest, RMSMappingQuality, DepthOfCoverage, FisherStrand, HardyWeinberg, HomopolymerRun.

We used the 7M biallelic SNPs in the mice cohort for imputation, using the method described below. To ensure quality of the imputed of SNPs used for downstream genetic analysis, we first extracted those SNPs imputed with high certainty using IMPUTE2-style INFO scores. We observed from inspecting allele distributions that an INFO score greater than 0.4 indicated markers where the three genotype classes were clearly separable. Thus we included only sites that met this criterion. We also discarded sites where more than 10% of mice had maximum genotype probability smaller than 0.9, and on autosomal chromosomes we discarded sites where the P-value for violation of Hardy Weinberg equilibrium was smaller than 10^-6. This resulted in a final set of 5.76M SNPs that we used for genetic mapping. Lastly, we used the most current release of the Sanger mouse genomes database (2016, REL-1505, comprising 36 genomes, almost twice the original number) to refine the set of novel SNPs. The number of novel sites among the 5.76M dropped from 799,133 (13.8%) to 152,671 (2.6%) (Supplemental Table S3). However, the TsTv ratios for the novel SNPs remained little changed, at 1.74 and 1.73 respectively.

Imputation

We developed a novel imputation algorithm, STITCH, described in a separate publication (Davies et al). This employed a hidden Markov model (HMM) that extended the population genetic methods of Li and Stephens⁵⁷, and more specifically the fastPHASE algorithm of Scheet and Stephens ⁵⁸. We assume that the CFW population was founded with K unknown ancestral haplotypes and that the chromosomes of each sequenced CFW mice are mosaics of the founder haplotypes. After some experimentation with different values of K we found that K=4 was optimal (ie the population was modeled as being founded from two individuals).

Simulating under the model (hidden ancestral states and sequencing reads) consists of: (i) choosing initial state probabilities (π_k) from one of the k haplotypes (ii) choosing where to recombine between ancestral haplotypes assuming G=100 of generations since the population’s founding and a genetic distance between SNPs t and t+1 (σ_t) (iii) choosing the ancestry within each segment with respect to the frequencies of each founder haplotype at that location (α_t,k), and (iv) sampling read locations, base qualities, underlying unobserved bases and observed sequenced bases, based on the relative probability that ancestral haplotype k emits a reference or ancestral base at SNP t (θ_t,k). Together, these represent the parameters of the model λ = (π, σ, α, θ).

To generate the probabilistic genotype of an individual CFW outbred mouse, we first calculate the probability of observing a given sequencing read given membership in ancestral haplotype k, as follows. We first removed SNPs with low base quality (<17) and SNPs in reads with low mapping quality (<17). For an individual read R_r indexed by r, let J_r be the number of SNPs in the read and P(s_r,j | g_i = i) = ϕⁱ_r,j the base-quality scaled emission probability of sequencing read s_r,j given true underlying genotype i. Let SNP j in read R_r correspond to SNP u_r,j. We assume the probability of a recombination within a read is low, so we assign each read as having been emitted from a central SNP t=c_r. Therefore, the probability of read R_r given it came from ancestral haplotype k is

$$P(R_r|q_t=k)={\displaystyle \prod _{j=1}^{Jr}\left({\theta }_{u_{r,j},k}{\varphi }_{r,j}^1+\left(1-{\theta }_{u_{r,j},k}\right){\varphi }_{r,j}^0\right)}$$

and the probability of observing all reads at SNP t in a diploid sample given diploid hidden state at SNP t of q_t = (k₁, k₂) is

$$P\left(O_t|q_t=\left(k_1,k_2\right)\right)={\displaystyle \prod _{r:c_r=t}\left(\frac{1}{2}P\left(R_r|q_t=k_1\right)+\frac{1}{2}P\left(R_r|q_t=k_2\right)\right)}$$

The full chromosome diploid probability is then calculated using the initial, recombination and transition probabilities in the normal manner.

We ran the method for 40 Expectation-Maximisation (EM) iterations, where in each iteration, during the expectation step, state probabilities are calculated for each mouse using the current parameters of the model, while in the maximization step, new initial, transition, recombination and emission parameters are estimated based on state probabilities. Upon completion, haplotype and genotype probabilities, as well as dosages, are calculated. For example, the dosage of the number of Alt alleles is 1* P(G = (Ref,Alt) / O, λ) + 2* P(G=(Alt,Alt) / O, λ) for a given mouse and SNP site.

Selection of tagging SNPs

We then identified a subset of 359,559 (353,697 autosomal) tagging SNPs with MAF > 0.1% and LD r²< 0.98. Genotypes at these sites were called based on maximum genotype probability from imputation; genotypes were only called based on maximum genotype probabilities of higher than 0.9, mice with maximum genotype probability of smaller than 0.9 at a particular site would have a missing genotype at the site.

Sample selection based on estimation of Identity by Descent (IBD) between samples

Pairwise Identity by Descent (IBD) was estimated by calculation of pairwise Identity by State (IBS) using PLINK (v1.07) at the tagging SNPs located on the autosomal chromosomes. Mice were excluded from further analysis if they had estimated PIHAT of higher than 0.5 with at least one other mice, or percentage IBS=1 of higher than 0.75 with at least one other mice, or percentage of IBS=0 of smaller than 0.25 with at least one other mice. 135 mice were excluded by the above criteria.

Sample Selection based on Principal Component Analysis (PCA)

Linkage Disequilibrium Adjusted Kinship (LDAK, version 5.9) ⁵⁹ was used to estimate local linkage disequilibrium (LD) by calculation of local pairwise correlations between SNPs and generating weightings of each SNP in the calculation of a genetic relatedness matrix (GRM) adjusted for local LD. The GRM was generated using hard-called genotypes at the tagging SNPs of MAF > 5% from all autosomes. Principal component analysis (PCA) was performed on the GRM to derive the top 20 principal components (PCs). PC2 separates out four mice from the rest; these four mice were excluded from further analysis.

Estimation of whole-genome SNP-based heritability

LDAK (version 5.9) was used to generate a new GRM using hard-called genoytpes of MAF > 5% at the same tagging SNPs in mice remaining in the analysis. Restricted maximum likelihood (REML) was used to estimate h² of each of the 200 phenotypes measured.

QTL mapping

We mapped quantitative trait loci (QTLs) at the tagging SNPs using purpose-written software in R. For each phenotype k, we used the quantile-normalised residuals y_k for QTL mapping and heritability analysis. Although we found little evidence of unequal degrees of relatedness between the CFW mice, as a precaution we used mixed models to control for cryptic relatedness and to avoid false positive QTL calls. We first used the imputed dosages of the tagging SNPs on the autosomal chromosomes to compute genome wide kinship matrices (K). Thus, if a_ip is the imputed reference allele dosage of SNP p in individual i then the genetic relationship K_ij between individuals i,j is defined to be the Pearson correlation coefficient of the vectors a_ip, a_jp across all autosomal tagging SNPs p. The i,j ‘th element of the population-wide genetic relationship matrix K is K_ij. We also computed leave-one-out kinship matrices K_c for each chromosome c, using all tagging SNPs not on chromosome c.

We modified the standard mixed model formulation for mapping QTLs by computing separate mixed models for each chromosome, in order to ameliorate the reduction in statistical significance of a locus caused by the same information being present in the kinship matrix. To test association between the phenotype k and tagging SNP p resident on chromosome, we estimated the phenotypic covariance matrix $V_{kc}={\sigma }_{gkc}^2{K}_c+{\sigma }_{ekc}^{2}I$ where the genetic and environmental variance components ${\sigma }_{gkc}^2,{\sigma }_{ekc}^2$ are estimated as above, and factorized it into its square root using the eigen-decomposition

$$V_{kc}=E_{kc}^{\prime }{\Lambda }_{kc}{E}_{kc}={\left(E_{kc}^{\prime }{\Lambda }_{kc}^{1/2}{E}_{kc}\right)}^2=A_{kc}^2$$

where E_kc is the orthogonal matrix of eigenvectors and Λ_kc the diagonal matrix of eigenvalues of V_kc. Then we fitted the transformed mixed model

$${\mathit{Z}}_{\mathit{k}\mathit{c}}=A_{kc}^{-1}{\mathit{y}}_{\mathit{k}}=\mu +\alpha (A_{kc}^{-1}{\mathbf{\text{a}}}_{\mathit{p}})+\mathit{e}$$

where μ, α are parameters to be estimated, and the error vector e is uncorrelated so the model can be fit efficiently by computing the correlation coefficient of ${\mathit{Z}}_{\mathit{k}\mathit{c}},A_{kc}^{-1}{\mathit{a}}_{\mathit{p}}\mathbf{.}$

Nominal statistical significance at a locus was measured as the logP (the negative log¹⁰ of the P-value of the ANOVA comparing the fit of the allele model to the null model). We defined a candidate QTL as any locus such that the logP was at a local maximum compared to the tests at neighbouring loci, and no other locus within 3Mb had a larger logP.

We estimated separate genome-wide thresholds for each phenotype, aiming to control the per-phenotype false discovery rate (FDR). We made Q = 100 permutations of each transformed phenotype vector Z_kc, keeping the transformed allele dosages fixed, and refitted the model. This is efficient because most of the computational effort in fitting a mixed model is reusable when fitting the permuted phenotypes. We found candidate QTLs in the permuted data in the same way and estimated the per-phenotype FDR of a QTL as

$$FD{R}_k\left(x\right)=\frac{P_k\left(x\right)}{Q{N}_k\left(x\right)}$$

where N_k(x), P_k(x) are the numbers of QTLs with logP ≥ x observed for phenotypek in the unpermuted and permuted data respectively, and Q = 100 is the number of permutations. Custom R code for QTL mapping, written specifically for this project, is available from R.M.

Fine mapping

Once a QTL had been mapped using the tagging SNPs and exceeded the FDR threshold, association was re-calculated with all imputed SNPs (from the 5.7M set) in a 20Mb window around the peak using the same mixed model.

Confidence Interval Estimation

Confidence intervals were estimated by simulation. First, at each QTL, a residual phenotype was constructed by removing the effect of the top SNP at the QTL from the phenotype vector used in the QTL mapping above. This ablated the QTL whilst maintaining genetic contributions from elsewhere in the genome. Next, 1000 SNPs were selected at random, subject to the constraint that they were within 2.5Mb of the top SNP and were polymorphic in the subset of individuals phenotyped for the trait (where the 95% interval estimate was 2.0 Mb or greater, we repeated the analysis using SNPs up to 10Mb from the top SNP). A causal variant was simulated at the SNP, with effect size matching that of the top SNP, taking account of the allele frequency, and its trait value added to the residual phenotype. A local scan of the region using the same mixed model but the simulated phenotype was performed and the location and logP of the top SNP recorded. Across the 1000 simulations, we estimated the distribution of the drop Δ in logP between the simulated top SNP and the simulated causal SNP (this was zero when the top and causal SNPs coincided). We used the fraction of simulations f(Δ) within Δ to determine confidence intervals for the original phenotype data. Thus we identified the range of SNPs within 2.5Mb of the top SNP and with a logP drop less than Δ to define the 100f(Δ)% confidence interval for the QTL. We did this using both the tagging SNPs and the fine-mapping SNPs.

Power Calculation

Since we applied an FDR approach to call QTLs we did not require a logP threshold that would be required in order to determine power. However, in order to estimate power and the effects of sample size and effect size, we determined approximate genome-wide thresholds based on permutations of the mixed-model transformed phenotypes z = A⁻¹y keeping the genotypes fixed in order to preserve LD structure. For each of the 200 phenotypes, we performed 100 permutations and computed the genome-wide maximum logP across the 359,559 tagging SNPs in order to define genome-wide thresholds T(p) at p = 0.5,0.1,0.5 levels of significance (e.g. the threshold T(p) is such that in a fraction p of simulations the genomewide maximum logP exceeds T(p). Thresholds vary slightly between phenotypes, so we used the thresholds obtained by pooling all 20,000 simulations to estimate power for sample sizes N = 1000,1732,2000,4000 and apparent effect sizes v = 0.01,0.016,0.02. (N = 1732 and v = 0.016 are the median sample size and effect size in the current study). Power π(N,v,T) to detect a QTL with effect size and sample size at genome-wide logP threshold T, was computed as $\pi (N,v,T)=\mathrm{Pr}(X>w(T)|X\sim {\chi }_{1,Nv}^2)$ where ${\chi }_{1,Nv}^2$ is the noncentral chi-square distribution on 1df with noncentrality parameter Nv, and w(T) is the quantile of a standard chi-squared distribution corresponding to logP T, ie $\mathrm{Pr}(X>w(T)|X\sim {\chi }_{1,0}^2)={10}^{-T}.$