Mutation Is a Sufficient and Robust Predictor of Genetic Variation for Mitotic Spindle Traits in Caenorhabditis elegans

Abstract

Different types of phenotypic traits consistently exhibit different levels of genetic variation in natural populations. There are two potential explanations: Either mutation produces genetic variation at different rates or natural selection removes or promotes genetic variation at different rates. Whether mutation or selection is of greater general importance is a longstanding unresolved question in evolutionary genetics. We report mutational variances (VM) for 19 traits related to the first mitotic cell division in Caenorhabditis elegans and compare them to the standing genetic variances (VG) for the same suite of traits in a worldwide collection C. elegans. Two robust conclusions emerge. First, the mutational process is highly repeatable: The correlation between VM in two independent sets of mutation accumulation lines is ∼0.9. Second, VM for a trait is a good predictor of VG for that trait: The correlation between VM and VG is ∼0.9. This result is predicted for a population at mutation–selection balance; it is not predicted if balancing selection plays a primary role in maintaining genetic variation.

THE question “What are the factors that govern genetic variation in natural populations?” has been central to the field of evolutionary genetics ever since its inception (Dobzhansky 1937; Lewontin 1974, 1997). Within a group of organisms, seemingly similar or related phenotypic traits can vary considerably, and consistently, in the extent of genetic variation in the trait. For example, in many organisms, resistance to acute heat stress is much less heritable and evolvable than resistance to acute cold stress (Hoffmann et al. 2013). If different traits in the same set of organisms have consistently different levels of genetic variation, there are two potential underlying evolutionary causes: mutation and/or selection. Traits may differ in the mutational target they present, i.e., the number and/or types of loci that potentially affect the trait, or in the rate at which those loci mutate. Traits may also differ in the average effect that mutations have on the trait; i.e., they may be differently robust to the effects of mutation. Alternatively, traits may be subject to differing strengths and/or kinds of selection.

In quantitative genetics, a few empirical conclusions seem fairly certain. First, traits that are direct components of fitness—life history traits—are typically more genetically variable than other classes of traits (Houle 1992; Lynch et al. 1999). Second, when scaled relative to the trait mean, life history traits experience greater input of genetic variation from mutation than other classes of traits (Houle et al. 1996; Halligan and Keightley 2009). Third, life history traits appear to be under stronger purifying selection than other classes of traits (Houle et al. 1996; Lynch et al. 1999; McGuigan et al. 2015).

A longstanding related, but unanswered, question is the relative influence of balancing selection on the maintenance of genetic variation (Dobzhansky 1955; Lewontin 1974; Charlesworth 2015). Presumably, a large fraction of mutations are unconditionally deleterious and are removed more or less efficiently by selection. However, if the mutation rate is high and selection is not too efficient, deleterious alleles segregating at mutation–selection balance (MSB) may represent a large fraction of the genetic variation. Alternatively, it is likely that some alleles are subject to balancing selection, and even if mutations subject to balancing selection are rare, they may in aggregate explain a substantial fraction of the standing genetic variation (Barton 1990).

Houle (1998) investigated the relationship between the standing additive genetic variance (VA) and the per-generation input of genetic variation by mutation [the mutational variance (VM)] for eight life history and morphological traits in Drosophila melanogaster and found a strong positive association between VM and VA (Spearman’s r = 0.95, P < 0.001; see figure 1 in Houle 1998). That result has a clear interpretation: Variation in mutation explains 90% of the variance in standing additive genetic variance among traits. Similar analysis of the genotypic variance (VG) and VM for nine morphological and life history traits in Daphnia pulex also reveals a strong positive correlation (r = 0.76, P < 0.02; data in table 1 and table 3 of Lynch et al. 1998). A positive association between the mutational variance and standing genetic variance is predicted if most genetic variation is due to deleterious alleles at MSB, because the equilibrium frequency of a deleterious allele has a linear dependence on the mutation rate ($\widehat{q}=\mu /s,$ where $\widehat{q}$ represents the equilibrium frequency of the deleterious allele, µ is the mutation rate, and s is the selection coefficient). Conversely, a relationship between VM and VG is not predicted if genetic variance is maintained by balancing selection, because the equilibrium frequencies of the segregating alleles do not depend on the mutation rate (Houle et al. 1996; Charlesworth and Hughes 2000). However, Charlesworth (2015) recently analyzed five decades of quantitative genetic and molecular data from D. melanogaster and reached the conclusion that MSB cannot be a sufficient explanation for genetic variation for fitness in that species, and hence there must be a significant contribution from balancing selection.

The biological particulars of Drosophila and Daphnia are quite different, except that in both species the relevant selection against deleterious mutations is in the heterozygous state. The population genetic milieu of Caenorhabditis elegans is very different from that of Drosophila or Daphnia. C. elegans reproduces predominantly by self-fertilization (Rockman and Kruglyak 2009), so the relevant selection against mutations is in the homozygous state. Moreover, C. elegans appears to have undergone one or more global selective sweep(s) within the past 600–1200 generations, resulting in (among other things) linkage disequilibrium that extends over entire chromosomes, little geographic substructure, a large excess of rare alleles (measured by Achaz’s Y statistic), and a global effective population size on the order of 10⁴ (Andersen et al. 2012). Here we report an analysis of mutational and standing genetic variation in 19 traits related to the first mitotic cell division in the nematode C. elegans, chosen on the basis of their relevance to cell biology.

Our primary question of interest is: What is the relationship between VG and VM? Because of the recent history of strong global selection in C. elegans, we can imagine two plausible alternative scenarios. First, since genetic variation was recently purged, mutation may predominate: The only genetic variation present is that introduced by new mutations since the recent purge. If so, we should see a strong positive association between VG and VM, and further, VG should consistently be no more than a few hundred generations of VM. Alternatively, because linkage disequilibrium is so strong and also because the purge of genetic variation was not complete (Thompson et al. 2015), idiosyncratic selection at linked loci may predominate, leading to a more or less random association between VG and VM.

Our data permit us to address an additional fundamental question: How consistent is the mutational process? For example, if trait X accumulates mutational variance 10 times faster than trait Y in one set of mutation accumulation (MA) lines derived from ancestor A, how closely does that relationship hold in an independent set of MA lines derived from ancestor B? Knowing the answer to that question will provide insight into the deeper question, “What would happen if the tape of life was replayed?” (Gould 1990).

Materials and Methods

MA lines

The details of the MA lines are reported in Baer et al. (2005). Briefly, sets of 100 replicate lines were initiated from highly homozygous populations of the N2 and PB306 strains of C. elegans in March of 2001 and maintained by serial transfer of a single immature hermaphrodite every generation for 250 generations, at which point each MA line was cryopreserved. The common ancestor (G₀) of each set of MA lines was cryopreserved at the outset of the experiment. At the time the experiments reported here were initiated, ∼70 MA lines from each strain remained extant, the others having been lost. Some lines were too sickly to collect sufficient animals for these experiments; we report results from 46 N2 MA lines and 47 PB306 MA lines. Ancestral (G₀) controls were thawed and 15 “pseudolines” were initiated from resuscitated individuals from each strain. The pseudolines were subsequently treated analogously to the MA lines. The purpose of including the G₀ pseudolines is to account for among-line variance resulting from any cause other than mutation accumulation (Lynch and Walsh 1998, p. 332).

Wild isolates

We assayed first cell division in a worldwide collection of 97 wild isolates of C. elegans. Strain identification numbers and collection information are reported in Supplemental Material, Table S1 or at www.elegansvariation.org.

Mitotic cell division phenotype assays

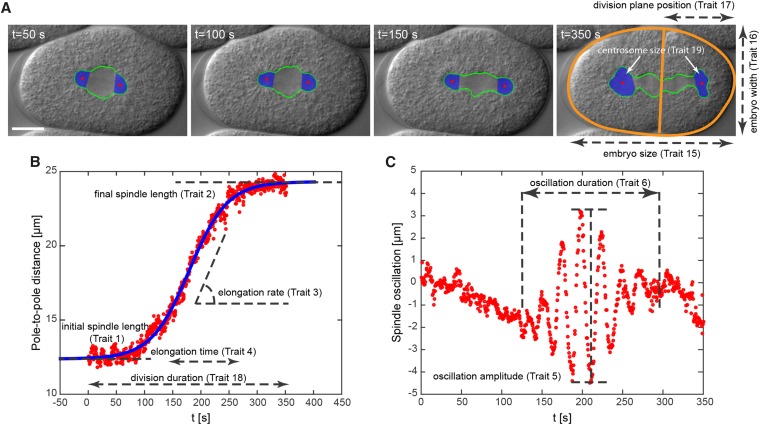
The details of maintenance, microscopy, and image processing of the first mitotic spindle in C. elegans embryos are reported in Farhadifar and Needleman (2014) and Farhadifar et al. (2015). Briefly, all lines were cultured at 24° on nematode growth media and fed the OP50 strain of Escherichia coli. We dissected and imaged the embryos on a 4% agar pad between a slide and coverslip by differential interference contrast (DIC) microscopy. We developed image-processing software to track the spindle poles in the DIC images (Figure 1A) (average sample sizes and trait numbers associated with trait descriptions are given in the first column of Table 1). For each embryo, we measured the pole-to-pole distance and fitted a sigmoid function $l\left(t\right)=l_0+l_1/\left(1+\exp \left(- {\left(t-T\right)}_l/\tau \right)\right)$ to the data (Figure 1B). We defined trait 1, $l_0,$ and trait 2, $l_0+l_1,$ as the initial and final length of the spindle (in micrometers), respectively (Figure 1B). Trait 3 (the elongation rate of the spindle in micrometers per minute, see Figure 1B) and trait 4 (the duration of spindle elongation in seconds) are defined as $l_1/4\tau$ and $\tau ,$ respectively. We quantified spindle oscillation by measuring the distance of the posterior and anterior centrosomes from the long axis of the embryo (Figure 1C). We defined trait 5 (oscillation amplitude of the posterior centrosome in micrometers) as the largest peak-to-trough distance of the posterior centrosome (Figure 1C) and trait 6 (oscillation duration of the posterior centrosome in seconds) as the total duration that the posterior centrosome oscillates (Figure 1C). We defined traits 7 and 8 for the anterior centrosome similar to traits 5 and 6 for the posterior centrosome. Traits 9 and 11 (in seconds) are defined as the time difference between the mid-spindle elongation ($T_l,$ see above) and the maximum oscillation peak for the posterior and anterior centrosomes, respectively. Traits 10 and 12 (in seconds) are defined as the time difference between the first oscillation peak and the mid-spindle elongation time for the posterior and anterior centrosomes, respectively. We defined traits 13 and 14 as the average frequency of centrosome oscillation (in min⁻¹) of the posterior and anterior centrosomes. Traits 15 and 16 are defined as the length and width of the embryo in micrometers (Figure 1A, far right). We defined trait 17 as the position of the division plane from the posterior end of the embryo in micrometers and trait 18 as the duration of the first division in minutes. Trait 19 is defined as the average size of the centrosomes for $t>T_l+e\tau$ (see above).

Figure 1.

Tracking and measurement of cell-division traits in the first mitotic division of C. elegans. (A) Automatic tracking of the spindle (green), centrosomes (blue), cellular boundary (orange, far right), and position of the division plane (orange, far right). Measurements for traits 15–17 are shown in the far right. Bar: 10 μm. (B) Pole-to-pole distance as a function of time (red dots). The blue curve is the sigmoid function fitted to the data (see Materials and Methods). Measurements for traits 1–4 and trait 18 are shown. Trait 4 (elongation time) is multiplied by a factor of 4 in the image for ease of visualization. (C) Spindle oscillation as a function of time (red dots). The distance of the posterior centrosome from the long axis of the embryo is plotted as a function of time. Measurements for traits 5 and 6 are shown.

Table 1. Trait means, with standard errors in parentheses.

	Mean (G0)		Mean (MA250)		ΔM (×104)
Trait	N2	PB306	N2	PB306	N2	PB306	Average
1. Initial spindle length (μm) $\overline{n}=23.6$	11.62 (0.059)	11.36 (0.102)	11.75 (0.040)	10.77 (0.068)	0.41 (0.24)	−2.10* (0.43)	−0.85 (0.25)
2. Final spindle length (μm) $\overline{n}=23.6$	24.20 (0.094)	25.61 (0.123)	24.19 (0.077)	25.75 (0.116)	−0.05 (0.21)	0.21 (0.26)	0.08 (0.17)
3. Elongation rate (μm/min) $\overline{n}=23.6$	5.62 (0.061)	6.17 (0.048)	5.55 (0.064)	6.16 (0.079)	−0.40 (0.61)	−0.10 (0.58)	−0.25 (0.42)
4. Elongation time (sec) $\overline{n}=23.6$	34.38 (0.540)	35.37 (0.395)	34.59 (0.421)	37.50 (0.396)	0.34 (0.78)	2.36* (0.63)	1.35 (0.50)
5. Posterior centrosome, oscillation amplitude (μm), $\overline{n}=22.6$	6.911 (0.064)	6.82 (0.060)	6.64 (0.084)	6.93 (0.079)	−1.60 (0.62)	0.68 (0.57)	−0.46 (0.41)
6. Posterior centrosome, oscillation duration (sec), $\overline{n}=22.6$	128.07 (1.867)	119.55 (1.716)	124.88 (1.40)	122.19 (1.540)	−1.00 (0.73)	0.92 (0.77)	−0.04 (0.53)
7. Anterior centrosome, oscillation amplitude (μm), $\overline{n}=22.6$	3.13 (0.071)	2.84 (0.076)	2.99 (0.073)	2.90 (0.065)	−1.80 (1.30)	0.67 (1.38)	−0.57 (0.95)
8. Anterior centrosome, oscillation duration (sec), $\overline{n}=22.6$	97.33 (1.979)	94.17 (2.221)	96.25 (1.903)	95.88 (2.120)	−0.40 (1.13)	0.73 (1.30)	0.17 (0.86)
9. Posterior centrosome, midelongation to maximum oscillation peak (sec), $\overline{n}=21.8$	−11.38 (0.878)	−17.22 (0.742)	−11.77 (0.715)	−14.14 (0.574)	−1.10 (3.32)	11.41 (3.48)	5.16 (2.40)
10. Posterior centrosome, first oscillation peak to midelongation (sec), $\overline{n}=21.8$	36.52 (1.075)	33.91 (0.955)	36.16 (0.923)	36.28 (0.755)	−0.80 (3.25)	5.39 (2.77)	2.30 (3.03)
11. Anterior centrosome, midelongation to maximum oscillation peak (sec), $\overline{n}=21.9$	−29.28 (0.848)	−29.81 (0.945)	−26.81 (0.780)	−27.25 (0.839)	5.52 (2.57)	5.91 (2.77)	5.72 (1.89)
12. Anterior centrosome, first oscillation peak to midelongation (sec), $\overline{n}=21.9$	15.78 (1.273)	13.64 (1.003)	18.27 (0.917)	15.81 (0.873)	5.36 (3.38)	4.99 (3.05)	5.18 (2.28)
13. Posterior centrosome, oscillation frequency (min−1), $\overline{n}=22.6$	2.66 (0.017)	2.79 (0.024)	2.66 (0.014)	2.873 (0.011)	−0.02 (0.34)	1.24 (0.38)	0.61 (0.25)
14. Anterior centrosome, oscillation frequency (min−1), $\overline{n}=22.6$	2.56 (0.017)	2.650 (0.018)	2.57 (0.012)	2.72 (0.011)	0.09 (0.29)	1.01 (0.30)	0.55 (0.21)
15. Embryo size (μm) $\overline{n}=24.4$	50.78 (0.166)	52.63 (0.207)	50.40 (0.152)	52.19 (0.239)	−0.30 (0.19)	−0.30 (0.24)	−0.30 (0.15)
16. Embryo width (μm) $\overline{n}=24.4$	33.93 (0.166)	33.72 (0.195)	34.05 (0.126)	34.40 (0.146)	0.09 (0.24)	0.79 (0.29)	0.44 (0.19)
17. Division plane position (μm) $\overline{n}=24.4$	22.31 (0.065)	22.89 (0.097)	22.24 (0.075)	22.54 (0.099)	−0.10 (0.18)	−0.60 (0.24)	−0.35 (0.15)
18. Division duration (min) $\overline{n}=24.5$	5.07 (0.051)	4.74 (0.045)	5.08 (0.039)	4.84 (0.039)	0.07 (0.51)	0.93 (0.49)	0.50 (0.35)
19. Centrosome size (μm2) $\overline{n}=24.9$	37.59 (0.303)	35.82 (0.422)	37.97 (0.316)	35.81 (0.325)	0.46 (0.47)	−0.03 (0.59)	0.21 (0.38)
Mean					0.05 (0.44)	1.80 (1.09)	1.02 (0.47)
Mean(Abs)					1.07 (0.26)	2.12 (0.66)	1.32 (0.44)
Median					−0.05	0.58	0.21
Median(Abs)					0.61	0.92	0.50

$\overline{n}$ is the mean number of individuals measured per line. Column headings are as follows: Trait, see Figure 1 for descriptions of traits; Mean (G₀), mean trait value of the ancestral G₀ control; Mean (MA250), mean of the MA lines; ΔM, percentage of per-generation change in the trait mean. ΔM for traits 9–13 (shaded rows) are standardized by the environmental standard deviation rather than the by the mean, and thus the per-generation change is given in units of phenotypic standard deviations rather than as a fraction of the mean. Values of ΔM marked by * are significantly different from 0 at the experiment-wide P < 0.05. Mean(abs) is the mean absolute value, Median(abs) is the median absoluted value.

Data analysis

With 19 traits, there are many more elements in the covariance matrix (190) than there are MA lines (46 or 47), which precludes formal matrix comparisons in the absence of some sort of data reduction. Because our primary interests relate to the organismal phenotype per se, we restrict the analyses to the univariate case, except for an exploratory principal components analysis intended to investigate the overall structure of phenotypic variation (explained in Results).

Data were analyzed for each set of MA lines (N2 and PB306) separately except as noted.

Trait standardization:

Meaningful comparisons among traits require that the traits be standardized on a common scale. Traits can be standardized either by the trait mean, in which case the mean-scaled genetic variance is the squared genetic coefficient of variation, or by the phenotypic standard deviation (SD), in which case the SD-scaled genetic variance is the heritability. The squared genetic coefficient of variation is naturally related to the evolvability of a trait (Houle 1992; Hansen et al. 2011), which is the “opportunity for selection” when the trait is fitness (Crow 1958). In some cases, however, mean standardization is not appropriate, e.g., when the trait value can be either positive or negative. Of the 19 traits, 4 (traits 9–12) cannot be meaningfully mean standardized. We report results for raw (unstandardized) data and SD standardized traits from the full data set and results for mean standardized traits from the reduced set of 15 traits. MA lines were mean standardized by dividing each data point by the mean of the G₀ ancestor and SD standardized by dividing each data point by the square root of the within-line (environmental) variance averaged over all lines (G₀ and MA). Wild isolates were mean standardized by the global mean of the wild isolates and SD standardized by the square root of the within-line variance of the wild isolates. In all cases, the important conclusions are qualitatively similar for the two different standardizations.

Evolution of trait means in MA lines (ΔM):

A directional change in the trait mean over the course of a MA experiment indicates a mutational bias. The per-generation change in the trait mean (ΔM) was determined from the slope of the regression of the (standardized) trait mean against generations of MA, i.e., $\Delta M=\left({\overline{z}}_{\mathrm{MA}}-{\overline{z}}_0\right)/{\overline{z}}_{0}t,$ where ${\overline{z}}_{\mathrm{MA}}$ and ${\overline{z}}_0$ are the means of the MA lines and the G₀ ancestors, respectively, and t is the number of generations of MA. Regression slopes were calculated from the general linear model

$$z_{\mathit{ijk}}=\mu +t_{\mathit{k}}+{\mathit{l}}_{\mathit{i}|\mathit{k}}+e_{ij|\mathit{k}},$$

where z_i is the standardized trait value of individual (equal to replicate) j of line i in treatment group k (G₀ ancestor or MA), µ is the overall trait mean (defined as 0 in the G₀ ancestor), t represents the number of generations of mutation accumulation (0 in the G₀ ancestor and 250 in the MA lines), l_j|k is the random effect of line (or pseudoline) i, and e_ij|k is the random residual associated with individual j of line i. Random effects are denoted conditioned on treatment group k because variance components of those effects were estimated independently for each treatment group. Analyses were performed using the MIXED procedure in SAS v.9.4. Variance components of the random effects were estimated by restricted maximum likelihood (REML) separately for each treatment group, using the GROUP= option in the RANDOM and REPEATED statements of the MIXED procedure (Fry 2004). Degrees of freedom were determined by the Kenward–Roger method (Kenward and Roger 1997). Statistical significance of the regression slope was determined by an F-test with type III sums of squares. Estimation of the regression slope from standardized traits fails to account for sampling variance of the G₀ controls, but with the sample sizes in this study (hundreds of control individuals) the bias is negligible, and the empirical 95% confidence intervals calculated by bootstrapping over lines (data not shown) are very close to those calculated from the linear model.

VM:

The mutational variance is half the difference in the among-line component of variance between the MA lines and the G₀ pseudolines, divided by the number of generations of MA; i.e., $\mathrm{VM}=\left(V_{\mathrm{L,MA}}-V_{\mathrm{L,}{\mathrm{G}}_{\mathrm{0}}}\right)/2t,$ where $V_{\mathrm{L,MA}}$ is the variance among MA lines, $V_{\mathrm{L,}{\mathrm{G}}_{\mathrm{0}}}$ is the variance among the G₀ pseudolines, and t is the number of generations of MA (Lynch and Walsh 1998, p. 330). To estimate VM, we first estimated variance components from the linear model given previously and then estimated the among-line variance from the model

$$z_{\mathit{ijk}}=\mu +t_{\mathit{k}}+{\mathit{l}}_{\mathit{ik}}+e_{ij|\mathit{k}},$$

the difference between the two models being that in the second model there is only a single among-line component of variance estimated, whereas in the first model the among-line variance is estimated separately for the G₀ and the MA groups. Statistical significance of VM is determined by a likelihood-ratio test (LRT) of the model with separate among-line variances of G₀ and MA compared to the model with a single among-line variance. The models are nested and differ by a single parameter, so the likelihood ratio is asymptotically chi-square distributed with a single degree of freedom. There are 38 significance tests (19 traits in two sets of MA lines), so the approximate experiment-wide 5% level of significance is P < 0.05/38.

VG of wild isolates:

The inferred rate of outcrossing among C. elegans in nature is very low (Rockman and Kruglyak 2009), so we treat the wild isolates as if they are homozygous lines. The genetic variance among a set of homozygous lines is half the among-line component of variance (Falconer 1989, p. 265). Variance components were estimated from the linear model z_ij = l_i + e_ij, where l_i represents the random effect of wild isolate i and e_ij is the random residual of individual j of wild isolate i. Significance of the among-line component of variance was assessed by LRT comparison of models with and without the line term included.

Data availability

Data (raw trait values) are deposited in Dryad (http://dx.doi.org/10.5061/dryad.js880).

Results

Multivariate trait architecture

Significant correlations exist between at least some of these traits (Farhadifar et al. 2015), so the possibility exists that the 19 traits are essentially only 1 or a few traits. To address that possibility, we carried out a principal component analysis (PCA) on the phenotypic correlation matrix (i.e., on SD standardized traits) of the MA lines, as implemented in the PRINCOMP procedure of SAS v.9.4. The resulting eigenvalues of the principal components are depicted in Figure S1 and the eigenvectors are given in Table S2. For N2, principal component 1 (PC1) explains ∼18% of the phenotypic variance (the expectation for uncorrelated traits is ∼6%), PC2 explains another ∼14% of the variance, and the first 9 PCs collectively explain ∼80% of the variance. Those values are almost exactly the same for PB306. Thus, although the traits are clearly correlated beyond the random expectation (Figure S4), there is also considerable scope for independent evolution of these traits. This conclusion is reinforced by inspection of the pairwise phenotypic correlations (Table S3). In N2, only 6 of the 171 pairwise absolute correlations are >0.5; in PB306, 9 are. The pairwise correlations are almost identical in the two sets of MA lines (r_N2,PB = 0.96, d.f. = 169, P < 0.0001).

Evolution of trait means in MA lines (ΔM)

Trait means evolved very little over the course of the MA experiment (Table 1). For the N2 lines, the median absolute change in the trait mean for the 15 traits that could be mean standardized was 0.0034% per generation; in no case was the change significant at the Bonferroni-corrected experiment-wide 5% level (0.05/(2 × 15), P < 0.0017). For the PB306 lines, the median absolute change was 0.0073% per generation, and only two traits (1 and 4) changed significantly at the experiment-wide 5% level. ΔM was not significantly correlated between the two sets of MA lines (r = 0.15, P > 0.60). Of the 19 traits, 9 changed in the same direction in both sets of lines and 10 changed in opposite directions, exactly as predicted if the direction of change was random. Moreover, these results are consistent with the traits being under some degree of stabilizing selection [perhaps collectively (Farhadifar et al. 2015)], because deleterious mutations do not have consistently directional effects. For a trait with a consistent mutational bias, at equilibrium selection must exactly counteract the mutational bias. Otherwise the trait would evolve without bound.

The ΔMs for these traits can be compared to ΔM for other traits expected to be under directional selection. For example, in these same sets of lines lifetime reproduction weighted by probability of survival (“total fitness”) decreased by ∼0.1% per generation (Baer et al. 2006) and body volume at maturity decreased by ∼0.07% per generation (Ostrow et al. 2007); in each case the change was highly significant and consistent between the two sets of lines.

VM

In 37 of 38 cases (19 traits in two sets of MA lines) the SD-standardized among-line variance of the MA lines is greater than the among-line variance of the G₀ controls, trait 13 in the PB306 lines being the sole exception (Table S4). However, in only two cases (traits 3 and 5 in the PB306 lines) is VM significant at the experiment-wide 5% level (P < 0.0013). To assess the overall significance of the differences in among-line variance in MA lines relative to the G₀ pseudolines, we performed paired t-tests on the N2 and PB306 lines, with each trait constituting a paired sample and a hypothesized difference of zero. In both cases, there was a highly significant overall increase in the SD-standardized among-line variance in the MA lines (N2, two-tailed t = −6.23, d.f. = 18, P < 0.0001; PB306, two-tailed t = −4.79, d.f. = 18, P < 0.0002). Thus, we proceed under the assumption that the point estimates of VM represent a reasonable approximation of the truth, even though they do not reach experiment-wide significance at the 5% level in most cases.

Averaged over the two sets of MA lines, mean-standardized VM varies by slightly under two orders of magnitude, from 3.3 × 10⁻⁷ per generation for trait 14 to 2.6 × 10⁻⁵ per generation for trait 7 (Table 2). These values can be put into context by comparison to a set of life history traits measured in these same sets of MA lines (Table S5). The average VM for the traits reported here (mean = 6 × 10⁻⁶ per generation, median = 2 × 10⁻⁶ per generation) is substantially smaller than that for the life history traits (mean = 9 × 10⁻⁵ per generation, median = 8 × 10⁻⁵ per generation), although the ranges of variability overlap.

Table 2. Variances of G₀ mean-standardized traits (squared coefficient of variation).

Trait	Strain	VL, G0 (×104)	VL, MA (×104)	VE, G0 (×104)	VE, MA (×104)	VM (×106)	Ave VM (×106)
1	N2	2.52 (1.44)	3.30 (1.13)	48.52 (3.15)	47.03 (2.13)	0.16 (0.37)	0.42 (0.62)
	PB	9.73 (4.73)	13.16 (3.51)	60.28 (4.50)	72.59 (3.29)	0.69 (1.18)
2	N2	2.47 (1.18)	3.60 (1.02)	24.24 (1.57)	23.26 (1.06)	0.23 (0.31)	0.64 (0.28)
	PB	2.28 (1.25)	7.56 (1.99)	23.31 (1.74)	35.47 (1.61)	1.06 (0.47)
3	N2	9.48 (6.20)	50.45 (12.89)	229.00 (14.88)	234.90 (10.66)	8.19 (2.86)	10.18 (2.13)
	PB	0	60.86 (15.85)	209.80 (15.34)	260.50 (11.85)	12.17 (3.17)
4	N2	30.67 (15.01)	47.83 (13.77)	346.30 (22.50)	372.90 (16.93)	3.43 (4.07)	5.26 (2.55)
	PB	5.50 (7.56)	40.98 (13.35)	327.40 (24.43)	372.20 (16.95)	7.10 (3.07)
5	N2	5.63 (5.57)	52.44 (14.28)	238.90 (18.75)	299.40 (13.94)	9.36 (3.07)	8.99 (1.95)
	PB	0	43.04 (12.06)	265.00 (20.17)	308.40 (13.98)	8.61 (2.41)
6	N2	22.83 (13.42)	36.39 (12.18)	405.90 (26.81)	410.20 (19.11)	2.71 (3.62)	5.96 (2.85)
	PB	11.11 (12.34)	57.13 (18.22)	451.70 (35.19)	437.90 (19.95)	9.20 (4.40)
7	N2	60.82 (31.62)	207.70 (52.44)	825.50 (54.43)	822.60 (38.26)	29.38 (12.25)	25.97 (8.79)
	PB	68.62 (40.18)	181.40 (48.66)	875.20 (68.00)	914.60 (41.52)	22.56 (12.62)
8	N2	42.13 (25.68)	130.10 (37.58)	850.40 (56.08)	939.00 (43.69)	17.59 (9.10)	22.99 (7.60)
	PB	41.14 (30.68)	183.10 (52.51)	964.40 (74.87)	1115.0 (50.63)	28.39 (12.16)
13	N2	5.48 (2.56)	11.28 (2.97)	49.77 (3.29)	54.92 (2.56)	1.16 (0.78)	0.58 (0.60)
	PB	8.83 (4.34)	3.82 (1.43)	57.95 (4.51)	57.76 (2.62)	0.00 (0.91)
14	N2	3.47 (2.05)	6.25 (2.15)	61.49 (4.06)	74.01 (3.46)	0.56 (0.59)	0.33 (0.41)
	PB	2.93 (2.36)	3.46 (1.52)	70.58 (5.50)	73.93 (3.36)	0.11 (0.56)
15	N2	1.59 (0.80)	3.27 (0.90)	20.25 (1.29)	21.30 (0.95)	0.34 (0.24)	0.81 (0.25)
	PB	1.62 (0.88)	8.07 (1.97)	17.85 (1.31)	30.63 (1.33)	1.29 (0.43)
16	N2	2.37 (1.41)	4.50 (1.39)	50.36 (3.22)	44.81 (2.00)	0.43 (0.40)	0.59 (0.33)
	PB	2.59 (1.85)	6.35 (1.82)	61.88 (4.55)	51.78 (2.24)	0.75 (0.52)
17	N2	0.31 (0.60)	3.38 (1.12)	39.57 (2.53)	134.70 (5.99)	0.61 (0.25)	0.81 (0.24)
	PB	1.44 (1.05)	6.51 (1.80)	32.49 (2.39)	46.32 (2.00)	1.01 (0.42)
18	N2	15.63 (6.40)	21.57 (5.81)	82.81 (5.28)	134.70 (5.99)	1.19 (1.73)	2.28 (1.18)
	PB	7.77 (4.74)	24.64 (6.42)	118.10 (8.61)	131.10 (5.73)	3.37 (1.60)
19	N2	5.38 (4.23)	24.84 (7.05)	191.80 (12.13)	179.20 (7.92)	3.89 (1.64)	3.54 (1.42)
	PB	11.23 (8.04)	27.20 (8.25)	255.60 (18.39)	253.70 (10.91)	3.19 (2.30)
Mean	N2					5.28 (2.20)	5.96 (2.19)
	PB					6.60 (2.30)
Median	N2					1.19	2.28
	PB					3.19

Standard errors are in parentheses. Column headings are as follows: VL, G₀, among-line variance of G₀ pseudolines; VL, MA, among-line variance of MA lines; VE, G₀, within-line variance of G₀ pseudolines; VE, MA, within-line variance of MA lines; VM, mutational variance (×10⁶); Ave VM, average VM of the two strains. Standard errors of VM for individual traits are calculated from the square root of the sum of the sampling variances of the G₀ pseudolines and MA lines. Standard errors of the among-trait mean VM are calculated as the among-trait variance divided by the square root of the number of traits.

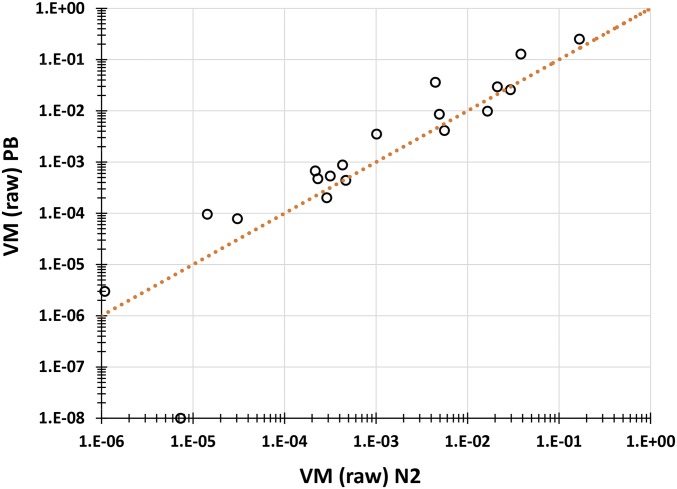
In contrast to the ΔMs, which are uncorrelated between the two sets of MA lines, the mutational variances are highly correlated between the N2 and the PB306 lines. For the full data set of 19 traits, the correlation between the raw (unstandardized) VMs in the two strains is 0.95 (P < 0.00001; Figure 2) and the correlation for the subset of 15 mean-standardized traits is 0.89 (P < 0.0001; Figure S2). The correlation between the mutational heritabilities in the two strains is smaller, although still significantly positive (r = 0.56, P < 0.02).

Figure 2.

Raw VM (PB306) plotted against raw VM (N2). The dotted line represents the line of equality.

VG of wild isolates

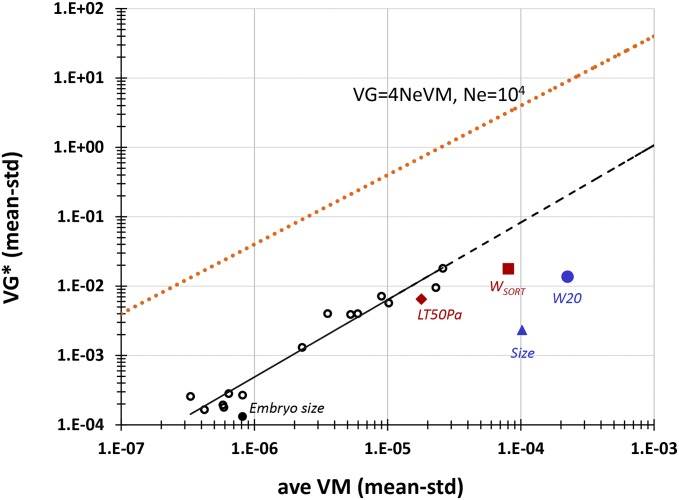
For all traits the among-line component of variance (raw and mean standardized) among the wild isolates is highly significantly different from zero (P < 0.0001 in all cases), as is the broad-sense heritability, H² (Table 3). However, the potentially nonzero among-line variance of the G₀ ancestors of the MA lines introduces the possibility that some fraction of the among-line variance of the wild isolates is not true genetic variance. To address that possibility, we subtracted the average of the two estimates of the among-line variance of the G₀ controls from the estimate of the among-line variance of the wild isolates before calculating VG; we refer to the corrected estimate of VG as VG* (Table 3). On average, VG* is reduced by ∼20–30% relative to the uncorrected VG (mean reduction = 27%; median reduction = 20%). For the full set of 19 unstandardized traits, the correlation between the average mutational variance VM and the genetic variance VG* is nearly perfect (r = 0.99, P < 0.0001; Figure S3); the correlation is essentially the same for the 15 mean-standardized traits (r = 0.95, P < 0.0001; Figure 3). The correlation between the mutational heritability and H² is somewhat smaller but remains highly significant (r = 0.69, P < 0.002).

Table 3. Summary statistics of wild isolates (standard errors in parentheses).

Trait	Mean	VG (raw)	VE (raw)	H2	VG* (std) (×103)	tp* (raw)	tP* (std)
1	11.61 (0.04)	0.06 (0.01)	0.74 (0.02)	0.07 (0.01)	0.17 (0.24)	419 (641)	394 (611)
2	24.89 (0.08)	0.25 (0.04)	1.40 (0.04)	0.13 (0.02)	0.28 (0.13)	414 (189)	441 (219)
3	5.76 (0.07)	0.20 (0.03)	0.80 (0.02)	0.17 (0.03)	5.71 (1.24)	544 (150)	561 (149)
4	35.67 (0.38)	6.24 (1.03)	43.56 (1.29)	0.11 (0.02)	3.91 (1.36)	763 (386)	743 (390)
5	7.38 (0.09)	0.40 (0.06)	1.45 (0.04)	0.18 (0.03)	7.16 (1.41)	878 (231)	797 (214)
6	126.4 (1.4)	78.50 (13.27)	629.0 (18.7)	0.10 (0.02)	4.01 (1.47)	781 (432)	674 (351)
7	3.49 (0.08)	0.26 (0.04)	1.03 (0.03)	0.17 (0.03)	18.07 (5.14)	953 (354)	696 (269)
8	105.6 (1.7)	128.8 (21.4)	878.0 (26.1)	0.11 (0.02)	9.54 (3.33)	524 (201)	415 (161)
9	−16.89 (0.60)	13.87 (2.50)	157.6 (4.8)	0.07 (0.01)		864 (529)
10	34.30 (0.77)	21.70 (4.15)	317.7 (9.7)	0.06 (0.01)		703 (359)
11	−32.65 (0.62)	11.45 (2.68)	330.8 (10.1)	0.03 (0.01)		448 (210)
12	15.41 (0.71)	16.59 (3.54)	343.0 (10.5)	0.04 (0.01)		599 (517)
13	2.75 (0.01)	0.004 (0.001)	0.037 (0.001)	0.09 (0.02)	0.19 (0.27)	404 (533)	335 (384)
14	2.62 (0.01)	0.003 (0.001)	0.046 (0.001)	0.05 (0.01)	0.26 (0.19)	708 (1147)	778 (989)
15	50.96 (0.12)	0.56 (0.10)	5.17 (0.15)	0.09 (0.02)	0.13 (0.08)	165 (65)	163 (66)
16	34.00 (0.10)	0.35 (0.07)	5.81 (0.17)	0.05 (0.01)	0.18 (0.14)	322 (211)	304 (195)
17	22.38 (0.06)	0.16 (0.03)	2.10 (0.06)	0.07 (0.01)	0.27 (0.10)	325 (116)	330 (121)
18	4.83 (0.03)	0.04 (0.01)	0.30 (0.01)	0.12 (0.02)	1.31 (0.59)	537 (320)	575 (326)
19	37.17 (0.38)	6.33 (1.00)	31.08 (0.88)	0.14 (0.02)	4.02 (1.00)	1194 (505)	1135 (494)
Mean				0.10 (0.01)	3.68 (1.29)	608 (59)	556 (65)
Median				0.09	2.61	544	561

Column headings are as follows: Mean, trait mean; VG (raw), standing genetic variation calculated from the raw data; VE (raw), environmental (within-strain) variance calculated from the raw data; H², broad-sense heritability; VG* (std), mean-standardized VG corrected by subtracting the average among-line variance of the MA controls; t_p* (raw), expected persistence time of a new mutation (t_p = VG/VM) calculated from raw data corrected by subtracting average among-line variance of MA controls from VG; t_p* (std), calculated from mean-standardized data.

Figure 3.

Mean-standardized VG* plotted against mean-standardized VM. The solid black line shows the best fit of the spindle trait data; the dashed black line represents the extension of the best-fit line. The orange dotted line shows 4N_eVM for N_e = 10⁴. See text for description of labeled traits and experimental details. Traits labeled in red were measured on the same set of wild isolates included in this study.

The ratio VG/VM has several interpretations, depending on the context. First, in an infinite population at MSB, it represents the persistence time (t_P) of a new mutation, i.e., the expected number of generations before the mutant allele is removed by selection (Garcia-Dorado et al. 2003). The stronger selection is, the shorter the persistence time. Second, for a neutral trait in a finite population, VG = 2N_eVM at mutation–drift equilibrium (Lynch and Hill 1986), so VG/VM is equal to 2N_e (4N_e in the case of obligate self-fertilization, which is approximately the case with C. elegans). Finally, VG/VM represents the number of generations of mutation required to produce a given amount of genetic variance, irrespective of other evolutionary forces.

For almost all of the traits in this study, the ratio VG*/VM (called t_P* in Table 3) falls within the relatively narrow window of 300–800. Two traits are obvious outliers: embryo size (trait 15; t_P* ≈ 160) and centrosome size (trait 19; t_P* > 1100). Embryo size has been previously inferred to be under long-term stabilizing selection (Farhadifar et al. 2015) and the reduced t_P is consistent with stronger selection on that trait than on the other traits. We have no intuition about why centrosome size is a high outlier. Balancing selection for some unknown reason is possible, although random chance seems equally plausible.

Discussion

Two robust conclusions emerge from this study, which inform several longstanding issues in evolutionary genetics. First, for this relatively large set of functionally related but (on average) only modestly correlated traits, the mutational process is highly repeatable: The correlation between estimates of trait-specific VM in two independent sets of MA lines derived from different ancestors is ∼0.9.

The high repeatability of the mutational process was hardly a foregone conclusion. To put this result in perspective, consider the contrast with fitness-related traits in D. melanogaster, which are notoriously noisy and inconsistent (Keightley and Eyre-Walker 1999). There are potentially several factors that underlie the differences between our results and those from Drosophila, including the demonstrable genetic variation for mutation rate in D. melanogaster (Schrider et al. 2013). Although we have yet to exhaustively characterize the mutational process in these two strains of C. elegans for all categories of molecular mutations, the base-substitution (Denver et al. 2012; F. Besnard and M-A. Felix, personal communication) and short tandem-repeat (Phillips et al. 2009) mutation rates are quite similar in the two strains.

The simplest explanation for the consistency of the results of this study (in contrast to the Drosophila work) is consistency in the experiments. The mutation accumulation lines were maintained in the same laboratory at the same time under the same conditions, and the phenotypic assays were done in the same laboratory by the same person at the same time under the same conditions. Further, the level of replication in these experiments is substantially greater (∼25 replicates per line) than in many, albeit not all, phenotypic assays of MA lines. This high level of replication is especially important because the mutational heritabilities for these traits are actually quite low (VM/VE ≈10⁻⁴; Table S4; compare to values in table 1 of Houle et al. 1996).

It is certainly possible that life history traits are somehow qualitatively different from the traits in this study. Our traits are restricted to a single, narrow window of time in development, so the phenotype, and thus the phenotypic variance, is not integrated over a long period. We have previously assayed lifetime productivity and size at maturity in these same lines. Averaged over six assays at two temperatures, VM for G₀ mean-standardized lifetime productivity varies by <3-fold between the two strains (data from table 2 of Baer et al. 2006); size at maturity varies by 1.5-fold (data from table 2 of Ostrow et al. 2007). Those values are well within the range of variation between the two strains for single traits in this study. In contrast, VM for egg-to-adult viability in D. melanogaster varies by at least 27-fold across studies, and VM for abdominal bristle number varies by at least 130-fold (data from table 1 of Houle et al. 1996). Thus, the difference in repeatability between this study and the Drosophila work does not seem to be due to a qualitative difference between categories of traits.

The second robust result is that VM almost perfectly predicts VG for these traits (Figure 3 and Figure S3). Again, this was not a foregone conclusion (Charlesworth 2015). This finding is not without precedent, however, as evidenced by figure 1 of Houle (1998). Houle calculated a correlation between VG and VM of 0.95 for eight life history and morphological traits in D. melanogaster. Lynch et al. (1998) reported similar data for nine life history and morphological traits in D. pulex, although they did not explicitly calculate the correlation between VG and VM (r = 0.75, reanalysis of data in their table 1 and table 3). An analogous relationship between VM and between-species divergence was reported for a set of several thousand gene-expression traits in D. melanogaster (Rifkin et al. 2005); the correlation between VM and between-species divergence ranged between 0.25 and 0.4 (P < 0.0001) for three species pairs. Similar data exist for other sets of traits and in other organisms, and we predict the correlation between mean-standardized VM and VG will generally be large and positive.

Two potentially interrelated underlying evolutionary mechanisms predict a positive correlation between VG and VM. The first is the interplay between mutation and random genetic drift. For a neutral trait at mutation–drift equilibrium (MDE) in a selfing organism, VG = 4N_eVM (Lynch and Hill 1986). Global N_e of C. elegans has been estimated from the standing nucleotide polymorphism (θ) to be on the order of 10⁴ (Andersen et al. 2012). In no case does VG of any of the traits investigated here come close to the value of 40,000 VM predicted for a neutral trait at MDE (dashed line in Figure 3); the average is ∼550 VM. However, C. elegans is almost certainly far from global MDE, so it seems intuitively obvious that VG should be well below the value predicted at MDE, even for a neutral trait. However, both VG and θ increase at a rate proportional to the mutation rate and decrease by drift at a rate inversely proportional to N_e. It is definitely possible that the loci that underlie most quantitative genetic variation mutate 70-fold more slowly than do single nucleotides. It seems less likely that N_e differs consistently by that much between the two categories of loci.

More importantly, it seems unlikely to us that these traits are neutral over the entire range of phenotypic space. An alternative, more reasonable possibility is that the traits are not neutral, but rather are subject to some degree of purifying selection, which probably manifests itself as stabilizing selection, either real or apparent (Kondrashov and Turelli 1992). If so, the observed positive relationship between VG and VM is predicted at MSB. In an infinite population at MSB, $\mathrm{VG}\propto \mathrm{VM/}S,$ where S is the mean strength of selection against a new mutation; the proportionality becomes equality if the average selective effects are assumed to be uniform (Bulmer 1989; Barton 1990). If the average selective effects are not uniform (and surely they are not), $\mathrm{VG}=\mathrm{VM/}S\left(1+C^2\right),$ where C is the coefficient of variation of mutational effects on fitness (Charlesworth 2015), but unless C is highly variable among traits, VM/VG provides a reasonable approximation of the relative strength of selection. Thus, if genetic variation is maintained by MSB, we expect a positive correlation between VG and VM unless the average strength of selection is different between traits and/or the CVs of the mutational effects are different. For example, if VM varies by two orders of magnitude, as it does here, selection would have to vary by nearly that much to remove the relationship between VG and VM.

The strong relationship between VG and VM implies that, perhaps with a couple of exceptions, selection must be remarkably uniform across this set of traits. Why might that be? One possibility is that the traits themselves are all highly genetically correlated, even though the phenotypic correlations are modest. If so, direct selection on one trait might lead to sufficient indirect selection on the other traits to produce the pattern. There are too few degrees of freedom to calculate the full set of quadratic selection gradients for these traits (Lande and Arnold 1983). However, a previous analysis of a subset of 6 of these traits (traits 1, 2, 3, 15, 17, and 19) revealed that stabilizing selection on embryo size (trait 15) of strength V_S = VM/(VG)² is sufficient to explain the observed standing genetic covariance matrix G for those traits, with no need to invoke selection on the other traits (Farhadifar et al. 2015). In that study, embryo size was chosen a priori as the likely target of stabilizing selection, for three reasons. First, from direct measurement of fecundity, we observed that embryo size showed the largest association with fecundity. Second, studies with many organisms have demonstrated that embryo size and size at birth are subject to stabilizing selection. And third, it showed the largest deviation from the neutral expectation. The results of this study reinforce the previous finding: t_P of embryo size is about half that of the next smallest t_P of the other 18 traits.

Any claim that direct selection on a favored trait(s) can explain the evolution of a set of correlated traits must be greeted skeptically, because all traits must be correlated with something, and we can never be certain we have accounted for all the relevant variables. Given the strong positive correlation between VM and VG for this particular set of traits, we can ask: Where do other traits fall out in VM-VG space? Might it be that any arbitrary trait falls out more or less on the same line, and if so, why?

VG and VM have been previously quantified for four other traits in C. elegans: lifetime reproduction weighted by survival measured under the MA conditions (W20), lifetime reproduction measured in a high-throughput “worm-sorter” assay (W_SORT), median lifespan when exposed to the pathogenic bacteria Pseudomonas aeruginosa (LT50Pa), and body volume at maturity (size) (Figure 3 and Table S5) (Etienne et al. 2015). Inspection of Figure 3 shows that fecundity (W20, W_SORT), body volume, and embryo size appear to fall farther below the line than the other traits, consistent with these traits being under stronger purifying selection than the others. Of the four traits, VG for W_SORT and LT50Pa were measured on nearly the same set of wild isolates as those reported in this study, so the values of VG and t_P are directly comparable with those reported here. Persistence time for W_SORT (166 generations) is almost identical to that for embryo size (163 generations), and t_P of LT50Pa (335 generations) is on the low end of the spindle trait values. Persistence times for W20 and size are substantially smaller, but VG for those traits was measured on a smaller subset of wild isolates, some of which may be very closely related. Unfortunately, only 11 isolates are common to the two data sets; for those 11 isolates VG and t_P for W20, and size are both more similar to each other and closer to the common line, but the confidence limits are so large that they make the interpretation tenuous if not meaningless.

It is certainly within the realm of possibility that t_P for more or less any trait measured in this set of wild isolates falls within the relatively narrow range observed here. We can think of at least two possible reasons why that might be. First, since C. elegans apparently experienced at least one hard, global, more or less genome-wide selective sweep within the recent past [∼600–1250 generations (Andersen et al. 2012)], selection at linked loci must necessarily have been very inefficient immediately following the sweep, in which case the standing genetic variation may mostly represent a few hundred generations of input of effectively neutral mutations. The average persistence time of ∼500 generations is consistent with that scenario. However, the two traits most clearly under selection on a priori grounds—embryo size and lifetime reproduction—fall farthest below the line, which suggests, unsurprisingly, that some mutations are sufficiently deleterious as to have been effectively purged by selection.

A second possibility is that the predominantly self-fertilizing life history of C. elegans, combined with relatively restricted recombination within gene-rich regions of the genome (Rockman and Kruglyak 2009), means that most traits experience approximately the same overall level of background selection, although again, certain traits clearly experience atypically strong (or weak) selection.

The peculiar population genetic features of C. elegans invite comparison of the persistence times reported here with those of other taxa, particularly Drosophila. On average, t_P for life history traits in D. melanogaster is on the order of 50 generations and about twice that for morphological traits (Houle et al. 1996). Fruit flies are obligate outcrossers, so selection against new mutations occurs primarily in heterozygotes, which implies that selection against mutant homozygotes must be substantially stronger. Persistence times of heterozygous mutations affecting life history traits in Daphnia are similar to those in D. melanogaster, on the order of 40 generations (Lynch et al. 1998).

Probably the most comparable data to ours in terms of the types of traits are from D. serrata, in which McGuigan et al. (2015) report VG and VM for eight cuticular hydrocarbons and 10 wing dimensions. The median t_P was ∼125 generations, again suggestive of substantially stronger selection against homozygotes. It appears that selection against homozygous mutations for these traits must be substantially weaker than selection against homozygous mutations in Drosophila. One possible explanation is that VG reported here is calculated from a global collection of wild isolates, whereas the Drosophila VG data are based on samples from small populations. However, the population genetic features of C. elegans suggest massive (i.e., global) recent gene flow (Andersen et al. 2012), so our estimate of VG would probably not be wildly different with a different sampling scheme (Salomon et al. 2009). Another possibility is that sexual selection is likely to be much more important in flies than in self-fertilizing nematodes.

For the traits reported in this study, the mean-standardized VM varies over nearly two orders of magnitude (∼80×). Stearns and Kawecki (1994) proposed that VM provides a measure of the robustness of a trait to the perturbing effects of new mutations, such that 1/VM is a meaningful estimate of mutational robustness. Houle (1998) dissented on the grounds that VM cannot provide an unambiguous measure of mutational robustness because different numbers of loci may affect different traits. Gibson and Wagner (2000) argued that “Comparing variabilities in ‘fitness’ with ‘wing shape’ is like comparing apples with oranges” (p. 377). However, the “number of loci” argument in its essence comes down to the distribution of mutational effects (DME), because in an infinitely large population all mutations at all loci in the genome will affect all traits, however small the effect, because all chemical reactions in an organism are ultimately coupled to some extent, however small. By the same logic, comparison of ΔM between traits provides an unambiguous measure of the average mutational effect on a trait, because all traits are subject to the effects of the same set of mutations. To take an opposing viewpoint from that of Gibson and Wagner (2000), perhaps “fitness” is a uniquely nonrobust phenotype precisely because so many mutations at so many loci have effects that are not vanishingly small.

A distinct but related issue concerning mutational robustness is the effect of genetic background: i.e., Are different genotypes differently robust to the effects of mutational perturbation? We can address that question with our data by pairwise comparison of VM for the same set of traits in the two genetic backgrounds, provided we are willing to make the assumption that the number of accumulated mutations does not differ significantly between the two stocks (as noted above, there is no reason to think it does). A paired t-test shows no significant difference in pairwise mean-standardized VM between the N2 and PB306 backgrounds (t = −1.33, d.f. = 14, two-tailed P > 0.20).

A second issue relating to mutational robustness concerns the relationship between genetic robustness (i.e., VM) and robustness to the effects of random environmental noise (variation due to the effects of unique environment, VE in the terminology of quantitative genetics). The extent to which genetic and environmental robustness have similar underlying mechanisms is an open empirical question (e.g., Fraser and Schadt 2010). Averaged over both sets of MA lines, there is a strong positive correlation between VM and VE (r ≈ 0.95). This result is commonly observed and is consistent with the idea that genetic variation and environmental variation have a common biochemical and/or physiological basis (Meiklejohn and Hartl 2002).

Conclusions and Future Directions

1. For this set of 19 functionally related traits, the mutational process is very repeatable. There are several other organisms for which there are extant MA lines from multiple starting genotypes, among them Chlamydomonas reinhardtii (Ness et al. 2016), C. briggsae and Oscheius myriophila (Baer et al. 2005), Arabidopsis thaliana (C. Fenster, personal communication), D. pulex (S. Schaack, personal communication), and probably others. Similar studies including suites of different types of traits will help establish the boundaries of repeatability and idiosyncrasy in the mutational process.

2. For these traits in this species, mean-standardized VM almost perfectly predicts VG. This result has been previously documented, in D. melanogaster (Houle 1998) and to a lesser extent in D. pulex (reanalysis of data in Lynch et al. 1998, above). It is the predicted result if genetic variation is predominantly due to mutation–selection balance or the interplay between mutation and drift. It is not predicted if balancing selection is of primary importance in the maintenance of genetic variation. C. elegans is, prima facie, an unlikely target for balancing selection because of the strong evidence for a recent episode of global strong directional selection (Andersen et al. 2012). However, recent evidence suggests that balancing selection may have maintained variation in numerous regions throughout the C. elegans genome (Thompson et al. 2015).

3. Looking farther afield, it has been convincingly argued that VM is not a sufficient predictor of VG for life history traits in Drosophila and that there must be a significant contribution to VG from balancing selection (Charlesworth 2015). If so, the effect of balancing selection would be to move the line of relationship between VG and VM (depicted in Figure 3) upward, i.e., to increase the intercept. If balancing selection contributes more to VG for life history traits than for other classes of traits, it implies that, all else equal, the slope of the relationship between VG and VM will be steeper than the line of neutrality, with persistence times of high-VM life history traits falling closer to the line of neutrality. All else is not equal, however; persistence times for life history traits in D. melanogaster and other taxa are, on average, less than half those for morphological or other traits (Houle et al. 1996; Houle 1998; Lynch et al. 1999). The discrepancy between the clear, compelling relationship between VM and VA and the apparent insufficiency of MSB to explain the standing genetic variation in D. melanogaster is an important unresolved issue in evolutionary genetics.