omniClassifier: a Desktop Grid Computing System for Big Data Prediction Modeling

Abstract

Robust prediction models are important for numerous science, engineering, and biomedical applications. However, best-practice procedures for optimizing prediction models can be computationally complex, especially when choosing models from among hundreds or thousands of parameter choices. Computational complexity has further increased with the growth of data in these fields, concurrent with the era of “Big Data”. Grid computing is a potential solution to the computational challenges of Big Data. Desktop grid computing, which uses idle CPU cycles of commodity desktop machines, coupled with commercial cloud computing resources can enable research labs to gain easier and more cost effective access to vast computing resources. We have developed omniClassifier, a multi-purpose prediction modeling application that provides researchers with a tool for conducting machine learning research within the guidelines of recommended best-practices. omniClassifier is implemented as a desktop grid computing system using the Berkeley Open Infrastructure for Network Computing (BOINC) middleware. In addition to describing implementation details, we use various gene expression datasets to demonstrate the potential scalability of omniClassifier for efficient and robust Big Data prediction modeling. A prototype of omniClassifier can be accessed at http://omniclassifier.bme.gatech.edu/.

1. INTRODUCTION

Prediction modeling is important in science and engineering disciplines, whether the goal is to classify stellar objects [1] or to determine the prognosis of a cancer patient [2]. Careful adherence to best-practice guidelines for prediction modeling in bioinformatics is especially important due to the properties of the data, e.g., these datasets typically have small sample sizes, but very large feature sizes. Published guidelines for bioinformatics prediction modeling highlight common pitfalls [3] and explicitly show the bias that can occur if these guidelines are not followed [4, 5]. Despite the availability of these guidelines, researchers occasionally report over-optimistic prediction results. Thus, it was necessary to revisit the importance of following good practices [2]. Reasons for the inconsistency in bioinformatics prediction modeling may include (1) the lack of a system for prediction modeling that is readily accessible not only to bioinformaticians, but also to biologists and medical researchers and (2) the prohibitive computational complexity of prediction modeling due to the growth of biomedical data. We address both of these challenges with omniClassifier, a web-based application that simplifies prediction modeling while following best-practice guidelines; and that uses desktop grid computing for unlimited scalability to large datasets.

A common pitfall for prediction modeling in bioinformatics is the failure to properly use cross validation to choose features and classifier parameters [3]. Subsequent to model selection, many studies also fail to evaluate their prediction model using independent validation data. Ambroise and McLachlan showed that improper implementation of cross validation can lead to overly optimistic estimates of prediction performance [4]. Specifically, using microarray gene expression data, they showed that when features are selected outside of cross validation, estimated prediction performance can be nearly perfect, even for randomly generated datasets in which feature vectors are independent of class labels. Furthermore, when cross validation encompasses both feature selection and classifier parameter selection, performance estimation bias can still occur [5]. Varma and Simon showed that a nested cross validation procedure can reduce this bias considerably [5]. Thus, we develop omniClassifier to closely follow these guidelines in order to achieve unbiased prediction modeling.

omniClassifier leverages desktop grid computing technology for increased scalability to better handle biomedical Big Data. We use the Berkeley Open Infrastructure for Network Computing (BOINC) middleware to manage distribution of work units to compute nodes [6]. Advantages of BOINC compared to traditional grid computing technologies include: (1) research scientists can quickly develop and deploy BOINC servers to commodity computers using open source software, (2) compute nodes have less restrictions in terms of operating system and hardware, (3) project administrators can spend less time maintaining computer systems and more time analyzing results, and (4) the project can be expanded to be a volunteer or publicresource computing project, which further increases the potential scale of projects. Because of these advantages, BOINC has been adopted for numerous computing projects in science and engineering. One of the earliest desktop grid computing applications is the SETI@home project, which allows users to dedicate their idle CPU cycles for processing radio telescope signals [7]. In the bioinformatics domain, Folding@home and Genome@home were developed as volunteer grid computing projects that simulate protein translation and folding [8, 9]. The physics and astronomy domain has led the way in adopting distributed computing platforms for solving problems [10–12]. In fact, “citizen science” or volunteer grid computing platforms have been popular enough to warrant studies to improve project visibility and to improve the quality of volunteer-contributed work [13].

The machine learning research community has produced a number of software packages that may be used in conjunction with omniClassifier, or are similar to omniClassifier. For example, Scikit-learn [14], SHOGUN [15], and Weka [16] are established machine learning packages that contain a large number of classification methods. These packages could be adopted to augment the set of classification methods available in omniClassifier. ML-Flex [17] and PARAMO [18] are similar to omniClassifier in terms of their parallel computing ability. MLFlex contains robust cross validation methods, but requires a dedicated cluster with a shared file system for parallel computing. PARAMO uses a Map-Reduce framework implemented by Apache for parallelization. However, this again requires a dedicated cluster. In contrast, omniClassifier’s use of the BOINC framework for desktop grid computing potentially enables scalability across heterogeneous and commodity compute nodes without the need for a dedicated compute cluster. The remainder of this paper is structured as follows. We describe the nested cross validation and external validation procedure for prediction modeling in the methods section, followed by specific feature selection and classification methods currently available in omniClassifier. Subsequently, we describe implementation details of omniClassifier including the web server, database, and BOINC server and clients. Finally, we use microarray gene expression datasets to evaluate the prediction modeling performance and efficiency of omniClassifier.

2. METHODS

2.1 Prediction Modeling

Using the guidelines presented by Varma and Simon, we implement a prediction modeling procedure that ensures unbiased optimization of all components of the model, including features and classifier parameters [5]. The procedure includes two steps: (1) performance assessment with nested cross validation and (2) final model selection and validation (Figure 1).

Figure 1.

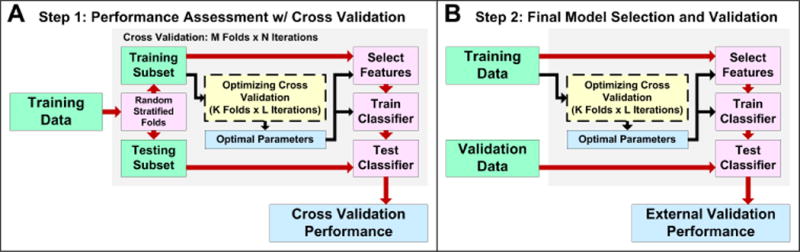
Prediction modeling procedure used for omniClassifier. (A) Using a training dataset, prediction performance is assessed using nested cross validation. (B) The final prediction model is optimized with the training data and evaluated with an independent dataset.

First, we use nested cross validation applied to only the training data to estimate prediction performance. Second, we apply cross validation to the training data to optimize a final prediction model and then validate this model using independent data. Our strategy assumes that the classification problem is binary, i.e., the goal is to classify data into two groups. Moreover, we use multiple iterations of k-fold cross validation. However, future implementations may be generalized to classify samples into three or more groups, and may use resampling methods such as bootstrapping or Monte Carlo cross validation [19, 20].

The first step of nested cross validation is random assignment of labeled samples into M stratified folds such that the prevalence of labels in each fold is approximately equal to that of the entire training data. M-1 folds are used as the ‘Training Subset’ and 1 fold is used as the ‘Testing Subset’. This is repeated M times such that each fold is used as a testing subset exactly once. The training subset is subject to an additional L iterations of K-fold cross validation, which is used to choose prediction model parameters (i.e., feature selection method, feature size, classifier, and classifier parameters). This is known as the ‘Optimizing Cross Validation’ procedure. The resulting prediction model parameters are then used to select features in the training subset, train the classifier, and test the classifier using the testing subset. A single iteration of nested cross validation produces M values of cross validation performance, which can be averaged into a single performance quantity. This entire process is then repeated for N iterations, resulting in N cross validation performance quantities.

Figure 1A summarizes cross validation performance assessment. After nested cross validation, it is important to choose a final prediction model and to validate this model using independent data. When choosing a final prediction model, the same ‘Optimizing Cross Validation’ procedure that was previously used in nested cross validation must be applied to the entire training data. Subsequently, the final model parameters should be used to select features and train the classifier. Then, samples from an independent validation dataset are used to quantify the external validation performance (Figure 1B). In summary, the ‘Optimizing Cross Validation’ procedure in Step 2 is an important component of prediction modeling in that it chooses the final model. Thus, the performance of this procedure is cross-validated in Step 1. Note that, due to sampling variance, the final parameters chosen in Step 2 may be different from the parameters chosen within the cross validation in Step 1. However, some variance is expected when choosing prediction modeling methods and this variance is generally smaller than the variance due to prediction endpoint [2].

2.2 Feature Selection and Classification Methods

omniClassifier currently supports seven feature selection methods and four classification methods. Supported feature selection methods include fold-change, T-test, two variations of minimum redundancy, maximum relevance (mRMR) [21], significance analysis of microarrays [22], rank-sum test, and rank products [23]. With the exception of mRMR, all feature selection methods rank features from most to least informative. mRMR searches for groups of features that maximize mutual information with the class labels while minimizing mutual information among features [21]. All feature selection methods can be optimized with a ‘size’ parameter, which controls the number of features selected. During prediction modeling, this parameter is generally varied to identify an optimal feature size. We implement all feature selection methods using C++ based on descriptions of the algorithms in their respective papers.

Classifiers supported by omniClassifier include Bayesian (or Gaussian model), k-nearest neighbors (KNN), logistic regression (LR), and support vector machine (SVM). The Bayesian classifier models the data with Gaussian distributions to estimate the class probability of future samples. Parameters of the Bayesian classifier control the covariance estimation method for multivariate Gaussian distributions. These parameters include pooled or un-pooled covariance and spherical, diagonal, or full covariance matrices [24]. The k parameter of the KNN classifier controls the number of training samples nearest the testing sample that are used to determine the class of the testing sample [25]. The logistic regression classifier contains no additional parameters. The SVM classifier can be optimized by choosing the kernel (e.g., linear or radial basis) and cost as well as the bandwidth, or gamma, of the radial basis kernel [26]. Table 1 summarizes all supported classifiers. We use the OpenCV library for the Bayesian and KNN classifiers [27]; the LIBSVM library for the SVM classifier [26]; and an open source package for the logistic regression classifier [28].

Table 1.

Supported Classifiers in omniClassifier

Classifier	Parameters	Possible Vallies
Bayesian	Covariance Pooling	0 = Not pooled, 1 = Pooled
	Covariance	0 = Spherical, 1 = Diagonal,
	Type	2 = Full Covariance
K-Nearest Neighbors	K	Integer ≥ 1
Logistic Regression	None	N/A
Support	Kernel	‘Linear’ or ‘Radial Basis’
Vector	Cost	Value >0
Machine	Gamma	Value > 0, “Radial Basis’ kernel only

2.3 System Implementation

The omniClassifier system consists of four components: the webinterface, the database, the BOINC server, and compute nodes (Figure 2). We describe implementation details and rationale for each component.

Figure 2.

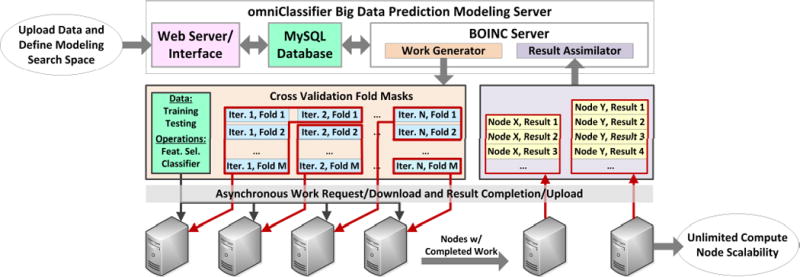
omniClassifier Prediction Modeling System. The system includes a web server with an interface for uploading data and submitting jobs, a MySQL database for storing datasets and prediction results, and the BOINC server. The BOINC server communicates with BOINC compute nodes to asynchronously distribute work units and collect results.

2.3.1 Web Interface

The web-interface enables researchers to queue prediction modeling jobs, to monitor submitted jobs, and to download results. The main page of the interface contains fields for job submission. Basic fields include data description, data files, prediction modeling parameters, and work distribution parameters (Figure 3). Users may fully customize the description of their prediction modeling job, allowing multiple users to submit jobs simultaneously to the system. Multiple testing datasets may be uploaded for each prediction modeling job. This is useful when multiple testing datasets cannot be combined due to batch effects. Since the majority of computation time is spent within the nested cross validation phase, inclusion of additional testing datasets does not substantially increase computation time.

Figure 3.

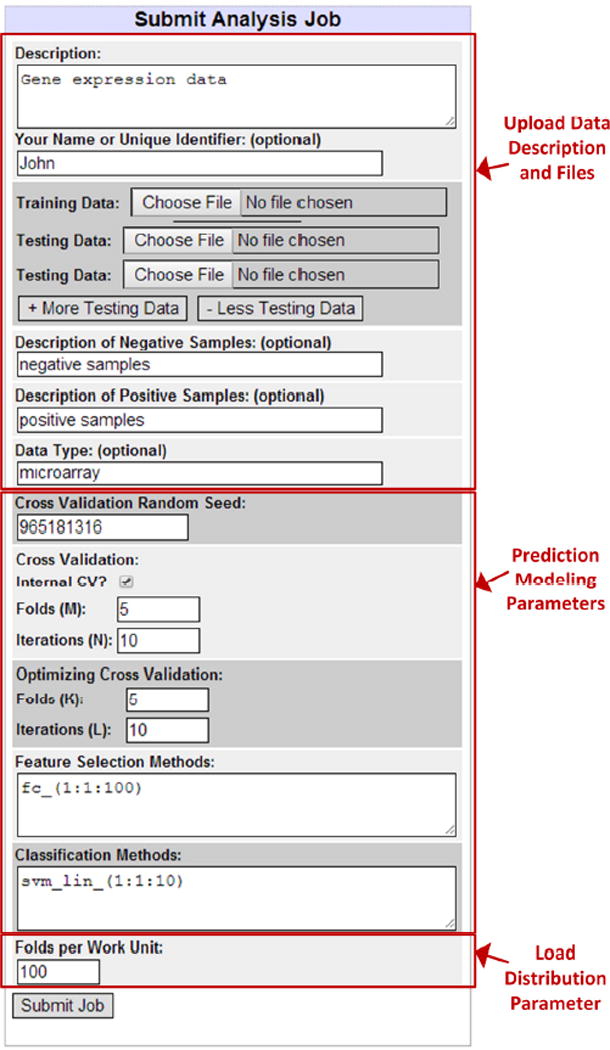
omniClassifier Web Interface for Job Submission. The interface allows users to upload datasets and select prediction modeling parameters.

After submitting prediction modeling jobs, users may monitor the status of their jobs on the omniClassifier result page (Figure 4). This page lists all submitted jobs and allows filtering and sorting. Jobs in progress are listed with an indicator for percentage complete. Each job is also listed with details of the data, feature selection and classification methods, and cross validation parameters. Once a job has completed, users can download results formatted as MATLAB data structures. These data structures are compatible with GNU Octave, an open-source alternative to MATLAB [29]. MATLAB/Octave code to parse the data structure will also be available from the omniClassifier web-interface. However, future versions may provide results in other formats.

Figure 4.

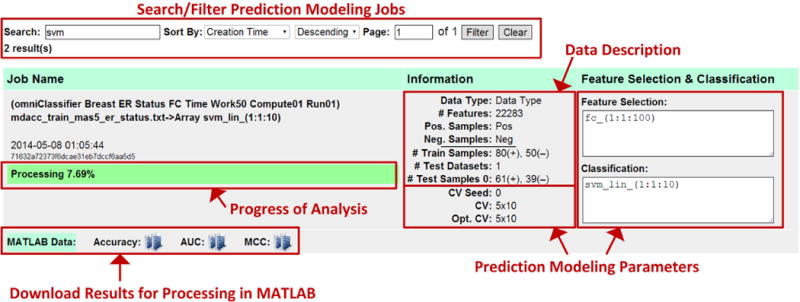
omniClassifier Web Interface for Result Monitoring, Browsing, and Download. This interface lists all submitted prediction modeling jobs and allows users to sort, filter, monitor progress, and download results.

2.3.2 Database

The omniClassifier database stores training and testing datasets, prediction modeling analysis parameters, and prediction results. It is implemented as a MySQL relational database with the following tables:

• Dataset: stores metadata for each training or testing dataset, including number of samples, number of features, and feature names.

• Sample: stores raw feature values for each sample of a dataset as well as the sample name and label.

• Analysis: stores meta information for each prediction modeling job, including data description, feature selection and classification methods, cross validation parameters, data distribution parameters, and job status.

In addition to these tables, the results of prediction modeling jobs are stored in four tables unique to each job:

• CV_Result: classification decision values for all MxN folds and iterations of the outer nested cross validation.

• Opt_CV_Result: classification decision values for all MxNxKxL folds and iterations of the inner nested cross validation (i.e., optimizing cross validation component of prediction modeling Step 1, Figure 1A).

• EV_Result: classification decision values for the final independent data validation.

• Opt_EV_Result: classification decision values for the KxL folds and iterations of the optimizing cross validation component of prediction modeling Step 2, Figure 1B.

Although we chose MySQL as the database for omniClassifier, any system for storing and retrieving structured data would suffice.

2.3.3 BOINC Server and Work Distribution

We use the Berkeley Open Interface for Network Computing (BOINC) middleware to manage the distribution of prediction modeling work units to compute nodes, and collection of results from each compute node. The BOINC server includes two processes: the ‘Work Generator’ and the ‘Result Assimilator’ (Figure 2).

The Work Generator periodically checks the database for new prediction modeling jobs and breaks these jobs into self-contained feature selection and classification work units. Jobs are divided by cross validation folds. For example, suppose that a prediction modeling job is submitted with 5×10 cross validation (i.e., 5 folds and 10 iterations), 3×5 optimizing cross validation, fold-change feature selection with feature sizes varying from 1 to 10, and KNN classification with K varying from 1 to 5. Each fold is a self-contained classification training and testing procedure. Thus, in this example, there are 5×10×3×5=750 procedures in the optimizing cross validation phase of Step 1, 5×10=50 procedures in the cross validation phase of Step 1, 3×5=15 procedures in the optimizing cross validation phase of Step 2, and 1 final procedure for the independent validation phase of Step 2. The total number of procedures is 750+50+15+1=816. In addition, each procedure tests all combinations of feature selection and classification. In this example, there are 10 feature sizes and 5 KNN parameters for a total of 10×5=50 combinations. Thus, each of the 816 procedures trains and tests a specific fold of data using 50 different combinations of feature selection and classification. The size of each work unit is controlled by the ‘Folds per Work Unit’ parameter during job submission (Figure 3). Work units are generated as text files, associated with data files, hosted on the BOINC server and downloadable by each compute node.

Compute nodes upload results of each work unit back to the BOINC server. As each result is uploaded, the Result Assimilator imports these results (i.e., classification decision values) into the omniClassifier database and updates the status and progress of the corresponding prediction modeling job. The updated status and progress is reflected in the omniClassifier result page (Figure 4).

2.3.4 Compute Nodes

Compute nodes can be attached to the BOINC server by installing the BOINC client. The BOINC client downloads work units and a platform specific executable for processing the work units. The omniClassifier prototype is attached to eight compute nodes with quad-core Intel Xeon E5405/E5504 CPUs (2.0 GHz) and at least 20 GB of RAM. Each compute node runs Red Hat Enterprise Linux Server with a minimum version of 6.4. Currently, only Linux compute nodes are supported. However, future omniClassifier BOINC clients may be compiled for Windows based compute nodes.

2.3.5 Result Data Structure

Once all work units have been completed for a prediction modeling job, results can be downloaded from the omniClassifier result page as a MATLAB data structure. The data structure contains metadata for the training and testing samples, prediction modeling parameters (i.e., feature selection methods and classifiers), and classifier decision values for all combinations of modeling parameters and all folds and iterations of nested cross validation. Using this data structure, we can identify optimal prediction modeling parameters. Currently, the system reports model performance using three metrics: accuracy, AUC (area under the receiver operating characteristic curve), and MCC (Matthew’s correlation coefficient). Any of these metrics can be used for model selection. We select a model with maximum average performance in the ‘Optimizing Cross Validation’ loop. In case of a tie between multiple models, we select the simplest model. The simplest models are defined as those with the smallest feature size, smallest cost and largest gamma for SVM models, and highest K for KNN models. Among Bayesian models, models with pooled covariance are simpler than un-pooled and models with spherical covariance are simpler than those with diagonal covariance. We have not assigned any preference to any particular classification method or feature selection method. Therefore, for each endpoint, it is possible to obtain multiple optimal models. Using these optimal model parameters, we report the average cross validation or external validation performance.

2.4 Case Study: System Evaluation using Microarray Gene Expression Data

2.4.1 Prediction Modeling Performance Evaluation

We use several microarray gene expression datasets to evaluate the prediction performance of omniClassifier (Table 2). Typical properties of gene expression data reflect one important characteristic of biomedical Big Data, i.e., dimension or feature size is much larger than sample size. We use datasets representing 14 clinical cancer endpoints, including treatment response, cancer detection, survival, and subtype diagnosis, among others. We include five breast cancer datasets focusing on estrogen receptor status [2, 30–32], with two of these datasets also investigating treatment response; three liver cancer datasets focusing on cancer detection [33–35]; two multiple myeloma datasets representing four different endpoints [2]; two neuroblastoma datasets representing four different endpoints [2]; four pancreatic cancer datasets focusing on cancer detection [36–39]; two prostate cancer datasets focusing on cancer detection [40, 41]; and four renal cancer datasets focusing on subtype classification [42–45].

Table 2.

Microarry Gene Expression Data Used for Evaluting omniClassifier

Cancer	Clinical Endpoint	# of Datasets	# of Features	# of Samples
Breast	Estrogen Receptor Status	5	22283	672
	Treatment Response	2	22283	230
Liver	Cancer Detection	3	22277	83
Multiple Myeloma (MM)	Overall Survival	2	54675	553
	Event-Free Survival	2	54675	553
	Gender*	2	54675	554
	Random**	2	54675	554
Neuroblastoma (NB)	Overall Survival	2	10707	420
	Event-Free Survival	2	10707	437
	Gender*	2	10707	482
	Random**	2	10707	504
Pancreas	Cancer Detection	4	22277	224
Prostate	Cancer Detection	2	12625	226
Renal	Subtype Diagnosis	4	8793	179

^*positive control,

^**negative control

Using omniClassifier, we analyze all combinations of training and validation datasets for each clinical endpoint. For example, we use each of the five breast cancer estrogen receptor status datasets in nested cross validation (i.e., Step 1 of prediction modeling) then validate each of the five resulting prediction models with the remaining four independent validation datasets. Thus, we obtain five cross validation performance estimates and 20 external validation performance estimates for the estrogen receptor status endpoint. We repeat this process for the datasets of each clinical endpoint. We use all seven feature selection methods, varying feature size from 1 to 100, and all four classification methods. We use four variants of the Bayesian classifier (pooled/unpooled and spherical/diagonal covariance estimation), vary the KNN K parameter from 1 to 10, and vary the linear SVM cost from 1 to 10. Thus, the size of the feature selection method and classifier search space is 700×(4+10+1+10)=17,500. Moreover, we use 10 iterations of 5-fold cross validation for both the outer cross validation as well as the optimizing cross validation.

2.4.2 Distributed Computing Performance Evaluation

We evaluate distributed computing performance using two breast cancer estrogen receptor status datasets, i.e., one as a training dataset and one as an independent validation dataset. Computation time and efficiency depend on factors such as number of compute nodes, data size, and prediction modeling methods. Thus, we use the following parameters:

• Four Classification Methods

  • ◦
    Bayesian (w/four variants)
  • ◦
    KNN (K=1…10)
  • ◦
    Logistic Regression
  • ◦
    Linear SVM (cost=1…10)
• Two Feature Selection Methods

  • ◦
    Fold-Change
  • ◦
    mRMR [21]

• Feature Sizes from 1 to 100

• Work Unit Sizes of 5 and 50

• Number of Compute Nodes from 1 to 4

For each combination of parameters, we measure the total computation time in minutes. We also use 10 iterations of 5-fold cross validation for both the outer cross validation and the optimizing cross validation.

3. RESULTS AND DISCUSSION

3.1 Prediction Modeling Performance

Prediction modeling results using several gene expression microarray datasets verify observations made in the MAQC-II study (Figure 5) [2]. In Figure 5, each colored cross represents a specific clinical endpoint with the vertical bar representing the range (i.e., standard error of the mean) of external validation performance and the horizontal bar representing cross validation performance. The optimal prediction model for each clinical endpoint is different (Table 3), reflecting the data-dependent nature of prediction modeling. Thus, it is important to consider a large number of methods when optimizing prediction models. Despite these differences, we observe that variance in prediction performance (measured using AUC) is dominated by the clinical endpoint, rather than by the feature selection or classification method, which is in agreement with results from the MAQC-II study. Moreover, cross validation performance (the X-axis of Figure 5) is able to predict external validation performance (the Y-axis of Figure 5) as indicated by the proximity of the data points to the diagonal line. We also observe that the negative controls and positive controls have the lowest and highest performances, respectively. This verifies that the system produces sensible results, i.e., samples in the negative control endpoints are randomly assigned to class labels and samples in the positive control endpoints correspond to easily predicted labels such as patient gender.

Figure 5.

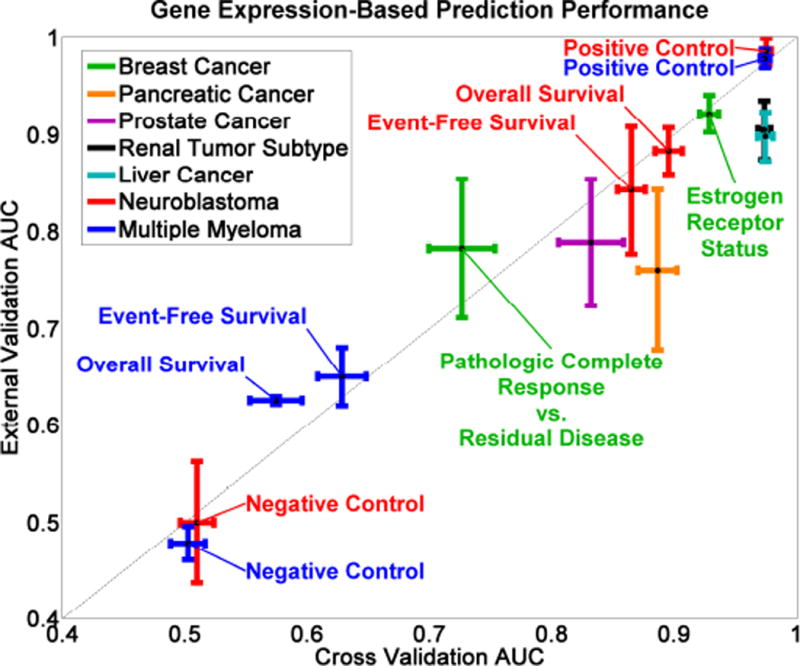
omniClassifier Prediction modeling results for 21 gene expression datasets, representing 14 clinical cancer endpoints. The X-axis represents cross validation AUC, and the Y-axis represents evaluation performance (AUC) of optimal prediction models using independent data.

Table 3.

Optimal feature selection and classification methods selected for each training dataset.^*

Clinical Endpoint	Train Dataset	Selection Method	Classification Method
Breast Cancer	1	Fold-Change	SVM
Estrogen	2	SAM	KNN
Receptor Status	3	mRMR	SVM
	4	Rank Prod.	LR
	5	Rank Sum	SVM
Breast Cancer	1	Rank Sum	SVM
Treat. Resp.	2	Fold-Change	Bayesian
Liver Cancer	1	Fold-Change	LR
Detection	2	SAM	SVM
	3	Fold-Change	SVM
MM Overall	1	Rank Prod.	SVM
Survival	2	Rank Sum	Bayesian
MM Event-	1	T-test	Bayesian
Free Surv.	2	SAM	Bayesian
MM Gender	1	Fold-Change	SVM
	2	T-test	LR
MM Random	1	SAM	LR
	2	Rank Prod.	SVM
NB Overall	1	Rank Prod.	SVM
Surv.	2	Rank Sum	SVM
NB Event-Free	1	mRMR	LR
Survival	2	T-test	SVM
NB Gender	1	T-test	KNN
	2	Fold-Change	SVM
NB Random	1	Fold-Change	SVM
	2	Rank Prod.	LR
Pancreatic	1	T-test	Bayesian
Cancer	2	Rank Prod.	SVM
Detection	3	SAM	SVM
	4	Fold-Change	SVM
Prostate Cancer	1	Fold-Change	Bayesian
Detection	2	Rank Sum	Bayesian
Renal Cancer	1	SAM	LR
Subtype	2	SAM	SVM
Diagnosis	3	Fold-Change	SVM
	4	Rank Prod.	LR

^*only one model is reported for each endpoint, however multiple models are possible in the event of ties

3.2 Distributed Computing Performance

Computing efficiency of omniClassifier is dependent on a number of factors, including feature selection method, classifier, work unit size, and number of compute nodes. Because there is computing overhead in the BOINC server due to generation of work units and gathering results from compute nodes, the number of compute nodes and work unit size should be carefully selected for each prediction modeling job.

Using fold-change feature selection and various classifiers to predict breast cancer estrogen receptor status, we observe that computing efficiency increases proportionally with the number of compute nodes (Figure 6). However, work unit size (i.e., number of folds in each work unit) also has a considerable effect on computing efficiency. Work unit sizes of 5 (Figure 6, X’s) can be up to three times slower than work unit sizes of 50 (Figure 6, squares). When work unit sizes are small, the total number of work units is larger. Thus, compute nodes must spend more time managing the download of work units and the upload of results, and less time on feature selection and classification. We also observe that the SVM classifier requires more compute time compared to the Bayesian, KNN, and logistic regression (LR) classifiers.

Figure 6.

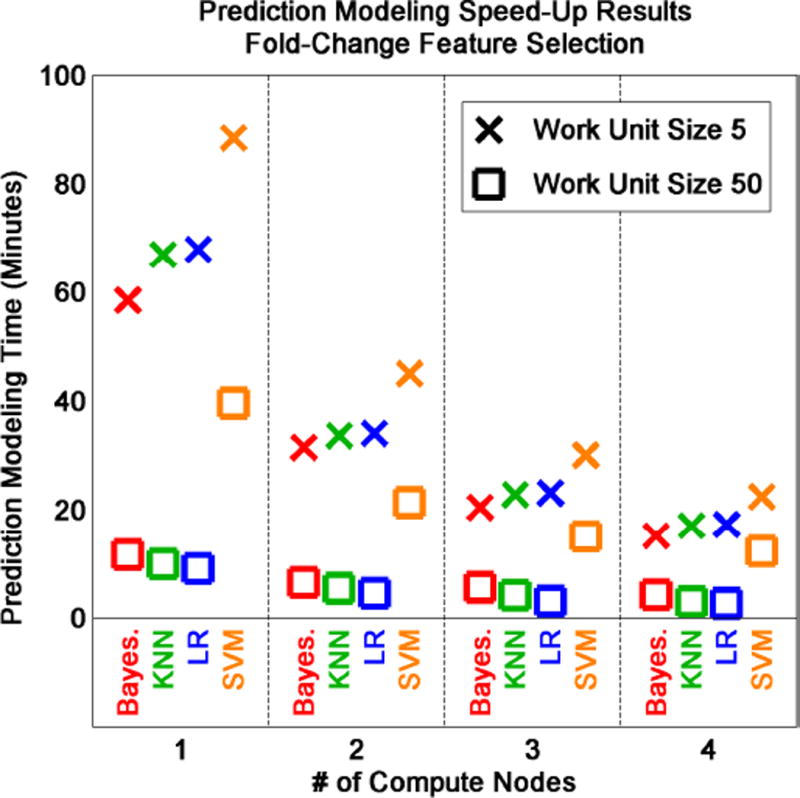
Evaluation of omniClassifier computing efficiency using two breast cancer datasets, fold-change feature selection, and four classifiers. Classifier, work unit size, and number of compute nodes affect prediction modeling time measured in minutes.

Using mRMR feature selection [21] changes the apparent effect of work unit size and classifier on computing efficiency (Figure 7). Computing efficiency still increases proportionally with the number of compute nodes. However, work unit size and classifier do not appear to affect computation time to the same degree. Overall, computation time increases for mRMR feature selection relative to fold-change feature selection. Thus, the computational complexity of mRMR dominates prediction modeling time relative to other factors. Work unit size should be optimized based on data size and computational cost of prediction modeling methods (i.e., classification and feature selection methods) to reduce computing overhead and to maximize efficiency.

Figure 7.

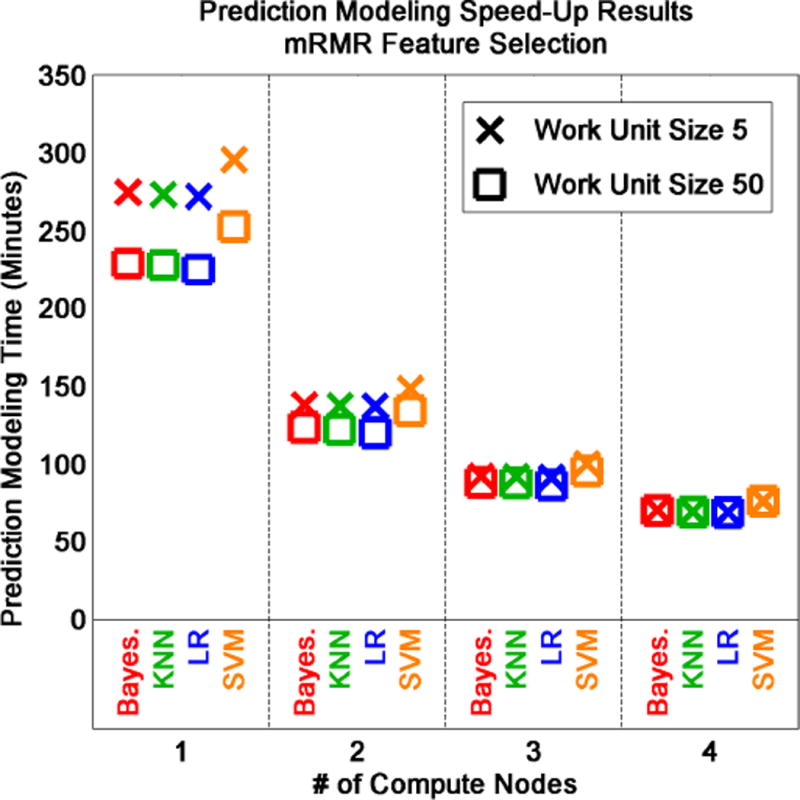
Evaluation of omniClassifier computing efficiency using two breast cancer datasets, mRMR feature selection, and four classifiers. Classifier, work unit size, and number of compute nodes affect prediction modeling time measured in minutes.

3.3 Limitations and Future Work

Future improvements to omniClassifier may include the ability for users to design and implement their own modules that can be plugged into the system. This would enable expansion of omniClassifier to include more classifiers and feature selection methods. In particular, inclusion of methods for ensemble classification [46] and multi-class classification (i.e., more than two classes) would greatly improve the utility of omniClassifier.

Although, the framework for omniClassifier has been targeted for classification, a generalized scientific computing framework would be feasible by enabling the integration of modules for tasks other than classification, e.g., image processing or genomic sequence alignment. Indeed, the BOINC framework has been used for a wide variety of scientific computing projects. However, implementation of such projects remains tedious. With a modular system for generalized desktop grid computing, parallel and high performance computing would become more tangible to the scientific community.

Finally, omniClassifier has primarily been tested within a controlled laboratory setup. We anticipate a number of technical challenges in a broader deployment of omniClassifier as a volunteer grid computing system. First, we will need to implement cross-platform versions (i.e., Linux, Microsoft Windows, and Apple OSX) of the omniClassifier BOINC client, and ensure that floating point computations are identical across CPU types. Second, the number of submitted computing jobs may increase dramatically, requiring improved disk, network, and database performance for the omniClassifier BOINC server. Third, users may want to deploy omniClassifier locally. Thus, we may release omniClassifier as an open-source package such that users can deploy it in a number of scenarios, including single-machine installations.

4. CONCLUSIONS

We developed omniClassifier, a Big Data prediction modeling application that uses desktop grid computing and enforces standardized practices for prediction modeling. We developed omniClassifier using BOINC, an open-source desktop grid computing middleware that can also be used as a volunteer or public-resource computing framework. Thus, BOINC enables scientists to utilize commodity desktop computers for unprecedented computing scalability. This scalability is important in the era of Big Data, in which individual datasets, especially those in the biomedical domain, have become too large to analyze within the computing and resource limits of small laboratories. omniClassifier also addresses the need for a standardized computing resource for prediction modeling. In the biomedical domain, analysis of large datasets (e.g., genomic, proteomic, imaging, and clinical) to predict clinical endpoints such as patient prognosis, optimal treatment regimen, and disease subtype, among others, has become a key area of research focus. But the lack of standardized resources for prediction modeling has led to issues with inconsistency and reproducibility of scientific results. We have demonstrated the utility of omniClassifier using 21 gene expression datasets that represent 14 different clinical cancer endpoints. We also demonstrated the computational scalability of omniClassifier by examining the efficiency under varying conditions such as work unit size and number of compute nodes. Although our case studies have used gene expression data, the system is scalable to any type of data in which samples can be represented as quantitative feature vectors. We plan to release omniClassifier as a public volunteer computing application. A prototype of the application can be accessed at http://omniclassifier.bme.gatech.edu/.