Dynamics of prebiotic RNA reproduction illuminated by chemical game theory

Significance

The origins of life required a means for information-containing molecules to compete with one another for survival and reproduction. Using an analysis based on game theory, we can predict the situations in which cooperation, selfishness, or a mixture of the two is beneficial to the future evolutionary success of RNAs.

Abstract

Many origins-of-life scenarios depict a situation in which there are common and potentially scarce resources needed by molecules that compete for survival and reproduction. The dynamics of RNA assembly in a complex mixture of sequences is a frequency-dependent process and mimics such scenarios. By synthesizing Azoarcus ribozyme genotypes that differ in their single-nucleotide interactions with other genotypes, we can create molecules that interact among each other to reproduce. Pairwise interplays between RNAs involve both cooperation and selfishness, quantifiable in a 2 × 2 payoff matrix. We show that a simple model of differential equations based on chemical kinetics accurately predicts the outcomes of these molecular competitions using simple rate inputs into these matrices. In some cases, we find that mixtures of different RNAs reproduce much better than each RNA type alone, reflecting a molecular form of reciprocal cooperation. We also demonstrate that three RNA genotypes can stably coexist in a rock–paper–scissors analog. Our experiments suggest a new type of evolutionary game dynamics, called prelife game dynamics or chemical game dynamics. These operate without template-directed replication, illustrating how small networks of RNAs could have developed and evolved in an RNA world.

A plausible description of a sequence of events that could have led to the origins of life on the Earth from a purely chemical milieu has long been desirable, yet remains elusive. The RNA world hypothesis has helped sharpen our focus on what could have taken place 4 Gya, in that RNA serves as a powerful model for a self-sustaining chemical system capable of evolutionary change (1–6). Although this hypothesis has engendered much debate, both in its general applicability and in the details of its implementation (7–9), there are some clear emerging trends. Among the recent advances in prebiotic RNA studies is the concept of an evolving “network” of RNAs being required to kick-start life, rather than a single selfish entity. This idea dates back to the formative studies of Eigen and Schuster in the 1970s (10, 11). However, it can be sharply seen in the 20+-y effort aimed at developing a generalized RNA replicase ribozyme in the laboratory: new successes have taken advantage of a fragmentation of the best such artificial ribozyme and invoke a network of reactions to provide for its assembly (12). Our own laboratories have focused on a variety of “prelife” (13, 14) and cooperative network (15, 16) approaches to understand how evolving RNA systems could have arisen from abiotic sources of nucleotides and short oligomers. Many others have also stressed the need for distributed functionality at the onset of life, both chemically (17) and in space and time (18, 19).

To advance a network approach to the “single biomolecule problem” in the RNA world, what is needed now is an understanding of how prebiotic networks could have evolved. Auspiciously, the mechanisms of network evolution are beginning to be unraveled (20–23). For example, Aguirre et al. (23) have recently provided a framework for studying how networks can actually compete with one another. To apply this type of thinking to prebiotic RNA networks, we first need to understand how pairs and small numbers of RNAs could influence the appearance and reproduction of others. In short, we need to understand the frequency-dependent dynamics of small clusters of RNAs before we can begin to decompose the mechanisms by which complex networks of RNAs could have evolved.

In this work, we provide an empirical demonstration of frequency-dependent dynamics that take place for small (one to three) numbers of catalytic RNA genotypes that interact while reproducing. Using the covalently self-assembling Azoarcus ribozyme system that we had previously elucidated (15, 16, 24), and in which a complex network ecology is possible (16), we quantify and model the growth rates of single genotypes as they compete with others for reproduction using RNA source fragments. We focus on interactions among pairs and in one triplet of RNAs to ask: which chemical behaviors engender the greatest numerical payoffs to various genotypes when mixed with others? We show that the dynamics of small networks can be studied in the laboratory, realizing the line of investigation first imagined by Eigen (10).

Moreover, we demonstrate that the resulting dynamics among RNA molecules can be interpreted, and in fact predicted, using concepts from evolutionary game theory. It has been noted before that both prebiotic evolution and the evolution of biological systems may follow similar equations (10, 11, 25). Using our empirical chemical system, we make this connection explicit. The game-theoretic framework provides an additional perspective on chemical kinetics. It allows us to summarize the dynamics between different genotypes in a single payoff matrix, whose values can easily be interpreted. Using only this matrix, we can calculate the final genotypic equilibria in two- or three-molecule interactions.

Results

The Chemical System.

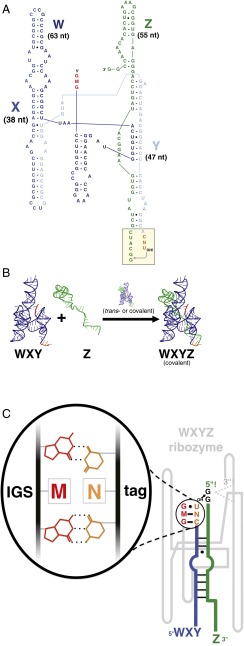
For a prebiotic system, we used the covalently self-assembling Azoarcus tRNA^Ile intron described previously (15, 24, 26). This ∼200-nt ribozyme (Fig. 1A) can be broken into two, three, or four pieces that can spontaneously reassemble into the covalently contiguous ribozyme when incubated in a warm (48 °C) MgCl₂ solution (24). The assembly process is initiated through a 3-nt base-pairing interaction between two RNA fragments, and, importantly, changing these nucleotide triplets can alter the specificity of which RNAs react with one another (26). For simplicity, we focused on the two-piece assembly reaction, which can be symbolized as WXY + Z → WXYZ, where W, X, Y, and Z represent roughly 50-nt sections of the Azoarcus ribozyme (Fig. 1 A and B). Various genotypes of WXY molecules can be created by altering one of the first (5′) three nucleotides in the W region, corresponding to the ribozyme’s internal guide sequence (IGS), and one of the last (3′) three nucleotides, corresponding to its “tag” that is recognized by a catalyst ribozyme to form a covalent bond with a Z fragment, creating a WXYZ molecule (Fig. 1C). We allowed fourfold variation in the middle nucleotide of both the IGS and the tag (M and N, respectively) to allow 16 possible molecular genotypes. For example, 1 of the 16 possible genotypes would be _GGGWXY_CAU, which can be abbreviated with just the middle nucleotides: GA in this case. These genotypes could be pitted against and among each other to form various small networks in which the shared resource Z molecule is required to create full-length, covalently contiguous WXYZ molecules.

Fig. 1.

Self-reproducing ribozyme system. (A) The Azoarcus ribozyme. The 148-nt WXY portion (blue) has an internal guide sequence (IGS) (GMG; red) on the 5′ end, and a 3-nt “tag” sequence (CNU; orange) on the 3′ end. The 55-nt Z portion is shown in green. Shaded box shows the trans-esterification reaction that occurs at the Y–Z junction. (B) The WXY + Z → WXYZ reaction. (C) The IGS-tag interaction determines assembly rates in the Azoarcus ribozyme broken into two pieces. The catalytically active ribozyme (gray) can be either a single covalently contiguous WXYZ molecule, or a noncovalent trans complex (24). Either catalyzes the formation of a covalent bond between WXY (blue) and Z (green) RNAs, guided by H bonding between the IGS (red) on the ribozyme and a tag (orange) on the WXY substrate.

Self-Assembly.

To dissect the dynamics of intragenotype and intergenotype interactions, we first compared the abilities of self-assembly among the 16 genotypes in isolation. We did this by measuring the autocatalytic rate constants (k_a) (cf. ref. 15) in WXY + Z → WXYZ reactions (SI Appendix, Fig. S1). As expected, when M and N are Watson–Crick pairs, much higher rates of self-assembly occur, but all possible pairings allow some degree of assembly (SI Appendix, Fig. S1). The autocatalytic rate constant is a measurement of the contribution of autocatalytic feedback to the overall self-assembly reaction (26). By doping various amounts of the fully formed autocatalyst WXYZ, we have previously measured values of k_a in similar Azoarcus ribozyme reactions (15), and here we used the same doping method (SI Appendix, Fig. S1) to measure it in these reactions. The efficiency of growth in self-reproducing systems (when autocatalysis is critical; e.g., prebiotic ones) is best reflected in the k_a parameter (27, 28), and thus we used this measure for all of our analyses below (SI Appendix).

Cross-Assembly.

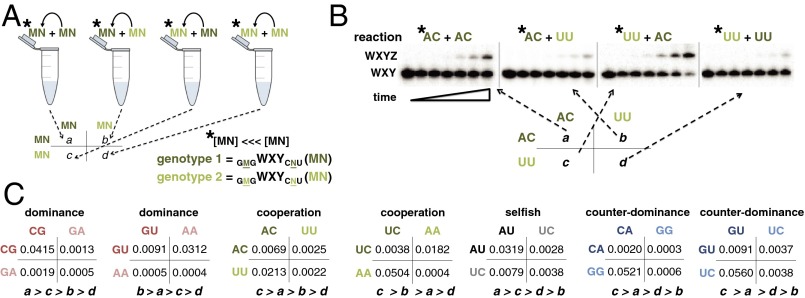
In an uncompartmentalized milieu, akin to a “warm little pond” scenario but extendable to other prebiotic scenarios, continuously interacting genotypes may be receiving assembly benefits from others as well as from like genotypes. Thus, our next step was to measure rates of cross-assembly. Cross-assembly has been studied in catalytic RNAs before, for example, in the case of two possible genotypes in a self-ligating ribozyme system (29). In our study, there are 120 possible pairwise interactions among dissimilar genotypes, and the reaction is by trans-esterification (i.e., recombination) rather than by ligation. We measured assembly rate constants when one genotype interacts with a different genotype in the same tube for 0–30 min. These rate constants are the dynamical variables in a setting when two genotypes compete for the shared resource Z. To do this, we tracked the amounts and proportions of each WXYZ genotype over time using differential ³²P labeling of the 5′ ends of the W-containing fragments (Fig. 2 A and B). By combining results from self- and cross-assemblies, we could now compile the four types of intramolecular and intermolecular events that could occur when two genotypes interact. These can be displayed in a 2 × 2 matrix that identifies the components of molecular “fitness” in a prebiotic competition. Although we did not measure all possible pairwise two-genotype interactions, we chose a few that would include competitions between both rapid and slow self-assembling RNAs. The data for seven representative matrices are given in Fig. 2C.

Fig. 2.

Single-round competitions between two WXY genotypes. (A) Differential ³²P-labeling method to separately obtain a, b, c, and d values (autocatalytic rate constants: k_a, in units of minutes^–1) in 2 × 2 matrices. The 5′-³²P•WXY RNA is a small (<<0.1%) dopant in 1 μM unlabeled WXY RNA plus 1 μM Z. Values a and d were obtained as in SI Appendix, Fig. S1, whereas b and c were obtained by doping genotype 1 into genotype 2. Asterisks (*) denote ³²P-labeled RNAs. (B) Example gel used for raw data. (C) Empirical matrices compiled from k_a values for seven selected competitions.

Serial Dilution Experiments.

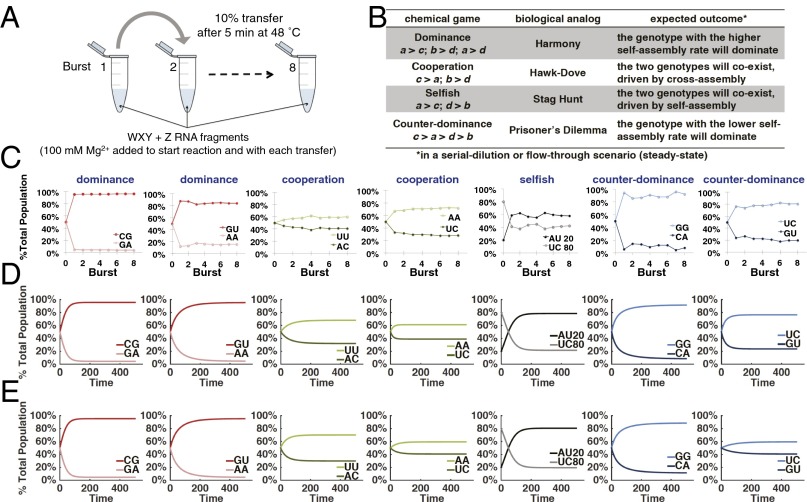
Having now both self- and cross-assembly rates for a single 30-min bout of competition for reproduction, we could compare their values and thus predict what would transpire when two genotypes of differing prelife fitnesses were allowed to compete iteratively over time in an evolutionary setting (30). We also hoped to be able to devise an analogous method with the potential to predict results from the myriad three-genotype interactions, and so on (see below). For the two-genotype experiments, we designed a serial-dilution technique in which a pair of WXY genotypes are mixed at some ratio, typically 1:1, provided Z, and then reacted for a brief period (5 min). At this time, when RNA production is still in exponential growth, we transferred a small fraction (10%) to a new reaction vessel in which new raw materials were present (Fig. 3A). In the receiving tube, we provided more unreacted WXY of each genotype, plus fresh Z and buffer. This technique was pioneered by Sol Spiegelman and coworkers (31) and has been used in many in vitro molecular evolution experiments with RNA (16, 32). We tracked the amounts and proportions of each WXYZ genotype over eight transfers using differential ³²P labeling. This allowed us to quantify the chemical equivalent of evolutionary success across generations (“bursts” of RNA assembly).

Fig. 3.

Serial-dilution experiments for two-genotype competitions. (A) Schematic of a serial-dilution experiment. (B) Classes of two-genotype (two-strategy) interactions in game theory. (C) Plots of relative frequencies of WXYZ genotypes as a function of time (bursts) in the serial-dilution format for the same seven competitions described in Fig. 2C. For the AU vs. UC competition, results from using skewed (AU:UC::20:80) genotype frequencies are shown; other ratios converge to the same qualitative result with AU > UC (SI Appendix, Fig. S2). (D) Predicted dynamics of the genotypes in these same competitions based on a simple ODE model in a flow reactor scenario using measured cross-assembly rates (Fig. 2C). (E) Modeling results using estimated cross-assembly rates in the 2 × 2 matrix (see text).

We pitted the seven pairs of WXY RNAs studied above against each other in two-genotype contests (Fig. 3B). Among these seven cases, we observed situations where one genotype clearly dominates, and cases in which coexistence of the two genotypes is attained after three to four bursts (Fig. 3C). In at least one case of the latter situation (AU vs. UC), we varied the genotype ratio across a broad range of values but always observed similar final steady-state frequencies reached by the two genotypes (SI Appendix, Fig. S2). Note that “extinction” is not possible in such serial dilution scenarios because fresh material is added each burst (31). However, the serial dilution format is prebiotically relevant in that it simulates a periodically replenished pool, as in wet–dry cycles.

Modeling Chemical Dynamics.

In parallel with the experimental results, we created ordinary differential equation (ODE) models of this system to visualize more clearly the dynamics of the genotypic assembly. We first developed a simple model in which the frequencies of two competing RNA types were tracked in a flow reactor setting that is a continuous analog of the serial dilution experiments. In this model, the frequency changes of the two strategies over time ($\dot{x}$ and $\dot{y}$) are described by the following:

$$\dot{x}=ax+by-\varphi x\hspace{0.17em};\hspace{0.17em}\dot{y}=cx+dy-\varphi y.$$ [1]

Here, a, b, c, and d are the rate constants of self-assembly (a and d) and cross-assembly (b and c), as visualized in a 2 × 2 matrix of possibilities when two genotypes interact (Fig. 2C). The death (or dilution) term, $\varphi =\left(a+c\right)x+\left(b+d\right)y$, guarantees that $\dot{x}+\dot{y}=0$ and x + y = 1. This parameterization is appropriate because the reaction rate is a linear function of RNA abundances, and because we maintained RNA assembly in its exponential growth phase across transfers (SI Appendix, Fig. S1). The unique equilibrium values, $\widehat{x}$ and $\widehat{y}$, for each competition are given by the following:

$$\widehat{x}=\frac{a-2b-d+\sqrt{{\left(a-d\right)}^2+4bc}}{2\left(a+c-b-d\right)},$$ [2]

and $\widehat{y}=1-\widehat{x}$ (SI Appendix). This model closely predicted the qualitative outcomes of the serial-dilution competitions (Fig. 3). With the a, b, c, and d values obtained empirically from Fig. 2 entered into the model, experimental data and model outcomes match in all cases, both qualitatively and quantitatively (compare Fig. 3 C and D). We could also predict the cross-assembly values from only the self-assembly values, and Fig. 3E shows that this technique still gives agreement between data and model. We explore this more in SI Appendix, Fig. S3, and in Discussion.

Game-Theoretic Treatment.

The ODE model based on chemical kinetics suggests a new type of evolutionary game theory. Game theory is a field that was first developed to study strategic and economic decisions among humans (33, 34). It later found its way into biology in the form of evolutionary game theory (35, 36). There, fitness depends on the frequency of different strategies (or phenotypes) in the population. The classical equation of evolutionary game theory is the so-called replicator equation (e.g., ref. 29): ${\dot{x}}_i=x_i\left[f_i\left(\overrightarrow{x}\right)-\varphi \left(\overrightarrow{x}\right)\right]$, where x_i is the frequency of genotype i, $f_i\left(\overrightarrow{x}\right)$ is the fitness of this genotype, and $\varphi \left(\overrightarrow{x}\right)$ is the average fitness of all genotypes. This describes a frequency-dependent replication rate. In contrast, in our system, there is no replication but rather frequency-dependent assembly.

To extend a game-theoretic treatment to an abiotic situation, we realized a parallel between the 2 × 2 matrix that exists to describe components of fitness (Fig. 2A) and a game-theoretic payoff matrix. In the latter, each matrix entry is the payoff to the row genotype when interacting with the column genotype. Importantly, the evolving entities need not be rational agents for a game-theoretic analysis to have explanatory power (30), and thus could be applied to a molecular system. In fact, there have been at least two recent predictions that game theory could be useful in the interpretation of biochemical behavior (37, 38), and the Azoarcus system in particular was singled out as a good candidate (37). Game theory has been proposed to be manifest at the chemical level (39–41), but this has never been shown empirically. We thus sought a practical demonstration that this could be the case, reasoning that game theory could augment our ODE analysis by offering a simple fitness-based explanation of how selection could choose, say, molecular cooperation.

Because there are four values in a 2 × 2 payoff matrix (Fig. 2), and, with the assumption that at the chemical level no two of these could be exactly the same, there are 24 possible strict ordinal rankings of these values (e.g., a > b > c > d) (30). Additionally, we can assume that a > d without loss of generality (otherwise, one only needs to relabel the genotypes), lowering the number of possible outcomes that could result from an iterative two-genotype interaction to 12. Based on groups of payoff matrix inequalities, we divided these outcomes into four categories (Fig. 3B) that will have evolutionary significance based on analogies with biological systems (30, 42), and we assigned names to various scenarios of experimental outcomes that we observed (Figs. 2 and 3). In the “Dominance” scenario, given by a > c and b > d, one genotype is expected eventually to dominate in frequency, in this case the genotype with the higher self-assembly rate (k_a). In the “Cooperation” scenario, c > a and b > d, such that cross-assembly will always exceed self-assembly, and hence the population will adopt a mixture of the two genotypes. In the “Selfish” scenario, a > c and d > b, such that self-assembly will always exceed cross-assembly, meaning that a coexistence mixture will also result, but for the opposite mechanism than in the Cooperation scenario. Finally, in the “Counter-dominance” scenario, c > a > d > b, the genotype with the lower self-assembly rate is, counterintuitively, expected to dominate in frequency. These four outcomes have rough parallels in the biological games (Fig. 3B). For example, a game with the payoffs of the Counter-dominance scenario can be interpreted as a prisoner’s dilemma (PD). In evolutionary biology, the PD is often taken as the baseline model for situations in which a group-beneficial trait—expressed by the a > d inequality—is selected against at the individual level because a < c and d > b. Similarly, the payoff configuration of the Selfish scenario corresponds to the so-called stag hunt game, in which a trait is only successful if it is common (as for example, when members of a group need to decide whether to join a stag hunt). Similar biological interpretations can be given for the other two classes (Fig. 3B) (30, 35, 36).

Among our two-genotype RNA competitions, we observed examples of all four of the categories described above (Figs. 2C and 3C). When CG is pitted against GA for example, CG dominates because it can assemble itself far better than can GA (SI Appendix, Fig. S1). The interactions between these two molecules are weak: the middle nucleotide of the IGS of one genotype does not pair well with the middle nucleotide of the other genotype’s tag. Self-assembly is the major determinant in this competition, leading to a Dominance outcome, because a >> c and b >> d. However, when we pitted CA against GG, the latter (GG) dominates despite its more than threefold worse self-assembly rate constant. This matchup is thus an example of the Counter-dominance scenario, in which a nonintuitive result emerges: in isolation, CA self-assembles far more robustly than GG (SI Appendix, Fig. S1), but when in competition with GG, this CA genotype is greatly outperformed for assembly. In this case, the interaction of CA with GG is very strong. The middle nucleotide of the IGS in CA forms a Watson–Crick interaction with the middle nucleotide of the tag of GG. Thus, the distinction between the “cooperator” (CA) and the parasitic genotype, or “defector” (GG), becomes clear, as in a classical PD. The PD has been biologically demonstrated in viruses (43) and yeast (44, 45). However, to our knowledge, our data are the first example of it manifesting at the pure molecular level, in which a genotype with a lower self-assembly rate can become predominant. Similar phenomena may explain the evolution of other biochemical functions such as single-turnover (“suicide”) enzymes, e.g., methyltransferases used in DNA repair.

We also observed examples of the other two categories of two-genotype competitions, those that lead to coexistence (Fig. 3C). When we pitted AC against UU, both genotypes persisted at high frequency (>40%) stably over time in a Cooperation outcome. Here, both self-assembly rates are expected to be moderate, along with one of the cross-assembly rates (UU → AC), whereas the other cross-assembly rate is strong (AC → UU). This leads to a situation where cross-assembly is generally more effective than self-assembly, with the consequence that each genotype predominantly assembles the other: a chemical analog to simultaneous reciprocal altruism. The result is that both genotypes are assembled to substantial frequencies. When we pitted AU against UC, genotypes with the same aggregate nucleotides as the AC vs. UU competition, again coexistence of both genotypes eventually resulted (Fig. 3C). However, the route to this result differed from that in the Cooperation scenario. In AU vs. UC, self-assembly is generally more effective than cross-assembly, such that the major dynamical determinant is each genotype doing the same, selfish, action of self-assembly. Thus, this contest is an example of a Selfish outcome. However, unlike the biological stag hunt game, where one expects bistability depending on starting ratios, different initial frequencies of the two chemical genotypes led to the same general outcome (SI Appendix, Fig. S2), highlighting a distinction between the biological replicator dynamics (35), and the chemical dynamics of our system. In a biological setting, a stag hunt scenario leads to the extinction of one the two strategies depending on the initial frequencies. However, in our chemical setting, we would expect a mixed population to result because the continual replenishment of genotypes in the serial dilution protocol prevents extinction, and we observed similar final frequencies when we varied genotype ratios in a Selfish scenario (SI Appendix, Fig. S2). Using only self-assembly data to estimate all four values in the payoff matrix (SI Appendix, Fig. S3), our ODE model could forecast what would result for many possible two-genotype contests (SI Appendix, Fig. S4). Generally, in a two-genotype contest, both genotypes will reach similar frequencies if a + b and c + d are approximately equal. This is less likely to happen in, for example, a Dominance scenario than in a Selfish one.

Rock–Paper–Scissors Competition.

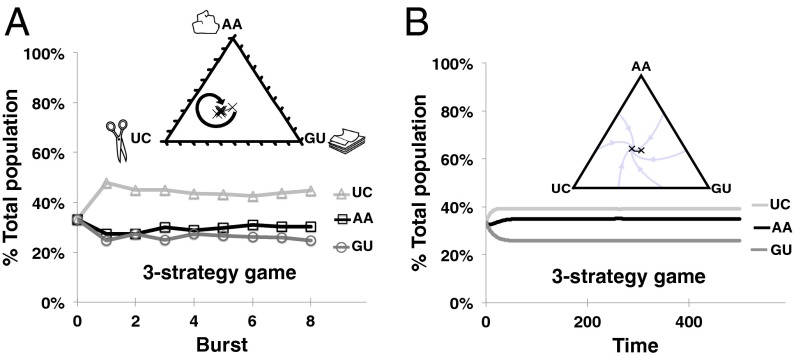
We were also able to manifest with RNA a well-known scenario with three genotypes (or “strategies”; Discussion), namely rock–paper–scissors (RPS) (Fig. 4). Inspired by the children’s game of the same name, RPS describes scenarios with a cyclical arrangement of dominance relationships; these have previously been identified in nature (46, 47). A well-known example involves the bacterium Escherichia coli, for which there is an evolutionary sequence from the wild type, to mutants that produce toxin together with an immunity protein, to mutants that only produce the immunity protein, and back to the wild type again (47). We were interested to see whether a similar scenario could also occur among molecular genotypes. RPS is one of ∼50 qualitatively different three-strategy game outcomes (48). It is a contest in which three genotypes will all attain substantial frequencies jointly despite the fact that the equilibrium frequency of any one would be far lower than another without the presence of the third. Based on our expectations from the results of other two-genotype contests, we chose three WXY genotypes—AA, UC, and GU—that we anticipated could generate an RPS game. In isolation, we would predict that AA beats UC, UC beats GU, and GU beats AA. When we pitted these genotypes against each other two-at-a-time in a serial-dilution format, we indeed saw that one genotype reaches at least 70% superiority in each game (Fig. 3C). However, when we pitted all three against each other in the same reaction vessel in a serial-dilution format, their joint frequencies quickly attained values near 30–40% and remained there (Fig. 4A). Notably the steady-state frequencies of each genotype in the RPS scenario were distinctly higher than their “losing” values in two-genotype games (Fig. 3C vs. Fig. 4A), and they appeared to converge on an internal point in a simplex plot. Again, using the simple ODE model described above, we were able to predict correctly these outcomes. To do this, we created a 3 × 3 payoff matrix (SI Appendix, Fig. S6) derived from the results of the three two-genotype payoff matrices (Fig. 2C). From this matrix, we calculated that there should be a stable internal equilibrium point (cf. ref. 36) consisting of 39% UC, 35% AA, and 26% GU, that agreed qualitatively with the empirical data in the three-strategy serial-dilution experiment (Fig. 4B).

Fig. 4.

A RPS competition among three WXY genotypes. (A) Empirical data from a serial-dilution experiment. The experiment was performed in the same fashion as in Fig. 3, except here three genotypes (AA, UC, and GU) were separately tracked. Each pair of two-genotype competitions is expected to give a clear winner (Fig. 3C); but here coexistence results. (B) Predictions from the ODE model. The simplex plots show (× symbols) the joint frequencies starting from the center and approaching a stable internal equilibrium point.

Discussion

We have characterized the dynamics that occur when two, and in one case three, RNA genotypes compete for reproduction using a common resource. By representing possible interactions in a 2 × 2 matrix, it is possible to predict rather accurately, based solely on a few lower-level data points, what would happen in various competition scenarios. This holds up qualitatively to the three-genotype interaction level and may extend beyond that. Likely, the complexity of the system and unpredictable interactions such as nonproductive binding events (16) will begin to play more important roles in larger networks. Prior efforts have focused on either simulation models of similar RNA network dynamics (e.g., refs. 11, 13, 37, and 49–51), or on broad-scale experimental data (e.g., refs. 12, 16, 29, 52, and 53). Here, we demonstrate that experiment and modeling can agree. Future work is now possible to understand how small networks can evolve into larger ones, and to extend these methods to other, simpler RNA systems.

This matrix approach has predictive power. To highlight this fact, we obtained 16 pieces of empirical data, which correspond to the diagonal values in the 2 × 2 matrix, i.e., the rate enhancement an RNA gets when interacting with its own genotype: a or d. For forecasting purposes, we can use these rate constants to estimate the off-diagonal terms in the matrix: b and c. Specifically, we used the corresponding nucleotide–nucleotide pairs from self-assembly to predict what would happen in cross-assembly (SI Appendix, Fig. S3). Then we input these four values into the ODE model to compare its outputs with the results from the serial dilution experiments. In Fig. 3E, the modeled dynamics are shown given the estimated values of b and c using this strategy (SI Appendix, Fig. S3). The outcomes using either measured or estimated b and c values both emulate the experimental results (Fig. 3C) almost perfectly. Such strong agreement of model and data underscores the utility of the 2 × 2 matrix approach to forecast complex dynamics from lower-dimensional data—the four values a, b, c, and d—and portend the ability to extend this type of analysis to three (or even more) interacting members of a prebiotic RNA network, as in the RPS scenario (Fig. 4). Thus, we demonstrate that self-assembly data alone can allow estimates of steady-state genotype frequencies; measurements of cross-assembly rates help refine these estimates but are not necessary for a qualitative prediction of dynamics. The static game theory tables organize the parameters that determine the dynamics into diagonal and off-diagonal terms that have clear meanings (autocatalytic and cross-catalytic).

Our experimental system is particularly amenable to a game-theoretic interpretation. The assembly rates of WXYZ molecules can be considered “payoffs” because WXYZs are covalently contiguous RNAs that would represent successful genotypes in an evolutionary contest, their rates of production being dependent on the current environment of other WXYZ molecules. New WXYZ molecules being produced are analogous to progeny in a biological setting. “Strategies” in a contest at the chemical level—molecular reproduction strategies—would be the phenotypes displayed by the genotypes: in our case, their abilities to catalyze the assembly of WXYZ RNAs. When provided with the Z molecule resource, these genotypes can assemble into WXYZ molecules, which then can catalyze even faster production of themselves because the covalently contiguous WXYZ has a roughly twofold higher catalytic activity than a noncovalent (trans) complex WXY-Z (16). Such phenotypes would be a combination of self-assembly, where a WXY drives the assembly of a WXYZ molecule of like genotype, and cross-assembly of other genotypes. In a molecular system, the genotype directly determines the phenotype, and hence the strategy, whose payoff is its fitness.

Our analyses lead to some subtle but important distinctions between what we describe here and classical evolutionary game theory (35, 36). Biological systems reproduce via template-directed polymerization, characterized by the replicator equation. In our chemical system, there is no replication per se. It is more de novo synthesis (reproduction rather than replication) that could be described as prelife (13, 14) in which the replicator equation does not apply. Here, Eq. 1 applies instead. The Azoarcus ribozyme system reproduces through a recombination of fragments rather than a polymerization of nucleotides (24). Specifically, the information that differentiates “self” from “nonself” is embodied in the thermodynamics of only a single nucleotide pair (Fig. 1C). Thus, there are only a few chemical moieties on the base-pairing surface of these nucleotides that influence the alternative strategies in a game-theoretic sense, rather than a large continuum of genotypes that would be available in a true biological system. However, a key facet of the dynamics of frequency changes of molecular genotypes is autocatalytic feedback, meaning that the strategies—such as intergenotype cooperation (54)—used by molecules in creating more molecules are optimized by kinetic selective forces (55). Explicit differences in kinetics lead to cases (e.g., the Selfish scenario) where chemical and biological game theory lead to qualitatively distinct outcomes. This can also be seen in the RPS scenario, where, although the results predicted from the replicator equation and from our chemical dynamics lead to qualitatively similar results (a stable interior equilibrium point), a small deviation in the quantitative results can be detected (SI Appendix, Fig. S7). Such variance reveals that, in prelife game dynamics, the specific outcomes of intergenotypic competitions can be predicted in a fashion parallel to, but not identical to, those used to calculate Nash equilibria (34) in classical games (SI Appendix). Thus, a game-theoretic approach gives us an appreciation of the chemical ecology of how reproduction (production from the environment) could evolve before biological replication. Knowing the mechanics behind the interactions among two and three genotypes, it should now be possible to predict how larger RNA networks could have evolved.

Materials and Methods

RNA Self-Assembly.

Reactions, containing WXY (1 μM), Z (1 μM), WXYZ (0–2 μM), and/or ³²P-labeled WXY (≤0.003 μM), were initiated with the addition of buffer (100 mM MgCl₂ and 30 mM EPPS, pH 7.5). Time point samples were drawn and immediately quenched at 0.5–30 min, and the WXY and WXYZ RNAs were separated by 8% (mass/vol) polyacrylamide/8 M urea gel electrophoresis. For serial-transfer experiments, after 5 min, 10% of each reaction was transferred to a new tube with fresh reagents, over eight transfers.

Autocatalytic Rate Constants.

Initial rates were calculated from slopes of the linear portion of plots of the product ratio versus time; for fast reactions this was ≤5 min and for slower reactions ≤10 min. The rate constant (k_a) was calculated from the slope of the initial WXYZ concentration versus the initial rate of the reaction (SI Appendix, Fig. S1) (15). For cross-assembly reactions, the WXY (1 μM) and WXYZ (0–2 μM) were of one genotype and ³²P-labeled WXY (≤0.003 μM) was a second. Values are averages of three separate trials. Each rank order of a, b, c, and d values was significant (P < 0.05; SI Appendix, Fig. S8).

Mathematical Modeling.

A dynamical ODE model was constructed assuming a flow-reactor scenario in which the frequency changes of two competing strategies were described by Eq. 1 above. This was extended to a competition among three or more strategies in a similar fashion (SI Appendix).