Modelling the coordination of the controls of stomatal aperture, transpiration, leaf growth, and abscisic acid: update and extension of the Tardieu–Davies model

Highlight

This paper reviews the control of water movement through the plant, stomatal aperture, and growth, and translates them into equations in a model. It includes recent progress in understanding intrinsic and environmental controls of tissue hydraulic conductance.

Abstract

Stomatal aperture, transpiration, leaf growth, hydraulic conductance, and concentration of abscisic acid in the xylem sap ([ABA] _xyl) vary rapidly with time of day. They follow deterministic relations with environmental conditions and interact in such a way that a change in any one of them affects all the others. Hence, approaches based on measurements of one variable at a given time or on paired correlations are prone to a confusion of effects, in particular for studying their genetic variability. A dynamic model allows the simulation of environmental effects on the variables, and of multiple feedbacks between them at varying time resolutions. This paper reviews the control of water movement through the plant, stomatal aperture and growth, and translates them into equations in a model. It includes recent progress in understanding the intrinsic and environmental controls of tissue hydraulic conductance as a function of transpiration rate, circadian rhythms, and [ABA] _xyl. Measured leaf water potential is considered as the water potential of a capacitance representing mature tissues, which reacts more slowly to environmental cues than xylem water potential and expansive growth. Combined with equations for water and ABA fluxes, it results in a dynamic model able to simulate variables with genotype-specific parameters. It allows adaptive roles for hydraulic processes to be proposed, in particular the circadian oscillation of root hydraulic conductance. The script of the model, in the R language, is included together with appropriate documentation and examples.

Introduction

The genetic controls of several physiological traits often involve common regions on the genome [quantitative trait loci (QTLs)] with consistent allelic effects (Tisne et al., 2010; Dignat et al., 2013; Peiffer et al., 2014). This is often interpreted as the effect of hubs that control and coordinate several traits jointly via common effectors (e.g. transcription factors, micro RNA, or hormones), thereby mimicking the central control of development and metabolism observed in animals (Baena-Gonzalez et al., 2007; Kellermeier et al., 2013). We have argued that this is not the only possibility for coordination in plants (Tardieu et al., 2011). Many traits are inter-related via deterministic relations based on physical laws, such as the relationship between stomatal conductance and photosynthesis based on gas diffusion at timescales of minutes to hours, or between biomass accumulation rate and leaf area based on intercepted light at timescales of days to weeks.

The most straightforward example of co-location of QTLs of traits associated with deterministic relations is flowering time, which shares QTLs with a large number of traits including growth, transpiration, and allometric relations (Vasseur et al., 2012; Peiffer et al., 2014). This commonality of QTLs does not necessarily indicate that the traits share part of their genetic control with flowering time. It can occur because the developmental programme of several organs is affected by flowering induction, so QTLs related to final organ size or cell number co-localize with those of flowering time (Tisne et al., 2010; Lievre et al., 2013). It can also occur because earlier flowering time often implies lower water or heat stresses during ovary fertilization and early growth, resulting in common QTLs of flowering time with final organ size/number or with the expression of stress-induced genes (Marchand et al., 2014). Finally, it can occur because of the intrinsic relationship between the duration of plant lifecycle and biomass accumulation. These intrinsic relations generate genetic correlations with opposite effects depending on environmental conditions and timescales (Munns et al., 2000; Tardieu, 2012; Tardieu et al., 2014), so they can be lost or seem erratic in phenotypic analyses.

Expansive growth (increase in plant volume) and growth in biomass have common trends over weeks to months but opposite trends over hours to days (Tardieu et al., 2014). Expansive growth is related to the opposite of stomatal conductance and of transpiration rate during the day, with higher values during the night than during the afternoon, during cloudy days compared to sunny days, and in genotypes with lowest stomatal conductance (Caldeira et al., 2014a). Conversely, growth in biomass is positively linked to stomatal conductance via photosynthetic rate and therefore reaches maximum values in the afternoon during sunny days and in genotypes with the highest stomatal conductance (Tardieu et al., 2014). Hence, growth rates whether expressed in terms of area or biomass react differently to environmental conditions, but interact over weeks via feedbacks linked to processes such as sugar sensing or source-sink relations (Minchin et al., 1993). The superposition of negative and positive effects of stomatal conductance on growth obscures phenotypic relationships in such a way that QTLs of expansive growth, organ size, and photosynthesis may or may not co-localize in the genome depending on climatic scenarios (Welcker et al., 2011). Genetic correlations between traits therefore depend on the timescale considered, with a better chance, a priori, that correlations established on a short timescale and in well defined conditions represent common genetic controls; those on longer timescales and/or established on complex data sets represent emerging properties combining different and often opposite processes (Tardieu et al., 2014).

A dynamic model potentially allows one to cross scales and to represent the consequences of deterministic relations, valid on short timescales, on the overall relations between traits on a longer timescale in a given climatic scenario (Hammer et al., 2006). This possibility has been explored for crop models with daily timesteps and simplified physiological hypotheses (Hammer et al. 2006, Martre et al. 2014). It is worth exploring it for models that simulate the explicit effects of one physiological trait on other traits with short timesteps, in order to analyse the part of genetic correlation linked to deterministic relations or to common genetic controls. This paper reviews the experimental and theoretical bases for a model that coordinates transpiration rate, stomatal conductance, abscisic acid (ABA) biosynthesis, the distribution of water potentials in the plant, and leaf expansion rate. In this regard, in tribute to Bill Davies, the paper follows that of Tardieu and Davies (1993), updating and extending it to more complex cases and the simulation of expansive growth. Although this model has been widely used since 1993 (Dewar, 2002; Gutschick and Simonneau, 2002; Ahmadi et al., 2009), many users found difficulties in running it because we did not publish the code. A function written in R, its documentation, and step-by-step examples are included with this paper as supplementary information.

The Tardieu–Davies model of stomatal conductance, transpiration, and circulation of water and ABA in the plant

Several sources of evidence suggest the participation of long-distance signals between root and shoot in stomatal control. The first comes from split-root experiments, in which the dehydration of part of the root system causes stomatal closure, although leaves are maintained at a high water potential (Davies and Zhang, 1991). Feeding well watered leaves with the sap of droughted plants also has a clear effect on stomatal closure (Zhang and Davies, 1991). Reciprocal grafting provides contrasting evidence, with a clear contribution of rootstock to stomatal control in Nicotiana plumbaginifolia (Borel et al., 2001a, b), a more complex pattern in some studies on tomato (Dodd et al., 2009), and no contribution in Arabidopsis thaliana (Christmann et al., 2007) or in other experiments on tomato (Holbrook et al., 2002). It has been proposed that both ABA in the xylem sap and leaf water status participate in stomatal control at a whole-plant level, with a different balance between these effects in different species (Tardieu and Davies, 1993; Tardieu and Simonneau, 1998). This hypothesis is implemented in the model, with stomatal conductance affected by ABA with a sensitivity (β) that depends on the leaf water potential at evaporative sites (Ψ _bundle) with a sensitivity δ [in A. thaliana, β increases with leaf age and is very low in the youngest leaves until they are subjected to episodes with high evaporative demand (Pantin et al., 2013b)]:

$$g_{\text{s}}=g_{\text{smin}}+\alpha \text{\hspace{1em}exp}\left[\beta {\mathrm{[\hspace{0.17em}}ABA]\hspace{0.17em}}_{\text{xyl}}\text{exp}\left(\delta {\psi }_{\text{bundle}}\right)\right]$$ (1)

where g _s (mol m^–2 s^–1) is the calculated stomatal conductance and [ABA] _xyl (µmol m^–3) is the concentration of ABA in the xylem sap. Ψ _bundle (MPa) is the water potential in bundle sheaths, considered as the evaporating sites in leaves. It differs from measured leaf water potential for reasons presented below. The variable g _smin is the minimum stomatal conductance resulting from cuticular conductance and from the conductance through closed stomata. α is a scale factor. The dependency of β on the hydraulic history of the leaf (Pantin et al., 2013b) has not yet been implemented in the model.

Eqn 1 overlooks the contributions to stomatal control of other compounds in the xylem sap, in particular sap pH (Wilkinson et al., 1998), ethylene (Sobeih et al., 2004), and other phytohormones (Wilkinson and Davies, 2002). Hence it considerably simplifies, for modelling purposes, the view that the balance of different compounds in the xylem sap is a platform that controls stomatal conductance (Wilkinson and Davies, 2002). It is noteworthy that the contribution of Ψ _bundle to stomatal control may account for the effects of chemical compounds that are not explicitly present in Eqn 1 but are correlated to Ψ _bundle. Eqn 1 results in a family of response curves of stomatal conductance to [ABA] _xyl that are increasingly sensitive with increasing values of β. The parameter δ depends on species and genotype: a zero value implies that Ψ _bundle does not participate in stomatal control, as in the case of sunflower, while the contribution of Ψ _bundle to stomatal control increases with δ in maize and poplar. We have proposed that this contribution drives iso- and anisohydric behaviours (Tardieu and Simonneau, 1998), but other hypotheses have also been proposed (see below).

The transpiration flux J _out (mm³ s^–1 plant^–1) is calculated with the Penman Monteith equation, taking into account plant leaf area in order to express transpiration per plant:

$$J_{\text{out}}=S\times \left(\text{s}{R}_{\text{n}}+\rho {\text{\hspace{1em}C}}_{\text{p}}{g}_{\text{a}}VPD\right)/\left(\lambda \times \left(\text{s}+\gamma \times \left(\text{1\hspace{1em}}+g_{\text{a}}/g_{\text{s}}\right)\right)\right)$$ (2)

where R _n (W m^–2) and VPD (Pa) are net radiation and air vapour pressure deficit, respectively; g _s and g _a are stomatal and aerodynamic conductance at the plant level, expressed in m s^–1; and S is leaf area (m^–2) corrected for self-shading. The conversion from expressions of g _s in mol m^–2 s^–1 to m s^–1 uses a temperature-dependent coefficient calculated by the following equation: –0.1424 × T _air + 43.917. Temperature-dependent coefficients ρ (kg m^–3), γ (Pa K^–1), λ (J kg^–1), and s (Pa K^–1) take into account air temperature at each step of the calculation (Jones, 1992). Cp is a temperature-independent coefficient (1012 J kg^–1 K^–1). The net radiation is calculated from incident radiation (Allen, 1998).

Roots synthesize ABA regardless of their branching order and distance to the apex, with a common linear response of synthesis rate per unit volume to root water potential in maize (Simonneau et al., 1998). A linear relationship between root water potential and concentration of ABA in roots was also observed in bean (Puertolas et al., 2013). These findings are implemented by considering that the amount of synthesized ABA is proportional to root water potential and diluted by the water flux through the plant, J _out, with an offset b (mm³ s^–1 plant^–1), analogous to a minimum flux that withdraws ABA from the xylem in proportion to [ ABA] _xyl, thereby avoiding unrealistic increases in [ ABA] _xyl at low water flows:

$${[\hspace{0.17em}ABA]\hspace{0.17em}}_{\text{xyl}}=–\text{\hspace{1em}a}{\Psi }_{\text{r}}/\left(J_{\text{out}}+\text{\hspace{1em}b}\right)$$ (3)

where Ψ _r is root water potential (MPa); and a (pmol s^–1 MPa^–1 plant^–1) is the plant’s ability to synthesize ABA at a given Ψ _r, calculated from data on roots (Simonneau et al., 1998; Puertolas et al., 2013) or fitted together with b from coupled observations of [ ABA] _xyl, J _out, and Ψ _r for the species and genotype considered (Tardieu et al., 1996; Tardieu and Simonneau, 1998). Root biomass affects the total ABA synthesis by a given plant or by parts of root systems distributed in soil compartments (Martin-Vertedor and Dodd, 2011). This effect is included in the value of a in Eqn 3.

Water flows from soil to air via plant compartments, following gradients of water potential from the rhizosphere (Ψ _soil) to roots (Ψ _r), xylem (Ψ _xyl), and leaf bundle sheaths (Ψ _bundle). Ψ _xyl (MPa) stands for the water potential in the leaf xylem near the leaf insertion point, close to the leaf-elongating zone in monocotyledons. Root water potential (Ψ _r) stands for the water potential at the outer root surface. Ψ _soil is related to the ratio of current to saturated soil water contents (W) via Eqn 4 (Van Genuchten, 1980). Soil hydraulic conductivity, k (Ψ _soil), is related to Ψ _soil by using Eqn 5 (Van Genuchten, 1980).

$${\psi }_{\text{soil}}(\hspace{0.17em}W)\hspace{0.17em}=\frac{{(\hspace{0.17em}1-W)\hspace{0.17em}}^{{\left(\frac{\text{n}}{\text{n}-\text{1}}\right)}^{\left(\frac{1}{\text{n}}\right)}}}{{(\hspace{0.17em}{\alpha }_{\text{v}}\times W)\hspace{0.17em}}^{\left(\frac{1}{\text{n}-\text{1}}\right)}}$$ (4)

$$\begin{array}{l}k\left({\psi }_{\text{soil}}\right)=\text{ks}{\left(\frac{1}{\left(1+{\hspace{0.17em}({\alpha }_{\text{v}}\times {\psi }_{\text{soil}})\hspace{0.17em}}^{\text{n}}\right)}\right)}^{\left(\text{p}-\frac{\text{p}}{n}\right)}\\ \times {\left(1-{\left(1-\left(\frac{1}{1+{\hspace{0.17em}({\alpha }_{\text{v}}\times {\psi }_{\text{soil}})\hspace{0.17em}}^{\text{n}}}\right)\right)}^{\left(1-\frac{1}{\text{n}}\right)}\right)}^2\end{array}$$ (5)

where ks (soil hydraulic conductivity at saturation), n, α_v, and p are coefficients that characterize a given soil. The resistance R _sp (MPa s mm^–3) between the rhizosphere and soil–root interface was calculated as in (Gardner, 1960):

$$R_{\text{sp}}=\text{\hspace{1em}ln\hspace{1em}}\left({\text{d}}^2/{\text{\hspace{1em}r}}^{\text{2}}\right)/\hspace{0.17em}(\text{4}\pi k\hspace{0.17em}({\Psi }_{soil})\hspace{0.17em})\hspace{0.17em}$$ (6)

where d and r are the mean distance between neighbouring roots and root radius, respectively. Ψ _soil can be considered the mean soil water potential in soil volumes with very dense root density, such as superficial soil layers or pots (i.e. the whole soil is a rhizosphere). Otherwise, the spatial variability of Ψ _soil should be taken into account via a model of soil water transfer (see below).

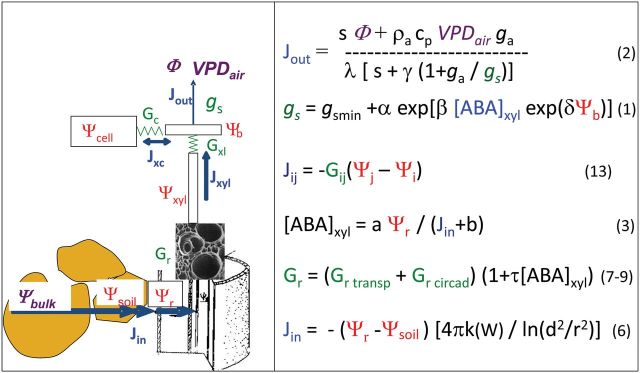
Stomatal conductance, [ABA] _xyl, water flux, and the water potentials in roots and bundle sheaths can be calculated by solving, at each timestep, five equations with five unknowns, namely Equations 1–3 and the two equations relating J _out to the differences in water potentials in the plant and from soil to roots (Eqn 13 in Fig. 1).

Fig. 1.

Schematic representation of the plant and of equations. Purple, environmental variables at the plant boundaries; red, water potentials; blue, fluxes; green, conductances. Numbers after equations refer to the numbers in the text, except Eqn 13. The water flows from the bulk soil (with water potential Ψ _bulk) to the root (Ψ _r) via the rhizosphere (Ψ _soil), then in the root (Ψ _r), the xylem (Ψ _xyl), and bundle sheaths (Ψ _b). Mature tissues (Ψ _cell) either divert part of the xylem flow or participate in transpiration, depending on the sign of (Ψ _cell – Ψ _b). J_in, J_xyl, J_xc, J_out: water flux entering into roots, in the xylem, from bundle sheaths to mature cells, and transpiration flux, respectively. G_r, G_xl, G_c, g _s: conductances for water in the roots, from the xylem to bundle sheaths, from bundle sheaths to mature cells, and stomatal conductance, respectively. Eqn 13 refers to all transport in the plant from point i to point j, with water potentials Ψ _i and Ψ _j, with a conductance for water G_ij from i to j.

Temporal changes in tissue hydraulic conductance and their implementation

Tissue hydraulic conductance changes with environmental conditions and time of day (Maurel et al., 2008; Maurel et al., 2010; Chaumont and Tyerman, 2014).

The circadian clock affects root hydraulic conductance under continuous light in A. thaliana (Takase et al., 2011) and maize (Caldeira et al., 2014b), with a peak in early morning and a period of 24h. The amplitude of circadian oscillations of hydraulic conductance and of ZmPIP (plasma membrane intrinsic protein) aquaporin transcripts depends on leaf water potential during previous days, associated with high VPD or soil water deficit (Caldeira et al., 2014b). Hence, plants keep a memory of the recent climatic scenarios in the control of ZmPIP expression and hydraulic conductance. The adaptive advantage of these oscillations is presented below (‘Tests and Uses of the Model’). This has been implemented (Caldeira et al., 2014b) by considering a circadian-dependent fraction of hydraulic conductance, Gr_circad (mm³ MPa^–1 s^–1):

$$\begin{array}{l}Gr\_circad={\tau }_{\text{circad}}\text{cos}\left(tim{e}_{\text{photo}}\times \pi /\text{12}\right)\times \\ \hspace{0.17em}({\Psi }_{xyl}max–{\Psi }_{xyl}min)\hspace{0.17em}\end{array}$$ (7)

where time _photo (h) is time in the photoperiod. Ψ _xyl min and Ψ _xyl max are the minimum and maximum Ψ _xyl during previous days; τ_circad (mm³ MPa^–2 s^–1) is the sensitivity to the amplitude of Ψ _xyl.

Diurnal variations of climatic conditions also affect root and leaf hydraulic conductances, which can be related to either light intensity (Cochard et al., 2007; Caldeira et al., 2014a) or transpiration rate (Vandeleur et al., 2014), although with some variation across species, especially in the case of A. thaliana (Prado et al., 2013). The effects of either light or transpiration provide similar results when tested in simulations (not shown). Implementing an effect of transpiration is more parsimonious because it is a linear function with two parameters, while a plateau is needed for a control using light to avoid unrealistically high conductances at high light. Hence, we propose an equation in which a fraction of root hydraulic conductance (Gr_transp, mm³ MPa^–1 s^–1) depends on transpiration, calibrated using data from Vandeleur et al. (2014):

$$Gr\_transp={\text{\hspace{1em}Gr}}_{\text{min}}+{\tau }_{\text{transp}}{J}_{–40}$$ (8)

where J _–40 is the mean transpiration rate for the period of time 60–20min before the time step considered and τ_transp is a sensitivity coefficient. Coefficients Gr_min (mm³ MPa^–1 s^–1) and τ_transp (MPa^–1) can be derived from Vandeleur et al. (2014) for maize and other species.

ABA most often increases root hydraulic conductance by inducing transcription factors that regulate the expression of PIP aquaporins (Kaldenhoff et al., 1996; Shinozaki et al., 1998) and affect a large number of PIP isoforms (Jang et al., 2004). At the whole-plant level, water deficit and salt stress usually decrease the root hydraulic conductivity (North et al., 2004; Vandeleur et al., 2009), but the specific effect of ABA is most often positive when analysed via the genetic manipulation of genes of ABA synthesis (Thompson et al., 2007; Parent et al., 2009). In our own study, overproduction of ABA caused an increase in the mRNA expression of most aquaporin ZmPIP genes with the opposite effect in lines which underproduced ABA. The same pattern was observed for the protein contents of four PIPs. This resulted in more than 6-fold differences between sense and antisense lines in root hydraulic conductivity, which translated into differences in whole-plant hydraulic conductance. The study of Thompson et al. (2007) also revealed an effect of ABA overproduction on the hydraulic conductivity of roots. In addition, ABA controls aquaporin PIP levels in the leaf (Aroca et al., 2006; Lian et al., 2006; Parent et al., 2009).

Overall, the tissue hydraulic conductance can be calculated as the sum of Gr_transp and Gr_circad, with a multiplying factor linked to [ABA] _xyl.with a sensitivity τ_ABA (m³ µmol^–1)

$$Gr=\hspace{0.17em}(Gr\_transp+Gc\_circad)\hspace{0.17em}\times \hspace{0.17em}(\text{1\hspace{1em}}+{\tau }_{\text{ABA}}{\hspace{0.17em}[ABA]\hspace{0.17em}}_{\text{xyl}})\hspace{0.17em}$$ (9)

This can be visualized in Fig. 2, which presents an experiment with one day of naturally fluctuating conditions of light and VPD, then constant conditions in a growth chamber (Caldeira et al., 2014b). The transpiration-dependent component of Gr oscillates with transpiration on the first day and is constant thereafter, while the circadian component of Gr oscillates equally in fluctuating and stable conditions. Note that both components of Gr are almost in opposite phase. Examples of Gr and Ψ _xyl outputs are provided in Supplementary Figure 1, with varying amplitudes of Ψ _xyl on previous days, different sensitivities to the amplitude of Ψ _xyl, and different sensitivities to transpiration rate.

Fig. 2.

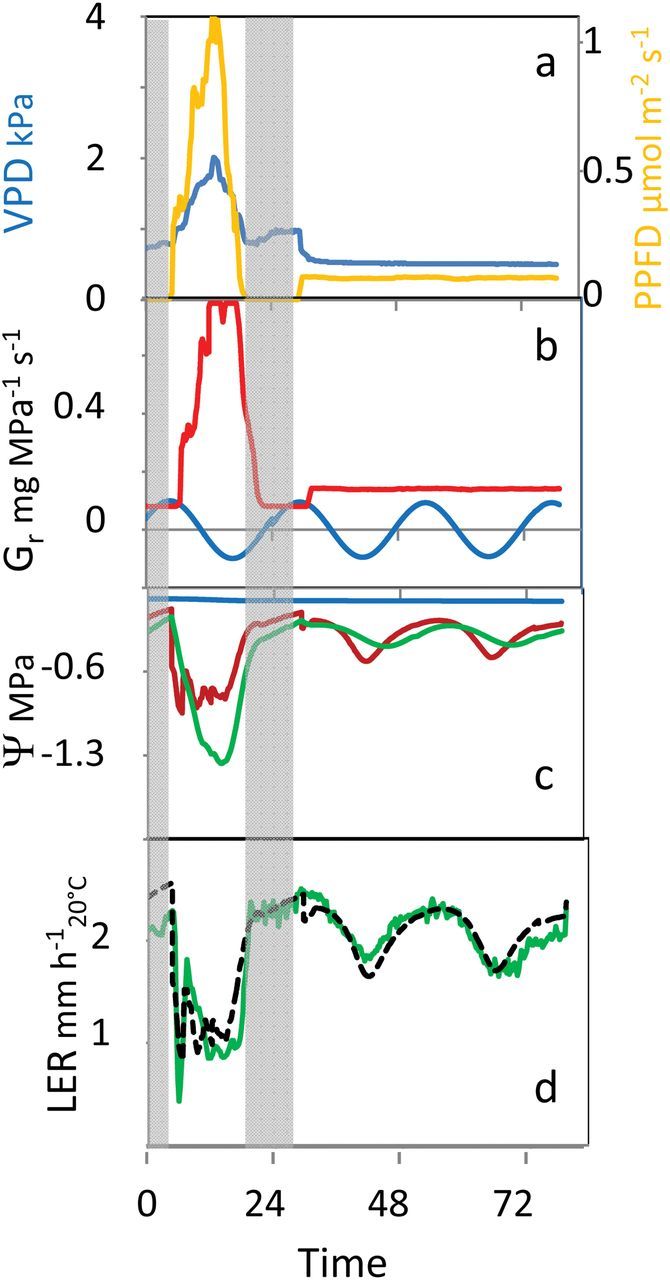
Simulations of the effects of circadian oscillations of root hydraulic conductivity. (A) Plants are first subjected to naturally fluctuating conditions in a greenhouse, then transferred to a growth chamber with stable photosynthetic photon flux density (PPFD) and air VPD. (B) Simulated root hydraulic conductance, with a term that depends on transpiration rate (red) and a term that depends on the circadian rhythm (blue). (C) Water potential of the xylem (red) and mature cells (green). (D) Leaf elongation rate (LER) oscillates in fluctuating conditions, but also in stable conditions. Green, measured LER; black dotted, simulated LER.

ABA may act in opposite directions on hydraulic conductance in roots and leaves. While it increases Gr in most studies, it decreases the conductance from the xylem to bundle sheaths (G _xl) in A. thaliana (Pantin et al., 2013a). This is probably not the case in maize (Parent et al., 2009), in which the expression of ZmPIP genes increases with ABA. In a re-analysis of various studies on roots and leaves (Dodd, 2013), the direction of the hydraulic conductance response to ABA turned out to be associated with the concentration used in the bioassays, suggesting that a common response in planta may apply to different plant tissues, with different impacts on hydraulic conductance depending on local distribution of the hormone. The effect of ABA in Eqn 9 should, therefore, be implemented in a case-to-case way. For better security, the current version of the model considers a very small ABA effect (τ_ABA = 0.1 m³ µmol^–1) as the default option in the calculation of hydraulic conductances.

Other environmental factors affect tissue hydraulic conductance, in particular tissue temperature via water viscosity (Cochard et al., 2000) and plant nutrient status (Clarkson, 2000; Trifilo et al., 2014). In addition, leaf hydraulic conductance tends to decrease with leaf age (Locke and Ort, 2014). These features have not been implemented in the model, but could be inserted via multiplying factors as in Eqn 9.

Measured leaf water potential is that of a capacitance, and appreciably differs from water potentials in the xylem and evaporation sites.

Measured leaf water potential varies considerably more slowly than leaf elongation rate upon rapid changes in environmental conditions (Caldeira et al., 2014a). In maize, it recovers with typical half times of 1–2h, compared with 30min for leaf elongation rate upon soil rehydration, and decreases more slowly than leaf elongation rate in the early morning, with similar half times compared with those upon rehydration. We have argued that the time course of leaf elongation rate is a good indicator of that of xylem water potential (Caldeira et al., 2014a), and that leaf water potential measured with a pressure chamber is that of mature tissues that act as capacitance connected to the bundle sheaths, thereby varying more slowly than Ψ _xyl. The rationale is that the tension on the apoplastic water is nullified when the leaf is cut, so the water is taken up by the symplast of the mature parts of the leaf. Pressurization refills the apoplast and xylem in such a way that the meniscus formed by the pressurized water appears on the petiole at a potential close to that of mature tissues. The same applies to measurement of leaf water potential with a psychrometer in mature tissues. This reasoning holds for monocotyledons, in which most symplastic water is located in the non-growing parts of leaves, but probably also applies to dicotyledon leaves at stages when they have nearly mature zones at their tips.

The water flowing in bundle sheaths contributes to transpiration or is diverted to mature leaf cells if the latter have a water potential lower than that in the xylem. Mature cells contribute to transpiration in the opposite case. The flux J _xc (mm³ plant^–1 s^–1) between mature tissues (with a water potential Ψ _cell) and bundle sheaths can be calculated as the product of the difference between Ψ _cell and Ψ _xyl and the conductance between both compartments (G _c, mm³ MPa^–1 s^–1). The latter is considered to depend on a circadian effect, on whole plant transpiration and on ABA in the same way as G _r (Equations 7–9). The differential equation for calculating the cell water potential Ψ _cell and J _xc can then be solved:

$$J_{\text{xc}}=d{V}_{\text{cell}}/dt=\hspace{0.17em}({\Psi }_{\text{bundle}}–{\Psi }_{\text{cell}})\hspace{0.17em}{G}_c$$ (10)

where V _cell (mm³) is related to Ψ _cell on the basis of a pressure volume curve parameterized using the same model as proposed for soils by Van Genuchten:

$$V_{\text{cell}}=V_{\text{res}}+\hspace{0.17em}(V_{\text{sat}}-V_{\text{res}})\hspace{0.17em}{\left(\frac{1}{1+{\hspace{0.17em}({\alpha }_{\text{cap}}-{\psi }_{cell})\hspace{0.17em}}^{{\text{n}}_{\text{cap}}}}\right)}^{\left(1-\left(\frac{1}{{\text{n}}_{\text{cap}}}\right)\right)}$$ (11)

with V _sat (mm³) the plant volume at saturation, V _res the residual water volume, and α_cap and n_cap fitted parameters representing the hydraulic properties of the capacitance. J _xc is calculated as the difference in V _cell between two different times for optimizing resolution of the differential equation.

The transpiration flux (J _out) is the sum of the flux through roots and xylem (J _in) and of the flux between the mature cells and the xylem (J _xc). Fig. 3C, D presents an example of the commonality of time courses of Ψ _cell with measured leaf water potential and of Ψ _xyl with leaf elongation rate.

Fig. 3.

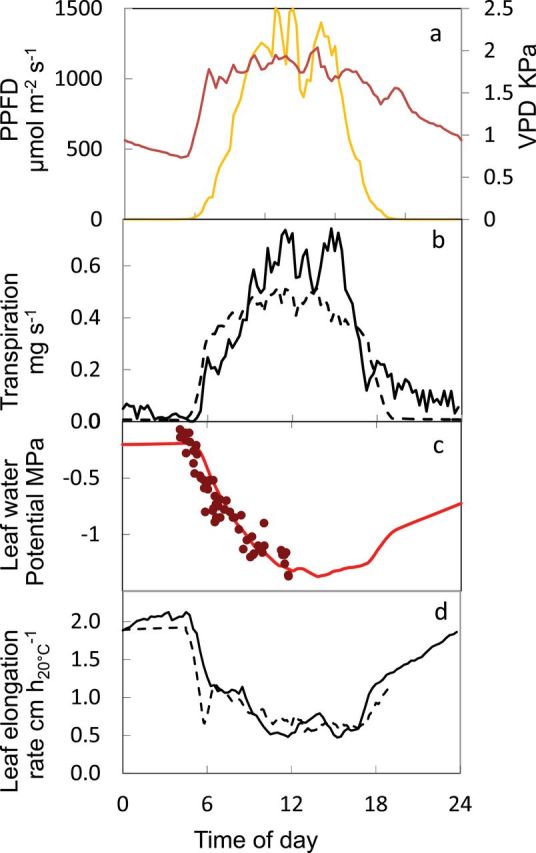
Outputs of the model and comparison with measured data. (A) Measured incident light (PPFD) and air VPD. (B) Measured and simulated transpiration. (C) Measured and simulated leaf water potentials. (D) Measured and simulated leaf elongation rates, normalized at 20°C. In (B) and (D): plain lines, measured; dotted lines, simulations. In c: dots, measurements; plain line, simulations.

Interpretation of isohydric vs anisohydric behaviours

A distinction between isohydric and anisohydric types was introduced to characterize plants which evolved with high or low efficacy in limiting the decrease in leaf water potential with increasing evaporative demand and/or soil water deficit (Stocker, 1956). The Tardieu–Davies model proposed the first mathematical expression for this distinction. Accordingly, a high value for δ in Eqn 1 captures the strong feedback control of stomatal conductance by leaf water status itself, thereby keeping leaf water potential at midday in a narrow range, as observed in isohydric plants (Tardieu and Davies, 1992). Conversely, a low value for δ makes stomata less responsive to leaf water potential and more dependent on [ABA] _xyl, accounting for anisohydric behaviour with larger variation of leaf water potential at midday as the soil dries or evaporative demand increases (Tardieu and Simonneau, 1998). Since then, a mixture between isohydric and anisohydric behaviours has been reported for some species depending on the time scale (Franks et al., 2007). A genetic continuum between the two behaviours has also been reported within species, including grapevine (Coupel-Ledru et al., 2014) and maize (Gholipoor et al., 2013). Recently, major evolution in stomatal physiology has been identified with a divergence in stomatal behaviour during the Paleozoic. In basal lineages of vascular plants (lycophytes and ferns), a simple hydropassive response of stomata to leaf water content was observed during the day, while gymnosperms and angiosperms evolved with stomatal sensitivity to ABA in addition to the hydropassive, feedback control by leaf water status (Brodribb and McAdam, 2011) with some intermediates (McAdam and Brodribb, 2014). Remarkably, and although considerable refinements have been gained in our understanding of ABA action on guard cells (Kim et al., 2010; Aliniaeifard and van Meeteren, 2013) and how it may interact with hydropassive control at a tissue level (Dewar et al., 2002), stomatal behaviours described in these works still fit in the initial proposal of the Tardieu–Davies model, with a mixed control of stomata by leaf water potential and ABA, the variable contribution of both processes being tunable by varying the value of δ in Eqn 1. Examples of effects of different δ values are presented in Supplementary Figure 1.

There is, however, growing evidence for an alternative, dominating role of hydraulic conductances operating upstream of stomata in controlling stomatal conductance and leaf water potential (Cochard et al., 2000; Franks et al., 2007), with some proposals that this may differentiate isohydric and anisohydric behaviours (Schultz, 2003; Vandeleur et al., 2009; Coupel-Ledru et al., 2014; Martinez-Vilalta et al., 2014). This makes sense, considering that leaf water potential relates to the balance between stomatal conductance (which controls water losses) and hydraulic conductances (which control water supply to the leaves). Consequently, differences in dynamic control of hydraulic conductance potentially has the same impact on isohydric or anisohydric behaviours as the differences induced by stomatal control implemented in Eqn 1. As mentioned above, the differential effect of ABA on hydraulic conductances in roots and leaves may differ between species and genotypes, so it is probably too early to routinely implement it in the model. A simulation is presented in Supplementary Figure 1, which shows that differential sensitivities of G_xl and Gr to [ABA] _xyl may have an effect on the degree of anisohydric behaviour. It will be worth progressing in this direction to test more extensively to what extent isohydric or anisohydric behaviours could become emergent properties of genotypic and environmental controls of hydraulic conductance at different points of water transport in the plant.

Taking into account water flux in the soil and soil hydraulic properties

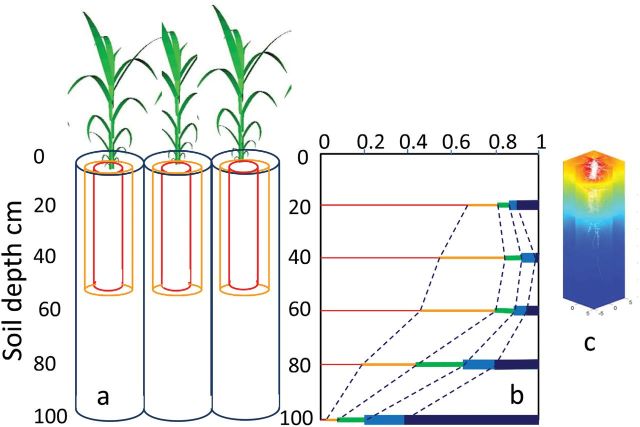
Patches of dry vs humid soil coexist at short distances, depending on the distance to the nearest root (Bruckler et al., 1991; Lobet et al., 2014). Hence, Equations 4–6, which consider the water transfer in a single soil compartment, are only valid in cases with a uniformly high root density in the whole rooting volume, a typical case for pots or fields with a shallow soil. In the opposite case, water continuously flows from humid patches to the (drier) rhizosphere, following the gradient of soil water potential (Lafolie et al., 1991; Javaux et al., 2008) (Fig. 4c). This flow is slowed down when the rhizosphere dries, due to the fact that soil hydraulic conductivity decreases by several orders of magnitude with soil water content in such a way that a dry rhizosphere becomes barely conductive to water (Lobet et al., 2014). Water transfer to such realistic root systems can be calculated via 3D numerical models that split the soil into small volumes (typically thousands), and calculate the water transfer between soil volumes depending on their water potentials, capacitances, and hydraulic conductances (Lafolie et al., 1991; Javaux et al., 2008) (Fig. 4c). This results in a complex model that can be simplified (Couvreur et al., 2012) in such a way that it becomes compatible with the model presented here. Recently, we have proposed an approach that mimics 3D soil-to-root water transfer by considering interlocked cylinders (Caldeira et al., 2014b; Fig. 4bc). The first one, in which all the soil is at <1mm from any root, represents the rhizosphere. In this cylinder, the distance between roots is calculated from total root length per plant; resistance to water transfer from soil to roots is calculated using Eqn 6. The second cylinder represents the soil localized at <4cm from the nearest root, and the third cylinder represents the ‘bulk soil’ available to one plant, with a volume that is the product of soil depth and the soil area occupied by one plant (i.e. the reciprocal of plant density). These respective volumes can be adjusted with those measured from maps of root impacts in the field (Tardieu, 1988) (Fig. 4bc). Water transfers between these interlocked soil volumes are chained using Ohm’s law analogy and Equations 4 and 5.

Fig. 4.

Representation of the rhizosphere and other soil compartments as a function of the distance to the nearest root. (A) Representation in the model used here, with three interlocked columns that represent classes of distances to the nearest roots. (B) Distribution of distances to the nearest root in field grown maize (Tardieu, 1988). At each depth, the thin red bars represent the proportion of soil located at <2cm from the nearest root. Orange, green, and blue bars indicate regions located at less than 4, 6, and 8cm from the nearest root. Thick black bars indicate regions located at >8cm from the nearest root. (C) 3D representation of the distribution of water potential in the soil using the RSWIMM model [based on Javaux et al. (2008)]. Colours represent water potentials as calculated by the model; white, root system. (From Caldeira C, Jeanguenin L, Chaumont F, Tardieu F. 2014b. Circadian rhythms of hydraulic conductance and growth are enhanced by drought and improve plant performance. Nature Communications 5, 5365.)

Simulation of expansive growth

Fluctuations of leaf expansion rate are associated with local events in the growth zone, with several potential candidates. Hydraulic processes are associated with expansive growth, with simultaneous changes in cell turgor and leaf elongation rate upon rapid variations of hydraulic conductivity (Ehlert et al., 2009) and/or with changes in the gradient of water potential between the xylem and growing tissues (Tang and Boyer, 2002). Cell wall mechanical properties are affected by water deficit in the growth zone with the involvement of ABA, potentially combined with other hormones or apoplastic pH (Tardieu et al., 2010). The abundance of expansin transcripts, which favour cell wall expansion, decreases with water deficit in the growth zones of maize leaves (Muller et al., 2007), while both cell wall peroxidase activity and caffeate O-methyltransferase (COMT) abundance increase, potentially slowing down expansion (Bacon et al., 1997; Vincent et al., 2005; Zhu et al., 2007). Cell division rate strongly decreases in the maize leaf under water deficit via the effect of p34CDC2 kinase, which blocks cells in the G1 phase (Granier et al., 2000). These mechanisms have markedly different time constants. A whole cell cycle takes about one day (Granier and Tardieu, 1998; Granier et al., 2000), changes in cell wall properties take minutes to hours (Chazen and Neumann, 1994), and hydraulic processes occur over seconds to minutes (Ye and Steudle, 2006; Caldeira et al., 2014a).

Consistent with the rapid temporal changes in leaf elongation rate presented above, we have proposed the simulation of expansive growth via its hydraulic control (Caldeira et al., 2014a). Leaf elongation rate (LER) is calculated as a maximum rate (a_ler), which is genotype dependent, and affected by xylem water potential with sensitivity c_ler, which can be extracted from the slope of the regression between night-time LER and pre-dawn leaf water potential (Welcker et al., 2011). A minor effect of ABA on LER was added via a relationship between LER and the concentration of ABA in the xylem sap, as in Tardieu et al. (2010), with a sensitivity a_r_aba. This was necessary in order to account for the inhibitory effect of ABA in transgenic plants (Tardieu et al., 2010).

$$\begin{array}{l}LER=\text{\hspace{1em}a}\_\text{ler\hspace{1em}}+\text{\hspace{1em}max\hspace{1em}}\hspace{0.17em}(0,–\text{a}\_\text{r}\_\text{aba\hspace{1em}}\\ \times \text{\hspace{1em}ln}{\mathrm{\hspace{0.17em}[ABA]\hspace{0.17em}}}_{\text{xyl}}\times \left(\text{1\hspace{1em}}+\text{\hspace{1em}c}\_\text{ler\hspace{1em}}\times {\Psi }_{\text{xyl}}\right)\end{array}$$ (12)

This formalism is implemented for maize and can be extended to other monocotyledons. In dicotyledons, a different formalism should be used, based on relative expansion rate (Granier and Tardieu, 1999).

Tests and uses of the model

The usefulness of the model has been tested in several published papers.

ABA effect

A key test has involved the analysis of transgenic plants affected in ABA synthesis via the zeaxantin epoxidase gene (Borel et al., 2001a, b) or the NCED gene (Parent et al., 2009; Tardieu et al., 2010). In both cases, the differential effect of ABA synthesis in sense, antisense, and wild-type plants was adequately described by the model, in which only one parameter was changed according to the genotype, namely the plant’s ability to synthesize ABA at a given root water potential (parameter a of Eqn 3; Fig. 5).

Fig. 5.

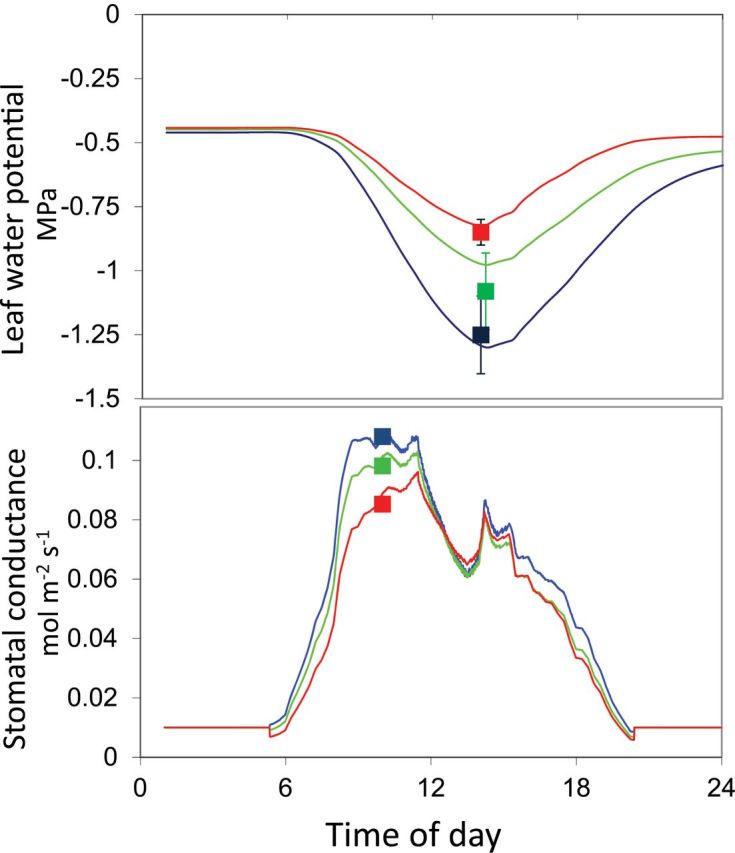
Simulated and measured values of stomatal conductance and leaf water potential in maize lines affected in the NCED-VP14 gene, over- or underproducing ABA. Green, wild type; red, S plants overproducing ABA; blue, AS plants underproducing ABA; squares, measured values.

Time courses and time constants

The ability of the model to jointly simulate the time courses of transpiration, leaf water potential, stomatal conductance, and leaf elongation rate has been reported in two recent papers in which measured and simulated values are compared (Caldeira et al., 2014a, b). One of these comparisons is presented in Fig 3, between measured leaf water potential and the simulated water potential of the capacitance, Vcell, as calculated in Equations 10 and 11. Fig. 3 also presents a comparison of measured and simulated LER, which is assumed to be controlled by Ψ _xyl as in Eqn 12. The model adequately simulated the slower decrease in leaf water potential than in leaf elongation rate in the morning. Simulated and measured values of leaf elongation rate and leaf water potentials of maize lines affected in ABA synthesis are presented for their behaviours during the early morning in Caldeira et al. (2014a) and upon soil rehydration in Parent et al. (2009).

Adaptive role of circadian oscillations of root hydraulic conductance

Finally, the ability of the model to reproduce the circadian rhythm and its adaptive advantage has been tested in experiments combining an entrainment period in the greenhouse with a period with continuous light in the growth chamber (Caldeira et al., 2014b). The circadian oscillation of Gr was sufficient to generate rhythmic growth, with amplitude depending on the alternations of xylem water potential during previous days (Fig. 2). The model suggests that circadian oscillations of root hydraulic conductance contribute to acclimation to water stress by increasing root water uptake over 24h. Indeed a temporarily high water uptake during the afternoon can have detrimental consequences on 24-h water uptake by considerably and almost irreversibly decreasing the hydraulic conductivity of the rhizosphere. Decreasing root water uptake during the afternoon (the time in which transpiration rate is at a maximum) has a transitory negative effect on plant water status, but avoids an excessive dehydration of the rhizosphere, which would dramatically decrease its hydraulic conductivity. Hence, high oscillations of root hydraulic conductance result in the maintenance of a higher water potential and hydraulic conductance in the rhizosphere, thereby favouring water uptake during the night and early morning. Conversely, high circadian oscillations have a negative effect on growth in well watered conditions, because they decrease root hydraulic conductivity and xylem water potential, at the time of maximum transpiration rate, without appreciable effect on water uptake during the night. This causes a decrease in 24-h growth and stomatal conductance, which is avoided via the ‘memory’ effect of water stress, which decreases oscillations of Gr in well watered conditions. A climatically driven control of root hydraulic conductance may therefore improve plant performances in both stressful and optimal conditions.

Concluding remarks

The model presented here has an intermediate status between multi-scale models that attempt to simulate the effects of gene networks and enzymes on plant behaviour (Chew et al., 2014), and crop models (Hammer et al., 2006) that consider robust simplifications of plant controls without explicit mechanisms such as the hydraulic mechanisms reviewed in (Parent and Tardieu, 2014). It has the capacity of hybridizing with both types of models. In particular, it may help to simplify detailed models by considering ecophysiological cause-and-effect processes for explicit simulations of environmental scenarios. It may also help to design crop models with simplified equations implying less requirements for data and genetic parameters than the model presented here, but still able to explicitly represent hydraulic processes. Finally, the parameters of the model presented here have values associated with genotypes, either directly via measurements or via genomic prediction (Tardieu and Tuberosa, 2010).

Supplementary material

Supplementary data can be found at JXB online.

Supplementary Figure S1. Environmental conditions in the example data set (climate) and simulation outputs of the examples provided in the R documentation file.

In addition:

A documentation file (or ‘help file’) of the R function modelhydro() performing simulations of the whole model presented in this paper.

model.hydro.RData: R environment containing the R function modelhydro() performing simulations of the whole model presented in this paper and the example data set (climate) used for running examples provided in the documentation file.

modelhydro.r: full script of the R function modelhydro(). It can be read with R code editor software (e.g. Rstudio and Tinn-R).

Appendix: implementation of the model.

The model provided in the Supplementary Material is written as an R function [modelhydro()] that can be run by specifying the environmental conditions at timesteps from 1min to 2 hours. Environmental data are provided as a data frame (data) containing at least the vectors hour (time, h), PPFD (Photosynthetic Photon Flux Density, µmol m ^–2 s^–1), T (temperature, °C) and VPD (air vapour pressure deficit, kPa). The whole set of biological variables is calculated every minute via the equations provided in this paper. Because environmental data are usually available at timesteps longer than 1min, a first routine calculates them every minute from data provided to the function via linear interpolation. The output is a data frame with environmental and biological variables every minute. The complete list of variables in the output table is provided in the documentary help file.

A complete list of parameters is provided in the documentary help file in SI (modelhydro.pdf). The default values of most parameters are for maize (mainly genotype B73). They can be changed by the user by specifying other values. Options (complexsoil and growth) are for a complex vs simple soil (see ‘Taking into account water flux in the soil and soil hydraulic properties’; Fig. 4) and for the calculation of leaf growth. Default options are FALSE, i.e. these calculations are not carried out.

The user must first load the R function modelhydro() and the example data set (climate) in the R environment (model.hydro.RData) that is provided in the Supplementary Material. After opening R:

setwd(“your directory”)

load (“model.hydro.RData”)

Then, the function can be called and the model can be run for specified environmental conditions and biological parameters. Here, the function is run for the example data set and with all default parameters.

mymodel <- modelhydro (data = climate)

mymodel

Parameter values can be changed in the list of arguments of the function. For example, changing the plant leaf area from 0.02 m² (the default value) to 0.03 m² can be done with:

Mod.LeafArea <- modelhydro (data = climate, surface = 0.03)

Mod.LeafArea

Others examples are provided in the function documentary in SI. They can be directly copied to R to launch the function and run examples presented in SI. Supplementary Figure S1 presents typical outputs. For more advanced R users, the code is also provided in SI for modifications (modelhydro.r).