β1-subunit–induced structural rearrangements of the Ca²⁺- and voltage-activated K⁺ (BK) channel

Significance

Large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channels play many physiological roles, ranging from the maintenance of smooth muscle tone to the modulation of alcohol tolerance. In most cases, this physiological versatility of the BK channel is due to the association of the pore-forming α-subunit with β-subunits. Therefore, it is of importance to know what the structural consequences of this association are. Here, using lanthanide-based resonance energy transfer, we were able to determine the extracellular position of transmembrane segments S0–S2 with and without the β1-subunit and the position of the two transmembrane segments of the β1 subunit in the α/β1-subunit complex. We concluded that β1 produces rearrangements of the BK voltage sensor domain.

Abstract

Large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channels are involved in a large variety of physiological processes. Regulatory β-subunits are one of the mechanisms responsible for creating BK channel diversity fundamental to the adequate function of many tissues. However, little is known about the structure of its voltage sensor domain. Here, we present the external architectural details of BK channels using lanthanide-based resonance energy transfer (LRET). We used a genetically encoded lanthanide-binding tag (LBT) to bind terbium as a LRET donor and a fluorophore-labeled iberiotoxin as the LRET acceptor for measurements of distances within the BK channel structure in a living cell. By introducing LBTs in the extracellular region of the α- or β1-subunit, we determined (i) a basic extracellular map of the BK channel, (ii) β1-subunit–induced rearrangements of the voltage sensor in α-subunits, and (iii) the relative position of the β1-subunit within the α/β1-subunit complex.

Important physiological processes involve Ca²⁺ entry into cells mediated by voltage-dependent Ca²⁺ channels. This divalent cation influx is essential for life because it permits, for example, the adequate functioning of smooth muscle or neurosecretion to occur. Some mechanism must be put into action, however, to control Ca²⁺ influx, either to dampen or to stop the physiological effects of the cytoplasmic increase in Ca²⁺. In many cases, this dampening mechanism is accomplished by one of the most broadly expressed channels in mammals: the large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channel (1–3). Because there is a single gene coding for the BK channel (Slowpoke KNCMA1), channel diversity must be a consequence of alternative splicing and/or interaction with regulatory subunits. In fact, both mechanisms account for BK channel diversity, but the most dramatic changes in BK channel properties are brought about through the interaction with regulatory subunits, membrane-integral proteins, denominated BK β-subunits (β1–β4) (4–7) and the recently discovered γ-subunits (γ1–γ4) (8, 9).

Structurally, the BK channel is a homotetramer of its pore-forming α-subunit and is a member of the voltage-dependent potassium (Kv) channel family. Distinct from Kv channels, however, BK channel subunits are composed of seven transmembrane domains S0–S6 (10, 11). Little is known about the detailed structure of the membrane-spanning portion of the BK channel, or of the α/β1-subunit complex. Here, we used a variant of Förster resonance energy transfer (FRET), called lanthanide-based resonance energy transfer (LRET), to determine the positions of the N terminus (NT) and S0, S1, and S2 transmembrane segments of the α-subunit of the BK channel, as well as the position of the β1-subunit in the α/β1-subunit complex. LRET uses luminescent lanthanides (e.g., Tb³⁺) as donor instead of conventional fluorophores. This technique has been successfully used to measure intramolecular distances and to track voltage-dependent structural changes in voltage-dependent K⁺ and Na⁺ channels (12–16). The advantages of this technique over FRET have been discussed in detail elsewhere (17), and only its highlights will be given here. Briefly, the isotropic emission of Tb³⁺ ensures that the maximum error in distance estimation due to the orientation factor (κ²) does not exceed ±10% in the range of 10–120 Å (17). Because Tb³⁺ has a spiked emission spectrum, it is possible to isolate the sensitized emission (SE) of the acceptor with relative ease by using an adequate optical filter. Additionally, we used the genetically encoded lanthanide-binding tag (LBT) to chelate Tb³⁺ donor within the protein structure (18) (Fig. 1A). Because the LBT-Tb³⁺ emission decay has a well-defined time constant of ∼2.4 ms, the donor-only (DO) emission (i.e., the donor emission in the absence of the acceptor) is very specific and distinguishable from background (13, 18, 19). Also, because the LBT is incorporated into the backbone of the protein, the donor becomes tied to the structure of the channel, likely decreasing the uncertainty of the donor position. Any distortion of the LBT structure that modifies Tb³⁺ accessibility to water will decrease its decay time constant. Therefore, by measuring the Tb³⁺ decay, it is possible to infer whether the LBT remains intact in the final structure. Moreover, the crystal structure of the LBT has been determined (18), making it possible to perform molecular dynamics (MD) simulations of the LBT-BK chimeric channels using homology-based models. The flexibility of the LBT–Tb³⁺ complex would place the Tb³⁺ atom at 5–8 Å from the LBT insertion site, giving us a concise picture of the general architecture of the external aspect of the BK channel (13).

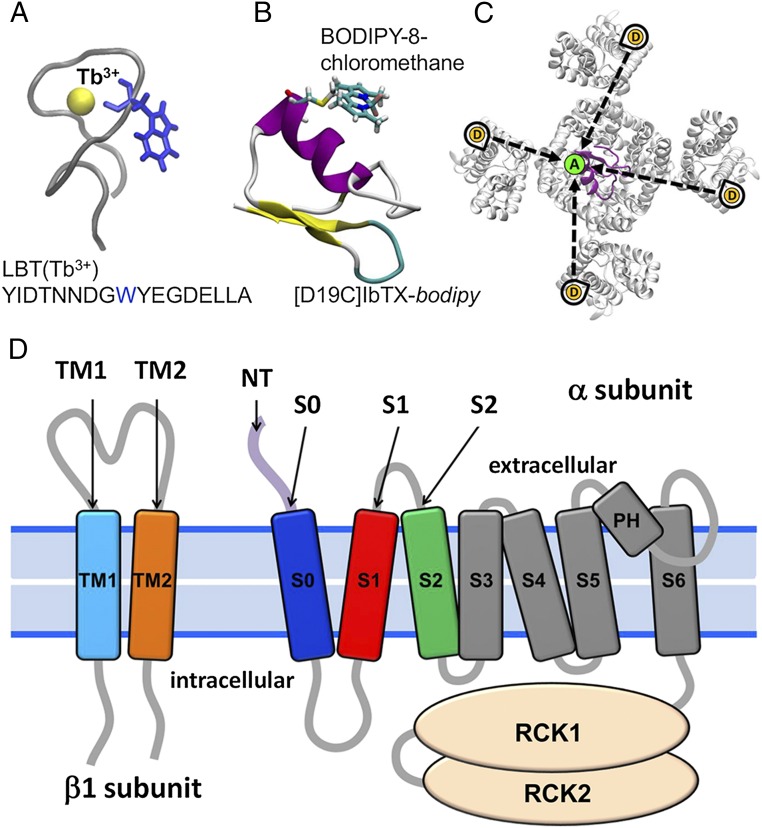
Fig. 1.

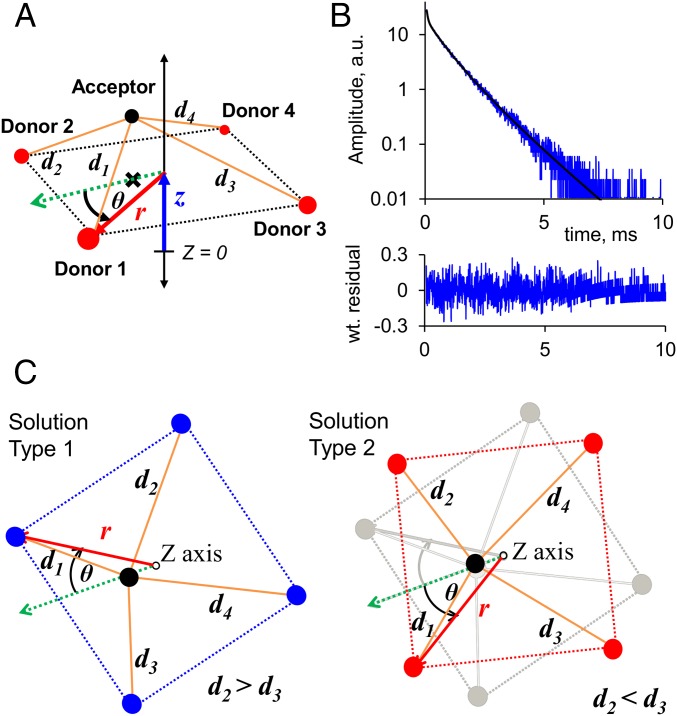
LRET strategy in the BK channel. (A) LBT binds a luminescent Tb³⁺ ion with high affinity, acting as a LRET donor. Highlighted in blue is the tryptophan, which serves as an antenna that sensitizes Tb³⁺ to become excited by a 266-nm laser pulse. (B) Fluorescent probe bodipy interacts via LRET with the LBT-chelated Tb³⁺ with an R₀ value of 39.7 Å. The bodipy molecule is covalently conjugated to IbTX at position D19C. (C) Due to the homotetrameric symmetry of the BK channel, each of the four donors (D) can transfer energy via LRET to the single acceptor (A) that is offset from the pore axis (dotted black arrows). The four different distances result in multiexponential decay of SE. (D) LBT constructs were engineered (one LBT at a time) within the BK α-subunit: NT; on the extracellular side of transmembrane segments S0, S1, and S2; and within the BK β1-subunit on the extracellular side of transmembrane segments TM1 and TM2. RCK, Regulator of Conductance of K+.

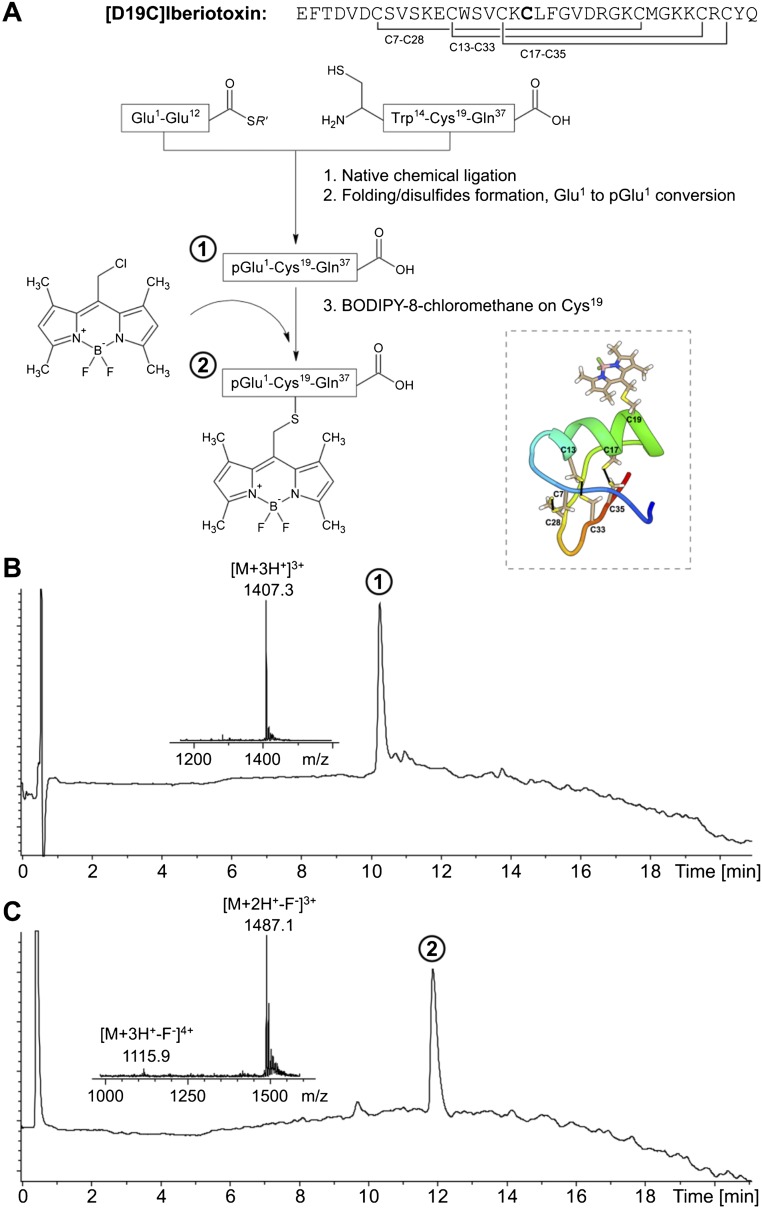
As a reference site to locate the acceptor, we used the successful approach of labeling BK with a specific pore-blocking toxin, the scorpion toxin iberiotoxin (IbTX), which binds to the external aspect of the BK pore with high affinity (13–15, 20, 21). One of the advantages of this approach is that the relative position of the acceptor can be modeled because the structure of a related toxin, charybdotoxin (CTX), in complex with the Kv1.2/2.1 paddle chimera has been determined (22). Because the BK channels are tetramers organized in an axial fourfold symmetry around the K⁺ selective pore, the location of the toxin, and hence the location of the acceptor fluorophore, can be modeled. We synthesized IbTX in solid phase with a modified cysteine at residue 19 and labeled with BODIPY-8-chloromethane (referred to as bodipy throughout this paper) as a fluorescent probe. The short linker of bodipy reduces uncertainty in the acceptor position (Fig. 1B). The labeled toxin was then used as an acceptor for the Tb³⁺ donor emission.

We used a methodology of analysis capable of extracting the position of the four donors from the SE of the acceptor, taking advantage of the fourfold symmetry of K⁺ channels (Fig. 1C). This method has been successfully tested in Shaker K⁺ channels (13). By changing the position of the LBT motif to different residues of the channel, we constructed a map of the extracellular arrangement of the S0, S1, and S2 segments, as well as the position of the NT of the BK channel, in the absence and presence of the auxiliary β1-subunit. In addition, by introducing the LBT in different positions of the β1-subunit, we located this subunit with respect to the α-subunit.

Results

LRET in LBT-Containing BK Channels.

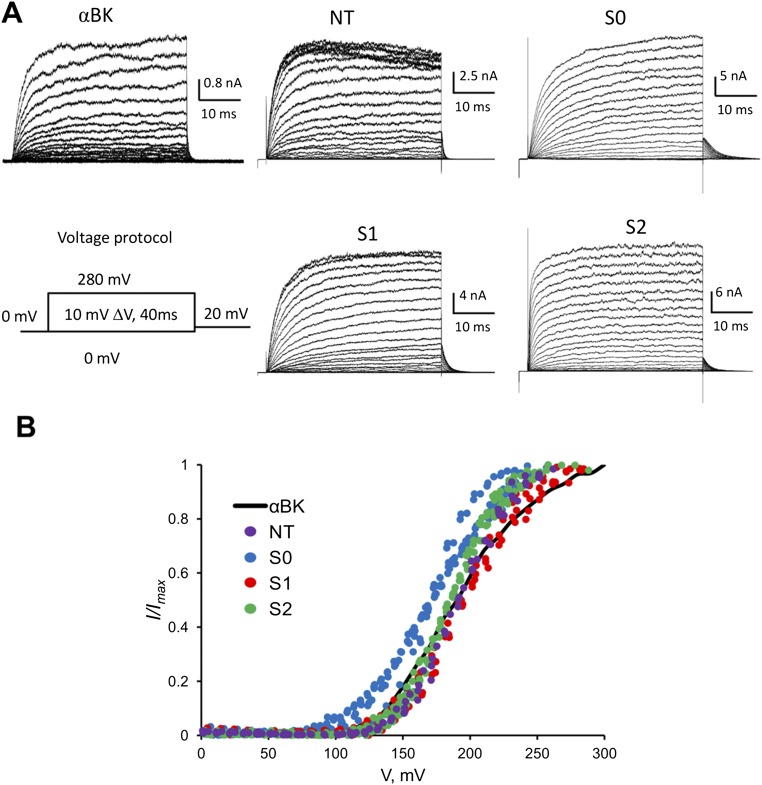
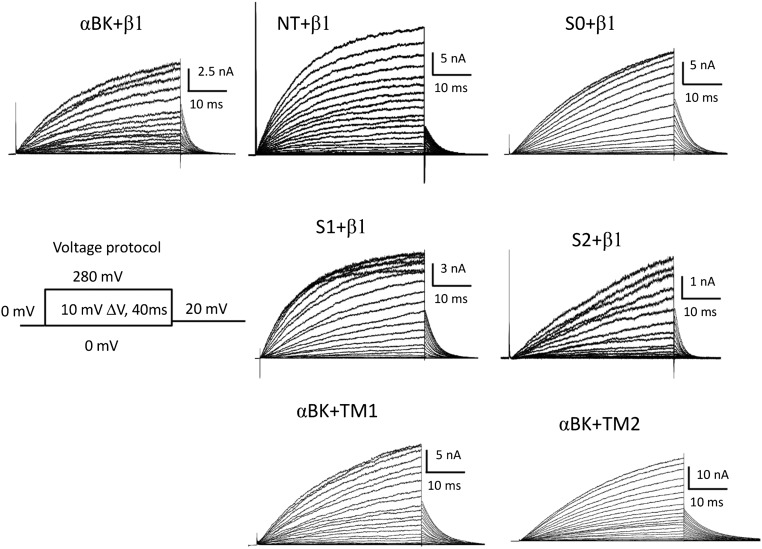
We selected LBT insertion sites within the BK α- and β1-subunits to estimate the location of the voltage sensor domain (VSD) with respect to the channel’s pore (i) in the absence of the regulatory β1-subunit and (ii) after coexpressing the BK α/β1-complex. Fig. 1D shows four insertion sites in the BK α-subunit that are in the extracellular face of the protein: NT (D15-LBT-S16), S0 (W22-LBT-W23), S1 (S134-LBT-S135), and S2 (D147-LBT-F148). Fig. 1D also shows insertion sites in the β1-subunit. They are located near the C terminus of transmembrane segment TM1 (L41-LBT-Y42) and near the NT of TM2 (R150-LBT-L151). All these constructs were expressed in the membrane of Xenopus laevis oocytes and tested with electrophysiological methods to confirm that they still operate as BK channels. No major alterations were observed after introduction of the LBT motif to any α-LBT constructs reported here (Fig. S1), suggesting that insertion of the LBT motif did not change the structure of the protein. The effect of the β1-subunit was also assessed with α-LBT constructs, as well as for TM1 and TM2 constructs coexpressed with wild-type (WT) α-BK subunit to confirm that they maintain the α/β1-BK phenotype (Fig. S2). In addition, several LBT insertion sites were designed and tested in the very short linker region between S3 and S4 of αBK. Although these constructs produced robust macroscopic currents, donor emission signal was absent, likely because of a defective LBT-Tb³⁺ structure.

Fig. S1.

α-LBT constructs expressed in the membrane of X. laevis oocytes. (A) Ionic current of inside-out membrane patches containing the four different α-LBT constructs in response to the indicated voltage pulse protocol. (B) Normalized tail current vs. voltage plots. Small changes in the slope and half-activation voltage suggest slight disruption of the voltage sensor structure in these four constructs.

Fig. S2.

α-LBT constructs (NT, S0, S1, S2) coexpressed with the β1-subunit and α-BK coexpressed with β1-LBT constructs (TM1, TM2). Ionic currents in response to the indicated voltage pulse protocol show the characteristic slowed activation and deactivation kinetics produced by the presence of the β1-subunit (compare with Fig. S1).

All LRET experiments described below were performed holding the membrane potential at −80 mV to ensure that all channels were closed with their voltage sensors in the resting state. LRET experiments at depolarizing voltages large enough to open the channels fully were not possible due to the high expression of the LBT-BK chimeras that precluded adequate voltage control of the oocytes at such high potentials.

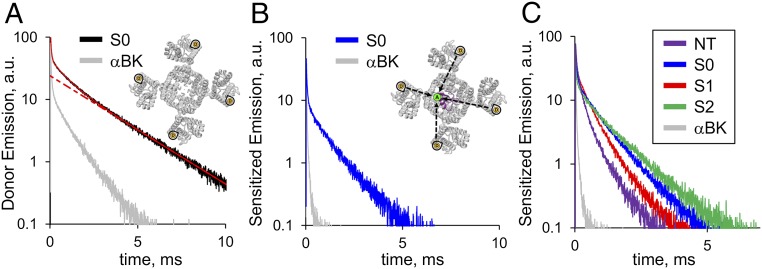
We tested the DO signal from all LBT-BK constructs by exciting the sample with a short laser pulse (5 ns) at 266 nm and obtained robust luminescence decays in all cases. Fig. 2A shows the time-resolved donor emission decay from an oocyte expressing the S0 construct. The slowest component of the decay has a time constant τ_D ∼ 2.4 ms [rate constant (k_D) ∼ 417 s⁻¹], which is absent in oocytes expressing WT BK channel (Fig. 2A, gray trace). This component is the expected decay of Tb³⁺ bound to LBT in the absence of acceptor (Fig. 2A, Inset). Our results show that all LBTs inserted in the α-subunit, as well as the β1-subunit, produced DO decay times greater than 2.15 ms, indicating that the LBT structure is maintained after insertion into either protein (Table S1).

Fig. 2.

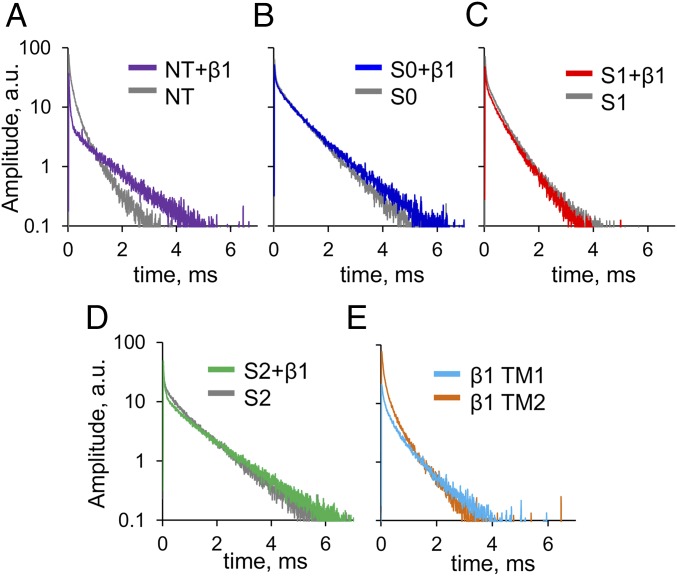
LRET measurements of LBT-tagged BK constructs. (A) Representative DO emission recording from an oocyte expressing the S0 construct. The red solid line represents a three-exponential fit. The slowest component with a time constant of ≈2.5 ms (red dotted line) corresponds to the decay from Tb³⁺ bound to LBT (Inset). (B) SE of the acceptor recorded after addition of IbTX-bodipy from the same oocyte of A. (Inset) Attached fluorophore acts as an LRET acceptor. Gray traces in A and B correspond to DO and SE control experiments, respectively, using WT BK α-subunit (α-BK). (C) Representative SE recorded from NT, S0, S1, and S2 constructs exhibited characteristic decay kinetics. Because there are four donors and one acceptor per channel, SE decays are composed of four energy transfer-based exponential components. Faster SE kinetics indicate that the four donors are positioned in closer proximity to the acceptor. a.u., arbitrary units.

Table S1.

DO lifetimes of BK-LBT constructs

Construct	τD, ms	n
S0	2.49 ± 0.08	34
S1	2.44 ± 0.05	29
S2	2.39 ± 0.07	50
NT	2.28 ± 0.05	13
S0 + β1	2.55 ± 0.04	29
S1 + β1	2.38 ± 0.06	16
S2 + β1	2.44 ± 0.03	23
NT + β1	2.31 ± 0.08	10
TM1	2.28 ± 0.05	17
TM2	2.19 ± 0.05	18

Values are given as mean ± SEM.

When 500 nM IbTX-bodipy is added to the bath solution, the excited donors (LBT-Tb³⁺) transfer energy by long-range dipole-dipole resonance to the attached fluorophore near the pore of the channel (Fig. 2B, Inset). Because the acceptor, bodipy, is fluorescent, it is possible to measure the SE, defined as the emission of acceptors excited only through energy transfer from donors. In LRET, the lifetime of the SE decay gives a direct measurement of the excited donor lifetime in the presence of acceptor, because the intrinsic acceptor lifetime is in the nanosecond scale, whereas the excited donor lifetime is in the millisecond scale (17, 23). We used a bandpass optical filter to isolate the SE of bodipy (Fig. 2B, blue trace) that effectively blocks any contamination from the donor emission. Because the acceptor is not located on the symmetry axis of the channel (Fig. 1C), there is more than one donor–acceptor distance, resulting in multiexponential SE decay (13–15). A comparison between the kinetics of SE traces from different constructs (Fig. 2C) reveals that the relative position of the donor relative to the static acceptor (offset from the pore axis) differs among constructs.

Dramatic effects are observed in the SE decay kinetics from different constructs when they are coexpressed with the β1-subunit. The effect of the β1-subunit is different for each of the four α-LBT constructs tested above. In the case of NT, β1 greatly slowed the SE kinetics (Fig. 3A). On the other hand, we observed less dramatic changes in the SE kinetics of S0, S1, and S2 (Fig. 3 B–D). These results suggest that the α/β1 interaction promotes a change in the architecture of the VSD of the BK channel.

Fig. 3.

LRET-based measurements reveal a rearrangement of the BK α-subunit when coexpressed with the β1-subunit. Representative SE decays recorded from oocytes independently expressing the α-LBT constructs coexpressed with the β1-subunit: NT (A), S0 (B), S1 (C), and S2 (D). For comparison, each panel shows in gray a representative SE trace of the corresponding construct expressed without the β1-subunit. Visual inspection shows that the most dramatic changes of LRET measurements occur in the NT construct. (E) SE from oocytes independently coexpressing the WT BK α-subunit with TM1 and TM2. Different kinetics indicate that the donors of these constructs are located in different parts of the channel structure.

As was done for the α-subunit, two LBT constructs of the β1-subunit were engineered with insertion sites near the extracellular side of the TM1 and TM2 segments (Fig. 1D). These constructs showed SE with characteristic kinetics indicating their different locations relative to the channel structure (Fig. 3E).

A Spatial Map of the Extracellular Face of the BK Channel.

To retrieve quantitative information from the SE recordings, we used the symmetrical nanopositioning system (SNPS) to generate a spatial map of the different donor positions (13). This methodology assumes a pyramid-like geometric model, which considers that the four donors are in the corners of a square pyramid base and the acceptor is above them at the apex (Fig. 4). The SNPS method finds the geometric configuration yielding theoretical SE decays that best fit an ensemble of experimental SE decays (13) (details are provided in SI Text, S1. LRET Calculations). The position of the acceptor was modeled from the available structure of CTX bound to the Kv1.2/2.1 paddle chimera (22), and thus acts as an absolute reference point for the position of the four donors with respect to the channel pore. Donor cylindrical coordinates determined by the SNPS are detailed in Table 1. This model yields two geometrically equivalent solutions corresponding to cases where intermediate distances are related by d₂ > d₃ (type 1) or d₂ < d₃ (type 2) (Fig. 4C). Despite this apparent ambiguity, it is possible to discard one of the two by comparing the resulting donor positions with the Kv1.2/2.1 crystal structure reference, assuming that the VSD of the BK channel keeps the basic VSD geometry. Furthermore there is no ambiguity for the case where the donor is near the symmetry line.

Fig. 4.

Geometric model used to fit experimental SE traces. (A) Three cylindrical coordinates, r (red arrow), θ (black arc), and z (blue arrow), determine the position of the four donors (red circles) with respect to the acceptor position (black circle). The SNPS fitting program calculates four effective distances (d₁ through d₄, orange lines) that determine the shape of the theoretical SE decay according to Eqs. S1–S3 (SI Text, S1. LRET Calculations). The black cross is the projection of the acceptor cloud center of mass onto the x–y plane containing the four donors. (B) Geometric fit to a single S0 construct SE decay (Top) and weighted (wt.) residuals (Bottom). Goodness of fit is evaluated with the reduced chi square (χ²_RG) value. a.u., arbitrary units. (C) Two equivalent geometric solutions are possible from a single fit, because the rotation angle may be ±θ with respect to the acceptor position.

Table 1.

Donor coordinates of BK-LBT constructs determined by nanopositioning (SNPS)

Construct	Solution	r (Å)	θ (º)*	z (Å)	${\chi }_{RG}^2$	n
S0	2	33.8 (−1.4, +1.2)	1.7 (−17.8,† +14.4)	24.4 (−3.1, +3.6)	1.028	18
S1	2	29.2 (−1.2, +1.1)	12.9 (−12.9, +11.6)	23.3 (−2.4, +2.7)	1.022	17
S2	2	38.9 (−0.8, +0.1)	0.0 (−14.2,† +14.2)	37.3 (−7.4, +7.4)	1.025	11
NT	2	33.1 (−1.0, +0.3)	45.0 (−8.2, +8.2)	37.3 (−8.4, +8.3)	1.039	8
S0 + β1	2	35.1 (−1.2, +1.2)	10.8 (−10.8, +10.3)	24.3 (−2.6, +3.3)	1.019	7
S1 + β1	2	24.2 (−1.4, +1.1)	23.3 (−11.9, +16.9)	15.4 (−1.5, +1.3)	1.026	20
S2 + β1	2	43.4 (−1.2, +0.1)	0.0 (−10.1,† +10.1)	37.3 (−9.6, +9.5)	1.027	5
NT + β1	2	41.9 (−1.2, +0.2)	0.0 (−10.9,† +10.9)	37.3 (−9.6, +9.5)	1.045	13
αBK + β1TM1	1	35.5 (−0.9, +0.4)	−22.7 (−13.3, +12.2)	37.4 (−7.6, +7.5)	1.026	6
αBK + β1TM2	1	31.1 (−1.5, +1.5)	−27.8 (−10.1, +5.2)	26.4 (−4.2, +8.7)	1.039	3

^*Rotation angle is relative to acceptor position: (x,y,z) = (−2.20,−4.21,37.36) Å, in absence of β1.

^†Confidence region crossed over into opposite solution space.

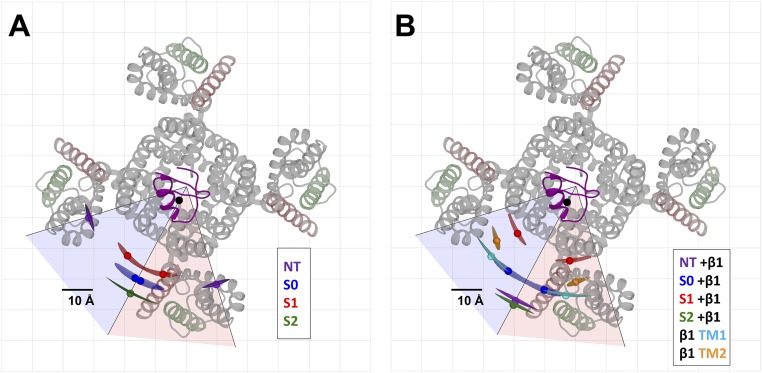
To summarize the selected LRET-SNPS results in the absence of the β1-subunit, Fig. 5A shows the relative position of donors for the four α-LBT constructs in the x–y plane, including 95% confidence isosurfaces. The donor of the S2 construct is located at the periphery of the channel at 38.9 Å from the pore axis, being the farthest of the four constructs from the symmetry axis of the channel. The S1 donor is the closest to the pore axis, with a radial distance of 29.2 Å. The S0 donor is located at 33.8 Å from the pore axis, between the S1 and S2 donors. Surprisingly, the NT donor appears to be far from the S0 donor, displaced by ∼23 Å in the x–y plane projection. When compared against the Kv1.2/2.1-CTX structure, the NT and S2 donors present no rotational ambiguity, whereas for the S1 construct, only solution type 2 fits over the VSD structure near the top of the S1 segment (Fig. S3A). Only the S0 construct displayed rotational ambiguity such that both solutions are equally probable, yet they are very close to the symmetry line (Fig. S3). Fig. 5B shows a lateral view of donor positions for the four constructs tested (x–y plane projection), where differences in the relative height of the donors can be observed.

Fig. 5.

Spatial map of the extracellular face of the BK VSD obtained from the geometric fit to SE traces. The position of each donor is represented by colored filled circles. The 95% confidence isosurfaces are shown as transparent volumes. For the sake of clarity, the donors from only one subunit are shown. The reference point is the acceptor (black circle) near the fourfold symmetry axis. The crystal structure of the pore section from the Kv1.2/2.1 paddle chimera (transparent gray) and the modeled IbTX-bodipy (purple) are presented in the background as references. The tentative area where the bulk of the BK VSD may be located is encircled by a black line. The space-filled boundary of the Kv1.2/2.1 paddle chimera is shown as a fainter gray line. (A and B) Top and side views, respectively, of the spatial map for BK constructs in the absence of the β1-subunit. (C and D) Top and side views, respectively, of the spatial map for BK constructs in the presence of the β1-subunit. Donors from the β1-LBT constructs TM1 and TM2 are shown as cyan and orange circles, respectively. For completeness, both solution types are shown for S0 + β1, TM1, and TM2 constructs. However, the less likely solutions are rendered transparent to reinforce the fact that they appear nonparsimonious.

Fig. S3.

Alternative solutions for the geometric model obtained by fitting the SE recordings. Donor positions are represented as colored spheres with their corresponding 95% confidence isosurfaces. Solution type 1 is within the transparent blue area, whereas solution type 2 is within the transparent red area. The central black segment from the origin is the symmetry line separating solution types 1 and 2. The other two black segments delimit the spatial region where solutions are allowed for Donor₁, given the tetrameric fourfold symmetry of the geometric model. (A) Geometric solutions for NT, S0, S1, and S2 constructs in the absence of the β1-subunit. (B) Geometric solutions for NT, S0, S1, and S2 constructs coexpressed with the β1-subunit, and also for the β1-TM1 and β1-TM2 constructs. The location of the acceptor (black circle) is referenced to the IbTX-bodipy model (shown in purple). The reference structure of the Kv1.2/2.1 paddle chimera is shown in transparent gray for comparison purposes. Transmembrane segments S1 and S2 of the paddle chimera are colored in red and green, respectively.

The External Architecture of the BK α/β1-Complex.

As expected by the changes observed in the SE kinetics, coexpression with the β1-subunit causes a change in the pattern of donor positions (Fig. 5 C and D). Donor solution types were selected to be most parsimonious with respect to the results obtained in the absence of the β1-subunit. For instance the S2 and NT constructs showed no rotational ambiguity, whereas S1 was kept as solution type 2 for the sake of parsimony. The solution type for the S0 donor coexpressed with β1 was selected as solution type 1 because (i) a counterclockwise rotation would place the S0 segment further into the VSD, which is not likely, and (ii) this solution type better agrees with reported interactions between the S0 segment and the TM1 or TM2 segment of the β1-subunit (24, 25). For the TM1 and TM2 constructs, the best choice was solution type 1; otherwise, these segments would be positioned inside the voltage sensor, a solution that has no physical meaning (Fig. 5C and Fig. S3B). The spatial map of Fig. 5 C and D shows that both the TM1 and TM2 donors are positioned between adjacent subunit VSDs and in the vicinity of the S0 donor, radially closer to the pore axis by 0.4 Å and 4 Å, respectively.

We noted that by maintaining the acceptor static, the donor position of all constructs except S1 clashed with an upper height boundary equal to the height of the acceptor. Because this picture seems unlikely, we shifted the acceptor position 1 Å radially outward from the pore axis for the complete dataset in the presence of the β1-subunit. The result was an overall decrease in individual fit error and the spreading of donor positions in the z axis (Fig. S4). This operation results in a more physically meaningful picture; therefore, the reported results in Fig. 5 C and D consider the shifted position of the acceptor, although this shift implies a slight change in the acceptor position due to the presence of the β1-subunit.

Fig. S4.

Effect of the acceptor position in the geometric model for BK-LBT constructs in the presence of the β1-subunit. (A) The z-coordinate of all donors except S1 clash with the upper boundary equal to the height of the acceptor (37.4 Å) when the acceptor radial shift is equal to 0, which corresponds to the best acceptor position for the data in absence of the β1-subunit (4.75 Å radial from the pore axis). We thus explored the possibility of a slight β1-induced acceptor perturbation by varying the acceptor radial distance to achieve a more structurally meaningful spread of z-coordinates among LBT constructs. A positive shift means further away from the z axis. When acceptor radial shift is >1 Å, the S1 donor drops below the extracellular face of the membrane (15 Å, dashed line). (B) Fit error (χ²_RG) vs. acceptor radial shift. χ²_RG decreases for all constructs as the acceptor is displaced away from the z axis. The average fit error of the entire dataset is shown as black diamonds.

The most dramatic structural rearrangement induced by the presence of the β1-subunit is the NT construct with a 29.8-Å displacement in the x–y plane. This rearrangement places the NT donor very near the new position of the S2 construct. At the same time, the S2 construct undergoes a displacement of 4.5 Å in the x–y plane away from the pore axis. The S1 construct shows a displacement toward the pore axis of 5 Å and a counterclockwise rotation of 10°. Finally, S0 moves 5.6 Å in the x–y plane with a clockwise rotation away from the S1 and S2 donors (S0 solution type 1 as a reference). Changes in the z-coordinate of each donor can also be observed. In particular, a downward displacement of the S1 donor by 7.9 Å is the most remarkable vertical shift. In contrast, NT, S0, and S2 have little change in the z-coordinate (<0.2 Å) when coexpressed with the β1-subunit. Fig. 6 summarizes the position changes of the donors in the α-subunit as a result of coexpressing the β1-subunit, as well as the position of the TM1 and TM2 donors of the β1-subunit.

Fig. 6.

Change in the donor position due to the presence of the β1-subunit. (A and B) Top and side views, respectively, of the changes in the donor positions as a consequence of coexpression with the β1-subunit. The 95% confidence isosurfaces are not displayed for clarity. Colored arrows indicate the direction of the change in position.

Discussion

Different from all other members of the Kv channels superfamily, in BK channels, not only the S4 segment but also the S2 and S3 segments of the VSD carry the electric charges that sense the membrane electric field (26–28). The translocation of these charged residues in the membrane electric field induces conformational changes in the VSD that can be tracked with site-directed voltage-clamp fluorometry (29–31). BK channels also have the additional S0 transmembrane segment preceding the six canonical segments (10, 11). Tryptophan scanning mutagenesis in S0 and fluorescence quenching by tryptophan W203 in the S3–S4 linker suggest that the NT of the S0 segment is in close contact with the VSD (S1–S4). This interaction would modulate the equilibrium between the resting and active states of the voltage sensor (32, 33).

Little is known about the detailed structure of the transmembrane portion of the BK channel, although some initial glimpses of the channel’s structure have been given using cryoelectron microscopy at a resolution of 17 Å (34). The BK structure resolved by this technique shows a large protrusion at the periphery of the VSD at ∼40 Å radial from the pore axis, which should correspond to the additional S0 helix and ∼40 extracellular N-terminal residues of the BK α-subunit. This observation is in good agreement with our measurement using LRET that places the S0 donor 33.8 Å radial from the pore axis.

BK Transmembrane Segments Pattern.

Information about the relative position of transmembrane segments was reported by using disulfide cross-linking experiments. There, S0 appeared to lie in close proximity to the S3–S4 loop, near the S1 and S2 segments and away from the S5 and S6 segments, based on the extent of disulfide bond formation between introduced cysteine residues (35). The best way to interpret these data was by positioning S0 surrounded by all the other transmembrane segments of the voltage sensor (S1–S4), preventing S0 from making contact with segments S5 and S6. More recently, using voltage-clamp fluorometry, it was found that a fluorescent label on the extracellular side of the S0 segment can be quenched by tryptophan W203 of the S3–S4 loop in a state-dependent manner, supporting the proximity of the S0 segment with the S3–S4 loop in the resting state (30). Using the same approach, after strategically locating the fluorescent probe and by introducing or substituting the quencher tryptophan, it was concluded that the S1 segment would be closer to W203 (which would be in close proximity to S0) than the S2 segment in the resting state (31). Our results place the position of the S0 donor nearly in-line between S1 and S2: a distance of 7.7 Å from S1 and 5.2 Å from S2 in the x–y plane (Fig. 5A).

The Transmembrane Segments Pattern of the BK α/β1-Complex.

The β1-subunit consists of two putative transmembrane segments joined together by a large extracellular loop (36). The BK β1-subunit increases the apparent Ca²⁺ sensitivity of the channel, slows down the macroscopic activation and deactivation kinetics, and decreases the voltage sensitivity (37–44). By stabilizing the voltage sensor in its active configuration, the β1-subunit has an important effect on the BK channel’s apparent Ca²⁺ sensitivity (43, 45). Therefore, it is reasonable to think that there is a close spatial relationship between the β1-subunit’s transmembrane segments and the VSD of the α-subunit. Our LRET experiments show that the α-subunit undergoes a change in the spatial pattern of its transmembrane segments when coexpressed with the β1-subunit (Fig. 5).

Using the disulfide cross-linking technique, Marx and co-workers (24, 25) also described the spatial distribution of BK transmembrane segments in the presence of the β1-subunit. Surprisingly, to best account for the results reported by Liu et al. (25), they no longer positioned the S0 segment surrounded by the other four transmembrane segments but in the periphery of the VSD facing the S3 and S4 segments. Their model does not allow direct contact of S0 with the S1 and S2 segments even though their results showed between 40% and 80% disulfide cross-linking between S0 and the S1 and S2 segments (25). In contrast, our results place the S0 segment in close proximity (<7 Å) to the S1 and S2 segments. In their work, the extent of cross-linking is only interpreted as relative differences in distances between cysteine residues, and the estimation is done a long time after cross-linking occurs. In contrast, our LRET measurements are performed in real time, with functional channels expressed in the membrane of a living cell, and the retrieved positions of donors anchored to the different transmembrane segments rely only on the modeled acceptor position and assumed fourfold channel symmetry (13).

Disulfide cross-linking between the β1-subunit and α-subunit suggested that both TM1 and TM2 segments are in close proximity to S0, S1, and S2; however disulfide bond formation is essentially prevented for the S3 to S6 segments (24, 25). This finding is consistent with our proposed location for the TM1 and TM2 segments, which appear adjacent to the S0-NT position (Fig. 5 C and D), and show that TM1 is 2.4 Å closer to S0 than TM2 in the x–y projection. These observations could give structural support to functional coupling between the S0/NT of the BK α-subunit and the β1-subunit (46). Due to the short distance to S0, TM1 is likely making contact with the α-subunit at this point, and these contacts may be responsible for the observed changes in the biophysical properties of the BK channel when coexpressed with the β1-subunit. Also, consistent with results reported by Liu et al. (25), our LRET experiments locate the TM1 and TM2 segments at the interface of adjacent voltage sensing domains (Fig. 5C), with both segments close to each other, allowing disulfide bond formation between these two segments.

A Model Structure of the External Aspect of the BK Channel.

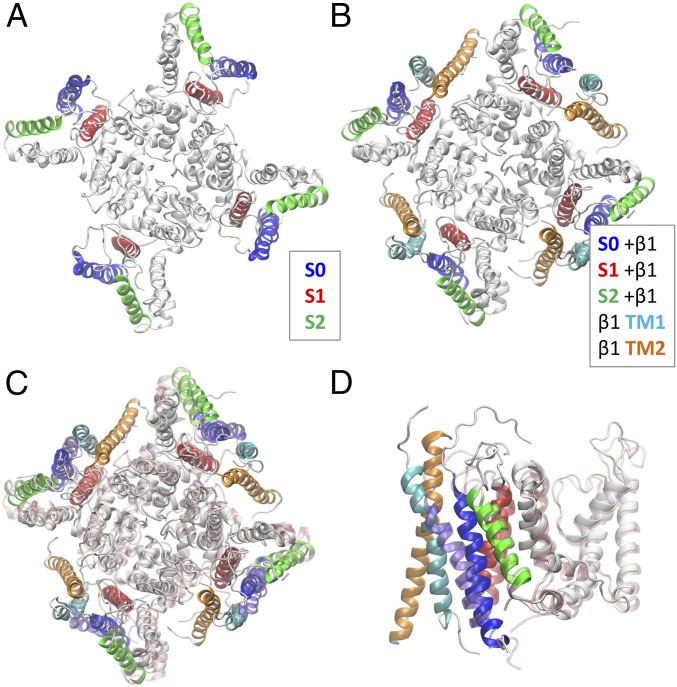
To account for our LRET findings in the structural context, we performed an LBT position-restrained MD protocol to refine a BK homology model according to our calculated donor positions (details are provided in Experimental Procedures). The BK structural model obtained using this approach is shown in Fig. 7A. The positions of segments S0, S1, and S2 are in agreement with these segments’ interactions reported previously (35). However, in our molecular model, the S0 segment is closer to the S1 and S2 segments than to the S3 and S4 segments.

Fig. 7.

 LRET-restrained molecular model of the BK channel. LBT insertions were sequentially included (one at a time) in LRET-restrained MD simulations used to construct the BK model. (A) Top view of the BK model in the absence of the β1-subunit. (B) Top view of the BK model in the presence of the β1-subunit. (C and D) Top and side views, respectively, of the BK model in the presence of the β1-subunit (solid white) compared with the model in its absence (transparent pink). The side view (D) includes only one subunit for clarity. The TM1 and TM2 segments were docked to match best the donor position obtained from β1-LBT constructs. LBT-labeled helices are colored consistent with LBT construct colors used throughout the paper.

To have the complete picture, we also performed a position-restrained model of the BK channel using the donor coordinates obtained in the presence of the β1-subunit (Fig. 7B). The structural changes in the BK model due to the presence of the β1-subunit are detailed in Fig. 7 C and D, including the transmembrane segments TM1 and TM2 docked in such a way that they best match LRET results. As a measure of β1-induced conformational change, we calculated the rmsd between the two models as 2.7 Å for the whole channel, 3.3 Å considering only the VSD (S0–S4), and 0.8 Å considering only the pore section (S5–S6). Our LRET-restrained model locates both the TM1 and TM2 segments of the β1-subunit near S0 and S1 in the space between two adjacent voltage sensors. This vicinity allows interaction between both transmembrane segments and also prevents interaction with S3–S4 segments as proposed by Liu et al. (24, 25).

The presence of the β1-subunit not only modifies the operation of the VSD but also dramatically slows the activation and deactivation kinetics (41, 43, 45, 47). The reported crucial role of the cytoplasmic domains of β-subunits (48, 49) requires close proximity of both cytoplasmic domains of the β1-subunit and the α-subunit VSDs. The molecular model proposed here for the BK α/β1-complex inferred from LRET experiments allows such interactions, given that the transmembrane segments of the α- and β1-subunits are close to each other.

Experimental Procedures

Donors and Acceptors.

The LBT, sequence YIDTNNDGWYEGDELLA (18), was inserted in chosen positions of the BK channel. LBT-BK channels were constructed using standard molecular biology techniques and a site-directed mutagenesis kit (QuikChange; Stratagene). Correct insertion of LBTs was confirmed by sequencing. As the LRET acceptor, we used the fluorophore bodipy attached to the peptidic scorpion toxin IbTX, a high-affinity pore blocker of BK channels. Labeled [D19C]IbTX was custom-synthesized in solid phase, and bodipy fluorophore was also custom-synthesized in-house (SI Text, S2. IbTX-Bodipy Synthesis and Fig. S5). We determined the Förster distance to be R₀ ≈ 39.7 Å for the LBT-Tb³⁺/[D19C]IbTX-bodipy pair (SI Text, S1. LRET Calculations).

Fig. S5.

Synthesis and characterization of synthetic bodipy-labeled IbTX. (A) Native chemical ligation-based synthesis scheme for [D19C]IbTX labeled with bodipy. (Inset) Structural model of toxin-dye conjugate, displaying all cysteine residues and its three disulfide bonds. (B) Analytical liquid chromatography (LC)-MS data for the purified and folded molecule [D19C]IbTX with N-terminal conversion to WT pyroglutamate, designated as product 1. (Inset) Electrospray mass spectrometry (ESMS) data: observed, 4,218.9 ± 0.3 Da; calculated, 4,219.0 Da [average (avg.) isotopes] with three disulfide bonds. (C) Analytical LC-MS data for the purified molecule [D19C]IbTX-bodipy, designated as product 2. (Inset) ESMS data: observed, 4,479.0 ± 0.3 Da (avg. isotopes); calculated, 4,479.1 Da (avg. isotopes). The MS data shown were collected across the main UV-absorbing peak in the chromatogram. We observed that 1 F⁻ was lost from the IbTX-bodipy molecule during the ionization process, which was also observed in MS measurement of bodipy alone.

Heterologous Protein Expression Electrophysiology.

For BK expression in oocytes, the WT and mutant channels’ cDNA was transcribed using an in vitro T7 polymerase transcription kit (Ambion). The transcribed cRNA (50 ng) was injected into Xenopus oocytes. Oocytes were incubated in SOS (100 mM NaCl, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 5 mM Hepes, pH 7.6) or ND96 (96 mM NaCl, 2 mM KCl, 1 mM CaCl₂, 1 mM MgCl₂, 5 mM Hepes, pH 7.6) solution at 18 °C for 3–5 d before recording. For electrophysiological characterization of BK-LBT constructs, patch-clamp experiments were performed with an Axopatch 200B amplifier in an inside-out configuration. The bath and pipette solution both contained 110 mM K-MES, 10 mM Hepes, and 5 mM EGTA (pH 7.4). In LRET experiments, a CA-1B amplifier (Dagan Corp.) in a two-electrode voltage-clamp configuration was used to keep the transmembrane voltage fixed at −80 mV. The internal microelectrodes’ resistance was 0.4–0.8 MΩ, and the pipette solution was 3 M KCl. For donor emission experiments, the bath solution composition was 110 mM N-methyl-d-glucamine-methanosulfonic acid, 10 mM Hepes, 2 mM CaCl₂, and 10 μM TbCl₃ (pH 7.4). For acceptor-SE experiments, the bath solution additionally contained 500 nM IbTX-bodipy. The acceptor-containing solution was made by adding 3 μL of 20 μM IbTX-bodipy solution to 117 μL of DO solution. Oocytes were incubated for 5–15 min in the IbTX-bodipy–containing solution before SE recording.

Optical Setup.

The optical setup used for simultaneous LRET and electrophysiology experiments was custom-designed and has been described before (13, 19). Briefly, to excite the donor, we used a 5-ns pulse at the 266-nm line of a quadrupled neodymium-yttrium aluminium garnet (Nd:YAG) laser (Spectra Physics). The laser excitation beam passes through excitation optics composed of a fused silica Pellin–Broca prism (Thorlabs) and UG11 cleanup filter, followed by a custom 266-nm laser dichroic with no antireflection (AR)-coating (Z266rdc; Chroma Technology). A 40× (1.25 N.A.) glycerol immersion quartz objective with no AR-coating (Partec GmbH) was used to collect the light from the sample. Emission filters were a long-pass E515LPv2 or a band-pass D520/20m (Chroma Technology) for DO emission or SE recordings, respectively. The optical signal was detected with a gated photomultiplier tube (Hamamatsu) coupled to a custom-made current/voltage converter. Analog fluorescence signal was filtered with an eight-pole Bessel filter at either 50 kHz or 100 kHz cutoff frequency, and acquired with a sample period of 2 μs using a 14-bit analog-to-digital converter. DO and SE traces were obtained by averaging 16–25 pulses.

SE Analysis.

Geometric models for all constructs were obtained by analyzing their respective SE decay measurements. The analysis was performed using the SNPS software developed by our group (13) using MATLAB (MathWorks). Briefly, the program generates a theoretical SE signal from a geometric model that takes into account the position of the four Tb³⁺ donors and the single acceptor in a pyramid-like model (Fig. 4A). The program routine finds the best geometry that simultaneously fits multiple experimental SE traces of a given LBT construct and conformational state. Solution types of the geometric model were selected according to the reference Kv1.2/2.1-CTX structure. Selection was made to have maximal overlap between the donor positions and the VSD of the paddle chimera. Details of this procedure can be found in SI Text, S1. LRET Calculations.

Acceptor Position Sampling by Dihedral Angle Scan.

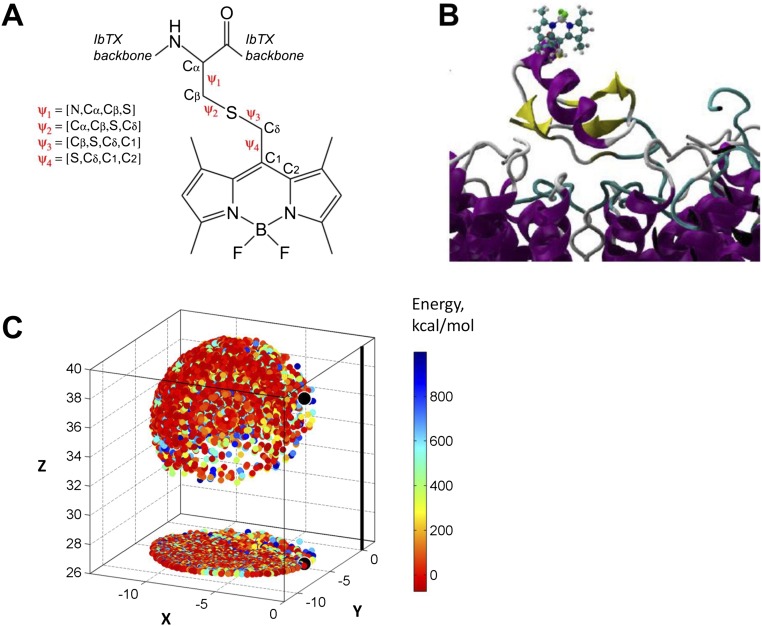
The conformational space of bodipy within the [D19C]IbTX–bodipy–BK complex model (SI Text, S3. Molecular Modeling and MD Simulations) was sampled by scanning the fluorophore–toxin complex dihedral angles Ψ₁, Ψ₂, Ψ₃, and Ψ₄ defined in Fig. S6A using 30° increments per dihedral (e.g., Ψ₁ = −150°, −120°, …, 180°). The scanned sample consists of 20,736 structures, which were evaluated in terms of their van der Waals (vdW) energy to discard clashed conformations (E_vdW > 1,000 kcal/mol or atomic distances < 1.4 Å). Each of the resulting 3,290 conformations was used to represent the accessible or diffusive volume of bodipy’s transition dipole moment (estimated as the geometric center of the chromophore’s central ring), such that each valid conformation is represented by a point, which, together, define the acceptor (cloud) position within the reference frame of the IbTX–BK complex (Fig. S6C).

Fig. S6.

Toxin-fluorophore conjugate and diffusive volume of the acceptor fluorophore. (A) Schematic of bodipy conjugated to IbTX at residue D19C. Ψ₁–Ψ₄ are the four dihedral angles that separate the chromophore from the toxin backbone. (B) Homology-based model of IbTX-bodipy bound to the BK pore. The bodipy full structure is shown as a ball and stick representation. The model was made using the CTX-bound Kv1.2/2.1 crystal structure (PDB ID code 4JTA) from Banerjee et al. (22). (C) Conformational space of bodipy attached to IbTX was modeled by rotating each of the four dihedral angles Ψ₁–Ψ₄ by 30° for a total of 20,376 conformations. All conformations that gave atomic distances less than 1.4 Å or with vdW potential energy >1,000 kcal/mol were discarded, resulting in a final set of 3,290 valid conformations. The final acceptor cloud is composed of discrete points, each of which represents the position of bodipy’s transition dipole moment per valid conformation (estimated as the geometric center of the chromophore’s central ring).

LRET-Restrained Molecular Modeling of BK.

Donor coordinates obtained from geometric fits to SE data were used as a constraint to refine an initial BK α-subunit model in the absence of the β1-subunit (SI Text, S3. Molecular Modeling and MD Simulations). The LBT peptide sequence was inserted into target sites accordingly to reproduce the LBT-BK constructs in silico using the same MD simulation size and parameters described for the [D19C]IbTX–bodipy–BK complex.

An LBT-Tb³⁺-restrained MD protocol was performed to refine the BK model according to donor coordinates. The Tb³⁺ Cartesian coordinates were restrained to its donor experimental position by means of a harmonic potential of 1 or 2 kcal⋅mol⁻¹⋅Ų using the colvar module of NAMD 2.9. The use of positional restraints allows smooth adaptation of the LBT-Tb³⁺ and the attached BK segment to the SNPS results. To maintain the LBT structure, a restraint of 2 kcal⋅mol⁻¹⋅Ų was also applied between the calcium (representing the terbium donor atom) and LBT’s charged side-chains.

Each LBT-BK system was simulated independently. The first system assembled included the LBT at the S1 insertion site. The positions of all four donor atoms were simultaneously restrained by coordinates obtained from the geometric fit. After 28 ns of simulation, the LBT structures were removed from S1 and inserted into the S2 site, extending the simulation by 28 ns with the donor positions restrained accordingly. Following the same strategy, the LBTs were inserted at the S0 site and simulated for 28 ns. The NT-LBT system was not simulated due to the intrinsic freedom of the NT. Finally, the LBTs were removed and the system was further relaxed for 40 ns.

Once each LBT segment was located at its experimental position by the above procedure, the subunit with the lowest energy conformation was considered to build a symmetrical tetramer of the BK α-subunit. The new symmetrical tetramer was used to build a membrane-embedded channel molecular system with the same dimensions and characteristics described above, and submitted to an MD simulation with restrained secondary structure. Symmetry was retained by means of harmonic restraints. The final production simulation lasted 20 ns.

The aforementioned BK channel was used to construct a 3D structural model of the BK α/β1-complex. The transmembrane segments of the β1-subunit were modeled using a generic α-helix due to lack of a crystal structure. The β1-subunit sequence obtained from the UniProt database (ID code Q16558) was analyzed using three secondary structure prediction algorithms [PSIPRED (50), MEMSAT (51) and TMHMM (52)] to define the transmembrane segments’ residues. The segments were modeled using the Prime module from the Schrödinger Suite, followed by a 5-ns MD protocol with the segments embedded in a phosphatidyloleoyl phosphatidylcholine (POPC) hydrated bilayer with 150 mM KCl. After 20 ns, the obtained structure was collected and used to build the initial BK α/β1-complex.

Both α- and β1-subunits were embedded in a POPC hydrated bilayer with 150 mM KCl. To represent the β1-subunit TM position calculated by LRET experiments, the α-carbon of the first residue of each segment was restricted to the x–y coordinates of its corresponding experimentally determined position (Ser45 for TM1 and Pro164 for TM2). This conformation was selected over other β1-subunits to minimize possible steric clashes among the extracellular loops. The final system containing BK α/β1-complex (final size of 210 × 210 × 111 ų, total of 371,560 atoms) was submitted to a 20-ns MD protocol using secondary and symmetry restraints as described above.

SI Text

S1. LRET Calculations.

R₀ Determination.

R₀ is the Förster distance at which energy transfer is 50% efficient (E = 0.5). R₀ was determined on the basis of measured spectral properties of the donor and acceptor (17) using the expression R₀ = 0.211(κ²n⁻⁴Q_DJ(λ))^1/6, with orientation factor κ² = 2/3, refractive index n = 1.4, donor quantum yield in absence of acceptor Q_D = (τ_D/τ_Di) = (2.5/4.75) = 0.526, and spectral overlap integral J(λ) = ∫ F_D(λ)ε_A(λ)λ⁴dλ. Q_D is equal to the ratio of experimental (τ_D) and intrinsic (τ_Di) DO time constants (in milliseconds). Due to partial donor quenching, slight variation in experimental τ_D (Table S1), and thus Q_D, were accounted for, resulting in a unique R₀ value per LBT construct. To calculate J(λ), the corrected donor emission spectrum F_D(λ) of Tb³⁺ ion complexed by custom-synthesized LBT peptide (Alpha Diagnostic International) was measured by spectrofluorometer (QuantaMaster; PTI) in a quartz cuvette (Hellma Analytics) at room temperature (RT). The solution contained 10 μM LBT peptide, 10 μM TbCl₃, and 10 mM Hepes (pH 7.5). Spectrofluorometer settings were λ_ex = 280 nm, λ_em = 400–800 nm, and slit widths = 1 mm, and the emission pathway included a FGL400 long-pass filter (Thorlabs). Spectral properties of bodipy fluorophore were carefully determined using both [D19C]IbTX-bodipy and cysteine-bodipy conjugates to account for conjugation effects, for example, the absorbance peak of free dye in methanol shifts from 523 nm to 512 nm after conjugation. Absorbance spectra were measured by a UV-Vis spectrophotomer (Cary 60; Agilent) in a quartz cuvette at RT. To calculate J(λ), the absorption spectrum of [D19C]IbTX-bodipy was measured at 10 μM concentration in 10 mM Hepes buffer (pH 7.5). The extinction coefficient of commercially available bodipy fluorophore is reported as ε_A = 74,000 M⁻¹⋅cm⁻¹ in methanol (CellTracker Green BODIPY; Molecular Probes). However, we observed extinction coefficient solvent dependence for both [D19C]IbTX-bodipy and cysteine-bodipy, which effectively reduced ε_A by ∼15% when transitioning from pure methanol to water. Taking this reduction into account, we estimated that ε_A ≈ 63,100 M⁻¹⋅cm⁻¹ for bodipy conjugate in aqueous solution. Cysteine-bodipy was prepared by addition of 20 μL of bodipy (5 mM in ACN) to a mixture of 80 μL of acetonitrile (ACN), 400 μL of MeOH, 100 μL of Hepes (10 mM, pH 7.5), 300 μL of dH₂0, and 100 μL of l-cysteine (0.5 M). The reaction was carried out to completion (1 h at RT), monitored by absorbance spectrum measurements. Toxin-dye and cysteine-dye conjugates were both fully soluble in pure methanol or water. We determined R₀ ≈ 39.7 Å for the LBT(Tb³⁺)/[D19C]IbTX-bodipy pair.

SE Geometric-Constrained Fit.

The theoretical SE trace is described by Eq. S1 (23):

$$I_s=B\exp (-t/{\tau }_{NS})+A{\displaystyle \sum _{i=1}^4[k_{Ti}\exp (-t(k_{Ti}+k_D))]+C},$$ [S1]

where the first exponential term is a fast-decaying nonspecific signal with amplitude B and time constant τ_NS (arising from delayed fluorescence, autophosphorescence, etc.). The nonspecific time constant was constrained to ensure it remains separated from the SE components (discussed below). A is the amplitude of the SE signal, C is the baseline, and t is time in milliseconds. k_i is the rate constant of the LRET interaction between the ith donor and the acceptor (Fig. 4A), and is a function of distance:

$$k_i=k_D{\left[\frac{R_0}{d_i}\right]}^6,$$ [S2]

where k_D is the rate constant of the DO emission (1/τ_D), obtained from the luminescence signal of the donor in absence of acceptor. R₀ is the distance at which k_i equals k_D. d_i represents the effective distance between the ith donor and the acceptor diffusion region in the rapid diffusion limit (13). Donor diffusion was modeled as a uniformly distributed sphere, and acceptor diffusion was modeled initially as a cloud of discrete points generated by molecular modeling (Fig. S5). Each of the four effective distances was calculated as follows:

$$d_i={\left({\displaystyle \sum _{j=1}^N{p}_j{\left(r_{i,j}^2-a_D^2\right)}^{-3}}\right)}^{-\frac{1}{6}},$$ [S3]

where r_j is the distance between the mean position of the ith donor and the jth discrete point of the acceptor cloud, each with probability p_j out of a total of N cloud points (Fig. S5), and a_D is the spherical diffusion radius of the donor volume, considered here as 3 Å (13). The acceptor cloud was fixed according to Cartesian coordinates obtained from molecular modeling, where the origin is set to the channel’s symmetry axis at the middle of the bilayer. Cylindrical coordinates of Donor₁ (radius r, angle θ, height z) determine the position of the other three donors, assuming that four of them are vertices of a square that is parallel to the x–y plane (Fig. 4A). Therefore, the three cylindrical coordinates determine the four effective distances between the donors and single acceptor. These three free parameters are part of the output of the SNPS software used to fit and generate the geometric models presented in this report. A comprehensive analysis throughout all datasets was made by allowing the initial acceptor cloud to shift its center of mass radially and optimize the probability of occupancies among rotamer-based subsets of points within the acceptor cloud. Such analysis was made to give our geometric model some flexibility, because we do not know a priori the real position or shape of the bodipy molecule’s diffusive volume. The final acceptor was treated as a single point offset by 4.75 Å from the z axis, because this way resulted in the best collective interpretation of all LRET data (discussed below). In the presence of the β1-subunit, including β1-LBT constructs, it was observed that the overall reduced chi squared (χ²_RG) diminished by radially displacing the acceptor 1 Å away from the pore (Fig. S4D), thus having a radial distance of 5.75 Å and still being within the shell of the originally modeled acceptor cloud.

Goodness of the geometric fits was evaluated by the χ²_RG value (13) and visual inspection of fit residuals (Fig. 4B). χ²_RG is the ratio of fit errors (reduced χ² for an ensemble of SE decays) between the geometric-constrained fit and a free multiexponential (unconstrained) fit with six components. For the entire dataset of all LBT constructs, the average χ²_RG was 1.03 ± 0.02 (SD, n = 121 SE traces), with a range of 1.01–1.08. The geometric model has two equivalent solutions as shown in Fig. 4C because the rotation angle can be ±θ with respect to the acceptor position: d₂ > d₃, solution type 1; d₂ < d₃, solution type 2 [details are provided in the study by Hyde et al. (13)]. The reported spatial maps were built by selecting the solution type of each construct that best matched the Kv1.2/2.1-CTX structure. For the sake of completeness, both solution types are reported in Fig. S3. In the case that one solution type could not be favored over the other (e.g., S0 construct), both solutions were displayed and then tested by constructing a donor position-restrained BK molecular model.

Optimization of the Acceptor Position.

The position of the bodipy acceptor fluorophore was initially modeled as a cloud of possible points accessible by diffusion of the probe about the IbTX labeling site, and with the IbTX docking position based on the CTX-bound Kv1.2/2.1 reference structure. Although a good starting point, we found that the actual acceptor position needed to be refined to minimize the error of the geometric fit (χ²_RG value) for all LBT constructs. Because we did not have a known position for any LBT construct a priori for use as a reference, we approached the acceptor position optimization problem by finding a globally optimal acceptor position under the constraint that all donor heights are within a structurally valid range of z = 15–35 Å. For each α-LBT construct (without β1), a geometric fit was performed with donor height fixed at a value from an evenly spaced set on [15,35] Å, but acceptor parameters were free to optimize (i.e., radial shift, point probabilities). For each fit, the acceptor cloud’s probability-weighted center of mass was calculated to represent its optimal position. Finally, the globally optimal acceptor point position was the position with maximum overlap from donor height scan series of all α-LBT constructs. For the dataset of α-LBT constructs expressed alone, this overlap point lies near, but within, the shell of the originally modeled acceptor cloud and has a radial distance of 4.75 Å from the channel’s symmetry axis (Fig. S5C). Due to its peripheral position relative to the original acceptor cloud, which may indicate a more confined diffusion volume (favoring Ψ₁ dihedral angles of 0°, 30°, and 60°), we chose to treat the acceptor as a single point for all subsequent analysis.

Nonspecific Decay Time-Constant Constraint.

The theoretical SE trace was described by Eq. S1, which included a fast-decaying nonspecific exponential with amplitude B and time constant τ_NS. LRET control experiments (SE, uninjected oocytes) showed that the nonspecific signal was best described by y_NS(t) ≈ 0.89exp[−t/37] + 0.11exp[−t/180] (time expressed in microseconds). Due to this complexity, we sought a robust strategy to determine the optimal τ_NS upper bound on a per decay basis. Because τ_NS is significantly faster than all distance components, Eq. S1 can be well fit to an SE decay excluding the nonspecific exponential (i.e., B = 0), provided that the fit start time t_start allows full decay of nonspecific signal (e.g., t_start > 3τ_NS). Optimal t_start was evaluated by performing a series of pyramid-constrained SE decay fits with variable t_start to construct a plot of <χ²_RG> vs. t_start for the ensemble of decays from a given LBT construct, which decayed to a steady-state level at approximately time t > 450 μs. As a smoothing function, this profile was fit by a three-exponential decay curve with offset c. Through simulation studies designed to recover geometric parameters optimally under these conditions, the optimal value t*_start occurred just before reaching steady-state level, specifically <χ²_RG> = 1.0025c. Finally, we defined the optimal τ_NS upper bound to equal (1/3)t*_start, which was 137 ± 30 μs (mean ± SD), with a range of 90–180 μs, among all SE datasets. For each LBT construct, SNPS fits using Eq. S1 were performed using t_start = 50–100 μs and optimal τ_NS upper bound set as determined by the above procedure. For completeness, we also fit all SE datasets without a nonspecific exponential (and t_start appropriately delayed) and recovered the same geometric parameters in both cases. Results presented herein were obtained with a fitted nonspecific exponential to maximize the number of fitted data points, and thus improve resolution of distances.

S2. IbTX-Bodipy Synthesis.

Reagents.

The 2-(1H-benzotriazol-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate and Nα-Boc protected L-amino acids (Peptide Institute) were obtained from Peptides International. Side-chain protecting groups used were Arg(Tos), Asp(OcHex), Cys(4-CH₃Bzl), Glu(OcHex), Lys(2Cl-Z), Ser(Bzl), Thr(Bzl), Trp(CHO), and Tyr(2Br-Z). Aminomethyl-resin (1.00 mmol/g) was prepared from Biobeads S-X (BioRad) (53). Diethyl ether, dichloromethane, N,N-dimethylformamide (DMF), HPLC-grade acetonitrile, and guanidine hydrochloride were purchased from Fisher. Trifluoroacetic acid (TFA) was obtained from Halocarbon Products. Hydrofluoric acid (HF) was purchased from Matheson. The 8-(chloromethyl)-4,4-difluoro-1,3,5,7-tetramethyl-4-bora-3a,4a-diaza-s-indacene (bodipy, calculated mass = 296.55 Da) was prepared and purified as previously described (54). All other reagents were purchased from Sigma–Aldrich and were of the purest grade available.

Peptide Synthesis.

Peptide segments were synthesized using manual “in situ neutralization” Boc chemistry protocols for stepwise solid-phase peptide synthesis (55). All peptides were synthesized on Boc-Phe-OCH₂-Pam-resin at a 0.5-mmol scale (56). The peptide-thioesters were synthesized on trityl-SCH₂CH₂CO-Ala-OCH₂-Pam-resin at a 0.5-mmol scale (57). After removal of the N-αBoc group, peptides were cleaved from the resin and simultaneously deprotected by treatment at 0 °C for 1 h with anhydrous HF containing 5% (vol/vol) p-cresol as a scavenger. After removal of HF by evaporation under reduced pressure, each crude peptide was precipitated and washed with diethyl ether and then dissolved in 50% (vol/vol) aqueous acetonitrile containing 0.1% TFA and lyophilized.

Formyl (CHO) Group Removal.

For synthesis of the peptide l-[Cys¹³-Gln³⁷], the formyl-protecting group on Trp¹⁴ was removed by treating the peptide-resin with 10% (vol/vol) piperidine and 5% (vol/vol) water in DMF three times for 20 min each time at RT before final Boc group removal, followed by cleavage and deprotection with HF.

Chemical Synthesis of Bodipy-Labeled IbTX.

[D19C]IbTX was prepared by native chemical ligation of two unprotected peptide segments and purification of the product 37-residue polypeptide, followed by folding/disulfide bond formation (Fig. S6A). l-[Glu¹-Glu¹²]-α-thioester (71 mg, 26.6 μmol) and l-[Cys¹³-Gln³⁷] (67.8 mg, 27.2 μmol) were dissolved in 2 mL of ligation buffer containing 6 M guanidine HCl, 0.1 M Na₂HPO₄, 100 mM Tris(2-carboxyethyl)phosphine hydrochloride, and 100 mM 4-mercaptophenylacetic that had been degassed for 15 min before use. The pH was adjusted to 7.0, and the reaction was kept for 48 h and purified by reverse-phase semipreparative HPLC (C18, 10 μm, 300 Å) using a linear gradient of 1–50% of buffer B in buffer A over 100 min at 40 °C (buffer A = 0.1% TFA in H₂O, buffer B = 0.08% TFA in acetonitrile). The purified linear (1–37) peptide product was then dissolved in 10 mL of 100 mM Na₂HPO₄, and the pH was adjusted to 8.0 and stirred under air at RT for 6 h. The pH of the solution was then adjusted to 6.7, and bodipy (3 eq in 5 mL of isopropanol and 2 mL of DMSO) was subsequently added dropwise. The solution was stirred overnight before HPLC purification to afford labeled product (2.7 mg, 6.1 nmol, 0.22% yield). The N-terminal pyroglutamate of this toxin (21) was replaced by glutamic acid for synthesis, which later converted to pyroglutamate (58) as demonstrated by MS data of the purified toxin molecule (Fig. S6B). The MS data of the toxin-dye conjugate (Fig. S6C) correspond to the molecule [D19C]IbTX-bodipy.

S3. Molecular Modeling and MD Simulations.

Human α-Subunit BK Initial Molecular Model.

The BK channel amino acid sequence was obtained using the nucleotide sequence code gi46396283 of the GenBank database (UniProt ID code Q12791.2). PSIPRED (50), and MEMSAT (59) prediction methods were combined to define the limits of the secondary structure elements and transmembrane segments, respectively. The predictions of these structures were contrasted with known experimental data, allowing us to divide the sequence into three characteristic regions: pore (S5–S6 segment), S1–S4, and S0 segments, which were evaluated independently to find appropriate structural templates for homology modeling. The pore was modeled using the multiple sequence alignment done by Carvacho et al. (60) together with the MthK crystallographic structure (61) [Protein Data Bank (PDB) ID code 4HYO], achieving an overall 35% sequence identity. The S1–S4 sequence was aligned against the Kv1.2/Kv2.1 chimera crystallographic structure (62) (PDB ID code 2R9R) based on a multiple sequence alignment previously described by Lu et al. (63), obtaining a 24% sequence identity. The S0 segment was built as a long α-helix according to secondary structure prediction results, mapping the S0 backbone structure on the S1 segment. The S0 segment was located between the S1 and S2 segments considering the differences between the S0 and NT segments’ donor coordinates of the BK α- and BK α/β1-complex. When required, the LBT structure (18), with calcium (considering a 3+ charge) representing the Tb³⁺ ion, was incorporated into different positions of the external loops of the α-subunit where LBTs were genetically encoded.

Bodipy Structure and Force Field Parameters.

The bodipy initial structure was sketched using GaussView software 3.07. The molecular geometry was then optimized using B3LYP/6-31G(d) level of theory. Geometry optimization and vibrational frequency calculations were carried out using Gaussian 03 software. The force constants of bond lengths, bond angles, dihedral angles, improper angles, and missing Lennard–Jones parameters were determined from the aforementioned quantum calculations or transferred the CHARMM force field and the corresponding parameters described for BODIPY-PC (64).

Bodipy–[D19C]IbTX–BK Complex Modeling and MD Simulation.

The IbTX 3D structure was obtained by homology modeling using the CTX structure as a template (PDB ID code 2A9H) and the alignment described by Johnson and Sugg (65). The program MODELLER 9v7 was used to generate several toxin models (66), which were sorted according to their Discrete Optimized Protein Energy potential. The best IbTX model was docked to the BK structure using as a reference the CTX-Kv1.2/2.1 complex structure (22), because the CTX toxin family complex with K⁺ channels has been described to have similar structural properties (67). Briefly, the BK initial model and the CTX-Kv1.2/2.1 complex were structurally aligned using their selectivity filter (sequence TVGYG) as a reference, maintaining the CTX-Kv1.2/2.1 coordinate frame. Afterward, the IbTX model was aligned to CTX using their α-carbon atoms as a reference, achieving an rmsd value of ∼1 Å between both toxin backbones. The IbTX–BK complex was energy-minimized and equilibrated by means of MD for 2 ns with backbone atoms restrained. Next, the [D19C]IbTX–bodipy–BK complex model was generated using MODELLER’s amino acid replacement methods. Bodipy was linked to IbTX by a covalent bond with the Asp19Cys mutant of IbTX, and submitted to a 2-ns MD simulation with the protein and toxin backbone restrained by 0.5 kcal⋅mol⁻¹⋅Ų of harmonic potential and the fluorophore set free to move. At the end of simulations, IbTX retained the CTX spatial position. The [D19C]IbTX-bodipy-BK system was embedded into a POPC bilayer. Subsequently, the model was hydrated, neutralized, and ionized at 0.110 M KCl. The simulated systems consisted of ∼450,000 atoms, and their dimensions were ∼19 × ∼19 × ∼14 nm³. All MD procedures were performed with the software NAMD 2.9 (68) using the CHARMM36 force field (69). BK’s pore secondary structure was restrained by means of a harmonic potential restraint of 0.5 kcal⋅mol⁻¹⋅Ų applied to its α-carbons. The initial conformations were energy-minimized until convergence and equilibrated for 1.2 ns at a constant volume and 300 K (Canonical ensemble), followed by 2 ns at a constant pressure and temperature (1 atm and 300 K, respectively), with fully anisotropic pressure coupling and absence of external surface tension components. The pressure was controlled using the Langevin piston method (70). The temperature was controlled using Langevin dynamics with a damping coefficient of 1 ps⁻¹. Periodic boundary conditions were used in all simulations. The equations of motion were integrated with a time step of 2, 2, and 4 fs for bonded, short-range, and long-range nonbonded interactions, respectively. An 8-Å spherical cutoff was used for short-range nonbonded interactions, including a switching function from 7 Å for the vdW term and shifted electrostatics (71). For long-range electrostatic interactions, the particle-mesh Ewald method was used with a grid spacing on the order of 1 Å or less. The TIP3P water model was used (72).