Visualizing weakly bound surface Fermi arcs and their correspondence to bulk Weyl fermions

Fermi arc states on the surface of a Weyl semimetal are revealed by the structure of their wave function.

Abstract

Fermi arcs are the surface manifestation of the topological nature of Weyl semimetals, enforced by the bulk-boundary correspondence with the bulk Weyl nodes. The surface of tantalum arsenide, similar to that of other members of the Weyl semimetal class, hosts nontopological bands that obscure the exploration of this correspondence. We use the spatial structure of the Fermi arc wave function, probed by scanning tunneling microscopy, as a spectroscopic tool to distinguish and characterize the surface Fermi arc bands. We find that, as opposed to nontopological states, the Fermi arc wave function is weakly affected by the surface potential: it spreads rather uniformly within the unit cell and penetrates deeper into the bulk. Fermi arcs reside predominantly on tantalum sites, from which the topological bulk bands are derived. Furthermore, we identify a correspondence between the Fermi arc dispersion and the energy and momentum of the bulk Weyl nodes that classify this material as topological. We obtain these results by introducing an analysis based on the role the Bloch wave function has in shaping quantum electronic interference patterns. It thus carries broader applicability to the study of other electronic systems and other physical processes.

INTRODUCTION

Topological states of matter harbor strikingly unique boundary states, such as the chiral edges of the quantum Hall effect (1), the surface states of topological insulators (2, 3), and the Majorana end modes of topological superconductors. The properties of these surface states, such as gapless surface spectrum, relativistic dynamics, and evasion of localization by disorder, are determined by the topological nature of the bulk and are protected by the energy gap in the bulk’s spectrum. These states cannot be realized as stand-alone systems without the coupling to the topological bulk. Surprisingly, these states exist even on two-dimensional surfaces of three-dimensional Weyl semimetals (4–9), despite the absence of a bulk energy gap (10). The defining characteristic of these states is the Fermi arcs, which may not be realized on stand-alone two-dimensional systems. Whereas in two-dimensional systems, lines of constant energy must form closed contours in momentum space, Fermi arcs are open contours that emanate and end in states associated with bulk Dirac cones whose nodes are termed Weyl nodes. Here, we use scanning tunneling microscopy (STM) and spectroscopy to study surface states in the Weyl semimetal tantalum arsenide (TaAs). Bulk and surface band structures of TaAs have been modeled (7–9) and mapped by photoemission spectroscopy (11–13), and its unique electrodynamics (14–18) have been probed in magnetotransport (19, 20). Previous STM studies of this material have identified scattering processes among the nontopological surface bands (21) and between these surface bands and a Fermi arc band, where absence of other scattering processes involving Fermi arc states was attributed to their connectivity with topological bulk bands (22). Here, we report an exhaustive visualization of the scattering processes available among the different surface bands, including intra-arc scatterings. Processes involving Fermi arc states are identified by their distinctive attributes and real-space structure. This provides a comprehensive characterization of the unusual properties of the Fermi arc states and their unique correspondence to topological bulk bands.

RESULTS

High-quality single crystals of TaAs (see Materials and Methods) were cold-cleaved at 80 K under ultrahigh vacuum, exposing a fresh (001) surface that was measured at 4.2 K in a commercial STM (UNISOKU). Quasiparticle interference (QPI) patterns that elastically scattered electrons embed in the local density of states were measured in differential conductance (dI/dV) mappings. We reveal four distinct attributes of the Fermi arcs by measuring different aspects of their scattering processes: (i) their relatively isotropic QPI profile, revealed by scattering off atomic vacancies (23–26); (ii) the linear energy dispersion and its relation with bulk Weyl nodes, by scattering off a crystallographic step edge; (iii) their localization on the Ta layer, by tracing the spatial origin of their QPI patterns with subatomic resolution; and (iv) the weak coupling to the surface atomic structure, as opposed to the strongly coupled trivial states, deduced from the manifestation of their wave function structure in the QPI pattern.

Visualizing the Fermi arc contour

An atomically resolved topographic image with several vacancies is shown in Fig. 1A. The QPI patterns seen in the dI/dV map (Fig. 1B) appear around those vacancies. In TaAs, these QPI patterns are superimposed on a spatial density modulation, commensurate with the lattice structure (inset). Fourier decomposition of the QPI pattern at a fixed energy (Fig. 1C) separates surface scattering processes according to their transferred momentum, q, between incoming and scattered electronic waves. We recognize three prominent QPI patterns: ellipse-shaped patterns around G_o and G_±Y, half of bowtie-shaped patterns at G_±X, and portions of rounded square-shaped patterns on the four corners of the central zone (dashed lines). These QPI patterns result from inter- and intraband scattering of nontopological surface states (21). To associate these QPI patterns with particular scattering processes, we plot in Fig. 1D the spin-selective scattering probability (SSP) calculated (see the Supplementary Materials) for the As-terminated Fermi surface of TaAs, based on its previously extracted dispersion (9, 13) and spin texture (Fig. 1E) (13, 27). By comparing the SSP with the central zone in the QPI map, we identify the ellipse QPI with scattering within the ellipse-shaped bands (blue arrow in Fig. 1E), and the square patterns (green in the SSP) with bowtie-to-ellipse scattering (green arrow). The detected splitting of the latter into two concentric squares originates from scatterings among the spin-split copies of the ellipse and bowtie bands and thus directly reflects the strong spin-orbit coupling in TaAs (28). Absence of double ellipse and bowtie QPI patterns manifests the scattering protection provided by these bands’ approximate helical spin textures (27, 29).

Fig. 1. Quasiparticle interference of trivial bands and Fermi arcs in TaAs.

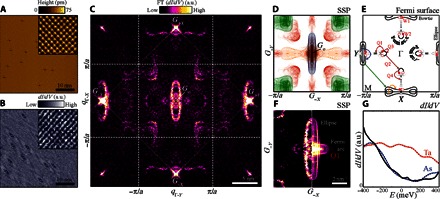
(A) Topography (V_B = −400 meV; I_t = 350 pA) of the (001) surface of TaAs with a few As vacancies. Inset: Atomic resolution with a lattice constant a = 3.47 Å. (B) dI/dV map of (A) (V_B = 0 meV) shows elongated QPI around vacancies on top of an atomically modulated local density of states (inset). (C) Fourier analysis of (B) reveals an intricate QPI pattern centered on both q = 0 and Bragg peaks. (D) SSP based on density functional theory (DFT) calculation shows marked resemblance to the central zone in (C): ellipse-shaped (blue) and bowtie-shaped (yellow) , spin-orbit-split double squares (green), intra–Fermi arc scattering around G_o (that is, q = 0) and inter–Fermi arc along G_o-G_M. Some SSP features appear in (C) around both G_o and the Bragg peaks G_±X, G_±Y. (E) DFT-calculated Fermi surface of As-terminated TaAs contains bowtie- and ellipse-shaped bands and topological Fermi arcs emanating from Weyl nodes W1 and W2 at energies −13 and 1.5 meV, respectively (red). Intra- and interband scattering processes are represented by colored arrows. Intra– (Q1, Q3, and Q4) and inter– (Q2) Fermi arc processes are labeled. (F) A magnified view of the G_o vicinity (left) reveals a round arc beyond the ellipse pattern (left). It agrees well with the SSP of scattering around the Fermi arc (Q1) and that of the ellipse (right). (G) Measured dI/dV spectrum (solid) and calculated density of states of As- and Ta-terminated (001) surfaces (blue and red, respectively), indicating the As termination of the measured sample.

Excellent agreement between the measured QPI and SSP as well as between the measured spectrum and the calculated density of states for As-terminated surface (Fig. 1G) confirms our identification of the As surface termination. We note that intraband scattering within the bowtie band (yellow in SSP) around G_o is hardly observed in the measured QPI at that energy. Its absence (addressed below) enables first detection of the Fermi arcs around G_o (magnified in Fig. 1F, left). We find two leaf-like features that peak beyond the ellipse (see also the Supplementary Materials). Quantitative agreement with the calculated SSP (Fig. 1F, right) identifies these features with the scattering processes between the Fermi arcs that emanate from the W2 Weyl node (defined in Fig. 1E) and the states located at their fine-structured tail (Q1 in Fig. 1E). Their arc-like shape directly reflects the contour of the Fermi arcs.

Fermi arc dispersion and its correspondence to the bulk Weyl nodes

The energy dispersion of the Fermi arcs is measured by electron-scattering off a crystallographic step edge that is oriented 49° with respect to the crystal axis (Fig. 2A). Accordingly, the interference pattern forms approximately along the G_o-G_M direction (Fig. 2B). The measured dI/dV line cut (Fig. 2C) displays clear dispersing interference patterns superimposed on commensurate (inset) nondispersing modulations. Fourier transforming this map (Fig. 2D) reveals the energy evolution of the QPI along G_o-G_M. The dispersing ellipse- and square-shaped QPI (blue and green arrows, respectively) are identified by comparison to SSP (Fig. 2E); between these two, we observe (red arrow) a scattering signature among the two Fermi arcs (Q2 in Fig. 1E). Upon increasing the energy toward W2, the extent of each arc shrinks (7–9, 11–13), resulting in a linear increase of the inter-arc separation, which corresponds to an average velocity of ~10⁵ m/s per arc. At the W2 energy (2 meV above Fermi energy), the inter-arc separation becomes the inter–Weyl node separation (see its evolution in the Supplementary Materials) and equals 5.4 ± 0.1 nm⁻¹, demonstrating a quantitative correspondence between the surface Fermi arc and the bulk Weyl node location in momentum space. Both values are consistent with our band structure modeling (9) and photoemission spectroscopy (11–13).

Fig. 2. Fermi arcs on Ta and trivial bands on As.

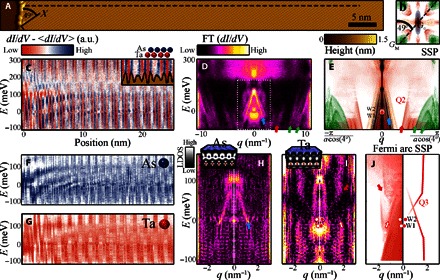
(A) Step edge topography oriented 49° with respect to the crystal axis. (B) Corresponding 49° cut (dashed line) across the SSP. (C) dI/dV map along the dashed line in (A) shows modulations in the density of states. Inset: Its commensuration with the topographic profile. It exhibits high density of states on As atoms and lower density of states on Ta, as well as dispersive interference patterns. (D) Fourier analysis of (C) shows the energy dispersion of the ellipse (blue arrow), the squares (green arrows), and the Fermi arcs (Q2 in Fig. 1E). (E) SSP cut along the dashed line in (B) identifies Q2 with inter–Fermi arc scattering, extending above and below the Weyl nodes’ energies (E_W2 ≈ 2 meV and E_W1 ≈ −13 meV, respectively). (F and G) Density of states on As sites (blue) and on Ta sites (red) reveals two different dispersing modes. (H) Fourier analysis of (F) detects the energy dispersion of the ellipse QPI. Inset: Calculated electronic local density of states (LDOS) of the ellipse band shows high localization on As sites. (I) Fourier analysis of (G) unveils QPI pattern associated with the Fermi arcs, which extrapolates to W2. Inset: Fermi arc wave function is localized on Ta sites. (J) Left: SSP of Fermi arcs only; right: dispersion extracted from left panel. Note its resemblance to (H). One of the modes extrapolates to the projection of W2 due to shrinkage of the Fermi arc (D, inset).

Common origin of surface Fermi arc and bulk Weyl bands

In contrast to trivial states that are bound to the surface by the local surface potential, the Fermi arcs’ existence is guaranteed by the bulk topology. We examined the distribution of the two types of bands with respect to the topmost As layer. To this end, we decompose (see the Supplementary Materials) the dI/dV map to submaps measured on As sites (Fig. 2F) and on Ta sites, located one monolayer deeper (Fig. 2G). The Fourier transforms of the two submaps display distinct patterns. QPI on the As layer matches that of the ellipse band (blue arrows in Fig. 2, E and H). In contrast, on the Ta layer, we find two opposite V-shaped curves (red arrows in Fig. 2I) that agree with the SSP of intra–Fermi arc processes (Q3 in Fig. 2J). Intriguingly, because of the shrinking extent of the Fermi arcs in momentum space toward the Weyl node, the upper dispersing branch extrapolates to the energy of the W2 Weyl node, again demonstrating the bulk-surface correspondence in energy and momentum. Furthermore, the distinct QPI patterns assert that the Fermi arc’s wave function is profoundly distinct from the nontopological dangling bond bands. Whereas the latter are confined to the As termination layer, the Fermi arc states, which relate to the bulk Weyl-cone Ta states (Fig. 2, H and I, insets), indeed reside on the Ta sites and extend further into the bulk.

Structure of the surface wave function and their topological classification

We now show that the Fermi arc bands differ from nontopological bands, also in their structure, parallel to the surface within the unit cell. Figure 3 shows QPI maps at three different energies (right panels), alongside dI/dV maps in a vacancy-free region (left panels). At −300 meV (below Fermi energy), the vacancy-free dI/dV map and the corresponding QPI map are approximately symmetric to 90° rotations, and the QPI patterns are concentrated around G_o. In contrast, at 85 meV, 130 meV, and the Fermi energy (Fig. 1B, inset), the vacancy-free dI/dV shows a clear chain structure that changes its crystallographic orientation with energy. The QPI features at corresponding energies are strongly replicated along that modulation direction. Modulation in a vacancy-free region ought to be attributed to the structure of the wave function. The correlation demonstrated in Fig. 3 is established by detailed comparison of the energy evolution of the intensities of the vacancy-free Bragg peaks (Fig. 4A) with that of the QPI scattering peaks (Fig. 4B). The Bragg peak intensity is extracted directly from the Fourier transform of a dI/dV map (Fig. 4A, inset) that is taken in a vacancy-free region, and the QPI intensities are extracted from the average intensity of the various QPI patterns (Fig. 4B, inset, and the Supplementary Materials). We note that small-momentum structure, which often arises from long-wavelength inhomogeneities, is completely absent in the vacancy-free image and hence cannot account for any features detected in the QPI at the zone center. Direct comparison of the two measures reveals that the intensity of vacancy-free dI/dV modulations along Γ-Y is fully correlated with the G_o-G_Y replications of the ellipse’s QPI; the same is observed for the bowtie along the Γ-X direction. The strong correlation between the two seemingly unrelated phenomena extends to all energies and suggests that both are dictated by the structure of the wave function rather than the details of the scatterer. In contrast to the trivial bands, the Fermi arcs’ QPI does not show any detectable replications, implying their relatively uniform distribution within the unit cell.

Fig. 3. Correlation between modulations and replications set by the electronic wave function.

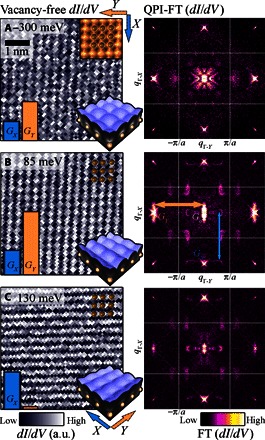
(A to C) Left panels: dI/dV in a vacancy-free region at three representative energies shows strong modulation, whose strength and orientation change with energy. The bars represent the Bragg peak intensities, ${|{\mathit{A}}_{{\mathit{G}}_{\mathit{X}},{\mathit{G}}_{\mathit{Y}}}|}^2$, along the two crystallographic directions. Insets: DFT calculation of the local charge density that captures a similar modulation. Right panels: Fourier analysis of extended dI/dV maps in the presence of vacancies at the corresponding energies. The intensity and anisotropy of the replications of QPI features are correlated with the modulation detected in the vacancy-free region.

Fig. 4. Replicated QPI patterns as a spectroscopic tool.

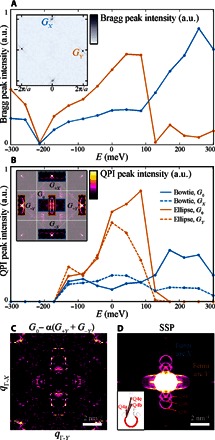
(A) Energy dependence of the Bragg peaks’ intensities in the vacancy-free region. Inset: Fourier transform of the dI/dV map from which the intensities are extracted. (B) Energy dependence of the QPI intensities of the bowtie and ellipse patterns (orange and blue, respectively; see this method of extraction in the Supplementary Materials) around q = 0 and around the Bragg peaks (see inset for legend). The ellipse is correlated with the Bragg peaks along Γ-Y, whereas the bowtie is correlated with Bragg peaks along Γ-X. (C) Subtraction of QPI peaks at G_±Y times α = 1.14 (the ratio between extracted intensities of ellipse QPI at G₀, and G_Y at E_F) from the central zone eliminates the ellipse from around q = 0, while leaving the QPI pattern of the Γ-X Fermi arc unaffected. Signatures of scatterings among the Γ-Y Fermi arc are revealed. (D) SSP of Fermi arcs alone. Inset: Contributing scattering processes (Q4a to Q4c) within the Fermi arc along Γ-Y.

Aiming at using this distinction to separate the different states, we note that both the dI/dV map in the vacancy-free regions and the QPI near vacancies reflect the coupling of the electrons to the periodic potential on the surface plane. The Bloch theorem constrains a state with a crystal momentum k to be a superposition of momenta k + G, where G is a vector in the two-dimensional reciprocal lattice, ${\mathrm{\Psi }}_{\mathit{k}}(\mathit{r})={\displaystyle {\sum }_{\mathit{G}}}{\mathit{C}}_{\mathit{G}}^{\mathit{k}}{\mathit{e}}^{\mathit{i}(\mathit{k}+\mathit{G})\cdot \mathit{r}}$. Consequently, the local density of states in a vacancy-free region becomes ∑_gA_ge^ig⋅r, where ${\mathit{A}}_{\mathit{g}}={\displaystyle {\sum }_{\mathit{G},\mathit{k}}}{\mathit{C}}_{\mathit{G}}^{*\mathit{k}}{\mathit{C}}_{\mathit{G}\prime }^{\mathit{k}}\mathrm{\delta }(\mathit{E}-{\mathit{E}}_{\mathit{k}})$ is the amplitude of the Bragg peak that corresponds to g = G − G′, r is the position, E is the energy, and E_k is the energy of the state with momentum k. A state with multiple substantial Bloch coefficients ${\mathit{C}}_{\mathit{G}}^{\mathit{k}}$ has a fine structure within the unit cell, which translates to multiple Bragg peaks. A vacancy violates the periodicity and adds a potential V(r), whose Fourier transform is V_q. The vacancy may scatter an electron between states Ψ_k(r) and Ψ_k′(r) through any momentum transfer q_g satisfying q_g = k − k′ + g. The amplitude for each of these processes is proportional, within the Born approximation, to ${\displaystyle {\sum }_{{\mathit{G}}^{\prime }}}{\mathit{V}}_{{\mathit{q}}_{\mathit{g}}}{\mathit{C}}_{{\mathit{G}}^{\prime }+\mathit{g}}^{*\mathit{k}}{\mathit{C}}_{{\mathit{G}}^{\prime }}^{{\mathit{k}}^{\prime }}$. Hence, the multiple substantial coefficients ${\mathit{C}}_{\mathit{G}}^{\mathit{k}}$ result in replicas of the QPI around multiple Bragg peaks (30), limited by the ability of the potential to provide the required momentum transfer (see the Supplementary Materials).

Accordingly, the replicated QPI observed in Fig. 3 originates from bands whose wave functions include several substantial Bloch components. We attempt to eliminate these states from the QPI map by subtracting their scaled replicated signals from the G_o signal. In Fig. 4C, we show the outcome of subtracting the ellipse QPI around G_±Y from that around G_o at E_F (dashed and solid orange squares, respectively, in the inset of Fig. 4B). Whereas the ellipse is eliminated, the Γ-Y Fermi arcs’ QPI signature remains unchanged. This elimination further exposes a signature of the Γ-X Fermi arcs (compare to SSP of Fermi arcs shown in Fig. 4D). This observation indicates that the Fermi arc wave function on the surface differs from that on nontopological bands because it is composed of a single dominant term (g = 0) or a combination of terms whose momentum difference (g = G − G^′) is larger than our resolution.

DISCUSSION

The topological nature of Weyl semimetals is manifested by the bulk Weyl nodes, their Berry flux, and the essential surface Fermi arcs that accompany them. The correspondence between the bulk and surface states gives rise to various physical phenomena that characterize the topological semimetals and their unique electrodynamics (14–18). However, in real systems, there are also nontopological surface states that overlap in space and energy with the topological Fermi arcs. These states, which may originate, for instance, from dangling bonds, are ubiquitous. Their effects on phenomena that involve the Fermi arcs, such as the cyclotron frequency of cyclotron orbits that connect opposite surfaces, are not determined by topological considerations alone; rather, it is affected by the combined energy-momentum dispersion of both types of states, by the wave functions of both types of states, and by impurity-induced scattering between the two types of states that we visualize.

The measurements we report here provide information on the interplay between the Fermi arc states and the nontopological ones as well as on their correspondence with the bulk Weyl nodes. We visualized scattering processes among the Fermi arc surface bands, processes that scatter Fermi arc states to trivial states, and processes that scatter between trivial states. The two processes that involve only topological states were found to be correlated with the energy-momentum location of the bulk Weyl nodes. The intra-arc scattering channel (Fig. 2, I and J) extrapolates to the momentum separation of a Weyl pair, whereas the momentum transfer of the inter-arc scattering channel (Fig. 2, D and E) entails the momentum separation between Weyl nodes of adjacent pairs. We stress that this quantitative correspondence between the topologically classified bulk dispersion and the momentum extent of the Fermi arcs is unique to semimetallic topology classes. All previously studied topological electronic phases have a gapped bulk spectrum, which is thus spectrally featureless. Bulk-surface correspondence is also evident by the structure of the Fermi arc wave function that resides predominantly on the subjacent Ta sites, from which the bulk Weyl cones are also derived (22).

We further showed that the lateral spatial structure of the Fermi arc wave functions within the unit cell is rather uniform and resembles a plane wave. It stands in stark contrast to the intricate structure of the nontopological surface bands, as captured by their strongly replicated QPI patterns. This observation demonstrates that the topologically derived Fermi arc states are fairly oblivious to the surface potential, which is a property that is not shared by the nontopological ones. The method of analysis that we developed and implemented, in which the replicated structure of QPI patterns is used to separate overlapping features in the pattern, will have further applicability in future studies of Fermi arcs in Weyl semimetals and in other electronic systems. Many topological surface states in different materials did not exhibit any clear replications in their QPI signatures (29, 31, 32), possibly signifying their surface resilience. A counter example that calls for a closer examination is that of topological crystalline insulators whose Dirac surface states’ QPI signatures were found to be replicated (33). Strongly correlated electronic systems may also be probed in a similar fashion. For instance, QPI patterns in high-temperature superconductors (34, 35), in which charge order has been recently reported, also exhibit replications. It would be enticing to apply our method of analysis to characterize the structure of the Bloch wave functions in such systems and to possibly unveil hidden spectroscopic features. On a yet broader scope, our resolution of the detailed structure of the Bloch wave function in local density of states and QPI measurements suggests that it will further affect other physical processes that involve quantum electronic interference. Among these are Friedel oscillations and their signature in transport, and surface state–mediated RKKY interactions. The role of the structure of the Bloch wave function in these processes calls for further theoretical elucidation alongside experimental verification.

MATERIALS AND METHODS

Sample synthesis

The single crystals of TaAs were grown using the chemical vapor transport method in a two-zone furnace on the basis of the precursor of polycrystalline samples, which were prepared by mixing high-purity (>99.99%) Ta and As elements. Both the polycrystalline TaAs powder and 0.46 mg cm⁻³ of iodine were loaded into a 24-mm-diameter quartz tube and then sealed under vacuum. Two ends of the tube were kept at 1150°C (charged part) and 1000°C for 21 days. The synthesized single crystals can be as large as 0.5 to 1 mm in size.

Spin-selective scattering probability

In the absence of a spin texture, measured QPI patterns are commonly compared to the calculated joint density of states (JDOS). The JDOS is the autocorrelation of the density of states across the Fermi surface ρ_E(k) and accounts for the summed amplitude of all available scattering processes of wave vectors (q) among the bands

$${\text{JDOS}}_{\mathit{E}}(\mathit{q})={\mathrm{\rho }}_{\mathit{E}}(\mathit{k})\otimes {\mathrm{\rho }}_{\mathit{E}}(\mathit{k})={\displaystyle \int }{\mathrm{\rho }}_{\mathit{E}}(\mathit{k}+\mathit{q}){\mathrm{\rho }}_{\mathit{E}}(\mathit{k})\mathit{d}\mathit{k}$$

A spin texture of a band will further attenuate otherwise available scattering processes on the basis of the spin overlap of initial and final states

$$\mathit{S}\mathit{S}{\mathit{P}}_{\mathit{E}}(\mathit{q})={\displaystyle \int }{\mathrm{\rho }}_{\mathit{E}}(\mathit{k}+\mathit{q}){\mathrm{\rho }}_{\mathit{E}}(\mathit{k}){|\langle {\mathrm{\sigma }}_{\mathit{k}+\mathit{q}}|{\mathrm{\sigma }}_{\mathit{k}}\rangle |}^2\mathit{d}\mathit{k}$$

Trigonometric identities can be used to cast this into a form that can be written as an autocorrelation.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/8/e1600709/DC1

Extended q-space map

dI/dV maps: Raw data and symmetrization

Fermi arc scattering signature

Agreement between vacancy- and step edge–induced QPI

Fermi arc dispersion

Correlation between scatterer-free dI/dV modulations and replications of QPI patterns

Correspondence between QPI patterns and Bloch wave function

Band structure calculations

Extracting the intensity of QPI features

Splitting the line-cut dI/dV into submaps

fig. S1. Extended q-space map.

fig. S2. dI/dV maps: Raw data and symmetrization.

fig. S3. QPI pattern involving Fermi arc scattering from a different vacancy distribution.

fig. S4. Agreement between vacancy- and step edge–induced QPI.

fig. S5. Calculated Fermi arc dispersion.

fig. S6. Structure of the Bloch wave function and its correspondence to QPI.

fig. S7. Wave function distribution.

fig. S8. Extraction of QPI feature intensities.

Reference (36)