Constrained Maximum Likelihood Estimation for Model Calibration Using Summary-level Information from External Big Data Sources

Abstract

Information from various public and private data sources of extremely large sample sizes are now increasingly available for research purposes. Statistical methods are needed for utilizing information from such big data sources while analyzing data from individual studies that may collect more detailed information required for addressing specific hypotheses of interest. In this article, we consider the problem of building regression models based on individual-level data from an “internal” study while utilizing summary-level information, such as information on parameters for reduced models, from an “external” big data source. We identify a set of very general constraints that link internal and external models. These constraints are used to develop a framework for semiparametric maximum likelihood inference that allows the distribution of covariates to be estimated using either the internal sample or an external reference sample. We develop extensions for handling complex stratified sampling designs, such as case-control sampling, for the internal study. Asymptotic theory and variance estimators are developed for each case. We use simulation studies and a real data application to assess the performance of the proposed methods in contrast to the generalized regression (GR) calibration methodology that is popular in the sample survey literature.

1 INTRODUCTION

Population based biomedical science is now going through a paradigm shift as extremely large data sets are becoming increasingly available for research purposes. Sources of such big data include, but are not limited to, population based census data, disease registries, health care databases and various consortia of individual studies. The power of such large data sets lies in their sample size. They, however, often do not contain detailed information at the level of individual analytic studies, which may be much smaller in size, but have been designed to answer specific hypotheses of interest. There is a growing need for a statistical framework for combining information from data sets that are large but have relatively crude information with that available from studies that are small but contain more detailed information on each subject. Methods that can work with summary level information, as opposed to individual level data, are particularly appealing due to practical reasons such as data sharing, storage and computing, as well as for ethical reasons, such as maintenance of the privacy of the study subjects and protection of the future research interests of data generating institutions and investigators.

In this article, we consider the problem of building regression models using individual level information from an analytic study while incorporating summary level information from an external large data source. Our goal is to work within a semiparametric framework that allows the distribution of all covariates to remain completely unspecified, so that analysis results are not sensitive to modeling assumptions. One class of methods that could potentially be used for this purpose is to use calibration techniques that are popular in sample-survey theory. Chen and Chen (2000), for example, studied the extension of the generalized regression (GR) method for developing regression models using data from double sampling or two-phase designs in cases where the internal study is a sub-sample of the external one. There exists a rich literature on how to form optimal calibration equations for improving efficiency of parameter estimates within various classes of unbiased estimators (Deville and Sarndal 1992; Robins, Rotnitzki and Zhao 1994; Wu and Sitter 2001; Wu 2003; Lumley, Shaw and Dai, 2011). Unlike GR, however, the application of many of these more optimal methods in the current setting requires access to individual level data from the external study.

The methodology for “model-based” maximum likelihood estimation has also been studied previously in some special cases of this problem, where it can be assumed that the covariate information available in the external data source can be summarized into discrete strata. In particular, in the setting of two-phase studies where it can be assumed that the internal study is a sub-sample of the external study, a number of researchers have proposed semiparametric maximum likelihood (SPML) methods for various types of regression models, while accounting for complex sampling designs (Scott and Wild 1997; Breslow and Holubkov 1997; Lawless, Wild and Kalbflesich 1999). Most recently, Qin et al. (2015) studied the problem of fitting a logistic regression model to case-control data utilizing information on stratum-specific disease probability rates from external sources. The assumption that only discretized information is available from the external source is a major limitation of these methods. In practice, the external data set may often include combinations of many variables and summarizing this information into strata can be subjective and inefficient.

In this article, we develop a general SPML estimation methodology, where we assume that the external information is summarized, not by a discrete set of strata defined by the study variables, but by a finite set of parameters obtained from fitting a model to the external data. We identify very general equations imposed by the external model, regard-less of whether the model is correctly specified or not, and use these equations to develop constrained maximum-likelihood estimation methodology. The broad framework allows arbitrary types of covariates and arbitrary types of regression models, including non-nested models for the internal and external data and complex sampling designs. For inference, we consider an empirical likelihood estimation technique, as well as a synthetic maximum likelihood approach that allows incorporating externally available estimates of the covariate distribution. We evaluate the performance of these maximum likelihood methods together with the GR-type calibration estimator in a wide variety of settings of practical interest. Finally, we illustrate an application of the method for developing an updated model for predicting risk of breast cancer using multiple data sources.

2 METHODS

2.1 Models and Notation

Let Y be an outcome of interest and X be a set of covariates. We assume a model for the predictive distribution g_θ(y|x) has been built based on an external big data set. In general, we will assume that we only have access to the model parameters, θ, but not necessarily to the individual level data from the “external” study based on which the original model was built. We assume that data on Y, X and a new set of covariates Z are available to us from an “internal” study for building a model of the form f_β(y|x, z). Throughout, we will refer to f_β(y|x, z) and g_θ(y|x) as the “full” and “reduced” models, respectively. We assume f_β(y|x, z) is correctly specified, but the external model g_θ(Y|X) need not be. In practice, although all models are going to be wrong to some extent, investigators will control the specification f_β(Y|X, Z) and can carry out suitable model diagnostics. Let F(X, Z) denote the distribution function of all risk factors for the underlying population, which, for the time being is assumed to be the same for the “external” and “internal” studies. This assumption, however, will be inspected more closely later.

2.2 The Key Constraints Relating Model Parameters of Full and Reduced Models

Let U(Y|X; θ) = ∂log{g_θ(Y|X)}/∂θ be the score function associated with the reduced model, and θ the parameter in the reduced model. The population parameter value θ* of θ underlying the external reduced model satisfies the equation

$$E\{U(Y|X,{\theta }^{*})\}=\int U(y|x,{\theta }^{*})\text{pr}(y|x)\text{pr}(x)dydx=0,$$ (1)

where pr(y, x) = pr(y|x)pr(x) is the true underlying joint distribution of (Y, X). When the model g_θ(y|x) is misspecified, g_θ(y|x) ≠ pr(y|x), but (1) still holds true under mild conditions (e.g. White 1882). Under the assumption that f_β(Y|X, Z) is correctly specified, we can write

$$\text{pr}(y|x)=\int f_{{\beta }_0}(y|z,x)\text{pr}(z|x)dz,$$

with β₀ the true value of β. Thus the constraint imposed by equation (1) can be re-written, after changing some ordering of integrals, as

$${\int }_{Z,X}\{{\int }_{Y}U(Y|X,{\theta }^{*})f_{{\beta }_0}(Y|X,Z)dY\}dF(X,Z)=0.$$ (2)

The equation essentially converts the external information to a set of constraints, which we utilize in our analysis of internal data to improve efficiency of parameter estimates and generalizability of models. The dimension of the constraints is the same as the number of parameters by which the external model has been summarized.

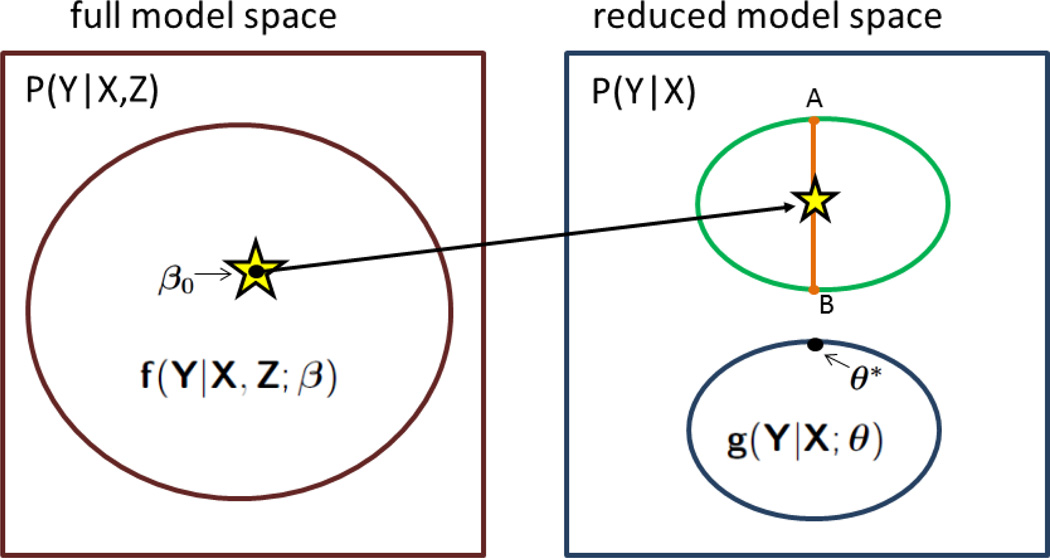
Figure 1 provides a geometric perspective for how the external reduced model provides information for building the full model based on the internal study. The true probability distribution for P₀(Y|X, Z) (shown in the left panel), which is assumed to belong to the class generated by a parametric family f_β(Y|X, Z), induces a true value for P₀(Y|X) = ∫ f_β0(Y|X, z)dF(z|X)dz (shown in the right panel). The reduced model space under consideration, g_θ(Y|X), may not contain P₀(Y|X). Nevertheless, a value of θ = θ* that solves the score equation E{U(Y|X, θ)} = 0 has a valid interpretation in that it minimizes the Kullback-Leibler distance (Huber 1967; White 1982) between the fixed P₀(Y|X) and the model space of g_θ(Y|X). Thus, from a reverse perspective, it is intuitive that if the value of θ* is given, then the search for β₀ could be constrained to a space so that P_θ*(Y|X) remains the minimizer between the model space of g_θ(Y|X) and any fixed point in the induced model space of P_β(Y|X) = ∫ f_β(Y|X, z)dF(z|X)dz. In the figure, the constrained space for the induced model is represented by the chord $\overline{AB}$.

Figure 1.

Geometric interpretation of the problem. The true distribution function P₀(Y|X) for Y given (X, Z) across all values of β is depicted in the left panel, with the true value of β, i.e., β₀ shown. In the right top panel, we see the true distribution function P₀(Y|X) for Y given X across all values of β with β₀ shown. The assumed external data model is given in the bottom right panel across all values of θ, with the solution θ* to (1) being shown as the minimizer of the Kullback-Leibler distance between the fixed P₀(Y|X) and the model space of g_θ(Y|X).

2.3 Semiparametric Maximum Likelihood

One class of methodology we consider is SPML methodology that allows the distribution F(X, Z) to be completely unspecified. Importantly, two-phase design maximum likelihood methodology requires X to be discrete as the number of constraints increases with the number of distinct levels of (Y, X). In contrast, here Y and X can be arbitrary in nature and yet the number of constraints, defined by the dimension of the reduced model parameter θ, remains finite.

2.3.1 Maximum-Likelihood Under Simple Random Sampling for the Internal Studies

Suppose we have data on (Y_i, X_i, Z_i) for i = 1, …, N randomly selected subjects in the internal study. The likelihood is given by

$$L_{\beta ,F}=\prod _{i=1}^N{f}_{\beta }(Y_i|X_i,Z_i)dF(X_i,Z_i).$$

Our goal is to maximize log{L_β,F} with respect to β and F(·) while maintaining the constraint given by (2). We assume that θ* is given to us externally, that is, θ is fixed at θ*. Thus, from now on, for simplicity we use θ to denote θ*.

Define

$$u_{\beta }(X,Z;\theta )={\int }_{Y}U(Y|X,\theta )f_{\beta }(Y|X,Z)dY.$$ (3)

We propose to maximize l_λ = log(L_β,F) + λ^T ∫ u_β(X, Z; θ)dF(X, Z), where λ is a vector of Lagrange multipliers with the same dimension as θ. Assuming that nonparametric maximum likelihood estimation (NPMLE) of F(X, Z) has masses only at the unique observed data points in the internal study, F(·, ·) can be characterized by the corresponding masses (δ₁, …, δ_m), where m denotes the number of unique values of (X_i, Z_i), i = 1 …, N. Using standard empirical likelihood (or profile likelihood) computation steps (see e.g. Qin and Lawless 1994; Scott and Wild 1997), we can show that the values of β and λ that satisfy the constrained maximum likelihood equations also satisfy the score-equations associated with a “pseudo-loglikelihood” given by

$$l_{\beta ,\lambda }^{*}=\sum _{i=1}^N\text{log }\left\{\frac{f_{\beta }(Y_i|X_i,Z_i)}{1-{\lambda }^T{u}_{\beta }(X_i,Z_i;\theta )}\right\}.$$ (4)

The derivation of (4) is given in Appendix.

2.3.2 Maximum Likelihood Under a Case-Control Sampling Design for the Internal Study

Even if we only have a case-control or retrospective sample from the internal study, as long as we have the external reduced model for the underlying population, we can estimate all of the parameters of the full model f_β(Y|X, Z) using this constrained maximum-likelihood approach. A special case is when the external information is simply the disease prevalence in the underlying population; it is well know that such information can be used to augment the case-control sample to estimate all of the parameters of a logistic or other binary disease risk models (see e.g., Scott and Wild 1992).

Suppose Y is binary and let p₁ = pr(Y = 1) = 1 − p₀ = ∫ f_β(Y = 1|x, z)dF(x, z) denote the underlying marginal disease probability in the population, for arbitrary values of β. The likelihood for the internal case-control study is given by

$$L_{\beta ,F}^{cc}=\{\prod _{i=1}^{N_1+N_0}{f}_{\beta }(Y_i|X_i,Z_i)dF(X_i,Z_i)\}\times p_1^{-N_1}{p}_0^{-N_0},$$ (5)

where N₁ and N₀ denote the numbers of cases and controls sampled. The goal is to maximize $l_{\lambda }^{cc}=\text{log}(L_{\beta ,F}^{cc})+{\lambda }^T\int u_{\beta }(X,Z;\theta )dF(X,Z)$. Again, assuming that the NPMLE of F(X, Z) has masses only within the unique observed data points of (X_i, Z_i), i = 1, …, N₁ + N₀, in Appendix we show that the constrained maximum likelihood estimation problem is equivalent to solving the score equation associated with the pseudo-loglikelihood

$$l_{\beta ,\lambda ,{\mu }_1}^{*,cc}=\sum _{i=1}^N\text{log }\left\{\frac{f_{\beta }(Y_i|X_i,Z_i)}{{\sum }_y{f}_{\beta }(y|X_i,Z_i){\mu }_y-{\lambda }^T{u}_{\beta }(X_i,Z_i;\theta )}\right\}+\sum _y{N}_y\text{log}({\mu }_y).$$ (6)

The pseudo-loglikelihood in the case-control sampling setting requires introduction of one additional nuisance parameter μ₁ = N₁/p₁, with μ₀ = N₀/p₀ defined by μ₁. In principle, this theory could be generalized to account for more complex stratified sampling designs for the internal study, assuming the external model is rich enough that it allows identification of all the parameters of the full logistic model even if certain parameters are not identifiable from the internal study.

The problem stated above has a strong connection with methodology in two-phase design semiparametric maximum likelihood estimation as developed by Scott and Wild (1997) and Breslow and Holubkov (1997). In fact, if the data (Y, X) from the external study can be summarized into a frequency table defined by fixed sets of strata, this problem essentially can be studied using previous theory with some modification for the fact that the internal study may not be a subset of the external study. The categorization of phase-I covariate data (X) is needed in these and other previously developed semiparametric methods, as all of them intrinsically rely on functionals that are smoothed over Z but not X. In contrast, in our maximum likelihood theory, the constraints are represented by functionals that are smoothed with respect to both X and Z. As a result, we avoid the “curse of dimensionality” problem that is typically faced in semiparametric estimation theory for covariate missing data and measurement error problems; see Roeder, Carroll, and Lindsay (1996) for a discussion on the latter topic.

2.3.3 Numerical Computation and Asymptotic Theory

For ease of exposition, when discussing computation and asymptotic theory, we transform the parameter μ₁ to α defined in Appendix S.2 of the Supplementary Material for the case-control design. Further, we absorb the parameter α into β in the case-control design, so that the notation for certain functions such as u_β(X, Z; θ) can be unified under both the simple random and case-control sampling designs.

As mentioned above and detailed in Appendix, the pseudo-loglikelihood given in (4) or (6) is in fact the Lagrange function for the constrained loglikelihood obtained by Lagrange multipliers and profiling out the infinite dimensional parameter F(·, ·). By the theory of Lagrange multipliers (Chiang and Wainwright, 1984), the proposed semiparametric constrained maximum likelihood estimator for β₀, denoted by β̂, is then obtained by directly solving for the stationary point, indeed the saddle point, over the expanded parameter space η = (β^T, λ^T)^T for the pseudo-loglikelihood function. We solve the resulting stationary equation to obtain β̂ by the usual Newton-Raphson method, which is quite stable and performs efficiently in our numerical studies when the initial value of λ is set to 0. In the simulations and data analysis performed in this work, all results converged within 10 iterations of the Newton-Raphson algorithm employed. Numerical optimizations were performed using PROC IML of SAS (version 9.3). Formulae for the score and Hessian for both simple random sampling and for case-control studies are given in Appendix S.2 of the Supplementary Material.

Let η̂ = (β̂^T, λ̂^T)^T be the stationary point of the pseudo-loglikelihood function given in (4) or (6); namely, η̂ is the solution to the score equation $\partial l_{\beta ,\lambda }^{*}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{*,cc}/\partial \eta =0$ when the internal study is under simple random or case-control sampling. Explicit expressions for the score function, the first derivative of the pseudo-loglikelihood with respect to η = (β^T, λ^T)^T, are given in Appendix S.2 in the Supplementary Material. The following result confirms that the constrained maximum likelihood estimator for β can be obtained by solving the score equation. The proof is detailed in Appendix S.5 of the Supplementary Material.

Lemma 1

Under regularity conditions for model f_β(y|x, z) and conditions (i)–(iv) given in Appendix S.4 of the Supplementary Material, the pseudo-loglikelihood function $l_{\beta ,\lambda }^{*}$ or $l_{\beta ,\lambda }^{*,cc}$ is maximized at β = β̂ with probability one, and η̂ = (β̂, λ̂) is the solution to $\partial l_{\beta ,\lambda }^{*}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{*,cc}/\partial \eta =0$.

The following proposition establishes the asymptotic normality of the constrained maximum likelihood estimator proposed.

Proposition 1

Let η̂ = (β̂^T, λ̂^T)^T be the solution to $\partial l_{\beta ,\lambda }^{*}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{*,cc}/\partial \eta =0$, and ${\eta }_0={({\beta }_0^T,0)}^T$ with β₀ the true value of β, 0 denoting a ℓ-vector of zeros and ℓ the dimension of λ. Under regularity conditions for f_β(y|x, z) and conditions (i)–(v) in Appendix S.4 of the Supplementary Material, as N → ∞, N^1/2(η̂ − η₀) converges in distribution to a zero-mean normal distribution with covariance matrix given by

$$\left(\begin{array}{cc}\hfill {(B+C{L}^{-1}{C}^T)}^{-1}\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill {(L+C^T{B}^{-1}C)}^{-1}\hfill \end{array}\right),$$ (7)

where B = E{i_ββ(Y, X, Z)}, C = E{c_β(X, Z; θ)}, and $L=E\{u_{\beta }(X,Z)u_{\beta }^T(X,Z)\}$, and where i_ββ(Y, X, Z) and c_β(X, Z; θ) are defined in (S.4) and (S.2), respectively, in Appendix S.2 in the Supplementary Material.

The proof is in Appendix S.5 of the Supplementary Material. A simple consistent estimator for the covariance matrix (7) is obtained by using the corresponding sample means for the expected quantities in the expression. In Section S.5 of the Supplementary Material, we show how to modify Proposition 1 when there is uncertainty about θ when it is estimated from a finite external study.

From Proposition 1 we see two interesting facts. First, the asymptotic variance of β̂ is (B + CL⁻¹CT)⁻¹ = B⁻¹ − B⁻¹C(L + C^TB⁻¹C)⁻¹C^TB⁻¹, and hence the constrained maximum likelihood estimator is asymptotically more efficient than the estimator based only on internal sample data, whose asymptotic variance is B⁻¹. Second, β̂ and λ̂ are asymptotically uncorrelated, a phenomenon also shared by other empirical likelihood methods such as that of Qin and Lawless (1994).

2.4 Synthetic Maximum Likelihood

So far we have assumed that the underlying populations for the internal and external studies are identical, which may be violated in practice. In particular, as we will demonstrate through simulation studies, various types of calibrations methods, either maximum likelihood or not, can lead to substantial bias in parameter estimates if the distributions of the underlying risk factors are different between the internal and external populations. In this section, we consider the situation when an external reference sample may be available for unbiased estimation of the covariate distribution for the external population.

Let F^†(X, Z) denote the underlying distribution for the external population, and consider the setting where it differs from the distribution F(X, Z) in the internal population. We continue to assume that the regression model f_β(Y|X, Z) correctly holds for both of the populations and that the underlying true parameters β₀ are the same. We assume data are available from the external reference sample in the form $(X_j^{†},Z_j^{†})$, j = 1, …, N_r, where N_r is the size of the external reference sample. When the internal study sample is obtained under the simple random sampling design, the synthetic constrained loglikelihood is defined as $l_{\beta ,\lambda }^{†}=\text{log}(L_{\beta ,F})+{\lambda }^T\int u_{\beta }(X,Z;\theta )d{\tilde{F}}^{†}(X,Z)$, with F̃^† the empirical distribution of (X^†, Z^†) in the external reference sample, and the synthetic constrained maximum likelihood (SCML) estimator (β̃, λ̃) for (β, λ) can be obtained by solving the estimating equations $\partial l_{\beta ,\lambda }^{†}/\partial \beta =0$ and $\partial l_{\beta ,\lambda }^{†}/\partial \lambda =0$, completely ignoring F(·, ·) because it factors out from the likelihood of the internal study.

When the internal sample represents a case-control study, however, the synthetic constrained loglikelihood is defined as

$$l_{\beta ,\lambda ,F}^{†,cc}=\text{log}(L_{\beta ,F}^{cc})+{\lambda }^T\int u_{\beta }(X,Z;\theta )d{\tilde{F}}^{†}(X,Z),$$

from which F(·, ·) cannot be factored out. As before, we consider NPMLE estimation of F(X, Z) allowing it to have masses at each of the unique observed data points of (X_i, Z_i) (i = 1 …, N₁ + N₀) in the internal study. In this setting, following Prentice and Pyke (1979) we can show that the SCML estimate of β can be obtained by maximization of a pseudo-loglikelihood of the form

$$l_{\beta ,\lambda ,\alpha }^{†,cc}=\text{log}(L_{\beta ,\alpha }^{cc})+{\lambda }^T\int u_{\beta }(X,Z;\theta )d{\tilde{F}}^{†}(X,Z),$$

where

$$L_{\beta ,\alpha }^{cc}=\prod _{i=1}^N{p}_{\beta ,\alpha }(Y_i|X_i,Z_i),$$

with

$$p_{\beta ,\alpha }(y|x,z)=\frac{{\mu }_y{f}_{\beta }(y|x,z)}{{\sum }_y{\mu }_y{f}_{\beta }(y|x,x)}=\frac{\text{exp}(\alpha y)f_{\beta }(y|x,z)}{{\sum }_y\text{exp}(\alpha y)f_{\beta }(y|x,z)}$$ (8)

and α = log (μ₁/μ₀). Here, $L_{\beta ,\alpha }^{cc}$ corresponds to the standard “prospective likelihood” for case-control data that is known to produce equivalent inference for β as the retrospective likelihood (Prentice and Pyke 1979; Scott and Wild 1997). In general, a likelihood of the form (8) may not be able to identify all of the parameters of the original model without additional information. In particular, for the logistic model, the intercept parameters become completely confounded by the nuisance parameters α and cannot be estimated from case-control data alone. However, in the setting considered here, the additional constraint (2) defined by the external model allows estimation of all of the parameters of the full model even when the distribution of the risk-factors may differ in the two underlying populations.

2.4.1 Computation and Asymptotic Theory

As in the procedure considered in Section 2.3, we use the Newton-Raphson method to solve the stationary equations for the synthetic constrained loglikelihood $l_{\beta ,\lambda }^{†}$ or $l_{\beta ,\lambda ,\alpha }^{†cc}$, depending on whether the internal study is based on simple random or case-control sampling. Formulae for the score and Hessian for simple random sampling and for case-control sampling are given in Appendix S.3 of the Supplementary Material.

As mentioned previously, to simplify exposition, in the case-control setting we absorb the nuisance parameter α into β, and let η = (β^T, λ^T)^T. Denote by q and ℓ the dimensions of β and λ. The following lemma shows that β̃ obtained from $\partial l_{\beta ,\lambda }^{†}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{†,cc}/\partial \eta =0$ indeed maximizes the log-likelihood function log(L_β,F) or $\text{log}(L_{\beta ,\alpha }^{cc})$ with probability tending to one under the constraint ∫ u_β(X, Z; θ)dF̃^†(X, Z) = 0.

Lemma 2

Suppose that q > ℓ, and N_r/N → κ > 0. Under regularity conditions for the model f_β(y|x, z) and conditions (i)–(iv) given in Appendix S.4 of the Supplementary Material, the loglikelihood functions log(L_β,F) or $\mathit{\text{log}}(L_{\beta ,\alpha }^{cc})$ is maximized at β = β̃ with probability approaching one under the constraint ∫ u_β(X, Z; θ)dF̃^†(X, Z) = 0, where β̃ is in the interior of a neighborhood of true parameter value β₀, and η̃ = (β̃^T, λ̃^T)^T is the solution to $\partial l_{\beta ,\lambda }^{†}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{†cc}/\partial \eta =0$.

We also provide asymptotic distribution theory for the SCML estimator η̃ = (β̃^T, λ̃^T)^T. The proofs of these theoretical results are given in Appendix S.5 of Supplementary Material.

Proposition 2

Recall that N_r/N → κ > 0. $\mathit{\text{Let }}{\eta }_0={({\beta }_0^T,0)}^T$ with 0 denoting a ℓ-vector of zeros and ℓ the dimension of λ. Under the assumptions in Lemma 2 and condition (v) in Appendix S.4 of the Supplementary Material, the estimator η̃ = (β̃^T, λ̃^T)^T satisfying $\partial l_{\beta ,\lambda }^{†}/\partial \eta =0$ or $\partial l_{\beta ,\lambda }^{†cc}/\partial \eta =0$ is asymptotically normal as N → ∞, such that N^1/2(η̃ − η₀) converges in distribution to a zero-mean normal distribution with covariance matrix

$$\left(\begin{array}{cc}\hfill B^{-1}-B^{-1}C{G}^{-1}(G-{\kappa }^{-1}L)G^{-1}{C}^T{B}^{-1}\hfill & \hfill -{\kappa }^{-2}{B}^{-1}C{G}^{-1}L{G}^{-1}\hfill \\ \hfill -{\kappa }^{-2}{G}^{-1}L{G}^{-1}{C}^T{B}^{-1}\hfill & \hfill {\kappa }^{-2}{G}^{-1}(G+{\kappa }^{-1}L)G^{-1}\hfill \end{array}\right),$$ (9)

where with E^† denoting expectation over the external covariate distribution F^†(X, Z), G = C^TB⁻¹C, B = E{i_ββ(Y, X, Z)}, C = E^†{c_β(X, Z; θ)}, $L=E^{†}\{u_{\beta }(X,Z)u_{\beta }^T(X,Z)\}$, and i_ββ(Y, X, Z) and c_β(X, Z; θ) defined in (S.4) and (S.2), respectively, in Appendix S.2 of the Supplementary Material.

The variance-covariance matrix (9) for η̃ can be readily estimated by replacing the component quantities in the expression with their sample analogies. In Section S.5 of the Supplementary Material, we show how to modify Proposition 2 when there is uncertainty in the parameter estimates of the external study.

From Propositions 1 and 2, we see differences between (β̂, λ̂) and (β̃, λ̃) in their asymptotic theory. First, unlike β̂, the SCML estimator β̃ is not guaranteed to be more efficient than the internal-sample only estimator. However, β̃ is usually more efficient than the latter estimator, especially when κ is large, i.e., the size of the reference sample for estimating F(·, ·) is sufficiently large relative to that of the internal sample. In particular, in the special case of κ → ∞, the matrix B⁻¹CG⁻¹C^TB⁻¹ is positive definite and hence β̃ is always more efficient than that of the internal-sample only estimator. Second, unlike (β̂, λ̂), (β̃ λ̃) are correlated asymptotically, although the correlation vanishes as κ → ∞.

3 SIMULATION STUDIES

We conduct simulation studies to evaluate the performance of the proposed methods in a wide variety of settings of practical interest. We consider developing models for a binary outcome Y using logistic and non-logistic link functions. In all simulations, it is assumed (X, Z) is bivariate normal with zero marginal means, unit marginal variances and a correlation of 0.3.

In other numerical studies (not shown here), the conclusions from simulation studies did not change qualitatively if we used an alternative to the bivariate normal distribution for simulating (X, Z).

We study three different settings, in two of which we assume that the full model of interest has the form

$$h^{-1}\{\text{pr}(D=1)\}={\beta }_0+{\beta }_{X}X+{\beta }_{Z}Z+{\beta }_{XZ}XZ,$$

where h⁻¹ denotes the inverse link function corresponding to a logistic or a probit model. In one of these settings, we assume that the external model is under-specified but involves both covariates with the form

$$h^{-1}\{\text{pr}(D=1)\}={\theta }_0+{\theta }_{X}X+{\theta }_{Z}Z,$$

and in the second setting we assume that the external model is missing the covariate Z altogether and has the form

$$h^{-1}\{\text{pr}(D=1)\}={\theta }_0+{\theta }_{X}X.$$

In the third setting, we consider a measurement error problem where it is assumed that Z is the true covariate of interest and X is a surrogate of Z in the sense that Y is independent of X given Z. In this setting, we assume that the full and reduced models of interest are

$$h^{-1}\{\text{pr}(D=1)\}={\beta }_0+{\beta }_{Z}Z\text{ and }{h}^{-1}\{\text{pr}(D=1)\}={\theta }_0+{\theta }_{X}X,$$

respectively.

In each setting, we simulate data under the correct full model given a set of parameter values and then obtain the values of external parameters by fitting the reduced model, which by definition is incorrectly specified, to a very large data set. In the under-specified and missing covariate scenarios, the parameter values of the true model (β₀, β_X, β_Z, β_XZ) = (−1.6, 0.4, 0.4, 0.2); in the measurement error scenario, they are (β₀, β_Z) = (−1.6, 0.4). In all models, the parameter specifications lead to a population disease prevalence around 20%. For simulating case-control samples for the internal study, in each simulation, we first generate a random sample and then select fixed and equal numbers of cases and controls. In both the simple random and case-control sampling settings, the size of the internal sample is N = 1000. The external data are generated with a very large sample size and fixed throughout the simulations.

As a benchmark for comparison, in each simulation, in addition to the constrained maximum likelihood estimator proposed, we obtain the internal-sample-only estimate β̂^I, and implement a generalized regression (GR) estimator, popular in the survey literature and developed for regression inference with double or two-phase sampling by Chen and Chen (2000). Specifically, the estimator takes the form

$${\hat{\beta }}^{GR}={\hat{\beta }}^I+H_1^{-1}{C}_{12}{C}_{22}^{-1}{H}_2({\hat{\theta }}^E-{\hat{\theta }}^I).$$ (10)

In (10), θ̃^E and θ̃^I are estimates for θ using the external and internal samples, respectively, while

$$H_1=E_I\{\partial s_{\beta }(Y,X,Z)/\partial {\beta }^T\}=-B,\hspace{1em}{H}_2=E_I\{\partial U(Y|X;\theta )/\partial {\theta }^T\},$$

$$C_{22}=E_I\{U(Y|X;\theta )U^T(Y|X;\theta )\},\hspace{1em}{C}_{12}=E_I\{s_{\beta }(Y,X,Z)U^T(Y|X;\theta )\},$$

where s_β(Y, X, Z) = ∂log f_β(Y|X, Z)/∂β, and where E_I denotes the sample expectation based on the internal study. In the current implementation of such a calibration method, unlike in the original proposal, we disregard the uncertainty associated with θ̂^E, since in the current setting such uncertainty is assumed to be negligible compared with the uncertainty in the internal sample. As shown in Chen and Chen (2000), the asymptotic covariance matrix of $\sqrt{N}{\hat{\beta }}^{GR}$ is given as

$$B^{-1}-B^{-1}{C}_{12}{C}_{22}^{-1}{C}_{12}^T{B}^{-1},$$ (11)

which accounts for the uncertainty of θ̂^I, and can be estimated by replacing each component quantity with its sample analogue.

Further, since the method of Chen and Chen (2000) was originally developed for simple random sampling designs only, when implementing their method for logistic regression analysis of a case-control design, we make an ad-hoc modification to GR estimator which we denote as mGR. Instead of applying the calibration formula (10) to the full set of regression parameters β, we apply it only to the subset of β excluding the intercept parameter. Such a modification is based on the rationale that, according to Prentice and Pyke (1979), for f_β(·) following a logistic regression model, the prospective maximum likelihood estimator provides valid and efficient estimates of all the parameters of the model except the intercept.

Tables 1–3 display simulation results with N = 1000. We also examine the cases with N = 400, which lead to similar conclusions and are relegated to Tables S.1–S.4 in the Supplementary Material. From Tables 1–3 we conclude that the constrained maximum likelihood estimator β̂^CML is always more efficient than the internal-sample-only estimator β̂^I. For the under-specified and missing covariate scenarios, substantial efficiency gains are observed for regression parameters corresponding to the covariates that are also included in the reduced model fitted with external data, i.e., for (β₀, β_X, β_Z) and (β₀, β_X), respectively. In the measurement error setting, the efficiency gain is observed for the main covariate of interest (Z) where the reduced model only includes an error-prone surrogate (X). These observations hold under both the simple random and case-control sampling designs. Under the simple random sampling design, the estimator β̂^GR performs similarly to or slightly worse than our estimator β̂^CML in the under-specified and missing covariate settings. However, in the measurement error setting, β̂^GR is far less efficient than β̂^CML. Under the case-control sampling design, the mGR estimator incurred substantial bias in the under-specified setting, but not in the other two settings. From these simulation results and those conducted in a smaller sample-size setting (N = 400), we can conclude that the asymptotic distribution theory provided in Proposition 1 for β̂^CML performs quite well, as seen by the generally close agreement between the estimated (ESE) and simulation standard errors (SE), and between the nominal and simulation coverage probabilities of the Wald-type confidence intervals based on asymptotic normality. Tables S.5–S.7 in the Supplementary Material show the performance of the different estimators in the setting of probit models under the random-sampling design. The results are generally similar to those for the logistic model in Tables 1–3.

Table 1.

Simulation results for the under-specification setting, in which the full model of interest has the form h⁻¹ {pr(D = 1)} = β₀ + β_XX + β_ZZ + β_XZXZ, where h⁻¹ denotes the inverse link function corresponding to a logistic model, and where the external model is under-specified but involves both covariates with the form h⁻¹ {pr(D = 1)} = θ₀ + θ_XX + θ_Z. Results multiplied by 10³ are presented, and the coverage probabilities (CP) are reported as percents.

	Int	β0 GR/ mGR	CML	Int	βX GR/ mGR	CML	Int	βZ GR/ mGR	CML	Int	βXZ GR/ mGR	CML
simple random; N = 1000
Bias	−8.94	−0.79	−1.12	2.42	2.16	2.46	1.29	1.29	1.65	1.39	1.30	1.87
SE	91.4	24.4	24.4	96.8	20.1	19.9	94.3	20.2	19.8	89.4	89.6	89.3
ESE	91.8	22.9	23.5	92.3	19.8	19.7	92.4	19.9	19.8	85.8	85.3	86.9
MSE	8.42	0.59	0.59	9.38	0.41	0.40	8.89	0.41	0.39	7.98	8.02	7.97
CP	95.4	88.6	90.8	94.3	94.6	95.2	94.6	94.4	95.5	93.6	93.4	93.8
case-control; N = 1000
Bias	-	-	1.70	2.40	28.4	2.23	5.06	27.6	1.73	−1.51	−1.20	−2.30
SE	-	-	17.4	75.7	11.3	16.7	72.2	11.4	16.6	72.9	72.8	71.7
ESE	-	-	16.6	73.3	11.6	16.5	73.1	11.6	16.5	71.4	71.3	70.1
MSE	-	-	0.30	5.73	0.93	0.28	5.24	0.89	0.28	5.31	5.29	5.15
CP	-	-	90.7	94.2	31.4	94.5	95.4	33.1	94.8	94.7	94.6	93.7

Int: internal-data only method

GR: generalized regression, mGR: modified GR for case-control sampling

CML: constrained maximum likelihood

ESE: estimated standard error

MSE: mean squared error

CP: coverage probability of a 95% confidence interval interval

Table 3.

Simulation results for the measurement error setting in which the full and reduced models are h⁻¹ {pr(D = 1)} = β₀ + β_ZZ and h⁻¹ {pr(D = 1)} = θ₀ + θ_XX, respectively, and where h⁻¹ denotes the inverse link function corresponding to a logistic model. Results presented are multiplied by 10³, and the coverage probability (CP) is in percents.

	Int	β0 GR/mGR	CML	Int	βZ GR/mGR	CML
simple random; N = 1000
Bias	−2.12	−3.73	0.20	0.80	1.23	1.13
SE	87.7	25.1	15.1	89.6	84.7	40.1
ESE	87.1	23.9	15.2	86.3	82.5	38.7
MSE	7.69	0.64	0.23	8.02	7.17	1.61
CP	95.9	92.6	94.1	94.2	94.0	94.1
case-control; N = 1000
Bias	-	-	0.99	2.85	2.91	1.74
SE	-	-	12.8	66.0	62.5	37.6
ESE	-	-	12.9	66.6	63.8	36.3
MSE	-	-	0.16	4.36	3.63	1.42
CP	-	-	95.6	95.7	96.1	94.6

Int: internal-data only method

GR: generalized regression, mGR: modified GR for case-control sampling

CML: constrained maximum likelihood

ESE: estimated standard error

MSE: mean squared error

CP: coverage probability of a 95% confidence interval interval

We next investigate the properties of the different estimators when the distribution of (X, Z) differs between the internal and external populations. All of the steps are identical as before except that we assume corr(X, Z) is 0.1 in the external population. In this scenario, we implement the SCML method assuming a reference sample for the external population is available to estimate the underlying covariate distribution. We assume that the sample size for the reference sample is the same as that of the internal study, and in each simulation the random reference sample for (X, Z) is drawn from the distribution that is the same as that for the external population. We obtain the value of the external parameter by fitting a reduced model to a very large data set simulated using the external covariate distribution. Table 4 shows the results under the missing covariate setting for logistic regression with simple random and case-control sampling.

Table 4.

Simulation results for the missing covariate setting as in the caption for Table 2, but when the covariate distributions are different between the internal and external populations. Results multiplied by 10³ are presented, and the coverage probabilities (CP) are reported as percents.

	Int	β0 CML	SCML	Int	βX CML	SCML	Int	βZ CML	SCML	Int	βXZ CML	SCML
simple random; N = Nr = 1000
Bias	−8.61	−32.4	−1.67	4.33	−85.2	2.63	1.10	0.30	−0.69	1.38	4.41	−0.04
SE	91.9	32.2	27.6	96.8	38.4	30.7	97.9	97.9	96.8	89.3	89.5	88.0
ESE	91.8	33.5	26.2	92.5	39.2	30.1	92.5	92.5	91.0	85.9	85.2	85.6
MSE	8.51	2.09	0.76	9.39	8.72	0.95	9.58	9.58	9.36	7,97	8.03	7.74
CP	95.3	90.6	92.0	93.5	42.3	93.0	93.2	93.3	93.4	93.5	93.6	93.9
case-control; N = Nr = 1000
Bias	-	−27.0	−1.13	0.76	−89.0	0.58	2.74	4.15	1.94	4.03	−1.90	2.30
SE	-	23.6	23.1	71.4	27.1	26.8	74.1	74.1	73.6	73.7	73.5	72.7
ESE	-	23.2	23.1	73.3	27.9	27.4	73.3	72.7	72.5	71.6	69.8	71.2
MSE	-	1.29	0.53	5.09	8.65	0.72	5.50	5.51	5.42	5.45	5.40	5.29
CP	-	82.0	94.2	95.0	7.9	93.7	94.3	94.0	94.1	93.6	93.5	94.3

Int: internal-data only method

CML: constrained maximum likelihood method

SCML: synthetic constrained maximum likelihood method

ESE: estimated standard error

MSE: mean squared error

CP: coverage probability of a 95% confidence interval

Since results from the regression calibration β̂^GR and the constrained maximum likelihood β̂^CML estimates are quite similar in this setting, results for the former are omitted in Table 4. As can be seen in Table 4, β̂, as well as β̂^GR, is subject to remarkable bias for parameters corresponding to the covariates included in the reduced model. This is expected since β̂, as well as β̂^GR, is derived under the assumption of complete homogeneity between the internal and external studies, and incorporation of the inconsistent external information can result in biased parameter estimates. On the other hand, we see from Table 4 that the SCML estimate β̃ performs quite well under both the simple random and case-control sampling: it is virtually unbiased, and more efficient than the estimate β̂^I based on the internal sample only. The efficiency gain of β̃ over β̂^I is particularly large for parameters corresponding to the covariates included in the reduced model. The standard error estimators and confidence intervals based on Proposition 2 for the synthetic constrained maximum likelihood estimation perform quite well in the settings considered.

4 DATA APPLICATION: BREAST CANCER RISK MODELING

We illustrate an application of our methodology by re-analysis of data from the Breast Cancer Detection and Demonstration Project (BCDDP) used by Chen et al (2006) for building a model for breast cancer risk prediction. The Breast Cancer Risk Assessment Tool (BCRAT), sometimes known as the Gail Model, is a widely used model for predicting the risk of breast cancer based on a handful of standard risk factors, including age at menarche (agemen), age at first live birth (ageflb), weight, number of first-degree relatives with breast cancer (numrel) and number of previous biopsies (nbiops). Chen et al (2006) developed an updated model, known as BCRAT2, to include mammographic density (MD), the areal proportion of breast tissue that is radiographically dense, that is known to be a strong risk factor for breast cancer. They used data available from 1217 cases and 1610 controls within the BCDDP study on whom data were available on these standard risk factors as well as MD. To increase efficiency, however, they used two-phase design methodology, utilizing data on standard risk factors that were available on a larger sample of subjects, including about 2808 cases and 3119 controls within the BCDDP study. Details of the BCDDP study design, case-control sample selections and two-phase design methodology used can be found in their previous publication (Chen et al. 2006; 2008).

Within the last decade, epidemiologic studies of cancers and many other chronic diseases have gone through a major transition due to the formation of various consortia that allow for the powerful analysis of common factors across many studies based on a very large set of samples. For example, two major consortia have been formed to study breast cancer: one based on cohort studies, e.g., the BPC3 study of Canzian et al, 2010, and others based on case-control studies (Breast Cancer Association Consortium, 2006) have been formed. These studies have led to extremely powerful investigation of various types of hypotheses, such as genetic association, based on tens of thousands of cases and controls depending on the types of risk factors that are being analyzed. Many of the studies participating in these consortia have standard risk factors available, although sometimes in a crude form. However, mammographic density (MD), which is much harder to evaluate, is rarely available in these studies.

To illustrate the utility of the proposed methodology, we develop a model for predicting breast cancer risk using data available on the full set of risk factors from the 1217 cases and 1610 controls of the “internal” BCDDP study and calibrating to the parameters from a standard risk factor model built from 12802 cases and 14296 controls from the “external” BPC3 consortium. The BPC3 standard risk factor model did not include mammographic density or the number of biopsies (nbiops); it included family history (famhist) as yes/no instead of the actual number of affected relatives, and recorded weight in tertiles as opposed to as a continuous variable. We used only summary level information from the BPC3 study, namely the estimates of the log-odds-ratio parameters and their standard errors. Our goal is to build a model similar to BCRAT2, i.e. a model with the standard risk factors as coded in BCRAT, and mammographic density.

Table 5 presents the results for model fit based on CML- and GR-based calibration approaches, together with the standard logistic regression analysis of the BCDDP data alone. In the model, the variable agemen is trichotomized according to age at menarche ≥ 14, 12–13, or < 12, and the two dummy variables for the latter two categories are denoted as agemen1 and agemen2; the variable ageflb is categorized into four groups according to age at first live birth < 20, 20–24, 25–29, and ≥ 30, and the latter three groups are denoted as ageflb1, ageflb2, and ageflb3. For both CML and GR methods, the standard errors were adjusted to account for uncertainty in the parameter estimates of the external model (see Appendix S.5 in Supplementary Material as well as in the proofs of Propositions 1 and 2). As expected, both CML and GR methods led to much smaller standard errors for the parameter estimates associated with covariates included in the external model than the analysis of the BCDDP data alone. For a number of these factors, including number of first-degree relatives with breast cancer and age at menarche, the use of the external model seems to change point estimates of model coefficients to a degree that cannot be explained by uncertainty alone. Closer inspection of the estimates of the parameters of the reduced model from the internal and external studies, also shown in Table 5, indicates that breast cancer associations for these two factors were different between the two studies to a degree that may be indicative of true population differences. Since BPC3 represents a consortium of cohort studies underlying a broader population than that underlying the BCDDP study, a risk model that is built based on the calibrated estimates could potentially be more broadly applicable. However, future validation studies would be needed to verify such an assertion.

Table 5.

Analysis results of BCDDP data. The variables in the full model include: number of first-degree relatives with breast cancer (numrel), age at menarche (two dummy variables agemen1–agemen2 according to ≥ 14, 12–13, or < 12 years), age at first live birth (three dummy variables ageflb1–ageflb3 according to < 20, 20–24, 25–29, and ≥ 30 years), weight (in kg), number of previous biopsies (nbiops), and mammographic density (MD). The variables in the reduced model include: family history (famhist, binary according to yes/no), age at menarche (two dummy variables agemen1–agemen2 according to ≥ 14, 12–13, or < 12 years), age at first live birth (three dummy variables ageflb1–ageflb3 according to < 20, 20–24, 25–29, and ≥ 30 years), and weight (two dummy variables weight1–weight2 according to < 62.6, 62.6–73.1, and ≥ 73.1 kg)

	Full model†				Reduced model†
variable	Internal data Est. (SE)	mGR Est. (SE)	CML Est. (SE)	variable	Internal data Est. (SE)	External data Est. (SE)
numrel	0.648 (0.090)	0.371 (0.038)	0.297 (0.033)	famhist	0.716 (0.101)	0.354 (0.030)
agemen1	0.083 (0.091)	0.074 (0.034)	0.077 (0.035)	agemen1	0.059 (0.090)	0.052 (0.030)
agemen2	0.468 (0.124)	0.185 (0.041)	0.167 (0.042)	agemen2	0.387 (0.120)	0.081 (0.031)
ageflb1	−0.018 (0.146)	−0.109 (0.054)	−0.117 (0.057)	ageflb1	0.046 (0.142)	−0.053 (0.048)
ageflb2	0.086 (0.144)	0.003 (0.052)	−0.005 (0.055)	ageflb2	0.261 (0.139)	0.171 (0.043)
ageflb3	0.251 (0.173)	0.173 (0.067)	0.163 (0.070)	ageflb3	0.449 (0.167)	0.358 (0.057)
weight	0.020 (0.004)	0.022 (0.003)	0.024 (0.002)	weight1	0.061 (0.088)	0.106 (0.031)
				weight2	0.135 (0.106)	0.214 (0.031)
nbiops	0.180 (0.070)	0.178 (0.069)	0.165 (0.073)
MD	0.430 (0.044)	0.428 (0.045)	0.441 (0.047)

^†: adjusted for 5-year age strata

mGR: modified GR for case-control sampling

CML: constrained likelihood method

Est.: estimated coefficient

SE: estimated standard error

Of the two calibration estimators, both CML and GR method produced comparable point estimates, but CML produced noticeably smaller standard errors for number of first-degree relatives with breast cancer and weight, two variables that were included in cruder forms in the external model. These results are consistent with higher efficiency of CML over GR in the simulation setting of measurement error. For the number of previous biopsies and mammographic density, two factors which were not included in the external model, both CML and GR produced results similar to the standard analysis of the BCDDP data alone. In Table S.8 of the Supplementary Material, we present results for CML and GR proceeding as though the external model parameters came from a data set that is so large that uncertainty can be ignored. In this case, as expected, we observe that the efficiency of both CML and GR further increases relative to BCDDP-only analysis. Moreover, the relative efficiency of CML over GR increases for the parameters associated with weight and number of first-degree relatives with breast cancer.

5 DISCUSSION

We have proposed alternative maximum likelihood methods for utilizing information from external big data sets while building refined regression models based on an individual analytic study. External information, when properly used, can increase both efficiency of underlying parameter estimates and the generalizability of the overall models to broader populations. In recognition of the potential of external data, survey methodologists have long used various types of “design-based” or “model-assisted” calibration techniques for estimating target parameters of interest without relying on a full probability model for the data. In this report, we provide a framework for a very general model-based, yet semiparametric, maximum likelihood inferential framework that requires only summary-level information from external sources.

Our simulation studies and data analysis show that the constrained maximum likelihood (CML) and synthetic constrained maximum likelihood (SCML) methods can achieve major efficiency gains over generalized regression (GR) type calibration estimators for covariates in a model that are measured with a poorer instrument in the external study. On the other hand, for covariates that are measured the same way in the external and internal studies, the efficiency of these two methods was similar. It is, however, noteworthy that the modified GR estimator we implemented for the case-control study is not a proper model-free calibration estimator in the sense survey methodologists use. The method is only applicable for logistic models and is likely to be more efficient than a proper design-based GR estimator when the model is correct. Future research is merited to explore the theoretical properties of such modified GR estimators and their connection with ML estimators.

Our simulation studies show that model calibration using external information has important caveats as well. In particular, if the risk factor distribution differs between the underlying populations for the internal and external studies, any type of calibration method, model-based or not, can produce severe bias in estimates of the underlying regression parameters, even when the regression relationship f_β(Y|X, Z) is exactly the same in the two populations. The assumption of complete exchangeability of populations that is required in calibration methods is more likely to be violated in the kind of applications we envision than in survey-sampling or two-phase design applications, where by design there is a common underlying population. Ideally, in this setting, model calibration should be performed with respect to a risk factor distribution that is representative of the external population. Our synthetic conditional maximum likelihood (SCML) method allows this by importing covariate distributions from an external reference sample. Even when such a sample is not available, the SCML method can be used to perform sensitivity analysis under various hypothetical or simulated covariate distributions that may be considered realistic for the external population. It is further important to note that likelihood-based methods require the assumption that the full model f_β(Y|X, Z) is correctly specified for both the internal and the external populations. Although the internal study can be used for performing model diagnostics for the underlying population, the assumption is not testable for the external population because of lack of information on Z and inaccessibility of individual level data.

The proposed methods may have applications in other areas, such as bench-marking small area estimates to match larger area estimates (Mugglin and Carlin, 1998; Bell, et al., 2013; Zhang, et al, 2014), analyzing randomized clinical trial data so that they are generalizable to larger populations (Greenhouse, et al., 2008; Frangakis, 2009; Stuart, et al., 2011; Pearl and Bareinboim, 2014; Hartman, et al., 2015) and standardization and control of confounding for observational studies (Keiding and Clayton, 2014). In general, we foresee that model synthesis using disparate types of data sources will be increasingly important for biomedical research in the future. The key constraints we identify to relate models of varying size, i.e. equation (2), could be useful for model synthesis in more general settings than we have considered here. More research is needed to extend the framework for developing models incorporating information from studies that may have collected different, possibly overlapping, sets of covariates. In this setting, each study or a combination of studies that collect similar covariates, can provide information on a particular type of reduced model. Future research is also merited to explore methods that can incorporate these constraints in a “softer” fashion to account for sources of uncertainty of the external models and their parameters.

Table 2.

Simulation results for the missing covariate setting, in which the full model of interest has the form h⁻¹ {pr(D = 1)} = β₀ + β_XX + β_ZZ + β_XZXZ, where h⁻¹ denotes the inverse link function corresponding to a logistic model, and where the external model is h⁻¹ {pr(D = 1)} = θ₀ + θ_XX. Results multiplied by 10³ are presented, and the coverage probabilities (CP) are reported as percents.

	Int	β0 GR/ mGR	CML	Int	βX GR/ mGR	CML	Int	βZ GR/ mGR	CML	Int	βXZ GR/ mGR	CML
simple random; N = 1000
Bias	−8.94	2.67	2.84	2.42	3.30	3.37	1.29	1.50	0.95	1.33	1.27	2.42
SE	91.4	32.5	32.4	96.8	39.0	38.9	94.3	94.4	94.3	89.4	89.4	89.5
ESE	91.8	32.1	32.3	92.3	38.8	38.9	92.4	92.3	92.5	85.8	85.6	86.9
MSE	8.42	1.06	1.06	9.38	1.53	1.53	8.89	8.91	8.89	7.98	7.99	8.01
CP	95.4	94.7	95.3	94.3	93.4	94.0	94.6	94.5	95.1	93.6	93.7	93.8
case-control; N = 1000
Bias	-	-	2.59	2.40	14.8	0.88	5.06	5.01	5.11	−1.51	−1.53	−1.57
SE	-	-	22.7	75.7	25.1	26.8	72.2	72.3	72.2	72.9	72.9	72.8
ESE	-	-	22.8	73.3	26.1	27.9	73.1	73.2	73.2	71.4	71.4	71.6
MSE	-	-	0.52	5.73	0.85	0.72	5.24	5.24	5.24	5.31	5.31	5.30
CP	-	-	94.7	94.2	91.3	96.2	95.4	95.6	95.4	94.7	94.4	94.5

Int: internal-data only method

GR: generalized regression, mGR: modified GR for case-control sampling

CML: constrained maximum likelihood

ESE: estimated standard error

MSE: mean squared error

CP: coverage probability of a 95% confidence interval interval

Appendix: Derivation of the Pseudo-Loglikelihood

We first derive the pseudo-loglikelihood (4) under the simple random sampling design. The semiparametric likelihood $L_{\beta ,F}={\mathrm{\prod }}_{i=1}^N{f}_{\beta }(Y_i|X_i,Z_i)dF(X_i,Z_i)$ is to be maximized under the constraint ∫ u_β(X, Z; θ)dF(X, Z) = 0, where u_β(X, Z; θ) is defined in (3), and F is treated nonparametrically by assigning masses (δ₁, …, δ_m) to the unique values of the data (X_i, Z_i) (i = 1, …, N), with m the number of unique data points and ${\sum }_{j=1}^m{\delta }_j=1$. Let n_j be the number of (X_i, Z_i) equal to the jth distinct pair value. For notational convenience, write f_β,i = f_β(Y_i, X_i, Z_i), u_β,i = u_β(X_i, Z_i; θ), and F_i = F(X_i, Z_i) (i = 1, …, N). Applying the Lagrange multiplier method, we solve the stationary point to

$$\sum _{i=1}^N\text{log }{f}_{\beta ,i}+\sum _{j=1}^m{n}_j\text{log }{\delta }_j+{\lambda }^T\sum _{j=1}^m{u}_{\beta ,j}{\delta }_j+\varphi (\sum _{j=1}^m{\delta }_j-1),$$

where λ and ϕ are Lagrange multipliers. By differentiating with respect to λ and ϕ, we obtain the stationary equation: ${\sum }_{j=1}^m{u}_{\beta ,j}{\delta }_j=0$ and ${\sum }_{j=1}^m{\delta }_j=1$, as desired. Further, by differentiating with respect to δ_j, we obtain the stationary equation

$$\frac{n_j}{{\delta }_j}+{\lambda }^T{u}_{\beta ,j}+\varphi =0,$$

which, by multiplying δ_j and summing over j on both sides leads to ϕ = −N since ${\sum }_{j=1}^m{u}_{\beta ,j}{\delta }_j=0$ and ${\sum }_{j=1}^m{\delta }_j=1$. Hence

$${\delta }_j=\frac{1}{n_j}\frac{1}{N-{\lambda }^T{u}_{\beta ,j}},j=1,\dots ,m.$$

Plugging this δ_j into log(L_β,F) results in a profile likelihood that is equivalent to (4), with λ rescaled by a factor of N.

Now consider the semiparametric constrained maximum likelihood under the case-control sampling design of the internal study. In this case we want to maximize the case-control loglikelihood $\text{log}(L_{\beta ,F}^{cc})$ given in (5) subject to the constraint ∫ u_β(X, Z; θ)dF(X, Z) = 0. Define $f_{\beta ,i}^y=f_{\beta }(Y_i=y|X_i,Z_i)$ for y = 0, 1, $p_1={\sum }_{j=1}^m{f}_{\beta ,j}^1{\delta }_j$ and $p_0=1-p_1={\sum }_{j=1}^m{f}_{\beta ,j}^0{\delta }_j$. By the characterization of F as above and the Lagrange multiplier method, we solve the stationary equation for

$$\sum _{i=1}^N\text{log}{f}_{\beta ,i}+\sum _{j=1}^m{n}_j\text{log}{\delta }_j+{\lambda }^T\sum _{j=1}^m{u}_{\beta ,j}{\delta }_j+\varphi (\sum _{j=1}^m{\delta }_j-1)-N_1\text{log}\sum _{i=1}^m{f}_{\beta ,j}^1{\delta }_j-N_0\text{log }(1-\sum _j{f}_{\beta ,j}^1{\delta }_j).$$

Again, by differentiating with respect to λ and ϕ, we obtain the stationary equations: ${\sum }_{j=1}^m{u}_{\beta ,j}{\delta }_j=0$ and ${\sum }_{j=1}^m{\delta }_j=1$. The stationary equation by differentiating δ_j leads to

$$\frac{n_j}{{\delta }_j}+{\lambda }^T{u}_{\beta ,j}+\varphi -N_1\frac{f_{\beta ,j}^1}{p_1}-N_0\frac{f_{\beta ,j}^0}{p_0}=0.$$

Multiplying by δ_j, and summing over j on both sides leads to ϕ = 0 given ${\sum }_{j=1}^m{u}_{\beta ,j}{\delta }_j=0$ and ${\sum }_{j=1}^m{\delta }_j=1$. Hence

$${\delta }_j=\frac{1}{{\mu }_1{f}_{\beta ,j}^1+{\mu }_0{f}_{\beta ,j}^0-{\lambda }^T{u}_{\beta ,j}},j=1,\dots ,m,$$

where μ_y = N_y/p_y (y = 0, 1) and μ₀ in fact links to μ₁ since p₀ = 1 − p₁. Plugging δ_j into $\text{log}(L_{\beta ,F}^{cc})$ then gives the profile likelihood equivalent to (6).