Kinetic Ductility and Force-Spike Resistance of Proteins from Single-Molecule Force Spectroscopy

Abstract

Ductile materials can absorb spikes in mechanical force, whereas brittle ones fail catastrophically. Here we develop a theory to quantify the kinetic ductility of single molecules from force spectroscopy experiments, relating force-spike resistance to the differential responses of the intact protein and the unfolding transition state to an applied mechanical force. We introduce a class of unistable one-dimensional potential surfaces that encompass previous models as special cases and continuously cover the entire range from ductile to brittle. Compact analytic expressions for force-dependent rates and rupture-force distributions allow us to analyze force-clamp and force-ramp pulling experiments. We find that the force-transmitting protein domains of filamin and titin are kinetically ductile when pulled from their two termini, making them resistant to force spikes. For the mechanostable muscle protein titin, a highly ductile model reconciles data over 10 orders of magnitude in force loading rate from experiment and simulation.

Introduction

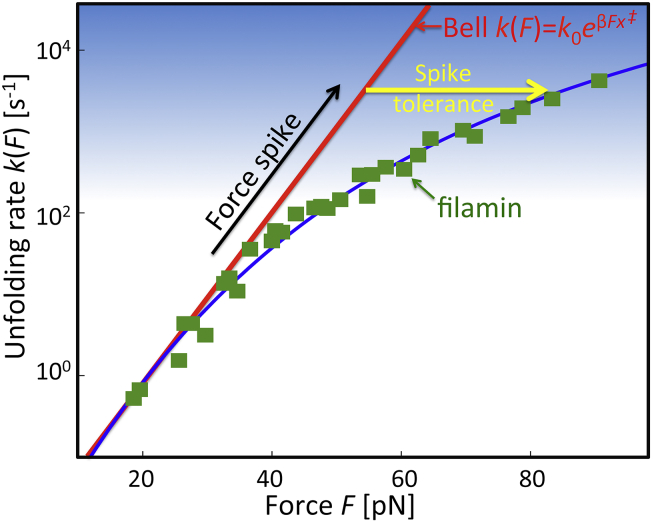
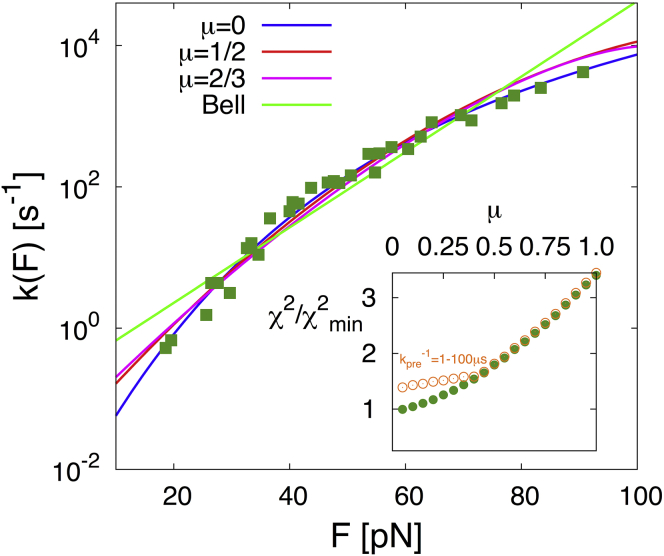
Proteins in muscle fibers, blood, or the cytoskeleton are subject to fluctuating forces. These forces can induce changes to their structure that range from reversible elastic deformations to dissociation of complexes and mechanical unfolding. According to the classical phenomenological theories (1, 2, 3), the rate of a conformational transition is expected to increase exponentially with force, $k\left(F\right)\approx k_0\text{exp}\left(\beta F{x}^{‡}\right)$, with $k_0$ as the intrinsic rate at zero force, $x^{‡}$ as the distance to the transition state, and β = 1/k_BT. As a consequence of the steep rise of the rupture rate with force, even transient force spikes can be highly destabilizing and carry the risk of quasi-irreversible damage from unfolding and eventual aggregation. Fig. 1 illustrates this problem with actual data (4, 5) for the ddFLN4 domain of filamin, a protein forming force-transmitting bridges in the actin network of the cytoskeleton. If the rise of the unfolding rate $k\left(F\right)$ with force F were strictly exponential as for the Bell’s model (3), a transient 1-ms force spike exceeding 50 pN would trigger unfolding with near certainty. However, at high force, the actual $k\left(F\right)$ drops below the Bell extrapolation. As a consequence, ddFLN4 is kinetically ductile, withstanding forces of nearly 80 pN for ∼1 ms on average. By contrast, the Bell rate extrapolated to this force would predict unfolding within 10 μs. Here, we develop the theoretical framework to relate the kinetic ductility reflected in the subexponential force dependence of $k\left(F\right)$ to the free energy landscape governing protein unfolding. We then use the theory to examine the force-spike resistance of different mechanoproteins.

Figure 1.

Resistance of proteins to transient force spikes. The force-dependent unfolding rates $k\left(F\right)$ of the filamin domain ddFLN4 (green symbols) drop below the exponential Bell model extrapolated from low force (red line). Rates $k\left(F\right)$ are from AFM measurements (4) cast into a master curve (5). As a result, larger force spikes (black arrow) into the critical regime (blue-shaded) can be tolerated. (Blue line) Fit to the experimental data of the kinetically ductile model (μ = 0 from Eq. 2). (Yellow arrow) Increased resistance to force spikes. To see this figure in color, go online.

Rupture rates, free energies of activation, and barrier locations can, in principle, be extracted quantitatively from single-molecule force spectroscopy experiments with the help of statistical mechanics. In microscopic theories (4, 6, 7, 8, 9, 10, 11, 12), molecular rupture under force is described in terms of diffusive dynamics on a unistable potential surface, for which the force dependence of the rupture rate can be found using Kramers theory (13). For constant loading rate, it appears that the rupture-force distribution, $p\left(F\right)$, can be expressed in terms of elementary functions only for two special cases of potentials: the linear-cubic (7, 9) and the harmonic-cusp potential (8). Dudko et al. (10) noted that for these two potentials and for Bell’s model, $k\left(F\right)$ and $p\left(F\right)$ can be written in a unified way by introducing a parameter ν. Specifically, values of ν = 1, 2/3, and 1/2 correspond to the Bell limit, and the linear-cubic and harmonic-cusp potential, respectively.

It was mentioned that ν could be treated as an adjustable parameter (10), but no specific form of the potentials was given for general ν. Lin et al. (11) considered polynomial approximations to the potential in the brittle regime (ν ≥ 1/2) that lead to the activation free energy of Dudko et al. (10). Hyeon and Thirumalai (12) constructed explicit potentials for ν = n/(n + 1) = 1/2, 2/3,… with n = 1,2,… that generalize the linear-cubic and harmonic-cusp models, and concluded that no physically reasonable potentials exist for 0 ≤ ν < 1/2. The ductile regime requiring a parameter from Dudko et al. (10) of ν < 1/2 has thus been associated with complex, multibarrier free energy landscapes (12, 14).

Here, we show that single-barrier potentials exist also in this ductile regime. The theory of force-induced rupture built on our newly introduced class of unistable potentials is fully analytical, and the potentials used in previous microscopic models are encompassed as special cases. By extending the range of potential surfaces, we can describe rupture kinetics from the ductile to the brittle extremes. We find that the regime corresponding to ν ≈ 0 results in kinetically ductile behavior described by a gradual stretching under force before eventual rupture. At the other extreme of brittle rupture, ν ≈ 1, the system does not yield significantly before breaking catastrophically. With the rupture-rate theory based on the new potentials, we examine the force-spike resistance of folded domains of the mechanoproteins titin, filamin, and gelsolin, which cover a broad range of mechanostabilities. For titin and filamin, the single-molecule pulling data (and molecular simulations in the case of titin) are consistent with high kinetic ductility.

Materials and Methods

Free energy surfaces

To extend the range of the analytic theory into the kinetically ductile regime, we consider a new class of smooth unistable potentials with continuous first derivatives,

$$G_0\left(x\right)=\frac{\Delta G^{‡}x}{\mu x^{‡}}\left[1-\left(1-\mu \right){\left(\frac{2x^2/x^{‡}}{\left|x\right|+x\text{sin}\theta }\right)}^{\mu /\left(1-\mu \right)}\right],$$ (1)

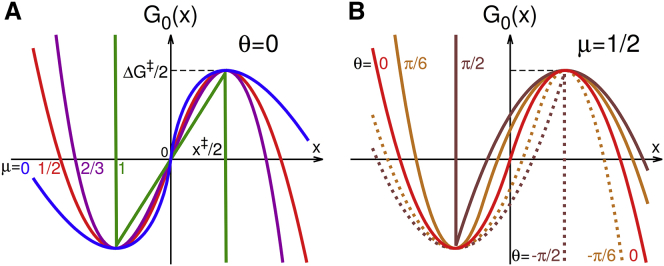
as illustrated in Fig. 2. The variable $x\in \left(-\infty ,\infty \right)$ is the pulling coordinate, $x^{‡}\equiv x^{‡}\left(F=0\right)$ is the distance from the well bottom to the barrier top without force, and $\Delta G^{‡}\equiv \Delta G^{‡}\left(F=0\right)$ is the activation free energy in the absence of force. The continuous parameters of kinetic brittleness, $\mu \in \left(\mathrm{0,1}\right)$, and well-barrier asymmetry, $\theta \in \left(-\pi /2,\pi /2\right)$, determine the shape of the potential with fixed activation free energy and distance to the transition state.

Figure 2.

Free energy profiles. (A) $G_0\left(x\right)$ for different kinetic brittleness μ = 0, 1/2, 2/3, and 1 with symmetric wells and barriers (θ = 0). (B) Asymmetric potentials $G_0\left(x\right)$ for μ = 1/2 and θ = 0, $\pm \pi /6$, and $\pm \pi /2$, shifted by $\left(\text{sin}\theta \right)/2$ along x to line up the extrema. For μ = 2/3 and θ = 0, $G_0\left(x\right)$ is the linear-cubic potential. For μ = 1/2, it is the harmonic-cusp potential when $\theta =-\pi /2$, and the matched-harmonic potential when θ = 0. As $\mu \to 1$, $G_0\left(x\right)$ becomes the saw-tooth potential. To see this figure in color, go online.

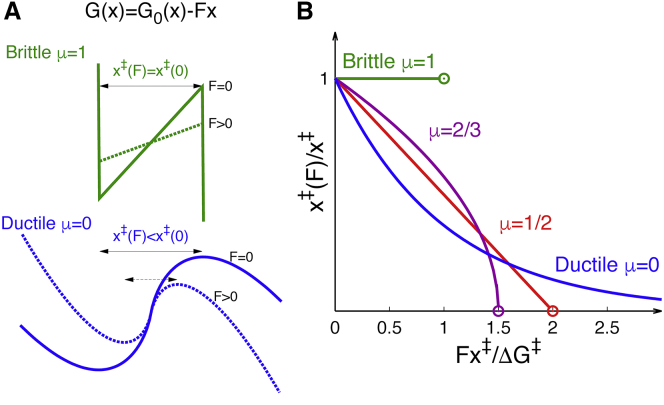
The class of potentials defined in Eq. 1 encompasses all previous microscopic models as special cases. For μ = 2/3 and θ = 0, we recover from $G_0\left(x\right)$ the linear-cubic potential (7, 9, 10), and for μ = 1/2 and θ = 0 the matched-harmonic. For μ = 1/2 and $\theta \to -\pi /2$, $G_0\left(x\right)$ reduces to the harmonic-cusp model (8). In the Bell limit $\mu \to 1$, we recover the saw-tooth potential (15) from $G_0\left(x\right)$. At a constant force F, the free energy is $G\left(x\right)=G_0\left(x\right)-Fx$ (Fig. 3 A).

Figure 3.

Brittle and ductile responses to force. (A) Free energy profiles, $G\left(x\right)=G_0\left(x\right)-Fx$, in the absence (F = 0; solid) and presence of a constant force (F > 0; dashed) for brittle (μ → 1) and ductile (μ → 0) systems with symmetric wells and barriers (θ = 0). (B) Normalized distance from the equilibrium position to the transition state, $x^{‡}\left(F\right)/x^{‡}$, as a function of the reduced force, $F{x}^{‡}/\Delta G^{‡}$, for μ = 0, 1/2, 2/3, and 1, for the class of potentials shown in Fig. 2. (Open circles) Disappearance of the barrier at the critical force. To see this figure in color, go online.

Kinetic ductility

The kinetic ductility of individual molecules is defined in terms of the response of the distance to the transition state $x^{‡}\left(F\right)$ to force before rupture (16) (Fig. 3). Perfectly brittle molecules rupture under force without any preceding drop in $x^{‡}\left(F\right)$, whereas for a perfectly ductile molecule, barring thermal fluctuations, $x^{‡}\left(F\right)$ would shrink indefinitely with F. This definition of brittleness differs from that adopted in some earlier studies, namely that brittle molecules have short distances to the transition state, such that the rupture rate depends relatively weakly on force. This latter definition requires a somewhat arbitrary choice of length scale to separate brittle from ductile. As we will show, under the definition of Hyeon and Thirumalai (16), even proteins with relatively short distances to the transition state can emerge as being ductile when being probed over a wide range of forces, making them resistant to transient force spikes.

For the class of unistable potentials defined in Eq. 1, the distance to the transition state depends on force as $x^{‡}\left(F\right)=x^{‡}{\left(1-F/F_c\right)}^{\left(1-\mu \right)/\mu }$ (Fig. 3 B), where the critical force $F_c=\Delta G^{‡}/\mu x^{‡}$ is the maximum sustainable force in the absence of thermal fluctuations. The value μ = 1/2 separates the kinetically ductile and brittle regimes with convex and concave $x^{‡}\left(F\right)$, respectively (Fig. 3 B). In the kinetically brittle limit (μ → 1), the saw-tooth potential perfectly maintains its distance to the transition state under force, $x^{‡}\left(F\right)=\text{const}.$, before collapsing catastrophically at the critical force. By contrast, in the fully ductile limit (μ → 0), the potential becomes $G_0\left(x\right)=\left(\Delta G^{‡}x/x^{‡}\right)\left[1-\text{ln}\left(2x^2/x^{‡}/\left(\left|x\right|+x\text{sin}\theta \right)\right)\right]$, and the metastable minimum persists for all finite forces, with the distance to the transition state decreasing exponentially with force, $x^{‡}\left(F\right)=x^{‡}\text{exp}\left(-F{x}^{‡}/\Delta G^{‡}\right)$. In practice, for any μ > 0, the barrier eventually disappears. Moreover, in a thermal system, barriers <k_BT are in essence negligible because of thermal fluctuations, and so the unruptured state does not persist to large force even when μ = 0.

Rupture-rate theory

We use Kramers theory (13) to calculate the force-dependent rate of molecular rupture $k\left(F\right)$, as modeled by the escape from the metastable minimum on the force-dependent free energy surface $G\left(x\right)$. For a smooth free energy profile near the extrema, one can expand $G\left(x\right)$ about the force-dependent minimum $\left(x_m\right)$ and maximum $\left(x_M\right)$ to second-order. For sufficiently high barriers, Kramers theory (13) leads to the expression $k\left(F\right)=\beta D{\left[G^{″}\left(x_m\right)\left|G^{″}\left(x_M\right)\right|\right]}^{1/2}\text{exp}\left[-\beta \Delta G^{‡}\left(F\right)\right]/2\pi$, where D is the diffusion coefficient and the force-dependent activation free energy is $\Delta G^{‡}\left(F\right)=G\left(x_M\right)-G\left(x_m\right)$. In this way, we find independent of the value of θ

$$k\left(F\right)=k_0{\left(1-\frac{\mu F{x}^{‡}}{\Delta G^{‡}}\right)}^{2-\frac{1}{\mu }}{e}^{\beta \Delta G^{‡}\left[1-{\left(1-\frac{\mu F{x}^{‡}}{\Delta G^{‡}}\right)}^{1/\mu }\right]},$$ (2)

where $k_0$ is the rate at zero force. For fixed $\Delta G^{‡}$ and $x^{‡}$ and decreasing μ, the range of forces for which Eq. 2 is valid, increases. In fact, $k\left(F_c\right)=0$ for $\mu >1/2$ (which is pathological). However, for $\mu <1/2$, $k\left(F\right)\to \infty$ as $F\to F_c$ (which fortuitously is more physically reasonable). In the fully ductile limit μ → 0, the rate becomes $k\left(F\right)=k_0\text{exp}\left[\beta \Delta G^{‡}\left(1-e^{-F{x}^{‡}/\Delta G^{‡}}\right)+F{x}^{‡}/\Delta G^{‡}\right]$.

The force-dependent activation free energy implicit in Eq. 2, $\Delta G^{‡}\left(F\right)=\Delta G^{‡}{\left(1-\mu F{x}^{‡}/\Delta G^{‡}\right)}^{1/\mu }$, is identical for all θ to that proposed by Dudko et al. (10) when μ → ν. However, the preexponential factors differ except when μ = 2/3, and this is why we use μ instead of ν. The reason for this is that the preexponential factors from Dudko et al. (10) for ν other than 1/2 and 2/3 were not derived from Kramers rate theory using an explicit free energy surface. In addition, for ν = 1/2, Dudko et al. (10) used a cusp-shaped potential surface, corresponding to μ = 1/2 and $\theta =-\pi /2$ here. For such potentials, when the second derivatives do not exist at the extrema, the preexponential factor should not be calculated as above, but in a different way (see section 3.5.3 of Hummer and Szabo (17)). For the harmonic-cusp model (8, 10, 18), μ = 1/2 and $\theta \to \pm \pi /2$, one then obtains a preexponential factor of $\left(1-F{x}^{‡}/\Delta G^{‡}\right)$ instead of 1, in agreement with Dudko et al. (10).

For soft linkers under the quasi-adiabatic assumption (see, e.g., Hummer and Szabo (8)), the distribution of rupture forces is

$$p\left(F\right)=\frac{k\left(F\right)}{\dot{F}}{e}^{-{\int }_0^{F}d{F}^{\prime }k\left(F^{\prime }\right)/\dot{F}},$$ (3)

where $\dot{F}=dF/dt$ is the force loading rate. For $k\left(F\right)$, in Eq. 2, it is valid for forces F well below F_c with activation barriers $\Delta G^{‡}\left(F\right)\gtrsim k_{\text{B}}T$. For a linear increase of the applied force with time t, $F\left(t\right)=\dot{F}t$ with $\dot{F}$ constant, we obtain

$$p\left(F\right)=\frac{k\left(F\right)}{\dot{F}}{e}^{{\Lambda }_0\left(\Gamma \left[3\mu -1,\beta \Delta G^{‡}\right]-\Gamma \left[3\mu -1,\beta \Delta G^{‡}{\left(1-\frac{\mu F{x}^{‡}}{\Delta G^{‡}}\right)}^{1/\mu }\right]\right)},$$ (4)

where ${\Lambda }_0=k_0{\left(\beta \Delta G^{‡}\right)}^{2-3\mu }{e}^{\beta \Delta G^{‡}}/\beta \dot{F}{x}^{‡}$ and $\Gamma \left[s,x\right]={\int }_x^{\infty }{t}^{s-1}{e}^{-t}dt$ is the incomplete Γ-function. The average rupture force $\langle F\rangle =\int Fp\left(F\right)dF$ is approximately

$$\langle F\rangle \approx \frac{\Delta G^{‡}}{\mu x^{‡}}\left[1-{\left(\frac{\text{lnΛ}}{\beta \Delta G^{‡}}\right)}^{\mu }\left(1+\frac{\mu \left(3\mu -2\right)\text{ln}\left(\text{lnΛ}\right)}{\text{lnΛ}}\right)\right],$$ (5)

where $\Lambda ={\Lambda }_0{e}^{\gamma }$ and $\gamma \approx 0.5772$ is the Euler-Mascheroni constant. For μ → 0, we find $\langle F\rangle =\left(\Delta G^{‡}/x^{‡}\right)\left[\text{ln}\left(\beta \Delta G^{‡}/\text{lnΛ}\right)+2\text{ln}\left(\text{lnΛ}\right)/\text{lnΛ}\right]$. Equation 5 can be obtained from Garg’s (7) asymptotic expansion by replacing ${\left({\text{lnΛ}}_0\right)}^{\mu }\left(1+\mu \gamma /{\text{lnΛ}}_0\right)$ with ${\left({\text{lnΛ}}_0+\gamma \right)}^{\mu }$.

Practical considerations

To combine different force spectroscopy experiments and simulations, rupture forces should be compared as a function of force loading rate, not of pulling velocity, because the effective spring constants in different experiments and simulations vary widely as a result of having used different pulling springs and/or molecular constructs with multiple domains and linkers. The relevant force loading rate is obtained as the product of the pulling speed v (in meters per second) and the effective spring constant ${\kappa }_{\text{eff}}$ of the combined molecular construct and pulling spring, $\dot{F}={\kappa }_{\text{eff}}v$. The value ${\kappa }_{\text{eff}}$ can be obtained from a wormlike-chain fit of the force-extension curves (5). More simply, in a plot of the force as a function of the entire extension (including the stretched pulling spring), the slope at rupture gives ${\kappa }_{\text{eff}}$ directly. As a function of the molecular extension (not including the stretched pulling spring), the slope κ has to be combined with the spring constant ${\kappa }_s$ of the pulling apparatus (8), ${\kappa }_{\text{eff}}={\kappa }_s\kappa /\left({\kappa }_s+\kappa \right)$. For the titin I91 and gelsolin domains, the slopes were obtained in this way from the published (19, 20, 21, 22) force extension curves just before rupture.

Model parameter interdependence is another concern. If the experimental data set is sufficiently large, it is possible to extract accurate values of the activation barrier, distance to the transition state, intrinsic rupture rate, and brittleness. However, if the data cover only a limited range, a wider range of models is consistent with experiment. For the titin I91 domain, the range of possible parameters and their interdependence are illustrated in Fig. S1 in the Supporting Material, which shows ${\chi }^2$ surfaces for μ = 0.3 fixed as a function of $\text{ln}\left(k_0\right)$ and $x^{‡}$ (top), and of $\Delta G^{‡}$ and $x^{‡}$ (bottom). The remaining parameters, $\Delta G^{‡}$ and $k_0$, were optimized. The best solutions show a linear correlation between the fitted $\text{ln}\left(k_0\right)$ and $x^{‡}$. These uncertainties can be reduced by incorporating prior knowledge, e.g., by assuming a physically reasonable value of the preexponential factor $k_{\text{pre}}=k_0\text{exp}\left(\beta \Delta G^{‡}\right)$.

Results and Discussion

Titin

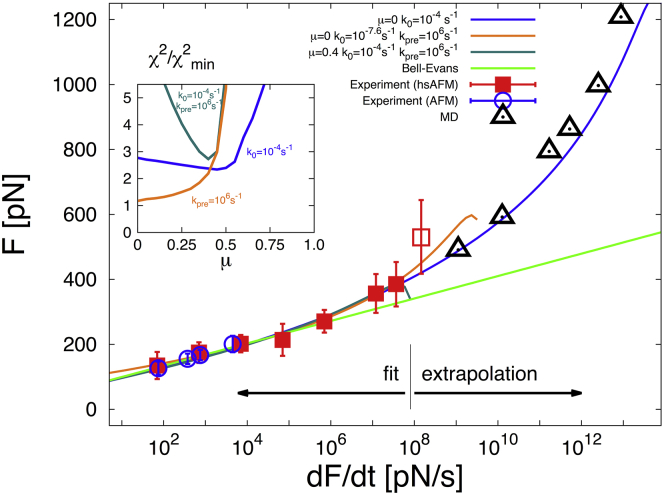
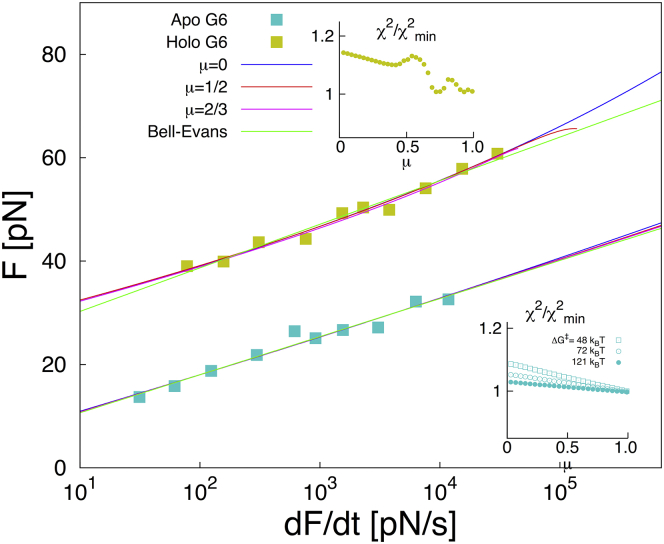
We focus first on the prototypical mechanostable protein titin from muscle fibers. Fig. 4 shows the mean unfolding forces of the titin I91 domain (I27 according to another numbering scheme) when pulled from its two termini, as a function of the force loading rate $\dot{F}$ from regular (19) and high-speed atomic force microscopy (hsAFM) experiments (20), and from all-atom molecular dynamics (MD) simulations (21). The dynamic range of the data is enormous because the I91 domain is exceptionally resistant to force. Using the harmonic cusp model (8), semiquantitative agreement between regular AFM and MD unfolding of titin I91 has been noted previously (21), although in an extrapolation to small force loading rates the experimental unfolding forces were overestimated by 50–100 pN. More recently, using the harmonic-cusp model, hsAFM measurements were shown to be consistent with the first point of low-speed MD (20), but even then there was a kink in the mean rupture force at the crossing of the hsAFM and MD regimes. Peculiarly, both of these studies obtained extremely low intrinsic (i.e., zero force) rates, $k_0\approx {10}^{-10}-{10}^{-11}{\text{s}}^{-1}$, six orders-of-magnitude smaller than expected from bulk rate measurements (19).

Figure 4.

Titin unfolding. Mean rupture force of the titin I91 domain, when pulled from its two termini, as a function of the logarithm of the force loading rate from hsAFM (red squares) (20) and regular AFM experiments (blue circles) (19), and from MD simulations (black triangles) (21). Error bars indicate SDs. The analytic expression for $\langle F\rangle$ in Eq. 5 was fitted only to hsAFM data (solid squares) (19). The point at the highest loading rate (open square) was not included in the fit because it proved difficult to estimate all the relevant correction factors (in particular the very large viscous drag correction, and the linker correction (see Cossio et al. (23) and the Supporting Material) required to determine the effective force loading rate). However, if these estimates are correct and the data value is proper, the overlap of experiment and MD would be poor. Least-square fits are shown for μ → 0 with fixed $k_0={10}^{-4}{\text{s}}^{-1}$ close to the bulk unfolding rate (blue line), and fixed kinetic prefactor $k_{\text{pre}}={10}^6{\text{s}}^{-1}$ (orange), and for μ = 0.4 with both $k_0$ and $k_{\text{pre}}$ fixed (dark green). (Inset) The error ${\chi }^2$ relative to the best fit as a function of brittleness μ. A fit of the perfectly brittle Bell-Evans model (3, 6) for $\dot{F}<{10}^6\text{pN}/\text{s}$ is shown as a light-green line. For the best fits $\left({\chi }^2/{\chi }_{\text{min}}^2<2.5\right)$, the distance to the transition state and the activation barrier are in the ranges $0.37\le x^{‡}\le 0.78\text{nm}$ and $24\le \Delta G^{‡}\le 32k_{\text{B}}T$, respectively. To see this figure in color, go online.

The wide class of potentials introduced here allows us to examine the effects of model choice on the extracted parameters. We find that $k_0$ from ${10}^{-10}{\text{s}}^{-1}$ to ${10}^{-3}{\text{s}}^{-1}$ leads to fits to the hsAFM data of comparable quality, with compensating changes primarily in $x^{‡}$. These large uncertainties could be reduced by using additional information. For instance, if we fix $k_0={10}^{-4}{\text{s}}^{-1}$, close to the equilibrium unfolding rate (19), we obtained excellent fits to the hsAFM data (20) for μ < 1/2 (see inset, Fig. 4), except for one point at the highest velocity, which has large uncertainties both in the force and in the estimated loading rate. These fits to the hsAFM data agree well also with regular AFM data (19), and, remarkably, the most ductile model, μ → 0, predicts the simulated rupture forces from MD simulation (21) for four orders of magnitude in loading rates beyond the fitting range. With $\Delta G^{‡}=32k_{\text{B}}T$ and $x^{‡}=0.38$ nm, the Kramers high-barrier approximation remains valid over the full force range (F < 1200 pN).

However, the excellent agreement in Fig. 4 over 10 orders of magnitude in the loading rate may be somewhat fortuitous. At the high speeds used in MD, the quasi-equilibrium assumption underlying the rupture rate theories may be violated (23). Another concern is that for μ → 0, the preexponential factor $k_{\text{pre}}=k_0{e}^{\beta \Delta G^{‡}}\approx 1/\left(25\text{ps}\right)$ obtained in the fit appears to be several orders-of-magnitude greater than what one would expect from measured transition path times for other biomolecules (24). If we fix both $k_0={10}^{-4}{\text{s}}^{-1}$ and $k_{\text{pre}}={10}^6{\text{s}}^{-1}$, with $\beta \Delta G^{‡}=\text{ln}\left(k_{\text{pre}}/k_0\right)\approx 24$, we find that optimal solutions to the experimental data are still ductile, $0.3<\mu <0.5$, but result in lower critical forces F_c ≤ 500 pN. As a consequence, the rupture-force curves break down immediately after the last experimental point (Fig. 4), well before the regime of MD simulations is reached. This would imply that experiments and MD simulations probe different unfolding mechanisms, with MD unfolding occurring faster than the characteristic time $1/k_{\text{pre}}=1\mu \text{s}$.

On the other hand, it is possible that for titin unfolding under high force, the preexponential factor is indeed faster than expected from equilibrium folding transitions of protein G and a WW domain (24). Experiments and simulations have been interpreted as force-induced unfolding being triggered by local events, such as the shearing of backbone hydrogen bonds (25) and additional breaking of side-chain interactions (26). Once these local interactions are broken, the transition state to unfolding is crossed at the relatively high forces exceeding 50 pN probed in the titin experiments. This local nature of the transitions under force is also consistent with the short, $x^{‡}\approx 0.4$ nm, distance to the transition state. The preexponential factor associated with such local motions could be considerably faster than the μs dynamics of folding. In turn, the transition path times to reach the first structures committed to the unfolded state would be faster than those seen in equilibrium unfolding experiments in the absence of force for other proteins (24), possibly because at the high forces of the titin force-ramp experiments (>150 pN, i.e., >36 k_BT/nm) the transition state is very close to the folded state, so that a structurally small perturbation of the right direction suffices to carry the protein over the barrier, beyond which it quickly unravels. A fast prefactor would rationalize the smooth transition from hsAFM to MD in Fig. 4, and support the conclusion that the unfolding transitions in fast MD pulling simulations with rupture forces F > 400 pN are relevant also in the experimental force range. In light of the rapid advances in both experiment and simulation, it should soon be possible to probe the mechanism in detail.

As noted above, the quasi-adiabatic approximation underlying Eq. 3 is expected to break down at sufficiently fast rupture speeds. Bullerjahn et al. (18) showed that for the harmonic-cusp potential, analytic formulas for the rupture-force distribution could be obtained in the limit of high loading rates, where small force-dependent barriers are probed. It remains to be seen if their approach can be extended to the class of potentials introduced here. Also, with the data at hand we could not account for the fact that, for multimodule titin constructs, both the effective spring-constant and the rupture rate depend on the number of domains that are still folded (8).

Filamin

Filamin is a protein forming force-transmitting bridges in the actin networks of the cytoskeleton. Its ddFLN4 domain is much less mechanostable than titin I91, withstanding forces only up to ∼90 pN in AFM experiments (4). In Fig. 5, we show the experimental rupture-force distributions (4) cast into a single k(F) master curve (5), and fitted k(F) curves for μ = 0, 1/2, 2/3, and the Bell model (3). To ensure validity of Eq. 2 over the entire force range $F<F_{\text{max}}=91$ pN, we constrained the fits so that $\Delta G^{‡}\left(F\right)\ge 1k_{\text{B}}T$. Additionally, we restricted the preexponential factor to the expected range (24), $1\mu \text{s}<k_{\text{pre}}^{-1}<100\mu \text{s}$ (inset, Fig. 5). In all cases, ductile models with μ < 0.4 produced acceptable fits, and the extracted parameters fall within relatively narrow ranges ($\Delta G^{‡}\approx 13.2-14.5k_{\text{B}}T$, $x^{‡}\approx 1.0-1.5\text{nm}$, and $k_0\approx {10}^{-3}-{10}^{-2}{\text{s}}^{-1}$; see Fig. S2 for fit details).

Figure 5.

Filamin unfolding. Force-dependent unfolding rates $k\left(F\right)$ of the filamin domain ddFLN4 from AFM measurements (4) (green squares) when pulled from its two termini. Fits of $k\left(F\right)$ are shown as lines for μ = 0 (blue), 1/2 (red), 2/3 (magenta), and the completely brittle Bell model (3) (light green). (Inset) The error ${\chi }^2$ relative to the best fit as a function of brittleness μ, with restricted prefactor, $1<k_{\text{pre}}^{-1}<100\mu \text{s}$ (orange), and without restriction on $k_{\text{pre}}$ (green). Minimum activation barriers of $\Delta G^{‡}\left(F\right)\ge 1k_{\text{B}}T$ were imposed over the entire force range, $0<F<F_{\text{max}}=91$ pN. To see this figure in color, go online.

Gelsolin

Our theory accounts also for brittle rupture, as exemplified by the sixth domain of gelsolin (G6), a calcium-activated protein that severs and caps actin filaments (27) (see Fig. 6), when pulled from its two termini. In its holo (active) state, the optimal brittleness parameter is $\mu \approx 0.75$ in a fit of the mean rupture forces measured as a function of force loading rate (22). In its apo (inactive) state, G6 is even more brittle, with μ → 1 producing the best fit. In fact, because Bell’s model is recovered from our theory when $\Delta G^{‡}\to \infty$ for all μ, we had to fix $\Delta G^{‡}$, and characterized the performance of the ${\chi }^2$ separately (bottom inset of Fig. 6). This shows that just two parameters are sufficient to describe the linear dependence of the experimental data, and $\Delta G^{‡}$ is undetermined. The optimal distance to the transition state and intrinsic rate are $x^{‡}\approx 1.2-1.4\text{nm}$ and $k_0\approx {10}^{-2}-{10}^{-1}{\text{s}}^{-1}$; and $x^{‡}\approx 1.6-2.0\text{nm}$ and $k_0\approx 5\times {10}^{-6}-5\times {10}^{-5}{\text{s}}^{-1}$ for the apo and holo states, respectively. The activation free energy for the holo state is $\Delta G^{‡}=22-24k_{\text{B}}T$, and the corresponding preexponential factor is within the expected range as $6\times {10}^5<k_{\text{pre}}<6\times {10}^6{\text{s}}^{-1}$. If the preexponential factor is fixed to ${10}^6{\text{s}}^{-1}$ for the apo state, then the corresponding activation barrier is $\Delta G^{‡}=16-18k_{\text{B}}T$. The difference in the force response of G6 and ddFLN4 is striking. Although both proteins can withstand forces up to ∼80 pN and exhibit comparable transition state distances, G6 and ddFLN4 are at opposite ends of the brittleness spectrum. However, the range of forces probed is relatively small in the case of G6, and as a result μ could not be determined with high statistical significance.

Figure 6.

Brittleness of the sixth domain of gelsolin along its end-to-end distance. Mean rupture force of the G6 gelsolin domain as a function of the logarithm of the force loading rate, in the absence (apo state; green) and presence of calcium ions (holo state; yellow). Fits of $\langle F\rangle$ are shown as lines for μ = 0 (blue), 1/2 (red), 2/3 (magenta), and the brittle Bell-Evans model (3, 6) (light green). (Inset) The error ${\chi }^2$ relative to the best fit. Brittle models are found to be optimal. Note that in the brittle limit, $\langle F\rangle$ grows linearly with $\dot{F}$, and one cannot extract $\Delta G^{‡}$ as a third parameter beyond $k_0$ and $x^{‡}$. Because for $\Delta G^{‡}\to \infty$, the fully brittle behavior is obtained from our theory for all μ, in fits of the apo state data $\Delta G^{‡}$ was fixed at different values to ensure numerical convergence. To see this figure in color, go online.

Conclusions

The potentials introduced in Eq. 1 lead to analytic expressions for the force-dependent rupture rate $k\left(F\right)$ in force-clamp experiments, and the rupture-force distributions $p\left(F\right)$ and the mean forces $\langle F\rangle$ in force-ramp experiments. These potentials can account for the widely varying responses of molecular constructs to force, from the brittle response of the gelsolin G6 domain to the ductile titin I91 and filamin ddFLN4 domains. In the ductile regime, relatively high peak forces can be sustained by each domain if the force is ramped up rapidly, as indicated by the sharp rise of $\langle F\rangle$ with $\dot{F}$ in Fig. 4 for titin, far exceeding the linear increase with $\text{ln}\dot{F}$ expected for a perfectly brittle material described by the Bell model (3, 6). In this way, ductility could limit the damage induced by force spikes (28), e.g., in muscle fibers (29, 30), where variations in the mechanical stabilities of the individual domains are expected to limit damage (31).

A need to account for the ductile regime has emerged also from earlier theoretical and molecular simulation studies of protein unfolding. Stretching forces required to destabilize some folded states were thermodynamically larger than previously expected (32), and both all-atom and coarse-grained simulations showed a nonlinear dependence of the activation barrier on force, indicative of kinetically ductile behavior (33, 34, 35).

Determining the brittleness of individual molecules has become possible by analyzing force spectroscopy measurements over a broad force range using the new potential surfaces. In practice, this requires that a wide range of forces have been probed because the brittleness manifests itself in the curvature of $\text{ln}k\left(F\right)$-versus-F (e.g., Fig. 1) or $\langle F\rangle$-versus-log-loading rate plots (e.g., Fig. 4). If the experimental data are limited, many parameter sets may be nearly equally consistent with experiment. If one is interested in extrapolated properties, such as the rate $k_0$ of rupture at zero force, the variability in the extrapolations for the different parameters μ provide an estimate of the uncertainties associated with model choice. The range of solutions can be reduced by making assumptions about the kinetics that may reflect additional information, as was done here for titin. In practical applications, we advocate a hierarchical approach in which the flexibility of the new formalism, which includes brittleness as an additional parameter, is exploited to first construct a wide range of numerically acceptable models that is then narrowed down by invoking additional information or imposing assumed physical constraints. Also, in a Bayesian formulation of the theory (36), prior distributions for the model parameters can be invoked to express parameter preferences transparently.

A corollary of Eq. 2 is that the exact shape of the molecular potential surface cannot be determined uniquely from force spectroscopy experiments. For the potentials in Eq. 1, the force-dependent activation barrier and distance to the transition state do not depend on the well-barrier asymmetry parameter θ. Thus, all the potentials in Fig. 2 B lead to essentially the same force dependence of the Kramers rate. Resolving the well-barrier asymmetry would be possible by additional high-precision measurements of the response of the equilibrium extension $\overline{x}\left(F\right)$ to force before rupture.

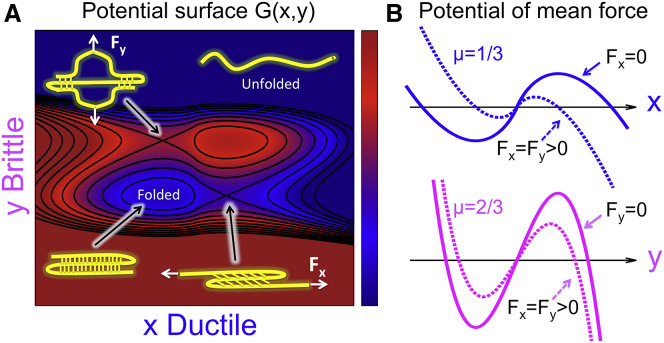
Brittleness is not a property of the entire protein because it can depend on the specific linkage used to apply the force. Proteins are inhomogeneous and anisotropic molecular structures. Consequently, the mechanical response depends on the direction of force, as demonstrated experimentally for ubiquitin (37) and green fluorescent protein (38, 39, 40) by probing a broad range of linkages. To illustrate this important point, we show in Fig. 7 A a schematic two-dimensional free-energy landscape for two different pulling directions, one ductile (x) and the other brittle (y). When force is applied in the x direction, escape from the single minimum in the bottom left will occur over the saddle point in the bottom right, governed by the one-dimensional potential of mean force along x (Fig. 7 B). As a result, the kinetics of forced rupture exhibits ductile characteristics. By contrast, when force is applied in the y direction, the saddle point in the upper-left gets lowered, and the one-dimensional potential of mean force along y becomes relevant. Consequently, the kinetics of forced rupture exhibits brittle properties. High forces will tend to favor transitions over saddle points in the pulling direction. Because different rupture channels can differ in their mechanical characteristics, the brittleness will, in general, depend on the pulling direction, just as $\Delta G^{‡}$ and $x^{‡}$ do (41).

Figure 7.

Changes in brittleness along different pulling directions. (A) Schematic representation of a two-dimensional potential surface, at zero force, as a function of a ductile coordinate x and a brittle coordinate y. The schematic structures of a folded/unfolded protein and of the two unfolding transition states are included purely for illustrative purposes, to indicate a possible change in unfolding mechanism for different pulling directions (i.e., transition states and brittleness could be quite different for actual three-stranded β-sheet proteins). (White arrows) Linkage of the force along each coordinate. (B) The potential of mean force along x (blue) and y (magenta) without force (solid lines), and with force $F_x=F_y>0$ (dashed lines). The brittleness parameter is μ = 1/3 along the ductile coordinate x and μ = 2/3 along the brittle coordinate y. To see this figure in color, go online.

Our theory assumes that the pulling direction is a good reaction coordinate, which is typically the case at high force (41). However, the rupture mechanism may change when probed over a large range of forces. Such changes can be accounted for by extending the formalism to treat M different rupture channels i in parallel, each with its effective one-dimensional free energy surface and corresponding parameters $k_{0i}$, $x_i^{‡}$, $\Delta G_i^{‡}$, and ${\mu }_i$,

$$k_{\text{eff}}\left(F\right)=\sum _{i=1}^{M}k\left(F|k_{0i},x_i^{‡},\Delta G_i^{‡},{\mu }_i\right),$$ (6)

or by going to a multidimensional framework (5, 42, 43, 44). On the schematic landscape in Fig. 7, a transition from one dominant mechanism to another would occur for a force acting on both x and y, say, by pulling along the one o’clock direction. At low forces, rupture would occur over the lower saddle in the bottom right. At high forces, however, the saddle in the upper-left becomes lower and thus dominant. Equation 6 approximates the overall rupture rate as that of the sum of the rates for the two rupture processes ($i=1$, and 2) for x and y, respectively, with effective parameters $k_{0i}$, $x_i^{‡}$, $\Delta G_i^{‡}$, and ${\mu }_i$. The effective intrinsic rate, activation barrier, and brittleness correspond to the true landscape along each direction. However, the effective distance to the transition state is reduced as a result of the projection of the force onto each coordinate.

But before invoking more complex rupture scenarios, it is important to show that the available data are indeed inconsistent with the predictions of the simple single-barrier potentials introduced here. Classic examples where this is the case are the biotin-avidin and LFA-1:ICAM1 complexes (12). On the other hand, it is interesting that biotin-streptavidin and LFA-1:ICAM2 complexes can be described rather well by our single-barrier models (see Fig. S3). The Src SH3 domain (44) is a more recent example where it is justified to invoke multiple pathways. In this case, the observed unfolding rate increases faster than exponentially with increasing force, whereas in a single-barrier model the behavior is predicted to be just the opposite (e.g., Fig. 5). Conversely, when our single barrier one-dimensional potentials work well over a broad range of forces, the molecular extension, at least in this range, is likely to be a meaningful coordinate. The usefulness of one-dimensional descriptions has been recently shown for the PrP protein by Neupane et al. (45) using transition path theory (46).

A limitation of the theory is that one cannot extract atomic details from the one-dimensional model or immediately relate the fitted parameters of the underlying potential surface to microscopic properties such as a specific hydrogen bond. Formally, the potential surface is defined by a projection of the high-dimensional conformation space onto the measured extension, which cannot be inverted. However, the characteristics of the potential surface may suggest mechanisms that can be tested, for instance, by performing mutations.

Finally, we note that the potentials introduced here for pulling may also prove useful in other fields. Encouraged by the remarkable equivalence of pulling and the behavior of Josephson junctions in the presence of time-varying fields (7, 47), we expect that the models introduced here may prove useful in diverse applications, from the dynamic theory of phase transitions to nanoscale friction and ionic currents under time-dependent electric fields.

Author Contributions

P.C., G.H., and A.S. developed theory, analyzed data, and wrote the article.

Editor: Matthias Rief.