Estimating differences and ratios in median times to event

Abstract

Time differences and time ratios are often more interpretable estimates of effect than hazard ratios for time-to-event data, especially for common outcomes. We developed a SAS macro for estimating time differences and time ratios between baseline-fixed binary exposure groups based on inverse probability weighted Kaplan-Meier curves. The macro uses pooled logistic regression to calculate inverse probability of censoring and exposure weights, draws Kaplan-Meier curves based on the weighted data, and estimates the time difference and time ratio at a user-defined survival proportion. The macro also calculates the risk difference and risk ratio at a user-specified time. Confidence intervals are constructed by bootstrap. We provide an example assessing the effect of exclusive breastfeeding during diarrhea on the incidence of subsequent diarrhea in children followed from birth to 3 years in Vellore, India. The SAS macro provided here should facilitate the wider reporting of time differences and time ratios.

INTRODUCTION

In longitudinal observational studies of the occurrence and timing of health outcomes, analyses often make extensive use of Cox proportional hazards models¹ to estimate adjusted hazard ratios. Hazard ratios have several methodological limitations,² and may be difficult to interpret when applied to common outcomes. For example, because almost all children will have multiple diarrhea episodes during the first few years of life, an estimate of increased relative hazard comparing two exposure conditions cannot be interpreted as a relative difference in the number of children experiencing the outcome between groups since the overall risk is near 100%. Here, estimates of the difference in timing of outcomes may be more relevant.

While the time ratio measure can be estimated parametrically using accelerated failure time models,^3,4 these models have the disadvantage of requiring parametric assumptions if there is no strong evidence that the data follow a particular distribution. Bayesian models can provide adjusted means and credible intervals of median times and ratios,⁵ and censored quantile regression provides an option to semiparametrically estimate contrasts in survival times using the Kaplan-Meier estimator.⁶ However, these methods are not widely used by epidemiologists. Here, we offer here an additional method in a SAS macro to estimate time differences and time ratios between baseline-fixed binary exposure groups based on inverse probability weighted Kaplan-Meier curves.

METHODS

Inverse probability weighting is a parametric approach to standardize functionals of the observed data to the total population distribution of confounders^7,8 and results in marginal effect estimates. Each stabilized exposure weight (SW_i^E) is the marginal probability of a subject’s observed exposure divided by the probability of her observed exposure conditional on her observed covariates, or

$${S{W}_i}^E=\mathrm{P}\mathrm{r}(X_i)/\mathrm{P}\mathrm{r}(X_i|Z_i)$$

where X_i is subject i’s exposure and Z_i is subject i’s covariates.

Censoring weights (SW_i,t^C)^9,10 are constructed over time as the marginal probability of a subject’s censoring status divided by the probability of her censoring status conditional on her observed baseline covariates. This quantity is multiplied by the same quantity at all previous time intervals, such that

$${S{W}_{i,t}}^C=\prod _{k=1}^t\mathrm{P}\mathrm{r}(C_{i,k}=0|C_{i,k-1}=0,X_i)/\mathrm{P}\mathrm{r}(C_{i,k}=0|C_{i,k-1}=0,X_i,Z_i)$$

where C_i,t is an indicator for censoring at time t, and t is the time interval ranging from 0 (baseline) to the interval of subject i’s event or censoring. Final inverse probability of exposure and censoring weights are calculated for each time interval as the product of the time-fixed exposure weight and the time-varying censoring weight, or $S{W}_{i,t}={S{W}_i}^{E}S{W}_{i,t}^C$. The weights can be truncated by resetting the values of weights outside extreme percentiles of the weight distribution to their values at specified percentile cut-offs. Further details on constructing inverse probability weights are available.¹¹

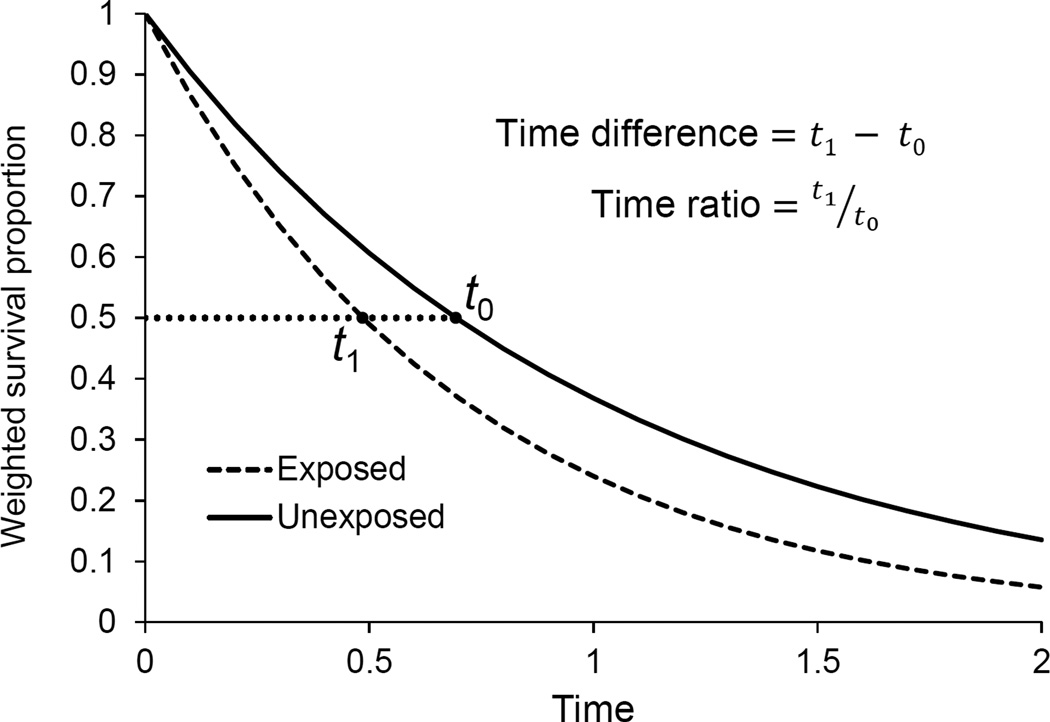
Time differences are defined as the difference in the time each exposure group reaches a given survival percentile p, t_1,p and t_0,p, and can be calculated by subtracting these times as read off the Kaplan-Meier curves, t_1,p − t_0,p. Time ratios are similarly defined as the ratio of these two times, $\raisebox{1ex}{$t_{1,p}$}\!\left/ \!\raisebox{-1ex}{$t_{0,p}$}\right.$. Figure 1 shows schematically how to calculate a median time difference and ratio (i.e. p=0.5) from two sample curves.

Figure 1.

Schematic showing the calculation of the median time difference and time ratio from inverse probability-weighted Kaplan-Meier curves.

Macro

Based on the above, the SAS macro provided here performs an analysis by calculating inverse probability of exposure and censoring weights for a binary exposure, drawing Kaplan-Meier curves based on the weighted data, and then estimating the effect measures requested by the user. First, the macro uses a logistic regression model (fit with PROC LOGISTIC) to calculate inverse probability of exposure weights stabilized by the marginal probability of exposure for a binary exposure.¹² Inverse probability of censoring weights^9,10 are then calculated by segmenting the time-scale into deciles based on the distribution of drop-out times. Probability of censoring is calculated in each time decile using pooled logistic regression (fit with PROC LOGISTIC) and censoring weights (SW_t^C) are constructed within time deciles. Final weights, calculated as the product of the exposure and censoring weights, are truncated at percentiles specified by the user.

Inverse probability-weighted Kaplan-Meier curves are drawn for exposed and unexposed groups (using PROC PHREG),^9,12,13 and the time difference (t_1,p − t_0,p) and time ratio $(\raisebox{1ex}{$t_{1,p}$}\!\left/ \!\raisebox{-1ex}{$t_{0,p}$}\right.)$ at p% survival are calculated. The macro also calculates the risk difference (R_1,t − R_0,t) and risk ratio $(\raisebox{1ex}{$R_{1,t}$}\!\left/ \!\raisebox{-1ex}{$R_{0,t}$}\right.)$ at time t = q, where R₁ and R₀ are the risks in the exposed and unexposed groups, respectively. The macro constructs 95% confidence intervals (CI) by non-parametric bootstrap with a user-defined number of simple random resamples each of the original sample size.¹⁴ Two confidence intervals are produced:¹⁵ directly using the 2.5^th and 97.5^th percentiles of the effect estimate distribution and using the standard deviation (SD) of the effect estimates to calculate Wald-based confidence limits $(X\pm 1.96*\sqrt{SD(X)})$. Comments in the eAppendix provide users with guidance on choosing confidence intervals and the number of bootstrap resamples.

To run the macro, the user inputs the dataset name, a subject ID variable, binary exposure indicator, list of covariates, time at outcome, binary outcome indicator, indicator for macro to include censoring weights (default is 1=yes), binary dropout indicator, low and high percentiles for truncating weights (default is 0 and 100 corresponding no truncation), survival proportion to calculate time differences/ratios (default is 0.5, corresponding to the median survival time), time to calculate risk differences/ratios, number of bootstrap resamples (default is 2000), and a seed for random sampling (see eAppendix for further information and annotated code).

Example

We provide an example using combined data from three prospective observational cohort studies of diarrhea among children from Vellore, India conducted between 2002 and 2013.^16–18 The studies were approved by the Institutional Review Boards of the Christian Medical College, Vellore, India and Tufts University Health Sciences campus, Boston, USA. The data set includes 982 children who were followed weekly or twice-weekly from birth to 3 years of age. We assessed the effect of exclusive breastfeeding during diarrhea on the incidence of subsequent diarrhea. The exposure was exclusive breastfeeding at a child’s first diarrhea episode, defined as feeding with breast milk only with the exception of vitamins, mineral supplements, and medicines.¹⁹ The event of interest was an incident second diarrhea episode, defined as at least three loose or watery stools in a 24-hour period.²⁰ Covariates were age and malnutrition status at first episode, child sex, low birth weight (<2.5 kg), socioeconomic status (based on the modified Kuppuswamy scale²¹), maternal education, and household hygiene (based on a composite score of water, food, and personal hygiene practices). 24 (2.4%) missing low birth weight values were set to the mean value. Censoring weights were not included since there were only 4 drop-outs. The inverse probability-weights were truncated¹¹ at the 0.5^th and 99.5^th percentiles with a mean of 0.92 and range from 0.46 to 9.85.

RESULTS

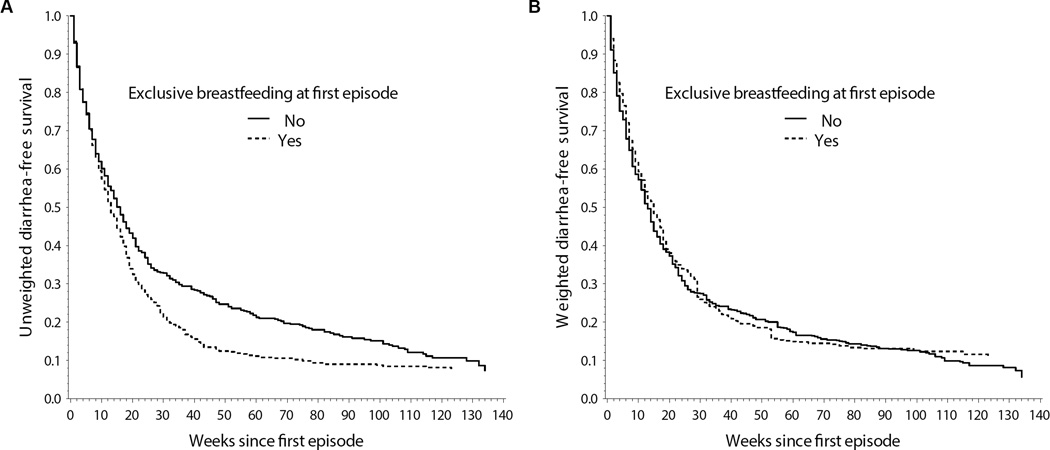
More than half of children stopped exclusively breastfeeding before their first diarrhea episode (n=548, 56%), and almost all children experienced a second diarrhea episode (n=848, 86%). Crude and inverse probability-weighted Kaplan-Meier curves are shown in Figure 2. After weighting, which largely adjusted for confounding by age, there was little evidence of an effect at all time points. The macro estimated that children who were exclusively breastfed at their first diarrhea episode had their second episode 2 weeks later than children who were not exclusively breastfed (weighted median time difference: 2 weeks, 95% CI: −2, 5). Median time ratio, 6-month risk difference, and risk ratio results are also shown in the Table. Both the crude and adjusted results were similar when using age as the timescale to account for confounding by age (Table, eFigure 1). For comparison with the estimated time difference of 2 weeks, the hazard ratio from a marginal structural Cox model with weights for the same baseline covariates was 0.95 (95% CI: 0.82, 1.1) and was 0.87 (95% CI: 0.73, 1.1) from a Cox model conditional on baseline covariates.

Figure 2.

Inverse probability-weighted Kaplan-Meier curves for time to second diarrhea episode by exclusive breastfeeding at the first episode among 982 children in birth cohorts from Vellore, Tamil Nadu, India 2002–2013. A – Crude (unweighted by covariates); B – Weighted by age at first episode, malnutrition status at first episode, child sex, low birth weight, socioeconomic status, maternal education, and household hygiene.

Table 1.

Estimated effect of exclusive breastfeeding at the first diarrhea episode on time to second episode among 982 children in birth cohorts from Vellore, Tamil Nadu, India 2002–2013.

	Crude			Weighteda
	Estimate	95% CIb	95% CIc	Estimate	95% CIb	95% CIc
Timescale: time since first episode
Median time difference (weeks)	−3	−5, 1	−6.0, −0.0	2	−2, 5	−2.0, 6.0
Median time ratio	0.8	0.7, 1.1	0.7, 1.0	1.15	0.9, 1.5	0.9, 1.5
6-month risk difference	0.08	0.03, 0.14	0.03, 0.14	−0.04	−0.12, 0.05	−0.13, 0.04
6-month risk ratio	1.1	1.0, 1.2	1.0, 1.2	0.94	0.83, 1.1	0.83, 1.1
Hazard ratio	1.2	1.1, 1.4d		0.95	0.82, 1.1d
Timescale: age
Median time difference (weeks)	1	−5, 5	−4.4, 6.4	1	−5, 5	−4.4, 6.4
Median time ratio	1.1	0.7, 1.5	0.7, 1.6	1.1	0.7, 1.5	0.7, 1.6
6-month risk difference	−0.03	−0.13, 0.06	−0.13, 0.06	−0.03	−0.12, 0.07	−0.13, 0.06
6-month risk ratio	0.96	0.86, 1.1	0.85, 1.1	0.96	0.85, 1.1	0.85, 1.1

^aWeighted by age at first episode, malnutrition status at first episode, child sex, low birth weight, socioeconomic status, maternal education, and household hygiene; weights truncated at 0.5^th and 99.5^th percentiles

^bConfidence interval using the 2.5^th and 97.5^th percentiles of 2000 bootstrap replicates

^cWald-based confidence interval with 2000 bootstrap replicates

^dWald-based confidence interval from Cox proportional hazards model

DISCUSSION

Time difference and ratio measures derived from inverse probability-weighted Kaplan-Meier curves provide highly interpretable summaries of time-to-event data, especially for common outcomes. Because the use of weighted Kaplan-Meier curves allows for adjustment for covariates without reliance on a proportional hazards assumption, several of the main disadvantages of the Cox model are circumvented.² The weighted survival curves presented here allow a visual representation of the potentially changing relationship between exposed and unexposed survival curves. Instead of being averaged over the duration of follow-up, time differences and ratios at a given survival proportion can be calculated at any survival proportion, or at several. Similarly, risk differences and risk ratios can be calculated at any time over follow-up. However, we recommend that clinically important proportions and times are chosen a priori to prevent selectively reporting results in which the magnitude of estimates is greatest. Presentation of adjusted Kaplan-Meier curves also eliminates the inherent selection bias of the hazard ratio² by focusing on survival, which accumulates with time and therefore does not continually restrict the samples under comparison.

The macro presented here is limited by the crude handling of measured informative censoring by calculating censoring weights within deciles of the time scale. This strategy allows users to input continuous time data with minimal dataset management. However, if censoring is common, discretizing time (e.g. into person-weeks) and calculating weights in smaller intervals will allow for finer control of selection bias. We provide a version of the macro for discrete time data (e.g., with one observation per person-week) in the eAppendix. The weights presented can be extended to further account for time-varying exposure.¹³

Adjusted Kaplan-Meier curves^9,12,13 and time differences and ratios should be reported more often as summary measures of effect; our hope is that the SAS macro provided here will facilitate their wider use.