Shape Selection of Surface-Bound Helical Filaments: Biopolymers on Curved Membranes

Abstract

Motivated to understand the behavior of biological filaments interacting with membranes of various types, we employ a theoretical model for the shape and thermodynamics of intrinsically helical filaments bound to curved membranes. We show that filament-surface interactions lead to a host of nonuniform shape equilibria, in which filaments progressively unwind from their native twist with increasing surface interaction and surface curvature, ultimately adopting uniform-contact curved shapes. The latter effect is due to nonlinear coupling between elastic twist and bending of filaments on anisotropically curved surfaces such as the cylindrical surfaces considered here. Via a combination of numerical solutions and asymptotic analysis of shape equilibria, we show that filament conformations are critically sensitive to the surface curvature in both the strong- and weak-binding limits. These results suggest that local structure of membrane-bound chiral filaments is generically sensitive to the curvature radius of the surface to which it is bound, even when that radius is much larger than the filament’s intrinsic pitch. Typical values of elastic parameters and interaction energies for several prokaryotic and eukaryotic filaments indicate that biopolymers are inherently very sensitive to the coupling between twist, interactions, and geometry and that this could be exploited for regulation of a variety of processes such as the targeted exertion of forces, signaling, and self-assembly in response to geometric cues including the local mean and Gaussian curvatures.

Introduction

All living cells have a wide variety of filamentous biopolymers associated with the cell or nuclear membranes that play vital roles in biological functions specifically through their interactions with these membranes. In eukaryotes, for example, the actin cortex that resides just inside the cell membrane and is linked to it via a number of actin-binding proteins, provides the cell with structural integrity and mediates signal transduction as well as cell adhesion (1). Other examples of membrane associated filamentous networks that provide mechanical stability include the actin-spectrin network in red blood cells and the nuclear lamin networks, which are anchored to the cell and nuclear membranes by a number of specific binding proteins (2, 3). Membrane-associated filaments can also be dynamic and exert forces such as the actin contractile ring in eukaryotes that provide the forces necessary for cell division (4). Cell-wall-associated microtubules in plants play a significant role in guiding synthesis activity during the elongation phase of the cell cycle (5). In bacteria, a similar role is accomplished by MreB, which directs cell wall synthesis (6, 7, 8), and the bacterial tubulin homolog FtsZ forms filaments that associate with the cell wall and function as contractile rings during division (7, 9). In many of these cases, the conformations and orientations of the membrane-bound filaments are critical for function, as they exert forces and guide growth.

Three very important physical parameters control these conformations and orientations: the helicity, or intrinsic twisted geometry, of the filaments; the strength of the binding interactions with the surface; and the local geometry or curvature of the surface. Although conformations of polymers in contact with interfaces and surfaces have been well studied in the past (10, 11), the interplay of helicity and surface curvature introduces rich new behaviors. Freely associating chiral polymers by themselves show novel phases in aggregates (12, 13, 14, 15), and we have shown recently that the interactions of a chiral polymer even with a flat surface dramatically restructures the filament shape and with nontrivial binding thermodynamics related to the Frenkel-Kontorova transition of incommensurate solids (16). We showed that there exists a critical binding strength, proportional to the torsional modulus of the filament and the square of its intrinsic twist, above which the filament unwinds to a zero-twist, surface-bound state, and below which the elastic energy of the filament causes the proliferation of weakly bound “twist domains”. For filaments with anisotropic bending stiffnesses, this transition is coupled to a dramatic change in the effective persistence length, with the twist walls functioning as floppy joints. Recently, it has also been shown that the interplay between twist elasticity and surface interactions can lead to nontrivial, metastable 3D morphologies including loops and helices that lift off the surface (17). Thus, the conformations of surface-bound helical polymers can depend sensitively on the binding interactions, and this has implications not only for biopolymers in vivo but also for experimental studies of biopolymers immobilized on surfaces (2) and for protein-based templated assemblies for nanotechnology applications (18, 19). For example, amyloid fibrils, which are essentially undesirable aggregates in vivo and are responsible for a number of pathological conditions (20), have been shown to be susceptible to membrane-binding-induced morphological changes in their twist states (21). Not only does this have implications for the cytotoxicity in vivo, but the coupling between binding and conformation via the twist may also be exploited for the design of amyloid-based functional nanomaterials.

Although the coupling between chirality and binding produces a rich behavior even on flat surfaces, curvature is an essential feature of many of the surfaces of relevance in vivo and also potentially a desirable feature for surfaces used in a variety of biotechnology applications. In this article, we take the first steps, to our knowledge, toward understanding the combined effect of surface curvature, chirality, and binding interactions on filament conformations. Specifically, we aim to understand how the 3D equilibrium shape of filaments (curvature and torsion) is controlled not only by the strength of surface interactions, but also by the shape of the interface itself to which it is bound. In the Model section, we present a general model of a helical filament adsorbed to an anisotropically curved (cylindrical) surface and construct the shape Hamiltonian of the filament. In Shape Transitions: Numerical Solutions, we present our numerical solutions of the shape equations of motion for filaments on surfaces of variable binding strength and surface curvature. Significantly, we showed that on anistropically curved surfaces, the equilibrium shape of filaments becomes increasingly curved as surface binding unwinds the helical twist of filaments, due to the nonlinear geometrical interplay of twist and writhe for filaments on curved surfaces. In Shape Sensitivity to Surface Curvature, we analyze the key limits of the rich shape evolution of helical filaments on curved surfaces, beginning with the case of strong surface binding and the transition from the strongly bound, untwisted filament to the weakly bound, twisted filament. We then look at the shape sensitivity of bound filaments in the limiting case of weak interactions with the curved surface, showing that even arbitrarily weak coupling between filament helicity and the surface leads to local changes of filament structure that are sensitive to surface curvature. In the last section, we discuss the implications of our results and potential experimental measurements.

Materials and Methods

All numerical solutions of differential equations in this article were obtained using the Mathematica (v10.4) package.

Model

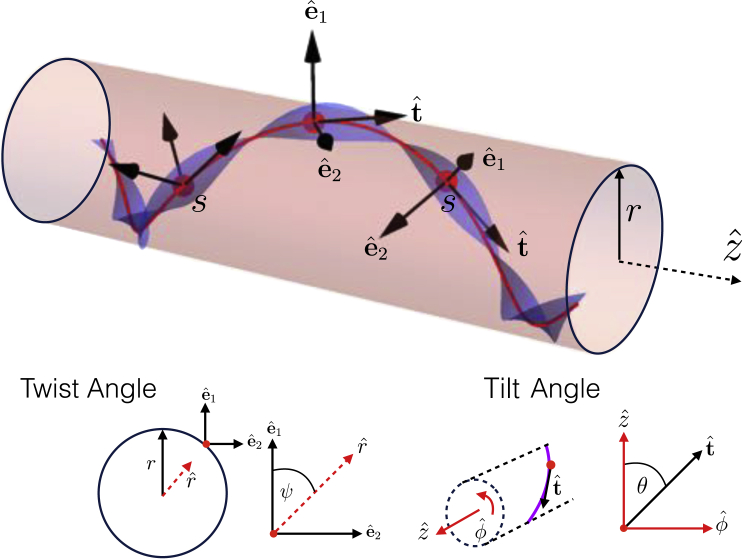
Our model considers a thin filament of length L that has a preferred intrinsic helical twist around its centroid of ${\omega }_0$ (radians/length). To depict the microscopic anisotropy of the filament, it is illustrated schematically as a helical ribbon in Fig. 1. We assume that the filament backbone, given by the curve $\mathbf{r}\left(s\right)$, where s is the contour length along the curve, is localized to a cylindrical membrane of fixed radius r, the simplest model of an extrinsically curved surface. The local geometry of the bound filament is described by its tangent, $\hat{\mathbf{t}}\left(s\right)$ (see Fig. 1),

$${\partial }_s\mathbf{r}=\hat{\mathbf{t}}=\text{cos}\theta \hat{z}+\text{sin}\theta \hat{\varphi }.$$ (1)

Figure 1.

A diagram depicting the model that we study. The triplet of axes are the filament tangent vector $\left(\hat{\mathbf{t}}\right)$, which is related to the tilt angle of the helix, and the two material frame coordinates $\left({\hat{\mathbf{e}}}_1,{\hat{\mathbf{e}}}_2\right)$, which are related to the twist angle of the filament. The radius of the cylinder is r. To see this figure in color, go online.

Here, $\theta \equiv \theta \left(s\right)$ is the tilt angle between the filament and the long axis of the cylinder and $\hat{z}$ and $\hat{\varphi }$ describe the local longitudinal and azimuthal directions on the cylinder. To describe the twist degree of freedom, we choose two orthonormal unit vectors defining the material frame,

$${\hat{\mathbf{e}}}_1=\text{cos}\psi \hat{r}+\text{sin}\psi \left(\hat{\mathbf{t}}\times \hat{r}\right)$$ (2)

and

$${\hat{\mathbf{e}}}_2=-\text{sin}\psi \hat{r}+\text{cos}\psi \left(\hat{\mathbf{t}}\times \hat{r}\right).$$ (3)

The angle $\psi \equiv \psi \left(s\right)$ is the angle between one “face” of the helical filament (for example, the wide face of the ribbon) and the local normal to the cylinder, $\hat{r}=\hat{\varphi }\times \hat{z}$. Using these three coordinate definitions we can compute the curvature of the filament in both of the principal material directions, ${\kappa }_i={\hat{\mathbf{e}}}_i\cdot {\partial }_s\hat{\mathbf{t}}$, as well as the rate of twist of the material frame, $\omega ={\hat{\mathbf{e}}}_1\cdot {\partial }_s{\hat{\mathbf{e}}}_2$ (i.e., the model assumes a “left-handed” convention for filament twist). The total curvature is given by

$${\kappa }^2={\left({\theta }^{\prime }\right)}^2+\frac{{\text{sin}}^4\theta }{r^2},$$ (4)

where the first and second contributions derive from the geodesic and normal curvatures of the filament on the cylinder. Similarly, the filament twist decomposes into two contributions,

$$\omega ={\psi }^{\prime }-\frac{\text{sin}\left(2\theta \right)}{2r},$$ (5)

where the first term represents the rotation of the material frame with respect to the local surface normal, and the second term derives from the rotation of the surface normal along the filament tangent.

The elastic mechanical energy stored in the filament,

$$E_{\text{mech}}=\frac{1}{2}{\int }_0^{L}ds\left[C{\kappa }^2+K{\left(\omega -{\omega }_0\right)}^2\right],$$ (6)

arises from two sources when it is bound to the cylinder: 1) bending energy, which is proportional to the local curvature (Eq. 4), the magnitude of which is set by the elastic constant C; and 2) the torsional elastic cost for deviations from the intrinsic twist of the filament, ${\omega }_0$, which we assume is harmonic and whose magnitude is set by K, the elastic twist stiffness (16). In the absence of external forces on the filament, the shape of the filament is straight $\left(\theta =0\right)$, with a twist rate of ${\omega }_0$. Here, we do not consider spontaneous curvature and neglect anisotropy in bending moduli for the ${\hat{\mathbf{e}}}_1$ and ${\hat{\mathbf{e}}}_2$ directions, though the model can easily be extended to consider these effects. To associate the cylindrical wall with the filament, we consider that the filament possesses strong binding domains distributed along its contour that are in register with the intrinsic twist of the filament. For the schematic example, “strong binding” may be considered to occur along the wider adhesive face shown in Fig. 1. Furthermore, we envision that it is these domains (faces with $\psi =n\pi$) that favor contact with the cylindrical wall at all times as opposed to the “off-face” binding (i.e., $\psi =\left(n+1/2\right)\pi$). As a minimal model of the interaction of the helical symmetry of the filament with the membrane, we introduce a periodic potential with a strength V,

$$E_{\text{bind}}=\frac{V}{2}{\int }_0^{L}ds{\text{sin}}^2\psi .$$ (7)

Note that the $\psi \to \psi +\pi$ symmetry is consistent with local $C_2$ symmetry of a double-helical filament cross section, though it is straightforward, in principle, to modify the interaction according to any n-start helical symmetry.

Combining the mechanical and binding energies (Eqs. 6 and 7) along with the curvature and twist expressions (Eqs. 4 and 5), we arrive at the Hamiltonian that describes the energetics of the conformational phase space that the filament can sample from, when it is bound to the cylinder.

$$\mathcal{H}=\frac{1}{2}{\int }_0^{L}ds\left[C{\left({\theta }^{\prime }\right)}^2+C\frac{{\text{sin}}^4\theta }{r^2}+K{\left({\psi }^{\prime }-\frac{\text{sin}\left(2\theta \right)}{2r}-{\omega }_0\right)}^2+V{\text{sin}}^2\psi \right].$$ (8)

By inspection, we see that helical filaments are frustrated by surface binding. On one hand, it is not possible even in the undeformed case $\left(\theta =0,{\psi }^{\prime }={\omega }_0\right)$ for the helical filament to maintain ideal contact with the cylinder surface, since the point of contact between the cylinder and the filament-binding domain will occur periodically at a distance of $\pi /{\omega }_0$ (i.e., half the helical pitch). On the other hand, maintaining uniform, ideal contact $\left(\psi =n\pi \right)$ leads generically to an elastic cost due to the preferred intrinsic twist. However, unlike the case of planar substrates $\left(r\to \infty \right)$ studied previously (16), any helical tilt of filaments on curved surfaces can relax the frustration through bending (i.e., $\theta \ne 0$). This is due to the geometric rotation of the surface normal along tilted paths, $\theta \ne n\pi /2$. Hence, although the transition from weakly bound, twisted filaments to strongly bound, untwisted filaments on flat surfaces is described by mathematics identical to the Frenkel-Kontorowa transition (16), on curved surfaces, the filament tilt acts as a gauge field coupled to the twist degree of freedom. As we find below, the strength of the coupling of the filament tilt to the twist, and its effect on the binding thermodynamics, is controlled by the dimensionless surface curvature, ${\left({\omega }_{0}r\right)}^{-1}$.

Results

Shape transitions: numerical solutions

In this section, we analyze the equilibrium shapes of bound helical filament conformations for varying surface-binding potential, V, for surfaces of varying curvature, ${\left({\omega }_{0}r\right)}^{-1}$, and filaments of varying ratios of bend to twist stiffness, $C\text{/}K$. For a given set of set parameters, V, ${\omega }_0$, r, C, and K, we consider equilibrium shapes for filaments of arbitrary (unlimited) length on infinite-length cylinders. Equilibrium shapes satisfy the following equations of motion, corresponding to torque balance about the surface normal,

$$C{\theta }^{″}=2C\frac{{\text{sin}}^3\theta \text{cos}\theta }{r^2}-K\frac{\text{cos}\left(2\theta \right)}{2r}\left({\psi }^{\prime }-\frac{\text{sin}\left(2\theta \right)}{2r}-{\omega }_0\right),$$ (9)

and about the filament tangent,

$$K{\left({\psi }^{\prime }-\frac{\text{sin}\left(2\theta \right)}{2r}\right)}^{\prime }=\frac{V}{2}\text{sin}\left(2\psi \right).$$ (10)

For the case of infinite-length filaments, we search for solutions that are periodic over an arc-distance $2\mathcal{L}$ (not the actual length, L, of the filament), and minimize the total energy per unit length of solutions with respect to $\mathcal{L}$. Because filament tilt compensates for frame rotation when ${\psi }^{\prime }\left(s\right)<{\omega }_0$, we assume that, for equilibrium shapes, $\psi \left(s\right)$ and $\theta \left(s\right)$ solutions remain “in phase” such that the magnitude of filament tilt reaches a maximum (minimum) at positions where the rotation rate, ${\psi }^{\prime }\left(s\right)$, is at a respective minimum (maximum). Hence, we solve Eqs. 9 and 10 numerically, subject to the boundary conditions

$$\psi \left(0\right)=0;\psi \left(\mathcal{L}\right)=\pi ;{\theta }^{\prime }\left(0\right)={\theta }^{\prime }\left(\mathcal{L}\right)=0.$$ (11)

In practice, Eqs. 9 and 10 are solved by fixing ${\psi }^{\prime }\left(0\right)\equiv {\psi }_0^{\prime }$ and using a standard shooting method to determine the values of initial tilt, $\theta \left(0\right)$, and half-period, $\mathcal{L}$. The energy per unit length of solutions is then calculated via Eq. 8 and minimized with respect to ${\psi }_0^{\prime }$, which is equivalent to minimization over $\mathcal{L}$, thus yielding both the equilibrium $\mathcal{L}$ and the equilibrium shape solutions, $\psi \left(s\right)$ and $\theta \left(s\right)$.

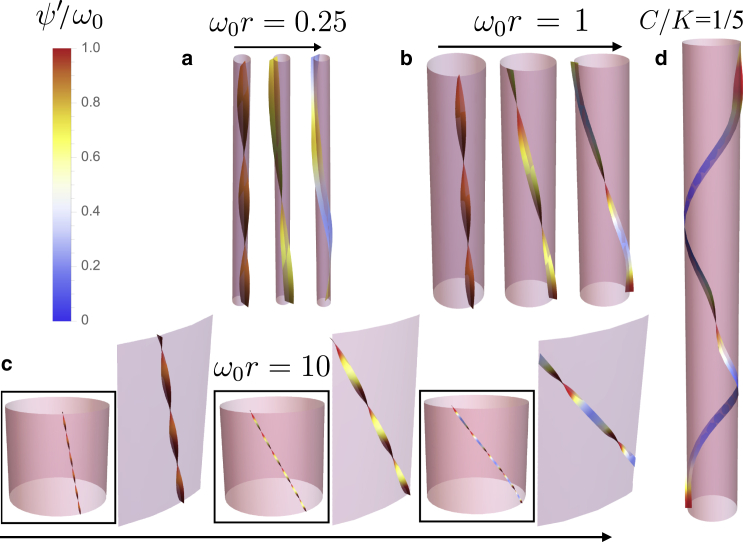
In Fig. 2, a–c, we present graphical portraits of the “phase diagram” to summarize the variation of equilibrium filament shape in the parameter space spanned by surface interactions and surface curvature. In particular, we show shape solutions for filaments with isotropic elastic properties, $C=K$, for three values of reduced curvature: ${\omega }_{0}r=10$ (low curvature), ${\omega }_{0}r=1$ (intermediate curvature), and ${\omega }_{0}r=0.25$ (high curvature). For each case, we see that as the interactions with the surface get stronger, the filament that originally prefers an axial orientation with native twist begins to untwist and the coupling with curvature causes the tilt angle to rise. Ultimately, above some critical binding strength, $V_{\text{c}}$, the filament is fully unwound and assumes a constant “face-on” configuration with uniform tilt angle θ.

Figure 2.

The numerically obtained shape solutions for filaments with isotropic elastic properties $C=K$ and ω₀r = 0.25, 1, and 10. (a–c) and for the case of $C=K/5,{\omega }_{0}r=1$ (d). (a–c) Three cases of increasing binding strength, V/V_c = 0.1, 0.5, and 0.95, are shown from left to right (arrows), where $V_{\text{c}}$ is the critical binding strength for each r. (d) The binding strength is close to the critical value $V=0.95V_{\text{c}}$, and the filament exhibits almost uniformly unwound helical regions separated by twist domains with pronounced axial straightening. To see this figure in color, go online.

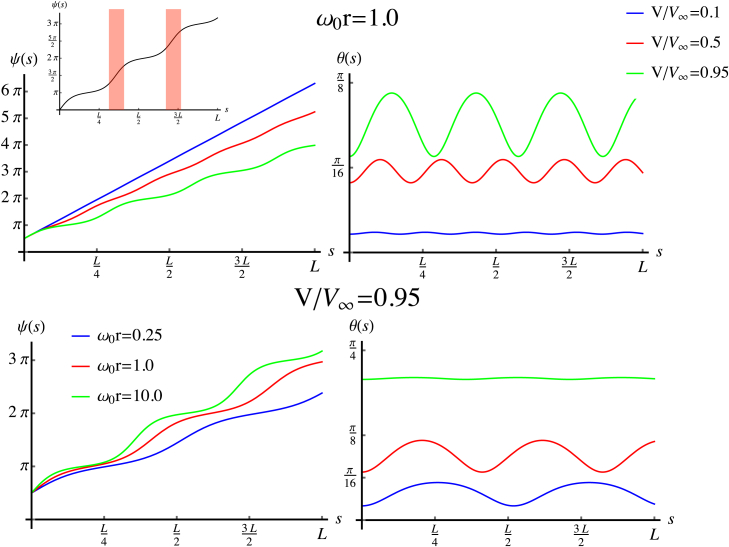
To probe these trends more quantitatively, we show, in Fig. 3, for the isotropic case $C=K$, the profiles of $\psi \left(s\right)$ and $\theta \left(s\right)$ for four values of the surface potential for a fixed value of curvature, ${\omega }_{0}r=1$. We see that the progression of rotation and tilt angle profiles with V shows a qualitatively similar sequence to what we observed from Fig. 2. As $V\to 0$, the solution approaches the elastically favorable intrinsic twist, ${\psi }^{\prime }\left(s\right)\to {\omega }_0$, and straight backbone, $\theta \left(s\right)\to 0$. As V increases, surface binding decreases (increases) the rate of ψ rotation near the maxima (minima) of the surface contact, leading to an oscillatory profile with a somewhat decreased mean value of $\langle {\psi }^{\prime }\left(s\right)\rangle <{\omega }_0$, along with an increase in the magnitude of the mean tilt angle, $\langle \theta \left(s\right)\rangle$. As values of the surface potential approach a critical value, $V_{\text{c}}$, that depends on the surface curvature, r (for the flat case, $V_{\text{c}}\equiv V_{\infty }={\pi }^{2}K{\omega }_0^2/4$ (16)), the solutions rapidly evolve toward a critical unwinding transition via inhomogeneous structures characterized by rapid jumps in $\psi \left(s\right)$ by π. These correspond to “twist domains” (highlighted in Fig. 3, inset) that are separated by increasing stretches of strong binding with nearly constant $\psi \approx n\pi$. Again, this progression toward the critical V is accompanied by a further increase in $\langle \theta \left(s\right)\rangle$.

Figure 3.

Variation of filament twist, ψ, and tilt, θ, with the contour length along the filament with $C=K$ for fixed curvature ${\omega }_{0}r$ and varying values of the potential, V (top), and for fixed potential and varying curvature (bottom). (Top left inset) Solution of the twist, ψ, for ${\omega }_{0}R=10.0$ and $V/V_{\infty }=0.95$, highlighting flat commensurate regions $\left({\psi }^{\prime }\simeq 0\right)$ that are flanked by rapid jumps in the twist $\Delta \psi \left(s\right)\simeq \pi$ (shaded vertical bars). To see this figure in color, go online.

Beyond this critical value of surface binding, filaments adopt a uniformly unwound, helical conformation with $\psi \left(s\right)=0$ and $\theta \left(s\right)=\text{const}.$, with shape independent of surface potential in this large-V region. In Fig. 3, we also show how $\psi \left(s\right)$ and $\theta \left(s\right)$ profiles vary when V is held fixed and the curvature, ${\omega }_{0}r$, is varied. Here, we see that curvature strongly influences both the tilt and twist of the filaments, with a higher degree of tilt and more pronounced, localized twist domains for larger radii surfaces.

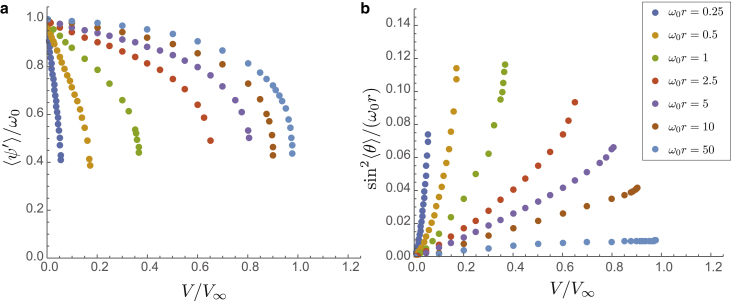
To probe the approach to the transition in more detail, we plot, in Fig. 4, $\langle {\psi }^{\prime }\rangle$, the mean rotation rate, and ${\text{sin}}^2\langle \theta \rangle /r$, a measure of the net curvature of the filament, as functions of surface-binding potential for a range of surface radii, $\left({\omega }_{0}r\right)$ = 0.25–50. Again, each of these shows a gradual decrease in the net rotation of the filament for small V followed by a precipitous drop to $\langle {\psi }^{\prime }\rangle =0$ at a critical surface potential, $V_{\text{c}}$, which decreases with increasing surface curvature. For the smallest curvature studied, we find that $V_{\text{c}}\simeq {\pi }^{2}K{\omega }_0^2/4$, approaching the asymptotic limit of binding on flat surfaces. For the largest curvature $\left({\omega }_{0}r=0.25\right)$, we observe $V_{\text{c}}\simeq 0.05\left({\pi }^{2}K{\omega }_0^2/4\right)$, a dramatic reduction in threshold surface interaction needed to unwind the filament.

Figure 4.

Plots of normalized twist rate, $\langle {\psi }^{\prime }\rangle /{\omega }_0$, and rescaled net filament curvature, ${\text{sin}}^2\langle \theta \rangle /\left({\omega }_{0}r\right)$, for equal bending and torsional stiffness, $C=K$. To see this figure in color, go online.

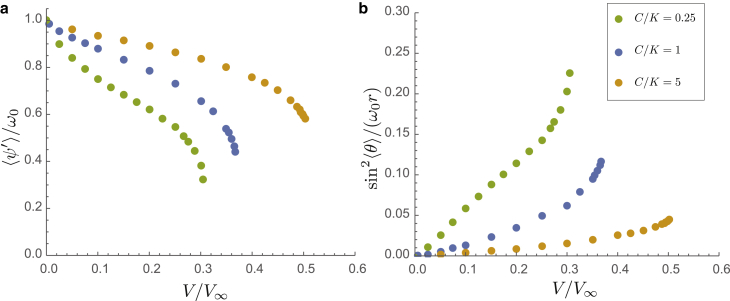
We analyze further how the coupling between twist and tilt degrees of filaments varies not only with surface curvature but with the ratio of bend to twist elastic constants, $C\text{/}K$. In Fig. 5, we plot $\langle {\psi }^{\prime }\rangle$ and ${\text{sin}}^2\langle \theta \rangle /r$ versus V at fixed curvature, ${\omega }_{0}r=1$, for three different elastic anisotropies, C/K = 0.25, 1, and 5. Due to the diminished effect of screening of the elastic cost of twist from helical bending (or tilt), increasing bending stiffness relative to twist stiffness increases the threshold surface binding for unwrapping the filament. In contrast, weakening the bending stiffness relative to twist leads to an increased sensitivity to surface binding and smaller $V_{\text{c}}$ (relative to ${\pi }^{2}K{\omega }_0^2/4$), and further to configurations which locally straighten significantly in the neighborhood of twist domains (see, e.g., Fig. 2 d).

Figure 5.

Plots of normalized twist rate, $\langle {\psi }^{\prime }\rangle /{\omega }_0$, and rescaled net filament curvature, ${\text{sin}}^2\langle \theta \rangle /\left({\omega }_{0}r\right)$, for varying ratios of bending and torsional stiffness, $C\text{/}K$, with fixed ${\omega }_{0}r=1$. To see this figure in color, go online.

Overall, these results illustrate that increasing the surface curvature and decreasing the relative bending stiffness, $C\text{/}K$, lead to a marked increase in the susceptibility of filament shape (both twist and curvature) to surface interactions that couple to the helical symmetry of the filament.

Shape sensitivity to surface curvature

In this section, we describe the mechanisms of shape selection for surface-bound helical filaments, and in particular, the sensitivity of filament shape to surface curvature. We begin by analyzing the limiting case of strong surface binding and the transition from the strongly bound, unwound filament to the weakly bound, twisted filament. We follow with an analysis of the shape sensitivity of bound filaments in the limiting case of weak interactions with the curved surface.

Strong-binding and unbinding transition

We begin by considering the shape of filaments in the $V\to \infty$ limit, where the strong-binding face or interaction sites on the filament are not free to peel way from the surface, which is the class of configurations in the model of (7). Assuming that filament orientation locally maximizes surface cohesion $\left(\psi =0\right)$, equilibrium configurations correspond to helices of constant $\theta ={\theta }_0$, determined by the strong-binding equation of state,

$$2C\frac{{\text{sin}}^3{\theta }_0\text{cos}{\theta }_0}{r^2}=K\frac{\text{cos}\left(2{\theta }_0\right)}{2r}\left(\frac{\text{sin}\left(2{\theta }_0\right)}{2r}+{\omega }_0\right),$$ (12)

obtained by setting $\psi =0$ in Eq. 9. The tilt equilibria are plotted in Fig. 6 as a function of reduced twist, $2{\omega }_{0}r$, showing a generic rise for $\theta =0$ to the tilt that provides the maximum rotation of the surface normal, $\theta =\pi /4$, and hence the largest possible relaxation of the twist elastic energy of the bound filament. It is straightforward to show that tilt equilibria have the asymptotic limits

$${\theta }_0=\{\begin{array}{cc}-{\text{sin}}^{-1}\left(2{\omega }_{0}r\right)/2\simeq {\omega }_{0}r& 2{\omega }_{0}r\ll 1\\ -\pi /4+\frac{C/K}{2{\omega }_{0}r-1+C/K}& 2{\omega }_{0}r\gg 1\end{array},$$ (13)

increasing linearly for small, reduced twist, and saturating at ${\theta }_0=\pi /4$ for large twist. We also plot, in Fig. 6, the dependence of ${\theta }_0$ on the ratio of bend to twist elastic constants, $C\text{/}K$, which illustrates that the shape of strongly bound filaments is determined not only by the degree of torsional strain, or ${\omega }_{0}r$, but also by the relative cost of relaxing that strain through bending deformations.

Figure 6.

Plots of the equilibrium tilt ${\theta }_0$, as a function of curvature, ${\omega }_{0}r$, in the strong binding limit for varying ratios of bending and torsional stiffness $C\text{/}K$. To see this figure in color, go online.

These constant-helix solutions have been previously studied as models of chiral filaments uniformly bound to cylindrical membranes, such as the bacterial cell wall (7). Here, we show the nonlinear evolution of the equilibrium shape with decreasing strength of filament-surface interactions, where sufficiently weak interactions allow filament conformations to peel away from uniform surface contact. In a previous study (16), we addressed the transition from weakly bound to strongly bound helical filaments for planar interfaces. Taking the limit of $r\to \infty$ in Eq. 8, we arrive at the planar model, described by the energy

$$\underset{r\to \infty }{\text{lim}}\mathcal{H}=\frac{1}{2}{\int }_0^{L}ds\left[C{\left|{\theta }^{\prime }\right|}^2+K{\left({\psi }^{\prime }-{\omega }_0\right)}^2+V{\text{sin}}^2\left(\psi \right)\right],$$ (14)

showing that bend- and twist-orientation degrees of freedom decouple on flat surfaces. As previously noted, the transition from strong to weak binding with decreasing surface potential, V, maps on to the commensurate-incommensurate transition of the Frenkel-Kontorowa model of surface adsorption (16, 22). The “unwound” filament with uniform $\psi =0$ (i.e., the commensurate state) is stable for $V>V_{\infty }$, where the critical potential is $V_{\infty }=\left({\pi }^2/4\right)K{\omega }_0^2$. Near to, but below this binding strength, localized jumps of $\psi$ by π over a length scale proportional to $\sqrt{K/V}$ become stable in the equilibrium shape, due to the (favorable) relaxation of the torsional strain at the expense of (unfavorable) unbinding from the surface. These localized “twist walls” (“discommensurations” in the language of incommensurate solids) are separated by a characteristic distance $\mathcal{L}$ that diverges as the potential approaches its critical value from below, $\mathcal{L}\sim -\text{ln}\left(V_{\infty }-V\right)$. As the binding strength is decreased far below $V_{\infty }$, distinct twist walls merge and the filament twist profile evolves continuously to the state of zero elastic strain and native twist $\left(\psi ={\omega }_{0}s\right)$ as $V\to 0$.

Noting that the binding threshold separating strong binding (uniform $\psi$, θ) from weak binding (nonuniform $\psi$, θ) is found to be strongly dependent on the coupling of local filament orientation to surface curvature, we propose a simple generalization of the flat-interface analysis for the critical surface potential on curved surfaces. When the uniform tilt solution of Eq. 13 is inserted into the elastic energy of Eq. 8, we note that the torsional strain is reduced from the native twist, ${\omega }_0$, by $-\left|\text{sin}\left(2{\theta }_0\right)/\left(2r\right)\right|$. Therefore, the torsional loading of the filament on the cylinder is reduced relative to a flat interface, and we expect the filament to be “unwound” by a far weaker critical potential, $V_{\text{c}}$, proportional to the square of a renormalized twist, ${\omega }_{\text{eff}}={\omega }_0-\left|\text{sin}\left(2{\theta }_0\right)/\left(2r\right)\right|<{\omega }_0$. Hence, we estimate the dependence of the critical potential on dimensionless twist, ${\omega }_{0}r$, as

$$V_c\left({\omega }_{0}r\right)=V_{\infty }{\left(1-\left|\frac{\text{sin}\left(2{\theta }_0\right)}{2{\omega }_{0}r}\right|\right)}^2.$$ (15)

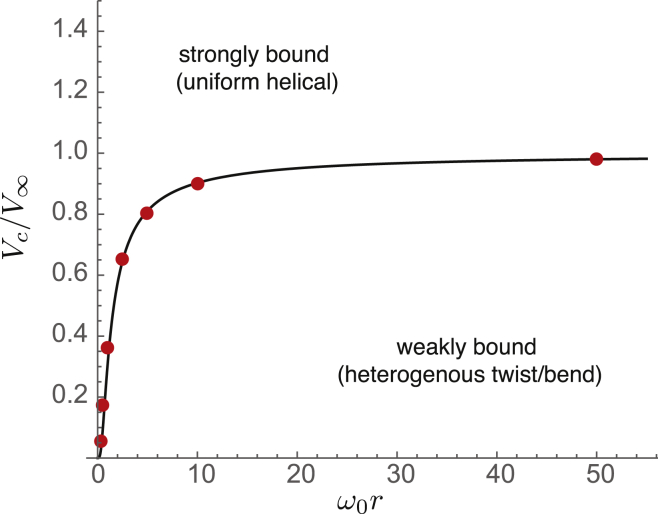
This estimate for the critical binding strength is compared to numerical results for the value of the binding potential at the transition between nonuniform and uniform $\psi$ solutions in Fig. 7 and shows strong agreement over the entire range from small to large curvatures. Using the solution of ${\theta }_0$ as ${\omega }_{0}r\to 0$, we estimate that, for large curvature, the critical binding strength vanishes as ${\text{lim}}_{r\to 0}{V}_c\approx V_{\infty }{\left({\omega }_{0}r\right)}^4$, due to the elimination of the elastic twist penalty to unwind the filament into perfect surface contact through small bending deformations. In the opposite limit, where ${\theta }_0\to \pi /4$ as ${\omega }_{0}r\to \infty$, we find a continuous increase of the critical potential to the critical value for the planar case, $V_{\text{c}}\to V_{\infty }$.

Figure 7.

Plot of critical potential, $V_c/V_{\infty }$, as a function of curvature, ${\omega }_{0}r$. The circles show the results of numerical solutions, whereas the solid curve is the prediction of the “renormalized” critical potential given by Eq. 15. To see this figure in color, go online.

Curvature sensitivity for weakly binding filaments

In this section, we illustrate the effect of surface interactions in the limit of $V\ll V_{\text{c}}$, where the filament structure is only weakly perturbed by surface interactions with its helical symmetry. The analysis is based on a perturbative solution to the filament-shape equations for weak binding (see Supporting Material for details). Here, we solve for the weakly perturbed filament conformation,

$$\psi \left(s\right)\simeq \omega s+\delta \psi \left(s\right);\theta \left(s\right)\simeq {\theta }_0+\delta \theta \left(s\right),$$ (16)

where ω and ${\theta }_0$ mean filament twist and tilt, respectively, and $\delta \psi \left(s\right)$ and $\delta \theta \left(s\right)$ represent zero-mean, longitudinal modulations of shape deriving from the position-dependent torques along the filament. First consider the planar case $r\to \infty$ and vanishing coupling between twist and tilt. In this case, expanding the equation of motion for small $\delta \psi$, the balance of torques about the filament axis sets $K\delta {\psi }^{″}\approx V\text{sin}\left(2\omega s\right)$. This implies a modulation of filament twist in registry with the mean twist, ω, which increases(decreases) the filament’s helical pitch where the filament-surface binding is locally maximal (minimal), with an amplitude proportional to $V/\left(K{\omega }^2\right)$. Hence, the net energy gain per unit filament length due to this weak-correlation effect is ∼ $-V^2/\left(K{\omega }^2\right)$, indicating a preference to unwind the natural twist of the filament. Balancing this preference is the elastic cost for altering the mean twist of the filament, $K{\left(\omega -{\omega }_0\right)}^2/2$, which, for small V, gives the parabolic dependence of torsional strain on potential,

$$\underset{V/V_c\ll 1}{\text{lim}}\left(\omega -{\omega }_0\right)=-\frac{V^2}{16K^2{\omega }_0^3}\text{for}r\to \infty .$$ (17)

For filaments on curved cylindrical surfaces, we find two additional effects. First, there is an additional contribution to the correlation energy, proportional to $-V^2/\left(C{\omega }^4{r}^2\right)$ per unit length, due to the enhanced ability of bound filaments to locally increase/decrease the rate of rotation of orientation though oscillatory “wobbling” of the filament tilt to further optimize local surface contact. The second, and perhaps more critical, difference is the screening of the elastic cost of mean torsional strain through tilt. In contrast to the harmonic cost on planar surfaces, in the $V\to 0$ limit, the elastic cost for deviations from native twist becomes much softer on curved surfaces, $C{\left(\omega -{\omega }_0\right)}^4{r}^2/2$ per unit length. Optimizing for mean twist in the $V\to 0$ limit, we find the torsional strain on curved surfaces with finite r.

$$\underset{V/V_{\text{c}}\ll 1}{\text{lim}}\left(\omega -{\omega }_0\right)=-{\left[\frac{V^2}{32C{\omega }_0^3{r}^2}\left(\frac{K^{-1}}{2}+\frac{3C^{-1}}{16{\omega }_0^2{r}^2}\right)\right]}^{1/3}$$ (18)

Therefore, we find that the sensitivity to surface potential of helical filament shape on curved surfaces is critically different from that on flat surfaces.

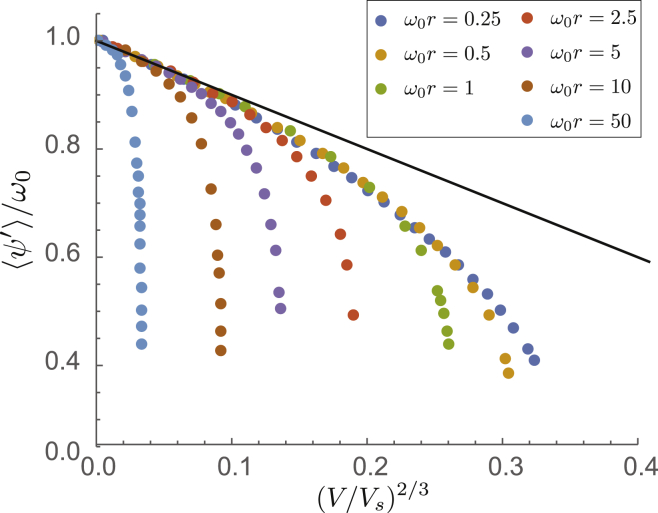
Most notably, we find that the power-law dependence of torsional strain, $\omega -{\omega }_0$, changes from the weaker $V^2$ on flat surfaces to $V^{2/3}$ on curved surfaces. Second, we observe that the torsional strain at small V is strongly dependent on surface curvature, r⁻¹, as well as on filament stiffness. This highlights the remarkable fact that the local structure of the filament is generically sensitive to the surface shape, even in the asymptotic limit of weak surface interactions. In Fig. 8, we verify the predicted dependence of torsional strain in the $V\to 0$ limit by replotting the mean twist, $\langle {\psi }^{\prime }\rangle =\omega$, versus the potential, V, rescaled by $V_s=\mathit{1}\mathit{6}C{\left({\omega }_0^{2}r\right)}^{\mathit{2}}{\{\mathit{2}K/[\mathit{8}C{\left({\omega }_{\mathit{0}}r\right)}^{\mathit{2}}+\mathit{3}K]\}}^{\mathit{1}/\mathit{2}}$, according to the right-hand side of Eq. 18 above. The collapse of points in the small V limit to a $V^{2/3}$ dependence for various ${\omega }_{0}r$ highlights the agreement. Finally, we note, by comparing the respective strain predictions for flat and curved surfaces, that we expect a crossover between the singular $V^{2/3}$ dependence at small potentials to the planar scaling, $V^2$, at a characteristic binding strength, $V_x\approx {\left(K^5{\omega }_0^6/C{r}^2\right)}^{1/4}$, indicating that the range of weak binding where strain exhibits strong curvature effects decreases with decreasing curvatures as ${\left({\omega }_{0}r\right)}^{-1/2}$.

Figure 8.

Plot of torsional strain versus rescaled potential at small V. The straight line indicates the $V^{2/3}$ scaling. To see this figure in color, go online.

Discussion

Our results show that for surface bound biopolymers, elasticity and chirality can combine in nontrivial ways with surface interactions and surface geometry to determine equilibrium morphology. For twisted filaments interacting with a flat surface, we previously showed (16) that there exists a critical interaction strength $V_{\infty }=\left({\pi }^2/4\right)K{\omega }_0^2$ above which the filament exists in an untwisted, strongly bound configuration that maximizes the interaction energy at the expense of torsion. Here, we show that the existence of surface curvature introduces an extra degree of freedom whereby the filament can transition to the untwisted state at lower values of the interaction strength by essentially relieving torsional strain via writhing to maintain surface contact. This results in a lowered value for the critical interaction strength— $V_c\left({\omega }_{0}r\right)=V_{\infty }{\left(1-\left|\text{sin}\left(2{\theta }_0\right)/2{\omega }_{0}r\right|\right)}^2$ —and a spontaneous preference for helical morphologies even in the absence of any spontaneous curvature simply due to the interplay between twist, writhe, surface interactions, and geometry.

This is of particular interest in the bacterial context where cytoskeletal filaments like FtsZ and MreB have specific orientations relative to cylindrical cell bodies that prove essential in applying forces and templating growth in the correct locations. To assess the significance of our results for bacterial cytoskeletal filaments, we consider the specific values of the elastic constants and geometric parameters that are involved and where this would situate these systems in our phase diagram. For FtsZ, the intrinsic twist, as reported by recent molecular dynamics (MD) simulations (23, 24), is in the range 3–20°, which we take to be of the order of $\sim {10}^{\circ }$ per monomer (of size 5 nm) resulting in ${\omega }_0\sim 0.03$ rad∙nm^–1. Given that cell radii for Escherichia coli bacteria are typically 100–500 nm, we get ${\omega }_{0}r\sim 3-15$. For single protofilaments of MreB, MD results (25) indicate a smaller angle of about $3^{\circ }$ per monomer, yielding ${\omega }_{0}r\sim 1-5$. To estimate the critical potential, $V_{\infty }$, we additionally require the torsional modulus, K. The variance, ${\sigma }^2$, of the fluctuations in the twist angle from independent MD simulations, gives a consistent value of ${\sigma }^2\approx 0.005$ rad² for FtsZ (23, 24). From this, one can estimate the torsional rigidity as $K=k_{\text{B}}T\ell /{\sigma }^2$, where $\ell \sim 5$ nm is the monomer size, giving us $K\sim 1200k_{\text{B}}T$ nm. For single MreB protofilaments, a similar analysis gives $K\sim 2000k_{\text{B}}T$ nm (25). This gives us a value of $V_{\infty }=\left({\pi }^2/4\right)K{\omega }_0^2\sim 2k_{\text{B}}T/\text{nm}$ for FtsZ and $0.5k_{\text{B}}T\text{/nm}$ for MreB. It is to be noted that these parameters could change for high order assemblies that occur in vivo. The actual interaction potentials between FtsZ/MreB and the membrane are complex and mediated by multiple linkers. An estimate of the binding affinity of FtsZ for ZipA-linker-coated substrates (26) allows us to approximate the interaction strength at about $1k_{\text{B}}T\text{/nm}$, yielding the ratio $V/V_{\infty }\sim 1/2$. In addition to specific interactions from linking molecules, nonspecific interactions such as electrostatics could also contribute significantly to the net interaction strength. Given that FtsZ (and also MreB) have linear charge densities comparable to actin ($\sim 4$ e/nm) (27) and that reasonable membrane charge densities under physiological conditions could give rise to $V_{\text{el}}\sim 1-2k_{\text{B}}T\text{/nm}$ for actin (16), we anticipate that $V_{\text{net}}\text{/}{V}_{\infty }$ could range from 0.2 to 1.5 for all cases considered. It is to be noted that these ranges of values for ${\omega }_{0}r$ and $V\text{/}{V}_{\infty }$ cover the region corresponding to the knee of the curve in Fig.7, indicating that these filaments are highly sensitive to changes in the global surface geometry and twist state, as well as in the interaction potential, wherein small changes in these parameters (e.g., the radius of curvature, r) can cause dramatic changes in morphology and orientation.

Another interesting feature of this coupling emerges when we consider that filaments can have spontaneous curvature as well. A transition in the twist state can be coupled to a reorientation or even the emergence of a plane of spontaneous curvature that can then lead to the exertion of forces (24). It has been observed with atomic force microscopy experiments on FtsZ polymerized on mica (28) that they can exist in two states, as long curved filaments or short straight filaments, which could arise from different torsional states in the two populations. Experiments on FtsZ adsorbed to curved lipid surfaces (29) have also shown that the resulting orientations cannot be accounted for by spontaneous curvature and must include a coupling to twist. These experimental observations lend support to our model and also suggest that the nonlinear interplay between geometry, twist, and surface interactions can be used to regulate force production. Furthermore, these in vitro systems are well suited to test the predictions of our theory, including the dependence of twist and tilt profiles on surface interactions, as well as the critical potentials as a function of curvature.

The coupling between filament bending and twist studied here for cylindrical surfaces, will arise on any surface which is anisotropically curved, a fact that has important biophysical implications. For a strongly bound filament whose material frame is locked to the local tangent frame of a binding surface, the twist has the form $2\left({\kappa }_1-{\kappa }_2\right)\text{sin}\left(2\theta \right)$, where ${\kappa }_1$ and ${\kappa }_2$ are the principal curvatures of the surface and θ is the angle between the filament tangent and the first principal axis. This formula shows that a strongly bound filament can maintain maximal twist by aligning at ${45}^{\circ }$ with respect to the principal axes of an anistropically curved surface. Combining this with the normal curvature for a filament ${\kappa }_1{\text{cos}}^2\theta +{\kappa }_2{\text{sin}}^2\theta$, we see that a surface of negative Gaussian curvature, where ${\kappa }_1{\kappa }_2\le 0$, allows filaments to bind with particularly low elastic energy, because there is always a straight path between the principal axes when principal curvatures have opposite signs. For example, for minimal surfaces, ${\kappa }_1=-{\kappa }_2$, binding at ${45}^{\circ }$ with respect to principal axes achieves the maximal twist of a strongly bound filament $\left(\pm 2{\kappa }_1\right)$ and requires no bending of the filament backbone. These arguments suggest that binding of helical filaments will be generically favored in regions of negative Gaussian curvature. This mechanism may have implications for the localization of bacterial cytoskeletal filaments to cell-wall geometries with negative curvature, such as the localization of crescentin that occurs in crescent-shaped Caulobacter crescentus (30), or that proposed for MreB either in a plastically deformed rod-like bacterium (31) or in maintaining rod shapes in growing cylindrical bacteria (32).

The fact that many biopolymers, both eukaryotic and prokaryotic, that are composed of proteins will have closely related properties indicates that this kind of coupling between twist, interactions and geometry could be exploited for regulation of a variety of processes. For example, adsorbing to the surface and unwinding could expose moieties on the monomer surfaces that could trigger biochemical pathways in response to geometric cues, such as the presence of regions with different curvatures. This could be of use in directing function to geometrically defined regions such as midplane constrictions for FtsZ or regions where extra cell-wall synthesis machinery mediated by MreB (as suggested in the preceding paragraph) could be directed. The transition could also be regulated by changing the intrinsic twist or even just the linear charge density by posttranslational modifications. Another interesting possibility is that the transition could be accompanied by the exposure of regions of the monomer surface that promote bundling or in-plane aggregation. This could then lead to an autocatalytic accumulation of filaments in targeted regions. One could imagine that such a mechanism would be valuable in the design of self-assembly pathways. For example, amyloid fibrils have been found to untwist upon interactions with lipid membranes (17, 21), which could in turn affect their aggregations and be exploited for the design of amyloid or protein-based functional nanomaterials (18) on arbitrarily curved surfaces that could be responsive to changing geometries. Finally, it is to be noted that many of these cytoskeletal filaments are in a state of dynamic turnover, and it has been shown (33) that coupling the kinetics of filament polymerization with cell-wall growth and mechanics can lead to nontrivial regulatory mechanisms. It would be interesting to consider the role of the coupling of our untwisting transition to these mechanisms.

Author Contributions

A.G. and G.M.G. designed the study. D.A.Q, A.G., and G.M.G. performed the research and wrote the article.

Editor: Sean Sun.