Abstract
Combining imaging with correlation spectroscopy, as in raster image correlation spectroscopy (RICS), makes it possible to extract molecular translational diffusion constants and absolute concentrations, and determine intermolecular interactions from single-channel or multicolor confocal laser-scanning microscopy (CLSM) images. Region-specific RICS analysis remains very challenging because correlations are always calculated in a square region-of-interest (ROI). In this study, we describe a generalized image correlation spectroscopy algorithm that accepts arbitrarily shaped ROIs. We show that an image series can be cleaned up before arbitrary-region RICS (ARICS) analysis. We demonstrate the power of ARICS by simultaneously measuring molecular mobility in the cell membrane and the cytosol. Mobility near dynamic subcellular structures can be investigated with ARICS by generating a dynamic ROI. Finally, we derive diffusion and concentration pseudo-maps using the ARICS method. ARICS is a powerful expansion of image correlation spectroscopy with the potential of becoming the new standard for extracting biophysical parameters from confocal fluorescence images.
Introduction
Fluorescence fluctuation spectroscopy (FFS) methods probe molecular parameters of diffusive fluorescent substances, classically by analyzing the temporal correlation function of fluorescence signals (1, 2, 3). FFS methods have seen a tremendous increase in popularity since the 1990s with the improvement and commercialization of confocal microscopes, which brought correlation analyses from the physics field to a broad scientific community. Combining FFS methods with fluorescence imaging, as originally done in image correlation spectroscopy (ICS) (4), allows quantitative molecular properties to be extracted from microscopy images. Many variations on the original ICS method have appeared over the years. For example, two-color image cross-correlation spectroscopy (ICCS) allows quantifying clustering of two types of fluorescently labeled molecules (5). Temporal ICS (TICS) can be used for measuring the dynamics of slowly diffusing complexes (6). Spatiotemporal ICS (STICS) is a method that can be used for quantifying the directionality and velocity of flow phenomena (7). Imaging mean squared displacement (iMSD) can be used to study diffusion mechanisms (8). The k-space ICS method (kICS) is used to efficiently deal with fluorophores that exhibit a significant blinking (9). Finally, the raster image correlation spectroscopy (RICS) method can be used to study the molecular translational diffusion constant (D), absolute concentration (c), and intermolecular binding constants of diffusive molecules in single or multicolor confocal laser scanning microscopy (CLSM) images (10, 11, 12).
ICS provides a popular powerful quantification and characterization tool for microscopy images. With RICS in particular, molecular parameters can be quantified in a (bio-)chemically interesting and exceptionally large dynamic range (D ≈ 0.1–500 μm2/s, c ≈ 10−6–10−9 M). RICS analyses suffer much less from photobleaching- and blinking-related artifacts than their single-point confocal counterparts, since fluorescence is probed over a large area (13). This larger probed area also increases experimental robustness against location-specific artifacts. Measurement times reduced to a few or even a single image frame suffice, in turn opening the door toward robust kinetic analysis. Most importantly, RICS can be carried out on almost any CLSM; most manufacturers nowadays offer plug-and-play RICS extensions, and different groups worldwide provide well-documented more-advanced RICS analysis software (10, 13, 14).
The RICS method, however, also has limitations that have prevented its widespread usage. For example, the classical algorithm used in RICS analysis only accepts n2 ROIs, where n is the number of pixels in each direction of the ROI (4). Placing a squared ROI inside an imaged sample, such as a cell or cell organelle, can be difficult. Decreasing n reduces this problem and even allows mapping of molecular parameters in a complex sample (15, 16), but limited statistics prevent an accurate spatial correlation analysis below n ≈ 64. A static square ROI is also disadvantageous when dealing with organelles such as the endoplasmic reticulum (ER) or mitochondria that have complex shapes and are dynamic in a live-cell imaging experiment.
Another limitation of FFS is that fluctuation analyses perform well only on relatively homogenous samples. For example, as little as a single contamination that is significantly brighter than the average fluorescent species is detrimental for the correlation function when not removed a priori from the data. A commonly used trick to deal with this during FCS analysis is to monitor the moving average count rate over time; when it temporarily exceeds a certain relative or absolute threshold, all photons detected during this period are omitted from the correlation analysis. To our knowledge, a similar approach has not yet been incorporated for spatial correlations.
Lastly, because molecular information is averaged over space, the RICS method has not been used for generating pixel-resolution diffusion or concentration maps, unlike imaging-based FFS methods such as scanning FCS (SFCS) (17, 18), TICS (5), imaging total internal reflection (ITIR)-FCS (19), and single-plane illumination microscopy (SPIM)-FCS (20). In these methods, however, diffusion maps are mostly obtained only for relatively slowly diffusing molecules, such as, e.g., membrane proteins. Finally, when imaging using a CLSM for methods based on correlation between consecutive frames, the maximal scanning speed of the laser determines the highest mobility of molecules that can be quantified, which in our experience was around D = 0.01 μm2/s (21). In addition to diffusion maps, concentration maps of slowly diffusing molecules can also be generated using imaging-based FFS methods. For fast diffusing molecules, concentration maps can also be generated using the number and brightness method (22), which derives concentration info from the photon distribution per pixel. However, being an obligate single-pixel analysis method such as TICS, a fair number of images are needed to obtain a map of sufficient quality.
In this work, we describe an adapted version of the original ICS algorithm that now accepts ROIs of any shape. We implemented our algorithm in an all-graphical ICS analysis program that utilizes ROIs that can be generated freehand or automatically. Hence, any arbitrarily shaped region from an image series can be selected before correlation analysis. Using different proof-of-principle experiments, we illustrate some of the possibilities of arbitrary-region RICS (ARICS): removing artifacts from images before a correlation analysis, simultaneous analysis of diffusion and concentration in the membrane and cytosol, quantifying diffusion near complex and dynamic organelles such as the ER, and finally, generating pseudo-maps of diffusion and concentration. Considering all the advantages of ARICS analysis, we expect this approach to be beneficial to a number of spatial correlation methods and to replace the classical RICS algorithm.
Theory
Classical ICS algorithm
For comparison, we first briefly summarize the classical ICS algorithm (4), in which correlations are typically calculated using the following fluctuation image δI(x,y):
| (1) |
where I is the original fluorescence intensity image of size X × Y, I(x,y) is the intensity of pixel (x,y) (Fig. 1 A), and is the mean image intensity. The unnormalized spatial autocorrelation function (SACF) over a selected ROI (Fig. 1 B) is typically defined as follows:
| (2) |
where denotes two-dimensional (2D) cross-correlation, i.e., , (X-|ξ|)(Y-|ψ|) is the number of times a particular spatial lag (ξ,ψ) can be sampled, and | | denotes the absolute value. As illustrated in Fig. 1 C, the correlation is averaged over fewer elements as the spatial lag increases. Analogously to fluorescence correlation spectroscopy, G(ξ,ψ) is typically normalized by so that the amplitude of the SACF scales inversely with the number concentration N (the reader is referred to Eq. 14 for the fitting model used for the RICS analysis). In ICS, the correlation is calculated for each frame individually and the resulting SACFs are averaged over all frames to increase signal-to-noise.
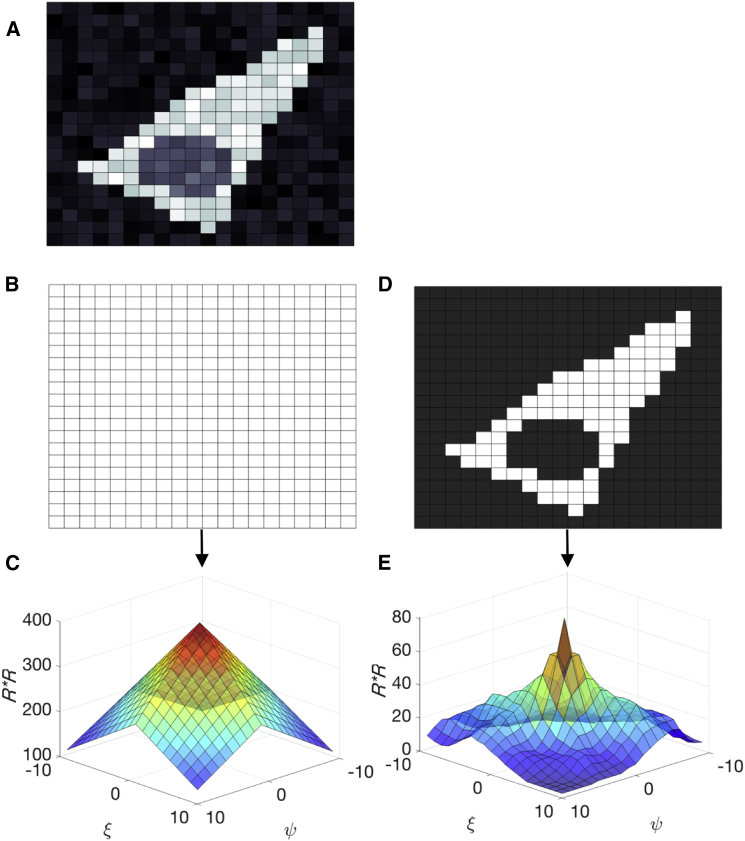
Figure 1.
Comparison of the ROI and ICS normalization in normal and generalized ICS. (A) Schematic representation of a 20 × 20 pixel2 image of a cell exhibiting fluorescence in the cytosol and, to a lesser extent, in the nucleus, is shown. (B) Normal ROI, encompassing the whole image including the cell and extracellular space is provided. (C) Graphical representation of the number of times a particular spatial lag is sampled, i.e., (X-|ξ|)(Y-|ψ|) in Eq. 2 or the denominator in Eq. 6. Spatial lags larger than half the ROI size are not used. (D) Arbitrary ROI mask, generated by intensity thresholding, encompassing only the cytosolic interior of the cell is shown. White pixels in the binary mask are unity; dark gray pixels are zero. (E) Spatial autocorrelation of the mask, displaying the number of times a particular spatial lag is sampled. For example, the lag (0,0) is sampled 81 times, which is equal to the number of unity pixels in the arbitrary ROI. To see this figure in color, go online.
ICS algorithm generalized for an arbitrary ROI
To generalize Eq. 2, we first define an arbitrarily shaped binary ROI mask R(x,y) with size equal to the image size, and with intensity one inside and zero outside the included region of interest (Fig. 1 D):
| (3) |
The image can then be masked by an elementwise multiplication with R:
| (4) |
and the fluctuation image δIR(x,y) can again be defined as follows:
| (5) |
where is now the mean intensity of all pixels included in the ROI. Then, similar to what has previously been done (23), we define the unnormalized SACF as follows:
| (6) |
where the correlation in the denominator again dictates the number of times a particular spatial lag (ξ,ψ) is sampled (Fig. 1 E). Hence, we average each shift in the correlation function by the number of times this shift is observable in the ROI. Finally, G(ξ,ψ) is normalized by the average intensity of the selected pixels, , and averaged over all frames. For both numerator and denominator, the same fast Fourier transform algorithm used for classical ICS can be applied to speed up the calculations. An additional change we made to the algorithm is to explicitly zero-pad images to avoid aliasing effects. The associated MATLAB (The MathWorks, Natick, MA) code and analysis software is available on request. Taken together, to generalize the ICS calculation algorithm for any ROI shape, we apply a ROI mask during image correlation, exploiting the fact that pixels with zero intensity cancel from the calculation, and normalizing the correlation at each spatial lag accordingly.
Generating the ROI
A ROI is classically defined in ICS as a square or rectangle positioned somewhere on an image in the image series. Here, we use three alternative ways for generating an ROI: 1) Many programming languages have built-in functions for manually drawing an arbitrarily shaped ROI, which can be useful for masking, e.g., an intracellular region. In MATLAB, we use the imfreehand command for this purpose. 2) Certain pixel characteristics can be used for defining the ROI, e.g., its absolute intensity:
| (7) |
where is the average intensity in an a × b area around pixel (x,y) and Ithreshold is an absolute intensity threshold above or below which pixel intensities should lie. Empirically, we found that a 5 × 5-pixel2 area worked well. For methods such as RICS where the correlation function is calculated on each image individually, the threshold selection criteria can be dynamic and the ROI variable for each frame. In this way, corrections can be made in movies where large aggregates or dark vesicles diffusing through the image series. Importantly, since thresholding is done using a spatial averaging filter, the pixels in the arbitrary ROI still constitute a complete intensity distribution histogram. This is important for spatial correlation methods such as RICS, as illustrated experimentally in this work, but also for methods in which the actual distribution is analyzed, e.g., photon counting histogram (24) or number and brightness analysis (22). Absolute or relative intensity or intensity variance thresholds can also be used, for which the reader is referred to the Supporting Material. 3) The ROI can be defined in another imaging channel, where a particular structure is specifically labeled.
Multiple ROIs can also be combined in various ways to obtain the final ROI. For example, if a freehand ROI (R1) is drawn on an image of a cell to roughly select the nuclear region, and an intensity thresholding is additionally carried out to select densely staining regions (R2), the final ROI R, used during correlation analysis, is obtained by an elementwise multiplication of the two ROIs, or in general for n ROIs as follows:
| (8) |
where n is the total number of ROIs.
Image preprocessing
For RICS analyses in live cells, slow fluctuations and spatial inhomogeneities are removed when necessary from the raw image data with a high-pass filter as follows:
| (9) |
where I(x,y,f) is the photon count of pixel (x,y) in frame f, is the moving average series from frames (f-ΔF) to frame (f+ΔF), and 〈I〉XYF is the mean intensity over all frames F with size X × Y. For live-cell experiments, a moving average of ΔF = 1 was used. Importantly, when performing temporal averages, pixels that were excluded from the ROI anywhere in the time window f ± ΔF also need to be excluded from the arbitrary ROI of frame f as follows:
| (10) |
IRICS and RRICS are subsequently used for correlation with Eq. 6. When performing a moving average, the image with the fluctuation of interest is included in the average and subtracted from the image. Hence, the amplitude of the fluctuation is decreased and the amplitude of the SACF in Eqs. 2 and 6 is also decreased. We correct for this artifact by rescaling the ACF:
| (11) |
Diffusion and concentration pseudo-maps
Since RICS is normally performed in large square image regions (typically > 642 pixel2) (Eq. 2), the spatial resolution is considerably lowered when molecular parameters (diffusion, concentration, brightness, stoichiometry, and interactions) are mapped. Although ARICS allows analysis in ROIs that do not need to be square (Eq. 6), enough pixels still need to be sampled to create a single correlation function. This leads to a similar resolution limit when mapping with ARICS. By exploiting particular image features, the ARICS method can also be used for creating pseudo higher-resolution maps of molecular parameters.
An example of such a feature is the average pixel intensity: most features that affect the local concentration of a molecule (interactions, exclusion zones, compartmentalization, etc.) also affect its apparent diffusion coefficient. Whereas mere changes in the mobility (e.g., because of different viscosities) create an inverse concentration and consequently intensity gradient in the sample (Fig. S4), interactions with cellular structures are much more complex and do not necessarily follow this relationship. Therefore, the different signal intensities in an image indicate local variations, and dividing an image into different ROIs depending on local intensity might reveal hidden interactions with or exclusions from the local environment.
Additionally, the ROIs do not necessarily have to be generated from the channel that is used for the actual correlation. By labeling an interaction partner or antagonist with a second color, or by imaging certain cellular markers (e.g., chromatin or organelles), the signal intensity in the second channel can then be used to create ROIs.
Practically, when the intensity of the images in a movie is broadly distributed, each image frame can easily be divided into m arbitrary ROIs Rm (e.g., m = 5), each encompassing pixels in a particular range of intensities (e.g., 0–200, 200–400, ... kHz). For every frame in the series, m SACFs are calculated (Eq. 6) and each SACF is averaged over all frames. The m SACFs are then fitted using Eq. 14 to extract D and N parameters for each of the m ROIs, termed Di and Ni, respectively. These parameters are subsequently assigned to every pixel in an image to create pseudo-maps of “single-frame” diffusion and concentration as follows:
| (12) |
respectively, where × denotes an elementwise multiplication. Although Eq. 12 assumes the m ROIs are completely nonoverlapping, only a small adaptation is needed to allow also overlapping ROIs. Finally, and as will also be shown experimentally, the m ROIs may move from one frame to the next. Therefore, an average over the single-frame pseudo-maps is performed as follows to generate a representative calculation of the diffusion and concentration pseudo-maps:
| (13) |
where F is the total number of frames minus any frames where, due to preprocessing stipulations (Eq. 10), the pixel was not assigned to a ROI.
Materials and Methods
Plasmids, cell culture, and transfection
pKHIVVenus encoding Gag.Venus was obtained from Barbara Müller (University of Heidelberg) and cloned as described previously (21). eGFP-LEDGF/p75 was cloned as described previously (25). pMyrPalm.mYFP was provided by Prof. R. Tsien (University of California San Diego, La Jolla, CA). PcsVenus and calreticulin-mRFP-KDEL/pcDNA3 plasmids were a gift of Prof. A. Miyawaki (26). HeLa cells (NIH Reagent program) were cultivated without antibiotics in low-glucose DMEM (Life Technologies, Darmstadt, Germany) supplemented with 10% heat-inactivated fetal bovine serum (complete medium) at 5% CO2 and 37°C in a humidified atmosphere. For transfection, 3 × 104 cells per well were plated in complete medium in eight-well cover slips (Lab-Tek II Chambered Coverglass, Thermo Scientific, Langenselbold, Germany). Plasmid DNA (500 ng in total) was mixed with 1.5 μL XtremeGene 9 transfection reagent (Roche Applied Science, Mannheim, Germany) in 50 μL OptiMEM and incubated for 15–20 min at room temperature, before addition of 100 ng pKHIVFP plasmid 6–8 h after cell seeding. For cotransfections a 1:1 plasmid weight ratio was used. All imaging experiments were performed at room temperature.
Venus FP imaging experiment
Previously described imaging data of the Venus fluorescent protein freely diffusing in a 10-cP viscosity buffer, acquired on a home-built confocal laser-scanning microscope (2 μW of 475-nm excitation at the sample) (13), was reanalyzed in this work. Imaging parameters were 200 frames, 12.5 × 12.5 μm2, 300 × 300 pixel2, line time τl = 3.33 ms, pixel dwell time τp = 11.11 μs, and pixel size δr = 41.7 nm.
Membrane diffusion experiment
Previously described imaging data of cells coexpressing cytosolic Venus and mCherry fluorescent proteins and membrane-targeted MyrPalm-mYFP, acquired on a home-built confocal laser-scanning microscope (0.8 μW of 475-nm excitation at the sample) (21), was reanalyzed in this work. Imaging parameters were 100 frames, 300 × 300 pixel2, line time τl = 3.33 ms, pixel dwell time τp = 11.11 μs, and pixel size δr = 41.7 nm. Before per-frame intensity thresholding (Eq. 7), a rough ROI covering the cell was manually drawn on the first image of the image series and kept constant for all frames.
Other imaging experiments
The Gag and LEDGF/p75 imaging experiments were carried out on a commercial Olympus Fluoview FV1000 confocal microscope. Raster-scanning was performed in the center of the scan range during 200 frames with the following settings: 256 × 256 pixel2, line time τl = 4.325 ms, pixel dwell time τp = 12.5 μs, and pixel size δr = 50 nm (i.e., zoom 16.4). Excitation light from a 488 nm Ar-ion laser (2% transmissivity, ∼2 μW in the sample) was reflected into a UPLSAPO-60XW objective (NA = 1.2) using a DM405/488/559/635 polychroic mirror. The optimal position of the objective cover slip correction collar was determined by maximizing the molecular brightness as measured by RICS of freely diffusing ATTO488-CA (ATTO-TEC, Siegen, Germany) at nM concentration in water. Emission was detected through a 130 μm pinhole (automatic setting) and a BA505-540 emission filter onto a photomultiplier tube operating in pseudo-photon counting mode. To convert pseudo-counts to real counts, an image intensity rescaling parameter S = 6 was used (27, 28). In the second imaging channel used for generating the ROI, 559-nm excitation (1% transmissivity) from a DPSS laser was used. Emission was separated from the other imaging channel using an SDM560 dichroic mirror and a BA575-675 emission filter. Before per-frame intensity thresholding (Eq. 7), a rough ROI covering the cytosol (Gag experiment) or nucleus (LEDGF/p75 experiment) was manually drawn on the first image of the image series and kept constant for all frames.
RICS fitting
The mean of the SACF series was analyzed as before (21) by nonlinear least squares fitting with a two-component (one mobile and one immobile) model for Brownian diffusion in a three-dimensional (3D) Gaussian PSF as follows:
where
| (14) |
is the time-dependent component of the correlation function ascribed to fast diffusing molecules. Amob and Aimm are the amplitudes of the mobile and immobile component in the correlation function, respectively and is a baseline correction term. The lateral and axial focus radii are denoted by ωr and ωz, respectively, defined as the distance from the focus center where the signal intensity decreases to 1/e2 of its initial value. The fraction of immobile molecules (on the RICS timescale) was described with a symmetrical 2D Gaussian function where ωimm represents the half-width of the function at 1/e2 of the maximal intensity of the immobilized objects. When the objects are smaller than the diffraction limit, ωimm becomes equal to ωr. is the average number of molecules in the point spread function (PSF) that are mobile on the RICS timescale, with γ = 2–3/2 the shape factor for a 3D Gaussian. Goodness-of-fit parameters were the weighted residuals parameter rw and reduced χ2 parameter. Because of the strong autocorrelation of the shot noise at (ξ = 0,ψ = 0), G(0,0) was not considered during fitting, and autocorrelation amplitudes were approximated by the average of G(1,0) and G(–1,0) for graphical representations.
Diffusion and concentration pseudo-maps
A freehand ROI was drawn around the nucleus of the cells, to exclude the cytosolic region a priori. Arbitrary ROIs were calculated using the H2B imaging channel and mapped onto the LEDGF/p75 channel. Moreover, in the H2B imaging channel, pixel intensities in each frame were rescaled such that the average image intensity in all frames was equal to that of the first frame. This procedure, which corrected the data for photobleaching, was important to render the threshold intensities applicable to all image frames.
Results
Outlier-free fluctuation imaging
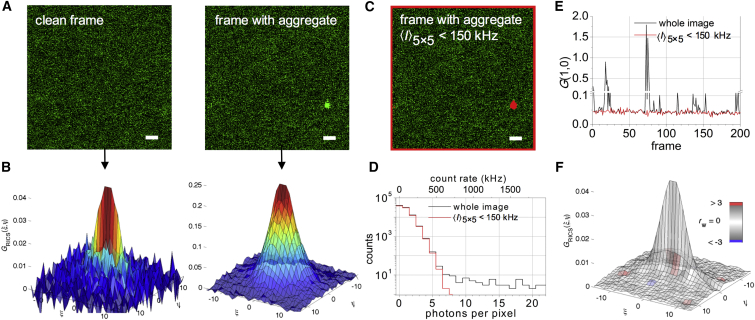
Many unwanted phenomena can give rise to confocal images with inhomogenously distributed fluorescence intensities: aspecific aggregation of molecules of interest, sticking of fluorophores to organelles, diffusing organelles lacking the molecule of interest, just to name a few. Although intrinsically part of the sample, when bright or dark artifacts move significantly from one frame to the next, they will adversely affect any quantitative (fluctuation) image analyses. A first application of the generalized ICS algorithm is cleaning up imaging data by removing fluorescent outliers before correlation and RICS analyses. As a proof-of-principle, we used a confocal image series of the freely diffusing Venus fluorescent protein at nM concentration in a buffer of roughly 10 times the viscosity of water. Fig. 2 A shows two frames: a clean frame and a frame in which a Venus aggregate coincidently diffused through the focal plane while the laser was scanning over it. We calculated the SACF of each frame (Fig. 2 B). Strikingly, although in the second frame, the aggregate was only detected in ∼1% of all pixels, its SACF looks completely different than that of the clean frame. To mask out the aggregate, we employed an absolute intensity threshold < 150 kHz (Eq. 7). This selectively removed the aggregate from the image while leaving the rest of the image untouched (Fig. 2 C). Consequently, the threshold removed the high-count tail from the overall pixel intensity distribution histogram, while leaving the shape of the low-count part unchanged (Fig. 2 D). To check whether the threshold held for all frames in the image series, we calculated all corresponding SACFs and plotted their amplitudes, approximated by the correlation value at ξ = 1, ψ = 0, as a function of frame number (Fig. 2 E). Clearly, when an arbitrary ROI was used, the variation on the SACF amplitude decreased tremendously. Finally, when the individual, artifact-free SACFs were averaged and the average SACF was fitted using Eq. 14, a single diffusing species (D = 7.7 ± 0.3 μm2/s) was observed with the fit model yielding 100% amplitude of the mobile fraction and 0% for an immobile species (reduced χ2 = 1.02) (Fig. 2 F). For comparison, Fig. S1 displays a RICS analysis of the raw imaging data, which is not described at all by Eq. 14 due to the presence of Venus aggregates. This proof-of-principle experiment clearly shows the generalized ICS algorithm can be used to specifically remove outliers from imaging data of freely diffusing Venus, resulting in RICS data that could be perfectly described by a single-component fit model.
Figure 2.
Cleaning up image series before RICS analysis. (A) Two image frames from a 200-frame confocal image series of freely diffusing Venus fluorescent protein are shown. In the right image frame, a protein aggregate was in focus while the laser scanned over it. Scale bars represent 1 μm. (B) SACFs were calculated from the frames in (A). The aggregate dictates the shape of the second SACF. (C) The frame containing the aggregate, with the pixels around which a 5 × 5 pixel2 area exhibited an average intensity exceeding 150 kHz depicted in red. To avoid edge effects during thresholding, the borders of the image were also omitted from the ROI. The scale bar represents 1 μm. (D) Intensity distribution histogram is provided of (black) all pixels in the frame containing the aggregate and (red) all pixels included in the arbitrary ROI of the same frame. For comparison, both the absolute photon counts and the count rate per pixel are displayed. (E) The amplitudes of the individual SACFs were calculated (black) using all image pixels with Eq. 2 or (red) using all pixels included in the arbitrary ROI with Eq. 6. Amplitudes were approximated by the correlation value at ξ = 1. For clarity, a break at 0.11–0.2 was introduced on the y-axis. (F) The averaged arbitrary-ROI SACF was fitted using Eq. 14 and color-coded using the weighted residuals goodness-of-fit parameter rw. Fig. S1 contains further details on the fitting, as well as a comparison with the raw-data average SACF fitting. To see this figure in color, go online.
Simultaneously measuring diffusion in the cytosol and membrane
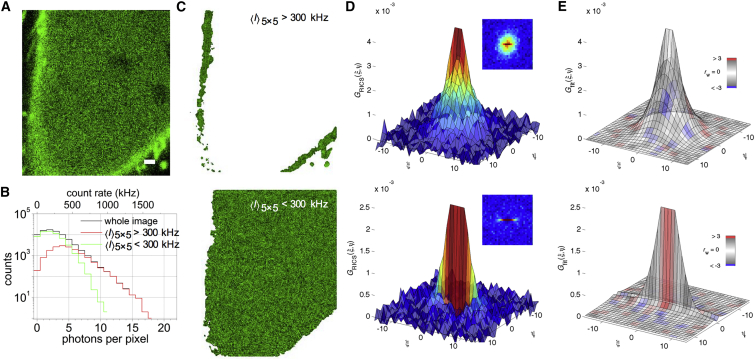
In a next experiment, we used absolute intensity thresholding in live cells to discern between species diffusing in the cell membrane and the cytosol. We coexpressed cytosolic Venus together with a membrane targeted MyrPalm-mYFP in HeLa cells (Fig. 3 A). We avoided imaging near the bottom and top cell membrane by an mCherry coexpression control and z-stacking (Fig. S2). We defined two arbitrary ROIs using Eq. 7 for selecting the membrane ( > 300 kHz) and cytosol ( < 300 kHz). By doing this, two complete pixel intensity distribution histograms were obtained, each one representing the molecules in the respective ROIs (Fig. 3 B). After preprocessing the image series using Eq. 9 (Fig. 3 C) and calculating the SACF of each image frame, the average SACF was obtained for the membrane and cytosolic ROI (Fig. 3 D, top and bottom graphs, respectively). In the membrane ROI, a circular SACF shape was observed, indicative of slower mobility. After fitting, a diffusion constant of D = 0.3 ± 0.1 μm2/s was obtained in the membrane ROI (Fig. 3 E, top graph), which is what is expected for the membrane-bound MyrPalm-mYFP protein (29). In the cytosol ROI, on the other hand, a line-shaped SACF was observed, with a corresponding diffusion constant of D = 30 ± 7 μm2/s (Fig. 3, D and E, bottom graphs), which in turn agrees with the expected value for fluorescent proteins diffusing freely in the cytosol (21, 25). Together, this experiment shows that arbitrary-region RICS can be used to simultaneously quantify diffusion in different compartments of the cell, as long as the ROIs can be discerned on the basis of the absolute fluorescence intensity.
Figure 3.
Absolute intensity thresholding for region-specific RICS analysis. (A) One image frame from a 100-frame confocal image series of a HeLa cell coexpressing cytosolic Venus fluorescent protein and membrane-targeted MyrPalm-YFP is shown. Scale bar represents 1 μm. (B) Intensity distribution histogram is provided of (black) all pixels in the frame, (red) an arbitrary ROI with > 300 kHz, and (green) an arbitrary ROI with < 300 kHz. For comparison, both the absolute photon count and the count rate per pixel are displayed. (C) The data from (A), were preprocessed using Eq. 9, and intensity-thresholded to select (top image) the membrane or (bottom image) the cytosol. (D) SACFs were calculated from the preprocessed ROI in (C). The inset is a top view of the SACFs. (E) The average arbitrary-ROI SACF was fitted using Eq. 14 and color-coded using the weighted residuals goodness-of-fit parameter rw. Fig. S2 contains further details on the experiment. Results for a representative cell are shown. The average error on the SACF data (% error on a data point relative to the SACF amplitude) was 3–4%, the error on D was 10–25%, and the reduced χ2 fit quality parameter was 1.9–2.4. To see this figure in color, go online.
Mobility near complex subcellular structures
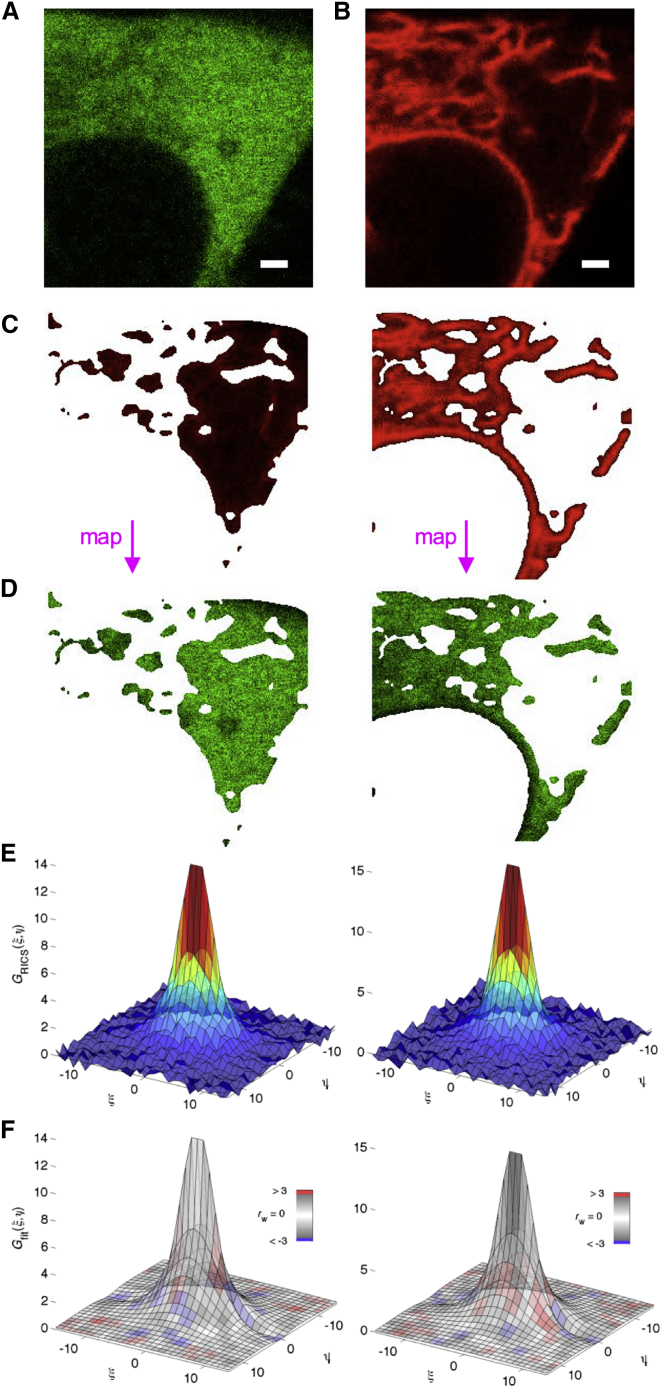
It would be of great interest to be able to measure the diffusion of proteins in different subcellular structures or organelles within a living cell. With the exception of the nucleus, this has not possible with RICS as the organelles are limited in size and are poorly described by rectangular ROIs. With ARICS, this becomes possible. When subcellular regions cannot be easily distinguished via the absolute fluorescence intensity as described above, a second channel can be used to image the subcellular structures or organelles. The ROI can then be generated from the fluorescence channel of the marker and then mapped back onto the image series of the molecule of interest. We used dual-color ARICS to study diffusion of the HIV-1 Gag, the protein that constitutes the protein shell of HIV-1 virions, near the ER. Previously, it had been shown that, under some conditions, the incorrect assembly of Gag can occur in the ER (30). Also, bridging conduits between macrophage cells that allow for cell-to-cell transfer of HIV consists of ER membranes (31). For the dual-color ARICS experiments, HIV-1 Gag was labeled with Venus and the ER membrane was labeled by fusing mRFP to an ER-targeting peptide (calreticulin-mRFP-KDEL). A typical confocal image of HeLa cells expressing Gag (as part of the MA-Venus-CA-NC-p6 construct) is shown in Fig. 4 A. The Gag protein is present in the cytosol but not in the nucleus. In the cytosol, regions with less Gag staining are visible (top left region in Fig. 4 A), which might correspond to the ER, but a reference image series of the ER was needed to confirm this. The image in Fig. 4 B corresponds to the image in Fig. 4 A, and shows the typical structure of the ER surrounding the nucleus, and staining densely in some cytosolic regions, but not in others. Based on intensity thresholding in the red imaging channel, we could define two ROIs: one staining only dimly in the ER imaging channel (Fig. 4 C, left) and one staining very intensely in the ER imaging channel (Fig. 4 C, right). These regions were consequently mapped onto the Gag imaging channel (Fig. 4 D) and a RICS analysis was performed (Fig. 4, E and F). Visually, the SACFs in cytosolic regions mostly devoid of ER membranes (Fig. 4 E, left) and enriched in ER membranes (Fig. 4 E, right) looked similar. After analyzing 10 cells, average diffusion coefficients of D = 3.5 ± 0.3 μm2/s (Fmob = 74 ± 1%) and D = 3.7 ± 0.3 μm2/s (Fmob = 72 ± 3%) were obtained respectively (Fig. 4 F). This can be interpreted in different ways: 1) the mobility of Gag in the cytosol and in the ER is similar, 2) the mobility of Gag near the ER as observed with ARICS is not decreased by interactions with the ER, or 3) diffusion in or interaction with the ER is not picked up at all by ARICS. To investigate whether ARICS is principally sensitive for diffusion inside confined areas, we performed simulations (Fig. S3). In brief, ARICS provided qualitative information on diffusion for confinements of similar size as the PSF, in that the SACFs got distorted from the freely diffusing species. For compartments that were significantly larger than the PSF, the algorithm could even extract correct diffusion constants. Although interpretations 1) and 2) cannot be ruled out, a complete absence of experimental SACF distortion suggests that Gag does not interact with or localize in the ER lumen at all, and the latter is likely also too small to affect the SACFs.
Figure 4.
Molecular mobility near complex cell organelles. (A and B) One image frame from a 200-frame two-color confocal image series of a HeLa cell coexpressing (A) Gag.Venus and (B) the endoplasmic reticulum marker calr-mRFP-KDEL are shown. Scale bars represent 1 μm. (C) The data from (B) was intensity-thresholded (Ithreshold = 500 kHz) to select (left image) regions devoid of ER membranes or (right image) regions with dense ER staining. (D) Selected pixels from (C) were used to create region-specific ROIs in the Gag.Venus imaging channel. (E) SACFs were calculated from the ROIs in (D); y-axes are ×10−3. (F) The average arbitrary-ROI SACF was fitted using Eq. 14 and color-coded using the weighted residuals goodness-of-fit parameter rw; y-axes are ×10−3. Results for a representative cell are shown, but a total of 10 cells were analyzed, using values for Ithreshold that visually separated the cytosol from the ER. Errors on fit parameters are the mean plus SE. The average error on the SACF data (% error on a data point relative to the SACF amplitude) was 1–4%, and the reduced χ2 fit quality parameter was 1.7–3.5. To see this figure in color, go online.
Taken together, molecular mobility can, in principle, be studied in or at particular subcellular structures using RICS by generating a dynamic arbitrary ROI of the structure in a second imaging channel and mapping this ROI onto the image series of the molecule of interest. For the mobility of Gag in or close to ER membranes, a significant difference could not be observed relative to regions with low/no ER staining.
Concentration and diffusion pseudo-maps
We exploited the generalized ICS algorithm to segment the image into several ROIs and map the mobility and concentrations of the different segments. As outlined in the Introduction, the ROIs are selected depending on a particular image characteristic. A RICS analysis is performed on each of the AROIs in each image and an average over the time series of the obtained RICS parameters is determined for each pixel in the image. We validated this approach using simulations (see the Supporting Material) where the diffusion coefficient varied depending on the position of the particle in the image. Slower diffusion leads to a higher concentration of particles and hence to higher intensity. Using fluorescence intensity for segmentation of the image, we could reconstruct the diffusion map (Fig. S4).
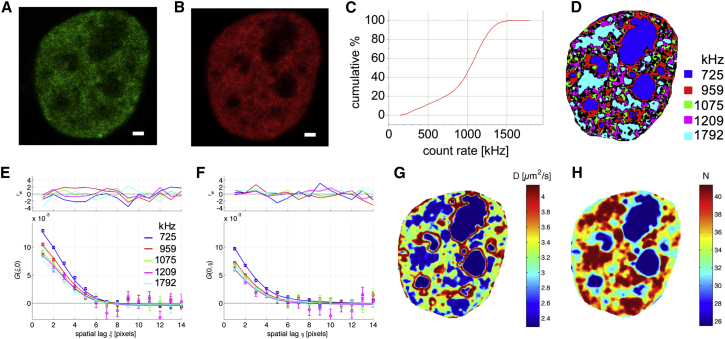
To test this method experimentally, we performed a RICS experiment on cells coexpressing the transcriptional coactivator LEDGF/p75 fused to eGFP (Fig. 5 A) as well as the core histone H2B fused to mRFP as a marker of chromatin density (Fig. 5 B) (25). We calculated the whole-series cumulative pixel intensity histogram of the H2B image series (Fig. 5 C), from which we defined five threshold intensities (725 kHz, 959 kHz, 1075 kHz, 1209 kHz, and 1792 kHz) that divided each image in the image series into five ROIs, as illustrated in Fig. 5 D. In each frame, we then calculated five SACFs and averaged these over the whole image series. After fitting, it was clear that the G(ξ,0) amplitude scaled inversely with the average fluorescence intensity of the mRFP-H2B protein. In other words, the eGFP-LEDGF/p75 density followed the mRFP-H2B density (Fig. 5 E). From the G(0,ψ) shape, on the other hand, it was clear that at least the lowest-intensity ROI seemed to contain molecules of overall lower mobility (Fig. 5 F). Using Eqs. 12 and 13, we then used the diffusion coefficients and number concentrations obtained from the five SACFs to create pseudo-maps of diffusion (Fig. 5 G) and concentration (Fig. 5 H). Several interesting features become obvious from this analysis: 1) The N map of LEDGF/p75 correlated with both the LEDGF/p75 and H2B intensity maps, suggesting that the intensity distribution in the intensity images is due to difference in concentration and not due to changes in the intrinsic fluorophore brightness. In addition, the concentration of LEDGF/p75 follows the chromatin density. This experiment can be viewed as a single-cell titration experiment as the segmentation leads to separate analyses for regions of different LEDGF/p75 concentrations. 2) Regions of low concentration, corresponding to the nucleoli as seen from the mRFP-H2B staining, correlated with regions of low mobility. 3) Other regions of low mobility correlated with regions of high eGFP-LEDGF/p75 concentration. As it is believed that LEDGF/p75 transiently interacts with DNA, slowing down its diffusion (25), the regions of lower mobility, corresponding to high chromatin densities, suggest that the affinity of eGFP-LEDGF/p75 for chromatin increases with concentration. 4) Lastly, the nucleoli are surrounded by regions of high mobility, suggesting a lower local viscosity in these regions. Since molecules naturally accumulate in regions of low mobility (the reader is referred to the simulation in Fig. S4), the absence of an excess LEDGF/p75 in the nucleolar regions suggests the protein has a hard time entering, or, is actively exported from these regions.
Figure 5.
Diffusion and concentration pseudo-maps with ARICS. (A and B) One-frame images from a 200-frame two-color confocal image series of a HeLa cell coexpressing (A) eGFP-LEDGF/p75 and (B) a chromatin density marker mRFP-H2B are shown. Scale bars represent 1 μm. (C) The cumulative pixel intensity histogram is provided of the complete mRFP-H2B image series for all pixels inside the nucleus. (D) Using intensity thresholding, each image can then be divided in five approximately equally sized ROIs, as displayed for the image frame from (B). The legend indicates the upper intensity threshold per ROI. Black regions correspond to pixels that switched between different ROIs within the moving average and are excluded by the preprocessing algorithm (Eq. 9). (E and F) The five averaged arbitrary-ROI SACFs (symbols and error bars) were fitted using Eq. 14 (solid line) and the (E) G(ξ,0) and (F) G(0,ψ) values and fits are displayed. Top panels show the weighted residuals goodness-of-fit parameter. (G) From the ARICS analysis, a pseudo-diffusion map and (H) pseudo-concentration map of eGFP-LEDGF/p75 averaged over all frames are shown. Results for a representative cell are shown. The average error on the SACF data (% error on a data point relative to the SACF amplitude) was 1–4%, the error on parameters in the pseudo-maps were 5–15% for D and 1–3% for N, and the reduced χ2 fit quality parameter was 1–2.5. To see this figure in color, go online.
To compare the results from the ARICS analysis with other FFS methods, we calculated the concentration map using an number and brightness (N&B) analysis (Fig. S5). The overall distribution and magnitude of number concentrations obtained with N&B and ARICS is similar, but because no spatial averaging was used for the N&B analysis, the noise in the number concentration image is higher. In summary, by categorizing image pixels in different intensity regions of another imaging channel, pseudo-maps of diffusion and concentration could be obtained for the transcription factor LEDGF/p75, which revealed an interesting correlation between diffusion and concentration, information that would otherwise be completely hidden in the SACF.
Discussion
The ability of RICS to extract biophysical information from fluorescence images makes it an exciting method for the biological and biophysical communities. Numerous studies of cytosolic or nuclear dynamics in cell types, such as HeLa cells, have been shown to be possible using RICS. However, accurate cellular RICS experiments are often difficult because of aggregates of high intensity or dark vesicles diffusing through the field of view. In addition, RICS is difficult with smaller cell types (for example T-cells or even bacteria or yeast cells) and nearly impossible when trying to measure diffusion in small organelles as the ROI is too small or ill-shaped for classical RICS. ARICS can circumvent many of these difficulties. As for any fluctuation experiment, enough (adjacent) pixels need to be sampled for the SACF to have meaningful statistics. As a rule-of-thumb, the statistics are generally sufficient for fitting the SACF to simple models when the standard deviation is smaller than 5% and the SACF does not contain a significant negative offset.
The freedom to correlate virtually any shape of ROI using ARICS opens up a number of possibilities. One possibility is the automatic detection and removal of undesired spatial fluctuations within images. For example, in live-cell measurements at 37°C, cell components (organelles, vesicles, membranes) move significantly from frame to frame, leading to the situation where many frame contains artifacts from moving dim or bright objects. As the SACF is calculated on each frame separately, one could delete each frame where such an artifact is observed. However, this can be time consuming and throws out data unnecessarily. By including predetermined criteria (e.g., minimum and maximum acceptable pixel intensity, maximum acceptable fluctuation from the pixel average, etc.), these artifacts can be detected and removed from the analysis as we demonstrated in our proof-of-principle Venus imaging experiment.
The strength of ARICS is that ROIs can be selected using a myriad of conditions, making it very powerful, not just to clean up artifacts but to perform biophysical characterization of biomolecules in cells with subcellular resolution. For example, we exploited the difference in absolute fluorescence intensity to discern between diffusion in the membrane and from the cytosol. Another alternative is to use a second imaging channel to perform the segmentation, as we demonstrated for labeling of the ER membrane. Hence, one can consider a wide range of parameters that could be used to select the ROIs for the ARICS analysis.
An additional advantage of ARICS is the ability to automate the analysis and to perform batch analyses. How well the process can be automated depends on how well one can automate the selection criteria for the different ROIs. Thus, we implemented a relative thresholding of a small (e.g., 5 × 5) versus a larger (e.g., 10 × 10) subregion in the image (as outlined in the Supporting Materials). In general, relative thresholds can be interesting for automated analysis, since they do not require a user-defined input of absolute intensities. Shape-sensitive ROI-generating algorithms for automatically detecting cells, nuclear membranes or cellular components (32) can also be implemented. Thus, ARICS holds promise for automated whole-cell and subcellular analysis by fluctuation methods.
We have also demonstrated the possibility of pseudo-mapping parameters using the ARICS method. To our knowledge, this is a versatile new way of looking at spatial correlation data. We deliberately termed it a pseudo-map, since it is based on the a priori definition of a number of ROIs between which the average properties are investigated. The quality of the pseudo-map depends on how well the ROIs are defined. When a particular parameter, such as D, varies largely within a single ROI, the pseudo-map will still provide a single averaged value. Any image feature (intensity, intensity variance, but possibly also higher moments) in any imaging channel can be used as input for generating the different ROIs. For example, a molecular brightness map can be made by dividing the average intensity image by the N pseudo-map. In this way, molecular stoichiometries can be imaged using ARICS just as with the N&B method. Conversely, the stoichiometry from an N&B analysis can also be used to generate ROIs and the dynamics of molecules having a particular stoichiometry investigated using ARICS.
Pseudo-mapping can principally also be used for creating D or N maps from TICS or imaging FCS (light sheet or total internal reflection fluorescence (TIRF)-based) data, where similar image features can be used as we proposed above, recorded in the same or another imaging channel. In general, the values for D that have to be quantified determine which fluctuation imaging methods are best suited. In terms of excitation power, a higher density is typically used in the RICS method, but regions are illuminated only briefly (μs pixel dwell times) in each frame, whereas a lower, but continuous density is typically used in TIRF and light sheet experiments. Finally, whereas the excitation light in confocal microscopy and light sheet microscopy travels throughout the cell (∼10 μm thickness and ∼20 μm length, respectively), in TIRF microscopy only a thin (< 200 nm) region is exposed to the excitation light.
In this work, we have described the principle of the ARICS approach and demonstrated some of its capabilities. However, there are a number of possibilities for extending the ARICS approach. ARICS can be extrapolated to a cross-correlation analysis of two or more channels or to other fluctuation analysis methods such as ICS, STICS, iMSD that analyze spatial fluctuations. The other spatial correlation methods will benefit from the same advantages as ARICS. The method can also be applied to other measuring modalities such as RICS combined with stimulated emission depletion microscopy (STED), which allows imaging dynamics on smaller spatial scales (33). Another extension of ARICS that we envision would be to give a statistical weight to the pixels within the ROIs. Fluorescence lifetime correlation spectroscopy (34), raster lifetime image correlation spectroscopy (13), and fluorescence spectral correlation spectroscopy (35) employ statistical filtering of fluorescence data during the correlation analysis. In a similar approach, the R(x,y) filter does not have to be binary but can be used as a statistical filter for weighting the ARICS data.
RICS and FCS both have particular advantages. FCS has the advantage of higher temporal resolution and, as the excitation volume is typically diffraction-limited, site-specific dynamics can be probed such as inside cell organelles or on the membrane. RICS has the advantage that the excitation energy is distributed over a much larger region in the sample. Hence, RICS and other imaging methods typically suffer much less from photobleaching-related artifacts (13). Secondly, because spatial correlation methods are carried out on a whole region in a sample, rather than a single point, much shorter measurement times are needed for obtaining adequate statistics. With ARICS, it is now possible to also probe dynamics inside cell compartments or membranes with RICS. In addition, nondesired heterogeneities within the sample, such as bright aggregates or dark organelles diffusing through the image, can be easily removed, making reliable RICS measurements much easier to perform. Lastly, since the ROI mask can move along with the imaged region-of-interest, ARICS makes it possible to probing molecular properties in dynamic subimage regions.
Conclusions
In this work, we present the ARICS method, which employs a generalized algorithm for spatial correlation analyses and can be applied to arbitrary regions-of-interest of a fluorescence image series. The way we have implemented ARICS is compatible with the fast Fourier transfer algorithms used typically in ICS and is not computationally cumbersome. ARICS sprouted from the many challenges we encountered in performing high-quality RICS data at 37°C in living cells. To illustrate the power of ARICS, we employed ARICS to clean up image series during correlation analysis, to perform cell organelle-specific correlation analysis, and to generate diffusion and concentration pseudo-maps. ARICS can be combined with any spatial correlation method and can be easily expanded to provide new modalities of analyzing RICS data. Hence, ARICS is a powerful successor of the classical RICS method with new functionalities and offers many exciting possibilities for further development.
Author Contributions
J.H. and T.D. designed the research. J.H. performed experiments and wrote the article. W.S. performed the simulations. All authors critically reviewed the article.
Acknowledgments
We thank Prof. Atsushi Miyawaki (RIKEN Brain Science Institute, Japan) for providing the Calr-mRFP-KDEL/pcDNA3 construct, Prof. Barbara Müller (Universitäts Klinikum Heidelberg, Germany) for the Gag.Venus construct, and Dr. Viola Baumgärtel (LMU Munich) for critically reading the manuscript. Prof. Johan Hofkens (KU Leuven) is gratefully acknowledged for the use of his microscope facilities.
Research was funded by the Research Foundation Flanders (FWO Vlaanderen), project n. G0B4915N. D.C.L. gratefully acknowledges the financial support of the “Deutsche Forschungsgemeinschaft” via the SFB1032 (Project B3) and the LMU via the LMUinnovativ program BioImaging Network and the Center for NanoScience (CeNS).
Editor: Paul Wiseman
Footnotes
Jelle Hendrix’s present address is Faculty of Medicine and Life Sciences and Biomedical Research Institute, Hasselt University, Diepenbeek, Belgium.
Supporting Material and Methods, Supporting Results, and five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30810-4.
Supporting Material
References
- 1.Magde D., Elson E., Webb W.W. Thermodynamic fluctuations in a reacting system—measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 1972;29:705. [Google Scholar]
- 2.Magde D., Elson E.L., Webb W.W. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 3.Elson E.L., Magde D. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 4.Petersen N.O., Höddelius P.L., Magnusson K.E. Quantitation of membrane receptor distributions by image correlation spectroscopy: concept and application. Biophys. J. 1993;65:1135–1146. doi: 10.1016/S0006-3495(93)81173-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wiseman P.W., Squier J.A., Wilson K.R. Two-photon image correlation spectroscopy and image cross-correlation spectroscopy. J. Microsc. 2000;200:14–25. doi: 10.1046/j.1365-2818.2000.00736.x. [DOI] [PubMed] [Google Scholar]
- 6.Srivastava M., Petersen N.O. Diffusion of transferrin receptor clusters. Biophys. Chem. 1998;75:201–211. doi: 10.1016/s0301-4622(98)00206-3. [DOI] [PubMed] [Google Scholar]
- 7.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 8.Di Rienzo C., Gratton E., Cardarelli F. Fast spatiotemporal correlation spectroscopy to determine protein lateral diffusion laws in live cell membranes. Proc. Natl. Acad. Sci. USA. 2013;110:12307–12312. doi: 10.1073/pnas.1222097110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kolin D.L., Ronis D., Wiseman P.W. k-space image correlation spectroscopy: a method for accurate transport measurements independent of fluorophore photophysics. Biophys. J. 2006;91:3061–3075. doi: 10.1529/biophysj.106.082768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Digman M.A., Brown C.M., Gratton E. Measuring fast dynamics in solutions and cells with a laser scanning microscope. Biophys. J. 2005;89:1317–1327. doi: 10.1529/biophysj.105.062836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Digman M.A., Sengupta P., Gratton E. Fluctuation correlation spectroscopy with a laser-scanning microscope: exploiting the hidden time structure. Biophys. J. 2005;88:L33–L36. doi: 10.1529/biophysj.105.061788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Digman M.A., Wiseman P.W., Gratton E. Detecting protein complexes in living cells from laser scanning confocal image sequences by the cross correlation raster image spectroscopy method. Biophys. J. 2009;96:707–716. doi: 10.1016/j.bpj.2008.09.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hendrix J., Schrimpf W., Lamb D.C. Pulsed interleaved excitation fluctuation imaging. Biophys. J. 2013;105:848–861. doi: 10.1016/j.bpj.2013.05.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gielen E., Smisdom N., Ameloot M. Diffusion of myelin oligodendrocyte glycoprotein in living OLN-93 cells investigated by raster-scanning image correlation spectroscopy (RICS) J. Fluoresc. 2008;18:813–819. doi: 10.1007/s10895-007-0308-8. [DOI] [PubMed] [Google Scholar]
- 15.Gielen E., Smisdom N., Ameloot M. Measuring diffusion of lipid-like probes in artificial and natural membranes by raster image correlation spectroscopy (RICS): use of a commercial laser-scanning microscope with analog detection. Langmuir. 2009;25:5209–5218. doi: 10.1021/la8040538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brewer J., Bloksgaard M., Bagatolli L.A. Spatially resolved two-color diffusion measurements in human skin applied to transdermal liposome penetration. J. Invest. Dermatol. 2013;133:1260–1268. doi: 10.1038/jid.2012.461. [DOI] [PubMed] [Google Scholar]
- 17.Petersen N.O. Scanning fluorescence correlation spectroscopy. I. Theory and simulation of aggregation measurements. Biophys. J. 1986;49:809–815. doi: 10.1016/S0006-3495(86)83709-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Berland K.M., So P.T., Gratton E. Scanning two-photon fluctuation correlation spectroscopy: particle counting measurements for detection of molecular aggregation. Biophys. J. 1996;71:410–420. doi: 10.1016/S0006-3495(96)79242-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kannan B., Guo L., Wohland T. Spatially resolved total internal reflection fluorescence correlation microscopy using an electron multiplying charge-coupled device camera. Anal. Chem. 2007;79:4463–4470. doi: 10.1021/ac0624546. [DOI] [PubMed] [Google Scholar]
- 20.Wohland T., Shi X., Stelzer E.H. Single plane illumination fluorescence correlation spectroscopy (SPIM-FCS) probes inhomogeneous three-dimensional environments. Opt. Express. 2010;18:10627–10641. doi: 10.1364/OE.18.010627. [DOI] [PubMed] [Google Scholar]
- 21.Hendrix J., Baumgärtel V., Lamb D.C. Live-cell observation of cytosolic HIV-1 assembly onset reveals RNA-interacting Gag oligomers. J. Cell Biol. 2015;210:629–646. doi: 10.1083/jcb.201504006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Digman M.A., Dalal R., Gratton E. Mapping the number of molecules and brightness in the laser scanning microscope. Biophys. J. 2008;94:2320–2332. doi: 10.1529/biophysj.107.114645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Leutenegger M., Lasser T., Robelek R. Imaging of G protein-coupled receptors in solid-supported planar lipid membranes. Biointerphases. 2008;3:FA136. doi: 10.1116/1.3054189. [DOI] [PubMed] [Google Scholar]
- 24.Chen Y., Müller J.D., Gratton E. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 1999;77:553–567. doi: 10.1016/S0006-3495(99)76912-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hendrix J., Gijsbers R., Engelborghs Y. The transcriptional co-activator LEDGF/p75 displays a dynamic scan-and-lock mechanism for chromatin tethering. Nucleic Acids Res. 2011;39:1310–1325. doi: 10.1093/nar/gkq933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.De Keersmaecker H., Fron E., Mizuno H. Photoconvertible behavior of LSSmOrange applicable for single emission band optical highlighting. Biophys. J. 2016;111:1014–1025. doi: 10.1016/j.bpj.2016.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dalal R.B., Digman M.A., Gratton E. Determination of particle number and brightness using a laser scanning confocal microscope operating in the analog mode. Microsc. Res. Tech. 2008;71:69–81. doi: 10.1002/jemt.20526. [DOI] [PubMed] [Google Scholar]
- 28.Ossato G., Digman M.A., Gratton E. A two-step path to inclusion formation of huntingtin peptides revealed by number and brightness analysis. Biophys. J. 2010;98:3078–3085. doi: 10.1016/j.bpj.2010.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zacharias D.A., Violin J.D., Tsien R.Y. Partitioning of lipid-modified monomeric GFPs into membrane microdomains of live cells. Science. 2002;296:913–916. doi: 10.1126/science.1068539. [DOI] [PubMed] [Google Scholar]
- 30.Fäcke M., Janetzko A., Kräusslich H.G. A large deletion in the matrix domain of the human immunodeficiency virus gag gene redirects virus particle assembly from the plasma membrane to the endoplasmic reticulum. J. Virol. 1993;67:4972–4980. doi: 10.1128/jvi.67.8.4972-4980.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kadiu I., Gendelman H.E. Macrophage bridging conduit trafficking of HIV-1 through the endoplasmic reticulum and Golgi network. J. Proteome Res. 2011;10:3225–3238. doi: 10.1021/pr200262q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Torrano A.A., Blechinger J., Bräuchle C. A fast analysis method to quantify nanoparticle uptake on a single cell level. Nanomedicine (Lond.) 2013;8:1815–1828. doi: 10.2217/nnm.12.178. [DOI] [PubMed] [Google Scholar]
- 33.Hedde P.N., Dörlich R.M., Nienhaus G.U. Stimulated emission depletion-based raster image correlation spectroscopy reveals biomolecular dynamics in live cells. Nat. Commun. 2013;4:2093. doi: 10.1038/ncomms3093. [DOI] [PubMed] [Google Scholar]
- 34.Böhmer M., Wahl M., Enderlein J. Time-resolved fluorescence correlation spectroscopy. Chem. Phys. Lett. 2002;353:439–445. [Google Scholar]
- 35.Benda A., Kapusta P., Gaus K. Fluorescence spectral correlation spectroscopy (FSCS) for probes with highly overlapping emission spectra. Opt. Express. 2014;22:2973–2988. doi: 10.1364/OE.22.002973. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.