Data-driven identification of prognostic tumor subpopulations using spatially mapped t-SNE of mass spectrometry imaging data

Significance

Mass spectrometry imaging provides untargeted spatiomolecular information necessary to uncover molecular intratumor heterogeneity. The challenge has been to identify those tumor subpopulations that drive patient outcomes within the highly complex datasets (hyperdimensional data, intratumor heterogeneity, and patient variation). Here we report an automatic, unbiased pipeline to nonlinearly map the hyperdimensional data into a 3D space, and identify molecularly distinct, clinically relevant tumor subpopulations. We demonstrate this pipeline’s ability to uncover subpopulations statistically associated with patient survival in primary tumors of gastric cancer and with metastasis in primary tumors of breast cancer.

Abstract

The identification of tumor subpopulations that adversely affect patient outcomes is essential for a more targeted investigation into how tumors develop detrimental phenotypes, as well as for personalized therapy. Mass spectrometry imaging has demonstrated the ability to uncover molecular intratumor heterogeneity. The challenge has been to conduct an objective analysis of the resulting data to identify those tumor subpopulations that affect patient outcome. Here we introduce spatially mapped t-distributed stochastic neighbor embedding (t-SNE), a nonlinear visualization of the data that is able to better resolve the biomolecular intratumor heterogeneity. In an unbiased manner, t-SNE can uncover tumor subpopulations that are statistically linked to patient survival in gastric cancer and metastasis status in primary tumors of breast cancer.

Mass spectrometry imaging (MSI) is a technology that simultaneously provides the spatial distribution of hundreds of biomolecules directly from tissue (1, 2). The two most common techniques, matrix-assisted laser desorption and desorption electrospray ionization, lead to minimal loss of histological information. Accordingly, the same tissue section can be histologically assessed and registered to the MSI dataset. In this manner, the mass spectral signatures of specific cell types or histopathological entities (e.g., tumor cells) can be extracted from the often highly heterogeneous tissues encountered in patient tumors (3). This high cellular specificity is behind the increasing popularity of MSI in cancer research and its proven ability to identify diagnostic and prognostic biomarkers (4).

There is growing awareness that MSI also can be used to annotate tissues based on the local mass spectrometry profiles and thereby differentiate tissues/regions that are not histologically distinct. Deininger et al. (5) were the first to report that MSI may reveal the biomolecular intratumor heterogeneity associated with a tumor’s clonal development. A hierarchical cluster analysis of the MSI data revealed a patchwork of molecularly distinct regions, which were postulated to reflect the tumor’s clonal evolution. It was recently demonstrated that such an approach, using multivariate analysis of the MSI data to identify regions with distinct mass spectral signatures and then linking these molecularly distinct regions to patient outcome, enables the identification of tumor subpopulations that are statistically associated with poor survival and tumor metastasis (6).

All methods used to date for revealing intratumor heterogeneity have been linear dimensionality-reduction techniques, but this linearity constraint focuses the results on the global characteristics of the data space at the expense of finer details (7). Accordingly, linear methods might not be sensitive to the subtle changes expected to demarcate the clonal progression of tumors, in which the molecular differences between nearly sequential subpopulations may be minor.

Nonlinear multivariate methods can preserve both local detail and the global data structure in a lower-dimensional representation by emphasizing similarities between data points. A technique known as t-distributed stochastic neighbor embedding (t-SNE) has rapidly established itself as a method of choice for summarizing high-dimensionality datasets owing to its ability to overcome the “crowding problem,” in which some of the higher-dimensional data similarities cannot be faithfully represented in a single map (7). t-SNE has been applied to high-dimensionality imaging data and has been shown to outperform other dimensionality-reduction techniques in several life-science applications. Mahfouz et al. (8) used it to visualize the spatial organization of gene expression across the mammalian brain. Ji (9) used it to study the relationship between gene expression and neuroanatomy in the developing mouse brain, demonstrating that the developmental neuroanatomy is preserved in transcriptome data. Fonville et al. (10) introduced t-SNE to the MSI field, demonstrating its superiority over linear multivariate methods for demarcating regions of tissues with different mass spectral signatures.

The foregoing examples testify to the ability of t-SNE to summarize the relationships among the molecular signatures from different subpopulations. Here we introduce a method, known as spatially mapped t-SNE, to automatically highlight the molecular intratumor heterogeneity revealed by MSI, and demonstrate that the different subpopulations can be statistically associated with different clinical outcomes. The key components of the method are (i) nonlinear dimensionality reduction using t-SNE, using the Barnes–Hut–SNE implementation for faster analysis of large, high-dimensionality datasets (11); (ii) visualization of the molecular intratumor heterogeneity revealed by the t-SNE embedding; and (iii) unbiased, image-driven clustering of the t-SNE maps to reveal distinct molecular tumor subpopulations.

In this paper, we report an automatic data-driven approach to reveal the intratumor heterogeneity of tumor tissue samples detected by MSI (SI Appendix, Materials and Methods). We applied this method to MSI datasets of tissue samples from 63 patients with gastric cancer and 32 patients with breast cancer after virtual microdissection, to focus the analysis on the MSI data of tumor areas. Linking the t-SNE clusters to the clinical outcomes of the patients revealed the subpopulations associated with survival and metastatic status.

Results

t-SNE Visualizes Molecular Tumor Heterogeneity in a Single Map.

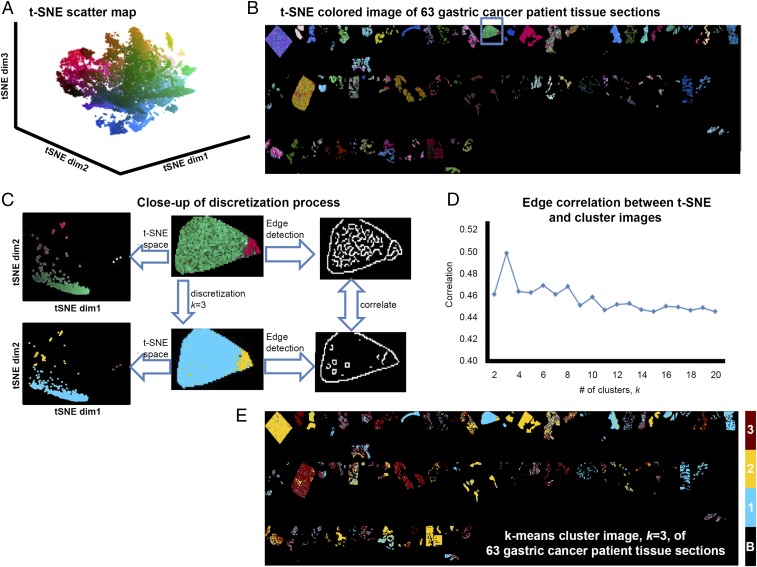
The t-SNE map of the gastric cancer dataset (Fig. 1A) represents the intertumor and intratumor heterogeneity within the tumor-specific MSI data of the entire 63-patient cohort. To illustrate this, SI Appendix, Fig. S1 shows scatterplots of the first and third t-SNE dimensions; A and B highlight three patient samples whose MSI datasets exhibit high intratumor heterogeneity, with data points scattered throughout the t-SNE data space, whereas C and D show three patient samples with lower intratumor heterogeneity, resulting in samples lying close to each other in the t-SNE map.

Fig. 1.

Nonlinear clustering of tumor cell-specific MSI data from 63 patients with gastric cancer. (A) The t-SNE scatterplot reveals clear structural separations based on molecular heterogeneity. (B) In the t-SNE image, each pixel is colored according to its location in the 3D t-SNE space using L*a*b* color coordinates, revealing a patchwork of subpopulations throughout the tumors. (C) Illustration of the discretization process of the spatially mapped t-SNE. (Upper) The molecularly distinct regions found by t-SNE are separated in the t-SNE space, yielding transitional boundaries in the image that can be highlighted using the Canny edge detector. (Lower) The same image after discretization (clustering) and Canny edge detection-based demarcation of cluster boundaries. (D) Pearson correlation metric of the edge images of the t-SNE and k-clustered images is then used to determine the discrete representation with the greatest correlation, here k = 3. (E) The k = 3 discrete approximation of the 63-tumor sample t-SNE image.

Spatially Mapped t-SNE Identifies Tumor Subpopulations Associated with Survival in Gastric Cancer.

To assess whether the structure revealed by t-SNE could be linked to clinical outcome, and thereby identify phenotypic tumor subpopulations, we clustered the t-SNE dataspace. First, we tested the ACCENSE algorithm (12), which is a density-based analysis of the data points in the t-SNE space to automatically locate clusters. The large number of clusters found by ACCENSE (more than 20) (SI Appendix, Fig. S2), undermined the ability to identify phenotypic subpopulations with statistical significance, because the patients were divided between too many groups. This result reflects the fact that t-SNE preserves the local structure of the data, and no information is used to help it differentiate between local differences due to different clones, different patient samples, or any measurement bias.

Consequently, we developed an alternative approach that exploits the local image structure of the MSI data. We hypothesized that edges in MSI data are natural boundaries of molecularly distinct subpopulations. To investigate this, we converted the 3D t-SNE space to a L*a*b color space (i.e., t-SNE coordinates become color coordinates) and colored each pixel’s data point using these laboratory color space coordinates. The resulting t-SNE image (Fig. 1B) clearly reveals the spatial structure of the molecularly distinct subpopulations.

We next clustered the t-SNE map. A bisecting k-means analysis (13) of the t-SNE data was applied with k ranging from 2 to 20, and k-means images were created by labeling each pixel according to its class label. The optimum number of clusters was defined as that in which the k-means image most closely resembled the t-SNE image. The similarity between the t-SNE image and the k-means images was computed by applying a Canny edge detector (14) to both images and computing their edge correlation (SI Appendix, Materials and Methods). Fig. 1C illustrates the clustering process in one of the gastric cancer tissue samples. The edge correlations between the t-SNE image and the corresponding k-means images for 2 ≤ k ≤ 20 are given in Fig. 1D, showing a maximum at k = 3. Fig. 1E shows the k-means image for k = 3, demonstrating the distribution of the molecularly distinct tumor subpopulations in the 63 patient tissue samples.

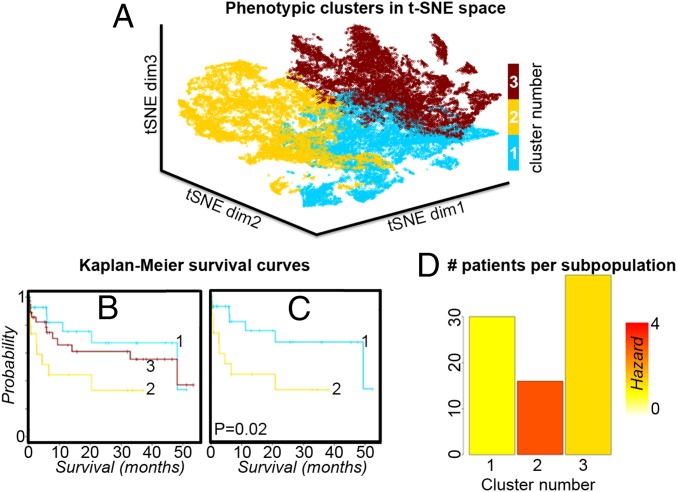
We then investigated the clinical relevance of the tumor subpopulations revealed by the spatially mapped t-SNE method by examining their association with patient survival. Each patient tissue contained one or more subpopulations. The patient survival data were assigned to a subpopulation only if it contributed more than would be possible by chance alone (i.e., >1/k × 100% of pixels). Fig. 2 shows Kaplan–Meier survival curves for the three subpopulations identified by the spatially mapped t-SNE method. There is a significant difference in survival between the two subpopulations encompassed by clusters one and two. The distribution of patients contributing to each of these subpopulations is given in Fig. 2D as a bar plot in which the bars are colored according to their Cox hazard ratio. The robustness of these findings with respect to the number of subpopulations is investigated in SI Appendix, Fig. S3, which compares the results for the optimal k = 3 with those obtained for the second- and third-ranked k values. The survival analysis data for all subpopulations is available in SI Appendix, Fig. S4, and P values for all pairwise comparisons of tumor subpopulations are provided in SI Appendix, Table S3.

Fig. 2.

(A) Clustering the t-SNE scatterplot using the highest-ranked value of k for the gastric cancer MSI data; k = 3. (B) Kaplan–Meier survival analysis shows the survival distribution for each of the clusters (subpopulations). (C) There are significant differences in survival between clusters 1 and 2; highlighting these clusters in the t-SNE scatterplot in A shows that they are from distinct regions of the t-SNE space. (D) The number of patients contributing to each of the clusters is shown as a bar plot in which the bar is colored according to the Cox hazard ratio.

Spatially Mapped t-SNE Identifies Subpopulations Associated with Metastasis in Breast Cancer.

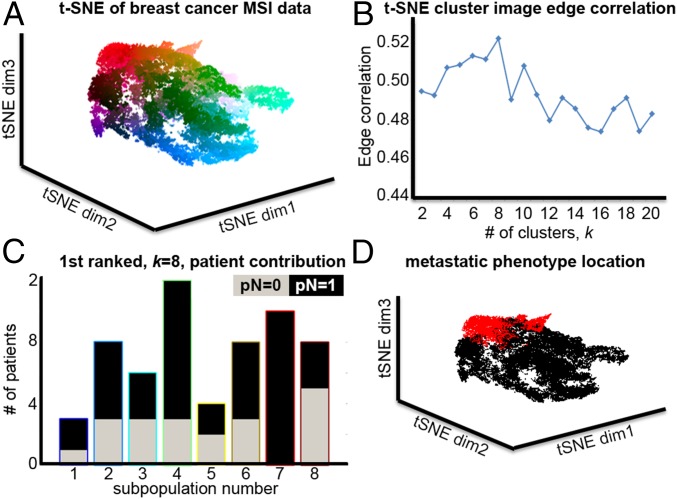
We applied the spatially mapped t-SNE method to a breast cancer dataset of primary tumors from 32 patients, of whom 21 had lymph node metastasis (pN = 1) and 11 were metastasis-free (pN = 0). Again the MSI datasets were first subjected to virtual microdissection to focus the analysis on tumor regions only. Fig. 3A shows the breast cancer MSI data in t-SNE space, with the data points colored based on their location. The spatial organization of mass spectral similarities, local and global, again produces a highly structured data space that reflects intratumor heterogeneity and patient variation. The edge correlations between the t-SNE image and the k-means images, for 2 ≤ k ≤ 20, are shown in Fig. 3B, which peaks at k = 8. The t-SNE image and the k-means image for k = 8 are shown in SI Appendix, Fig. S5 and again reveal spatially coherent and molecularly distinct subpopulations in the patient tissues.

Fig. 3.

(A) Nonlinear visualization of tumor cell-specific MSI data from 32 patients with breast cancer using t-SNE. (B) An edge-based image correlation is then used to determine the discrete representation with the highest correlation, here k = 8. (C) Visualization of the metastasis-associated subpopulations in the breast cancer MSI data as revealed by t-SNE shows the contributions of metastatic (black) and nonmetastatic patients (gray) to the eight clusters in a grouped histogram. A statistical analysis found cluster 7 to be exclusively associated with a metastatic phenotype. (D) This subpopulation, highlighted in red in the t-SNE scatterplot, occupies a distinct region of the t-SNE space.

Fig. 3C shows the contribution of metastasized and nonmetastasized patients to the eight subpopulations. It can be seen that subpopulation 7 has an exclusively metastatic phenotype. The data points represented by subpopulation 7 are highlighted in red in the t-SNE plot shown in Fig. 3D. SI Appendix, Fig. S6 shows the same bar charts and t-SNE plots for k = 7 and k = 6, which are the k-means images with the second- and third-highest gradient correlation with the t-SNE image and in which subpopulation 6 also has an exclusively metastatic phenotype. In each case, the cluster of data points with the metastatic phenotype is localized in the same distinct region of the t-SNE space (for k = 6, 7, and 8), demonstrating the efficiency of t-SNE in finding molecular signatures that group together patients with similar clinical outcomes.

The foregoing results demonstrate that the molecular signatures of tumor subpopulations with distinct phenotypes cluster together in the t-SNE space, that the clusters can be captured using the spatially mapped t-SNE methodology, and that the process is generalizable to other cancers and clinical phenotypes.

Spatially Mapped t-SNE–Based Prediction of Tumor Subpopulations and Patient Outcomes.

We next investigated whether we could build a pixel classifier that can assign clinical outcomes to previously unseen MSI data. In brief, we used significance analysis of microarrays (SAM) (15) to determine which protein ions can differentiate between the spatially mapped t-SNE clusters (false discovery rate, 0.001). Using only those m/z values, we built a k-nearest-neighbor (kNN; k = 5) classifier (16). The pixel labels for the classifier training were those obtained from the spatially mapped t-SNE clustering along with their clinical association (e.g., poor-survival subpopulation). To train and cross-validate this kNN pixel classifier, we performed an unbiased cross-validation experiment, hereinafter referred to as leave one patient out (LOPO), a schematic of which is shown in SI Appendix, Fig. S9.

For each LOPO iteration, we set one patient apart, executed the foregoing procedure on the remaining patients (spatially mapped t-SNE, clustering, phenotype association, SAM analysis, kNN classification), and then classified the pixels in the MSI data of the withheld patient. We repeated this process for all patients, giving an unbiased error of the pixel-based classifier. Prediction results are reported in Dataset S1.

We found that the breast cancer subpopulation associated with lymph node metastasis contributed between 0% and 98% of the withheld patient’s primary tumors, and the gastric cancer subpopulation associated with poor survival contributed between 0 and 95%. In the absence of a ground truth of the intratumor heterogeneity of each patient sample with which the results of the pixel classification could be compared, we sought to use the (known) patient outcomes for the validation. It is currently unknown what proportion of a tumor should be represented by a phenotypic subpopulation for it to manifest itself in the clinic (e.g., different patient survival/lymph node metastasis). Thus, we tested a simple patient-based classifier; if a tissue has more than t1 pixels of the poor-outcome subpopulation and less than t2 pixels of the good-outcome subpopulation, then we classify the patient as poor outcome (and vice versa).

For predicting metastasis in breast cancer tissue, we used Youden’s index (17) to set these values (i.e., t1 = 2% and t2 = 100%). Using these thresholds and predictions from our pixel classifier, we obtained 75% correct classifications (19 metastasized and 5 nonmetastasized), which is significant according to Fisher’s exact test (SI Appendix, Table S4). Note that the evaluations were performed on the patients set apart to ensure unbiased estimates. For predicting poor survival in gastric cancer, we used t1 = 10% and t2 = 50% for the patient-based classifier. These predictions resulted in significant survival time differences between the predicted patient groups, as shown by Kaplan–Meier survival analysis and the log-rank test (P = 0.0104) (SI Appendix, Fig. S10).

Spatially Mapped t-SNE Enables Identification of Discriminative m/z Features.

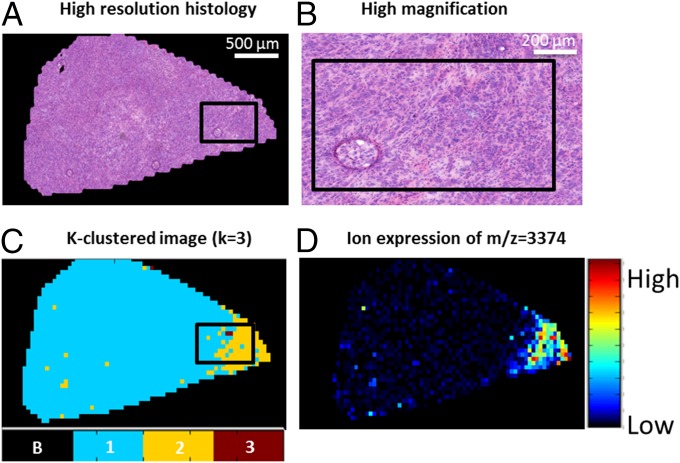
In the foregoing classification experiment, we performed the SAM analyses to determine which protein ions differentiated the subpopulations. In these analyses, a number of protein ions were consistently found (>80% of LOPO runs) to characterize the phenotypic subpopulation for gastric cancer survival—m/z = [3,374, 3,409, 3,445, 3,670, 3,711, 4,967, and 14,021] (SI Appendix, Fig. S11A)—and for breast cancer lymph node metastasis—m/z = [4,965, 4,999, 5,067, 5,171, 6,650, 6,980, 7,009, 9,265] (SI Appendix, Fig. S12A). This provides the opportunity to detect the different subpopulations based on only a few targeted protein ions (instead of analyzing the full mass spectrometry spectrum). In SI Appendix, Figs. S11B and S12B are t-SNE maps in which the data are colored for each of these m/z features for gastric cancer and breast cancer, respectively. The figures confirm that these protein ions demarcate data points in specific areas of the t-SNE map. Of note, those features that were detected in all LOPO runs had the highest differential expression for the detrimental subpopulation; for gastric cancer, this was m/z = 3,374 and 3,445 (Fig. 4A), and for breast cancer, it was m/z = 4,965 and 4,999 (Fig. 4B). Close examination of the MSI data shows that the spatial distributions of these ions coincided with those of the phenotypic subpopulations revealed by the t-SNE clustering (Fig. 5). Fig. 5 also presents the histological image of the tissue section, to demonstrate that although the subpopulations are molecularly and phenotypically distinct, they are histologically identical. Similar results were found for different patients and protein ions in both the breast cancer and gastric cancer cohorts (SI Appendix, Figs. S13 and S14).

Fig. 4.

(A) A 3D t-SNE map of the gastric cancer MSI dataset (Fig. 1A) color-coded with the intensities of m/z 3,374 and 3,445, protein ions detected in all LOPO runs, with localized overexpression in the yellow, poor-survival subpopulation (Fig. 2A). (B) A 3D t-SNE map of the breast cancer MSI dataset (SI Appendix, Fig. S5), color-coded with the intensities of m/z 4,965 and 4,999, protein ions detected in all LOPO runs, and with localized underexpression in the exclusively metastatic subpopulation (Fig. 3D).

Fig. 5.

Comparison of tissue histology and MSI of α-defensin protein ion detected at m/z 3,374. (A) Histological image of a tissue section from a patient with gastric cancer. (B) Higher-magnification image of a selected region in A showing uniform histology. (C) Close-up of a tissue section in the k = 3 discrete approximation of the 63-tumor sample t-SNE image, showing the presence of the poor survival subpopulation (cluster number 2, yellow). (D) MSI of the α-defensin protein ion detected at m/z = 3,374 showing heterogeneity within the histologically uniform tissue, in which it is highly expressed in the poor-survival subpopulation.

Discussion

Identification of the tumor subpopulations that impact patient outcomes is essential for better characterizing the molecular changes that accompany tumor development and for optimizing patient management (18, 19). MSI has several key characteristics that make it well suited to this task; it is an untargeted analysis that can simultaneously analyze hundreds of molecular ions, it can be directly applied to tissue sections, it is inexpensive, and it is fast. Several previous studies have reported MSI’s ability to uncover tumor subpopulations in histologically identical regions of tumor tissue (5, 20, 21). Here we have used dimensionality reduction based on t-SNE followed by bisecting k-means clustering to automatically segment the tumor-specific MSI data from a patient series into an optimum number of subpopulations. We used t-SNE because it is a nonlinear mapping technique that preserves the local and global similarity structure of the dataspace in a lower-dimensionality representation. t-SNE has previously been shown to be a superior representation for the spatial organization of MSI and gene expression data (10). We reasoned that t-SNE’s nonlinear nature would also better equip it to distinguish the mass spectrometry differences between tumor subpopulations.

Mapping of the tumor-specific MSI data from patients with gastric and breast cancer into the lower-dimensional t-SNE space revealed structured 3D data spaces. The application of ACCENSE density-based partitioning (12) to the t-SNE map led to the detection of a large number of clusters, but the Kaplan–Maier curves lacked statistical significance (SI Appendix, Fig. S2B).

Given that the spatial organization of pixels is lost in the t-SNE map, and that neighboring pixels in the MSI data are more likely to constitute the same tumor subpopulation, we set out to cluster the t-SNE map using bisecting k-means clustering, with k optimized on spatial congruency. We chose bisecting k-means because it is insensitive to initial conditions, convergences to a global optimum, and scales better to large datasets because it has a linear time and memory complexity (13). To estimate the optimum number of clusters (subpopulations), we calculated the correlation between the t-SNE image and the k-means image. Because of the difficulty of comparing a continuous t-SNE image with a discrete k-means cluster image, and to focus the analysis on the borders between tumor subpopulations, we used an edge correlation function to compare the images. This technique is an established image analysis method for comparing continuous and discrete imaging modalities (22).

We previously reported a clinical data-driven approach for identifying phenotypic tumor subpopulations (6). This approach was based on the consensus of five different linear multivariate methods (20) to locate tumor subpopulations, but required the user to prespecify the number of subpopulations. The resulting cluster data were then compared with the clinical data to assess their statistical significance. Here we developed an MSI data-driven approach to determine the optimum number of subpopulations (even if those subpopulations are characterized by relatively minor differences in molecular profiles) and assess their clinical significance. We thus exploited the greater capacity of t-SNE to reveal heterogeneity in the MSI data, allowing automatic identification of subpopulations.

Of note, the t-SNE approach distinguishes the phenotypic subpopulations for patient survival in gastric cancer for k = 3, whereas our previously reported agreement analysis approach (6) begins to identify these differences only at significantly higher values of k (figure 4 in ref. 6). Furthermore, the prognostic signature reported and extensively validated here for gastric cancer involves more proteins; of the seven protein ions reported here, namely m/z = 3,374, 3,409, 3,445, 3,670, 3,711, 4,967, and 14,021, only m/z 3,445 (DEFA-1) and 14,021 (histone H2A) were reported previously. The lower separation power of the earlier linear multivariate methods may explain why the previously detected subpopulations had mixed contributions from nonphenotypic as well as phenotypic subpopulations. This would dilute any observable differences and thus limit the ability to identify protein ions associated with phenotype.

Using the spatially mapped t-SNE, we were able to build a pixel classifier and a patient-based classifier for outcome, which were able to demarcate the intratumor heterogeneity and predict patient survival (in gastric cancer) or metastasis status (in primary breast cancer). In all examples, the molecular and phenotypic intratumor heterogeneity was not apparent in the conventional histological images. This opens up much needed possibilities for assessing the clinical impact of intratumor heterogeneity and clonal evolution in cancer by, for example, using the pixel classification for spatially resolved sample selection for RNA sequencing of tumor subpopulations with different clinical phenotypes.

Concluding Remarks

Intratumor heterogeneity is a key factor in tumor progression, affecting patient outcomes and treatment. Tumor subpopulations can be histologically indistinguishable but still have molecular phenotypes that drive tumor progression and determine disease outcome (18, 23). The identification of these clinically relevant tumor subpopulations is of utmost importance for understanding cancer development and the management of cancer patients (24). Although localized genomic techniques have established branched evolution of tumors (25) and single-cell transcriptional heterogeneity (26), the cost and throughput of these techniques are prohibitive for large-scale multisite sequencing of patient tissues. The automated identification of phenotypic tumor subpopulations reported here will allow better targeting of these powerful genomic methods to those subpopulations that are statistically associated with patient outcomes.

Materials and Methods

Tumor-specific signatures obtained by protein matrix-assisted laser desorption MSI analysis of primary tumors of gastric cancer (n = 63) and breast cancer (n = 32) were nonlinearly mapped to a 3D space using t-SNE. Using the perceptually linear L*a*b color map to color each pixel according to its position in the t-SNE space, a t-SNE colored image can be obtained that depicts regions characterized by similar mass spectral profiles with similar colors. To segment the image into a discrete number of clusters, bisecting k-means and edge-correlation algorithms were applied. The resulting clusters, or tumor subpopulations, were then statistically compared with the patients’ clinical data (survival for gastric cancer and lymph node metastasis for breast cancer) to identify the subpopulations statistically associated with patient phenotype. LOPO pixel-based and patient-based classifiers were built to cross-validate the identification of tumor subpopulations and patient outcomes. Detailed descriptions of the clinical tissue samples, MSI experiments, data processing, technical validation, and algorithms are provided in SI Appendix, Materials and Methods. This study was approved by the Institutional Review Board and the Ethics Committee of the Faculty of Medicine of the Technische Universität München, with informed consent from all subjects and patients.