HPLC-based kinetics assay facilitates analysis of systems with multiple reaction products and thermal enzyme denaturation

Abstract

Glucosinolates are plant secondary metabolites abundant in Brassica vegetables that are substrates for the enzyme myrosinase, a thioglucoside hydrolase. Enzyme-mediated hydrolysis of glucosinolates forms several organic products, including isothiocyanates (ITCs) that have been explored for their beneficial effects in humans. Myrosinase has been shown to be tolerant of non-natural glucosinolates, such as 2,2-diphenylethyl glucosinolate, and can facilitate their conversion to non-natural ITCs, some of which are leads for drug development. An HPLC-based method capable of analyzing this transformation for non-natural systems has been described. This current study describes (1) the Michaelis–Menten characterization of 2,2-diphenyethyl glucosinolate and (2) a parallel evaluation of this analogue and the natural analogue glucotropaeolin to evaluate effects of pH and temperature on rates of hydrolysis and product(s) formed. Methods described in this study provide the ability to simultaneously and independently analyze the kinetics of multiple reaction components. An unintended outcome of this work was the development of a modified Lambert W(x) which includes a parameter to account for the thermal denaturation of enzyme. The results of this study demonstrate that the action of Sinapis alba myrosinase on natural and non-natural glucosinolates is consistent under the explored range of experimental conditions and in relation to previous accounts.

1. Introduction

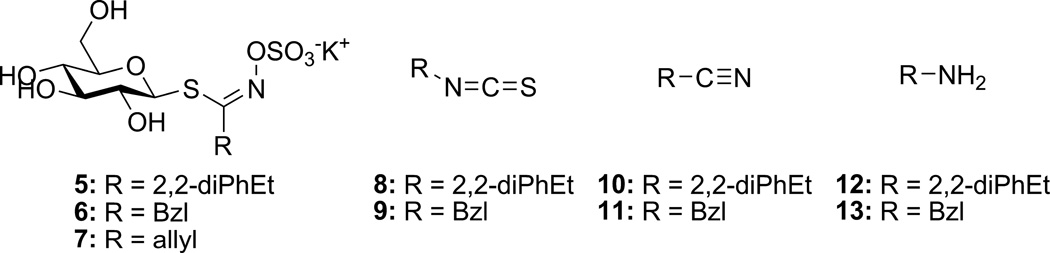
Organic isothiocyanates (ITCs, 2, Scheme 1) are a well-studied class of compounds with an array of documented biological applications, including anti-inflammatory [1,2,3,4,5], antioxidant [6,7,8,9], and antitumor effects [10,11,12,13,14]. Of note, consumption of many Brassica vegetables (e.g. broccoli, cauliflower, kale, cabbage) confers anti-cancer properties in part due to their high natural concentration of glucosinolates (1), β-thioglucoside-N-hydroxysulfate precursors of ITCs. Over 200 naturally-occurring variants of 1 have been discovered which vary in the aglycone sidechain (R) [15]. The enzyme myrosinase (β-thioglucoside glucohydrolase, EC 3.2.3.1) catalyzes hydrolysis of the thioglucosidic bond in 1 in a mechanism that follows Michaelis–Menten kinetics [16]. While ITCs are the principle hydrolysis product at physiological pH and temperature, nitriles (3) have been observed to form at acidic pH [17,18], and amines (4) can result when the electrophilic ITC is hydrolyzed by water to a carbamic acid that rapidly undergoes decarboxylation [17].

Scheme 1.

Myrosinase-catalyzed hydrolysis of glucosinolates and possible resultant organic products.

Although natural glucosinolates and their ITCs have been relatively well-described, fewer accounts have been made concerning non-natural analogues, those compounds bearing sidechains structures not observed in natural sources [19]. Screening efforts have identified non-natural ITC leads with promising activity against human disease [20,21,22,23]. These results have been aided by a key 2008 study which demonstrated that non-natural glucosinolates are substrates for myrosinase, and that these precursors can be quantitatively converted to non-natural ITCs by the enzyme [23]. However, the broader structural diversity of non-natural analogues challenged the traditional ultraviolet-visible (UV–Vis) spectrophotometric methods of monitoring this enzymatic method of unmasking bioactive ITCs [16]. In 2014, a novel HPLC approach for analyzing reaction kinetics was described and validated against the UV–Vis method; key advantages of the HPLC approach were the ability to chromatographically separate and simultaneously track analytes with diverse polarity/solubility profiles, such as 1 and 2 [19]. This methodology has more recently been expanded to LC–MS systems to aid in the evaluation of samples from complex mixtures and has broader implications as an analytical approach [24].

2,2-Diphenylethyl ITC (8) is one example of a non-natural analogue that demonstrates promise as an anticancer agent. Mutations to p53 are estimated to be present in about half of human cancers, and limit the ability of p53 to exert its normal function as a tumor suppressor [25]. Mutant p53 has also been implicated in promoting tumorigenesis through a gain of function mechanism [26]. A 2011 study identified 8 as a potent and selective inhibitor of mutant p53 [22]. This same ITC was also one of the three lead compounds identified in a 2008 evaluation of non-natural ITCs, where the authors noted its consistent, potent antiproliferative effects against an array of human cancer cell lines [23]. Importantly, this study demonstrated that the synthetic non-natural glucosinolates 5 was a substrate for myrosinase and, upon exposure to the enzyme, was converted to its analogous ITC 8 [23,27]. More recent efforts further demonstrate that non-natural ITCs can be generated in situ via the reaction of non-natural glucosinolates and myrosinase [19]. Together, this combined work supports the premise that non-natural ITCs and their glucosinolate prodrugs are viable targets for the rational design of novel anticancer agents, a field that has not been extensively explored.

Although non-natural glucosinolates are known substrates for myrosinase, the kinetic studies conducted to date have been focused on the goals of proof-of-principle [23] and validation of the general HPLC methodology [19]. A comprehensive evaluation of myrosinase toward non-natural substrates has not been conducted to demonstrate that these analogues mirror the outcome(s), tolerance, and mechanism exhibited by natural glucosinolates. Since myrosinase does not require any additional cofactors for complete function [28], the major parameters that affect its role as a catalyst are pH and temperature. Kinetic evaluation of 7 in unbuffered conditions demonstrated both time-dependence of increasing acidity and preferential formation of the nitrile product (3) at low pH [18]. Studies describing the pH-dependence of myrosinase catalytic activity on natural substrates have noted a maximum efficiency at pH 6.5 for enzyme isolated from Sinapis alba [29] and pH 6.5–8.5 for Carica papaya [30]. Similarly, thioglucohydrolases demonstrate an Arrhenius-type increase in the rate of catalysis of natural glucosinolates between 0–40 °C, an optimum temperat ure range between 40–55 °C, and complete thermal inactivation by 80 °C [30,31,32]. If the ca talytic mechanism of myrosinase on non-natural glucosinolate substrates parallels the mechanism for natural substrates, it would be expected that similar dependence patterns on pH, temperature, and their effects on the ratio of organic product distribution (e.g. 2–4) would be observed.

The underlying motivation for this study was to test the hypothesis that the myrosinase-catalyzed hydrolysis of non-natural glucosinolate 5 would mirror the parameters observed for natural glucosinolates. The validated HPLC approach is ideally suited for these enzymological studies, as it offers the possibility of simultaneously and independently evaluating glucosinolate and any resultant organic product(s), a feature which has broader methodological considerations and applications [19]. Initial rates (V₀) for glucosinolate hydrolysis and product formation would be obtained from nonlinear reaction progress curves fit with the Lambert W(x) [19,33]; these elucidated V₀ would provide explicit rate information, an advantage over many previous accounts which solely reported relative rates [31,32].

To test this hypothesis, two glucosinolates were selected as representative examples of natural and non-natural analogues. 2,2-Diphenylethyl glucosinolate (5) was a non-natural glucosinolate that has not yet been subject to complete kinetic characterization, whose resultant ITC (8) has potential utility as an anticancer agent [23]. Its inclusion was secondarily intended to provide greater understanding of the enzyme-catalyzed conversion of 5 to 8 toward future cellular studies directed at the use of 5 as a prodrug for 8. Glucotropaeolin (6) was a natural glucosinolate whose Michaelis–Menten and specific activity characterization has been previously described [19]; its inclusion would allow parallel evaluation and direct comparison of both natural and non-natural glucosinolate substrates in pH and temperature experiments. Through the implementation of reaction progress curves tracking each analyte, these studies would provide detailed information on the optimal conditions for both glucosinolate hydrolysis and formation of organic product(s). A similar enzymatic profile across natural and non-natural glucosinolates would support the hypothesis of a conserved catalytic mechanism and the general ability to utilize myrosinase as a means to generate non-natural ITCs.

Beyond the underlying experimental hypothesis, these studies would provide the opportunity to evaluate the general methodological applicability of using the reaction progress curve approach. More broadly, the capability to simultaneously analyze multiple reaction components using reaction progress curves would be useful methodology which has not been extensively described in the literature. Similarly, there have been no notable accounts on the use of reaction progress curve analysis with experiments conducted at either elevated temperatures or non-physiological pH. Consequently, it was plausible that the Lambert W(x) would no longer accurately model the system under these extreme conditions and that alterations to the model would need to be made to account for new features, such as thermal or chemical denaturation of the enzyme.

2. Materials and Methods

2.1. General Information

All reactions were carried out under nitrogen unless indicated otherwise. All reagents were obtained from available commercial sources and were used without further purification unless otherwise noted. The silica gel used in flash chromatography was 60 Å, 230–400 mesh. Analytical TLC was performed on Uniplate 250 µm silica gel plates with detection by UV light. NMR spectra were acquired on a JEOL ECS-400 400 MHz NMR spectrometer with multinuclear capability and 24-sample autosampler, with solvent as internal reference; the chemical shifts are reported in ppm, in δ units. Infrared spectra were acquired on a Nicolet Avatar FTIR. Ultraviolet-visible spectroscopy experiments were conducted on a Shimadzu UV-2450 spectrometer fitted with a TCC-240A temperature-controlled cell chamber. HPLC experiments were conducted using an Agilent 1200 system with a degasser, photodiode array detector, and temperature-controlled autosampler. High resolution mass spectroscopic data were obtained at the Mass Spectrometry & Analytical Proteomics Laboratory at the University of Kansas (Lawrence, KS). Regression analyses were completed using the GraphPad Prism 6 software suite.

2.2. Preparation and Characterization of ITCs and Glucosinolates

The detailed synthetic protocols and spectral characterization toward glucosinolate 5 and ITC 8 are described in Klingaman et. al. [34].

2.3. Calibration of Myrosinase Specific Activity

The specific activity of commercial Sinapis alba myrosinase (Sigma-Aldrich, T4528) was determined using the established method [16].

2.4. General HPLC Method

The general HPLC method was similar to the established procedure [19], with the following notable changes. The autosampler was maintained at 37 °C fo r most experiments; alternate temperatures were used for studies assessing the effect of variable temperature. Integration events were automated with the following features: tangent skim mode = standard; tail peak skim height ratio = 0.00; front peak skim height ratio = 0.00; skim valley ratio = 20.00; baseline correction = classical; peak to valley ratio = 500.00; slope sensitivity = 5; peak width = 0.05; area reject = 5; height reject = 1; shoulders = off.

2.5. HPLC Kinetics Assay

Evaluations of reactions using HPLC were conducted similar to the established procedure [19], with the following notable changes. Standardization of nitriles 10–11 and amines 12–13 (1000 µM in Buffer A, 37 °C) was conducted similar to the procedure used for ITCs. Chromatograms were independently analyzed at multiple wavelengths (5/8/10/12: 220, 227, 235, 241 nm; 6/9: 227, 235, 241 nm; 11/13: 210 nm).

Each hydrolysis reaction contained glucosinolate (1000–31.3 µM), myrosinase (5: 8.83 or 7.06 U; 6: 1.77 U) and Buffer A, with a total volume of 1.000 ml [19]. Variable pH and temperature experiments were conducted similarly, substituting either 0.1 M phosphate buffer (pH range 2–10) or the reaction incubation temperature (range 9.0–85.0 °C), as appropriate. Re action pH was tested before and after each hydrolysis reaction and temperature was monitored continuously to ensure integrity. Reaction time was measured from addition of myrosinase to the times of injection (10 µl), which occurred at 0.85 min, 15.67 min, 30.50 min, 45.33 min, 60.17 min, and 75.00 min.

Glucosinolate ([Gluc]_t), ITC ([ITC]_t), and nitrile ([nitrile]_t) reaction progress curves were fitted to a temporal closed-form solution of the Michaelis–Menten equation incorporating the Lambert W(x) function (M. Goličnik, Eq. 11) [19,33]. Initial variable values for nonlinear regression were [Gluc]₀ = 500 µM, K_m = 1.0 µM, and V_max = 8.0 µM min⁻¹. Variable pH and temperature studies used a modified version of the Lambert W(x), which included a term to account for potential first-order enzyme denaturation (Equation 1) [35]. Initial variable values for the modified nonlinear regression were [Gluc]₀ = 250 µM, K_m = 500 µM, V_max = 8.0 µM min⁻¹, and k_d = 1.0 × 10⁻⁷ min⁻¹, with the following constraints: [Gluc]₀ = 0–400 µM, K_m = 0– 1200 µM, V_max = 0–50 µM min⁻¹, and k_d = 0–0.1 min⁻¹. Velocities were normalized for the concentration of myrosinase (U ml⁻¹) to provide V₀ [Myr]⁻¹ data.

2.6. Michaelis-Menten Analysis

Velocity data generated by the HPLC method were fitted to the Michaelis–Menten equation using nonlinear regression in GraphPad Prism 6.0 [19,33]. Initial variable values for nonlinear regression were K_m = 1.0 µM, and V_max = 1.0 µM min⁻¹; K_m was restrained to ensure that the converged value was greater than zero. Best-fit values for K_m and V_max were reported with correlation coefficients (r², range = 0.9903 to 0.9934).

3. Results and Discussion

3.1. Myrosinase Standardization

The specific activity of myrosinase was determined spectrophotometrically at 227 nm using 7 as substrate [16,23]. To maintain consistency with past standardization methods, Δε₂₂₇ = 6458 M⁻¹ cm⁻¹ was used to calculate initial reaction velocities and one unit of myrosinase was defined as the amount of enzyme able to hydrolyze 1 nmol 7 per minute at pH 7.4 and 37 °C when the initial co ncentration of 7 ([7]₀) was 250 µM [16,19].

3.2. Michaelis–Menten Analysis and Specific Activity of 2,2-Diphenylethyl Glucosinolate

Kinetic analysis of 5 was achieved using the general reverse phase HPLC methodology that has been previously developed and validated [19,23]. Unlike previous studies which were limited to physiological conditions, the broader spectrum of experimental conditions required by later aspects of this work had the increased likelihood of producing organic products beyond solely the ITC 8. Consequently, standards were prepared for glucosinolate 5, ITC 8, nitrile 10, and amine 12, and it was found that the peaks for all four analytes were resolved using the described HPLC solvent gradient [19]. The increased nonpolar nature of the sidechain in 5 and related analogues versus those described in 2014 resulted in slightly increased retention times for both 5 (3.77 min) and 8 (5.58 min); the peaks for amine 12 (4.05 min) and nitrile 10 (5.07 min) were intermediate between these extremes and reflective of their relative polarity. Peak areas for each analyte were proportional to the amount injected (range = 12.50–0.25 nmol, Fig. 14 in Ref. [34]) and facilitated construction of standard curves (see Fig. 15 to 22 in Ref. [34]).

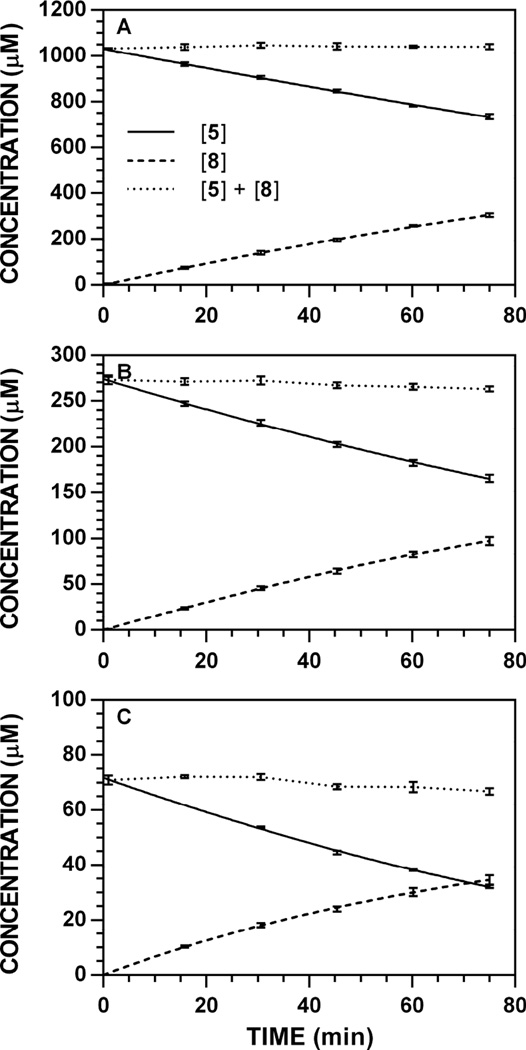
Hydrolysis reactions of 5 conducted at pH 7.4 and 37 °C produced non-linear reaction progress data for the glucosinolate ([Gluc]_t) and ITC ([ITC]_t) that were fit to the Lambert W(x), a closed-form solution of the Michaelis–Menten equation [19,33]. Initial rates (V₀) of glucosinolate hydrolysis (Δ[Gluc] Δt⁻¹) and ITC formation (Δ[ITC] Δt⁻¹) were obtained from their slopes at t = 0 min (see Tables 2 and 3 in Ref. [34]). Representative reaction progress curves monitored at 227 nm for the conversion of 5 to 8 are provided (Fig. 2); progress curves for all other concentration/wavelength combinations are available [34]. For this substrate, [ITC]_t data (Fig. 2, dashed lines) were fit using the full W(x) approximation, unlike previous accounts where a simplified approximation was necessary [19]. Overall, there was minimal loss of the detectable concentration balance ([Gluc] + [ITC], Fig. 2, dotted lines).

Figure 2.

Representative reaction progress curves for the conversion of 5 to 8 at pH 7.4 and 37 °C (227 nm). The concentration of myrosinase was constant (8.83 U ml⁻¹). HPLC chromatogram peak areas were used to determine [5] and [8] at each timepoint and the data (n = 3) was fitted to a reaction progress curve using nonlinear regression. The dotted line denotes the sum of [Gluc] + [ITC] at each timepoint and its slope represents ITC loss over time. Reaction progress curves for each [5]₀-wavelength combination are available [34]. A. [5]₀ = 1000 µM. B. [5]₀ = 250 µM. C. [5]₀ = 62.5 µM.

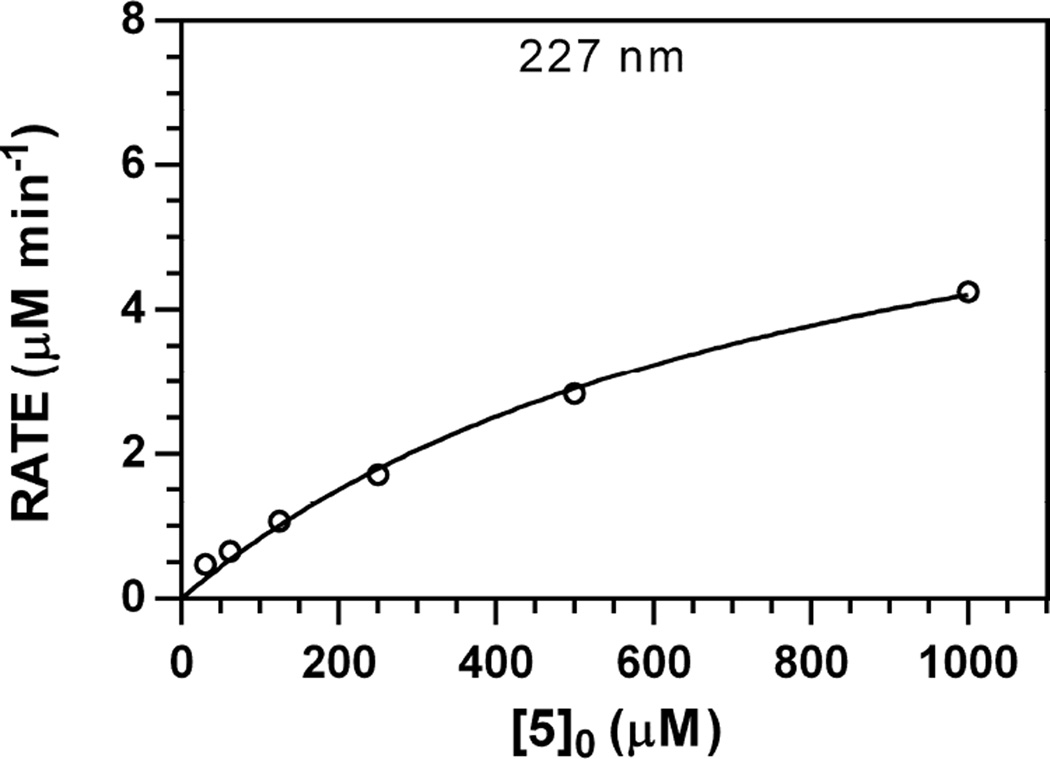
Michaelis–Menten curves were independently generated for each wavelength monitored [19]; a representative Michaelis–Menten plot for 5 (227 nm) is depicted in Fig. 3; analogous plots for other wavelengths are available [34]. Each Michaelis–Menten curve was fit with a high correlation (r² > 0.9903), and converged K_m and V_max values were consistent across independently monitored wavelengths, as evidenced by results from pooled wavelength data (r² = 0.9911, Table 1) [19]. The K_m range for 5 was 710–946 µM, higher than what has been determined for both 6 (83.9–105.2 µM) and 7 (142–233 µM) [19]; these results are consistent with the increased size of the aglycone in 5 and its resultant reduced affinity for the myrosinase active site. Similarly, the normalized maximum velocity (V_max [Myr]⁻¹) for 5 ranged from 0.78–0.93 min⁻¹, corresponding to 41–49% the relative maximum velocity of 7 (1.91 min⁻¹) [19].

Figure 3.

Representative Michaelis–Menten plot for V₀ vs. [5]₀ data (pH 7.4, 37 °C, 227 nm). The concentration of myrosinase was constant (8.83 U ml⁻¹). Plots for other wavelengths are available [34].

Table 1.

Michaelis–Menten kinetic constants for the action of Sinapis alba myrosinase on glucosinolate 5. Results were independently evaluated using the HPLC method, at multiple wavelengths; regression analysis of pooled wavelength data for each glucosinolate/ITC pair are also included. The Michaelis–Menten constant ± SE (K_m, µM) and maximum velocity ± SE (V_max, µM min⁻¹) are shown. Calculated V_max were normalized to the concentration of myrosinase ([Myr], U ml⁻¹) to yield normalized rate constants (min⁻¹) and relative % rates versus 7 (1.91 min⁻¹, 227 nm) [19].

Entry	λ (nm)	Km (µM)	Vmax (µM min−1)	Vmax [Myr]−1 (min−1)	Relative Rate (%)
5 to 8	220	710 ± 121	6.92 ± 0.64	0.78	41
	227	824 ± 152	7.66 ± 0.80	0.86	45
	235	741 ± 151	7.20 ± 0.81	0.81	42
	241	946 ± 224	8.29 ± 1.16	0.93	49
	Pooled	798 ± 71	7.48 ± 0.37	0.85	45

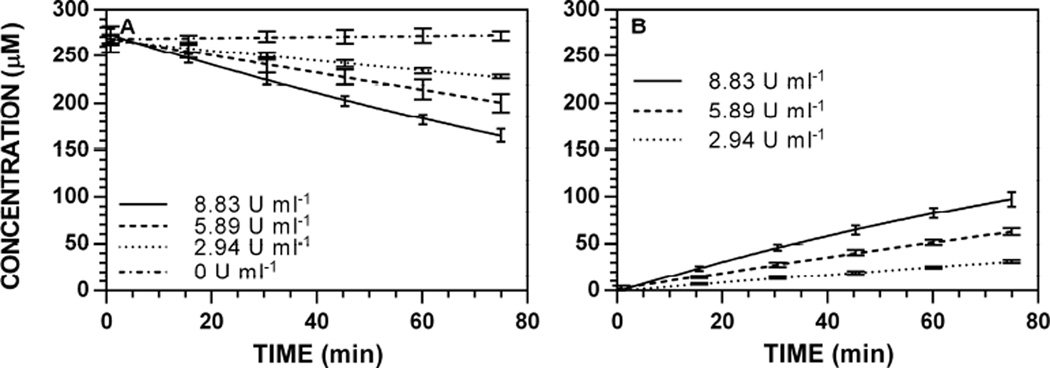
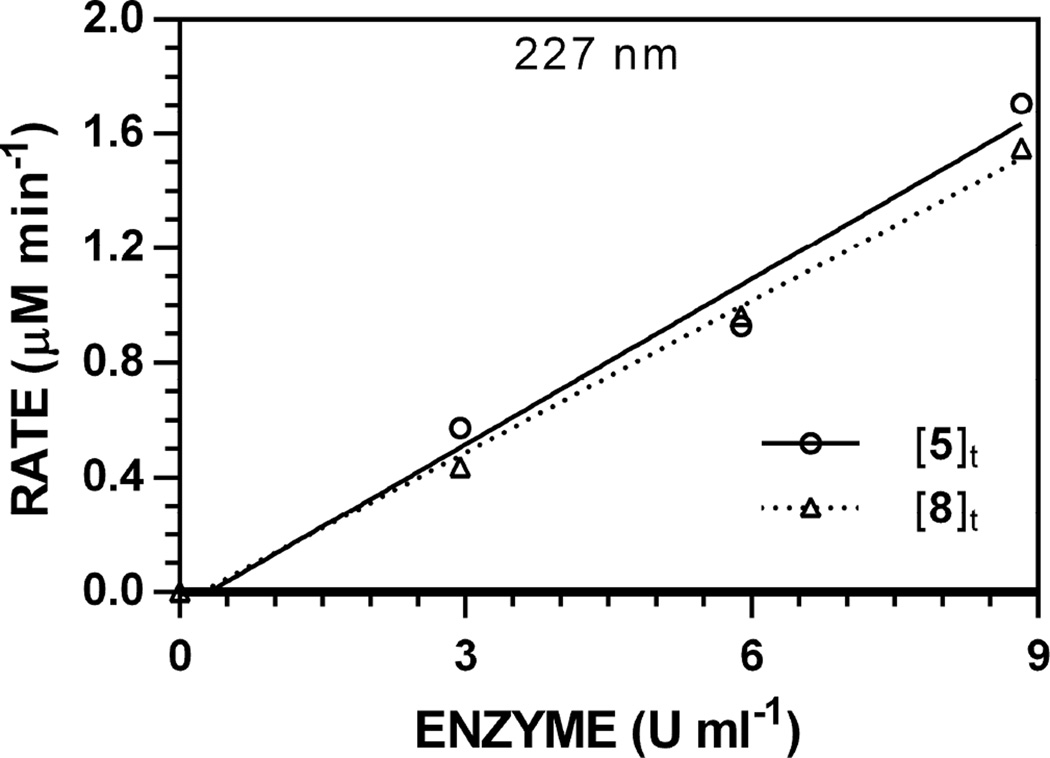
Hydrolysis reactions of 5 ([5]₀ = 250 µM) were conducted using variable [Myr] (100, 67, 33, and 0% of maximum, 8.88 U ml⁻¹) and used to generate reaction progress curves to validate the proportional relationship between [Myr] and V₀. Representative reaction progress curves at 227 nm are depicted in Fig. 4; progress curves for all other wavelengths are available [34]. Similar to previous accounts [19], detectable [Gluc]_t and [ITC]_t did not change over time in the absence of enzyme. The V₀ scaled linearly with [Myr] (r² > 0.9770) when monitoring both [Gluc]_t and [ITC]_t (Fig. 5); specific activity plots for all other wavelengths are available [34]. Specific activities of 5 versus the standard ([7]₀ = 250 µM, 0.94 min⁻¹) ranged from 19–20%.

Figure 4.

Enzyme-dependence on reaction progress curves for [5]_t and [8]_t at pH 7.4 and 37 °C ([5]₀ = 250 µM, 227 nm). HPLC chromatogram peak areas were used to determine [5] and [8] at each timepoint and the data (n = 3) was fitted to a reaction progress curve using nonlinear regression. Progress curves for other wavelengths are available [34]. A. [5]_t. B. [8]_t.

Figure 5.

Representative specific activity plot for the hydrolysis of 5 (pH 7.4, 37 °C, [5]₀ = 250 µM, 227 nm). HPLC data for [5]_t and [8]_t were independently tracked. Plots for other wavelengths are available [34].

3.3. Effects of Variable pH

The underlying hypothesis of this study was that the action of myrosinase on non-natural glucosinolates mirrors the process and outcome(s) that are observed when natural glucosinolates are substrates. Using our representative non-natural (5) and natural glucosinolate (6), experiments were conducted to evaluate the effects of the two major uncharacterized variables: pH and temperature. Although glucosinolate 6 and ITC 9 were earlier standardized using this HPLC approach [19], standards of nitrile 11 and amine 13 were prepared and evaluated in a similar fashion. Unfortunately, the UV-Vis spectra of analytes 11 and 13 did not strongly absorb light at 227, 235, and 241 nm, the three wavelengths previously used to characterize 6 and 9; ensuring a comparable dynamic range of analyte detection (12.50–0.25 nmol) necessitated evaluation at wavelengths below 220 nm. While both 200 and 210 nm were monitored for 11 and 13, data collected at 200 nm did not scale linearly with concentration (data not shown); it is believed that this resulted from incomplete baseline subtraction and significant absorption by the mixed solvent gradient.

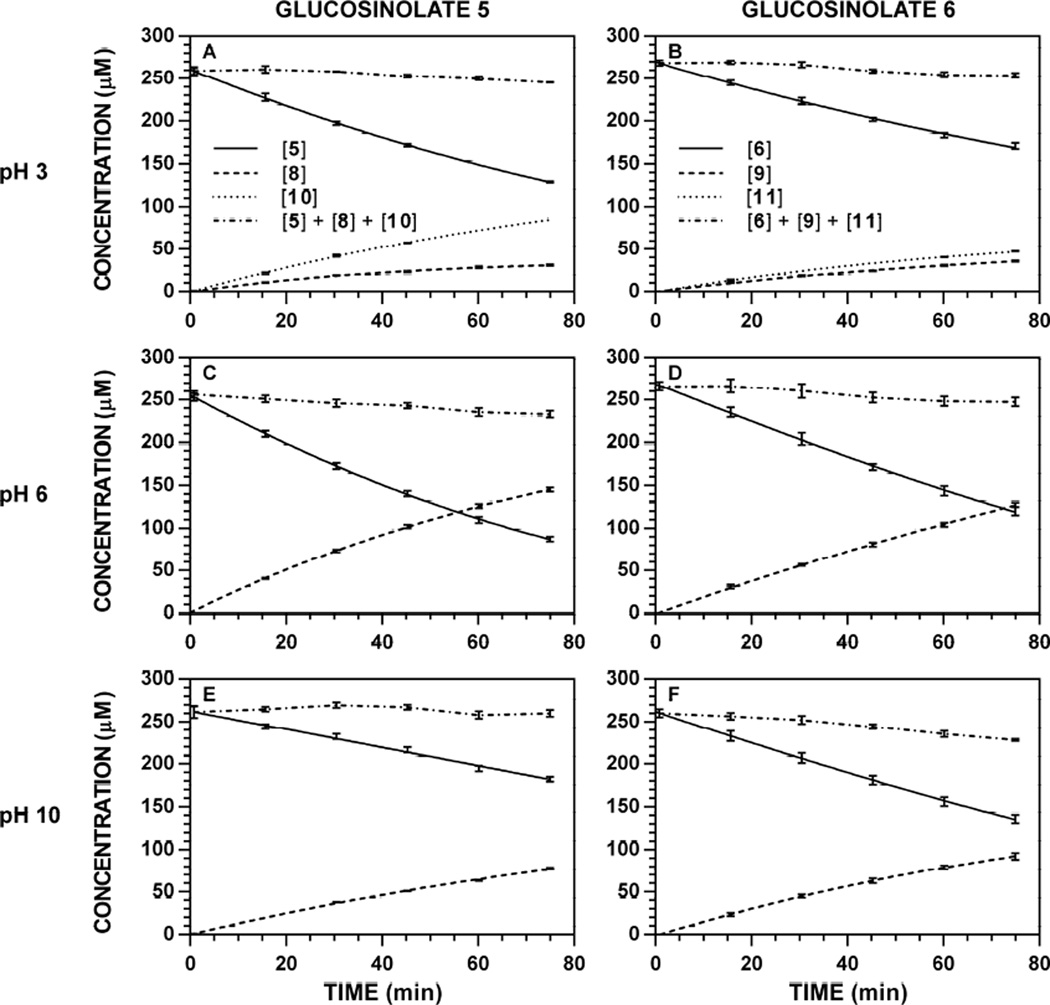
Hydrolysis reactions of 5 and 6 ([Gluc]₀ = 250 µM) were conducted at 37 °C in 0.1 M phosphate buffe r at variable pH (2–10). Since myrosinase-catalyzed hydrolyses conducted in unbuffered aqueous media demonstrate a significant change in pH over the course of the reaction [18], it was important to ensure that the buffer capacity of 0.1 M phosphate was not exceeded, especially for buffers adjusted to a pH distant from one of phosphate’s three pK_a values. None of the hydrolysis reactions conducted in various 0.1 M phosphate buffers demonstrated a change in pH over the course of the reaction. Especially at acidic pH, HPLC chromatograms indicated the time-dependent formation of the corresponding nitrile, which could be evaluated in addition to [Gluc]_t and [ITC]_t. Each set of concentration data was fit to the Lambert W(x), and used to calculate either its initial velocity of hydrolysis or initial velocity of formation. Representative reaction progress curves at 227 nm are depicted in Fig. 6; progress curves for all other wavelength-pH combinations are available [34]. For each pH evaluated, (1) the detectable concentration balance (Fig. 6, dotted lines) was consistent and (2) no change in [Gluc]_t was observed in the absence of myrosinase (data not shown), suggesting that the calculated velocities result solely from the action of myrosinase.

Figure 6.

Representative reaction progress curves for the hydrolysis of glucosinolates ([Gluc]₀ 250 µM) at variable pH and 37 °C. The concentration of myro sinase was constant for each substrate: 5, 8.83 U ml⁻¹; 6, 1.77 U ml⁻¹. HPLC chromatogram peak areas at specific wavelengths were used to determine [Gluc]_t, [ITC]_t, and [nitrile]_t at each timepoint, and the data (n = 3) was fitted to a reaction progress curve using nonlinear regression: 5, 227 nm; 8, 227 nm; 10, 227 nm; 6, 227 nm; 9, 227 nm; 11, 210 nm. The dotted line denotes the sum of [Gluc] + [ITC] + [nitrile] at each timepoint, and its slope represents product loss over time. Reaction progress curves for all other pH-wavelength combinations are available [34]. A. Hydrolysis of 5, pH 3.0. B. Hydrolysis of 6, pH 3.0. C. Hydrolysis of 5, pH 6.0. D. Hydrolysis of 6, pH 6.0. E. Hydrolysis of 5, pH 10.0. F. Hydrolysis of 6, pH 10.0.

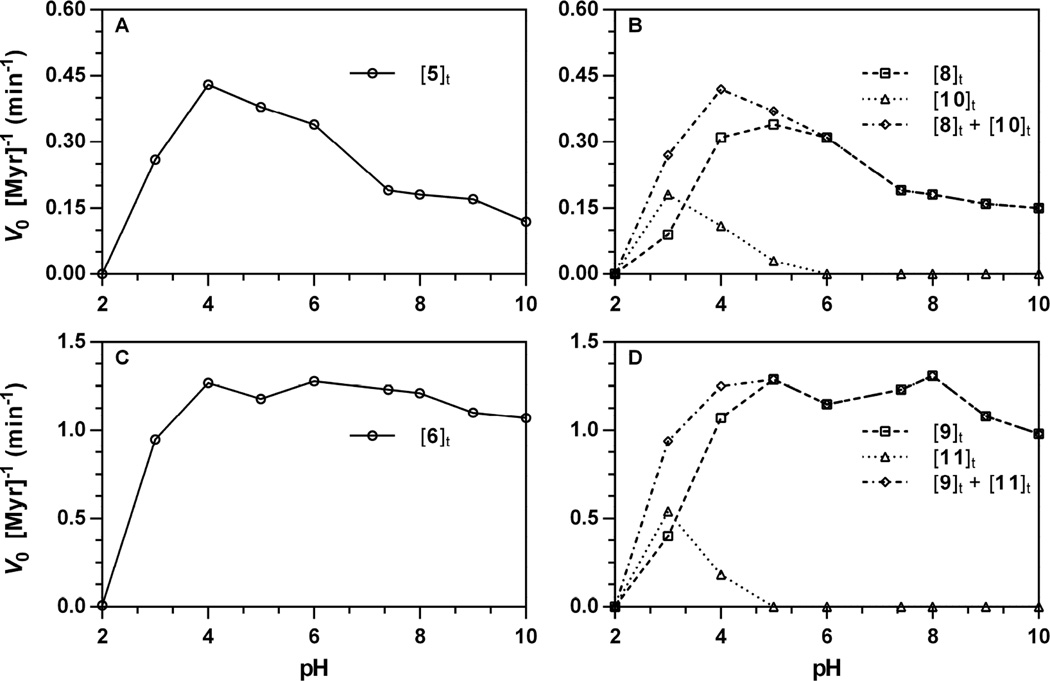
Normalized initial velocities for each analyte were plotted versus pH. Representative data acquired at 227 nm (210 nm for 10, 11) is depicted in Fig. 7; pH-dependence plots for all other wavelength-substrate combinations are available [34]. Right panels (Fig. 7A and 7C) depict V₀ for glucosinolate hydrolysis and left panels (Fig. 7B and 7D) depict V₀ for each product and the total V₀ for all products (hashed lines). The concentration of amines (12, 13) did not exceed the lower limit of detection at any of the pH evaluated; these results were surprising, considering the rapid rate at which ITCs are hydrolyzed to carbamic acids, then amines under basic conditions [36]. It is possible that the absence of the amine may be, in part, due to the low concentrations of ITCs evolved during the 75 minute reaction of an enzyme hydrolysis experiment. Control experiments conducted at pH 11 with aqueous solutions of pure ITC ([ITC]₀ = 250 µM) demonstrated rapid conversion to both amine and other minor unidentified organic products (data not shown); ITC 9 was noted to be particularly susceptible to hydrolysis under basic conditions at pH 10 and above. ITC stability studies are currently ongoing and will be reported in due course. However, it is important to note that the observed rates of hydrolysis are congruent with the sum of rates of product formation (Fig 7B, 7D, hashed lines) for each glucosinolate.

Figure 7.

pH Dependence of the action of Sinapis alba myrosinase on glucosinolates ([Gluc]₀ = 250 µM, 37 °C). Rates of hydrolysis and product formation w ere independently obtained from progress curves tracking glucosinolate ([Gluc]_t), isothiocyanate ([ITC]_t), and nitrile ([nitrile]_t) at a specific wavelength, then normalized for the concentration of myrosinase (V₀ [Myr]⁻¹, min⁻¹): 5, 227 nm; 8, 227 nm; 10, 227 nm; 6, 227 nm; 9, 227 nm; 11, 210 nm. pH-Dependent rate constants for other wavelength-substrate combinations are available [34]. The sum of rate constants for product formation ([ITC]_t + [nitrile]_t) are included to demonstrate conservation of rates. A. Hydrolysis of 5 (227 nm). B. Formation of 8 (227 nm), 10 (227 nm), and sum. C. Hydrolysis of 6 (227 nm). D. Formation of 9 (227 nm), 11 (210 nm), and sum.

For both 5 and 6, the optimal rate of hydrolysis with Sinapis alba myrosinase occurred at pH 4, at rates roughly proportional to the ratio of substrate specific activities calculated at physiological pH 7.4 [19]. This pH represented a true maximum for non-natural glucosinolate 5, which demonstrated a decline in normalized velocity with increasing pH; in contrast, 6 maintained a relatively constant normalized velocity over the same range. This optimal pH range, especially for 5, is somewhat lower than what has been previously disclosed in the literature for thioglucohydrolases: Sinapis alba, optimal pH 6.5 [29], Carica papaya, optimal pH 6.5–8.5 [30]. Previous mechanistic studies suggest that pH-dependent changes in myrosinase activity do not result from conformational changes, but rather ionic changes to the enzyme active site [37]. Although proposals have been made towards a mechanism of thioglucosidase action, there does not appear to be a clear consensus [29,38,39]. It is plausible that the larger steric size of the aglycone in 5 confers greater susceptibility to pH-dependent changes in hydrolysis velocity, as ionic changes to the active site may become less accommodating to its greater bulk. The relationship between the data presented in this manuscript, prior studies, and the mechanism of myrosinase action on both natural and non-natural glucosinolates is currently under investigation and will be reported in due course.

Stronger support for the conservation of myrosinase action between natural and non-natural glucosinolates stems from the organic product distributions that occur below pH 6. It has been reported that nitriles (3) become the principle organic product following hydrolysis conducted under acidic conditions; one account demonstrated the nitrile becomes the major product in the hydrolysis of 7 at pH 3 [18]. The data in Fig. 7 support this trend, demonstrating that nitriles 10 and 11 begin to appear at and below pH 5, becoming the principle product versus ITCs 8 and 9 by pH 3. At pH 3, the nitrile:ITC ratio is observed to be between 3:1 to 2:1 for both substrates. No enzyme-catalyzed reactivity was observed at pH 2 for either glucosinolate; interestingly, the thioacetal linkage in both glucosinolates appear to be stable at pH 2 and 37 °C over a 75 minute duration, as reaction progress curves did not indicate a change in detected concentration over time (see Fig. 29 through 35 in Ref. [34]). However, the overall similarities in the pH dependence of myrosinase action on 5 and 6 are supportive of a shared enzymatic mechanism for natural and non-natural glucosinolates.

3.4. Effects of Variable Temperature

To test the impact of temperature on the ability of myrosinase to accommodate natural and non-natural substrates, hydrolysis reactions of 5 and 6 ([Gluc]₀ = 250 µM) were conducted at pH 7.4 in 0.1 M phosphate buffer, incubated at a range of temperatures (9–85 °C). The temperature of each trial was monitored continuously with a calibrated thermometer to ensure thermal homogeneity of samples. For temperatures below 40 °C, the variance in temperatu re over a 75 minute reaction was less than ±0.5 °C; at higher temperatures, the variance was ±1.0 °C. N one of the temperatures assessed indicated the formation of nitrile (10, 11) or amine (12, 13) products. For reactions conducted at temperatures above 65 °C, it was noted that [Gluc]_t decreased early in a trial, then appeared to stagnate; nonlinear regression of these data were poorly fit to the Lambert W(x). Previous accounts have noted thermal stability of Sinapis thioglucosidase activity up to this temperature range: Sinapis negra, 60 °C [31], Sinapis hirta, 60 °C [40].

Based on these data, it was hypothesized that this feature was due to the thermal denaturation of the enzyme, and it became desirable to modify the Lambert W(x) in such a way as to generate a nonlinear function that accounts for time-dependent inactivation of enzyme function. A previous study on α-amylase indicated that its thermal denaturation occurred through a first-order kinetic process [35]. Since the Lambert W(x) is expressed in terms of the variables in the Michaelis–Menten equation (see Equations SD-1 through SD-3 in supplementary material), enzyme denaturation would cause the V_max term to no longer be constant (V_max)₀, but rather decrease over time (V_max)_t. Consequently, each occurrence of the (V_max)₀ variable in the Lambert W(x) was modified with an exponential relationship expressed in terms of the deactivation rate constant (k_d) (Equation 1). To ensure regression solutions that were within the logical confines of the experiment, variable range restrictions were necessary. Thus, for scenarios where denaturation was not a factor, the k_d term would approach zero and (V_max)_t would converge on (V_max)₀; if denaturation was occurring, nonlinear regression would converge on larger k_d values to fit the experimental data.

$${(V_{\text{max}})}_t={(V_{\text{max}})}_0(e^{-k_{\mathrm{d}}t})$$ (Equation 1)

Since the modified Lambert W(x) contained an additional variable (k_d) and had the risk of overfitting the experimental data, the new model was statistically compared to the original Lambert W(x) using the corrected Akaike information criterion (AICc), a variation of the AIC which contains a correction for sample size [41,42]. AICc analysis provided a means to compare the quality of two similar regression models where the goodness of fit was offset by a penalty related to the number of parameters in the model [43,44]. The difference in AICc (ΔAICc) between Lambert W(x) (simple) and modified Lambert W(x) (advanced) model fits of pH and temperature [Gluc]_t data was calculated using GraphPad Prism 6.0 (Table 3 and Table 4); negative reported ΔAICc values suggest that the preferred (non-overfit) model was the simple, unmodified Lambert W(x). Calculated ΔAICc values were also translated to a probability statement that the modified Lambert W(x) was the preferred model for a dataset. As shown in Table 3, progress curve datasets for variable pH experiments uniformly had a negative ΔAICc and low probability at all pH for both substrates. These data demonstrate that the simple Lambert W(x) was preferred vs. the modified Lambert W(x), suggesting that variance in pH does not appreciably lead to enzyme denaturation and the need to employ the modified Lambert W(x). Datasets for variable temperature experiments (Table 4) showed similar ΔAICc trends at low temperatures (< 65 °C). Above th is temperature range, ΔAICc was positive and there was high probability that the modified Lambert W(x) was preferred to model the data. Since the modified Lambert W(x) only differs by its inclusion of the k_d parameter to model first-order enzyme denaturation, these data suggest that significant enzyme denaturation was occurring above 65 °C. Interestingly, this range was slightly higher (> 75 °C) for glucosinolate 6, suggesting that this substrate was more tolerant to thermal denaturation. Although additional studies will need to be conducted to further explore this difference, it was hypothesized that this observation may be due to steric differences between aglycone sidechains.

Table 3.

Statistical analysis of model fits on variable pH [Gluc]_t reaction progress curves ([Gluc]₀ = 250 µM). AIC analysis was conducted between Lambert W(x) (simple) and modified Lambert W(x) (advanced) model fits in GraphPad Prism 6.0. For each substrate-wavelength-pH dataset, the ΔAICc is reported along with the percent probability that the modified Lambert W(x) model is preferred. DNC = did not converge.

			pH
Entry	Statistical Parameter	λ (nm)	2	3	4	5	6	7.4	8	9	10
[5]t	ΔAICc	220	DNC	−3.93	−15.62	−7.20	−6.71	−4.21	−3.98	−3.99	−4.18
		227	DNC	−4.19	−19.88	−9.88	−6.71	−4.17	−4.63	−3.99	−5.62
		235	DNC	−3.53	−26.65	−12.06	−6.13	−3.93	−4.80	−4.16	−3.93
		241	DNC	−3.72	−24.33	−9.73	−5.90	−3.92	−3.47	−4.01	−4.13
	Probability (%)	220	DNC	12.3%	0.0%	2.7%	3.4%	10.9%	12.0%	12.0%	11.0%
		227	DNC	11.0%	<0.01%	0.7%	3.4%	11.1%	9.0%	12.0%	5.7%
		235	DNC	14.6%	<0.01%	0.2%	4.5%	12.3%	8.3%	11.1%	12.3%
		241	DNC	13.4%	<0.01%	0.8%	5.0%	12.3%	15.0%	11.9%	11.3%
[6]t	ΔAICc	227	DNC	−3.59	−5.22	−11.20	−6.75	−11.71	−5.24	−4.74	−5.18
		235	DNC	−3.06	−5.32	−9.72	−7.90	−11.40	−5.48	−4.74	−5.42
		241	DNC	−3.44	−5.11	−10.82	−9.35	−10.51	−5.57	−4.58	−5.33
	Probability (%)	227	DNC	14.3%	6.8%	0.4%	3.3%	0.3%	6.8%	8.5%	7.0%
		235	DNC	17.8%	6.5%	0.8%	1.9%	0.3%	6.1%	8.5%	6.3%
		241	DNC	15.2%	7.2%	0.4%	0.9%	0.5%	5.8%	9.2%	6.5%

Table 4.

Statistical analysis of model fits on variable temperature [Gluc]_t reaction progress curves ([Gluc]₀= 250 µM). AIC analysis was conducted between Lambert W(x) (simple) and modified Lambert W(x) (advanced) model fits in GraphPad Prism 6.0. For each substrate-wavelength-temperature dataset, the ΔAICc is reported along with the percent probability that the modified Lambert W(x) model is preferred. DNC = did not converge; NT = not tested.

			Temperature (°C)
Entry	Statistical Parameter	λ (nm)	5	15	25	37	45	50	55	60	65	70	75	85
[5]t	ΔAICc	220	DNC	−3.83	−3.54	−3.93	−7.16	NT	−3.65	5.28	13.46	12.04	−2.15	NT
		227	DNC	DNC	−3.45	−3.95	−7.31	NT	−3.37	−1.69	8.20	6.02	25.34	NT
		235	−3.92	−3.88	−3.92	−3.95	−7.29	NT	−3.51	−2.49	12.17	9.68	−2.58	NT
		241	−3.93	DNC	−3.96	−3.90	−7.52	NT	−3.60	−2.77	9.88	8.90	−2.41	NT
	Probability (%)	220	DNC	12.8%	14.5%	12.3%	2.7%	NT	13.9%	93.3%	99.9%	99.8%	25.4%	NT
		227	DNC	DNC	15.1%	12.2%	2.5%	NT	15.7%	30.0%	98.4%	95.3%	>99.99%	NT
		235	12.3%	12.6%	12.3%	12.2%	2.5%	NT	14.7%	22.3%	99.8%	99.2%	21.6%	NT
		241	12.3%	DNC	12.1%	12.5%	2.3%	NT	14.2%	20.1%	99.3%	98.9%	23.1%	NT
[6]t	ΔAICc	227	−3.92	−4.18	−4.33	− 11.71	−18.68	−54.06	−27.09	−38.61	−3.91	NT	18.74	−3.81
		235	−3.93	−4.23	−4.70	− 11.40	−18.28	−63.53	−26.77	−41.61	−3.89	NT	−0.18	65.30
		241	−3.91	−3.93	−4.79	− 10.51	−17.91	−61.51	−26.21	−42.13	−3.89	NT	10.55	0.19
	Probability (%)	227	12.3%	11.0%	10.3%	0.3%	<0.01%	<0.01%	<0.01%	<0.01%	12.4%	NT	>99.99%	13.0%
		235	12.3%	10.8%	8.7%	0.3%	0.0%	<0.01%	<0.01%	<0.01%	12.5%	NT	47.7%	>99.99%
		241	12.4%	12.3%	8.4%	0.5%	0.0%	<0.01%	<0.01%	<0.01%	12.5%	NT	99.5%	52.4%

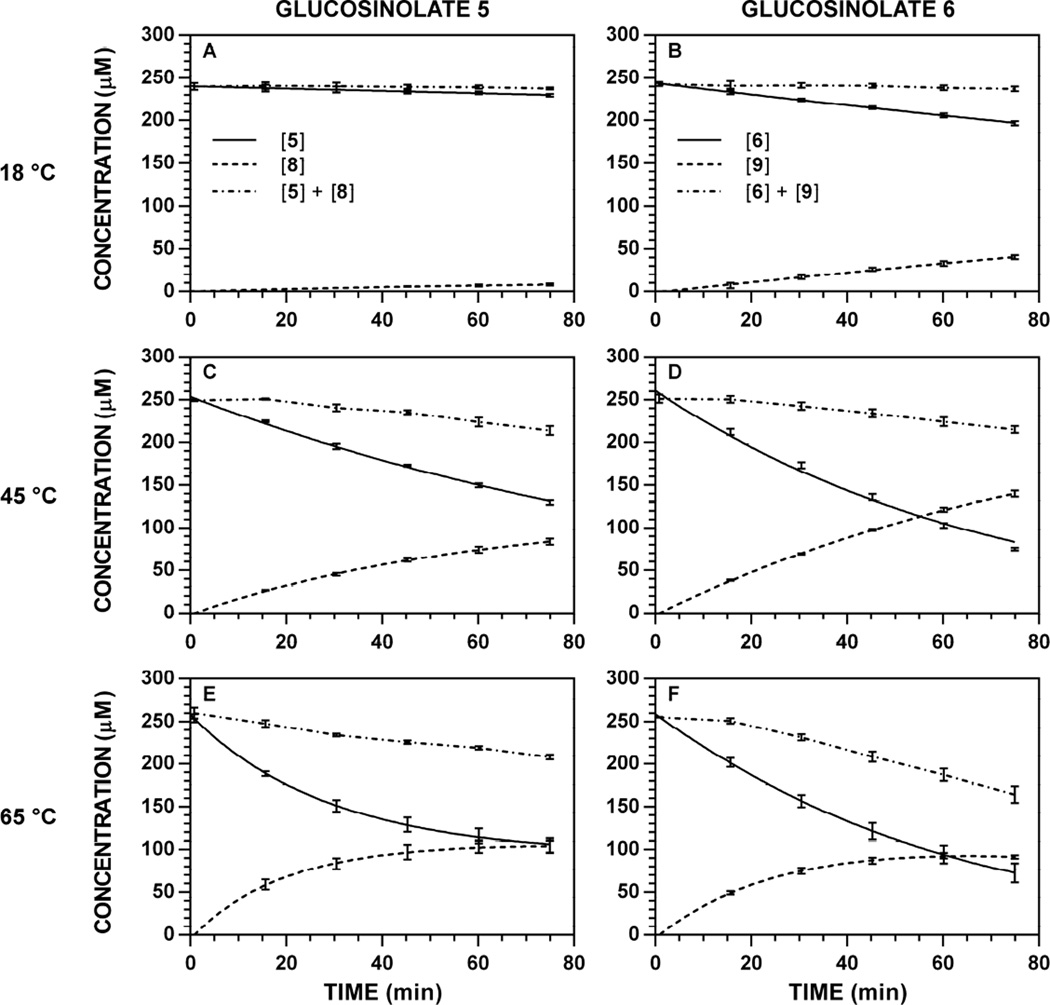
Application of the modified Lambert W(x) (see Equation SD-8 in supplementary material for the textual definition) provided excellent curves that fit each set of [Gluc]_t and [ITC]_t data well under both denaturing (> 65 °C) and non-denaturing (< 65 °C) conditions. Representative reaction progress curves at 227 nm are depicted in Fig. 8; progress curves for all other wavelength-temperature-substrate combinations are available [34]. From these data, initial velocities of hydrolysis or initial velocities of formation were calculated. In these plots, the detectable sum of concentrations (Fig. 8, dotted lines) was no longer constant and demonstrated an increasingly negative slope at higher temperatures. Since no change in [Gluc]_t was observed in the absence of myrosinase at any temperature (9–85 °C), this net loss must necessarily be attributable to the loss of [ITC]_t from the system; this effect can be observed by a stagnation, flattening, or even decrease in [ITC]_t at later reaction times (e.g. Fig. 8F) [18].

Figure 8.

Representative reaction progress curves for the hydrolysis of glucosinolates ([Gluc]₀ = 250 µM) at variable temperature and pH 7.4 (227 nm). The concentration of myrosinase was constant for each substrate: 5, 7.06 U ml⁻¹; 6, 1.77 U ml⁻¹. HPLC chromatogram peak areas at specific wavelengths were used to determine [Gluc]_t and [ITC]_t, at each timepoint, and the data (n = 3) was fitted to a reaction progress curve using nonlinear regression. The dotted line denotes the sum of [Gluc] + [ITC] at each timepoint, and its slope represents product loss over time. Reaction progress curves for all other temperature-wavelength combinations are available [34]. A. Hydrolysis of 5, 18 °C. B. Hydrolysis of 6, 18 °C. C. Hydrolysis of 5, 45 °C. D. Hydrolysis of 6, 45 °C. E. Hydrolysis of 5, 65 °C. F. Hydrolysis of 6, 65 °C.

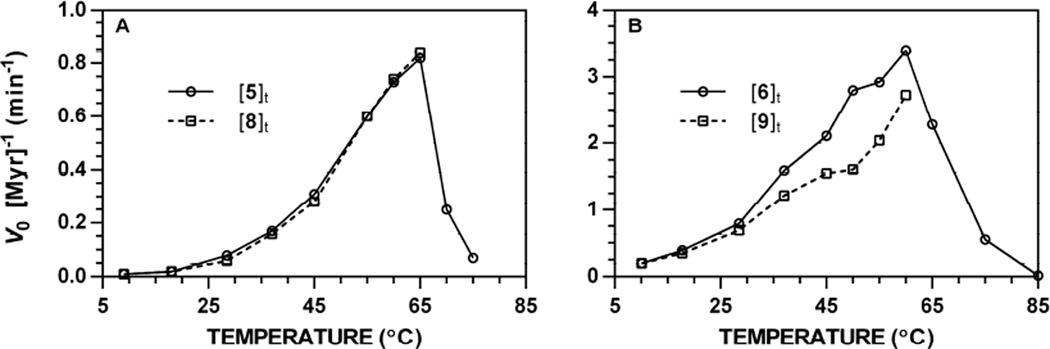
Normalized initial velocities for each analyte were plotted versus temperature. Representative data acquired at 227 nm is depicted in Fig. 9; temperature-dependence plots for all other wavelength-substrate combinations are available [34]. Both glucosinolate substrates demonstrated a temperature-dependent increase in normalized rate, reaching a maximal V₀ between 60–65 °C. Velocities rapidly dropped at higher temperatures, reaching complete enzymatic inactivation between 75–85 °C. These optimal temperatures are supported by other accounts on thioglucosidase activity, which show variations based on species of origin: Brevicoryne brassicae, optimal temperature 35–45 °C [32], Carica papaya, optimal temperature 40–50 °C [30], mustard (Sinapis) variants have demonstrated relatively higher thermal stability [31,40].

Figure 9.

Temperature dependence of the action of Sinapis alba myrosinase on glucosinolates ([Gluc]₀ = 250 µM, pH 7.4, 227 nm). Rates of hydrolysis and product formation were independently obtained from progress curves tracking glucosinolate ([Gluc]_t) and isothiocyanate ([ITC]_t) at a specific wavelength, then normalized for the concentration of myrosinase (V₀ [Myr]⁻¹, min⁻¹). Temperature-dependent rate constants for other wavelength-substrate combinations are available [34]. A. Hydrolysis of 5 and formation of 8. B. Hydrolysis of 6 and formation of 9.

Similar to variable pH studies, the maximum V₀ for 5 and 6 were roughly proportional to the ratio of substrate specific activities calculated at physiological temperature (37 °C). While the thermal aqueo us stability of glucosinolates renders data tracking [Gluc]_t as the more accurate metric for assessing V₀, [ITC]_t data (Fig. 9, dashed lines) followed the same trends and closely mirrored [Gluc]_t data, especially at temperatures below 37 °C. Between 37 °C and 60–65 ° C, ITC 8 demonstrated greater thermal stability than ITC 9, with [ITC]_t V₀ data that more similar to those acquired from [Gluc]_t. Beyond these temperatures, both 8 and 9 demonstrated an initial increase in concentration, followed by significant and consistent decrease that led to poor fits with the Lambert W(x) and data that was not representative of actual reaction outcomes (see Fig. 36 to 42 in Ref. [34]). Indeed, control studies conducted with pure 8 and 9 at high temperatures support their rapid degradation to amines (4) and other, unidentified organic products. Although substrates 5 and 6 were hydrolyzed at different rates by myrosinase, their temperature profiles were congruent and supportive of a shared mode of catalytic action.

3.5. Conclusions

The underlying hypothesis of this study was that the action of Sinapis alba myrosinase on non-natural glucosinolate would mirror its action for natural glucosinolates. The complete kinetic characterization of non-natural analogue 2,2-diphenylethyl glucosinolate (5) was accomplished, with results that were consistent, given its structural differences relative to previously-described natural analogues. These data represent the first complete, documented kinetic assessment for this compound. Together with glucotropaeolin (6), these two analogues were evaluated to examine the effects of pH and temperature on initial rates of hydrolysis and product formation. Both compounds demonstrated similar optimal pH and temperature profiles that are consistent with a shared mode of action by myrosinase. For reasons that remain unclear, the optimal pH was lower than has been previously reported for this enzyme; this data necessitates continued evaluation to determine whether there are broader implications to this observation. Both natural and non-natural analogues demonstrated congruent relative rates of product formation that were in support of previously-documented trends.

Beyond the scope of the explicit hypothesis of this study, the broader impact of this work lies in two main facets: (1) the continued support for use of the HPLC-based kinetic method and (2) expansion of the Lambert W(x) with a term which accommodates time-dependent enzyme denaturation. With every kinetic assessment that our group has performed, the advantages provided by the HPLC method have become more apparent. The automated ability to sample reactions at intervals to determine analyte concentrations and velocities is highly convenient. Furthermore, this study tested and confirmed the ability of the sharp solvent gradient to resolve and analyze a mixture of four components with a significant range of structural polarity. In this work, particularly for reactions conducted at acidic pH, the capability to independently analyze and simultaneously determine velocities of reaction and velocities of formation for multiple organic products provides a level of kinetic information that has been absent using traditional methods. Our adaptation of the Lambert W(x) to include a term to describe enzyme denaturation was an unintended and significant outcome of these studies that we hope can be applied toward the study of other enzymatic systems. Towards the purposes of this project, this modification allowed determination of initial velocities under at elevated temperatures. The converged values for k_d demonstrated the expected trend of increasing with temperature [35]; however, the density of data points would likely need to be increased, especially early in a reaction, in order for this approach to become a viable method for experimentally-determining k_d for an enzyme.

Figure 1.

Glucosinolates, isothiocyanates, nitriles, and amines.

Table 2.

Specific activities (V₀, min⁻¹) for the hydrolysis of glucosinolate 5 ([Gluc]₀ = 250 µM) by Sinapis alba myrosinase. HPLC data for [5]_t and [8]_t were independently tracked. Specific activities were normalized to the specific activity of 7 (0.94 min⁻¹, 227 nm) [19].

		V0 [Myr]−1 (min−1)		Relative Specific Activity (%)
Entry	λ (nm)	[5]t	[8]t	[5]t	[8]t
5 to 8	220	0.19 ± 0.02	0.18 ± 0.01	20	19
	227	0.18 ± 0.02	0.18 ± 0.01	19	19
	235	0.18 ± 0.02	0.19 ± 0.01	19	20
	241	0.19 ± 0.01	0.18 ± 0.01	20	19