Measuring Cell Viscoelastic Properties Using a Microfluidic Extensional Flow Device

Abstract

The quantification of cellular mechanical properties is of tremendous interest in biology and medicine. Recent microfluidic technologies that infer cellular mechanical properties based on analysis of cellular deformations during microchannel traversal have dramatically improved throughput over traditional single-cell rheological tools, yet the extraction of material parameters from these measurements remains quite complex due to challenges such as confinement by channel walls and the domination of complex inertial forces. Here, we describe a simple microfluidic platform that uses hydrodynamic forces at low Reynolds number and low confinement to elongate single cells near the stagnation point of a planar extensional flow. In tandem, we present, to our knowledge, a novel analytical framework that enables determination of cellular viscoelastic properties (stiffness and fluidity) from these measurements. We validated our system and analysis by measuring the stiffness of cross-linked dextran microparticles, which yielded reasonable agreement with previously reported values and our micropipette aspiration measurements. We then measured viscoelastic properties of 3T3 fibroblasts and glioblastoma tumor initiating cells. Our system captures the expected changes in elastic modulus induced in 3T3 fibroblasts and tumor initiating cells in response to agents that soften (cytochalasin D) or stiffen (paraformaldehyde) the cytoskeleton. The simplicity of the device coupled with our analytical model allows straightforward measurement of the viscoelastic properties of cells and soft, spherical objects.

Introduction

Although it has been long understood that soluble factors from the cellular microenvironment can strongly influence cellular behavior, it is becoming increasingly clear that physical, and especially mechanical, inputs can also affect cell behaviors such as migration, proliferation, and differentiation (1, 2, 3, 4). Cells frequently respond to mechanical stimuli by adaptively tuning their intrinsic mechanical properties, and significant evidence suggests that this “mechanoadaptation” is key to transducing these inputs into biochemical signals that mediate cell behavior. Moreover, because disease states are often accompanied by changes in cell and tissue mechanics, there has been growing interest in using cell mechanical properties as a label-free biomarker (5, 6, 7, 8, 9). As a result, there is much interest in developing platforms to quickly and accurately quantify cellular mechanical properties. These new platforms would not only facilitate advances in understanding how cells stabilize their shape and process mechanical cues but would also give rise to novel clinical diagnostic tools.

Traditional techniques for studying the mechanical properties of single cells include micropipette aspiration (MPA), atomic force microscopy (AFM), optical stretching, and magnetic bead cytometry (10, 11, 12). Although these methodologies have been instrumental in elucidating the molecular basis of cellular mechanics, they require highly skilled operators and sophisticated equipment and, most importantly, suffer from low experimental throughput. For example, AFM and optical stretching techniques have sampling rates on the order of 1 cell/min (if not slower), which severely reduces statistical power and complicates, if not precludes, the identification of rare cellular subpopulations. Additionally, many of these techniques require direct contact between a probe and cell, adhesion to two-dimensional culture substrates, or both, which may invite measurement artifacts.

To address these issues, microfluidic tools have recently been explored as a strategy to measure cellular structural and mechanical properties with a rapidity that may be better suited to drug discovery and clinical application (13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24). Although these approaches have indeed massively improved measurement throughput and reduced operator skill/bias issues relative to traditional measurements, the extraction of cell mechanical properties (e.g., elastic modulus) remains challenging, primarily due to complex viscous forces that severely complicate analysis of deformations.

Recently, Guck and colleagues performed rapid cell deformability measurements with a device that squeezed cells into a bullet shape as the cells passed through square constriction channels (18, 19). By using a viscous medium (viscosity of μ ∼ 15 mPa·s vs. 1 mPa·s for water at room temperature), the device could be operated at low Reynolds number (Re ∼ 0.1), thereby enabling the development of an analytical model from which elastic moduli of cells could be determined from the resulting deformations (19). Although this method has proven quite powerful, it is analytically demanding and requires accurate edge detection of a complicated shape to extract elastic properties.

In an attempt to achieve high-throughput mechanical measurements within a simpler geometry, Di Carlo and colleagues developed higher-Reynolds-number (Re > 40) microfluidic systems that measure cell deformability with throughput ranging from 1000 cells/s (14) to 65,000 cells/s (15). By elongating cells at the stagnation point of extensional flow or pinching cells with two sheathing flows, they successfully developed population “signatures” based on distributions of cell deformability versus size. These population signatures responded in expected ways to cytoskeletal drugs in the pinched-flow sheathing device for which strain rates and imposed cell strains were not too large (15) (the expected effects of cytoskeletal depolymerization drugs were not detected in the high-strain-rate, high-strain-extensional-flow device (13)) and enabled prediction of disease state from clinical samples (13, 14). Nonetheless, this work did not present an analytical route for extracting cell constitutive model parameters, instead requiring numerical solutions due to the high inertial component of the flow. Thus, there remains a significant need for microfluidic strategies to measure cellular viscoelastic properties in a simple geometry subject to well-defined deformation forces.

In this study, we present, to our knowledge, a novel cross-slot microfluidic system that addresses these limitations. By strategically choosing our device geometry and suspending fluid, we are able to greatly simplify both the experimental workflow and mechanical analysis and thereby arrive at a single analytical equation that relates deformation, channel geometry, and cellular viscoelastic parameters. The expected elliptical deformed shape is more easily analyzed and less sensitive to noise in image processing compared to a more complicated shape with rapid changes in curvature. We validate the approach by measuring the elastic properties of cross-linked dextran hydrogel particles, using independent MPA measurements and previously published values for stiffness as comparisons. We then apply this system to measure the apparent shear modulus and fluidity (viscosity parameter) of 3T3 fibroblasts and primary glioblastoma tumor initiating cells (GBM TICs) and show that we can capture expected changes in cell stiffness in the presence of specific pharmacologic agents.

Materials and Methods

Microfluidic device fabrication

Microfluidic cross-slots were fabricated using standard soft lithography. This geometry, consisting of two channels that intersect at 90°, is a convenient platform for generating a planar extensional flow. Masters for the cross-slots used for the cell experiments were made from SU-8 patterned on silicon wafers according to standard soft lithography approaches (25). Briefly, silicon wafers were precleaned with piranha solution (3:1 sulfuric acid to hydrogen peroxide), washed with deionized water, and baked at 120°C for 20 min to remove any moisture. After spin-coating a 30-μm layer of SU-8 2025 photoresist (Microchem, Boston, MA) onto the wafer, the wafer was exposed to 365-nm ultraviolet light at ∼40 mW/cm² for 12 s under a mylar mask printed with the cross-slot pattern (Artnet Pro, San Jose, CA). After development, wafers were pretreated with trichloro (1H,1H,2H,2H-perfluoroocytl)silane to prevent adhesion of the polydimethylsiloxane (PDMS) to the silicon wafer. PDMS and curing agent (Sylgard 184, Dow Corning, Midland, MI) were mixed in a 10:1 ratio, degassed, and poured over the silicon master. The PDMS was cured overnight at 80°C before the PDMS patterns were removed. Inlet and outlet holes were punched with an 18-gauge blunt needle (McMaster Carr, Elmhurst, IL). The PDMS devices were bonded to glass microscope slides after oxygen plasma treatment, and bonding was finalized by curing the PDMS/glass device in an oven at 80°C overnight. The cross-slot channel geometries for the cell experiments had widths of 70 or 100 μm, a depth of 30 μm, and channel lengths to the cross-slot region of 1 or 2 mm.

For the dextran particle experiments, which required very deep devices, masters were made from dry-film photoresist on stainless steel wafers. Before lamination, the steel wafers were rinsed with acetone and water. Two layers of 100-μm-thick dry-film photoresist (Riston GoldMaster GM100 photoresist, DuPont, Research Triangle Park, NC) were laminated onto the steel wafer with the rollers heated to 120°C (Akiles Prolam Ultra, Mira Loma, CA). The dry-film photoresist was exposed to 365-nm ultraviolet light at ∼40 mW/cm² for 10 s under a mylar mask printed with the cross-slot pattern (Artnet Pro). The laminate was developed with 10% K₂CO₃ solution and then dried. The PDMS cross-slot devices were prepared from the dry-film photoresist masters in the same manner as from the SU-8 masters. These large devices, with 200 μm depth, 400 μm width, and channel lengths of 2 mm, accommodated the large (40- to 100-μm diameter) dextran hydrogel particles.

Cell culture

NIH 3T3 mouse fibroblasts (ATCC, Manassas, VA) were cultured on tissue culture plastic in complete medium consisting of Dulbecco’s modified Eagle’s medium (Gibco, Carlsbad, CA) with 10% calf serum (JR Scientific, Woodland, CA) and 1% penicillin/streptomycin (Gibco). The primary GBM TIC line, L0, was collected in a previous study after informed consent from male patients who underwent surgical treatment and Institutional Review Board approval (26). The TIC neurospheres were propagated in neurosphere assay growth conditions (27) with serum-free medium (Neurocult NS-A Proliferation kit, Stem Cell Technologies, Vancouver, Canada) supplemented with epidermal growth factor (20 ng/mL, R&D Systems, Minneapolis, Minnesota), basic fibroblast growth factor (R&D Systems) and 2 μg/mL heparin (Sigma-Aldrich, St. Louis MO) The gliomaspheres were serially passaged every 5–7 days, when the spheres reached a diameter of ∼150 μm. Gliomaspheres were dissociated with trypsin/ethylenediaminetetraacetic acid (0.05%) for 2 min and then replated in fresh media with the addition of epidermal growth factor, basic fibroblast growth factor, and heparin. Both cell cultures were grown in a humidity-controlled 5% CO₂ incubator at 37°C.

Pharmacologic studies

For studies with cytochalasin D (CytoD), cells were incubated with 10 μM CytoD (Sigma-Aldrich) for 30 min before the experiment. CytoD was then also added to the suspending solution at 10 μM to ensure exposure to a constant CytoD concentration during cross-slot deformation. For paraformaldehyde (PFA) studies, cells were fixed with 4% PFA (Alfa-Aesar Haverhill, MA) in phosphate-buffered saline (PBS) for 10 min in culture and then washed three times with PBS to remove any residual PFA before resuspension. Because PFA irreversibly cross-links cellular proteins upon transient treatment, it was not necessary to include PFA in the medium during measurement.

Cross-slot deformation experiments

Cells and dextran hydrogel particles were suspended in 20% (cells), 30%, or 40% (dextran particles), w/v, 20000 Da polyethylene glycol (PEG20000)/PBS solution to operate in the low-Reynolds-number regime and to reliably focus the majority of cells/particles during cross-slot deformation. The PEG had a viscosifying effect so that a given fluid stress could be applied at lower fluid velocities to make image capture and analysis of cell and dextran particle deformation easier. The viscosity of the PEG20000/PBS solution was measured at 25°C using an Anton Paar (Graz, Austria) Physica MCR 301 rheometer with a 50 mm parallel plate geometry. The measured viscosities were nearly constant across the tested strain rates (1–2000 s⁻¹): 35–50 mPa·s for 20% w/v solutions, ∼100 mPa·s for 30% w/v solutions, and ∼200 mPa·s for 40% w/v solutions (Fig. S1 in the Supporting Material). The high concentration of PEG also increased the density of the suspending solution to 1.03–1.05 g/mL so that cells and dextran particles were approximately neutrally buoyant. Thus, during observation of deformation at the midchannel height (i.e., 15 μm above the glass-bottom surface for cells in the 30-μm-deep device), most cells and particles were in focus and candidates for measurement. 3T3 and GBM TIC cells were trypsinized into a single-cell suspension and then resuspended in the PEG20000/PBS solution. For cells treated with CytoD, drug at the same concentration as for incubation was included in the solution to prevent recovery of the cytoskeleton from the depolymerization. Typical cell densities were 8–10 million cells/mL as measured by a hemocytometer. The cross-linked dextran beads were Sephadex G200 beads in powder form (GE Healthcare, Little Chalfont, United Kingdom) and were simply added to the PEG20000/PBS solution.

The cell and dextran particle suspensions were loaded into 1 mL syringes (BD Falcon, San Jose, CA). Cell and particle suspensions were infused into the cross-slot device using a syringe pump (74900 series dual syringe pump, Cole-Parmer, Vernon Hills, IL) at constant flow rates ranging from 50 to 1400 μL/h for the cells and from 2.5 to 40 mL/h for the dextran hydrogel particles. To account for the compliance in the microfluidic device and tubing, the system was allowed at least 2 min to equilibrate before data capture after each new flow-rate adjustment.

Cells or dextran particles flowing in both cross-slots were elongated at constant strain rate in extensional flow and observed passing through the stagnation point region. Deformation was imaged in phase contrast mode using a Nikon (Tokyo, Japan) TE2000-E2 microscope with a 40× objective (∼2 px/μm), and the plane of focus was the device centerplane. Images were captured by using a high-speed Phantom Miro M310 camera (Vision Research, Wayne, NJ) at 2000 frames/s with 20 μs exposure to obtain several images per cell or particle, thereby capturing the evolution of the deformation, and to minimize blurring due to cell or particle movement. All movies were captured within 30 min of the trypsinization process.

Cell and dextran particle deformation images were analyzed with custom software written for ImageJ (NIH) and Matlab (2013v, Mathworks, Natick, MA). Cell strain was defined as ε = (a − b)/(a + b), where a and b are the long and short axes, respectively, of an ellipse fitted manually to the outer edge of the cell membrane (Fig. 1 A; Fig. S3). Our definition of cell strain is equivalent to the Taylor deformation parameter (28) historically used to define droplet deformation (29, 30, 31) and adapted to quantify red blood cell deformations (20, 24, 32). The cell strain measurement was taken at the time point at which the cell was closest to the stagnation point. Additionally, this definition of ε is also the magnitude of engineering strain along the x and y axes: ε = |(R − R₀)|/R₀ = |ΔR|/R₀ where the change in sphere radius at the surface is ΔR > 0 along the y axis (outlet flow axis) and −ΔR along the x axis (inlet flow axis). Note that the sphere strain along the z axis is zero for planar extensional flow due to zero velocity in the z-coordinate direction and therefore no contribution to the velocity gradient that determines the viscous fluid stresses acting on the sphere surface.

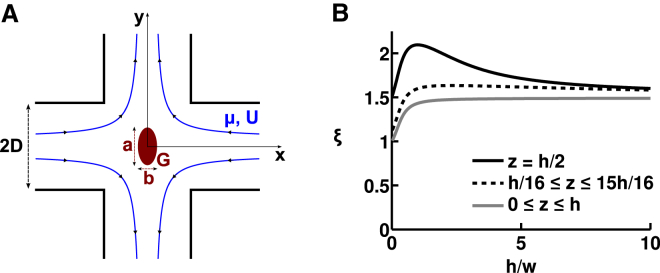
Figure 1.

Cross-slot flow field. (A) Cross-slot device containing a body (red) that is initially spherical but then elliptically deforms under elongational viscous fluid stresses (flow streamlines in blue). D is the channel’s half-width. a and b, respectively, denote the long and short axes of the ellipse. G is the shear modulus of the body. μ is the fluid dynamic viscosity and U is the mean flow velocity. (B) Normalized entrance velocity, ξ = U_in/U, at the entrance to the cross-slot stagnation point region (|x| = sqrt(x² + y²) ≤ D), as a function of the channel’s aspect ratio, A = h/w, where h and w (w = 2D) are the channel height and width, respectively. Values for normalized entrance velocity are computed using our derived analytical expression for ξ_max and ξ_min. z denotes the position of the vertical axis, with the channel occupying 0 ≤ z ≤ h. ξ_max is plotted as a black line and corresponds to an object at the vertical center of the channel, where the velocity is maximal. ξ_min is plotted as a gray line and corresponds to objects that are in the middle of the channel’s width but distributed equally along the height of the channel. The dotted black line indicates an example of the normalized entrance velocity, ξ, for objects that are in the middle of the channel’s width and distributed equally along the height of the channel with the exclusion of the very bottom and the very top of the channel (in this example, we excluded 1/8 of the total channel height). This final value (dotted black line) is the one that best matches experimental observations. To see this figure in color, go online.

Cells were excluded from analysis if one of the following criteria was met:

• •The cell was not spherical before entry into the cross-slot, as the analytical model becomes invalid in such a case, since the assumed initial state for deformation computation is incorrect.
• •The cell was not sufficiently centered in the channel width direction (i.e., it was closer than 25% of the channel width to the walls) or was adherent to another object (e.g., another cell), as the analytical model becomes invalid since the object does not experience the assumed strain rate.
• •The cell membrane appeared damaged.
• •The cell was either very large or very small compared to other cells (for a distribution of the cell size of the analyzed population of cells, see Fig. S4), as such cells may be apoptotic, multinucleated, or otherwise abnormal and empirically demonstrated very large or very small deformations far outside the population average.

The same exclusion criteria applied to dextran hydrogel particles, though the criterion related to the assumed strain rate was the only one that applied in practice, because the particles were all initially spherical and intact.

The mechanical properties of cells and dextran particles were determined from the analysis of the deformation due to the known viscous forces. At a given flow rate, cell type, and drug treatment, the reported deformation under those experimental conditions was computed as the average deformation of 10 ≤ n ≤ 30 cells with an uncertainty defined as the standard error of the mean. Mechanical property parameters were obtained through linear regression with a least-squares fit of the observed strain, ε, to cross-slot extensional strain rate, ξU/D (for cells, a log-log plot), or viscous stress, μξU/D (for dextran particles, a linear plot) based on the theory described in the Results section, where ξ, U, and D are defined. The uncertainties in the linear fits and the significance of the differences in measured material properties between the cell pharmacologic studies are evaluated using analysis of covariance.

MPA experiments

Micropipettes were fabricated from glass capillaries as described in Guillou et al. (33) and mounted on motorized micromanipulators. The aspiration pressure was applied using an air-filled syringe and determined using a home-made pressure sensor as described in Hogan et al. (34). Aspiration pressure was increased from 0 to 10 kPa by incremental steps of 2 kPa. After each pressure step, an image of the aspirated Sephadex bead was acquired using a 40× objective.

Results

Theoretical analysis of the deformation of an elastic body in a cross-slot device

We begin by calculating the viscous stresses experienced by spherical bodies flowing through the stagnation point region of a cross-slot device and apply these findings to the simple case of an isotropic, linearly elastic spherical particle. Our result is valid in the limit of low-Reynolds-number flow and small deformations of the particle. Indeed, these two modeling assumptions were met in the upcoming results as we observed cell strains of 0.01 < ε < 0.18 under operating conditions in which the flow Reynolds number was small, specifically, 0.006 < Re < 0.2 (range of all experimental parameters given in Table S1). Therefore, the effects of fluid inertia can be assumed to be negligible compared to viscous fluid forces and omitted from our model. In contrast, the Reynolds number in the cross-slot devices of Di Carlo and colleagues (13, 15) were finite at operating conditions (Re > 40) and therefore fluid inertia would need to be included in the modeling of cell deformation in their system.

Our system parameters are the channel half-width, D, the channel height, h, the medium dynamic viscosity, μ, the fluid density, ρ, and the mean flow velocity U (see Fig. 1). We define the flow Reynolds number as Re = ρUD/μ and consider only the case where Re ≪ 1. Hence, viscous forces dominate inertial forces and we assume Stokes flow. The cross-slot generates approximately planar extension flow, in which the velocity field is v = Ω(−xi + yj) and Ω is the uniform extensional strain rate. Therefore, in the stagnation point region under these laminar flow conditions, the velocity gradient is nearly constant. In particular, along the inlet center streamline (x axis), the velocity gradient is approximately Ω = U_in/D, indicating that the velocity decreases linearly from U_in, the velocity at the entry of the cross-slot region (|x| = D), to zero at the stagnation point. Other investigators previously measured this velocity behavior along the center streamline using micro-PIV measurements (35), and we confirmed the uniform strain rate with our own measurements in the device used for the cell experiments (Fig. S8). We introduce the normalized entrance velocity, ξ = U_in/U, and the stagnation-point-region velocity gradient is Ω = U_in/D = ξU/D. Because U and D are set by the experimental conditions, ξ is the only remaining factor that must be derived to obtain the velocity gradient in the stagnation point region.

In a first step, we restrict our analysis to the position of maximal in-plane (x-y) velocity gradient, corresponding to an object that is at the channel’s vertical center (z = h/2) and in the middle of the channel’s width (y = 0), where U_in = U_max. In such a case, ξ = ξ_max = U_max/U. Using the known velocity profile for laminar flow through a rectangular channel (36), we are able to derive an analytical expression for ξ_max in terms of a Fourier series in the channel aspect ratio, A = h/(2D) = h/w:

$${\xi }_{\max }=\frac{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-6\sum _{\text{n}=0}^{\infty }\frac{{\left(-1\right)}^{\text{n}}}{{\lambda }_{\text{n}}\cosh \left({\lambda }_{\text{n}}/A\right)}}{1-6A\sum _{\text{n}=0}^{\infty }\frac{\tanh \left({\lambda }_n/A\right)}{{\lambda }_{\text{n}}^5}}\text{where}{\lambda }_{\text{n}}=\frac{\left(2\text{n}+1\right)\pi }{2}.$$ (1)

We note that for A < 1, both infinite series in Eq. 1 can be approximated by their first term with an error for ξ_max of <1%. For 1 < A < 3, one must add the second series term to maintain an error of <1%. Further, we verified that in the quasi-two-dimensional (2D) limit where A goes to 0 (corresponding to a very flat channel), ξ_max converges to 3/2, the well-known maximum-to-mean velocity ratio in a 2D parabolic flow. We also note that because inverting the width and height affects neither the maximum nor the mean velocity, ξ_max(A) = ξ_max(1/A).

In a second step, we relax the constraint that the body must be located at the channel midheight, because it is difficult to perfectly focus all cells in experiments. Still assuming that the body is at the center of the channel width direction, the body may now be located anywhere on the vertical axis so that U_in = U_w/2. We use the same approach as above, and derive the normalized velocity, ξ_min = U_w/2/U, in terms of a Fourier series:

$${\xi }_{\text{min}}=\frac{1-6\text{A}\sum _{\text{n}=0}^{\infty }\frac{1}{{\lambda }_{\text{n}}^4\cosh \left({\lambda }_{\text{n}}/\text{A}\right)}}{1-6A\sum _{\text{n}=0}^{\infty }\frac{\tanh \left({\lambda }_{\text{n}}/\text{A}\right)}{{\lambda }_{\text{n}}^5}},\text{where}{\lambda }_{\text{n}}=\frac{\left(2\text{n}+1\right)\pi }{2}.$$ (2)

ξ_min is plotted for aspect ratios between 0 and 10 in Fig. 1 B (solid gray line). We note that for A < 1, both infinite series in Eq. 2 can be approximated to their first term with an error for ξ_min of <1%. For 1 < A < 3, one must add the second series term to maintain an error of <1%.

In experiments, objects were predominantly near the midplane of the channel, so ξ assumed values that lie between ξ_min and ξ_max. To further refine the expression for the experimental value of ξ, we adjust Eq. 2 to take into account the radius of the object being deformed, in which case we find that the normalized velocity is almost always close to 1.5 (see Fig. 1 B; see the Supporting Results for more details), except for high-aspect-ratio channels that are seldom used in microfluidics, in part because objects will often be out of focus as a consequence. For simplicity, we retain this value of 1.5 in our subsequent experimental analysis. Thus, the velocity gradient in our device is Ω = ξU/D, where ξ is expressed analytically as a function of the aspect ratio, A = h/w, of the device. In the experiments reported here, ξ ∼ 1.5.

By scaling arguments and analysis of the cross-slot flow field, we can therefore reasonably assume that objects sufficiently close to the stagnation point are deformed by our derived strain rate, ξU/D. The results for ξ are derived in the absence of cells or particles. We verified that the size of cells was sufficiently small to avoid perturbations to the flow, as evidenced by the small value of the Stokes number, Stk ∼10⁻⁶ ≪ 1 (see details in the Supporting Results and Fig. S7). Our Hele-Shaw simulation results of the cross-slot flow field and our micro-PIV measurements (Fig. S8), as well as other reported particle-image velocimetry measurements (Fig. S2 in (37); Fig. 5 D in (35)), indicate that the strain rate is constant in the stagnation-point region. According to our Hele-Shaw simulations, for distances <25% of the channel width away from the stagnation point, the local strain rate is within 95% of the maximum value at the stagnation point (Fig. S2).

Having characterized the velocity gradient in the device, we consider the simple case of an isotropic, linearly elastic material deforming in a pure and infinite planar extensional flow. Murata (38) analyzed the general problem of an incompressible elastic sphere deforming in an arbitrary, low-Reynolds-number flow field in the limit of small deformations (ε ≪ 1). From Murata’s example solution for the surface of a sphere deforming in planar extensional flow, we obtain the following relation for the strain in this flow field: ε = (5Ωμ)/(2G), where G is the shear modulus and the strain is defined as ε = (a − b)/(a + b) (Fig. 1 A). Plugging in our expression for the velocity gradient, Ω, we find an expression for the strain of an elastic sphere deforming in our cross-slot device:

$$\epsilon =\frac{\text{a}-\text{b}}{\text{a}+\text{b}}=\frac{5}{2}\xi \frac{\text{U}}{\text{D}}\frac{\mu }{\text{G}}.$$ (3)

Extension of the theory to the deformation of a viscoelastic body in a cross-slot device

We next extend the relation to the deformation of a viscoelastic body in planar extensional flow. Because the fluid velocity gradient is uniform in a cross-slot and because the fluid forces exerted on a cell are largely dominated by viscous forces that are proportional to this homogeneous velocity gradient, a body moving through the cross-slot’s central region (|x| ≤ D) will be submitted to viscous stresses proportional to τ ∼ μξU/D, assuming the disturbance to the velocity field due to the presence of the cell is small (see details in Supporting Results). Although for an elastic body, the uniform viscous stresses means an instantaneous and constant deformation, the deformation of viscoelastic bodies such as suspended cells changes with time under loading by a constant stress and depends not only on the force magnitude but also on the rate at which the force is applied. One choice of model to capture viscoelastic behavior is the simple two-parameter power law for a time-dependent cell stiffness. This phenomenologic law has been shown to describe cell mechanical behavior for several cell types over a wide range of timescales as measured by several techniques, including optical magnetic twisting cytometry (39, 40), atomic force microscopy indentation (41), and microfluidic constriction channel traversal (17). The power law can be expressed mathematically as (39)

$$\text{G}\left(\text{t}\right)={\text{G}}_0{\left(\frac{\text{t}}{{\text{t}}_0}\right)}^{-\alpha },$$ (4)

where t₀ is an arbitrary reference time, G₀ is the value of the shear modulus at time t₀, and the fluidity parameter α describes the dependence of the shear modulus on time. The case of a purely elastic body is recovered by choosing α = 0, and a Newtonian fluid corresponds to α = 1. For a viscoelastic material with 0 < α < 1, the power-law model predicts that as the deforming force is applied more quickly (smaller t), the material appears stiffer (larger G(t)). A rigorous implementation of this relaxation modulus G(t)—the viscoelastic, time-dependent analog of the shear modulus G for an elastic material—requires a more complicated stress-strain relationship involving an integral in time. This constitutive law would need to be incorporated into the time-dependent version of the governing equations for the solid undergoing infinitesimal deformations, which are more complicated than the steady-state versions used to derive Eq. 3. In a simplistic approach, we will not explicitly consider the time-dependent modulus G(t) in the governing equations, but rather will consider the cell to be an elastic sphere with an “effective” shear elastic modulus, G(t_cs), where G(t_cs) is G(t) evaluated at timescale t_cs of cross-slot deformation. Thus, we have taken a phenomenological approach as opposed to a rigorous mechanics derivation by replacing G in Eq. 3 with G(t_cs). We show below that, despite these simplifications, this power-law adequately describes our own measurements of suspended cells.

We observed the deformation of single cells at the time point nearest to the stagnation point and thus extract the time-dependent shear modulus at a certain time after the start of deformation. By varying the flow rate, we sample a range of deformation times and strain rates. Using our knowledge of the well-defined extensional flow field, we calculate the average time of deformation at a given flow rate experienced by the cells as they travel from the end of the channel toward the stagnation point. This time of deformation is expected to scale with D/U. By symmetry, we considered the upper quadrant of the cross-slot defined by x > 0 and y > 0. When entering the cross-slot, the body travels at a velocity of the extensional flow field, v = ui + vj, where u(x) = −Ωx and v(y) = Ωy. Therefore, choosing t = 0 to be the point in time where the body enters the cross-slot region at |x| = D and starts being exposed to the extensional stresses, integration along the streamline yields the x coordinate of cell position to be x = Dexp(−Ωt). This is equivalent to a time of extensional deformation t = −1/Ωln(|x/D|) for an object that started at x = D at t = 0 and is now located at a new x < D after flowing entrained in the extensional flow field. We restrict the analysis to bodies whose centers are located in the region where x є [0;D/2] and y є [0;D/2], equivalent to our experimental criteria that bodies are imaged close to the stagnation point. The average time of deformation for cells observed in the region x,y є [0, D/2] is therefore

$${\text{t}}_{\text{cs}}=\frac{-1}{\text{D}/2}\underset{0}{\overset{\text{D}/2}{\int }}\frac{1}{\Omega }\text{ln}\left(\frac{\text{x}}{\text{D}}\right)\text{dx}=\frac{1+\text{ln}\left(2\right)}{\Omega }.$$ (5)

This equation yields the expected scaling with D/U, apparent when rewritten as t_cs = (1 + ln(2))D/(ξU). Notwithstanding this result, we note that any other choice of zone is possible; both derivation methods for the normalized velocity, ξ, and the time spent in the cross-slot, t_cs, would have remained valid and would have just led to different final equations. For instance, choosing the entire cross-slot would have led to t_cs = 1/Ω.

This derivation of t_cs assumes that the cell travels at the fluid velocity. We performed several particle-tracking measurements and found that, within experimental error, cells traveled close to the expected maximum fluid velocity (see Fig. S9 for details). Our results are supported by theoretical and simulation results from Guck and colleagues showing that objects travel at >90% of the maximal fluid velocity when the degree of confinement is r_cell/R_eq < 0.4 where r_cell is the cell diameter and R_eq is the equivalent channel radius (Fig. 2 A in (19)). Defining R_eq based on the hydraulic mean radius of our rectangular channels (R_h = 23 μm), these results predict that cells with diameter r_cell < 9.2 μm travel at >90% of the maximal fluid velocity. Thus, r_cell < 9.2 μm is an upper bound on cell size for the range of applicability of our model. The histograms of cell size presented in Fig. S4 show that the cells measured are below this upper bound, with an average cell radius around 7 μm.

Combining Eqs. 3, 4, and 5, we present the following analytical relation that relates the observed body deformations with the cross-slot dimensions, the suspending fluid viscosity, and the applied flow rate via two fitting parameters, α and G₀, that describe the body’s viscoelastic behavior:

$$\epsilon =\frac{5}{2}\frac{\mu }{{\text{G}}_0}{\left(\frac{1+\text{ln}\left(2\right)}{{\text{t}}_0}\right)}^{\alpha }{\left(\frac{\xi \text{U}}{\text{D}}\right)}^{1-\alpha }.$$ (6)

G₀ corresponds to the apparent stiffness for a given time, t₀. In our analysis of cell deformation, we will choose t₀ = 5 ms, the average t_cs across all cell experiments, as a timescale that is naturally suited to the apparent stiffness.

Experimental validation of the deformation of an elastic body in a cross-slot device

To experimentally assess the validity and accuracy of the model, we performed studies on a model elastic body whose mechanical properties had been previously determined using other systems. Our theory required that this body be initially spherical and that it deform at low Reynolds number. We chose Sephadex G200 cross-linked dextran beads with diameters ranging from 40 to 100 μm, which are the most deformable of all commercially available Sephadex beads due to their large porosity. These particles are spherical in a stress-free state and deformed in cross-slot experiments operated at low Reynolds number (0.001 < Re < 0.1). Our experimental system required that the average flow velocity, U, be <∼0.18 m/s, as velocities above this value precluded accurate tracking of deformations.

We introduced Sephadex G200 beads into our cross-slot device and observed deformations in the vicinity of the stagnation point (Fig. 2 A). Since with the employed magnification, a Sephadex bead is typically 50–100 pixels in diameter, the lowest strains (engineering strains) detectable for an individual Sephadex is of the order of 1% (the fitting of an ellipse rounds up or down to the nearest pixel). By employing solutions of varying viscosities (105, 179, and 201 mPa·s) and flow rates (2.5–40 mL/h), we sampled a wide range of strain rates (ξU/D ∼ 65–1300 s⁻¹). As predicted by Eq. 3, the mean particle deformation was linearly related to the applied stress, with a shear modulus (slope) of G = 8.6 ± 0.5 kPa (Fig. 2 B).

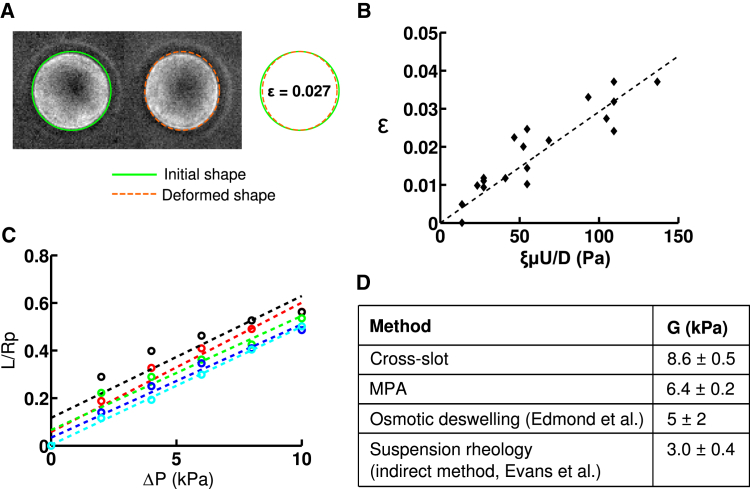
Figure 2.

Validation of cross-slot mechanical measurements with cross-linked dextran hydrogel particles. (A) Time-lapse of a Sephadex G200 cross-linked dextran particle stretching in extensional flow as it passes through the stagnation point region. The shear modulus is extracted from the observed deformation. Cross-slot dimensions are 400 μm wide and 200 μm deep. The strain rate is ξU/D ∼ 520 s⁻¹ at a 20 mL/h flow rate. Right: Overlay of the ellipses manually fitted to images of the dextran particle at the entrance of the cross-slot region and at the location closest to the stagnation point. The deformation was chosen to be an average case of all observed deformations. (B) Deformation of Sephadex G200 beads as a function of the applied stress. Suspending fluids with three viscosities were used, μ = 105 mPa·s, 179 mPa·s, and 201 mPa·s. A linear regression of ε = 5ξμU/(2GD) provides the shear modulus of G = 8.6 ± 0.5 kPa. Reported uncertainties of our measurements are the standard errors of the mean values of the population of dextran beads. (C) Micropipette aspiration of Sephadex G200 beads. The entry length, L, is normalized by the micropipette radius, R_p, and plotted as a function of the applied pressure, ΔP. Each color represents a different bead (n = 5 beads), and the shear modulus is inversely proportional to the slope. (D) Comparison of shear-modulus values obtained with our cross-slot measurements, our MPA measurements, and previously published values based on osmotic deswelling (43) and suspension rheology (44). To see this figure in color, go online.

We then validated these stiffness measurements by performing MPA experiments on the same Sephadex G200 beads in the same suspending PEG/PBS medium (Fig. 2 C). Application of linear elasticity theory (42) to relate the entry length of the dextran beads inside the micropipette with the aspiration pressure yielded shear moduli of G_asp = 6.4 ± 0.2 kPa. This is in reasonable agreement with our cross-slot measurement and in order-of-magnitude agreement with previous measurements by osmotic deswelling (43) and suspension rheology (44) (Fig. 2 D). Microscale mechanical measurements are expected to be more sensitive than bulk measurements to microscopic structural inhomogeneities, such as defects or variations in cross-linking density (45). This means that measured values are quite sensitive to the method of force application. For instance, localized application of force (aspirating one region of particle in MPA) could be expected to give different results than more homogeneous applied forces (elongation in a uniform velocity gradient in cross-slot microfluidic devices) that may present a more averaged response that masks microparticle structural inhomogeneity. Furthermore, each method makes simplifying assumptions to extract material properties from primary measurements such as deformation, thereby introducing systematic error that is not included in reported measurement uncertainty, typically a population standard deviation or standard error of the mean.

Measuring the viscoelastic properties of 3T3 and GBM TICs

Having validated our analysis and experimental platform, we progressed to measuring mechanical properties of living cells. For proof-of-principle studies, we focused on NIH 3T3 fibroblasts, which have been mechanically characterized by AFM (46, 47), optical stretching (48, 49), and MPA (50). To explore the potential of our cross-slot device for novel discovery, we also characterized GBM TICs, a stem-like subpopulation of GBM tumors thought to drive tumor initiation, recurrence, and therapeutic resistance (26, 51, 52). Importantly, manipulation of mechanics and mechanotransductive signaling in GBM TICs was recently shown to significantly reduce tissue invasion and extend survival (53).

Our model’s assumption that the deforming body is initially spherical is a reasonable approximation for cells in suspension in general (54), and for circulating white blood cells in particular (55, 56). For a subset of cells, we measured a deformation (mean ± SE) of ε = 0.0004 ± 0.004 (n = 21,) and ε = 0.007 ± 0.003 (n = 28) for 3T3 and GBM TICs, respectively, before entry into the central region of the cross-slot (each sample set taken from two separate experiments on two different days). As another measure of cell sphericity, we also evaluated cell circularity index, defined as c = 4πA/(P²) where A is the cell area and P is the cell perimeter. (A value of c = 1 indicates a perfect circle and a value of c = 0 indicates a line.) From the ellipses manually fitted to the same subset of cells, we found c = 0.998 ± 0.001 and c = 0.998 ± 0.001 for 3T3 cells and GBM TICs, respectively, showing that cells are spherical before entering the cross-slot central region.

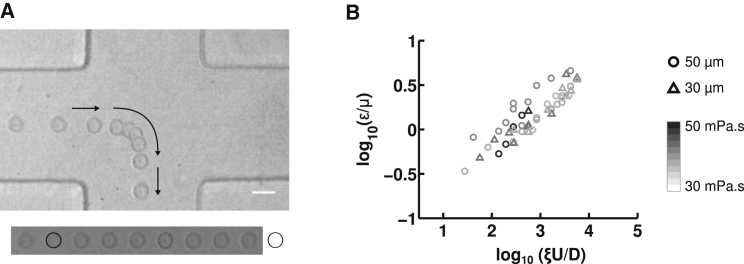
In separate experiments, we infused both cell types through the device at various flow rates (50–1400 μL/h) that produce a wide range of strain rates (ξU/D ∼ 280–6800 s⁻¹) and imaged cellular deformations at the stagnation point as with the Sephadex particles (Fig. 3 A). We found that the deformation agreed well with the power-law model in Eq. 6, as demonstrated by the linearity of the log-log plots of cell strain, ε, versus cross-slot velocity gradient ξU/D (Fig. 4, B and C). This relationship continued to hold when we independently varied cross-slot width (w = 2D), fluid viscosity (μ), and flow rate (determines average flow velocity, U = Q/A), which are the three tunable parameters in the power-law model (Fig. 3 B).

Figure 3.

Measurement of cellular viscoelastic properties. (A) Time-lapse images of a 3T3 fibroblast stretching in extensional flow as it passes through the stagnation point region. Arrows denote the direction of movement. Viscoelastic power-law constitutive model parameters are extracted from the observed deformation. Cross-slot dimensions are 100 μm wide and 30 μm deep and the strain rate is ξU/D ∼ 1690 s⁻¹ at a 500 μL/h flow rate. The time between images is 0.5 ms, and the scale bar is 20 μm. We can observe that cell deformation increases as cells pass through the central region of the cross-slot, as is further detailed in Fig. S5. (B) Control TIC cross-slot deformation at various flow rates in devices of varying dimensions and for different suspending fluid viscosities. Each data point represents a separate experimental condition, with 10 ≤ n ≤ 30 fitted for the reported average deformation. Marker color indicates fluid viscosity, μ, using a gray scale (from white, 30 mPa·s, to black, 50 mPa·s), and the pattern indicates the cross-slot half-width, D (triangles, 35 μm; circles, 50 μm). Flow rates varied between 10 μL/h and 1000 μL/h. Height was kept constant at 30 μm.

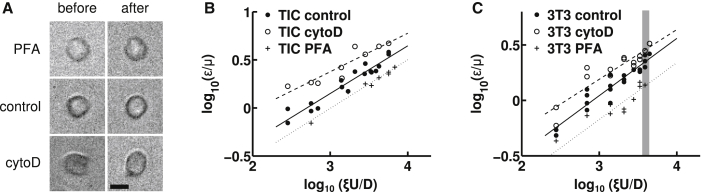
Figure 4.

Softening and stiffening effects of drugs that affect the cytoskeleton on TIC and 3T3 deformations measured in the cross-slot. (A) Images of 3T3 fibroblasts before (left) and during (right) deformation by the extensional flow in the cross-slot. We took a cell from all three cases: incubation in PFA (top), control (middle), and incubation in cytochalasin D (bottom). In all three cases, ξU/D ∼ 4100 s⁻¹. Cells were chosen to be representative of the average deformation at this strain rate. The scale bar is 10 μm. (B and C) Linear regression of the log-log plots based on ε = 5ξμU/2GD (solid lines, control; dashed lines, cytoD, dotted lines, PFA) yield the cell power-law material properties under control and drug conditions; the fluidity parameter, α, is obtained from the slope and the shear modulus, G₀, at a specified timescale, t₀ = 5 ms, is obtained from the intercept. The cross-slot deformations of both GBM TICs (B) and 3T3 fibroblast cells (C) are consistent with the power-law model, as indicated by the linearity of the log-log plots. Each data point represents a separate experimental condition (i.e., the ξU/D strain rate and drug condition), with 10 ≤ n ≤ 30 cells fitted for the reported average deformation. In (C), the gray zone corresponds to the strain rate chosen for the cells in (A). For clarity, error bars reflecting the uncertainty in strain measurements (mean ± SE) is omitted. See Fig. S6 for versions of (B) and (C) with vertical error bars and Table S3 for the cross-slot extensional strain rate (ξU/D), strain (ε), and strain uncertainty for each point plotted in (B) and (C).

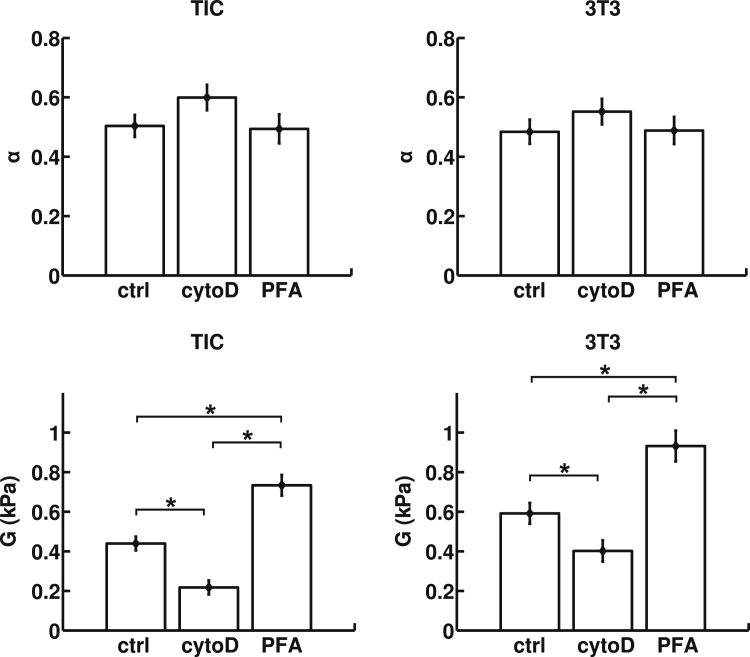
The power law relationship in Eq. 6 predicts that a log-log plot of viscosity-normalized strain (ε/μ) versus strain rate (ξU/D) would be linear and may be fitted to extract the cellular shear modulus (G) and fluidity parameter (α). Accordingly, for 3T3 cells, we obtained a shear modulus of G₀(t₀) = 0.59 ± 0.05 kPa (Fig. 5) for t₀ = 5 ms. Previous measurements on suspended 3T3 cells using optical stretchers yielded shear moduli of ∼70–80 Pa ((49); extracted from Figs. 2 A and 3 B from (49)) and 100 ± 10 Pa (extracted from Fig. 2 from (48)) for a deformation timescale of t = 200 ms. In turn, if we set our timescale t₀ to 200 ms in our cross-slot experiment, we find that G₀(200 ms) = 101 ± 8 Pa, which is very consistent with the values found using an optical stretcher. For GBM TICs, we measured a stiffness of G₀(t₀) = 0.44 ± 0.03 kPa. Again, this value is in close proximity to previous AFM measurements on this same cell line that found values of 0.8–0.9 kPa (53). The measured cell fluidity parameter was similar for both cell types: α = 0.48 ± 0.04 for 3T3 cells and 0.50 ± 0.04 for TICs.

Figure 5.

Power-law material parameters, the fluidity parameter, α, and the shear modulus, G = G₀(t₀), evaluated at the average timescale of cell cross-slot deformation, t₀ = 5 ms for GBM TICs and 3T3 fibroblasts under different pharmacological interventions. The values of α and G are determined by linear regression, and the error bars are derived from analysis of covariance. Although the fluidity of the cells does not change appreciably, both cell types are significantly softened by CytoD and stiffened by PFA (^∗p ≤ 0.01).

We next explored the sensitivity of the measurement to perturbations of cytoskeletal assembly and mechanics. For our softening studies, we used CytoD (10 μM), which has been previously shown to disrupt the 3T3 actin cytoskeleton (57, 58). As expected, inhibition of actin polymerization by treatment with CytoD increased cellular deformation at all strain rates and reduced shear modulus (0.40 ± 0.05 kPa for 3T3 cells and 0.22 ± 0.04 for TICs). Those values are statistically significantly different from the control case, with p ≤ 0.01 between all groups (see Table S2 for individual p-values). Conversely, covalent cross-linking of cells with PFA increased the shear modulus (0.93 ± 0.08 kPa for 3T3 cells and 0.73 ± 0.05 for TICs). Here, also, the values were statistically different from the control case, with p ≤ 0.01 between all groups. Despite these changes in stiffness, neither CytoD nor PFA produced statistically significant changes in fluidity for either cell type.

Discussion

Cellular mechanical properties serve as a powerful and promising label-free marker for gaining insight into molecular changes within the cell or characterizing different cellular states for potential diagnostic information. Recent advances in microfluidic technology have allowed the high-throughput measurement of cellular mechanical properties with single-cell resolution. Such platforms are strongly positioned to detect potential differences in rare subpopulations of cells that may drive disease progression, which would otherwise be masked in bulk- or population-based mechanical measurements. To improve on previous studies, we have developed an analytical equation for a simple PDMS-based microfluidic platform to measure and quantify cellular mechanical properties. The strength of our model lies in its simplicity, with a single equation that uses easily obtainable parameters, as well as its adaptability, as it can be readily extended to account for other viscoelastic material laws.

It is interesting to note that although at least one previous study (13) has successfully captured changes in stiffness and correlated these differences to phenotype, the authors did not report changes in stiffness when cells were treated with cytoskeletal depolymerization drugs. The authors hypothesized that this may be because the high strain rates in their system (ξU/D ∼2 × 10⁵ s⁻¹) effectively fluidize the cytoskeleton and are instead dominated by the viscous properties of the cytosol and chromatin. Consistent with this explanation, the lower strain rates employed in our device (300 ≤ ξU/D ≤ 7000 s⁻¹) and many other single-cell platforms (e.g., optical tweezers) would facilitate measurement of cytoskeletal mechanics. Key to achieving this regime is our use of high-viscosity fluid medium (μ ∼40 mPa·s), which enabled us to achieve similar stresses and cellular deformations at much lower strain rates, similar to those of Guck and colleagues, who used a viscosified suspending solution of μ = 15 mPa·s (19). Another factor that may contribute to the ability to detect the effects of cytoskeletal depolymerization drugs is the magnitude of cell strain. A different high-throughput device from Di Carlo and colleagues (15) extended cells asymmetrically with pinching sheathing flows so that the leading edge of the cell experienced higher shearing stresses than the trailing edge. The device was operated at strain rates (ξU/D ∼ 1 × 10⁵ s⁻¹, though this is a less accurate estimate, because the flow is not pure extensional flow) similar to those in their cross-slot device in (13), but deformed the cells less. The high-strain-rate cross-slot device in (13) deformed cells to strains of ε ∼ 0.32 for control and depolymerization-drug-treated cells, whereas the pinched-flow stretching device in (15) deformed control cells to ε ∼ 0.15 and treated cells to ε ∼ 0.2–0.3. Our high-viscosity cross-slot system only deformed cells up to a maximum of ε = 0.18, a relatively small strain. Consequently, we were able to detect the effect of both softening (CytoD) and stiffening (PFA) interventions in two different cell lines. Moreover, these interventions did not significantly change cell fluidity, further consistent with the notion that the strain rates we imposed were insufficient to fluidize the cytoskeleton.

Although our stiffness measurements of both the Sephadex beads and 3T3 cells are of the same order of magnitude as previously published results, there is still a slight variation among all the values, as well as among previously published results. These variations may be due to differences in measurement modalities across these reports. Although the cross-slot platform measures the deformation on a 1–10-ms timescale, the other methods employed (AFM, MPA, osmotic deswelling, and suspension rheology) are performed on a 1–10-s timescale. Additionally, previous measurements have shown that Sephadex bead stiffness increases by ∼30% when the deformation timescale is decreased from 10⁴ to 10 s (44). Hence, we speculate that when decreasing the timescale farther from 1 s to 1–10 ms, one would expect some moderate stiffening to occur.

Similarly, for 3T3 cells, reduced timescales unsurprisingly seem to lead to higher apparent stiffnesses. Indeed, in another study, a millisecond-timescale platform measured higher cellular stiffness values than did AFM, which typically involves measurements on the timescale of seconds (59). In the future, it would be valuable to measure bead or cellular mechanical properties across various timescales within the same device. These studies would clarify the exact relationship between the timescale of measurement and the resulting values. Modulation of the viscosity of the suspension medium within our device, as well as the flow rate and the device dimensions, may offer the opportunity to systematically explore these timescales.

We also note some differences in cell deformation behavior in pure extensional flow in a cross-slot channel compared to previous observations of red blood cell deformation in extension-dominant but nonzero shear flows in a converging-width channel. In a channel converging linearly from large (100 μm wide) to small (20 μm wide) widths over a downstream distance of 70 μm (height a constant 40 μm), four modes of deformation, stretching, twisting, tumbling, and rolling, were observed for cells at different cross-stream positions (23). The stretching mode occurred for red blood cells on the channel centerline where the velocity gradient was symmetric about the cell. In our study, although we did observe rolling of cells with visible defects in the entrance channels of the cross-slot device (shear dominant Poiseuille flow), we never observed tumbling or rolling in the stagnation-point region (pure extensional flow), only stretching. The existence of one deformation mode in extensional flow—stretching—is expected from cell-mimetic vesicle simulations (60, 61) and experiments (37, 62). Thus, the differences in our observation of one deformation mode compared to the previous four modes of deformation are a result of the different flow fields. In our cross-slot system, the close proximity of the top and bottom walls of the 30-μm-deep channel prevents pure planar (z-independent) extensional flow. However, our observations that cells only stretch near the stagnation point indicates that any shear velocity gradient effects due to the top and bottom walls contribute negligibly to cell deformation. This stands in contrast to the study described earlier in which four modes of deformation were observed (23), which featured significant, nonzero shear components in straight, narrow regions of the channel downstream of the extension-dominant converging section.

Conclusions

We have developed an experimental and analytical strategy to measure cellular mechanical properties based on deformations within a microfluidic cross-slot device. By creating measurement conditions that reduce strain rates and developing an analytical model, we successfully detected perturbations to cytoskeletal assembly and mechanics, which is a significant innovation for cross-slot-based systems and enables comparison with more traditional single-cell mechanics measurements. We envision that this technology will prove valuable for the rapid mechanical characterization of living cells in suspension, thereby accelerating fundamental studies of cellular mechanics and establishing a platform for future diagnostic technologies.

Author Contributions

S.J.M., S.K., L.G., J.B.D., and J.G.L. designed research; L.G., J.B.D., and J.G.L. performed research; A.I.B., J.H., S.J.M., and S.K. supervised research; L.G., J.B.D., and J.G.L. analyzed data; and all authors wrote the manuscript.

Editor: Alexander Dunn.

Supporting Citations

Reference (63) appears in the Supporting Material.