Segmentation of 3D Trajectories Acquired by TSUNAMI Microscope: An Application to EGFR Trafficking

Abstract

Whereas important discoveries made by single-particle tracking have changed our view of the plasma membrane organization and motor protein dynamics in the past three decades, experimental studies of intracellular processes using single-particle tracking are rather scarce because of the lack of three-dimensional (3D) tracking capacity. In this study we use a newly developed 3D single-particle tracking method termed TSUNAMI (Tracking of Single particles Using Nonlinear And Multiplexed Illumination) to investigate epidermal growth factor receptor (EGFR) trafficking dynamics in live cells at 16/43 nm (xy/z) spatial resolution, with track duration ranging from 2 to 10 min and vertical tracking depth up to tens of microns. To analyze the long 3D trajectories generated by the TSUNAMI microscope, we developed a trajectory analysis algorithm, which reaches 81% segment classification accuracy in control experiments (termed simulated movement experiments). When analyzing 95 EGF-stimulated EGFR trajectories acquired in live skin cancer cells, we find that these trajectories can be separated into three groups—immobilization (24.2%), membrane diffusion only (51.6%), and transport from membrane to cytoplasm (24.2%). When EGFRs are membrane-bound, they show an interchange of Brownian diffusion and confined diffusion. When EGFRs are internalized, transitions from confined diffusion to directed diffusion and from directed diffusion back to confined diffusion are clearly seen. This observation agrees well with the model of clathrin-mediated endocytosis.

Introduction

Single-molecule detection in aqueous solution has advanced our knowledge in molecular and cellular biology since its introduction in early 1990s (1, 2, 3). Whereas single-molecule imaging has led to the development of pointillism microscopy (4), such as PALM (5, 6) and STORM (7), complex molecular trafficking and interaction dynamics inside live cells often cannot be deciphered by pointillism microscopy because of its limited temporal resolution (8). For nearly four decades, cellular dynamic processes have been probed using two ensemble and time-averaging techniques—fluorescence recovery after photobleaching (FRAP (9)) and fluorescence correlation spectroscopy (FCS (10)). Although FRAP and FCS provide sufficient temporal resolution (submilliseconds) to monitor fast molecular dynamic processes, their spatial resolution is limited by diffraction (11). Alternatively, rapid molecular dynamics can be studied at high spatial resolution using single-particle tracking (SPT (11, 12, 13, 14, 15, 16, 17, 18, 19)). Whereas SPT has made important discoveries that change our view of plasma membrane organization (17, 19) and molecular motor dynamics (20), the use of SPT in monitoring “intracellular” processes is rather limited because of the lack of three-dimensional (3D) tracking capacity that can follow a single particle inside a live cell for a long period of time. In the past decade, new SPT techniques have been developed to visualize molecular motion in the 3D space (termed 3D-SPT), including multiple imaging planes (21, 22), orbital tracking (23, 24, 25), point spread function engineering (26, 27), and confocal tracking (28, 29). Although allowing for direct observation of transport processes from membrane to cytoplasm, current 3D-SPT methods often suffer from shallow imaging depth (because of the use of one-photon excitation) and limited z-tracking range (e.g., astigmatism-based, nonfeedback tracking systems (27)), which prevent these methods from tracking single molecules inside multicellular models such as spheroids (see our review in (8)).

Our group has recently developed a new, to our knowledge, 3D-SPT method termed TSUNAMI (Tracking of Single particles Using Nonlinear And Multiplexed Illumination) that enables high-resolution tracking of single epidermal growth factor receptor (EGFR) complexes in live cancer spheroids (∼100 μm thick), with track duration up to 10 min and vertical tracking depth up to tens of microns (30, 31, 32, 33). As a wealth of information about membrane structure, interior organization, and receptor biology can be derived from the long 3D trajectories acquired by TSUNAMI, a sophisticated tool is needed to segment and classify these trajectories according to their motional modes (34, 35, 36, 37), extract physical parameters of the motion (30, 38), and correlate that motion to the surrounding environment (39), all with the goal of understanding the physical scenarios behind the observed motion (40, 41). Considerable effort has been devoted to the identification of change points in motion (36) or diffusivity (38) along the same trajectory and to the visualization of spatial regions with different dynamic behaviors (34, 35, 38, 42). Such an analysis is called trajectory segmentation and classification (11), which is often carried out by calculating a number of classification parameters over the trajectory using methods such as rolling window analysis (34, 36, 43), supervised segmentation (44), mean-squared-displacement (MSD) curvature (34, 35, 45, 46), maximum likelihood estimator (38), Bayesian methods (47, 48), F-statistics (49), hidden Markov model (50, 51), and wavelet analysis (42, 52).

In this study, we demonstrate an integrated trajectory analysis tool that adopts a combination of analytical strategies (34, 35, 36, 37, 39) and classification parameters (MSD scaling exponent (53, 54, 55, 56), directional persistence (36, 57), and confinement index (37, 58)) in achieving effective segmentation and classification of both simulated and real-world trajectories. Our algorithm has achieved 81% accuracy in classifying segments along simulated 3D trajectories. From visual inspection, we find most of the misidentified segments near the change points of different motional modes. When analyzing 95 EGF-stimulated EGFR trajectories acquired in live skin cancer cells, we find that these trajectories can be separated into three groups—immobilization (24.2%), membrane diffusion only (51.6%), and transport from membrane to cytoplasm (24.2%). When EGFRs are membrane-bound, they show an interchange of Brownian diffusion and confined diffusion. When EGFRs are internalized, transitions from confined diffusion to directed diffusion and from directed diffusion back to confined diffusion are clearly seen. As expected, the speed observed in the directed diffusion matches well with the speed of the typical molecular motor-mediated transport (0.5–2 μm/s) (59, 60, 61, 62). When compared with the stimulated EGFRs, the untreated EGFRs clearly show increased mobility on membrane. Reduced mobility for stimulated EGFRs is likely due to EGFR dimerization (50, 63), which induces endocytosis (64).

Materials and Methods

TSUNAMI tracking microscope

TSUNAMI is a feedback-control tracking system that employs a spatiotemporally multiplexed two-photon excitation and temporally demultiplexed detection scheme (Figs. S1 and S2 in the Supporting Material). Submillisecond temporal resolution (under high signal-to-noise conditions) and subdiffraction tracking precision in all three dimensions have been previously demonstrated (30). Tracking can be performed at depths up to 200 μm in highly scattering environments (30, 31).

Excitation of 835 nm from a Ti:Al₂O₃ laser (Mira 900, Coherent, Santa Clara, CA) is used for tracking experiments. Following the optical multiplexer, the beams pass through a galvo scanning system (6125H, Cambridge Technology, Bedford, MA), before being focused through a 60 × N.A. 1.3 silicone oil objective (UPLSAPO 60X, Olympus, Center Valley, PA). The total laser power was ∼8mW at the objective back aperture. For a typical 40 nm red fluorescent bead (F8770, Thermo Fisher Scientific, Waltham, MA), photon count rates were in the range of 200–500 kHz. Background fluorescence signal was on the order of 3 kHz that includes a 150 Hz background signal from the detector. Signal-to-noise ratios were typically above 20. Demultiplexed detection is performed electronically via time-correlated single-photon counting (TCSPC) analysis. Fluorescence signals are detected by a cooled GaAsP photomultiplier tube with 5 mm square active area (H7422PA-40, Hamamatsu, Bridgewater, NJ) in nondescanned configuration. The current output from the PMT is amplified through a 2 GHz cutoff bandwidth preamplifier (HFAC-26, Becker and Hickl, Berlin, Germany) and sent into a photon-counting board (SPC-150, Becker and Hickl, Berlin, Germany) to be counted and correlated to the 76 MHz reference clock of the laser oscillator. The instrument response function (IRF) is measured to be 230 ps FWHM. Every 1–20 ms a photon histogram is sampled from the TCSPC module and processed in the software loop run in LabVIEW (National Instruments, Austin, TX). The tracking algorithm employs a proportional control to convert the error signals to new stage positions. New voltages are sent out through a DAQ card (PCIe-6353, National Instruments, Austin, TX) to their respective actuators—galvo mirrors for x and y tracking and piezo objective stage for z tracking. The saved voltages are converted to build a 3D tracking trajectory.

Trajectory segmentation and classification

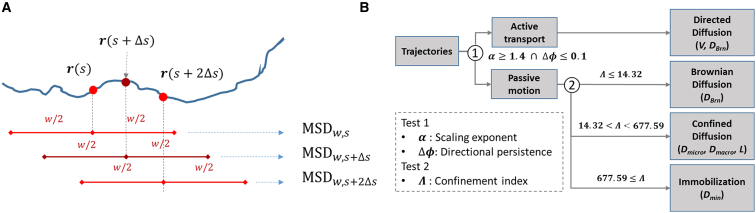
We have developed a procedure to perform trajectory segmentation and classification (Fig. 1). First, a temporal rolling window of length w centered at time s on the trajectory (34, 36) is adopted for calculating the segmented MSD at s (MSD_w,s, Fig. 1 A). As the motional mode of the tracked particle can vary significantly from one segment to another, a wide distribution of the segmented MSD curves is expected. We then perform a two-step test (Fig. 1 B) to classify the motion of each segment into four modes: 1) directed diffusion, 2) Brownian diffusion, 3) confined diffusion, and 4) immobilization. Within each segment only one of these motional modes is assigned.

Figure 1.

Procedure for segmentation and classification of trajectories. (A) The rolling window analysis is conducted at a given time point s with the length of rolling window of 1.6 s (w = 1.6 s) and the sliding time step (Δs) of 0.1 s. (B) The transient behaviors of a trajectory are identified using the three classification parameters: scaling exponent of MSD curve (α), directional persistence (Δϕ), and confinement index (Λ). The MSD curve of each segment is fitted with the proper model to extract the dynamic parameters including V, D_Brn, D_micro, D_macro, L, and D_min. To see this figure in color, go online.

The first step of the test is to differentiate directed motion (active transport) from Brownian diffusion, confined diffusion, and transient immobilization (passive motion) by evaluating two parameters from the segmented trajectories and their derived MSD curves—scaling exponent (α) (34) and directional persistence (Δϕ) (36). By fitting each segmented MSD curve with the following power-law equation (41), a single α value is obtained and is assigned to each time point s along the trajectory as follows:

$$\text{MSD}\left(t\right)\sim t^{\alpha }.$$ (1)

Directional persistence function (Δϕ) in a temporal rolling window of length w centered at time s is defined as (36) follows:

$$\Delta \varphi \left(t\right)={\langle {\left(\varphi \left(t^{\prime }+t\right)-\varphi \left(t^{\prime }\right)\right)}^2\rangle }^{\frac{1}{2}},t^{\prime }\in \left[s-\frac{w}{2},s+\frac{w}{2}\right],$$ (2)

where ϕ is the directional vector at each data point (see Fig. S3 B). Although, each rolling window centered at s generates a directional persistence function Δϕ(t), we use the single value, Δϕ(w/4), to represent the direction persistence Δϕ at s. The time lag of w/4 is chosen in consideration of the microtubule bending during a motor-driven event (36). The Δϕ is equal to zero when the motion is unidirectional. Similar angle analysis (e.g., jump angle analysis) is used to probe diffusion bias inside nucleus (65, 66).

The segment at time s is classified as active transport when α ≥ 1.4 and Δϕ ≤ 0.1 (test 1 in Fig. 1 B). Otherwise the segment is classified as passive motion (threshold optimization is discussed in the Supporting Material and Fig. S4). In the complex intracellular environment, the active transport along microtubules has α values ranging from 1.4 to 2 (53). Whereas some biological studies also used the α value of 1.4 as a criterion for classification (54, 55), an α value of 1.7 was used in a microfluidic experiment (36). In the same report, the criterion of Δϕ ≤ 0.1 was found suitable to achieve sufficient discrimination between active and passive motion (36). The threshold values of α and Δϕ have also been validated in our simulated movement experiment (SME; see the detailed discussion on SME below).

The second step of test is to classify passive motion into Brownian diffusion, confined diffusion, and immobilization by evaluating confinement index (Λ) from the segmented trajectories (test 2 in Fig. 1 B). Confinement index (Λ) is defined as (37, 58) follows:

$$\Lambda =\frac{D_{max}w}{var\left(r\right)},$$ (3)

where D_max is the unconstrained diffusivity of particles and var(r) stands for the variance of particle positions (r) within a temporal rolling window of length w. In the early reports, confinement index is defined as the ratio of D_maxw and $r_{max}^2$, where r_max is the largest displacement from the starting point within the rolling window (43). Under Brownian diffusion, $r_{max}^2$ scales linearly with D_maxw. But when the particle is confined in a domain of linear size L, $r_{max}^2$ is limited by L². Thus the value of Λ becomes significantly larger than that in Brownian diffusion. In Eq. 3, $r_{max}^2$ is replaced with var(r) in the Λ calculation. As a result, Λ becomes the ratio of the variance of Brownian diffusion (D_maxw) and the variance of trajectory segmented under study (var(r)). This modified definition of Λ has advantage in detecting confinement in a wider class of trapping potential shapes (37). Two threshold values were selected: Λ_Brn = 14.32 and Λ_Im = 677.59. Based on these thresholds, trajectories were classified into Brownian diffusion (Λ ≤ Λ_Brn), confined diffusion (Λ_Brn < Λ < Λ_Im), and immobilization (Λ ≥ Λ_Im). Threshold optimization is discussed in Discussion (also see Fig. S5).

For trajectory segmentation and classification, the length of temporal rolling window (w) should be sufficiently long to ensure good estimation of α, Δϕ, and Λ (36). On the other hand, the w should be kept short to maintain decent temporal resolution. Optimization of rolling window length is discussed in the Supporting Material (Fig. S4). We found that the reasonably short rolling window of 1.6 s (w) can effectively differentiate active transport from passive motion (Fig. S4) and distinguish confined diffusion from Brownian diffusion (Fig. S5). The sliding time step (Δs) for the rolling window analysis is set as 0.1 s, whereas the time step for position acquisition (Δt) is either 2.5 ms for simulated trajectories or 20 ms for experimental trajectories. In our simulations, we also found that the confinement index of Brownian motion is independent of the rolling window length (w), but the scaling exponent (α) of directed diffusion, the directional persistence (Δϕ) of directed diffusion, and the confined index (Λ) of confined diffusion are all functions of the rolling window length (Figs. S4 and S5).

Extracting dynamic parameters from MSD

The typical approach to analyze a single-particle trajectory starts with the calculation of MSD, which describes the average squared distance $\left(r^2\right)$ that the particle has explored in space at a given time lag (t) (see Fig. S3 A). Because the cellular environment is highly crowded with a compartmentalized structure, the dynamics for receptors, even of the same type, can be highly heterogeneous (67). Observed motion in a live cell can be comprised of periods of Brownian diffusion, directed diffusion, confined diffusion, and transient immobilization, all within an individual receptor trajectory. For Brownian diffusion, the MSD can be calculated as the variance of the solution to the Fick’s law of diffusion and it scales linearly with t as follows:

$$\text{MSD}\left(t\right)=\langle {\left(\mathit{r}\left(t^{\prime }+t\right)-\mathit{r}\left(t^{\prime }\right)\right)}^2\rangle =2d{D}_{Brn}t,$$ (4)

where d represents the dimensionality of the space in which the motion takes place, D_Brn is the Brownian diffusion coefficient, and r is the position vector of the particle.

Directed diffusion corresponds to the superposition of a ballistic movement and Brownian diffusion. It is characterized by the following quadratic scaling relationship (68):

$$\text{MSD}\left(t\right)=2d{D}_{lateral}t+{\left(Vt\right)}^2,$$ (5)

where V represents the speed of the ballistic movement that is most likely caused by molecular motor-assisted active transport along microtubules. As Brownian diffusion is most noticeable in the lateral direction of ballistic movement, D_lateral is used to represent it.

Confined diffusion, the constrained particle diffusion due to receptors being trapped in small cellular compartments such as cortical cytoskeleton, membrane cavities, and vesicles (37), is featured by an abrupt change of slope in the MSD curve (35) after a characteristic equilibration time τ (see Fig. S8 for discussion on various types of confined diffusion). Although the exact expression of MSD depends on the shape of the confining region and on spatial dimensionality, the two-dimensional (2D) MSD of confined diffusion can be approximated by (39, 69)

$${\text{MSD}}_{2D}\left(t\right)\cong \frac{L^2}{3}\left[1-\text{exp}\left(-\frac{t}{\tau }\right)\right]+4D_{macro}t,$$ (6)

where D_macro is the long-term “macroscopic” diffusion coefficient (69) and L is the linear dimension of the confinement. The characteristic equilibration time τ can be related to L by the following (39):

$$\tau =\frac{L^2}{12\left(D_{micro}-D_{macro}\right)},$$ (7)

where D_micro is the short-term “microscopic” diffusion coefficient (39, 69). This intradomain diffusivity D_micro is measured using the same method as described in Brownian diffusion section.

Transient immobilization takes place when the diffusivity falls below a predefined value D_min (1.9 × 10⁻⁴ μm²/s), which is the detection limit of our TSUNAMI microscope (see Fig. S6 for detailed discussion).

MSD curve fitting

Curve fitting of segmented MSD using Eqs. 4–6 can extract local dynamic parameters such as Brownian diffusion coefficient (D_Brn and D_lateral), active transport speed (V), linear dimension of compartments (L), macroscopic diffusivity (D_macro), and microscopic diffusivity (D_micro). For each segment classified as Brownian diffusion, the associated D_Brn is optimally determined using a covariance-based estimator (70). Here we define the instantaneous diffusivity (D₀) as the linear MSD fitting result of each rolling window (regardless the classification result of that rolling window). Since MSD at a longer time lag is averaged over fewer samples (i.e., noisier), typically only the first 1–20 data points in the MSD curve are used for diffusivity estimation in a short time period (35, 69, 71, 72, 73). The optimal number of data points used for D₀ estimation should be determined by expected diffusion coefficient, tracking error, size of time step, and track duration. Considering these factors in our experiments, we estimate D₀ based on the first 3–5 points in the MSD curve. The detection limit of the TSUNAMI microscope is currently at 1.9 × 10⁻⁴ μm²/s (D_min, Fig. S6).

Following the definition of D₀, we define the instantaneous velocity (V_i) as the absolute displacement within a rolling window divided by the length of that rolling window, regardless of the classification result of that rolling window. In this report, D_Brn and V are the dynamic parameters derived from the segments classified as Brownian and directed diffusion, respectively, whereas D_o and V_i are the parameters derived from all segments regardless their classification results. Readers are advised to pay attention to these different notations and their associated definitions.

For segments classified as directed diffusion or confined diffusion, a least squares regression line is fitted through the first N_f points of the MSD curve with each point weighted by the reciprocal of its relative variance var_rel (68):

$$va{r}_{rel}\left(t\right)=\frac{t\left(2t^2+1\right)}{w-t+1},$$ (8)

where w is the length of rolling window and t is the time lag of MSD curve. The values of N_f are typically N/3 (N_f = 16) (74), N/2 (N_f = 28) (75), and 2N/3 (N_f = 50), where N is the number of total MSD data points (34). As a precise measure of the dynamic parameters requires a sufficient number of MSD points, we choose N_f = 40 (N/2, N = 80 (w = 1.6 s and Δt = 20 ms)) in calculating the dynamics parameters of directed and confined diffusion.

Verifying 3D tracking and trajectory analysis algorithm using SME

The accuracy of dynamic parameters extracted from MSD curves is limited by the tracking error of our system. To precisely quantify the tracking error of TSUNAMI microscope, we tracked a fixed fluorescent bead (200 nm, F-8810, Thermo Fisher Scientific) loaded on an independent xyz piezo stage (P-733K130, Physik Instrumente (PI), Karlsruhe, Germany), which is programmed to carry out motion patterns generated by Monte Carlo simulation. This control experiment is termed the SME (Fig. S1) and the simulation-generated trajectory is termed the prescribed trajectory. To characterize the tracking error in a scattering environment, fluorescent beads were embedded in 1.3% agarose within chambered coverglasses. We neglected the finite differences between the Monte-Carlo-simulation-generated trajectory (that was used to command the movement of the xyz piezo stage) and the trajectory that the stage actually performed (determined by the capacitive sensors of the stage). The tracking error of TSUNAMI microscope is defined as the standard deviation of the differences between the stage trajectory and the TSUNAMI tracking trajectory. The tracking error was found less than 20 nm in x and y and ranged from 51–91 nm in z, depending on the diffusivities used in the SME (Fig. S9). In a prescribed motion that mimicked the typical 2D confined diffusion of membrane receptors, the TSUNAMI tracking error was found to be 16 nm in xy and 43 nm in z (Fig. S10). Tracking error can also be caused by the thermomechanical instability of the microscope (69). For 100 s tracking experiments, the static error is found significantly smaller than the dynamic error (Fig. S6).

Cell culture

Used as the model system, EGFR-overexpressed A431 skin cancer cell was purchased from ATCC and grown in DMEM (Dulbecco’s Modified Eagle Medium, 11995-065, Thermo Fisher Scientific) supplemented with 10% fetal bovine serum (16140-071, Thermo Fisher Scientific). The cell cultures were kept in humidified atmosphere with 5% CO₂ at 37°C. Single suspensions were prepared by mild enzymatic dissociation using a 0.25% trypsin/EDTA solution (25200-056, Thermo Fisher Scientific). For EGFR tracking in monolayer cells, A431 cells were seeded onto optical imaging eight-well chambered coverglasses (154534, Thermo Fisher Scientific) with cell density of 1 × 10⁵ cells per well and allowed to adhere overnight.

Multicellular spheroid preparation

Agarose-coated 96-well plates (130188, Thermo Fisher Scientific) were used to cultivate A431 spheroids. Agarose coating was conducted by filling each well with 50 μL DMEM sterilized agarose solution (1.5% by weight, A9539-100G, Sigma-Aldrich). The spheroids were prepared following the procedure described in literature (76) and the plates were incubated for 96 h in humidified atmosphere with 5% CO₂ at 37°C. To generate spheroids with various sizes, single-cell suspensions from liquid overlay culture were seeded onto agarose-coated plates at different cell densities: 125, 250, 500, 1000, 1500, 2000, and 3000 cells per well (Fig. S15). Considering the penetration depth of the cell membrane dye (CellMask Deep Red, C10046, Thermo Fisher Scientific) and the working distance of the objective, spheroids with diameters of 90 to 110 μm (seeding density ∼125 cells per well) were selected for the tracking experiments.

Fluorescent probe labeling to EGFRs

Anti-EGFR antibody-conjugated fluorescent nanoparticles were used to label EGFRs for tracking. Biotinylated monoclonal anti-EGFR IgG (Ab-3, MS-311-B, Thermo Fisher Scientific) was mixed at 1:1 ratio with 40 nm red fluorescent nanoparticles (F8770, Thermo Fisher Scientific) in 1.5% BSA/phosphate-buffered saline solution (BSA, S7806, Sigma-Aldrich). The antibody-conjugated fluorescence nanoparticles (∼30 nM, the stock solution) can be stored at 4°C for up to 1 week. The number of antibodies per nanoparticle should follow a Poisson distribution (77). In our experiments, we cannot rule out the possibility of cross-linking due to conjugating multiple antibodies on a single nanoparticle. The brightness of an antibody-conjugated fluorescent nanoparticle was characterized by fluorescence correlation spectroscopy and tracking of fixed particles (Fig. S16).

Before tracking experiments, both monolayer cells and spheroids were kept under serum-starvation conditions for 24 h. For monolayer samples, cells were stained with CellMask Deep Red (1:1000 dilution in DMEM) for 10 min at 37°C. For spheroid samples, spheroids were transferred from a 96-well plate to an 8-well chambered coverglass using micropipette (8 to 10 spheroids per well). To ensure thorough membrane staining, a higher concentration of CellMask Deep Red (1:500 dilution) and a longer incubation time (1 h) were employed. After membrane staining, the staining buffer was replaced with the EGFR-labeling solution (antibody-conjugated fluorescent nanoparticles at 100 pM) diluted from the stock solution (30 nM). The reaction was incubated for 30 min at 37°C (preparation steps are graphically presented in Fig. S17). The EGFR-labeling solution was removed, and the samples were washed twice using phosphate-buffered saline to remove the unbound fluorescent nanoparticles. Under these conditions, each A431 cell was expected to have 3–8 EGFRs labeled with a single fluorescent bead. At such a low labeling density, the chance for one fluorescent bead to encounter another bead or to crosslink multiple EGFRs was minimal. Without anti-EGFR antibodies in reaction, very few fluorescent beads (typically aggregates) were found on the cell membrane (<0.27 bead/cell) (Fig. S18).

Upon completion of membrane staining and EGFR labeling, the chambered coverglass was immediately put on the TSUNAMI microscope for tracking experiments. Internalization of EGFR was initiated by replacing the media with DMEM containing 10 ng/ml EGF (recombinant human epidermal growth factor, PHG0311L, Thermo Fisher Scientific) (64). As membrane-bound EGFRs were typically internalized within 30 min upon EGF stimulation (78), 2–4 EGFR trajectories (duration ranged from 2–10 min) were typically obtained from each well. The volumes of all solutions and washing buffers used in staining were 200 μl per well.

Results

Verifying 3D tracking and trajectory analysis algorithm using SME

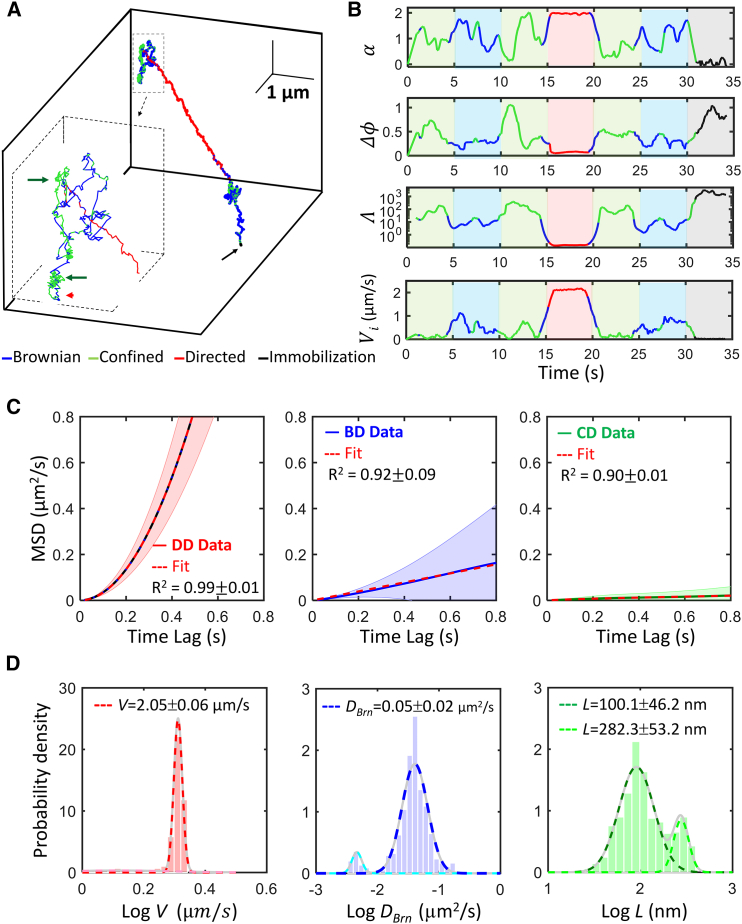
The reliability of the TSUNAMI 3D tracking microscope and the trajectory analysis algorithm was verified by following prescribed trajectories that imitated EGFR trafficking in live cells. One 35 s representative prescribed trajectory (Fig. 2) was divided into seven 5-s-long regions, where three were encoded with confined diffusion (green areas), two were encoded with Brownian diffusion (blue), one was encoded with directed diffusion (red), and the last one was encoded with immobilization (gray). In our trajectory analysis, every 0.1-s-long segment was classified into one of the four motional modes (the sliding time step (Δs) was 0.1 s, Fig. 1) and color-coded for visual inspection. It is obvious to see that one classification parameter alone could not well identify the motional modes (Fig. 2 B). In this example, our algorithm successfully recovered the seven regions and reached 81% overall segment classification accuracy.

Figure 2.

Verifying the trajectory analysis algorithm using SME system (n = 16). (A) A representative prescribed trajectory is composed of Brownian diffusion (BD), confined diffusion (CD), directed diffusion (DD), and immobilization (IM). Simulated conditions are Brownian diffusivity D_pre = 0.08 μm²/s, linear dimension of the confinement L_pre = 100 nm, probability of penetration P = 0.01, and speed of directed diffusion V_pre = 2 μm/s. The track duration is 35 s, and the trajectory is equally divided into seven 5-s-long regions in which the tracked particle exhibits four types of motional modes in the following sequence: CD→BD→CD→DD→CD→BD→IM. The red arrowhead marks the starting point of the trajectory. The green arrows mark the regions exhibiting confined diffusion and the black arrow marks the immobilization region. (B) Time traces of the three classification parameters (α, Δϕ, Λ) and instantaneous velocity (V_i) of the representative trajectory shown in (A). (C) The ensemble-averaged MSD curves from the classified regions were fitted with the proper models to recover the dynamic parameters (D_Brn, L, and V). The R-squared values were employed to evaluate the goodness-of-fit. Ribbons represent the standard deviations. (D) Normalized histograms of experimentally derived dynamic parameters logV (red), logD_Brn (blue), and logL (green) are provided. The means and standard deviations were from curve fitting with a Gaussian mixture model. The total number of trajectories analyzed is 16 in (C) and (D). To see this figure in color, go online.

The misclassified segments concentrated near the change points between regions. In particular, misidentification of confined diffusion as Brownian diffusion took place when the motion changed from confined diffusion (green, 10–15 s) to directed diffusion (red, 15–20 s). Similarly, when motion changed from Brownian diffusion (blue, 25–30 s) to immobilization (gray, 30–35 s), misclassification of immobilization as confined diffusion was also noticed. These systematic misidentifications around the change points were understandable as the classification parameters were averaged over a 1.6-s-long rolling window (w), which could span two or more distinctive motion modes. Because of these misclassifications, the experimentally derived dynamic parameters often needed to be fitted with a Gaussian mixture model (MATLAB, The MathWorks, Natick, MA). For the directed diffusion region (red areas in Fig. 2 B), the predetermined active transport speed (V_pre) and the experimentally recovered active transport speed (V) were 2 μm/s and 2.05 ± 0.06 μm/s, respectively (where the error was the standard deviation of the Gaussian fit, Fig. 2 D). Here the 2.05 ± 0.06 μm/s was the major population, whereas the overall population (considering the presence of subpopulation) was calculated to be 1.96 ± 0.28 μm/s. For the Brownian diffusion regions (blue areas), the predetermined diffusivity (D_pre) and the experimentally recovered diffusivity (D_Brn) were 0.08 μm²/s and 0.05 ± 0.02 μm²/s, respectively (whereas the overall population to be 0.04 ± 0.03 μm²/s). For the confined diffusion regions (green areas), the predetermined confinement size (L_pre) and the experimentally recovered confinement size (L_exp) were 100 nm and 100.1 ± 46.2 nm, respectively (whereas the overall population to be 131.1 ± 84.2 nm). More SME results that demonstrate the reliability of the trajectory analysis algorithm can be found in Figs. S11–S13.

Revealing membrane dynamics of EGFRs

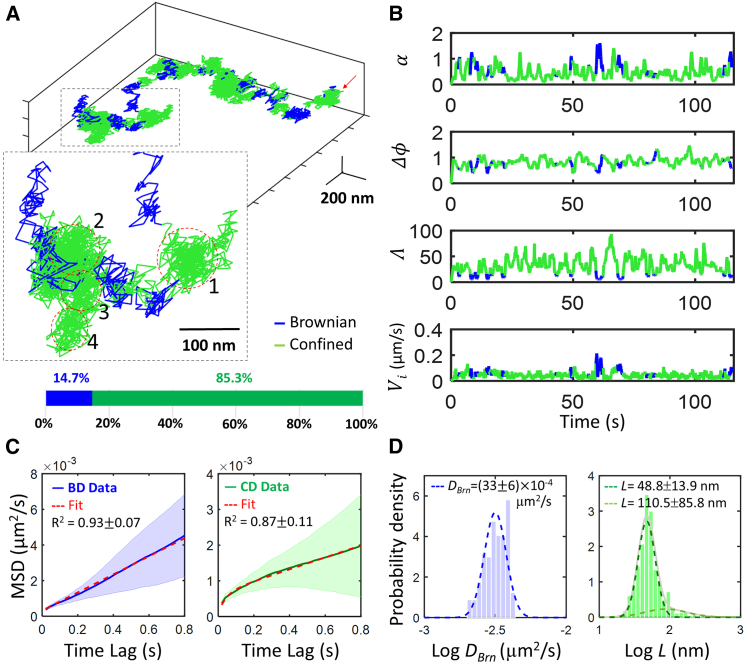
We used the developed algorithm to analyze 112 EGFR trajectories acquired in live A431 epidermoid carcinoma cells (95 with stimulation of EGFs and 17 without stimulation). These trajectories all started on the apical surfaces of the cells, and consequently were expected to exhibit an interchange of confined diffusion and Brownian diffusion at the beginning (16). One representative 120-s-long trajectory clearly showed these two motional modes on the cell membrane, with the fractions of confined time and free-diffusing time being 85% and 15%, respectively (Fig. 3). For Brownian diffusion segments (blue), the measured diffusivity, D_Brn, was (3.2 ± 0.5) × 10⁻³ μm²/s. For confined diffusion, the measured diffusivities, D_micro and D_macro, were (3.3 ± 0.6) × 10⁻³ μm²/s and (0.5 ± 0.7) × 10⁻³ μm²/s, respectively. The linear dimension of confinement, L, was found to have two distributions: 48.8 ± 13.9 nm and 110.5 ± 85.8 nm (Fig. 3 D). These values agree with previous observation of membrane-bound EGFR dynamics using 2D single-particle tracking techniques (50, 58).

Figure 3.

Interchanging of confined diffusion and Brownian diffusion on cell membrane. (A) A representative trajectory of EGFR membrane diffusion is shown. The green and blue colors represent confined diffusion and Brownian diffusion, respectively. The zoom-in view (inset) shows the membrane confinements based on visual inspection. The fractions of free diffusion time and confinement time were 14.7% and 85.3%, respectively. (B) Time traces of the three motion classification parameters (α, Δϕ, Λ) and instantaneous velocity (V_i) of the representative trajectory shown in (A) are provided. (C) The ensemble-averaged MSD curves from the classified segments were fitted with the proper models to extract D_Brn and L. The R-squared values were employed to evaluate the goodness-of-fit. Ribbons represent the standard deviations. (D) Histograms of logD_Brn and logL derived from the classified segments are provided. These histograms were fitted with a Gaussian mixture model. To see this figure in color, go online.

Monitoring EGFR trafficking from membrane to cytoplasm in live cells

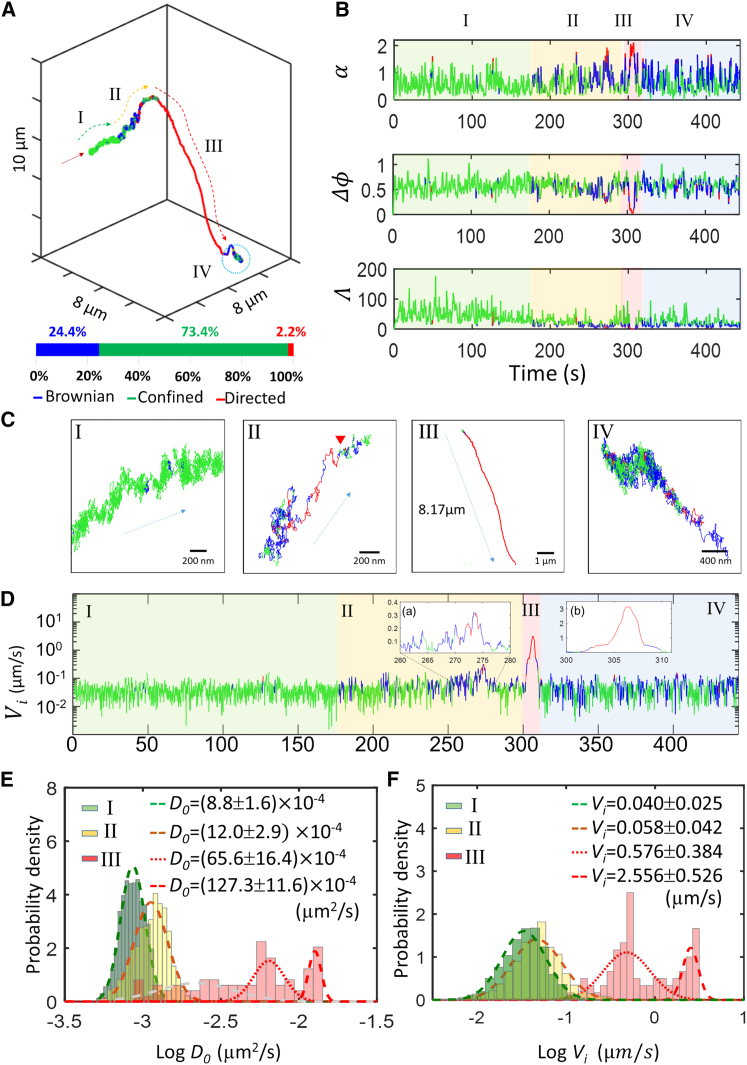
TSUNAMI is one of the few high-spatiotemporal-resolution 3D tracking techniques (8, 23, 25, 79, 80) that allow for monitoring intracellular processes and generating 3D trajectories over a large z depth (>30 μm) and a long period of time (∼10 min). One representative 442-s-long trajectory clearly exhibited features of EGFR trafficking from membrane to cytoplasm (Fig. 4 A). After the trajectory was segmented, classified, and color-coded, four different phases could be clearly identified: confined diffusion on the cell membrane (phase I), onset of the internalization process (phase II), active intracellular transport (phase III), and confined diffusion in a vesicle (phase IV). The durations of these four phases were 177, 124, 10, and 131 s, respectively (Fig. 4 B).

Figure 4.

Trafficking from membrane to cytoplasm. (A) A representative trajectory of EGFR trafficking from cell membrane to cytoplasm is shown. The green, blue, and red colors represent confined, Brownian, and directed diffusion, respectively. The dark red arrow marks the starting point of the trajectory. The fractions of free diffusion time, confinement time, and active transport time were 24.4%, 73.4%, and 2.2%, respectively. The trajectory can be divided into four phases by visual inspection. (B) Time traces of the three motion classification parameters (α, Δϕ, Λ) is shown. Corresponding periods of the four phases are color-coded in these time traces. (C) Zoom-in views of the four phases, which clearly show the differences in the receptor motion in these phases. In this case, EGFR complex traveled 8.17 μm into the cytoplasm at phase III. (D) Time trace of instantaneous velocity (V_i) is shown. A small peak was noted around 273 s in phase II (inset a) and a large peak took place around 307 s in phase III (inset b), which mark the onset of internalization and the motor-mediated transport, respectively. (E) Histograms of logD₀ in phases I–III are provided. (F) Histograms of logV_i in phases I–III are provided. The values shown in (E) and (F) represent the means and standard deviations from Gaussian mixture model fitting. The logD₀ and logV_i of phase III clearly show two distributions. These two distributions are indicated with dotted line and dashed line, respectively. To see this figure in color, go online.

Phase I was featured by high confinement indices (average Λ = 45.6 ± 22.8) and very small displacements within 20 ms (average absolute displacement = 13.3 ± 6.5 nm per 20 ms), indicating confined diffusion on the cell membrane. As the cell membrane was stained with CellMask, we confirmed that the phase I trajectory was indeed on the cell membrane by superimposing the trajectory over the two-photon scanning image of the cell. Interestingly, we often observed EGFR movement toward one direction on membrane (Fig. 4, C-I). This type of the “linear” confined diffusion of transmembrane proteins has previously been reported by other groups (81), possibly reflecting diffusion within a linear confinement.

Phase II was featured by an interchange of Brownian and directed diffusion, which we believe marked the onset of the internalization. If internalization of EGFR is carried out by clathrin- and actin-mediated endocytosis, phase II should represent the pulling of clathrin-coated pits toward the interior of the cell by the movement of the growing actin network (82) and the formation of endosome mediated by dynamins (83). There was a noticeable peak in the instantaneous velocity (V_i) time trace in phase II, from 266 to 275 s (Fig. 4 D, inset a). The average V_i within this 9-s window was significantly higher than the background level (0.16 vs. 0.05 μm/s). This increased velocity agreed well with the clathrin-mediated endocytosis model as the internalization speed of clathrin-coated pits is found on the order of 0.1 μm/s (84). Upon a closer examination of the color-coded phase II trajectory (Fig. 4, C-II), a change point (marked by a red arrow) from the red-blue-mixing region to the green-blue-mixing region was clearly noted. We believe this change point marked the transition from the actin-cytoskeleton-mediated movement (red-blue-mixing) to the confined diffusion in an early endosome (green-blue-mixing).

A sudden increase of instantaneous velocity at 302 s marked the beginning of phase III, which was featured by a large linear displacement (8.17 μm in Fig. 4, C-III) within a short period of time (10 s). Phase III was believed to be the active transportation of endosome on microtubules (i.e., directed diffusion) (34, 60). Both the average instantaneous velocity of 1.20 ± 1.06 μm/s (V_i) and the active transport speed of 1.39 ± 0.99 μm/s (V, from Eq. 5) derived from phase III matched well with the typical motor protein-mediated transport speed of 0.5 to 2 μm/s (59, 60, 61, 62). The two separate populations of V_i in phase III might represent the two classes of runs (the short-slow run and the long-fast run) observed in active transport (85, 86) (Fig. 4 F). The short-slow run represents motors engaged in a tug-of-war between oppositely directed molecular motors attached to the same cargo (87, 88). The long-fast run (∼4 μm displacement and ∼3 s duration, such as the movement within 305 to 308 s in phase III, Fig. 4 D, inset b) indicates that dynein motors become dominate in the intracellular transportation. The length and duration of active transport of EGFRs (derived from the 95 EGF-stimulated EGFR trajectories) were 3.89 ± 1.69 μm and 5.05 ± 4.50 s, respectively.

The instantaneous velocity suddenly decreased to the background level at 311 s (∼0.05 μm/s), which marked the end of active transportation and the beginning of phase IV. Featured by a mixture of confined and Brownian diffusion (Fig. 4 C-IV), phase IV was believed to be a diffusion confined within a vesicle (late endosome) that itself diffused (69) (called cage diffusion in Fig. S8).

The histograms of logD_o were clearly distinguishable for phases I, II, and III (Fig. 4 E). The logD_o histogram of phase IV was similar to that of phase I and was thus not shown (Fig. S14). Similarly, the histograms of logV_i were also distinguishable for phases I, II, and III. Whereas logD₀ and logV_i of phases I and II had a normal distribution, those of phase III clearly had a much broader distribution. The average D_Brn, L, D_micro, D_macro, V_i, and V values for each phase are summarized in Table 1. For the entire trajectory (442 s long), the fractions of free diffusion time, confinement time, and active transport time were 24.4%, 73.4%, and 2.2%, respectively.

Table 1.

Comparison of Dynamic Parameters in Different Phases of EGFR Trafficking

Dynamic Parameters	DBrn (μm2/s)	L (nm)	Dmicro (μm2/s)	Dmacro (μm2/s)	$\overline{V}$i (μm/s)	V (μm/s)
Phase I	–	88.0 ± 71.6	(0.9 ± 0.2) × 10−3	(1.7 ± 2.5) × 10−3	0.04 ± 0.02	–
Phase II	(1.3 ± 0.03) × 10−3	96.3 ± 61.8	(1.2 ± 0.2) × 10−3	(5.7 ± 16.2) × 10−3	0.06 ± 0.04	0.24 ± 0.08
Phase III	–	–	–	–	1.20 ± 1.06	1.39 ± 0.99
Phase IV	(1.1 ± 0.02) × 10−3	102.8 ± 65.3	(1.0 ± 0.2) × 10−3	(1.7 ± 3.2) × 10−3	0.05 ± 0.03	–

Distributions of the dynamic parameters of EGFR

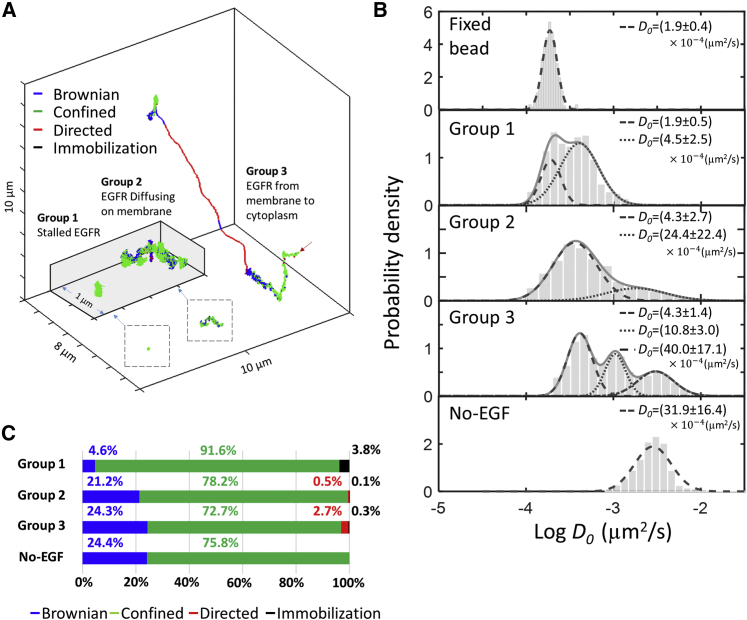
Based on the classification results, the 95 EGF-stimulated EGFR trajectories were divided into three groups—group 1: stalled EGFRs (n = 23, 24.2%), group 2: membrane diffusing EGFRs (n = 49, 51.6%), and group 3: membrane to cytoplasm trafficking EGFRs (n = 23, 24.2%) (Fig. 5 A showing a representative trajectory in each group). Group 1 trajectories were characterized by either immobilization (Λ ≥ Λ_Im) or confined diffusion within a region of linear size of 500 nm or smaller. The low D₀ feature (centered around (1.9 ± 0.5) × 10⁻⁴ μm²/s) might indicate trapping of EGFRs in plasma membrane compartments, such as clathrin-coated pits (89), or formation of EGFR clusters (90). In addition, EGFRs can associate with integrins in a signal transduction system (91). Group 2 trajectories, on the other hand, showed an interchange of Brownian diffusion and confined diffusion, but without any active transport component. Group 3 trajectories exhibited directed diffusion that lasted for at least 0.5 s or longer. Instead of further dividing each trajectory into distinct phases and computing their dynamic parameters separately (as Table 1), here we treated each trajectory as a whole and built histograms of D₀ based on the entire trajectories. The D₀ histograms not only discriminated EGF-stimulated trajectories from no-EGF trajectories, but they also differentiated among EGF-stimulated groups 1, 2, and 3 trajectories themselves (Fig. 5 B). Clearly without EGF stimulation, EGFRs were more mobile on the membrane. Dimerization of EGFRs was believed to the cause of reduced mobility for EGF-stimulated EGFRs (50, 63), which also induced endocytosis (64). Although untreated EGFRs were more mobile, their time proportions in Brownian and confined diffusion were similar to those of EGF-stimulated EGFRs (Fig. 5 C). In addition, no significant differences between trajectories collected from monolayer cells and those from spheroids were noticed.

Figure 5.

Dividing EGFR trajectories into three groups. (A) 95 EGF-stimulated EGFR trajectories were categorized into three groups that represent stalled EGFRs (group 1, n = 23), membrane-diffusing EGFRs (group 2, n = 49), and membrane-to-cytoplasm-trafficking EGFRs (group 3, n = 23). The inset shows a zoom-in view of the representative trajectories from groups 1 and 2. The trajectories are color-coded to indicate different motional modes within each segment. The dark red arrow marks the starting point of the trajectory of the group 3 representative trajectory. (B) Histograms of logD₀ derived from EGF-stimulated EGFR trajectories (groups 1–3) and the ones without EGF stimulation (No-EGF, n = 15) are provided. These histograms were fitted with a Gaussian mixture model. The detection limit (D_min) is estimated by tracking of fixed beads. (C) Percentages of the four motional modes within the trajectories of the three EGF-stimulated groups and the no-EGF group are provided. To see this figure in color, go online.

Discussion

Rationale behind the thresholds used for trajectory classification

How reliably our rolling-average algorithm can identify the motional mode associated with each trajectory segment depends on the thresholds that we select for the classification parameters (scaling exponent α, directional persistence Δϕ, and confinement index Λ) and the length that we choose for the rolling window (w). Other than the misclassification issue around the change points, 100% classification accuracy cannot be achieved as pure random walks can also transiently exhibit movement similar to confined or directed diffusion (Fig. 2 B). Here we use prescribed trajectories embedded with physiologically relevant receptor dynamics (D_pre, L_pre, and V_pre) to train the algorithm and obtain a set of thresholds that minimizes the chance of segment misclassification. For example, movement of an internalized early endosome is mostly assisted by molecular motors on microtubules, which exhibits a characteristic transport speed of ∼1 μm/s (60, 92) with lateral diffusivity (D_lateral) around 3 × 10⁻³ μm²/s (53). By analyzing the prescribed trajectories built on these practical dynamic parameters, we confirm that the thresholds of 1.4 for α and 0.1 for Δϕ work well in distinguishing active transport from passive transport (Fig. S4). These results also indicate that the length of the rolling window has to be sufficiently long, on the order of 1.6 s, to accurately identify the directed diffusion. Since motor protein-assisted active transport typically lasts for 1–2 s or longer (34, 57), the 1.6 s rolling window (w) with 0.1 s sliding time step (Δs) is appropriate to resolve motor protein-assisted directed diffusion.

As for the confinement index Λ, the upper-bound and the lower-bound thresholds for Λ are chosen such that there is a less than 5% probability for Brownian diffusion or immobilization being misidentified as confined diffusion (Fig. S5). Since reliable differentiation of confined diffusion from Brownian diffusion is the most critical classification step in our analysis, we define the “power of confinement detection” to be the successful rate to capture each confined diffusion. We further test these Λ thresholds with different lengths of rolling window and find that the rolling window has to be longer than 1.6 s for the power of confinement detection being greater than 90% (Fig. S5). We emphasize that the thresholds used in our trajectory segmentation and classification method are calibrated computationally (via Monte Carlo simulation, Fig. S5) and validated experimentally (via SME, Figs. 2, S4, and S7). Although here we only demonstrate the analysis of EGFR trajectories, our method should be applicable to many other trajectories acquired from biological samples with minor modifications. The detailed information of threshold optimization and the calculation of these three classification parameters were summarized in Supporting Material (Table S1; Fig. S3).

Challenges in molecular trajectory analysis

Analysis of complex trajectories faces three major challenges: 1) observing transient behaviors in motion patterns that span the spatiotemporal scale from nanometer to micron and from millisecond to second, 2) discriminating mechanisms that give similar subdiffusive MSD curves, and 3) identifying the physical scenarios behind the observed molecular trajectories. In this study we have tackled the first challenge, and future work will focus on the final two. Other than the mechanisms in confined geometries that lead to subdiffusive behaviors (corralled, hop, and cage diffusion, as discussed in Fig. S8), mechanisms in “unconfined” geometries, such as continuous time random walk (93, 94, 95), fractional Brownian motion (96, 97), and random walk on a fractal structure (98), can also give subdiffusive MSD curves (11, 41, 99). A sophisticated differentiation decision tree, such as the one proposed by Meroz’s group (41), should be established and rigorously tested. Such a decision tree can be used in conjunction with ours in Fig. 1 B for identifying the mechanisms behind the subdiffusive behaviors in both confined and unconfined geometries.

Whereas different confinement models and simulations have been carried out by other groups (34, 37, 39, 100) and us (Fig. S8), it is currently difficult to rule out one model (e.g., cage diffusion (69)) from other models (e.g., hop diffusion (100)) when explaining the mechanisms behind the observed confined diffusion. Since MSD fits alone do not fully distinguish between different models for the diffusion, additional information is often needed. For instance, Kusumi’s group determined that phospholipids undergo hop diffusion in cell membrane based on the control experiments that modified or depleted membrane skeleton (100). On the other hand, Salome’s group believed that a G-protein-coupled receptor follows cage diffusion based on their visual inspection of the trajectories—only few hops from one domain to another were observed (69). With a close examination, our results resemble the hop diffusion described by Kusumi based on 40 nm gold particle tracking (Fig. 3 A) (101). Although the conventional 2D-SPT results suggested that all phospholipid and transmembrane proteins exhibit short-term confined diffusion within a compartment and long-term hop movement from one domain to another (so-called the skeleton fence model) (101), more-advanced techniques, such as the scanning STED-FCS that provides even higher spatiotemporal resolution in molecular motion analysis, showed no evidence of nanodomains but rather suggested transient interactions with immobile or slowly moving entities, possibly proteins (102). Since particle size effect on the tracking experiment has not been completely elucidated, hop diffusion as a general molecule diffusion phenomenon on membrane is still under debate (49). Anyhow, it becomes clear that to derive biological meaning from single-particle trajectories, one cannot simply rely on a single analysis tool or a single parameter such as MSD. Proper controls are also critically important.

Trade-offs in temporal resolution and probe size

Although our TSUNAMI microscope is capable of performing 3D tracking at 50 μs temporal resolution (20 kHz) when the tag is very bright (30), in the current experiments the feedback loop was set to be 20 ms so more photons could be collected for a better position estimate. The trade-off of this adjustment is the reduced capacity in resolving transient confinement of EGFRs on plasma membrane. Lagerholm’s group has shown that EGFRs are transiently confined in compartments with linear dimension of 100–150 nm and a mean confinement duration of 50–100 ms, using the 2D-SPT method with 1.75kHz frame rate (49). We have observed a similar confinement size in our 3D-SPT experiments (Table 1) but a longer confinement duration. Although high temporal resolution will certainly improve the estimate of transient confinement duration, significantly larger nanoparticle tag is often needed. Recently Yang’s group demonstrated 3D-SPT at 10 μs temporal resolution using a giant polystyrene bead and quantum dot assembly (∼100 nm) (79). Although larger (also brighter and more photostable) nanoparticle tags have provided us with excellent localization accuracy and temporal resolution in single-particle tracking, there is generally a doubt that how much these large particles may influence the mobility of molecules under investigation (e.g., by inducing cross-linking with other biomolecules or by blocking molecule’s interactions with environment) (11, 103). It has been reported that transmembrane proteins tagged with a 40 nm gold nanoparticle could diffuse three to seven times slower than the same proteins tagged with an Alexa 594 dye due to steric hindrance and crosslinking effect (104). EGFRs tagged with a 40 nm gold particle exhibit a diffusivity (∼3 × 10⁻³ μm²/s) lower than that of EGFRs tagged with a commercial quantum dot (∼0.04 μm²/s) (50) or fused with an EGFP (∼0.2 μm²/s) (106). Although large nanoparticle labels have also been used for high-resolution tracking of a wide range of membrane proteins (such as glycine receptors (107), GPI anchor proteins (17), α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid and N-methyl-D-aspartate receptors (108), integrins (109), and cystic fibrosis transmembrane conductance regulator channel proteins (110, 111)), smaller particle labels (diameter < 10 nm) are recently developed and tested for SPT in a confined space (such as synaptic receptors in synaptic cleft (27)), providing less steric hindrance and reduced cross-linking. To completely eliminate cross-linking, we are currently developing monovalent EGFR labeling techniques based on site-specific biotinylation of membrane receptors (113), monovalent streptavidin (114, 115), and monovalent nanoparticles (116).

Outlook of high-resolution 3D tracking of EGFR

The combination of the TSUNAMI microscope and the classification algorithm is capable of revealing the dynamics of complex EGFR trajectories from the plasma membrane into deep cytoplasm at 20 ms temporal resolution and 16/43 nm (xy/z) spatial resolution, with track duration ranging from 2 to 10 min and vertical tracking depth up to tens of microns. We can monitor the onset of EGFR internalization process (phase II in Fig. 4 A) and directly observe the change points of motional modes along the trajectory (Fig. 4 C). Since the 2D-SPT techniques can only probe the diffusion process on membrane (phase I) (49, 50, 58), very few results have been published about the endocytosis and intracellular transport dynamics of membrane receptors (34, 60). In this study we report the physical parameters associated with these processes (Table 1) and show the statistics of our 3D trajectory classifications (Fig. 5). Interestingly, our results suggest that there are three populations of EGFRs that respond differently (immobilization, membrane diffusion, and active transportation) upon ligand stimulation. It will be worthwhile to further investigate the molecular mechanisms causing the difference.

Defective endocytosis of EGFR can be caused by altered ubiquitination (117, 118), altered cytoskeletal interactions (119), and derailed endocytosis. All of these causes of EGFR dysfunction can be associated with oncogenic alterations (120). Therefore, the outlined 3D-SPT method and trajectory classification would be a highly desirable tool for monitoring EGFR intracellular trafficking dynamics at distinct phenotypic transition stages in cancer development. Additionally, our study may also provide a unique means to identify how the therapeutic drugs (such as monoclonal antibodies and tyrosine kinase inhibitors) affect receptor dynamics (anywhere from actin network reorganization (121) to derailed endocytosis (119)), which could have significant impact in the treatment of cancer.

Author Contributions

Y.-L.L. and H.-C.Y. conceived the project and wrote the article. E.P.P. built the microscope and developed the control software. Y.-L.L., E.P.P., and P.Y. performed the 3D tracking experiments. Y.-L.L. and C.L. performed Monte Carlo simulations and developed the trajectory analysis algorithm. Y.-L.L. and P.Y. prepared cell samples and analyzed the data. C.-K.C. and M.-C.H. helped analyze the EGFR trajectories. H.-C.Y. and A.K.D. supervised the project.

Editor: Julie Biteen