Push-pull and feedback mechanisms can align signaling system outputs with inputs

Summary

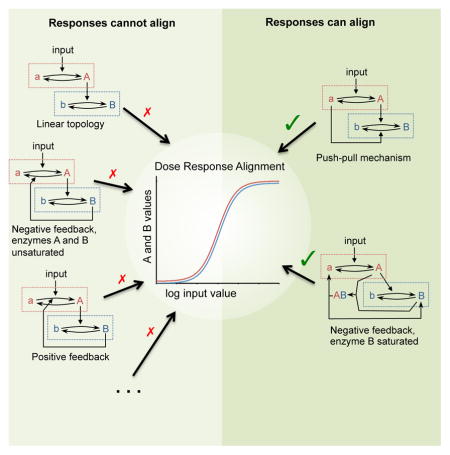
Many cell signaling systems, including the yeast pheromone response system, exhibit “dose-response alignment” (DoRA), in which output of one or more downstream steps closely matches the fraction of occupied receptors. DoRA can improve the fidelity of transmitted dose information. Here, we searched systematically for biochemical network topologies that produced DoRA. Most networks, including many containing feedback and feedforward loops, could not produce DoRA. However, networks including “push-pull” mechanisms, in which the active form of a signaling species stimulates downstream activity and the nominally inactive form reduces downstream activity, enabled perfect DoRA. Networks containing feedbacks enabled DoRA, but only if they also compared feedback to input and adjusted output to match. Our results establish push-pull as a non-feedback mechanism to align output with variable input and maximize information transfer in signaling systems. They also suggest genetic approaches to determine whether particular signaling systems use feedback or push-pull control.

eTOC blurb

Diverse signaling systems adjust downstream outputs to track the fraction of occupied cell surface receptors. We show how signaling reaction networks can achieve this alignment using push-pull or feedback control with a comparator-adjuster, and suggest experimental tests to tell these apart.

Introduction

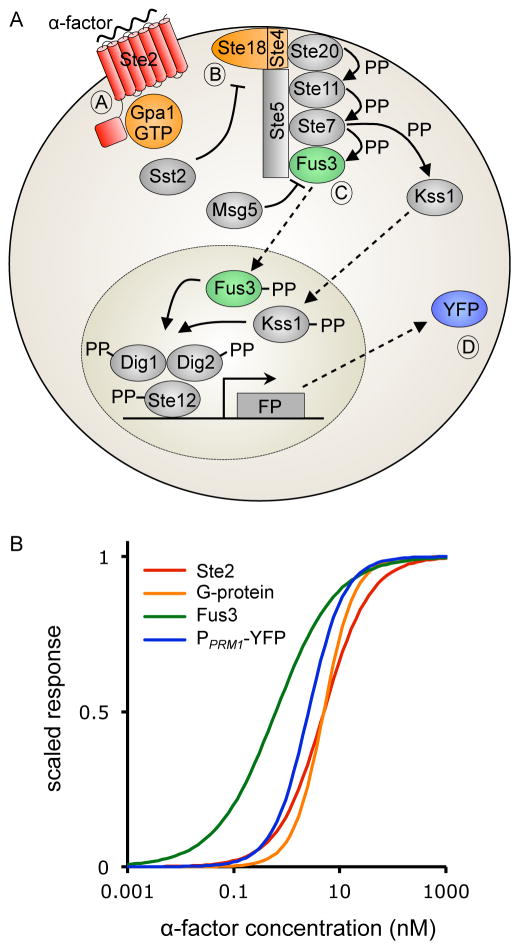
Cell signaling systems sense extracellular conditions and transmit information about those conditions into the cell. Cells then make decisions, including fate decisions, based on this information. The Saccharomyces cerevisiae Pheromone Response System (PRS) is such a system. MATa and MATα haploid cells sense each other’s secreted mating pheromones (a-factor and α-factor, respectively) through pheromone binding to receptors. In MATa cells, pheromone binding to Ste2^GPCR triggers a chain of events, including changes in the intracellular portion of the receptor, dissociation of the heterotrimeric G-protein, recruitment of a scaffold protein to the membrane, activation of protein kinases that activate other protein kinases including Fus3^MAPK and Kss1^MAPK, and phosphorylation of transcription activators. PRS operation induces gene expression, cell cycle arrest, growth toward the mating partner, and eventual fusion and formation of a diploid cell (Figure 1A, reviewed in (Bardwell, 2005; Dohlman and Thorner, 2001; Kurjan, 1992)). Each quantifiable molecular event in this chain defines the system output at that particular measurement point (Brent, 2009). We and others have quantified these outputs, including for G-protein dissociation (Yi et al., 2003), reporter gene induction (Colman-Lerner et al., 2005; Yu et al., 2008), and scaffold recruitment (Bush and Colman-Lerner, 2013).

Figure 1.

(A) The yeast pheromone response system (PRS). Binding of mating pheromone, α-factor, to the G-protein coupled receptor Ste2^GPCR activates a G-protein (Gpa1-Ste18-Ste4). Its βγ subunit (Ste18-Ste4) causes the Ste5 scaffold protein to translocate from the cytoplasm to the cell membrane and initiates a mitogen-activated protein (MAP) kinase cascade, operating on Ste5. The final cascade elements, Fus3^MAPK and Kss1^MAPK, carry the signal to the nucleus where it activates transcription of fluorescent reporter genes (FP), including the P_PRM1. -YFP fusion that generated data here (Yu et al., 2008). (B) Dose Response Alignment (DoRA) in the PRS. Red line represents pheromone binding to Ste2^GPCR, orange represents G-protein dissociation (Yi et al., 2003), green represents Fus3 phosphorylation (Yu et al., 2008), and blue represents YFP expression from the PRM1 promoter (Yu et al., 2008). Responses are scaled to range from 0 to 1.

Upon induction by a step increase in extracellular pheromone, PRS output at each measurement point increases, peaks, and declines toward an apparent plateau (Yu et al., 2008), and system output is constant over several hours (Colman-Lerner et al., 2005) (in bar1⁻ cells, from which the data used here derive). These behaviors are consistent with a system that settles to a steady state. At many measurement points, steady-state system output closely matches the percent of bound receptors (Moore, 1983; Yi et al., 2003) (Figure 1B). In the PRS, this substantial Dose Response Alignment (DoRA) (Yu et al., 2008) is robust to changes in protein abundance during the response (Jenness et al., 1986; Thomson et al., 2011) and to artificially-provoked changes in the number of Ste2^GPCR receptors (Gehret et al., 2012; Leavitt et al., 1999; Reneke et al., 1988; Shah and Marsh, 1996). This implies that the PRS senses and transmits the fraction of ligand-bound receptors, even as its protein abundance changes (Brent, 2009). Many other signaling systems, including the insulin, acetylcholine, TSH, angiotensin II, and EGF receptor systems also exhibit DoRA (Yu et al., 2008); in the EGF and EPO systems, downstream alignment is maintained in the face of changes in the number of active surface receptors over time (Knauer et al., 1984, Becker et al. 2010, Oyarzún et al. 2014). Systems that exhibit DoRA use the entire dynamic range of the signal from bound receptor, which can enable downstream outputs to exhibit more distinguishable responses (Yu et al., 2008). DoRA also protects systems from amplification of stochastic noise during signal transmission (Yu et al., 2008). By these means, systems that maintain DoRA maximize the precision with which cells can respond to changing external conditions (Yu et al., 2008).

DoRA is implicit, though not named, in Alan Clark’s supposition that the binding of drugs to cellular molecules that he called receptors caused the drug’s effects (Clark, 1933). In this idea, a cell’s response was necessarily directly proportional to the fraction of receptor molecules bound. Clark’s conception of receptors largely endured (Stephenson, 1956) until receptors were isolated, after which it became apparent that receptors often exert their effects via signal transduction involving intermediary proteins (Rodbell, 1980).

It is far from obvious how chains of biochemical reactions can produce DoRA, or maintain it as protein abundances change. To the contrary, several researchers have shown that typical reaction chains do not produce DoRA. Using non-mechanistic models of sequential reactions, two groups (Black and Leff, 1983; Strickland and Loeb, 1981) showed that downstream responses exhibit higher sensitivities (respond at smaller doses) and reduced dynamic ranges compared to receptor binding curves. Goldbeter and Koshland (Goldbeter and Koshland, 1981) used mechanistic models to show that enzyme saturation in chains of enzymatic reactions make downstream response curves progressively flatter at the ends and steeper in the middle, which they termed zero-order ultrasensitivity. Huang and Ferrell (Huang and Ferrell, 1996) built on that work to investigate protein kinase cascades, as in the PRS, in which upstream protein kinases phosphorylate and activate downstream kinases. They also found that downstream responses exhibited increased sensitivity and ultrasensitivity.

Human-built systems that maintain the linear input-output relationships required for DoRA often use negative feedback to do so (Black, 1934). They compute the difference between the output and the input, yielding the error value, and then adjust the output to reduce the error (Astrom and Murray, 2008; Franklin et al., 1994). Such systems employ different approaches to adjustment, including proportional control, in which the output adjustment is proportional to the error, and integral control, in which the output adjustment depends on the integral of the error. Integral control can produce perfect adaptation, meaning that the output exactly returns to the ideal value even in the face of perturbations (Doyle, 2016). Many evolved systems also use negative feedback, for example to maintain constant concentrations of metabolites (Umbarger, 1978), to regulate the response to DNA damage (Brent and Ptashne, 1980, 1981), and to linearize integrated responses to extracellular signals (Becker et al., 2010; Oyarzún et al., 2014). In the PRS, negative feedback maintains alignment at one measurement point: the kinase activity of Fus3^MAPK is needed to shift the Fus3^MAPK phosphorylation dose-response curve to the right, toward alignment (Yu et al., 2008). These findings suggested that negative feedback might maintain DoRA at other measurement points as well.

Here, we searched for reaction mechanisms that could align upstream activity (e.g. receptor occupancy) with downstream responses to produce DoRA. To do so, we developed a scheme to represent reaction networks in signaling pathways and a quantitative measure of differences between dose-response curves. We used these to assess how well different network architectures could produce DoRA. For broad classes of models, we found that adding negative feedback loops could not produce DoRA. However, topologies that used non-linear reaction kinetics improved alignment. Most significantly, topologies that incorporated “push-pull” mechanisms, in which both the active and nominally inactive states of signaling proteins exerted downstream effects, produced DoRA. This result is consistent with recent experimental findings that Ste2^GPCR carries out push-pull control on G-proteins (Bush and Colman-Lerner, in revision). Additionally, we found that negative feedback can produce DoRA, but only when the system includes a mechanism that compares output with input and then adjusts output using this result. Our results establish push-pull control as a mechanism to generate DoRA, and provide guidance for experimental tests to identify feedback and push-pull control.

During the course of this work another study (Yan et al., 2012) was published describing network architectures that could produce DoRA. It used different methods and arrived at different conclusions, in particular finding that a much a larger number of topologies could produce alignment. We discuss these differences and their significance.

Results

Modeling signaling system topologies and assessing model performance

We represented the molecular species composing signaling systems as interconverting between two states: active and nominally inactive. We defined system output at a given measurement point, or node, as the fraction of that node’s species in the active state. We indicated interactions between these species using arrows, in which the active or nominally inactive fraction of one node catalyzed interconversions within other nodes. This idea built on the cyclic cascades introduced by Stadtman and Chock (Chock and Stadtman, 1977; Stadtman and Chock, 1977) and investigated further by Goldbeter and Koshland (Goldbeter and Koshland, 1981; Goldbeter and Koshland, 1982), Huang and Ferrell (Huang and Ferrell, 1996), and others (Sauro and Kholodenko, 2004; Ventura et al., 2008). We then computationally screened different reaction networks (as done, for example, in (Ma et al., 2009; Yan et al., 2012)) to see how well each could produce DoRA.

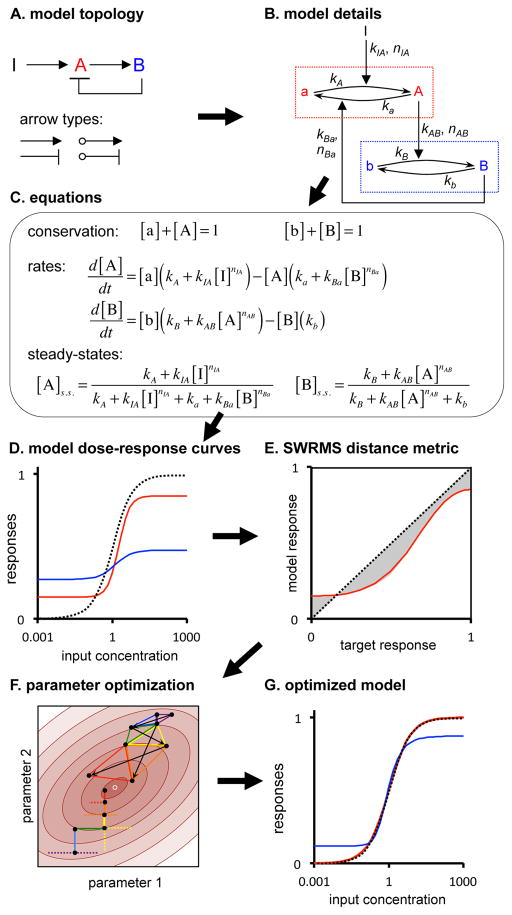
Figure 2A depicts the topology of one such network. In it, the input is I (a ligand concentration), the signal proceeds to node A and then to node B, and a negative feedback loop originates at B and acts on A. Because biological signaling systems depend on linear chains of cause and effect, in which each active species activates the next in the chain, all tested topologies contained a core sequence of arrows that represented that linear reaction chain. Our topologies also contained control arrows that exerted feedback and feedforward regulation, respectively upstream and downstream of their node of origin. Control arrows could also act directly upon their node of origin, promoting its activation or inactivation, and could act on other arrows, where they increased or decreased the rate constant associated with the targeted reaction (Document S1). In such cases, we avoided perturbing the core linear reaction diagram by adding a second arrow and modifying its rate instead. We show an arrow with a plain tail if it originates from the active component of a node and with a circular tail if it originates from the nominally inactive component; we called these latter arrows low-true by analogy with digital electronics (Horowitz and Hill, 1989). Also, we show an arrow with a pointed heads, a positive arrow, if it increases the amount of the active component in the destination node and with a T-bar head, a negative arrow, if it decreases the amount of the active component. For example, the model in Figure 2A includes two positive arrows that represent the linear reaction chain, plus a negative feedback control arrow. We note that this representation resembles that used by others but some terminology differs. For example, a topology with two sequential positive arrows and a positive feedforward loop is sometimes called a coherent feedforward loop (Shen-Orr et al., 2002) and, when found, is thought to produce delayed response to a stimulation (Alon, 2007). Our terminology is more general and does not presuppose specific function.

Figure 2.

Modeling scheme, illustrated by a two-node network with negative feedback. (A) Model topology; ‘I’ is the input, A and B are nodes, and arrows types depict interactions. (B) Detailed representation; dotted boxes are nodes, showing nominally inactive and active states and interconversion reactions, and black text symbols are model parameters. (C) Model equations; brackets denote concentrations of node species and the “s.s.” indicates steady-state. (D) Steady-state dose-response curves for the same model, using arbitrary parameters. The black dashed line is the target function, the red line is the node A response, and the blue line is the node B response. (E) SWRMS distance using the node A dose-response curve shown in panel D, now with the target response as the x-axis. (F) Parameter optimization. Brown ellipses show a contour graph of SWRMS distances near a minimum (small white circle). Four intermediate steps are shown in progressively warmer colors (blue, green, yellow, red) for each approach. Black dots mark the parameter estimates. Vertical and horizontal lines depict greedy random walk steps while triangles depict downhill simplex method steps. (G) Dose-response curves after optimization of model parameters for agreement with the target function.

Figure 2B shows a detailed representation of the same network. It depicts each node with a dotted box within which capital letters denote active species and small letters denote nominally inactive species. Reactions (barbed arrows), with activating (k_A and k_B) and inactivating (k_a and k_b) rate constants, interconvert these states. The control arrows introduced above add to the interconversion rates through catalysis that is performed by either the input or components of other nodes. Rate constants (k_IA, k_AB, and k_Ba) and reaction orders (n_IA, n_AB, and n_Ba), where subscripts indicate arrow origin and destination, parameterize these arrows. Reaction orders represent the reaction rate dependence on enzyme concentration. Non-first order, or cooperative, reactions are often found in biological systems due to protein oligomerization (Chadwick et al., 1970) and allosteric interactions in multi-protein complexes (Koshland et al., 1966; Monod et al., 1965).

This detailed representation leads to three sets of equations (Figure 2C). Conservation equations state that the sum of the active and nominally inactive species in each node is constant. Rate equations represent interconversion rates within each node, assuming simple mass action kinetics. Steady-state equations represent steady-state node activities as functions of node inputs; they arise from setting the rate equations to zero and applying the conservation equations. When arrows altered the rates of other arrows, we typically combined their effects into a single rate constant and multiplied the concentrations of the species at the two arrow origins. For example, in one topology (T14), node B is activated by two forward arrows from A, of which the second one is positively influenced by the concentration of B through a feedback. Here, the rate equation for B is

$$\frac{d\left[\mathrm{B}\right]}{dt}=\left[\mathrm{b}\right]\left(k_B+k_{AB}{\left[\mathrm{A}\right]}^{n_{AB}}+k_{\mathit{ABB}}{\left[\mathrm{A}\right]}^{n_{\mathit{ABB}1}}{\left[\mathrm{B}\right]}^{n_{\mathit{ABB}2}}\right)-\left[\mathrm{B}\right]\left(k_b\right)$$ (1)

We wrote software, NodeSolver, to compute steady-state activities for specific inputs and model parameters (Methods). By scanning over the input values, it computed model dose-response curves (Document S1; Figure 2D).

We defined target dose-response curves using the Hill function,

$$y=B+A\frac{x^N}{E^N+x^N}$$ (2)

where x is the dose, y the response, B the baseline, A the amplitude, E the EC₅₀, and N the Hill coefficient (a measure of steepness). To compare model and target dose-response curves, we developed the Slope-Weighted Root Mean Square (SWRMS) distance metric, d, a weighted integral of the differences between the two curves (Methods and Document S1). It is best illustrated using a parametric plot (Figure 2E), in which increasing deviations from the diagonal line depict increasing fit distances. NodeSolver used stochastic optimization (Figure 2F, Methods) to adjust model parameter values to achieve the minimum SWRMS distance between model and target dose-response curves, thus producing an optimized model (Figure 2G). We combined analytical work, manual parameter exploration with NodeSolver, and simulations with COPASI (Hoops et al., 2006) to explore each topology’s characteristics, such as why it could or could not produce DoRA, over what parameter range it could produce DoRA, and whether it led to monostable or bistable outputs.

Most two-node model topologies did not produce DoRA

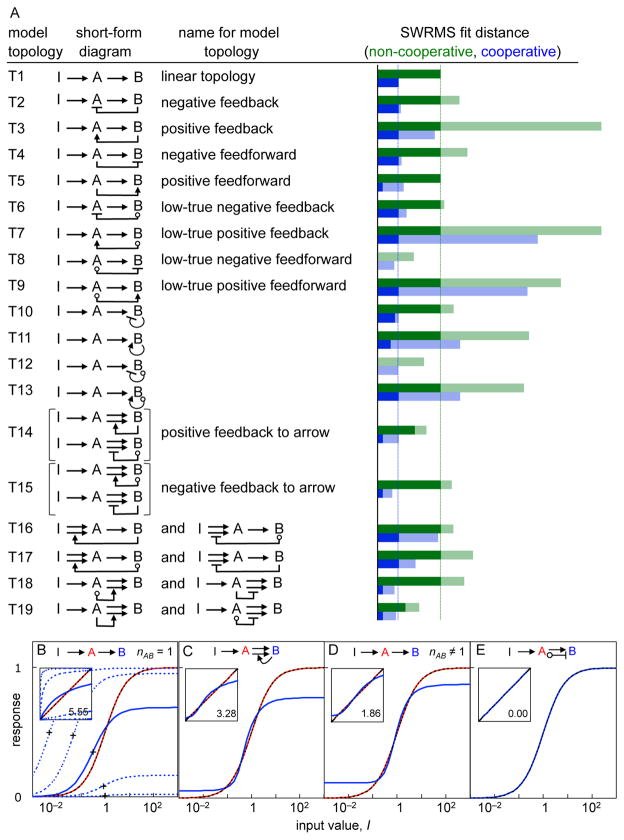
We tested a series of two-node topologies to identify which could produce DoRA (Figure 3A). In each case, the target dose-response curves were Hill functions of the input value that gave zero baseline, unit amplitude, unit EC₅₀, and unit Hill coefficient for each node. We used non-cooperative reactions at first so that we could distinguish differences due to network topology from any effects that might be caused by reaction cooperativity. We found that the linear topology (T1), which lacks control arrows, could not produce DoRA. Upon adjustment of the model rate constants, we could align EC₅₀s or amplitudes, but not both (Figure 3B). The best compromise, judged by SWRMS distance, had a 69% EC₅₀ decrease and a 31% amplitude decrease (Document S1).

Figure 3.

Survey of two-node models. (A) All model topologies, showing topology designation, representation, name, and SWRMS distances. Green bars show fit distances with non-cooperative reactions and blue bars for cooperative reactions. Control arrow reaction rates were fixed for the shaded portions of the bars and optimized for the solid portions. Vertical dashed lines show fit distances for linear topologies. (B–E) Best fits for linear topology (T1), a positive feedback to an arrow (T14), linear topology with cooperative reactions (T1), and push-pull (T8), all with non-cooperative reactions except as noted. Colors are as in Figure 2. Insets show target responses on the x-axis and list SWRMS distances. Dashed lines in (B) show the node B responses with different values of k_AB, while crosses show EC₅₀ values.

We tested all 18 two-node topologies that incorporated a single control arrow. We first chose a fixed rate constant for the control arrow and optimized all other model parameters (Figure 3A, light green bars). This was a consistent method to observe each arrow’s influence. In only four topologies (T8, T12, T14, T19) did adding the control arrow reduce the SWRMS distance. We then re-optimized the models while allowing the control arrow rate constant to vary (Figure 3A, dark green bars). This tested whether there were any parameters for which control arrow improved the fit. The same four topologies showed a lower SWRMS distance, while the others gave the same SWRMS distance as the linear topology. In these, inspection showed that the control arrow rate constants had been optimized to zero, thus simplifying them to the linear topology. Significantly, negative feedback loops (e.g. T2 and T6) did not improve DoRA.

Topologies that steepened response curves improved DoRA

We examined topologies T14 and T19 to determine how they achieved smaller SWRMS distances than the linear topology. We found that their control arrows increased node B output at high inputs while leaving it low at low inputs (Figure 3C). This steepened the node B response (increased the effective Hill coefficient) but improved EC₅₀ and amplitude alignment.

To investigate whether increasing the downstream response steepness improved DoRA more generally, we re-surveyed the two-node topologies while optimizing reaction orders as well as rate constants. Indeed, this improved alignment for all topologies (Figure 3A, blue bars). For example, the linear topology fit distance improved 3-fold from 5.55 to 1.86 (Figure 3D). In this case, the reaction order (n_AB) increased to 2.8, suppressing node B sensitivity to A at low inputs and increasing it at high inputs. This improved alignment by increasing the node B amplitude and EC₅₀, despite also raising the effective Hill coefficient from 1 to 1.8. Increasing (or decreasing) reaction orders did not qualitatively affect dose-response curves in other ways.

Most other topologies exhibited similar 3-fold improvements. However, a positive feedforward loop (T5) decreased the fit distance about 13-fold to 0.42. Here, the two arrows from A to B had different reaction orders, so one dominated at low inputs and the other at high inputs. The other four topologies that contained this control arrow (T14, T15, T18, and T19) improved in the same way, again with fit distances decreasing to 0.42. These became equivalent to T5 during optimization.

Push-pull topologies produced perfect DoRA

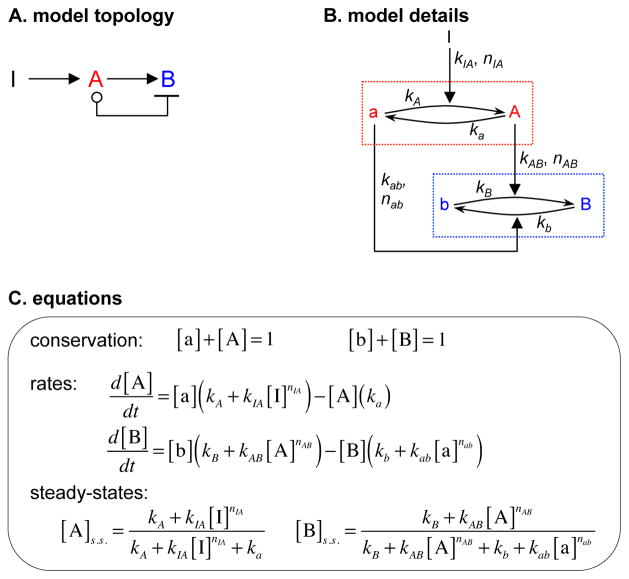
Two topologies, T8 and T12, allowed perfect DoRA (d = 0; Figure 3E). Both included control arrows from nominally inactive species that decreased the value of node B. However, the output from T12, in which the control arrow came from node B, was bistable; it either equaled the node A activity, giving DoRA, or got stuck in a fully active state (Document S1). We did not consider it further. For T8, in which the control arrow came from node A, the steady-state node B activity was (Figure 4)

Figure 4.

Push-pull mechanism. This figure is similar to Figure 2, except that it shows topology T8.

$${\left[\mathrm{B}\right]}_{s.s.}=\frac{k_B+k_{AB}{\left[\mathrm{A}\right]}^{n_{AB}}}{k_B+k_{AB}{\left[\mathrm{A}\right]}^{n_{AB}}+k_b+k_{ab}{\left[\mathrm{a}\right]}^{n_{ab}}}$$ (3)

If k_b and k_B equal zero, k_ab equals k_AB, n_AB and n_ab equal 1 and [A]+[a] equals 1, then the right side of this equation simplifies to just [A], meaning perfect DoRA. Restated, T8 yielded perfect alignment if the control arrow had the same rate constant as the arrow from the core sequence, that rate was much larger than the downstream node’s uncatalyzed rate constant, and both arrows acted with first order kinetics (these kinetics are required for alignment, as opposed to being imposed as fitting constraints). We named this topology push-pull by analogy with the electronic circuits sometimes used for audio and servo amplifiers, in which one part of the circuit supplies current to a downstream load, while a symmetrical part sinks current from it. In T8, the arrow in the core sequence from active A “pushes up” (increases) node B activity while the low-true control arrow, catalyzed by nominally inactive a, “pulls down” node B activity (see Figure 4, (Chock and Stadtman, 1977)).

Results for 4-node models were similar to those for 2-node models

We surveyed a wide range of 4-node topologies, again fitting model dose-response curves to the same target function (a Hill function with B = 0, A = E = N =1). The SWRMS distances were generally larger than for 2-node topologies, arising from the fact that dose-response curve misalignment is cumulative, but our qualitative results were essentially identical. In particular, a model with a linear topology and non-cooperative arrows exhibited poor alignment (Figure 5A) but alignment improved about 3-fold when reaction orders were allowed to vary (Figure 5B). Use of the longer reaction chain revealed a new result, that topologies with positive feedforward loops that skipped over nodes exhibited improved DoRA (Figure 5C). The rate constants for the core sequence of arrows were reduced to zero, so activation did not proceed along a chain but fanned out from a common origin through the control arrows. As before, topologies with push-pull mechanisms produced perfect DoRA, which was true whether the pull arrow originated from the immediate upstream node (Figure 5D) or farther upstream. In fact, DoRA improved substantially between the input and terminal step if these were connected with a pull arrow, even without intermediate control arrows (Figure 5E, note node A and D response alignment).

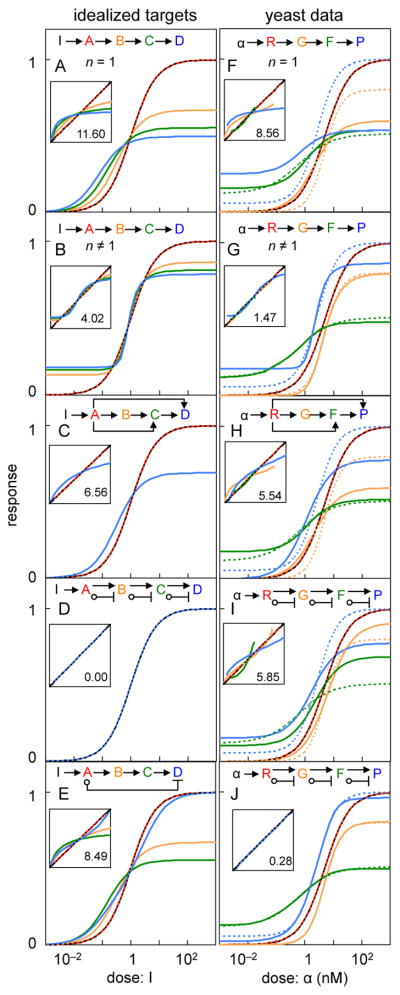
Figure 5.

Results for 4-node models. Left column represents idealized models, for which the target responses are shown with a black dashed line, node A in red, node B in orange, node C in green, and node D in blue. Right column represents models fit to experimental yeast PRS data. Hill function fits to the data (target functions) are shown with dashed lines and model fits are shown with solid lines. Node GPCR is shown in red, G-protein in orange, Fus3 in green, and PRM1-YFP in blue. (A) and (F) show results for linear topologies with non-cooperative reactions, (B) and (G) show results for linear topologies with cooperative reactions, (C) and (H) show results for topologies constructed with positive feedforward loops that skip over intermediate nodes, (D) and (I) show results for push-pull mechanisms, (E) shows a pull arrow that skips intermediate nodes, and (J) shows push-pull mechanisms with cooperative reactions. The insets are analogous to those shown in Figure 3.

The same mechanisms enabled excellent fit to experimental data

We defined new target dose-response curves based on experimental data from four yeast measurement points (Figure 1, Document S1) and again searched for topologies that could fit them. The nodes were (i) Ste2^GPCR, whose activity was defined by the fraction bound by α-factor, (ii) G-protein, defined as active when the Ste4/Ste18 subunits were dissociated from the Gpa1 subunit, (iii) Fus3^MAPK, defined as active when the protein was phosphorylated on its Thr180 and Tyr182 residues (Gartner et al., 1992), and (iv) YFP expression from the PRM1 promoter, defined as active when P_PRM1 directed maximal YFP production. In contrast to the idealized targets used before, now all four Hill function parameters varied between the target curves.

Our results were essentially the same as before. A linear topology and non-cooperative arrows fit the data poorly (Figure 5F) and most topologies with additional control arrows did not improve fits. However, topologies with cooperative arrows (Figure 5G), positive feedforward loops that skipped over nodes (Figure 5H), and push-pull mechanisms (Figure 5I) improved fits substantially. The push-pull topology in Figure 5I was limited to non-cooperative reactions, so it could not fit the different Hill coefficients. Relieving this constraint produced a nearly perfect fit (Figure 5J).

Negative feedback loops modeled using Henri-Michaelis-Menten kinetics could give perfect DoRA

We derived our model rate equations while assuming simple mass action kinetics, meaning that reaction rates were directly proportional to reactant concentrations. For example, in T1, and assuming non-cooperative reactions and no uncatalyzed activation for simplicity, we treated the net formation rate of B as (see Figure 2)

$$\frac{d\left[\mathrm{B}\right]}{dt}=k_{AB}\left[\mathrm{A}\right]\left[\mathrm{b}\right]-k_b\left[\mathrm{B}\right]$$ (4)

However, enzymatic reactions are often better described by Henri-Michaelis-Menten kinetics, in which enzyme A associates with substrate b in an Ab complex, which makes product B. This representation is often (see (Kholodenko et al., 1997; Russo and Silhavy, 1991; Yan et al., 2012)) simplified by using steady-state Michaelis-Menten equations, which do not explicitly represent enzyme-substrate complexation. This simplified Michaelis-Menten approach yields the formation rate of B in T1 as

$$\frac{d\left[\mathrm{B}\right]}{dt}=\frac{k_c\left[\mathrm{A}\right]\left[\mathrm{b}\right]}{K_M+\left[\mathrm{b}\right]}-k_b\left[\mathrm{B}\right]$$ (5)

where k_c is the catalytic rate constant and K_M is the Michaelis constant (note that the equation is valid if the enzyme-substrate concentration is effectively constant (Briggs and Haldane, 1925); here, this condition automatically met due to our assumption of steady-state conditions). When K_M ≫ [b], the limit of low saturation where most A is not bound to b, this reduces to eq. 4. In other words, the simple mass action and simplified Michaelis-Menten approaches are identical when enzyme saturation is low. When K_M ≪ [b], the limit of high saturation where most A is bound to b, eq. 5 simplifies to show that the formation rate of B becomes independent of the substrate concentration. Instead, it depends only on [A], putting the reaction in the “zero-order region” with respect to the substrate b (Goldbeter and Koshland, 1981). Here, the steady-state solution for eq. 5 is

$$\left[\mathrm{B}\right]=\frac{k_{c,AB}}{k_b}\left[\mathrm{A}\right]$$ (6)

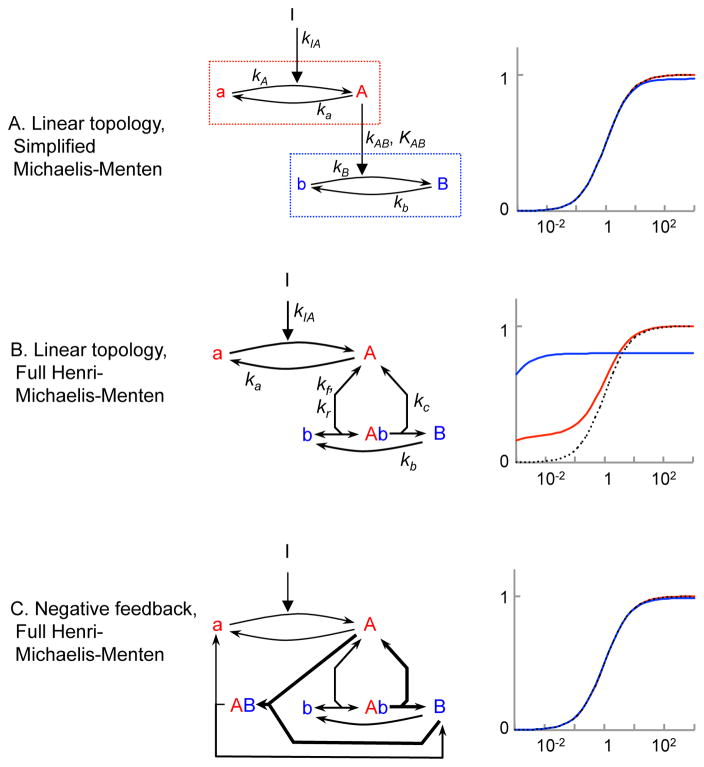
If k_c,AB = k_b, which is reasonable, this represents DoRA (Figure 6A, Document S1). This result, that a linear topology can produce DoRA when modeled with simplified Michaelis-Menten kinetics, contrasts with our prior results using mass action kinetics.

Figure 6.

(A,B) Dose-response behavior of linear topology (T1) when the first step is modeled with simple mass action kinetics and the second step with Henri-Michaelis-Menten kinetics. Each row shows a reaction network and the dose-response curves that result from it using the parameters [A_tot.] = [B_tot.] = k_IA = k_a = k_b = k_r = 1, k_f = 10,000, and k_c = 9; from these, K_M = 0.001. (A) shows simplified Michaelis-Menten kinetics; it approaches DoRA as K_M approaches 0. (B) shows full Henri-Michaelis-Menten kinetics; note retroactivity effect on node A. (C) Topology with a negative feedback loop (T2) in which the first step is modeled with simple mass action kinetics and other reactions with full Henri-Michaelis-Menten kinetics. Optimal parameters are depicted here using bold arrows for fast reactions and single-headed arrows for irreversible reactions.

We explored this discrepancy by modeling topology T1 yet again, but now with full Henri-Michaelis-Menten kinetics, explicitly including the Ab complex. We defined node activity as the fraction of the total species in the active state, as before, but now also included species in complexes. We optimized model parameters as described above, except that we computed dose-response curves with COPASI (Hoops et al., 2006), computed SWRMS distances with Microsoft Excel, and optimized by trial and error, because these kinetics are outside of NodeSolver’s scope (Document S1). The optimal model (d = 5.55) turned out to be in the limit of low saturation (K_M ≫ [b]). As a result, it was effectively identical to the one from our original treatment using simple mass action kinetics. We found that the high saturation limit did not enable DoRA because the A and b species became sequestered into Ab complexes (Blüthgen et al., 2006). Importantly, the amount of A that is sequestered is affected by the concentration of b and this sequestration of A shifts the equilibrium of node A towards its active state. As a result, changes in the node B activity affect the node A activity (Document S1). This effect, in which sequestration causes downstream elements to affect upstream elements, is well known and called “hidden feedback” (Ventura et al., 2010; Ventura et al., 2008) or “retroactivity” (Del Vecchio et al., 2008). In this case, the hidden feedback shifted the node A dose-response curve substantially, causing it to fit less well to the target function. This then increased the node B activity, making the node B curve fit less well too. These results show that simplified Michaelis-Menten kinetics allow enzyme saturation but ignore its consequences, and so, when used in multi-step models are internally inconsistent and lead to incorrect solutions, whereas simple mass action kinetics (which implicitly assume negligible enzyme-substrate complexation) are internally consistent and lead to correct solutions.

We also investigated the negative feedback and push-pull topologies (T2 and T8, respectively) with full Henri-Michaelis-Menten kinetics to see if the different kinetics would affect their abilities to exhibit DoRA. As with the linear topology, we found that the best fit for the push-pull topology (d = 0.00) was in the low saturation regime (Document S1). This result again supported the use of simple mass action kinetics in the rest of this work. In contrast, we found that the negative feedback topology T2 could exhibit essentially perfect DoRA (Figure 6C, Document S1). This occurred when the control reaction was saturated and the others were unsaturated. Consideration of this result showed that DoRA arose in this network from a comparator-adjustor mechanism, described next.

Models combining negative feedback with a comparator-adjuster gave perfect DoRA

We were initially puzzled why topologies with negative feedback loops, such as T2, T10, and T15, did not produce DoRA when we modeled them using simple mass action kinetics (Figure 3). We then realized that they lacked elements found in even the earliest artificial controlled systems for which system output tracked variable input (e.g. servomechanisms and telephone amplifiers) (Black, 1934; Mindell, 2002). Such feedback control systems incorporate an explicit controller; more precisely, they use a comparator-adjuster, which compares system output with input, then uses this information to adjust output so that it matches the input (Figure 7A). Such comparator-adjustors can align output with input in different ways, including use of high gain and proportional feedback control, and use of integral feedback control (e.g. (Ang et al., 2010; Astrom and Murray, 2008; Doyle, 2016; Muzzey et al., 2009; Yi et al., 2000)). In this work, models T2, T10, and T15 modeled with mass action kinetics had negative feedback that affected output, but lacked comparator-adjusters.

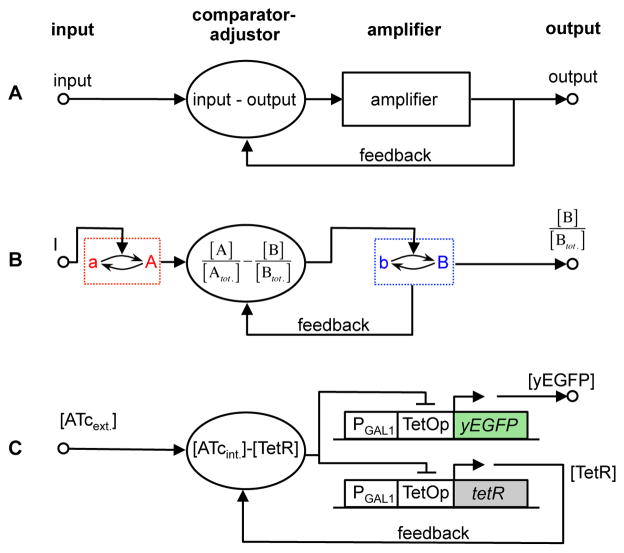
Figure 7.

Alignment by feedback and comparator-adjuster. (A) Control theory diagram, where “amplifier” is a device to be controlled and “comparator-adjuster” compares input to output and adjusts signal in proportion to the difference. (B) Biochemical reaction network where nodes have active and nominally inactive states. Feedback alone cannot produce alignment in such a network, but can if network contains a comparator-adjuster, shown with an unspecified mechanism. (C) A human-built cell system that aligned output with variant input using feedback and a comparator-adjuster (Nevozhay et al. (2009). An inhibitor, anhydrotetracycline (ATc) diffuses into (and out of) yeast cells slowly. ATc binds and inactivates tetracycline repressor, TetR. If ATc level rises so that intracellular ATc exceeds TetR, then all TetR is bound, while some ATc is free. Because all TetR is inactivated, it does not repress yEGFP expression, so system output increases. Meanwhile, TetR synthesis driven by an identical promoter is derepressed. Once total TetR concentration exceeds that of ATc, some TetR remains free and active. Free TetR represses yEGFP expression, capping yEGFP synthesis and TetR synthesis at a new, higher level. The comparator uses binding between ATc and TetR to compute their concentration difference, and the adjuster (free TetR) aligns system output (yEGFP and total TetR) with the input, ATc.

Figure 7B shows a conceptual two-node topology that incorporates negative feedback and a comparator-adjuster. Here, the extracellular signal, I, sets the node A activity level, which is then sent to the comparator-adjuster. This component, via an unspecified proportional control mechanism, computes the difference between the node A and node B activities, amplifies the difference, and uses the final result to activate node B. Meanwhile, node B loses activity through an uncatalyzed reaction. This closed-loop control architecture can produce perfect DoRA if the comparator-adjuster output is amplified (Document S1). We know no examples of such control in eukaryotic signaling systems. However, Nevozhay et al. (Nevozhay et al., 2009) recently imported the regulatory logic of the prokaryotic Tn10 tet repressor system into yeast cells to engineer a system in yeast cells that does use feedback control to align output with input (Figure 7C, Document S1). This control mechanism uses binding between input ligand and Tet repressor as a comparator and regulated protein expression for amplification. Our investigation of topology T2 with full Henri-Michaelis-Menten kinetics showed that it also aligned output with input using a comparator-adjuster-like mechanism. In this case, tight binding between species A and species B forms a comparator, leaving free A or free B if amounts are unequal; these unbound species then adjust the total amount of B to bring the system back to alignment. If there is free A, then A catalyzes conversion of b to B at rate k_f,AB[A][b], a rate directly proportional to the amount of free A. If there is free B, then B is converted to b at rate k_b[B], which is directly proportional to the amount of free B. In both cases, the rate of change is directly proportional to the difference between A and B.

Together, these results suggest that multistep cell signaling systems could use negative feedback to achieve DoRA, but that to do so, they would require a mechanism to compare output with input and use the result to adjust output.

Discussion

The problem of control

The yeast PRS amplifies the weak effects of ligands binding to receptors to carry out dramatic but tightly regulated responses, for example the wholesale expression of pheromone-induced proteins. These responses depend on chains of biochemical reactions among components that diffuse in space and vary in number. To transmit information accurately through this chain, the PRS, and many other cell signaling systems, maintains Dose-Response Alignment, or DoRA, in which fractional downstream output equals the fraction of receptor occupied at the cell surface. Framed in this way, the PRS addresses and solves a problem that human engineers solved in the 20th century (Mindell, 2002). Mechanical engineers designed servomechanisms to steer ships and aim guns, and communication engineers designed feedback controlled amplifiers to relay signals over continent-sized distances, in each case precisely converting weak time-variant input to more powerful outputs (Astrom and Murray, 2008; Franklin et al., 1994). These are problems of control.

To better understand how systems like the PRS effect control through chains of chemical reactions, we searched for reaction arrangements (topologies) that could transmit fractional receptor occupancy faithfully. We found that most topologies could not yield DoRA when constrained to non-cooperative reactions but yielded better alignment with cooperative reactions. Given that PRS operation requires receptor oligomerization (Overton et al., 2005), multiple Fus3^MAPK protein modifications (Gartner et al., 1992), and Fus3^MAPK conformational changes when other proteins bind the Ste5 scaffold (Good et al., 2009), we find such cooperative reactions likely.

Alignment via push-pull control

We also found that alignment can arise from push-pull mechanisms, in which the active species at a node activates a downstream node, while the nominally inactive species deactivates it. There is evidence supporting operation of push-pull mechanisms in the PRS. First, phosphorylated Fus3^MAPK and Kss1^MAPK induce PRS gene expression (Breitkreutz et al., 2001; Elion et al., 1993; Good et al., 2009; Madhani et al., 1997) while unphosphorylated Kss1^MAPK diminishes PRS gene expression (Bardwell et al., 1998a; Bardwell et al., 1998b). Second, ligand-bound Ste2^GPCR causes G-protein dissociation (Bardwell, 2005) while unbound Ste2^GPCR causes G-protein association (Bush and Colman-Lerner, in revision).

In addition, we found that long-range push-pull (multistep topologies in which the nominally inactive form of a protein exerts a negative effect on steps far downstream) can improve downstream alignment. This may explain an otherwise puzzling finding: PRS gene expression aligns well with receptor occupancy (Figure 1B) despite the fact that the dose-response for Ste5 scaffold recruitment is more sensitive than that for receptor occupancy (Bush and Colman-Lerner, 2013) and blocking the Fus3^MAPK negative feedback, which sensitizes the dose-response curve for Fus3^MAPK phosphorylation (Yu et al., 2008), does not sensitize recruitment further (Bush and Colman-Lerner, 2013). A pull reaction originating upstream of Ste5 recruitment would explain these results.

Push-pull mechanisms are inherent to phosphorelay systems, found in bacteria and plants. In the E. coli EnvZ-OmpR system (Batchelor and Goulian, 2003; Russo and Silhavy, 1991, 1993), phosphorylated EnvZ (a histidine protein kinase) transfers its phosphate to and activates OmpR, losing its phosphate in the process (unlike the serine-threonine protein kinases in the PRS), while unphosphorylated EnvZ is a phosphatase that removes the phosphate from and inactivates OmpR-P, gaining a phosphate in the process. This push-pull mechanism is said to make the downstream response robust to protein concentration fluctuations (Batchelor and Goulian, 2003; Russo and Silhavy, 1991, 1993; Shinar et al., 2007). Some phosphorelay systems have additional proteins that relay phosphate groups from the sensor (Grefen and Harter, 2004) to the downstream transcription factor. In Arabadopsis thaliana, for example, cytokinin ligand binding to histidine kinase membrane receptors causes them to phosphorylate Arabadopsis Histidine Phosphotransfer (AHP) proteins, which then pass phosphates to type B Arabadopsis Response Regulators (ARRs), which bind DNA and activate transcription. Examination of published data (Stolz et al., 2011) shows that these systems exhibit DoRA. Although our work here does not apply to phosphorelay systems directly, because we assumed that upstream components are not changed when they activate or deactivate downstream components, it may be that these systems use push-pull to achieve DoRA.

Alignment by feedback and comparator-adjuster

Negative feedback control is common in biology. In E. coli leucine biosynthesis, for example, the cell maintains a high substrate concentration but limits its flux into the pathway using negative feedback from the leucine product (Umbarger, 1978). This feedback suppresses leucine biosynthesis when the cell has adequate supply. Similarly, in the E. coli SOS response, depletion of LexA protein derepresses the LexA promoter, which makes more LexA protein (Brent and Ptashne, 1980, 1981). This stabilizes LexA concentration during normal growth and helps restore it after the SOS response. These systems promote homeostasis by comparing system output to a set-point determined by evolution and adjusting output accordingly. We showed here that quantitatively aligning output to variable input requires not only negative feedback but also component(s) that act as a comparator-adjuster, comparing output to variable input and adjusting output to match. Such components are common in human-designed control systems (Mindell, 2002) and are present in an engineered eukaryotic control circuit that imported Tet repressor control from the bacterial transposon Tn10 into yeast (Nevozhay et al., 2009) (Figure 7C). However comparator-adjusters have not been described for natural eukaryotic signaling systems and this work suggests they may not have evolved.

Comparison with prior work

In a previous study, Yan et al. (Yan et al., 2012) also searched for reaction networks that could produce DoRA. In contrast to our results, they found that many topologies, including linear topologies and topologies with negative feedback loops (but without comparator-adjusters) could produce DoRA. Our results show that this difference has two main causes. First, Yan et al. (2012) defined DoRA as similarity in EC₅₀s and Hill coefficients of response curves, but did not account for differences in amplitudes. We chose to include curve amplitudes (and baselines) in our definition of DoRA and SWRMS criterion because a) we could estimate them from experimental data, b) they are functionally important: signaling systems with larger response amplitudes can give greater ranges of distinguishable responses to different input signals (Yu et al., 2008) and c) by including these parameters, we represented the biological system more accurately. In fact, if we exclude response amplitude from our alignment criteria, we find that linear topologies give perfect alignment, but at the cost of flattening downstream response curves (see Figure 3B). Second, Yan et al. modeled reactions using the simplified Michaelis-Menten approach, while we modeled reactions using mass action. We showed in this work that use of the simplified Michaelis-Menten approach allows a linear topology to exhibit DoRA (see eq. 6) while use of mass action or full Michaelis-Menten equations do not allow these topologies to exhibit DoRA.

In a third difference between our work and the previous study, Yan et al. asserted that a topology could produce DoRA if a large enough proportion of models (>0.15%) with randomly chosen parameters gave alignment defined by their criteria, whereas we asserted that a topology could produce DoRA based on the alignment (defined by our SWRMS score) given by optimum parameter values. We will consider elsewhere arguments about the general biological relevance of robustness of signaling system models to changes in parameter values. Here, to compare the studies, we quantified the fraction of the models that could produce partial alignment (d<3) with randomly chosen parameters (Document S1). We found that topologies with better optimum values tended to be more likely to produce partial alignment. Thus, we conclude that the fact that we found only a few topologies that produced DoRA was because our criteria for alignment included amplitude, and that our modeling scheme used less simplified, more accurate means to represent enzyme kinetics.

Genetic tests for control mechanisms

For systems that do exhibit DoRA, our results suggest genetic tests to determine whether these control mechanisms are operating. One approach to establish push-pull control would be to design and ectopically express mutant proteins locked in either push or pull forms (Conde et al., 2009; Russo and Silhavy, 1993). For example, for a step carried out by a protein kinase, one would engineer and ectopically express mutant forms of the protein constitutively in the active kinase state or nominally inactive phosphatase state. The locked push kinase would increase basal downstream response and the locked pull form would decrease the maximum response. In closed-loop control systems regulated by negative feedback with a comparator adjuster, these perturbations should have no effect.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Steve Andrews: steven.s.andrews@gmail.com

METHOD DETAILS

SWRMS distance

We defined the SWRMS distance (Document S1) between target and model dose-response curves, y_t(I) and y_m(I), respectively, as

$$d=100\sqrt{\underset{0}{\overset{\infty }{\int }}{\left[y_m\left(I\right)-y_t\left(I\right)\right]}^2\left[c_t\left|\frac{{dy}_t\left(I\right)}{dI}\right|+c_m\left|\frac{{dy}_m\left(I\right)}{dI}\right|\right]dI}$$ (7)

where

$$c_t=\frac{1}{2|y_t(\infty )-y_t\left(0\right)|}{c}_m=\frac{1}{2|y_m(\infty )-y_m\left(0\right)|}$$

It is a standard weighted sum of squared errors calculation (Larsen and Marx, 2012; Press et al., 1988) in which the integral is the sum, the [(y_m(I)-y_t(I)]² term is the squared error, and the second term in brackets is the weighting. These weights are proportional to the slopes of the two dose-response curves and the equation is scaled to give a unitless fit value between 0 (perfect fit), and 100 (no fit). This metric accounts for differences in baseline, slope, amplitude and EC₅₀, and weights these differences most heavily around their EC₅₀s, where responses are most distinct. We computed the overall distance for multiple nodes as the mean of the distances for the individual nodes.

NodeSolver software

NodeSolver computed steady-state node activities by making initial guesses and then refining these guesses repeatedly using the steady-state equations until activities changed by less than 1 part in 10⁵, which typically took between 3 and 8 iterations. It repeated these steps over a range of different input doses to yield steady-state dose-response curves. NodeSolver optimized model parameters by starting with user-supplied initial parameters and optimizing them using greedy random walk and/or downhill simplex (Press et al., 1988) methods to minimize the SWRMS distance. It computed the SWRMS distances with eq. 7, performing the integration with the midpoint rule with dose values sampled from the smallest EC₅₀ of the target Hill functions divided by 110, to the largest EC₅₀ of the target Hill functions multiplied by 110, with logarithmically spaced doses (multiples of 1.1). We deemed a solution optimal only when we found it repeatedly from many different starting values. See Document S1 for details.

QUANTIFICATION AND STATISTICAL ANALYSIS

We quantified fit quality using the SWRMS fit distance, described above in the Method Details section. Our statistical analyses used the Akaike Information Criterion and a robustness test in which we computed the fraction of trial models that had SWRMS distances within 3 units of an optimum value. Document S1 describes these methods in detail.

DATA AND SOFTWARE AVAILABILITY

Software

The NodeSolver software is licensed under LGPL and is available in Data S1.

Data Resources

Document S1 provides additional details on all of our important quantitative results and sources of all experimental data sets. Contact the authors for any other results.

Highlights.

1. In many signaling systems, output is closely aligned with fraction bound receptor

2. In push-pull, nominally-inactive proteins inhibit, and align downstream output

3. Networks can also form comparator-adjusters, enabling alignment by feedback

4. Genetic tests can distinguish feedback-based alignment from push-pull control