Active hair-bundle motility harnesses noise to operate near an optimum of mechanosensitivity

Abstract

The ear relies on nonlinear amplification to enhance its sensitivity and frequency selectivity to oscillatory mechanical stimuli. It has been suggested that this active process results from the operation of dynamical systems that operate in the vicinity of an oscillatory instability, a Hopf bifurcation. In the bullfrog's sacculus, a hair cell can display spontaneous oscillations of its mechanosensory hair bundle. The behavior of an oscillatory hair bundle resembles that of a critical oscillator. We present here a theoretical description of the effects of intrinsic noise on active hair-bundle motility. An oscillatory instability can result from the interplay between a region of negative stiffness in the bundle's force-displacement relation and the Ca²⁺-regulated activity of molecular motors. We calculate a state diagram that describes the possible dynamical states of the hair bundle in the absence of fluctuations. Taking into account thermal fluctuations, the stochastic nature of transduction channels' gating, and of the forces generated by molecular motors, we discuss conditions that yield a response function and spontaneous noisy movements of the hair bundle in quantitative agreement with previously published experiments. We find that the magnitude of the fluctuations resulting from the active processes that mediate mechanical amplification remains just below that of thermal fluctuations. Fluctuations destroy the phase coherence of spontaneous oscillations and restrict the bundle's sensitivity as well as frequency selectivity to small oscillatory stimuli. We show, however, that a hair bundle studied experimentally operates near an optimum of mechanosensitivity in our state diagram.

The mechanosensory hair cells of the vertebrate ear amplify their inputs to enhance sensitivity and frequency selectivity to weak oscillatory stimuli (reviewed in refs. 1–3). Although the cellular mechanisms that mediate this active process have remained elusive, in vitro (4–6) as well as in vivo (7) experiments have revealed that the mechanosensory organelle of the hair cell, the hair bundle, can generate active oscillatory movements that might underlie frequency-selective amplification. Four essential properties define active hair-bundle motility. First, a hair bundle can oscillate spontaneously (ref. 8 and references therein). Second, the response to weak oscillatory mechanical stimuli can be amplified (4, 6). Third, amplification is frequency selective, being the greatest at stimulus frequencies near the bundle's characteristic frequency of oscillation (4, 6). Finally, the response to stimuli of increasing magnitudes displays a compressive nonlinearity that is well characterized by a power law (6). All four properties have been recognized as signatures of a dynamical system operating near an oscillatory instability, a Hopf bifurcation (6, 9–11). Because these properties would be observed for any dynamical system on the verge of an oscillatory instability, however, they do not pinpoint the specific microscopic mechanism that underlies the amplificatory process.

Oscillatory instabilities of the hair bundle can be generated by at least three active mechanisms. First, a collection of molecular motors with a region of negative slope in the force-velocity relation becomes self oscillatory when the motor assembly is coupled to an elastic element (12). In the hair bundle, the myosin-based adaptation motors in the stereocilia (reviewed in ref. 13), as well as the dynein motors in the kinocilium (10), could provide such an instance. Second, coupling Ca²⁺-mediated reclosure of the transduction channels (14–17) with gating kinetics (9) or intracellelular Ca²⁺ dynamics (18) can yield hair-bundle oscillations. Finally, the interplay between negative hair-bundle stiffness and the Ca²⁺-dependent activity of the adaptation motors can generate oscillations (8, 19). This third mechanism provides the most convincing description of the hair-bundle oscillations observed in the bullfrog's sacculus.

Although the observed hair-bundle movements are noisy and lose phase coherence after approximately one cycle of oscillation (5), previous theoretical studies neglected the effects of fluctuations on active hair-bundle motility. Noise blurs the distinction between active oscillations and fluctuations and thus conceals the bifurcation between oscillatory and nonoscillatory states. Here, we show that only by taking fluctuations into account, we can provide a quantitative theoretical description of a hair bundle's responsiveness to oscillatory stimuli.

Active Hair-Bundle Mechanics

At steady state, an external force F_ext applied at a hair bundle's top is balanced by the elastic restoring forces provided by the parallel combination of gating springs and stereociliary pivots: K_gsY + K_spX = F_ext. Here, K_gs characterizes the combined stiffness of the gating springs, K_sp that of the pivots, X is the position of the hair-bundle tip along the axis of the applied force, and Y = ℓ/γ accounts for the extension ℓ of the gating springs projected on the X axis. The geometric coefficient γ relates the shearing motion between contiguous stereocilia to movement at the top of the bundle (20). We assume that the N stereocilia of the hair bundle move as a unit and that the gating springs operate in parallel. Channel opening yields a decrease of the gating-spring extension by an amount d, a phenomenon called gating compliance (14). At the bundle's top, this gating swing corresponds to a displacement D = d/γ. As a consequence, the average extension of the gating springs can be expressed as Y = X - X_a - DP_o, where P_o denotes the open probability of the transduction channels and X_a the value of Y for X = 0 if all channels are closed. In a two-state model for channel gating (21), the open probability can be written as

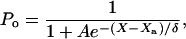[1]

where A = exp([ΔG + (K_gsD²)/(2N)]/k_BT) accounts for the intrinsic energy difference ΔG between the open and the closed states of a transduction channel and δ = Nk_BT/(K_gsD). Here, k_B is the Boltzmann constant and T denotes the temperature.

The dynamic behavior of the hair bundle can be described by the following three coupled equations:

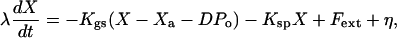[2]

[3]

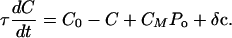[4]

Eq. 2 describes the dynamics of the hair-bundle position X. The hair bundle is subjected to friction, characterized by the coefficient λ, as well as to the elastic forces -K_spX and -K_gsY and the external force F_ext. Active hair-bundle movements result from forces exerted by a collection of N_a molecular motors within the hair bundle. By adjusting the gating-spring extension, these motors mediate mechanical adaptation to sustained stimuli (reviewed in ref. 13). The variable X_a can be interpreted as the position of the motor collection. Eq. 3 describes the mechanics and the dynamics of these motors by a linear force-velocity relation of the form λ_adX_a/dt = -F₀ + F_mot, where λ_a characterizes the slope of the force-velocity relation. In the hair bundle, the motors experience an elastic force F_mot = K_gsY. At stall, these motors produce an average force F₀ = N_aγfp that is proportional to the force f generated by a single motor and to the probability p that a motor is bound to an actin filament. Active force production by the motors corresponds to motors climbing up the stereocilia, i.e., dX_a/dt < 0, which tends to increase the extension of the gating springs and to open transduction channels. In Eq. 3, we neglect the fact that adaptation is incomplete. Incomplete adaptation could be described by introducing an additional elastic element (22). Because mechanical adaptation is regulated by Ca²⁺ (ref. 23; reviewed in ref. 24), we assume that the probability for an adaptation motor to be bound to actin p(C) depends on the intracellular Ca²⁺ concentration C at the motor site. Eq. 4 describes the dynamics of C, which relaxes with a time constant τ. The steady-state Ca²⁺ concentration maintained by the cell if the transduction channels are closed is denoted C₀ and the concentration C_M >> C₀ is the maximal Ca²⁺ concentration at the location of the adaptation motors. It is expected to be proportional to the Ca²⁺ concentration in the endolymph (8). In the following, we ignore nonlinearities in p(C) and truncate a general expansion to linear order: p(C) ≃ p₀ + p₁C. We define the strength of the calcium feedback on the motor force F₀ by the dimensionless parameter S = -C_M p₁/p₀. As detailed in the next section, we have added noise terms η, η_a, and δc to account for fluctuations that result from several types of stochastic processes.

State Diagram in the Absence of Noise

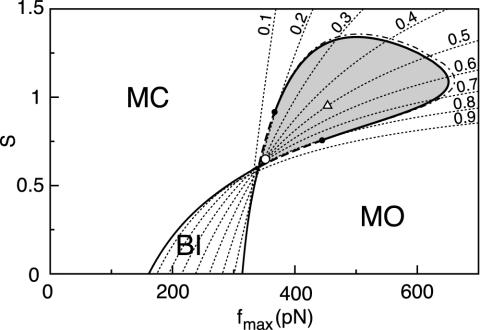
To explore the dynamic behaviors of the system described by Eqs. 2, 3, 4, we first ignore the effects of fluctuations and assume F_ext = 0. Steady states satisfy dX/dt = 0, dX_a/dt = 0, and dC/dt = 0. Linear stability analysis of these steady states reveals conditions for stability as well as for oscillating instabilities that lead to spontaneous oscillations by a Hopf bifurcation (25). Because calcium dynamics at the motor site is expected to be much faster than the hair-bundle oscillations observed in the bullfrog's sacculus (26), we determined the state diagram for τ = 0 (Fig. 1). The state diagram is a function of two parameters: the maximal force f_max = N_afp₀ produced by adaptation motors along their axis of movement, and the dimensionless feedback strength S of the Ca²⁺ regulation. We assume that increased Ca²⁺ levels at the motor site reduce active force generation by the motors (p₁ < 0).

Fig. 1.

State diagram of a hair bundle as a function of the maximal force f_max that adaptation motors produce and of the strength S of Ca²⁺ feedback on motor activity. Lines of equal open probability P_o of the transduction channels (dotted lines) are superimposed and each are indexed by the corresponding value for P_o. The diagram is parsed into regions in which the hair bundle can be monostable with transduction channels mostly closed (MC) or mostly open (MO), bistable (BI), or oscillatory (gray). Hopf bifurcations occur along the line separating oscillating from stable states: for small f_max, the bifurcation is subcritical (broken line), whereas the bifurcation becomes supercritical for larger motor forces (solid line). For f_max = 352 pN and S = 0.65 with P_o = 0.5 (○), stochastic simulations of the system closely matched the behavior of a hair bundle that was studied experimentally (see Figs. 2 and 3). For f_max = 439 pN and P_o = 0.5 (▵), the noisy system displayed a global maximum of sensitivity to small stimuli (see Fig. 4). The quality factor of the bundle's spontaneous oscillations was also close to the global maximum there. The state diagram was calculated by assuming that the calcium dynamics is instantaneous τ = 0. In the case of τ = 0.1 ms, the oscillatory region expands slightly toward regions of larger motor forces (dot-dash line). Parameters used are listed in Table 1.

The state diagram exhibits different regimes (Fig. 1). If the force f_max is small, the motors are not strong enough to pull transduction channels open. In this case, the system is monostable with most of the channels closed. Increasing f_max leads to channel opening. For intermediate forces and weak Ca²⁺ feedback, the system is bistable, i.e., open and closed channels coexist. For strong Ca²⁺ feedbacks, however, the motors cannot sustain the forces required to maintain the channels open. In this case, the system is again monostable with most channels closed. Spontaneous oscillations occur in a region of both intermediate forces and feedback strengths. The boundary between a stable state and an oscillatory state corresponds to a Hopf bifurcation. This bifurcation is subcritical near the bistable region (broken line in Fig. 1) but becomes supercritical at larger motor forces (solid line in Fig. 1). Note that there is no oscillation in the absence of Ca²⁺ feedback, i.e., for S = 0.

The behavior of the system in the presence of an external force can be described by response functions. However, the calculated linear response functions of the noiseless system in an oscillatory state display sharp singularities that are not observed experimentally (see Fig. 5, which is published as supporting information on the PNAS web site).

Fluctuations and Noise

Spontaneous hair-bundle oscillations are noisy (5). Noise terms η, η_a, and δc in Eqs. 2, 3, 4 formally take into account the effects of various sources of fluctuations that destroy the phase coherence of hair-bundle movements. The stochastic forces η and η_a act on X and X_a, respectively. The consequences of these forces have been analyzed for nonoscillating hair bundles (27). The fluctuations δc of the Ca²⁺ concentration in the stereocilia result from stochastic transitions between open and closed states of the transduction channels (28). Noise terms are zero on average. Their strengths are characterized by autocorrelation functions 〈η(t)η(0)〉, 〈η_a(t)η_a(0)〉, and 〈δc(t)δc(0)〉, respectively. We assume that different noise sources are uncorrelated and that noise is Gaussian.

Assuming that the motors are deactivated (f = 0), we first discuss thermal contributions to the noise. The noise term η in Eq. 2 then results from Brownian motion of fluid molecules that collide with the hair bundle and from thermal transitions between open and closed states of the transduction channels. By changing the gating-spring extension, this channel clatter generates fluctuating forces on the stereocilia. The fluctuation-dissipation theorem implies that 〈η(t)η(0)〉 = 2k_BTλδ(t). The friction coefficient λ = λ_h + λ_c results from two contributions: λ_h ≃ 1.3 10^-7 N·s·m^-1 accounts for hydrodynamic friction, which depends on bundle geometry and fluid viscosity (14, 29), whereas λ_c results from channel clatter. The contribution λ_c can be estimated from the autocorrelation function of the force η_c that results from stochastic opening and closing of N transduction channels

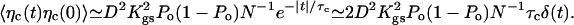[5]

This expression shows that noise is correlated in time with a correlation time given here by the characteristic dwell time τ_c of the transduction channels' open and closed states. However, channel clatter is fast compared with hair-bundle oscillations and we can focus on the low-frequency limit of friction. With 〈η_c(t)η_c(0)〉 ≃ 2k_BTλ_cδ(t), Eq. 5 yields

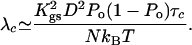[6]

Recent single-channel recordings indicate that τ_c ≃ 1 ms (30), which is consistent with earlier measurements of the transduction kinetics of a group of hair cells (31). By using parameter values listed in Table 1 and P_o = 0.5, we find that channel clatter dominates friction and λ ≃ 3 10^-6 N·s·m^-1.

Table 1. Parameter values for the simulations.

Parameter	Definition	Value	Ref.
λ	Friction coefficient of hair bundle	2.8 μN·s·m-1
λa	Friction coefficient of adaptation motors	10 μN·s·m-1	23
Kgs	Combined gating-spring stiffness	750 μN·m-1	19
Ksp	Combined stiffness of stereociliary pivots and load	600 μN·m-1	19
d	Gating-spring elongation on channel opening	8.7 nm	19
γ	Geometrical gain of stereociliary shear motion	0.14	20
τ	Time constant of calcium feedback	0.1 ms
τc	Dwell time of transduction channels	1 ms	30
C0	Intracellular Ca2+ concentration with channels closed	0 mM
N	No. of stereocilia	50	20
Na	No. of motors in the hair bundle	3000	13
ΔG	Intrinsic energy change on channel opening	10 kBT	38
Ta	Effective temperature for Eq. 3	1.5 T

The noise term η_a in Eq. 3 describes fluctuating forces acting on the motors. In the case of deactivated motors (f = 0), thermal binding and unbinding of molecular motors, respectively, to and from actin filaments generates friction with a coefficient λ₀ ≃ γ²N_apkτ₁ (32). Here, p = τ₁/(τ₁ + τ₂) is the probability for a motor to be attached to an actin filament, where τ₁ and τ₂ denote the lifetimes of the attached and detached states, respectively, and k is the stiffness of a single motor. By using P ≃ 0.05, k ≃ 500 μN/m, and τ₁≃ 10 ms, we estimate λ₀ ≃ 1.5 10^-5 N·s·m^-1. The strength of the thermal contribution η₀ to η_a is 〈η₀(t)η₀(0)〉 ≃ 2k_BTλ₀δ(t).

We now turn to the more interesting situation of active motors (f ≠ 0). Measurements of the initial adaptation rate as a function of the magnitude of step stimuli (23) imply that λ_a ≃ 1.3 10^-5 N·s·m^-1, which is in agreement with the value of the friction coefficient λ₀ estimated above for deactivated motors. We thus neglect the effect of motor activity on motor friction. However, the stochastic activity of motors generates an active contribution η_m to η_a with

[7]

Here, we have assumed that the N_a motors fluctuate independently and that relevant time scales for a hair-bundle oscillation are longer than τ_a, where 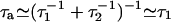is the characteristic time of force production by the motors. This noise strength can be described by introducing an effective temperature T_m defined by 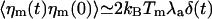. With f ≃ 1 pN, τ_a ≃ 10 ms, and p ≃ 0.05, we find T_m/T ≃ N_aγ²p(1 - p)f²τ_a/(k_BTλ_a) ≃ 0.5. Writing 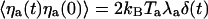, we thus get T_a ≃ 1.5 T.

Assuming that channel dynamics equilibrates rapidly enough, we neglect the effect of spontaneous motion on the channels' statistics and assume that Eq. 1 is valid even if motors are active. In this case, the fluctuations in Eq. 2 remain thermal and satisfy a fluctuation-dissipation relation.

Ca²⁺ dynamics is also subjected to fluctuations that are described by the noise term δc in Eq. 4. Similarly as above, the autocorrelation function of δc is approximated by

[8]

We can assess the significance of these fluctuations in the limit where C relaxes instantaneously. The system is in turn reduced to Eqs. 2 and 3, with C = C₀ + C_MP_o + δc. The fluctuations of the Ca²⁺ concentration can then be written as 〈δC(t)δC(0)〉 ≃ 〈δc(t)δc(0)〉. Because the probability p of motor binding to actin filaments depends on the Ca²⁺ concentration, fluctuations of C result in the generation of fluctuating forces η_c by the motors. We estimate this random force η_c ≃ γN_afp₁δC. For times large compared with τ_c, we find

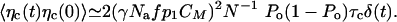[9]

Introducing an effective temperature T_c, with 〈η_c(t)η_c(0)〉 = 2k_BT_cλ_aδ(t), we find T_c/T ≃ (γf_maxS)²P_o(1 - P_o)τ_c/(Nk_BTλ_a) ≃ 0.13 for f_max = 350 pN, S = 0.65, P_o = 0.5 and parameter values from Table 1. This result suggests that fluctuations of the motor force evoked by Ca²⁺ fluctuations are below the unavoidable thermal fluctuations.

In our simulations of Eqs. 2, 3, 4, we used the noise strengths 〈η(t)η(0)〉 = 2k_BTλδ(t), 〈η_a(t)η_a(0)〉 = 2k_BT_aλ_aδ(t) with T_a = 1.5 T and 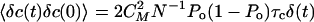, with parameter values listed in Table 1. Note that it is not necessary to know the value of C_M if S and f_max are given.

Spontaneous Movements and Response Function

Fluctuations destroy the phase coherence of spontaneous oscillations and conceal the bifurcations between the dynamic states displayed in the state diagram (Fig. 1). The response of a noisy oscillating system to a periodic force 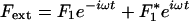thus behaves effectively as that of a stable system. The response function χ(ω) = X₁/F₁, where X₁ is the amplitude of the phase-locked response, can be described for small stimulus amplitude by

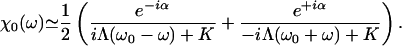[10]

This response function is characterized by the stiffness K and the friction coefficient Λ. The phase α describes the phase lag of the bundle's displacement with respect to the stimulus at the characteristic frequency ω₀. As shown in Supporting Text, which is published as supporting information on the PNAS web site, this form of the linear response function is that of a noiseless stable system that operates in the vicinity of a Hopf bifurcation. In addition, the spectral density G(ω) of hair-bundle displacements can be approximated by:

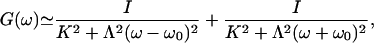[11]

where I is the noise strength (5). The parameters have been measured in the case of a spontaneously oscillating hair bundle from the bullfrog's sacculus (5): K ≃ 100 μN·m^-1, λ ≃ 6.5 μN·s·m^-1, I ≃ 0.14 pN²·s and α ≃ 0.

The response of the hair bundle to larger stimulus amplitudes reveals the existence of nonlinearities (6). The dominant non-linearity is described by the generic expression for the sensitivity , which defines the nonlinear coefficient B (10). For the data published in ref. 6, |B|≃1.5 10¹² N·m^-3. In the nonlinear regime 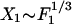, and the sensitivity decreases approximately according to the power law .

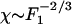Numerical Results

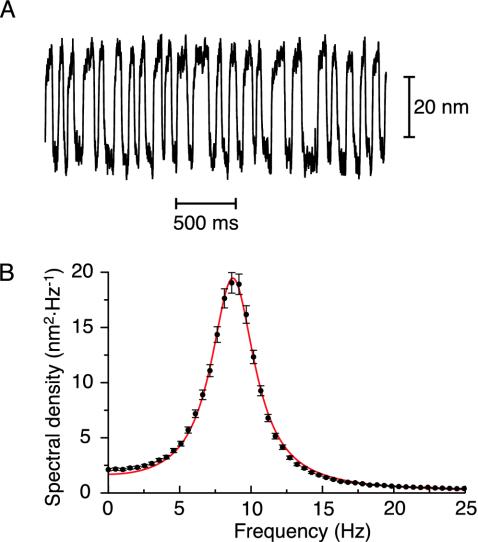
We performed numerical simulations of Eqs. 2, 3, 4 (see Supporting Text). Most of the model parameters were fixed (Table 1). The only free parameters were the feedback strength S and the maximal motor force f_max. In endolymph containing Ca²⁺at a concentration of 250 μM, the opening probability for which the adaptation motors reach steady state is between 0.25 and 0.5 (23, 31). Along a line of constant open probability P_o in the state diagram (Fig. 1), we determined the parameters in Eq. 10 as a function of f_max in the presence of noise. For P_o = 0.5, the characteristic frequency of spontaneous oscillations varied between a few Hertz and ≈50 Hz in the range f_max = 330–800 pN within which a peak was detected in the spectral density of spontaneous movements. Because α ≃ 0 ensures that the linear response function has the same shape as that observed experimentally (5), we elected the value of the motor force f_max ≃ 352 pN at which this condition was satisfied for P_o = 0.5 (Fig. 1). At this operating point, the system displayed noisy spontaneous oscillations X(t) that were strikingly similar to the hair-bundle oscillations observed in the bullfrog's sacculus (Fig. 2A). Their spectral density was peaked at a characteristic frequency ν₀ = ω₀/2π = 8.7 Hz and had a width at half the maximal value of δν = 3.7 Hz, corresponding to a quality factor Q = ν₀/δν = 2.4 (Fig. 2B).

Fig. 2.

Spontaneous noisy oscillations for parameters corresponding to the operating point (○) in Fig. 1. (A) Spontaneous hair-bundle movements X(t)as a function of time. This oscillation has an rms magnitude of 15 nm. (B) Spectral density of the movements depicted in A. The spectrum was fitted (red line) by Eq. 11 with I = 0.105 pN²·s, K = 74 μN·m^-1, λ = 6.3 μN·s·m^-1, and ν₀ = 2πω₀ = 8.7 Hz. The hair-bundle oscillation measured in ref. 5 is strikingly similar to that simulated here. Here, and in the subsequent figures, error bars correspond to the SD obtained for 4–10 successive realizations of the simulation.

We calculated the linear response function χ₀ as a function of frequency (Fig. 3 A and B) and found that it agreed quantitatively with the experimental observations (5). At the characteristic frequency of the spontaneous oscillations, the sensitivity |χ| of the system to mechanical stimulation exhibited the three regimes observed experimentally (6) as a function of the stimulus amplitude |F₁| (Fig. 3C): a linear regime of maximal sensitivity |χ̂₀| = 8.5 km·N^-1 at ω = ω₀ for small stimuli, a compressive nonlinearity for intermediate stimuli and a linear behavior of low sensitivity for large stimuli. The maximal sensitivity as well as the breadth of the nonlinear region were also in quantitative agreement with experiments. An important parameter that influenced the system's maximal sensitivity was the stiffness of the load to which the hair bundle is coupled (see Fig. 6, which is published as supporting information on the PNAS web site). For f_max ≃ 352 pN, power spectra of spontaneous oscillations and response functions were not significantly affected by varying P_o in the range 0.2–0.8. Thus, agreement between simulations and experiments did not qualify a particular value of P_o.

Fig. 3.

Responsiveness to sinusoidal stimulation. (A) The real part of the linear response function χ₀ displays a peak near the bundle's frequency of spontaneous oscillation, and is positive everywhere. (B) The imaginary part 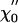changes sign at a frequency near that of the bundle's spontaneous oscillation. The external sinusoidal force had an amplitude of 2 pN. From the fit (red lines) of the response function χ₀ by Eq. 10, we found α ≃ 0, K = 74 μN·m^-1, Λ = 4.3 μN·s·m^-1, and ν₀ = 2πω₀ = 8.6 Hz, which is in quantitative agreement with the response function measured for an oscillatory hair bundle (5). (C) The sensitivity |χ| displays a nonlinear compression in a regime of intermediate forces 3 - 30 pN when the magnitude of an external sinusoidal force is increased at the frequency of the spontaneous oscillations. This nonlinearity is consistent with a power law with an exponent of -2/3 (red line). A fit to the relation yielded the nonlinear coefficient |B| ≃ 1.2 10¹²N·m^-3. For stimuli smaller than ≃ 1 pN, the sensitivity saturates at 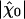≃ 8.5 km·N^-1 (green line). For stimuli larger than ≃ 300 pN, the sensitivity approaches a constant, minimal value of 1 km·N^-1 (green line). The parameters used in the simulation are the same as in Fig. 2.

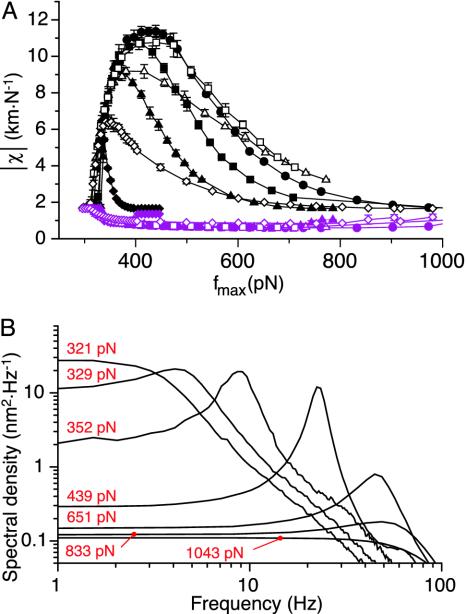
Is the hair bundle's operating point optimal? To address this issue, we determined, for different open probabilities of the transduction channels, how the sensitivity to small stimuli at resonance 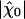varied with the maximal force f_max that the motors produce (Fig. 4A). We found that this sensitivity was at the global maximum 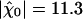km·N^-1 for P_o ≃ 0.5 and f_max ≃ 439 pN, near the center of the oscillatory region in the state diagram (Fig. 1). At this point, the spontaneous oscillation displayed a characteristic frequency of ν₀ = 24.7 Hz and a quality factor Q = 5.4 that was also near the global maximum (Fig. 4B). This point was clearly distinct from the operating point of the hair bundle (Fig. 1). There, the hair bundle was characterized by a sensitivity to small stimuli that was 25% lower than that at the optimum.

Fig. 4.

Sensitivity and spontaneous movements as a function of the hair bundle's operating point. (A) Maximal (black symbols) and minimal (purple symbols) sensitivity |χ| as a function of the maximal motor force f_max for P₀ = 0.1 (♦), 0.3 (▴), 0.4 (▪), 0.5 (•), 0.6 (□), 0.7 (▵), and 0.9 (⋄). The sensitivity displays a global maximum for f_max ≃ 439 pN and P_o = 0.5. Responses of maximal sensitivity 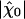were obtained in response to small sinusoidal stimuli at the characteristic frequency of spontaneous bundle oscillation, whereas the minimal sensitivity was observed for intense stimuli (see Fig. 3). The ratio of maximal and minimal sensitivities determines the gain of the amplificatory mechanism. (B) Spectral density of spontaneous movements along the line P_o = 0.5 for the different values of f_max indicated in red.

Discussion

The Importance of Fluctuations. We have presented a physical description of active hair-bundle motility that emphasizes the role played by fluctuations. The mechanical properties of oscillatory hair bundles can be described quantitatively only when fluctuations are taken into account. Fluctuations arise in part from Brownian motion of fluid molecules and from the stochastic gating of transduction channels. By consuming energy, the motors power frequency-selective amplification but also generate nonthermal fluctuations that add to the inevitable thermal fluctuations. We find, however, that the magnitude of fluctuations due to active processes remains below the level of thermal noise.

In the absence of fluctuations, an operating point on the line of Hopf bifurcations in the state diagram would result in diverging sensitivity, infinite frequency selectivity, and a compressive nonlinearity over many decades of stimulus magnitudes. This situation is ideal for detecting oscillatory stimuli (9–11, 33, 34). As exemplified by our analysis, fluctuations restrict the system's sensitivity and frequency selectivity to oscillatory stimuli as well as the range of stimulus magnitudes over which the compressive nonlinearity of the bundle's response occurs. Despite fluctuations, a single hair bundle amplifies its response to small stimuli and, correspondingly, the characteristic compressive nonlinearity that arises near a Hopf bifurcation remains (Fig. 3). One can define the gain of the amplificatory process as the ratio of the sensitivity at resonance to small stimuli 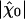and that to intense stimuli. Both experiments and simulations indicate that active hair-bundle motility provides a gain of ≈10. Our theoretical analysis demonstrates that significant amplification happens inside the area of the state diagram where the noiseless system oscillates (Fig. 4A). Interestingly, the global optimum of mechanosensitivity is obtained at an operating point located near the center of the oscillatory region in the state diagram, thus far from the line of Hopf bifurcations of the noiseless system. Furthermore, the sensitivity is largest if the open probability of the transduction channels is 0.5. In addition, variations of 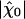to small stimuli in the state diagram mirror that of the quality factor Q ≃ ω₀λ/2K (Fig. 4). In particular, the point at which Q is at a global maximum is near the global optimum of sensitivity. The quality factor characterizes the coherence of spontaneous movements and is related to the system's ability to discriminate frequencies: the sharper the spectral density of spontaneous oscillations, the greater the selectivity.

Sensitivity and Friction. The value of the coefficient λ that characterizes friction of the hair bundle has a significant effect on the sensitivity 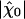that the system can achieve. Decreasing this friction coefficient to the physical limit λ ≃ λ_h ≃ 2 10^-7N·s·m^-1 given by hydrodynamic friction, indeed results in a threefold increase of sensitivity. This coefficient was estimated previously in experiments where the hair cells were immersed entirely in standard saline solution and did not, or very rarely, show spontaneous oscillations of their hair bundles (29). Because the Ca²⁺ concentration in standard saline is 16 times higher than in artificial endolymph, the feedback strength S = -C_M p₁/p₀ is probably much stronger in standard saline. A more efficient Ca²⁺ feedback could explain why the system operates in a monostable state with transduction channels mostly closed (Fig. 1). Under these circumstances, the experiments suggested that hydrodynamic friction alone accounted for the observed hair-bundle friction. For hair bundles immersed in artificial endolymph, our present analysis indicates instead that the contribution of channel clatter dominates friction λ ≃ λ_c ≃ 3 10^-6 N·s·m^-1. This apparent discrepancy can be explained by considering the Ca²⁺ dependence of the transduction channels' open probability P_o and possibly of the channels' gating swing d. In standard saline, the average open probability is only P_o ≃ 0.15 (23, 31). If in addition, the channel swing were reduced to d ≃ 4 nm, as suggested by measurements of bundle stiffness in this ionic environment (14), the contribution of channel clatter to friction would be at the level of hydrodynamic friction (see Eq. 6). In addition, the dwell time τ_c of transduction channels is also probably shorter in standard saline than it is in artificial endolymph (30, 31). Faster transduction channels would yield greater mechanosensitivity than that observed so far in the bullfrog's sacculus. A dwell time of τ_c ≃ 1ms is probably fast enough for saccular hair cells to operate in a frequency range of 5–130 Hz, but auditory hair cells could have shorter dwell times, therefore reduced friction λ and increased mechanosensitivity. The calcium dependence of parameters such as P_o, d, or K_gs can also account for the fast mechanical “twitches” that occur in standard saline when the hair bundle is deflected by abrupt step stimuli (14, 15, 17). Because these movements are beyond the scope of the present work, however, we have neglected these effects in our physical description.

Operating Point. We can only speculate about what determines the operating point of the hair bundle in the state diagram. It has been suggested that a general self-regulation mechanism adjusts a control parameter of the system to bring it close to a point of high sensitivity (10). An important issue is to identify possible parameters that the cell could regulate to optimize its behavior. Our work suggests that the feedback strength S and the maximal motor force f_max are natural candidates. If the hair cell could regulate both parameters, it could achieve high sensitivity by moving toward the point where the quality factor Q is the largest. For that purpose, the hair cell might take advantage of a filter (18), such as that provided by an electrical oscillator in the basolateral membrane of the hair cell (35, 36). The hair cell might also control one parameter, for instance, if the maximal motor force f_max were determined only by the intrinsic properties of the adaptation motors and the number of motors per stereocilium. By regulating S at fixed f_max, the hair cell could nevertheless find an operating point of high sensitivity if the properties of the motors were such that f_max fell in an appropriate range. The hair cell could regulate the feedback strength S for example by controlling the intracellular level C₀ of Ca²⁺. Such a mechanism might also affect f_max.

The ability of a single hair bundle to detect oscillatory stimuli by using critical oscillations is limited by fluctuations which conceal the critical point. This limitation could be overcome if an ensemble of hair cells with similar characteristic frequencies were mechanically coupled. Coupled noisy oscillators could approach the ideal case of a critical oscillator near a Hopf bifurcation. In an intact mammalian cochlea, the gain that characterizes amplification of basilar-membrane motion is up to 10³ (37), which can be compared to a gain of only ≈10 for a single hair bundle in the bullfrog's sacculus. This finding suggests that in the cochlea the effects of fluctuations of individual hair cells could be reduced by the cooperative action of many oscillatory cells, whether the oscillations are provided by active hair-bundle motility or by a different mechanism.