Summary
Models of cortical dynamics often assume a homogeneous connectivity structure. However, we show that heterogeneous input connectivity can prevent the dynamic balance between excitation and inhibition, a hallmark of cortical dynamics, and yield unrealistically sparse and temporally regular firing. Anatomically based estimates of the connectivity of layer 4 (L4) rat barrel cortex and numerical simulations of this circuit indicate that the local network possesses substantial heterogeneity in input connectivity, sufficient to disrupt excitation-inhibition balance. We show that homeostatic plasticity in inhibitory synapses can align the functional connectivity to compensate for structural heterogeneity. Alternatively, spike-frequency adaptation can give rise to a novel state in which local firing rates adjust dynamically so that adaptation currents and synaptic inputs are balanced. This theory is supported by simulations of L4 barrel cortex during spontaneous and stimulus-evoked conditions. Our study shows how synaptic and cellular mechanisms yield fluctuation-driven dynamics despite structural heterogeneity in cortical circuits.
Keywords: cortical networks, dynamics, balance, adaptation, inhibition, homeostatic plasticity
Highlights
-
•
Structural heterogeneity threatens the dynamic balance of excitation and inhibition
-
•
Reconstruction of cortical networks reveals significant structural heterogeneity
-
•
Spike-frequency adaptation can act locally to facilitate global balance
-
•
Inhibitory homeostatic plasticity can compensate for structural imbalance
Landau et al. show that anatomical variability is expected to generate substantial heterogeneity in the input connectivity of local cortical networks. This heterogeneity threatens the balance of excitation and inhibition. Balance can be recovered by spike-frequency adaptation or homeostatic plasticity.
Introduction
Cortical neurons receive thousands of excitatory and inhibitory synaptic inputs, both long-range and from local circuits. Balancing between the resultant excitatory and inhibitory currents is therefore crucial to keep the neurons at a functional dynamic range, namely near their firing threshold, allowing them to rapidly elicit action potentials in response to changes in their inputs. Substantial perturbation of this balance may lead to either a strongly inhibited circuit, where most of the neurons remain quiescent, or an epileptic state with “runaway” firing. Indeed, excitation-inhibition imbalance has been implicated in several neurological and psychiatric diseases (Yizhar et al., 2011, Dehghani et al., 2016).
It has been shown that under conditions where recurrent neuronal circuits are connected via strong synapses, the firing rates of excitatory and inhibitory populations adjust dynamically, resulting in an asynchronous balanced state (van Vreeswijk and Sompolinsky, 1996). In this state, the neurons are driven by the fluctuations in their net excitatory and inhibitory inputs. This fluctuation-dominated state has many spatial and temporal response properties that resemble those of cortical neurons (Brunel, 2000, Renart et al., 2010, Roxin et al., 2011, Hansel and van Vreeswijk, 2012, Pehlevan and Sompolinsky, 2014, Wimmer et al., 2015).
However, the emergence of balanced states in excitation-inhibition networks is based on the common assumption of a uniform connection probability, namely that all neurons in a population have similar total number of connections. Yet recent studies reported that cortical neurons exhibit significant heterogeneity in their input probability (Okun et al., 2015) and in their total synaptic current (Xue et al., 2014). Such heterogeneity is already apparent from anatomical studies of the first stage of input into the cortex: the innervation of layer 4 (L4) neurons by thalamocortical axons (da Costa and Martin, 2011, Furuta et al., 2011, Schoonover et al., 2014). The assumption of uniform connectivity is hence questionable, and we therefore investigated how heterogeneity in input connectivity will impact the excitation-inhibition dynamics of cortical networks.
We first study this issue in abstract network models in which the structural variability in the total synaptic input to postsynaptic cells across the population is much larger than expected from that of uniform connection probability. We show theoretically and by simulations that the dynamic cancelation between excitation and inhibition is undermined, and a majority of neurons are completely suppressed while a small number of neurons fire action potentials regularly at unrealistically high rates. Correlations in the connectivity structure can mitigate this imbalance. We present a quantitative measure of the structural imbalance, accounting for both correlations and heterogeneity, which predicts whether excitation-inhibition balance can be achieved.
We identify two cellular mechanisms that can recover excitation-inhibition balance. The first is homeostatic synaptic plasticity, which adjusts the functional connectivity patterns in the network to compensate for the structural imbalance. An alternate mechanism that does not involve synaptic plasticity is spike-frequency adaptation. We show that this adaptation current generates local negative feedback that cancels the excess synaptic input at the single-cell level. This leads to a novel adaptation-facilitated balance, in which the adaptation current enables neurons to remain near threshold and fluctuations drive irregular, asynchronous activity.
We study the effect of heterogeneity on excitation-inhibition balance and the possible mechanisms to recover balance in a realistic network model of L4 of the D2 column of the vibrissal part of rat primary somatosensory cortex (vS1; i.e., barrel cortex). There is strong anatomical evidence that the L4 barrel comprises a relatively complete local network, with axons and dendrites of both excitatory and inhibitory neurons remaining largely restricted to the barrel, and thalamic ventral posteromedial nucleus (VPM) axons defining the barrel boundaries. Using a statistical connectivity model based on reconstructions of the detailed 3D anatomy of the barrel cortex (Egger et al., 2014), we provide realistic estimates of the heterogeneity in input connectivity in the local L4 circuits (i.e., within the barrel) and study the resulting dynamics in an anatomically constrained network of linear integrate-and-fire (LIF) point neurons (Gerstner and Kistler, 2002). We find that non-uniformities in the distributions of excitatory and inhibitory somata (Meyer et al., 2013), and morphological diversity within and across L4 cell types (Koelbl et al., 2015, Narayanan et al., 2015) yield substantial heterogeneity in input connectivity. The estimated levels of correlations between excitatory and inhibitory input connectivity are significant but still yield substantial structural imbalance, and are therefore not sufficient to restore a balanced state. In numerical simulations, we find that structural heterogeneity has dramatic impact on the activity in the major thalamo-recipient layer, for example, allowing only a fraction of neurons to be responsive to sensory input.
We test both homeostatic plasticity and the novel adaptation-facilitated balance on our anatomically constrained model of L4 in rat vS1. We show that over the necessary long timescales of homeostatic plasticity, functional in-degrees can be adjusted to recover realistic firing. Furthermore, we show that on more rapid timescales, adaptation currents with strengths and time courses comparable with those observed experimentally are sufficient to counteract the structural heterogeneity of the L4 network, thereby yielding an asynchronous balanced state with realistic firing rates during both periods of spontaneous and periods of stimulus-evoked activity.
Results
Broken Balanced State
Network models often assume a homogeneous probability of connection between pairs of neurons, given their cell types. In such networks, the in-degree, i.e., the total number of inputs to individual neurons, is narrowly distributed around its mean, K. Specifically, the SD σk is proportional to the square root of the mean. In the cortex, typical in-degrees are on the order of thousands, so that in these homogeneous network models the SD of the in-degree is small relative to the mean (Figure 1A, left).
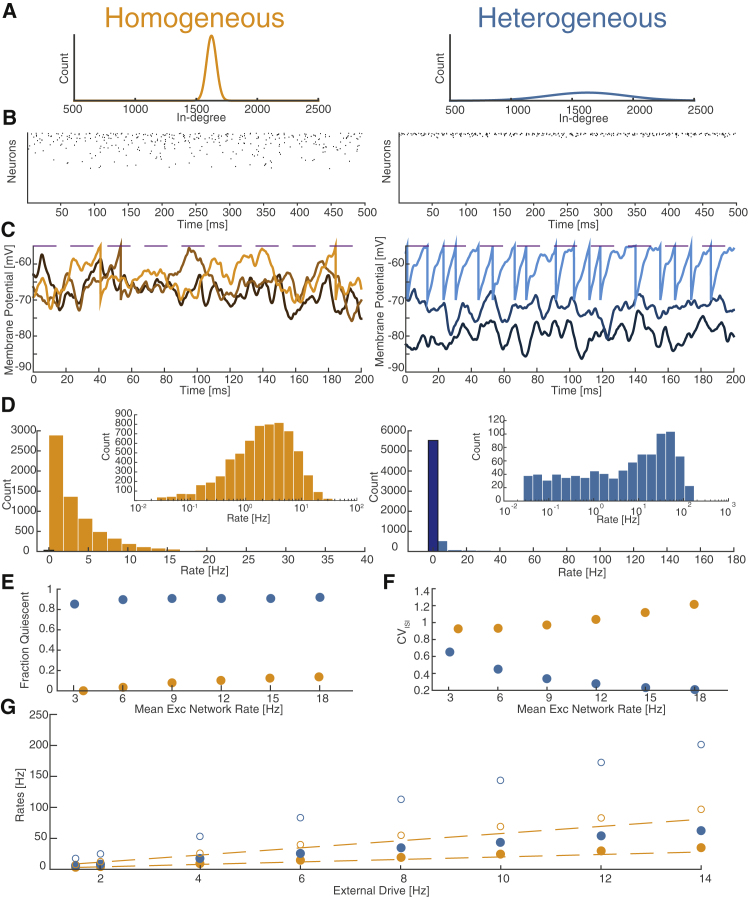
Figure 1.
Structural Heterogeneity Breaks the Balanced State
Comparison of the dynamics of homogeneous (Hom.) network (left, orange) with a heterogeneous (Het.) network (right, blue) (coefficient of variation of in-degree, CVK = 0.2). Excitatory drive is chosen so that mean rates of the two networks are comparable.
(A) In-degree distributions.
(B) Raster plots of networks firing near 3 Hz reveal exceedingly sparse and relatively regular firing in Het. network.
(C) Two hundred milliseconds of membrane potential traces from three typical neurons from each network (lighter colors indicate higher-firing neurons). The three neurons in the Hom. network have membrane potentials that fluctuate significantly near threshold and are highly overlapping; their corresponding firing rates are 0.6, 7.6, and 26.5 Hz. The three neurons from the Het. network have membrane potentials whose means are quite separated and fluctuations are smaller. Two of the neurons never fire, whereas one of them fires fairly regularly at 94.6 Hz.
(D) Rate histograms of the same networks from 60 s trial. Totally quiescent neurons enumerated by bar with black edges and slightly darker color. In the Het. network, more than 75% of neurons are totally quiescent, whereas some neurons reach rates of more than 150 Hz. Inset: log-histogram shows the Hom. network follows a roughly log-normal rate distribution, whereas the Het. network is far more skewed.
(E) Fraction of neurons quiescent for entire 60 s trial as a function of network rate.
(F) CVISI as a function of network rate.
(G) Mean rates of both populations (open symbols represent inhibitory [Inh], filled symbols represent excitatory [Exc]) versus external drive. Dotted lines indicate prediction from balanced-state theory.
All panels display results from Exc population except where indicated. Inh results were qualitatively similar.
To analytically study the effect of deviating from this homogeneity assumption, we consider networks with heterogeneous in-degrees and characterize their distribution by the coefficient of variation, . In homogeneous networks, CVk is much smaller than 1; networks are said to be heterogeneous if they have CVk of order unity (Figure 1A, right).
We study heterogeneous networks with three cell types: excitatory (E) and inhibitory (I) neurons as well as an excitatory external population denoted by O. We write the mean in-degree from type B onto type A as KAB. We also write K as the mean connectivity across the entire network. We focus here on the first- and second-order statistics of the connectivity structure, assuming negligible higher-order statistics such that the identities of a neuron’s postsynaptic targets are independent of its own in-degree. Furthermore, we assume the network is in an asynchronous state characterized by population rates: rE, rI, and rO.
We write the three in-degrees of the ith neuron of type A = E, I as for B = E, I, O, where the “relative in-degree,” , is neuron i’s in-degree from cell-type B divided by the mean over all postsynaptic neurons of type A. Then the total mean synaptic current to this neuron is
| (Equation 1) |
where JAB is the strength of synaptic connections from neurons of type B onto neurons of type A scaled by the mean number of connections KAB.
As in the balanced network of van Vreeswijk and Sompolinsky (1998) we assume that the synapses are strong, such that action potentials in a small fraction of presynaptic neurons are sufficient to evoke an action potential in the postsynaptic neuron. Therefore, the excitatory and inhibitory synaptic currents in Equation 1 are each large relative to threshold, and for the net current to be within range of the threshold, the excitatory and inhibitory contributions need to approximately cancel each other, yielding a set of linear equations that we refer to as the balance conditions:
| (Equation 2) |
For a network with small CVk, all are approximately 1. Thus, the near-threshold condition reduces to the two linear equations of the balanced state of homogeneous networks, two equations for the two unknowns rE and rI. In such a network it has been shown that the mean population rates will dynamically adjust their value and arrive rapidly at a steady state that satisfies these equations. This balancing of the net excitatory and inhibitory currents yields a state where most of the neurons are near threshold and driven by the fluctuations in synaptic current (van Vreeswijk and Sompolinsky, 1998).
However, in the case where CVk is non-negligible, each relative in-degree may be substantially different, and therefore there is no pair of excitatory and inhibitory population rates that can combine to satisfy Equation 2 for more than a small fraction of the population. Due to the substantial difference between in-degrees within the network, any given population rates will only balance synaptic current of a small fraction of neurons. The remaining neurons will either have a larger ratio of inhibitory to excitatory in-degrees, and therefore be completely suppressed by strong total inhibitory current, or they will have a smaller ratio, in which case they will be driven to high firing rates with regular inter-spike intervals (ISIs). Thus, we expect the dynamic balance between excitation and inhibition to fail in heterogeneous networks (see Experimental Procedures).
We have numerically confirmed these predictions by generating heterogeneous networks and simulating them with LIF point neurons (Experimental Procedures). Even in a network with only moderate heterogeneity (CVk = 0.2), the lack of balance is immediately apparent in the dynamics of both the population firing (Figure 1B) and the individual neuron subthreshold potentials (Figure 1C). The population rate distributions are highly skewed, with over 75% of neurons completely quiescent and an extremely long tail of neurons with very high firing rates and low average coefficient of variation of ISI (CVISI) (Figures 1D–1F). In such a state even the mean current over all postsynaptic neurons is not balanced, reflected in population firing rates versus input strength that deviate from the linear population balance predictions (Figure 1G). Evidently, substantial heterogeneity of input connectivity leads to a breakdown of the balanced state.
Impact of In-Degree Correlations
The above analysis was based on the assumption that excitatory and inhibitory in-degrees are uncorrelated. If, however, they are correlated, this could potentially restore the excitation-inhibition balance. Indeed, evidence of correlations between postsynaptic excitatory and inhibitory currents has been reported recently (Xue et al., 2014). In the extreme case where all three vectors of relative in-degrees are the same, , the set of balance equations (Equation 2) can be effectively reduced to the pair of population equations of the homogeneous case, and the dynamic balance of the population rates will guarantee that the net mean current on all postsynaptic neurons is canceled and balance is restored.
Writing , where is the mean of the three vectors , we introduce a measure of “structural imbalance”:
| (Equation 3) |
where the average is over neurons and type-to-type pathways. In the Supplemental Information, we show that to achieve excitation-inhibition balance, must be at most of order . Note that can be small either if in-degrees are uncorrelated but narrowly distributed, such as in homogeneous networks, or if in-degrees are broadly distributed but highly correlated. This bound implies that the structural demands for maintaining balance in the face of heterogeneity are extremely stringent: in heterogeneous networks, the cell-to-cell variability of the input connectivity must be close to fully correlated across all presynaptic populations to enable the emergence of the balanced state.
To check the above prediction, we generated heterogeneous networks scanning the two-dimensional parameter space consisting of CVk and the correlation coefficient between in-degrees from each pair of presynaptic populations (Experimental Procedures). In agreement with our theoretical bound, simulations reveal that only networks that are sufficiently homogeneous or have sufficiently correlated in-degrees exhibit the dynamics of excitation-inhibition balance (Figure 2). For example, for networks with correlation coefficients as high as 0.7, as CVk increases from 0 to 0.3, we observe a crossover from a state in which all neurons are active with CVISI around 1 to a state in which more than 80% of neurons are quiescent throughout the trial (Figure 2A) and those that fire have CVISI less than 0.5 (Figure 2B).
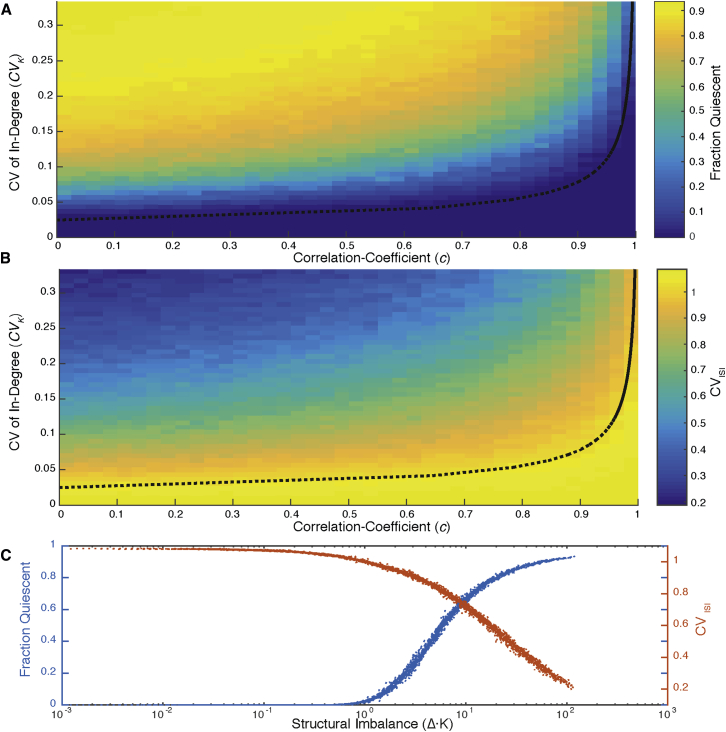
Figure 2.
Structural Bounds on the Balanced State
Heterogeneous networks are generated with each presynaptic population having identical CVK and correlation coefficient between in-degrees from pairs of populations given by .
(A and B) Color maps of simulation results scanning the 2D structural parameter space of heterogeneous networks firing at 10 Hz for a 60 s trial. Dotted black line shows the theoretical bound (Δ ⋅ K ≈ 1) below which we expect balance to hold. (A) Fraction of neurons quiescent throughout the 60 s trial. (B) CVISI over the same parameter space. Similar qualitative results are obtained at different firing rates.
(C) Fraction quiescent (blue) and CVISI (red) (from A and B) plotted against the deviation from fully correlated in-degrees (given by Δ ⋅ K) shows that this deviation determines the dynamics of networks independent of respective values of CVK and c.
Furthermore, by plotting both CVISI and the fraction of quiescent neurons as a function of structural imbalance (Δ) for networks with a range of structural parameters, we confirm that Δ is an effective measure for predicting dynamical imbalance (Figure 2C). Our simulations indicate that in-degree correlations mitigate the impact of structural heterogeneity, but balance is restored only for extremely high correlations.
Recovering Balance by Homeostatic Plasticity
If the relative in-degree vectors are not highly correlated, excitation-inhibition balance can still be achieved if the synaptic weights are properly tuned. Such a relation between synaptic efficacies and structural connectivity may emerge via homeostatic synaptic plasticity. A simple scenario is that the strength of each synapse is scaled by a factor proportional to the inverse of the in-degree of the postsynaptic neurons, , which will compensate for the structural heterogeneity. Indeed, as we show in the Supplemental Information (Figure S1), such a scaling of all synaptic strengths in the network yields balanced dynamics. However, such a scaling would require extensive plastic changes in the synaptic efficacies of all pathways, and the outcome will be a network with net synaptic currents that are homogeneous across each population.
In fact, a recent study reported broadly distributed net synaptic currents across a cortical population, although with significant correlations between total excitatory and inhibitory synaptic currents. That study suggested that these correlations might be in part the consequence of plasticity of inhibitory synapses (Xue et al., 2014). In addition, two recent theoretical and numerical studies have proposed inhibitory plasticity as a mechanism for balancing excitatory and inhibitory inputs (Luz and Shamir, 2012, Vogels et al., 2011). These results motivate the question: can plasticity in the inhibitory synaptic weights alone recover balance?
To explore this possibility, we assume a network with heterogeneous, uncorrelated in-degrees and initial homogeneous synaptic weights. We study plastic changes that depend only on postsynaptic activity and write the relative change in inhibitory synaptic strength onto the ith neuron of type A as . This plasticity can be thought of as changing the “functional in-degree” of each neuron, , so that the mean net synaptic input to neuron i is still given by Equation 1, but with , where is the structural in-degree.
It is straightforward to see that plastic changes to the functional inhibitory in-degrees can be sufficient to bring the net current of each neuron near threshold, satisfying the balance conditions of Equation 2. In fact, the plastic changes that will satisfy those equations yield functional inhibitory in-degrees that are coplanar (i.e., lie in the plane spanned by the excitatory and external in-degrees), of the form
| (Equation 4) |
where the coefficients αE and αO must both be positive and they determine the firing rates (relative to rO) that will dynamically balance the net synaptic currents (see Supplemental Information for further details).
To check whether a plausible homeostatic inhibitory plasticity can reach this solution, we simulated a homeostatic plasticity rule on inhibitory synapses, reminiscent of synaptic scaling (Turrigiano et al., 1998, Rannals and Kapur, 2011, Keck et al., 2013), in which changes in synaptic strength depend only on postsynaptic firing (Experimental Procedures). This plasticity rule increases the strength of inhibition in proportion to the postsynaptic neuron’s firing rate, thus preventing neurons from firing at extremely high rates. Neurons firing at high rates due to structural imbalance will have their functional inhibition gradually increased, while quiescent neurons will have their functional inhibition reduced until Equation 4 is satisfied self-consistently across the population (see Supplemental Information).
Indeed, applying this plasticity rule on inhibitory synapses, we found that the network recovered excitation-inhibition balance by yielding coplanar functional in-degrees (Figure 3A), decreasing the functional imbalance throughout the time of plasticity (Figure 3B), and generating irregular firing dynamics with reasonable rate distributions (Figures 3C and 3D).
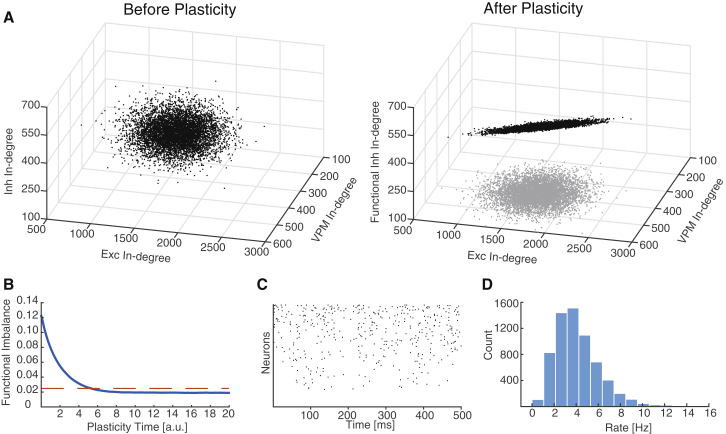
Figure 3.
Recovering Balance by Homeostatic Inhibitory Plasticity
Results of inhibitory (Inh) plasticity. We initialize a heterogeneous network with CVK = 0.15 and zero in-degree correlations.
(A) 3D scatterplot of the in-degrees of excitatory (Exc) neurons from each of the three populations (Exc, Inh, VPM). Left: initial. Right: After plasticity, correlations have increased such that the functional in-degrees are coplanar. Gray shadow is the projection of the in-degrees in the Exc-VPM plane, which is unchanged throughout plasticity.
(B) Functional imbalance (defined in the Supplemental Information) decreases throughout the plasticity session and reaches a steady state that is less than (red dashed line).
(C) Sample raster plot after plasticity reveals irregular firing.
(D) Rate histogram shows network has recovered reasonable rate distribution, with nearly all neurons active.
As explained in the Supplemental Information, the solution of coplanar functional in-degrees achieved by homeostatic plasticity is qualitatively different from the situation of low structural imbalance presented earlier. With low structural imbalance, balance can be achieved for the same broad range of synaptic strength parameters, JAB, as for homogeneous networks. In contrast, after homeostatic plasticity, the functional in-degrees are aligned for the particular values of JAB, as reflected in Equation 4.
Local Facilitation of Balance by Adaptation
Homeostatic synaptic changes such as described earlier (Equation 4) depend on the structural in-degrees of the external drive. Because homeostatic plasticity is relatively slow, of timescales of hours to days (Turrigiano et al., 1998, Rannals and Kapur, 2011, Keck et al., 2013), this mechanism will be unable to react fast to changes in the identity of the external population that drives the circuit. It is thus important to explore faster mechanisms for restoring balance in structurally heterogeneous networks.
Adaptation currents have been widely reported in cortical neurons with decay times on the order of seconds, and may be generated by a number of possible cellular mechanisms including Na+- or Ca2+-dependent K+ conductances (Sanchez-Vives et al., 2000, Stocker, 2004). Here we show that spike-frequency adaptation currents can compensate for the imbalance due to heterogeneous connectivity.
To explore this scenario analytically, we introduce a spike-frequency adaptation current such that after a neuron fires a spike it receives a negative current with amplitude Jad that is on the order of magnitude of a single postsynaptic current and has a decay time, τad, of the order of a second. Such current will add to the net current of ith neuron of type A (Equation 1), a negative term, , where is the neuron’s firing rate.
Because the decay time of adaptation is much larger than the membrane time constant, the adaptation current accumulated over time may be large; we assume that it is of the same order of magnitude as the synaptic currents. Therefore, adaptation can counter the local imbalance in the synaptic inputs and ensure that most neurons are in a near-threshold steady state. Requiring that the net current on the active neurons is balanced yields an equation for the local firing rates
| (Equation 5) |
where is x for x > 0 and zero otherwise. Averaging these relations over all neurons in a population yields self-consistency equations for the population firing rates (Supplemental Information).
Note that the neurons for which the net synaptic input is negative will be quiescent. The fraction of quiescent neurons is controlled by the strength of the adaptation or its time constant. For instance, for a fixed τad, as the adaptation current amplitude Jad increases, the fraction of neurons that are quiescent decreases; above some critical value all neurons are active (Supplemental Information). In this parameter regime, the above equations for the local firing rates become linear and averaging them over the full population yields the following linear equations for the population rates, as a function of the external drive,
| (Equation 6) |
To test our theory, we simulated a network model with parameterized input heterogeneity and correlations (Figure 4). We find that: (1) the above linear equations predict very well the mean network rates (Equation 6; Figure 4A), (2) the fraction of quiescent neurons is near zero (Figure 4B), and (3) the CVISI is near 1 (Figure 4C). Our theory yields a good prediction not only for the mean rates, but also for the individual neuron rates (Equation 5; Figure 4D). The adaptation current facilitates the dynamic balancing of net current despite the heterogeneous in-degrees and enables the emergence of substantial membrane potential fluctuations (Figure 4E), which drive irregular firing (Figure 4F).
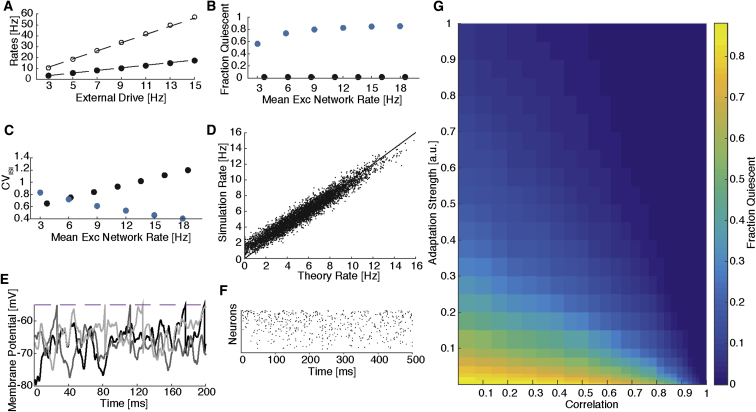
Figure 4.
Adaptation-Facilitated Balanced State in Heterogeneous Network
(A–F) Simulation of a network with , and spike-frequency adaptation. (A) Mean rate of excitatory (Exc; filled symbols) and inhibitory (Inh; open symbols) populations in the adaptation-facilitated network versus external drive. Dotted lines show the prediction from theory (Equation 6). (B and C) Comparison with network with the same structural heterogeneity, but without adaptation (blue). (B) Fraction of neurons quiescent versus mean firing rate. (C) CVISI versus mean firing rate. (D) Scatterplot of single neuron firing rates: simulation versus theory, with black line equality (r2 = 0.95). (E) Two hundred milliseconds of membrane potential traces from three typical neurons. Membrane potentials are concentrated near threshold and fluctuate significantly. The three neurons fire at rates 5.2, 7.3, and 9.5 Hz, respectively. (F) Sample 500 ms raster plot. Population exhibits asynchronous irregular firing.
(G) Fraction of neurons quiescent throughout 60 s. Color map of the 2D phase-space consisting of adaptation strength (units relative to amplitude of a single postsynaptic current) versus correlation coefficient. All networks constructed with CVK = 0.2, and external drive chosen to drive the network at 10 Hz. The fraction of quiescent neurons decreases with adaptation strength, and increased correlations allow weaker adaptation to recover balance.
Furthermore, our theory predicts that the strength of the adaptation current necessary to recover balance depends on the extent of in-degree correlations. In fact, the measure of structural imbalance, as given by the deviation from full correlation, Δ (Equation 3), determines the strength of adaptation necessary to recover balance (Experimental Procedures). For fixed CVK = 0.2, we explored the impact of varying both correlations and adaptation strength on the dynamical state of the network (Figure 4G). We observed that for a network with fully uncorrelated in-degrees to guarantee that only 5% of neurons were quiescent required that the post-spike amplitude of the adaptation current be about the same size as a single excitatory postsynaptic current (EPSC). However, in a network with in-degree correlations c ≈ 0.7, for example, an adaptation current with one-third the amplitude was sufficient to achieve the same recovery of balance.
We note that the adaptation-driven balanced state is qualitatively different from the balanced state of homogeneous networks in which the heterogeneity of firing rates emerges from the fluctuation-driven dynamical state even if all neurons have nearly the same number of inputs. Here individual firing rates are determined by the individual input connectivity (Equation 5), and in the parameter regime where all neurons are active these rates are a linear function of the in-degree (Supplemental Information).
Finally, we observe that this solution to structural imbalance is robust. In contrast with the homeostatic plasticity solution, which achieves balance only for a particular pattern of activity of external populations and responds to changes only over long timescales, adaptation reacts rapidly to changes in the relative activity of external populations with independent connectivity statistics.
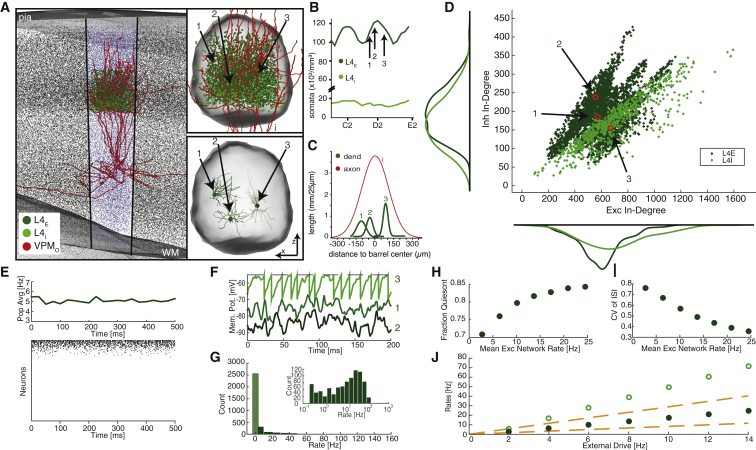
Anatomically Realistic Structural Heterogeneity
To obtain realistic estimates of the extent of heterogeneity and correlations in the input connectivity within a cortical circuit, we use an anatomically well-constrained connectivity model of an L4 barrel in rat vS1 and its thalamic inputs (Figure 5). As described previously (Egger et al., 2014) and reviewed in the Supplemental Information, a full-scale matrix of the probability of connections between all neurons in vS1 (“dense statistical connectome”) was generated on the basis of precisely measured 3D distributions of excitatory and inhibitory somata, which are non-uniform and cell-type specific even within L4 (Figure 5B), and 3D reconstructions of in vivo- and in vitro-labeled dendrite and axon morphologies, which are highly variable even within cell types (Figure 5C). Cell-type average connection probabilities have been validated (Egger et al., 2014) by comparison with studies that used paired recordings (Feldmeyer et al., 1999, Constantinople and Bruno, 2013) or correlated light and electron microscopy (Schoonover et al., 2014).
Figure 5.
Anatomical Sources of Heterogeneity and the Resulting Dynamics
(A) Dense statistical model of rat barrel cortex. Somata in the barrel column representing the D2 whisker are highlighted. Neurons with somata located in the L4 barrel of the D2 column were simulated; dark green represents excitatory (Exc), light green represents inhibitory (Inh), and red represents VPM axons. Top right: L4 barrel with three typical excitatory neurons identified. Bottom right: Dendritic morphology of the three example neurons.
(B) Soma density versus horizontal location with the locations of the three example neurons.
(C) Dendritic extent from barrel center of the three example neurons, with axonal extent of a single VPM axon.
(D) Scatterplot of Inh and Exc in-degrees with marginal histograms, with the three example neurons identified. Both postsynaptic populations are shown.
(E) Mean population firing rate and sample raster plot of 200 randomly chosen neurons ordered by decreasing firing rate.
(F) Two hundred milliseconds of membrane potential traces from the three example neurons shown in (A). Neuron 3 has a firing rate of 76.2 Hz, whereas the other two are quiescent.
(G) Rate histogram of the same network. Totally quiescent neurons enumerated by lighter bar with black edges.
(H) Fraction of neurons totally quiescent for 60 s as a function of network rate.
(I) CVISI as a function of network rate.
(J) Mean rates of both populations as a function of external drive. Dotted lines show prediction from balanced-state theory.
In the present study, we examine a network consisting of 3,283 excitatory neurons, comprising spiny stellate and star pyramidal cell types (Feldmeyer et al., 1999), and 680 inhibitory interneurons (Koelbl et al., 2015), representing the L4 barrel in the D2 column. In addition, all neurons in the network are innervated by 311 neurons located within the somatotopically aligned “barreloid” in the ventral posterior medial division of the thalamus (VPM) (Land et al., 1995).
Analysis of the resulting anatomically constrained connectivity reveals that the non-uniformities in the underlying anatomy give rise to substantial heterogeneity in the excitatory, inhibitory, and VPM input connectivities (Figure 5D). The resulting in-degree distributions are significantly broader than those of homogeneous networks; in particular, we find values of CVK around 0.3 (Table 1). Our analysis also shows that the excitatory and inhibitory in-degrees are strongly correlated, with correlation coefficients ranging from 0.55 to 0.79 for input to excitatory cells and up to 0.91 for inhibitory cells (Table 1). Thus, an important question is whether these high correlations are sufficient to yield a balanced state.
Table 1.
In-Degree Distributions of Anatomically Constrained L4 Network
| Exc Neurons | 599 | 0.27 | 195 | 0.31 | 119 | 0.30 | 0.55 | 0.79 | 0.69 | 11.3 |
| Inh Neurons | 709 | 0.35 | 172 | 0.38 | 130 | 0.36 | 0.88 | 0.90 | 0.91 | 5.6 |
Mean total number of inputs (connections with neurons located outside the L4 barrel were not considered), , and coefficient of variation, , from each of the three populations—excitatory (Exc), inhibitory (Inh), and the VPM thalamus (O)—the correlation coefficient, cAB, between each pair of populations, and the deviation from fully correlated as measured by the structural imbalance, Δ ⋅ K. The in-degree distributions are significantly broader than would be obtained in a homogeneous network, and despite substantial correlations the deviation from fully correlated is significant.
An initial answer is given by the network’s structural imbalance (Equation 3). We find for the anatomically constrained network Δ ⋅ K > 10, which predicts a substantial imbalance of the dynamics. We test this answer by simulating the dynamics of a network of LIF neurons with the anatomically constrained connectivity matrix. Indeed, we find that the network deviates significantly from a balanced state (Figures 5E and 5F), despite the substantial in-degree correlations. The rate distributions are extremely skewed with a large fraction of neurons quiescent (Figures 5G and 5H), individual neurons fire regularly especially at moderate rates (Figure 5I), and the mean population rates deviate from the linear balance equations (Figure 5J).
Nevertheless, the presence of correlations between the in-degrees does have a significant impact on the level of spike irregularity, reflected in a moderate CVISI, especially at low mean population rates. At low rates, the total excitatory and inhibitory currents are not substantially larger than threshold and therefore, in spite of the remaining imbalance, residual fluctuations continue to contribute significantly to the dynamics of active neurons, even as they account for less than one-third of the population. For higher mean firing rates (10 Hz and above), however, the mean currents dominate and firing becomes regular (Figure 5).
Our analysis shows that anatomical variability within the local recurrent network is expected to yield broken balance dynamics in the major thalamo-recipient layer. Furthermore, we applied the anatomically constrained connectivity estimate to the excitatory circuit across the entire D2 column and we find that structural heterogeneity is substantial within and across all layers (Table S1).
As we show in the Supplemental Information, inhibitory homeostatic plasticity as described earlier on abstract network models succeeds similarly in the anatomically constrained network, aligning the functional in-degrees so that all neurons fluctuate near threshold and recover the realistic firing patterns generated by excitation-inhibition balance (Figure S2). Next we explore whether a biologically plausible spike-frequency adaptation can maintain balance on behaviorally relevant timescales.
Dynamics of Anatomically Realistic Networks with Adaptation
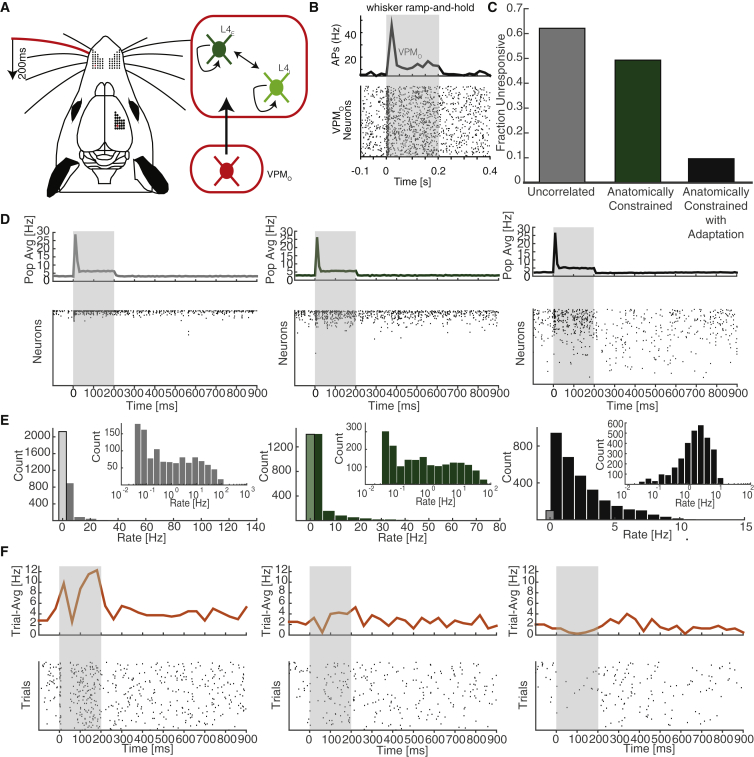
To test whether adaptation is a biologically plausible solution for the expected imbalance in local cortical networks due to structural heterogeneity, we introduced an adaptation current into our anatomically constrained network model and tested its effect in realistic spontaneous as well as stimulus-evoked states (Figure 6).
Figure 6.
Impact of Correlations and Adaptation on Spontaneous and Stimulus-Evoked Activity
(A) Schematic of stimulus protocol.
(B) Sample VPM peristimulus time histogram (PSTH) and raster plot of simulated stimulus-response. VPM rates were chosen to produce similar PSTHs across all three networks.
(C–E) Comparison of three networks (C). Fraction of neurons unresponsive to stimulus throughout all 100 trials is shown for network with uncorrelated in-degrees, marginal distributions constrained by anatomy, without adaptation (gray bar); anatomically constrained network without adaptation (green bar); and anatomically constrained network with adaptation (black bar). (D) Top: Trial-averaged population PSTH. Bottom: Single-trial raster plots reveal substantial difference in underlying population activity of the three networks. (E) Spontaneous population rate histogram from 60 s trial, black-line bin enumerates totally quiescent neurons. Inset: Log-histogram of the rates of active neurons. Only the network with both correlations and adaptation produces a roughly log-normal rate distribution.
(F) Top: trial-averaged PSTH of the three exemplary neurons from Figure 5A reveals consistency in the single-neuron response and heterogeneity within the population. Each neuron is active with realistic response profile. Bottom: raster plot of single neuron response to repeated trials shows trial-to-trial variability of single neuron response.
Spontaneous Dynamics
We simulated our network with external input from a population of VPM neurons with spontaneous firing rate set to drive the excitatory population at mean firing rate near 2.5 Hz for 60 s. Using an adaptation current comparable with that found empirically (Gupta et al., 2000, Rauch et al., 2003, La Camera et al., 2006), the network exhibited balanced dynamics: neurons fired irregularly and only 3% of neurons were quiescent, while the maximal firing rate was 15 Hz. Moreover, the shape of the rate distribution was roughly log-normal as observed empirically (Buzsáki and Mizuseki, 2014) (Figure 6E, right).
To gain insight into the respective role of adaptation and in-degree correlations, we compare our network to the same anatomically constrained network but without adaptation and also to a network without correlations but with the same marginal in-degree distributions (Experimental Procedures; Figure 6E). The uncorrelated network has structural imbalance more than five times larger than the anatomically constrained network, yielding Δ ⋅ K ≈ 55. As expected, all three networks fired irregularly at these low firing rates, but in the uncorrelated network without adaptation, 57% of excitatory neurons were quiescent throughout the entire 60 s simulation while active neurons reached rates greater than 90 Hz. In the anatomically constrained network with correlations intact but without adaptation, the percentage of excitatory quiescent neurons was significantly lower, 37%, with maximum rates well more than 60 Hz. As predicted by our theory, in-degree correlations due to the underlying anatomy moderately reduce the extent of imbalance, but nevertheless an adaptation current is necessary to bring the anatomically constrained network into a balanced steady state.
Furthermore, similar to the abstract network (Figure 4G, top), in-degree correlations in the anatomically constrained network act in concert with the adaptation current to recover balance. The same strength adaptation current when applied to the uncorrelated network was only sufficient to reduce the fraction of quiescent neurons to 15%. An adaptation current four times larger was required to achieve a comparable level of 3% in the uncorrelated network.
Stimulus Response
We now ask how our network model responds to realistic stimulus settings. To address this question, we simulated 100 trials of a well-studied stimulus protocol called the “ramp-and-hold” stimulus, in which the principal whisker (PW; i.e., the one that corresponds to the somatotopic location of the barreloid-barrel) is deflected for 200 ms and then released (Figure 6A) (Simons and Carvell, 1989, Brecht and Sakmann, 2002, Minnery et al., 2003, de Kock et al., 2007). We simulated the VPM neurons in our model so that at stimulus onset they fired at elevated rates for an initial 10 ms followed by moderate rates throughout the end of stimulus duration (Simons and Carvell, 1989) (Figure 6B).
In the uncorrelated network, on any given trial 88% of neurons were unresponsive to the stimulus and even more significantly, 73% of neurons were completely unresponsive to the stimulus throughout all 100 trials. The correlations present in the anatomically constrained network reduced the percentage of neurons unresponsive to the stimulus on any given trial to 78%, while 49% of the neurons never responded to the stimulus. Finally, after introducing adaptation, the percentage of neurons unresponsive on a given trial declined to 55% and that of completely unresponsive declined to less than 10% (Figures 6C and 6D).
Our theoretical analysis above describes the steady-state balance generated by the adaptation current. It is therefore important to inquire how fast the balancing effect of adaptation sets in. Our simulations of the transient response to a 200 ms stimulation show that the adaptation current in fact accumulates enough to recover balance at timescales that are a fraction of the adaptation time constants, which are in the range of 500 to 2,000 ms, and is sufficient to dramatically impact the transient network dynamics during stimulus response (Figure 6D, right).
We conclude that a biologically plausible adaptation current together with high input connectivity correlations derived from the anatomical constraints are capable of recovering fluctuation-driven balance and realistic cortical firing in L4 during both spontaneous and stimulus-evoked states.
Discussion
Studies in cat visual cortex (da Costa and Martin, 2011) and rat barrel cortex (Furuta et al., 2011, Schoonover et al., 2014) have shown that the first stage of input into sensory cortex has remarkably heterogeneous connectivity: the total number of innervating thalamic synapses differs substantially from cell to cell in L4. The anatomically constrained estimates of connectivity presented here support this conclusion and expand it to the recurrent connectivity as well. Our theoretical and numerical results show that such input heterogeneity can have dramatic impact on the balance between excitation and inhibition in the L4 recurrent network. Lacking a mechanism to recover balance, such networks will exhibit extreme population sparsity with a majority of neurons quiescent throughout both spontaneous and stimulus-evoked epochs and with active cells firing at high rates with temporal regularity.
Some research suggests that trial-to-trial variability in the L4 barrel cortex is externally generated, and thus excitation-inhibition balance may not be a feature of this network (Hires et al., 2015). Others have found that cortical interactions even in L4 are in fact a rich source of variability (Cohen-Kashi Malina et al., 2016). In our simulations, individual neurons display variability that is due to VPM input and additional trial-to-trial variability due to cortical interactions (Figure 6F). Regardless of how this open question is settled, however, the impact of heterogeneous connectivity on excitation-balance has far broader implications. Our anatomy-based estimates of connectivity predict substantial heterogeneity in all cortical layers (Table S1). Thus, it is crucial to address how local networks maintain the dynamic balance of excitation and inhibition in spite of heterogeneous connectivity across cortical regions and layers.
To assess the structural heterogeneity in cortical circuits and its impact on dynamics, it is necessary to quantify the extent of correlations in the net input from different presynaptic populations. Correlations between total excitatory and inhibitory synaptic current onto cortical neurons were observed via in vivo intracellular recordings (Xue et al., 2014), and they are shown here to arise at least in part because of anatomical variability underlying local networks (see Anatomical Sources of Heterogeneity below). We show that these correlations ensure that a large component of heterogeneous synaptic inputs cancel out at the level of net current. We have presented a measure of the net structural imbalance that takes into account both the heterogeneity and the correlations in net inputs and predicts the extent of dynamic imbalance.
We have proposed two cellular mechanisms capable of restoring excitation-inhibition balance in local networks despite substantial heterogeneity: homeostatic plasticity and adaptation.
Homeostatic Plasticity
Plasticity in parvalbumin-expressing inhibitory neurons was implicated for equalizing excitation-inhibition ratios in sensory cortex (Xue et al., 2014), and another study suggested that inhibitory neurons may contribute to homeostatic stabilization via synaptic scaling of postsynaptic GABAA receptor expression (Rannals and Kapur, 2011). We show that homeostatic plasticity of inhibitory synapses in heterogeneous networks can align functional in-degrees to precisely balance the combined excitatory input from recurrent and external sources. We use a simple plasticity rule, reminiscent of synaptic scaling (Turrigiano et al., 1998), in which changes in synaptic strength depend only on the activity of postsynaptic neurons. It is worth noting that this solution would require long timescales to align the in-degrees to a particular external population driving the network, and we therefore sought a solution that would be robust to more rapid changes to the identity of the primary external drive.
Adaptation-Facilitated Balance
Spike-frequency adaptation has been widely studied for its coding properties (Wark et al., 2007). Here we study the dynamical impact of adaptation on the emergent fluctuation-driven balanced state in heterogeneous networks. We show that the local negative feedback generated by spike-frequency adaptation balances out the excess synaptic current due to the structural heterogeneity, resulting in a new adaptation-facilitated balanced state. We note that while in other circuits adaptation generates synchronous oscillations (van Vreeswijk and Hansel, 2001, Ladenbauer et al., 2012), in the present parameter regime it enables the emergence of a fluctuation-driven state, thereby yielding irregular firing.
We found that the adaptation parameter regime necessary to recover balance is consistent with available estimates of the strength and time course of adaptation in cortical neurons.
Pyramidal neurons in the cortex have been widely reported to exhibit spike-frequency adaptation with timescales between 300 and 500 ms (Rauch et al., 2003). Certain types of inhibitory neurons (low-threshold spiking, for example) exhibit substantial adaptation at timescales around 1 s (Gibson et al., 1999, Gupta et al., 2000). Furthermore, studies that have recorded from fast-spiking (FS) inhibitory neurons for long durations have found that they exhibit adaptation on even longer timescales (Descalzo et al., 2005, La Camera et al., 2006). We have modeled inhibitory adaptation with the small relative strength of adaptation compared with excitatory neurons as reported by La Camera et al. (2006). The overall amplitude of adaptation sufficient to restore the balanced state was of the same order of magnitude but somewhat larger than reported (Rauch et al., 2003, La Camera et al., 2006). We have also studied a connectivity matrix based on slightly different assumptions regarding the relationship between morphology and connectivity, which yield somewhat higher correlations between excitatory and inhibitory input connectivity (Supplemental Information). In this connectivity model, setting the adaptation strength to the value reported in the literature was sufficient to recover balance (Figure S3). We also anticipate that the quantitative estimates of the required adaptation strength will vary if additional realistic features are added to our simple LIF dynamics, for example, synaptic depression, which has been widely observed in the barrel cortex (Koelbl et al., 2015, Beierlein et al., 2003, Chung et al., 2002).
Anatomical Sources of Heterogeneity
Both the large heterogeneity and the substantial correlations we observe in our anatomically constrained dense statistical connectome model of the L4 barrel result from a number of underlying anatomical sources of variability. As previously reported, the soma density distribution of L4 excitatory cells is non-uniform with respect to the horizontal barrel axes (decreasing toward the septa between barrels), which is not the case for L4 inhibitory cells. On the other hand, the L4 inhibitory soma density is non-uniform with regard to the vertical cortex axis (increasing toward the L4-L5 border) (Figures 3A and 3B) (Meyer et al., 2013). The innervating VPM axons also have non-uniform density within the L4 barrel (Oberlaender et al., 2012, Furuta et al., 2011). These underlying cell-type-specific spatial heterogeneities contribute significantly to the heterogeneity observed in our anatomically constrained network. Another source of both variability and correlations in in-degrees is the large variability of dendrite and axon morphologies within and across excitatory cell types (e.g., dendritic length, layer-specific axon innervation) as reported in Narayanan et al. (2015). These combined sources of heterogeneity and correlation are not easily disentangled; for example, comparing neurons with identical dendritic lengths, we find both heterogeneous in-degrees and correlations between in-degrees from different populations (Figure S4). The same is also true for neurons located within the same sub-region of the barrel (Figure S4). The Xue et al. (2014) study suggested that inhibitory plasticity could be a source for correlations in total excitatory and inhibitory synaptic input. We show that significant correlation is expected to arise from anatomical properties.
Our dense statistical connectivity model assumes that for a given set of connection probabilities, individual contacts between a pair of neurons are drawn independently. Past studies have reported a bimodal distribution in the number of contacts, suggesting statistical dependencies between multiple contacts between the same pair, and this has been supported by a recent electron microscopy (EM) reconstruction study (Kasthuri et al., 2015). At present, it is unclear whether these features extend to connections between neurons throughout an entire layer and column. However, such dependencies are unlikely to have a major impact on the overall heterogeneity or correlations of input connectivity, because they are likely to increase cell-to-cell variability rather than decrease it.
To avoid additional assumptions about either the distribution of the number of contacts or the relationship between synaptic strength and number of contacts, our study makes the simplifying assumption that (in the absence of homeostatic plasticity) the synaptic matrix is binary: neurons of a given cell-type pair are either unconnected or they are connected by a synapse of a fixed strength. In this framework the heterogeneity in total synaptic current arose from the probability of input connection, which was dependent on the identity of the postsynaptic neuron. Equivalently, our theory applies also to networks where the main source of heterogeneity is not the number of input connections, but their strength. In the Supplemental Information we show the results of simulating an anatomically constrained L4 barrel network in which both the number and the strength of incoming connections exhibit large variance. Here the distribution of synaptic strength shows long tails similar to experimental observations (Song et al., 2005, Lefort et al., 2009). This network exhibits a loss of balance, as well as recovery of balance by correlations and adaptation, qualitatively similar to the network with fixed synaptic strength (Figure S5).
Previous Work on Connectivity and Dynamics
Several studies numerically explored the dynamics of networks with different degree distributions. In particular, Pernice et al. (2013) performed simulations of LIF neuron networks in asynchronous irregular states with widely varying degree distributions. Similar to our findings, they observed that larger SD of in-degree was correlated with lower CVISI. Their study, however, did not offer a theoretical account of this finding, and they suggest that the lower CVISI may be primarily because of higher population firing rates. Neither did they explore mechanisms for establishing balance in such networks. We make use of the balanced-state theoretical framework and show that independent of population firing rates, broader in-degree distributions push the network into a mean-driven regime where activity is inevitably more regular and the CVISI is lower. Another recent study concurs with our observation that heterogeneous in-degrees threaten excitation-inhibition balance (Pyle and Rosenbaum, 2016). They study a simple model in which excitatory and inhibitory populations are each divided into two populations with distinct in-degrees. They show that balance can be recovered by introducing connection selectivity between the subgroups. Such higher order connectivity statistics are beyond the scope of our study. Several studies have begun to develop theoretical frameworks relating structure to dynamics (Pernice et al., 2011, Hu et al., 2014) and, in particular (Shkarayev et al., 2012) have studied mean-field theory of networks with heterogeneous in-degree, similar to our local balance equations; however, they focus on mean-driven states, whereas we study fluctuation-driven balanced dynamics.
Our study compared heterogeneous networks with homogeneous networks in which all neurons from a given pair of types have the same probability of connection. It is worth noting that network models in which the probability of connection between a pair of neurons depends on factors such as the distance between them (Rosenbaum and Doiron, 2014) often exhibit similarly narrow in-degree distributions. To capture the realistic variability of cortical circuits, such network models should incorporate heterogeneity in the total input connectivity as we have done here.
The advent of connectomics has triggered great interest in the fine details of connectivity patterns of neuronal circuits. Yet it remains unclear, in general, how and to what extent these details affect the dynamics and function of these circuits. Here we have shown that a specific feature, heterogeneity in incoming connectivity, has a significant qualitative impact on local cortical dynamics, and that the circuits’ proper function depends on the interplay between connectivity structure and single neuron dynamical properties.
Experimental Procedures
Generative Model for Heterogeneous Connectivity
We generate connectivity matrices for heterogeneous networks consisting of populations E and I, and external population O, where population sizes are NE, NI, and NO, respectively. Because the dynamics are directly influenced by the statistics of convergent input, we assume for simplicity that the input connectivity varies between postsynaptic neurons, but not between presynaptic neurons. This restriction can be relaxed without changing the qualitative results of this study.
In our heterogeneous generative model, we draw each neuron’s set of relative in-degrees from a 3D truncated Gaussian distribution with means 1, SDs , and correlation coefficient c between each pair of presynaptic populations.
Given a neuron i’s relative in-degree, we assign it presynaptic partners at random from population B. For simplicity, we set , the mean connection probability, to be uniform across pathways.
We write for the resulting binary, {0,1}, connectivity matrix from neuron j of type B onto neuron i of type A.
In our anatomically constrained network, is a Bernoulli random variable with probability generated from the anatomical data as described in the Supplemental Information.
To construct a matrix with the same marginal input connectivity distributions as the anatomically constrained matrix, but without correlations (Figures 5C–5E), we shuffle the rows of each matrix independently.
Single-Neuron Dynamics and Simulations
We study LIF point neurons whose dynamics are given by the equations:
where is the membrane potential of neuron i of type , is the neuron’s normalized synaptic trace, a difference of exponentials with rise time and decay time . , where is the strength of a single connected synapse from population B onto population A. is cell-specific external current, VL is the equilibrium leak-potential, VR the reset potential, and VTh the threshold potential (Table 2).
Table 2.
System Parameters
| Intrinsic Neuron Properties | Synaptic Scaling Parameters | ||
|---|---|---|---|
| −70 mV | |||
| −70 mV | |||
| −55 mV | |||
| 10 ms | |||
| 250 pF | (constant-input simulations) | ||
| 1 ms | (constant-input simulations) | ||
| 3 ms | (spiking-input simulations) | ||
| 0.5 ms | (spiking-input simulations) | ||
| 1.5 ms | |||
| Synthetic Network Parameters | Anatomically Constrained Network Size | ||
| 6500 | 3283 | ||
| 1500 | 680 | ||
| 0.25 | 311 | ||
| 1.625 s | 0.5 s | ||
| 6.5 s | 2 s | ||
| (fixed adaptation-strength simulations) | 60 pA | 75 pA | |
| (fixed adaptation-strength simulations) | 1.5 pA | 2 pA | |
Parameters used in simulations, as described in Experimental Procedures.
We write JAB = KABWAB, the mean total strength of synapses from population B onto population A.
For simulating the synthetic networks from our generative model, as well as for the initial analysis of the anatomically constrained network, we use time-independent external current .
For simulations of realistic spontaneous and whisker-stimulus conditions, the cell-specific external input is the synaptic current from the Poisson-firing population, O, which is given by
The anatomically constrained network parameters yield excitatory to excitatory postsynaptic potentials (EPSPs) equal 0.36 mV.
Simulations were conducted in MATLAB with a first-order Euler method and step size of 0.05 ms.
Heterogeneous Balance Theory
We consider the time-averaged synaptic current to a neuron i:
The temporal average of is simply the average single-neuron rate . Because is independent of , we can write (as in Equation 1)
Following van Vreeswijk and Sompolinsky (1998), we make synapses strong by scaling individual synapses by . For ease of notation, we define the strength of a synapse from connected neurons of type B onto type A as , where jAB have units of total charge and are of the same order of magnitude as the threshold current multiplied by membrane time constant, or equivalently, cmVTh (Table 2).
Then the net time-averaged synaptic current onto the ith neuron of type A is
With this scaling, we can see that if the excitatory and inhibitory synaptic currents do not cancel the external current, then the net synaptic current will be large, . The requirement that the synaptic currents be O(1), i.e., of the same order of magnitude as threshold-current yields balance equations
which must be fulfilled up to order . If then for most neurons, and these equations reduce to two equations with two unknowns, which are readily solved.
If CVK is not small, however, then the balance equations cannot be generically solved unless . We treat this case in the Supplemental Information and derive the structural bounds on balance.
Homeostatic Plasticity Rules
We model a homeostatic plasticity rule on inhibitory synapses as an additive synaptic scaling in which individual synapse strength depends on postsynaptic firing:
where is obtained by low-pass filtering neuron i’s spike train:
where is the time of the kth action potential of neuron i of type A. This plasticity rule applies only to connected neurons, i.e., those with CAI = 1.
τw sets the timescale of a “weight-decay” component of the plasticity dynamics. To limit simulation duration, we use τw = 40 s. τl sets the timescale of the filtering of the neuron’s activity. In our simulations we use τl = 200 ms. ηA sets the timescale of the homeostatic component of the plasticity dynamics; the relationship between ηE and ηI controls the relationship between mean population rates, rE and rI, at steady state. In our simulations we use and . See the Supplemental Information.
Adaptation Dynamics and Theory
We introduce to each neuron an additional current that has dynamics given by
where tk is the time of the kth spike.
We write , where is of the order of magnitude of the threshold-current, and , where is of the order of magnitude of the synaptic time constant.
Note that has units of current and that the area under the curve, i.e., the total charge due to a single spike, depends on . The accumulated adaptation current for a neuron firing at rate is , which is of the same order of magnitude as the total synaptic currents above. The net current onto neuron i is therefore
which yields local-balance equations (Equation 5)
which must be solved self-consistently. We show the conditions under which all neurons will be active and solve the rate equations under these conditions in the Supplemental Information.
Note that if the firing is irregular, then the variance in the adaptation current will be , such that it contributes only after the dominant term in the net current is balanced.
Throughout our simulations, we fix and , which are approximately the relations found empirically (La Camera et al., 2006). For realistic spontaneous and stimulus-evoked states, we use time constants of 2 and 0.5 s, for inhibitory and excitatory, respectively, and peak amplitudes of 2 and 75 pA, respectively, which is the same order of magnitude as found empirically.
Interaction between Structural Imbalance and Adaptation
We rewrite , where are . We claim that in order to facilitate balance it suffices for the accumulated adaptation current to be order . Suppose that and scale the adaptation strength , then
This yields a self-consistent solution to the balance conditions in which the mean rates are given by , where are the homogeneous balance solutions . With these mean rates, the individual firing rates are given by
and the correction terms, δrA, are recovered self-consistently. In the case where all neurons are active they are given by
Author Contributions
H.S. and I.D.L. developed the theory and performed the analytical calculations. I.D.L. performed the numerical simulations. M.O. developed the connectivity model. R.E., V.J.D., and M.O. generated implementations of the connectivity model. I.D.L., R.E., M.O., and H.S. performed data analysis and wrote the manuscript.
Acknowledgments
We thank Idan Segev for helpful conversations, as well as Dirk Feldmeyer and Bert Sakmann for providing reconstructions of L4 inhibitory neuron morphologies. This study was partially supported by the Max Planck-Hebrew University Center, established between the Max Planck Institute of Neurobiology, Martinsried, Germany, and the Hebrew University, Jerusalem, Israel. Partial funding was also provided by the MPHUC (I.D.L., V.J.D.); the Max Planck Institute for Biological Cybernetics (R.E., M.O.); the Gatsby Charitable Foundation (H.S.); the Studienstiftung des Deutschen Volkes (R.E.); the Bernstein Center for Computational Neuroscience, funded by German Federal Ministry of Education and Research grant BMBF/FKZ 01GQ1002 (R.E., M.O.); the Zuse Institute Berlin (V.J.D.); and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant 633428 to M.O.).
Published: November 17, 2016
Footnotes
Supplemental Information includes Supplemental Experimental Procedures, five figures, and one table and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2016.10.027.
Supplemental Information
References
- Beierlein M., Gibson J.R., Connors B.W. Two dynamically distinct inhibitory networks in layer 4 of the neocortex. J. Neurophysiol. 2003;90:2987–3000. doi: 10.1152/jn.00283.2003. [DOI] [PubMed] [Google Scholar]
- Brecht M., Sakmann B. Dynamic representation of whisker deflection by synaptic potentials in spiny stellate and pyramidal cells in the barrels and septa of layer 4 rat somatosensory cortex. J. Physiol. 2002;543:49–70. doi: 10.1113/jphysiol.2002.018465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000;8:183–208. doi: 10.1023/a:1008925309027. [DOI] [PubMed] [Google Scholar]
- Buzsáki G., Mizuseki K. The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci. 2014;15:264–278. doi: 10.1038/nrn3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung S., Li X., Nelson S.B. Short-term depression at thalamocortical synapses contributes to rapid adaptation of cortical sensory responses in vivo. Neuron. 2002;34:437–446. doi: 10.1016/s0896-6273(02)00659-1. [DOI] [PubMed] [Google Scholar]
- Cohen-Kashi Malina K., Mohar B., Rappaport A.N., Lampl I. Local and thalamic origins of correlated ongoing and sensory-evoked cortical activities. Nat. Commun. 2016;7:12740. doi: 10.1038/ncomms12740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constantinople C.M., Bruno R.M. Deep cortical layers are activated directly by thalamus. Science. 2013;340:1591–1594. doi: 10.1126/science.1236425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Costa N.M., Martin K.A.C. How thalamus connects to spiny stellate cells in the cat’s visual cortex. J. Neurosci. 2011;31:2925–2937. doi: 10.1523/JNEUROSCI.5961-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Kock C.P.J., Bruno R.M., Spors H., Sakmann B. Layer- and cell-type-specific suprathreshold stimulus representation in rat primary somatosensory cortex. J. Physiol. 2007;581:139–154. doi: 10.1113/jphysiol.2006.124321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehghani N., Peyrache A., Telenczuk B., Le Van Quyen M., Halgren E., Cash S.S., Hatsopoulos N.G., Destexhe A. Dynamic balance of excitation and inhibition in human and monkey neocortex. Sci. Rep. 2016;6:23176. doi: 10.1038/srep23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Descalzo V.F., Nowak L.G., Brumberg J.C., McCormick D.A., Sanchez-Vives M.V. Slow adaptation in fast-spiking neurons of visual cortex. J. Neurophysiol. 2005;93:1111–1118. doi: 10.1152/jn.00658.2004. [DOI] [PubMed] [Google Scholar]
- Egger R., Dercksen V.J., Udvary D., Hege H.C., Oberlaender M. Generation of dense statistical connectomes from sparse morphological data. Front. Neuroanat. 2014;8:129. doi: 10.3389/fnana.2014.00129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D., Egger V., Lubke J., Sakmann B. Reliable synaptic connections between pairs of excitatory layer 4 neurones within a single ‘barrel’ of developing rat somatosensory cortex. J. Physiol. 1999;521:169–190. doi: 10.1111/j.1469-7793.1999.00169.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furuta T., Deschênes M., Kaneko T. Anisotropic distribution of thalamocortical boutons in barrels. J. Neurosci. 2011;31:6432–6439. doi: 10.1523/JNEUROSCI.6154-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W., Kistler W.M. Cambridge University Press; 2002. Spiking Neuron Models: Single Neurons, Populations, Plasticity. [Google Scholar]
- Gibson J.R., Beierlein M., Connors B.W. Two networks of electrically coupled inhibitory neurons in neocortex. Nature. 1999;402:75–79. doi: 10.1038/47035. [DOI] [PubMed] [Google Scholar]
- Gupta A., Wang Y., Markram H. Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science. 2000;287:273–278. doi: 10.1126/science.287.5451.273. [DOI] [PubMed] [Google Scholar]
- Hansel D., van Vreeswijk C. The mechanism of orientation selectivity in primary visual cortex without a functional map. J. Neurosci. 2012;32:4049–4064. doi: 10.1523/JNEUROSCI.6284-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hires S.A., Gutnisky D.A., Yu J., O’Connor D.H., Svoboda K. Low-noise encoding of active touch by layer 4 in the somatosensory cortex. eLife. 2015;4:e06619. doi: 10.7554/eLife.06619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Y., Trousdale J., Josić K., Shea-Brown E. Local paths to global coherence: cutting networks down to size. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014;89:032802. doi: 10.1103/PhysRevE.89.032802. [DOI] [PubMed] [Google Scholar]
- Kasthuri N., Hayworth K.J., Berger D.R., Schalek R.L., Conchello J.A., Knowles-Barley S., Lee D., Vázquez-Reina A., Kaynig V., Jones T.R. Saturated reconstruction of a volume of neocortex. Cell. 2015;162:648–661. doi: 10.1016/j.cell.2015.06.054. [DOI] [PubMed] [Google Scholar]
- Keck T., Keller G.B., Jacobsen R.I., Eysel U.T., Bonhoeffer T., Hübener M. Synaptic scaling and homeostatic plasticity in the mouse visual cortex in vivo. Neuron. 2013;80:327–334. doi: 10.1016/j.neuron.2013.08.018. [DOI] [PubMed] [Google Scholar]
- Koelbl C., Helmstaedter M., Lübke J., Feldmeyer D. A barrel-related interneuron in layer 4 of rat somatosensory cortex with a high intrabarrel connectivity. Cereb. Cortex. 2015;25:713–725. doi: 10.1093/cercor/bht263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- La Camera G., Rauch A., Thurbon D., Lüscher H.R., Senn W., Fusi S. Multiple time scales of temporal response in pyramidal and fast spiking cortical neurons. J. Neurophysiol. 2006;96:3448–3464. doi: 10.1152/jn.00453.2006. [DOI] [PubMed] [Google Scholar]
- Ladenbauer J., Augustin M., Shiau L., Obermayer K. Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Comput. Biol. 2012;8:e1002478. doi: 10.1371/journal.pcbi.1002478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Land P.W., Buffer S.A., Jr., Yaskosky J.D. Barreloids in adult rat thalamus: three-dimensional architecture and relationship to somatosensory cortical barrels. J. Comp. Neurol. 1995;355:573–588. doi: 10.1002/cne.903550407. [DOI] [PubMed] [Google Scholar]
- Lefort S., Tomm C., Floyd Sarria J.C., Petersen C.C. The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron. 2009;61:301–316. doi: 10.1016/j.neuron.2008.12.020. [DOI] [PubMed] [Google Scholar]
- Luz Y., Shamir M. Balancing feed-forward excitation and inhibition via Hebbian inhibitory synaptic plasticity. PLoS Comput. Biol. 2012;8:e1002334. doi: 10.1371/journal.pcbi.1002334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer H.S., Egger R., Guest J.M., Foerster R., Reissl S., Oberlaender M. Cellular organization of cortical barrel columns is whisker-specific. Proc. Natl. Acad. Sci USA. 2013;110:19113–19118. doi: 10.1073/pnas.1312691110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minnery B.S., Bruno R.M., Simons D.J. Response transformation and receptive-field synthesis in the lemniscal trigeminothalamic circuit. J. Neurophysiol. 2003;90:1556–1570. doi: 10.1152/jn.00111.2003. [DOI] [PubMed] [Google Scholar]
- Narayanan R.T., Egger R., Johnson A.S., Mansvelder H.D., Sakmann B., de Kock C.P., Oberlaender M. Beyond columnar organization: cell type- and target layer-specific principles of horizontal axon projection patterns in rat vibrissal cortex. Cereb. Cortex. 2015;11:4450–4468. doi: 10.1093/cercor/bhv053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberlaender M., de Kock C.P., Bruno R.M., Ramirez A., Meyer H.S., Dercksen V.J., Helmstaedter M., Sakmann B. Cell type-specific three-dimensional structure of thalamocortical circuits in a column of rat vibrissal cortex. Cereb. Cortex. 2012;22:2375–2391. doi: 10.1093/cercor/bhr317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okun M., Steinmetz N.A., Cossell L., Iacaruso M.F., Ko H., Barthó P., Moore T., Hofer S.B., Mrsic-Flogel T.D., Carandini M., Harris K.D. Diverse coupling of neurons to populations in sensory cortex. Nature. 2015;521:511–515. doi: 10.1038/nature14273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pehlevan C., Sompolinsky H. Selectivity and sparseness in randomly connected balanced networks. PLoS ONE. 2014;9:e89992. doi: 10.1371/journal.pone.0089992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernice V., Staude B., Cardanobile S., Rotter S. How structure determines correlations in neuronal networks. PLoS Comput. Biol. 2011;7:e1002059. doi: 10.1371/journal.pcbi.1002059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernice V., Deger M., Cardanobile S., Rotter S. The relevance of network micro-structure for neural dynamics. Front. Comput. Neurosci. 2013;7:72. doi: 10.3389/fncom.2013.00072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pyle R., Rosenbaum R. Highly connected neurons spike less frequently in balanced networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2016;93:040302. doi: 10.1103/PhysRevE.93.040302. [DOI] [PubMed] [Google Scholar]
- Rannals M.D., Kapur J. Homeostatic strengthening of inhibitory synapses is mediated by the accumulation of GABA(A) receptors. J. Neurosci. 2011;31:17701–17712. doi: 10.1523/JNEUROSCI.4476-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauch A., La Camera G., Luscher H.R., Senn W., Fusi S. Neocortical pyramidal cells respond as integrate-and-fire neurons to in vivo-like input currents. J. Neurophysiol. 2003;90:1598–1612. doi: 10.1152/jn.00293.2003. [DOI] [PubMed] [Google Scholar]
- Renart A., de la Rocha J., Bartho P., Hollender L., Parga N., Reyes A., Harris K.D. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum R., Doiron B. Balanced networks of spiking neurons with spatially dependent recurrent connections. Phys. Rev. X. 2014;4:021039. [Google Scholar]
- Roxin A., Brunel N., Hansel D., Mongillo G., van Vreeswijk C. On the distribution of firing rates in networks of cortical neurons. J. Neurosci. 2011;31:16217–16226. doi: 10.1523/JNEUROSCI.1677-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Vives M.V., Nowak L.G., McCormick D.A. Cellular mechanisms of long-lasting adaptation in visual cortical neurons in vitro. J. Neurosci. 2000;20:4286–4299. doi: 10.1523/JNEUROSCI.20-11-04286.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoonover C.E., Tapia J.C., Schilling V.C., Wimmer V., Blazeski R., Zhang W., Mason C.A., Bruno R.M. Comparative strength and dendritic organization of thalamocortical and corticocortical synapses onto excitatory layer 4 neurons. J. Neurosci. 2014;34:6746–6758. doi: 10.1523/JNEUROSCI.0305-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shkarayev M.S., Kovačič G., Cai D. Topological effects on dynamics in complex pulse-coupled networks of integrate-and-fire type. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:036104. doi: 10.1103/PhysRevE.85.036104. [DOI] [PubMed] [Google Scholar]
- Simons D.J., Carvell G.E. Thalamocortical response transformation in the rat vibrissa/barrel system. J. Neurophysiol. 1989;61:311–330. doi: 10.1152/jn.1989.61.2.311. [DOI] [PubMed] [Google Scholar]
- Song S., Sjöström P.J., Reigl M., Nelson S., Chklovskii D.B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stocker M. Ca(2+)-activated K+ channels: molecular determinants and function of the SK family. Nat. Rev. Neurosci. 2004;5:758–770. doi: 10.1038/nrn1516. [DOI] [PubMed] [Google Scholar]
- Turrigiano G.G., Leslie K.R., Desai N.S., Rutherford L.C., Nelson S.B. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C., Hansel D. Patterns of synchrony in neural networks with spike adaptation. Neural Comput. 2001;13:959–992. doi: 10.1162/08997660151134280. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C., Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C., Sompolinsky H. Chaotic balanced state in a model of cortical circuits. Neural Comput. 1998;10:1321–1371. doi: 10.1162/089976698300017214. [DOI] [PubMed] [Google Scholar]
- Vogels T.P., Sprekeler H., Zenke F., Clopath C., Gerstner W. Inhibitory plasticity balances excitation and inhibition in sensory pathways and memory networks. Science. 2011;334:1569–1573. doi: 10.1126/science.1211095. [DOI] [PubMed] [Google Scholar]
- Wark B., Lundstrom B.N., Fairhall A. Sensory adaptation. Curr. Opin. Neurobiol. 2007;17:423–429. doi: 10.1016/j.conb.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wimmer K., Compte A., Roxin A., Peixoto D., Renart A., de la Rocha J. Sensory integration dynamics in a hierarchical network explains choice probabilities in cortical area MT. Nat. Commun. 2015;6:6177. doi: 10.1038/ncomms7177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue M., Atallah B.V., Scanziani M. Equalizing excitation-inhibition ratios across visual cortical neurons. Nature. 2014;511:596–600. doi: 10.1038/nature13321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yizhar O., Fenno L.E., Prigge M., Schneider F., Davidson T.J., O’Shea D.J., Sohal V.S., Goshen I., Finkelstein J., Paz J.T. Neocortical excitation/inhibition balance in information processing and social dysfunction. Nature. 2011;477:171–178. doi: 10.1038/nature10360. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.