A new hydrogen-bonding potential for the design of protein–RNA interactions predicts specific contacts and discriminates decoys

Abstract

RNA-binding proteins play many essential roles in the regulation of gene expression in the cell. Despite the significant increase in the number of structures for RNA–protein complexes in the last few years, the molecular basis of specificity remains unclear even for the best-studied protein families. We have developed a distance and orientation-dependent hydrogen-bonding potential based on the statistical analysis of hydrogen-bonding geometries that are observed in high-resolution crystal structures of protein–DNA and protein–RNA complexes. We observe very strong geometrical preferences that reflect significant energetic constraints on the relative placement of hydrogen-bonding atom pairs at protein–nucleic acid interfaces. A scoring function based on the hydrogen-bonding potential discriminates native protein–RNA structures from incorrectly docked decoys with remarkable predictive power. By incorporating the new hydrogen-bonding potential into a physical model of protein–RNA interfaces with full atom representation, we were able to recover native amino acids at protein–RNA interfaces.

INTRODUCTION

The interactions of DNA- and RNA-binding proteins with nucleic acids play central roles in gene expression and its regulation. If we had available proteins that could control these interactions at will, we could interfere with gene expression pathways and gain a much better understanding of gene expression networks. Combinatorial methods such as phage display have been used to engineer DNA-binding proteins with new specificity, but inevitably have limitations (1,2) and have met only limited success when they were applied to RNA-binding proteins (3,4). If we understood the principles of nucleic acid recognition better, we could then use rational approaches to design new RNA- and DNA-binding proteins. By establishing a design cycle involving both computational design and experimental validation, we would also be able to examine the molecular origin of recognition. The first requirement to the development of computational tools to design new RNA-binding proteins is a physical model capable of reliably quantifying the molecular interactions responsible for affinity and specificity between proteins and RNA.

A number of authors have recently analyzed protein–nucleic acid interfaces computationally using visualization and statistical tools analogous to those used with proteins (5–18). In these important studies, common interaction patterns between amino acids and nucleotides were reported. The relative roles of packing, hydrogen-bonding and electrostatic interactions in molecular recognition were described as well. In some cases, it was possible to attribute interaction propensities (e.g. arginine–guanine, etc.) to specific patterns of hydrogen-bonding and electrostatic interactions (5,9). However, no systematic attempt has so far been made to correlate these geometrical preferences with quantitative estimates of the relative contribution of each interaction to the total free energy of binding. Computational studies on protein–nucleic acid interactions remain very few when compared with the body of theoretical and experimental work dedicated to understanding interactions within protein cores and at protein–protein interfaces, and to redesigning new protein structures and interfaces (19–31). In other words, the knowledge encoded in the ever-growing database of protein–nucleic acid structures remains to be exploited in the quantitative dissection of energetic features responsible for affinity and specificity and in the development of predictive tools to be used in protein design.

The strong orientational character of hydrogen-bonding interactions (32) makes them particularly important in determining the specificity of protein recognition and folding (33). Protein–nucleic acid interfaces are significantly more polar compared to protein–protein interfaces and to protein cores (10): interactions involving ion pairs and hydrogen bonds should play a key role in dictating specificity between proteins and nucleic acids (7–9,34). However, the quantitative description of the orientational features of hydrogen-bonding interactions from the first principles is not straightforward. For example, the direction of the lone electron pair cannot simply be assumed by the hybridization of the acceptor, because hydrogen-bond formation may perturb the hybridization state of the acceptor atom (35,36). Most current force fields used in molecular dynamics simulations describe hydrogen bonds through a combination of Coulomb and Lennard–Jones interactions with refined atomic charges and lack explicit directionality (37–39). Furthermore, differences in entropy costs associated with freezing exposed and buried side chains or solvent-dependent effects are difficult to model.

An attractive approach to the description of hydrogen-bonding interactions relies on the statistical examination of hydrogen bonds observed in high-resolution crystal structures (40–42). The statistical preferences observed experimentally can then be converted into a mean-field potential by inverting Boltzmann statistics (43). The mean-field potentials relate the probabilities of occurrence of atom–atom interactions in a database to the energies of these interactions (43–46) and incorporate implicitly environmental effects such as solvation and side-chain entropy. Although several theoretical limitations of this approach have been described previously (47,48), an orientation-dependent hydrogen-bonding potential was reported to contributing significantly to the correct prediction of hot spots in protein interfaces by providing a superior description of polar interactions compared to a purely Coulombic description of electrostatics (49,50). The physical basis for such a potential has been demonstrated by its striking correspondence, at least for protein side chains, with quantum mechanical calculations of hydrogen bonded dimers (51).

The present study describes the development of a physical model for protein–RNA interfaces. The model is based on physical potentials to describe van der Waals interactions, solvation, and on a distance and orientation-dependent hydrogen-bonding potential developed from the statistical analysis of hydrogen bonds observed in high-resolution structures of protein–nucleic acid complexes. We observe that hydrogen bonds involving nucleic acids are more orientationally constrained compared to proteins. The predictive power of the atomic model is demonstrated through its ability to recover the native amino acids at protein–RNA interfaces. A scoring function based on the new hydrogen-bonding potential very successfully discriminates native protein–RNA structures from a large set of decoys.

METHODS

Construction of protein–nucleic acid structure database

Protein–DNA and protein–RNA structures were downloaded from the Protein Data Bank (PDB) (52). Only X-ray crystal structures with a resolution of 2.5 Å or better and a crystallographic R-factor of 0.25 or better were included in the statistical analysis. The database contains 42 protein–RNA and 125 protein–DNA complexes as of March 2004. However, the protein–RNA complexes include the 50S ribosome structure comprising 2 RNA and 28 individual polypeptide chains (53); therefore, the dataset effectively contains nearly 70 independent protein–RNA structures. For crystals with multiple complexes in a unit cell, only one representative structure was included. The database was checked with BLAST and MACAW to remove redundant protein structures (more than 30% sequence homology), but homologous proteins were retained when bound to DNA or RNA sequences that were significantly different.

Analysis of hydrogen-bonding geometry

Hydrogen atoms are generally not included in the coordinates derived from the crystal diffraction data. Thus, polar hydrogen atoms were added when the position of the hydrogen itself is clearly defined by the chemistry of the donor atom. For proteins, hydrogens were added to all backbone amide protons and to the tryptophan indole, histidine imidazole, asparagine and glutamine amides, and arginine guanidinium groups. For nucleic acids, imino and amino hydrogens were added. The bond length between proton and donor was set to 1.01 Å for NH bonds (as established by CHARMM27) (54). Angles were defined using the same method as used by HBPLUS (55), with the exception of the protein backbone amide protons, where the angles of C–N–H and Cα–N–H were set to be equal (the difference is only 4° in HBPLUS). It is difficult to define the orientations of Asn, Gln and His side chains in X-ray crystal structures at resolutions approximately >1 Å. Therefore, incorrect placement (flip over) is possible in the X-ray structures; this feature was not corrected here as it would require assumptions about hydrogen-bonding energies. The protonation state of histidine was assumed to be the most common Nε2 protonation state (55). No attempt was made to add rotatable polar hydrogens to the OH groups of Ser, Thr and Tyr, to the amino group of Lys and to the RNA 2′-OH. These hydrogens are not observed explicitly in the models derived from X-ray diffraction studies and cannot be located in an unbiased way in the absence of neutron diffraction data. Because of these omissions, the distributions of hydrogen-bonding interactions among different amino acids and nucleobases differ somewhat from previous studies (5,7,8).

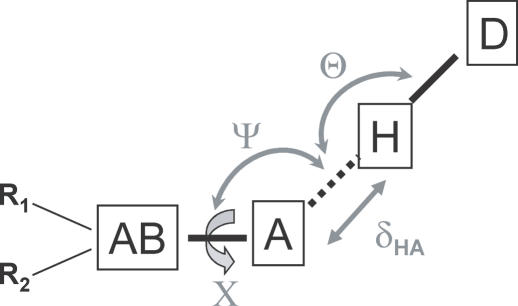
One of the goals of our study was to generate a self-consistent model for the description of proteins, nucleic acids and their complexes for design purposes. Therefore, the parameters chosen to describe hydrogen bonds in nucleic acids (Figure 1) were equivalent to those used to describe hydrogen bonds in proteins (49). Four geometrical parameters were used to describe hydrogen-bond geometry (Figure 1): (i) the distance δ_HA between the hydrogen and acceptor atoms; (ii) the angle Θ at the hydrogen atom; (iii) the angle ψ at the acceptor atom; and (iv) the dihedral angle X corresponding to the rotation around the acceptor–acceptor base bond. For the dihedral angle around phosphate oxygen (e.g. O1P) and phosphorous, the reference atom (R) was chosen as the second phosphate oxygen (e.g. O2P); therefore, the plane defined by O1P–P–O2P defines ‘planarity’ for phosphate oxygen acceptors. A pre-defined cut-off range (1.4–2.6 Å) was set for distance between hydrogen and acceptor atoms, while an upper limit of 4 Å was chosen for the donor-to-acceptor heavy-atom distance; no pre-condition was applied for the three angular parameters describing hydrogen-bond formation. In the analysis of geometric preferences, bin sizes of 0.1 Å and 10° were assigned to describe distance (δ_HA) and angular distributions (Θ, Ψ, X), respectively. After counting the number of observed hydrogen-bonding contacts in each bin, raw counts were corrected for the different volume elements encompassed by the bins to ensure that the number of observations in each bin is representative of the density of points and is not affected by the different bin size (42). Angular corrections of sin Θ and sin Ψ were applied to achieve this correction, but no correction was applied to the X angle because the volume elements considered for the dihedral angle are of equal size. A distance correction (δ_HA²) was also applied.

Figure 1.

Schematic representation of the geometric parameters used to describe hydrogen-bond geometry. δ_HA represents the distance between the hydrogen and acceptor atoms; Θ, the angle at the hydrogen atom describes the linearity of hydrogen bond; Ψ, the angle at the acceptor atom; (X represents the dihedral angle given by rotation around the acceptor–acceptor base bond; for sp² hybridized acceptors, it is a measure of the planarity of the hydrogen bond. A, acceptor; D, donor; H, hydrogen; AB, acceptor base; and R₁, R₂, reference atoms bound to the acceptor base.

Construction of a potential of mean force for hydrogen-bonding interactions

The orientational hydrogen-bonding potential comprises a distance-dependent energy term [E(δ_HA)] and three angular-dependent energy components: E(Θ) (the angle at the hydrogen atom), E(Ψ) (the angle at the acceptor atom) and E(X) (the dihedral angle of the hydrogen bond). The hydrogen-bonding potential was generated using reverse Boltzmann statistics by converting observed frequency distributions into a potential of mean force. In doing so, we implicitly assume that the total energy of a system can be partitioned as the sum of independent contributions (40,49):

where f_pdb(p) is the frequency at which a geometric parameter p is observed in a certain bin in the dataset and f_random(p) is a reference frequency value assuming an unbiased distribution in all bins. The hydrogen-bond energy (E_HB) was then derived from the linear combination of the four distance and orientational terms under the assumption that they are independent of each other:

Energy evaluation for native amino acid recovery test at protein–RNA interfaces

All energy calculations were carried out using the protein–nucleic acid interaction module of ROSETTA developed by Jim Havranek, Chuck Duarte and David Baker. The total free energy of protein–RNA interactions was modeled as the linear combination of physical and knowledge-based potentials describing (i) van der Waals interactions [attractive part of a Lennard–Jones potential (E_LJattr) and a distance-dependent repulsive term (E_LJrep)]; (ii) the orientation-dependent hydrogen-bond potential (E_HB); (iii) the implicit solvation-free energy (G_sol) (27); (iv) the amino acid backbone-dependent rotamer probability [E_rot(aa, φ, ψ)] (56); (v) the amino acid type (aa)-dependent backbone φ, ψ probabilities [E_Θ/Ψ(aa)]; and (vi) the amino acid type-dependent reference energies (E_aa^ref).

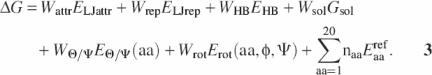
Two types of orientation-dependent hydrogen-bonding potentials were used: one is based on the previous study for hydrogen bonds between amino acids (49) and the other is directly derived from the current result for hydrogen bonds between amino acids and nucleic acids. All parameters for the hydrogen-bonding potential between amino acids and nucleic acids are listed in Supplementary Material. When the hydrogen-bonding potential was supplemented with a Coulombic model of charge–charge interactions, a linear distance-dependent dielectric constant was used and partial charges were taken from the CHARMM19 parameter set for proteins (38) and from CHARMM27 for RNA (47,54).

The weights W of the different components of the model were obtained by requiring the energy function to optimally reproduce the native amino acids at the protein–RNA interfaces. We used a training set of 25 protein–RNA complexes. Amino acid-dependent reference energies that approximate the free energy of the unfolded reference state were also obtained in the same fitting procedure. The remaining 17 complexes were set aside as a testing set. The list of protein–RNA complexes used in the training and testing sets can be found in Supplementary Material. During the fitting procedure, each of the components of the energy function for all protein rotamers at each interfacial position was computed assuming a constant environment for all other amino acids in their native conformation. The weights were then optimized using a conjugate gradient method to maximize the probability of the native amino acid type at each position. The rotamer library was from Dunbrack (56). Additional rotamers were included with small deviations (10–20°) of the χ₁ and χ₂ angles for buried residues. All RNA atoms were fixed except for 2′-OH, whose position was searched using a rotamer approach (58) to optimize the local hydrogen-bonding network. The protein–RNA interface was defined according to the distance cut-off values between the C1′ of nucleic acids and Cβ of amino acids. Depending on the size of the amino acid side chain, the distance cut-off value varies from 10 to 15 Å.

Decoy sets

A set of 2000 decoys for each of the five representatives protein–RNA complexes were generated using the protein–ligand docking module of ROSETTA developed by Jens Meiler. Rigid-body perturbations of the relative position and orientation of the two partners were carried out in the protein–RNA complexes (59). RNA was treated as a rigid molecule during docking and the protein backbone was fixed as well. However, interfacial amino acid side chains were repacked and minimized using a backbone-dependent rotamer packing algorithm after rigid-body docking (60). Decoys were scored and compared to the native structure based on the hydrogen-bonding scoring function derived directly from the statistical analysis of protein–nucleic acid hydrogen-bond geometries (Equation 1) without any weight. For infrequent distance and angular values, the score was set to 0 and no penalties were applied. A Z-score was defined as follows:

where

is the average energy of N decoys and

is the standard deviation of decoy energies. E_ref is the energy of the native structure experimentally determined by the X-ray diffraction.

RESULTS

We describe the development and validation of a distance and orientation-dependent hydrogen-bonding potential derived from the statistical analysis of protein–nucleic acid complexes. We then incorporate the potential into a general physical model of protein–nucleic acid interfaces.

Database construction

The PDB currently (Spring 2004) includes ∼167 high-resolution (<2.5 Å) protein–nucleic acid (DNA, RNA) crystal structures. Considering the complexity of the ribosomal structure (28 proteins and 2 RNAs), the total number of independent structures included in the database is close to 200. The database contains 3445 distinct hydrogen bonds involving protein and DNA or RNA. The phosphate oxygens provide the largest number of hydrogen-bond acceptors (53%), while the amino groups of amino acid side chains (1167) and the backbone NH's (672) are the most common donors. This number certainly under-represents the total number of hydrogen-bonding interactions between amino acid side chains and nucleic acids, since sp³ hydrogen-bond donors (Ser, Thr and Tyr OH's and especially Lys NH₃) were excluded from the analysis because their hydrogens cannot be positioned explicitly without assumptions about hydrogen-bonding energies.

The current structural database is too small to analyze each possible pair of hydrogen-bond donor and acceptor types at the interface of protein and nucleic acid while generating statistically significant results. Therefore, different types of donor and acceptors were grouped together according to the structural and chemical similarity. Subtle differences between related hydrogen-bonding groups (e.g. all base nitrogens were classified as a single atom type) are inevitably lost, but smooth distributions could be generated for most acceptor/donor pairs, suggesting that the statistical sample is large enough to yield reliable results. In choosing how to partition hydrogen bonds, we followed criteria similar to those used in analogous studies of proteins to ensure consistency in the description of hydrogen-bonding interactions (49). Thus, five types of hydrogen-bond donors and acceptors were defined for nucleic acids and five for proteins based on whether the atom belongs to the protein and nucleic acid backbone or side chain and on the hybridization state of the acceptor (Table 1). Separate statistics were collected for protein side-chain acceptors of sp² and sp³ hybridization to take into account different electronic distributions around the acceptor atoms. Phosphate and ribose oxygens were separated as well because of their different hybridization states. This classification partitions all hydrogen bonds between proteins and nucleic acids into 11 different classes (Table 2).

Table 1. Partition of nucleic acid and protein hydrogen-bond donors and acceptors.

Nucleic acids (DNA, RNA)
Donor	na_NH	A N6, G N1 N2, C N4, T and U N3	aa_sc_NH	His Nε2, Trp Nε1, Asn Nδ2, Gln Nε2, Arg Nε, Nη1, Nη2
			aa_bb_NH	Backbone amide N
Acceptor	na_base_O	G O6, C O2, T and U O2 and O4	aa_sc_sp2	Asp Oδ1 Oδ2, Glu Oε1 Oε2, His Nδ1, Asn Oδ1, Gln Oε1
	na_base_N	A N1 N3 N7, G N3 N7, C N3	aa_sc_sp3	Ser Oγ, Thr Oγ1, Tyr Oη
	na_P	O1P, O2P	aa_bb_O	Backbone carbonyl O
	na_O	O5*, O4*, O3*, O2*

Table 2. Partition of hydrogen bonds between nucleic acid and proteins among different types of hydrogen-bond donors and acceptors.

RNA/DNA		Protein		Number (3445)
Donor	na_NH	Acceptor	aa_sc_sp2	284
			aa_sc_sp3	51
			aa_bb_O	174
Acceptor	na_P	Donor	aa_sc_NH	1167
			aa_bb_NH	672
	na_O		aa_sc_NH	238
			aa_bb_NH	80
	na_base_O		aa_sc_NH	352
			aa_bb_NH	94
	na_base_N		aa_sc_NH	289
			aa_bb_NH	44

Hydrogen bonds at protein–nucleic acid interfaces

In the following, we briefly analyze the distance and angular distributions for hydrogen-bond donor and acceptor pairs observed in protein–nucleic acid complexes according to the four geometrical parameters shown in Figure 1.

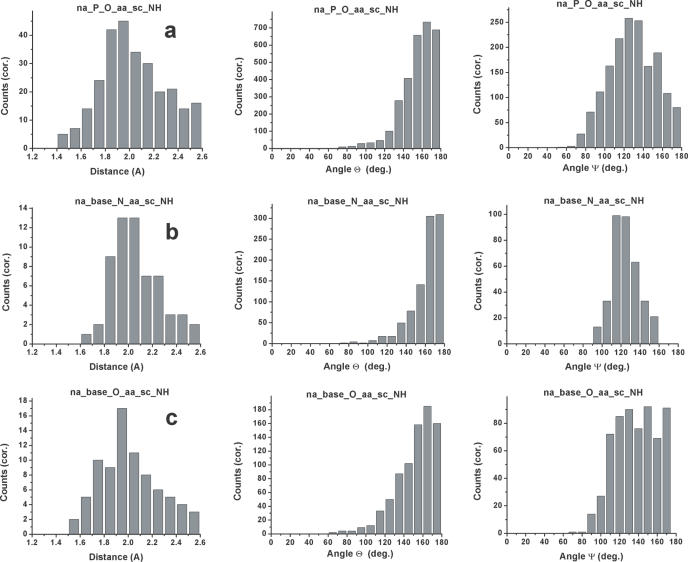
Hydrogen-bond distance δ_HA—the maxima in the distance distributions between hydrogens and hydrogen-bond acceptors are generally centered between 1.8 and 2.0 Å, with small differences between different classes of hydrogen bonds. However, the breadth of the distribution differs when different donor–acceptor pairs are examined. Interactions between phosphate oxygens and both protein backbone and side-chain NH's are the most common polar contacts at protein–nucleic acid interfaces (7–10). For both sets of contacts, we observe well-defined maxima in the distributions, as would be expected for interactions with strong hydrogen-bonding (as opposed to purely electrostatic) character (Figure 2a). The distance distribution for protein backbone NH interactions with phosphate oxygens (data not shown) is centered over a narrower range compared to side-chain NH/NH₂ (Figure 2a), probably reflecting the structural constraints imposed by the protein secondary structure. Although hydrogen bonds to base N are not numerous, the relatively sharp distance distribution observed suggests that these interactions are energetically very favorable and geometrically highly constrained (Figure 2b). Interactions between base NH's and protein backbone carbonyl O are also not numerous, but have a relatively sharp distance distribution (data not shown), suggesting that the steric and structural constraints imposed by the protein backbone and the RNA bases result in relatively few energetically favorable interaction geometries.

Figure 2.

Distance (δ_HA), linear angle (Θ) and angular (Ψ) distributions for selected hydrogen bonds at protein–RNA/DNA interfaces: (a) phosphate oxygens to protein side-chain NH/NH₂; (b) base N to protein side-chain NH/NH₂; and (c) base O to protein side-chain NH/NH₂.

The hydrogen-bond angle Θ measures the linearity of the hydrogen bond: if a hydrogen bond was perfectly linear, its value would be 180°. As expected, hydrogen bonds between nucleic acids and proteins are almost always very close to linear: the distributions generally have maxima in the Θ angle range between 160° and 180°. Interactions between the RNA backbone phosphate oxygens and the protein backbone NH display particularly strong linearity (data not shown), while the side-chain NH's have broader distributions with a maximum slightly removed from the linear value (Figure 2a). Interactions between base nitrogens and protein backbone NH have nearly perfect linear distributions (data not shown), but broader spreads are observed for contacts between base nitrogens and protein side-chain NH's (Figure 2b). The distributions for hydrogen bonds between base oxygens and protein backbone and side-chain NH's have the maxima skewed to values slightly smaller than linear; the distribution is particularly broad for interactions involving the protein side chains (Figure 2c).

The angle Ψ represents the acceptor hydrogen-bond angle. Interactions between phosphate oxygens and protein donors are ideally centered at 120° with a broad distribution especially for interactions involving protein side chains (Figure 2a). Hydrogen bonds between nucleic acid base N and the protein side-chain NH's (Figure 2b) have Ψ distributions resembling those observed for interactions involving protein side chains (49). In contrast, hydrogen bonds to base O have much broader distributions skewed to values much closer to linear, particularly for hydrogen bonds involving protein side-chain NH's, where almost a flat distribution is observed between 120° and 180° (Figure 2c). Nearly linear acceptor angles are often observed between protein side-chain NH's and base O when base O is involved in base-pairing interactions; e.g. in contacts between Arg and GC pairs, or between Asp and AU pairs (11).

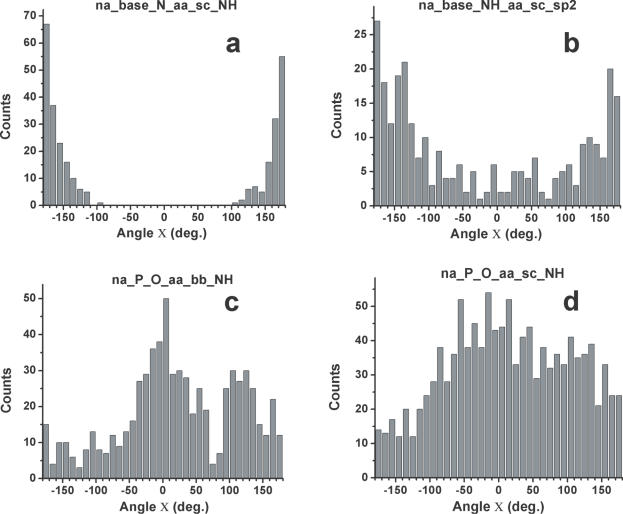
The dihedral angle X measures the planarity of the hydrogen bond. A value of 0° (or ±180°) occurs when the hydrogen is located in the plane defined by the acceptor, acceptor base and reference atom (Figure 1). Protein backbone and side-chain amide groups make strongly planar interactions with base nitrogen acceptors. This preference is more significantly marked for protein side chains (Figure 3a) because of a larger statistical sample, but it is also clear for the protein backbone (data not shown). This observation places strong constraints on the direction of the hydrogen bonds between amino acids and the RNA/DNA bases (see Discussion). The planar preference for base carbonyl oxygens is not as marked as for the ring nitrogens, but still clearly observable. Although interactions between nucleic acid base NH and protein backbone carbonyl oxygens are devoid of any statistical preference (data not shown), weak but clear preferences for a planar arrangement are observed for interactions between nucleic acid NH and NH₂ donors and sp²-hybridized acceptors on the side chains of proteins (Figure 3b). Hydrogen bonds involving phosphate oxygens tend to be planar when paired with amino acid backbone NH, but less clearly so when paired with side-chain donors (Figure 3c and d).

Figure 3.

Dihedral angular distributions (X) for hydrogen bonds at the interface of proteins and RNA/DNA: (a) base N to protein side-chain NH/NH₂ donors; (b) base NH/NH₂ to protein side-chain sp² hybridized acceptors; (c) phosphate O to protein backbone NH; and (d) phosphate O to protein side-chain NH/NH₂.

Construction of a knowledge-based hydrogen-bonding potential

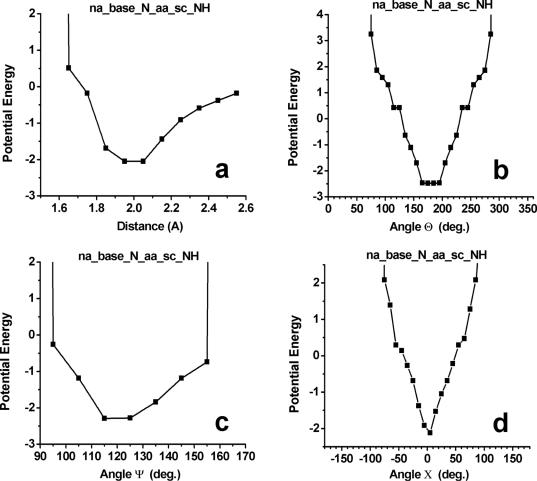
The potential of mean force describing hydrogen-bonding interactions at protein–nucleic acid interfaces was derived by reversing Boltzmann distribution by taking the negative logarithm of the probability distributions for each hydrogen-bond acceptor–donor pair. The total hydrogen-bonding potential is composed of the linear combination of the distance-dependent energy term [E(δ_HA)] and the three angle-dependent energy components [E(Θ), E(Ψ), E(X)] (see Methods). Figure 4 shows the result of this analysis for hydrogen bonds between base N and protein side-chain NH groups. Clear minima appear in the energy profiles reflecting the strong distance and directional preferences as observed in the database of high-resolution crystal structures. In other words, the strong distance and orientation dependence of the hydrogen-bonding reflect significant energetic restrictions on the relative positions of the donor and acceptor atoms at protein–nucleic acid interfaces.

Figure 4.

Hydrogen bonding-potential of mean force for interactions between base N and protein side-chain NH/NH₂ donors. (a) Distance δ_HA; (b) angle Θ; (c) angle Ψ; and (d) angle X. The knowledge-based potentials were calculated from the negative logarithm of the observed frequency distributions (see Methods).

Prediction of the native protein sequence identity at protein–RNA interfaces

Two tests were carried out to demonstrate the importance of the distance and orientation-dependent effects in hydrogen bonds at the protein–RNA interface and validate the ability of the model to capture these effects. The first test probes the ability of the model to recover the native protein sequence at a protein–RNA interface. This test is based on the assumption that the substitution of the sequences of protein at protein–RNA interface with non-native amino acids generally results in an increase in free energy compared with the naturally occurring sequence. In order to assess the importance of the hydrogen-bonding potential, we repeated the same test first by eliminating the orientational components of the hydrogen bond and then by replacing hydrogen-bonding potential with electrostatic Coulomb potential using a linear distance-dependent dielectric constant.

The complete energy function used to score protein–RNA complexes includes van der Waals interactions, solvation, amino acid rotamer and backbone conformational preferences in addition to the statistical-based hydrogen-bonding potential. In weighting for the different components of the total free energy, we used 25 protein–RNA complexes (4500 amino acid positions) and set aside the remaining 17 independent structures (850 amino acid positions) to execute the amino acid recovery test. The weights for the energy terms in each of the experiments were re-optimized (see Methods) for each test (complete hydrogen-bonding function; no orientation-dependent components; no hydrogen-bonding potential instead using a Coulomb potential). Cysteine residues were not included in the substitution profile because potential disulfide bonds remain to be modeled.

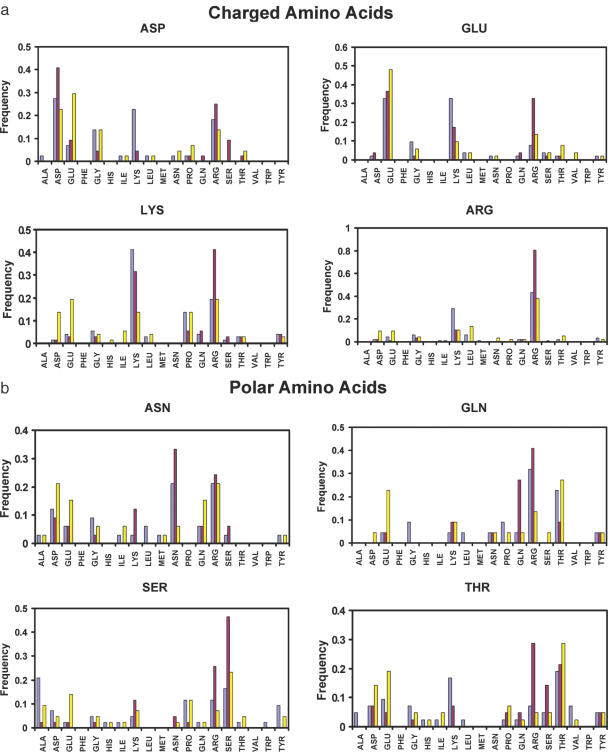
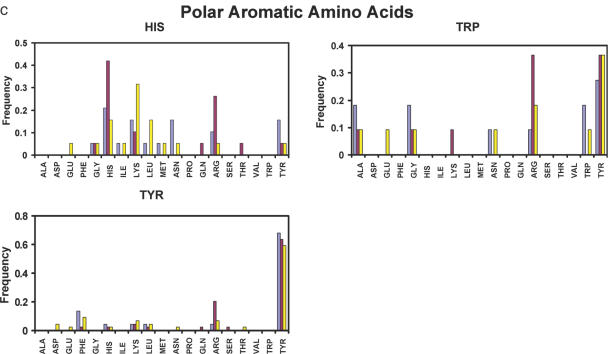
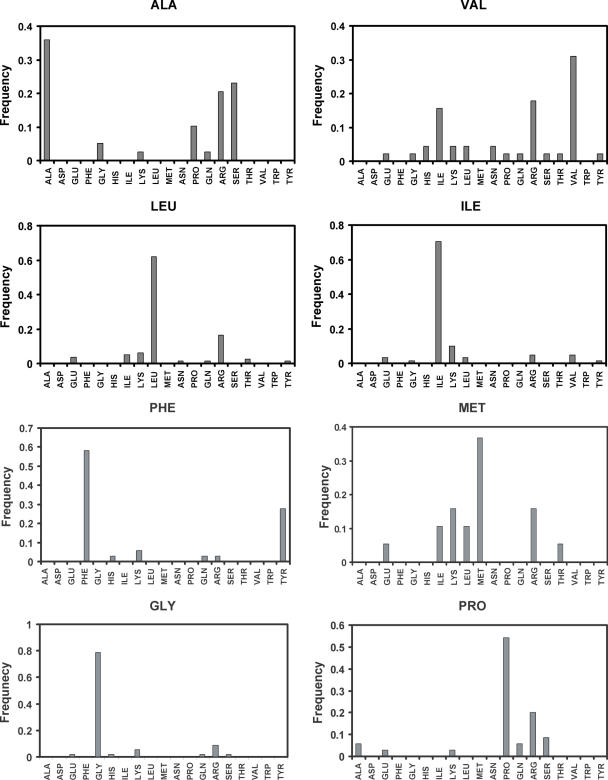
The results of the test are shown in Figures 5 and 6, where we report how often the native amino acids were found to be energetically most favorable. The overall recovery rate is 44%: this result compares well with what is observed on single domain proteins (52% for buried positions and 26% for all positions) and protein–DNA interfaces (43%) by similar tests (49,74). This lower recovery rate compared with the protein core is expected because the identities of the native amino acids at protein–RNA interfaces like protein–protein interfaces are not only determined by energetic considerations, but also by functional and solubility constraints. The complete hydrogen-bonding potential identifies the native amino acids most often as the energetically most favorable replacement for most charged (A, D, K and R), polar (N, Q, S and T) and polar aromatic (H, W and Y) amino acids (Figure 5). The exceptions are Lys, Gln, Thr and Trp. However, the overall prediction accuracy for these residue classes remains worse than that for hydrophobic amino acids (A, I, L, V, F, M, G and P), which are all predicted with the highest frequency (Figure 6).

Figure 5.

Native protein sequence recovery at protein–RNA interface derived from a test set of 17 protein–RNA complexes. Different energy functions are used to test the substitution profile: red bars, complete energy function, as described in the text; light blue bars, energy function with the angular terms of hydrogen-bonding potential turned off; yellow bars, the hydrogen-bonding potential was substituted with a purely Coulombic interaction model. The bars show how often the native amino acids are calculated to be energetically most favorable at each interfacial position probed. (a) Charged amino acids; (b) polar amino acids; and (c) polar aromatic amino acids.

Figure 6.

Recovery of hydrophobic amino acids at the interface of protein–RNA complexes using the complete energy function including the hydrogen-bonding potential.

Significantly, worse results are observed in nearly each case when the orientational component of the hydrogen bond is removed; the model performs even worse when the hydrogen-bonding term is substituted with a purely electrostatic description of polar interactions (Figure 5). Replacing hydrogen-bonding interactions with a purely Coulombic term gives the worst recovery rate in all cases except Glu and Thr. Combining both the hydrogen-bonding and electrostatic potentials, only slightly improves the overall performance of the total energy function in recovering the native sequence (data not shown). Based on these results, the electrostatic potential was not included in the current model.

Recovery frequencies for individual amino acids are revealing. Arg has the highest recovery frequency (over 79%) among all 19 amino acids and is also preferred to the native amino acid for Lys, Gln, Thr and Trp. This is consistent with the high occurrence of Arg (over 15%) at protein–nucleic acid interfaces (7,9). Lys was not recovered most frequently when hydrogen-bonding potential was included, but was found most often when the angular terms of the hydrogen bonds were switched off. This is probably due to the limited conformational sampling of the rotamer approach, which makes it difficult for long polar amino acids to find optimal hydrogen-bonding geometries. Lys was also not initially included in the hydrogen-bonding geometrical analysis because its polar hydrogen atoms cannot be placed without assumptions about hydrogen-bonding energies. Currently, it uses hydrogen-bonding potential based on the analysis of other protein side-chain donors. Thr is most often recovered when a purely electrostatic potential is used but not when the hydrogen-bonding potential is used instead. For polar aromatic amino acid, Trp is less favorable compared with Tyr, which has the second highest frequency of recovery (66%). The high recovery rate for Tyr is presumably due to the hydrogen-bonding properties of its OH groups as well as its ability to form stacking interactions. Although stacking interactions are not explicitly modeled, steric constraints included in the Lennard–Jones term are likely to recapture at least some aspects of the base–amino acid stacking interactions observed in many protein–RNA complexes. Trp is present in only a very small number of cases (11 positions) in our test set, and it is the only polar aromatic amino acid not selected correctly with high frequency of recovery. Its large aromatic ring could sterically clash if conformational space is not sampled adequately.

Decoy discrimination in protein–RNA docking

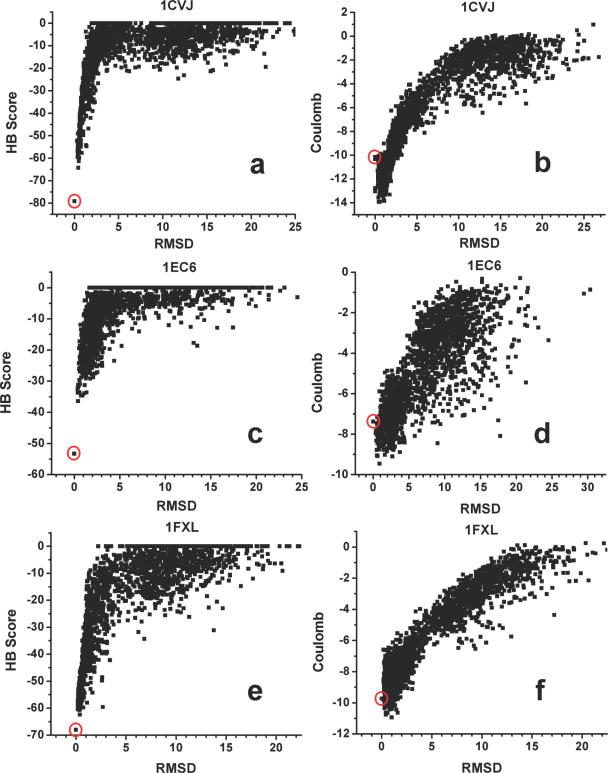
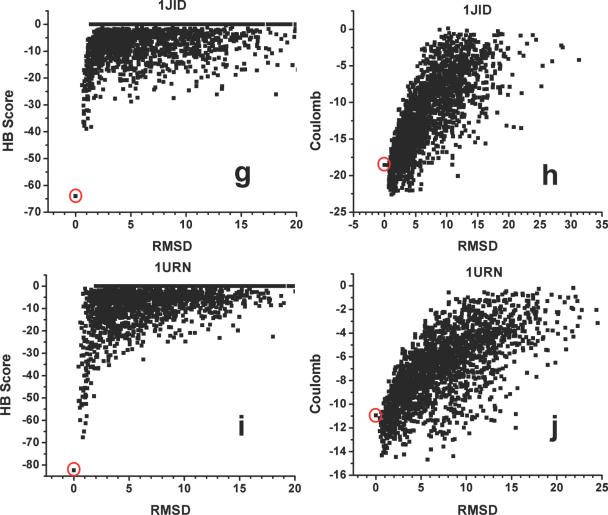
In a second test, we assessed the ability of the new hydrogen-bonding function to discriminate native from non-native protein–RNA structures (Figure 7). This test is based on the assumption that native protein–RNA interfaces, like protein–protein interfaces, are generally energetically optimized when compared to alternative binding conformations (49,61–63). We selected five protein–RNA complexes and generated 2000 decoy structures covering a range of root-mean-square distance (RMSD) values from below 1 Å to over 20 Å. The five structures were chosen according to their sizes (<200 amino acids and RNA between 8 and 29 nt), crystallographic resolution (1CVJ, 2.60 Å; 1EC6, 2.40 Å; 1FXL, 1.80 Å; 1JID, 1.80 Å; and 1URN, 1.90 Å) and characteristics of the interface. Four complexes represent single-strand RNA interacting with one or two RNA recognition motifs (RRMs); 1JID provides an example of a protein bound to the major grove of an irregular helix RNA (Table 3). These are the major interaction modes between protein and RNA. Starting from the native structures, small perturbations (translation and rotation) were applied to obtain both near-native decoys and decoys with larger RMSD values. Protein backbone conformations in all decoys were kept fixed as in the native structures, but the protein side-chain conformations were modeled using standard rotamer library to allow the extensive rearrangement of the side chains in the protein–RNA interface during docking. RNA molecules were kept in the same conformation as in the native structures.

Figure 7.

Scatter plots obtained by scoring five sets of protein–RNA decoys using either hydrogen-bonding potential (a, c, e, g and i) or a Coulombic potential with distance-dependent dielectric constant (b, d, f, h and j). A total of 2000 decoys are created for each of the five test structures using the small perturbation method. The scores of the native structures are highlighted using red circles: (a and b) 1CVJ; (c and d) 1EC6; (e and f) 1FXL; (g and h) 1JID; and (i and j) 1URN.

Table 3. Z-scores for the five protein–RNA complex decoy sets.

PDB code	RNA-binding mode	Z-score
		Coulomb	HB
1CVJ	Single-strand (SS) RNA interacts with two protein RRM motifs	1.19	5.11
1EC6	Protein loop interacts with SS RNA	1.09	6.53
1FXL	SS RNA interacts with two RRMs	1.55	2.70
1JID	Protein interact with RNA major groove and tetraloop	1.36	9.12
1URN	SS RNA interacts with RRM	1.35	8.39

The following potential functions are used: (i) Coulomb electrostatics with a linear distance-dependent dielectric constant (Coulomb) and (ii) hydrogen-bonding potential (HB) based on the present study.

Figure 7 shows the results graphically, while Table 3 shows the Z-score values measuring the discrimination of the native structures from all other decoy conformations. We compared the full hydrogen-bonding potential with the performance of a Columbic potential with a linear distance-dependent dielectric constant. In all cases, the hydrogen-bonding potential successfully discriminated the native structures, with the lowest Z-score of 2.70 (success is defined as Z-score > 1). The hydrogen-bonding potential performs much better than the Columbic model, especially in the low-RMSD range (up to 3 Å) where correct and incorrect structures are most difficult to discriminate. When the angular terms of the hydrogen-bonding potential are removed, the Z-score values are only slightly affected, but three out of five native structures are not discriminated well from the rest of the decoys. The results of this test suggest that native protein–RNA complexes maximize the number of hydrogen-bonding interactions in the interface, while hydrogen-bonding plays a significant role in the affinity and specificity of protein–RNA interactions. It also suggests that explicit treatment of the directionality of the hydrogen bond is required to fully capture its importance.

We expected the model to perform best when recognition was primarily of single-stranded nucleotides compared to more structured RNAs that have more backbone contacts. Consistent with this, the shape of the score distribution at low-RMSD values was not as distinct for the complex involving a structured RNA (1JID) compared to the other four decoys sets, although the Z-score value remains very high (9.12). In this structure, the protein binds to the major groove and tetraloop of a helical RNA, with few direct protein–base contacts. A complex network of highly ordered water molecules is also present in this protein–RNA interface. The presence of water molecules is certain to affect the accuracy of the hydrogen-bonding potential, since they are not modeled in the scoring functions and are discarded in the docking process. Despite these difficulties, discriminations between correct and incorrect structures remain effective and in fact the Z-score is the best of all tests.

DISCUSSION

The increase in the number of RNA–protein structures in the last few years has been remarkable. We now know the structures of most if not all major RNA-binding protein families and how they bind to RNA (64–66). However, even in the best-studied case, RRM, the molecular basis of specificity in protein–RNA recognition remains far from clear (64,67). A fruitful approach in understanding the molecular determinants of protein–protein interactions has been the establishment of computational tools to redesign specificity (68–71). The computational redesign of proteins and protein–protein interfaces is providing experimental test of our knowledge of the interaction principle, as well as design cycles to successively improve tools for design and prediction based on the experimental results. The aim of the present manuscript is to establish comparable tools to study protein–RNA recognition.

The starting point for the present work is the statistical analysis of hydrogen-bond geometries at the interfaces between proteins and nucleic acids as they are observed in high-resolution crystal structures. Several recent studies have analyzed the statistical properties of protein–RNA interfaces and provided insight into amino acid preferences in the interactions with certain bases and macroscopic characteristics such as polarity and average size (5–11). However, the quantitative analysis of the energetic features responsible for specificity and affinity in protein–RNA recognition remains to be executed. None of the existing computational studies has until now been expanded to develop a testable model of protein–nucleic acid interfaces with predictive power. We use the statistical analysis to establish a distance and orientation-dependent hydrogen-bonding potential which is fully compatible (indeed inspired by it) with a successful model to describe hydrogen bonding in protein cores and protein–protein interfaces (49,68). We demonstrate that this potential of mean force provides a quantitative tool to analyze protein–RNA interfaces by conducting two independent tests: (i) it successfully recovers native amino acids at protein–RNA interfaces and (ii) it successfully discriminates native structures of protein–RNA complexes from a very large set of docking decoys.

The statistical-based hydrogen-bonding potential recovers native amino acids at the interface ∼44% of the time when included in a complete physical model of protein–RNA interfaces that contains Lennard–Jones potentials and solvation. This result is comparable to similar studies conducted with single domain proteins and protein–DNA complexes (49,74), which also used orientation-dependent hydrogen-bonding potential but based on the geometries of hydrogen bonds in protein crystal structures. In the study with protein–DNA complexes, a potential term derived from the present study to restrict the acceptor angle of aromatic nitrogen was included as well in the total hydrogen-bond potential. The success of current model is particularly encouraging when one considers that this is the first version of a model that remains to be refined through successive rounds of computational prediction and experimental validation. We demonstrate that the successful recovery of polar and aromatic-polar amino acids is compromised when the hydrogen-bonding angular terms in the potential are removed (i.e. the hydrogen bond is assumed to be radially symmetric) and when a Coulombic potential is used instead of the hydrogen-bonding potential. As observed for proteins (49), even if van der Waals and other components of the model are retained and undoubtedly provide geometric restriction to the possible intermolecular interactions, they are not sufficient to discriminate the native amino acid sequence from random mutations. Arg is among the most frequently observed amino acids in protein–nucleic acid interfaces, so the weights and reference energy calculation process will certainly provide some bias toward this residue. Furthermore, distance cut-off used to define the protein–RNA interface is generous. It is possible that certain amino acids (e.g. Asp and Glu; Figure 5) on the protein surface are defined as interface residues even if they do not directly interact with RNA: they may be replaced with Arg providing more favorable electrostatic contacts. Using direct contacts (VDW and hydrogen bond) to define protein–RNA interfacial residues and weighting the amino acid frequency from the database of protein–nucleic acid interactions will probably reduce the preference for more dominant residues.

The current hydrogen-bonding potential also discriminates native protein–RNA structures from large sets of decoys prepared by small-perturbation method and greatly outperforms a purely Coulombic model, especially in the most challenging low-RMSD range. The hydrogen-bonding potential has much better discrimination power in this close-to-native case compared with Coulombic potential. However, in the high-RMSD range (up to 15 Å), the distance-dependent Coulombic potential has a better score-RMSD linear relationship compared with hydrogen-bonding potential. Perhaps, the two scores could be successfully combined during the de novo modeling of protein–RNA interfaces. The electrostatic potential can guide the two partners during the initial searches leading to rough models that can be refined using the more accurate hydrogen-bonding potential.

We compared the performance of hydrogen-bonding potentials based on the current protein–RNA/DNA database with a previously published hydrogen-bonding model based on protein structures. The comparison was carried out by mapping atom types to each other based on similar chemistry. The recovery tests yielded comparable overall results, although the recoveries of individual amino acids differ somewhat between the two tests. We notice, however, that the current hydrogen-bonding potential for proteins employed in Rosetta treats aromatic nitrogens based on the results of the protein–nucleic acid database illustrated here. Furthermore, Rosetta uses a rotamer library to search the amino acid side-chain conformations, and this approximation most probably introduces errors that are greater than the difference between the two hydrogen-bonding potentials. Finally, protein–nucleic acid interfaces have a significant number of protein–protein hydrogen bonds, in addition to protein–nucleic acid hydrogen bonds. These three effects mitigate the differences observed between the two hydrogen-bonding potentials.

Hydrogen bonds involving the nucleic acid bases are undoubtedly an important source of specificity in protein–RNA/DNA recognition (7,9). However, they are much fewer than the contacts with the backbone phosphates; in RNA, e.g. 60–70% of all interactions involves the backbone (9). What features of the hydrogen bond between proteins and nucleic acids are the most significant determinants of its importance in recognition?

1. Hydrogen bonds between the protein side chain and backbone atoms and RNA/DNA bases are constrained over narrow distance and (especially) angular values. The sharp distance and orientational preferences observed in the present study reveal very narrow minima in the potential of mean force subtending these interactions. They are energetically constrained within surprisingly narrow (compared to protein–protein interactions) geometrical parameters.

2. Hydrogen bonds involving the nucleic acid bases have very strong preference for planarity. The planarity of hydrogen bonds involving the nucleic acid bases is particularly stunning (Figure 3). By way of comparison, contacts between protein side chains only display mild planar preference for sp²-hybridized acceptors. Backbone contacts in proteins deviate significantly from planarity with maxima in the distribution near −120° for α-helices, −100° for irregular structures, while a bimodal distribution centered around −130° and a broad peak near 0° for β-sheet structures (49). The very strong preference for planarity of the hydrogen bond in nucleobases may reflect the electron distributions of the planar ring systems as well as the steric constraints in interaction with bases. Whatever its origin, this observation places very significant constraints on the type of intermolecular hydrogen bonds between proteins and nucleic acids that are energetically favorable. This observation may also have implications for drug design. Many existing drugs contain heteroaromatic rings, including nucleosides, which are likely to share hydrogen-bonding characteristics with the nucleic acid bases.

3. Interactions of phosphate oxygens with proteins have strong hydrogen-bonding character. We observed clear maxima in the distance distributions for hydrogen bonds between proteins and the phosphate oxygens, corresponding to typical hydrogen bonds. Purely electrostatic interactions would generate distributions that increase monotonically with distance and would not be strongly directional (9,49). The distance and angle distributions for phosphate oxygen acceptors (Figure 2a) are only slightly broader compared with other hydrogen-bonding distributions described here, suggesting that the contributions from charge–charge interactions are marginal. Furthermore, some residues (e.g. Arg) can form one strong and one weak hydrogen bonds with the two phosphate oxygens, affecting the geometry of the hydrogen bond. Phosphate oxygen acceptors provide the majority of intermolecular hydrogen-bonding interactions between proteins and nucleic acids. Very often, these interactions involve basic side chains such as Arg or Lys (5,7). Although their contribution to affinity has long been recognized as very important, their contribution to specificity (indirect recognition) has been more difficult to dissect. The observation of clear distance and orientational constraints indicates that only certain structural arrangements are conducive to favorable interactions between nucleic acid phosphates and proteins. This is probably a major reason why a purely Coulombic model performs less satisfactorily compared to the orientation-dependent hydrogen-bonding model derived from existing protein–nucleic acid structures.

It is clear from this discussion that the formation of hydrogen bonds at protein–nucleic acid interfaces places very strong orientational constraints on the relative placement of hydrogen-bonding atom pairs. These preferences define the kind of interactions that are energetically favorable between nucleic acid and proteins. Interactions involving the bases are especially directional and tightly constrained geometrically. Direct recognition of RNA and DNA functional groups, even by the protein backbone (as is very commonly observed in RNA–protein interactions) (9), is a highly effective way to achieve specific recognition because of these strong geometric constraints. Interactions involving phosphate oxygens are also most favorable within relatively narrow distance ranges and are remarkably directional. By controlling the spatial location of phosphate groups and therefore dictating which interactions between the phosphates and protein side chains are energetically favorable or even feasible, nucleic acid structure contributes to the indirect recognition of a nucleic acid sequence.

The present work and the concomitant prediction of protein–DNA interactions introduce a validated computational tool for the redesign of specificity in nucleic acid-binding proteins. Such proteins would provide valuable new probes for biological interactions and, potentially, new therapeutic agents. Combinatorial methods such as phage display are effective for at least some classes of nucleic acid-binding proteins (1,2,72,73), however, it would be highly advantageous to be able to alter the specificity of existing nucleic acid-binding proteins in a predictive way using design algorithms that have become increasingly powerful in the design of proteins and protein–protein interface (22–26,49). The physical model presented here is capable of energetically quantifying the molecular interactions between proteins and nucleic acids based on a full atom representation that comprises both physical and statistical components. We are currently working at improving the model by allowing for RNA flexibility, by improving the description of electrostatic and by including cation–π interactions, guided by the results of amino acid substitutions. We are also experimentally testing the predictive power of the model by redesigning specificities at model protein–RNA interfaces.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.