Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 11;7:39315. doi: 10.1038/srep39315

Two-Layer Elastographic 3-D Traction Force Microscopy

Begoña Álvarez-González 1,2, Shun Zhang 2, Manuel Gómez-González 2, Ruedi Meili 1,2, Richard A Firtel 1, Juan C Lasheras 2,3,4, Juan C del Álamo 2,4,a
PMCID: PMC5225457  PMID: 28074837

Abstract

Cellular traction force microscopy (TFM) requires knowledge of the mechanical properties of the substratum where the cells adhere to calculate cell-generated forces from measurements of substratum deformation. Polymer-based hydrogels are broadly used for TFM due to their linearly elastic behavior in the range of measured deformations. However, the calculated stresses, particularly their spatial patterns, can be highly sensitive to the substratum’s Poisson’s ratio. We present two-layer elastographic TFM (2LETFM), a method that allows for simultaneously measuring the Poisson’s ratio of the substratum while also determining the cell-generated forces. The new method exploits the analytical solution of the elastostatic equation and deformation measurements from two layers of the substratum. We perform an in silico analysis of 2LETFM concluding that this technique is robust with respect to TFM experimental parameters, and remains accurate even for noisy measurement data. We also provide experimental proof of principle of 2LETFM by simultaneously measuring the stresses exerted by migrating Physarum amoeboae on the surface of polyacrylamide substrata, and the Poisson’s ratio of the substrata. The 2LETFM method could be generalized to concurrently determine the mechanical properties and cell-generated forces in more physiologically relevant extracellular environments, opening new possibilities to study cell-matrix interactions.

The mechanical properties of the extracellular environment affect cellular behavior and processes such as cell migration, proliferation, growth, differentiation, and spreading1,2,3. Cells can feel the mechanical properties of their extracellular environment and regulate their adhesions by a process known as mechanosensing4,5,6. Traction forces exerted by the cells are known to regulate not only cell locomotion but also many other cellular processes7,8. Several traction force microscopy methods have been developed to measure the forces exerted by stationary and/or migrating cells on flat elastic polymer-based hydrogels9,10,11,12,13,14,15. These gels exhibit a linearly elastic behavior in the range of the small deformations produced by the cells16,17,18. The calculation of the traction forces in these TFM methods requires a precise knowledge of the constitutive equations of the substratum, which for linearly elastic materials depend only on two parameters: the Young’s modulus of elasticity and the Poisson’s ratio19. The Young’s modulus of polyacrylamide and other elastic materials commonly used in these TFM methods are well-known, and there are established methods for their measurement17. On the other hand, the value of their Poisson’s ratio is often not well characterized.

Flexible polymer hydrogels have been shown to exhibit Poisson’s ratios close to 0.5. However, a wide range of values has been reported for these gels in the literature (0.27–0.49), depending on their specific composition and method of preparation20,21,22. Pioneering TFM studies that assumed 2-D substratum deformation and infinite substratum thickness reported a weak dependence of the traction stresses on the Poisson’s ratio23. However, more recent analyses that consider the finite thickness of the substratum and three-dimensional deformations have indicated that this dependence is stronger than previously believed24. The uncertainty in the Poisson’s ratio poses an important limitation to TFM methods since for a given deformation field, not only the magnitude but also the spatial distribution of the traction forces depends on the Poisson’s ratio25. To address this issue, we have developed a new traction force microscopy method that enables the simultaneous calculation of the Poisson’s ratio of the gel and the traction forces that a cell exerts on it. Furthermore, this method allows for measuring the Poisson’s ratio at each specific measurement time and location, in order to account for possible spatial and temporal variations of the mechanical properties of the substratum when measuring cellular traction forces, cell-cell tensions25,26, and potentially other biomechanical quantities of interest.

When cells adhere to an elastic substratum, they apply forces on its surface producing deformations deep throughout the substratum27. These deformations depend on the value of the Poisson’s ratio of the substratum’s material, σ24. If the Poisson’s ratio is known, it is possible to solve the elastostatic equation

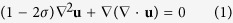graphic file with name srep39315-m1.jpg

to determine the 3-D deformation everywhere inside the substratum, u(x, y, z), from the 3-D deformation measured on a single plane, u(x, y, z = constant)24. Thus, knowing the 3-D substratum deformation on two different planes, u(x, y, z = h0) and u(x, y, z = h1), makes equation (1) highly overdetermined. In this paper, we exploit this overdetermination to develop a two-layer elastographic traction force microscopy (2LETFM) method that allows us to estimate σ while simultaneously calculating the traction forces exerted by the cell. It is important to note, however, that this method cannot determine the Young’s modulus of the substratum because this parameter modulates the deformations in the same manner everywhere in the substratum and, thus, it does not affect the deformation patterns.

2LETFM is rooted in the analytical solution to the elastostatic equation (1) developed for Fourier Traction Force Microscopy10,24,28. We use this solution together with the deformation measured at the first plane (z = h0) to calculate the deformation on the second plane (z = h1) as a function of the Poisson’s ratio. Then, we determine the Poisson’s ratio by iteratively minimizing the least-squares error between the measured and calculated deformations at z = h1. The obtained value of σ is subsequently used to calculate the 3-D traction stresses exerted by the cell following the approach described by del Álamo et al.24. To test the accuracy and robustness of the new 2LETFM method, we use synthetic deformation fields with prescribed background noise. This analysis indicates that, in the range of values of the Poisson’s ratio typically encountered in experiments (σ > 0.3), 2LETFM can accurately and robustly determine σ for a wide range of experimental design parameters, and even in the presence of significant measurement noise. As way of illustration, we perform 2LETFM experiments on Physarum microamoebae migrating on the flat surface of polyacrylamide substrata. The elastographic TFM analysis can be immediately extended to the case of cells embedded inside linearly elastic 3-D matrices.

Methods

Two-layer elastographic traction force microscopy analysis

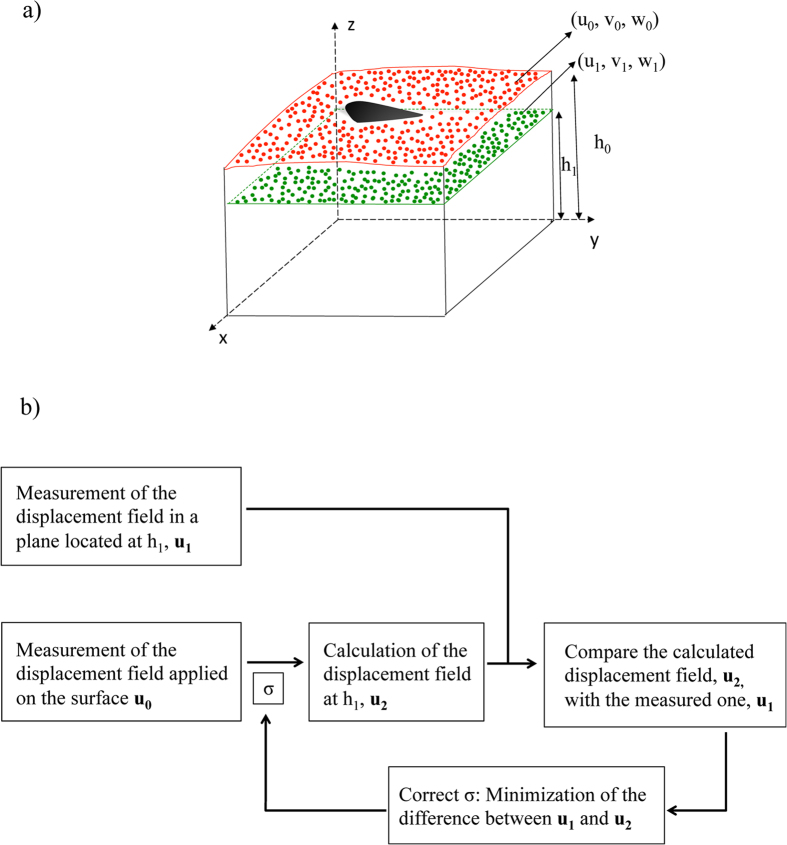
Consider the two-layer TFM setup in Fig. 1a, where the 3-D deformation of the substratum is measured at two separate horizontal planes, u0 = u(x, y, z = h0) and u1 = u(x, y, z = h1). For this exposition, we will consider that h ≥ h0 > h1 where h is the substratum thickness. Using u0 as boundary condition together with zero deformation at the bottom of the substratum, it is possible to find an exact solution to the elastostatic equation (1) where the Poisson’s ratio is a free parameter24. This solution provides the full 3-D deformation vector field everywhere inside the substratum, including at the second measurement plane z = h1.

Figure 1.

Figure 1

Open in a new tab

(a) Sketch of the configuration of the experiment. The substratum has a layer embedded with red beads at the surface and another layer embedded with green beads in a plane below the surface. As a cell adheres to the substratum, the deformations that it applies in both layers embedded with beads are measured. (b) Overview of the method. Diagram indicating the steps followed in this method for the calculation of the Poisson’s ratio of the substratum.

The solution procedure, which was explained in detail by del Álamo et al.24,28, is summarized as follows. We expand the deformation vector field in Fourier series in the x and y directions,

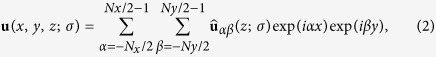graphic file with name srep39315-m2.jpg

where Nx and Ny are respectively the number of measurement points in x and y, and α and β are the corresponding wavenumbers. This transformation allows us to obtain a second-order, ordinary boundary value problem for 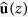Inline graphic. The solution to this problem is

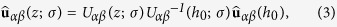graphic file with name srep39315-m4.jpg

where Uαβ(z; σ) is the resolvant matrix of the boundary value problem, which can be found in closed analytical form in ref. 24, and 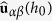Inline graphic are the Fourier coefficients of the deformation measured at z = h0. By plugging z = h1 in equations (2, 3), we calculate the substratum deformation at the second measurement plane from the substratum deformation measured at the first plane,

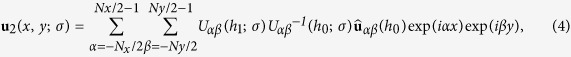graphic file with name srep39315-m6.jpg

which is equivalent to 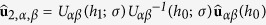Inline graphic. The Poisson’s ratio appears as a free parameter in the calculation of u2. Thus, comparing u2(x, y; σ) with the deformations measured at the second plane, u1(x, y), allows for estimating the value of the Poisson’s ratio σr that maximizes their agreement.

The resolvant matrix of the traction force microscopy problem has a form that can amplify or suppress experimental noise28,29. Specifically, it is straightforward to see that deformations with spatial patterns of wavelength 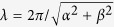Inline graphic much smaller than substratum thickness (λ ≪ h) vary as as 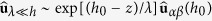Inline graphic28. This dependence justifies our choice h0 > h1, which naturally introduces a low-pass filter for the noise contained in the deformations measured at z = h0. Note that the alternative option, h0 < h1, would exponentially amplify measurement noise. Experimental errors can be decreased further given that the comparison u2(x, y; σ) = u1(x, y) is done at Nx × Ny different points (see eq. 4). Having Nx × Ny conditions to estimate one single parameter makes the calculation of σr highly overdetermined and renders the error of the recovered Poisson’s ratio significantly lower than that of the traction stresses themselves, as is shown below. To solve the overdetermined problem, we followed a least-squares approach using an iterative Levenberg-Marquardt algorithm that minimized a global cost function to calculate σ. This iterative algorithm is similar to those employed in our previous studies30,31,32 and is summarized in Fig. 1b.

We tested two different cost functions,

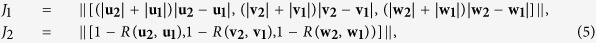graphic file with name srep39315-m10.jpg

where R stands for the correlation coefficient. The main difference between these two functions is that J1 penalizes differences in magnitude whereas J2 penalizes differences in spatial patterns.

Once the value of σr has been estimated, the traction stresses at the cell-substratum interface are obtained as described by del Álamo et al.24. Specifically, these stresses are determined from the calculated displacements and their z-derivatives by applying Hooke’s law in Fourier space,

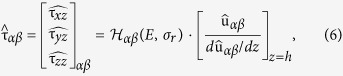graphic file with name srep39315-m11.jpg

where the 6 × 3 matrix 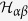Inline graphic, which only depends on the material properties of the substratum (E and σr) and the wavenumbers of each Fourier mode, was given in the Supporting Information of del Álamo et al.24.

Cell culture

We cultured Physarum polycephalum plasmodia in agarose plates with oatmeal33,34. We excised small pieces from the parent plasmodium, and grew them on agarose plates without oatmeal during 10 hours. We subsequently excised 200-μm sized pieces with a scalpel and placed them over the polyacrylamide gel. This process produces highly motile amoebae35,36. We then removed the surrounding water using a small glass capillary tube, and covered the polyacrylamide gel with the amoebae using an agar cap. To fabricate the agar cap, we boiled a 100 mM agar solution and poured 100 μl of this solution on a glass coverslip mounted with a 12-mm washer, and waited until the agar solidified. The weight of the agar cap generated a pressure on the amoebae comparable to but smaller than the traction stresses generated by the cells, thus generating a gentle confinement36. Such confinement prevented the gel from drying out and rendered the cell easier to visualize, while still allowing the cell to exert significant deformations in the substratum.

Substratum fabrication

We fabricated 12-mm diameter polyacrylamide gels of 5% acrylamide and 0.225% bisacrylamide (Young’s modulus approximately 8 KPa37) mounted on 22-mm square # 1 glass coverslips38,39. To independently measure the substratum deformation at a plane near its surface (z = h0) and at a second plane below the surface (z = h1), we fabricated a polyacrylamide substratum with four layers: the bottom layer contained no beads, the second layer contained 0.07% carboxylate modified yellow latex beads of 0.5 μm diameter (Fluospheres, Invitrogen, Carlsbad CA), the third layer contained no beads, and the top layer contained 0.07% carboxylate modified red latex beads of 0.5 μm diameter (Fluospheres, Invitrogen, Carlsbad CA). Figure 1a shows a sketch of the experimental configuration. The layers were verified to adhere well to each other under experimental conditions by confirming continuity of deformation across different layers, similar to our previous work24. To further establish if the layers were properly attached to each other so that there were no jumps in deformation across different layers, we verified the continuity of the substratum deformation in x − z planes under the cells (see Figure S1 in the Supplementary Information). We mounted the coverslips with the gels in Petri dishes with circular openings at their bottom using silicon grease (Dow Corning, Midland, Michigan). We made the gels physiologically compatible by cross-linking collagen I to the surface of the polyacrylamide. We used 1 mM Sulfo-SANPAH (Thermo Sci, Rockford, Il) after UV activation to cross-link 0.25 mg/ml collagen I. The gels were incubated overnight at room temperature. After washing, the gels were stored in 0.05 M HEPES buffer and antibiotic (40 μM Ampicillin) for up to a week. The thickness of the gels was approximately 100 μm and the distance between the two layers containing beads was approximately 15 μm. In each experiment, we measured the exact thickness of the gel and the distance between the two layers containing beads. The thickness of the gel was measured by locating the top and bottom planes and subtracting their z-positions and, in a similar manner, the distance between the two layers containing beads was measured by locating these layers and subtracting their z-positions.

Microscopy

The 3-D deformation of the substratum at two different planes beneath the surface, z = h0 and z = h1, was measured by tracking respectively the red and yellow fluorescent beads. We acquired time-lapse sequences of image z-stacks using a Leica DMI6000 B inverted microscope (Leica Microsystems, Inc., Buffalo Grove, IL) equipped with a Zyla 4.2 sCMOS camera (Andor Technology Ltd., Belfast, UK) and a 20x objective lens. The imaging setup was controlled by the open source microscopy software Micro-Manager40,41. Each z-stack consisted of 20 images at 0.5 μm increments, and was vertically centered at the plane of maximum fluorescence intensity as determined by the autofocus system. The position and shape of the cell at each instant of time was recorded with an additional bright-field phase contrast image. We acquired the two fluorescent z-stacks and the phase-contrast image of the cell every 60 seconds.

Measurement of substratum deformation

We determined independently the 3-D deformation at the center plane of the two imaged z-stacks by analyzing the images of the red and yellow beads separately. For each color, we cross-correlated an instantaneous z-stack with the cell in the center of the x − y field of view, and a reference z-stack that was obtained after the highly motile cell had moved away of the field of view, similar to our previous works8,24,28,36,42,43,44,45,46. Enough time was given for the cell to move away from the field of view so that the edges of the reference images were non-deformed. We note that the agar cap was not removed to acquire the reference z-stack, and thus the polyacrylamide gel was still supporting the weight of the cap. However, this does not preclude the calculation of the traction stresses because the weight exerted by the agar cap is constant, and the polyacrylamide gel behaves linearly (see detailed demonstration in the Supplementary Information). To measure deformation, both the instantaneous and reference z-stacks were divided into smaller 3-D interrogation boxes, as is done in particle image velocimetry47. In order to balance spatial resolution and signal-to-noise ratio while minimizing phototoxic effects, we chose interrogation boxes of size 64 × 64 × 20 pixels in the x, y and z directions, with 50% overlap in the x and y directions. The resulting spatial resolution (20 μm) was sufficient for the Physarum amoebae considered in our experiments, which had a typical size of 200-μm.

Results

Synthetic-field analysis of 2LETFM

As discussed in the Methods section, the relative position of the measurement planes may influence the performance of 2LETFM in the presence of experimental noise. The Poisson’s ratio and the nature (tangential vs. normal) of the cell-generated traction forces could also affect the accuracy of the new technique, because they modulate how stress and deformation propagate throughout the substratum24. To systematically determinate the accuracy and robustness of 2LETFM as a function of these parameters, we applied the new method to synthetic deformation fields with prescribed noise. The synthetic deformation fields were defined by the equations

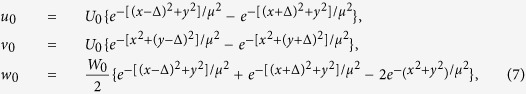graphic file with name srep39315-m13.jpg

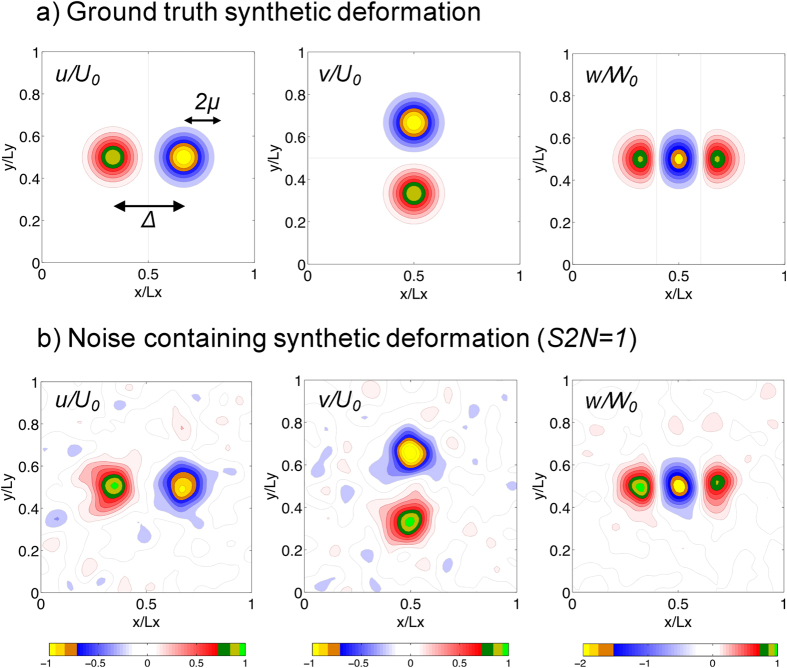
and are shown in Fig. 2. These synthetic data mimic the substratum deformation generated by migrating amoeboid cells13, including the Physarum amoebae reported in the Results Section below (see also ref. 36). The parameter μ in these equations represents the length scale of the deformation patterns, whereas the parameters U0 and W0 represent the magnitude of the deformations. To simplify the analysis, we reduced the number of parameters by assuming that the top measurement plane was located at the surface of the substratum, h = h0.

Figure 2. Example of the synthetic deformations used for the in silico analysis of 2LETFM.

Figure 2

Open in a new tab

(a) Ground truth synthetic deformation, u0 = (u0, v0, w0) at the surface of the substratum, given by eq. 7. The parameters Δ (distance between positive and negative deformation patterns) and μ (size of each the deformation pattern) are explained in the plot. (b) Noise containing synthetic field obtained by adding a normally distributed random field that has been low-pass filtered with a Gaussian filter of size μ/2. The signal-to-noise ratio of this example is S2N = 1. The in-plane (u0, v0) and out-of-plane (w0) deformations are given normalized with U0 and W0 respectively, and their values correspond to the colorbars at the bottom of each column.

We used the synthetic deformation field u0 as boundary conditions for the elastostatic equation, and calculated u1(x, y) at z = h1 from eq. 4 for given values of the Poisson’s ratio σe that was considered as exact. Then, we studied how accurately the two-layer algorithm could recover σe under different conditions.

Effect of Experimental Noise

To model experimental noise, we used u0 and u1 as ground truth data, and added an independent random field on each of these deformation fields. Noise fields unois with spatial patterns that resembled experimental conditions were generated in the Fourier domain, with a Gaussian spectrum of wavenumber width δ, i.e.

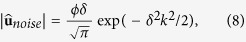graphic file with name srep39315-m14.jpg

where 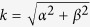Inline graphic, and uniformly random phase. The noise fields generated by this model are also Gaussian in the physical domain (x, y), and have a characteristic length scale δ. Unless otherwise specified, we used δ = μ/2 in our simulations so that the length scales of the noise and the ground truth are comparable. Note that this is a conservative scenario that makes it challenging to low-pass or high-pass filter the noise without affecting the ground truth measurements. Additional simulations were performed for other values of δ. The results of these simulations, reported in Figure S3 in the Supplementary Information, indicate that the conclusions presented here are independent of δ. The S2N of the noise-containing fields was defined as the ratio between the ground truth fields and the root mean squares of the noise,

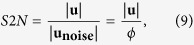graphic file with name srep39315-m16.jpg

and was varied in the range 0.25 ≤ S2N ≤ 10 via the coefficient ϕ in eq. (8). An example of a 3-D noise-containing deformation field with signal-to-noise ratio (S2N) equal to one is shown in Fig. 2b.

We simulated gels with values of the Poisson’s ratio in the range 0.1 < σe < 0.5. This range was chosen for completeness, even though values σ < 0.3 have not been reported for the elastic hydrogels used in TFM. For each pair of values of σe and S2N, we ran N = 100 realizations with different random noise distributions. We plugged the noise-containing deformation fields into the least-squares iterative procedure described in Fig. 1 to recover the Poisson’s ratio of the substratum, σr, and compared the result to σe. In these simulations, we kept the positions of the two measurement planes fixed at h1 = 0.85 h and h0 = h. The effect of the relative position of the measurement planes, h0 − h1 is discussed below.

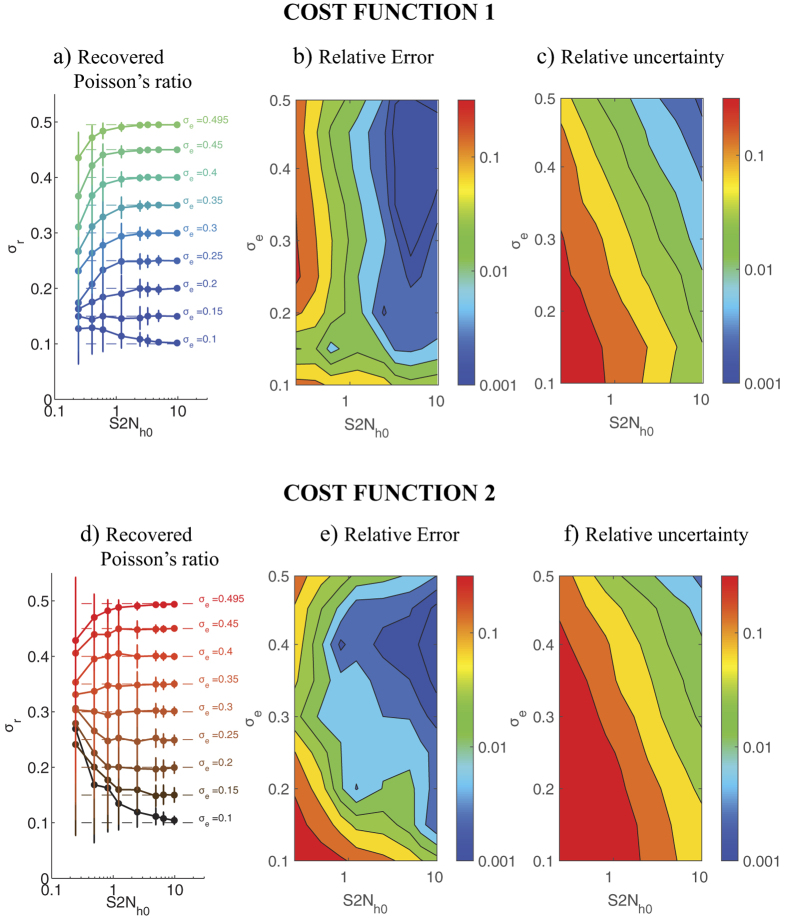
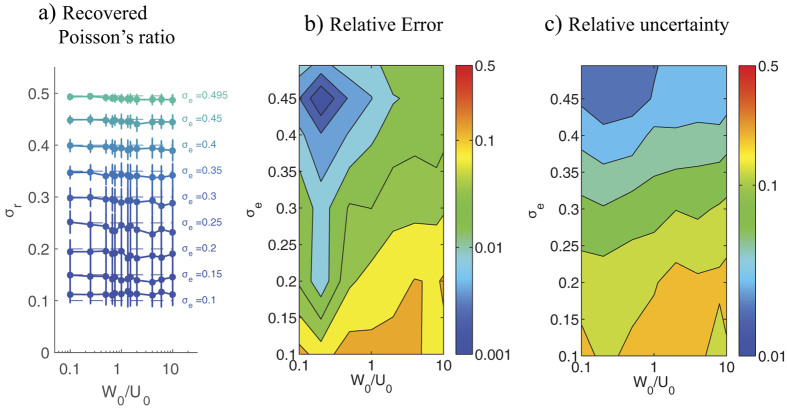
Figure 3 shows the statistics (mean ± standard deviation) of the recovered Poisson’s ratio σr as a function of the exact value σe and the S2N for the two different cost functions presented in equation 5. The data show that 2LETFM can accurately determine the Poisson’s ratio even for noisy displacement fields. The method is particularly accurate and robust for the values of the Poisson’s ratio typically found in TFM substrata (i.e. 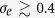Inline graphic). In this range, both |σr − σe| and the standard deviation of σr are less than 10% of σe for S2Ns as low as 0.5. When the S2N is lower than 0.5, the Poisson’s ratio can be underestimated for σe ≥ 0.2 − 0.3, while it is overestimated for lower values of σe (Fig. 3a,d). It is worth noting that the determination of σ by 2LETFM is substantially more accurate than the calculation of the traction stresses when the same level of noise is present in the measured deformations. In fact, comparing Fig. 3b,e with Figure S3 in the Supplementary Information reveals that the error in σr is about 10 times lower than the error in the traction stresses.

Figure 3. Accuracy and robustness of 2LETFM in the presence of zero-average, normally distributed random noise.

Figure 3

Open in a new tab

(a) Value σr of the Poisson’s ratio recovered by 2LETFM using the difference cost function J1 (eq. 5). The data are plotted as a function of the signal-to-noise ratio S2Nh0 of the deformations prescribed at z = h0, and represented as mean ± standard deviation obtained from N = 100 random realizations. Each curve is obtained for a different value σe of the exact Poisson’s ratio that is being recovered. This exact value is indicated with a dashed horizontal line in each case. (b) Contour plot of the relative error of σr obtained with the cost function J1 as a function of S2Nh0 and σe. The relative error is defined as |σr − σe|/σe. (c) Contour plot of the relative uncertainty of σr obtained with the cost function J1 as a function of S2Nh0 and σe. The relative uncertainty is defined as r.m.s.(σr)|/σe. (d) Value σr of the Poisson’s ratio recovered by 2LETFM using the correlation cost function J2 (eq. 5). The data are plotted in the same manner as in panel (a). (e) Contour plot of the relative error of σr obtained with the cost function J2 as a function of S2Nh0 and σe. (f) Contour plot of the relative uncertainty of σr obtained with the cost function J2 as a function of S2Nh0 and σe. The data were obtained for h0 − h1 = 0.15h0 = 2.5μ and U0 = W0.

The recovery of the Poisson’s ratio is relatively independent of the cost function employed in the least-squares optimization algorithm. However, the cost function based on the difference between deformations (J1, see eq. 5) (Fig. 3a–c) performs somewhat better than the one based on cross-correlating the spatial patterns of the deformations (J2, see eq. 5) (Fig. 3d–f), particularly for very low S2Ns. Unless otherwise indicated, the results presented below are obtained using J1.

Effect of the position of the measurement planes

The position of the second measurement plane, z = h1, might be a key factor in the experimental design of 2LETFM. To investigate if there is an optimal position that maximizes the accuracy of 2LETFM, we ran simulations varying the value of h1 and with the noise-containing synthetic fields described above (keeping the S2N = 1). The results of these simulations are summarized in Fig. 4 as a function of h0 − h1.

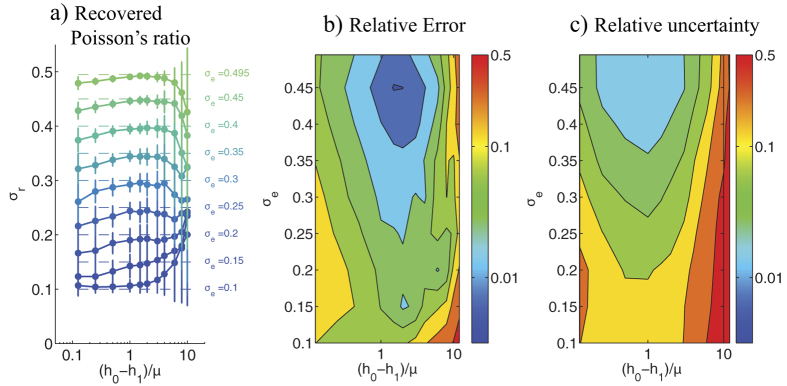
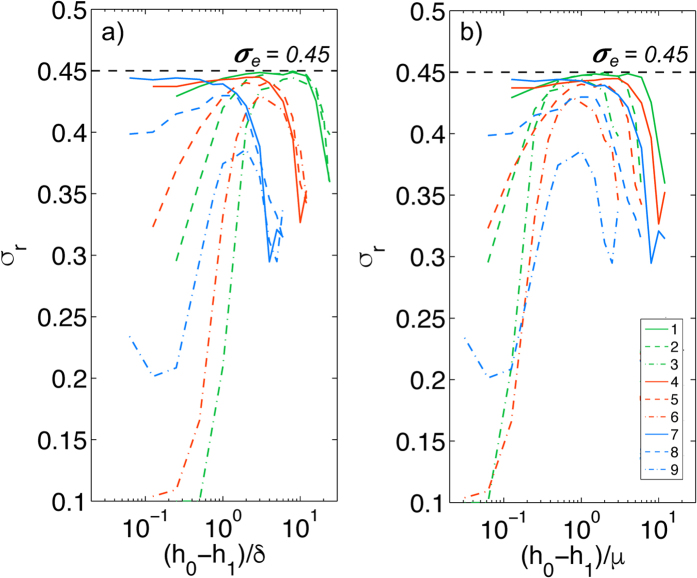
Figure 4. Accuracy and robustness of 2LETFM as a function of the ratio of the distance between the two measurement planes h0 − h1 and the length scale of the deformation field at the top plane μ.

Figure 4

Open in a new tab

(a) Recovered value σr of the Poisson’s ratio, plotted as a function of h0 − h1. The data are represented as mean ± standard deviation obtained from N = 100 random realizations. Each curve is obtained for a different value σe of the exact Poisson’s ratio that is being recovered by 2LETFM. This exact value is indicated with a dashed horizontal line in each case. (b) Contour plot of the relative error of σr as a function of h0 − h1 and σe. The relative error is defined as |σr − σe|/σe. (c) Contour plot of the relative uncertainty of σr as a function of h0 − h1 and σe. The relative uncertainty is defined as r.m.s. (σr)|/σe. The data were obtained for S2N = 1 and U0 = W0.

Consistent with the data shown in Fig. 3, the performance of the technique improved as σe approached 0.5, both in terms of the average σr (Fig. 4a) and its relative error and relative uncertainty (Fig. 4b,c). Furthermore, we found a non-monotonic dependence of these parameters with h0 − h1. The algorithm’s performance was optimal when the distance between the two measurement planes, h0 − h1 was comparable to the length scale of the deformation patterns at the substratum’s surface, μ (see eq. 7). These results can be explained considering that when the second plane is located at a distance from the surface much larger than μ, the deformation measured on that plane is negligible28. On the other hand, if h1 ≈ h0, the deformations measured on the two planes are almost the same. In both cases, the TFM problem is hardly overdetermined and the accuracy of the two-layer approach deteriorates. Despite this non-monotonic behavior, the relative error of the recovered σr remains below 10% in a wide range of values of h0 − h1.

In the simulations presented so far, the length scale of the ground-truth synthetic displacements was proportional to that of the noise. Specifically, the 1/e-width of the deformation patterns was equal to the root mean square of the ground truth synthetic deformation, μ (eq. 7) and the spectral width of the noise distribution was fixed as half that value, δ = μ/2 (eq. 8). To verify that the optimal inter measurement plane distance is proportional to the length scale of the deformation applied by the cell (μ) and not to the length scale of the noise, (δ), we performed simulations varying both δ and μ in addition to h1. Figure 5 shows the average σr as a function of h0 − h1 for σe = 0.45 for varying the values of μ and δ in the range 0.01h0–0.04h0. The figure shows that when h0 − h1 is is normalized with the length scale of the noise patterns (δ), σr is scattered (Fig. 5a). However, when h0 − h1 is normalized with the length scale of the ground-truth deformation patterns (μ), the different curves collapse reasonably well. Thus, we conclude that the optimal separation between the measurement planes is associated with the length scale of the cell-generated deformation and not to the measurement noise. Furthermore, the data suggests that σr is closest to σe for h0 − h1 ≈ μ.

Figure 5. Recovered value σr of the Poisson’s ratio, obtained for σe = 0.45 and for different values of μ and δ, and plotted as a function of inter measurement plane distance h0 − h1.

Figure 5

Open in a new tab

The legend indicates the different cases considered. Case 1: μ/h0 = 0.02, δ/h0 = 0.01. Case 2: μ/h0 = 0.02, δ/h0 = 0.02. Case 3: μ/h0 = 0.02, δ/h0 = 0.04. Case 4: μ/h0 = 0.04, δ/h0 = 0.01. Case 5: μ/h0 = 0.04, δ/h0 = 0.02. Case 6: μ/h0 = 0.04, δ/h0 = 0.04. Case 7: μ/h0 = 0.08, δ/h0 = 0.01. Case 8: μ/h0 = 0.08, δ/h0 = 0.02. Case 9: μ/h0 = 0.08, δ/h0 = 0.04. (a) The inter measurement plane distance h0 − h1 is normalized with the length scale of the background noise (δ). (b) The inter measurement plane distance h0 − h1 is normalized with the length scale of the deformation field at the top plane (μ). The data were obtained for S2N = 1 and U0 = W0.

Effect of normal/tangential traction force ratio

When cells apply traction stresses on the surface of their substratum, the normal component of the cell-generated deformation decays slower with the distance to the surface than the tangential ones24. Because 2LETFM relies on detecting differences in the transmission of deformation throughout the substratum, we hypothesized that this technique will be less accurate when cells exert predominantly normal traction stresses in substrata with σ ≈ 0.5. To test this hypothesis, we made the synthetic horizontal and vertical deformations using two different length scales, U0 and W0 (see eq. 7), and determined the dependence of the error of 2LETFM on the ratio W0/U0. The results of this analysis (Fig. 6a–c) confirm our hypothesis, and indicate that the error in the recovered Poisson’s ratio increases with the ratio W0/U0. The data also indicates that σ can be recovered with reasonable accuracy regardless of W0/U0 as long as σe > 0.4.

Figure 6. Accuracy and robustness of 2LETFM as a function of the ratio of normal to tangential deformation created by the cell on the substrate, W0/U0.

Figure 6

Open in a new tab

(a) Recovered value σr of the Poisson’s ratio, plotted as a function of W0/U0. The data are represented as mean ± standard deviation obtained from N = 100 random realizations. Each curve is obtained for a different value σe of the exact Poisson’s ratio that is being recovered by 2LETFM. This exact value is indicated with a dashed horizontal line in each case. (b) Contour plot of the relative error of σr as a function of W0/U0 and σe. The relative error is defined as |σr − σe|/σe. (c) Contour plot of the relative uncertainty of σr as a function of W0/U0 and σe. The relative uncertainty is defined as r.m.s. (σr)|/σe. The data were obtained for S2N = 1 and h0 − h1 = 0.15h0 = 2.5 μ.

Experimental demonstration of two-layer elastographic traction force microscopy

To demonstrate the experimental feasibility of 2LETFM, we applied this technique to simultaneously measure the traction stresses generated by migrating Physarum amoebae and the Poisson’s ratio of the polyacrylamide substrata where they adhere. For this purpose, we manufactured polyacrylamide gel substrata embedded with fluorescent beads of two different colors in two different layers located at the substratum surface and below it (see Fig. 1). The 3-D substratum deformations in these two layers were independently measured by tracking the displacements of the two sets of fluorescent beads as described in the Methods Section. Using these data, we implemented the two-layer algorithm presented above to estimate the Poisson’s ratio σ of the polyacrylamide gel and, once σ was known, determined the traction stresses generated by the cell.

Recovered Poisson’s ratio. Effect on deformations and traction stresses

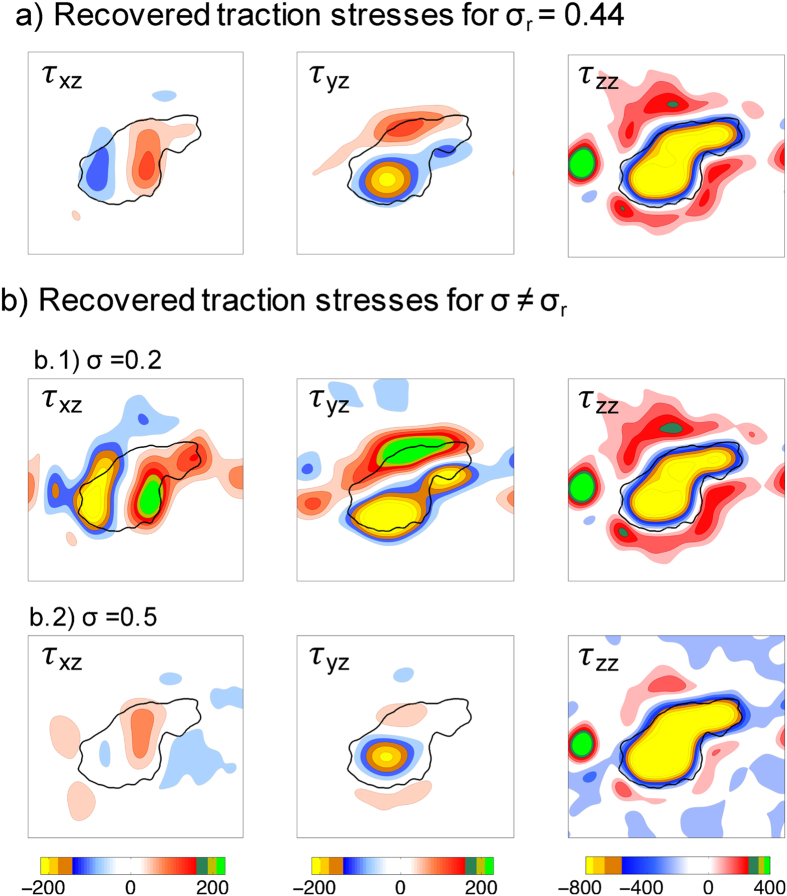
Figure 7 shows a representative example of a two-layer deformation measurement. Panel (a) shows the experimental measurements, including the bright field image used to segment the cell contour (a.1), and the deformations measured at z = h0 (u0, a.2) and z = h1 (u1, a.3). We applied the 2LETFM algorithm to these measurements and recovered a value of σr = 0.44, which agrees well with previous measurements of the Poisson’s ratio of polyacrylamide gels20,48,49. As expected, the deformation u2 calculated at z = h1 for σr (panel b) agreed with the measured one better than for other values of σ ≠ σr. For reference, panel (c) shows maps of u2 calculated for values of the Poisson’s ratio below (σ = 0.2, c.1) and above (σ = 0.5, c.2) the recovered value.

Figure 7. Experimental demonstration of 2LETFM.

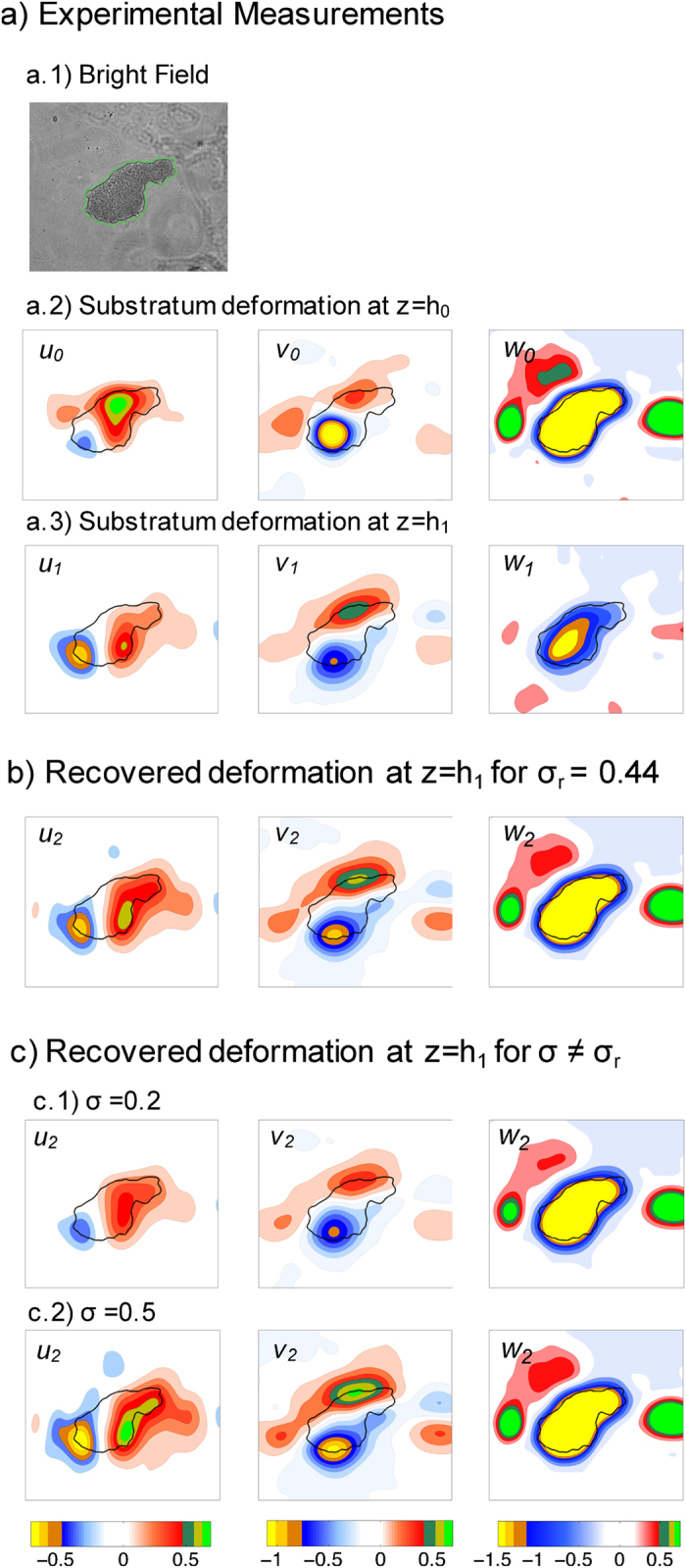
Figure 7

Open in a new tab

(a) Experimental measurements of the deformation applied by a motile Physarum amoebae, (a.1) bright field image of the amoeba with its detected contour plotted in green, (a.2) 3-D substratum deformation generated by the amoeba, u0, measured at the top surface of the substratum (z = h0 ≈ h = 170 μm), (a.3) 3-D substratum deformation generated by the amoeba, u1, measured at a second plane underneath the surface (z = h1 = 154 μm). (b) 3-D deformation u2 at z = h1 calculated from the measured u0 for the value of the Poisson’s ratio recovered by the two-layer approach, σr = 0.44. (c) 3-D deformation u2 at z = h1 calculated from the measured u0 for two values of the Poisson’s ratio below and above σr. (c.1) σ = 0.2. (c.2) σ = 0.5. All the deformations are given in microns according to the colorbars at the bottom of each column.

Apart from offering potentially useful information about the material properties of the substratum, an accurate determination of σ is important to quantify the magnitude and spatial distribution of the traction stresses exerted by a cell. To demonstrate this point, we compared the 3-D traction stresses determined from the substratum deformations generated by the same amoeba for the actual value of the Poisson’s ratio recovered by 2LETFM, σr, (Fig. 8a), and for two hypothetical values lower (σ = 0.2) and and higher (σ = 0.5) and than σr (Fig. 8b). It is important to note that since the cell is sandwiched between the substratum and an agar cap (see Materials and Methods), the computed traction stresses need not balance to zero. The results from these calculations indicate that carrying out the TFM analysis with erroneous values of the Poisson’s ratio leads to an underestimation (σ > σr) or an overestimation (σ < σr) of the traction stresses for the same values of measured deformations. Moreover, using inaccurate values of the Poisson’s ratio can also significantly alter the spatial patterns of the traction stress.

Figure 8. Effect of Poisson’s ratio on the 3-D traction stresses recovered from measured substratum deformation.

Figure 8

Open in a new tab

The data comes from the same Physarum amoebae shown in Fig. 7. (a) 3-D traction stress vector (τxz, τyz, τzz) obtained using the value of the Poisson’s ratio recovered by the two-layer approach, σr = 0.44. (b) 3-D traction stress vector obtained for σ ≠ σr. The two Poisson’s ratios considered are σ = 0.2 (b.1) and σ = 0.5 (b.2). All the stresses are given in Pascals according to the colorbars at the bottom of each column.

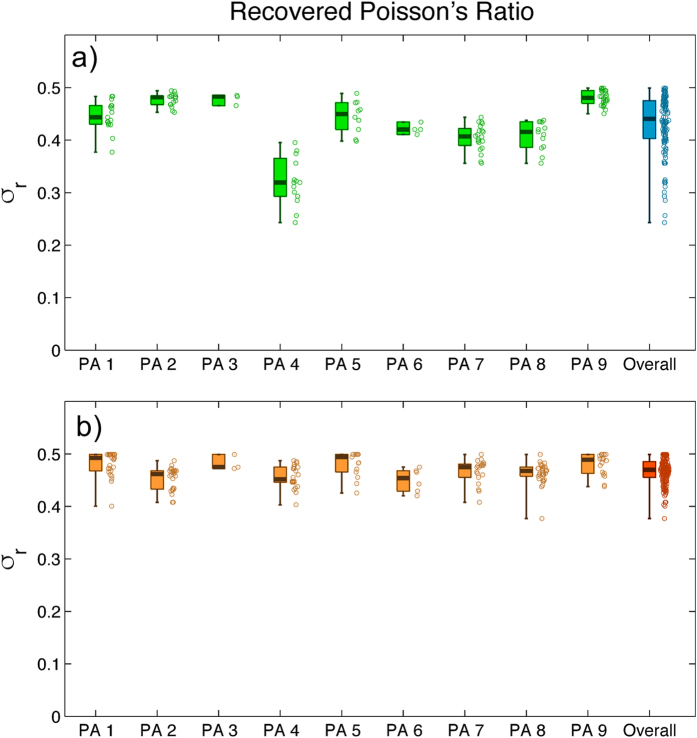
Poisson’s ratio of polyacrylamide gels determined by two-layer elastographic TFM

We applied 2LETFM to Physarum amoebae migrating over 9 different polyacrylamide gels that were manufactured using the same protocol. For each substratum, we obtained several repeated measurements of σ for a period long enough for the amoebae to move out of the field of view. Figure 9 shows the results of these experiments for both cost functions considered in the optimization algorithm (see eq. 5). When using the cost function J1 based on the difference between measured and calculated displacements fields, the mean ± standard deviation of the recovered Poisson’s ratio were 0.43 ± 0.05, whereas the median, first and third quartiles were respectively 0.44, 0.40 and 0.47. On the other hand, when using the cost function J2 based on cross-correlation, the mean ± standard deviation of the recovered Poisson’s ratio were 0.47 ± 0.03, whereas the median, first and third quartiles were respectively 0.47, 0.45 and 0.49. Combining the results obtained from the two different cost functions, we obtain that σ = 0.45 ± 0.06. The two sets of results agree with each other reasonably well, and are also in good agreement with previous direct measurements of σ20,48,49.

Figure 9. Statistics of Poisson’s ratio values determined in nine different experiments using polyacrylamide (PA) substrata.

Figure 9

Open in a new tab

The data are presented in the form of boxplots showing the median, the lower and upper quartiles, and the minimum and maximum values of the distribution. The distribution of values for each case is represented scattered to the right of each boxplot. Each data point corresponds to an instantaneous 2LETFM measurement as the cell migrates over the substratum. Each individual substratum is represented by a boxplot, whereas all the data are pooled in the last panel at the right of the graph. The Poisson’s ratios were obtained using the cost functions J1 and J2 (eq. 5) in panels (a) and (b) respectively.

Discussion

Linearly elastic polymer-based hydrogels such as polyacrylamide are broadly used as substrata to calculate the traction stresses exerted by cells. A priori knowledge of the mechanical properties of these substrata is crucial for a precise calculation of the traction stresses. In linearly elastic materials the stresses are related to the deformations by two parameters, the Young’s modulus of elasticity (E) and the Poisson’s ratio (σ). Since the traction stresses are directly proportional to E, significant efforts have been devoted to characterize this parameter in the context of traction force microscopy. There are well-established techniques to accurately measure E such as indentation, atomic force microscopy and manipulation of spherical beads50,51. On the other hand, less effort has been devoted to characterizing σ due to the assumption that this parameter barely influences the traction stresses. However, we recently showed that the calculation of the traction stresses exerted by cells can be highly dependent on σ, particularly for the nearly incompressible gels with σ ≈ 0.5 that are used in traction force microscopy24. Of note, whereas errors in E only affect the magnitude of the traction stresses, errors in σ also distort their spatial patterns (see Fig. 8). The latter may lead to qualitative misinterpretations of a traction force microscopy experiment.

This work introduces a novel two-layer elastographic 3D traction force microscopy (2LETFM) method to measure the Poisson’s ratio of an elastic substratum, while simultaneously calculating at each time point the traction stresses. The method is based on 3D measurements of substratum deformation performed on two different planes beneath the surface. The deformation measured at the first plane is used to calculate the deformation at the second plane, which is also measured. Then, it employs an optimization algorithm that recovers σ by iteratively minimizing a least-square cost function that penalizes differences between the calculated and measured deformations at the second plane.

We have simulated this new 2LETFM method in silico using synthetic 3D fields that mimic the deformation caused by large motile amoebae36, including random noise of different levels. By means of these simulations, we have studied the effect of several algorithmic and experimental parameters on the accuracy and robustness of 2LETFM. The results suggest that 2LETFM can accurately determine the substratum Poisson’s ratio even for noisy experimental data with signal-to-noise ratios lower than one. These simulations show that the error in the recovered Poisson’s ratio is in fact much lower than that of the recovered traction stresses, consistent with the recovery of σ being highly overdetermined. The method performs particularly well for σ ≥ 0.4, which coincides with the range of reported values of the Poisson’s ratio of hydrogels used in traction force microscopy. We found these results to be relatively independent of the cost function used in the optimization algorithm. Our in silico analysis with zero-mean random noise shows that a cost function based on the difference between deformations slightly over-performs a cost function based on cross-correlation. However, additional simulations (not shown) suggest that cross-correlation may be better suited to compare deformations that contain systematic errors.

We have also found that, while the position of the second measurement plane only has a modest influence on the efficacy of 2LETFM, there is an optimal inter measurement plane distance that minimizes the error of the technique. Our simulations suggest that this optimal distance is similar to the size of the spatial patterns of the deformation measured the top plane (the 1/e witdh μ, see Fig. 2). According to del Álamo et al.28, that is the characteristic distance of propagation of the cell-generated deformations into the substratum. Thus, if the second plane is located below the optimal position, the deformation measured at that plane would be very small. On the other hand, if the second plane is located above the optimal distance, the difference between the deformations measured at the two planes becomes hard to distinguish from the background noise. Consistently, the error in the recovered Poisson’s ratio increases when the cell-generated normal traction stresses are larger in magnitude than the tangential ones, because the substratum deformation changes little between the measurement planes in that case. We argued that this behavior is due to the fact that cell-generated stresses propagate deeper into the substratum when they are applied in the direction normal to the substratum surface24,52. Overall, our simulations allowed us to determine the experimental parameter values that minimize the error of the recovered σ, and also showed that 2LETFM can accurately and robustly recover σ for a wide range of experimental parameter values.

To provide proof of principle of 2LETFM, we carried out experiments with motile Physarum amoebae crawling on top of polyacrylamide gels, and jointly recovered the 3-D cell generated traction stresses and the gel Poisson’s ratio. Overall, these experiments resulted in σ = 0.45 ± 0.06, which agrees well with previously reported values of σ obtained by direct measuring methods15. For polyacrylamide gels with similar composition as in our experiments, Takigawa reported that σ = 0.46 by measuring the stretch ratio between the elongation of the gel in the directions perpendicular and parallel to the mechanically stretched one48. Also, Bodou et al. determined a value of 0.49 by measuring the deformation exerted through micropipette aspiration experiments49. More recently, Chippada measured the displacements of non-spherical magnetic inclusions moved by a magnetic manipulator to obtain a value close to 0.520.

In all these methods, an external force is applied to the substratum by a relatively invasive apparatus prior to recovering the Poisson’s ratio. It is important to note that in 2LETFM, the external force is generated in the least possible disruptive manner (i.e. by the cell itself), and at the site of interest. This poses an advantage with respect to existing methods since the internal microstructure of polyacrylamide gels is not perfectly uniform53,54. The differences in the internal composition increase with the ratio of cross-linking to monomer53, and this inhomogeneous gel microstructure has an effect on its mechanical properties. Additionally, it has been suggested that the percentage of acrylamide and bisacrylamide and the amount of ammonium per sulfate influence the value of the Poisson’s ratio20,21.

Two-layer ETFM works by applying a mechanical equilibrium constraint on a set of over-determined substratum deformation measurements. This same principle, either using the same or a different mathematical formulation, could be exploited in a wide range of different scenarios. For example, one could adapt the current formulation to determine the 3D traction stresses generated by a cell from 2D-only measurements of the deformation in two planes. Fibrous extracellular matrices (ECMs) formed by collagen or fibrin are more physiologically relevant environments than polymer hydrogels55. However, the material properties of these matrices are non-linear and may also be anisotropic depending on the orientation of the fibers56,57. Extending 2LETFM to these ECMs would require reformulating the mechanical equation of equilibrium (1) to take into account large strain and anisotropy. Another potential extension of 2LETFM could be the study of the interaction between tumor cells and the ECM. Oncogenic processes commonly trigger ECM remodeling by the secretion of metalloproteinases and other ECM digestive enzymes58,59. Our method could be extended to characterize the spatial and temporal changes in the ECM in migrating cancer cells and could aid in the understanding of the involvement of the ECM in tumor development60,61.

Additional Information

How to cite this article: Álvarez-González, B. et al. Two-Layer Elastographic 3-D Traction Force Microscopy. Sci. Rep. 7, 39315; doi: 10.1038/srep39315 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep39315-s1.pdf (1MB, pdf)

Acknowledgments

This work was supported by grants NSF CBET – 1055697 and NIH R01 GM084227. The authors would like to thank Joshua François’ valuable comments on the manuscript.

Footnotes

Author Contributions B.A.-G., R.M., R.A.F., J.C.L. and J.C.A. planned the research. S.Z., M.G.-G. and R.M. contributed experimental techniques and helped build the experimental setup. B.A.-G. and J.C.A. performed the research. B.A.-G., J.C.L. and J.C.A. wrote the manuscript.

References

  1. Pelham R. J. & Wang Y. l. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA 94, 13661–13665 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Chowdhury F. et al. Material properties of the cell dictate stress-induced spreading and differentiation in embryonic stem cells. Nat Mater 9, 82–88 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ulrich T. A., de Juan Pardo E. M. & Kumar S. The mechanical rigidity of the extracellular matrix regulates the structure, motility, and proliferation of glioma cells. Cancer Res. 69, 4167–4174 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Vogel V. & Sheetz M. Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 7, 265–275 (2006). [DOI] [PubMed] [Google Scholar]
  5. Li B., Moshfegh C., Lin Z., Albuschies J. & Vogel V. Mesenchymal stem cells exploit extracellular matrix as mechanotransducer. Sci Rep 3, 2425 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Holle A. W. & Engler A. J. More than a feeling: discovering, understanding, and influencing mechanosensing pathways. Curr. Opin. Biotechnol. 22, 648–654 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ananthakrishnan R. & Ehrlicher A. The Forces Behind Cell Movement. International Journal of Biological Sciences 3, 303–317 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Álvarez-González B. et al. Three-Dimensional Balance of Cortical Tension and Axial Contractility Enables Fast Amoeboid Migration. Biophysical Journal 108, 821–832 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dembo M. & Wang Y.-L. Stresses at the Cell-to-Substrate Interface during Locomotion of Fibroblasts. Biophysical Journal 76, 2307–2316 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Butler J. P., Tolić-Nørrelykke I. M., Fabry B. & Fredberg J. J. Traction fields, moments, and strain energy that cells exert on their surroundings. American Journal of Cell Physiology 282, 595–605 (2002). [DOI] [PubMed] [Google Scholar]
  11. Maskarinec S. A., Franck C., Tirrell D. A. & Ravichandran G. Quantifying cellular traction forces in three dimensions. Proc. Natl. Acad. Sci. USA 106, 22108–22113 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Delanoë-Ayari H., Rieu J. & Sano M. 4D traction force microscopy reveals asymmetric cortical forces in migrating Dictyostelium cells. Physical Review Letters 105, 248103 (2010). [DOI] [PubMed] [Google Scholar]
  13. Alvarez-Gonzalez B. et al. Cytoskeletal Mechanics Regulating Amoeboid Cell Locomotion. Appl Mech Rev 66 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Style R. W. et al. Traction force microscopy in physics and biology. Soft Matter 10, 4047–4055 doi: 10.1039/C4SM00264D (2014). [DOI] [PubMed] [Google Scholar]
  15. Polio S. R., Rothenberg K. E., Stamenovic D. & Smith M. L. A micropatterning and image processing approach to simplify measurement of cellular traction forces. Acta Biomater 8, 82–88 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Levental I. et al. A simple indentation device for measuring micrometer-scale tissue stiffness. J Phys Condens Matter 22, 194120 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Frey M. T., Engler A., Discher D. E., Lee J. & Wang Y. L. Microscopic methods for measuring the elasticity of gel substrates for cell culture: microspheres, microindenters, and atomic force microscopy. Methods Cell Biol. 83, 47–65 (2007). [DOI] [PubMed] [Google Scholar]
  18. Legant W. R. et al. Measements of mechanical tractions exerted by cells in three-dimensional matrices.. Nature Methods 7, 969–971 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Landau L. D. & Lifshitz E. M. Theory of Elasticity, vol. 7 (Elsevier Ltd., 1986). [Google Scholar]
  20. Chippada U., Yurke B. & Langrana N. A. Simultaneous determination of Young’s modulus, shear modulus, and Poisson’s ratio of soft hydrogels. Journal of Materials Research 25, 545–555 (2011). [Google Scholar]
  21. Li Y., Hu Z. & Li C. New Method for Measuring Poisson’s Ratio in Polymer Gels. Applied Polymer Science 50, 1107–1111 (1993). [Google Scholar]
  22. Geissler E., Hecht A.-M., Horkay F. & Zrinyi M. Compressional Modulus of Swollen Polyacrylamide Networks. Macromolecules 21, 2594–2599 (1988). [Google Scholar]
  23. Wang N. et al. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. American Journal of Physiology - Cell Physiology 282, C606–C616 (2002). [DOI] [PubMed] [Google Scholar]
  24. del Alamo J. C. et al. Three-Dimensional Quantification of Cellular Traction Forces and Mechanosensing of Thin Substrata by Fourier Traction Force Microscopy. PLOS ONE 8, e69850 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hur S. S. et al. Roles of cell confluency and fluid shear in 3-dimensional intracellular forces in endothelial cells. Proceedings of the National Academy of Sciences 109, 11110–11115 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Tambe D. T. et al. Monolayer stress microscopy: limitations, artifacts, and accuracy of recovered intercellular stresses. PloS one 8, e55172 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Sen S., Engler A. J. & Discher D. E. Matrix strains induced by cells: computing how far cells can feel. Cellular and molecular bioengineering 2, 39–48 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. del Alamo J. C. et al. Spatiotemporal analysis of eukaryotic cell motility by improved force cytometry. Proceedings of the National Academy of Sciences 104, 13343–13348 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schwarz U. S. et al. Calculation of forces at focal adhesions from elastic substrate data: the effect of localized force and the need for regularization. Biophysical Journal 83, 1380–1394 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Del Alamo J. C. & Jiménez J. Estimation of turbulent convection velocities and corrections to Taylor’s approximation. Journal of Fluid Mechanics 640, 5–26 (2009). [Google Scholar]
  31. Mijailovich S. M. et al. Resolution and uniqueness of estimated parameters of a model of thin filament regulation in solution. Computational biology and chemistry 34, 19–33 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Bermejo J. et al. Diastolic chamber properties of the left ventricle assessed by global fitting of pressure-volume data: improving the gold standard of diastolic function. Journal of Applied Physiology 115, 556–568 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Daniel J. W. & Rusch H. P. The pure culture of Physarum polycephalum on a partially defined soluble medium. J. Gen. Microbiol. 25, 47–59 (1961). [DOI] [PubMed] [Google Scholar]
  34. Wohlfarth-Bottermann K. E. Plasmalemma Invaginations as Characteristic Constituents of Plasmodia of Physarum Polycephalum. Journal of Cell Science 16, 23–37 (1974). [DOI] [PubMed] [Google Scholar]
  35. Ueda M. & Ogihara S. Microtubules are required in amoeba chemotaxis for preferential stabilization of appropriate pseudopods. J. Cell. Sci. 107 (Pt 8), 2071–2079 (1994). [DOI] [PubMed] [Google Scholar]
  36. Lewis O. L., Zhang S., Guy R. D. & del Alamo J. C. Coordination of contractility, adhesion and flow in migrating Physarum amoebae. J R Soc Interface 12 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tse J. R. & Engler A. J. Preparation of hydrogel substrates with tunable mechanical properties. Curr Protoc Cell Biol Chapter 10, Unit 10.16 (2010). [DOI] [PubMed] [Google Scholar]
  38. Wang Y. L. & Pelham R. J. Preparation of a Flexible, Porous Polyacrylamide Substrate for Mechanical Studies of Cultured Cells. Methods in Enzymology 298, 489–496 (1998). [DOI] [PubMed] [Google Scholar]
  39. Engler A. et al. Substrate Compliance versus Ligand Density in Cell on Gel Responses. Biophysical Journal 86, 617–628 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stuurman N., Amdodaj N. & Vale R. Micro-Manager: Open Source Software for Light Microscope Imaging. Microscopy Today 15, 42–43 (2007). [Google Scholar]
  41. Edelstein A., Amodaj N., Hoover K., Vale R. & Stuurman N. Computer Control of Microscopes Using Micro-Manager. Current Protocols in Molecular Biology 14.20.1–14.20.17 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Meili R. et al. Myosin-II is essential for the spatiotemporal organization of traction forces during cell motility. Molecular Biology of the Cell 21, 405–417 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Bastounis et al. Role of the scar/wave complex in regulating traction forces during amoeboid motility. Molecular Biology of the Cell 22, 3995–4003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Alonso-Latorre B., del Alamo J. C., Meili R., Firtel R. A. & Lasheras J. C. An Oscillatory Contractile Pole-Force Component Dominates the Traction Forces Exerted by Migrating Amoeboid Cells. Cellular and molecular bioengineering 4(4), 603–615 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Bastounis E. et al. Both contractile axial and lateral traction force dynamics drive amoeboid cell motility. Journal of Cell Biology 204(6), 1045–1061 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Bastounis E. et al. Cooperative cell motility during tandem locomotion of amoeboid cells. Molecular Biology of the Cell 27(8), 1262–1271 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Willert C. E. & Gharib M. Digital Particle Image Velocimetry. Experiments in Fluids 10, 181–193 (1991). [Google Scholar]
  48. Takigawa T., Morino Y., Urayama K. & Masudab T. Poisson’s Ratio of Polyacrylamide (PAAm) Gels. Polymer Gels and Networks 4, 1–5 (1996). [Google Scholar]
  49. Boudou T. et al. An extended modeling of the micropipette aspiration experiment for the characterization of the Young’s modulus and Poisson’s ratio of adherent thin biological samples: numerical and experimental studies. J Biomech 39, 1677–1685 (2006). [DOI] [PubMed] [Google Scholar]
  50. Dimitriadis E. K., Horkay F., Maresca J., Kachar B. & Chadwick R. S. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 82, 2798–2810 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Long R., Hall M. S., Wu M. & Hui C. Y. Effects of gel thickness on microscopic indentation measurements of gel modulus. Biophys. J. 101, 643–650 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Aung A. et al. 3D traction stresses activate protease-dependent invasion of cancer cells. Biophysical journal 107, 2528–2537 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Cohen Y., Ramon O., I. J. K. & Mizrahi S. Characterization of inhomogeneous polyacrylamide hydrogels. Journal of Polymer Science Part B: Polymer Physics 30, 1055–1067 (1992). [Google Scholar]
  54. Baselga J., Hernandez-Fuentes I., Pierola I. F. & Llorente M. A. Elastic properties of highly crosslinked polyacrylamide gels. Macromolecules 20, 3060–3065 (1987). [Google Scholar]
  55. Lai V. K. et al. Microstructural and mechanical differences between digested collagen-fibrin co-gels and pure collagen and fibrin gels. Acta Biomater 8, 4031–4042 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Holzapfel G. A. & Ogden R. W. Constitutive modelling of arteries. Proceedings of the Royal Society A 466, 1551–1597 (2010). [Google Scholar]
  57. Xu B., Chow M. J. & Zhang Y. Experimental and modeling study of collagen scaffolds with the effects of crosslinking and fiber alignment. Int J Biomater 2011, 172389 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Jinka R., Kapoor R., Sistla P. G., Raj T. A. & Pande G. Alterations in Cell-Extracellular Matrix Interactions during Progression of Cancers. Int J Cell Biol 2012, 219196 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Lu P., Weaver V. M. & Werb Z. The extracellular matrix: a dynamic niche in cancer progression. J. Cell Biol. 196, 395–406 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Lochter A. & Bissell M. J. Involvement of extracellular matrix constituents in breast cancer. Semin. Cancer Biol. 6, 165–173 (1995). [DOI] [PubMed] [Google Scholar]
  61. Gilkes D. M., Semenza G. L. & Wirtz D. Hypoxia and the extracellular matrix: drivers of tumour metastasis. Nat. Rev. Cancer 14, 430–439 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep39315-s1.pdf (1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES