The timing of eukaryotic evolution: Does a relaxed molecular clock reconcile proteins and fossils?

Abstract

The use of nucleotide and amino acid sequences allows improved understanding of the timing of evolutionary events of life on earth. Molecular estimates of divergence times are, however, controversial and are generally much more ancient than suggested by the fossil record. The limited number of genes and species explored and pervasive variations in evolutionary rates are the most likely sources of such discrepancies. Here we compared concatenated amino acid sequences of 129 proteins from 36 eukaryotes to determine the divergence times of several major clades, including animals, fungi, plants, and various protists. Due to significant variations in their evolutionary rates, and to handle the uncertainty of the fossil record, we used a Bayesian relaxed molecular clock simultaneously calibrated by six paleontological constraints. We show that, according to 95% credibility intervals, the eukaryotic kingdoms diversified 950–1,259 million years ago (Mya), animals diverged from choanoflagellates 761–957 Mya, and the debated age of the split between protostomes and deuterostomes occurred 642–761 Mya. The divergence times appeared to be robust with respect to prior assumptions and paleontological calibrations. Interestingly, these relaxed clock time estimates are much more recent than those obtained under the assumption of a global molecular clock, yet bilaterian diversification appears to be ≈100 million years more ancient than the Cambrian boundary.

Reconstructing and dating the early evolutionary history of eukaryotes have proven challenging questions due to the scarcity of the fossil record, especially for protists (1). In the Archean eon, biomarker compounds characteristic of possibly extinct stem eukaryotes are found ≈2,700 million years ago (Mya) (2). Morphological clues for eukaryotes seem to occur in the Paleoproterozoic, but convincing microfossil evidence appears ≈1,500 Mya in Lower Mesoproterozoic successions (3). Fossils that can be interpreted as crown eukaryotes are found in Upper Mesoproterozoic/Lower Neoproterozoic rocks, ≈1,200 Mya for red algae (4) and 1,000 Mya for stramenopiles (5). Chlorophytes and testate amoebae are found in Middle to Late Neoproterozoic formations at ≈750 Mya (5, 6). Special attention has been attracted to the origin of the animal phyla. Bilaterian metazoans first appeared at the end of the Late Proterozoic (≈600 Mya at the Doushantuo Formation) (7) and were already quite diversified ≈530 Mya (8), suggesting a rapid diversification known as the Cambrian explosion.

The advent of molecular data started a new era by providing an independent approach to address the history of life on Earth and thus creating a closer connection among geology, paleontology, and biology (9). The constancy of molecular evolutionary rate over time, i.e., the molecular clock hypothesis, was suggested early on (10). Calibration of this clock based on taxa with a rich fossil record allowed the inference of divergence times for other living organisms (11). Yet DNA and protein age estimates of land plants, fungi, and animal phyla possibly appeared several hundred million years (Myr) older than indicated by paleontology (12).

A major concern in molecular dating is that independent studies based on multiple genes yielded highly variable estimates. For example, the protostome/deuterostome divergence time ranges from 573 to 1,200 Mya, albeit either close to or drastically more ancient than the Cambrian explosion (13–23). The observed discrepancy between clocks and rocks might be due to an extended period of Precambrian metazoan diversification without any trace in the fossil record (24) but also to biases in molecular dating methods. Among the limitations of the latter approaches, the nonclocklike behavior of genes and proteins (25), the limited power of the relative rate tests used to detect lineage-specific rate variation (26), and the existence of a systematic bias toward overestimation of evolutionary time scales (27) are the most confounding. For example, incorrectly assuming a clocklike property of the sequence data involves higher (22, 28, 29) or lower (30) divergence times. Consequently, dating methods have been developed to relax molecular clock assumptions by allowing rate variations along branches of a phylogenetic tree (28, 31–33).

To estimate the timing of eukaryotic evolution while reducing the impact of stochastic error due to the finite length of the sequences, we used a large data set of 129 combined nuclear proteins for 36 animals, fungi, plants, and protists. Despite the expectation that potential lineage-specific evolutionary rate variations from one protein to another might be counterbalanced in large-scale analysis (34), extensive among-species variations in the rate of amino acid replacements were identified. We thus took advantage of a relaxed molecular clock approach developed in a Bayesian framework, which approximates divergence times by a Markov chain Monte Carlo (MCMC) numerical method (32, 33). Such a relaxed clock method has three major advantages: (i) the biologically unverified hypothesis of a constant evolutionary rate over the history of eukaryotes is unnecessary, (ii) the incorporation of prior constraints on divergence times is preferred over the use of fixed time points to handle the inherent uncertainties of paleontological data (fossils never match exactly on nodes of phylogenetic trees), and (iii) several independent calibrations can be used simultaneously. Because divergence times based on this relaxed protein clock were much more recent than those based on a global (constant) clock, computer simulations were used to explore the reliability of the Bayesian dating method.

Materials and Methods

The assembly of the data set of 129 proteins from 36 eukaryotes and its partitioned maximum likelihood analysis are provided elsewhere (35). Due to ambiguous alignment, two-thirds of the sites were conservatively removed to ensure the sitewise homology of the remaining 30,399 positions at this deep evolutionary time scale. Alignments are available from H.P. upon request. We verified orthology through the analysis of each gene with standard phylogenetic methods, and we discarded several proteins, including some that were frequently used for studying eukaryotic evolution (tubulins, actin, and HSP70). Our reasonable taxon coverage in this large multiprotein framework involves that some genes are lacking for some taxa, leading to ≈25% of missing character states. The best topology (Fig. 1) was rooted by Dictyostelium, as suggested by a derived gene fusion separating opisthokonts (animals, choanoflagellates, and fungi) from bikonts (eukaryotes ancestrally with two cilia) (36, 37). However, because of the potential homoplasy of gene fusion and fission characters (38), a more classical rooting along the kinetoplastid branch was also considered.

Fig. 1.

Divergence time estimates (Mya) among eukaryotes, based on a Bayesian relaxed molecular clock applied to 30,399 amino acid positions. The topology is the highest-likelihood one, with branch lengths proportional to the absolute ages of the subtending nodes. Dictyostelium rooted the tree but was pruned from dating analyses. White rectangles delimit 95% credibility intervals on node ages. Stars indicate the six nodes under prior paleontological calibration (lower bound only for the white star; lower and upper bounds for black stars). Gray areas encompass the bounds between which calibration nodes stand a posteriori during the Bayesian search. Primary and secondary plastid endosymbioses are indicated, respectively, by the circled 1 and 2. Double horizontal arrows and dotted lines indicate the displacement of 95% credibility intervals for eight selected nodes after rerooting the tree along the kinetoplastid branch. Paleozoic, Mesozoic, and Cenozoic are indicated by I, II, and III, respectively. Transitions between Meso-/Neo-Proterozoic and Cambrian are indicated by vertical dashed lines.

Relaxed Molecular Clock Analyses. Divergence times were estimated under a Bayesian relaxed molecular clock (33), constrained by six independent fossil references. To explicitly incorporate the inherent uncertainty of paleontological estimates, each primary calibration was defined as a prior time constraint, with lower and/or upper bounds. In a conservative approach, we used the stratigraphic range of the geological period to which key fossils for the node under focus were attributed: (i) the Eudicot/Liliopsida split during Jurassic (144–206 Mya), just before the first record of angiosperm pollen grains in the Neocomian (see ref. 39); (ii) the Bryophyta/Tracheophyta split during Ordovician (443–490 Mya), as attested to by the oldest land plant spores (40); (iii) the origin of ascomycotans before Devonian (417 Mya; ref. 41); (iv) the Actinopterygii/Mammalia split during Devonian (354–417 Mya), because actinopterygian and sarcopterygian remains are dated from this period (42); (v) the split between Diptera and Lepidoptera + Hymenoptera during the Devonian–Carboniferous (290–417 Mya; ref. 42); and (vi) the Chelicerata/Insecta split during Cambrian (490–543 Mya), as suggested by the oldest remains of these groups (42). Relaxing the molecular clock assumption involved two steps. First, the program estbranches (Version 5b; ftp://statgen.ncsu.edu/pub/thorne; ref. 33) estimated the branch lengths and their variance–covariance matrix from the concatenated 30,399 sites, under the Jones–Taylor–Thornton model. Second, the program divtime (Version 5b) estimated the posterior ages of all nodes within the ingroup. Prior gamma distributions on three parameters of the relaxed clock model were assumed and specified through the mean and SD of the root age, root rate, and rate autocorrelation; 1,000 Mya (SD = 500 Mya) for the expected time between tips and root without node time constraints, 0.036 (SD = 0.018) amino acid replacements per 100 sites per Myr at the ingroup root node, 0.001 (SD = 0.001) for the parameter (ν) that controls the degree of rate autocorrelation per Myr along the descending branches of the tree. The highest possible time between tips and root was 4,500 Mya. The MCMC were started from random values. After conservatively discarding 100,000 generations as the burn-in, they were run for 10 million generations. A sample was taken each 100 generations. Posterior divergence times were identical for different MCMC started independently, evidencing convergence of the Bayesian dating procedure. The uncertainty of divergence time estimates was characterized by 95% credibility intervals, calculated after sorting the 100,000 MCMC samples, and then reporting the 2,501st and 97,500th values.

Simulation Studies. Simulation studies were conducted to evaluate (i) the ability of the global and relaxed clock approaches to accurately estimate divergence times when rates do correlate or not along tree branches, and (ii) the impact of missing data. We generated 10 matrices of 36 taxa and 30,399 amino acid positions (i.e., 1,094,364 character states) under pseq-gen (43) by using empirical amino acid frequencies, and a gamma distribution parameter (α = 0.70) for rate heterogeneity among sites. Each branch length was set equal to the product of its rate (i.e., the average of the rates at the nodes that begin and end it) by its time duration (i.e., the age difference between its beginning and ending nodes) as measured by divtime. For each of these 10 simulated data sets, we applied the six calibration constraints and computed the Bayesian divergence times as described above. Then, we removed each character corresponding to the missing data of the original data set (281,517 amino acids, i.e., ≈25% of the data) and again calculated the divergence times. Age estimates computed with and without missing data were then compared for each node.

Moreover, a second set of 10 complete matrices was generated under a global clock model. The same topology, amino acid frequencies, gamma parameter, and distribution of node times were used, but a single (constant) rate of 0.025 amino acid replacement per 100 sites per Myr was enforced for branch length entries. Autocorrelated-rate and constant-rate matrices were analyzed under estbranches. Then, MCMC runs were conducted under divtime to estimate divergence times, assuming either rate autocorrelation along branches (mean and SD for ν ≠ 0) or a perfect clock (mean and SD for ν = 0).

Results

A Molecular Time Scale for the Main Eukaryote Clades. The phylogeny resulting from the maximum likelihood analysis of the 30,399 unambiguously aligned amino acid positions (Fig. 1) is in agreement with current opinion about eukaryotic relationships (44). The log-likelihoods (lnL) of the phylogenetic tree were lnL_{unconstrained} = -779,284 without a molecular clock constraint and lnL_clock = -783,020 under the global clock and a rooting by Dictyostelium. A likelihood ratio test significantly rejected the hypothesis of a clocklike behavior of our data (P < 0.0001). Thus, the rate of amino acid replacements extensively changed among the eukaryote lineages here analyzed. For example, trypanosomes and nematodes evolved two and three times faster than mammals, respectively (data not shown).

The relaxed molecular clock based on the 129 proteins was calibrated by six time constraints spread over the phylogenetic tree and defined within green plants, animals, and fungi. Credibility intervals at 95% indicated that the basal split between the major eukaryotic kingdoms documented here occurred 950–1,259 Mya (mean 1,085), followed by their diversification in <200 Myr (Fig. 1). Plantae originated 892–1,162 Mya (mean 1,010), and red algae branched off 825–1,061 Mya (mean 928), whereas stem land plants separated from green algae 662–812 Mya (mean 729). This suggests that the endosymbiosis of a free-living cyanobacterium that led to primary plastids (surrounded by two membranes) occurred between 825 and 1,162 Mya (Fig. 1). Plastids surrounded by four membranes originated from secondary endosymbiosis, in which a red alga was engulfed and retained by a flagellate protist. This event probably happened along the branch leading to stramenopiles + alveolates, i.e., between 767 and 1,072 Mya, shortly after the primary endosymbiosis (Fig. 1).

Among opisthokonts, most of the inferred divergence times were more recent than previous molecular multigene estimates. The divergence between animals and fungi was, for example, estimated 872–1,127 Mya (mean 983 Mya), whereas others provide estimates up to 1,600 Mya (45). The divergence between choanoflagellates and animals was estimated during the Late Proterozoic, between 761 and 957 Mya (mean 849). The major transition during animal evolution from unicellular to multicellular state might have thus occurred at least 200 Myr before the Cambrian explosion. Interestingly, the divergence time between protostomes and deuterostomes (Fig. 1) was 642–761 Mya (mean 695). This value is much lower than most of the previously published ones (12, 17, 46) but is close to recent estimates (22, 23), reducing to ≈40 Myr the minimum gap between the protein relaxed clock timing and the first indisputable bilaterian fossil (7). Within fungi, the divergence between ascomycetes and basidiomycetes is estimated ≈629–837 Mya (mean 727), whereas a recent study using a global clock method on a similar number of proteins, but a lower number of taxa and calibration points, yielded 1,200 Mya (45).

Global vs. Relaxed Clock Estimates. Our molecular time scale for the major eukaryotic clades is on average 1.5 times more recent than the one based on a global clock (12). To evaluate the accuracy and precision of dates estimated under linear versus autocorrelated rates extrapolations beyond calibrations, we conducted simulations. Table 1 recapitulates the age estimates of two selected nodes, bilaterians and our tree root, calculated under either global or relaxed clock assumptions onto data simulated with or without a constant rate of evolution. Relaxed clock timings were accurate, although slightly deeper when estimated on constant-rate data. They were also less precise, as attested by 95% credibility interval widths relative to global clock estimates, because of the greater number of parameters involved (22). However, constant-rate extrapolations conducted with all other conditions being identical yield less accurate, i.e., 1.2–1.4 deeper divergence times when actual rates do vary. The simulations therefore indicate that the autocorrelation model of substitution-rate evolution does not underestimate ages on clocklike data, whereas a linear extrapolation on rate-variable data markedly overestimates divergence times (Table 1).

Table 1. Relaxed and global clock average age estimates (in Mya) for bilaterians and the tree root.

		Simulations
	Clock	Variable rates	Constant rate
Bilateria	Relaxed	692 ± 6 (119 ± 4)	706 ± 7 (52 ± 6)
	Global	864 ± 9 (22 ± 0.4)	700 ± 7 (35 ± 5)
Root	Relaxed	1,083 ± 15 (308 ± 14)	1,122 ± 11 (89 ± 8)
	Global	1,541 ± 14 (41 ± 1)	1,079 ± 8 (54 ± 7)

Divergence times are computed on 30,399-aa-long data for 36 taxa, simulated under variable (autocorrelated) or constant rates of evolution, by using either a relaxed or a global molecular clock. Expected (simulated) ages are 695 Mya for bilaterians and 1,085 Mya for the root. The 95% credibility interval widths are given in parentheses. All values are averages ± SE of 10 replicates.

Impact of Missing Data on Divergence Times. Despite the expectation that the large size of our dataset would have likely buffered the impact of missing data (47), our dating estimates might have been seriously influenced by the absence of ≈25% of amino acids. This point was evaluated on simulated protein sequences, by comparing divergence times inferred from complete and gapped alignments (Fig. 3, which is published as supporting information on the PNAS web site). The presence of missing data leads to slightly under- or overestimated divergence ages, depending on the node under focus, and induces a mean difference of -0.2% ± 2.8 over all nodes (extreme values, -9.8 to + 8.7%). On average, the relative differences are, respectively, + 1.7% and -2.5% for ages that are over- and underestimated by missing data. This corresponds to variations of approximately +17 Myr to -25 Myr for a 1,000-Myr-old node. For the root age, these values are indeed twice less than the actual SD measured by the Bayesian approach. Interestingly, the random introduction of an additional 25% of missing data, yielding a data set with 50% of missing amino acids, again provides very similar dates relative to the original data set (data not shown). The relaxed clock method is therefore efficient, even when the alignment contains partial sequences.

Sensitivity of Posterior Divergence Ages upon Prior Assumptions. Because Bayesian posteriors might depend on priors, we evaluated the sensitivity of our dating results upon a priori hypotheses. Different expected numbers of time units between tree root and tips were tested by comparing posterior ages obtained using different gamma-distributed priors: 540 ± 270 Mya (the Cambrian boundary), 1,000 ± 500 Mya [earliest body fossils of stramenopiles (5)], 2,000 ± 1,000 Mya [a recent molecular estimate for eukaryotes origin (12)], and 3,000 ± 1,500 Mya [a deep value for stem eukaryotes (2)]. Posterior ages were plotted against the four independent root priors for each of the 34 tree nodes. This resulted in 34 regression lines with a mean slope of 0.016 (range, -0.002 ± 0.0005 to 0.067 ± 0.007). Such an average impact over all nodes indicated that a 1,000-Myr variation of the root prior will involve a posterior divergence age variation of only 16 Myr, which is far less than the order of magnitude of the uncertainty on the divergence ages themselves. Posterior divergence times thus appeared only slightly sensitive to huge changes in prior specification of root age. Furthermore, comparison of a priori and a posteriori age estimates for calibration nodes did not reveal any systematic trend (Table 3, which is published as supporting information on the PNAS web site), suggesting that paleontological uncertainties did not bias our calculations, because they were incorporated in the dating procedure (31, 33).

Changes in reference topology may potentially affect molecular dating (39). Because the root location is uncertain among eukaryotes (44), we recalculated divergence times after moving the root from the branch leading to the cellular slime mold to the one leading to kinetoplastids (Fig. 1). Divergence times in opisthokonts, especially among animals, were not sensitive to this modification (e.g., we obtained 627–738 Mya for bilaterians). The kinetoplastid rooting actually involved deeper divergences among Plantae (899–1,191 Mya). The main clades of eukaryotes also diverged earlier (1,042–1,412 Mya; Fig. 4, which is published as supporting information on the PNAS web site), likely because such an alternative root location involves a pectinate tree shape. Thus, we confirm that the above-mentioned observations of Middle to Late Proterozoic cladogeneses among most eukaryotes were not the result of a rooting artifact.

Molecular clock approaches are also sensitive to the choice of calibrations (48). For example, divergence time estimates under the single vertebrate calibration were on average 1.4 times deeper than those measured with the six calibrations (Table 4, which is published as supporting information on the PNAS web site). We systematically studied the effect of calibration selection by analyzing all of the possibilities of choosing one or combining 2, 3, 4, 5, or 6 calibrations. Whereas divergence times averaged over all possibilities of using a given number of simultaneous calibrations seems not to vary much with those numbers, the minimum and maximum estimates may dramatically vary depending upon the choice of a given combination of fossil references (Table 2). However, a reduction of the uncertainty on divergence times was clearly associated to the increase of the number of simultaneous calibrations. Importantly, our datings were robust against the random exclusion of one or two calibration points.

Table 2. Posterior divergence ages for bilaterians and tree root computed on real data under a relaxed molecular clock calibrated by different combinations of one to six time constraints.

	Bilaterians		Root
C	Ages (range)	δ Credl	Ages (range)	δ Credl
1	694 (452–999)	330 ± 201	1,140 (751–1,617)	578 ± 307
2	708 (536–999)	199 ± 97	1,147 (885–1,621)	379 ± 135
3	709 (560–863)	157 ± 73	1,132 (908–1,361)	329 ± 82
4	706 (642–845)	136 ± 56	1,117 (1,029–1,298)	312 ± 68
5	699 (669–757)	123 ± 32	1,099 (1,045–1,174)	301 ± 39
6	695 (—)	119	1,085 (—)	309

Mean ages, range of ages, and mean 95% credibility interval widths (δ Credl) are computed on the 6, 15, 20, 15, 6, or 1 possibility of incorporation of, respectively, C = 1, 2, 3, 4, 5, or 6 simultaneous calibrations.

Discussion

Robustness of the Relaxed Clock Estimates. Molecular clocks are highly controversial, dates from various sources being often so different that some researchers doubt that molecular dating of evolutionary events is possible (49). Three points are of crucial importance: (i) the size of the molecular sample (i.e., stochastic errors due to a limited number of species and/or genes), (ii) the efficiency of the dating method (i.e., systematic errors in the inference), and (iii) the quality of the fossil calibrations (i.e., amplification of paleontological uncertainties). We tried to reduce the impact of all these potential issues.

Our divergence time estimates should not be seriously affected by the stochastic error, because we used a very large data set (129 genes; 30,399 amino acid positions), corresponding to proteins involved in different functional pathways like translation, transcription, cytoskeleton, and metabolism. Contrary to all previous studies with such a large sample of genes, a reasonable taxonomic diversity (36 species) was sampled. Here, half of the total number of proteins contains at most three missing taxa over 36, and 25% of the amino acids are missing in our final alignment. Nevertheless, our dating estimates are robust upon missing data (Fig. 3, which is published as supporting information on the PNAS web site). Indeed, a potentially reduced phylogenetic (and/or dating) accuracy associated with missing data is primarily caused by the occurrence of too few complete characters rather than too many missing positions (47). Presently, because the shortest concatenated sequence includes 7,500 amino acids, our complete alignment retains a strong phylogenetic and dating signal.

Second, our relaxed molecular clock datings (Fig. 1) appear to be robust to the specification of prior distributions on model parameters. This suggests that much posterior dating information regarding measure of divergence times among eukaryotes is attributable to the 129 concatenated proteins rather than to prior specifications. Moreover, the relaxed clock approach retrieves the true divergence times (Table 1) when substitution rates are distributed according to the autocorrelated-rate model developed by Thorne et al. (32).

Third, the concomitant use of six calibration constraints chosen among plants, fungi, and animals (Fig. 1) also helped to more accurately measure the absolute amino acid replacement rates in these three distinct clades and stabilized the Bayesian divergence times on the whole tree. An alternative procedure (22, 28) is to use several independent calibrations and, for each gene, to average the corresponding divergence estimates. However, such an approach is “inferior to a simultaneous analysis of multiple genes under the constraints of multiple calibrations” (22). Accordingly, we have shown that the use of simultaneous calibrations reduces the uncertainty on age estimates (Table 2).

Variable-Rate and Constant-Rate Molecular Clocks. The greatest discrepancy between age estimates without and with the clock assumption is observed for the Saccharomyces/Candida split, here estimated at 168–308 (mean 235) Mya (Fig. 1) compared with 841 Mya (45). These two fungi appear to be fast evolving (data not shown), and such high rates are probably not accommodated by global clock based methods. When we constrained a perfect molecular clock under the Bayesian approach, this divergence was estimated at 439–468 Mya (mean 454). On average, the divergence times among eukaryotes were 1.7 times deeper with a global clock than with a relaxed clock (Table 5, which is published as supporting information on the PNAS web site). The greatest contrast (ratio >2.0) between global and relaxed clock ages is observed for alveolates, nematodes, and kinetoplastids, i.e., the fastest-evolving taxa for the 129 proteins here evaluated. A similar result was obtained for animals under various models of clock relaxation (22, 28) and for mitochondrial genomes of mammals (29).

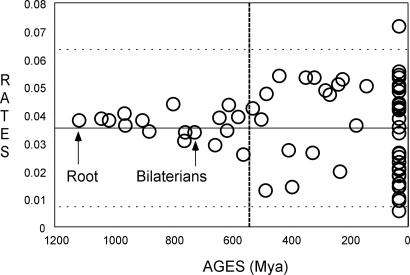
How should we evaluate which method, either a global or a relaxed clock, is better for describing the data at hand? Estimating a time scale by the mean of age extrapolation beyond animal, fungi, and plant calibrations may possibly lead to biased estimates. Whereas interpolation of date estimates is certainly less biased because evolutionary rates are bounded by zero, extrapolation could conduct to rates increasing on average when moving far back in time. Thus, increased rates, faster earlier and slower since the Neoproterozoic/Cambrian transition, may result in estimates that are apparently too recent for deeper nodes. Two elements suggest that our analyses have not been affected by such a trend. First, we plotted the posterior evolutionary rate of each node against its mean posterior age estimate as measured on our concatenated data set (Fig. 2). No trend toward a rate increase far back in time is observed, and the rate for the last common bilaterian ancestor is close to the mean rate measured along the eukaryotic phylogeny. In particular, our 129 proteins did not record the Late Precambrian episodic burst of evolutionary rates detected on 22 mitochondrial and nuclear genes (22). Second, simulation studies (Table 1) indicate that, at least in the present case, the autocorrelated rates model does not underestimate divergence times, neither on clocklike nor on relaxed clock sequences.

Fig. 2.

Relationship between node rates and node times. For each node of the chronogram, the amino acid replacement rate has been plotted against the estimated divergence times. The Cambrian boundary is indicated by the vertical line. The mean and ± 2 SDs of the rates are indicated by the continuous and dashed horizontal lines, respectively.

Comparison with Other Relaxed Molecular Clock Datings. Recently, two relaxed clock dating studies, among metazoans (23) and photosynthetic eukaryotes (50), yielded results that are at first sight incongruent with our estimates. The use of seven concatenated proteins and the nonparametric rate smoothing r8s approach (31) indicate a more recent occurrence of the last common bilaterian ancestor, between 556 and 592 Mya (23) instead of 642–761 here. Importantly, these estimates were obtained without taking into account among-site rate variation. In the same paper, calculations conducted by modeling such a rate variation with a gamma distribution yield a confidence interval of 636–678 Mya for the bilaterian diversification, i.e., an estimate overlapping with ours.

On the basis of a tree derived from five concatenated plastid proteins, calibrated by five intervals under the r8s approach, Yoon et al. (50) suggested a red–green algae split between 1,591 and 1,757 Mya, instead of 825–1,061 or 899–1,191 Mya here, depending on the root location. Our reanalysis of this data set under the divtime relaxed molecular clock approach suggests a major incompatibility between “green” and “red” calibrations. Under the maximum likelihood topology inferred from the five plastid proteins, and enforcing the angiosperms, spermatophytes, and land plant nodes between 90 and 130, 290 and 320, and 432 and 476 Mya (50), would involve a red algae diversification between 392 and 761 Mya (mean 551 Mya) and a Chondrus/Palmaria split between 165 and 381 Mya. This is incompatible with the respective 1,174- to 1,222- and 594- to 603-Mya constraints used in reference (50). Reciprocally, if we use the latter two “red” calibrations, angiosperms, spermatophytes, and land plants would have diversified 106–336, 344–809, and 626–1,237 Mya. Actually, calibrations among land plants only yield a red algae/chlorobionts split between 925 and 1,576 Mya, a credibility interval that partially overlaps with ours. Further analyses, including longer plastid sequences, are required to evaluate the degree of congruence between molecular and paleontological data in red algae (4, 50). More generally, molecular dating still needs to be refined by improved sampling of genes, and especially of species, and improved methods with more realistic models of rate variation.

Toward a Partial Reconciliation of Clocks and Rocks. Deeper molecular dates are actually expected, because the fossil record documents only the first appearance of a morphologically recognizable (crown) group and not the actual time of genetic divergence (51). Previous molecular datings yielded molecular ages always more ancient than paleontological ones, but often to a large extent (12, 15, 20, 46). Interestingly, our molecular dating (Fig. 1) does not appear to be biased in such a systematic way. Molecular ages are more recent than the fossil record for red algae but more ancient for animals. We dated the divergence between green plants and red algae between 825 and 1,061 Mya (Fig. 1), whereas a fossil of 1,200 Mya has been interpreted as belonging to a specific subgroup of red algae, i.e., bangiophytes (4). Molecular dating with a kinetoplastid rooting would be in better agreement with this fossil (95% credibility interval, 899-1191; Fig. 1), but such a rooting might represent a tree reconstruction artifact (36). Actually, single fossils may also bear their load of uncertainty in taxonomy identification and geological ages (11). Illustrating the latter case, the age of the Bangiomorpha assemblage is in fact bounded between 1,267 and 723 Mya (52). For bilaterians, the discrepancy between our molecular estimates (642–761 Mya) and the fossil record (7) is reduced to a minimum of 40 Myr. According to protein data, the divergence of the main stem groups of metazoans (Deuterostomia, Ecdysozoa, and Lophotrochozoa) would have occurred in the Late Neoproterozoic, but their diversification would date close to the Precambrian–Cambrian boundary. This suggests that the stem lineages would have been organisms with a poor fossil record because of their small size, taphonomic problems, or undistinguishable morphology.

The use of a relaxed molecular clock on our large data set estimated the diversification time of most extant eukaryotic kingdoms at ≈1,100 Mya in the mid-Proterozoic (Fig. 1). Even if cytoskeletal and ecological prerequisites for eukaryote diversification were already established some 1,500 Mya (3), the postulated anoxic and sulfidic redox status of oceans between ≈2,000 and 1,000 Mya might have limited the rise of photosynthetic eukaryotes (53). Around 1,000 Mya, the diversification of plants may have been facilitated by the primary endosymbiotic event that led to plastids. Moreover, it has been proposed that a major increase in atmospheric oxygen level occurred between 1,000 and 640 Mya (54). In association with the Neoproterozoic appearance of more fully oxic oceans (53), this major transition toward a more oxygenic environment could possibly have accelerated the diversification of the eukaryotic organisms, thanks to the aerobic respiration provided by mitochondria (55). Close to the Meso-/Neo-Proterozoic transition, choanoflagellates diverged from their closest animal relatives, marking the dawn of cellular cooperation in animals. The major eukaryotic kingdoms therefore originated much more recently than previously thought (12) but did not seem to have been affected by the postulated global glaciations (“snowball Earth” hypothesis) between 750 and 600 Mya (56). The present study illustrates how geological and biological records of organismal evolution might be partially reconciliated by using molecular relaxed clock datings from large genomic comparisons.