Food availability affects adult survival trajectories depending on early developmental conditions

Abstract

Food availability modulates survival in interaction with (for example) competition, disease and predators, but to what extent food availability in natural populations affects survival independent of these factors is not well known. We tested the effect of food availability on lifespan and actuarial senescence in a large population of captive zebra finches by increasing the effort required to obtain food, reflecting natural contrasts in food availability. Food availability may not affect all individuals equally and we therefore created heterogeneity in phenotypic quality by raising birds with different numbers of siblings. Low food availability had no effect on lifespan for individuals from benign developmental conditions (raised in small broods), but shortened lifespan for individuals from harsh developmental conditions. The lifespan difference arose through higher baseline mortality rate of individuals from harsh developmental conditions, despite a decrease in the rate of actuarial senescence. We found no evidence for sex-specific environmental sensitivity, but females lived shorter than males due to increased actuarial senescence. Thus, low food availability by itself shortens lifespan, but only in individuals from harsh developmental conditions. Our food availability manipulation resembles dietary restriction as applied to invertebrates, where it extends lifespan in model organisms and we discuss possible reasons for the contrasting results.

1. Introduction

In natural populations, food availability is a key factor in population dynamics and life-history evolution, because survival and fecundity are thought to increase when food becomes more abundant [1,2]. However, the exact mechanisms through which food availability affect survival and reproduction remain unclear, because food abundance interacts with other ecological factors [3–5]. For example, an increase in food availability is likely to reduce starvation risk but also affects exposure to predators because animals are often more vulnerable when foraging, and high food abundance allows for a reduction in the time spent foraging. Thus, an increase in food availability could affect survival primarily through an effect on predation rate, with a negligible contribution of altered starvation rate [3]. Alternatively, increased food availability may increase the local density of conspecifics, which can result in an increase in the number of predators to the extent that per capita predation rate is increased [6]. That the relation between food availability and survival is complex is further illustrated by the finding that dietary restriction in laboratory animals generally increases survival and lifespan [7]. Perhaps due to a combination of these processes, a recent meta-analysis concluded that food supplementation in natural populations had no demonstrable effect on survival [5]. Thus, the extent to which food abundance in isolation affects survival in natural populations is an open question, at least in the food availability range where animals occur naturally. This is unfortunate, because insight into the mechanisms mediating demographic effects of food availability may be essential to predict such effects in our ever-changing world. Experiments are required to resolve this issue, and we here present the results of a large-scale and long-term experiment in which we test for an effect of food availability on lifespan and ageing in zebra finches Taeniopygia guttata. An essential aspect of our approach is that we manipulated food availability in a way that mimics natural variation in food availability—namely by manipulating foraging costs [8], here defined as the effort required to obtain a unit of food. Thus, animals could respond to lower food availability by increasing their foraging effort, as they can in natural conditions. At the same time, in the foraging cost manipulation in adulthood, density was controlled and there were no predators, and thus food availability effects on adult survival can be attributed to food availability per se.

Variation among individuals (individual heterogeneity) with respect to susceptibility to environmental factors such as food abundance can have interesting demographic consequences [9–11]. Environmental factors contribute to the development of individual heterogeneity at all ages, but environmental conditions during development are thought to be of particular importance in determining individual heterogeneity in lifespan and, more generally, adult health [12–16]. The link between developmental conditions and lifespan can be complex when the effects depend on the environmental conditions in adulthood [17,18]. For example, benign developmental conditions may yield high-quality phenotypes that cope better with harsh conditions in adulthood relative to phenotypes from harsh developmental conditions (the ‘silver spoon hypothesis’ [19]). By contrast, the match–mismatch hypothesis states that environmental challenges faced during development may prepare individuals to cope with similar environmental challenges during adulthood, while a mismatch may cause health problems [16,20–22]. Lastly, specific stressors experienced during development may prime the development of resistance against such stressors in adulthood (known as a hormesis effect; e.g. [23]). Experimental studies of developmental effects on lifespan have generally considered only high quality environmental conditions during adulthood (e.g. standard laboratory conditions), or considered animals in a (uniform) environment, and thus cannot distinguish silver spoon from match–mismatch scenarios. Such a test requires the independent manipulation of the environment during development and in adulthood in a crossover design, which needs a level of control that usually requires a laboratory setting. There are few such experiments and these have generally failed to find such interaction effects [24–28] (but see [29]). However, these studies all used species with indeterminate growth and/or developmental phases of flexible duration. Such developmental patterns increase the opportunity to mitigate effects of harsh developmental conditions in ways that are not open to species with determinate growth such as birds and humans. Thus, to what extent lifespan is subject to match–mismatch effects versus silver spoon effects is unknown for species with determinate growth.

We here report the results of an experiment aimed to tease apart effects of foraging costs during development and in adulthood on lifespan and senescence. The zebra finch is a suitable species because it has determinate growth, and developmental conditions have previously been shown to affect the phenotype in ways that are important for adult health and lifespan (review in [30]). The experiment had a 2 × 2 design, independently manipulating foraging costs during development and adulthood, so that we could test for interaction effects between food availability at different life stages. We manipulated the foraging costs during development by cross-fostering chicks to either small or large broods (as in [31]), which in a sense increases ‘foraging costs’ because chicks have to beg more per item food reward [32] (also in our study species [33]). In adulthood, we experimentally increased the flight costs per food reward (as in [8]), and individuals were maintained in these conditions until natural death.

When age at death follows a Gompertz distribution, variation in lifespan can arise via two distinct but not mutually exclusive ways: a change in the (age-independent) baseline mortality rate (vulnerability to the ageing process) and/or a change in the age-dependent mortality rate (actuarial senescence or ‘ageing rate’ [34–38]). Identifying which parameter changed when there is a change in lifespan is informative because these effects are likely to be caused by different biological processes [39,40]. We therefore analysed our data in two steps. First, we identified treatment effects on lifespan using Cox proportional hazard (CPH) analyses [41,42]. Next, we evaluated the contribution of differences in age-independent and age-dependent mortality to the observed lifespan differences by fitting the Gompertz mortality function [34,35]. In this way, we tested effects of foraging costs during development and in adulthood on lifespan, and on the parameters that describe the mortality trajectory.

2. Material and methods

(a). Development

Birds for the experiment were reared by randomly paired birds housed indoors on a 14 L : 10 D schedule at around 25°C and 60% humidity in a cage (L × H × D: 80 × 40 × 40 cm) with a nest-box and nesting material (hay). Drinking water, sepia and a commercial tropical seed mixture were available ad libitum. A teaspoon of fortified canary food (‘eggfood’, by Bogena, Hedel, the Netherlands) was given three times a week until hatching of the first chick (no ‘eggfood’ was given during the nestling phase to avoid possible diet variation between birds growing up in large and small broods). Nest-boxes were checked daily. When the oldest chick of a brood was 4–5 days old, all chicks of that nest were cross-fostered randomly to small and large broods. We created experimentally small broods (89% with two chicks and 11% with three chicks) and large broods (80% with six chicks, 7% with five, 9% with seven, and 4% with eight chicks). These brood sizes are within the range observed in wild [43]. Behavioural observations [33] showed that birds in large broods had to beg more per feeding bout from the parents, confirming that the effort required per unit of food was higher in large broods when compared with small broods. At the age of 15 days birds were ringed, and from the age of 35 days until approximately 120 days young were housed in larger indoor cages with up to 40 other young of the same sex and two male and two female adults for sexual imprinting.

At the age of 15 days, i.e. just before fledging, growing up in a large brood resulted in 1.4 g (12%) lower mass without altering the variance (s.d.: 1.4 in both groups; n = 478; electronic supplementary material, figure S1) in agreement with earlier reports [31,44]. Selective disappearance of low-quality individuals, reducing heterogeneity, can bias estimates of the long-term effects of developmental conditions, but survival between cross-fostering and age 120 days was high and independent of the number of siblings after cross-fostering (see electronic supplementary material 1 for details).

(b). Adulthood

From an age of 120 days onwards, birds were housed in eight single sex outdoor aviaries (L × H × W: 310 × 210 × 150 cm) located in Groningen, The Netherlands (53°13′0″ N/6°33′0″ E). Four aviaries had low foraging costs and four had high foraging costs, equally divided between sexes, and with a balanced spatial distribution. Thus, all foraging costs/sex combinations were replicated. We manipulated foraging costs as in [8]. In brief, in each aviary a food container (L × W × H: 120 × 10 × 60 cm) with 10 holes in the sides was suspended from the ceiling. This number was sufficiently large that we never observed competition for feeding holes (more than 14 h of observation; M.B., E.K., J.J.B., B.J. & S.V. 2011, unpublished data). In the low-foraging-cost (benign) treatment, food containers have perches below the holes, while in the high-foraging-cost (harsh) treatment these perches are absent. Therefore, birds in the harsh treatment need to fly from a distant perch to the food container, hover to get the seed(s) and fly back to the perch to consume it.

The adult phase of the experiment started on 9 December 2007 and we used data collected till 1 January 2015 in this paper. In each aviary, we entered an approximately equal number of birds reared in small or large broods. Mass at ages 15 and 120 days did not differ between birds entered in the hard or easy foraging treatment (table 1). As birds died, new birds, reared in small or large broods as described above, were added periodically to keep densities within aviaries within a limited range, which has the added advantage that this allows the separation of temporal effects from age effects in the statistical analyses. The starting population (2007) contained 249 birds, and the following numbers were added in subsequent years: 2008, 45; 2009, 44; 2011, 95; 2012, 62; 2013, 27; 2014, 28 (i.e. 301 birds added in total, bringing total birds in experiment to 550). Birds were entered in the aviaries when three to four months old, except for the first batch which was 3–24 months old when the experiment started. The age at the start of the foraging cost experiment did not differ significantly among groups (table 1), and we took age at start of the experimental treatment into account in the analysis. The first batch was housed in the same aviaries prior to the start of the experiment in 2007, but with food supplied in bowls on the floor. Before the start of the foraging cost experiment, all birds were trained on the harsh foraging treatment to ensure that birds in the benign and harsh adult foraging treatment were strictly comparable in case not all birds managed to cope with the harsh foraging treatment. Of the 562 birds trained, 12 died during training, equally divided among birds reared in small and large broods.

Table 1.

Descriptive statistics (mean (s.d.)) of the experimental groups. dev, developmental conditions; ad, adult conditions.

	benign dev		harsh dev
statistic	benign ad	harsh ad	benign ad	harsh ad
n birds entered into adult experimental conditions	129	136	133	152
proportion of males	0.50	0.50	0.51	0.53
age (years) when entering adult experimental conditions	0.95 (0.55)	0.93 (0.54)	0.99 (0.60)	1.01 (0.60)
n deaths on 1 Jan 2015	90	83	92	112
n censoreda	39	53	41	40
mass (g) at age 15 days; during growth	11.4 (1.4)	11.2 (1.4)	10.2 (1.6)	9.7 (1.5)
mass (g) at age three months; early adulthood	15.0 (1.5)	15.0 (1.6)	14.4 (1.6)	14.3 (1.6)

^aOf the censored animals, 97.5% outlived the experiment, the remaining 2.5% died in accidents of various kinds.

(c). Statistical analyses

Mortality may have been affected by fixed effects besides our manipulations (e.g. sex and starting age of the adult treatment). Furthermore, several random effects may have affected mortality (birth nest, genetic mother, genetic father, rear nest, rear mother, rear father, birth batch and aviary). To identify whether these were of interest to take into account when testing for manipulation effects, we used CPH analyses and model selection [45,46], based on the Akaike information criterion (AICc), to identify the model best supported by the data (see electronic supplementary material, S2), for which, as a rule of thumb, a change in AICc of −2 is considered significant [45]. These analyses revealed that higher ‘starting age’ increased mortality, but there was no support for the inclusion of interactions between starting age and experimental manipulation (electronic supplementary material, table S2). We thus fitted parametric mortality models (see below) correcting for starting age (exponentially transformed and mean centred). CPH analyses also showed evidence for female biased mortality but not for sex-specific experimental effects (electronic supplementary material, table S3). We thus fitted parametric mortality models excluding sex-specific experimental effects. Of all the random effects tested (see above), including or excluding them never altered any of the conclusions of the CPH analyses. Aviary was the best supported, but still explained little variance (p > 0.10), and we here report all CPH results including aviary as a random effect.

We employed parametric mortality models to quantify experimental effects on age-dependent and age-independent mortality components. Our sample sizes more than fulfil the minimum requirements for fitting mortality models [47]. Of the various mortality models fitted to our data, the Gompertz model fitted best (electronic supplementary material, table S4). We here further discuss two mortality models. In the exponential model the force of mortality at time t (M_t) is a constant k (M_t = k) and thus there is no senescence. In the Gompertz function (M_t = Ae^Bt or, in the notation we use, log(M_t) = log(A) + Bt), the force of mortality at time t (M_t) is a function of baseline parameter A and increases exponentially with age according to the parameter B, which quantifies actuarial senescence. We used these Gompertz parameters to derive population characteristics such as (i) the mortality rate doubling time (MRDT), another measure of the rate of senescence, given by MRDT = 0.693/B (Finch [48], pp. 22–24), (ii) the life expectancy at start of the treatment, and (iii) the standard deviation in ages at death as a measure of lifespan inequality. Standard deviation of ages at death were estimated based on simulations of populations of 10 000 individuals given the Gompertz parameter estimates (table 2).

Table 2.

Lifespan characterizations of the experimental groups. Time was taken to be time elapsed since birds entered the adult treatment. dev, developmental conditions; ad, adult conditions.

	benign dev		harsh dev
statistic	benign ad	harsh ad	benign ad	harsh ad
ln(Gompertz A), age-independent mortality (±s.e.)	−2.21 (0.21)	−2.22 (0.20)	−1.91 (0.19)	−1.41 (0.16)
Gompertz B, age-dependent mortality (±s.e.)	0.37 (0.07)	0.41 (0.06)	0.28 (0.06)	0.18 (0.06)
mortality rate doubling time (years)	1.78	1.69	2.48	3.85
life expectancy at start treatment (years)	3.28	3.21	3.20	2.66
standard deviation in age at death (years)a	1.67	1.60	1.83	1.79

^aSimulation based using the Gompertz estimates in this table.

We fitted these models using the function ‘basta’ in the R package ‘Bayesian Survival Trajectory Analysis' (BaSTA) [49], which optimizes parametric survival functions using Markov chain Monte Carlo (MCMC) procedures. Starting age was included as a covariate. We fitted the parametric mortality models using four parallel MCMC runs with 500 000 iterations, 100 000 burn-in period and a thinning of 1000. Potential scale reduction factors (all less than the maximum of 1.1) and trace plots (electronic supplementary material, figure S2) indicated appropriate model convergences, and the levels of autocorrelation were low (less than 0.04). Parameter comparison between groups was done using the Kullback–Leibler discrepancy (KLD) [50,51]. KLD describes to what extent the posterior distributions of parameters between groups are similar and ranges from 0.5 (identical distribution) until 1 (no overlap).

3. Results

For brevity, we refer to the four experimental groups as BB, BH, HB and HH, where the first letter stands for benign (B) or harsh (H) developmental conditions (i.e. small or large brood size), and the second letter stands for benign (B) or harsh (H) foraging conditions in adulthood.

(a). Lifespan

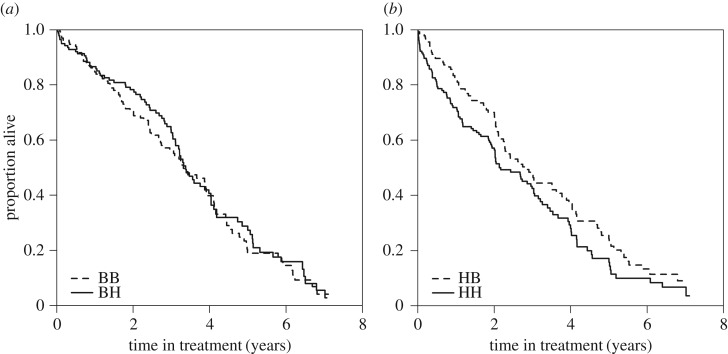
The foraging cost manipulation had little effect on the life expectancy of birds reared in benign developmental conditions (figure 1a and table 2; BB versus BH: ΔAICc > +0.67; electronic supplementary material, table S1A). By contrast, the foraging cost manipulation had a strong effect on the life expectancy of birds reared in harsh developmental conditions, with HH birds living six months (17%) shorter than HB birds (figure 1b and table 2; HB versus HH: ΔAICc = −3.61; electronic supplementary material, table S1b). The interaction between developmental and adult conditions was included in the best-fitting model (ΔAICc = −1.22; electronic supplementary material, table S1e). Thus high foraging costs shortened lifespan, but only for birds that had experienced harsh developmental conditions.

Figure 1.

High foraging costs shorten survival for birds from harsh (b) but not from benign (a) developmental conditions. Survival curves were corrected for age at start of the adult treatment (table 1). Graphs for the four groups together are shown in electronic supplementary material, figure S3a. Treatment abbreviations: B, benign conditions; H, harsh conditions (in chronological order; e.g. BH indicates benign development followed by harsh adult conditons).

(b). Senescence

To test for actuarial senescence, an increase in mortality rate with age, we compared the fit of the exponential model (that assumes a constant mortality rate with age) with that of the Gompertz model (which assumes an exponential change in mortality rate with age). The Gompertz model fitted the data better than the exponential model (ΔDIC = −241; electronic supplementary material, table S4) and showed that the risk of dying increased over time. Thus, our population of zebra finches experienced significant actuarial senescence.

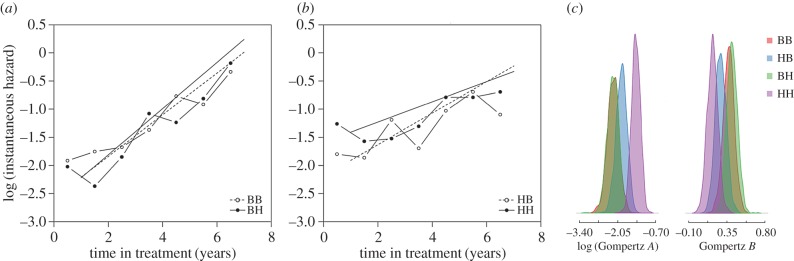
Having established that there was actuarial senescence we investigated whether changes in Gompertz baseline mortality rate and/or actuarial senescence could explain the experimental effects on lifespan. Baseline mortality rate (or ‘vulnerability’, the age-independent A in the Gompertz equation) varied twofold between groups (table 2). For birds from benign developmental conditions (BB versus BH), foraging costs had little effect on Gompertz A (figure 2a) and posterior parameter distributions overlapped moderately (KLD = 0.84; figure 2c). By contrast, for birds from harsh developmental conditions (HB versus HH), high foraging costs increased Gompertz A (figure 2b) and there was no overlap in posterior parameter distributions (KLD = 1.00; figure 2c). Thus, high foraging costs increased baseline mortality for birds that grew up in harsh relative to those from benign developmental conditions.

Figure 2.

High foraging costs had little effect on mortality rates for birds from (a) benign developmental conditions. In contrast, for birds from (b) harsh development conditions, high foraging costs increased baseline mortality rate (Gompertz A) and decreased actuarial senescence (Gompertz B). Dots show mortality per half year. Lines show Gompertz fits. Graphs for the four groups together are shown in electronic supplementary material, figure S3b. (c) Posterior distributions of Gompertz parameters overlap for birds from benign developmental conditions (BB and BH) but little for birds from harsh developmental conditions (HB and HH). Treatment abbreviations as for figure 1. (Online version in colour.)

Age-independent and age-dependent mortality rate often correlate negatively (see Discussion). Consistent with this general finding, the age-dependent mortality rate (actuarial senescence or ‘ageing rate’, B in the Gompertz equation) was higher for the experimental groups with low Gompertz A. For birds from benign developmental conditions (BB versus BH) foraging costs had little effect on Gompertz B (figure 2a) and posterior parameter distributions overlapped moderately (KLD = 0.82; figure 2c). By contrast, for birds from harsh developmental conditions (HB versus HH), high foraging costs decreased Gompertz B (figure 2b) and there was virtually no overlap in posterior parameter distributions (KLD = 0.99; figure 2c). In agreement with these findings, the MRDT was longer for birds reared in harsh relative to those from benign developmental conditions, in particular when they lived in a harsh adult environment (HH; table 2). Thus, high foraging costs decreased age-dependent mortality rate, but only for birds from harsh developmental conditions.

A common measure of variation in lifespan is the standard deviation in age at death (s.d.), and other measures of lifespan inequality correlate well with the s.d. [52]. We found that the s.d. of age at death was higher for birds from harsh developmental conditions, independent of foraging costs in adulthood (table 2). Thus, while benign foraging costs mitigated the negative effects of harsh developmental conditions on mean lifespan, this was not the case for variation in lifespan.

(c). Sex differences

Males lived on average one month longer than females (electronic supplementary material figure S4a and table S3; ΔAICc = −3.1), but there was no evidence for sex-specific experimental effects (+1.0 < ΔAICc < +6.5; electronic supplementary material, table S3). To understand whether the differences in lifespan between the sexes arose due to differences in age-independent and/or age-dependent mortality rate, we fitted the Gompertz model per sex (electronic supplementary material, figure S4b). The sexes did not differ in age-independent mortality rate (Gompertz A; KLD = 0.50; electronic supplementary material, figure S4c), but females showed accelerated age-dependent mortality rate relative to males (Gompertz B; KLD = 0.93; electronic supplementary material, figure S4c). Thus, sexes differed in lifespan because females aged faster than males.

4. Discussion

Whether food availability affects survival in natural populations has remained elusive due to interactions between food availability and factors such as predation and competition [4,5]. We therefore studied the effect of manipulated food availability on survival and lifespan in a setting where confounding effects of predation and competition were excluded. A unique aspect of our experiment is that we manipulated food availability in a vertebrate by increasing foraging costs, mimicking how animals experience natural variation in food availability. To our surprise, an increase in foraging costs that resulted in doubling of the time spent foraging [8] had no effect on survival of birds that were reared in benign conditions (i.e. in small broods), despite the fact that the birds were housed in outdoor aviaries and were thus exposed to large fluctuations in ambient temperatures, and hence energy needs [53]. By contrast, birds reared in harsh conditions (large broods) were susceptible to the foraging cost manipulation, attaining a shorter lifespan when facing increased foraging costs. Apparently, birds reared in benign conditions could compensate behaviourally or physiologically for the increase in foraging costs in a way that did not compromise their survival or lifespan, while birds reared in harsh conditions did not have this opportunity. Thus, we conclude that the effect of food availability on survival and lifespan depends on the developmental history of the individual, with individuals in poorer conditions developing to be more vulnerable to an increase in foraging costs. To the best of our knowledge, this is the first experimental demonstration that foraging costs affect survival and lifespan of a vertebrate in a setting that fully excludes confounding effects of predation and competition. Further research is required to elucidate the mechanism that mediates the foraging cost effect on lifespan and why it depends on developmental history.

Dietary and caloric restriction (DR/CR) extend lifespan in traditional model species [7], and the effect of food availability on model species has therefore been well studied. In vertebrates, food intake is generally restricted by providing less food than the animal would normally eat, or, in some cases, by setting the food intake to zero on alternate days (intermittent fasting experiments). By contrast, in invertebrate studies food is often diluted in medium, forcing animals to spend more resources per unit energy intake. Our study applied the latter approach for the first time in relation to ageing in a vertebrate. The two approaches differ in the control that subjects have over their energy budget, being either experimenter-imposed or self-regulated in response to higher foraging costs. While these approaches are often implicitly assumed to be similar, because they have similar effects on lifespan in model organisms, their effects on size and allocation of the energy budget are likely to be very different [54,55]. Indeed, this may explain the contrast between the lifespan extending effect of DR/CR in laboratory rodents [7] and our findings of shortened lifespan when foraging costs were increased. It should be noted in this context that we applied only two foraging cost levels, and therefore cannot rule out that other levels of foraging costs will have a different effect on lifespan, as previously found in invertebrates [56].

Different predictions have been made with respect to the dependence of long-term fitness effects of developmental conditions on the environment experienced as adult. In a silver spoon scenario, individuals from good developmental conditions perform better than those from harsh developmental conditions [19], while according to the match–mismatch scenario individuals from harsh developmental conditions are better prepared to cope with similar challenges during adulthood [16,20–22]. There is empirical support for both scenarios, and to some extent they are not mutually exclusive. Moreover, in practice one can only observe the net outcome of the different processes combined. Our results clearly point to the silver spoon hypothesis being the most important in our experiment, because individuals reared in small broods were less susceptible to an increase in foraging costs than those reared in large broods. This may at least in part be due to the fact that zebra finches, like other bird species, have determinate growth, which reduces the opportunity to adjust development to environmental conditions. The match–mismatch hypothesis was also tested using data of humans suffering famines, and also there the ‘silver spoon’ effect appeared to dominate the finding [57]. This lack of support for the match–mismatch hypothesis also fits the results of a taxonomically broad meta-analysis of experiments with similar designs to ours that measured a variety of traits [58] and with the results of (non-experimental) cohort studies in wild vertebrates [59].

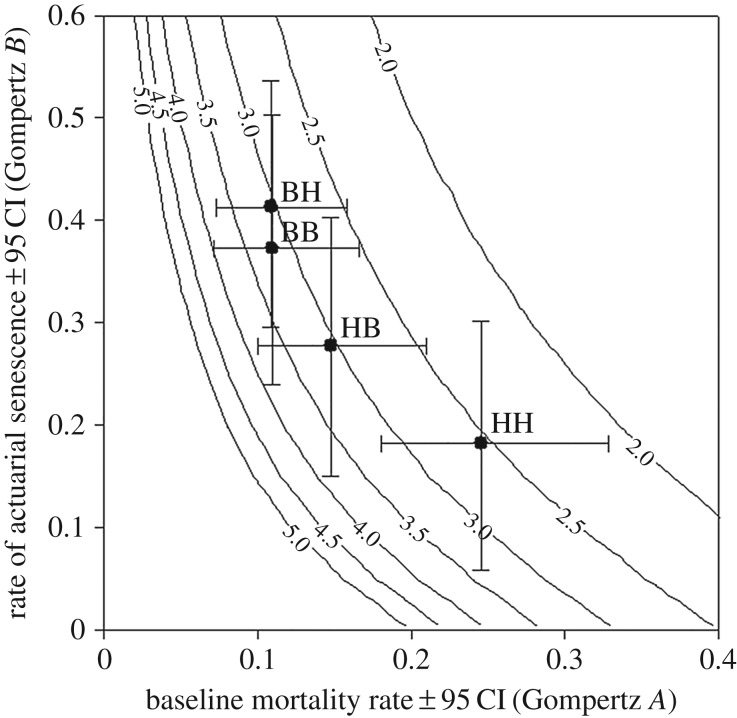
Different combinations of baseline mortality (‘A’) and actuarial senescence (‘B’) can result in the same lifespan (figure 3), and hence variation in lifespan can arise in different ways. How lifespan variation arises is of interest because it affects population demography, including, for example, the proportion of old individuals in a population, and thereby the evolution of senescence and traits that are expressed late in life [60] and extinction risk [61]. There is usually a negative association between the Gompertz parameters A and B among different populations of a species, known as the compensation law of mortality or Strehler–Mildvan correlation [37,62,63], and we find a similar relation among the four groups in our experiment (figure 3). Figure 3 further shows that birds subjected to the HH treatment had shorter lifespan than birds subjected to the BH treatment due to a higher age-independent mortality rate, and despite a decrease in actuarial senescence. A difference in the same direction, but of considerably smaller magnitude, was found between birds in the HB and BB treatment groups. The negative effect of developmental conditions on lifespan was mediated via an immediate (vulnerability) rather than latent (actuarial senescence) mortality cost. This is interesting because the importance of developmental conditions for mortality patterns in adulthood has not been fully resolved, even in humans [64–66]. Mortality rates of birds with different developmental backgrounds (B versus H) converged to similar levels at high ages (figure 2), which is reminiscent of similar patterns in humans when comparing age-dependent mortality rates between birth cohorts within a country or between developing and industrialized countries [62,67–70] (but see [71]). Such a response can arise because of heterogeneity in population composition: in groups with high baseline mortality rate the more vulnerable individuals disappear at younger ages, leaving only less vulnerable individuals at old ages [72]. It is noteworthy that while the developmental effects on life expectancy were reduced by benign conditions in adulthood, the effect on the standard deviation of age at death, a measure of lifespan inequality and population health [52,68], was not (table 2). Hence, benign conditions in adulthood only partly mitigate effects of harsh developmental conditions.

Figure 3.

Gompertz parameter estimates (±95 CI) for the different treatment combinations. Iso-life expectancy lines show life expectancy (years) at start foraging treatment for different combinations of the two parameters. Treatment abbreviations as for figure 1.

Ethics

All methods and experimental protocols were carried out under the approval of the Animal Experimentation Ethical Committee of the University of Groningen, licence 5150A. All methods were carried out in accordance with these approved guidelines.

Data accessibility

Data are available from the Dryad Digital Repository [73].

Authors' contributions

S.V. conceived and designed the experiment. M.B., E.K. and B.J. performed the experiment. M.B. analysed the data with the help of J.J.B. M.B. and S.V. wrote the paper, and all authors went through later stages of the manuscript.

Competing interests

We have no competing interests.

Funding

E.K. was supported by NWO Vici grant 865.04.003 to S.V. and J.J.B. by NWO open competition grant 823.01.009 to S.V.