Detecting subnetwork-level dynamic correlations

Abstract

Motivation: The biological regulatory system is highly dynamic. The correlations between many functionally related genes change over different biological conditions. Finding dynamic relations on the existing biological network may reveal important regulatory mechanisms. Currently no method is available to detect subnetwork-level dynamic correlations systematically on the genome-scale network. Two major issues hampered the development. The first is gene expression profiling data usually do not contain time course measurements to facilitate the analysis of dynamic relations, which can be partially addressed by using certain genes as indicators of biological conditions. Secondly, it is unclear how to effectively delineate subnetworks, and define dynamic relations between them.

Results: Here we propose a new method named LANDD (Liquid Association for Network Dynamics Detection) to find subnetworks that show substantial dynamic correlations, as defined by subnetwork A is concentrated with Liquid Association scouting genes for subnetwork B. The method produces easily interpretable results because of its focus on subnetworks that tend to comprise functionally related genes. Also, the collective behaviour of genes in a subnetwork is a much more reliable indicator of underlying biological conditions compared to using single genes as indicators. We conducted extensive simulations to validate the method’s ability to detect subnetwork-level dynamic correlations. Using a real gene expression dataset and the human protein-protein interaction network, we demonstrate the method links subnetworks of distinct biological processes, with both confirmed relations and plausible new functional implications. We also found signal transduction pathways tend to show extensive dynamic relations with other functional groups.

Availability and Implementation: The R package is available at https://cran.r-project.org/web/packages/LANDD.

Contacts: yunba@pcom.edu, jwlu33@hotmail.com or tianwei.yu@emory.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

High-throughput expression data, such as gene expression, metabolomics and proteomics data, comprehensively profile the expression levels of thousands of biological units. Such data can reveal complex regulatory patterns in the biological system. Methods to explore patterns in high-throughput expression data include clustering, dimension reduction, sparse factorization, etc. Such methods are mostly based on pairwise relations between the biological units. However, the expression levels of the biological units are the outcome of complex biological regulatory networks, the links of which may be turned on and off in response to certain biological conditions (Barzel and Barabasi, 2013; Ideker and Krogan, 2012; Luscombe et al., 2004; Ocone et al., 2013). As a result, at the gene expression level, many correlations are dynamic, changing from positive correlation in some biological conditions to negative or no correlation in other biological conditions. Such conditions may not be major phenotype changes, e.g. disease/non-disease in case-control studies, but they may be more subtle and unobserved within each phenotype group (Li, 2002; Li et al., 2004).

To analyze dynamic correlations in gene expression profiling data, the expression levels of certain genes are treated as indicators of cellular states, and correlation changes conditioned on such genes are computed (Boscolo et al., 2008; Chen et al., 2011; Li, 2002). The selection of such genes may be ad hoc and subjective, and the resulting gene pairs with dynamic correlation may be functionally divergent and difficult to interpret. To address such issues, we consider the existing biological networks, such as protein-protein interaction (PPI) network and signal transduction network. Such networks provide known functional links between the biological units. Integrating expression data with existing biological networks has proven to be an effective approach to reduce spurious findings and achieving more interpretable results (Barabási, 2007; Barabási et al., 2011; Chan and Loscalzo, 2012). By allowing genes to borrow information from those of related biological functions, such methods can better resist the tendency of generating false positive results in the presence of measurement noise. So far such work has been solely focused feature selection—finding subnetworks that associate with certain disease outcomes (Chen et al., 2013; Ciriello et al., 2012; Nie and Yu, 2013; Sanguinetti et al., 2008; Su et al., 2010; Taylor et al., 2009; Wei and Pan, 2010; Wei and Pan, 2012; Yang et al., 2014; Zhao et al., 2014). Not much attention has been paid to the behavior of the network itself. In this work, our purpose is to develop a new method that can find sub-regions of the genome-scale network that show dynamic relationships between each other. We utilize Liquid Association (LA) for gene-level dynamic correlation detection (Li, 2002), and the ego-network concept to define subnetworks (Yang et al., 2014).

An ego-network is a sub-network that involves a particular node that is called ego, and a neighborhood around this node (Borgatti et al., 2009). The ego node is the focal point, and a K-step ego-network includes the ego node itself, and all nodes to which the ego node has a connection at path length ≤K, as well as all the edges between them. Every node in the overall network can be an ego node. Using the ego network concept, it is straightforward to delineate subnetworks. Biologically, an ego node itself may not exhibit certain behavior at the expression level, while other nodes in its neighborhood can provide evidence that the ego node is in fact relevant, which is valid because the activities of many proteins are regulated in a post-translational manner, and may not be reflected by measurements of gene expression. Moreover, focusing on one ego node at a time means the computation can be conducted efficiently using deterministic iterations (Yang et al., 2014).

Liquid Association (LA) is a method that detects three-way interactions between genes (Li, 2002), which has been shown to reveal dynamic relations in gene expression that are not found by traditional correlation-based methods (Chen et al., 2012; Li et al., 2007). LA reveals the change of co-expression pattern for a pair of genes. A third gene called LA-scouting gene is used to indicate the cellular state change (Li, 2002). Focusing on LA relations between regions of the existing biological network can greatly improve the interpretability of the results. By combining LA with the ego-network approach, and using mixture models for LA scores through local false discovery rate (lfdr) inference (Efron and Tibshirani, 2002), our method finds network regions where the LA scouting genes to a given ego-network are concentrated. Using real data, we show that the method not only recovers existing knowledge about regulatory relations between the biological functions represented by the subnetworks, but also discovers new and plausible relations that could help future biological studies.

2 Methods

2.1 Calculating liquid association (LA) score

The goal of LA is to reveal the dynamics of co-expression patterns for a pair of genes. There are different methods to detect LA activities between a pair of genes X and Y, and here a third gene Z called LA-scouting gene is used following the original work by Li (2002). Specifically, between the three random variables (genes), Li defined $LA\left(XY\right|Z)=E(XY\left|Z\right)$ as the LA score to measure the dynamic correlation between X and Y, with Z as the biological state indicator, and derived the theory that $LA\left(XY\right|Z)=E(XYZ)$ following proper data standardization to have mean 0 and variance 1 (Li, 2002). The sample version of the LA score is $LA\left(XY \right| Z)={\sum }_i{x}_i{y}_i{z}_i/n$, where n is the sample size.

The LANDD algorithm takes an existing network and gene expression data matrix as input data (Fig. 1a). In the network data, each node represents a gene, and each edge represents a biological link, e.g. physical interaction or signal transduction, depending on the choice of the network. Our method assumes the network is given, and does not attempt to modify the network. We further discuss the choice of network in the Discussions section. In the gene expression matrix, each row represents a gene and each column is a specific sample. First, data cleaning is performed to find common genes between the network and the expression matrix. Second, the n × m expression matrix is normalized using normal score transformation for every row. This is to simplify the calculation of LA scores as recommended in (Li, 2002).

Fig. 1.

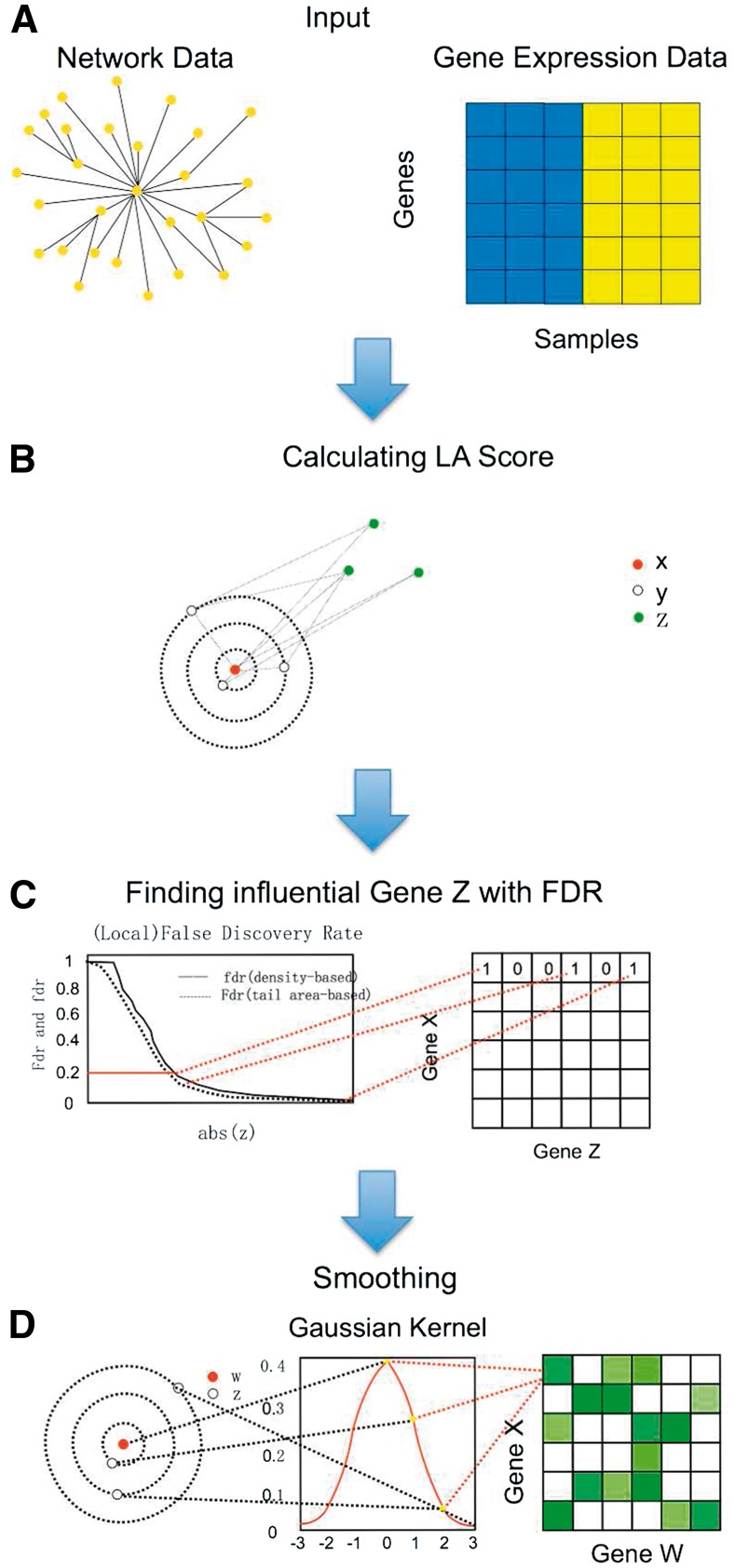
The workflow of the LANDD method (Color version of this figure is available at Bioinformatics online.)

2.2 Selecting scouting genes for ego-networks

The algorithm then iteratively scans through all genes in the network as gene X (Box 1). For each X, it finds the K-step ego-network. Every gene in the ego-network is connected to gene X at a certain path length ranging from 1 to K. The algorithm iterates through all genes in the ego-network as gene Y. All other genes in the network are treated as gene Z for the calculation of LA score (Fig. 1b).

Box 1.

The pseudocode for conducting LA scouting gene search on the network.

Finding scouting genes

Input: G (graph of gene network), M (expression matrix), K (neighborhood order), $T$ (local fdr threshold)

Output: Scouting genes: S

Standardize each row of M

n = the number of rows (genes) in M

m = the number of columns (samples) in M

for each node X in G do

  Scouting genes S_X= Φ

  N = neighborhood within K steps of X

  for each node Y in N do

    for each node Z_i in G do

      LA_i = (x₁y₁z_i1+…+x_my_mz_im)/m

      Fit {LA_i}_{i = 1,…,n} from all genes to mixture model using fdrtool to find {lfdr_i}_{i = 1,…,n}

      $S_X=S_X \cup \left\{Z_i: {lfdr}_i\le T\right\}$

    End for

  End for

End for

Return S = {S_X, for every gene X in G}

After LA scores for all possible Z’s are calculated for a pair of gene X and gene Y. We need to determine which gene, among all the nodes of the network, have significant LA relationship with the (X, Y) pair. We achieve this goal by fitting a mixture model to all the LA scores for the X–Y pair. When X, Y and Z all follow normal distribution, and when Z is unrelated to X and Y, the LA score LA(XY|Z) approximately follows a normal distribution, even if X and Y are correlated (Supplementary Fig. S1). A true scouting gene Z will bring the LA score to more extreme values compared to the normal distribution. Thus we can consider all the LA scores between an X–Y pair and all the potential Z’s to follow a mixture model of two components:

$$f\left(LA\right)={\pi }_0{f}_0\left(LA\right)+(1-{\pi }_0)f_1\left(LA\right),$$

where f is the mixture density for the observed LA score, $f_0$ and $f_1$ are the respective densities of the statistic of the null (non-scouting) and non-null (scouting) genes, and ${\pi }_0$ is the proportion of true null genes. Here $f_0$ is a normal distribution with unknown parameters that depend on the joint distribution of X and Y, and $f_1$ is an unknown distribution. This setup follows exactly the literature on local false discovery rate (lfdr) (Efron and Tibshirani, 2002). Based on the mixture model, the local fdr methods can estimate the probability of each candidate Z gene belongs to the null (non-scouting) category by density estimation procedures. In this study we used the R package fdrtool (Strimmer, 2008) to fit the LA scores and separate LA scouting genes from the rest (Fig. 1c).

Each ego node X may have multiple neighbors in the K-step neighborhood that can serve as Y. The above procedure is repeated for every Y. The null distribution of each (X, Y) pair may be different from others. As long as a gene is found to be a scouting gene for one (X, Y) pair, it is considered a scouting gene for the ego-network centered at X (Fig. 1c).

2.3 Finding scouting ego nodes using kernel smoothing

Usually, there are several scouting genes Z for each gene X. Finding network regions where scouting genes are enriched can shed light on the functional implications on the LA relations, as well as reduce the impact of false positives. We employ the truncated Gaussian kernel to find nodes around which scouting genes for a given X is concentrated (Fig. 1d). We consider one X node at a time. For every scouting node Z selected for X, we spread its signal to its network neighborhood. Let k be the distance of a node in the neighborhood to Z. We assign a weight of $\varphi \left(k\right)$ to the node, where $\varphi \left(\right)$ is the density of standard Gaussian distribution. We only considered nodes up to two steps from Z.

Given that the number of nodes around every Z is different, normalization needs to be conducted. We provide three different ways for users to choose from, which are normalizing with the total weight, the square root of total weight, and no normalization. The first normalization method results in the total weight of the neighborhood of every Z, including Z itself, to be exactly 1. The other two favor nodes around large hubs.

Similar to the ego-network approach, this procedure allows us to find nodes around which scouting genes are concentrated, even when the node itself is not a scouting gene. After this procedure, every node on the network is assigned a value. Then we can use thresholding to select the nodes with highest scores. As they may or may not be the scouting nodes (Z) originally selected, we name such nodes ‘scouting ego nodes’, and use W to denote them.

2.4 Finding network communities of scouting ego nodes

Up to this step, we can find a list of scouting ego nodes for every ego-network. Data interpretation can be conducted at the scouting ego node (W) level. In order to further simplify the result and provide a high-level summary, we further divide the scouting ego nodes for each ego-network into dense sets, using the network connectivity structure between them.

For this purpose, we apply a well-established method that detects dense sub-graphs from a sparse graph by short random walks (Pons and Latapy, 2005). The scouting ego nodes (W) are grouped into communities. After detecting several communities among the W nodes, we use the GOstats method to evaluate the biological functions of each community of W (Falcon and Gentleman, 2007), based on the Gene Ontology biological processes. In the output object, the significant biological processes for the W nodes are juxtaposed side-by-side with the significant biological processes of the corresponding ego-network (X and Y nodes) for the ease of results interpretation. In addition, the median semantic distances on the GO system between the communities of the W nodes and the X node are calculated to facilitate the comparison (Yu et al., 2010).

3 Results

3.1. Simulation study

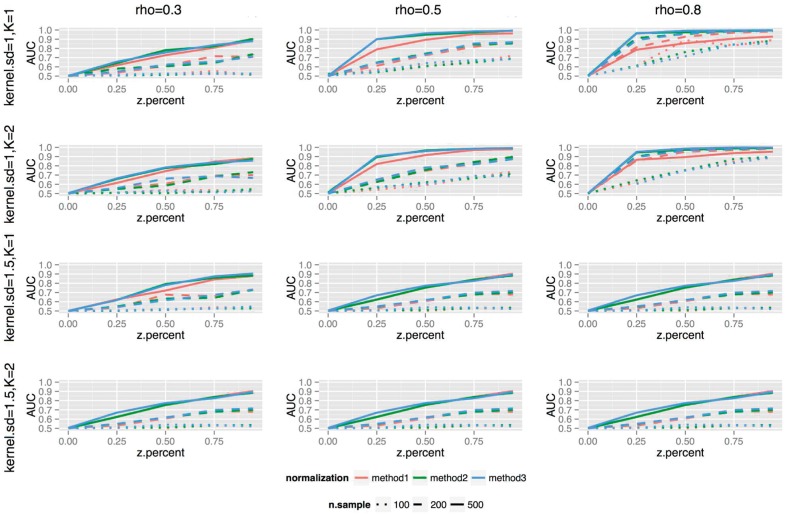
An R package of the method is available at https://cran.r-project.org/web/packages/LANDD. We conducted a systematic study using simulated data. In each simulation, (1) a scale-free network of 5000 nodes was generated using the Barabasi-Albert model (Barabasi and Albert, 1999), with a connectivity level similar to the real network used in the next section. (2) The expression data matrix was generated using multivariate normal distribution, in which the covariance structure was determined by the network structure. The covariance between any pair of genes was set to 0.4^k, where k was the shortest distance between the two nodes, and the variance of each gene was set to 1. (3) We then randomly selected one ego node whose 2-step ego network contained 20 to 40 nodes as the X node. (4) A portion of the nodes in the 2-step ego-network were randomly selected as the Y nodes. (5) For the W node, we randomly selected a node that was at least 5 steps away from the X node, which also has more 2-step neighbors than the number of Y nodes, and randomly selected a Z node in its two-step neighborhood for each Y node selected in step 4. (6) For each Z node, the expression vector was replaced by generating new expression values that are rank-correlated with the $X\times Y$ values, such that LA relationships were established. Three parameters were used to control the signal strength in the data: (a) rho, which controls the strength of LA relationship. Three levels were used: weak, medium and strong (rho = 0.3, 0.5, 0.8). (b) The proportion of Y nodes among all nodes in the X ego network (z.percent = 0, 0.25, 0.5, 0.75, 0.95). (c) Sample size in the simulated expression data (n.sample = 100, 200, 500).

After data generation, we analyzed the data using LANDD at different parameter settings. They include the size of the ego network (K = 1, 2), normalization methods (method 1, method 2, method 3), normalization Gaussian kernel standard deviation (kernel.sd = 1, 1.5). Every parameter combination was run 50 times. We evaluated the results by the receiver-operating characteristic (ROC) analysis, which evaluates the capability of all X–W scores to differentiate true W genes from the rest. The area under the curve (AUC) of ROC was used to summarize the results.

The simulation results showed that when no true LA relation is present (z.percent = 0 in each plot), the AUC is close to the theoretical minimum of 0.5 in all cases (Fig. 2). When z.percent (left to right of each sub-plot) or the LA strength (left to right columns) increases, the AUC also increases. The three normalization methods exhibit the same trend, while the normalization methods that favor nodes with higher degrees (blue and green curves) showed slightly better performance. However, this could be due to the generation process of the simulations, which favored the selection of higher-degree nodes when selecting the true W nodes. The K value (1st row versus 2nd row; 3rd row versus 4th row) did not impact the results much, while the smoothing kernel standard deviation (top two rows versus bottom two rows) impacted the results substantially, with kernel.sd = 1 performing better than kernel.sd = 1.5. Higher sample size yielded higher AUC (different line types). In summary, the capability of LANDD to rank the correct W genes higher, i.e. sensitivity, increases with the sample size and LA relation strength. When the LA strength is medium to strong, and LA relation is pervasive between two sub-networks, LANDD has a high likelihood to give high score to the correct W genes.

Fig. 2.

Simulation results. In each sub-plot, the X-axis represents the proportion of Y nodes among all nodes in the X ego network; the Y-axis represents the area under the curve (AUC) of the receiver-operating characteristic (ROC) curve that measure the association between W node scores with the true W node locations. Line colors represent normalization methods, and line types represent sample sizes. The columns of sub-plots represent different LA association strengths, and the rows represent combinations of K values, i.e. ego network size, and kernel standard deviations used in the kernel smoothing to calculate W scores

3.2. Real data analysis

To assess the performance of LANDD, we conducted real data analysis of an expression dataset. The data we used in this study is the GSE10255 dataset downloaded from the Gene Expression Omnibus (GEO). The data contained gene expression in diagnostic bone marrow leukemia cells in patients with primary acute lymphoblastic leukemia (ALL). ALL is a blood cancer with the typical outcome of the accumulation of abnormal leukemia cells that can't mature properly. We selected the probesets with known ENTREZ Gene IDs. For genes represented by more than one probesets, we merged the corresponding probesets by taking the mean expression levels. The data matrix contained 12 704 rows (genes) and 161 columns (samples). Although the original study was focused on associating gene expression with methotrexate (MTX) treatment, the data was generated at baseline and feasible to study general gene expression patterns in diagnostic bone marrow leukemia cells (Sorich et al., 2008). In this study we consider the general interaction patterns between genes on the known biological network. For the network, we used the protein-protein interaction (PPI) network from the HINT database (Das and Yu, 2012), which combines data from several databases and filters the interactions manually to remove erroneous interactions. The network we used contained 8292 proteins and 27 493 binary interactions. After finding overlaps between the expression data and the network, 6856 common nodes remained.

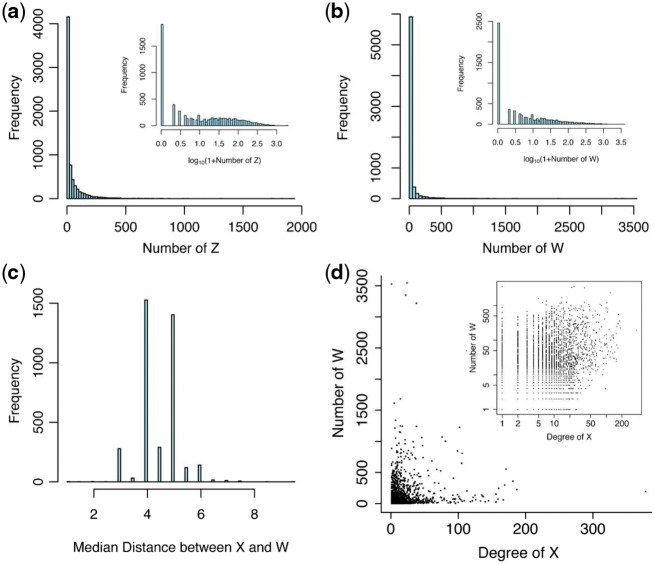
We applied the new method LANDD to the data, using ego network size limit K = 2, lfdr cutoff value 0.2 to select Z nodes, and W node selection threshold 0.2. Over all the ego-networks, the distribution of the number of Z nodes and the number of W nodes are highly skewed, which indicates LA relations are important only for a portion of genes (Fig. 3). Because of the heavy skewness of the data (Fig. 3a, b), median values better summarize the results than mean values. The median number of Z nodes detected for any X node is 9; for 1910 X nodes, no Z node was detected (Fig. 3a). The median number of W nodes detected for any X node is 4; for 2459 X nodes, no W node was detected (Fig. 3b). Figure 3(c) shows the distribution of median network distance between X and its W nodes. The overall median for all X’s is 4.5. The number of W nodes detected didn’t have much relation with the connectivity (degree) of X nodes (Fig. 3d).

Fig. 3.

Summary plots of the results from GSE10255 and the HINT interaction database. (a) Histogram of the number Z genes found for each X; (b) histogram of the number of W genes found for each X; (c) histogram of the median graph distance between W nodes and X nodes, for each X; (d) scatter plot of the number of W nodes found against the degree of the X nodes. Insets: plots on log10 scale

The full results of the W genes found for each X, as well as their main biological functions as defined by over-represented gene ontology (GO) biological process terms found by the GOstats package (Falcon and Gentleman, 2007) are listed in the supplementary file at http://web1.sph.emory.edu/users/tyu8/LANDD%20Supplements/Spt_2_all_W.xls.

For each X node, when a number of W nodes were found, we further conducted community detection among the W nodes. The biological functions of the detected communities are listed in the supplementary file at http://web1.sph.emory.edu/users/tyu8/LANDD%20Supplements/Spt_3_W_community.xls. We further selected a few examples to illustrate the results.

In the first example, the X gene, 26 119, encodes the low-density lipoprotein receptor adaptor protein 1 (LDLRAP1, or ARH), which contains a phosphotyrosine binding domain (Dvir et al., 2012). The phosphotyrosine binding domain of LDLRAP1 binds to the tail of low-density lipoprotein receptor (LDLR) in a sequence-specific manner (He et al., 2002). The function analysis of the two-step ego-network around 26 119 indicated that the major functions of LDLRAP1 and its interacting proteins include immune effector process (Hermansson et al., 2010) and cholesterol and sterol homeostasis (Cohen et al., 2003; Garuti et al., 2005).

As shown in Figure 4, two W communities were identified for gene 26 119, together with some individual W genes. The first W community (W1) contains 15 genes (indicated as blue dots), which are all related to tyrosine kinase superfamily. They include genes ABL1, EGFR, ERBB2, YFN, GH1, GHR, GRB2, PIK3R1, PKD1, PKD2, PTPN6, PTPRC, SRC and TEC. There are many studies indicating that tyrosine kinase family regulates LDL receptor and LDL adapter protein. For example, The estrogen-induced transcription of the low-density lipoprotein receptor (LDL-r) depends on tyrosine kinase (TK) and protein kinase C (PKC) activation (Distefano et al., 2002). So the genes in W1 community are likely involved in the regulation of the homeostasis of lipid, one of the major direct biological functions of gene X, 26 119.

Fig. 4.

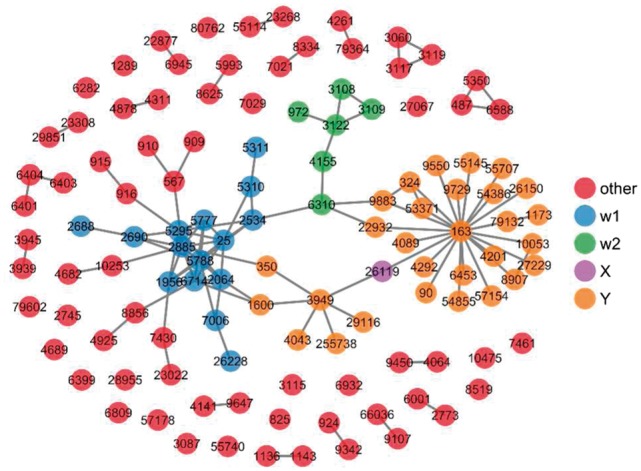
The two-step ego-network of gene 26 119, and the detected W genes for the ego-network. The detected communities of W genes are colored differently

The second W community (W2) contains six genes, which are indicated in green dots (Fig. 4). The proteins encoded by these genes are involved in the major histocompatibility complex II molecules (the class II MHC complex). MHC II are a family of molecules normally found only on antigen-presenting cells, including dendritic cells, T cells and B cells and play important role in immune process development. Studies have indicated that MHC II processing pathways are critically associated with the immune-related biological function of gene X, 26 119. It has been shown that plasma LDL and oxLDL levels constitute signals that can up-regulate MHC II in immature dendritic cells (Zaguri et al., 2007), in which LDLRAP1 is likely to play a role.

Given that a number of W nodes didn’t fall into any network community (Fig. 4, red nodes), we also studied the biological functions of all W nodes together using Gene Ontology. As shown in Table 1, the most significant GO terms are concentrated in immune system functions and immune-related signal transduction pathways.

Table 1.

Top 25 over-represented GO biological processes for genes 26 119 and 924.^a

X gene: 26119

Leukocyte cell-cell adhesion: 5.4694e-16

T cell costimulation: 6.212e-14

T cell activation: 4.6677e-13

T cell aggregation: 4.6677e-13

T cell receptor signaling pathway: 5.1054e-10

Antigen receptor-mediated signaling pathway: 6.115e-10

Lymphocyte differentiation: 1.7846e-07

Antigen processing and presentation of exogenous antigen: 1.239e-06

Immune response-activating signal transduction: 1.2725e-06

Lymphocyte proliferation: 1.6325e-06

Response to interferon-gamma: 2.6283e-06

Interferon-gamma-mediated signaling pathway: 2.9274e-06

Leukocyte differentiation: 5.1616e-06

Response to cytokine: 7.4043e-06

Antigen processing and presentation: 8.9682e-06

T cell differentiation: 1.1261e-05

Cellular response to interferon-gamma: 1.2995e-05

Antigen processing and presentation of exogenous peptide antigen via MHC class II: 2.5379e-05

Antigen processing and presentation of peptide or polysaccharide antigen via MHC class II: 3.0822e-05

Thymic T cell selection: 3.4917e-05

Cellular response to cytokine stimulus: 4.3809e-05

Antigen processing and presentation of exogenous peptide antigen: 4.568e-05

Calcium ion transport: 5.0122e-05

Immune effector process: 5.5959e-05

B cell activation: 0.00010786

X gene: 924

Leukocyte cell-cell adhesion: 3.8768e−15

Leukocyte aggregation: 7.339e−15

Regulation of T cell activation: 2.0694e−13

T cell costimulation: 1.4367e−11

Antigen receptor-mediated signaling pathway: 2.3406e−09

Lymphocyte differentiation: 5.8768e−09

T cell proliferation: 1.0758e−06

T cell selection: 1.1524e−06

Regulation of immune response: 2.4014e−06

Immune response-regulating signaling pathway: 8.3202e−06

Antigen processing and presentation of exogenous peptide antigen via MHC class II: 1.3205e−05

Interferon-gamma-mediated signaling pathway: 1.6072e−05

Phosphatidylinositol 3-kinase signaling: 2.3359e−05

Response to cytokine: 2.6589e−05

Positive regulation of intracellular signal transduction: 3.8474e−05

Hemopoiesis: 4.2317e−05

Phosphatidylinositol-mediated signaling: 4.6578e−05

Platelet activation: 6.6332e−05

Hematopoietic or lymphoid organ development: 8.1033e−05

Regulation of peptidyl-tyrosine phosphorylation: 0.00020249

Fibroblast growth factor receptor signaling pathway: 0.00024721

Response to fibroblast growth factor: 0.00045182

Regulation of ERK1 and ERK2 cascade: 0.00049142

Adenylate cyclase-modulating G-protein coupled receptor signaling pathway: 0.00076589

Fc-gamma receptor signaling pathway involved in phagocytosis: 0.00082535

^aGO terms are followed by P-value; some redundancies manually removed.

Another example ego (X) node is gene 924, which encodes CD7, a member of the immunoglobulin superfamily. CD7 plays an essential role in T cell interactions and T-cell and B-cell interactions during early lymphoid development. CD7 is an important immunological marker in ALL. Aberrant expression of CD7 is associated with acute myeloid leukemia (AML) (Cruse et al., 2005; Rausei-Mills et al., 2008). The function analysis indicates that the CD7 is involved in the pathways related to vesicle transport, fusion docking and localization. A single community was found for 924. As shown in Figure 5, there are 18 genes in the W community (indicated as blue dots). The genes in W community include ADRB2, B2M, CD3D, CD3E, CTNNB1, EGFR, FYN, GRB2, NUBP1, PIK3R1, PTPN6, PTPRC, SRC, SYK, SPRY2, SEMA4D, GNA15, CD1B. They regulate the aggregation, adhesion, activation and differentiation of different immune cells including leukocyte, lymphocyte, T cell and so on, which are closely related to the biological function of the X gene 924.

Fig. 5.

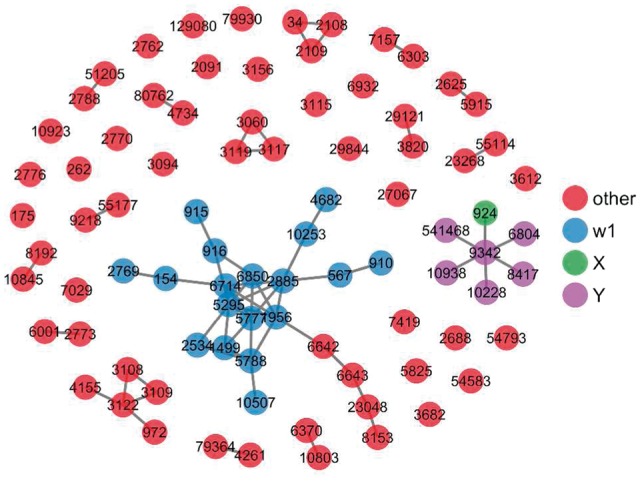
The two-step ego-network of gene 924, and the detected W genes for the ego-network. The detected communities of W genes are colored differently

Again we also studied the biological functions of all W nodes together using Gene Ontology (Table 1). Similar to gene 26 119, the most significant GO terms are concentrated around immune system functions and signal transduction pathways. Given the ego node 924 (CD7) is a member of the immunoglobulin superfamily, and is directly involved in T cell interactions and T-cell and B-cell interaction, the results clearly conform to existing knowledge.

On the other hand, some genes that have no obvious association with leukemia and/or immune system were also found. As an example, the gene 8192 (caseinolytic mitochondrial matrix peptidase proteolytic subunit, CLPP) was found to be one of the LA scouting ego nodes for 924 (CD7). The protein encoded by this gene is a member of the peptidase family S14. It is located in the mitochondria and hydrolyzes proteins in the presence of ATP and magnesium. Recent work has found the inhibition of this protease has therapeutic effect on Acute Myeloid Leukemia (AML) (Cole et al., 2015; Larkin and Byrd, 2015), indicating a potential functional relationship between the W gene 8192 with the immune-related functions surrounding CD7.

When we consider all X nodes together, we found some nodes tend to serve as LA scouting ego nodes (W) for many X nodes. We selected the top 50 nodes that have the highest frequency to be W nodes, and analyzed their biological function using GOstats (Table 2). Among the top 25 significant GO terms, we can see the functions are clustered around three themes: immune system function, signal transduction (mostly in relation to immune system), as well as differentiation and development. 17 of the 50 genes fall into enzyme linked receptor protein signaling pathways. Because LA relationship implies potential regulative relations, the excess of signal transduction related genes in the top W nodes is expected.

Table 2.

Top 25 over-represented Gene Ontology biological process terms of the top 50 LA scouting ego genes (W genes), after manual removal of overly broad and overlapping terms

GOBPID	P-value	Count	Size	Term
GO:0002768	5.59E−09	13	261	Immune response-regulating cell surface receptor Signaling pathway
GO:0045321	7.87E−09	16	447	Leukocyte activation
GO:0032386	1.76E−08	13	287	Regulation of intracellular transport
GO:0038093	2.17E−08	11	190	Fc receptor signaling pathway
GO:0032880	3.79E−08	14	366	Regulation of protein localization
GO:0002252	1.44E−07	14	407	Immune effector process
GO:0050776	1.51E−07	16	551	Regulation of immune response
GO:0002764	2.32E−07	13	357	Immune response-regulating signaling pathway
GO:0071495	4.44E−07	17	677	Cellular response to endogenous stimulus
GO:0006913	1.24E−06	11	283	Nucleocytoplasmic transport
GO:0031295	1.32E−06	6	56	T cell costimulation
GO:0048546	1.34E−06	5	31	Digestive tract morphogenesis
GO:0071822	1.42E−06	19	917	Protein complex subunit organization
GO:0044744	1.47E−06	9	177	Protein targeting to nucleus
GO:0043066	1.94E−06	14	504	Negative regulation of apoptotic process
GO:0000904	3.37E−06	14	528	Cell morphogenesis involved in differentiation
GO:0010647	4.41E−06	17	797	Positive regulation of cell communication
GO:0048699	5.23E−06	17	807	Generation of neurons
GO:0071214	5.42E−06	8	155	Cellular response to abiotic stimulus
GO:0009719	5.74E−06	18	907	Response to endogenous stimulus
GO:0042060	7.21E−06	13	484	Wound healing
GO:0042177	8.06E−06	5	44	Negative regulation of protein catabolic process
GO:0042325	9.17E−06	17	841	Regulation of phosphorylation
GO:0048565	9.36E−06	6	78	Digestive tract development
GO:0071363	1.01E−05	13	499	Cellular response to growth factor stimulus

4 Discussion

In this manuscript we present a method LANDD, which finds sub-networks with concentrated Liquid Association relationships. The calculation of Liquid Association scores is done one gene triplet at a time, independent from other genes. The network structure is then imposed to select LA scouting genes and LA scouting ego nodes for each ego-network. For each X–Y pair, a mixture model was fit by the local fdr approach to best separate LA scouting and non-scouting genes. We note that between the LA scores of different Z genes for each X–Y pair, and more broadly between different X–Y pairs, correlations exist. Thus the local fdr results are only used as heuristics to separate the mixture and select scouting genes, but cannot be taken as posterior probabilities.

LANDD is a heuristic method that combines several approaches. Thus several parameters can impact the results. There are three key parameters. The parameter K, i.e. the size of the ego network to consider, reflects the user’s belief of how wide a neighborhood on the network is considered to be ‘local’ to the ego node. In other words, how close do two nodes need to be for their biological function to be related and their dynamic correlation to be meaningful. Another important parameter is the normalization method, which reflects the consideration of whether to favor nodes with a higher number of connections. In the biological system, often hub nodes play important roles. The third key parameter is the standard deviation of the kernel. Similar to the parameter K, it reflects our belief of how concentrated on the network the scouting signal should be. In our simulation studies (Fig. 2), we have shown these parameters could change the sensitivity to detect true LA relationships. We next conduct a comparison using the real data.

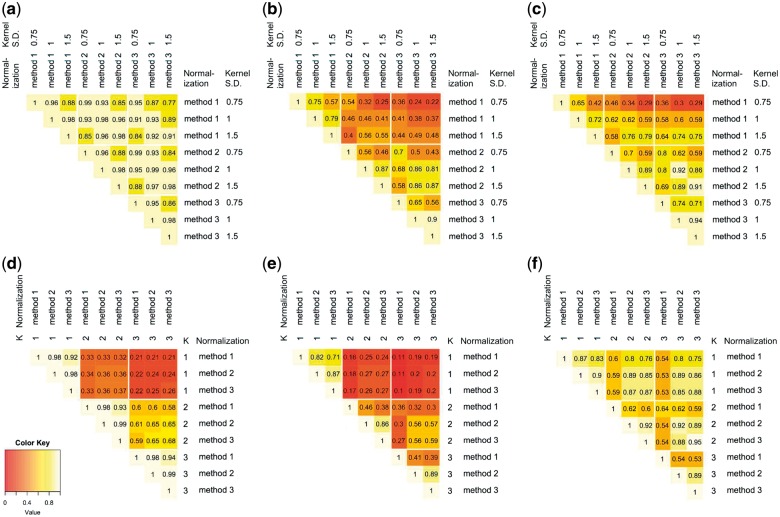
First fixing K = 2, we varied the normalization method and the kernel SD, and made pairwise comparisons between parameter settings with regard to the median column-wise correlation of the raw LA relation scores in the n by n matrix with X genes in the row and W in the column, the overlap of all selected X–W pairs, and the overlap between the selected top 50 scouting egos (Fig. 6a–c). Because the score distribution, hence the selection threshold, depends on the parameter settings, to simplify the comparison, we fixed the quantile for selecting X–W pairs to the same as reported in Section 3.2, such that roughly the same number of X–W pairs were selected at every parameter setting.

Fig. 6.

Comparisons of the results generated from different parameter combinations. Top row: fixing K = 2 and vary the normalization method and kernel standard deviation (SD). (a) Median correlation of each node’s W score; (b) proportion of overlap between the selected lists of X–W pairs; (c) proportion of overlap between the selected lists of top 50 scouting ego nodes. Bottom row: fixing normalization Gaussian kernel SD = 1, and vary K and normalization method. (d) Median correlation of each node’s W score; (e) proportion of overlap between the selected lists of X–W pairs; (f) proportion of overlap between the selected lists of top 50 scouting ego nodes (Color version of this figure is available at Bioinformatics online.)

Changing the normalization methods and kernel SD, we observed that the correlation of X–W pair scores were relatively high across all settings (Fig. 6a), ranging from 0.77 to 0.99. After thresholding the scores to obtain the top X–W pairs, we observed relatively high overlap rate between normalization methods 2 and 3, as well as between kernel SD 1 and 1.5 (Fig. 6b). The selection of top 50 W scouting egos appears to be more consistent across different parameter settings (Fig. 6c). This is expected as the selection of top 50 scouting egos is an aggregation over the selected X–W pairs.

We then fixed the kernel SD at 1, and varied the value of ego network size K and the normalization method (Fig. 6 d–f). With regard to the X–W score correlation (Fig. 6d), and the selected X–W pair overlap (Fig. 6e), clearly K had a much bigger impact than the normalization method. Within each K value setting, normalization methods 2 and 3 agreed better with each other. Overall, between K = 2 and K = 3, the agreement was reasonably high. On the other hand, the agreement of the top 50 scouting egos was much less impacted by the K value, especially between normalization methods 2 and 3 (Fig. 6f).

Overall, we observed reasonable agreement when changing the parameters. The parameter that showed the largest impact was K, the size of the ego network. The biological network can have varying characteristics in different sub-regions. One set of parameter may not be optimal for all sub-regions of the networks. Thus the differences in the results using different parameter settings may partially reflect different sensitivity each parameter setting has on different sub-regions of the network. We will explore methods for adaptive parameter tuning across the whole network in future studies.

Multi-gene relationships can be difficult to discover and interpret. However when correctly identified, they can bring deeper understanding to the high dimensional data. Approaches similar to LA, such as likelihood-based methods and those using information theory, have also been proposed (Boscolo et al., 2008; Chen et al., 2011). In this study, we anchored LA relations on existing biological network, and pooled information from network neighborhoods using the ego-network concept. Such a procedure limits the search space of gene triplets, and hence the computing cost. In addition, genes in ego-networks tend to be functionally related. Focusing on ego networks and ego scouting nodes makes the results easily interpretable.

Our method relies on an existing biological network. There are a number of databases available on protein-protein interaction networks, signal transduction networks, etc. We point the reader to some recent reviews (Chowdhury and Sarkar, 2015; Szklarczyk and Jensen, 2015). Characteristics of the network, such as the degree distribution, the diameter of the graph, etc., and more importantly, the local functional consistency of the network, are expected to impact optimal parameter setting. To fully understand their impacts, a systematic study will be necessary, which should include large scale simulations and more importantly, analysis of the characteristics of existing biological networks. This is out of the scope of the current work. We plan to conduct the study in the near future.

LANDD limits the computation of LA scores to gene pairs that are within a certain path length on the network. Suppose the network consists of N nodes, and there are in total M_k node pairs that are within K steps of distance. Because the network structure can vary, we cannot express M_K as a function of N and the average degree. However given that we use a K that is small, we expect M_K≪N². The step of calculating LA scores to find the Z genes has a computing complexity of O(NM_K). In the following step of kernel smoothing and finding the W genes, we used a truncated kernel that only spread the signal up to 2 steps, then the complexity is O(NM₂). Supplementary Figure S2 shows the computing time at different network size and K values, under the setting of the simulation study (Section 3.1), using a laptop computer with a 2.8 GHz Intel core i7 CPU and 16 Gb memory. With 5000 nodes and K = 2, and sample size of 500, the computation takes 4.3 min. With K = 3, the computation takes 21 min, because the M₃ is much larger than M_2.

There are certain caveats to our method. The first is some truly related gene triplets may not be close on the existing network, given the limitations of current knowledge of the biological network. They will be missed by the method. Secondly, although ego-network is a very convenient concept to use in generating subnetworks, it has its limitations, the most critical of which is the fact that different ego-networks can be partially overlapping. Nonetheless, it has been demonstrated that with some expert input and targeted examination of the results, methods using the ego-network concept yield easily interpretable results. In addition, using the ego-network concept allows users to easily focus on pre-selected genes of biological relevance.

Overall, the method LANDD (Liquid Association for Network Dynamics Detection) extracts new dynamic correlation relations on the genome-scale network that are not detected using existing methods. It can help to generate new biological insights and testable hypotheses.

Funding

This work was partially supported by NIH grants 2U19AI057266 and R15GM113120, Ministry of Science and Technology of China National Key Research Program grant No. 2016YFC0206507, 973 Program grant No. 2013CB967101, Natural Science Foundation of China No.41476120, No.61572362, and No.81571347, Shanghai Eastern Scholar program, and Shanghai Science Committee Foundation (13PJ1433200).

Conflict of Interest: none declared.