Abstract
We develop a transport formula for predicting overall cumulative vaccine efficacy through time t (VE(t)) to prevent clinically significant infection with a genetically diverse pathogen (e.g., HIV infection) in a new setting for which a Phase III preventive vaccine efficacy trial that would directly estimate VE(t) has not yet been conducted. The formula integrates data from (1) a previous Phase III trial, (2) a Phase I/II immune response biomarker endpoint trial in the new setting where a follow-up Phase III trial is planned, (3) epidemiological data on background HIV infection incidence in the new setting; and (4) genomic epidemiological data on HIV sequence distributions in the previous and new settings. For (1), the randomized vaccine versus placebo Phase III trial yields estimates of vaccine efficacy to prevent particular genotypes of HIV in participant subgroups defined by baseline covariates X and immune responses to vaccination S(1) measured at a fixed time point τ (potential outcomes if assigned vaccine); often one or more immune responses to vaccination are available that modify genotype-specific vaccine efficacy. The formula focuses on subgroups defined by X and S(1) and being at-risk for HIV infection at τ under both the vaccine and placebo treatment assignments. For (2), the Phase I/II trial tests the same vaccine in a new setting, or a refined new vaccine in the same or new setting, and measures the same baseline covariates and immune responses as the original Phase III trial. For (3), epidemiological data in the new setting are used to project overall background HIV infection rates in the baseline covariate subgroups in the planned Phase III trial, hence re-calibrating for HIV incidence differences in the two settings; whereas for (4), data bases of HIV sequences measured from HIV infected individuals are used to re-calibrate for differences in the distributions of the circulating HIV genotypes in the two settings.
The transport formula incorporates a user-specified bridging assumption function that measures differences in HIV genotype-specific conditional biological-susceptibility vaccine efficacies in the two settings, facilitating a sensitivity analysis. We illustrate the transport formula with application to HIV Vaccine Trials Network (HVTN) research. One application of the transport formula is to use predicted VE(t) as a rational criterion for ranking a set of candidate vaccines being studied in Phase I/II trials for their priority for down-selection into the follow-up Phase III trial.
Keywords: Case-control design, Case-cohort design, Clinical trials, Generalizability, Immune correlate of protection, Principal stratification, Vaccine efficacy trial
1. Introduction
Ideally, decisions on licensure and deployment of a vaccine for various settings would be based on direct data on efficacy to prevent a clinical endpoint from Phase III trials in each and every setting. However, there are a vast number of different settings, defined by (1) features of the vaccine regimen such as schedule, dose, adjuvant, delivery vector, combination of components, and vaccine strains; (2) features of study participants such as demographics, genetics, and exposure to the pathogen under study; and (3) features of the pathogen such as genotype, serotype, or other phenotypes. Because resource and ethical constraints prohibit this fully direct approach, regulatory agencies allow decisions to be based on immune response data in a new setting (without direct efficacy data) provided that the selected immune response biomarkers are credibly valid immune correlates of protection (FDA Guidance Document, 2007), i.e., are approximately valid surrogate endpoints that can be used to reliably predict the level of vaccine efficacy against the clinical endpoint (Plotkin and Gilbert, 2012). Despite the ubiquity of this application and its critical importance, there do not appear to be published formal statistical formulas that aide such predictions (albeit formulas from other work could certainly be extended to this application). We provide such a bridging transport formula, which lays out the specific component terms that need to be correctly specified or estimated to obtain an accurate prediction, and exposit the several assumptions that are needed, highlighting the difficult challenges posed to succeeding in this objective without collecting the direct efficacy data. We also show how to quantify uncertainty in the prediction, and provide a framework of sensitivity analysis to violation of key assumptions. We develop the formula supposing two experiments, the original Phase III efficacy trial (or series of similar trials) that is used to estimate how type-specific vaccine efficacy varies across participant subgroups defined by baseline covariates and immune responses to vaccination, and a subsequent Phase I/II trial in the new setting that measures the same baseline covariates and immune responses. The formula also inputs epidemiological data on background disease incidence in the new setting and genomic epidemiological data on the distributions of pathogen types in the two settings.
Literature for methods tackling a similar objective include Cole and Stuart (2010) and Pearl and Bareinboim’s (2011) transport formula, the latter of which uses causal selection diagrams to formally encode knowledge of how the original and new settings differ. We use an alternative approach that encodes the bridging assumptions using the principal stratification framework (Frangakis and Rubin, 2002), which entails expressing how pathogen type-specific vaccine efficacy (VE) in subgroups defined by baseline covariates and immune responses to vaccination differs between the original and new settings. Moreover, our formula addresses three major issues not addressed in most previous work: (1) time-varying VE; (2) mark-varying VE (the “mark” is a genotypic or phenotypic feature of the infecting pathogen that is only measured in clinical endpoint cases); and (3) the fact that some clinical endpoints occur before the immune responses are measured. In our motivating application of preventive HIV vaccines, all three new issues are important, as VE typically varies over time [e.g., Durham et al. (1998) and Robb et al. (2012)] and varies against different HIV-1 genotypes [e.g., Gilbert, McKeague, and Sun (2008) and Rolland et al. (2012)], and a sizable fraction of HIV infection events (e.g., about 30% in Hammer et al., 2013) occur before the primary time point for measuring immune responses. Therefore, the proposed transport formula accounts for all five issues of baseline covariate re-calibration, post-randomization intermediate endpoint re-calibration, time-varying vaccine efficacy, mark-varying vaccine efficacy, and early clinical events.
Section 2 describes the randomized trial designs, notation, and parameters of interest. Section 3 provides the transport formula, and Section 4 describes procedures for estimating the terms in the formula and for obtaining uncertainty assessment. Section 5 applies the formula to the HIV example with expanded details relegated to the Supplementary Materials. Section 6 concludes with discussion. Supplementary Materials A discusses how our transport formula can be altered to swap principal stratification treatment effects for controlled effects (Robins and Greenland, 1992; Pearl, 2001). It is also of interest to compare our transport formula to those of Pearl and Bareinboim (2011) and their subsequent work; we describe a few connections in Section 3.3.
2. Trial Design, Notation, Vaccine Efficacy Parameters
2.1. Set-Up of the Randomized Phase III Trial for Assessing Vaccine Efficacy
We consider a double-blind clinical trial that randomizes n participants to vaccine or placebo, with Z the indicator of assignment to vaccine. Participants are followed for occurrence of the primary clinical study endpoint, clinically significant pathogen infection (Clements-Mann, 1998), with maximum follow-up τ1, and T is the time from randomization until the clinical endpoint. Let S be immune response biomarkers (that are potentially modifiers of vaccine efficacy) measured at fixed time τ < τ1 post-randomization in vaccine recipients. Because S is expensive to measure, a case-cohort or case-control sampling design is used; let R be the indicator that S is measured. Let X be baseline covariates. Let C be the time from randomization until right-censoring, with Y ≡ min(T, C) and Δ ≡ I(Y = T). Let V be a “mark” variable measuring features of the infecting pathogen for disease endpoint cases; T and V are only observed if Δ = 1 (Juraska and Gilbert, 2013). In the sixties, D.R. Cox introduced the terminology “mark” to refer to any information collected from failure cases, which is not observable or meaningful until failure occurs (e.g., the sequence of an HIV infecting a person is only observable and relevant once HIV infection occurs). With key paper Prentice et al. (1978), many statistical methods in the competing risks failure time literature have focused on a discrete mark variable, where the different levels of the mark are the competing risks. A mark is conceptually distinct from a covariate–covariate levels define subgroups who are followed for occurrence of the outcome whereas mark levels define types of the outcome; thus vaccine efficacy parameters of interest condition on covariates but not on marks.
Let W(z) ≡ (R(z), R(z)S(z), T(z), C(z), Δ(z), V(z)) be the potential outcomes if assigned treatment z, for z = 0, 1, where S(z) is defined if and only if T(z) > τ. The observed data are O ≡ (Z, X, R, ZRS, Y, Δ, ΔV). We make the typical assumptions for randomized clinical trials of SUTVA (no-interference between units and only one version of treatment) (Rubin, 1978), ignorable treatment assignment (Z ⊥ W(1), W(0)), random censoring (C(z) ⊥ R(z), R(z)S(z), T(z), V(z)) for z = 0, 1, whether S is observed depends only on the observed data O (missing at random), and W1, ···, Wn and O1, ···, On are independent copies of W and O, respectively.
2.2. Vaccine Efficacy Curve Parameters for Enabling Bridging
In general, principal stratification analysis assesses treatment effects in “principal strata subgroups” defined by joint potential outcomes under each treatment assignment (Frangakis and Rubin, 2002). For our problem, we first define principal strata by early failure status I(T(z) > τ), and secondly intersect S(1) with these principal strata to form a finer stratification that delineates the subgroups for inference. Four principal strata subgroups are defined by the cross-classification of I(T(1) > τ) and I(T(0) > τ):
Gilbert and Hudgens (2008) and sequel articles including Gabriel and Gilbert (2014) developed methods for estimating the “VE surface,” which contrasts risks of the clinical endpoint over time under the two treatment assignments in principal strata defined by the immune response (S(1), S(0)) in the EAS stratum, the only one of the four in which both S(1) and S(0) are defined:
| (1) |
for z = 0, 1. The closely related marginal VE curve contrasts the treatment-specific clinical risks averaged over the distribution of S(0),
where the principal strata of interest are defined by {T(1) > τ, T(0) > τ, S(1) = s1}.
A transport formula could be developed based on riskz(·|s1, s0) or on mriskz(·|s1). We restrict attention to the latter marginal risks, with the corresponding conditional cumulative vaccine efficacy defined as
We focus on the marginal risks because they are easier to estimate than the risks, given the lower dimensionality of the principal strata, and because there are many applications amenable to working with the marginal risks. In particular, one major application area has S(0) constant (the “Constant Biomarker” scenario), including for our HIV vaccine example where S(0) is zero in all placebo recipients (Gilbert and Hudgens, 2008). For this application area riskz(·|s1, s0) = mriskz(·|s1), such that the analysis is identical using risks or marginal risks. In scenarios where S(0) is not constant, the other major application area where the marginal risks approach works is if one can assume that S(0) does not modify vaccine efficacy after accounting for S(1) and X. While this is typically a strong assumption warranting caution, there may be applications where the assumption is plausible, for example if X includes a measurement of S at baseline, such that S(0) is a repeated measure of the same variable measured at baseline (Gabriel and Gilbert, 2014).
We similarly define the mark-specific VE curve, VE(t, v|s1) ≡ 1 − mrisk1(t, v|s1)/mrisk0(t, v|s1), where
for z = 0, 1. The parameters may also condition on X: VE(t, v|s1, x) = 1 − mrisk1(t, v|s1, x)/mrisk0(t, v|s1, x), VE(t, v|x) ≡ 1 − risk1(t, v|x)/risk0(t, v|x), and VE(t|x) = 1 − risk1(t|x)/risk0(t|x), with riskz(t, v|x) ≡ P(T(z) ≤ t, V(z) = v|T(1) > τ, T(0) > τ, X = x) and riskz(t|x) ≡ P(T(z) ≤ t|T(1) > τ, T(0) > τ, X = x). Study of these VE curves is a study of effect modification–how does VE vary with (X, S(1)) across EAS subgroups defined by (X, S(1))? Table 1 defines the terms needed for the transport formula.
Table 1.
Notations and Definitions of Terms used in the Transport Formula
| Source | Notation/Term | Definition | |
|---|---|---|---|
| Phase III trial | Z | Treatment assignment (Z = 1, vaccine; Z = 0, placebo) | |
| Phase III trial | X | Baseline covariates | |
| Phase III trial | τ | Fixed time point after randomization for measuring immune responses S | |
| Phase III trial | τ1 | End of follow-up period where τ < τ1 | |
| Phase III trial | S(z) | Immune responses under assignment to vaccine (z = 1) or placebo (z = 0) | |
| Phase III trial | T(z) | Time to the primary clinical endpoint if Z = z | |
| Phase III trial | V(z) | ‘Mark’ measuring a feature of the pathogen in endpoint cases if Z = z | |
| Phase III trial | F(s1|x) | P(S(1) ≤ s1|T (1) > τ, T(0) > τ, X = x) | |
| Phase III trial | H(x) | P(X ≤ x|T(1) > τ, T(0) > τ) | |
| Phase III trial | risk0(t|x) | P(T(0) ≤ t|T(1) > τ, T(0) > τ, X = x) | |
| Phase III trial | risk0(t, v|x) | P(T(0) ≤ t, V(0) = v|T(1) > τ, T(0) > τ, X = x) | |
| Phase III trial | mriskz (t, v|s1, x) | P(T(z) ≤ t, V(z) = v|T(1) > τ, T(0) > τ, S(1) = s1, X = x) | |
| Phase III trial | VE(t, v|s1, x) | 1 − mrisk1(t, v|s1, x)/mrisk0(t, v|s1, x) | |
| Phase I/II trial | Z* | Treatment assignment (Z* = 1, vaccine; Z* = 0, placebo) | |
| Phase I/II trial | X*, S(z*), T(z*), V(z*) | Same as X, S(z), T(z), V(z) for the Phase I/II trial (new setting) | |
| Phase I/II trial | F*(s1|x) | P(S(1*) ≤ s1|T(1*) > τ, T(0*) > τ, X* = x) | |
| Phase I/II trial | H*(x) | P(X* ≤ x|T(1*) > τ, T(0*) > τ) | |
| Phase I/II trial |
|
P(T(0*) ≤ t|T(1*) > τ, T(0*) > τ, X* = x) | |
| Phase I/II trial |
|
P(T(0*) ≤ t, V(0*) = v|T(1*) > τ, T(0*) > τ, X* = x) | |
| Phase I/II trial |
|
P(T(z*) ≤ t, V(z*) = v|T(1*) > τ, T(0*) > τ, S(1*) = s1 X* = x) | |
| Phase I/II trial | VE*(t, v|s1, z) |
|
|
| Both trials | ϕ(t, v|s1, x) | Bridging assumption function VE*(t, v|s1, x)/VE(t, v|s1, x) | |
| Both trials | VEd*(t) | Target parameter to estimate: P(T(1*) ≤ t) − P(T(0*) ≤ t) | |
| Both trials | VE*(t) | Target parameter to estimate: 1 − P(T(1*) ≤ t)/P(T(0*) ≤ t) | |
| Epidemiological study | wInc(t|x) | Placebo risk calibration | |
| Epidemiological study | wV (t, v|x) | Circulating endpoint type frequencies calibration |
We develop the results assuming “No-early-VE”, P(I(T(1) > τ) = I(T(0) > τ)) = 1, which implies that the EH and EP strata are empty and can be ignored, greatly simplifying identifiability. No-early-VE has been assumed in most articles on the evaluation of principal surrogate endpoints, and is discussed further in Section 3.4. We also develop the results relaxing No-early-VE to “No-early-harm”, P(T(1) ≤ τ, T(0) > τ) = 0, under which the EP stratum may not be empty and must be dealt with. This second approach allows beneficial VE before the immune responses are measured, which can readily occur (e.g., Capeding et al., 2014; Villar et al., 2015). Because it is more complicated, we relegate it to Supplementary Materials B. The No-early-harm assumption is a monotonicity assumption commonly used in causal inference that simplifies identifiability, and No-early-VE is a stronger version that is equivalent to monotonicity in both directions.
2.3. Is Use of a Surrogate Endpoint S Critical for Bridging?
Traditionally, bridging is based on a surrogate (i.e., replacement) endpoint, which may be defined conceptually as an intermediate response endpoint measured in both treatment groups that can be used for reliable inferences about clinical treatment efficacy without needing to measure the clinical endpoint (FDA Guidance Document, 2007). Here we avoid the term surrogate, because the needed attribute of S for the transport formula is that it modifies vaccine efficacy, and being an effect modifier is a distinct property from being a valid surrogate endpoint (Gilbert et al., 2015). For example, our transport formula makes no assumptions about whether S satisfies the Prentice (1989) criteria for a valid surrogate endpoint; rather it requires inclusion of all effect modifiers S regardless of the extent to which they adhere to the Prentice criteria.
3. Immuno-Bridging Transport Formula
3.1. Set-Up
Suppose a previous Phase III vaccine efficacy trial showed significant overall benefit VE(t) > 0 for a fixed time t ∈ (τ, τ1] of interest, as for our motivating example the RV144 trial. Our goal is to estimate VE(t) in a new setting of interest based on (1) the estimated VE(t, v|s1, x) curve from the previous Phase III trial(s), (2) assumptions about how this curve transports to the new setting, (3) data on the distributions of X, S(1), V, and (4) information on background risk mrisk0(t, v|s1, x) in the new setting. A Phase I/II randomized trial is conducted in the new setting, which randomizes m participants to the new vaccine or new placebo (Z = 1* or Z = 0*), and uses identical procedures for measuring the same covariates X and immune responses S(1). Participants are followed until time τ when samples are collected for measuring S(1). The trial has most of the same random variables as the previous efficacy trial, with potential outcomes (S(z*), T(z*), C(z*), Δ(z*)) for z* = 0, 1 and observed random variables (Z*, X*, S*, Y*, Δ*), except that (Y(z*), Δ(z*)) is observed only if Y(z*) ≤ τ and hence (Y*, Δ*) is observed only if Y* ≤ τ. Because the Phase I/II trial does not follow participants long enough to directly assess VE*(t) ≡ 1 − P(T(1*) ≤ t)/P(T(0*) ≤ t) for time points t > τ, interest centers on estimating VE*(t) for a fixed time t ∈ (τ, τ1] based on the full data set from the previous efficacy trial and on the data set ( ), i = 1, ··· m from the Phase I/II trial, where . Based on these data we develop a transport formula for additive-difference vaccine efficacy, VEd*(t) ≡ P(T(1*) ≤ t) − P(T(0*) ≤ t), and for multiplicative-reduction vaccine efficacy, VE*(t) = 1 − P(T(1*) ≤ t)/P(T(0*) ≤ t).
Let F*(s1|x) be the cdf of S(1*) conditional on X* and T(1*) > τ, T(0*) > τ; H*(x) be the cdf of X* conditional on T(1*) > τ, T(0*) > τ; and F*(s1, x) ≡ P(S(1*) ≤ s1, X* ≤ x|T(1*) > τ, T(0*) > τ) be the joint conditional cdf. Define [and ] parameters identical to the mrisk0(·) [risk0(·)] parameters with (T(0), V(0), S(1), X) replaced with (T(0*), V(0*), S(1*), X*). Define the “bridging assumption function”
| (2) |
which measures the ratio of vaccine efficacies for the new and original settings for each value of (t, v, s1, x), thereby expressing a bridging assumption of how the mark-specific VE curve differs in the two settings. This ratio has approximate interpretation as the ratio of multiplicative vaccine-reductions in average mark-specific per-exposure probabilities of acquisition of HIV (Gilbert, McKeague, and Sun, 2008), which aids thoughtful specification of ϕ(·). Specification of bridging assumptions through the function ϕ(·) is a key difference of the current approach compared to Pearl and Bareinboim’s (2011) approach.
3.2. Transport Formula
For any fixed t ∈ (τ, τ1], the “immuno-bridging transport formula” is
| (3) |
and VE*(t) = −VEd*(t)/P(T(0*) ≤ t) (Supplementary Material C provides a proof). This formula averages VE(t, v|s1, x) over the EAS* new study population using four weighting factors: (1) the relationship between VE*(t, v|s1, x) and VE(t, v|s1, x), ϕ(t, v|s1, x); (2) the conditional biomarker distribution in the new setting, F*(s1|x); (3) the baseline covariate distribution in the new setting, H*(x); and (4) the background/placebo arm conditional marginal risk in the new setting. Factors (2) and (3) may be re-written as [dF*(s1|x)/dF(s1|x)]dF(s1|x) and [dH*(x)/dH(x)]dH(x), highlighting re-calibration by differences in the immune response and baseline covariate distributions, and similarly for factor (4) as we discuss below.
Estimation of VEd*(t) and VE*(t) is achieved by substituting estimates for VE(t, v|s1, x), F*(s1|x), H*(x), , P(T(0*) > τ), and P(T(0*) ≤ t) into equation (3), and assuming a specified form for ϕ(t, v|s1, x). We next list a set of assumptions sufficient for consistently estimating VEd*(t) and VE*(t) using the formula, followed by some proposed approaches to estimating terms. The list of the assumptions will make evident that it is highly challenging to assure valid implementation of the transport formula. Indeed, an objective of this work is to explain in specific and component terms the challenges posed to reliably inferring VE*(t) in a new setting without directly estimating VE*(t) using the clinical endpoint data.
3.3. Assumptions for the Transport Formula
The set of assumptions needed for the transport formula to provide consistent estimates of VEd*(t) and VE*(t) for a fixed t ∈ (τ, τ1] are listed below.
Assumptions for the original Phase III trial: (A) Standard assumptions in a randomized trial listed in Section 2.1; (B) No-early-VE: P(I(T(1) > τ) = I(T(0) > τ)) = 1; (C) VE(t, v|s1, x) is consisently estimated.
Assumptions for the new Phase I/II trial: (A) Standard assumptions in a randomized trial listed in Section 2.1; (B) F*(s1|x) and H*(x) are consistently estimated; (C) No-early-VE*: P(I(T(1*) > τ) = I(T(0*) > τ)) = 1.
Assumptions combined over the two trials: (A) The support of (X*, S(1*), V*) is contained in the support of (X, S(1), V); (B) The variables (X, S(1), V) and (X*, S(1*), V*) used in the transport formula are selected such that, for each v in the support of V*, (X, S(1)) includes all modifiers of VE(t, v|s1, x) and (X*, S(1*)) includes all modifiers of ; (C) ϕ(t, v|s1, x) is correctly specified.
Assumptions about background risk in the new setting: is consistently estimated. Separate assumptions are not listed for P(T(0*) > τ) and P(T(0*) ≤ t) because these terms can be consistently estimated given the other assumptions above, based on formulas (8) and (9) in Section 4.3. [These assumptions assure consistent estimation of the integrands in (8) and (9), therefore assuring consistent estimation of the integrals.]
The common support assumption 3(A) is needed for the transport formula to provide empirical estimates of VE*(t); without it, the formula can only provide predictions of VE*(t) for what-if modeling scenarios. The critical assumptions 3(B) and 3(C) require subject-matter knowledge for achieving plausibility. Because the three major factors (1) VE(t, v|s1, x), (2) , and (3) ϕ(t, v|s1, x) in the transport formula modularly measure distinct scientific elements, we stated the sufficient conditions 3(B) and 3(C) in terms of capturing the effect modifiers of vaccine efficacy in the original Phase III trial [factor (1)] and capturing the prognostic factors in the new setting [factor (2)], combined with correctly specifying the bridging assumption function ϕ(·) for these selected variables [factor (3)]. Because the effect modifiers and prognostic factors may be different for different disease types v, the practioner must seek to include all modifying covariates for any type V = v of disease. In particular, this is seen by expressing 3(B) as follows. Let Xall and Sall(1) represent all participant covariates at baseline and time τ under vaccine assignment, measured or unmeasured, and similarly let Vall represent all pathogen features at the time of the disease endpoint. Then 3(B) states that (X, S(1), V) and (X*, S(1*), V*) used in the transport formula satisfy and for all (x, s1, v) in the support of (X*, S(1*), V*).
For specifying ϕ(t, v|s1, x) in critical assumption 3(C), note that, in principle, ϕ(t, v|s1, x) should approximately equal 1 in the hypothetical scenario that (Xall, Sall(1), Vall) were used in the transport formula, because after all characteristics are accounted for there are no remaining factors to create differential vaccine efficacy in the two settings. Thus, the scientist aims to select sufficiently rich (X, S(1), V) to make ϕ(t, v|s1, x) plausibly near one and to narrow the range of the sensitivity analysis that varies ϕ(t, v|s1, x). 3(C) with ϕ(t, v|s1, x) = 1 is more readily credible for applications where the identical vaccine is tested in the original and new settings. Estimation via the transport formula combines empirical evidence with a bridging assumption, where consistent estimation may be obtained if ϕ(·) is correctly specified, e.g., as unity. For bridging to a new vaccine in the same setting, such a “perfect bridging assumption” ϕ(·) = 1 states that, within each baseline subgroup X = x, a vaccine-induced immune response of S(1) = s1 corresponds to the same level of protective efficacy whether the original vaccine or new vaccine generated the response. This interpretation naturally extends for bridging to a new vaccine in a new setting. Carroll et al. (2006) defined transportability in the measurement error problem context where measurement error from one study can be corrected using information on the measurement error process from independent data. They stated that parameters of a model can be transported from one study to another if the model holds with the same parameter values in both studies. Carroll et al.’s (2006) transportability assumption corresponds to our perfect bridging assumption ϕ(·) = 1, where the vaccine efficacy model as a function of X and S(1) is the same between the original setting and the new setting.
In the special case of no right-censoring, no mark V, and no clinical events before τ, the above transport formula collapses to the formula of Huang, Gilbert, and Wolfson (2013) based on S alone, which is similar to a formula in Follmann (2006). In addition, with no V, no clinical events before τ, and a different type of perfect bridging assumption, our transport formula is similar to one of Pearl and Bareinboim’s (2011) transport formulas (their Equation 5). In particular, their Equation 5 in our notation is
| (4) |
for z = 0, 1, which makes a perfect bridging assumption of invariant (s, x)–specific average causal effects in the two settings [surmised to be P(Y(1*) = 1|S(1*) = s, X* = x) − P(Y(0*) = 1|S(0*) = s, X* = x) = P(Y(1) = 1|S(1) = s, X = x) − P(Y(0) = 1|S(0) = s, X = x)]. This formula is the same as ours for , but for it differs, in that P(Y(0) = 1|S(0) = s, X = x) in (4) conditions on the observable S(0) = s instead of on the counterfactual S(1) = s. This difference means that a new distribution is used in Pearl and Bareinboim’s formula (4) that is not used in our formula.
Under the assumptions, VE*(t) can be accurately estimated by substituting fixed terms and estimated terms into (3). In addition, the uncertainty in the bridging estimation can be quantified by accounting for multiple uncertainty sources including estimator sampling variability, potential misspecification of models used in estimating VE(t, v|s1, x) and , partial non-identifiability of VE(t, v|s1, x), and potential misspecification of ϕ(·). Below we implement this via bootstrap-based procedures for obtaining estimated uncertainty intervals (EUIs) (Vansteelandt et al., 2006).
3.4. Plausibility and Evaluation of the No-early-VE and Common Support Assumptions
The No-early-VE assumption is often violated in trials with a series of vaccinations and τ substantially after baseline, given the accrual of protective immunity over time. It is straightforward to diagnose a violation, by testing if vaccine efficacy by τ differs from 0. If relatively few clinical events happen by τ this violation may only minorly bias results; otherwise use of the method removing the No-early-VE assumption may be warranted.
The multivariate nature of (X, S(1), V) makes it challenging to check the common support assumption. For each marginal univariate distribution of the components of X and S(1), methods in the literature for testing for a common support of two distributions could be used, for example accessing tests of ‘support overlap’ in the propensity score matching causal literature. These diagnostic procedures can be carried out because samples of (X, S(1)) and (X*, S(1*)) are available. In addition, domain knowledge aids in checking the assumption; for example immunological assays used to measure S(1) typically have lower and upper quantification readout limits, and based on knowledge of the vaccine regimens and immunology it may be expected that the whole range would be represented in both settings.
The more challenging problem involves checking the support assumption in terms of the mark variable V. Whereas a sample of (X, S(1), V) is available, as is a sample of (X*, V*), no sample is available for (X*, S(1*), V*) in the new setting, because the Phase I trial that measures S(1*) is not designed to capture clinical endpoints and hence measure V*. Consequently, domain knowledge is necessary for judging credibility of the common support assumption, which cannot be fully empirically checked until the future Phase III trial is conducted. If V is discrete categorical and is highly represented among circulating pathogen types in both the original and new settings across the levels of X, then the assumption may be quite plausible.
4. Estimation of the Terms in the Transport Formula
4.1. Estimation of the Mark-Specific VE Curve in the Original Phase III Trial
Qin et al. (2008) and Gabriel et al. (2014, 2015) developed methods for estimation of VE(t|s1, x) from an efficacy trial, accommodating the right-censoring of T. These papers did not consider competing risks data but could be straightforwardly extended to estimate VE(t, v|s1, x) for a discrete V via a cause-specific Cox proportional hazards model (Prentice et al., 1989). For the application we apply an alternative, new method for estimating VE(t, v|s1, x) for the special case of a dichotomous mark V (with levels 0 and 1) based on structural multinomial logistic regression modeling (described in Supplementary Materials D).
If the support of (X*, S(1*), V*) is contained in that of (X, S(1), V), then all values of needed in the estimated transport formula can be obtained from estimates in the original efficacy trial. If not, for example if the new vaccine generates higher immune responses S(1*) than observed in the original trial, then application of the formula requires specification of VE(t, v|s1, x) at covariate levels (X* = x, S(1*) = s1) where there is no empirical data support from the original trial. For such applications the transport formula does not provide “estimates” of VEd*(t) and VE*(t) per se, but rather provides projections based on a what-if modeling scenarios.
4.2. Estimation of Covariate Distributions in the Phase I/II Trial in the New Setting
Under the assumptions of Section 3.3, F*(s1|x) = P(S(1*) ≤ s1|min(T*, C*) > τ, Z* = 1, X* = x), such that F*(s1|x) can be directly estimated from vaccine recipients in the Phase I/II trial who attend the study visit at time τ HIV negative with samples collected for measuring S(1*). Similarly, under No-early-VE, H*(x) = P(X* ≤ x|min(T*, C*) > τ), such that H*(x) can be estimated from the same participants as F*(s1|x), and, optionally, placebo recipients may also be included.
4.3. Estimation of Background Disease Risk in the New Setting
Estimation of is a challenging problem, because it is not possible for epidemiological data to be available for direct empirical estimation, due to the basic fact that the follow-up Phase III trial will occur in the future. However, epidemiological data on recent background disease incidence for V* = v-specific disease within baseline covariate levels X* = x in the new setting can be used for estimation of , under assumptions about how S(1*) affects these disease risks after accounting for X*, and assuming that the recent epidemiological data are representative of the future Phase III trial setting. We consider two approaches to estimating based on recent epidemiological data. For Approach 1, we assume
| (5) |
for some specified paired functions wS(s1|x) and g(s1|x) chosen to ensure both constraints and risk0(t, v|x) = ∫ mrisk0(t, v|s1, x)dF(s1|x) for all (t, v, x), which with (5) require
| (6) |
The idea of Approach 1 is to shift the problem from estimation of , which is hard, to the simpler problems of estimation of and mrisk0(t, v|s1, x). To estimate the former term, we factor it into two ratios reflecting (i) different background overall conditional disease cumulative incidences,
and (ii) different distributions of circulating and infecting pathogen types V,
The numerator of wV(t, v|x) measures the relative fraction of the circulating pathogen types potentially exposing and infecting subgroup X* = x participants in the new setting that are of type v, while the denominator measures this relative fraction in the original setting. Under Approach 1,
| (7) |
We illustrate two choices of (wS, g) that satisfy the constraint (6). First, if F(s1|x) and F*(s1|x) are continuous functions, then an equipercentile assumption may be expressed as g(s1|x) = F−1(F*(s1|x)) and wS(s1|x) = 1 where F−1(·|x) is the inverse of F(·|x). Second, under a location-shift model dF*(s1|x) = dF((s1 − μ(x))/σ(x)|x), we set g(s1|x) = (s1 − μ(x))/σ(x) and wS(s1|x) = 1.
To implement Approach 1, we need to estimate mrisk0(t, v|s1, x) and both terms wInc(t|x) and wV(t, v|x). The term mrisk0(t, v|s1, x) is estimated as part of the process for estimating the VE curve as addressed in Section 4.1. For wV(t, v|x), estimation of must be based on epidemiological data in the new setting that depends on the quality of surveillance for incident disease cases and on the cataloging of the types v of disease cases. The numerator of wInc(t|x) may be estimated based on an epidemiological cohort study in the new setting, and the denominator through straightfoward analysis of the original Phase III trial. Because risk0(t|x) appears in the denominator of wInc(t|x), estimation could be unstable if risk0(t|x) is close to zero; thus reasonably precise estimation of risk0(t|x) for each x is needed (which is achieved in the RV144 Example due to ample sample size). The numerator of wV(t, v|x) may be estimated from a genomic epidemiological study of circulating pathogen types in the new setting, and denominator either through a genomic epidemiological study in the original setting or through straightforward analysis of the original Phase III trial.
Our Approach 2 to estimating makes the stronger assumption that and mrisk0(t, v|s1, x) = risk0(t, v|x), i.e., T(0*), V(0*) ⊥ S(1*)|X*, T(1*) > τ, T(0*) > τ and T(0), V(0) ⊥ S(1)|X, T(1) > τ, T(0) > τ. Plausibility of this assumption requires rich X that leaves no residual prognostic value of S(1*), which is unverifiable and typically not credible, such that Approach 1 may be better justified.
Approach 2 is implemented by estimating in the same way as under Approach 1, e.g., as . Approach 2 also has mathematical convenience that it majorly simplifies the estimation of VE(t, v|s1, x) in the original Phase III trial, because mrisk0(t, v|s1, x) becomes estimable without needing to impute the missing counterfactual immune response S(1) in participants assigned placebo Z = 0 (Follmann, 2006).
Lastly, the terms P(T(0*) ≤ τ) and P(T(0*) ≤ t) should be estimated compatibly with the approach taken to estimation of . For Approach 1, using (7), this means that P̂(T(0*) ≤ t) should be compatible with P(T(0*) ≤ t) =
| (8) |
For Approach 2, this means that P̂(T(0*) ≤ t) should be compatible with
| (9) |
4.4. Sensitivity Analysis to the Perfect Bridging Assumption
Given that direct data on clinical efficacy for the new setting of interest are not available, theories of mechanisms of protection, as encoded in the specified bridging assumption function ϕ(·), must be combined with empirical data to make bridging inferences. Because the form of ϕ(·) cannot be directly estimated until the new efficacy trial, a sensitivity analysis is warranted. One approach specifies a fixed constant Γ and estimates VE*(t) under each of a grid of constants , setting ϕ(t, v|s1, x) ≡ γ. Following the approach of Rosenbaum (2010), by estimating VEd*(t) [or VE*(t)] with a 95% confidence interval for each fixed γ, one obtains an estimated ignorance interval and a 95% estimated uncertainty interval for VEd*(t) [or VE*(t)] (Vansteelandt et al., 2006). A more sophisticated sensitivity analysis would follow this program using fixed constant functions Γ(s1, x) and γ(s1, x) or even Γ(t, v|s1, x) and γ(t, v|s1, x).
5. Application to HIV Vaccine Efficacy Trials
We consider bridging the multiplicative-reduction vaccine efficacy through 39 months of follow-up of the ALVAC-gp120 prime-boost vaccine versus placebo [VE(t = 39)] that was observed in the RV144 Thai trial (Rerks-Ngarm et al., 2009), to estimate VE*(t = 39) in the planned HIV Vaccine Trials Network (HVTN) 702 Phase III trial in South Africa. HVTN 702 will test a similar ALVAC-gp120 prime-boost vaccine regimen versus placebo and has primary objective to estimate VE*(t) over time t with particular interest in the durability of efficacy out to 39 months, VE*(t = 39). The RV144 trial provided the HIV vaccine field the first result of a partially efficacious HIV vaccine [estimated VE(t = 39) = 0.31, 95% 0.004 to 0.52], and HVTN 702 builds on this partial success in testing the efficacy of a putatively improved version of the RV144 vaccine regimen. The HVTN 702 trial is preceded by the HVTN 100 Phase IIa trial in the same study population in South Africa that is currently studying the immune responses induced by the vaccine.
The RV144 and HVTN 702 efficacy trials differ in (1) the vaccine regimens [different HIV sequences in the ALVAC and gp120 vaccines (two subtype AE strains and one subtype B strain for RV144 and three subtype C strains for HVTN 702) and different adjuvants used to deliver the gp120 boost (Alum for RV144 and MF59 for HVTN 702)]; (2) circulating HIV-1 genotypes and phenotypes exposing trial participants (e.g., subtype AE in RV144 and subtype C in HVTN 702); (3) immune responses induced by the vaccine regimens; (4) host immune genetics; (5) participant demographics including country, race/ethnicity, gender, BMI, and level and pattern of HIV risk-taking behavior (RV144 participants were Thai, low risk, and low BMI whereas HVTN 702 participants will be mostly Black South African, high risk, and higher BMI for women); and (6) intensity of HIV exposure (much higher exposure in HVTN 702). We select V as the indicator of whether the amino acid (AA) at position 169 in an HIV infected individual’s V2 Envelope HIV sequence sampled at diagnosis of infection mismatches the corresponding AA in the HIV strains contained in the vaccine (Rolland and Edlefsen et al., 2012). In addition, we select S as the magnitude of binding antibodies to the V1V2 portion of a gp70-scaffolded Envelope protein (Haynes et al., 2012), and select X as the indicator of whether an individual carried a CC or TT (CT/TT) genotype at position 126 in intron 2 of the Fc-γ receptor 2C gene locus (Li et al., 2014). These choices are based on published results that the vaccine efficacy in RV144 significantly depended on these variables after multiplicity correction (see Supplementary Materials A for details).
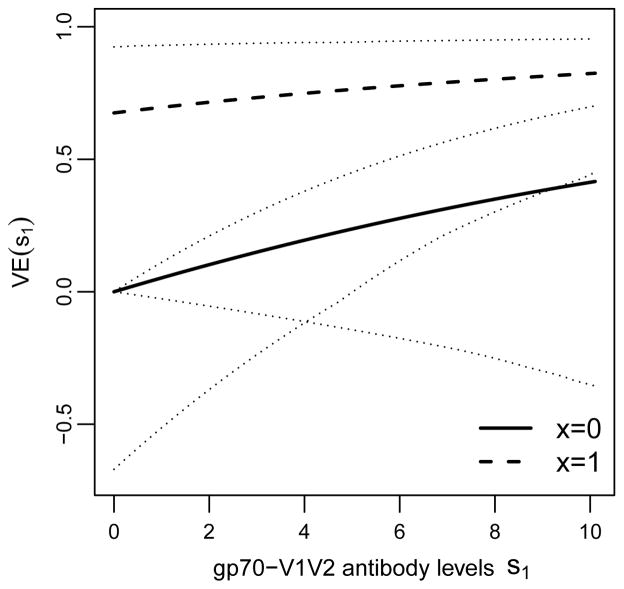
For the input terms VE(t = 39, v|s1, x), for v = 1, we set for all s1 and x, because (95% CI = −2.58 to 0.33); this choice invokes the assumption that the vaccine did not increase the risk of v = 1 HIV infection (which “de-noises” the estimation). Alternatively, VE(t = 39, v = 1|s1, x) could be estimated similarly as VE(t = 39, v = 0|s1, x) without making the assumption of zero vaccine efficacy against type v = 1 HIV. For v = 0, we set based on estimation methods described in Section 4.2 and Supplementary Materials B and D; Figure 1 shows as a function of S(1) = s1 for the subgroups x = 0 (CC genotype) and x = 1 (CT/CT).
Figure 1.
Based on the RV144 Phase III efficacy trial data, estimated vaccine efficacy curves with 95% bootstrap confidence intervals by the method described in Supplementary Material D with v = 0 an HIV with Lysine at position 169 of the HIV Envelope protein and immune response S(1) = s1 the binding antibody level to a scaffolded gp70-V1V2 protein (Zolla-Pazner et al., 2014), in the two subgroups of trial participants defined by x = 0 (CC at position 126 in intron 2 of the Fc-γ receptor 2C gene locus) and by the complement subgroup x = 1 (CT or TT at this locus). The analysis assumes average causal necessity (ACN) for the X = 0 subgroup, VE(t = 39, v = 0|s1 = 0, x = 0) = 0.
Because S(1) is missing in Z = 0 participants, there is a non-identifiability issue in estimating all parameters in the conditional risks that constitute the VE(t = 39, v = 0|s1, x) parameters. As one approach to achieve identifiability, our estimation approach assumes VE(t = 39, v = 0|s1 = 0, x = 0) = 0, which is the “average causal necessity” (ACN) scenario (Gilbert and Hudgens, 2008) for the X = 0 subgroup. We could alternatively carry out the estimation enforcing an additional assumption of ACN for X = 1 as well as for X = 0, but it is not necessary for identifiability, such that we leave the risk for the S(1) = 0, X = 1 subgroup to be estimated. (Here we seek to only specify the minimum assumptions needed to achieve identifiability.) In the RV144 trial, vaccine efficacy for the X = 0 subgroup was estimated to be near 0 whereas vaccine efficacy for the X = 1 subgroup was estimated to be well above 0, making it more consistent with empirical data to assume ACN for X = 0 but not for X = 1. Below we also report a sensitivity analysis that instead assumes ACN for the X = 1 subgroup.
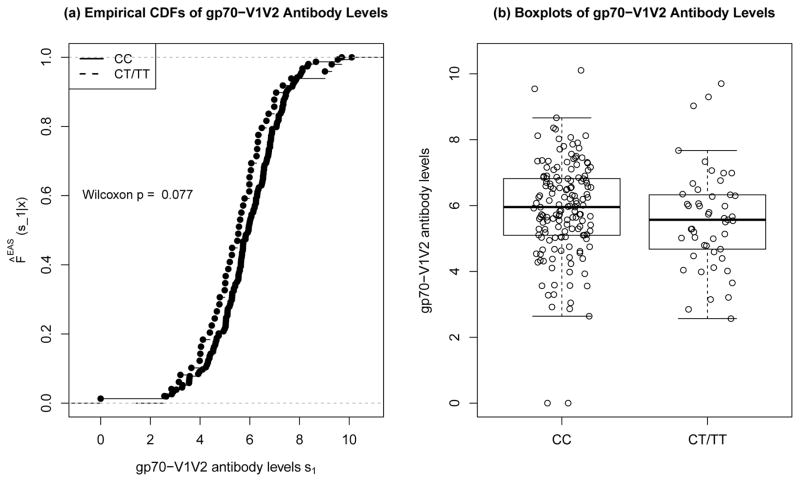
We estimate F*(s1|x) and H*(x) based on the ongoing HVTN 100 Phase IIa trial. HVTN 100 is enrolling 212 vaccine recipients, and will measure baseline covariates X* in all of these participants and immune responses S(1*) in all who attend the Month 6 visit HIV negative (i.e., with min(T*, C*) > 6 months). Because the data are not yet available for HVTN 100, for illustrative purposes we first use the data from the RV144 trial [assuming S(1*)|X*, T(1*) > τ, T(0*) > τ =d S(1)|X, T(1) > τ, T(0) > τ], and secondly consider scenarios where the new vaccine increases immune responses compared to RV144. Figure 2 shows the empirical estimates of F*(s1|x) for each subgroup x = 0, 1 in RV144. We estimate H*(x) based on a Fc-γ receptor genetics in a sample of n = 131 Black South Africans (Lassauniere et al., 2014). Because 49% carried CT or TT, we set P̂(X* = 1|T(1*) > τ, T(0*) > τ) = 0.49 (compared to 0.28 in RV144; Table S8 of Li et al., 2014).
Figure 2.
Based on RV144 data from 205 HIV uninfected vaccine recipients of S(1*) the binding antibody level to a scaffolded gp70-V1V2 protein measured by BAMA at τ = Month 6.5, panel (a) shows nonparametric maximum likelihood estimates of F*(s1|x) = P(S(1*) ≤ s1|T(1*) > τ, T(0*) > τ, X* = x) for each of the two subgroups x = 0 (CC) and x = 1 (CT or TT). Panel (b) shows boxplots of S(1*)|X* = x.
Supplementary Materials A describes the full details of the methods used for estimation of for each v, x ∈ {0, 1} via equation (5), which we accomplish by assuming the equipercentile model for F*(s1|x) described in Section 4.3 and estimating the three terms wInc(t|x), wV(t, v|x), and mrisk0(t, v|s1, x) separately. The numerator of wInc(t|x) is estimated from a recent HIV vaccine efficacy trial in South Africa (Gray et al., 2014) in a study population expected to be similar to the HVTN 702 study population, and the denominator is estimated from RV144. The numerators and denominators of wV(t, v|x) are estimated from the LANL HIV Sequence Data Base, the numerator based on 254 HIV-1 sequences from South Africans collected between 2008 and 2013 (60% with v = 0) and the denominator based on 207 HIV-1 sequences from Thais collected during the RV144 trial between 2003 and 2009 (72% with v = 0). Lastly, mrisk0(t, v|s1, x) is estimated as a component step for estimating VE(t, v|s1, x). The estimates of the individual terms are shown in Table 2.
Table 2.
Estimation of the Terms in the Transport Formula for Bridging RV144 to Estimation of VE*(t = 39) in HVTN 702
| Term | Data Source | Method | (v, x) Level | ||||
|---|---|---|---|---|---|---|---|
| (0,0) | (0,1) | (1,0) | (1,1) | ||||
|
|
RV144 | Structural MLR | Figure 1 | Figure 1 | 0.01 | 0.01 | |
|
|
RV144 | From above2 | Not shown | NS | NS | NS | |
| F̂*(s1|x) | HVTN 1003 | Empirical NPMLEs | Figure 2 | Figure 2 | Figure 2 | Figure 2 | |
| Ĥ*(x) for x = 0 (CC) and x = 1 (CT/TT) | Host genetics database | Frequency of CC, CT/TT in n = 131 Black South Africans | 0.51 | 0.49 | 0.51 | 0.49 | |
|
| |||||||
| ŵInc(t = 39|x) numer: | HVTN 503 trial in RSA (2007–2013) (Gray et al., 2014) | IPW Kaplan-Meier NPMLEs | 0.1214 | 0.1214 | 0.1214 | 0.1214 | |
| ŵInc(t = 39|x) denom: | RV144 | IPW Aalen-Johansen | 0.0070 | 0.012 | 0.0070 | 0.012 | |
| ŵInc(t = 39|x) | 17.3 | 10.08 | 17.3 | 10.08 | |||
|
| |||||||
| ŵV(t = 39, v|x) numer: | HIV sequence database | Frequency of v = 0 (169K) and v = 1 (X169K) in the RSA IPW Aalen-Johansen + database | 0.605 | 0.605 | 0.405 | 0.405 | |
| ŵV(t = 39, v|x) denom: | RV144 | 0.706 | 0.766 | 0.336 | 0.206 | ||
| ŵV(t = 39, v|x) | 0.86 | 0.79 | 1.22 | 2.03 | |||
Estimated as 0.0 because (95% CI = −2.58 to 0.33) and the belief that the vaccine did not increase infection risk.
Estimated as part of the method for estimating (details in Supplementary Appendix B).
Because HVTN 100 has not yet completed, the data from RV144 were used.
The estimates are the same for x = 0 and x = 1 because data on X were not available in the HVTN 503 trial.
The estimates are the same for v = 0 and v = 1 because data on X were not available in HVTN 503; the estimates are empirical fractions from 254 HIV-1 sequences of South Africans in the LANL database from 2008 to 2013.
Initial estimates from RV144 (IPW Aalen-Johansen) and final estimates using empirical fractions from 207 HIV-1 sequences of Thais in the LANL database from 2003 to 2009 (See Supplementary Appendix B).
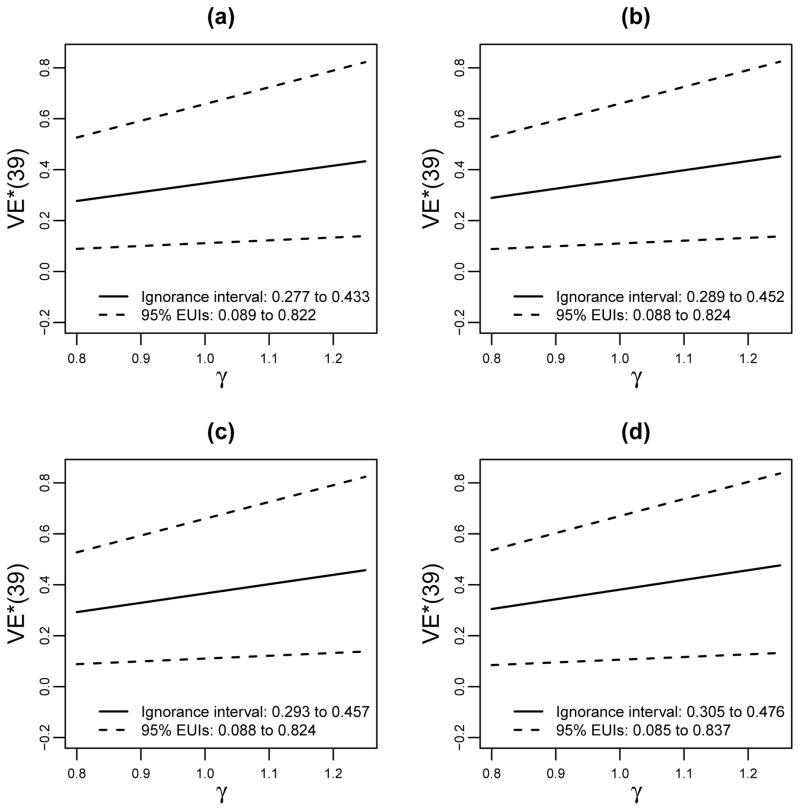
We apply the transport formula under the perfect bridging assumption ϕ(·) ≡ 1 by plugging the estimated terms into the formula (3), yielding with 95% bootstrap confidence interval 0.11 to 0.66. (See Supplementary Materials E for a description of the bootstrap procedure.) As a sensitivity analysis, we repeated the analysis for a grid of fixed γ = ϕ(t, v|s1, x) values varying between and Γ with Γ = 1.25 (Figure 3a), which gives an estimated ignorance interval of 0.28 to 0.43 and a 95% EUI of 0.09 to 0.82. Next, we repeated the analysis of Figure 3a supposing the vaccine in HVTN 100 produces higher immune responses than in RV144, in one or both of the genotype subgroups. In particular, we modified the estimates F̂*(s1|x) of Figure 2 in three ways by moving a random sample of 75% of the original Si(1) values with percentile p ≤ 0.50 in RV144 to the percentile p* = p + 0.50, for (b) all CC participants; (c) all CT/TT participants; or (d) all participants. Figures 3b–d show the resulting estimates of VE*(t = 39), showing similar estimated ignorance intervals compared to Figure 3a and to each other, with estimated VE*(t = 39) only slightly increasing for the scenarios with increased V2 immune responses in the new setting. Thus, the overall result is that vaccine efficacy is predicted to be slightly higher in the new setting than was previously observed in RV144 (also summarized in Table 3). This only-slight increase is explained by the fact that the VE curves only slightly increased with S(1) (Figure 1), limiting the impact of improving V2 responses, combined with the facts that for all (s1, x) and the frequency of v = 1 is greater in South Africans (40%) than Thais (28%).
Figure 3.
For bridging the vaccine efficacy of the RV144 trial to the HVTN 100/702 trial setting: Estimated VE*(t = 39 months) with 95% bootstrap confidence intervals for fixed sensitivity parameter γ varying from 0.8 to 1.25 and under average causal necessity for the X = 0 subgroup, assuming (a) F̂*(s1|x) is from RV144; or F̂*(s1|x) is from RV144 modified by moving a random sample of 75% of the original SI values with percentile p ≤ 0.50 in RV144 to the percentile p* = p + 0.50, for (b) the x = 0 (CC) subgroup; (c) the x = 1 (CT/TT) subgroup; or (d) all participants. Estimated ignorance intervals and 95% estimated uncertainty intervals (EUIs) are listed.
Table 3.
Estimated VE*(t = 39) × 100% in the New Setting (HVTN 702) Under Different Estimation and Modeling Approaches1
| S(1*) Distribution | ACN Assump. |
|
|||
|---|---|---|---|---|---|
| Est. (95% CI) γ = 1 | Ign. int.2 | 95% EUI1 | |||
| Same as RV144 (Fig. 3A) | for X = 0 | 34.6 (11.1, 65.8) | (27.7, 43.3) | (8.9, 82.2) | |
| Higher3 for X* = 0 (Fig. 3B) | for X = 0 | 36.1 (11.0, 65.9) | (28.9, 45.2) | (8.8, 82.4) | |
| Higher3 for X* = 1 (Fig. 3C) | for X = 0 | 36.6 (11.0, 65.9) | (29.3, 45.7) | (8.8, 82.4) | |
| Higher3 for All (Fig. 3D) | for X = 0 | 38.1 (10.6, 67.0) | (30.5, 47.6) | (8.5, 83.7) | |
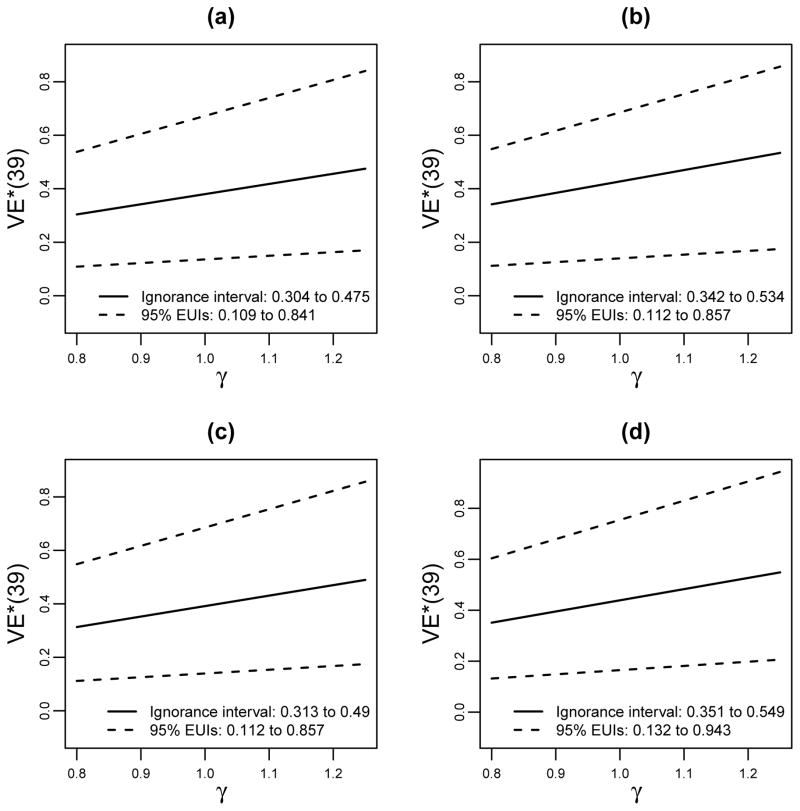
| Same as RV144 (Fig. 4A) | for X = 1 | 38.0 (14.0, 67.2) | (30.4, 47.5) | (10.9, 84.1) | |
| Higher3 for X* = 0 (Fig. 4B) | for X = 1 | 42.7 (14.0, 68.5) | (34.2, 53.4) | (11.2, 85.7) | |
| Higher3 for X* = 1 (Fig. 4C) | for X = 1 | 39.2 (14.0, 68.5) | (31.3, 49.0) | (11.2, 85.7) | |
| Higher3 for All (Fig. 4D) | for X = 1 | 43.9 (16.5, 75.5) | (35.1, 54.9) | (13.2, 94.3) | |
| Higher4 for All | for X = 0 | 40.7 (6.7, 74.2) | (31.8, 50.9) | (2.6, 93.4) | |
| Higher4 for All | for X = 1 | 55.8 (23.2, 94.0) | (44.8, 70.1) | (19.3, 100) | |
| Model Adding a v = 1 Strain Assuming
| |||||
| Higher3 for All | for X = 0 | 52.3 (15.1, 92.7) | (41.8, 65.3) | (12.0, 100) | |
| Higher3 for All | for X = 1 | 60.3 (23.6, 100) | (48.2, 75.4) | (18.8, 100) | |
| Higher4 for All | for X = 0 | 55.8 (6.3, 100) | (44.1, 69.6) | (0.0, 100) | |
| Higher4 for All | for X = 1 | 76.7 (33.3, 100) | (61.5, 96.3) | (26.9, 100) | |
The estimation is done as described in Table 2, except for new elements listed in this table.
Computed for ϕ(t, v|s1, x) = γ with γ ranging over [ Γ] for Γ = 1.25, where ϕ(t, v|s1, x) ≡ VE*(t = 39, v|s1, x)/VE(t = 39, v|s1, x).
Estimation scenario of equal support of (X*, S(1*)) and (X, S(1)), where the distribution of S(1*) follows a modification of F̂*(s1|x) from RV144 data (Figure 2) by moving a random sample of 75% of the original Si(1) values with percentile p ≤ 0.50 in RV144 to the percentile p* = p + 0.50.
Estimation scenario of equal support of (X*, S(1*)) and (X, S(1)), where the distribution of S(1*) is uniformly distributed in the highest range of immune responses supported by the binding assay, [9, 10.1].
To examine the common support assumption 3(A), note that the BAMA assay used for measuring S(1) has lower and upper readout limits, and from RV144 we directly observed that S(1) takes values over the whole range for each subgroup X = 1 and X = 0. Moreover, we know that S(1*) also takes values over the whole range for each subgroup X* = 1 and X* = 0, by the way we simulated the data. Lastly, V is simple, being binary, and the data on (X, V) and (X*, V*) show that each of the four possible levels is well-represented in each of the original and new settings. Taken together these results strongly suggest (but do not prove) the common support assumption.
We repeated the analysis assuming average causal necessity (ACN) for the x = 1 (higher protected) subgroup instead of for the x = 0 subgroup (Figure 4, Table 3). Now the increase in V2 immune responses S(1) leads to a greater increase in estimated VE*(t = 39), which occurs because the estimated VE(t = 39, v = 0|s1, x = 1) curve is steeper than in the previous analysis.
Figure 4.
The analysis of Figure 3 repeated assuming average causal necessity for the X = 1 subgroup instead of the X = 0 subgroup, VE(t = 39, v = 0|s1 = 0, x = 1) = 0, under which the estimated curves are steeper in s1 (stronger effect modification).
We also consider the scenario where all vaccine recipients achieve S(1*) in the highest region of possible immune responses supported by the binding assay, uniformly distributed between 9 and 10.1 (10.1 is the upper quantification limit of the assay). This scenario represents a case where a “putatively much stronger” vaccine is identified in HVTN 100. The predicted VE*(t = 39) increases by 20% to 30% (Table 3).
Lastly, to illustrate how the method can be used to project what overall vaccine efficacy could be achievable if additional HIV strains are added to a refined multivalent version of the vaccine regimen, we consider the scenario that a v = 1 HIV strain is added to the vaccine construct. This follows the paradigm for traditional vaccinology to put multiple pathogen genotypes in a vaccine to broaden protection against genetically diverse pathogens (e.g., Capeding et al., 2014; Villar et al., 2015). We consider the scenario that the v = 1 and v = 0 strains protect equally well against pathogen-matched type v disease, expressed as VE(t, v = 1|s1, x) = VE(t, v = 0|s1, x). As such, in implementing the transport formula we use an estimated VE(t, v = 1|s1, x) equal to the estimated VE(t, v = 0|s1, x) in the previous analyses. The resulting estimated ignorance intervals for the scenarios in Figures 3(d) and 4(d) are now 0.42 to 0.65 and 0.44 to 0.70, respectively (Table 3). The predicted VE*(t = 39) majorly increases because 40% of the circulating HIV-1s in South Africa are of type v = 1, against which a vaccine without a v = 1 strain confers no protection.
6. Discussion
This article develops an immuno-bridging transport formula for predicting overall vaccine efficacy VE*(t) in a new setting based on a previous Phase III vaccine efficacy trial(s) and a Phase I/II biomarker endpoint trial in the new setting, plus epidemiological data on disease incidence in the new setting and genomic epidemiological data on the pathogen genotypes in the previous and new settings. One application is quantifying uncertainty about predicting VE*(t) in the absence of an efficacy trial, explaining in specific and component terms the challenges posed to reliably inferring VE*(t) in a new setting without directly estimating VE*(t) from clinical endpoint data. A second application is “Go/No-Go” decision-making about whether a new vaccine tested in a Phase IIa trial should be advanced to an efficacy trial in the original or new setting (elaborated in Supplementary Materials F). For example, the HVTN is testing multiple candidate HIV vaccines in Phase I/II trials in South Africa with objective to down-select up to three vaccines into an efficacy trial. The transport formula provides a criterion for advancement, where regimens with higher estimated VE*(t) would be favored. While this article focuses on the vaccine field, the Go/No-Go application is of broad relevance across clinical trials research. A third highly related application is guidance for selecting study endpoints in Phase I/II vaccine/treatment trials prior to the next efficacy trial; for example biomarkers S(1) that are stronger effect modifiers of vaccine/treatment efficacy in the previous efficacy trial(s) may be preferred.
6.1. Which Variables (X, S(1), V) to Include in the Transport Formula?
A basic challenge posed to applying the transport formula is how to choose the baseline covariates X, intermediate response endpoints S(1), and marks V to make the formula accurate? As stated above, for validity the (X, S(1)) selected for use in the transport formula must be the only effect modifiers of mark-specific vaccine efficacy in the original and new settings and be the only prognostic factors for disease in the new setting, for each type V of disease. This condition implies that application of the formula depends on the integration of subject-matter knowledge. Selecting (X, S(1), V) will generally be easier when the new setting entails a nearly identical vaccine as studied originally, and more difficult for a new vaccine, moreso the extent to which it differs from the original vaccine. Pearl and Bareinboim (2011) provide various criteria for covariates that are necessary to include versus necessary to not include.
In practice, often particular S(1) variables are known to be strong effect modifiers of VE(t, v), making it obvious to pick these variables. Moreover, commonly vaccine efficacy is known to vary with a particular pathogen feature V such as serotype, making it obvious to include this feature. A recent dengue vaccine efficacy trial illustrates this situation, which tested a vaccine containing four dengue strains, one of each serotype (Capeding et al., 2014; Villar et al., 2015). The trial assessed vaccine efficacy against each serotype v = 1, 2, 3, 4, and measured the level of neutralization to each of the four dengue strains in the vaccine (four variables Sv(1), v = 1, 2, 3, 4). Prior to the trial, the dengue vaccine field had knowledge that for each v = 1, 2, 3, 4, VE(t, v|s1, x) would likely be higher for subgroups with higher levels of Sv(1) = s1.
6.2. How to Handle the Dimensionality of X?
If X is discrete categorical with a reasonable amount of data support at each level, then the transport formula can be applied without invoking parametric models for the conditional distribution of S(1) given X, and mriskz (t, v|s1, x) can be estimated separately for each x. However, if X is higher dimensional, then some parametric modeling assumptions are needed, and if X is high dimensional, then specialized p > n regression models are needed. One approach to addressing both issues would estimate mriskz (t, v|s1, x) using a supervised statistical learning approach that considers a large set of potential models defined by different sets of the covariates within X and different models, for example using nonparametric loss-based ensemble learning (van der Laan et al., 2007), with cross-validated area-under-the ROC curve as a criterion for model selection (van der Laan, Hubbard, and Pajouh, 2013). Existing supervised statistical learning methods may be applied to estimate mrisk1 (t, v|s1, x) given the identifiability of this parameter from the observed data. For mrisk0(t, v|s1, x), additional research would be needed given the identifiability challenge.
6.3. How to Specify the Bridging Assumption Function ϕ(·|·)?
For the transport formula to work well in applications it is neccessary that the bridging assumption function ϕ(t, v|s1, x) = VE*(t, v|s1, x)/VE(t, v|s1, x) can be meaningfully specified and varied in a sensitivity analysis. We suggest that if ϕ(t, v|s1, x) is approximately a ratio of multiplicative vaccine-reductions in average mark-specific per-exposure probabilities of acquisition of the pathogen under study, then ϕ(·|·) can be interpreted as a “pure biological susceptibility” parameter akin to a challenge trial, thus making a default assumption ϕ(t, v|s1, x) = 1 reasonable given carefully selected (X, S(1), V), and facilitating an interpretable sensitivity analysis. This biological parameter approximation is more accurate for a rare event trial (Gilbert, 2001), suggesting that the formula may be most appropriate for such settings, which are the norm in vaccine efficacy trials. Moreover, while our approach focuses on cumulative vaccine efficacy parameters, the approach could be adapted to instead use proportional mark-specific hazards vaccine efficacy parameters (Gilbert and Sun, 2014), and applied to settings where the proportional hazards assumption is approximately true (e.g., Capeding et al., 2014; Villar et al., 2015). The advantage of the hazard ratio approach is that ϕ(t, v|s1, x) has a closer approximation to a ratio of average per-exposure vaccine efficacies (Gilbert, 2001). However, a disadvantage is that the proportional hazards VE parameter is only a causal effect of treatment assignment under a strong assumption that will fail if there is treatment efficacy, such that it is only an approximately causal approach (Hernán, 2010); whereas in contrast the cumulative vaccine efficacy approach is based on true causal effects.
6.4. VE Curve Principal Stratification Versus Observables-Only Transport Formula
Our transport formula is based on VE curves VE(t, v|s1, x) that measure vaccine efficacy in sub-populations defined by (X, S(1)), which are not identifiable from the standard assumptions in the Phase III efficacy trial and the observed data, because the vaccine-induced immune responses S(1) are not directly measurable in placebo recipients (Follmann, 2006). The rationale for this approach is that for many vaccine fields one or more immune response biomarkers are known or hypothesized to be (very) strong effect modifiers of vaccine efficacy (Plotkin, 2010), and the principal stratification framework studies treatment effect modification across such post-randomization subgroups (Frangakis and Rubin, 2002; Gilbert and Hudgens, 2008; Gilbert et al., 2015). To avoid the identifiability challenge, an alternative transport formula would be based purely on parameters identifiable from the standard assumptions and observed data. However, a challenge posed to this observables approach is how to specify an interpretable bridging function that expresses a perfect bridging scenario as a special case and provides a basis for sensitivity analysis? A difficulty is that bridging functions based purely on observables may aggregate biological and behavioral/ecological differences between the old and new settings, which may be dominated by behavioral/ecological factors; for example in the HIV vaccine illustration the cumulative infection rate in placebo recipients is approximately 10 times higher in the new setting than the old setting. Nevertheless, the “purely observables” approach certainly merits full investigation, given its advantage in avoiding the use of partially non-identified parameters, and it is beyond the scope of this work to make this comparison. We do note, however, that under our Approach 2 for estimating described in Section 4.3, our transport formula is a version of an observables-only transport formula, because with this approach VE(t, v|s1, x) is identified from the standard assumptions in randomized trials (albeit Approach 2 makes a strong assumption that must be used with caution). In addition, if the principal stratification framework is deemed unappealing for an application but controlled effects can be well-defined and are appealing, our alternative version of the transport formula based on controlled effects may be considered (Supplementary Materials A).
6.5. Transport Formula Under the No-Early-Harm Assumption
Supplementary Materials G develops the transport formula relaxing the No-early-VE assumption to the No-early-harm monotonicity assumption, showing that the formula becomes more complicated, for example involving three bridging assumption functions instead of one. Therefore the problem of immuno-bridging is majorly simplified if one can at least approximately assume no vaccine efficacy by the time τ that immune responses/intermediate endpoints are measured. Accordingly, most of the principal surrogate endpoint evaluation literature has assumed No-early-VE or has considered the simplified scenario that no clinical events happen before the potential surrogates are measured. The current research indicates that in some settings this issue must be accounted for to achieve a cogent transport formula, for example in the two Phase III dengue vaccine efficacy trials mentioned above, the immune responses were measured far after randomization (τ = 13 months) and No-early-VE was clearly majorly violated (Capeding et al., 2014; Villar et al., 2015). The simpler transport formula will be most easily justified in settings where strong effect modifying biomarkers are available shortly after vaccine/treatment initiation, for which No-early-VE may be justified, or minor violations will not materially affect the bridging prediction. Moreover, the controlled effects approach may be best suited to settings where no or very few clinical events occur before τ, given the difficulty in conceiving of the intervened biomarker-specific vaccine efficacy curve otherwise.
6.6. Final Remarks
Implementation of the proposed transport formula entails estimation of ignorance intervals and uncertainty intervals, in order to account for sampling variability as well as for: (1) partial non-identifiability of the mark-specific conditional vaccine efficacy curve VE(t, v|s1, x), (2) uncertainty in the assumptions used to estimate , and (3) possible deviations from the perfect bridging assumption. This research shows that, even under No-early-VE, a large amount of data from the original efficacy trial(s) is needed for precise estimation of VE*(t), highlighting the importance of conducting direct clinical endpoint Phase III trials. However, the identical immuno-bridging formula applies if a set of previous efficacy trials is used instead of a single efficacy trial, where trial-level and subject-level features of the trials can be included as covariates in the transport formula. In some areas of clinical research, meta-analysis data are available from a large number of mega-trials (Staessen et al., 2005), illustrating that, in principle, it is possible in practice to generate the requisite data for obtaining relatively precise inferences.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by the National Institute Of Allergy And Infectious Diseases (NIAID) of the National Institutes of Health (NIH) under Award Numbers R37AI054165 and UM1AI068635, and by the Bill and Melinda Gates Foundation Award Number OPP1110049. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or BMGF. The authors thank the participants, investigators, and sponsors of the HVTN 503 and RV144 trials, for the latter including the U.S. Military HIV Research Program (MHRP); U.S. Army Medical Research and Materiel Command; NIAID; U.S. and Thai Components, Armed Forces Research Institute of Medical Science; Ministry of Public Health, Thailand; Mahidol University; SanofiPasteur; and Global Solutions for Infectious Diseases.
References
- Capeding MR, Tran NH, Hadinegoro SRS, Ismail HIHM, Chotpitayasunondh T, Chua MN, Luong CQ, Rusmil K, Wirawan DN, Nallusamy R, et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: a phase 3, randomised, observer-masked, placebo-controlled trial. The Lancet. 2014;384:1358–1365. doi: 10.1016/S0140-6736(14)61060-6. [DOI] [PubMed] [Google Scholar]
- Carroll R, Ruppert D, Stefanski L, Crainiceanu C. Measurement Error in Nonlinear Models: A Modern Perspective, Second Edition. Chapman and Hall; London: 2006. [Google Scholar]
- Clements-Mann M. Lessons for AIDS vaccine development from non-AIDS vaccines. AIDS Research and Human Retroviruses. 1998;14(Suppl 3):S197–S203. [PubMed] [Google Scholar]
- Cole S, Stuart E. Generalizing evidence from randomized clinical trials to target populations the ACTG 320 trial. American Journal of Epidemiology. 2010;172:107–115. doi: 10.1093/aje/kwq084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durham L, Longini I, Halloran M, Clemens J, Nizam A, Rao M. Estimation of vaccine efficacy in the presence of waning: application to cholera vaccines. American Journal of Epidemiology. 1998;147:948–959. doi: 10.1093/oxfordjournals.aje.a009385. [DOI] [PubMed] [Google Scholar]
- FDA Guidance Document. FDA Guidance for Industry: Clinical trial endpoints for the approval of cancer drugs and biologics 2007 [Google Scholar]
- Follmann D. Augmented designs to assess immune response in vaccine trials. Biometrics. 2006;62:1161–1169. doi: 10.1111/j.1541-0420.2006.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frangakis C, Rubin D. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel E, Gilbert P. Evaluating principle surrogate endpoints with time-to-event data accounting for time-varying treatment efficacy. Biostatistics. 2014;15:251–265. doi: 10.1093/biostatistics/kxt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabriel EE, Sachs MC, Gilbert PB. Comparing and combining biomarkers as principle surrogates for time-to-event clinical endpoints. Statistics in Medicine. 2015;34:381–395. doi: 10.1002/sim.6349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, Gabriel E, Huang Y, Chan I. Surrogate endpoint evaluation: Principal stratification criteria and the prentice definition. Journal of Causal Inference. 2015;3(2):157–175. doi: 10.1515/jci-2014-0007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, Hudgens M. Evaluating candidate principal surrogate end-points. Biometrics. 2008;64:1146–1154. doi: 10.1111/j.1541-0420.2008.01014.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, McKeague I, Sun Y. The two-sample problem for failure rates depending on a continuous mark: an application to vaccine efficacy. Biostatistics. 2008;9:263–276. doi: 10.1093/biostatistics/kxm028. [DOI] [PubMed] [Google Scholar]
- Gilbert P, Self G, Rao M, Naficy A, Clemens J. Sieve analysis: Methods for assessing how vaccine efficacy depends on genotypic and phenotypic pathogen variation from vaccine trial data. Journal of Clinical Epidemiology. 2001;54:68–85. doi: 10.1016/s0895-4356(00)00258-4. [DOI] [PubMed] [Google Scholar]
- Gilbert P, Sun Y. Testing for vaccine efficacy against a spectrum of pathogen sequences in stratified mark-specific proportional hazards models with missing marks, with application to the RV144 HIV vaccine efficacy trial. Journal of the Royal Statistical Society Series C. 2014;64:49–73. doi: 10.1111/rssc.12067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray GE, Moodie Z, Metch B, Gilbert PB, Bekker LG, Churchyard G, Nchabeleng M, Mlisana K, Laher F, Roux S, Corey L. Recombinant adenovirus type 5 HIV gag/pol/nef vaccine in South Africa: unblinded, long-term follow-up of the phase 2b HVTN 503/Phambili study. The Lancet Infectious Diseases. 2014;14:388–396. doi: 10.1016/S1473-3099(14)70020-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer S, Sobieszczyk M, Janes H, Karuna S, Mulligan MJ, Grove D, et al. Efficacy trial of a DNA/rAd5 HIV-1 preventive vaccine. New England Journal of Medicine. 2013;369:283–292. doi: 10.1056/NEJMoa1310566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haynes B, Gilbert P, McElrath M, et al. Immune correlates analysis of the ALVAC-AIDSVAX HIV-1 vaccine efficacy trial. New England Journal of Medicine. 2012;366:1275–1286. doi: 10.1056/NEJMoa1113425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernán MA. The hazards of hazard ratios. Epidemiology. 2010;21:13–15. doi: 10.1097/EDE.0b013e3181c1ea43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Gilbert P, Wolfson J. Design and estimation for evaluating principal surrogate markers in vaccine trials. Biometrics. 2013;69:301–309. doi: 10.1111/biom.12014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juraska M, Gilbert P. Mark-specific hazard ratio model with multivariate continuous marks: An application to vaccine efficacy. Biometrics. 2013;69:328–337. doi: 10.1111/biom.12016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lassauniere R, Tiemessen C. HIV Research for Prevention 2014 (HIV R4P) Cape Town, South Africa: 2014. Fc-gamma receptor variability in the South African population– Will this impact on HVTN097 and vaccine efficacy? Abstract P37.05. [Google Scholar]
- Li S, Gilbert P, Tomaras G, et al. Association of FCGR2C polymorphisms with vaccine efficacy and correlates of HIV-1 infection risk in the RV144 trial. Journal of Clinical Investigation. 2014;124:3879–3890. doi: 10.1172/JCI75539. * Contributed equally. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. Direct and Indirect Effects. Morgan Kaufmann; San Francisco: 2001. [Google Scholar]
- Pearl J, Bareinboim E. Transportability of causal and statistical relations: A formal approach. Proceedings of the Twenty-Fifth National Conference on Artificial Intelligence; Menlo Park, CA. 2011. pp. 247–254. [Google Scholar]
- Plotkin S, Gilbert P. Nomenclature for immune correlates of protection after vaccination. Clinical Infectious Diseases. 2012;54:1615–1617. doi: 10.1093/cid/cis238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plotkin SA. Correlates of protection induced by vaccination. Clinical Vaccine Immunology. 2010;17:1055–1065. doi: 10.1128/CVI.00131-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice R. Surrogate endpoints in clinical trials: definition and operational criteria. Statistics in Medicine. 1989;8:431–440. doi: 10.1002/sim.4780080407. [DOI] [PubMed] [Google Scholar]
- Prentice R, Kalbfleisch J, Peterson A, Fluornoy N, Farewell V, Breslow N. The analysis of failure time in the presence of competing risk. Biometrics. 1978;34:541–554. [PubMed] [Google Scholar]
- Qin L, Gilbert P, Follmann D, Li D. Assessing surrogate endpoints in vaccine trials with case-cohort sampling and the Cox model. Annals of Applied Statistics. 2008;2:386–407. doi: 10.1214/07-AOAS132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rerks-Ngarm S, Pitisuttithum P, Nitayaphan S, et al. Vaccination with ALVAC and AIDSVAX to prevent HIV-1 infection in thailand. New England Journal of Medicine. 2009;361:2209–2220. doi: 10.1056/NEJMoa0908492. [DOI] [PubMed] [Google Scholar]
- Robb M, Rerks-Ngarm S, Nitayaphani S, et al. Risk behaviour and time as covariates for efficacy of the HIV vaccine regimen ALVAC-HIV (vCP1521) and AIDSVAX B/E: a post-hoc analysis of the thai phase 3 efficacy trial RV144. Lancet Infectious Diseases. 2012;12:531–537. doi: 10.1016/S1473-3099(12)70088-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins J, Greenland S. Identifiability and exchangeability of direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Rolland* M, Edlefsen* P, Larsen B, et al. Increased HIV-1 vaccine efficacy against viruses with genetic signatures in Env V2. Nature. 2012;490:417–420. doi: 10.1038/nature11519. * Contributed equally. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum P. Design of Observational Studies. Springer; New York: 2010. [Google Scholar]
- Rubin D. Bayesian inference for causal effects. Annals of Statistics. 1978;6:34–58. [Google Scholar]
- Staessen J, Yan L, Lutgarde T, Wang JG. Blood pressure reduction and cardiovascular prevention: An update including the 2003–2004 secondary prevention trials. Hypertension Research. 2005;28:385–407. doi: 10.1291/hypres.28.385. [DOI] [PubMed] [Google Scholar]
- van der Laan MJ, Hubbard AE, Pajouh SK. UC Berkeley Division of Biostatistics Working Paper Series. 2013. Statistical inference for data adaptive target parameters. Working Paper 314. [DOI] [PubMed] [Google Scholar]
- van der Laan MJ, Polley EC, Hubbard AE. Super learner. Statistical Applications in Genetics and Molecular Biology. 2007;6 doi: 10.2202/1544-6115.1309. [DOI] [PubMed] [Google Scholar]
- Vansteelandt S, Goetghebeur E, Kenward M, Molenberghs G. Ignorance and uncertainty regions as inferential tools in a sensitivity analysis. Statistica Sinica. 2006;16:953–979. [Google Scholar]
- Villar L, Dayan GH, Arredondo-García JL, Rivera DM, Cunha R, Deseda C, Reynales H, Costa MS, Morales-Ramírez JO, Carrasquilla G, et al. Efficacy of a tetravalent dengue vaccine in children in latin america. New England Journal of Medicine. 2015;372:113–123. doi: 10.1056/NEJMoa1411037. [DOI] [PubMed] [Google Scholar]
- Zolla-Pazner S, DeCamp A, Gilbert P, et al. Vaccine-induced IgG antibodies to V1V2 regions of multiple HIV-1 subtypes correlate with decreased risk of HIV-1 infection. PLoS One. 2014;9:e87572. doi: 10.1371/journal.pone.0087572. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.