Parametric mediational g-formula approach to mediation analysis with time-varying exposures, mediators, and confounders

Abstract

The assessment of direct and indirect effects with time-varying mediators and confounders is a common but challenging problem, and standard mediation analysis approaches are generally not applicable in this context. The mediational g-formula was recently proposed to address this problem, paired with a semi-parametric estimation approach to evaluate longitudinal mediation effects empirically. In this paper, we develop a parametric estimation approach to the mediational g-formula, including a feasible algorithm implemented in a freely available SAS macro. In the Framingham Heart Study data, we apply this method to estimate the interventional analogues of natural direct and indirect effects of smoking behaviors sustained over a 10-year period on blood pressure when considering weight change as a time-varying mediator. Compared with not smoking, smoking 20 cigarettes per day for 10 years was estimated to increase blood pressure by 1.2 (95 % CI: −0.7, 2.7) mm-Hg. The direct effect was estimated to increase blood pressure by 1.5 (95 % CI: −0.3, 2.9) mm-Hg, and the indirect effect was −0.3 (95% CI: −0.5, −0.1) mm-Hg, which is negative because smoking which is associated with lower weight is associated in turn with lower blood pressure. These results provide evidence that weight change in fact partially conceals the detrimental effects of cigarette smoking on blood pressure. Our work represents, to our knowledge, the first application of the parametric mediational g-formula in an epidemiologic cohort study.

Introduction

Mediation analysis, a method to decompose the total effect of an exposure on an outcome into direct and indirect effects through a mediator, is essential for investigating pathways or mechanisms in epidemiology and in the social sciences. Causal mediation analysis, defining natural direct and indirect effects based on counterfactual models, extends traditional mediation analysis to settings involving nonlinearities and interactions^1,2. Numerous methodologic approaches based on causal mediation analysis have been developed in recent years allowing different outcome scales, including additive, multiplicative, and odds ratio scales, as well as other models for time-to-event data^3–8. Most of the approaches mentioned above only consider a point exposure and a subsequent point mediator. When conducting causal mediation analysis with longitudinal data, the restriction of only one single exposure and mediator neglects exposures or mediators at other time-points, which thus potentially results in loss of valuable information.

Robins has proposed the g-formula to estimate the total effect in settings with time-varying exposures and confounders⁹. In addition, when mediators can be intervened upon, the g-formula can estimate the controlled direct effect by comparing the effects of two different exposure levels and specifying the mediators at certain fixed values. For mediation, however, the natural direct effect and the natural indirect effect involved in effect decomposition are, unfortunately, not identified. VanderWeele and Tchetgen Tchetgen¹⁰ proposed the mediational g-formula to overcome the methodologic challenges of causal mediation analysis with time-varying mediators. As discussed below, this method decomposes the randomized interventional analogue of total effect into interventional analogues of natural direct effect and indirect effect and moves beyond the limitations of a single exposure and a single mediator. Time-varying confounders can also be accounted for provided no unobserved confounding is present. For estimation of the randomized natural direct and indirect effects, VanderWeele and Tchetgen Tchetgen proposed a semi-parametric approach based on inverse probability weighted estimators. As with standard inverse probability weighting, this approach is potentially unstable if the exposure is continuous or the weights are highly variable. Instead, we consider an alternative approach that is potentially more stable and efficient, by implementing a fully parametric mediational g-formula approach, using a user-friendly algorithm implemented in freely available software. We then apply this method to the Framingham Heart Study (FHS) data to investigate the effect of smoking on blood pressure mediated by weight change.

Case study for Framingham dataset: smoking, weight, and blood pressure

In past research, the association between smoking and blood pressure has been controversial^11–16. In some studies, average blood pressure, as measured using a domestic blood pressure monitor^17–19, is lower among smokers than among non-smokers at particular times of the day^14,20. According to most literature, among former smokers, smoking cessation is associated with increased blood pressure^21,22 while some studies fail to observe this association²³.

Three possible mechanisms might explain this association. First, smoking activates the autonomic nervous system to increase blood pressure directly, but smoking cessation also activates the autonomic nervous system, increasing blood pressure among former smokers^24,25. Second, smoking elevates blood pressure through exacerbating arterial stiffness. Third, smoking decreases blood pressure through weight loss²¹. The adverse effect of smoking on elevated blood pressure might thus be partially concealed by weight loss. Because both smoking status and weight change vary over time, the mediational g-formula can be used to study the extent of this adverse effect mediated by weight loss. In this study, we obtain the estimates by applying our method to the FHS data and demonstrate an application of causal mediation analysis with time-varying mediators.

Methods Development

Notation and review for causal mediation analysis

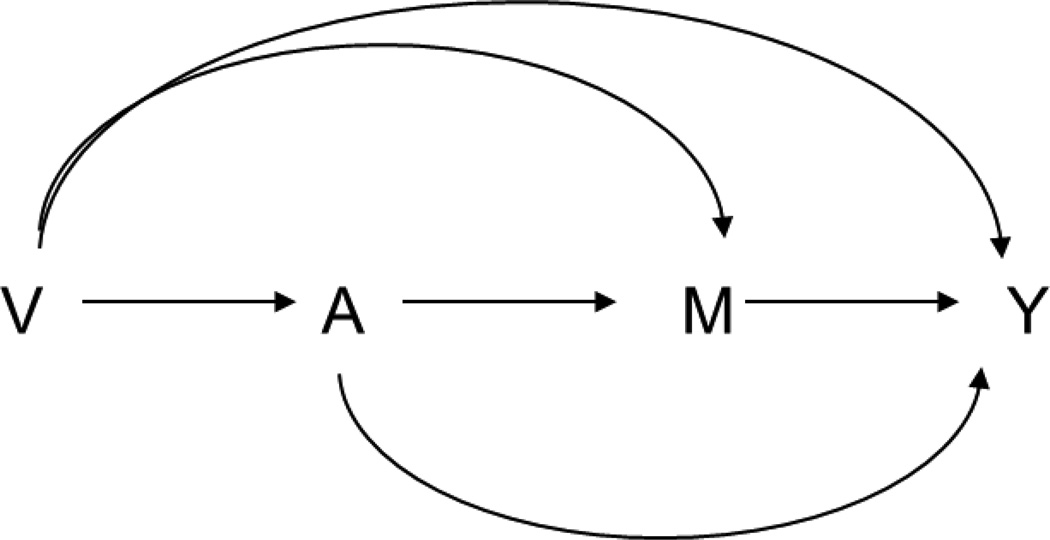
First consider a setting with an exposure, mediator, and outcome measured at a single time. Let A denote an exposure, Y an outcome, and M a mediator. Let V denote a set of baseline covariates not affected by the exposure. The relationships among these variables are described in Figure 1. Under counterfactual models^26,27, Y_a and M_a denote the counterfactual values of the outcome and the mediator, respectively, if exposure A is set to level a. Y_am denotes the counterfactual value of the outcome if exposure A is set to level a, and mediator M is set to level m. In addition, Y_aMa* denotes the counterfactual value of the outcome if exposure A is set to level a and mediator M is set to level M_a*. Under the consistency assumption^6,28,29, Y_a = Y and M_a = M if A = a; Y_am = Y if A = a and M = m; and the composition assumption that Y_aMa* = Y if A = a and M = M_a*.

Figure 1.

Simple model for mediation analysis.

Mediation analysis decomposes the overall effect into a direct effect (the effect not through the mediator) and an indirect effect (the effect through the mediator). Under the above counterfactual models, causal mediation analysis usually defines the total effect, natural direct effect, and natural indirect effect to represent the overall, direct, and indirect effects, respectively. Let A = a and A = a^* denote two hypothetical intervention statuses, exposure and non-exposure, respectively. The total effect is defined as E[Y_a − Y_a*] or equivalently, E[Y_aMa − Y_a*Ma*]; the natural direct effect is defined as E[Y_aMa* − Y_a*Ma*], and the natural indirect effect is defined as E[Y_aMa − Y_aMa*]. These effects have been described extensively elsewhere and arguments have been made that they are theoretically appealing for effect decomposition^1,2,6. However, in the presence of time-varying confounders, the natural direct effect and natural indirect effect are not generally identified from data even if these confounders are observed^30,31. To address the problem of identification, an alternative definition uses the randomized analogue of total effect, randomized natural direct effect, and randomized natural indirect effect to represent the overall, direct, and indirect effects, respectively^32–34. Let G_a denote a random draw from the distribution of the mediator amongst those with exposure status A = a. When exposure is set to a (or a*), the distribution of mediator among whole population is also determined. Therefore, for every individual, a random draw from this distribution, G_a (or G_a*), will be independent of the counterfactual mediator, M_a (or M_a*) and outcome (Y_am). The randomized analogue of total effect is defined as E[Y_aGa] − E[Y_a*Ga*]. The randomized natural direct effect is defined as E[Y_aGa*] − E[Y_a*Ga*], which can be interpreted as an effect on the outcome comparing exposure versus no exposure with the mediator in both cases randomly drawn from the distribution of the population when given no exposure. Finally, the randomized natural direct effect is defined as E[Y_aGa] − E[Y_aGa*], interpreted as an effect on the outcome of randomly assigning an individual who is given exposure to a value of the mediator drawn from the distribution of the mediator amongst those given exposure versus not given exposure. We have the decomposition: E[Y_aGa]− E[Y_a*Ga*] = (E[Y_aGa] − E[Y_aGa*]) + (E[Y_aGa*] − E[Y_a*Ga*]), so the overall effect decomposes into the sum of the effect through the mediator (i.e. the indirect effect) and the direct effect.

Both natural direct and indirect effects can be identified under four assumptions: (1) Y_am^⊥A|V (no unmeasured exposure-outcome confounder); (2) Y_am^⊥M|V, A (no unmeasured mediator-outcome confounder); (3) M_a^⊥A|V (no unmeasured exposure-mediator confounder); and (4) Y_am^⊥M_a*|V (no mediator-outcome confounder affected by exposure)^6,30, when ⊥ denotes independence and X ⊥ Y | Z denotes that X is independent of Y conditional on Z. Under these assumptions, natural direct effects (NDE) and indirect effects (NIE) are identified by the following expressions:

$$\mathrm{N}\mathrm{D}\mathrm{E}={\mathrm{\Sigma }}_{\mathrm{v}}{\mathrm{\Sigma }}_{\mathrm{m}}\{\mathrm{E}[\mathrm{Y}|\mathrm{a},\mathrm{m},\mathrm{v}]-\mathrm{E}[\mathrm{Y}|{\mathrm{a}}^{*},\mathrm{m},\mathrm{v}]\}\mathrm{P}(\mathrm{m}|{\mathrm{a}}^{*},\mathrm{v})\mathrm{P}(\mathrm{v})$$ (1)

$$\mathrm{N}\mathrm{I}\mathrm{E}={\mathrm{\Sigma }}_{\mathrm{v}}{\mathrm{\Sigma }}_{\mathrm{m}}\mathrm{E}[\mathrm{Y}|\mathrm{a},\mathrm{m},\mathrm{v}]\{\mathrm{P}(\mathrm{m}|\mathrm{a},\mathrm{v})-\mathrm{P}(\mathrm{m}|{\mathrm{a}}^{*},\mathrm{v})\}\mathrm{P}(\mathrm{v})$$ (2)

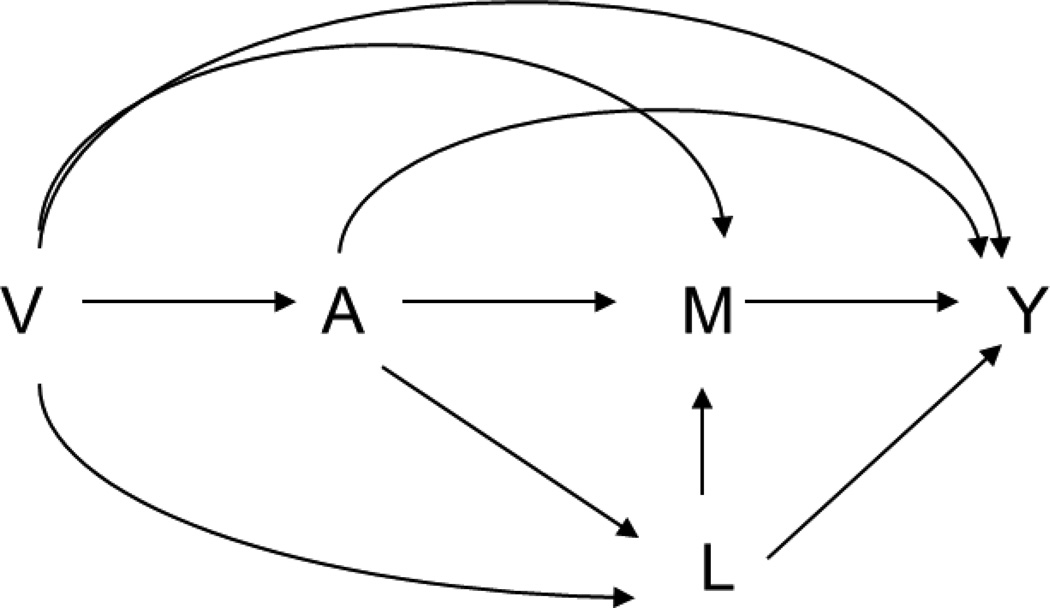
The fourth assumption holds only under a non-parametric structural equation model and would be violated under several settings. The most common one is the existence of a mediator-outcome confounder L that is affected by exposure (Figure 2), in which case the fourth assumption fails, even if this confounder is observed. When this confounder is a single binary variable, Tchetgen Tchetgen and VanderWeele proposed a method to identify the NDE and NIE by assuming the monotonicity about the effect of exposure on this confounder³⁵. A severe shortcoming of this assumption is that even if the mediator is restricted to occurring immediately after the exposure, the assumption cannot be ensured. As a result, this approach is not generally applicable for settings with time-varying mediators. However, even if this assumption fails, given assumptions (1) to (3) hold and the mediator-outcome confounder is observed, the randomized natural direct effect (rNDE) and randomized natural indirect effect (rNIE) in the second definition are still identifiable from the data by the empirical expressions given by³⁴:

$$\mathrm{r}\mathrm{N}\mathrm{D}\mathrm{E}={\mathrm{\Sigma }}_{\mathrm{v},\mathrm{l},\mathrm{m}}\{\mathrm{E}[\mathrm{Y}|\mathrm{a},\mathrm{l},\mathrm{m},\mathrm{v}]\mathrm{P}(1|\mathrm{a},\mathrm{v})-\mathrm{E}[\mathrm{Y}|{\mathrm{a}}^{*},\mathrm{l},\mathrm{m},\mathrm{v}]\mathrm{P}(1|{\mathrm{a}}^{*},\mathrm{v})\}\mathrm{P}(\mathrm{m}|{\mathrm{a}}^{*},\mathrm{v})\mathrm{P}(\mathrm{v})$$ (3)

$$\mathrm{r}\mathrm{N}\mathrm{I}\mathrm{E}={\mathrm{\Sigma }}_{\mathrm{v},\mathrm{l},\mathrm{m}}\mathrm{E}[\mathrm{Y}|\mathrm{a},\mathrm{l},\mathrm{m},\mathrm{v}]\mathrm{P}(\mathrm{l}|\mathrm{a},\mathrm{v})\{\mathrm{P}[\mathrm{m}|\mathrm{a},\mathrm{v}]-\mathrm{P}(\mathrm{m}|{\mathrm{a}}^{*},\mathrm{v})\}\mathrm{P}(\mathrm{v})$$ (4)

Figure 2.

Mediation analysis with a mediator-outcome confounder L that is affected by exposure.

To understand the difference in the effects better, note that the natural direct effect and natural indirect effect cannot be checked by designing a randomized trial even if we were able to intervene on both the exposure and the mediator. However, it is possible to design a two-stage trial to estimate randomized natural direct and indirect effects. A randomized trial could first be conducted to obtain the empirical distribution of counterfactual mediator given exposed and non-exposed by randomizing the exposure and measuring the mediator distributions. We can then estimate randomized natural indirect effect in a second trial by the effect on the outcome of assigning an individual who is given the exposure to a value of the mediator sampled from the marginal distribution of the mediator amongst those given exposure versus no exposure, using the empirical distributions of the mediator estimated from the first randomized trial. Similarly, we can estimate randomized natural direct effect by a direct effect comparing exposure versus no exposure with the mediator in both cases randomly drawn from the empirical distribution of the population when given no exposure, which was also estimated from the first randomized trial.

Notation and review of mediation analysis with time-varying mediators and the mediational g-formula

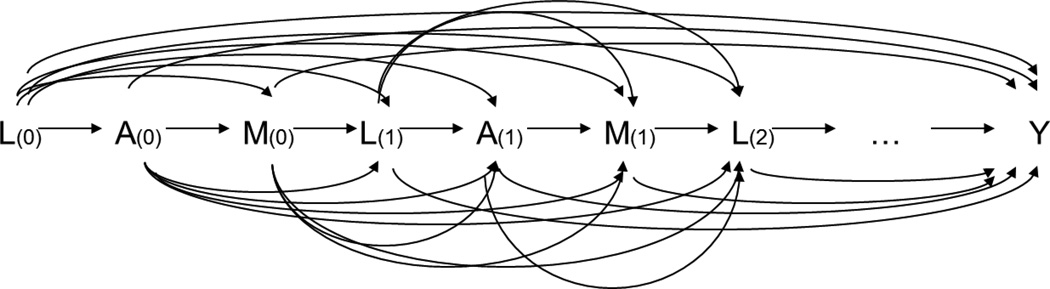
Consider exposures, mediators, and confounders that vary over time in longitudinal settings with T measurements at time t = 0, 1, 2, …, T−1. Let (A(0), A(1), …, A(T−1)), (M(0), M(1), …, M(T−1)), and (L(0), …, L(T−1)) denote values of the time-varying exposures, mediators, and confounders at periods 1, …, T, with the final outcome of interest Y. The initial baseline confounders are included in L(0). Figure 3 depicts a possible data generating mechanism under which these assumptions would hold.

Figure 3.

Time-varying mediation with ordering of variables of A(t), M(t), L(t), for t = 0 to T−1.

For any variable W, let $\overline{\mathrm{W}(\mathrm{t})}=(\mathrm{W}(0),\mathrm{W}(1),\dots ,\mathrm{W}(\mathrm{t}))$ and let $\overline{\mathrm{W}}=\overline{\mathrm{W}(\mathrm{T}-1)}=(\mathrm{W}(0),\mathrm{W}(1),\dots ,\mathrm{W}(\mathrm{T}-1))$. Let ${\mathrm{Y}}_{\overline{\mathrm{a}\mathrm{m}}}$ be the counterfactual value of Y given Ā is set to ā and M̅ is set to m̅. Let M_ā(t) be the counterfactual value of M(t) given $\overline{\mathrm{A}(\mathrm{t})}$ is set to $\overline{\mathrm{a}(\mathrm{t})}$. Let G_ā(t) denote a random draw from the distribution of the mediator M_ā(t). Let Ā = ā and $\mathrm{Ā}=\overline{{\mathrm{a}}^{*}}$ denote two hypothetical intervention statuses, for example, exposed from t = 0 to T−1 and non-exposed from t = 0 to T−1, respectively. In this setting, we define total effect as $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}}]$ (i.e. $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\overline{\mathrm{M}}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\overline{\mathrm{M}}\overline{\mathrm{a}*}}]$), natural direct effect, as $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\overline{\mathrm{M}}\overline{\mathrm{a}*}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\overline{\mathrm{M}}\overline{\mathrm{a}*}}]$, and natural indirect effect $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\overline{\mathrm{M}}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\overline{\mathrm{M}}\overline{\mathrm{a}*}}]$; we aslo define randomized analogues of total effect as $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\mathrm{Ḡ}\overline{\mathrm{a}*}}]$, randomized analogue of natural direct effect as $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\overline{\mathrm{a}*}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\mathrm{Ḡ}\overline{\mathrm{a}*}}]$, and randomized analogue of natural indirect effect as $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\overline{\mathrm{a}*}}]$. We can decompose the total effect into the natural direct effect and natural indirect effect. Similarly, randomized analogue of total effect is decomposed into randomized analogues of natural direct effect and of natural indirect effect (i.e., $\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\mathrm{Ḡ}\overline{\mathrm{a}*}}]=\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\overline{\mathrm{a}*}}]-\mathrm{E}[{\mathrm{Y}}_{\overline{\mathrm{a}*}\mathrm{Ḡ}\overline{\mathrm{a}*}}]+\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\mathrm{ā}}]-\mathrm{E}[{\mathrm{Y}}_{\mathrm{ā}\mathrm{Ḡ}\overline{\mathrm{a}*}}]$.

If the entire vector $\mathrm{Ā}=\overline{\mathrm{A}(\mathrm{T}-1)}$ is taken as the joint exposure of interest and $\overline{\mathrm{M}}=\overline{\mathrm{M}(\mathrm{T}-1)}$ as the mediators of interest, then assumption (4) is violated because the variable L(1) is affected by A(0) and confounds the mediator-outcome relationship between M(1) and Y (similarly, the L(t) is affected by $\overline{\mathrm{A}(\mathrm{t}-1)}$ and confounds the relationship between M(t) and Y, when t = 1, …, T−1). Therefore, natural direct and indirect effects cannot be identified in this setting. However, randomized natural direct and indirect effects are still identifiable under the following three assumptions for all t: (1) ${\mathrm{Y}}_{{\overline{\mathrm{a}\mathrm{m}}}^{\perp }}\mathrm{A}(\mathrm{t})|\overline{\mathrm{A}(\mathrm{t}-1)},\overline{\mathrm{M}(\mathrm{t}-1)},\overline{\mathrm{L}(\mathrm{t})}$ (no exposure–outcome confounding conditional on the past variables), (2) ${\mathrm{Y}}_{{\overline{\mathrm{a}\mathrm{m}}}^{\perp }}\mathrm{M}(\mathrm{t})|\overline{\mathrm{A}(\mathrm{t})},\overline{\mathrm{M}(\mathrm{t}-1)},\overline{\mathrm{L}(\mathrm{t})}$ (no mediator–outcome confounding conditional on the past variables), and (3) ${\mathrm{M}}_{\mathrm{ā}}(\mathrm{t})\perp \mathrm{A}(\mathrm{t})|\overline{\mathrm{A}(\mathrm{t}-1)},\overline{\mathrm{M}(\mathrm{t}-1)},\overline{\mathrm{L}(\mathrm{t})}$ (no exposure–mediator confounding conditional on the past variables)¹⁰. Given the three assumptions, VanderWeele and Tchetgen Tchetgen¹⁰ show that the randomized natural direct (rNDE) and indirect effects (rNIE) are identified non-parametrically by the following equations:

$$\mathrm{r}\mathrm{N}\mathrm{D}\mathrm{E}=\mathrm{Q}(\mathrm{ā},\overline{{\mathrm{a}}^{*}})-\mathrm{Q}(\overline{{\mathrm{a}}^{*}},\overline{{\mathrm{a}}^{*}})$$ (5)

$$\mathrm{r}\mathrm{N}\mathrm{I}\mathrm{E}=\mathrm{Q}(\mathrm{ā},\mathrm{ā})-\mathrm{Q}(\mathrm{ā},\overline{{\mathrm{a}}^{*}})$$ (6)

$$\text{where }\mathrm{Q}({\mathrm{ā}}_1,{\mathrm{ā}}_2)=\sum _{\overline{\mathrm{m}}}\sum _{\overline{\mathrm{l}}}\mathrm{E}[\mathrm{Y}|\overline{{\mathrm{a}}_1},\overline{\mathrm{m}},\overline{\mathrm{l}}]\prod _{\mathrm{t}=0}^{\mathrm{T}-1}\mathrm{P}(\mathrm{l}(\mathrm{t})|\overline{{\mathrm{a}}_1(\mathrm{t}-1)},\overline{\mathrm{m}(\mathrm{t}-1)},\overline{\mathrm{l}(\mathrm{t}-1)})\times \sum _{\overline{\mathrm{l}\prime }}\prod _{\mathrm{t}=0}^{\mathrm{T}-1}\mathrm{P}(\mathrm{m}(\mathrm{t})|\overline{{\mathrm{a}}_2(\mathrm{t})},\overline{\mathrm{m}(\mathrm{t}-1)},\overline{\mathrm{l}\prime (\mathrm{t})})\mathrm{P}(\mathrm{l}\prime (t)|\overline{{\mathrm{a}}_2(\mathrm{t}-1)},\overline{\mathrm{m}(\mathrm{t}-1)},\overline{\mathrm{l}(\mathrm{t}-1)})$$ (7)

As in VanderWeele and Tchetgen Tchetgen, we refer to this expression Q(ā₁, ā₂) above as the mediational g-formula. When there are no mediators, i.e. M̄ equals empty, this formula (7) reduces to the standard g-formula:

$$\mathrm{Q}(\mathrm{ā})=\sum _{\overline{\mathrm{l}}}\mathrm{E}[\mathrm{Y}|\overline{{\mathrm{a}}_1},\overline{\mathrm{l}}]\prod _{\mathrm{t}=0}^{\mathrm{T}-1}\mathrm{P}(\mathrm{l}(\mathrm{t})|\overline{{\mathrm{a}}_1(\mathrm{t}-1)},\overline{\mathrm{l}(\mathrm{t}-1)})$$ (8)

Further, rNDE (5) and rNIE (6) reduce to the natural direct effect and natural indirect effect, respectively, when there are no time-varying confounders¹⁰.

Parametric mediational g-formula

VanderWeele and Tchetgen Tchetgen described how to use inverse probability weighting of marginal structural models to estimate the mediational g-formula Q(ā₁, ā₂) (7) in realistic high-dimensional settings¹⁰. However, this approach can perform poorly with continuous exposures and mediators and can also be inefficient. As an alternative, an adaptation of the standard parametric g-formula^9,36 can be used to parametrically estimate the mediational g-formula in high-dimensional settings and, in turn, the randomized natural direct effect (5) and randomized natural indirect effect (6).

We begin by briefly reviewing the standard parametric g-formula. This approach parametrically estimates the standard g-formula by (i) fitting parametric models for the joint density of the outcome and time-varying covariates and (ii) using the estimated parameters of these models to simulate many covariate histories consistent with the exposure intervention ā. Specifically, the following algorithm, which is implemented in a publicly available SAS macro³⁷, can be used to parametrically estimate the standard g-formula Q(ā):

1. Fit parametric models for the observed data:

   • (1a)
     For times t ≥ 0, fit parametric models for the joint density of the confounders and exposures at t given the measured past.
   • (1b)
     Fit a parametric model for the mean of the outcome at the end of follow-up given the measured past.
2. Set baseline confounders and exposures to the observed sample values. Recursively, for each subject i = 1, …, n and for each time t = 0, 1, 2, …, T−1:

   • (2a)
     For t ≥ 0, generate time t confounders and exposures based on the estimated model coefficients of (1a) and previously generated exposures and confounders under intervention.
   • (2b)
     Assign time t exposures under intervention ā.

3. Simulate the outcome for each of the n generated histories in step 2 based on the estimated model coefficients of (1b).

4. Take the mean over n simulated outcomes in (3) to estimate Q(ā).

Here, we have adapted the above algorithm and associated SAS macro code to parametrically estimate the mediational g-formula Q(ā₁, ā₂), the randomized analogues of total effect, of natural direct effect, and of natural indirect effect. The primary difference between the parametric g-formula and the parametric mediational g-formula is, under the latter algorithm, the estimated model coefficients from step (1) are additionally used to estimate the joint distribution of the time-varying mediators (marginal over all other covariates) under both exposure interventions ā and $\overline{{\mathrm{a}}^{*}}$. These are then used to assign values of the mediator under the joint exposure and mediator interventions (ā,Ḡ_ā), $(\mathrm{ā},{\mathrm{Ḡ}}_{\overline{a^{*}}}),(\overline{{\mathrm{a}}^{*}},{\mathrm{Ḡ}}_{ā})$ and $(\overline{{\mathrm{a}}^{*}},{\mathrm{Ḡ}}_{\overline{a^{*}}})$. The algorithm is as follows:

1. Fit parametric models for the observed data:

   • (1a)
     For times t ≥ 0, fit parametric models for the joint density of the confounders, exposures and mediators at t given the measured past.
   • (1b)
     Fit a parametric model for the mean of the outcome at the end of follow-up given the measured past.
2. Estimate the joint distribution of time-varying mediators under time-varying exposure interventions ā and $\overline{{\mathrm{a}}^{*}}$:

   • (2a)
     Set baseline (t = 0) covariates to the observed values for subject i. Recursively, for each time t = 0, …, T−1 and each subject i = 1, …, n:

     • (2a.i)
       For t ≥ 0, generate time t confounders, exposure, and mediator based on the estimated model coefficients of (1a) and previously generated covariates under the time-varying exposure intervention ā through t−1.
     • (2a.ii)
       Assign time t exposure under the intervention ā.
   • (2b)
     For each t = 0,…T−1, randomly permute the n values of the joint mediators assigned under intervention ā in (2a). For each t, save this permutation for use in (3) below (we obtain Ḡ_ā in this step).
   • (2c)
     Repeat (2a) replacing intervention ā with $\overline{{\mathrm{a}}^{*}}$.
   • (2d)
     Repeat (2b) replacing intervention ā with $\overline{{\mathrm{a}}^{*}}$ (we obtain ${\mathrm{Ḡ}}_{\overline{a^{*}}}$ in this step).
3. Estimate Q(ā, ā), $\mathrm{Q}(\mathrm{ā},\overline{{\mathrm{a}}^{*}}),\mathrm{Q}(\overline{{\mathrm{a}}^{*}},\mathrm{ā})$ and $\mathrm{Q}(\overline{{\mathrm{a}}^{*}},\overline{{\mathrm{a}}^{*}})$ by repeating the following for each $(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})=(\mathrm{ā},\mathrm{ā}),(\mathrm{ā},\overline{{\mathrm{a}}^{*}}),(\overline{{\mathrm{a}}^{*}},\mathrm{ā})$ and $(\overline{{\mathrm{a}}^{*}},\overline{{\mathrm{a}}^{*}})$:

   • (3a)
     Recursively for each time t = 0,…,T−1 and each subject i = 1,…,n:

     • (3a.i)
       Repeat (2a.i) but replacing “time-varying exposure intervention ā through t−1” with the joint “time-varying exposure and mediator intervention $(\overline{{\mathrm{a}}_1},{\mathrm{Ḡ}}_{\overline{a_2}})$”.
     • (3a.ii)
       Assign the time t mediator as the i^th component of the permuted vector for time t from (2b) $(\text{if }\overline{{\mathrm{a}}_2}=\mathrm{ā})$ or (2d) $(\text{if }\overline{{\mathrm{a}}_2}=\overline{{\mathrm{a}}^{*}})$.
     • (3a.iii)
       Assign time t exposure under the intervention $\overline{{\mathrm{a}}_1}$.
   • (3b)
     Simulate the outcome given each of the i = 1,…,n histories based on the estimated model coefficients of (1b) and the histories generated in (3a).
   • (3c)
     Estimate $\mathrm{Q}’(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$ as the mean over the n simulated outcomes in (3b).
   • (3d)
     Repeat (1) to (3c) for some fixed number K (e.g. 25) times, using different permutation in (2b) for each time.
   • (3e)
     Estimate $\mathrm{Q}(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$ as the mean of the K (e.g. 25) values of $\mathrm{Q}’(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$ in (3d).

The algorithm can stop at (3c) and use the $\mathrm{Q}’(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$ as the unbiased estimate of $\mathrm{Q}(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$. However, the repeated steps in (3d) can improve standard errors for smaller sample sizes. Estimates of the randomized natural direct and indirect effects are then calculated from the estimates of the four $\mathrm{Q}(\overline{{\mathrm{a}}_1},\overline{{\mathrm{a}}_2})$ in (3). 95% confidence intervals are calculated based on repeating the above algorithm in 500 bootstrap samples of the original n observations. This algorithm can be implemented with the mgformula macro, freely accessible with documentation at http://www.hsph.harvard.edu/causal/software/. However, the data are not available on the website. Please see the eAppendix for details.

Data Application

Beginning in 1948 in Framingham, Massachusetts, the FHS is a longitudinal cohort study. The original cohort consists of 5,209 participants aged from 30 to 62 years old without cardiovascular disease (CVD) history at baseline. All the participants underwent examinations at the beginning of the study and routinely every two years after that. During each exam, potential CVD risk factors were collected, including socio-demographic data, lifestyle characteristics, detailed medical history, physical examination data, and blood samples. Further details on the design of FHS have been described elsewhere^23,38. All participants had provided written informed consent and the protocol was approved by the Institutional Review Board at Boston University Medical Center. The purpose of the analysis here is to illustrate the parametric meditational g-formula approach and software.

We specify exam 3 as the first exam and exams 1 and 2 as pre-baseline covariates to allow the function of the past in the models of step (1) of the estimation algorithm to depend on two lagged periods of the covariates. We follow the cohort for ten years (i.e. five visits) to reduce the proportion of death or loss to follow up to limit selection bias by death. Four exclusion criteria are listed below: (1) death or loss to follow up during the period before exam 7 (the end of follow-up); (2) no record at baseline on weight, height, smoking status, former smoking history, systolic blood pressure (SBP), or total cholesterol; (3) diagnosis of diabetes, cancer, or CVD at baseline; and (4) missing value for smoking status or BMI missing more than once. After these exclusions, 3,116 participants remain eligible for our analysis. For simplicity, we now refer to the original FHS exams 3,…, 7 as exams 1,…, 5.

SBP at exam 5 is the outcome Y. BMI during follow-up (exam 1 to 5) is the mediator M̅. The exposure Ā is smoking status during follow up, measured as self-reported average number of cigarettes smoked per day. For missing BMI value or smoking status at a single time period, we carry forward the last observed value/status for one exam period only. We consider "smoking 20 cigarettes per day" and "no smoking" during follow-up as two hypothetical intervention levels Ā = ā and $\mathrm{Ā}=\overline{{\mathrm{a}}^{*}}$. Time-varying covariates L̅ include the exam number, the systolic blood pressure (mm-Hg) at last exam, total non-fasting cholesterol level (mg/dl), and the usage of antihypertensive drugs. Baseline covariates include gender, age (years), height (meters), education (≤ 8^th grade, some high school, high school graduate, some college, college graduate, post-graduate), occupation before retirement (executive/supervisory, technical, laborer, clerical, sales, housewife), marital status (single, married, widowed/divorced), and tobacco use at baseline (never user, current user, and past user). All covariates and the corresponding models are listed in Table 1.

Table 1.

Summary of covariate models.

Variable	Type of model when used as dependent variable	Functional form when used as predictor
Non-modifiable
Gender	Not predicted	Indicator
Age	Not predicted	Quadratic linear
Height	Not predicted	Quadratic linear
Education level	Not predicted	Six categoriesa
Occupation	Not predicted	Six categoriesa
Marital status	Not predicted	Three categoriesb
Baseline smoking	Not predicted	Three categoriesb
Modifiable
SBP	Linear	Quadratic linear
Smoking	Logistic then log-linearc	Quadratic linear
Cholesterol	Linear	Quadratic linear
Anti-hypertension   drug	Linear	Three categoriesb

^aEducation level categories are ≤ 8^th grade, some high school, high school graduate, some college, college graduate, and post-graduate. Occupation categories are executive/supervisory, technical, laborer, clerical, sales, and housewife.

^bMarital status categories are single, married, and divorce or widowed. Baseline smoking are smoking, not smoking, and quitting. Anti-hypertension drug are regular use, not use, and sporadic use.

^czero-continuous variables such as cigarettes per day are predicted in two stages, first a logistic regression on an indicator of whether the variable is nonzero and then a linear regression of the log of the nonzero values.

The parametric g-formula is used to estimate the total effect of smoking 20 cigarettes per day v.s. no smoking on SBP and on BMI at exam 5, by the g-formula macro. The parametric mediational g-formula is applied to conduct mediation analysis with time-varying mediators and exposures by our newly developed mgformula macro. We specify models for the outcome mean, as well as for each time-varying covariate (including mediator, exposure, and confounders) at each time point. We use current covariates and covariates at one period back (one lagged model) as the predictors. Specifically, we regress Y on main effects for A(5), M(5), L(5), A(4), M(4), and L(4). For t = 0, 1, 2, …, 5, we regress L(t) on A(t−1), M(t−1), and L(t−1); regress M(t) on A(t), A(t−1), M(t−1), L(t), and L(t−1); and regress A(t) on A(t−1), M(t−1), L(t), and L(t−1) (please refer to the eAppendix for more details). All analyses are conducted using SAS 9.4 (Cary, NC).

Results

The demographic and baseline health characteristics for smokers (n = 1,759), non-smokers (n = 1,174), and quitters (n = 183) are shown in Table 2. Compared with non-smokers, smokers have higher male proportion, younger age, and better education level. The majority of non-smokers are female (84%) and half of them have the occupation of housewife. The occupations of the smokers are mainly supervisor, laborer, and housewife. At baseline, the smokers appear to have better health status for lower systolic blood pressure, cholesterol level, and BMI.

Table 2.

Baseline characteristics of eligible participants grouped by former smoking status.

Characteristic	Quitters (n = 183)	Non-smokers (n = 1,174)	Smokers (n = 1,759)
Male (%)	128 (69)	188 (16)	1049 (59)
Age, year (Mean (SD))	50 (8.5)	49 (8.5)	46 (8.0)
SBP, mmHg (Mean (SD))	128 (18)	132 (22)	126 (18)
BMI (Mean (SD))	26 (4)	26 (4)	25 (4)
Chol (Mean (SD))	234 (44)	232 (45)	228 (43)
Height (Mean (SD))	66 (3)	63 (3)	65 (3)
Education (%)
<High school	65 (36)	507 (43)	675 (38)
High school	64 (35)	420 (36)	707 (40)
College or higher	51 (28)	227 (19)	350 (20)
Missing	3 (2)	20 (2)	27 (2)
Work (%)
Supervisory	58 (32)	156 (13.3)	419 (23.8)
Technical	20 (10.9)	31 (2.6)	130 (7.4)
Laborer	48 (26.2)	238 (20.3)	517 (29.4)
Clerical	12 (6.6)	76 (6.5)	109 (6.2)
Sales	8 (4.4)	19 (1.6)	91 (5.2)
Housewife	36 (19.7)	647 (55.1)	478 (27.2)
Missing	1 (0.5)	7 (0.6)	15 (0.9)
Marital (%)
Married	163 (89.1)	935 (80)	1580 (90)
Single	10 (6)	145 (12)	105 (6)
Divorced	10 (6)	94 (8)	74 (4)

SBP: systolic blood pressure; BMI: body mass index; Chol: cholesterol level;

No one use the anti-hypertensive drugs at the beginning.

We use the g-formula to estimate the total effect of smoking (20 cigarettes per day v.s. no smoking for 10 years) on SBP and BMI in Table 3. Smoking elevates SBP by 1.2 mm-Hg and reduces BMI by 0.2 kg/m². In Table 4, we use the parametric mediational g-formula to simulate systolic blood pressure at the end of 10-year follow-up under no smoking with BMI distributed as the BMI under no smoking, smoking 20 cigarettes per day with BMI distributed as the BMI under smoking 20 cigarettes per day, no smoking with BMI distributed as the BMI under smoking 20 cigarettes per day, and smoking 20 cigarettes per day with BMI distributed as the BMI under no smoking. We then estimate the randomized total effect, randomized natural direct effects, and randomized natural indirect effects of smoking on systolic blood pressure mediated by BMI. The estimate of randomized analogue of total effect is 1.2 (95 % CI: −0.7, 2.7) mm-Hg, the estimate of randomized analogue of natural direct effect is 1.5 (95 % CI: −0.3, 2.9) mm-Hg, and the estimate of randomized analogue of natural indirect effect is −0.3 (95 % CI: −0.5, −0.1) mm-Hg. The directions of randomized natural direct and indirect effects are different, suggesting that the seemingly protective mediated effect of smoking through BMI may partially mask the detrimental direct effect of smoking on systolic blood pressure.

Table 3.

Estimates of the total effect of smoking 20 cigarettes per day for 10 years (compared with no smoking) on SBP and BMI.

Intervention	SBP (mm-Hg)	Change in SBP (95% CI)	BMI (kg/m2)	Change in BMI (95% CI)
No intervention	136.2	0.5 (−0.1, 1.0)	25.8	−0.00 (−0.2, 0.1)
No smoking	135.7	Reference	25.9	Reference
20 cigarettes/day	136.9	1.2 (−1.0, 3.1)	25.7	−0.2 (−0.4, 0.0)

SBP: systolic blood pressure; BMI: body mass index; CI: confident interval.

Table 4.

Randomly interventional analogue of total effect, of natural direct effect, and of natural indirect effect for the effect of smoking 20 cigarettes per day for 10 years (compared with no smoking) on SBP, mediated by BMI change over time.

	Estimate	95% CI
E[Y0G0]	135.691	134.93, 137.11
E[Y1G0]	137.211	135.76, 138.80
E[Y0G1]	135.336	134.57, 136.69
E[Y1G1]	136.874	135.64, 138.37
rTE	1.18	−0.68, 2.69
rNDE	1.52	−0.25, 2.90
rNIE	−0.34	−0.52, −0.13

rTE: randomly interventional analogue of total effect; rNDE: randomly interventional analogue of natural direct effect; rNIE: randomly interventional analogue of natural indirect effect; CI: confident interval; E[Y0G0], E[Y1G0], E[Y0G1], and E[Y1G1]

represent “no smoking with BMI distributed as the BMI under no smoking”,

“smoking 20 cigarettes per day with BMI distributed as the BMI under no smoking”,

“no smoking with BMI distributed as the BMI under smoking 20 cigarettes per day”,

and “smoking 20 cigarettes per day with BMI distributed as the BMI under smoking 20 cigarettes per day”, respectively.

Discussion

To our knowledge, this is the first paper to provide a fully parametric method for causal mediation analysis with time-varying mediators. We develop an algorithm and corresponding SAS macro to use the mediational g-formula parametrically. We use the parametric approach to obtain estimates for the mediational g-formula by adapting the g-formula macro externally to build our SAS macro. Similar to the g-formula, we use Monte-Carlo simulation and bootstrapping methods for point and interval estimation, respectively. Since the estimation is an approximation of the maximum likelihood estimation, this estimation is asymptotically efficient provided the regression models are all correctly specified, while the inverse probability weighting does not achieve the efficiency bound in a model where parametric assumptions about the weights and the marginal structural modeling are correct. In addition, like other simulation-based methods³⁹, the approach here has the advantage of allowing for very flexible models such as quadratic linear models.

The parametric mediational g-formula provides a powerful method to investigate the mechanisms of an effect through time-varying mediators. Traditional techniques, allowing only one observation of the mediator and restricting it to variables occurring immediately after the exposure, inadequately capture the indirect effect when the exposures affect the mediators over time. One alternative approach is to estimate the controlled direct effect, the effect of the exposures on the outcome when fixing the mediators at certain values. Obtained by applying the g-formula and specifying the mediators to these values, the controlled direct effect estimate provides valuable information for policy makers. For example, from FHS data we can provide the effect of smoking cessation decreasing systolic blood pressure if BMI is fixed to a certain level. This is also described elaborately elsewhere⁴⁰. The effects from the meditational g-formula will, however, further allow for effect decomposition.

This study provides direct evidence for the hypothesis that “the adverse effect of smoking on high blood pressure is partially concealed by weight loss”^13,21. The concealment of the effect is partial because smoking is not substantially associated with weight loss (Table 3). Some studies report that smoking cessation increases blood pressure^21,22. The discrepancy with these studies might be attributed to a different analysis approach or simply the special characteristics of FHS participants.

Several limitations of this study should be noted. First, the use of analogue of total effect, randomized natural direct effect, and randomized natural indirect effect, defined based on the stochastic interventions, results in different interpretations from the total effect, natural direct effect, and natural indirect effect³⁴. This is inevitable for causal mediation analysis with time-varying mediators because the natural direct and indirect effect are not generally identified by empirical data in the presence of time-varying confounders, randomized natural direct and indirect effect can still serve as an analogue of natural direct and indirect effect, and have the advantage that they can be verified by randomized controlled trial, while natural direct and indirect effect cannot. Second, in the macro we have developed, the outcome can only be affected by the covariates at the most recent three exams because of a similar restriction of the g-formula macro employed for continuous/binary outcome types. This is not a limitation of the methodology itself, but only of the current implementation. The earlier covariates affect the outcome only through these recent covariates. We specify the outcome variables in previous exams (i.e. the previous systolic blood pressure values) as the time-varying covariates. Thus, the earlier covariates can also affect the outcome through the previous outcome variables. Third, we have not adjusted for selection bias here. Selection bias or truncation by death is a difficult problem for causal inference generally and for mediation analysis, even with only one single mediator. Most of the literature makes a sequential ignorability assumption that survival is effectively randomized conditional on the past. Under this assumption, the result can be interpreted as what would happen to the population if one could intervene to prevent death for everyone. Alternatively, one could also pursue sensitivity analysis approaches and there are also alternative stronger assumptions that would allow one to interpret the results without necessarily intervening upon death^41,42. We hope to address this in future work but the extension of this to time-varying exposures and mediators is substantial. For the purposes of the illustration, we have simply focused on complete-case data and restricted our follow-up to ten years to partially address this selection bias. The relatively low proportion of loss to follow-up (< 20%) perhaps partially mitigates this problem. A general disadvantage of our proposed approach is that it may be particularly prone to bias due to model misspecification. Some misspecification may be theoretically guaranteed in complex longitudinal settings as considered here when the null hypothesis of no causal time-varying treatment effect is true, a problem known as the g-null paradox⁴³. The magnitude of bias implied by the g-null paradox is not guaranteed and, depending on the setting, may be large or small. For some further consideration of the g-null paradox using numerical examples, see Young and Tchetgen Tchtegen⁴⁴. The aforementioned inverse probability weighting estimator offers an alternative method which is not subject to the g-null paradox and might be used for the population estimands considered here⁴⁵. Finally, the analysis is subject to potential violation of the confounding assumptions. Future research could develop sensitivity analysis techniques for violations of these assumptions for our method.

Conclusion

The parametric mediational g-formula serves as a powerful and useful tool for mediation analysis with longitudinal data. Researchers can apply our method to disentangle the complicated causal mechanisms arising from time-varying mediators, exposures, and confounders. Further issues concerning the interpretation of the interventional direct and indirect effects can be found in VanderWeele and Tchetgen Tchetgen¹⁰. Using this method, we provide evidence that weight change in fact partially conceals the detrimental effect of cigarette smoking on blood pressure.