The Genetic Architecture of Gene Expression in Peripheral Blood

Abstract

We analyzed the mRNA levels for 36,778 transcript expression traits (probes) from 2,765 individuals to comprehensively investigate the genetic architecture and degree of missing heritability for gene expression in peripheral blood. We identified 11,204 cis and 3,791 trans independent expression quantitative trait loci (eQTL) by using linear mixed models to perform genome-wide association analyses. Furthermore, using information on both closely and distantly related individuals, heritability was estimated for all expression traits. Of the set of expressed probes (15,966), 10,580 (66%) had an estimated narrow-sense heritability (h²) greater than zero with a mean (median) value of 0.192 (0.142). Across these probes, on average the proportion of genetic variance explained by all eQTL $\left(h_{COJO}^2\right)$ was 31% (0.060/0.192), meaning that 69% is missing, with the sentinel SNP of the largest eQTL explaining 87% (0.052/0.060) of the variance attributed to all identified cis- and trans-eQTL. For the same set of probes, the genetic variance attributed to genome-wide common (MAF > 0.01) HapMap 3 SNPs $\left({\mathit{h}}_{\mathit{g}}^2\right)$ accounted for on average 48% (0.093/0.192) of h². Taken together, the evidence suggests that approximately half the genetic variance for gene expression is not tagged by common SNPs, and of the variance that is tagged by common SNPs, a large proportion can be attributed to identifiable eQTL of large effect, typically in cis. Finally, we present evidence that, compared with a meta-analysis, using individual-level data results in an increase of approximately 50% in power to detect eQTL.

Introduction

In the past decade, genome-wide association studies (GWASs) have identified thousands of loci for complex traits and diseases. Most associated variants are not located in protein-coding regions and are instead highly enriched for regulatory regions of the genome. Thus, it has been suggested that for many variants, the functional mechanisms by which they affect disease susceptibility is through regulation of gene expression.^{1, 2} GWA-type approaches have been used to map loci, termed expression quantitative trait loci (eQTL), that influence the expression levels of thousands of transcripts. To date, the majority of identified eQTL are located proximal to their transcript (i.e., cis).^{3, 4, 5, 6, 7} The mean of the estimates of heritability across expressed mRNA transcripts in peripheral blood ranges from 0.14 to 0.24,^{7, 8, 9} although these studies vary in numerous aspects of their design and methodological approaches. We consider the proportion of transcript narrow-sense heritability not explained by the heritability attributed to identified eQTL as the missing heritability of gene expression.^{10, 11, 12, 13} On average, the proportion of heritability explained by eQTL across mRNA transcripts, which is largely attributed to cis variants, ranges from 0.20 to 0.38,^{3, 4, 7, 8} suggesting that to date much of the heritability for gene expression is still unaccounted for.

By using individual-level data, we can investigate some of the hypotheses for missing heritability in more detail. One of the proposed hypotheses is that there is a large contribution from rare variants of large effect. Typically, rare variants are not included on SNP arrays and are not well tagged through imputation to a common reference panel. Another hypothesis is that the majority of missing heritability is due to common variants of small effect that are not detected at the level of genome-wide significance. If the second hypothesis is true, increasing sample size will be more important than extending variant coverage for continued progress in understanding cellular or higher-order complex traits.¹⁴ For gene expression, much of the remaining variation is hypothesized to be hidden in trans-eQTLs of small effect.^{4, 7, 8, 9, 15}

We use data from the Consortium for the Architecture of Gene Expression (CAGE), which comprises individual-level whole-blood expression and genotype data on 2,765 individuals. For all transcript expression traits (also referred to as probes), we use the method presented in Zaitlen et al.¹⁶ to estimate concurrently the total narrow sense heritability (h²) and the proportion of phenotypic variance explained by all common SNPs $\left({\mathit{h}}_{\mathit{g}}^2\right)$ using a linear mixed model (LMM) that relies on a partitioned identity-by-state (IBS) genetic relationship matrix and takes advantage of both the related and unrelated individuals present in the data. To summarize the extent of missing heritability across expression traits, h² and $h_g^2$ are compared to the proportion of genetic variance explained by eQTLs identified from an exhaustive association study. Furthermore, we investigate the relative power of meta-analyses versus mega-analyses with individual-level data for eQTL detection.

Material and Methods

Consortium for the Architecture of Gene Expression

We investigated the genetic architecture underlying gene expression variation in peripheral blood tissue using data from 2,765 individuals within CAGE (Table S1). For the full details of the cohorts contributing to CAGE and their sample preparation, normalization, and imputation, see the Supplemental Note. In brief, the 2,765 samples consisted of data from five cohorts: BSGS (n = 916),^{5, 17} CAD (n = 147),¹⁸ CHDWB (n = 449),¹⁹ EGCUT (n = 1,065),²⁰ and Morocco (n = 188).²¹ We conducted the quantification of gene expression for each cohort by isolating RNA from whole blood and then hybridizing RNA to Illumina Whole-Genome Expression BeadChips (HT12 v.3, HT12 v.4). Genotype data were acquired using different genotyping platforms and were imputed to the 1000 Genomes Phase 1 Version 3 reference panel,²² resulting in 7,763,174 SNPs passing quality control. The gene expression levels in each cohort were initially normalized using variance stabilization,²³ followed by a quantile adjustment to standardize the distribution of expression levels across samples using the software of Ritchie et al.²⁴ The PEER software²⁵ was used to concurrently correct for the measured covariates such as age, gender, cell counts, and batch effects, which are known to explain variation in gene expression, and hidden heterogeneous sources of variability. Not all cohorts had measurements for all covariates and thus we relied on the PEER software to correct for these in their absence. For all cohorts we chose the maximum number of relevant factors in the PEER analysis to be 50. The residuals from PEER for each cohort were then standardized to z-scores and concatenated across cohorts. We retained only those probes that passed quality control in all cohorts, resulting in 38,624 taken forward. We performed a further PEER correction analysis on the concatenated data with the covariate gender included and then transformed the residuals for each probe using the rank normal transformation of Blom,²⁶ which alters the distribution of the residuals to be normally distributed with a mean of 0 and a standard deviation of 1. Finally, probes measuring expression levels of genes located on the X and Y chromosomes were removed from the analysis, leaving 36,778 for analysis.

Heritability Estimation

The 2,765 CAGE samples consist of a mix of both highly related individuals and different ancestral groups (Figures S7 and S8). To avoid problems associated with population stratification, we chose to estimate heritability using data from individuals of European ancestry. To investigate ancestry for the 2,765 individuals in CAGE, the relationship between the first two principal components (PCs) of the CAGE genotype matrix relative to the HapMap 3 ancestry cohorts (i.e., projected PCs^{27, 28}) showed mixed population backgrounds within CAGE (Figure S7). Non-European individuals were defined to be those exceeding the bounds of [lower quartile − 1.5 × IQR, upper quartile + 1.5 × IQR] of the first projected PC²⁸ (where IQR is the inter-quartile range); this threshold removed 311 individuals leaving 2,454 with European ancestry (see Table S3 for a detailed summary of data subsets used across analyses).

We utilized a method presented by Zaitlen et al.¹⁶ to estimate the narrow-sense heritability (h²) and the proportion of phenotypic variance explained by genotyped SNPs $\left({\mathit{h}}_{\mathit{g}}^2\right)$ via the use of a two-variance component LMM that requires an IBS genetic relationship matrix (GRM) (denoted K_IBS). This method, here termed Big K/Small K, makes use of both the unrelated and related European individuals present in the CAGE dataset by partitioning the phenotypic covariance matrix as Σ = K_IBS>t ($h_{IBS>t}^2$ − $h_g^2$) + ${\mathbf{K}}_{\text{IBS}}{h}_g^2$ + I(1 − $h_{IBS>t}^2$). The K_IBS>t matrix is estimated by setting the off-diagonal elements of K_IBS less than the off-diagonal threshold t to zero. The resultant estimate of h² is the proportion of phenotypic variance attributed to the sum of the two variance component parameters. The method was implemented in the GCTA software²⁹ for all European individuals (n = 2,454), with t = 0.05 and SNPs common to the HapMap 3 set and the 7.8 M CAGE SNPs (893,626) used to construct the GRM (Figure S9). The first ten PCs of the genotype matrix for the European individuals were included as fixed effects in the REML analysis to control for any residual population stratification in the European individuals. For comparison, the unconstrained and constrained versions of the REML algorithm in GCTA were run. The narrow-sense heritability and proportion of phenotypic variance explained by genotyped SNPs from the unconstrained algorithm are denoted as $h^{2\ast }$ and $h_g^{2\ast }$, respectively, to differentiate from the constrained values.

In order to make inferences regarding the proportion of narrow-sense heritability explained by genome-wide SNPs and identified eQTL, we made comparisons across a set of probes that overlapped with those reported to be expressed in the study of Kirsten et al.⁴ This set was chosen because the Kirsten et al.⁴ data are completely independent from CAGE, had expression levels determined from peripheral blood, and had a similar data size to CAGE (n = 2,112). The probe list was downloaded from the GEO website and consisted of 18,738 probes that mapped uniquely to the genome and had a probe annotation quality score of at least “good” as per the protocol of Barbosa-Morais et al.³⁰ Of the set of 18,738 well-expressed probes, 15,966 overlapped with the CAGE data, which formed the comparative set.

eQTL Discovery

BOLT-LMM Association Analysis

We used a LMM, implemented in the BOLT-LMM software,³¹ to identify SNP-probe associations across 36,778 mRNA transcript level phenotypes in a computationally efficient manner, while accounting for the population structure present in the data. BOLT-LMM was chosen because it has high computational efficiency, performs LMM analysis, and uses a mixture of two normal distributions for the genetic effects. The standard LMM, referred to as the “the infinitesimal model,” implicitly assumes that all variants have an effect that is drawn from independent Gaussian distributions. BOLT-LMM relaxes the assumptions of the infinitesimal model by using a mixture of two Gaussian distributions as the prior on the genetic effects, giving the model greater flexibility to accommodate SNPs of large effect, which are often present for expression traits, while maintaining effective modeling of genome-wide effects (for example, ancestry).³¹

We estimated SNP effects for each combination of 7,763,174 autosomal SNPs against 36,778 probes using data from all 2,765 individuals. To increase computational efficiency while maintaining power and correction for confounding, we used the modelSnps option in BOLT-LMM, which requires the specification of a set of linkage disequilibrium (LD) pruned SNPs, and was set to be the HapMap 3 set of SNPs.

COJO Refinement of SNP-Probe Associations

To subset the extensive set of SNP-probe association results generated by BOLT-LMM, we performed a conditional and joint (COJO) stepwise model selection³² procedure. The method was implemented in the GCTA software and uses the summary statistics generated from the BOLT-LMM analysis. Probes were carried forward for this analysis if they had a SNP-probe association with a p value < 5 × 10⁻⁸. To avoid overfitting in the COJO model selection procedure, an initial clumping of the BOLT-LMM association summary statistics was performed for each probe. This analysis was completed with the PLINK 2 software³³ with an LD threshold R² of 0.1 and the default clump distance of 250 kb. The clumped summary statistics were then used for the COJO analysis.

The COJO analysis selects SNPs (cis and trans) on the basis of conditional p values thresholded at p < 5 × 10⁻⁸ and then estimates the joint effects of all selected SNPs after the model has been optimized. GCTA allows for the individual-level genotype data to be used in the procedure; thus, we used the CAGE genotype data as an LD reference for the COJO analysis. An estimate of the proportion of phenotypic variance explained by the identified COJO eQTL was calculated for each probe by fitting the selected SNPs in a multiple linear regression model in the R programming language³⁴ (with ten PCs fitted as fixed effects to correct for population stratification), and the resultant ratio of the genetic variance and the phenotypic variance taken to be the heritability estimate $\left(h_{COJO}^2\right)$. The genetic variance was calculated as Var(X $\hat{\mathit{\beta }}$), where $\hat{\mathit{\beta }}$ is the vector of estimated SNP effects from the multiple regression model and X the corresponding genotypes. Additionally, for the probes that had an identified eQTL, the proportion of phenotypic variance explained by the sentinel SNP (defined to be the SNP with the smallest association p value for each probe) was calculated by fitting the selected SNP in a linear regression model (with ten PCs added to correct for population structure) and estimating the proportion of phenotypic variance explained by that SNP $\left(h_S^2\right)$ as above for the COJO set of SNPs.

Power to Detect SNP-Probe Associations: Mega- versus Meta-analysis

We investigated the statistical power for eQTL discovery using individual-level data versus a meta-analysis by comparing association results from using the CAGE data to those presented in Westra et al.⁶ In Westra et al.,⁶ Spearman’s rank correlations were used to measure the association between genotypes and phenotypes for each of the gene expression data cohorts. These correlations were converted to t scores, and then, via the inverse normal distribution, to z values. For each dataset i, the z value for each SNP j and probe m was weighted by the square root of the sample size for the dataset used to calculate the z value for the SNP tested in the association test, i.e.,

$$z_{w_{ijm}}=\sqrt{n_{ij}}{z}_{ijm}$$

For each cis-eQTL association present after controlling the false discovery rate at 0.05, Westra et al.⁶ reported the weighted z value $z_{w_{ijm}}$. If at least three cohorts had results for a SNP-probe pair, the combined z value was calculated as

$$z_{met{a}_{jm}}=\frac{1}{\sqrt{n}}{\sum }_i{z}_{w_{ijm}},$$

where n is the total number of individuals contributing a weighted z score; this statistic was then used to calculate the presented p value. To be consistent with the data present in Westra et al.,⁶ a set of unrelated European individuals was determined by removing individuals from the subset of 2,454 European individuals in the CAGE dataset via a threshold of 0.05 on the off-diagonals of the genetic relationship matrix (GRM) (Figure S9). This resulted in the removal of a further 706 individuals, leaving n = 1,748 individuals for comparison. We recalculated the $z_{met{a}_{jm}}$ values from the Westra et al.⁶ study using the DILGOM cohort³⁵ (n = 509) and the largest Fehrmann cohort³⁶ (n = 1,240), which resulted in n = 1,749 individuals. These cohorts were chosen because they were the largest cohorts that when summed had a similar number of individuals to the set of unrelated Europeans from the CAGE dataset. The resultant z values were converted to ${\chi }^2$ statistics by squaring these values. We preferred to make comparisons between the ${\chi }^2$ statistics because they are on the scale of the number of individuals and are all positive. Additionally, a comparison between effect sizes was made by estimating ${\hat{\beta }}_{jm}$ from the recalculated $z_{met{a}_{jm}}$ statistics. This required the estimation of an approximate standard error for each ${\hat{\beta }}_{jm}$, which was calculated as σ $\left({\hat{\beta }}_{jm}\right)$ = $1/\sqrt{2p_j\left(1-p_j\right)\left(n+z_{met{a}_{jm}}^2\right)}$ where p_j is the allele frequency for SNP j (obtained from a large independent dataset of unrelated Europeans) and n = 1,749.

To compare the results from the two datasets, the sentinel SNP (from the cis set of results in Westra et al.⁶) for each of 3,450 overlapping probes reported in Westra et al.⁶ were used. For the 3,450 probes, an association analysis using the BOLT-LMM software was run on the set of unrelated European individuals in CAGE. To provide further comparison, SNP-probe associations for the overlapping sentinel SNPs were investigated using a standard single-SNP linear association analysis performed in the PLINK 2 software, with the first ten PCs of the genotype matrix used as covariates. This analysis was chosen to provide a baseline comparison with a standard analysis performed in the literature and reflected a methodology closer to that used in Westra et al.⁶

We investigated a potential deflation of the test statistics as a function of the amount of variance explained by an individual SNP. BOLT-LMM uses an approximate method that first estimates the variance components of the LMM under the null model (no SNP effect) and then keeps the variance components from the null model fixed when testing the effect of each SNP. This reduces computation time, but the assumption that the variance explained by each SNP is approximately zero is a good approximation only for highly polygenic traits. For eQTL that explain a large proportion of phenotypic variance (up to 60% observed for a single eQTL in the CAGE analysis), this assumption leads to a deflation of the ${\chi }^2$ statistics by a factor of approximately 1/(1 − R²). For SNPs that explain a large amount of phenotypic variance, an exact test that repeatedly estimates variance components when performing each association is desirable. Zhou and Stephens³⁷ presented an efficient exact method, referred to as genome-wide efficient mixed-model association (GEMMA), that makes approximations unnecessary in many contexts but is computationally less efficient than BOLT-LMM and thus was not viable for the full CAGE analysis. To provide more exact estimates of ${\chi }^2$ statistics for reference and comparison, we performed a LMM eQTL analysis using the GEMMA software for the 3,450 overlapping probes.

To make comparisons between sets of ${\chi }^2$ statistics for the sentinel SNPs from the different methodologies, a linear model was fitted with no intercept term. Regression slopes were then used to measure whether the ${\chi }^2$ statistics were on average greater than those calculated in Westra et al.⁶

Results

Expression Quantitative Trait Loci

We performed an eQTL analysis on 2,765 individuals for each of the 36,778 mRNA transcript phenotypes and 7,763,174 SNPs using a LMM implemented in the BOLT-LMM software.³¹ A total of 2,733,370 SNP-probe associations were identified at a p value threshold of 5 × 10⁻⁸. Each probe with one or more associations at this threshold was taken forward for clumping using the PLINK 2 software and then for conditional and joint (COJO) analysis.³² The COJO analysis selects SNPs (cis and trans) on the basis of conditional p values (thresholded at p < 5 × 10⁻⁸) and estimates the joint effects of all selected SNPs after the model has been optimized. The COJO analysis identified a total of 17,608 eQTLs for 11,829 unique probes and 9,190 HGNC genes. Of this set, 2,613 eQTL (1,862 probes) were for probes with a genome annotation quality score of less than “good” as per the protocol of Barbosa-Morais et al.,³⁰ making them unreliable for classification as cis or trans. The remaining 14,995 eQTL corresponded to 9,967 probes with 11,204 (75%) located in cis and 3,791 (25%) in trans (Table 1). cis-eQTL were defined to be those associations where the SNP was located on the same chromosome as the gene, and trans-eQTL the complement of this. We identified multiple independent eQTLs for 2,306 probes in cis and 360 in trans (Table S4). All SNP-probe associations below a p value threshold of 1 × 10⁻⁶ and the complete set of COJO eQTL are publicly available to download or query using the CAGE Shiny online application (see Web Resources).

Table 1.

Summary of Identified eQTL

No. eQTL per Probe	Probes	Genes	eQTL	cis-eQTL	trans-eQTL
$\mathrm{\geqq }1$	9,967	8,080	14,995	11,204	3,791
1	6,617	5,707	6,617	4,692	1,925
2	2,231	2,050	4,462	3,419	1,043
3	754	708	2,262	1,775	487
4	242	232	968	780	188
$\mathrm{\geqq }5$	123	112	686	538	148

Summary of eQTL mapping from the BOLT-LMM and COJO analyses of the whole CAGE dataset. Of the set of 11,829 probes with at least one COJO eQTL, there were 1,862 probes with a genomic annotation quality score of less than “good” as per the protocol of Barbosa-Morais et al.,³⁰ and thus the results for 9,967 probes are presented. Genes correspond to the number of unique HGNC gene names for each set of probes. cis-eQTL were defined to be those associations such that the SNP was located on the same chromosome as the gene and trans-eQTL the complement of this.

Heritability of Gene Expression

For the 36,778 transcripts passing quality control, we estimated narrow-sense heritability (h²) and the proportion of phenotypic variance explained by genotyped SNPs $\left({\mathit{h}}_{\mathit{g}}^2\right)$ via the Big K/Small K method of Zaitlen et al.¹⁶ This analysis was implemented in the GCTA software using both the unconstrained and constrained REML algorithms²⁹ (see Figure S10 for full distributions of heritability estimates). Poor convergence of the REML algorithm was observed for 6,811 probes in the unconstrained Big K/Small K analysis, and thus to obtain estimates for these probes we used the –reml-force-converge option in the GCTA software. The majority of the probes with poor convergence had heritability estimates that were close to 0. As an initial benchmark, we also estimated narrow-sense heritability using just the K_IBS>t matrix of estimated relatedness and the unconstrained REML algorithm. The unconstrained narrow-sense heritability estimates from this model showed very similar results to the sum of the two variance components estimated using the unconstrained Big K/Small K method (Figure S11A), and thus we focused on the results from the Big K/Small K method.

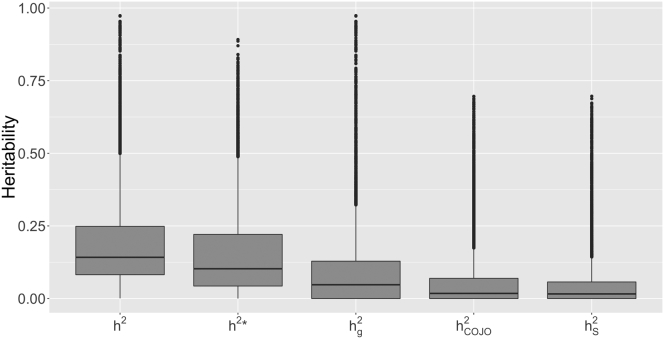
To make conclusions about the proportion of h² explained by genotyped SNPs, COJO eQTL, and the sentinel SNP, we compared means and medians across the set of 15,966 overlapping expressed probes from the study of Kirsten et al.⁴ This is in contrast to the COJO eQTL results, which are reported for all probes that had a COJO eQTL. To investigate whether this preselection of probes was reasonable, we calculated the average number of identified COJO eQTL in the overlapping expressed probes from the study of Kirsten et al.⁴ and for the complement set of probes (20,812). For the overlapping Kirsten et al.⁴ probes, the average number of eQTLs per probe was 0.72 and for the complement the average number was 0.29. Therefore, for the comparative set, we observed a greater than 2-fold enrichment for identified eQTLs, implying that our preselected set was much more likely to contain probes with a genetic contribution to variation. For the set of 15,966 overlapping probes, the mean and median estimates of h² from the constrained algorithm were 0.139 and 0.089 (Table 2 and Figure S12). Average standard errors across the 15,966 probes for h² and $h^{2\ast }$ were approximately 0.053 and 0.052, respectively (Figure S13). Of the set of 15,966 probes, 10,580 probes (66%) had a ${\hat{h}}^{2\ast }$ greater than 0, representing 8,842 unique HGNC genes (Table 2). The mean and median from the constrained algorithm for these probes were 0.192 and 0.142, respectively, with smaller estimates from the unconstrained algorithm of 0.158 and 0.103 (Table 2 and Figure 1).

Table 2.

Summary of Heritability Estimates across Overlapping Probes from the Study of Kirsten et al.⁴

Threshold		h2	${\mathit{h}}^{2\mathbf{\ast }}$	${\mathit{h}}_{\mathit{g}}^2$	${\mathit{h}}_{\mathit{g}}^2$	${\mathit{h}}_{\mathit{COJO}}^{\mathbf{2}}$	${\mathit{h}}_{\mathit{S}}^{\mathbf{2}}$
Expressed probes (15,966)	mean	0.139	0.089	0.068	0.052	0.041	0.036
	median	0.089	0.042	0.022	0.036	0.000	0.000
${\hat{h}}^{2\ast }$ > 0 (10,580)	mean	0.192	0.158	0.093	0.079	0.060	0.052
	median	0.142	0.103	0.048	0.056	0.018	0.016
${\hat{h}}^{2\ast }$ > 0.05 (7,560)	mean	0.241	0.212	0.116	0.104	0.081	0.070
	median	0.193	0.158	0.074	0.077	0.036	0.029
${\hat{h}}^{2\ast }$ > 0.1 (5,383)	mean	0.294	0.268	0.142	0.136	0.106	0.091
	median	0.245	0.218	0.100	0.100	0.060	0.047
${\hat{h}}^{2\ast }$ > 0.2 (2,987)	mean	0.391	0.368	0.194	0.198	0.158	0.135
	median	0.349	0.329	0.148	0.148	0.117	0.090
${\hat{h}}^{2\ast }$ > 0.4 (997)	mean	0.566	0.538	0.304	0.330	0.273	0.234
	median	0.536	0.512	0.264	0.264	0.258	0.205

Numbers in parentheses indicate the total number of probes used to calculate estimates. For Big K/Small K narrow-sense heritability estimates (h² and $h^{2\ast }$) and the proportion of phenotypic variance explained by genome-wide HapMap 3 SNPs ($h_g^2$ and $h_g^{2\ast }$), all European individuals in CAGE with varying degrees of relatedness were used (n = 2,454). The asterisk (^∗) notation refers to the results from the unconstrained variance components REML algorithm implemented in the GCTA software. The parameters $h_{COJO}^2$ and $h_S^2$ correspond to the proportion of phenotypic variance explained by COJO eQTL and the sentinel SNPs, respectively.

Figure 1.

Boxplot Summary of Heritability Estimates

The summarized results are for the set of 10,580 probes that had a ${\hat{h}}^{2\ast }$ greater than 0 from the set of overlapping expressed probes from the Kirsten et al.⁴ study. Estimates from the Big K/Small K method are displayed for the narrow-sense heritability from the constrained algorithm (h²), the narrow-sense heritability from the unconstrained algorithm ($h^{2\ast }$), and the proportion of phenotypic variance explained by genome-wide HapMap 3 SNPs ($h_g^2$) from the constrained REML algorithm, which used European individuals (n = 2,454). The parameters $h_{COJO}^2$ and $h_S^2$ refer to the proportion of phenotypic variance explained by COJO eQTL and the sentinel SNP.

Missing Heritability for Gene Expression

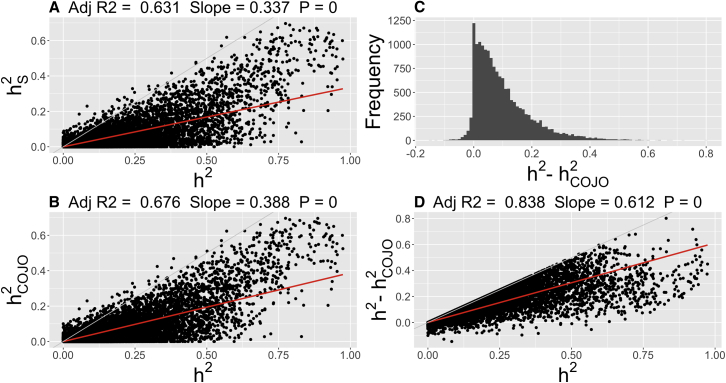
For all probes, estimates of the proportion of variance explained by significant eQTLs $\left(h_{COJO}^2\right)$ were summarized to investigate the extent of missing heritability for gene expression. Across the set of 15,966 probes, the sentinel SNP of the largest eQTL for a gene explained on average 88% (0.036/0.041) of the variance attributed to all identified cis- and trans-eQTL $\left(h_{COJO}^2\right)$. Across this same set of probes, $h_{COJO}^2$ explained on average 30% (0.041/0.139) of h², suggesting that 70% of the heritability is missing (Table 2). For the set of expressed probes with a $h^{2\ast }$ estimate greater than zero (10,580 probes), 6,585 (62%) had one or more independent significant eQTL identified from the COJO analysis, leaving 3,995 having no significant eQTL. For those probes with no significant eQTL, $h_{COJO}^2$ was set to zero when calculating averages across probes, as were all probes without a COJO eQTL across other ${\hat{h}}^{2\ast }$ threshold summaries. For these probes, similar on average proportions were seen, with 87% (0.052/0.060) of $h_{COJO}^2$ being explained by $h_S^2$ and 31% (0.060/0.192) of h² explained by $h_{COJO}^2$ (Table 2). For transcripts with a ${\hat{h}}^{2\ast }$ > 0.4 (997 probes), on average 48% (0.273/0.566) of h² could be attributed to $h_{COJO}^2$. Of the set of 15,966 probes, a total of 2,634 probes (2,387 unique genes) had an estimate of $h_{COJO}^2$ that explained greater than 50% of h², indicating that their genetic architecture is predominantly driven by a few loci of large effect. We also observed a positive linear relationship between estimates of h² and $h_{COJO}^2$, suggesting that as the heritability of gene expression transcripts increases, so does the proportion of phenotypic variance explained by identified QTLs (Figure 2B).

Figure 2.

Missing Heritability

Scatterplot and density summaries of narrow-sense heritability estimates (constrained REML algorithm) from the Big K/Small K method (h²), the proportion of phenotypic variance explained by COJO eQTL ($h_{COJO}^2$), and the proportion of phenotypic variance explained by the sentinel SNP ($h_S^2$). Displayed summaries are across 15,966 overlapping expressed probes from the Kirsten et al.⁴ study.

(A) Scatterplot of Big K/Small K heritability estimates versus the proportion of phenotypic variance explained by the sentinel SNP.

(B) Scatterplot of Big K/Small K heritability estimates versus the proportion of phenotypic variance explained by the COJO eQTL.

(C) Histogram of the difference between Big K/Small K heritability estimates and the proportion of phenotypic variance explained by the COJO eQTL.

(D) Scatterplot of Big K/Small K heritability estimates versus the difference from (C).

For (A), (B), and (D), the fitted regression line (red) and 95% confidence interval (shaded) is plotted with the key statistics of this regression (no intercept term fitted) displayed at the top of the panels. The light gray line represents the y = x line. The p value is with regard to the regression slope.

The ratio of $h_{COJO}^2$ and $h_g^2$ gives an indication of the degree of “hiding” heritability, which is most likely due to common variants of small effect.³⁸ Across the set of 15,966 probes, on average 60% (0.041/0.068) of $h_g^2$ is explained by $h_{COJO}^2$, with the proportion increasing to 65% (0.060/0.093) for expressed transcripts with a ${\hat{h}}^{2\ast }$ > 0. Average standard errors for $h_g^2$ and $h_g^{2\ast }$ across the 15,966 probes were approximately 0.129 and 0.126, respectively (Figure S13). For transcripts with a ${\hat{h}}^{2\ast }$ > 0.4, on average 90% (0.273/0.304) of $h_g^2$ could be attributed to $h_{COJO}^2$ (Table 2). These results suggest that for more heritable probes there is less hiding heritability.

The ratio of $h_g^2$ and h² represents the “still-missing” heritability, which is most likely due to variants that are poorly tagged by genotyped SNPs, for example due to rare variants. An alternative explanation is that h² is biased upward due to confounding by non-additive or non-genetic factors. Across the set of 15,966 probes, on average 49% (0.068/0.139) of h² could be attributed to $h_g^2$, suggesting that 51% is still missing (Table 2). For the set of probes with ${\hat{h}}^{2\ast }$ > 0, a similar on average proportion of 48% (0.093/0.192) was observed, which increases to 54% (0.304/0.566) for transcripts with a ${\hat{h}}^{2\ast }$ > 0.4. These results suggest that on average approximately half of the narrow-sense heritability is captured by genome-wide HapMap 3 SNPs. This is in contrast to results for human complex traits, where it has been observed across 49 human phenotypes that $h_g^2$ is approximately one third of h².³⁹ The proportion of hiding and still-missing heritability for each probe is available to download at the CAGE Shiny online application (see Web Resources).

Mega- versus Meta-analysis Chi-Square Statistics

We investigated the relative statistical power to identify eQTL when using individual-level data versus meta-analyzed summary statistics by comparing the results from the analysis of the CAGE data to a published meta-analysis.⁶ Association chi-square $\left({\chi }^2\right)$ statistics for 3,450 sentinel SNPs (common to both studies) were compared between the meta-analysis and those obtained by analyzing the CAGE data using a single SNP analysis in PLINK and a LMM fitted with BOLT-LMM. Comparisons between association ${\chi }^2$ statistics for all common sentinel SNPs were made via regressing the ${\chi }^2$ statistics generated from CAGE on those obtained in the meta-analysis.

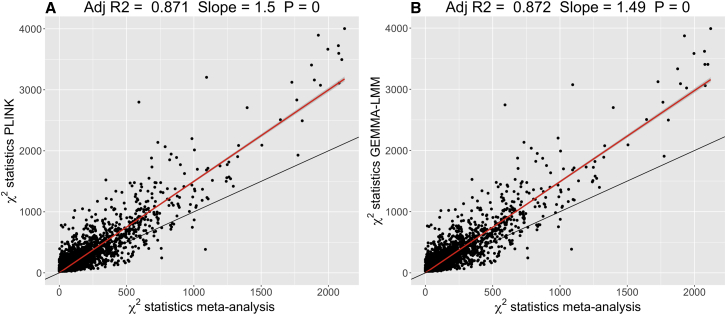
Linear regressions of mega-analysis association ${\chi }^2$ statistics (CAGE), generated using single-SNP regression in PLINK 2 and a LMM in BOLT-LMM, on meta-analysis ${\chi }^2$ statistics showed slope coefficients of 1.5 and 0.86, respectively (Figures 3 and S14A). We expected the slopes of the single-SNP regression analysis and the LMM to be approximately the same, but we observed a deflation in the ${\chi }^2$ statistics from BOLT-LMM relative to the PLINK analysis. Upon investigation, this deflation is expected from theory (see Material and Methods). A deviation between PLINK and BOLT-LMM was seen after a ${\chi }^2$ statistic of ≈100 (Figure S14D), which has little practical consequence for discovery and significance given that such test statistics are large.

Figure 3.

Mega- versus Meta-analysis Chi-Square Statistics

Comparison of association ${\chi }^2$ statistics for the sentinel SNP from the top 3,450 cis probes generated from a subset of the meta-analysis of Westra et al.⁶ (n = 1,749) and analyses of CAGE data using European unrelated individuals (n = 1,748).

(A) Comparison of the set of association ${\chi }^2$ statistics generated using a linear model analysis of sentinel SNPs from the CAGE dataset (analyzed in PLINK and corrected for ten PCs) versus those from the meta-analysis.

(B) Comparison of the association ${\chi }^2$ statistics for sentinel SNPs from the GEMMA-LMM analysis (GRM generated from HapMap 3 SNPs) and the meta-analysis. All panels include the fitted regression line (red) and its 95% confidence interval (shaded) with the key statistics of this regression (no intercept term fitted) displayed at the top of each panel. The p value is with regard to the regression slope. Additionally, the y = x line (black) line is plotted for reference.

The deviation between the BOLT-LMM and GEMMA-LMM statistics for the set of overlapping sentinel SNPs is substantial, with the same parabolic deflation seen as in the comparison of BOLT-LMM and PLINK (Figure S14C). The regression slope from the GEMMA-LMM comparison with the Westra et al.⁶ meta-analysis was 1.49 (Figure 3) and thus, the CAGE data have ${\chi }^2$ statistics for sentinel SNPs across 3,450 probes that are on average approximately 50% greater than the meta-analysis ${\chi }^2$ statistics. This increase in ${\chi }^2$ statistics is partially due to an increase in estimated effect sizes. A regression slope of 1.20 was observed when regressing ${\hat{\beta }}_{jm}$ statistics from the PLINK and GEMMA-LMM analyses in the CAGE data on those from the approximate effects calculated from the meta-analysis z values (Figures S14E and S14F).

Discussion

We have presented results from the examination of the genetic architecture of gene expression in blood tissue from 2,765 individuals. We identified 11,204 cis- and 3,791 independent trans-eQTLs using a two-step analysis of all 36,778 probes in CAGE, with multiple independent eQTLs detected for 2,306 probes in cis and 306 in trans. Using information on both closely and distantly related individuals, we estimated heritability for all probes in the CAGE dataset. We showed that across overlapping expressed probes from the study of Kirsten et al.⁴ that had a $h^{2\ast }$ estimate greater than zero (10,580), on average $h_{COJO}^2$ explained 31% (0.060/0.192) of h², suggesting that 69% is missing. For this same set of probes, on average 48% (0.093/0.192) of h² could be attributed to additive genetic values captured by genome-wide HapMap 3 SNPs ($h_g^2$), suggesting that approximately half of the heritability of gene expression is “still” missing³⁸ for these probes. Additionally, 65% (0.060/0.093) of the variance explained by genotyped SNPs ($h_g^2$) could be detected at a genome-wide significance threshold; this value increased to 90% (0.273/0.304) for transcripts with ${\hat{h}}^{2\ast }$ > 0.4. Therefore, for this set of transcripts, approximately half of the variance for gene expression is not tagged by common SNPs, while the majority of variance that is tagged is due to detected eQTL. Additionally, we observed a positive linear relationship between the heritability of probes and the proportion of phenotypic variance that can be explained by COJO-eQTL, implying that, on average, more heritable probes have larger effects. This is in contrast to what is observed for the majority of complex traits and common diseases.⁴⁰

There is the potential for h² estimates to be inflated due to effects such as dominance, shared environment, and epistatic variance,^{16, 41} although there is little evidence that non-additive genetic variation contributes considerably to variation in gene expression.⁸ In addition to these sources of bias, we acknowledge that the presented mean Big K/Small K heritability estimates across probes are biased due to sampling variance. The estimates of $h_{COJO}^2$ and $h_S^2\text{also}$ contain a contribution from overestimated effects due to the winner’s curse, although the contribution to the mean is likely to be small given that the effects are large for the majority of expression traits. Furthermore, the heritability estimates from the constrained REML algorithm are potentially biased due to the bounded variance component parameter space, which is alleviated by the reporting of the estimates from the unconstrained REML algorithm. Schweiger et al.⁴² showed that the reported standard errors from the constrained REML algorithm led to the construction of confidence intervals with inaccurate coverage probabilities. However, the reported mean standard error from the constrained REML algorithm is a meaningful measure of the uncertainty in these estimates due to the law of large numbers. Additionally, the array technology used in this study may lack sufficient resolution to identify variation in lowly expressed genes, which may be abated by studying large cohorts with RNA-seq. The ideal set for making conclusions about missing heritability would be the set of probes with a genetic contribution to gene expression variation in peripheral blood. In reality, no selection of probes is perfect for comparison and thus we made a selection based upon external data, where each probe had evidence for variation of which additive genetic variation could be a potential contributor. The set of probes chosen showed a greater than 2-fold enrichment for identified eQTLs, which reinforced our preselection of this set of probes.

The estimated value of $h_g^2$ is an upper bound on the proportion of variation that can be attributed to all SNPs on a given genotyping platform and is almost entirely made up of common variation. One potential reason for the differences between $h_g^2$ and h² is that rare variation accounts for a significant fraction of the total narrow-sense heritability. Recently, Zhao et al.⁴³ showed that an excess of rare variants contributed to both the high and low expression levels of many genes in blood. It is important to recognize that blood is a heterogenous tissue made up of multiple cell types, and although it is likely that cis effects will be shared across cell types,⁹ we expect some variability in average heritability estimates for expression transcripts across blood cell types, meaning that our estimates are likely to reflect averaged effects. This heterogeneity may be particularly evident for immune-specific cells, where Brodin et al.⁴⁴ showed that for many of the component parts of the immune system, a considerable amount of the variation in humans is driven by non-heritable factors.

The individual-level data of the CAGE resource allowed for a genome-wide eQTL analysis to be performed using a LMM, which accounts for population stratification and cryptic relatedness and improves statistical power due to joint modeling of all genotyped markers. Additionally, the LMM methodology used has increased flexibility to model SNPs of large effect, which are often present for gene expression phenotypes. The results from the COJO-eQTL analysis allowed for a characterization of independent eQTL signals with 17,608 eQTLs identified for 11,829 transcripts (9,190 unique genes). The majority of the identified eQTL are located in cis with 25% of the identified eQTL being in trans. A similar percentage (29%) of genes were identified as being trans-regulated (relative to all genes with an eQTL) in the study of Kirsten et al.⁴ While the majority of COJO eQTLs are likely to tag independent causal variants, there is the possibility that multiple eQTLs could be in LD with a single causal variant of very large effect.³² The meta-analysis comparison also showed that linear mixed model methods that reduce computational burden by assuming that the variance components estimated under the null model of no effect at the candidate marker,⁴⁵ or the variance explained by a single SNP is small, may not be adequate for gene expression traits because many loci can explain a large amount (>10%) of the phenotypic variance. We demonstrated that using individual-level data can increase the ${\chi }^2$ statistics for eQTLs on average, with a 50% increase in ${\chi }^2$ statistics compared with a meta-analysis. However, it is important to note that the meta-analysis of Westra et al.⁶ is more powerful given its larger sample size. The information differences shown here may be caused by the difficulties inherent in sharing summary statistics and the heterogeneity caused in cohort processing.⁴⁶ A final additional benefit of using raw-level data is the ability to employ a variety of data normalization pipelines and more complex analyses such as the LMM, to account for cryptic relatedness and population structure, and conditional single SNP modeling.

This resource has allowed for an exhaustive eQTL analysis and has characterized the heritability of gene expression by studying thousands of mRNA profiles using contrasting methods. Our eQTL results are a valuable resource to explore the relevance of SNPs identified in current as well as future GWASs. These results and data will form the basis of further study into the genetic basis of gene expression with the dataset opening the door to explore questions, such as multivariate modeling of joint cis effects of SNPs on gene expression variation, genetic co-regulation of mRNA transcripts within peripheral blood across all probes, and sexual dimorphism in gene expression.

Published: January 5, 2017; corrected online February 2, 2017

Web Resources

• CAGE Shiny, http://cnsgenomics.com/shiny/CAGE/

• GEO, http://www.ncbi.nlm.nih.gov/geo/

• International HapMap Project, ftp://ftp.ncbi.nlm.nih.gov/hapmap/