Bayesian Model Assessment in Joint Modeling of Longitudinal and Survival Data with Applications to Cancer Clinical Trials

Summary

Joint models for longitudinal and survival data are routinely used in clinical trials or other studies to assess a treatment effect while accounting for longitudinal measures such as patient-reported outcomes (PROs). In the Bayesian framework, the deviance information criterion (DIC) and the logarithm of the pseudo marginal likelihood (LPML) are two well-known Bayesian criteria for comparing joint models. However, these criteria do not provide separate assessments of each component of the joint model. In this paper, we develop a novel decomposition of DIC and LPML to assess the fit of the longitudinal and survival components of the joint model, separately. Based on this decomposition, we then propose new Bayesian model assessment criteria, namely, ΔDIC and ΔLPML, to determine the importance and contribution of the longitudinal (survival) data to the model fit of the survival (longitudinal) data. Moreover, we develop an efficient Monte Carlo method for computing the Conditional Predictive Ordinate (CPO) statistics in the joint modeling setting. A simulation study is conducted to examine the empirical performance of the proposed criteria and the proposed methodology is further applied to a case study in mesothelioma.

1 Introduction

Recently, joint modeling of longitudinal and time-to-event outcomes has become more popular in the analysis of patient-reported outcomes (PROs) for the purpose of evaluating the efficacy and tolerability of cancer treatment. In oncology applications, information from the patients’ perspectives can be useful in evaluating actual patients’ experiences on dimensions known to be important to them and also associated with treatment outcomes. The field of PROs has evolved and reached a common understanding about good clinical practices for the use of PROs (Rothman et al., 2009). In addition, the U.S. and European regulators have published guidance on the use of these measures to support PRO-based claims in pharmaceutical product labeling (European Medicines Agency, 2005; US Food and Drug Administration Guidance for Industry, 2009) (DeMuro et al., 2013). Siddiqui et al. (2014) reviewed and addressed issues regarding the “why, how, and what” of PROs as well as cancer survivorship because it closely relates to PROs. Building on previous joint modeling work in a highly symptomatic and particularly fatal cancer (Wang et al., 2012; Hatfield et al., 2011, 2012; and Zhang et al., 2014, 2015a), we develop new Bayesian methodology on how to evaluate the distinct effects of longitudinal and time-to-event outcomes on the fit of a joint model.

A popular approach in joint modeling of longitudinal and survival data is based on shared random effects, where the longitudinal component and the survival component of the joint model share common random effects and these random effects then induce correlation between the longitudinal and survival data. There are two basic formulations of the joint model. The first is the “trajectory model” (TM), where one substitutes the time trajectory function from the longitudinal component into the hazard function of the survival component, and in this case, the trajectory function acts like a time-varying covariate in the survival component. The second formulation is the shared parameter model (SPM), which directly includes the random effects as covariates in the survival component. One of the main advantages of the TM is that it leads to a straightforward interpretation of the association between the longitudinal measure and survival time through the direct inclusion of the trajectory function in the hazard. For the SPM, the characterization of the association is much more complex and can only be analytically determined once the random effects have been integrated out, as the two components of the model are independent conditional on these random effects. However, the TM is computationally more expensive compared to the SPM. In addition, the TM requires extrapolation beyond the last time at which the longitudinal measure is observed in the survival component. The SPM typically fits the survival component of the joint model better as it directly includes the random effects as covariates in the survival component. There is a very rich literature concerning these two basic approaches. The TM has been considered in Schluchter (1992), Hogan and Laird (1997), Law et al. (2002), Brown and Ibrahim (2003), Chen et al. (2004) Ibrahim et al. (2004), Brown et al. (2005), Chi and Ibrahim (2006), Chi and Ibrahim (2007), and Ibrahim et al. (2010) for joint modeling with biomedical applications. There has also been much work on using the SPM, including Pawitan and Self (1993), DeGruttola and Tu (1994), Lavalley and DeGruttola (1996), Henderson et al. (2000), Xu and Zeger (2001a, 2001b), and Song et al. (2002) for univariate or multivariate longitudinal data. An excellent review on joint modeling of longitudinal and survival data is given in Tsiatis and Davidian (2004) and an overview of joint models for longitudinal and time-to-event data can be found in Ibrahim, Chen, and Sinha (2001, Chapter 7) and Rizopoulos (2012a). There are several R packages available in fitting joint models, including JM (Rizopoulos, 2012b), JMbayes (Rizopoulos, 2014), and joineR (Philipson et al., 2012). There is also a Stata module stjm (Crowther, 2012; Crowther et al., 2013), which fits shared random effects models. In addition, another R package, lcmm (Proust-Lima et al., 2014), fits joint models based on shared latent classes.

One important issue in the joint modeling of longitudinal and survival data concerns the separate contribution of the model components to the overall goodness-of-fit of the joint model. Zhang et al. (2014) developed a decomposition of AIC and BIC to assess the fit of each component of the joint model. A SAS macro, called JMFit, (Zhang et al., 2015b) implements a variety of popular joint models and provides several model assessment measures including the decomposition of AIC and BIC as well as ΔAIC and ΔBIC. Within the Bayesian framework, Hanson et al. (2011) proposed to use LPML to predict survival times conditional on the longitudinal component of the model. In this paper, we derive a novel decomposition of the DIC and LPML criteria into additive components that will allow us to assess the goodness of fit for each component of the joint model. Such a development is extremely important since it not only allows us to quantify the contribution of the longitudinal data to the fit of the survival data or the contribution of the survival data to the fit of the longitudinal data, but it also allows us to identify which PROs are most highly associated with survival outcomes, a finding with significant clinical implications. In addition, we also develop a new Monte Carlo (MC) method for computing the CPO statistics which may involve intractable high-dimensional integrals. The proposed MC approach for computing the CPO has a potential to lead to a gain in computing time compared to a numerical approximation approach, particularly in the joint modeling setting. To illustrate our proposed method, we only consider (i) polynomial trajectories and independent and identically distributed Gaussian noise for longitudinal measures and (ii) the Cox model with a piecewise constant baseline hazard function for survival data in our simulation study and real data analysis. However, the proposed method can be applied to other types of longitudinal trajectories and other types of survival models such as those considered in Hanson et al. (2011).

The rest of the paper is organized as follows. Section 2 presents the joint models and the likelihood and posterior. The first decomposition (Decomposition I) of DIC and LPML (i.e., DIC= DIC_Long + DIC_Surv|Long and LPML= LPML_Long+LPML_Surv|Long), the corresponding two new criteria (i.e., ΔDIC_Surv and ΔLPML_Surv), as well as a new Monte Carlo method for computing CPO are also developed in Section 2. A simulation study is conducted in Section 3, and a comprehensive analysis of the longitudinal and survival data from a cancer clinical trial is carried out in Section 4. We conclude the paper with a brief discussion in Section 5. Prior specification and posterior computation are discussed in Appendix A of the supplementary material. In addition, we develop the second decomposition (Decomposition II) of DIC and LPML (i.e., DIC= DIC_Surv + DIC_Long|Surv and LPML= LPML_Surv + LPML_Long|Surv) and the corresponding ΔDIC_Long and ΔLPML_Long criteria to assess the fit of the longitudinal data using the information from the survival data in Appendix B of the supplementary material.

2 Bayesian Assessment of Model Fit in the Joint Model

2.1 The Joint Models

Suppose that there are n subjects. For the i^th subject, let y_i(t) denote the longitudinal measure, which is observed at time t ∈ {a_i1, a_i2, . . . , a_imi}, where 0 ≤ a_i1 < a_i2 < · · · < a_imi and m_i > 1. Note that y_i(0) corresponds to the baseline value. Also let x_i and z_i denote two vectors of covariates, which may include the treatment indicator. We assume a mixed effects regression model for y_i(t) given by

$$y_i\left(a_{ij}\right)=\mathit{g}{\left(a_{ij}\right)}^{\prime }{\theta }_i+{\mathit{x}}_i^{\prime }\gamma +{ϵ}_i\left(a_{ij}\right),$$ (2.1)

where g(a_ij) denotes a (q+1)-dimensional vector of functions of a_ij for j = 1, . . . , m_i, θ_i denotes a (q+1)-dimensional vector of random effects, and γ denotes a vector of regression coefficients. In (2.1), we further assume θ_i ~ N(θ, Ω), where θ is a (q+1)-dimensional vector of overall effects, Ω is a (q+1) × (q+1) positive definite covariance matrix, ε_i(a_ij) is the measurement error term, which is assumed to follow a N(0, σ²) distribution and is independent of θ_i. We note that in (2.1), if q = 1, g(a_ij) = (1, a_ij)′ and (g(a_ij))′ θ_i represents a linear trajectory; if q = 2, $\mathit{g}\left(a_{ij}\right)={(1,a_{ij},a_{ij}^2)}^{\prime }$ and (g(a_ij))′ θ_i leads to a quadratic trajectory; and if g(a_ij) = (1, B₁(a_ij), . . . , B_q(a_ij))′, where {B_k(·), k = 1, 2, . . . , q} is a q-dimensional basis for spline functions over a finite interval, (g(a_ij))′θ_i represents a spline trajectory considered in Brown et al. (2005).

Let t_i and δ_i denote the failure time and the censoring indicator, respectively, where δ_i = 1 if t_i is a failure time and 0 if t_i is right-censored for the i^th subject. The hazard function for failure time t_i is assumed to have the form

$$\lambda (t\mid {\lambda }_0,\alpha ,\beta ,{\theta }_i,\mathit{g}\left(t\right),{\mathit{z}}_i)={\lambda }_0\left(t\right)\exp \{h(\alpha ,{\theta }_i,\mathit{g}\left(t\right))+{\mathit{z}}_i^{\prime }\beta \},$$ (2.2)

where λ₀(t) is the baseline hazard function, h(·) is a linear function of g(t) and θ_i with α being a vector of regression coefficients. Note that λ₀, α, and β are the fixed effects parameters pertaining to the survival component of the joint model. When h(α, θ_i, g(t)) = {g(t)′θ_i}α, where α is a scalar, the hazard function (2.2) leads to the TM. When h does not depend on g(t), that is, $h(\alpha ,{\theta }_i,\mathit{g}\left(t\right))={\theta }_i^{\prime }\alpha$, where α is a (q + 1)-dimensional vector, the hazard function specified by (2.2) defines the SPM. Under the TM, g(t)′θ_i acts a time-varying covariate in the survival component while under the SPM, the random effects θ_i are included as q + 1 covariates in the survival component.

2.2 The Likelihood and Posterior

We first introduce some notation. We rewrite (2.1) as

$${\mathit{y}}_i={\mathit{X}}_i{({\theta }_i^{\prime },{\gamma }^{\prime })}^{\prime }+{ϵ}_i,$$

where y_i = (y_i(a_i1), . . . , y_i(a_imi))′, ${\mathit{X}}_i={({(\mathit{g}{\left(a_{ij}\right)}^{\prime },{\mathit{x}}_i^{\prime })}^{\prime },j=1,\dots ,m_i)}^{\prime }$, and ε_i = (ε_i(a_i1), . . . , ε_i(a_imi))′ ~ N(0, σ²I_mi). Then, the probability density function (pdf) of y_i conditional on θ_i is given by

$$f({\mathit{y}}_i\mid \gamma ,{\sigma }^2,{\theta }_i,{\mathit{x}}_i)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{\frac{m_i}{2}}}\exp \left\{-\frac{1}{2{\sigma }^2}{({\mathit{y}}_i-{\mathit{X}}_i{({\theta }_i^{\prime },{\gamma }^{\prime })}^{\prime })}^{\prime }({\mathit{y}}_i-{\mathit{X}}_i{({\theta }_i^{\prime },{\gamma }^{\prime })}^{\prime })\right\},$$

and the pdf of θ_i is given by

$$f({\theta }_i\mid \theta ,\Omega )=\frac{{\mid \Omega \mid }^{-\frac{1}{2}}}{{\left(2\pi \right)}^{\frac{q+1}{2}}}\exp \left\{-\frac{1}{2}{({\theta }_i-\theta )}^{\prime }{\Omega }^{-1}({\theta }_i-\theta )\right\},$$

for i = 1, . . . , n. Letting λ be a vector of parameters for the baseline hazard function λ₀(t), we write

$$f(t_i\mid \lambda ,\alpha ,\beta ,{\theta }_i,{\delta }_i,{\mathit{z}}_i)={\left[\lambda (t_i\mid {\lambda }_0,\alpha ,\beta ,{\theta }_i,\mathit{g}\left(t_i\right),{\mathit{z}}_i)\right]}^{{\delta }_i}\exp \left\{-{\int }_0^{t_i}\lambda (u\mid {\lambda }_0,\alpha ,\beta ,{\theta }_i,\mathit{g}\left(u\right),{\mathit{z}}_i)du\right\},$$

where λ(t|λ₀, α,β,θ_i, g(t), z_i) is defined in (2.2). We note that when δ_i = 1, f(t_i|λ, α, β, θ_i, δ_i = 1, z_i) reduces to the density of t_i, and when δ_i = 0, f(t_i|λ, α, β, θ_i,δ_i = 0, z_i) is the survival function evaluated at t_i.

Let φ = (θ, γ, σ², Ω, λ, α, β). The joint distribution of (y_i, t_i, θ_i) is written as

$$f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)=f(t_i\mid \lambda ,\alpha ,\beta ,{\theta }_i,{\delta }_i,{\mathit{z}}_i)f({\mathit{y}}_i\mid \gamma ,{\sigma }^2,{\theta }_i,{\mathit{x}}_i)f({\theta }_i\mid \theta ,\Omega ),$$ (2.3)

and the marginal joint distribution of (y_i, t_i) is given by

$$f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)=\int f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)d{\theta }_i,$$ (2.4)

for i = 1, . . . , n. Letting D_obs = {(y_i, t_i, θ_i, x_i, z_i), i = 1, . . . , n} denote the observed data, the observed-data likelihood is given by

$$L(\phi \mid D_{\mathrm{obs}})=\prod _{i-1}^{n}f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i).$$ (2.5)

Using (2.5), the joint posterior of φ takes the form

$$\pi (\phi \mid D_{\mathrm{obs}})=\frac{L(\phi \mid D_{\mathrm{obs}})\pi \left(\phi \right)}{c\left(D_{\mathrm{obs}}\right)},$$ (2.6)

where π(φ) is the joint prior, which is specified in Appendix A, and the normalizing constant is given by

$$c\left(D_{\mathrm{obs}}\right)=\int \prod _{i=1}^{n}f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)\pi \left(\phi \right)d\phi .$$ (2.7)

We write ${\theta }^R={({\theta }_1^{\prime },\dots ,{\theta }_n^{\prime })}^{\prime }$, which is the vector of all the random effects. Then, the augmented posterior distribution of (φ, θ^R) is given by

$$\pi (\phi ,{\theta }^R\mid D_{\mathrm{obs}})=\frac{{\prod }_{i=1}^{n}f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)\pi \left(\phi \right)}{c\left(D_{\mathrm{obs}}\right)},$$ (2.8)

where f(y_i, t_i, θ_i|φ, δ_i, x_i, z_i) is defined in (2.3). It is easy to see that ∫ π(φ, θ^R|D_obs)dθ^R = π(φ|D_obs). The implementation details of the Gibbs sampling algorithm to sample (φ, θ^R) from (2.8) are given in Appendix A.

2.3 Deviance Information Criterion

The Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002) for the joint model is defined as

$$\mathrm{DIC}=\mathrm{Dev}\left(\stackrel{‒}{\phi }\right)+2p_D,$$ (2.9)

where Dev(φ) is the deviance function, $p_D=\overline{\mathrm{Dev}}\left(\phi \right)-\mathrm{Dev}\left(\stackrel{‒}{\phi }\right)$ is the effective number of model parameters, and $\stackrel{‒}{\phi }$ and $\overline{\mathrm{Dev}}\left(\phi \right)$ are the posterior means of φ and Dev(φ), respectively, with respect to the posterior distribution in (2.6). To assess the overall fit of the joint model, we specify the deviance function as

$$\mathrm{Dev}\left(\phi \right)=-2\log L(\phi \mid D_{\mathrm{obs}}),$$

where L(φ|D_obs) is given by (2.5). From (2.5), we see that Dev(φ) involves the computation of n integrals as shown in (2.4).

The integration over the random effects specified in (2.4) always poses a major challenge in computing the observed-data likelihood of the joint model. One possible approach is to use a Monte Carlo (MC) approach, but this may be computationally intensive. Adaptive Gaussian quadrature (AGQ) (Pinheiro and Bates, 1995) is another approach to approximate (2.4), and is implemented here to calculate DIC when the dimension of θ_i is low.

2.3.1 DIC Decomposition

To assess the contribution of the longitudinal data to the fit of the survival data, we develop a novel decomposition of DIC in (2.9). Specifically, we decompose DIC into two parts: one part for the longitudinal data and the other part for the survival data conditional on the longitudinal data. Write φ₁ = (θ, γ, σ²,Ω) and φ₂ = (λ, α, β). Let f(θ_i|φ₁, y_i, x_i) be the conditional density of the random effects θ_i given y_i, and also let f(y_i|φ₁, x_i) = ∫ f(y_i| γ, σ², θ_i, x_i)f(θ_i|θ, Ω)dθ_i, which is the marginal density of y_i. Let ${\stackrel{‒}{\phi }}_1$ and ${\stackrel{‒}{\phi }}_2$ denote the posterior means of φ₁ and φ₂. Define ${\mathrm{Dev}}_{\mathrm{Long}}\left(\stackrel{‒}{\phi }\right)=-2{\sum }_{i=1}^n\log f({\mathit{y}}_i\mid {\stackrel{‒}{\phi }}_1.{\mathit{x}}_i)$, $p_{D\left[\mathrm{Long}\right]}=E[-2{\sum }_{i=1}^n\log f({\mathit{y}}_i\mid {\phi }_1,{\mathit{x}}_i)\mid D_{\mathrm{obs}}]+2{\sum }_{i=1}^n\log f({\mathit{y}}_i\mid {\stackrel{‒}{\phi }}_i,{\mathit{x}}_i)$, ${\mathrm{Dev}}_{\mathrm{Surv}\mid \mathrm{Long}}\left(\stackrel{‒}{\phi }\right)=-2{\sum }_{i=1}^n\log \int f(t_i\mid {\stackrel{‒}{\phi }}_2,{\theta }_i,{\delta }_i,{\mathit{z}}_i)f({\theta }_i\mid {\stackrel{‒}{\phi }}_1,{\mathit{y}}_i,{\mathit{x}}_i)d{\theta }_i$, and $p_{D[\mathrm{Surv}\mid \mathrm{Long}]}=E[-2{\sum }_{i=1}^n\log \int f(t_i\mid {\phi }_2,{\theta }_i,{\delta }_i,{\mathit{z}}_i)f({\theta }_i\mid {\phi }_1,{\mathit{y}}_i,{\mathit{x}}_i)d{\theta }_i\mid D_{\mathrm{obs}}]+2{\sum }_{i=1}^n\log \int f(t_i\mid {\stackrel{‒}{\phi }}_2,{\theta }_i,{\delta }_i,{\mathit{z}}_i)f({\theta }_i\mid {\stackrel{‒}{\phi }}_1,{\mathit{y}}_i,{\mathit{x}}_i)d{\theta }_i$. We are led to the following result.

Result 1

DIC and p_D in (2.9) have the following decomposition:

$$\begin{array}{cc}\hfill & \mathrm{DIC}={\mathrm{DIC}}_{\mathrm{Long}}+{\mathrm{DIC}}_{\mathrm{Surv}\mid \mathrm{Long}},\hfill \\ \hfill & p_D=p_{D\left[\mathrm{Long}\right]}+p_{D[\mathrm{Surv}\mid \mathrm{Long}]},\hfill \end{array}$$ (2.10)

where ${\mathrm{DIC}}_{\mathrm{Long}}={\mathrm{Dev}}_{\mathrm{Long}}\left(\stackrel{‒}{\phi }\right)+2p_{D\left[\mathrm{Long}\right]}$, and ${\mathrm{DIC}}_{\mathrm{Surv}\mid \mathrm{Long}}={\mathrm{Dev}}_{\mathrm{Surv}\mid \mathrm{Long}}\left(\stackrel{‒}{\phi }\right)+2p_{D[\mathrm{Surv}\mid \mathrm{Long}]}$.

In (2.10), DIC_Long measures the contribution of the longitudinal data to the total DIC while DIC_Surv|Long quantifies the contribution to the total DIC due to the survival data given the additional information from the longitudinal data.

The marginal distribution of y_i follows

$${\mathit{y}}_i\mid {\phi }_1,{\mathit{x}}_i\sim N\left({\mathit{X}}_i\left(\begin{array}{c}\hfill \theta \hfill \\ \hfill \gamma \hfill \end{array}\right),\left({\sigma }^2{I}_{m_i}+{\mathit{X}}_i\left(\begin{array}{cc}\hfill \Omega \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right){\mathit{X}}_i^{\prime }\right)\right)$$

and the conditional distribution of the random effects θ_i given the longitudinal data takes the form

$${\theta }_i\mid {\phi }_1,{\mathit{y}}_i,{\mathit{x}}_i\sim N\left({\Omega }_{{\theta }_i}\left[\frac{1}{{\sigma }^2}\left(I_{q+1}0\right){\mathit{X}}_i^{\prime }\left({\mathit{y}}_i-{\mathit{X}}_i\left(\begin{array}{c}\hfill 0\hfill \\ \hfill I_p\hfill \end{array}\right)\gamma \right)+{\Omega }^{-1}\theta \right],{\Omega }_{{\theta }_i}\right),$$

where ${\Omega }_{{\theta }_i}={({\Omega }^{-1}+\frac{1}{{\sigma }^2}\left(I_{q+1}0\right){\mathit{X}}_i^{\prime }{\mathit{X}}_i\left(\begin{array}{c}\hfill I_{q+1}\hfill \\ \hfill 0\hfill \end{array}\right))}^{-1}$. These are the quantities needed to apply Result 1.

2.3.2 ΔDIC_Surv

When we fit the survival data alone, i.e., α = 0 in (2.2), the hazard function reduces to $\lambda (t\mid {\lambda }_0,\alpha =0,\beta ,{\theta }_i,{\mathit{z}}_i)={\lambda }_0\left(t\right)\exp \left({\mathit{z}}_i^{\prime }\beta \right)$ and the density for t_i becomes $f_0(t_i\mid \lambda ,\beta ,{\delta }_i,{\mathit{z}}_i)={\left\{{\lambda }_0\left(t_i\right)\exp \left({\mathit{z}}_i^{\prime }\beta \right)\right\}}^{{\delta }_i}\exp [-\exp \left({\mathit{z}}_i^{\prime }\beta \right)\left\{{\int }_0^{t_i}{\lambda }_0\left(u\right)du\right\}]$ Write D_{Surv, obs} = {(t_i, δ_i, z_i), i = 1,...,n} and let

$${\mathrm{DIC}}_{\mathrm{Surv},0}={\mathrm{Dev}}_{\mathrm{Surv},0}(\stackrel{‒}{\lambda },\stackrel{‒}{\beta })+2p_{D[\mathrm{Surv},0]},$$

where ${\mathrm{Dev}}_{\mathrm{Surv},0}(\stackrel{‒}{\lambda },\stackrel{‒}{\beta })=-2{\sum }_{i=1}^n\log f_0(t_i\mid \stackrel{‒}{\lambda },\stackrel{‒}{\beta },{\delta }_i,{\mathit{z}}_i)$, and $p_{D[\mathrm{Surv},0]}=E[-2{\sum }_{i=1}^n\log f_0(t_i\mid \lambda ,\beta ,{\delta }_i,{\mathit{z}}_i)\mid D_{\mathrm{Surv},\mathrm{obs}}]+2{\sum }_{i=1}^n\log f_0(t_i\mid \stackrel{‒}{\lambda },\stackrel{‒}{\beta },{\delta }_i,{\mathit{z}}_i)$. We now propose the following model assessment criterion:

$$\Delta {\mathrm{DIC}}_{\mathrm{Surv}}={\mathrm{DIC}}_{\mathrm{Surv},0}-{\mathrm{DIC}}_{\mathrm{Surv}\mid \mathrm{Long}}.$$ (2.11)

In (2.11), ΔDIC_Surv measures the gain of the fit in the survival component due to the longitudinal data with a penalty for the additional parameters in the survival component of the joint model. A model with a large value of ΔDIC_Surv is more preferred. When $2(p_{D[\mathrm{Surv}\mid \mathrm{Long}]}-p_{D[\mathrm{Surv},0]})>{\mathrm{Dev}}_{\mathrm{Surv},0}(\stackrel{‒}{\lambda },\stackrel{‒}{\beta })-{\mathrm{Dev}}_{\mathrm{Surv}\mid \mathrm{Long}}\left(\stackrel{‒}{\phi }\right)$, then ΔDIC_Surv < 0. That is, when the penalty for the additional parameters in the survival component outweighs the gain of the fit in the survival component, ΔDIC_Surv can be negative.

2.4 Conditional Predictive Ordinate

2.4.1 CPO Computation

Let $D_{\mathrm{obs}}^{(-i)}=\{({\mathit{y}}_j,t_j,{\delta }_j,{\mathit{x}}_j,{\mathit{z}}_i),j=1,\dots ,i-1,i+1,\dots ,n\}$ denote the observed data with the i^th subject deleted. The Conditional Predictive Ordinate (CPO) (e.g., Geisser and Eddy, 1979; Gelfand et al., 1992; and Gelfand and Dey, 1994) for the i^th subject is defined as

$${\mathrm{CPO}}_i=\int f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)\pi (\phi \mid D_{\mathrm{obs}}^{(-i)})d\phi ,$$ (2.12)

where

$$\pi (\phi \mid D_{\mathrm{obs}}^{(-i)})=\frac{{\prod }_{j\ne i}f({\mathit{y}}_j,t_j\mid \phi ,{\delta }_j,{\mathit{x}}_j,{\mathit{z}}_j)\pi \left(\phi \right)}{c\left(D_{\mathrm{obs}}^{(-i)}\right)},$$ (2.13)

and $c\left(D_{\mathrm{obs}}^{(-i)}\right)$ is the normalizing constant, i.e., $c\left(D_{\mathrm{obs}}^{(-i)}\right)=\int {\prod }_{j\ne i}f({\mathit{y}}_j,t_j\mid \phi ,{\delta }_j,{\mathit{x}}_j,{\mathit{z}}_j)\pi \left(\phi \right)d\phi$. Following Chen et al. (2000), we obtain the first CPO identity.

CPO Identity I

CPO_i in (2.12) can be rewritten as

$${\mathrm{CPO}}_i=\frac{1}{\int \frac{1}{f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi (\phi \mid D_{\mathrm{obs}})d\phi }.$$ (2.14)

The proof of this identity directly follows from Chapter 10 of Chen et al. (2000). CPO Identity I leads to the development of a popular Monte Carlo estimate of CPO using Gibbs samples from the posterior distribution given D_obs instead of $D_{\mathrm{obs}}^{(-i)}$. Letting {φ_b, b = 1, . . . , B} denote a Gibbs sample of φ from π(φ|D_obs) and using (2.14), a Monte Carlo estimate of ${\mathrm{CPO}}_i^{-1}$ is given by

$${\widehat{\mathrm{CPO}}}_i^{-1}=\frac{1}{B}\sum _{b=1}^B\frac{1}{f({\mathit{y}}_i,t_i\mid {\phi }_b,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}.$$ (2.15)

The numerical approximation of ${\mathrm{CPO}}_i^{-1}$ in (2.15) involves the integral over the random effects and can be calculated using AGQ to approximate (2.4). However, this method would likely be computationally intensive when the dimension of the random effects is high. To circumvent this numerical integration issue in (2.15), we develop a second CPO identity and then propose a new efficient MC method which directly uses the Gibbs samples generated from the augmented posterior distribution π(φ, θ^R|D_obs) in (2.8) to calculate ${\mathrm{CPO}}_i^{-1}$.

CPO Identity II

Let w_i(θ_i) be a normalized weight function such that ∫ w_i(θ_i)dθ_i = 1. Then, CPO_i in (2.12) can be expressed as

$${\mathrm{CPO}}_i=\frac{1}{\int \frac{w_i\left({\theta }_i\right)}{f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi (\phi ,{\theta }^R\mid D_{\mathrm{obs}})d{\theta }^{R}d\phi }.$$ (2.16)

Now, let $\{({\phi }_b,{\theta }_b^R),b=1,\dots ,B\}$ denote a Gibbs sample of (φ, θ^R) from π(φ, θ^R|D_obs). Using the CPO Identity II in (2.16), a Monte Carlo estimate of ${\mathrm{CPO}}_i^{-1}$ is given by

$${\widehat{\mathrm{CPO}}}_i^{-1}=\frac{1}{B}\sum _{b=1}^B\frac{w_i\left({\theta }_{ib}\right)}{f({\mathit{y}}_i,t_i,{\theta }_{ib}\mid {\phi }_b,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}.$$

Under certain ergodic conditions, ${\widehat{\mathrm{CPO}}}_i^{-1}$ is unbiased and consistent for any normalized weight function w_i. However, the Monte Carlo error of ${\widehat{\mathrm{CPO}}}_i^{-1}$ depends on the choice of w_i. The following theorem characterizes the optimal choice of w_i in minimizing the variance of the Monte Carlo estimator ${\widehat{\mathrm{CPO}}}_i^{-1}$ when $\{({\phi }_b,{\theta }_b^R),b=1,\dots ,B\}$ is a sample from π(φ, θ^R|D_obs).

Theorem 1

Let

$$w_{i,\mathrm{opt}}\left({\theta }_i\right)=\frac{f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}{f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}.$$

Then, for any normalized weight function w_i, we have

$$\mathrm{Var}\left(\phantom{\mid }\frac{w_{i,\mathrm{opt}}\left({\theta }_i\right)}{f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\mid D_{\mathrm{obs}}\right)\le \mathrm{Var}\left(\phantom{\mid }\frac{w_i\left({\theta }_i\right)}{f({\mathit{y}}_i,t_i,{\theta }_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\mid D_{\mathrm{obs}}\right),$$

where the variance is taken with respect to the posterior distribution π(φ, θ^R|D_obs).

Remark 1

The result established in Theorem 1 provides the best choice of w_i. However, this optimal weight function is expensive to compute. Since the optimal weight function w_i,opt is analogous to the optimal weight function in the importance-weighted marginal density estimation (IWMDE) of the marginal posterior density proposed by Chen (1994), we may follow the guidelines discussed in Geweke (1989) and Chen (1994) to construct a good weight function w_i which is similar to w_i,opt. One possible choice of w_i is a multivariate normal density, which is constructed via the Laplace approximation to the joint density f(y_i, t_i, θ_i|φ, δ_i, x_i, z_i) in (2.3). Another possible choice of w_i is w_i,cond(θ_i) = f(θ_i|φ₁, y_i, x_i), which is the conditional density of the random effects θ_i given y_i. Note that when y_i and t_i are independent, w_i,cond(θ_i) = w_i,opt. Therefore, w_i,cond(θ_i) may be a reasonable choice for computing the CPO_i.

2.4.2 CPO Decomposition

In this subsection, we first establish the third CPO identity which will lead to the decomposition of CPO.

CPO Identity III

The CPO in (2.12) can also be expressed as

$${\mathrm{CPO}}_i=\frac{c\left(D_{\mathrm{obs}}\right)}{c\left(D_{\mathrm{obs}}^{(-i)}\right)}=\frac{f({\mathit{y}}_i,t_i\mid \phi ,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)\pi (\phi \mid D_{\mathrm{obs}}^{(-i)})}{\pi (\phi \mid D_{\mathrm{obs}})},$$ (2.17)

which is true for all φ.

Since plugging in any numerical value for φ in (2.17) results in the CPO, we have

$${\mathrm{CPO}}_i=\frac{f({\mathit{y}}_i,t_i\mid {\phi }^{\ast },{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)\pi ({\phi }^{\ast }\mid D_{\mathrm{obs}}^{(-i)})}{\pi ({\phi }^{\ast }\mid D_{\mathrm{obs}})},$$ (2.18)

where φ* is a fixed value of φ, which may be chosen as the posterior mean. We note that (2.18) is similar to the identity of Chib (1995). Let ${\phi }_1^{\ast }$ and ${\phi }_2^{\ast }$ denote the posterior means of φ₁ and φ₂. From (2.4) and (C.1), we have

$$f({\mathit{y}}_i,t_i\mid {\phi }^{\ast },{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)=f({\mathit{y}}_i\mid {\phi }_1^{\ast },{\mathit{x}}_i)f(t_i\mid {\phi }_2^{\ast },{\phi }_1^{\ast },{\delta }_i,{\mathit{y}}_i,{\mathit{x}}_i,{\mathit{z}}_i),$$

where $f(t_i\mid {\phi }_2^{\ast },{\phi }_1^{\ast },{\delta }_i,{\mathit{y}}_i,{\mathit{x}}_i,{\mathit{z}}_i)=\int f(t_i\mid {\phi }_2^{\ast },{\theta }_i,{\delta }_i,{\mathit{z}}_i)f({\theta }_i\mid {\phi }_1^{\ast },{\mathit{y}}_i,{\mathit{x}}_i)d{\theta }_i$. We also observe that

$$\begin{array}{cc}\hfill & \pi ({\phi }^{\ast }\mid D_{\mathrm{obs}}^{(-i)})=\pi ({\phi }_i^{\ast }\mid D_{\mathrm{obs}}^{(-i)})\pi ({\phi }_2^{\ast }\mid {\phi }_1^{\ast },D_{\mathrm{obs}}^{(-i)}),\hfill \\ \hfill & \pi ({\phi }^{\ast }\mid D_{\mathrm{obs}})=\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}})\pi ({\phi }_2^{\ast }\mid {\phi }_1^{\ast },D_{\mathrm{obs}}).\hfill \end{array}$$ (2.19)

Using (2.18) and the facts of the joint densities stated above, we propose the CPO decomposition:

$${\mathrm{CPO}}_i={\mathrm{CPO}}_{i,\mathrm{Long}}\cdot {\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}},$$ (2.20)

where

$${\mathrm{CPO}}_{i,\mathrm{Long}}=\frac{f({\mathit{y}}_i\mid {\phi }_i^{\ast },{\mathit{x}}_i)\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}}^{(-i)})}{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}})},$$ (2.21)

and

$${\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}}=\frac{f(t_i\mid {\phi }_2^{\ast },{\phi }_1^{\ast },{\delta }_i,{\mathit{y}}_i,{\mathit{z}}_i)\pi ({\phi }_2^{\ast }\mid {\phi }_1^{\ast },D_{\mathrm{obs}}^{(-i)})}{\pi ({\phi }_2^{\ast }\mid {\phi }_1^{\ast },D_{\mathrm{obs}})}.$$ (2.22)

Remark 2

Let D_Long,obs = {(y_i, x_i), i = 1, . . . , n} denote the observed longitudinal data and D_Surv,obs = {(t_i, δ_i, z_i), i = 1, . . . , n} denote the survival data, respectively. Also let $D_{\mathrm{Long},\mathrm{obs}}^{(-i)}=\{({\mathit{y}}_i,{\mathit{x}}_i),j=1,\dots ,i-1,i+1,\dots ,n\}$ and $D_{\mathrm{Surv},\mathrm{obs}}^{(-i)}=\{(t_i,{\delta }_i,{\mathit{z}}_i),j=1,\dots ,i-1,i+1,\dots ,n\}$ denote the observed longitudinal and survival data with the i^th subject deleted, respectively. Assume that D_Long,obs and D_Surv,obs are independent and π(φ₁, φ₂) = π(φ₁)π(φ₂). Under these assumptions, we have

$${\mathrm{CPO}}_{i,\mathrm{Long}}={\mathrm{CPO}}_{i,\mathrm{Long}\mathrm{alone}}=\int f({\mathit{y}}_i\mid {\phi }_i,{\mathit{x}}_i)\pi ({\phi }_i\mid D_{\mathrm{Long},\mathrm{obs}}^{(-i)})d{\phi }_1,$$ (2.23)

$${\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}}={\mathrm{CPO}}_{i,\mathrm{Surv}0}=\int f_0(t_i\mid {\phi }_2,{\delta }_i,{\mathit{z}}_i)\pi ({\phi }_2\mid D_{\mathrm{Surv},\mathrm{obs}}^{(-i)})d{\phi }_2,$$ (2.24)

and

$${\mathrm{CPO}}_i=\int f({\mathit{y}}_i\mid {\phi }_1,{\mathit{z}}_i)\pi ({\phi }_1\mid D_{\mathrm{Long},\mathrm{obs}}^{(-i)})d{\phi }_1\times \int f_0(t_i\mid {\phi }_2,{\delta }_i,{\mathit{z}}_i)\pi ({\phi }_2\mid D_{\mathrm{Surv},\mathrm{obs}}^{(-i)})d{\phi }_2,$$

where

$$\begin{array}{c}\hfill \pi ({\phi }_1\mid D_{\mathrm{Long},\mathrm{obs}}^{(-i)})=\frac{{\prod }_{j\ne i}f({\mathit{y}}_j\mid {\phi }_1,{\mathit{x}}_j)\pi \left({\phi }_1\right)}{\int {\prod }_{j\ne i}f({\mathit{y}}_j\mid {\phi }_1,{\mathit{x}}_j)\pi \left({\phi }_1\right)d{\phi }_1},\hfill \\ \hfill \pi ({\phi }_2\mid D_{\mathrm{Surv},\mathrm{obs}}^{(-i)})=\frac{{\prod }_{j\ne i}{f}_0(t_j\mid {\phi }_2,{\delta }_j,{\mathit{z}}_j)\pi \left({\phi }_2\right)}{\int {\prod }_{j\ne i}{f}_0(t_j\mid {\phi }_2,{\delta }_j,{\mathit{z}}_j)\pi \left({\phi }_2\right)d{\phi }_2},\hfill \end{array}$$

and f₀(t_j|φ₂, δ_j, z_j) is defined in Section 2.3.2 with φ₂ = (λ α = 0, β). Therefore, CPO_i,Long and CPO_i,Surv|Long reduce to the usual CPOs for the longitudinal data and the survival data separately, and the CPO decomposition (2.20) holds under the usual definition of CPO.

Next, we develop useful in the following theorem for $\frac{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}}^{(-i)})}{\partial ({\phi }_1^{\ast }\mid D_{\mathrm{obs}})}$, CPO_i,Long, and CPO_i,Surv|Long, which facilitate the computation and further understanding of these quantities.

Theorem 2

For CPO_i, CPO_i,Long, and CPO_i,Surv|Long, we have the following identities:

$$\frac{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}}^{(-i)})}{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}})}={\mathrm{CPO}}_i\int \frac{1}{f({\mathit{y}}_i,t_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi ({\phi }_2\mid {\phi }_1^{\ast },D_{\mathrm{obs}})d{\phi }_2,$$

$${\mathrm{CPO}}_{i,\mathrm{Long}}={\mathrm{CPO}}_i\int \frac{1}{f(t_i\mid {\phi }_2,{\phi }_1^{\ast },{\delta }_i,{\mathit{y}}_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi ({\phi }_2\mid {\phi }_1^{\ast },D_{\mathrm{obs}})d{\phi }_2,$$ (2.25)

and

$${\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}}=\frac{1}{\int \frac{1}{f(t_i\mid {\phi }_2,{\phi }_1^{\ast },{\delta }_i,{\mathit{y}}_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi ({\phi }_2\mid {\phi }_1^{\ast },D_{\mathrm{obs}})d{\phi }_2}.$$ (2.26)

Remark 3

The identity in (2.26) is quite attractive as it has a similar form as the usual CPO_i in (2.14). We also see from (2.26) that CPO_i,Surv|Long is free of ${\phi }_2^{\ast }$. In addition, CPO_i,Surv|Long can be directly calculated from (2.26). Thus, if only CPO_i,Surv|Long is of interest, it is not necessary to compute the overall CPO_i. However, it does not appear possible that CPO_i,Long can be computed directly without knowing CPO_i and CPO_i,Surv|Long.

Remark 4

To avoid the calculation of $f({\mathit{y}}_i,t_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)$, we use the same idea as in (2.16) and obtain

$$\frac{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}}^{(-i)})}{\pi ({\phi }_1^{\ast }\mid D_{\mathrm{obs}})}={\mathrm{CPO}}_i\int \frac{w_i\left({\theta }_i\right)}{f({\mathit{y}}_i,t_i,{\theta }_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi ({\phi }_2,{\theta }^R\mid {\phi }_1^{\ast },D_{\mathrm{obs}})d{\theta }^{R}d{\phi }_2,$$

where the optimal choice of w_i(θ_i) is $\frac{f({\mathit{y}}_i,t_i,{\theta }_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}{f({\mathit{y}}_i,t_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}$. Similarly,

$${\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}}=\frac{1}{f({\mathit{y}}_i\mid {\phi }_1^{\ast },{\mathit{x}}_i)\int \frac{w_i\left({\theta }_i\right)}{f({\mathit{y}}_i,t_i,{\theta }_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}\pi ({\phi }_2,{\theta }^R\mid {\phi }_1^{\ast },D_{\mathrm{obs}})d{\theta }^{R}d{\phi }_2},$$

where the optimal choice of w_i(θ_i) is $\frac{f({\mathit{y}}_i,t_i,{\theta }_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}{f({\mathit{y}}_i,t_i\mid {\phi }_1^{\ast },{\phi }_2,{\delta }_i,{\mathit{x}}_i,{\mathit{z}}_i)}$.

2.4.3 LPML and LPML Decomposition

The logarithm of the Pseudo marginal likelihood (LPML) (Ibrahim et al., 2001) is defined as

$$\mathrm{LPML}=\sum _{i=1}^n\log \left({\mathrm{CPO}}_i\right).$$

We note that there is a relationship between the DIC and the LPML in large samples (see Draper and Krnjajić (2005, Section 4)). Using the decomposition of CPO in (2.20), we are led to the following result.

Result 2

LPML can be decomposed as

$$\mathrm{LPML}={\mathrm{LPML}}_{\mathrm{Long}}+{\mathrm{LPML}}_{\mathrm{Surv}\mid \mathrm{Long}},$$

where ${\mathrm{LPML}}_{\mathrm{Long}}={\sum }_{i=1}^n\log {\mathrm{CPO}}_{i,\mathrm{Long}}$, ${\mathrm{LPML}}_{\mathrm{Surv}\mid \mathrm{Long}}={\sum }_{i=1}^n\log {\mathrm{CPO}}_{i,\mathrm{Surv}\mid \mathrm{Long}}$ and CPO_i,Long and CPO_i,Surv|Long are given by (2.21) and (2.22), respectively.

2.4.4 ΔLPML_Surv

Define ${\mathrm{LPML}}_{\mathrm{Surv},0}={\sum }_{i=1}^n\log \left({\mathrm{CPO}}_{i,\mathrm{Surv}0}\right)$, where CPO_i,Surv0 is given by (2.24). We propose the model assessment criterion

$$\Delta {\mathrm{LPML}}_{\mathrm{Surv}}={\mathrm{LPML}}_{\mathrm{Surv}\mid \mathrm{Long}}-{\mathrm{LPML}}_{\mathrm{Surv},0}.$$

ΔLPML_Surv quantifies the gain of the fit in the survival component due to the longitudinal data with a penalty for the additional parameters in the survival component of the joint model. A model with a large value of ΔLPML_Surv is more preferred. From Remark 3, it is easy to see that if our interest is on ΔLPML_Surv only, we do not need to compute the overall LPML for the joint model. Similar to ΔDIC_Surv, it is not guaranteed that ΔLPML_Surv is non-negative.

3 A Simulation Study

We conduct a simulation study to evaluate the empirical performance of ΔDIC_Surv and ΔLPML_Surv in selecting the true model or identifying the true longitudinal data. We generate longitudinal and survival data under the SPM with the simple exponential baseline. Specifically, we first simulate θ_i = (θ_0i, θ_1i)′ N(θ, Ω), where θ = (θ₀, θ₁)′ = (0.1, 0.5)′ and $\Omega =\left(\begin{array}{cc}\hfill {\Omega }_{00}\hfill & \hfill {\Omega }_{01}\hfill \\ \hfill {\Omega }_{10}\hfill & \hfill {\Omega }_{11}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 0.7\hfill & \hfill -0.1\hfill \\ \hfill -0.1\hfill & \hfill 0.06\hfill \end{array}\right)$. We then simulate the longitudinal data from a N(μ_i(a_ij), σ²) distribution with a linear trajectory μ_i(a_ij) = θ_0i + a_ij θ_1i + x_iγ. For the survival data, we set z_i = x_i and generate t* from an exponential regression model, i.e., $t_i^{\ast }{[-\lambda \exp \{{\theta }_{0i}{\alpha }_1+{\theta }_{1i}{\alpha }_2+z_i\beta \}]}^{-1}\log (1-U)$, where U ~ U(0, 1), and draw the censoring times C_i from an exponential distribution with mean 10. Then, we compute $t_i=\min \{t_i^{\ast },C_i\}$ and δ_i = 1 if $t_i^{\ast }\le C_i$ and 0 otherwise. The treatment indicator x_i is generated from a Bernoulli(0.5) distribution. For each subject, 6 or 7 time points (a_ij, j = 1, . . . , 6 or 7) for the longitudinal measures are chosen to be (0 + ζ_i1, 21 + ζ_i2, 42 + ζ_i3, 63 + ζ_i4, 84 + ζ_i5, 105 + ζ_i6)/30.4375 if ζ_i7 > 0 and (0 + ζ_i1, 21 + ζ_i2, 42 + ζ_i3, 63 + ζ_i4, 84 + ζ_i5, 105 + ζ_i6, 126 + ζ_i7)/30.4375 if ζ_i7 ≤ 0, where ζ_ij ~ U(−3, 3) for j = 1, . . . , 7, and 30.4375 = 365.25/12. The design values of the parameters are given as Ω₀₀ = 0.7, Ω₁₀ = Ω₀₁ = −0.1, Ω₁₁ = 0.06, δ² = 0.3, θ₀ = 0.1, θ₁ = 0.5, γ = −0.2, α₁ = 0.3, α₂ = 1.6, β= −0.4, and λ = 0.08. 500 datasets are simulated independently with n = 400 subjects in each simulated dataset. The resulting censoring percentage is about 40%.

Let D_T denote the dataset generated from the true SPM model. One additional set of longitudinal data is generated by adding noise to the true longitudinal measures. More specifically, it is simulated from a N(μ_ℓi(a_ij), δ²) distribution with linear trajectories μ_ℓi(a_ij) = (θ_0i + τ_ℓ0i) + a_ij(θ_1i + τ_ℓ1i) + x_iγ, where (τ_ℓ0i, τ_ℓ1i)′ ~ N(0, 0.2²I₂), and the values of the other parameters remain the same as before. By combining this longitudinal dataset with the same survival data in D_T, we obtain the additional dataset and denote it as D_W.

We consider the following scenarios to fit different joint models to the datasets D_T and D_W:

1. TRUE: Fit the true joint model to D_T . In the true joint model, (2.1) becomes

   $$y_i\left(a_{ij}\right)={\theta }_{0i}+a_{ij}{\theta }_{1i}+x_i\gamma +{ϵ}_i\left(a_{ij}\right),$$ (3.1)

   and (2.2) becomes

   $$\lambda \exp \{{\theta }_{0i}{\alpha }_1+{\theta }_{1i}{\alpha }_2+z_i\beta \}.$$ (3.2)

2. Long: Fit the joint model with (3.1) and (3.2) to D_W. In this case, D_W is fit by the joint model with misspecified longitudinal submodel.

3. SurvI: Fit the joint model with (3.1) and misspecified survival submodel to D_T. In this joint model, (3.2) reduces to λexp{θ_0i α₁ + z_i β}.

4. SurvII: Fit the joint model with (3.1) and misspecified survival submodel to D_T. In this joint model, (3.2) reduces to λexp{θ_1i α₂ + z_i β}.

5. TM: Fit the joint model with (3.1) and misspecified survival submodel to D_T. In this joint model, (3.2) becomes λexp{(θ_0i + θ_1it)α + z_i β}.

6. Long&Surv: Fit the joint model with misspecified longitudinal and survival submodels to D_T. In this joint model, (3.1) becomes y_i(a_ij) = θ_0i + x_iγ + ε_i(a_ij), and (3.2) reduces to γexp{θ_0i α₁ + z_i β}.

In all the six scenarios, the exponential regression model, namely, λexp{z_i β}, fits the true survival data D_T in computing DIC_{Surv, 0} and LPML_{Surv, 0}. Thus, the values of DIC_{Surv, 0} and LPML_{Surv, 0} are the same for all of the six scenarios. Since ΔDIC_Surv = DIC_{Surv, 0} − DIC_Surv|Long and ΔLPML_Surv = LPML_Surv|Long − LPML_{Surv, 0}, ΔDIC_Surv and ΔLPML_Surv can be used to assess the fit of the survival component of the joint model for all of the six scenarios. We also note that in scenario (ii), both components of the joint model are correctly specified but fit to the longitudinal data, which are less correlated to the survival data; in scenarios (iii), (iv), and (v), the longitudinal component is correctly specified, the survival component is misspecified, and both components fit the true longitudinal and survival data; and in scenario (vi), both components of the joint model are misspecified but fit the true data.

For each simulated dataset, we take 5000 Gibbs samples with 100 burn-in iterations. The means of ΔDIC_Surv and ΔLPML_Surv as well as the frequencies of ranking each model as best based on ΔDIC_Surv and ΔLPML_Surv are reported in Table 1. From this table, we see that True has the largest means of ΔDIC_Surv and ΔLPML_Surv, which are 18.72 and 9.37, and gets ranked as the best with 423 times out of 500 by both criteria, while SurvI has the smallest means of ΔDIC_Surv and ΔLPML_Surv and never gets ranked as the best by these two criteria in these 500 simulated datasets. These results show that both ΔDIC_Surv and ΔLPML_Surv can correctly identify the true model or the true data.

Table 1.

Means of ΔDIC_Surv and ΔLPML_Surv and frequencies of ranking each model as best based on ΔDIC_Surv and ΔLPML_Surv

	ΔDICSurv		ΔLPMLSurv
Data	Mean	Frequency	Mean	Frequency
True	18.72	423	9.37	423
Long	10.67	27	5.35	28
SurvI	1.31	0	0.63	0
SurvII	10.54	19	5.23	22
TM	4.09	8	1.92	6
Long&Surv	10.59	23	5.30	21

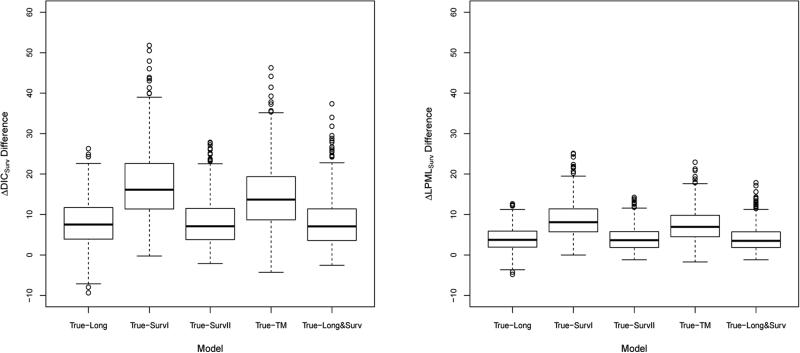
Figure 1 shows boxplots of the ΔDIC_Surv and ΔLPML_Surv differences between True and each of Long, SurvI, SurvII, TM, and Long&Surv. We see from this figure that boxplots for ΔDIC_Surv and ΔLPML_Surv differences are almost above zero, indicating that the true model does fit the true data much better than other models based on either ΔDIC_Surv or ΔLPML_Surv. These results are consistent with those based on the means of ΔDIC_Surv and ΔLPML_Surv and the frequencies of ranking each model as best as shown in Table 1.

Figure 1.

Boxplots of the ΔDIC_Surv differences and the ΔLPML_Surv differences between True and each of Long, SurvI, SurvII, TM, and Long&Surv.

4 Analysis of the EMPHACIS Data

We consider a dataset from a multicenter, randomized, single-blind, EMPHACIS lung cancer clinical trial (Evaluation of MTA in Mesothelioma in a Phase III Study with Cisplatin) (Vogelzang et al., 2003). The study drug was multi-targeted antifolate (MTA) pemetrexed given in combination with cisplatin (the PEM/Cis arm), and the active-treatment comparator was cisplatin alone (the Cis arm). The treatment for both arms was structured as six 21-day cycles of therapy; patients receiving treatment benefit could receive additional cycles based on investigator discretion. Malignant pleural mesothelioma is characterized by rapid disease progression, high symptom burden, and a relatively short median survival of 12 months after diagnosis (Thompson et al., 2014). Accordingly, patient-reported assessments are important for evaluation of disease progression and patients’ response to therapy. In oncology, the patients’ importance ratings on the magnitude of progression-free survival improvement has been shown to depend on the severity of disease-related symptoms (Bridges et al., 2012). We analyzed the disease-specific patient-reported Lung Cancer Symptom Scales (LCSS) (Patricia et al., 2006) to evaluate the patient-level association of five of the six instrument items (i.e., anorexia, cough, dyspnea, fatigue, and pain) with progression-free survival using the EMPHACIS trial data. Progression free survival time (PFS) is defined as the time from randomization to the time until documented progression or death from any cause. We are interested in the association between post-baseline LCSS measurements and PFS. The main goal of applying joint models in this study is to assess the association of each longitudinal LCSS symptom with PFS and the treatment effects on each LCSS item and PFS simultaneously. More importantly, with the decomposition of DIC and LPML, the longitudinal LCSS symptoms can be compared in terms of their contribution to the fit of the PFS data as well as the gain in the fit of the longitudinal data for each LCSS symptom using the information from the PFS data can be determined.

Our study cohort consists of 425 patients with at least one post-baseline value of each longitudinal measure and seven binary covariates, including race (x_i1 = 1 if white), gender (x_i2 = 1 if male), age (x_i3 = 1 if age ≥ 65), Karnofsky status (x_i4 = 1 if Karnofsky status is high), baseline stage of disease (x_i5 = 1 if stage I/II), vitamin supplementation (x_i6 = 1 if full vitamin supplementation), and treatment assignment (x_i7 = 1 if the i^th patient is in the pemetrexed/cisplatin arm). Among the 425 patients, 394 patients experienced disease progression. Among these 394 patients, there were only 129 distinct disease progression times. In all the computations, we used z_i = x_i and standardized these five LCSS measures, where the means and standard deviations were 30.79 and 27.19, 11.48 and 17.93, 31.41 and 26.33, 39.38 and 27.06, and 24.64 and 24.90 for anorexia, cough, dyspnea, fatigue, and pain, respectively. The total numbers of longitudinal measures (i.e., ${\sum }_{i=1}^n{m}_i$) including the baseline measures were 5504, 5544, 5553, 5530, and 5546 for anorexia, cough, dyspnea, fatigue, and pain.

In (2.2), we assume a piecewise constant hazard function for λ₀(t) defined as

$${\lambda }_0\left(t\right)={\lambda }_k,t\in (s_{k-1},s_k]\text{for}k=1,\dots ,K,$$ (4.1)

where 0 = s₀ < s₁ < s₂ < . . . < s_K−1 < s_K = ∞ is a finite partition of the time axis. The s_k's in (4.1) were constructed based on the percentiles such as the first (Q₁), second (Q₂), and third (Q₃) quartiles of the PFS times. Let D_anorexia, D_cough, D_dyspnea, D_fatigue, and D_pain denote the five observed LCSS longitudinal datasets and also let D_Surv denote the observed PFS data. We fit the shared parameter model and the trajectory model with a linear trajectory, denoted by SPML and TML, respectively, to each pair of the PFS data and one of the five LCSS longitudinal outcomes corresponding to anorexia, cough, dyspnea, fatigue, and pain, namely, D_anorexia + D_Surv, D_cough + D_Surv, D_dyspnea + D_Surv, D_fatigue + D_Surv, and D_pain + D_Surv. The prior π(g=f) in (2.6) is specified in Appendix A of the supplementary material. For TML, we specify a N(0, 10000) prior distribution for α.

To construct the partition {s_k, k = 0, 1, . . . , K}, we adopt the left bi-sectional quantile partition (LBSQP) method proposed in Zhang et al. (2015b). We use DIC_{Surv, 0} and LPML_{Surv, 0} to determine the number of intervals (K) in (4.1). We start with a large value of K, which is close to the number of distinct PFS times, and work down to a smaller value of K. For the EMPHACIS data, K = 100 should be sufficiently large given that there were only 129 distinct PFS times. We determine an “optimal” value of K according to DIC_{Surv, 0} and LPML_{Surv, 0} by fitting the PFS data alone. Table S1 of the supplementary material shows the results for various values of K. From Table S1, we see that the respective values of DIC_{Surv, 0} and LPML_{Surv, 0} were 2070.61 and −1070.94 for K = 100; 2022.56 and −1012.62 for K = 35; 2018.49 and −1010.07 for K = 30; 2026.85 and −1014.27 for K = 25; and 2206.05 and −1103.10 for K = 2. Thus, the piecewise constant baseline hazard function with K = 30 fit the PFS data alone best according to both DIC_{Surv, 0} and LPML_{Surv, 0}. We then fit each of the LCSS longitudinal and PFS data, D_anorexia + D_Surv, D_cough + D_Surv, D_dyspnea + D_Surv, D_fatigue + D_Surv, and D_pain + D_Surv, with the “best” value of K = 30 in fitting the PFS data alone along with K = 25 and K = 35. We used the Laplace approximation to construct a multivariate normal density for w_i in computing LPML (MC), LPML_Surv|Long (MC), and ΔLPML_Surv (MC). Table 2 shows DIC, DIC_Surv|Long, ΔDIC_Surv, LPML, LPML_Surv|Long, and ΔLPML_Surv using the proposed MC method for each of the five PROs for K = 25, 30, and 35 under SPML and TML, respectively. The values of p_D and p_D[Surv|Long] associated with DIC and DIC_Surv|Long are given in Table S2 of the supplemental material. Table S3 of the supplemental material shows LPML, LPML_Surv|Long, and ΔLPML_Surv using the AGQ approach. We see from Table 2 and Table S3 that LPML (MC), LPML_Surv|Long (MC), and ΔLPML_Surv (MC) are very close to LPML (GQ), LPML_Surv|Long (GQ), and ΔLPML_Surv (GQ). We also see from Table 2 that (a) according to DIC_Surv|Long and LPML_Surv|Long, the joint model with K = 30 fit the longitudinal and survival data better than those models with K = 25 and K = 35 under both SPML and TML; and (b) according to DIC and LPML, SPML fit D_anorexia + D_Surv, D_dyspnea + D_Surv, D_fatigue + D_Surv, and D_pain + D_Surv better than TML except for D_cough + D_Surv. Among the five PROs, pain had the largest values of ΔDIC_Surv and ΔLPML_Surv while cough had the smallest values of ΔDIC_Surv and ΔLPML_Surv under both SPML and TML. These results indicate that pain led to the most gain in fitting the PFS data while cough had the least contribution to the fit of the PFS data. We mention here that the overall DIC and LPML were not able to determine the contribution of the longitudinal data in fitting the survival data for these five LCSS longitudinal measures under the joint modeling framework. From Table 2, we observe that the smallest DIC_Long (or largest LPML_Long) value was the main reason for dyspnea having the smallest DIC (largest LPML) value, which had no implication on the contribution of the LCSS data to the fit of the PFS data. In addition, DIC and LPML were not directly comparable among these five PROs since the total numbers of longitudinal measures were different.

Table 2.

The Decompositions of DIC and LPML for five PROs under SPML and TML with different K

K	Model		Anorexia	Cough	Dyspnea	Fatigue	Pain
25	SPML	DIC	14022.37	14271.39	11920.73	13001.30	12843.70
		DICSurv|Long	2004.52	2022.77	2007.75	1995.93	1975.15
		ΔDICSurv	22.33	4.08	19.10	30.91	51.70
		LPML	−7015.02	−7145.62	−5965.58	−6504.33	−6428.93
		LPMLSurv|Long	−1003.19	−1012.15	−1004.82	−998.63	−988.28
		ΔLPMLSurv	11.08	2.12	9.45	15.63	25.99
	TML	DIC	14024.40	14269.30	11927.25	13007.29	12858.02
		DICSurv|Long	2006.64	2020.66	2015.58	2001.91	1990.13
		ΔDICSurv	20.20	6.19	11.27	24.93	36.71
		LPML	−7016.13	−7144.96	−5968.82	−6507.33	−6436.08
		LPMLSurv|Long	−1004.31	−1011.09	−1008.75	−1001.89	−995.99
		ΔLPMLSurv	9.96	3.17	5.51	12.38	18.27
30	SPML	DIC	14014.67	14262.97	11911.96	12993.00	12835.64
		DICSurv|Long	1996.62	2014.65	1999.37	1987.86	1967.00
		ΔDICSurv	21.86	3.84	19.11	30.62	51.49
		LPML	−7011.19	−7141.36	−5960.94	−6500.14	−6424.85
		LPMLSurv|Long	−999.00	−1008.05	−1000.58	−994.65	−984.21
		ΔLPMLSurv	11.07	2.02	9.48	15.41	25.86
	TML	DIC	14016.65	14260.43	11919.21	12999.26	12849.74
		DICSurv|Long	1998.91	2012.10	2007.31	1994.24	1982.24
		ΔDICSurv	19.58	6.39	11.18	24.25	36.24
		LPML	−7012.14	−7140.22	−5964.61	−6503.19	−6431.90
		LPMLSurv|Long	−1000.25	−1006.79	−1004.63	−997.96	−991.98
		ΔLPMLSurv	9.82	3.28	5.44	12.11	18.09
35	SPML	DIC	14018.84	14267.09	11914.40	12997.21	12839.63
		DICSurv|Long	2000.43	2018.43	2002.76	1991.57	1970.54
		ΔDICSurv	22.13	4.13	19.81	31.00	52.02
		LPML	−7013.76	−7143.93	−5962.76	−6502.81	−6427.37
		LPMLSurv|Long	−1001.53	−1010.42	−1002.91	−997.12	−986.54
		ΔLPMLSurv	11.09	2.20	9.71	15.50	26.07
	TML	DIC	14019.89	14264.71	11923.25	13002.92	12853.22
		DICSurv|Long	2002.30	2015.98	2011.28	1998.05	1986.04
		ΔDICSurv	20.27	6.58	11.28	24.52	36.52
		LPML	−7014.31	−7143.10	−5967.13	−6505.60	−6434.11
		LPMLSurv|Long	−1002.67	−1009.37	−1007.04	−1000.34	−994.39
		ΔLPMLSurv	9.95	3.25	5.58	12.28	18.23

Tables 3 and 4 show the posterior estimates and 95% highest posterior density (HPD) intervals of the hazard ratio (HR) of the overall treatment effect on PFS (β₁) and the estimates (Est) of the regression coefficients α associated with the random effects under SPML and TML with K = 30, respectively. We observe that except for dyspnea under SPML, the HRs under the joint model (ranging from 0.614 to 0.634 under SPML and ranging from 0.608 to 0.636 under TML) were smaller than or close to the HR of 0.638 when fitting the PFS data alone.

Table 3.

Parameter estimates under SPML with K = 30

	β 1		α 1		α 2
PRO	HR	95% HPD Int.	Est	95% HPD Int.	Est	95% HPD Int.
Anorexia	0.614	(0.495, 0.756)	0.365	(0.202, 0.530)	1.178	(0.449, 1.893)
Cough	0.634	(0.516, 0.777)	0.200	(0.060, 0.343)	0.608	(−0.060, 1.230)
Dyspnea	0.641	(0.522, 0.790)	0.203	(0.068, 0.343)	1.412	(0.770, 2.069)
Fatigue	0.620	(0.498, 0.765)	0.367	(0.205, 0.534)	1.437	(0.706, 2.176)
Pain	0.622	(0.502, 0.776)	0.349	(0.206, 0.489)	1.938	(1.354, 2.537)

When fitting the PFS data alone, the estimate and 95% HPD interval of exp(β₁) are 0.638 and (0.526, 0.785).

Table 4.

Parameter estimates under TML with K = 30

	β 1		α
PRO	HR	95% HPD Int.	Est	95% HPD Int.
Anorexia	0.620	(0.501, 0.760)	0.320	(0.186, 0.455)
Cough	0.636	(0.520, 0.782)	0.192	(0.064, 0.318)
Dyspnea	0.631	(0.518, 0.776)	0.223	(0.098, 0.340)
Fatigue	0.620	(0.501, 0.759)	0.343	(0.215, 0.478)
Pain	0.608	(0.491, 0.751)	0.391	(0.273, 0.515)

We used the overlapping batch statistics approach with a batch size of 2000 (Meketon and Schmeiser, 1984; and Chen et al., 2000, Section 3.3) to compute the Monte Carlo (MC) standard errors of DIC_Surv|Long, ΔDIC_Surv, LPML_Surv|Long, and ΔLPML_Surv under SPML and TML. The results are reported in Table 5. From this table, we see that (i) the MC standard errors ranged from 0.074 to 0.620 for all of DIC_Surv|Long, ΔDIC_Surv, LPML_Surv|Long, and ΔLPML_Surv, which were reasonably small compared to the magnitudes of their estimated values; and (ii) the MC standard errors of LPML_Surv|Long (GQ) and LPML_Surv|Long (MC), and ΔLPML_Surv (GQ) and ΔLPML_Surv (MC) were very close, which empirically confirmed that the proposed MC approach for estimating LPML_Surv|Long and ΔLPML_Surv were as accurate as the numerical approximation approach for computing these quantities. Table 6 shows the running times in minutes on an Intel i686 processor machine with 16 GB of RAM memory using a GNU/Linux operating system for computing ΔDIC_Surv, ΔLPML_Surv (GQ), and ΔLPML_Surv (MC) under SPML and TML with K = 30 based on an Markov chain Monte Carlo (MCMC) sample size of 20,000. From Table 6, we see that (i) the running times for computing ΔLPML_Surv (MC) were similar to those for computing ΔDIC_Surv under SPML though ΔLPML_Surv (MC) required two MCMC samples; (ii) SPML required much less running time than TML; and (iii) ΔLPML_Surv (GQ) required the most running time.

Table 5.

MC Standard Errors of DIC_Surv|Long, ADIC_Surv, LPML_Surv|Long, and ΔLPML_Surv under SPML and TML with K = 30 based on an MC sample size of 20,000

Model		Anorexia	Cough	Dyspnea	Fatigue	Pain
SPML	DICSurv|Long	0.391	0.263	0.397	0.396	0.458
	ΔDICSurv	0.530	0.444	0.535	0.534	0.581
	LPMLSurv|Long (GQ)	0.248	0.246	0.200	0.196	0.225
	LPMLSurv|Long (MC)	0.248	0.246	0.201	0.197	0.222
	ΔLPMLSurv (GQ)	0.314	0.313	0.278	0.275	0.297
	ΔLPMLSurv (MC)	0.314	0.313	0.279	0.275	0.294
TML	DICSurv|Long	0.288	0.346	0.451	0.512	0.370
	ΔDICSurv	0.460	0.498	0.576	0.624	0.515
	LPMLSurv|Long (GQ)	0.104	0.125	0.114	0.073	0.074
	LPMLSurv|Long (MC)	0.104	0.125	0.114	0.073	0.074
	ΔLPMLSurv (GQ)	0.219	0.230	0.224	0.206	0.207
	ΔLPMLSurv (MC)	0.219	0.230	0.224	0.206	0.207

Table 6.

Running Times in Minutes for Computing ΔDIC_Surv, ΔLPML_Surv (GQ), and ΔLPML_Surv (MC) under SPML and TML with K = 30 based on an MC sample size of 20,000

Model		Anorexia	Cough	Dyspnea	Fatigue	Pain
SPML	MCMC Sampling	6.0	5.9	5.8	6.3	5.9
	ΔDICSurv	16.0	14.9	18.3	17.7	16.9
	ΔLPMLSurv (GQ)	18.2	17.6	21.0	20.3	21.4
	ΔLPMLSurv (MC)	17.6	16.0	18.5	17.9	18.5
TML	MCMC Sampling	523.9	526.2	525.7	521.9	516.6
	ΔDICSurv	1142.7	1070.9	1195.1	1153.4	1245.6
	ΔLPMLSurv (GQ)	1681.2	1711.8	1704.2	1718.3	1665.4
	ΔLPMLSurv (MC)	1488.4	1494.2	1397.0	1486.3	1373.8

Finally, we computed relevant quantities under the second decomposition of DIC and LPML given in Appendix B of the supplementary material to quantify the contribution of the PFS data to the fit of the longitudinal data. The results are shown in Table 7. As mentioned earlier, the total numbers of observations for these five symptoms were different, implying that ΔDIC_Long and ΔLPML_Long were not directly comparable for the EMPHACIS data. Therefore, we consider the relative ΔDIC_Long and ΔLPML_Long defined by

$$\mathrm{R}\Delta {\mathrm{DIC}}_{\mathrm{Long}}=\frac{\Delta {\mathrm{DIC}}_{\mathrm{Long}}}{{\mathrm{DIC}}_{\mathrm{Long},\mathrm{alone}}}\times 1000$$

and

$$\mathrm{R}\Delta {\mathrm{LPML}}_{\mathrm{Long}}=\frac{\Delta {\mathrm{LPML}}_{\mathrm{Long}}}{\mid {\mathrm{LPML}}_{\mathrm{Long},\mathrm{alone}}\mid }\times 1000.$$

From Table 7, we see that pain had the largest relative improvement in terms of both RΔDIC_Long and RΔLPML_Long (MC), which were 5.00 and 6.18 under SPML and 3.52 and 4.83 under TML, and cough had the smallest relative improvement with RΔDIC_Long = 0.35 and RΔLPML_Long = 1.46 (MC) under SPML and RΔDIC_Long = 0.57 and RΔLPML_Long = 1.90 (MC) under TML. The values of RΔDIC_Long and RΔLPML_Long (MC) for anorexia, dyspnea, and fatigue, were 1.89 and 2.77, 1.89 and 3.04, and 2.91 and 3.89, respectively, under SPML; and 1.68 and 2.76, 1.09 and 2.33, and 2.26 and 3.43, respectively, under TML.

Table 7.

Decomposition II of DICs and LPMLs under SPML and TML with K = 30

Model		Anorexia	Cough	Dyspnea	Fatigue	Pain
Long alone	DICLong,alone	12017.52	12248.60	9911.66	11005.02	10867.34
	LPMLLong,alone	−6011.72	−6133.68	−4959.88	−5505.25	−5439.62
SPML	DICSurv	2019.87	2018.65	2019.26	2019.99	2022.59
	(pD[Surv])	37.28	37.32	36.94	37.06	36.42
	DICLong|Surv	11994.80	12244.31	9892.94	10973.01	10813.05
	(pD[Long|Surv])	15.17	14.95	15.70	15.10	15.94
	ΔDICLong	22.72	4.28	18.73	32.00	54.29
	RΔDICLong	1.89	0.35	1.89	2.91	5.00
	LPMLLong|Surv (GQ)	−5995.08	−6124.71	−4944.80	−5483.84	−5405.97
	LPMLLong|Surv (MC)	−5995.08	−6124.70	−4944.78	−5483.83	−5406.03
	ΔLPMLLong (GQ)	16.64	8.97	15.08	21.41	33.65
	ΔLPMLLong (MC)	16.64	8.98	15.09	21.42	33.59
	RΔLPMLLong (GQ)	2.77	1.46	3.04	3.89	6.19
	RΔLPMLLong (MC)	2.77	1.46	3.04	3.89	6.18
TML	DICSurv	2019.31	2018.87	2018.34	2019.08	2020.69
	(pD[Surv])	37.29	37.20	37.28	37.26	36.89
	DICLong|Surv	11997.34	12241.56	9900.87	10980.18	10829.05
	(pD[Long|Surv])	14.15	14.12	14.03	14.12	14.53
	ΔDICLong	20.18	7.04	10.79	24.84	38.29
	RΔDICLong	1.68	0.57	1.09	2.26	3.52
	LPMLLong|Surv (GQ)	−5995.20	−6122.07	−4948.57	−5486.61	−5413.59
	LPMLLong|Surv (MC)	−5995.11	−6122.04	−4948.30	−5486.38	−5413.33
	ΔLPMLLong (GQ)	16.51	11.61	11.30	18.64	26.03
	ΔLPMLLong (MC)	16.60	11.64	11.58	18.87	26.29
	RΔLPMLLong (GQ)	2.75	1.89	2.28	3.39	4.78
	RΔLPMLLong (MC)	2.76	1.90	2.33	3.43	4.83

5 Discussion

In this paper, we have developed two versions of the DIC and CPO decomposition as well as two sets of new criteria in Section 2 (ΔDIC_Surv, ΔLPML_Surv) and in Appendix B (ΔDIC_Long, ΔLPML_Long). The decompositions, DIC = DIC_Long + DIC_Surv|Long and LPML = LPML_Long + LPML_Surv|Long (Decomposition I), are most useful when our primary goal is to make inferences about the parameters in the survival component of the joint model while using the information from longitudinal data through the joint model. In practice, DIC_Surv|Long and LPML_Surv|Long can be used to select the survival component of the joint model and the main utility of ΔDIC_Surv and ΔLPML_Surv is to determine which longitudinal marker leads to the most gain in the fit of the survival data or which longitudinal marker is most highly associated with the survival outcome. The simulation study in Section 3 and the real data analysis in Section 4 empirically demonstrated that DIC_Surv|Long, LPML_Surv|Long, ΔDIC_Surv, and ΔLPML_Surv are quite effective and promising in selecting the survival component of the joint model and identifying the importance of longitudinal biomarkers in fitting the survival data. Decomposition II and the corresponding RΔDIC_Long and RΔLPML_Long criteria are useful when the main focus of a clinical trial is on the longitudinal markers and the primary goal is to make inferences about the parameters in the longitudinal component of the joint model while using the information from the survival data through the joint model. Similar to Decomposition I, DIC_Long|Surv and LPML_Long|Surv can be used to choose the longitudinal component of the joint model and RΔDIC_Long and RΔLPML_Long are useful to determine the gain in the fit of the longitudinal data while using the information from the survival data through the joint model.

In the AIC decomposition developed in Zhang et al. (2014), dim(φ₁) and dim(φ₂) were manually allocated to AIC_Long and AIC_Surv|Long, respectively, as the dimensions of the parameters. However, the parameters φ₁ are also involved in computing AIC_Surv|Long. Thus, the appropriateness of these dimension allocations needs to be further validated. The DIC decomposition developed in this paper automatically calculates the dimensions of the parameters, p_D[Long] and p_D[Surv|Long], in DIC_Long and DIC_Surv|Long. The real data analysis in Section 4 and the results shown in Table S2 of the supplementary material empirically demonstrated that p_D[Long] ≈ dim(φ₁) and p_D[Surv|Long] ≈ dim(φ₂). Since the DIC approximates the AIC as discussed in Spiegelhalter et al. (2002) for Gaussian posteriors (or very large samples), our empirical results based on the DIC decomposition confirm that the dimension allocations of the model parameters in the AIC decomposition are quite appropriate. Both the AIC decomposition and the DIC decomposition require the numerical approximation of an intractable integral ∫ f(y_i, t_i, θ_i|φ, δ_i, x_i, z_i)dθ_i in (2.4) for computing the joint distribution of y_i and t_i. The proposed LPML decomposition avoids the calculation of this integral. As demonstrated in both the simulation study and the real data analysis, LPML_Surv|Long and ΔLPML_Surv performed equally well as DIC_Surv|Long and ΔDIC_Surv in selecting the survival model and identifying the important longitudinal markers. In addition, as shown in Table 6, LPML_Surv|Long (MC) and ΔLPML_Surv (MC) require less computing time than LPML_Surv|Long (GQ) and ΔLPML_Surv (GQ). Thus, the LPML decomposition may be potentially more useful in practice.

In Section 2, we proposed two approaches (AGQ and MC) for computing CPO related criteria. As shown in Section 4, both approaches yielded almost identical results. However, the proposed MC method requires less computing time and is more applicable to models involving high-dimensional random effects than the AGQ approach. In Section 4, the LPML_Surv|Long's were calculated based on the CPO decomposition in (2.18) by taking φ* as the posterior mean of φ. We also calculated the LPML_Surv|Long's by taking φ* as the posterior median of φ. For the EMPHACIS Data, under SPML with K = 30, the LPML_Surv|Long's calculated based on the posterior medians were −998.95, −1008.13, −1000.64, −994.54, and −984.13 for anorexia, cough, dyspnea, fatigue, pain, respectively. These values are very close to those given in Table 2. Thus, LPML_Surv|Long is relatively robust to the choice of φ*.

Hanson et al. (2011) introduced the conditional CPO and LPML. Using our notation, the conditional CPO is defined as

$${\mathrm{CPO}}_{i,\mathrm{Surv}}^c=\int f(t_i\mid {\phi }_2,{\theta }_i,{\delta }_i,{\mathit{z}}_i)\pi (\phi ,{\theta }^R\mid D_{\mathrm{Long},\mathrm{obs}},D_{\mathrm{Surv},\mathrm{obs}}^{(-i)})d{\theta }^{R}d\phi ,$$

where $\pi (\phi ,{\theta }^R\mid D_{\mathrm{Long},\mathrm{obs}},D_{\mathrm{Surv},\mathrm{obs}}^{(-i)})$ is the joint posterior of (φ, θ^R) given D_Long,oba and $D_{\mathrm{Surv},\mathrm{obs}}^{(-i)}$ with the survival data deleted for the i^th subject. The conditional LPML in Hanson et al. (2011) is thus defined by

$${\mathrm{LPML}}_{\mathrm{Surv}}^c=\sum _{i=1}^n\log \left({\mathrm{CPO}}_{i,\mathrm{Surv}}^c\right).$$

For the purpose of assessing the fit of the survival data, ${\mathrm{CPO}}_{i,\mathrm{Surv}}^c$ and ${\mathrm{LPML}}_{\mathrm{Surv}}^c$ do correspond to CPO_i,Surv|Long and LPML_Surv|Long. However, they are not the same unless the longitudinal data are independent of the survival data. Although ${\mathrm{CPO}}_{i,\mathrm{Surv}}^c$ and ${\mathrm{LPML}}_{\mathrm{Surv}}^c$ cannot be used to assess the overall fit of the joint model or to determine the gain in the fit of the longitudinal data while using the information from the survival data through the joint model, they are quite attractive due to computational simplicity if the primary goal is to make inferences about the parameters in the survival component. We defer to a future project for further investigation of theoretical and empirical comparisons between ${\mathrm{LPML}}_{\mathrm{Surv}}^c$ and LPML_Surv|Long.

Although the proposed Bayesian criteria are developed under the joint model in Section 2, they can be easily extended to models for other types of data such as longitudinal binary/ordinal response or count data as well as other types of survival models such as cure rate models, nonproportional hazards models, and competing risks models discussed in Klein et al. (2013). Furthermore, the proposed MC method for computing CPO is applicable for a variety of Bayesian models involving random effects or latent variables. The potential applications of the proposed methodology to other types of longitudinal data such as multi-dimensional longitudinal data and more complex survival data, such as survival data in the presence of competing risks and/or semi-competing risks, are currently under investigation.

In Sections 3 and 4, we carried out all computations using the FORTRAN 95 software with double precision and IMSL subroutines. The FORTRAN 95 code is available upon request. We are currently working on a user-friendly R interface of the FORTRAN code that has been developed for this paper so that it would be available to practitioners.