Abstract
Simulation and control of a system containing compliant mechanisms such as cardiac catheters often incur high computational costs. One way to reduce the costs is to approximate the mechanisms with Pseudo-Rigid-Body Models (PRBMs). A PRBM generally consists of rigid links connected by spring-loaded revolute joints. The lengths of the rigid links and the stiffnesses of the springs are usually chosen to minimize the tip deflection differences between the PRBM and the compliant mechanism. In most applications, only the relationship between end load and tip deflection is considered. This is obviously not applicable for MRI-actuated catheters which is actuated by the coils attached to the body. This paper generalizes PRBM parameter optimization to include loading and reference points along the body.
I. Introduction
MRI-actuated catheters, proposed in [1], is a new robotic catheter for catheter ablation of atrial fibrillation. It uses MRI’s soft-tissue visualization capability for navigation and its strong magnetic field for steering. The catheter is made of a flexible tube with current-carrying coils attached to its body as shown in Fig. 1. The coils are capable of producing mutually orthogonal magnetic moments that are used to deflect the catheter under MRI’s magnetic field. Deflection is controlled by varying the currents going through the coils and calculating exactly how much current is needed to deflect the catheter to a desired position requires a good model of the catheter.
Fig. 1.
MRI-actuated catheter with two sets of actuation coils.
Pseudo-Rigid-Body Models (PRBMs) have been used to model compliant mechanisms in various applications [2]. PRBMs are useful because they reduce the degrees of freedom (DOF) of the mechanism down to a finite one. This makes simulation and control of a system containing compliant mechanisms more tractable. A PRBM often consists of rigid links joined by revolute joints. The compliance of the mechanism is represented by springs attached to the joints. The accuracy of a PRBM increases with the number of joints it has. On the other hand, high DOF leads to high computational cost. One way to reconcile the two opposing goals is to fix the DOF to a reasonable value, and optimize spring stiffnesses and link lengths so that the PRBM closely approximates the continuum model as much as possible with the limited DOF.
Previous work on PRBM parameter optimization consider tip deflection under tip loading [3]–[6]. This is not sufficient for the MRI catheter for several reasons. First, the coils actuate the catheter by creating torques on the body of the catheter. Thus, parameters optimization has to be able to take loadings along the body into account. Moreover, since the actuation torques are proportional to the cross product between the magnetic moments at the coils and MRI’s magnetic field, the orientations of the coils are essential for calculating the catheter deflections resulting from the currents sent to the coils [7]. So, the objective function of the optimization problem has to include configurations of points along the body of the mechanism as well.
This paper presents parameter optimization of a PRBM with n revolute joint under combined loading. Parameter optimization is generalized by consideration of external loads and reference points on the body of the PRBM. The optimization algorithm compares static deflections of the PRBM and the continuum model under a set of loads and chooses link lengths and spring stiffnesses that minimize the difference between the two models. The continuum model used as the reference model is presented in [8], [9].
The optimization problem is difficult to solve for several reasons. First, there are many local minima because the relationship between PRBM parameters and the resulting deflections is nonlinear. Moreover, the dimension of the problem is relatively large. Each new link introduces one link length and at least one spring stiffness. Finally, objective function evaluation takes a long time because solving for many static deflections is required. To address these problems we use Particle Swarm Optimization (PSO) to overcome non-convexity of the problem. We sidestep the other two problems by breaking the optimization down into subproblems. This helps keeping PSO focus its computation effort on a more relevant subspace as the dimension of the problem grows.
The rest of the paper is organized as follows. Parameter optimization algorithm is described in Section II. Parameter optimization of the MRI catheter is presented in Section III. Conclusions are presented in Section IV.
II. Parameter Optimization Algorithm
Parameter optimization of a PRBM consists of two parts. First, static deflections of the PRBM under different external loads are calculated. Then the optimization algorithm compares the configurations of the PRBM with those of the continuum model under the same loads and makes adjustments to the parameters of the former. Calculation of static deflections under given external loads is described in Section II-A. The optimization problem is formulated in Section II-B. Finally, the optimization algorithm is presented in Section II-C.
A. Static Configuration Calculation
A static deflection occurs when the joint torques from the load equal to the internal joint torques from the springs, namely,
| (1) |
The stiffness matrix K ∈ ℝn×n is a diagonal matrix with spring stiffness coefficients as its diagonal elements. The joint angle vector θ ∈ ℝn specifies how much each of the catheter’s n joints bends. The manipulator Jacobian Ji(θ) ∈ ℝ6×n associated with the coordinate frame of the external load is written in the body frame [10]. The external load is a wrench Fi ∈ ℝ6 that consists of a force fi ∈ ℝ3 and a joint torque τi ∈ ℝ3. Joint angles that satisfy this condition can be calculated by solving (1) iteratively.
B. Problem Formulation
The optimization algorithm adjusts link lengths and spring stiffnesses of the PRBM such that its static deflections match those of the continuum model under the same set of external loads. The closeness of the two models are determined from the configurations of a set of reference points on the two models. The parameter optimization problem is given by, min
| (2a) |
| (2b) |
| (2c) |
| (2d) |
The inner summation sums over all reference points, q ∈ 𝒬, where |𝒬| denotes the number of reference points. Each term inside the summation consists of xhij ∈ ℝ3 and uhij ∈ ℝ3, which are the position and orientation of the coordinate frame attached to the reference point qj on the PRBM subjected to external load Fi ∈ ℱh applied at loading point ph. Similarly, x̂hij and ûhij are the position and the orientation of the corresponding point from the reference model subjected to the same load. The positions, xhij and x̂hij, are made dimensionless by normalizing them with the length of the catheter. The orientations, uhij and ûhij, are unit vectors tangent to the body of the catheter at the reference point.
The weights, denoted by αi and βi specify the relative importance of the position and the orientation of the ith reference point. The next summation sums over all external loads, F ∈ ℱh, at the hth loading point, where |ℱh| denotes the number of external loads. The outermost summation in the objective function sums over all loading points, p ∈ 𝒫, where |𝒫| denotes the number of such points.
The objective function (2a) is the cumulative weighted sum of the orientation errors and the position errors of the reference points under all external loads at all loading points. The optimization is performed over normalized link lengths and spring stiffnesses denoted by r ∈ ℝn+1 and k ∈ ℝn. The lengths and stiffnesses are bounded from above and below by (2b) and (2c) to limit the search in a reasonable region. Finally, The sum of the lengths must also be equal to the total length as specified by the constraint (2d).
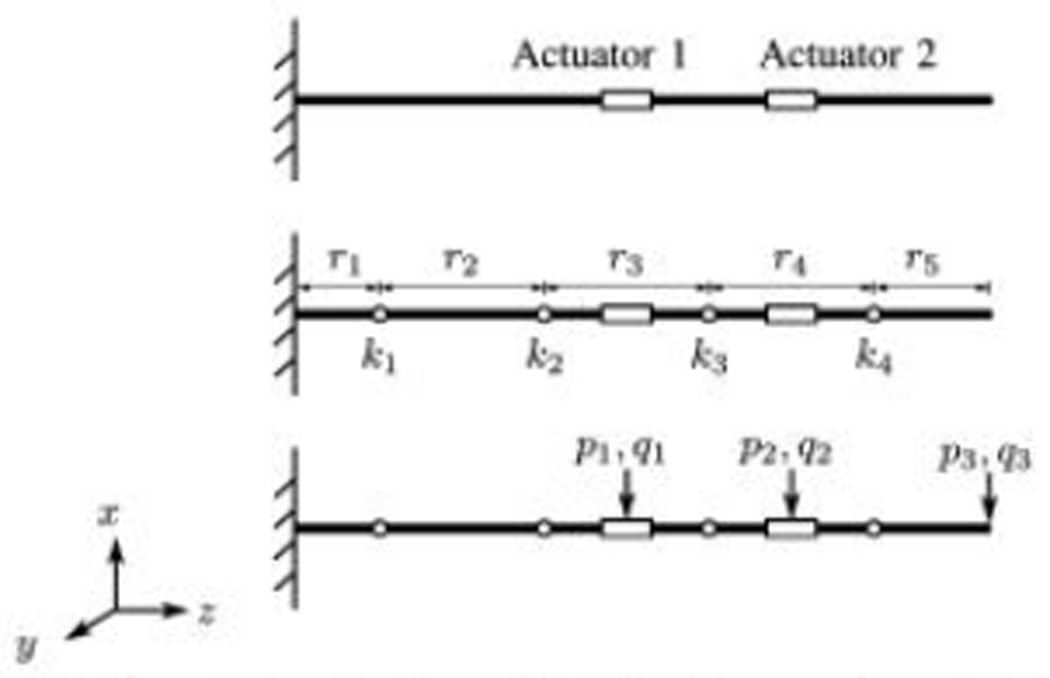
As a concrete example of (2), consider a catheter and its PRBM is illustrated in Fig. 2. Since we wish to match the positions and orientations of the coils and the tip, the reference points, 𝒬 = {q1, q2, q3}, are placed at the two coils and the tip, respectively. The loading points, 𝒫 = {p1, p2, p3}, are also located at the two coils and the tip. The loadings ℱ1 and ℱ2 at p1 and p2 represent the actuations and the weights of the coils. The loading ℱ3 at p3 represents the contact force the catheter will experience during ablation. We wish to determine the lengths [r1, r2, r3, r4, r5] and [k1, k2, k3, k4] that minimize the position and angular errors of all reference points in q ∈ 𝒬 when the catheter is subjected to all wrenches F ∈ ℱh at all loading points ph ∈ 𝒫.
Algorithm 1.
Parameter optimization
Fig. 2.
The catheter (top) and its PRBM approximation (middle) with the external loads (bottom).
C. Optimization Algorithm
Since the optimization problem is non-convex, a global optimization such as Particle Swarm Optimization (PSO) is chosen. PSO maintains a set of particles that is updated every iteration. Each particle maintains its personal best and its current velocity. The particles interact with one another by changing its velocity towards its personal best as well as the global best [11].
It is possible to attempt to solve the problem described in (2) directly. However, solving the optimization problem for all of the parameters simultaneously using all possible loads and their effects on all reference points can be computationally expensive. To alleviate the problem, the optimization problem is decomposed into subproblems in which the solutions of the previously solved subproblems are used to initialize the latter ones.
The optimization problem is decomposed as follows. First, only the first reference point and the loading points between the base and the first reference point is considered. In the next subproblem, one reference point and the loading points between the base and the new reference point are considered. The solution of the first subproblem is used to setup appropriate bounds on the lengths and stiffnesses of the new subproblem. The last subproblem eventually contains all original loading and reference points and its objective function is the same as the original problems, but its bounds on the lengths and the stiffnesses are much tighter, which allow the particles to be distributed more efficiently. The optimization algorithm is summarized in Algorithm 1.
For example, consider the PRBM depicted in Fig. 2. First, only q1 and the loadings at p1 are considered. The solution to this first subproblem is r1, r2, k1, and k2. In the second subproblem, q1 and q2, and the loadings at p1 and p2 are considered. The solution from the first subproblem is used to setup the bounds for this subproblem. Finally, all reference and loading points are considered in the third subproblems.
III. Parameter Optimization a PRBM of MRI-Actuated Catheters
This section presents parameter optimization of the PRBM for MRI-actuated catheter depicted in Fig. 2. Since the catheter has two sets of coils, a PRBM with four joints is chosen. The first three joints from the base of the catheter give the PRBM enough degrees of freedom to deflect when the coils are energized. The last joint represents the compliance of the catheter when in contact with a surface. The external loads include the torques and the weight of the coils, and forces exerted to the tip. While real data is more desirable, the continuum model gives more flexibility in terms of the ability to generate a richer data set for parameter identification. The parameters of the continuum model are listed in Table I [8].
TABLE I.
Catheter parameters
| Parameter | Value |
|---|---|
| Young’s modulus (MPa) | 350 |
| Poisson’s ratio | 0.3 |
| Inner radius (mm) | 0.45 |
| Outer radius (mm) | 0.50 |
| Total length (mm) | 60.0 |
| Location of coils 1 (mm) | 22.5 |
| Location of coils 2 (mm) | 37.5 |
| Coil weight (g) | 1.0 |
Since the catheter is axially symmetric, parameter optimization is performed only in the xz-plane. So, only forces in the xz-plane and the torques along the y-axis are considered in the optimization. The result are validated in a 3-dimensional setting afterwards.
The optimization problem is decomposed into three subproblems. The first subproblem concerns the first coil set and its effects on the orientation and the position of the coil set itself. That is, [r1, r2], [k1, k2] are calculated from the loading at the first coil set with the reference point on the coil. The forces and moments applied at the first coil set, denoted by f1x and τ1y, are listed in Table II. The weights in the objective function are α = 1.0 and β = 1.0.
TABLE II.
External loads used to optimize the parameters
| Load | Min | Max | Increment |
|---|---|---|---|
| f1x (N) | 3 × 10−3 | 15 × 10−3 | 3 × 10−3 |
| τ1y (Nmm) | 1 × 10−1 | 5 × 10−1 | 1 × 10−1 |
| f2x (N) | 3 × 10−3 | 15 × 10−3 | 3 × 10−3 |
| τ2y (Nmm) | 1 × 10−1 | 5 × 10−1 | 1 × 10−1 |
| f3x (N) | 5 × 10−3 | 9 × 10−3 | 1 × 10−3 |
| f3z (N) | 5 × 10−3 | 9 × 10−3 | 1 × 10−3 |
The parameters calculated from the first subproblem are then used in solving the second subproblem concerning the second coil set and [r1, r2, r3] and [k1, k2, k3]. The forces and moments of the second coil set, denoted by f2x and τ2y, are listed in Table II. The weights in the objective function are α = [0.0, 1.0] and β = [1.0, 1.0]. The position of the first coil set is dropped from the objective function (first element of α) to focus on optimizing the position and the orientation of the second coil set.
The last subproblem concerns tip deflection under bending and axial loads, with [r1, r2, r3, r4] and [k1, k2, k3, k4]. Bending and axial forces, denoted by f3x and f3z, are listed in Table II. To prevent buckling, a constant f3x = 1 × 10−3 N is applied in addition to f3z during optimization. The weights in the objective function are α = [0.0, 0.0, 1.0] and β = [1.0, 1.0, 1.0]. For this subproblem, the positions of both actuators are dropped. Note that while there are five links, only four of them are considered explicitly. This is because the constraint (2d) reduces the degrees-of-freedom of link lengths by one.
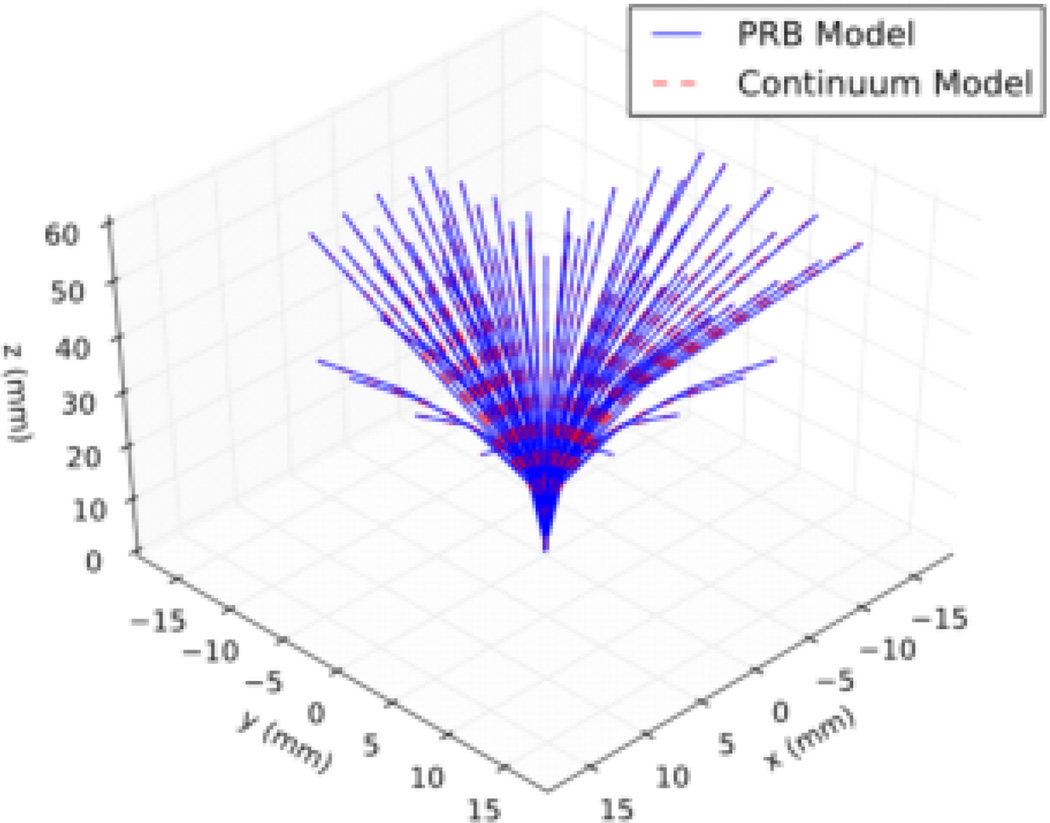
The parameters calculated from the three subproblems are listed in Table III. The results are validated using a set of external loads listed in Table IV. The RMS errors of the positions and the orientations of the reference points subjected to different external loads are listed in Table V. The position errors are the distance between the reference point on the continuum model and the PRBM subjected to the same load. The errors are then averaged over the range of loading as in Table IV. The average errors of the orientation are calculated in a similar manner using the orientation of the reference points. The results show that the PRBM closely approximates the continuum model with maximum errors of 2.81 × 10−1 and 2.25 × 10−1 rad for the orientations of the two coils, and 3.55 ×10−3 mm for the position of the tip. The deflections of the continuum model and PRBM under the external loads are compared in Fig. 3.
TABLE III.
PRBM optimal parameters
| Parameter | Value |
|---|---|
| r (Normalized) | [0.01655, 0.2181, 0.2893, 0.2455, 0.2306] |
| k (rad/Nmm) | [8.884, 3.659, 3.996, 2.701] |
TABLE IV.
External loads used in validating the results
| Load | Min | Max | Increment |
|---|---|---|---|
| f1x (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| f1y (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| τ1x (Nmm) | 0.5 × 10−1 | 3.5 × 10−1 | 1.0 × 10−1 |
| τ1y (Nmm) | 0.5 × 10−1 | 3.5 × 10−1 | 1.0 × 10−1 |
| f2x (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| f2y (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| τ2x (Nmm) | 0.5 × 10−1 | 3.5 × 10−1 | 1.0 × 10−1 |
| τ2y (Nmm) | 0.5 × 10−1 | 3.5 × 10−1 | 1.0 × 10−1 |
| f3x (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| f3y (N) | 4.5 × 10−3 | 10.5 × 10−3 | 3 × 10−3 |
| f3z (N) | −4.5 × 10−3 | −10.5 × 10−3 | 3 × 10−3 |
TABLE V.
RMS of position and orientation errors of the actuators and the catheter tip.
| RMS Error | Max Error | |
|---|---|---|
| Actuator 1 Position (mm) | 2.65 × 10−3 | 6.34 × 10−3 |
| Actuator 1 Angle (rad) | 3.41 × 10−3 | 2.81 × 10−1 |
| Actuator 2 Position (mm) | 2.17 × 10−3 | 5.89 × 10−3 |
| Actuator 2 Angle (rad) | 4.47 × 10−3 | 2.25 × 10−1 |
| Tip Position (mm) | 9.79 × 10−4 | 3.55 × 10−3 |
| Tip Angle (rad) | 1.45 × 10−3 | 4.43 × 10−2 |
Fig. 3.
Deflection of the PRBM and the continuum model under torques applied to actuator 1 and 2, and bending forces applied at the tip. The magnitude of the torques and forces are the same as in Table IV, but the directions are altered so that the catheter bends in different quadrants under different loads.
IV. Conclusions
A general method for parameter optimization of a PRBM is presented in this paper. The method extends the current PRBM parameter optimization by including external loads and reference points along the body. The optimization is simplified by solving subproblems sequentially. Particle Swarm Optimization is used in the optimization procedure. Simulation results are presented. The results demonstrate that the PRBM successfully approximates the continuum catheter model.
Acknowledgments
This work was supported in part by the National Science Foundation under grant CISE IIS-1524363, and National Institutes of Health under grant R01EB018108.
References
- 1.Gudino N, Heilman JA, Derakhshan JJ, Sunshine JL, Duerk JL, Griswold MA. Control of intravascular catheters using an array of active steering coils. Medical Physics. 2011;38(7):4215–4224. doi: 10.1118/1.3600693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Howell LL, Magleby SP, Olsen BM. Handbook of compliant mechanisms. Wiley Online Library; 2013. [Google Scholar]
- 3.Su H-J. A Pseudorigid-Body 3R Model for Determining Large Deflection of Cantilever Beams Subject to Tip Loads. Journal of Mechanisms and Robotics. 2009;1(2) [Google Scholar]
- 4.Chen G, Xiong B, Huang X. Finding the optimal characteristic parameters for 3R pseudo-rigid-body model using an improved particle swarm optimizer. Precision Engineering. 2011;35:505–511. [Google Scholar]
- 5.Khoshnam M, Patel RV. Robotics and Automation (ICRA), 2013 IEEE International Conference on. IEEE; 2013. May, A pseudo-rigid-body 3R model for a steerable ablation catheter; pp. 4427–4432. [Google Scholar]
- 6.Venkiteswaran VK, Su H-J. A parameter optimization framework for determining the pseudo-rigid-body model of cantilever-beams. Precision Engineering. 2014 [Google Scholar]
- 7.Greigarn T, Cavusoglu MC. Pseudo-Rigid-Body Model and Kinematic Analysis of MRI-Actuated Catheters; Robotics and Automation (ICRA), 2015 IEEE International Conference on; [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu T, Cavusoglu MC. Robotics and Automation (ICRA), 2014 IEEE International Conference on. Hong Kong, China: IEEE; 2014. Three Dimensional Modeling of an MRI Actuated Steerable Catheter System. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu T, Lombard Poirot N, Franson D, Seiberlich N, Griswold M, Cavusoglu M. Modeling and Validation of the Three Dimensional Deflection of an MRI-Compatible Magnetically-Actuated Steerable Catheter. 2015 doi: 10.1109/TBME.2015.2510743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murray RM, Li Z, Sastry SS, Sastry SS. A Mathematical Introduction to Robotic Manipulation. 1st. CRC Press: 1994. Mar, [Google Scholar]
- 11.Chong EKP, Zak SH. An introduction to optimization. John Wiley & Sons; 2008. [Google Scholar]