Inferring Recent Demography from Isolation by Distance of Long Shared Sequence Blocks

Abstract

Recently it has become feasible to detect long blocks of nearly identical sequence shared between pairs of genomes. These identity-by-descent (IBD) blocks are direct traces of recent coalescence events and, as such, contain ample signal to infer recent demography. Here, we examine sharing of such blocks in two-dimensional populations with local migration. Using a diffusion approximation to trace genetic ancestry, we derive analytical formulas for patterns of isolation by distance of IBD blocks, which can also incorporate recent population density changes. We introduce an inference scheme that uses a composite-likelihood approach to fit these formulas. We then extensively evaluate our theory and inference method on a range of scenarios using simulated data. We first validate the diffusion approximation by showing that the theoretical results closely match the simulated block-sharing patterns. We then demonstrate that our inference scheme can accurately and robustly infer dispersal rate and effective density, as well as bounds on recent dynamics of population density. To demonstrate an application, we use our estimation scheme to explore the fit of a diffusion model to Eastern European samples in the Population Reference Sample data set. We show that ancestry diffusing with a rate of $\sigma \approx 50--100\hspace{0.5em}\text{km}/\sqrt{\text{gen}}$ during the last centuries, combined with accelerating population growth, can explain the observed exponential decay of block sharing with increasing pairwise sample distance.

THERE has been a long-standing interest in estimating demography, as migration and population density are key parameters for studying evolution and ecology. Demographic models are essential for disentangling the effects of neutral evolution from selection, and are crucial to understanding local adaptation. Moreover, the inference of demographic parameters is important for conservation and breeding management. Given the intensive nature of obtaining such parameters by direct observations, which are moreover necessarily limited to short timescales, the increasing availability of genetic markers has spurred efforts to develop inference methods based on genetic data.

This work focuses on estimating dispersal rate and population density in two-dimensional habitats by analyzing the geographic distribution of so-called identity-by-descent (IBD) blocks, which are commonly defined as co-inherited segments delimited by recombination events (see Figure 1). It has now become feasible to detect long regions of exceptional pairwise similarities from dense SNP or whole genome sequences (Gusev et al. 2009; Browning and Browning 2011). For regions longer than a few cM, the bulk mostly consists of a single IBD block unbroken by recombination, at least when inbreeding is rare (Chiang et al. 2016). This yields novel opportunities for inferring recent demography, as one can study the direct traces of coancestry.

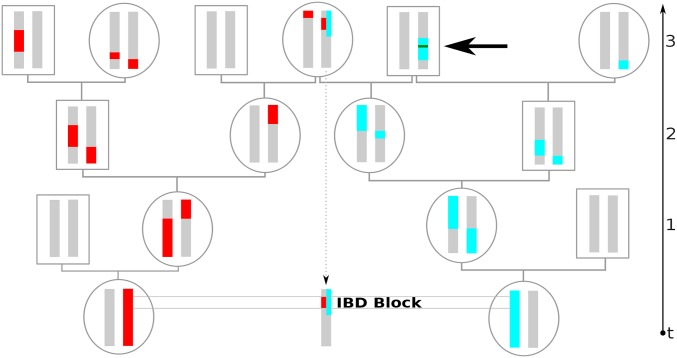
Figure 1.

Example of an IBD block co-inherited from a common ancestor three generations back. Going back in time, recombination splits up genetic ancestry (colored red and blue here) into blocks distributed among ancestors. If, as depicted here, such ancestral blocks overlap in a recent common ancestor, the intersecting stretch of the genome will be shared and both individuals will carry few distinguishing mutations. Here, we define IBD blocks to be delimited by any recombination events on the genealogical path to the most recent common ancestor. Thus, the recombination events that are fused again quickly by inbreeding loops, as depicted by the blue chromosome (thick arrow), also delimit IBD blocks. However, this recombination is not detectable in practice, and the two adjacent IBD blocks would be identified as one long IBD segment.

Moreover, the length of shared blocks contains information about their age. That is, the longer the time to the most recent common ancestor, the shorter the expected IBD length, as recombination has more chances to break up ancestral genetic material. The probability that no recombination occurs in a block of a given map length decays exponentially, going back in time. Hence, long IBD blocks originate mostly from very recent coancestry and provide insight into the recent history of a population. Shared long blocks between pairs of populations can be used to infer the distribution of recent coalescence times (Ralph and Coop 2013), and fitting deme and island models can yield information on recent population sizes (Palamara et al. 2012; Browning and Browning 2015) and migration patterns (Palamara and Pe’er 2013). These works are complementary to the analysis of short identical segments, which are informative about deeper timescales (Li and Durbin 2011; Harris and Nielsen 2013), and they showcase the utility of long IBD blocks for inferring recent demography.

Here, we focus on a pattern of isolation by distance of IBD blocks within populations extended in two dimensions with local migration. For such populations, the classical Wright–Malécot formula describes an increase of mean pairwise genetic diversity with increasing geographic separation (Wright 1943; Malécot 1948). Several inference methods use such classical isolation by distance patterns as signals to infer the parameters of recent demography. For example, fitting increasing pairwise genetic diversity with geographic distance is widely used (Rousset 1997, 2000; Vekemans and Hardy 2004), and approximate-Bayesian-computation methods have been applied (Joseph et al. 2016). Similarly, the extent of geographic clustering of rare frequency alleles can be used as a signal for inference (Novembre and Slatkin 2009). While the signal of locally decreased pairwise genetic diversity mostly stems from recent times (Leblois et al. 2004), such patterns can be severely confounded by deeper, often unknown, ancestral patterns (Meirmans 2012). Moreover, such methods can usually only infer the neighborhood size $4\pi D_e{\sigma }^2,$ which is proportional to the product of dispersal rate ${\sigma }^2$ with effective density $D_e.$ Usually, these important parameters cannot be estimated separately, as the underlying signal is mostly based on a short-term equilibrium between local drift and dispersal. An exception is quickly mutating organisms such as viruses, for which phylogeographic diffusion approaches yield separate estimates of σ (Lemey et al. 2010). However, the mutation rates are usually too low to provide significant additional information on recent demography (Barton et al. 2013). In summary, inference schemes based on pairwise genetic diversity suffer from several fundamental limitations.

To overcome these problems, this work builds upon the ideas of Barton et al. (2013), who observed that the analysis of long shared IBD blocks would, in principle, allow one to estimate dispersal and population density separately. They argued that such an inference scheme would be robust to confounding by ancestral structure, since long IBD blocks mostly originate from not long ago. Here, we introduce a practical inference scheme based on this idea. We first expand the theoretical results of Barton et al. (2013). We use a model of spatial diffusion of ancestry, which yields analytical formulas for block-sharing patterns. We then fit these results using a composite-likelihood framework, similar to Ralph and Coop (2013). This approach allows one to readily include error estimates for block detection, such as limited detection power or wrongly inferred block lengths, which are problems that usually arise when IBD segments are called from genotype data (Browning and Browning 2012; Ralph and Coop 2013). Recently, Baharian et al. (2016) independently derived similar equations for block sharing under the diffusion approximation and used them for demographic inference by fitting binned data. We extend this work in several ways. We additionally deal with growing and declining populations, and our composite-likelihood method offers several significant advantages over fitting binned data. Importantly, as a major part of this article, we extensively evaluate our estimation scheme on simulated data. We test its power to recover demographic parameters for several geographic models and we investigate how model deviations, such as nearby habitat boundaries, affect inference. This yields valuable novel insight into the validity of the underlying idealized diffusion model and examines the scope of the inference scheme.

Currently, large IBD block data sets are available, mainly for humans. To showcase a practical application of our inference scheme, we use it on a subset of the Population Reference Sample (POPRES) data set, which Ralph and Coop (2013) previously analyzed for long IBD blocks. Although human demography is without doubt very complex, the diffusion model provides a good fit to the data, which allows us to draw conclusions about the extent of human ancestry spread in continental Europe during the last centuries. We also infer a rapidly increasing population density, which stresses the importance of accounting for rapid population growth when analyzing human IBD sharing.

Methods

The model

To describe block sharing in two spatial dimensions with local migration, we use two basic model assumptions to approximate a wide range of scenarios. Obviously, the true demographic history of a population is more complex than any such simple model. Thus, the aim is not to have a mathematically rigorous model, which is often formally problematic (Felsenstein 1975; Nagylaki 1978) and only holds exactly in specific settings, but to have an accurate approximation that captures general patterns that can be used for robust inference of basic demographic parameters. In the following, we outline these two central modeling assumptions.

Poisson recombination:

We approximate recombination as a homogeneous Poisson process, i.e., crossover events are assumed to occur at a uniform rate along a chromosome. Throughout this work, the unit of genetic distance will therefore be the Morgan, which is defined as the distance over which the expected average number of intervening chromosomal crossovers in a single generation is one. Small-scale processes, such as gene conversion, are not captured by the Poisson approximation, but for the large genomic scales of typically several cM considered here this can be neglected (Lynch et al. 2014). Similarly, we ignore the effect of interference, which is reasonable when describing the effects of recombination over several generations. Since the female and male recombination rate can be markedly different, for our purposes we use the sex-averaged rate $r=r_{\mathrm{m}}+r_{\mathrm{f}}/2.$ In every generation, loci on autosomes have an equal chance to trace back to a female or male ancestor. Thus, the female and male Poisson processes together are described by a single Poisson process with the averaged recombination rate. Generalizing this line of thought, any individual differences in map length can be modeled by a single Poisson process with the population-averaged rate.

Diffusion approximation:

Following a long tradition of modeling individual movement in space with diffusion (Fisher 1937; Wright 1943; Malécot 1948; Nagylaki 1978), we approximate the spatial movement of genetic material back in time using a diffusion process. The position of ancestral material at some time t in the past is the sum of the migration events until then, which are often correlated only on small timescales. Therefore, using the central-limit theorem, the probability density for the displacement of a lineage can be approximated using a Gaussian distribution with axial variance of ${\sigma }^{2}t$ (Figure 2). This approximation does not depend on details of the single-generation dispersal kernel, provided its variance is finite. It seems plausible that diffusion of ancestry is often an accurate approximation on recent to intermediate timescales (Barton et al. 2002), which are important for the sharing of long IBD blocks.

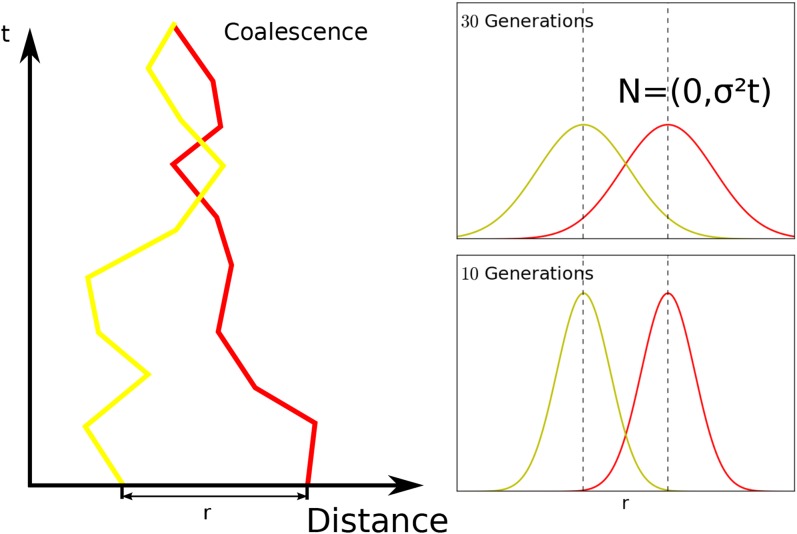
Figure 2.

Diffusion model visualized in one spatial dimension. Our model is in fact two dimensional, but is qualitatively similar. Left panel: One realization of the movement of ancestry of two homologous loci initially separated by distance r. In our model, there is a chance that they coalesce every time they come close, which is indirectly proportional to the local effective density parameter $D_e$ (see Appendix A). Right panel: In our model, the probability density function of having moved distance $\Delta x$ at time t generations back spreads out as a Gaussian distribution $N\left(0,{\sigma }^{2}t\right)$ with linearly increasing variance of ${\sigma }^{2}t.$

If consecutive single-generation dispersal events are uncorrelated, ${\sigma }^2$ is the average squared axial parent-offspring distance (Rousset 1997). Even with small-scale spatial or temporal correlations between dispersal events, one can model the spread of ancestry using the diffusion approximation (Robledo-Arnuncio and Rousset 2010). In this case, ${\sigma }^2$ has to be interpreted as a parameter that describes the rate of the spread of ancestry back in time (Barton et al. 2002), which can differ markedly from the single-generation squared axial parent-offspring distance.

Here, we will need to describe the chance that pairs of lineages of homologous loci come into close proximity. For this, we assume that the two lineages diffuse independently. In this case, the sum of their movements can be described using a two-dimensional Gaussian distribution with twice the variance of a single lineage. The probability density that two lineages that were initially separated by $\left(x_0,y_0\right)$ have a pairwise distance of zero along each axis at time t, or equivalently, that the sum of the movements is $\left(-x_0,-y_0\right),$ is therefore:

$$\frac{1}{4\pi t{\sigma }^2}\exp \left(-\frac{x_0^2+y_0^2}{4t{\sigma }^2}\right)=\frac{1}{4\pi t{\sigma }^2}\exp \left(-\frac{r^2}{4t{\sigma }^2}\right),$$ (1)

where $r=\sqrt{x_0^2+y_0^2}$ is defined as the initial Euclidean distance between the two lineages.

This ignores the fact that once coalesced, lineages remain at a pairwise distance of zero. Wilkins (2004) gave recursions and approximate formulas (formulas A15 and A17) that account for this interference of lineages in two spatial dimensions. They show that complex interference terms can be neglected as long as previous coalescence is sufficiently rare. Thus, for describing the chance of pairwise coalescence in the relatively recent past, Equation 1 usually represents an accurate approximation, particularly for well-separated samples. Other causes of correlations of movements are often of local geographic nature, as in the cases of density fluctuations or local barriers. Such small-scale heterogeneities often average out when viewed on larger scales, and the approximation that lineages move independently remains accurate on these scales (Barton et al. 2002).

IBD sharing in the model

Using similar assumptions, Barton et al. (2013) calculated the probability that two individuals a certain distance apart share an IBD block longer than a minimum length starting from a specified locus. For this specific purpose they could directly apply the Wright–Malécot formula by replacing mutation with recombination. For practical inference from IBD blocks, more general formulas describing the total number of shared blocks of a specific length L are advantageous. In this section, we derive such equations.

IBD blocks of age t:

Following Ralph and Coop (2013), we first partition $N_L,$ the number of shared blocks of map length L for a given pair of samples, into $N_L^t,$ the number of blocks coalescing at time t:

$$E\left[N_L\right]={\displaystyle {\int }_0^{\mathrm{\infty }}E\left[N_L^t\right]dt}.$$ (2)

Throughout this article, such terms are always understood as a density with respect to block length and time. Following the ancestry of two chromosomes back in time, a change of genealogy only occurs when there is a recombination event somewhere along the lineage. Between these discrete jumps, genetic material can be traced as a single locus. This allows us to further split $E\left[N_L^t\right]$ into the product of the expected number of blocks of length L obtained by splitting the two chromosomes according to the Poisson recombination over time t with the probability that a single locus coalesces time t ago. We denote the first factor by $E\left[K_L^t\right],$ and the second factor, commonly known as the coalescence time distribution, by $\psi \left(t\right):$

$$E\left[N_L^t\right]=E\left[K_L^t\right]\psi \left(t\right).$$ (3)

Number of candidate blocks:

Under our model assumptions, the position of all recombination events on two independent chromosomes traced back until time t is given by a Poisson process with rate $2t.$ The expected number of all block pairs overlapping at an intersection length L can then be calculated as follows. A recombination event occurs in a small region of map length $\Delta L$ with a probability of $2t\Delta L,$ and the probability that a region of length L does not recombine follows the exponential distribution $\exp \left(-2Lt\right).$ For chromosomes of map length G, summing the possible start sites yields the expected total number of blocks of length L:

$$E\left[K_L^t\right]=2\cdot 2t\exp \left(-2Lt\right)+\left(G-L\right)4t^2\exp \left(-2Lt\right),$$ (4)

where the first term describes the blocks starting at either edge and the second term the fully interior blocks, which require two delimiting recombinations. Neglecting the effects of chromosome edges $\left(G\gg L\right),$ this is approximated by:

$$E\left[K_L^t\right]\approx G4t^2\exp \left(-2Lt\right).$$ (5)

We will use Equation 5 to derive an approximate formula for capturing the qualitative behavior of mean IBD sharing. The slightly more complex result, including edge effects used for inference, is derived analogously (see Appendix B).

Single locus coalescence probabilities:

The probability $\psi \left(t\right)$ that two homologous loci have their last common ancestor time t ago depends on their pairwise sample distance r and the parameters of the demographic model. We can follow Barton et al. (2002) and approximate the probability of a recent coalescence as the product of the probability of the pairwise sample distance being zero (Equation 1) and a rate of local coalescence which, following Barton et al. (2013), we shall denote by $1/2D_e.$ In Appendix A, we justify this approximation and give a formal definition of this so-called effective density $D_e.$ To describe a globally growing or declining population, which is particularly important for the human case studied in this article, we let $D_e$ depend on time t. Together, this yields:

$$\psi \left(t\right)=\frac{1}{2D_e\left(t\right)}\frac{1}{4\pi t{\sigma }^2}\exp \left(-\frac{r^2}{4t{\sigma }^2}\right).$$ (6)

Full formula:

Substituting Equations 5 and 6 into Equation 3 gives:

$$E\left[N_L^t\right]=\frac{Gt}{2D_e\left(t\right)\pi {\sigma }^2}\exp \left(-\frac{r^2}{4t{\sigma }^2}-2Lt\right).$$ (7)

To determine the total number of expected shared blocks, we have to integrate all possible coalescence times t. For the class of power density functions, where

$$D_e\left(t\right)=D{t}^{-\beta }D>0,\beta \in \mathrm{ℝ},$$ (8)

the integral yields explicit formulas. The important case of $\beta =0$ models a constant population density, while $\beta >0$ and $\beta <0$ describe populations with a growing or declining density, respectively. With $\beta >0,$ the density approaches infinity for $t=0,$ which corresponds to a negligible chance of coalescence in the present. However, since we effectively fit block sharing on intermediate timescales (see Figure 9), this obvious problem of the model is not very limiting in practice. This class of functions has been used to fit human demographic growth (Von Foerster et al. 1960). Importantly, linear combinations of such terms can be used to build more complex density functions, including polynomials for the special case $\beta \in \mathrm{\mathbb{N},}$ which then also yield analytical formulas.

Figure 9.

Left panel: Age of shared IBD blocks. Density of blocks of certain length originating t generations ago, as calculated from the $1/T$ population density growth model with best fit parameters. Most of the signal is predicted to have arisen within the last 50 generations (green line). Block sharing would have been more recent assuming a constant population density. Right panel: Distribution of block lengths used in our analysis of empirical human data. Pw: Pairwise.

Performing the integral of Equation 2 gives the main result:

$$E\left[N_L\right]=2^{\frac{-3\beta }{2}-3}\frac{G}{\pi D{\sigma }^2}{\left(\frac{r}{\sqrt{L}\sigma }\right)}^{2+\beta }{K}_{2+\beta }\left(\sqrt{2L}\frac{r}{\sigma }\right).$$ (9)

Integrating this formula with respect to the block length gives the expected number of shared blocks longer than the threshold length $L_0:$

$$\begin{array}{c}E\left[N_{>L_0}\right]={\displaystyle {\int }_{L_0}^{\mathrm{\infty }}E\left[N_L\right]dL}=\\ 2^{\frac{-5-3\beta }{2}}\frac{G}{\pi D{\sigma }^2}{\left(\frac{r}{\sqrt{L_0}\sigma }\right)}^{1+\beta }{K}_{1+\beta }\left(\sqrt{2L_0}\frac{r}{\sigma }\right),\end{array}$$ (10)

where $K_{\gamma }$ denotes the modified Bessel function of the second kind of degree γ (Abramowitz and Stegun 1964). We analyze Equations 9 and 10 qualitatively in the Discussion section, and Figure 3 depicts their accuracy on simulated data.

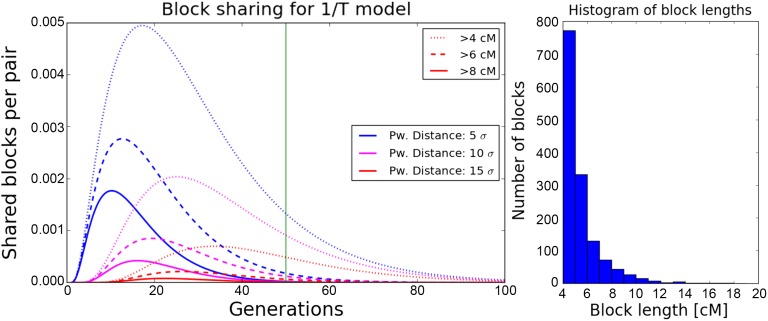
Figure 3.

Simulated IBD block sharing compared with theoretical expectations. We show values normalized to give rates per pair and cM. Theoretical expectations are calculated for each length bin using Equation 10. For the five models described in the Methods section, we kept the population density constant at $D_e=1,$ with a dispersal rate of $\sigma =2$ on a torus of size 180, and simulated IBD sharing between 150-cM chromosomes spread out on a subgrid with nodes two distance units apart. (For a full set of specific simulation parameters, see File S1.) For every model, we ran 20 replicate simulations. Distances are measured in dispersal units $\left(\text{so that}\sigma =1\right)$ and error bars depict the estimated SDs for each bin among the 20 runs to visualize the uncertainty of the estimates.•’s are spread out for better visualization around their original positions (middle •).

For a widely used functional form of population-density change, an exponential growth with rate β, the integral converges only for blocks of length $2L>\beta .$ Otherwise, the exponential rate at which the long blocks are broken up is slower than the exponentially increasing chance of local coalescence, and the expected number of blocks does not vanish for large t. However, we can approximate exponential growth on intermediate timescales by approximating it by using the standard Taylor expansion up to a certain term, and then using our results for the power density functions. Again, this effectively fits a population density up to the intermediate timescales, where the Taylor approximation is accurate, while circumventing the pathological behavior of the distant past.

Inference scheme

To learn about recent demography, we fit the observed block sharing between a set of samples to Equation 9. Here, we use a likelihood method in which we approximate the likelihood function $f:\theta \to \mathrm{Pr}\left(x|\theta \right)$ of the observed data x for a given set of parameters θ (σ, D, β) with a composite likelihood $\stackrel{\sim }{f}\left(\theta \right).$ This allows us to estimate the approximate standard deviations and confidence intervals from the empirical Fisher information matrix. One can use standard numerical optimization techniques to find the maximum likelihood estimates ${\widehat{\theta }}_{\text{MLE}}.$ In our analysis we use the Nelder–Mead method, as implemented in the class GenericLikelihoodModel of the Python package statsmodels, which proved to be numerically robust and quick.

Poisson model:

We can construct an approximate likelihood of observed block sharing by using an approach that follows Ralph and Coop (2013). First, for every pair of samples, we bin block sharing with respect to shared block length into small length bins. Then, we model the number of shared blocks within each of these bins as independent Poisson distributions around expected rates ${\lambda }_i,$ which, for a small enough bin $\left[L_i,L_i+\Delta L\right]$ can be approximated using Equation 9:

$${\lambda }_i\left(r,\theta \right)=E\left[N_{L_i}\left(r,\theta \right)\right]\Delta L.$$ (11)

Using this equation, we can calculate a composite likelihood of the observed data given the demographic parameters θ (see Appendix C).

Block detection errors:

The detection of IBD blocks from genetic data is not a trivial task. In practice, one often has to deal with erroneous detection (Browning and Browning 2012). Blocks might be called in the absence of true IBD blocks (false positives), and only a fraction of true IBD blocks of a given length are detected (limited power), and there is a probability of assigning them the wrong length (error). Following Ralph and Coop (2013), we can include these errors into our likelihood framework. Careful analysis allows one to estimate block detection errors (Ralph and Coop 2013), and the expected rates per bin can be updated accordingly (see Appendix D).

Assumption of independence:

This Poisson approximation assumes that all shared blocks are the outcomes of independent processes. This is obviously an oversimplification. Block sharing can be correlated along chromosomes and among different sample pairs because of the initially shared movement of genetic material. Taking all these correlations into account would go beyond the simple pairwise diffusion model. However, maximizing the likelihood of actually correlated observations (composite likelihood) is a widely used practice in inference from genetic data (e.g., Fearnhead and Donnelly 2002). It still gives consistent and asymptotically normal estimates, although the errors calculated from the curvature of the maximum likelihood surface at its maximum (Fisher information matrix) will be too tight when the observations are actually correlated (Lindsay 1988; Coffman et al. 2016). Moreover, in many cases, correlations among blocks can be expected to remain fairly weak, since initial correlations in spatial movement are broken up quickly by recombination. When analyzing well-separated samples, sharing of long blocks is a rare event and, thus, most of the observed block sharing will originate from independent coalescent events.

Adjacent IBD blocks:

The theory and inference scheme introduced here is based on IBD blocks that have been defined to be ended by any recombination event on the path to the common ancestor. However, multiple, consecutive IBD blocks of recent coancestry, for unphased data from all four possible pairings of two sets of diploid chromosomes, produce an unbroken segment of exceptionally high similarity that is detected as a single long IBD block in practice. This can significantly inflate the number of observed IBD blocks of a given length beyond the true value, especially for shorter IBD segments (Chiang et al. 2016).

If adjacent IBD blocks happen to be neighbors, the error estimation model by Ralph and Coop (2013), which is based on introducing artificial IBD segments of known length, partly accounts for this effect. However, this does not estimate the effect of short inbreeding loops where ancestral genetic material that was broken up by a recombination fuses together again quickly (Figure 1), rendering the IBD block ending recombination event ineffective (Barton et al. 2013).

Intuitively, for a large neighborhood size (a parameter proportional to the product of ${\sigma }^2$ and effective density $4\pi {\sigma }^2{D}_e)$ short inbreeding loops that significantly extend a recent IBD block by quick recoalescence are rare, and our approach remains valid. However, for a population with small neighborhood size, ineffective recombination events can potentially confound observed block-sharing patterns and the estimates based on them. This effect is driven mostly by coalescence within a few generations, before the blocks migrate away from each other. Hence, local dispersal and breeding patterns are important; however, the diffusion of ancestry usually only becomes accurate on intermediate timescales. Therefore, a generally applicable theoretical treatment of this issue is not feasible. In this article, we study the effects of this model inaccuracy using simulations, and show that the inference scheme is not greatly affected in the simulated scenarios.

Simulations

To test our equations and inference scheme, we simulated the sharing of IBD blocks in a set of samples by tracing the ancestry of the chromosomes back in time for a variety of spatial population models. Simulations were mostly done on a two-dimensional torus that was large enough that IBD sharing over more than half of the torus was very unlikely; thus we effectively simulated a two-dimensional population without boundary effects. Since sharing of long IBD blocks is very unlikely to originate far back in time, we ran the simulations up to a maximal time $t_{\max }.$ If not otherwise stated, we analyzed the sharing of true IBD blocks, in which every recombination event was assumed to be effective.

Grid models:

In our grid models, the nodes of a rectangular grid were occupied by a prespecified number of pairs of homologous chromosomes to mimic diploid individuals. Similar to the classic Wright–Fisher model of panmictic populations, for every chromosome, a parent was chosen independently for every discrete generation back, with the probabilities described by a prespecified dispersal kernel. Poisson recombination events along the chromosome induced a switch between the two parental chromosomes. Whenever the ancestral material of the two distinct initial chromosomes fell on the same chromosome and overlaps for longer than a given threshold chromosome length, we stored the resulting IBD block. We simulated the dispersal following discretized uniform, Gaussian, and Laplace probability densities along each axis to have representatives of dispersal kernels with low, intermediate, and high kurtosis. To analyze the effects of a growing or declining population density, we simulated a varying number of multiple pairs of homologous chromosomes per node. A chromosome then first picks an ancestral node as before, and subsequently a random diploid ancestor from this node. The grid model was also easily modified to simulate a classic nearest neighbor stepping stone model (Kimura and Weiss 1964). Nodes were grouped into demes, and each chromosome either chose its parent uniformly from within its own or one of the neighboring demes.

Continuous model: spatial λ-Fleming-Viot process:

We additionally simulated a model in which each individual occupied a position in continuous space. For this, we used DISCSIM, a fast implementation (Kelleher et al. 2014) of the recently introduced spatial λ-Fleming-Viot process. Summarizing briefly, this model introduced by Barton et al. (2010) follows lineages backward in time and events are dropped randomly with a certain rate parameter and uniform spatial density. In each such event, every lineage within radius R is affected with the probability u by this event. A prespecified number of parents, here two, are dropped uniformly within the disc, and every affected lineage jumps to them, switching parents according to the recombination rate. Given an initial set of loci, DISCSIM generates their coalescence tree up to a specified time. The output contains a list of all coalescent nodes, which we further analyzed to detect IBD sharing.

Application to Eastern European data

Currently, population genomic data sets which allow one to analyze long IBD blocks are available mainly for humans. To test the inference scheme, we applied a data set of blocks shared between Europeans, which was generated previously by Ralph and Coop (2013), and includes detailed error estimates for IBD block detection. They reported significant differences in patterns of block sharing between Eastern and Western European populations. Therefore, we concentrated our analysis on block sharing in the Eastern European subset, as diffusion should be a better approximation for modeling the spread of ancestry in continental regions. Moreover, Eastern European countries are on average geographically more compact and, thus, the position data at the country level is expected to be more accurate.

The data:

The detection method and error analysis of the IBD block data were described in detail by Ralph and Coop (2013). Summarizing briefly, IBD blocks were called for a subsample of the POPRES data set (Nelson et al. 2008) and genotyped at ∼$500,000$ SNPs using the fastIBD method, as implemented in Beagle version 3.3 (Browning and Browning 2011). Every sample used in the analysis was required to have all reported grandparents from the same country. We analyzed block sharing between 125 Eastern European samples (see Supplemental Material, File S1). We followed the geographic classification of Ralph and Coop (2013), but excluded the six Russian and one Ukrainian samples, as location data at the country level are likely very inaccurate for these two geographically extended countries. We analyzed shared blocks >4 cM. Within our subsample, $1824$ such blocks were reported (Figure 9). We set the position of each country to its current demographic center, defined as the weighted mean location (File S1). In our analysis, we used sex average map lengths of autosomes given by the deCODE map (Kong et al. 2002), consistent with Ralph and Coop (2013).

Data analysis:

Throughout the analysis, we worked with block length bins ranging from 0 to 30 cM with a bin width of $\Delta L=0.1$ cM, and applied the error function estimates reported by Ralph and Coop (2013). For maximizing the likelihood, we calculated the likelihood of block sharing in the bins from $4$ to $20\hspace{0.5em}\text{cM}\hspace{0.17em},$ which is informative about the last few centuries (see Figure 9). We excluded the longer shared blocks from our analysis since these blocks have a considerable chance of originating in the last few generations, which is not expected to be accurately captured in the diffusion model. Longer shared blocks are also confounded by the sampling scheme that excluded individuals with reported grandparents from different countries.

We used our inference scheme to fit several specific models of past density D as follows:

1. For a constant population: $D=C.$

2. For a population growing at accelerating rate: $D=C/t.$

3. For a growth model where the growth rate is fitted as well: $D=C{t}^{-\beta }.$

In each case, t measured time back in generations. To learn about the certainty of estimates, in addition to using the curvature of the likelihood surface (Fisher information matrix), we bootstrapped the data. Since we suspected strong correlations and systematic deviations from the model, we resampled different units. We bootstrapped on the level of blocks by redrawing each block a number of times following a Poisson distribution of mean 1, and similarly over country pairs, since we suspected systematic correlations on this level.

Furthermore, we analyzed the deviation of pairwise block sharing between pairs of countries from the expected value predicted by the best fit model. For this, we assumed that the observed block sharing was Poisson distributed around the predicted block sharing. Transforming the block count data $x\to 2\sqrt{x}$ converts these Poisson distributions into approximately Gaussian distributions with an SD of 1, which helped visual inspection of the statistical significance of residuals.

Data availability

We implemented the described methods to simulate and analyze IBD sharing data in Python. The source code was uploaded to the freely available Github repository https://git.ist.ac.at/harald.ringbauer/IBD-Analysis. The preprocessed human IBD block-sharing data, including the detection-error estimates used here, were the result of the analysis of Ralph and Coop (2013), and can be freely accessed at http://www.github.com/petrelharp/euroibd.

Results

Block sharing in simulated data

We compared simulated block-sharing patterns with the theoretical expectations. For each bin, we depicted rates per pair and normalized for a rate per cM.

Constant population density:

For a constant population density, the theoretical expectation (Figure 3) is given by Equation 9:

$$E\left[N_L\right]=\frac{G}{8\pi D{\sigma }^2}{\left(\frac{r}{\sqrt{L}\sigma }\right)}^2{K}_2\left(\sqrt{2L}\frac{r}{\sigma }\right),$$

where $K_2$ denotes the modified Bessel function of the second kind of degree two (Abramowitz and Stegun 1964). This formula predicts that block sharing approaches exponential decay with distance, as Bessel functions $K_{\gamma }\left(x\right)$ converge to $\sqrt{\pi /2r\exp \left(-r\right)}$ for $r\gg 1$ (Abramowitz and Stegun 1964). This decay then dominates the polynomial terms in front of the Bessel functions, and the slope of this exponential decay (on a log scale) converges to $\sqrt{2L}/\sigma$ as $\sqrt{2L}r/\sigma >1.$ For the long blocks considered here, this quick decay is approached for pairwise sample distances of a few σ. In all simulations, block-sharing patterns were very similar among the five different simulated models, and closely followed the theoretical expectation (Figure 3).

Growing and declining populations:

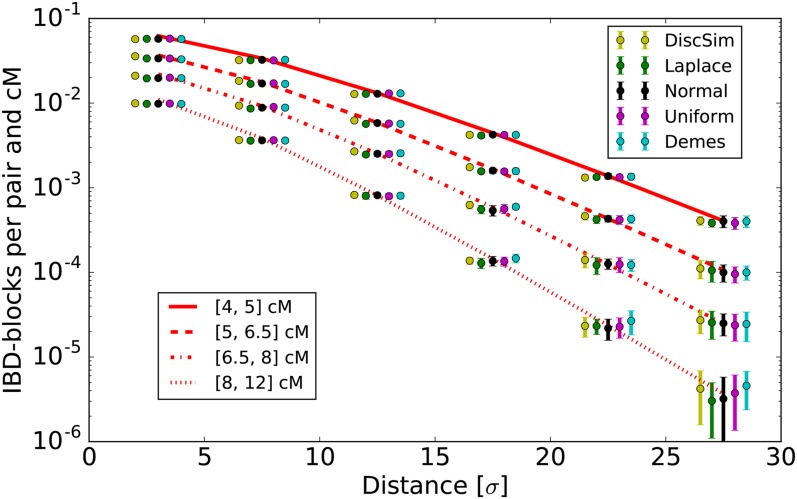
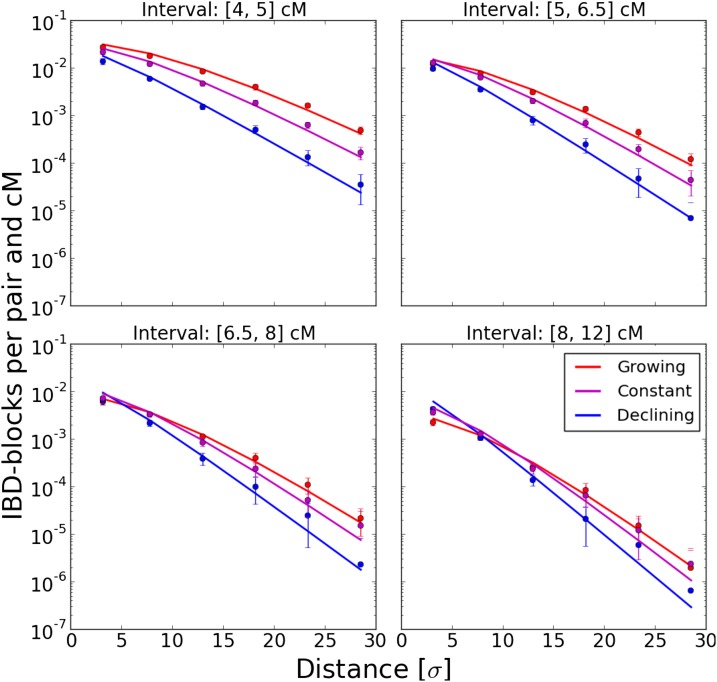
We simulated block sharing for three scenarios of a growing, declining, and constant population with growth parameters $\beta =1,0,-1.$ Figure 4 shows that the results are again in good agreement with theory. We depicted the result for the simulated Laplace dispersal; the other dispersal kernels yielded almost identical results. In all scenarios, the decay of block sharing with distance approached exponential decay with rate $\sqrt{2L}/\sigma ,$ where the specific density scenario determined the speed of convergence.

Figure 4.

Various population density scenarios. Simulated IBD block sharing per pair and cM in various density scenarios was compared to theoretical expectations based on Equation 9. The block sharing of a subset of 150-cM chromosomes four distance units apart placed on an initial grid was analyzed. Along each axis, dispersal was modeled by a Laplace distribution with $\sigma =1,$ and the number of diploid individuals per node n either remained constant at $n=10,$ grew as $n\left(t\right)=t,$ or declined as $n\left(t\right)=200/t;$ in all cases, t denotes the time back measured in generations, and at every step $n\left(t\right)$ was rounded to the nearest integer value. For each scenario, 20 replicate runs were done. •’s depict the mean and error bars the SD for every bin. The solid lines show the theoretical prediction based on Equation 9.

Inference in simulated data

We tested our parametric inference scheme and analyzed its ability to recover the underlying demographic parameters from simulated block-sharing data. For every simulated block data set, we numerically computed the maximum likelihood estimates ${\theta }_{\text{MLE}}$ for shared blocks between 4 and 20 cM, put into bins of width 0.1 cM.

Constant population density:

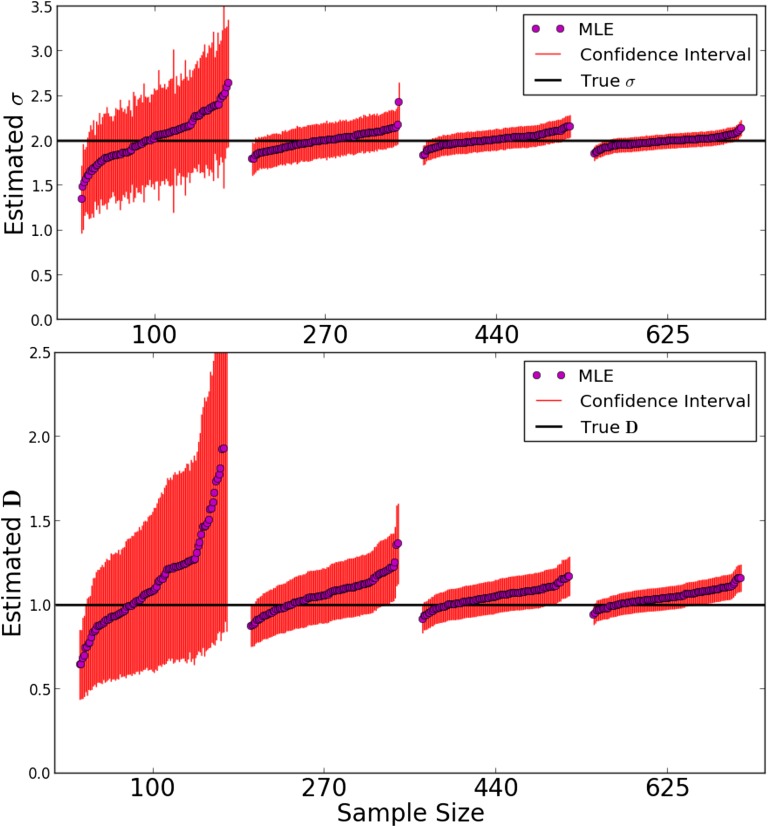
Results for the parameter inference for a population of constant density are depicted in Figure 5. We simulated a varying number of samples on a grid, consisting of one chromosome each, to test the behavior of the inference scheme with respect to limited sample size. Naturally, the variance of estimates increased with decreasing sample size, but the bias remained small. Moreover, the estimated SEs captured the true estimator variance relatively well (see File S2). This confirms that most of the shared blocks were the result of uncorrelated coalescence events, as heuristically argued above. The typical log-likelihood surface for a single simulated IBD block-sharing data set was found to be smooth (Figure S2), and in all cases, numerical maximization did not result in spurious maxima, even for initial estimates orders of magnitudes off. Moreover, estimates of density and dispersal rate were only slightly correlated in the scenario considered here (File S2).

Figure 5.

Maximum likelihood estimates. We simulated a Laplace model on a grid of nodes of torus length 180 for $t=200$ generations back. We set the dispersal rate at $\sigma =2$ and the number of individuals per node to $D=1.$ In every run, a random subset of 100, 270, 440, or 625 chromosomes of map length 150 cM was picked from an initial sample grid spaced two nodes apart. For each sample size, 100 simulations and subsequent parameter estimates were run. Every • depicts the maximum likelihood parameter estimate of a single run. The $95\text{\%}$ confidence intervals were calculated from the Fisher information matrix. MLE, maximum likelihood estimate.

Varying population density:

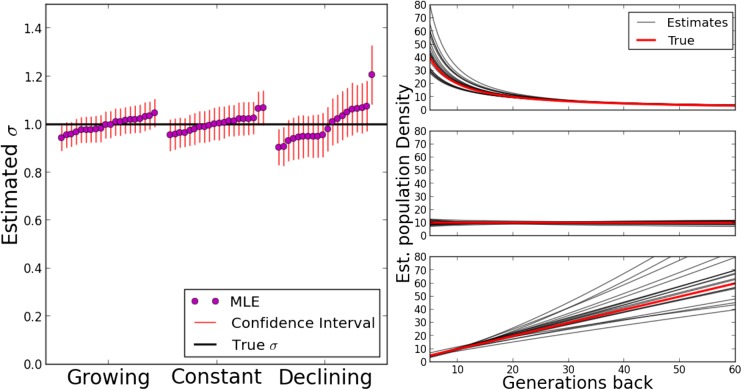
We also tested the ability of the inference scheme to detect recent changes in population densities. For this, we simulated three scenarios of a growing, declining, and constant population with growth parameters $\beta =1,0,-1.$ Results are depicted in Figure 6. The estimates of the demographic parameters allowed us to robustly distinguish these three scenarios. Interestingly, accurate estimates of the dispersal rate were feasible in all these demographic scenarios; even when fitting a model with constant population size to the other two scenarios of a recently, quickly changing, population size (Figure S1). This can be explained by the fact that the eventual rate of decay, the main signal for estimating σ from fitting Equation 9, remains the same, independent of the specific population density scenario. The speed of convergence varies, but in all cases the eventual rate is approached relatively quickly within several dispersal distances (Figure 4).

Figure 6.

Likelihood estimates for various population density scenarios. The same scenarios used in Figure 4 were simulated. For 20 runs each, 625 chromosomes of length 150 cM were randomly picked from a sample grid and traced back using a Laplace dispersal kernel with $\sigma =1;$ and the maximum likelihood fits and $95\text{\%}$ confidence intervals were calculated from their block sharing. For the estimated population density, the true value of the simulations and the maximum likelihood estimate for every run are shown. MLE, maximum likelihood estimate.

True vs. detectable IBD blocks:

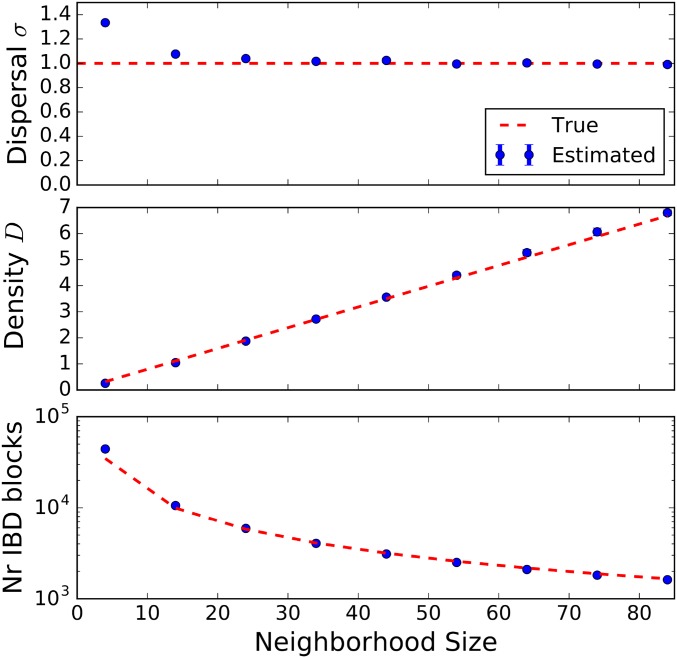
In Figure 7, the effect of undetected recombination events on estimates of demographic parameters and overall IBD block number is depicted. This was investigated with simulations in the DISCSIM model, as it allowed easy and continuous tuning of the neighborhood size $4\pi {\sigma }^2{D}_e$ through the parameter describing the probability that an event hits an individual within its range (Barton et al. 2013). Pairwise coalescence times for all pairs of loci along the chromosome were extracted, but now only the effective recombination events were counted, which were defined as jumps of coalescence times between adjacent pairs of loci with at least one coalescence time older than a preset time threshold of 1000 generations back, the time at which the backward simulations were run. This would capture most short recombination-coalescence loops, while still being well below the bulk of ancestral coalescence times. The effect of the nondetectable recombination events became significant only for very low neighborhood sizes $\left(<15\right)$ when the detected number of IBD blocks of a certain length was inflated by wrongly inferring multiple shorter blocks as a single longer block. While estimates for density remained almost unbiased, the inferred dispersal rates increased significantly, likely due to an excess of block sharing for distant samples. However, even for very low neighborhood sizes, when the effective density of individuals measured in dispersal units was about one (for neighborhood size $4\pi D_e{\sigma }^2\approx 12.6),$ the upward bias remained <50%.

Figure 7.

Observable IBD blocks and estimates compared with the theoretical predictions for true IBD blocks. Simulations were run with DISCSIM for an initial grid of 150-cM chromosomes that were three distance units apart on a torus with axial size 90. Dispersal rate was set to one. IBD blocks were detected as consecutive runs of coalescence times $<1000$ generations, and then used to estimate demographic parameters. For various densities corresponding to neighborhood sizes 4–86, 10 DISCSIM runs were simulated. The mean of these runs was compared with the theoretical prediction using Equation 9, which assumes that every recombination event is effective.

Sampling guidelines

Edge effects:

In practice, populations are not extended infinitely beyond the sampling area, but have range boundaries. This forces lineages to deviate from the simple diffusion model, as they cannot wander out of the species range (Wilkins and Wakeley 2002; Wilkins 2004). This might be a common violation of our model assumptions. We assessed how much our inference method was affected using simulated data from habitats of limited size. In these simulations, we assumed that the lineages were reflected once they reached a range boundary.

Our results (File S3) indicated that, in cases when the boundaries were close to the samples such that the distance to the nearest samples was on the same order of magnitude as σ, the estimates for the dispersal rate σ and density D become biased downward; an effect also observed for the inference method of Novembre and Slatkin (2009) which is based on the sharing of rare alleles. Similarly, we observed that the estimates for D and σ become biased downward for habitats of width $\approx 10\sigma .$ Therefore, we recommend to always check whether most of the samples are collected far from the habitat edges $\left(>\sigma \right)$ and whether the habitat is sufficiently large $\left(\text{diameter}>10\sigma \right).$

For the special case of rectangular habitats with reflecting boundaries, the method of images described by Wilkins (2004) gives a simple way of calculating the coalescence probabilities for two spatially diffusing lineages (Equation 6). In principle, it is straightforward to update our formulas for expected block sharing accordingly. One simply has to add terms describing the expected block sharing with ghost samples reflected at the edges. However, we did not implement this correction, as this approach cannot be extended to more irregularly shaped habitats and boundary edges, as usually encountered in reality.

Clumped sample distribution:

In practice, samples are not always evenly distributed, but are often clumped due to sampling constraints. To investigate how such clustered sampling affects our inference scheme, we compared the results of various scenarios of clumping (File S3). The estimates and their inferred uncertainty were not affected substantially; only in the cases of very asymmetric clumping did we observe a small upward bias of dispersal estimates. This overall robustness is not surprising as the distribution of pairwise sampling distances is not changed much as long as the clumping is not overly pathogenic (i.e., a very low number of sample clusters).

Inference in POPRES data

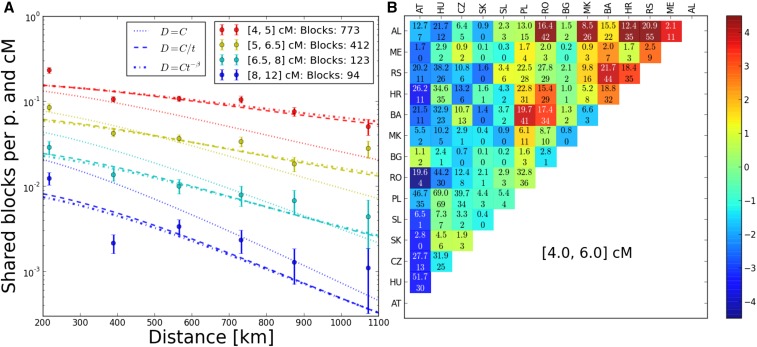
When fitting our models to the Eastern European subset of the POPRES IBD data, the model of quick population growth with a population density $D_e\left(t\right)=1/t$ fit markedly better than a model of constant population size, which underestimated sharing of short blocks (Figure 8) at the maximum likelihood parameters. In the more complex model, $D_e\left(t\right)=t^{-\beta },$ the growth rate parameter β was estimated to be close to one. The increase of likelihood was small $\left(\Delta L=1.1\right),$ especially when considering that there are correlations in the data that make the difference of true likelihood even smaller (Coffman et al. 2016). Similarly, fitting several, more complex, density functions as sums of power terms did not significantly increase the likelihood. In all three models, the estimates for dispersal σ were $\sim 60\text{—}70\hspace{0.5em}\text{km}/\sqrt{\text{gen}},$ even under the likely misspecified constant population size model (Table 1), and bootstrapping on the country-pair level yielded $95\text{\%}$ confidence intervals that ranged from $45\text{—}80\hspace{0.5em}\text{km}/\sqrt{\text{gen}}.$

Figure 8.

Fit of models to Eastern European block-sharing data. (A) To better visualize the data, observed block sharing was binned into distance and block length bins. The •’s depict the average block sharing within each bin and the lines are predictions from the best fit models. The error bars represent SDs under the assumption of Poisson counts in every bin; some are clearly too tight and there are outliers, which hints at more systematic deviations at the country-pair level (see also Figure 5). p., pair. (B) Residuals for pairs of countries for blocks of length 4–6 cM. Upper line in every field: total number of IBD blocks predicted by the best fit model. Lower line: observed number of IBD blocks. Color of every field is determined by statistical significance (z-value when transformed $x\to 2\sqrt{2x}).$ AL, Albania; AT, Austria; BA, Bosnia; BG, Bulgaria; CZ, Czech Republic; HR, Croatia; HU, Hungary; ME, Montenegro; MK, Macedonia; PL, Poland; RO, Romania; RS, Serbia; SK, Slovakia; SL, Slovenia.

Table 1. Maximum likelihood estimates for Eastern European IBD data.

Density model	Parameter	MLEa	$95\text{\%}$ C.I.b	$95\text{\%}$ C.I. bootstrapc
$D_e=D$	D	0.047	0.043–0.051	0.038–0.065
	σ	67.8	62.9–72.8	53.03–81.50
$D_e=D/t$	D	1.71	1.48–1.94	1.22–2.87
	σ	62.6	56.1–69.0	42.2–82.6
$D_e=D{t}^{-\beta }$	D	2.13	1.39–2.86	1.16–5.83
	σ	63.0	56.2–69.8	44.2–82.4
	β	1.05	0.98–1.13	0.90–1.25

MLE, maximum likelihood estimate.

^aAll units so that distances are measured in km and time in generations.

^bCalculated from Fisher information matrix.

^cCalculated from 100 estimates on data bootstrapped over country pairs.

The estimated parameter uncertainty when bootstrapping over single blocks was only slightly larger than was estimated from the curvature of the likelihood, but bootstrapping over country pairs gave markedly increased confidence intervals (Figure S3), which implies that there are systematic correlations at this level in the data. This was further confirmed by the analysis of the residuals for the country pairs, which yielded a gradient toward the Balkans for more block sharing than predicted by the best fit models. The deviations were statistically most significant for short blocks because of the increased power due to the higher number of shared blocks (Figure 5); however, the overall pattern also held for longer blocks (Figure S4).

Discussion

The main goal of this article was to develop a robust inference scheme for populations extended in two spatial dimensions that uses pairwise shared long IBD blocks to reliably estimate the dispersal rate σ and the effective population density $D_e$ separately. For this, we derived analytical formulas for block sharing under a model of diffusion of ancestry that extended the previous work of Barton et al. (2013), and fit these results by maximizing a composite likelihood similar to that used by Ralph and Coop (2013). Using extensive tests on data simulated under a variety of scenarios, we demonstrated that our method could robustly perform this task.

Baharian et al. (2016) recently independently arrived at similar formulas for block sharing under a model of spatial diffusion, which they fit by regressing block sharing data binned according to pairwise geographic distance and block length. Our work is conceptually similar, but provides several important extensions. We additionally described the effect of recent population density changes, which seems especially relevant for human populations. For the special case of a constant population size, our results matched an equivalent result of Baharian et al. (2016), and our approach allowed us to additionally incorporate chromosomal edge effects. Moreover, our likelihood framework offers several advantages over regressing binned data because it makes use of the information contained in the lengths of shared blocks. It can also be used to quantify the uncertainty of the parameter estimates, and can readily include error estimates for block detection. Another major contribution is our extensive testing on simulated data. These simulations yielded insights into the general accuracy of the underlying idealized model assumptions. They also helped us to investigate how several deviations from the model that might occur in practice; including ineffective recombination events, wrongly specified growth models, irregular sample distribution, and nearby habitat boundaries; affect inference.

Exponential decay of IBD sharing with distance and block length

The derived formulas for sharing long IBD blocks under diffusion of ancestry are structurally similar to the Wright–Malécot formula (Barton et al. 2013) which describes allelic identity by state using similar approximations. A polynomial factor is multiplied with a Bessel function of the second kind, $K_{\gamma }\left(\sqrt{2\lambda }\frac{r}{\sigma }\right);$ for allelic correlation $\lambda =\mu$ (the mutation rate), while here $\lambda =L$ (the IBD block map length). For long blocks, L is much larger than typical mutation rate μ. This allows us to probe the tail of the Bessel function $\left(\sqrt{2\lambda }r/\sigma >1\right),$ where it approaches exponential decay that dominates the polynomial factor. This exponential decay occurs with both an increasing block length $\sqrt{L}$ and an increasing geographic distance r. The theory predicts that for long blocks, this decay can be over orders of magnitude when pairwise geographic sample distance increases multiple dispersal distances (Figure 3), which is observed in the human data (see Figure 8). This pattern persists even in the case of recent population density changes (see Figure 4). When global density changes can be modeled as the sums of power terms of the form in Equation 8, the result for expected block sharing will be given by the sums of the corresponding Bessel functions (Equation 9). Each of those approaches exponential decay with rate $\sqrt{2L}/\sigma ;$ thus, also their sum does. Therefore, estimates of the dispersal rate σ that use the decay rate in the exponential regime can be expected to be relatively robust with respect to recent demographic history (see also Figure S1).

Implications for demographic inference

The fast rate at which long blocks are broken up and the ability to probe the exponential regime of decay offer several significant advantages for demographic inference, which our inference scheme can use. First, long blocks typically stem from very recent times (see Figure 9). This is clearly advantageous for populations that have been in equilibrium for only a relatively short time, as is likely often the case. Inference methods that rely on allelic correlations probe recent timescales as well (Barton et al. 2013). They similarly pick up locally increased identity by state by recent coancestry. However, this is often only a small signal on top of a majority of identity by state stemming from ancient times. Thus, these methods are much more susceptible to confounding by ancestral structure (Meirmans 2012), and have stringent, often unrealistic, equilibrium time requirements (Leblois et al. 2003), which our method can avoid. For instance, in the human case, the best fit model predicts that most long blocks stem from within the last 50 generations (Figure 9). Second, quick exponential decay, both with sampling distance and block length, offers a very robust signal for demographic inference. As demonstrated, the expected number of blocks that are multiple cM long decays by orders of magnitude over a geographic scale of several dispersal distance units. This pattern should be relatively robust with respect to small-scale heterogeneities of habitat or dispersal. Such quick decay also aids robust inference, as shown by the accuracy of the inference method on simulated data. This is in contrast to inference that is based on classic measures of pairwise genetic similarity. Such measures usually only decay with the logarithm of distance (Barton et al. 2002), which causes low and often problematic signal-to-noise ratios (Watts et al. 2007). Third, using the logarithmic regime of the Wright–Malécot formula only allows one to infer the neighborhood size proportional to the product of density and dispersal. Naturally, however, their separate values are of interest. As demonstrated, inference based on long IBD blocks allows one to obtain robust separate estimates of these two important demographic parameters.

Analysis of human data

The analysis of human data nicely demonstrates our inference scheme. The true demographic scenario is doubtless more complex, including heterogeneous, time-dependent migration rates and large-scale migrations. However, qualitatively the patterns of IBD sharing appear to fit well with our diffusion model. Despite several significant deviations, the best fit model explains the overall broad trends in the empirical data (Figure 8), such as the decay of the number of shared blocks with both increasing geographic distance and block length. Using our inferred model, we predicted most of the shared blocks we used (>4 cM) and hence our signal originates within the last 50 generations (Figure 9), which corresponds to the past 1450 years (assuming 29 years per generation; Fenner 2005). This mostly postdates the period of large-scale migrations in Europe (“Völkerwanderung”; Davies 2014). Our inferred demographic parameters seem to be plausible. There is a clear signal for rapidly accelerating recent population growth, which is in agreement with historical estimates (McEvedy and Jones 1978) and previous genetic studies based on the allele-frequency spectrum (Keinan and Clark 2012; Gao and Keinan 2016). Historical dispersal estimates infer values of typical migration distances per generation ranging from a few to several dozen kilometers (Wijsman and Cavalli-Sforza 1984; Pooley and Turnbull 2005). While agreeing on orders of magnitude, these are somewhat lower than our estimates $\left(\sigma \approx 50-100\hspace{0.5em}\text{km}/\sqrt{\text{gen}}\right).$ However, there is also evidence that preindustrial individual human migrations over large distances are rare, but occur at a significant rate (Pooley and Turnbull 2005).

We detected a systematic, large-scale deviation from a simple diffusion model with uniform population density, as there is a clear gradient for higher block sharing in the direction of the Balkan countries (Figure 5). This was already observed by Ralph and Coop (2013). They hypothesized that this could be due to the historic Slavic expansion, a hypothesis supported by admixture analysis (Hellenthal et al. 2014). However, the pattern of increased block sharing also holds for longer, typically younger, blocks, which could hint additionally at a consistently lower population density in these regions. Such systematic regional deviations from the diffusion model also imply that care should be taken when estimating parameters and their uncertainty ranges.

Outlook

Our inference scheme based on long IBD blocks requires large amounts of data, as it needs dense genotype data from a few dozen individuals, spatial information of the samples, and a linkage map. However, the novel opportunities and advantages for inference of recent demography should justify the effort. The possibility to accurately estimate dispersal distances and past effective population densities could yield interesting novel insights for a whole range of organisms. The necessary data sets are within reach for several systems, and they will become even more accessible in the near future with increasing genotyping capacities.

A salient extension of our model would be to address complications such as anisotropy (Jay et al. 2013) and large-scale heterogeneities in migration patterns or population densities across the landscape. For classic measures of genetic similarity, elaborate computational techniques have been recently applied for inference within such complex demographic scenarios (Duforet-Frebourg and Blum 2014; Petkova et al. 2016). As argued above, analysis of IBD blocks would be even more suited to this task, as the length of shared blocks gives additional information. However, analytical solutions, which hugely facilitate inference, are likely no longer feasible. Inference will have to be based on numerical predictions, although using block sharing of different lengths will be even more computationally intensive than extracting information from a single genetic similarity matrix. Consequently, this challenge is beyond the scope of this article. We hope that future work will help to fully use the potential of shared IBD blocks, and that our inference scheme marks only one step in a new era of demographic inference.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.196220/-/DC.

Appendix A: Effective Density

We use diffusion to model the separation of two lineages backward in time. Let $r\left(x,t\right)$ denote the probability density of the vector $x$ of pairwise distances along each axis at time t back. In our model, two lineages coalesce instantaneously at an average coalescence rate $\nu \left(x\right)$ depending on $x.$ For the probability of coalescing at time t ago, we get:

$$\psi \left(t\right)={\displaystyle {\int }_{{\text{R}}^2}r\left(x,t\right)\nu \left(x\right)dx}.$$

In cases where only discrete sample distances $x$ are possible, such as the stepping stone model, the integral has to be replaced with a sum. The key observation is that $\nu \left(x\right)$ is usually negligible outside a small area around the origin, since in most models only very close samples $\left(\left|x\right|\approx \sigma \right)$ have an appreciable chance to coalesce. Within such small areas around the origin, for $t\gg 1$ we approximate $r\left(x,t\right)$ with $\approx r\left(0,t\right)$ and get:

$$\psi \left(t\right)\approx r\left(0,t\right){\displaystyle {\int }_{{\text{R}}^2}\nu \left(x\right)dx}=r\left(0,t\right)\frac{1}{2D_e},$$ (A1)

where we have defined $\frac{1}{2D_e}:={\displaystyle {\int }_{{\text{R}}^2}\nu \left(x\right)dx}.$ It can be shown that stepping stone models asymptotically converge to this model when rescaling appropriately (Barton et al. 2002, 2013). With demes separated by one distance unit, $D_e$ corresponds to the number of diploid individuals per deme, which motivates the name effective density. Here we give this more general definition of $D_e$ to allow one to directly calculate its value in various scenarios we simulated above (see File S2).

Appendix B: Chromosomal Edge Effects

Here, we give the full result for block sharing that includes chromosomal edge effects, which we use for inference. We shall denote the Equation 9 with fixed $G=1\text{M}$ with $n_L\left(\beta \right),$ where the dependencies other than β are suppressed for ease of notation. Then, integrating Equation 4 yields:

$$E\left[N_L\right]=\left(G-L\right)n_L\left(\beta \right)+n_L\left(\beta -1\right),$$

the formula for one chromosome of length G. For multiple chromosomes of different lengths, one has to sum this formula over all chromosomes. For pairs of diploid individuals, the resulting formula also has to be multiplied by a factor of four, since for every pair of individuals four pairs of chromosomes are compared.

Appendix C: Likelihood

Using the Poisson approximation (Equation 11), the likelihood of a pair of samples $\left(j\right)$ at distance r sharing blocks of length $\overrightarrow{L}=L_1,L_2,\dots ,L_n$ falling into a set of bins $i_1,i_2,\dots ,i_n$ is given by:

$$\stackrel{\sim }{f_j}=\text{Pr}\left(\overrightarrow{L}|r,\theta \right)=C{\lambda }_{i_1}{\lambda }_{i_2}\cdots {\lambda }_{i_n}\exp \left(-{\displaystyle \sum }_i{\lambda }_i\right),$$ (C1)

where C absorbs all constants that do not depend on the model parameters θ—this constant can be dropped when doing likelihood-based analysis. Continuing to assume independence, we take the product over all pairwise likelihoods $\stackrel{\sim }{f_j}$ to get the total composite likelihood:

$$\stackrel{\sim }{f}\left(\overrightarrow{L},\theta \right)={\displaystyle \prod _{\text{Pairs }j}\stackrel{\sim }{f_j}\left(\overrightarrow{L^j},r_j,\theta \right)},$$

where $\overrightarrow{L^j}$ denotes the shared blocks of the jth pair.

The number of pairs $n\left(n-1\right)/2$ increases quadratically with sample size n. This scaling is advantageous for an inference scheme, but implies that the runtime also grows with the square of sample size. However, algorithms to maximize functions with a low number of parameters are very efficient, so even sample sizes of hundreds of individuals can easily be handled. Calculation can be also sped up by grouping pairs with the same pairwise distance—such as when analyzing multiple individuals from a population with the same spatial coordinates—since then the ${\lambda }_i$ does not have to be calculated repeatedly for every individual pair. Denoting the length bins of blocks shared over all pairs by $i_1,i_2,\dots ,i_n$ and the number of pairwise comparisons by k yields:

$$Pr\left(\overrightarrow{L}|r,\theta ,k\right)=C{k}^n{\lambda }_{i_1}{\lambda }_{i_2}\cdots {\lambda }_{i_n}\exp \left(-k{\displaystyle \sum _i{\lambda }_i}\right),$$

where the factor $C{k}^n$ does not depend on the model parameters and can be dropped when maximizing the likelihood.

Appendix D: Block Detection Errors

The probability density $\stackrel{\sim }{\lambda }\left(y\right)$ of actually observing a pairwise shared block of length y can be calculated from the theoretical probability $\lambda \left(x\right)$ of sharing true blocks of length x:

$$\stackrel{\sim }{\lambda }\left(y\right)=f\left(y\right)+{\displaystyle {\int }_0^{G}R\left(y,x\right)c\left(x\right)\lambda \left(x\right)dx},$$ (D1)

where $f\left(y\right)$ describes the false-discovery-rate function depending on block length y, $c\left(x\right)$ is the power to detect a block of length x, and $R\left(y,x\right)$ is the probability of detecting a block of true length x as block of length y. Doing a careful analysis using techniques such as manually inserting shared blocks and rerunning the IBD block detection allows one to estimate these error functions (Ralph and Coop 2013).

In the likelihood framework, for every block length bin of a pair of samples, first the predicted true sharing λ is calculated for a set of demographic parameters θ, and then updated according to Equation D1 with the detection error estimates to get the final predicted rates $\stackrel{\sim }{\lambda },$ from which the likelihood of observed block sharing can be computed as before. This error model is straightforwardly included into the framework of working with small length bins.