Abstract
Readmission following discharge from an initial hospitalization is a key marker of quality of health care in the United States. For the most part, readmission has been studied among patients with ‘acute’ health conditions, such as pneumonia and heart failure, with analyses based on a logistic-Normal generalized linear mixed model (Normand et al., 1997). Naïve application of this model to the study of readmission among patients with ‘advanced’ health conditions such as pancreatic cancer, however, is problematic because it ignores death as a competing risk. A more appropriate analysis is to imbed such a study within the semi-competing risks framework. To our knowledge, however, no comprehensive statistical methods have been developed for cluster-correlated semi-competing risks data. To resolve this gap in the literature we propose a novel hierarchical modeling framework for the analysis of cluster-correlated semi-competing risks data that permits parametric or non-parametric specifications for a range of components giving analysts substantial flexibility as they consider their own analyses. Estimation and inference is performed within the Bayesian paradigm since it facilitates the straightforward characterization of (posterior) uncertainty for all model parameters, including hospital-specific random effects. Model comparison and choice is performed via the deviance information criterion and the log-pseudo marginal likelihood statistic, both of which are based on a partially marginalized likelihood. An efficient computational scheme, based on the Metropolis-Hastings-Green algorithm, is developed and had been implemented in the SemiCompRisks R package. A comprehensive simulation study shows that the proposed framework performs very well in a range of data scenarios, and outperforms competitor analysis strategies. The proposed framework is motivated by and illustrated with an on-going study of the risk of readmission among Medicare beneficiaries diagnosed with pancreatic cancer. Using data on n=5,298 patients at J=112 hospitals in the six New England states between 2000–2009, key scientific questions we consider include the role of patient-level risk factors on the risk of readmission and the extent of variation in risk across hospitals not explained by differences in patient case-mix.
Keywords: Bayesian survival analysis, cluster-correlated data, illness-death models, reversible jump Markov chain Monte Carlo, shared frailty, semi-competing risks
1 Introduction
Cancer of the pancreas is one of the most deadly. In 2013, an estimated 38,460 individuals died from pancreatic cancer in the United States making it the fourth most prevalent cause of cancer death (American Cancer Society, 2013). Unfortunately, since there are no effective screening tests for pancreatic cancer, most patients are diagnosed at a late stage of the disease, specifically once it has metastasized to other parts of the body. As a result, survival is poor with 1-year and 5-year mortality rates are of 75% and 94%, respectively (Shin and Canto, 2012). In practice, since prognosis is poor and mortality rates high, the treatment and management of patients diagnosed with pancreatic cancer generally focuses on palliative care aimed at enhancing quality of end-of-life care (PLoS Medicine Editors, 2012). Such care is expensive, however, with patients diagnosed with pancreatic cancer accruing an estimated $165,000 in health care costs in their last year of life (Mariotto et al., 2011).
Despite the huge costs, there are currently no comprehensive national efforts to monitor quality of end-of-life care for pancreatic cancer nor for any of a broad range of other ‘advanced’ health conditions for which the management of disease focuses on palliative care. Outside the context of these conditions, however, there is substantial interest in understanding variation in quality of health care. The recent literature, in particular, has focused on readmission as a key marker of quality of care, in part because it is expensive but also because it is thought of as an often-preventable event (Vest et al., 2010; Warren et al., 2011; Brooks et al., 2014; Stitzenberg et al., 2015). In addition, as the nation’s largest payer of health care costs in the United States, the Centers for Medicare and Medicaid Services (CMS) uses hospital-specific readmission rates as a central component in two programs: the Hospital Inpatient Quality Reporting Program, which requires hospitals to annually report, among other measures, readmission rates for pneumonia, heart failure and myocardial infarction in order to receive a full update to their reimbursement payments (CMS, 2013a); and, the Readmission Reduction Program, which requires CMS to reduce payments to hospitals with excess readmissions (CMS, 2013b).
Across all of these efforts, investigations of readmission in the literature have invariably used a logistic-Normal generalized linear mixed model (LN-GLMM) to analyze patients clustered within hospitals (Normand et al., 1997; Ash et al., 2012). While reasonable for health conditions with effective treatment options and low mortality, direct application of this model to investigate variation in risk of readmission following a diagnosis of pancreatic cancer is inappropriate because of the strong force of mortality. Consider, for example, n=5,298 Medicare beneficiaries diagnosed with pancreatic cancer at J=112 hospitals in six New England states between 2000–2009 and suppose interest lies in understanding determinants of readmission 90 days post-discharge. While additional detail is given below, we note at the outset that 1,257 patients (24%) died within 30 days of discharge without experiencing a readmission event; furthermore, 1,912 patients (36%) died within 90 days of discharge without experiencing a readmission event. Naïve application of a standard LN-GLMM to these data ignores the fact that a substantial portion of the patients are not at risk to experience the event of ‘readmission by 90 days’ for much of the timeframe. Such an analysis may lead to bias and, if incorporated into existing CMS programs, could have a major impact on how hospitals are penalized for poor quality of care.
In the statistics literature, data that arise from studies in which primary scientific interest lies with some non-terminal event (e.g. readmission) whose observation is subject to a terminal event (e.g. death) are referred to as semi-competing risks data (Fine et al., 2001). Broadly, published methods for the analysis of semi-competing risks data can be classified into three groups: methods that specify dependence between the non-terminal and terminal events via a copula (Fine et al., 2001; Peng and Fine, 2007; Hsieh et al., 2008); methods based on multi-state models that induce dependence via a shared patient-specific frailty (Kneib and Hennerfeind, 2008; Xu et al., 2010; Zeng et al., 2012; Han et al., 2014; Zhang et al., 2014; Lee et al., 2015); and, methods based on principal stratification (Zhang and Rubin, 2003; Egleston et al., 2007; Tchetgen Tchetgen, 2014). Common to all of these methods, however, is that their development has focused exclusively on settings where individual study units are independent. As such, the methods are not design to address scientific questions that arise naturally in the context of cluster-correlated data (Diggle et al., 2002; Fitzmaurice et al., 2012). In the context of readmission following a diagnosis of pancreatic cancer, such questions include: (i) the investigation of between- and within-hospital risks factors for readmission while acknowledging death as a competing force, (ii) characterizing and quantifying between-hospital variation in risk of the terminal event not explained by differences in patient case-mix, and (iii) estimating, and quantifying uncertainty for, hospital-specific effects, as well as ranking. Furthermore, it is well-known that if one is to perform valid inference all potential sources of correlation must be accounted for in the analysis.
To our knowledge, while the literature on the related competing risks problem has considered methods for cluster-correlated data settings (Katsahian et al., 2006; Chen et al., 2008; Gorfine and Hsu, 2011; Zhou et al., 2012; Gorfine et al., 2014), only one paper on the analysis of cluster-correlated semi-competing risks data has been published. Specifically, Liquet et al. (2012) recently proposed a multi-state model that incorporated a hospital-specific random effect to account for cluster-correlation. Estimation and inference was performed within the frequentist paradigm, based on an integrated likelihood that marginalizes over the random effect, implemented in the frailtypack R package (Rondeau et al., 2012). For our purposes, however, their approach is limited in a number of important ways. First, the analyses presented in Liquet et al. (2012) permit either a patient-specific frailty to account for dependence between T1 and T2 or a hospital-specific random effect to account for cluster-correlation but not both simultaneously. Second, the proposed specification assumed that the hospital-specific random effect for the non-terminal event is independent of the hospital-specific random effect for the terminal event, precluding a potentially important form of dependence. Third, towards understanding variation in risk of readmission, the hospital-specific random effects are themselves key parameters of scientific interest and not nuisance parameters to be marginalized over. Finally, evaluation of the integrated likelihood requires the specification of a parametric distribution for the hospital-specific random effects. While estimation and inference for regression parameters is generally robust to misspecification of random effects distributions in GLMMs, misspecification is known to adversely impact the shape of the estimated distribution of the random effects themselves (McCulloch et al., 2011; McCulloch and Neuhaus, 2011; Neuhaus and McCulloch, 2011). This is particularly important in quality of health care studies where identifying a hospital as being in the tail of the distribution can have a substantial impact on their evaluation.
Towards overcoming these limitations, we develop a novel, comprehensive hierarchical multi-state modeling framework for cluster-correlated semi-competing risks data. A key feature of the framework, and its implementation, is that it permits either parametric or non-parametric specifications for a range of model components, including baseline hazard functions and distributions for hospital-specific random effects. This gives analysts substantial flexibility as they consider their own analyses. Estimation and inference is performed within the Bayesian paradigm which facilities the straightforward quantification of uncertainty for all model parameters, including hospital-specific random effects and variance components. The remainder of this paper paper is organized as follows. Section 2 introduces an on-going study of readmission among patients diagnosed with pancreatic cancer, and provides a description of the available Medicare data. Section 3 describes the proposed framework, including specification of prior distributions; Section 4 provides a brief overview of an efficient computational algorithm for obtaining samples from the joint posterior, its implementation and methods for comparing goodness-of-fit across model specifications. Section 5 presents a comprehensive simulation study investigating the performance of the proposed framework, including a comparison with the methods of Liquet et al. (2012). Section 6 reports on a detailed analysis of the motiving pancreatic cancer study; sensitivity analyses regarding the specification of certain model parameters are reported in Section 7. Finally Section 8 concludes the paper with a discussion. Where appropriate, detailed derivations and additional results are provided in an online Supplementary Materials document.
2 Risk of Readmission Among Patients Diagnosed with Pancreatic Cancer
As mentioned in the Introduction, readmission is a key marker of quality-of-care (Ash et al., 2012; CMS, 2013a,b). To-date, however, studies of readmission have focused on health conditions that have relatively good prognosis and/or low mortality including heart failure, myocardial infarction and pneumonia (Krumholz et al., 1997, 2011; Joynt et al., 2011; Epstein et al., 2011). Beyond these conditions, however, little is known about variation in risk of readmission for patients diagnosed with terminal conditions such as pancreatic cancer. We are therefore currently engaged in a collaboration investigating readmission among Medicare enrollees diagnosed with pancreatic cancer. The overarching goals of the study are to improve end-of-life quality of care for these patients by first understanding patient-level risk factors associated with readmission and second understanding variation in risk at the level of the hospital (i.e. that not explained by differences in patient case-mix). Towards this we identified all n=5,298 Medicare enrollees who were diagnosed with pancreatic cancer during a hospitalization at one of J=112 hospitals in the six New England states (Connecticut, Maine, Massachusetts, New Hampshire, Rhode Island and Vermont) between 2000–2009. Information on the initial hospitalization and diagnosis, patient characteristics and co-morbid conditions, discharge destinflation and subsequent readmissions is obtained from the Medicare Fee-For-Service inpatient claims file (Part A). Specific covariates of interest include sex (0/1 = male/female), age, race (0/1 = white/non-white), the patients Charlson/Deyo comorbidity score (Sharabiani et al., 2012), information on entry route for the initial admission (0/1 = from the ER/transfer from some other facility), whether or not the patient underwent a pancreatic cancer-specific procedure (resection, bypass, or stent), the length of hospitalization and the discharge destinflation. For the latter, patients could have been discharged to their home, their home with care, a hospice, an intermediate care or skilled nursing facility (ICF/SNF) or some other facility (e.g. a rehabilitation facility or to inpatient care). Table 1 provides a summary of observed distributions for these covariates.
Table 1.
Covariate and outcome information for n=5,298 Medicare beneficiaries diagnosed with pancreatic cancer in the six New England states during a hospitalization between 2000–2009. Outcome information is considered with administrative censoring applied at 30 and 90 days post–discarge.
| n | Percent | ||
|---|---|---|---|
| Covariate information | |||
| Sex | Female | 3,037 | 57.3 |
| Male | 2,261 | 42.7 | |
| Age, years | 65–69 | 727 | 13.7 |
| 70–74 | 1,052 | 19.9 | |
| 75–79 | 1,226 | 23.1 | |
| 80–84 | 1,129 | 21.3 | |
| ≥ 85 | 1,164 | 20.0 | |
| Race | White | 4,982 | 94.0 |
| Non-white | 316 | 6.0 | |
| Charlson/Deyo comorbidity score | ≤ 1 | 4,854 | 91.6 |
| > 1 | 444 | 8.4 | |
| Entry route | Emergency room | 2,255 | 42.6 |
| Transfer from another facility | 3,043 | 57.4 | |
| Procedure during hospitalization | Yes | 1,291 | 24.4 |
| No | 4,007 | 75.6 | |
| Length of hospitalization, days | 1–7 | 3,170 | 59.8 |
| 8–14 | 1,465 | 27.7 | |
| ≥ 15 | 663 | 12.5 | |
| Discharge destination | Home | 1,823 | 34.4 |
| Home with care | 1,571 | 29.7 | |
| Hospice | 419 | 7.9 | |
| SNF/ICF | 1,219 | 23.0 | |
| Other facility | 266 | 5.0 | |
| Outcome information with administrative censoring at 30 days | |||
| Readmission and death | 205 | 3.9 | |
| Readmission and censored prior to death | 853 | 16.1 | |
| Death without readmission | 1,257 | 23.7 | |
| Censored prior to readmission or death | 2,983 | 56.3 | |
| Outcome information with administrative censoring at 90 days | |||
| Readmission and death | 608 | 11.5 | |
| Readmission and censored prior to death | 930 | 17.6 | |
| Death without readmission | 1,912 | 36.1 | |
| Censored prior to readmission or death | 1,848 | 34.9 | |
Also provided in Table 1 is a summary of the observed outcome information at 30 and 90 days post-discharge. Specifically, each patient is classified into one of four groups: (1) they experienced a readmission event and were subsequently observed to die; (2) they experienced a readmission event but were censored prior to death; (3) they were observed to die without having experienced a readmission event; and, (4) they were censored prior to experiencing either a readmission or death event. The administrative censoring at 30 and 90 days is driven by a several important factors. First, scientific and health policy interest regarding readmission has generally focused on a patient’s experience in the immediate months following discharge (CMS, 2013a). The primary rationale for this is that post-discharge management for patients diagnosed with pancreatic cancer generally focuses on palliative care, with a specific emphasis on pain management. As patients and their health care providers coordinate this care, the early phases are particularly important for long-term success and are therefore of key interest. A second consideration is that readmission events that occur soon after a patient is discharged are more likely to be directly related to their diagnosis and subsequent care. Readmission events that occur a long time after diagnosis are less likely to be directly related to the quality of care they receive in the immediate aftermath of the diagnosis and, arguably, should not count against a hospitals performance.
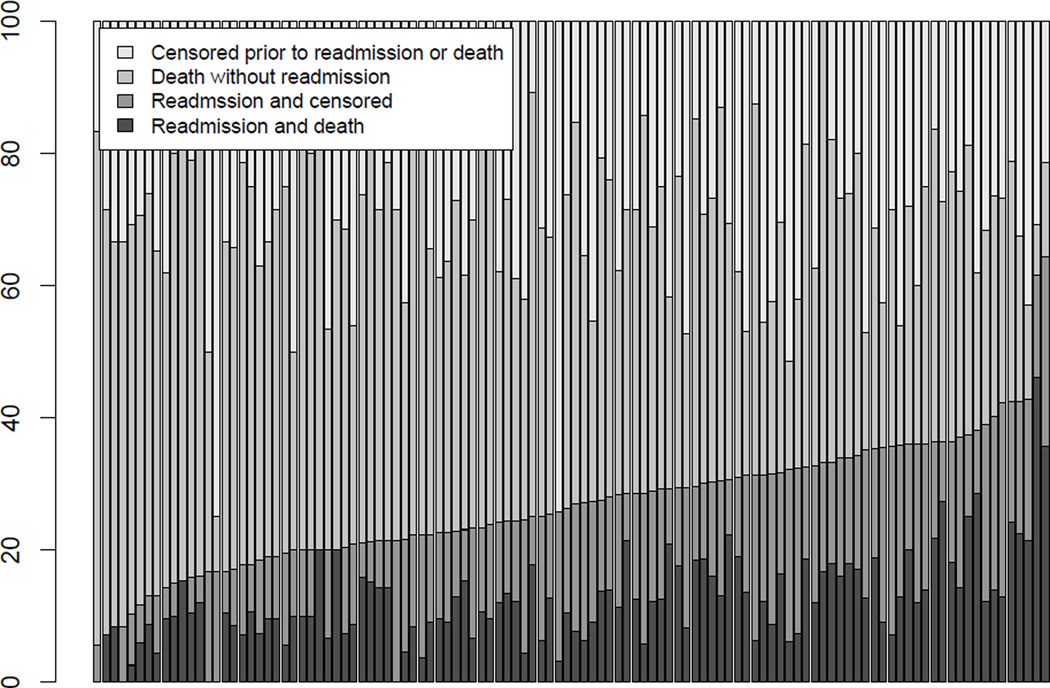
A central feature of the Medicare data is that the n=5,298 patients are clustered within J=112 hospitals; cluster sizes vary from 10–420 with a median of 30 patients. The inherent clustering of patients within hospitals is important from both a statistical and a scientific perspective: valid inference requires acknowledging potential correlation among patients and understanding between-hospital variation in readmission rates is a key scientific goal. Towards the latter, Figure 1 provides a barplot of the hospital-specific distributions of the four outcome groups based on censoring at 90 days. While there are many ways in which the J=112 hospitals could be ordered, Figure 1 orders them according to the total percentage of patients readmitted within 90 days (i.e. with or without a subsequent death event). From the figure we see that there is substantial variation in observed readmission rates across hospitals, with the lowest being 5.6% and the highest being 64.3%. Moving beyond these raw adjusted rates would need to first account for case-mix differences across the hospitals, second account for death as a competing risk and third account for the cluster-correlation.
Figure 1.
Hospital-specific distributions of the outcome information for n=5,298 Medicare beneficiaries diagnosed with pancreatic cancer at one of J=112 hospitals in the six New England states between 2000–2009. Outcomes have been administratively censored at 90 days and distributions ordered according to the observed percentage of deaths (with and without readmission).
3 A Bayesian Framework for Cluster-Correlated Semi-competing Risks Data
3.1 Model specification
Viewing ‘discharge’, ‘readmission’ and ‘death’ as three states, the underlying data generating mechanism that gave rise to these data can be represented by a multi-state model, specifically an illness-death model (Andersen et al., 1993; Putter et al., 2007; Xu et al., 2010). In the context of our motivating New England Medicare application, individuals may undergo one or more of three transitions between the three states: (i) discharge to readmission; (ii) discharge to death; and (iii) readmission to death. Letting T1 denote the time to non-terminal event and T2 the time to the terminal event, the illness-death model is characterized by three hazard functions that govern the rates at which patients transitions between the states: a cause-specific hazard for readmission, h1(t1); a cause-specific hazard for death, h2(t2); a hazard for death conditional on a time for readmission, h3(t2|t1). Specifically, we define
| (1) |
| (2) |
| (3) |
In practice, analyses based on the illness-death model characterized by (1)–(3) proceeds by placing structure on these functions, specifically as a function of covariates and frailties/random effects. Towards this, let Tji1 and Tji2 denote the time to the non-terminal event and time to the terminal event for the ith patient in the jth cluster, respectively, for i = 1, …, nj and j = 1, …, J. Furthermore, let Xjig be a vector of time-invariant covariates for the ith patient in the jth cluster that will be considered in the model for the gth transition, g=1,2,3. Consider the following general modeling specification:
| (4) |
| (5) |
| (6) |
where γji is a shared patient-specific frailty, Vj = (Vj1, Vj2, Vj3) is a vector of cluster-specific random effects, each specific to one of the three possible transitions, and βg is a transition-specific vector of fixed-effect log-hazard ratio regression parameters. As described by Xu et al. (2010), model (6) is often simplified in practice by either assuming that h03(tji2|tji1) = h03(tji2) or that h03(tji2|tji1) = h03(tji2 − tji1). Given the former specification, the model is referred to as being Markov in the sense that the hazard for death given readmission does not depend on the actual time of readmission; under the latter specification, the model is referred to as semi-Markov. For simplicity we focus the exposition in this section on Markov models although note that the methods and computational algorithms have also been developed and implemented for the semi-Markov model; the analyses in Sections 6 and 7 also consider both models.
3.2 The observed data likelihood
To complete the notation developed so far, let Cji denote the right censoring time for the ith patient in the jth cluster. Furthermore, let Yji1 = min(Tji1, Tji2, Cji), Δji1 = 1 if Yji1 = Tji1 (i.e. a readmission event is observed) and 0 otherwise, Yji2 = min(Tji2, Cji) and, Δji2 = 1 if Yji2 = Tji2 (i.e. a death event is observed) and 0 otherwise. Finally, let 𝒟ji = {yji1, δji1, yji2, δji2} denote the observed outcome data for the ith patient in the jth cluster and H0g(·) the cumulative baseline hazard function corresponding to h0g(·). Let γ⃗ and V⃗ denote the collections of the γji and Vj, respectively. Following Putter et al. (2007), for a given specification of (4)–(6), the observed data likelihood as a function of the unknown parameters Φ = {β1, β2, β3, h01, h02, h03, γ⃗, V⃗}, is given by:
| (7) |
where and r(tji1, tji2) = [H01(tji1)ηji1 + H02(tji1)ηji2 + {H03(tji2) − H03(tji1)}ηji3].
In the remainder of this section, we complete the specification of the Bayesian model by providing detail on a range of possible choices for specification of the baseline hazard functions in (4)–(6), the population distribution for the hospital-specific random effects and, finally, prior distributions. To facilitate the exposition, Table 2 provides a summary of four possible specifications of the model along with the hyperparameters that require specification by the analyst.
Table 2.
Summary of four models based on parametric and non-parametric specifications of the baseline hazard functions and hospital-specific random effects distributions. Hyperparameters that require specification by the analyst are provided in parenthesis. Note, (aθ, bθ), the hyper-parameters for the patient-specific frailty variance component, require specification in all of four models.
| Hospital-specific random effects, Vj | ||
|---|---|---|
| Baseline hazard functions, h0g (·) | MVN (Ψυ, ρυ) |
DPM† (Ψ0, ρ0, τ) |
| Weibull (aα,g, bα,g, aκ,g, bκ,g) | Weibull-MVN | Weibull-DPM |
| PEM† (αKg, aσ,g, bσ,g) | PEM-MVN | PEM-DPM |
PEM: piecewise exponential model; DPM: Dirichlet process mixture
3.3 Baseline hazard functions
Within the frequentist paradigm estimation and inference for time-to-event models is often based on a partial likelihood which conditions on risk sets, removing the need for analysts to specify baseline hazard functions. In the Bayesian paradigm, however, one is required to specify these functions. Here, we consider two strategies. The first assumes that the underlying transition times follow Weibull(αw,g, κw,g) distributions, parameterized so that h0g(t) = αw,gκw,gtαw,g − 1. While such a parametric specification is appealing due to its computational simplicity, especially in small-sample settings, the Weibull is somewhat restrictive in that the corresponding hazard function is strictly monotone. As an alternative, we consider a non-parametric specification based on taking each of the log-baseline hazard functions to be a flexible mixture of piecewise constant functions (McKeague and Tighiouart, 2000). Briefly, let sg,max denote the maximum observed time for transition g and partition (0, sg,max] into Kg + 1 intervals: sg = {sg,0, sg,1, …, sg,Kg + 1}, with sg,0 ≡ 0 and sg,Kg + 1 ≡ sg,max. Given the partition (Kg, sg), we assume
| (8) |
where λg,k is the (constant) height of the log-baseline hazard function on the interval (sg,k − 1, sg,k]. We refer to this specification as a piecewise exponential model (PEM) for the baseline hazard function. Note, while numerous options are available for specifying these functions (e.g. Ibrahim et al., 2001), a key benefit of this structure is that it balances flexibility and computational convenience, since the integrals in the likelihood (specifically for the cumulative hazard functions) are replaced with summations (Lee et al., 2015).
3.4 Hospital-specific random effects
As with specification of the baseline hazard functions, we consider two options for the specification of the population distribution for the J hospital-specific vectors of random effects. First, motivated by the current standard for analyses of readmission (i.e. a LN-GLMM), we consider a specification in which the Vj arise as i.i.d draws from a mean-zero multivariate Normal distribution with variance-covariance matrix ΣV. The diagonal elements of the 3×3 matrix ΣV characterize variation across hospitals in risk for readmission, death and death following readmission, respectively, that is not explained by covariates included in the linear predictors. Crucially, that each random effect has its own variance component allows the characterization of differential variation across hospitals for each of the three transitions. In addition, the off-diagonals of ΣV permit covariation between the three random effects across the hospitals giving researchers the ability to characterize, for example, whether or not hospitals with high mortality rates tend to have low readmission rates.
While conceptually simple and computationally convenient, the Normal distribution it is often criticized as being a strong assumption. As an alternative we consider the use of a so-called Bayesian nonparametric specification for the population distribution of Vj, specifically a Dirichlet process mixture of multivariate Normal distributions (DPM-MVN) (Ferguson, 1973; Bush and MacEachern, 1996; Walker and Mallick, 1997). One representation of this model is as follows:
| (9) |
where μj, Σj are the cluster-specific latent mean and variance of Vj, which are taken to be draws from some (unknown) distribution G to which a Dirichlet process prior is assigned. Finally the Dirichlet process is indexed by G0, the so-called centering distribution, and τ, the so-called precision parameter.
3.5 Hyperparameters and prior distributions
The proposed Bayesian framework is completed with the specification of prior distributions for unknown parameters introduced in Sections 3.1–3.4.
3.5.1 Stage one parameters
For each of the transition-specific regression parameters, βg for g=1,2,3, a non-informative at prior on the real line is adopted. For the shared patient-specific frailties, γji, we assume that they arise from a Gamma(θ−1, θ−1) distribution, parameterized so that E[γji] = 1 and V [γji] = θ. In the absence of prior knowledge on the frailty variance component, a Gamma(aθ, bθ) hyperprior for the precision θ−1 is adopted.
3.5.2 Baseline hazard functions
For the parametric Weibull baseline hazard functions, since the hyperparameters have support on (0, ∞), we complete the specification of this model by adopting gamma prior distributions for both; that is, we take αw,g ~ Gamma(aα,g, bα,g) and κw,g ~ Gamma(aκ,g, bκ,g), g=1,2,3.
To complete the non-parametric PEM model specification, we specify that the Kg + 1 heights arise from a multivariate Normal distribution. Specifically, letting λg = (λg,1, …, λg,Kg, λg,Kg + 1) denote the transition-specific heights, we assume that , where μλg is the overall mean, is a common variance component for the Kg + 1 elements and Σλg is a correlation matrix. To induce a priori smoothness in the baseline hazard functions we view the components of λg in terms of a one-dimensional spatial problem, so that adjacent intervals can ‘borrow’ information from each other. To do this we specify Σλg via a Gaussian intrinsic conditional autoregression (ICAR)(Besag and Kooperberg, 1995). Additional technical details regarding the corresponding MVN-ICAR are provided in Supplementary Materials A. Finally, we specify a series of hyperpriors for the additional parameters introduced in the MVN-ICAR. In particular, we adopt a at prior on the real line for μλg and a conjugate Gamma(aσ,g, bσ,g) distribution for the precision . For the ICAR specification, we avoid reliance on a fixed partition of the time scales by permitting the partition (Kg, sg) to vary and be updated via a reversible jump MCMC scheme (Green, 1995). Towards this we first adopt a Poisson(αKg) prior for the number of splits in the partition, Kg. Conditional on the number of splits, we take the locations to be a priori distributed as the even-numbered order statistics:
| (10) |
Jointly, these choices form a time-homogeneous Poisson process prior for the partition (Kg, sg) so that a posteriori, after mixing over partitions as they arise in the MCMC scheme, the value of λg(t) in any given small interval of time is characterized as a smooth exponentiated mixture of piecewise constant functions (Arjas and Gasbarra, 1994; McKeague and Tighiouart, 2000; Haneuse et al., 2008).
3.5.3 Hospital-specific random effects
For the parametric specification of a single MVN3(0, ΣV) distribution, we adopt a conjugate inverse-Wishart(Ψυ, ρυ) prior for the variance-covariance matrix ΣV. Completion of the non-parametric DPM-MVN model requires specification of prior choices for the centering distribution and the precision parameter. Here we take G0 to be a multivariate Normal/inverse-Wishart (NIW) distribution for which the probability density function can be expressed as the product:
where fD(·|θD) is the density function for a distribution D indexed by θD. This choice is appealing in that one can exploit prior-posterior conjugacy in the MCMC scheme (Neal, 2000). Finally, we treat hyperparameter the precision parameter in DPM-MVN specification, τ, as unknown and assign a Gamma(aτ, bτ) hyperprior (Escobar and West, 1995).
4 Posterior Inference and Model Comparison
4.1 Markov Chain Monte Carlo
To perform estimation and inference for each of the models in Table 2 we use a random scan Gibbs sampling algorithm to generate samples from their joint posterior distributions. In the corresponding Markov chain Monte Carlo (MCMC) scheme, parameters are updated by either exploiting conjugacies inherent to the model structure or using a Metropolis-Hastings step. For models that adopt a PEM specification for the baseline hazard functions, updating the partition (Kg, s) requires a change in the dimension of the parameter space and a Metropolis-Hastings-Green step is used (Green, 1995). A detailed description of proposed computational scheme is given in Supplementary Materials B; as mentioned in Section 3.1, the computation scheme has been developed for both the Markov and semi-Markov models for h03(·).
Finally, we note that the algorithms are implemented in the SemiCompRisks package for R (R Development Core Team, 2014). Given the complexity of the proposed models, and the numerous updates in the MCMC scheme, C has been used as the primary computational engine to ensure that analyses can be conducted within a reasonable timeframe.
4.2 Model comparison
In practice, analysts have to balance model complexity with the realities of sample size and availability of information. While each of models in Table 2 has its own merit and utility, it may be of interest to directly compare their goodness of fit to the observed data. To this end, we consider two model assessment metrics: the deviance information criterion (DIC; Spiegelhalter et al., 2002), and the log-pseudo marginal likelihood statistic (LPML; Geisser and Eddy, 1979; Gelfand and Mallick, 1995). Although DIC is often the default choice for model comparison in the Bayesian paradigm, its use in the context of complex hierarchical models requires care (Celeux et al., 2006). Specifically for models that condition on latent parameters, such as the patient-specific γji in models (4)–(6), DIC computed on the basis of a likelihood that is marginalized with respect to these parameters performs more reliably as a metric for comparison than DIC computed on the basis of a likelihood that conditions on them (Millar, 2009). For our purposes, since the Vj random effects are of intrinsic scientific interest, we propose to evaluate DIC and LPML on the basis of a partially marginalized likelihood, one that integrates solely over the distribution of the patient-specific frailties:
| (11) |
where Φ* = {β1, β2, β3, h01, h02, h03, θ, V⃗}, ℒ(𝒟ji|·) is given by expression (7) and f(·; θ) is the density of a Gamma(θ−1, θ−1) distribution (see Section 3.5.1).
Given expression (11), we therefore compute DIC as:
| (12) |
where is the (marginal) deviance and is the posterior mean of Φ*. The penalty term, pD, is given by , where D̅(Φ*) is the posterior mean of D(Φ*). Note, a model with smaller DIC indicates a better fit of the model for the data.
The LPML statistic is computed as , the sum of the logarithms of the patient-specific conditional predictive ordinate (CPO) (Geisser, 1993), each defined as:
| (13) |
where 𝒟(−ji) denotes the data with the observation from the ith patient in the jth cluster removed. Intuitively, the CPOji is the posterior probability of the observed outcome for ith patient in the jth cluster, i.e. (yji1, δji1, yji2, δji2), on the basis of a model fit to a dataset that excludes that particular patient. Thus, large values of CPOji attribute high posterior probability to the observed data and, therefore, indicate a better fit. Although a closed form expression for CPOji is not available for our proposed models, following Shao and Ibrahim (2000) we approximate CPOji via a Monte Carlo estimator:
| (14) |
where {Φ*(q); q = 1, 2, …, Q} are MCMC samples drawn from the (marginal) joint posterior distribution of Φ*.
5 Simulation Studies
The performance of the proposed models is investigated through a series of simulation studies. The overarching goals of the simulation studies are to investigate the small sample operating characteristics of the models summarized in Table 2 under a variety of scenarios as well as to compare their performance with the methods of Liquet et al. (2012).
5.1 Set-up and data generation
Towards developing a comprehensive understanding of the performance of the proposed methods we consider six data scenarios that vary in terms of the true underlying baseline hazard distributions, the true distribution of the cluster-specific random effects and the true extent of variation in the patient-specific frailties. Table 3 provides a summary. In scenarios 1–5, the baseline hazard functions are set to correspond to the hazard of a Weibull distribution so that the event rates in the simulated data are similar to those in the observed Medicare data when the outcomes are administratively censored at t=90; specifically, we set (αw,1, κw,1)=(0.8, 0.05), (αw,2, κw,2)=(1.1, 0.01), and (αw,3, κw,3)=(0.9, 0.01). To evaluate the performance of the model when the baseline hazard functions do not correspond to a Weibull, scenario 6 takes them to be piecewise linear functions: h0g(t) = {(kg−bg)t/40+bg}I(t≤40) + {(3kg−bg)/2−(kg−bg)t/80}I(t>40), with b1=0.1, b2=0.05, b3=0.15, and k1=k2=k3=0.0005 specified so that the true baseline hazard functions are not monotone increasing or decreasing functions like a Weibull.
Table 3.
Summary of six simulation scenarios explored in Section 5.
| Scenario | Distribution of baseline hazard functions |
Distribution of cluster-specific random effects, Vj |
θ | |
|---|---|---|---|---|
| 1 | Weibull | MVN(0, 0.25·I) | 0.50 | |
| 2 | Weibull | MVN(0, 0.25·I) | 1.00 | |
| 3 | Weibull | 0.50 | ||
| 4 | Weibull | MVN(0, 0.25·I) | 0.00 | |
| 5 | Weibull | 0.5·MVN(0, I)+0.5·MVN(0, 0.01·I) | 0.50 | |
| 6 | Piecewise linear | MVN(0, 0.25·I) | 0.50 |
With regard to the ‘true’ distribution of the cluster-specific random effects, scenarios 1, 2, 4 and 6 consider a multivariate Normal distribution in which the components are independent. Scenario 3 expands on this by considering the impact of covariation across the Vj, while Scenario 5 examines the performance of the models when the true distribution is a mixture of two multivariate Normal distributions.
Finally, with regard to the ‘true’ variance of the patient-specific frailties, scenarios 1, 3, 5 and 6 consider a base value of θ=0.5. This value was chosen as a compromise across the posterior medians from the fits of the four models in Table 2 to the Medicare data (see Table 9 below). Scenario 2 considers the impact of greater variation in the patient-specific frailties, while Scenario 4 corresponds to a misspecification of the proposed model with the ‘true’ θ set to 0.
Table 9.
Posterior summaries (medians (PM) and 95% credible intervals (CI)) for standard deviations (SD) of the underlying population distributions for the patient-specific frailties and hospital-specific random effects. Estimates of population correlation components, between hospital-specific random effects, are also provided.
| Weibull-MVN PM (95% CI) |
Weibull-DPM PM (95% CI) |
PEM-MVN PM (95% CI) |
PEM-DPM PM (95% CI) |
|
|---|---|---|---|---|
| Patient-specific frailties |
||||
| 1.03 (0.94, 1.12) | 1.03 (0.95, 1.12) | 0.61 (0.50, 0.71) | 0.61 (0.49, 0.71) | |
| Hospital-specific random effects |
||||
| SD(Vj1) | 0.26 (0.20, 0.34) | 0.27 (0.21, 0.35) | 0.25 (0.19, 0.32) | 0.25 (0.20, 0.32) |
| SD(Vj2) | 0.37 (0.28, 0.47) | 0.37 (0.28, 0.47) | 0.32 (0.25, 0.41) | 0.32 (0.25, 0.42) |
| SD(Vj3) | 0.37 (0.27, 0.50) | 0.37 (0.27, 0.50) | 0.33 (0.25, 0.44) | 0.33 (0.25, 0.45) |
| corr(Vj1, Vj2) | −0.04 (−0.40, 0.33) | −0.04 (−0.40, 0.33) | −0.12 (−0.44, 0.23) | −0.12 (−0.45, 0.24) |
| corr(Vj1, Vj3) | 0.06 (−0.32, 0.42) | 0.06 (−0.32, 0.43) | 0.03 (−0.32, 0.38) | 0.03 (−0.33, 0.39) |
| corr(Vj2, Vj3) | 0.39 (−0.02, 0.67) | 0.37 (−0.03, 0.67) | 0.28 (−0.12, 0.59) | 0.29 (−0.11, 0.59) |
For each of the six scenarios we generated R=500 simulated datasets under the semi-Markov illness-death model described in Section 3.1. Across all simulated datasets, we set the number of clusters and cluster-specific sample sizes to be those observed in the Medicare data. Furthermore, we specified that each of the three transition-specific hazard functions depended on three covariates: Xjig,1 and Xjig,2 both Normal(0, 1) random variables and Xjig,3 a Bernoulli(0.5) random variable. The regression coefficients are set to β1=β2=(0.5, 0.8, −0.5) and β3=(1.0, 1.0, −1.0), so that the covariate effects on the risk of the terminal event depend on whether or not the non-terminal event has occurred. Finally, we note that the function used to simulate the semi-competing risks data is available in the SemiCompRisks package.
5.2 Analyses
For each of the R=500 datasets under each of the six scenarios we fit each of the four models in Table 2. For the proposed models in which the baseline hazard function was specified via a Weibull distribution, we set (aα,g, bα,g) = (0.5, 0.01) and (aκ,g, bκ,g) = (0.5, 0.05) for the transition-specific shape and rate parameters. For models in which a non-parametric PEM specification was adopted for the baseline hazard function, we set the prior Poisson rate on the number of intervals to be αg = 10. For the precision parameter in the MVN-ICAR specification, we set (aσ,g, bσ,g) = (0.7, 0.7) so that the induced prior for had a median of 1.72 and 95% central mass between 0.23 and 156.
For the variance component associated with the patient-specific frailties, we set (aθ, bθ) = (0.7, 0.7); that is the same prior was used for the precision θ−1 for the γji frailties as the precision component in the MVN-ICAR specification for the PEM model. For the hospital-specific random effects variance components, given a MVN specification, we set (Ψυ, ρυ) = (I3, 5) so that the induced prior on ΣV has a prior mean given by the 3×3 identity matrix. The same prior was adopted for the variance-covariance matrix of the centering distribution of the DPM-MVN specification, G0; that is, we set (Ψ0, ρ0) = (I3, 5). Finally, for the precision parameter in the DPM-MVN specification we set (aτ, bτ) = (1.5, 0.0125) so that a priori τ had a mode of 40 and standard deviation of 98. Given the prior specifications, two independent chains were run for a total of six million scans each; the Gelman-Rubin potential scale reduction (PSR) statistic (Gelman et al., 2013) was used to assess convergence, specifically requiring the PSR to be less than 1.05 for all model parameters.
In addition to the models in Table 2, we analyzed each simulated dataset using the methods of Liquet et al. (2012). Specifically, we considered the ‘shared frailty’ (SF) model implemented in the frailtypack package for R (Rondeau et al., 2012) and summarized using notation consistent with that adopted in this manuscript in Supplementary Materials Section C. Briefly, this model adopts a Cox-type regression structure for each transition-specific hazard, as we do in expressions (4)–(6). For the baseline hazard functions, two options are available: one that corresponds to a Weibull distribution and another where each hg(·) is specified via a flexible penalized smoothing spline. To distinguish these models, we refer to them as the Weibull-SF and Spline-SF models, respectively. In contrast to the specification in (4)–(6), the SF model introduces a cluster-specific frailties as a multiplicative factors for each transition-specific hazard. Two options are available for the distribution of these factors across the clusters; either they arise from three independent gamma distributions or they arise from three independent log-Normal distributions. For either option, estimation and inference is performed within the frequentist paradigm specifically based on an integrated likelihood that marginalizes out the cluster-specific frailties; estimation of the latter is performed via empirical Bayes. In this paper, we present the results from the SF models that adopt independent gamma distributions for cluster-specific frailties while we provide those from the SF models with independent log-Normal frailties in Supplementary Materials D. Finally, we note that in contrast to the specification in expressions (4)–(6), the SF model does not account for within-patient correlation. That is there is no quantity that corresponds to the patient-specific γji terms in the proposed models.
5.3 Results
5.3.1 Baseline survivor functions
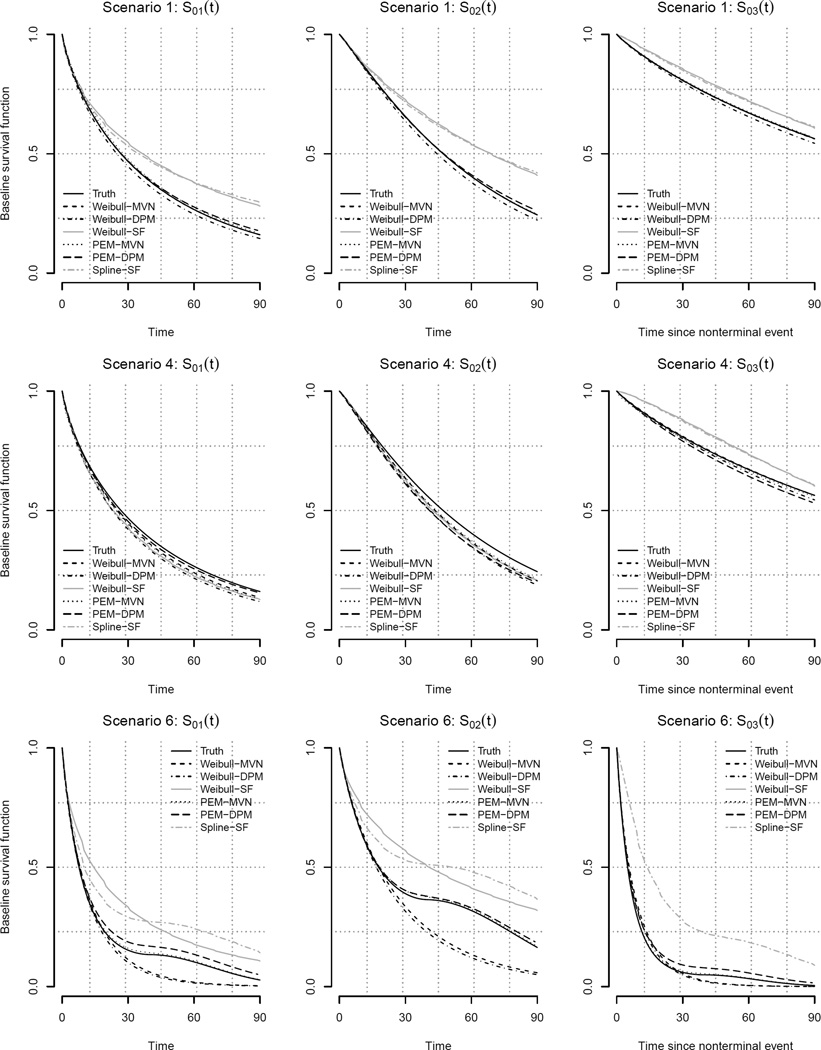
Figure 2 presents the mean estimated transition-specific baseline survival functions under scenarios 1, 4 and 6 across the six models. Under scenarios 1 and 4, for which the baseline hazard functions are Weibull, all four of the proposed models estimate the three baseline survivor functions very well. In contrast the two SF models only perform well in scenario 4 for which θ=0. This is to be expected since, as described in detail in Supplementary Materials Section C, the SF model does not include patient-specific frailties; effectively, it assumes that θ=0 even when it is not. In scenario 6, for which the baseline hazard functions are not Weibull, the proposed PEM-MVN and PEM-DPM specifications capture the true shape of the baseline survivor functions well; all four of the models that assume the baseline hazard function to be a Weibull, however, are unable to capture the shape.
Figure 2.
Estimated transition-specific baseline survival functions, S0g(·) = exp(−H0g(·)), for each six analyses described in Section 5.2 under simulation scenarios 1, 4 and 6.
5.3.2 Regression parameters and θ
Focusing on scenarios 1–3, each corresponding to a ‘true’ Weibull-MVN model, Table 4 indicates that all four of the proposed models in Table 2 perform very well in terms of estimation and inference for β1 and θ. Across the board, we find that percent bias is no larger than 3.2% and the estimated coverage probabilities are all close to the nominal 0.95. In contrast, both the Weibull-SF and Spline-SF models yield point estimates of β1 that are significantly biased and, as such, have poor coverage probabilities. The poor performance of the SF models is likely tied to the fact that they do not account for within-patient correlation; hence θ is not estimated by these models. The results for these models, however, is dramatically improved under scenario 4 for which the true value of θ is zero (i.e. the scenario they explicitly accommodate). Interestingly, the four proposed models each exhibit a small amount of bias under this scenario (up to approximately 5%). In addition the coverage probabilities for β11 and β12 are poor, particularly for the two models that adopt a PEM specification for the baseline hazard function. In scenario 5, we again see that all four of the proposed models perform well. Finally, under scenario 6 we see that the PEM-MVN and PEM-DPM models perform very well in terms of bias and coverage. In contrast, the Weibull-MVN and Weibull-DPM models perform poorly, particularly with respect to estimation of θ, illustrating the potential danger of adopting a parametric Weibull baseline hazard function when the truth is not a Weibull.
Table 4.
Estimated percent bias and coverage probability for β1 and θ for six analyses described in Section 5.2, across six simulation scenarios given in Table 3. Throughout values are based on results from R=500 simulated datasets.
| Percent Bias | Coverage Probability | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | True value |
Weibull -MVN |
Weibull -DPM |
Weibull -SF |
PEM -MVN |
PEM -DPM |
Spline -SF |
Weibull -MVN |
Weibull -DPM |
Weibull -SF |
PEM -MVN |
PEM -DPM |
Spline -SF |
|
| 1 | β11 | 0.50 | 0.1 | 0.2 | −19.8 | 0.4 | 0.4 | −21.0 | 0.96 | 0.96 | 0.01 | 0.95 | 0.96 | 0.00 |
| β12 | 0.80 | 0.2 | 0.3 | −19.7 | 0.5 | 0.4 | −21.0 | 0.95 | 0.95 | 0.00 | 0.96 | 0.97 | 0.00 | |
| β13 | −0.50 | 0.3 | 0.3 | −19.8 | 0.3 | 0.3 | −21.2 | 0.97 | 0.96 | 0.31 | 0.96 | 0.96 | 0.25 | |
| θ | 0.50 | 1.0 | 1.3 | 1.4 | 1.2 | 0.95 | 0.95 | 0.93 | 0.94 | |||||
|
| ||||||||||||||
| 2 | β11 | 0.50 | −0.1 | −0.0 | −31.8 | 0.1 | 0.1 | −32.8 | 0.94 | 0.94 | 0.00 | 0.94 | 0.93 | 0.00 |
| β12 | 0.80 | 0.1 | 0.2 | −31.7 | 0.4 | 0.3 | −32.7 | 0.97 | 0.97 | 0.00 | 0.94 | 0.95 | 0.00 | |
| β13 | −0.50 | 1.2 | 1.3 | −31.1 | 1.1 | 1.1 | −32.2 | 0.94 | 0.95 | 0.05 | 0.94 | 0.94 | 0.04 | |
| θ | 1.00 | 0.4 | 0.7 | 0.7 | 0.6 | 0.94 | 0.95 | 0.94 | 0.95 | |||||
|
| ||||||||||||||
| 3 | β11 | 0.50 | 0.3 | 0.3 | −19.9 | 0.7 | 0.7 | −21.0 | 0.94 | 0.94 | 0.00 | 0.93 | 0.94 | 0.00 |
| β12 | 0.80 | 0.4 | 0.4 | −19.8 | 0.8 | 0.8 | −20.9 | 0.94 | 0.94 | 0.00 | 0.94 | 0.94 | 0.00 | |
| β13 | −0.50 | 0.4 | 0.3 | −20.1 | 0.5 | 0.6 | −21.2 | 0.96 | 0.96 | 0.31 | 0.95 | 0.96 | 0.27 | |
| θ | 0.50 | 2.0 | 2.1 | 3.2 | 3.2 | 0.96 | 0.96 | 0.93 | 0.95 | |||||
|
| ||||||||||||||
| 4 | β11 | 0.50 | 3.7 | 3.7 | 0.2 | 4.7 | 4.6 | 0.3 | 0.87 | 0.86 | 0.96 | 0.81 | 0.83 | 0.96 |
| β12 | 0.80 | 3.6 | 3.6 | −0.0 | 4.5 | 4.5 | 0.1 | 0.80 | 0.79 | 0.95 | 0.69 | 0.70 | 0.95 | |
| β13 | −0.50 | 4.0 | 4.0 | 0.2 | 4.8 | 4.7 | 0.2 | 0.93 | 0.94 | 0.94 | 0.93 | 0.93 | 0.93 | |
| θ | 0.00 | |||||||||||||
|
| ||||||||||||||
| 5 | β11 | 0.50 | −0.3 | 0.1 | −20.3 | 0.0 | 0.3 | −21.1 | 0.94 | 0.95 | 0.00 | 0.96 | 0.96 | 0.00 |
| β12 | 0.80 | 0.0 | 0.3 | −20.0 | 0.3 | 0.6 | −20.9 | 0.95 | 0.95 | 0.00 | 0.96 | 0.96 | 0.00 | |
| β13 | −0.50 | −0.2 | 0.2 | −20.4 | −0.2 | 0.2 | −21.3 | 0.94 | 0.94 | 0.29 | 0.94 | 0.94 | 0.25 | |
| θ | 0.50 | −0.2 | 1.0 | 0.4 | 1.3 | 0.95 | 0.95 | 0.95 | 0.96 | |||||
|
| ||||||||||||||
| 6 | β11 | 0.50 | 9.3 | 9.4 | −22.1 | 0.4 | 0.3 | −25.9 | 0.58 | 0.57 | 0.00 | 0.94 | 0.94 | 0.00 |
| β12 | 0.80 | 9.7 | 9.8 | −22.0 | 0.5 | 0.5 | −25.8 | 0.20 | 0.20 | 0.00 | 0.94 | 0.95 | 0.00 | |
| β13 | −0.50 | 10.2 | 10.2 | −21.6 | 0.8 | 0.7 | −26.1 | 0.81 | 0.80 | 0.21 | 0.93 | 0.94 | 0.10 | |
| θ | 0.50 | 52.8 | 53.0 | 1.8 | 1.7 | 0.00 | 0.00 | 0.95 | 0.96 | |||||
While Table 4 explores estimation and the (valid) quantification of uncertainty, Table 5 examines the relative merits of the various analysis approaches in terms of efficiency. Specifically, we computed the average relative width of 95% credible/confidence intervals for β1 and θ under each analysis with the Weibull-MVN model taken as a common referent. Comparing the Weibull-DPM to the Weibull-MVN as well as the results between the PEM-MVN and PEM-DPM we see that there is no loss of efficiency for any of the regression parameters, and minimal loss for θ, if one adopts the flexible DPM specification for the cluster-specific random effects, even if the true distribution is a MVN. Under all five scenarios for which the true baseline hazard functions were Weibull hazard functions, the two models that adopt a PEM specification have somewhat wider credible intervals particularly for θ. However, as expected, the 95% credible intervals for the two PEM models under scenario 6 are somewhat tighter indicating improved efficiency when the true baseline hazard functions are not Weibull hazard functions. Finally, across all scenarios, the estimated 95% confidence intervals for the two SF models are substantially tighter than those for any of the proposed analyses, although this must be balanced with the high bias shown in Table 4.
Table 5.
Average relative width of 95% credible/confidence intervals for β1 and θ, with the Weibull-MVN model taken as the referent, across six simulation scenarios given in Table 3. Throughout values are based on results from R=500 simulated datasets.
| Scenario | Weibull -MVN |
Weibull -DPM |
Weibull -SF |
PEM -MVN |
PEM -DPM |
Spline -SF |
|
|---|---|---|---|---|---|---|---|
| 1 | β11 | 1.00 | 1.00 | 0.81 | 1.02 | 1.02 | 0.81 |
| β12 | 1.00 | 1.00 | 0.77 | 1.04 | 1.04 | 0.77 | |
| β13 | 1.00 | 1.00 | 0.84 | 1.00 | 1.01 | 0.83 | |
| θ | 1.00 | 1.00 | 1.10 | 1.12 | |||
| 2 | β11 | 1.00 | 1.00 | 0.73 | 1.02 | 1.02 | 0.73 |
| β12 | 1.00 | 1.00 | 0.69 | 1.03 | 1.04 | 0.69 | |
| β13 | 1.00 | 1.00 | 0.76 | 1.00 | 1.00 | 0.76 | |
| θ | 1.00 | 1.00 | 1.12 | 1.14 | |||
| 3 | β11 | 1.00 | 1.00 | 0.81 | 1.02 | 1.02 | 0.81 |
| β12 | 1.00 | 1.00 | 0.76 | 1.04 | 1.04 | 0.77 | |
| β13 | 1.00 | 1.00 | 0.83 | 1.00 | 1.01 | 0.83 | |
| θ | 1.00 | 1.00 | 1.10 | 1.13 | |||
| 4 | β11 | 1.00 | 1.00 | 0.95 | 1.02 | 1.01 | 0.96 |
| β12 | 1.00 | 1.00 | 0.94 | 1.03 | 1.03 | 0.95 | |
| β13 | 1.00 | 1.00 | 0.96 | 1.01 | 1.01 | 0.96 | |
| θ | 1.00 | 1.00 | 1.09 | 1.09 | |||
| 5 | β11 | 1.00 | 1.00 | 0.81 | 1.02 | 1.02 | 0.81 |
| β12 | 1.00 | 1.00 | 0.77 | 1.03 | 1.03 | 0.77 | |
| β13 | 1.00 | 1.00 | 0.83 | 1.00 | 1.00 | 0.83 | |
| θ | 1.00 | 1.00 | 1.09 | 1.09 | |||
| 6 | β11 | 1.00 | 1.00 | 0.74 | 0.94 | 0.95 | 0.73 |
| β12 | 1.00 | 1.00 | 0.72 | 0.96 | 0.97 | 0.71 | |
| β13 | 1.00 | 1.00 | 0.76 | 0.93 | 0.93 | 0.75 | |
| θ | 1.00 | 1.00 | 0.89 | 0.90 | |||
5.3.3 Cluster-specific random effects
Finally, Table 6 investigates the relative performance of the various analyses with respect to estimation of the cluster-specific random effects. Specifically, we calculated the mean squared error of prediction (MSEP) given by:
| (15) |
where Vrjg is the cluster-specific random effect for the jth cluster in the transition g for the rth simulated data set, r=1,…,R. For each of the four proposed models, V̂rjg was taken as the corresponding posterior median. For the two SF models, V̂rjg was taken as a the log of the empirical Bayes estimates of the transition/cluster-specific frailties (see Supplementary Materials C for details). We note, however, that for some of the simulated datasets, the empirical Bayes estimates returned by the current implemented in the frailtypack package were zero. Since taking the log of these estimates would yield V̂rjg = −∞, we calculated MSEP over the random effects for which the empirical Bayes estimate was non-zero; to place these values in context, Table 6 also reports the percentage of instances where a frailty was estimated to be zero.
Table 6.
Mean squared error of prediction (×10−2) for cluster-specific random effects based on six analyses described in Section 5.2, across six data scenarios given in Table 3. Throughout values are based on results from R=500 simulated datasets.
| Scenario | Weibull -MVN |
Weibull -DPM |
Weibull -SF |
PEM -MVN |
PEM -DPM |
Spline -SF |
|||
|---|---|---|---|---|---|---|---|---|---|
| %F† | %F | ||||||||
| 1 | V1 | 5.25 | 5.27 | 6.40 | 17.8 | 5.27 | 5.27 | 6.39 | 0.2 |
| V2 | 7.66 | 7.70 | 8.70 | 7.67 | 7.72 | 8.68 | |||
| V3 | 9.91 | 9.95 | 12.13 | 9.91 | 9.96 | 12.11 | |||
| 2 | V1 | 6.36 | 6.41 | 8.10 | 10.4 | 6.37 | 6.41 | 8.09 | 0.0 |
| V2 | 8.76 | 8.85 | 10.23 | 8.77 | 8.86 | 10.20 | |||
| V3 | 11.13 | 11.19 | 13.85 | 11.13 | 11.19 | 13.91 | |||
|
| |||||||||
| 3 | V1 | 5.03 | 5.04 | 6.27 | 15.8 | 5.04 | 5.04 | 6.22 | 0.0 |
| V2 | 6.34 | 6.34 | 8.28 | 6.36 | 6.36 | 8.24 | |||
| V3 | 7.55 | 7.49 | 11.66 | 7.57 | 7.55 | 11.69 | |||
|
| |||||||||
| 4 | V1 | 3.84 | 3.85 | 4.99 | 12.8 | 3.87 | 3.87 | 5.01 | 0.4 |
| V2 | 6.25 | 6.27 | 7.19 | 6.25 | 6.27 | 7.12 | |||
| V3 | 7.89 | 7.90 | 9.57 | 7.90 | 7.91 | 9.52 | |||
|
| |||||||||
| 5 | V1 | 6.95 | 6.26 | 10.87 | 12.8 | 6.96 | 6.27 | 10.86 | 0.2 |
| V2 | 11.52 | 10.50 | 14.95 | 11.50 | 10.52 | 14.92 | |||
| V3 | 15.46 | 14.66 | 25.04 | 15.46 | 14.72 | 24.94 | |||
|
| |||||||||
| 6 | V1 | 5.05 | 5.01 | 6.34 | 5.4 | 4.89 | 4.85 | 6.26 | 1.4 |
| V2 | 7.58 | 7.55 | 8.60 | 7.41 | 7.39 | 8.49 | |||
| V3 | 6.72 | 6.65 | 13.42 | 6.44 | 6.40 | 13.70 | |||
% of times SF models yield at least one of V̂j being −∞, resulting in MSEP being ∞
From Table 6 we see that under scenarios 1–4, for which the true model is a Weibull-MVN model, the Weibull-MVN analysis generally performs the best. Comparing the Weibull-MVN and PEM-MVN results across these scenarios, we see that over-specification of the baseline hazard functions (i.e. adoption of the more flexible PEM specification) does not meaningfully impact MSEP. In addition, comparing the Weibull-MVN and Weibull-DPM results we see that over-specification of the random effects structure (i.e. adoption of the more flexible DPM specification) does not adversely affect MSEP either. When the true distribution of the random effects is not a multivariate Normal distribution, however, as in scenario 5, both the Weibull-DPM and PEM-DPM models outperform their MVN counterparts, illustrating the potential benefit of the more flexible DPM specification. Furthermore, when the true baseline hazard functions do not correspond to a Weibull distribution, the MSEP for the two PEM models are, as expected, smaller than the corresponding values for the two Weibull models, illustrating the potential benefit of the more flexible PEM specification. Finally, we find that the empirical Bayes estimates of the cluster-specific random effects from the SF models perform relatively poorly when compared to the corresponding estimates from the proposed methods. For example, the Spline-SF model yields approximately 14% to 55% higher MSEP than our proposed PEM-MVN model across the six scenarios.
6 Analysis of Medicare Data
6.1 Analysis details and prior specifications
Returning to the motivating application of readmissions following a diagnosis of pancreatic cancer, we fit each of the four models summarized in Table 2 to the Medicare data under both the Markov and semi-Markov assumption for h3(·) (see Section 3.1). Based on the rationale provided in Section 2, we administratively censored observation time at 90 day. Given the results from the simulation studies, specifically with respect to estimation of the cluster-specific random effects, we decided not to fit the shared frailty models of Liquet et al. (2012). We did, however, perform an analysis based on a LN-GLMM model since this model is the current standard for analyzing variation in the risk of readmission and we believed it would be instructive to examine the potential impact of ignoring death as a competing force. Towards this, let be a binary indicator of whether or not the ith patient in the jth hospital readmitted within 90 days of discharge. Note, if a patient died prior to readmission within 90 days their outcome was set to . The LN-GLMM is then given by:
| (16) |
where is a hospital-specific random effect for readmission taken to be Normally distributed with mean zero and a constant variance, . To complete the Bayesian specification of this model, we adopted a Gamma(0.7, 0.7) prior for the precision . For the four proposed models, the hyperparameters outlined in Table 2 are specified as in Section 5.2
Throughout the analyses, to ensure the baseline hazard functions in the proposed models and the (overall) intercept in the LN-GLMM retained reasonable interpretations, age was standardized so that ‘zero’ corresponded to age 77 years and a one-unit increment corresponded to a 10-year contrast. Furthermore, length of stay during the initial hospitalization was also standardized so that ‘zero’ corresponded to 10 days and a one-unit increment corresponded to a 7-day contrast.
6.2 MCMC
Towards obtaining summaries of the joint posterior distributions we ran 3 independent chains of the proposed MCMC scheme, each for a total of 6 million scans. Convergence was evaluated by inspection of trace plots as well as calculation of the PSR statistic; an MCMC scheme was determined to have converged if the PSR statistic was less than 1.05 for all parameters in the model (see Supplementary Materials E). Although the hierarchical models are complex and include a large number of parameters, the proposed algorithm achieved an overall acceptance rate of 35% across the various Metropolis-Hastings and Metropolis-Hastings-Green steps. To provide a sense of computational time, the most complex of our proposed models (i.e. the PEM-DPM model), the implementation in our R package is able to generate 1 million scans in 30 minutes on a 2.5 GHz Intel Core i7 MacBook Pro; for the least complex of the models (i.e. the Weibull-MVN model), the implementation is able to generate 1 million scans in 10 minutes on the same machine.
6.3 Results
6.3.1 Overall model fit
Table 7 provides DIC and LPML for the eight model fits. For the DIC measure, a general rule of thumb for model comparison is to consider differences of less than 2 to be negligible, differences between 2 and 6 to indicative of positive support for the model with the lower value and differences greater than 6 to be strong support in value of the model with the lower value (Spiegelhalter et al., 2002; Millar, 2009). For LPML, one can compute the so-called pseudo Bayes factor (PBF) for two models by exponentiating difference in their LPML values (Hanson, 2006). While the conventional Bayes factor (Kass and Raftery, 1995) tends to find which model explains the observed data best, predictive methods such as PBF attempt to find which model gives the best predictions for future observations when the same process as the original data is used to generate the observations (Kadane and Lazar, 2004)
Table 7.
DIC and LPML for eight models fit to the New England Medicare data.
| DIC | LPML | ||
|---|---|---|---|
| Markov | Weibull-MVN | 46184.3 | −23101.6 |
| Weibull-DPM | 46174.1 | −23101.2 | |
| PEM-MVN | 45609.2 | −22812.6 | |
| PEM-DPM | 45606.8 | −22810.7 | |
| semi-Markov | Weibull-MVN | 46163.7 | −23088.8 |
| Weibull-DPM | 46153.0 | −23086.7 | |
| PEM-MVN | 45574.1 | −22790.9 | |
| PEM-DPM | 45569.0 | −22789.3 | |
Based on pairwise comparisons of the values in Table 7 we draw a number of conclusions. First, each of the models in which a semi-Markov specification is made for h03(·) has a substantially better fit to the data than the corresponding model in which a Markov assumption is made for h03(·); differences in DIC and the PBF range between 20.6–37.8 and the order of 105–109, respectively. Second, both DIC and LPML indicate that models for which a PEM specification was adopted for the baseline hazard functions have substantially better fit to the data than models for which a Weibull hazard function was adopted; differences in DIC and the PBF range between 567.3–589.6 and the order of 10125–10129, respectively. Finally, although DIC indicates a somewhat better fit for models that adopt a DPM for the random effects distribution compared to a MVN specification, the LPML values are less convincing in this regard; differences in DIC and the PBF range between 2.4–10.7 and 1.5–8.2, respectively.
6.3.2 Baseline survival functions
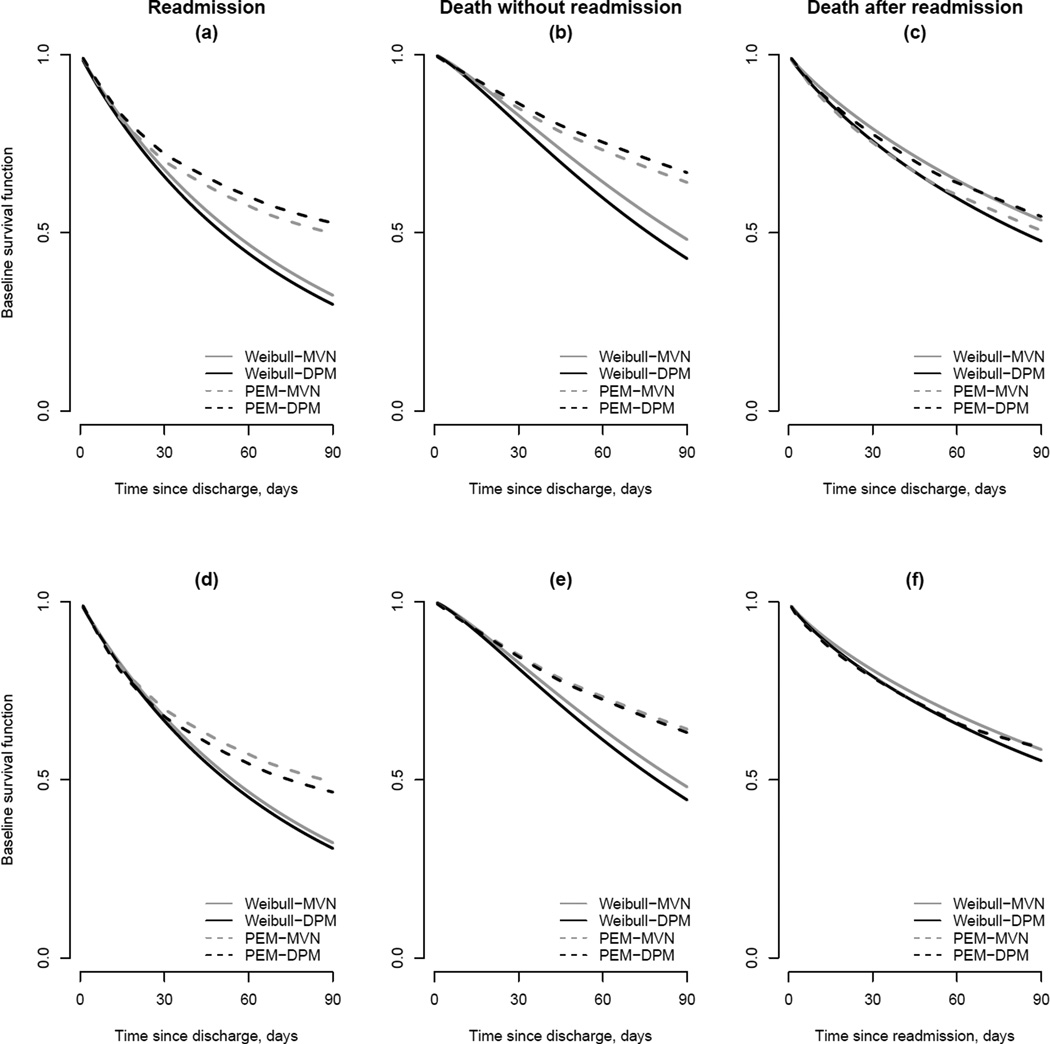
Since hazard functions are notoriously difficult to interpret, Figure 3 provides estimates of the corresponding baseline survival functions. Specifically, they provide pointwise time-specific posterior medians for S0g(·) for a 77-year old white female patient who had a Charlson/Deyo comorbidity score of 0 or 1, whose initial hospitalization lasted 10 days and during which they had no pancreatic cancer-related procedures, and were eventually discharged to their own home. In panels (a)–(c) results are presented for models for which a Markov assumption was adopted for h03(·); panels (d)–(f) present results for models for which a semi-Markov assumption was adopted.
Figure 3.
Estimated transition-specific baseline survival functions, S0g(·) = exp(−H0g(·)), for the eight models fit to the New England Medicare data (see Table 7). Panels (a)–(c) are estimates based on a Markov specification for h03(·); panels (d)–(f) are estimates based on a semi-Markov specification. Note the difference in time scale between panels (c) and (d) due the differing specifications for h03(·).
From panels (a) and (d) we see that all eight models indicate similar risk of readmission within the first 30 days. After 30 days, however, models with a parametric Weibull specification for the baseline hazard functions indicate substantially higher overall risk for readmission. Note, most of the observed readmission events occur relatively soon after discharge with a median of 18 days and 75% of observed events occurring within 40 days. As such, the posterior mass is being assigned to values of the two Weibull hyperparameters, (αg, κg), that fit the early time periods well to the detriment of fitting late periods relatively poorly. From panels (b) and (e) a similar phenomenon is observed for the baseline survival function for death without readmission for which the median event time is 20 days and, again, approximately 75% of observed events occurring within 40 days. In contrast, since the distribution of time to death following readmission is more spread out (median=43 days, IQR=40 days) the estimated baseline survival functions under the Weibull and PEM are more similar (see panels (c) and (f)).
6.3.3 Regression parameters
Posterior summaries for the vector of hazard ratio (HR) parameters for readmission, exp(β1), are presented in Table 8. For brevity, based in part on the conclusions drawn from Table 7, results are only presented for models for which a semi-Markov specification was adopted for h03(·); additional results, particularly for exp(β2) and exp(β3) are provided in Supplementary Materials E. In addition, posterior summaries for the vector of odds ratio (OR) parameters, exp(β*) from model (16), are also presented.
Table 8.
Posterior summaries (medians and 95% credible intervals (CI)) for hazard ratio (HR) parameters for readmission, exp(β1), from semi-competing risks data analyses and odds ratios (OR) based on a LN-GLMM. For the latter, results are reported for models for which a semi-Markov specification was adopted for h03(·)
| LN-GLMM OR (95% CI) |
Weibull-MVN HR (95% CI) |
Weibull-DPM HR (95% CI) |
PEM-MVN HR (95% CI) |
PEM-DPM HR (95% CI) |
|
|---|---|---|---|---|---|
| Sex | |||||
| Male | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Female | 0.91 (0.80, 1.03) | 0.80 (0.70, 0.90) | 0.79 (0.70, 0.90) | 0.85 (0.76, 0.96) | 0.85 (0.76, 0.95) |
| Age† | 0.87 (0.83, 0.92) | 0.90 (0.86, 0.95) | 0.90 (0.86, 0.95) | 0.91 (0.87, 0.94) | 0.91 (0.87, 0.95) |
| Race | |||||
| White | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Non-white | 1.17 (0.90, 1.51) | 1.12 (0.86, 1.45) | 1.12 (0.86, 1.46) | 1.11 (0.89, 1.40) | 1.12 (0.89, 1.38) |
| Source of entry to initial hospitalization | |||||
| Emergency room | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Other facility | 0.99 (0.86, 1.14) | 1.18 (1.03, 1.36) | 1.19 (1.03, 1.35) | 1.12 (1.00, 1.27) | 1.13 (1.00, 1.28) |
| Charlson/Deyo score | |||||
| ≤ 1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| >1 | 1.31 (1.05, 1.64) | 1.50 (1.19, 1.85) | 1.49 (1.20, 1.85) | 1.41 (1.15, 1.68) | 1.40 (1.15, 1.70) |
| Procedure during hospitalization | |||||
| No | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Yes | 0.73 (0.61, 0.86) | 0.45 (0.38, 0.53) | 0.44 (0.37, 0.54) | 0.56 (0.48, 0.66) | 0.57 (0.48, 0.66) |
| Length of stay* | 1.14 (1.06, 1.22) | 1.15 (1.07, 1.24) | 1.15 (1.07, 1.24) | 1.12 (1.05, 1.18) | 1.12 (1.05, 1.19) |
| Discharge location | |||||
| Home without care | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Home with care | 0.68 (0.58, 0.79) | 0.95 (0.82, 1.11) | 0.96 (0.82, 1.11) | 0.90 (0.79, 1.02) | 0.89 (0.78, 1.02) |
| Hospice | 0.06 (0.04, 0.10) | 0.39 (0.22, 0.62) | 0.39 (0.22, 0.62) | 0.27 (0.15, 0.45) | 0.27 (0.16, 0.43) |
| ICF/SNF | 0.44 (0.36, 0.53) | 0.88 (0.72, 1.07) | 0.88 (0.73, 1.08) | 0.76 (0.64, 0.90) | 0.76 (0.65, 0.90) |
| Other | 0.56 (0.41, 0.76) | 1.04 (0.75, 1.42) | 1.06 (0.75, 1.44) | 0.91 (0.70, 1.18) | 0.90 (0.68, 1.18) |
Standardized so that 0 corresponds to an age of 77 years and so that a one unit increment corresponds to 10 years
Standardized so that 0 corresponds to 10 days and so that a one unit increment corresponds to 7 day
Recognizing that the interpretation of the HR and OR parameters differ (due to the different set of frailties/random effects that are conditioned upon), the results in Table 8 indicate that the LN-GLMM qualitatively identifies a different set of risk factors for readmission than the results based on the proposed framework. For instance, while there is evidence of lower risk for readmission among females diagnosed with pancreatic cancer under the semi-competing risks approach (e.g. HR 0.80; 95% CI 0.70, 0.90 in Weibull-MVN), one cannot draw the same conclusion based on the LN-GLMM (OR 0.91; 95% CI 0.80, 1.03). In addition, under the LN-GLMM model there is no evidence of a relationship between source of entry to the initial hospitalization (OR 0.99; 95% CI 0.86, 1.14) while under each of the semi-competing risks analysis models there is evidence that patients who enter the initial hospitalization via some route other than the emergency room are at higher risk of readmission (e.g. HR 1.12; 95% CI 1.00, 1.28). Conflicting results are also found with respect to discharge destinflation. In particular, under the LN-GLMM model patients who are discharged to home with care, a hospice, a ICF/SNF or some ‘other’ facility (e.g. a rehabilitation center) have statistically significant lower estimates odds of readmission than patients discharged to their home without care. In contrast, results from the semi-competing risks analyses fail to indicate differences between patients discharged to home without care and those discharged to home with care (e.g. HR 0.90; 95% CI 0.79, 1.02) or to some other facility. Furthermore, while patients discharged to either a hospice or ICF/SNF have significantly lower odds of readmission, the estimated effects are substantially attenuated (e.g. compare OR=0.06 under the LN-GLMM to HR=0.27 under the PEM-MVN model). Finally, consistent with the assessment of model fit in Table 7, Table 8 indicates that for estimation and inference for regression parameters differs somewhat between models based on a Weibull baseline hazard specification and models based on a PEM specification. Comparing the Weibull-MVN model to the PEM-MVN model, for example, estimates for gender, Charlson/Deyo score and whether or not the patient underwent a procedure during the hospitalization are all attenuated; in contrast estimates for discharge location are generally strengthened under the PEM-MVN model, in some cases achieving statistical significance.
6.3.4 Variance components
Table 9 provides posterior summaries for the standard deviation of the patient-specific frailty distribution, , as well as components of the variance-covariance matrix for the hospital-specific V = (V1, V2, V3) from models in which a semi-Markov specification was adopted for h03(·). For the latter, the summaries are directly with respect to the components of ΣV under a MVN specification; under the two DPM specifications, posterior summaries are reported for the marginal total variance-covariance matrix obtained by applying the law of total cumulance: , where (Ohlssen et al., 2007). From the Table we see that the components of variation (particularly the standard deviation components) are generally smaller in magnitude for models in which a PEM specification for the baseline hazard functions was adopted. For example, under the Weibull-MVN model the posterior median of is 1.03, whereas the corresponding posterior median under the PEM-MVN model is 0.61. This is likely due to the γji patient-specific frailties not only representing patient-level heterogeneity but also accounting, in part, for misspecification of the Weibull model when the underlying baseline hazard functions are not Weibull. Qualitatively, across all four model specifications, we find that there is less variation across hospitals in the random effects specific to readmission compared to the random effects for mortality (either prior to or post-readmission); compare the posterior summaries for SD(Vj1) to those of SD(Vj2) and SD(Vj2). Furthermore, while there is no evidence of correlation between hospital-specific random effects for readmission and corresponding random effects for mortality, there is some evidence of a positive correlation between hospital-specific random effects for mortality pre- and post-readmission, although the 95% CIs each cover 0.
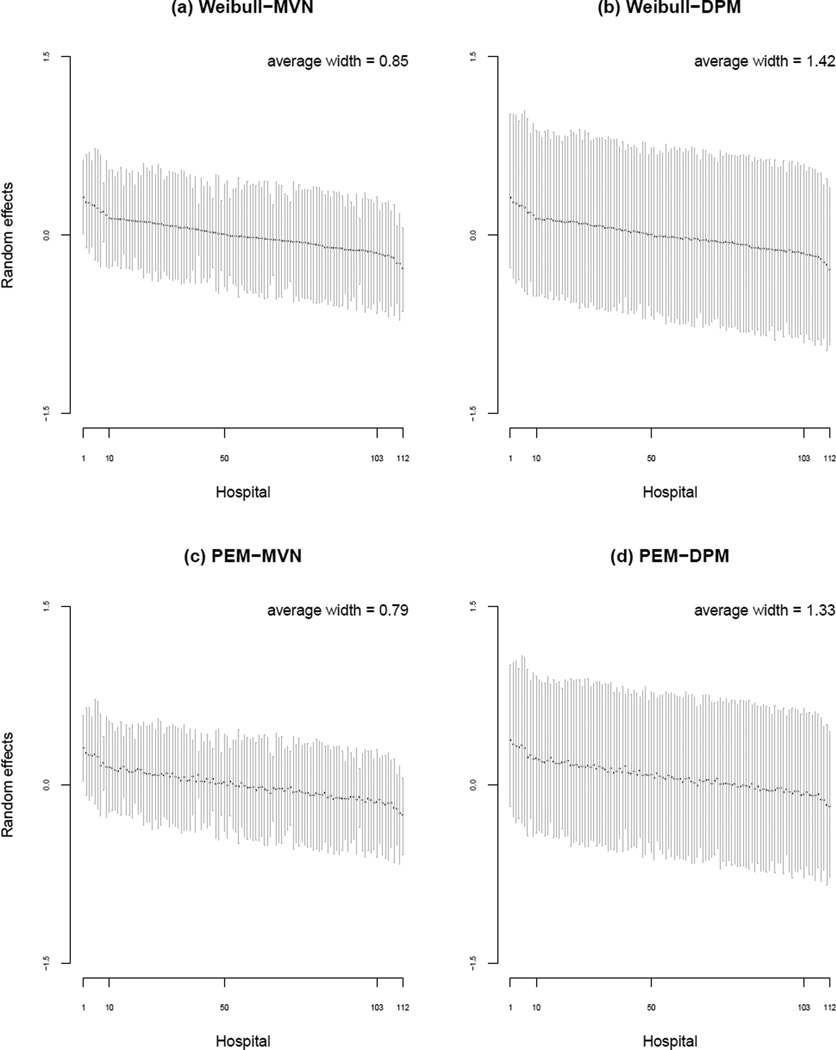
6.3.5 Hospital-specific random effects
As noted, a key advantage of embedding the analysis of cluster-correlated semi-competing risks data in the Bayesian framework is the relatively straightforward nature of obtaining posterior summaries for the hospital-specific random effects themselves. Figure 4 provides posterior medians and 95% CIs for V1j, j = 1, …, 112, based on the four models in which a semi-Markov specification is adopted for h03(·). Note, across the four panels, the ordering of the hospitals is based on the magnitude of the posterior median under the Weibull-MVN model. Comparing the panels we see that posterior uncertainty for the V1j is generally greater under models that adopt a DPM for the hospital-specific V compared to those that adopt a MVN specification. This may not be surprising given the additional complexity of the DPM specification, although we do find that the more ‘complex’ PEM specification for the baseline hazard functions yields lower posterior uncertainty than the Weibull specification.
Figure 4.
Posterior summaries (median and 95% credible interval) for the hospital-specific random effects for readmission, V1j, under four models for which a semi-Markov specification for h03(·) was adopted. In each panel, the hospitals are ordered according to the posterior median under the Weibull-MVN model.
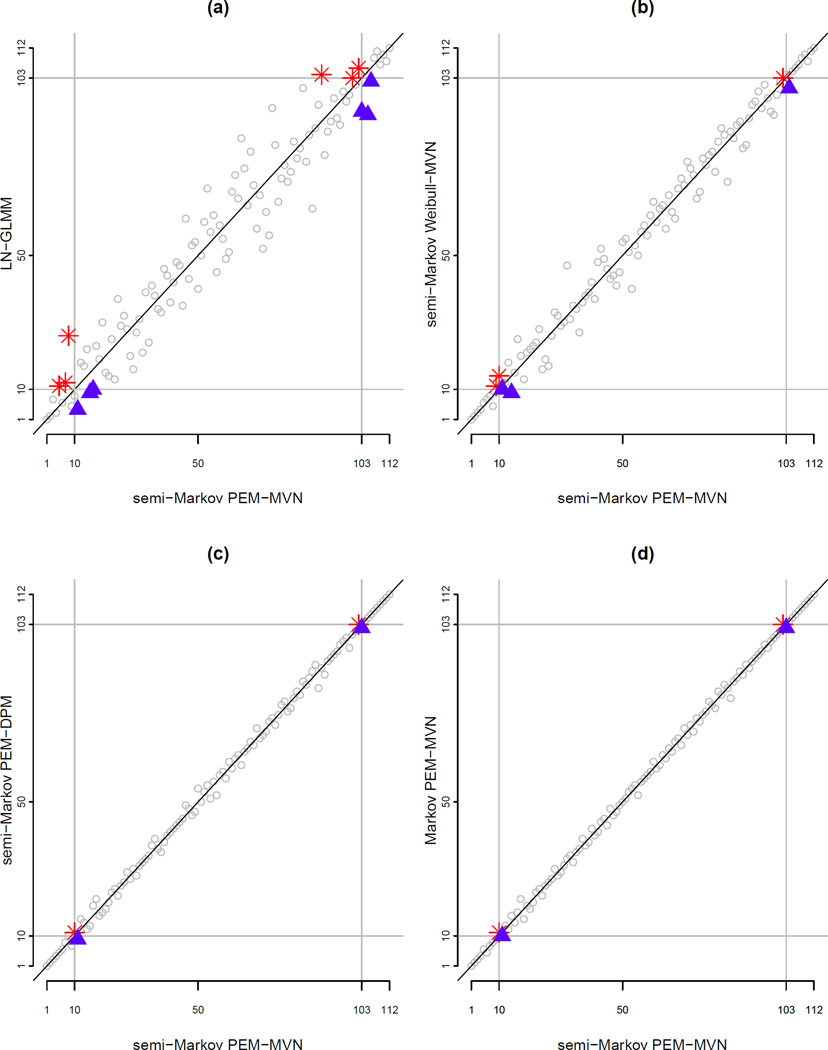
6.3.6 Hospital-specific ranks
In addition to examining the absolute values of the hospital-specific V1j, we also considered their rank ordering. Figure 5 compares the ranks of the J=112 hospitals according to the posterior median of V1j under the PEM-MVN model with a semi-Markov specification for h03(·) to the corresponding ranks based on four other models: (a) LN-GLMM; (b) Weibull-MVN with a semi-Markov specification for h03(·); (c) PEM-DPM with a semi-Markov specification for h03(·); and, (d) PEM-MVN model with a Markov specification for h03(·). In each panel, the grey horizontal and vertical lines mark the ‘top 10’ hospitals (i.e. ranks 1–10) and ‘bottom 10’ hospitals (i.e. ranks 103–112).
Figure 5.
Comparison of ranks of J=112 hospitals in the Medicare data on the basis of the posterior median for hospital-specific random effects for readmission, V1j. Panels compare the ranks on the basis of one of four models to a referent set of ranks based on a PEM-MVN model with a semi-Markov specification for h03(·) (see Section 6.3.6 for details). Hospitals marked with a ✳ suffer under the given model compared to the referent under the referent semi-Markov PEM-MVN model; hospitals marked with a ▲ benefit.
From panel (a) we see that the correspondence between the ranks under a semi-Markov PEM-MVN model and those under a LN-GLMM it is far from exact. Crucially, from the lower-left portion of the panel, three hospitals that would have been ranked in the top 10 under the semi-Markov PEM-MVN model are ranked outside the top 10 under the LN-GLMM (specifically, those marked with a ✳). Correspondingly there are three hospitals (marked with a ▲) who are indicated as being in the top 10 under the LN-GLMM while the semi-competing risks analysis under the semi-Markov PEM-MVN would have ranked them outside the 10 top. Furthermore, from the top-right portion of the panel, three hospitals ranked in the bottom 10 under the semi-Markov PEM-MVN model are ranked above the bottom 10 under the LN-GLMM model (i.e. those marked with a ▲).
From panels (b)–(d) we find that there is greater correspondence in the ranks of the 112 hospitals across the models within the proposed hierarchical framework. Comparing the ranks under the semi-Markov PEM-MVN specification to the semi-Markov Weibull-MVN specification in panel (b) we see that twos hospital that would have been ranked in the top 10 is now outside the top 10; there is also one hospital that is ranked in the bottom 10 under the semi-Markov PEM-MVN specification but outside the bottom 10 when a more restrictive Weibull model is used for the baseline hazard functions. Panels (c) and (d) are qualitatively similar in that the same two hospitals switch ranks at the lower end and the same two switch at the upper end; more generally, consistent with the conclusions we draw from Table 7, there is very close correspondence in the ranks across the three models represented in these two panels.
7 Sensitivity Analyses
As outlined in Section 3.5 and Table 2, the proposed Bayesian framework requires the specification of a number of hyperparameters. In practice comprehensive sensitivity analyses should be conducted to examine the extent to which conclusions are robust with respect to this specification, especially across key targets of estimation and inference. Here we focus our attention on the choice of hyperparameters for the prior distribution of ΣV, the variance-covariance matrix of underlying population distributions for hospital-specific random effects, and their influence on estimation/inference for the random effects as well as τ, the precision parameter in the DPM specification of the baseline hazard function. Towards this, we conducted sensitivity analyses based on the semi-Markov PEM-MVN and PEM-DPM models, specifying a range of values for (Ψυ, ρυ) and (Ψ0, ρ0) such that Ψυ=Ψ0=Ψ*(ρ* − 4)I3 and ρυ=ρ0=ρ*, where,ψ*=0.01, 0.1, 1, 10 and ρ*=5, 10, 50, 100. Note, these specifications correspond to a prior distribution for ΣV with a mean of ψ*I3 and a variance of diagonal elements of 2ψ*2/(ρ* − 6).
Table 10 presents the results. First, we focus Case I–IV, where ψ*=1, ρ* = 100, 50, 10, 5 which correspond to prior distributions of ΣV having a mean of I3 and a standard deviation of diagonal elements of 0.15, 0.21, 0.71, 3.16; for Case IV we note that the (induced) prior standard deviation was calculated from 100,000 random draws from the prior. From the results we see that when the prior distribution is centered around the identity matrix the posterior assigns mass to smaller values of SD(Vj1) as one increases the prior variance (dictated by decreasing ρ*). This is likely due to the discrepancy between the actual variation on the cluster-specific random effects for h1() and the choice the identity matrix, I3, as the prior mean for ΣV (since ψ*=1) together with the strength attributed to that choice (i.e. the prior variance for ΣV dictated by ρ*). When a prior mean of I3 is chosen for ΣV together with a high value of ρ* the overall prior overcomes the information in the data such that the posterior for SD(Vj1) is pushed ‘closer’ to 1.0. As ρ* decreases, however, and less prior mass is given to ΣV = I3, the likelihood is able to overcome the less informative prior so that the posterior is able to move away from the prior mean. Interestingly, based on both the DIC and LPML measures, we find that the overall fit of the data across Cases I–IV improves as the prior variance increases. We therefore interpret these results collectively as indicating that the variation across the (true underlying) Vj1 is meaningful but relatively small. Turning to Cases V and VI, we note that the induced prior distributions of ΣV are centered around relatively small values, specifically 0.01I3 and 0.1I3, with induced prior standard deviations of diagonal elements of 0.07 and 0.22, respectively. From the DIC and LPML values, these specifications of (Ψ*, ρ*) further improve the overall fit of the model from Case IV, we the posterior summaries for SD(Vj1) again indicating that the variation in the Vj1 is relatively small.
Table 10.
Sensitivity analyses for prior specification for hospital-specific random effects. We obtain the fits from PEM-MVN and in PEM-DPM conditioning on a range of values for (Ψυ, ρυ) and (Ψ0, ρ0): Ψυ=Ψ0=Ψ* (ρ* − 4)I and ρυ=ρ0=ρ*, where, ψ*=0.01; 0.1; 1, 10 and ρ*=5, 10, 50, 100. For each model DIC, LPML, and posterior medians (PM) and 95% credible intervals (CI) for standard deviations (SD) of the underlying population distributions for hospital-specific random effects are reported, as well as the average posterior standard deviation of hospital-specific random effects estimates on readmission (σ̄Vj1). Also presented are the PM for τ under the PEM-DPM model.
| Case | (Ψ*, ρ*) | Model | DIC | LPML | SD(Vj1) PM (95% CI) |
σ̄Vj1 | τ PM |
|---|---|---|---|---|---|---|---|
| I | (1, 100) | MVN | 45784.6 | −22905.0 | 0.77 (0.69, 0.85) | 0.36 | |
| DPM | 45779.3 | −22902.4 | 0.77 (0.70, 0.85) | 0.70 | 0.14 | ||
| II | (1, 50) | MVN | 45758.2 | −22890.1 | 0.66 (0.59, 0.75) | 0.34 | |
| DPM | 45754.4 | −22888.0 | 0.66 (0.59, 0.75) | 0.72 | 0.14 | ||
| III | (1, 10) | MVN | 45642.5 | −22828.0 | 0.39 (0.33, 0.47) | 0.27 | |
| DPM | 45644.0 | −22828.7 | 0.39 (0.33, 0.47) | 0.47 | 0.14 | ||
| IV | (1, 5) | MVN | 45574.1 | −22790.9 | 0.25 (0.19, 0.32) | 0.20 | |
| DPM | 45569.0 | −22789.3 | 0.25 (0.20, 0.32) | 0.32 | 0.15 | ||
| V | (0.01, 5) | MVN | 45549.4 | −22777.8 | 0.08 (0.04, 0.16) | 0.08 | |
| DPM | 45550.6 | −22778.8 | 0.09 (0.04, 0.18) | 0.12 | 0.31 | ||
| VI | (0.1, 5) | MVN | 45545.7 | −22776.7 | 0.14 (0.09, 0.21) | 0.13 | |
| DPM | 45540.6 | −22774.0 | 0.15 (0.10, 0.24) | 0.18 | 0.23 |
While there are clear differences in the posterior summaries for SD(Vj1) across Cases I–VI, within each case we see that there is little difference in the corresponding summaries between the MVN and DPM specifications; that is the conclusions one draws regarding the variation of the true underlying Vj1 are robust to this choice. However we do find that there are substantial differences in the average posterior standard deviations for the J cluster-specific Vj1. In Case II, for example, σ̄Vj1 is 0.34 under the MVN specification and 0.70 under the DPM specification. Generally, this ordering is consistent across the six cases, as well as with the results presented in Figure 4. When combined with the posterior summaries for SD(Vj1), the results suggest that for our application the trade-off of using the more flexible DPM specification is somewhat detrimental to the analyses; use of the DPM specification rather than the MVN does not serve to change our conclusions regarding the variation across the true Vj1 but has, rather, served to increase the posterior uncertainty regarding any given specific Vj1.
Finally, the last column of Table 10 presents the posterior median for τ, the precision parameter in the DPM specification. If one interprets the DPM specification as a mixture of MVN distributions (see Supplementary Materials Section B), τ dictates, in part, the number of mixture components and, hence, the complexity of the overall specification. From the results, however, we see that the posterior median of τ, which takes on values in (0, ∞), tends towards quite small values and is generally robust to the specification of (Ψ*, ρ*). To further investigate the role of τ in our analyses, we conducted a series of additional analyses where τ was fixed at values ranging from 0.1 to 100 (i.e. we did not adopt a gamma hyperprior as described in Section 3.5.3). Although details are not reported here, we found that results of our analyses to be very robust to the specific value of τ, again indicating few gains associated with use of the more flexible DPM specification for our application.
8 Discussion
In this paper, we propose a comprehensive, unified Bayesian framework for the analysis of cluster-correlated semi-competing risks data. The framework is flexible in that it lets researchers take advantage of the numerous benefits afforded by the Bayesian paradigm including the natural incorporation of prior information and the straightforward quantification of uncertainty for all parameters including hospital-specific random effects. The framework is also flexible in that it gives researchers choice in adopting parametric and/or semi-parametric specifications for various model components, a key consideration in practice when small sample size may require pragmatism during the analysis. To facilitate model choice, we have also developed DIC and LMPL measures for model comparison within the proposed framework. Finally, computationally efficient algorithms have been developed and implemented, and are readily-available in a freely-available R package.
The work in this paper was motivated by an on-going collaboration investigating variation in risk of readmission following a diagnosis of pancreatic cancer. Towards this, we applied the framework to a sample of 5,298 Medicare enrollees diagnosed with pancreatic cancer at one of 112 hospitals between 2000–2009. The results from our analysis indicate a number of important determinants of risk of readmission including gender, age, co-morbidity status (as measured by the Charlson/Deyo score), whether or not they underwent a procedure during the index hospitalization, the length of stay of the index hospitalization and the location to which the patients was eventually discharged. The analyses also revealed that there is substantially less between-hospital variation in risk of readmission than the risk of death (either prior to or post-readmission), after accounting for patient case-mix. To our knowledge these are the first reported results of this kind in the literature and we are currently expanding our analyses to consider patients across the entire U.S.
More generally, in the clinical and health policy literature, the standard analysis approach for investigating risk of readmission is based on a LN-GLMM (Normand et al., 1997; Ash et al., 2012). In the specific context of our application, compared with results based on the proposed framework, such an analysis yields meaningfully different conclusions regarding which patient-level characteristics are associated with risk of readmission, the magnitude and statistical significance of those associations and the ranks of hospitals. Given the relative robustness across models within the proposed framework, the fact that a LN-GLMM yields different conclusions is likely related to the fact that death is completely ignored as a competing risk. As a concrete example consider the hospital in Figure 5(a) that is ranked 8th under the semi-Markov PEM-MVN model and 26th under the LN-GLMM. Closer inspection of the raw data reveals that very few patients diagnosed at this hospital died within the 90-day window we consider. At other hospitals, the force of mortality is stronger and patients die at higher rates within the 90-day window; that these patients die is overlooked by the LN-GLMM which assumes that they remain ‘at risk’ to experience a readmission event. Hence their estimated readmission rates are too small in the LN-GLMM (since the denominator is erroneously inflated). Unfortunately the hospital ranked 8th under the semi-Markov PEM-MVN model suffers from their low mortality rate in the sense that they do not benefit from erroneous inflation of the readmission rate denominator, as other hospitals do. Hence the change in rank.
As indicated, results across models within the proposed framework were relatively robust in our main application. We did find, however, that models which adopted the flexible PEM specification for the baseline hazard functions had substantially better fit to the data than models that adopted a Weibull specification. While models based on a semi-Markov specification for death following readmission generally had better fit to the data than models based on a Markov specification we note that this choice does not affect the interpretation of the model for readmission (i.e. model (4)) the investigation of which was our primary scientific goal. With this in mind, we have not reported on the results for the two models for death (i.e. models (5) and (6)) although they are available in the Supplementary Materials E. In practice, researchers may be interested in readmission and death jointly in which case the choice of specification for h03(·) will become critical from a scientific perspective (Lee et al., 2015). In our main application, since the data are relatively rich in terms of sample size and the event rates, we have taken the PEM-MVN and PEM-DPM models as our primary models for comparison of ranks of hospitals and sensitivity analyses. In other less-rich data settings, however, analysts may be in a position where structure is needed either in the forms of the baseline hazard functions or for the random effects. Finally, we note that in our application a MVN specification for the population distribution of the vector of hospital-specific random effects, Vj, appeared to be adequate. That is, the so-called Bayesian non-parametric DPM specification did not yield any additional insight into our understanding of variation in risk of readmission nor did it change meaningfully the ranking of hospitals. In other applications this may, of course, not be the case and the proposed framework gives researchers important choice in this regard.
In Section 5, we show that incorrect assumption of the underlying distribution for cluster-specific random effects or baseline hazard functions result in lower efficiency of the incorrect parametric estimators. In addition, the computational efficiency of proposed models with non-parametric specification of parameters heavily depends on underlying distributions of model parameters. For PEM models, if the underlying hazard function has an intricate shape, the model estimates a posterior distribution αg to be centered around a larger value, resulting in expensive computation due to more parameters (λg,k’s) to be estimated. For DPM models, if data suggest a larger value of τ, the model will introduce more latent classes in the mixture, implying more parameters to be estimated.
Our analysis focuses on readmission 90 days post-discharge. However, we note that the computational performance of our proposed approach would not be challenged in the cases when an administrative censoring is not imposed. In particular, the proposed PEM model is flexible in that it allows the time scale for each of three hazard functions to be different for each transition. Following McKeague and Tighiouart (2000) and Haneuse et al. (2008), we suggest the last observed event time points be the upper bound in general problems where an administrative censoring is not imposed. In our application, however, since most of patients diagnosed with pancreatic cancer die within 1-year period, we would expect the estimates of baseline hazard functions have a relatively greater uncertainty in the late periods if the administrative censoring is not considered. In addition, in the context of our study, patients can experience multiple readmission events prior to death. The literature on recurrent event semi-competing risks would likely be useful for this setting and thus the development of methods that can accommodate recurrent non-terminal events in the cluster-correlated data setting is a promising area for future development.
In this paper, we considered a gamma distribution for the within-patient frailty because of its computational tractability. When the frailty distribution is mis-specified, the resulting estimator is not guaranteed to be consistent, with the extent of asymptotic bias depending on the discrepancy between the assumed and true frailties distributions. However, Hsu et al. (2007) studied the effect of mis-specification of frailty distribution on the marginal regression estimates and hazard functions when gamma distribution is assumed. Their results show that the biases are generally low, even when the true frailty distribution is substantially different from the assumed gamma distribution. Therefore, if the regression parameters and hazard function are of primary interest, the gamma frailty model can be a reasonable choice in practice. During the review process, one reviewer suggested that we examine the potential for non-proportional hazards in the motivating Medicare application. Towards this, we developed and implemented an extension of the so-called heteroscedastic Weibull model (Hsieh, 2001; Nikulin et al., 2006) to the semi-competing risks context, specifically for the semi-Markov Weibull-MVN model. Although details are given in the Supplementary Materials E, Briefly, this model permits the shape parameters for each of the three Weibull baseline hazard functions to depend upon covariate values. Results from this model are also presented in the Supplementary Materials E. Interestingly, a number of covariates did exhibit non-proportionality in their impact on the risk of readmission including source of entry and whether or not the patient underwent a procedure during their hospitalization. Based on this, and general considerations in applied survival analysis, it is clear that expanding the scope of the entire proposed framework (i.e. beyond the semi-Markov Weibull-MVN model) is important. Indeed, it is a key aspect of our on-going work.
Finally, we conclude by emphasizing that the proposed framework significantly improves and expands the set of statistical tools researches have to study quality of end-of-life care. While our focus has been on pancreatic cancer, the proposed framework is broadly applicable to all ‘advanced’ health conditions for which current treatment options are limited and the force of mortality is strong. Such studies will be of paramount importance in the near-future because many of these conditions, including other cancers as well as neurodegenerative conditions such as Alzheimers’ disease, directly affect large segments of an increasingly aging population. In addition, although it has not been in the focus of this paper, the proposed framework will also be critical in helping policy-makers understand and ultimately control the increasing costs of health care delivery in the U.S. In particular, the proposed framework provides CMS appropriate statistical tools with which to expand the scope of the Hospital Inpatient Quality Reporting Program and the Readmission Reduction Program to include to conditions with strong forces of mortality.
Supplementary Material
Acknowledgments
This work was supported by National Cancer Institute grant (P01 CA134294-02) and National Institutes of Health grants (ES012044, K18 HS021991, R01 CA181360-01).
Footnotes
Title: In online Supplementary Materials, we provide a detail description of Metropolis-Hastings-Green algorithm to fit our proposed models. Additional details regarding the Medicare data and results from the application are also provided. (pdf file)
R-package ‘SemiCompRisks’: R-package SemiCompRisks contains codes to implement proposed Bayesian framework described in the article. The package is currently available in CRAN.
Contributor Information
Kyu Ha Lee, Epidemiology and Biostatistics Core, The Forsyth Institute, Department of Oral Health Policy and Epidemiology, Harvard School of Dental Medicine.
Francesca Dominici, Department of Biostatistics, Harvard T.H. Chan School of Public Health.
Deborah Schrag, Department of Medical Oncology, Dana Farber Cancer Institute.
Sebastien Haneuse, Department of Biostatistics, Harvard T.H. Chan School of Public Health.
References
- American Cancer Society. Cancer Facts & Figures 2013. 2013 [Google Scholar]
- Andersen PK, Borgan O, Gill RD, Keiding N. Statistical models based on counting processes. Springer; 1993. [Google Scholar]
- Arjas E, Gasbarra D. Nonparametric Bayesian inference from right censored survival data, using the Gibbs sampler. Statistica Sinica. 1994;4:505–524. [Google Scholar]
- Ash AS, Fienberg SF, Louis TA, Normand S-LT, Stukel TA, Utts J. Statistical issues in assessing hospital performance. Commissioned by the Committee of Presidents of Statistical Societies for the CMS. 2012 [Google Scholar]
- Besag J, Kooperberg C. On conditional and intrinsic autoregressions. Biometrika. 1995;82(4):733–746. [Google Scholar]
- Brooks GA, Li L, Uno H, Hassett MJ, Landon BE, Schrag D. Acute hospital care is the chief driver of regional spending variation in Medicare patients with advanced cancer. Health Affairs. 2014;33(10):1793–1800. doi: 10.1377/hlthaff.2014.0280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush CA, MacEachern SN. A semiparametric Bayesian model for randomised block designs. Biometrika. 1996;83(2):275–285. [Google Scholar]
- Celeux G, Forbes F, Robert CP, Titterington DM, et al. Deviance information criteria for missing data models. Bayesian Analysis. 2006;1(4):651–673. [Google Scholar]
- Chen BE, Kramer JL, Greene MH, Rosenberg PS. Competing risks analysis of correlated failure time data. Biometrics. 2008;64(1):172–179. doi: 10.1111/j.1541-0420.2007.00868.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CMS. Hospital inpatient quality reporting program. [accessed 20 November 2014];2013a URL https://www.cms.gov/Medicare/Quality-Initiatives-Patient-Assessment-Instruments/HospitalQualityInits/HospitalRHQDAPU.html.
- CMS. Readmissions reduction program. [accessed 20 November 2014];2013b URL http://www.cms.gov/Medicare/Medicare-Fee-for-Service-Payment/AcuteInpatientPPS/Readmissions-Reduction-Program.html.
- Diggle P, Heagerty P, Liang K-Y, Zeger S. Analysis of longitudinal data. Oxford University Press; 2002. [Google Scholar]
- Egleston BL, Scharfstein DO, Freeman EE, West SK. Causal inference for non-mortality outcomes in the presence of death. Biostatistics. 2007;8(3):526–545. doi: 10.1093/biostatistics/kxl027. [DOI] [PubMed] [Google Scholar]
- Epstein AM, Jha AK, Orav EJ. The relationship between hospital admission rates and rehospitalizations. New England Journal of Medicine. 2011;365(24):2287–2295. doi: 10.1056/NEJMsa1101942. [DOI] [PubMed] [Google Scholar]
- Escobar MD, West M. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90(430):577–588. [Google Scholar]
- Ferguson TS. A Bayesian analysis of some nonparametric problems. The Annals of Statistics. 1973;1(2):209–230. [Google Scholar]
- Fine J, Jiang H, Chappell R. On semi-competing risks data. Biometrika. 2001;88(4):907–919. [Google Scholar]
- Fitzmaurice GM, Laird NM, Ware JH. Applied longitudinal analysis. Vol. 998. John Wiley & Sons; 2012. [Google Scholar]
- Geisser S. Predictive inference. CRC Press; 1993. [Google Scholar]
- Geisser S, Eddy WF. A predictive approach to model selection. Journal of the American Statistical Association. 1979;74(365):153–160. [Google Scholar]
- Gelfand AE, Mallick BK. Bayesian analysis of proportional hazards models built from monotone functions. Biometrics. 1995;51(3):843–852. [PubMed] [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian Data Analysis. Chapman and Hall/CRC Boca Raton; 2013. [Google Scholar]
- Gorfine M, Hsu L. Frailty-based competing risks model for multivariate survival data. Biometrics. 2011;67(2):415–426. doi: 10.1111/j.1541-0420.2010.01470.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorfine M, Hsu L, Zucker DM, Parmigiani G. Calibrated predictions for multivariate competing risks models. Lifetime Data Analysis. 2014;20(2):234–251. doi: 10.1007/s10985-013-9260-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green P. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82(4):711–732. [Google Scholar]
- Han B, Yu M, Dignam JJ, Rathouz PJ. Bayesian approach for exible modeling of semicompeting risks data. Statistics in Medicine. 2014;33(29):5111–5125. doi: 10.1002/sim.6313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haneuse S, Rudser K, Gillen D. The separation of timescales in Bayesian survival modeling of the time-varying effect of a time-dependent exposure. Biostatistics. 2008;9(3):400–410. doi: 10.1093/biostatistics/kxm038. [DOI] [PubMed] [Google Scholar]
- Hanson TE. Inference for mixtures of finite polya tree models. Journal of the American Statistical Association. 2006;101(476):1548–1565. [Google Scholar]
- Hsieh F. On heteroscedastic hazards regression models: theory and application. Journal of the Royal Statistical Society: Series B. 2001;63(1):63–79. [Google Scholar]
- Hsieh J, Wang W, Ding A. Regression analysis based on semicompeting risks data. Journal of the Royal Statistical Society, Series B. 2008;70(1):3–20. [Google Scholar]
- Hsu L, Gorfine M, Malone K. On robustness of marginal regression co-efficient estimates and hazard functions in multivariate survival analysis of family data when the frailty distribution is mis-specified. Statistics in Medicine. 2007;26(25):4657–4678. doi: 10.1002/sim.2870. [DOI] [PubMed] [Google Scholar]
- Ibrahim J, Chen M-H, Sinha D. Bayesian survival analysis. Springer; 2001. [Google Scholar]
- Joynt KE, Orav EJ, Jha AK. Thirty-day readmission rates for medicare beneficiaries by race and site of care. Journal of the American Medical Association. 2011;305(7):675–681. doi: 10.1001/jama.2011.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadane JB, Lazar NA. Methods and criteria for model selection. Journal of the American Statistical Association. 2004;99(465):279–290. [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. Journal of the American Statistical Association. 1995;90(430):773–795. [Google Scholar]
- Katsahian S, Resche-Rigon M, Chevret S, Porcher R. Analysing multicentre competing risks data with a mixed proportional hazards model for the subdistribution. Statistics in Medicine. 2006;25(24):4267–4278. doi: 10.1002/sim.2684. [DOI] [PubMed] [Google Scholar]
- Kneib T, Hennerfeind A. Bayesian semiparametric multi-state models. Statistical Modeling. 2008;8(2):169–198. [Google Scholar]
- Krumholz HM, Lin Z, Drye EE, Desai MM, Han LF, Rapp MT, Mattera JA, Normand S-LT. An administrative claims measure suitable for profiling hospital performance based on 30-day all-cause readmission rates among patients with acute myocardial infarction. Circulation: Cardiovascular Quality and Outcomes. 2011;4(2):243–252. doi: 10.1161/CIRCOUTCOMES.110.957498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumholz HM, Parent EM, Tu N, Vaccarino V, Wang Y, Radford MJ, Hennen J. Readmission after hospitalization for congestive heart failure among medicare beneficiaries. Archives of Internal Medicine. 1997;157(1):99–104. [PubMed] [Google Scholar]
- Lee KH, Haneuse S, Schrag D, Dominici F. Bayesian semiparametric analysis of semicompeting risks data: investigating hospital readmission after a pancreatic cancer diagnosis. Journal of the Royal Statistical Society, Series C. 2015;64(2):253–273. doi: 10.1111/rssc.12078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liquet B, Timsit J-F, Rondeau V. Investigating hospital heterogeneity with a multi-state frailty model: application to nosocomial pneumonia disease in intensive care units. BMC Medical Research Methodology. 2012;12(1):79. doi: 10.1186/1471-2288-12-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mariotto AB, Yabroff KR, Shao Y, Feuer EJ, Brown ML. Projections of the cost of cancer care in the United States: 2010–2020. Journal of the National Cancer Institute. 2011;103(2):117–128. doi: 10.1093/jnci/djq495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCulloch CE, Neuhaus JM. Prediction of random effects in linear and generalized linear models under model misspecification. Biometrics. 2011;67(1):270–279. doi: 10.1111/j.1541-0420.2010.01435.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCulloch CE, Neuhaus JM, et al. Misspecifying the shape of a random effects distribution: why getting it wrong may not matter. Statistical Science. 2011;26(3):388–402. [Google Scholar]
- McKeague I, Tighiouart M. Bayesian estimators for conditional hazard functions. Biometrics. 2000;56(4):1007–1015. doi: 10.1111/j.0006-341x.2000.01007.x. [DOI] [PubMed] [Google Scholar]
- Millar RB. Comparison of hierarchical Bayesian models for overdispersed count data using DIC and Bayess’ factors. Biometrics. 2009;65(3):962–969. doi: 10.1111/j.1541-0420.2008.01162.x. [DOI] [PubMed] [Google Scholar]
- Neal RM. Markov chain sampling methods for dirichlet process mixture models. Journal of Computational and Graphical Statistics. 2000;9(2):249–265. [Google Scholar]
- Neuhaus JM, McCulloch CE. Estimation of covariate effects in generalized linear mixed models with informative cluster sizes. Biometrika. 2011;98(1):147–162. doi: 10.1093/biomet/asq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikulin MS, Commenges D, Huber C. Probability, Statistics, and Modelling in Public Health. Springer; 2006. [Google Scholar]
- Normand ST, Glickman ME, Gatsonis CA. Statistical methods for profiling providers of medical care: issues and applications. Journal of the American Statistical Association. 1997;92(439):803–814. [Google Scholar]
- Ohlssen DI, Sharples LD, Spiegelhalter DJ. Flexible random-effects models using bayesian semi-parametric models: applications to institutional comparisons. Statistics in Medicine. 2007;26(9):2088–2112. doi: 10.1002/sim.2666. [DOI] [PubMed] [Google Scholar]
- Peng L, Fine J. Regression modeling of semicompeting risks data. Biometrics. 2007;63(1):96–108. doi: 10.1111/j.1541-0420.2006.00621.x. [DOI] [PubMed] [Google Scholar]
- PLoS Medicine Editors, editor. Beyond the numbers: describing care at the end of life. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Putter H, Fiocco M, Geskus R. Tutorial in biostatistics: competing risks and multi-state models. Statistics in Medicine. 2007;26(11):2389–2430. doi: 10.1002/sim.2712. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2014. [Google Scholar]
- Rondeau V, Mazroui Y, Gonzalez JR. frailtypack: An R Package for the Analysis of Correlated Survival Data with Frailty Models Using Penalized Likelihood Estimation or Parametrical Estimation. Journal of Statistical Software. 2012;47(4):1–24. [Google Scholar]
- Shao Q, Ibrahim JG. Monte Carlo methods in Bayesian computation. Springer; 2000. [Google Scholar]
- Sharabiani MT, Aylin P, Bottle A. Systematic review of comorbidity indices for administrative data. Medical Care. 2012;50(12):1109–1118. doi: 10.1097/MLR.0b013e31825f64d0. [DOI] [PubMed] [Google Scholar]
- Shin EJ, Canto MI. Pancreatic cancer screening. Gastroenterology Clinics of North America. 2012;41(1):143. doi: 10.1016/j.gtc.2011.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, Series B. 2002;64(4):583–639. [Google Scholar]
- Stitzenberg KB, Chang Y, Smith AB, Nielsen ME. Exploring the burden of inpatient readmissions after major cancer surgery. Journal of Clinical Oncology. 2015;10(33):455–464. doi: 10.1200/JCO.2014.55.5938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ. Identification and estimation of survivor average causal effects. Statistics in Medicine. 2014;33(21):3601–3628. doi: 10.1002/sim.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vest J, Gamm LD, Oxford BA, Slawson KM. Determinants of preventable readmissions in the United States: a systematic review. Implementation Science. 2010;5(88):1–28. doi: 10.1186/1748-5908-5-88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker SG, Mallick BK. Hierarchical generalized linear models and frailty models with Bayesian nonparametric mixing. Journal of the Royal Statistical Society: Series B. 1997;59(4):845–860. [Google Scholar]
- Warren J, Barbera L, Bremner K, Yabroff K, Hoch J, Barrett M, Luo J, Krahn M. End-of-life care for lung cancer patients in the United States and Ontario. Journal of the National Cancer Institute. 2011;103(11):853–862. doi: 10.1093/jnci/djr145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Kalbeisch J, Tai B. Statistical analysis of illness-death processes and semi-competing risks data. Biometrics. 2010;66(3):716–725. doi: 10.1111/j.1541-0420.2009.01340.x. [DOI] [PubMed] [Google Scholar]
- Zeng D, Chen Q, Chen M-H, Ibrahim JG, et al. Estimating treatment effects with treatment switching via semicompeting risks models: an application to a colorectal cancer study. Biometrika. 2012;99(1):167–184. doi: 10.1093/biomet/asr062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang JL, Rubin DB. Estimation of causal effects via principal stratification when some outcomes are truncated by death. Journal of Educational and Behavioral Statistics. 2003;28(4):353–368. [Google Scholar]
- Zhang Y, Chen M-H, Ibrahim JG, Zeng D, Chen Q, Pan Z, Xue X. Bayesian gamma frailty models for survival data with semi-competing risks and treatment switching. Lifetime Data Analysis. 2014;20(1):76–105. doi: 10.1007/s10985-013-9254-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou B, Fine J, Latouche A, Labopin M. Competing risks regression for clustered data. Biostatistics. 2012;13(3):371–383. doi: 10.1093/biostatistics/kxr032. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.