Abstract
Intrathecal drug and gene vector delivery is a procedure to release a solute within the cerebrospinal fluid. This procedure is currently used in clinical practice and shows promise for treatment of several central nervous system pathologies. However, intrathecal delivery protocols and systems are not yet optimized. The aim of this study was to investigate the effects of injection parameters on solute distribution within the cervical subarachnoid space using a numerical platform. We developed a numerical model based on a patient-specific three dimensional geometry of the cervical subarachnoid space with idealized dorsal and ventral nerve roots and denticulate ligament anatomy. We considered the drug as massless particles within the flow field and with similar properties as the CSF, and we analyzed the effects of anatomy, catheter position, angle and injection flow rate on solute distribution within the cerebrospinal fluid by performing a series of numerical simulations. Results were compared quantitatively in terms of drug peak concentration, spread, accumulation rate and appearance instant over 15 seconds following the injection. Results indicated that solute distribution within the cervical spine was altered by all parameters investigated within the time range analyzed following the injection. The presence of spinal cord nerve roots and denticulate ligaments increased drug spread by 60% compared to simulations without these anatomical features. Catheter position and angle were both found to alter spread rate up to 86%, and catheter flow rate altered drug peak concentration up to 78%. The presented numerical platform fills a first gap towards the realization of a tool to parametrically assess and optimize intrathecal drug and gene vector delivery protocols and systems. Further investigation is needed to analyze drug spread over a longer clinically relevant time frame.
Introduction
Intrathecal drug and gene vector delivery (IT) to the central nervous system (CNS) is a procedure involving the release of therapeutic agents into the cerebrospinal fluid (CSF) via an inserted catheter [1]. The CSF is a water-like fluid that resides in the subarachnoid space (SAS) surrounding the brain and spinal cord and is also contained within four fluid filled reservoirs within the brain called ventricles. Total CSF volume in an adult is approximately 150 ml [2] with ≃80 ml contained within the spinal SAS [3]. CSF in the SAS is bounded on the outside by the arachnoid membrane and dura and on the inside, covering the CNS tissue surface, by the delicate pia mater.
Traditional oral or parenteral drug administration for CNS diseases is limited, mainly due to the shielding effect of the blood-brain barrier to macromolecules. Conversely, thanks to the proximity of the CSF to the brain and spinal cord parenchyma, IT allows many drugs to directly penetrate into the CNS tissue by the leptomeningeal spaces [4–7] thereby requiring a lower drug dosage and resulting in less potential toxic effects [8, 9].
The strong interest in IT stems from the fact that CNS disorders are the world’s leading cause of disability and necessitate more prolonged care and hospitalizations than almost all other diseases [5]. In particular, many CNS pathologies, such as neurodegenerative and enzymatic disorders (e.g. Parkinson’s, amyotrophic lateral sclerosis and Mucopolysaccharidosis), as well as functional recovery after spinal cord injuries, may benefit from IT [1, 10–12]. IT is presently used for treatment of spasticity and chronic pain caused by multiple sclerosis and cancer [3, 4]. IT systems, also known as pain pumps, consist of a pump that is surgically placed beneath the skin. The pump contains a medication that is released into the CSF via a flexible catheter [4]. For these patients, a bolus injection trial, whose injection is performed for approximately 1 minute, is used to test patient tolerance to the administered drug [13]. Another application of IT with several ongoing experimental trials is gene therapy, a procedure in which gene vectors are delivered and distributed to the CNS tissue via the CSF [14, 15].
IT is affected by several parameters, many of which are little understood. These parameters are as follows: 1. Solute baricity and chemical properties; 2. Catheter type, placement and orientation; 3. Infusion flow rate, volume and concentration; 4. Patient characteristics [16]. Additional complex biophysical aspects that affect the IT outcome include drug advection and diffusion within the CSF [17], absorption across the arachnoid membrane and interstitial penetration within the tissue [5]. At present, optimal IT protocols are not yet established. Therapy control is needed to provide an adequate therapeutic effect while minimizing possible risks, complications (e.g. catheter tip granuloma) and costs [17, 18]. In particular, gene therapy drugs can cost as much as 1 million USD per patient [19].
Several clinical and experimental studies have been performed to investigate the intrathecal drug distribution within the CSF. Experimental studies on non-human primates were carried out to investigate transport and tissue penetration mechanisms [1, 11], as well as pharmacokinetics and bioavailability [20], of the injected macromolecules. Papisov [1] found that drug and macromolecules delivery to the CNS can be pursued through the intrathecal route although several aspects affecting it, such as drug-cell interaction and CSF drainage, are not fully understood. Clinical studies in humans were performed in [21] to understand how continuous IT flow rates affect analgesia and observed that at a higher flow rate the patient’s pain feeling increased, a factor likely due to the increased drug dilution. An in vitro model was carried out in [22] to investigate the dependence of anaesthetic distribution on flow rate, catheter size and angle through and it found that all these parameters affect drug distribution and peak concentration. An in vitro model was also developed in [23] to investigate CSF dynamics around a catheter tip and it reported that steady streaming introduced by adjacent CSF vortices was the main driver of drug movement. Finally, a recent in vitro model was developed by Tangen et al. [24] to investigate the effects of the body position and lumbar drainage rates on the treatment of the subarachnoid hemorrhage.
Several numerical modeling studies have investigated drug transport in the spinal SAS. Myers [25] completed the first numerical model of IT in an idealized three-dimensional (3D), axisymmetric elliptic-shaped-geometry of the spinal SAS. This model did not include small anatomic features such as the spinal cord nerve roots, but it parametrically evaluated the influence of injection rate, catheter orientation and spinal-column size on drug distribution over a maximum period of five minutes. The authors found that low values of the ratio of the SAS and catheter cross-sectional dimensions produce more uniform drug distribution and that effects of catheter orientation are more pronounced at higher injection flow rates. More recently, [26] performed numerical simulations of lumbar IT in a 3D reconstruction of the spinal SAS (C1 to L2 levels) with approximated elliptical cross-sections and moving boundaries. The authors computed drug concentration in the CSF over a period of one hour after bolus injection and noticed that local drug distribution differences occurring between slow or bolus injection dissipate on a longer time scale. This model lacked a catheter geometry within the CSF and did not focus on the effects of specific injection parameters. Hsu [27] developed a two-dimensional model of the complete SAS (cerebral and spinal) and ventricles and showed that a 2X increase in CSF frequency and stroke volume enhanced drug dispersion and decreased peak concentration by 26 and 28%, respectively. This model also lacked small anatomic features within the CSF such as spinal cord nerve roots and arachnoid trabeculae. In another study, [28, 29], performed Lattice Boltzmann simulations (with periodic boundary conditions) on an elliptic SAS annulus that included idealized fine anatomical structures (i.e. nerves bundles and trabeculae) and showed that these anatomical structures produce CSF stirring effects and consequently enhance drug dispersion by a factor of 5 to 10. The effective longitudinal drug dispersion was found to be 1000 times higher than a reference molecular diffusivity. Finally, [30] showed that in models of the cervical SAS with NRDL, assuming CSF incompressibility and fixed SAS walls, the presence of microanatomical structures can speed up drug dispersion.
Despite the outstanding contributions available in literature, to the best of our knowledge, a 3D anatomically-detailed model has not been used to investigate the possibility and a range of effects of injection parameters on IT. We present a numerical model of catheter drug injection based on a patient-specific 3D geometry of the cervical SAS with idealized anatomical structures, namely dorsal and ventral spinal cord nerve rootlets and denticulate ligaments (NRDL).
Materials and methods
We conducted a series of numerical simulations to investigate the impact of the following parameters on drug distribution within the CSF: (a) NRDL, (b) catheter position, (c) catheter angle and (d) injection flow rate. All simulations were carried out for a period up to 20 cardiac cycles (T = 0.78 s being the period), and drug injection was assumed to be continuous over that time span. Drug distribution was quantified in terms of drug peak concentration, axial spread, accumulation rate and appearance instant.
Geometry and flow conditions
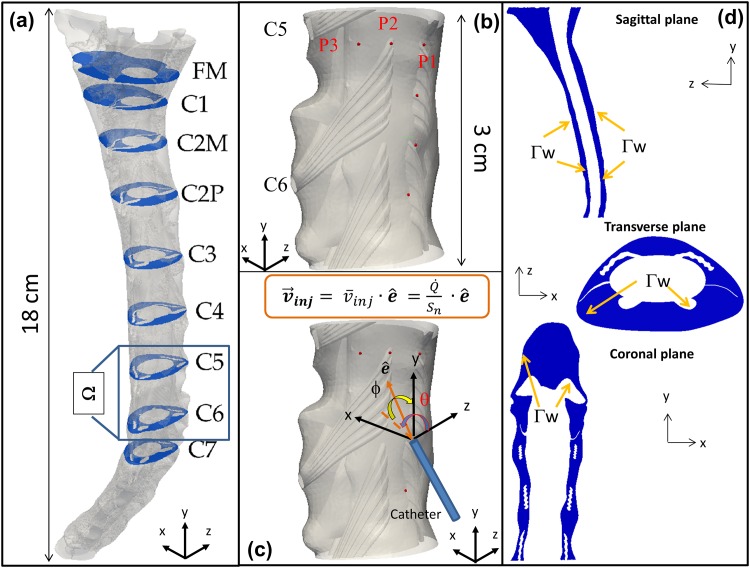
We considered two different 3D geometries of the cervical SAS (ranging from the foramen magnum to ∼5 cm caudal to the seventh cervical vertebra (C7), as reported in Fig 1(a)) with rigid walls. A SAS geometry without NRDL (previously published by [31]) was obtained from manual segmentation of T2-weighted MRI sequences on a 22-years-old male healthy subject using ITK-Snap (Version 2.2, University of Pennsylvania). A more complex geometry of the SAS with detailed anatomical structures, was obtained by the addition of artificially constructed NRDL, based on anatomical ex-vivo measurements in the literature and reference to the MR images (further details are reported in [32]).
Fig 1. Geometry of the anatomical domain.
(a) 3D geometry of the cervical SAS with NRDL also showing relevant anatomical cross sections; (b) Injection positions; (c) Spherical system to define catheter angle; (d) Illustrative sections of the cervical SAS: sagittal (x = 1.7 cm), transverse (y = 6 cm) and coronal (z = 0.85 cm).
A patient-specific CSF flow rate, based on 4D Flow MRI measurements obtained for the same 22-years-old subject as above, was imposed at the flow inlet on the caudal end of the model (5 cm below the C7 level shown in Fig 1(a)). Furthermore, we applied no-slip boundary conditions at the SAS walls, a reference pressure value at the flow outlet on the cranial end of the model and a null-velocity as the initial condition.
Finally, to simulate drug infusion, we assumed that the characteristic size of the catheter tip (≈0.2 mm representative of the inner radius of a 22-gauge catheter) is small compared to that one of the SAS cross-section. Moreover, since we were not interested in assessing the effect of catheter tip penetration into the SAS, we assumed injection to occur in a tiny volume hereafter denoted by Ωn. In particular, Ωn was defined by intersecting the SAS with a sphere having radius equal to the catheter inner radius and centered at the injection position on the arachnoid wall (specified below, when discussing the injection parameters). Hence, we enforced the injection velocity (vinj in Fig 1(c)) through a Dirichlet boundary condition within Ωn. The injection direction was defined according to the angles θ and ϕ shown in Fig 1(c).
Drug parameters
The injected drug was considered to be isobaric as in [27], with identical properties as water at body temperature having a kinematic viscosity and density of 7 ⋅ 10−7 m2/s and 1 ⋅ 103 kg/m3, respectively. Moreover, molecular diffusion of the drug was not considered because typical values of drug diffusivity in the CSF are ∼10−10 − 10−11 m2/s [3, 33], rendering advection to be the dominant factor leading to drug spread. Furthermore, as observed by [30], diffusion has little affect on intrathecal drug dispersion. In addition, based on the considered short time window (∼ 15 s), we neglected drug absorption-desorption and degradation mechanisms that can play a major role on a longer time scale. By virtue of these positions, drug transport reduced to the transport of a passive scalar simply advected with the CSF.
Injection simulations and parameters
The following numerical simulations, Si (Table 1), were conducted to understand the impact of catheter position, angle, injection flow rate and CSF space anatomy:
S1-S6 to evaluate the effects of catheter position (perpendicular injection with a 6 cm/s injection speed);
S2, S7, S8 to evaluate the effects of catheter angle in a frontal position (injection at P2 with a 6 cm/s injection speed);
S6, S9, S10 to evaluate the effects of catheter angle in a lateral position (injection at P6 with a 6 cm/s injection speed);
S2, S11, S12 to evaluate the effects of injection speed (perpendicular injection at P2).
Table 1. Summary of injection simulations and parameters analyzed.
| Test Case | Position | θ | ϕ | |
|---|---|---|---|---|
| S1 | P1 | 0 | 0 | 6 |
| S2 | P2 | 0 | 0 | 6 |
| S3 | P3 | 0 | 0 | 6 |
| S4 | P4 | 0 | 0 | 6 |
| S5 | P5 | 0 | 0 | 6 |
| S6 | P6 | 0 | 0 | 6 |
| S7 | P2 | 0 | 45° | 6 |
| S8 | P2 | 45° | 0 | 6 |
| S9 | P6 | 0 | 45° | 6 |
| S10 | P6 | 45° | 0 | 6 |
| S11 | P2 | 0 | 0 | 3 |
| S12 | P2 | 0 | 0 | 0 |
| P1 | 0 | 0 | 6 |
Position: Six different injection positions were considered at the cervical level (between C5-C7 vertebra levels), located either on the dorsal (P1-P4) or on the dorsolateral side (P5-P6) of the spinal SAS, within the CSF close to the outer arachnoid wall, as shown in Fig 1(b). We located the catheter injection positions dorsally between consecutive nerve bundles, a location that is also accessible by a needle that can penetrate the intervertebral disks.
Angle: We considered three different catheter angles at a single fixed injection position. In particular, we assumed the injection jet perpendicular (θ = ϕ = 0°) to the spinal cord, inclined 45°-up (θ = 0°, ϕ = 45°) and 45°-right (θ = 45°, ϕ = 0°), where θ and ϕ are respectively the azimuth and elevation angles between the z-axis and the injection direction shown in Fig 1(c).
Flow: We also investigated the effect of the injection speed (). The main value we adopted, i.e. , was estimated as the ratio between a volumetric flow rate through a cross section Sn of a clinically used 22-gauge catheter [34–36]. This flow rate is also representative of the ongoing screening trial for intrathecal Baclofen administration [37–39]. Moreover, to account for slower injections, we also considered 3 and 0 cm/s (the latter value describes a limit case where the drug starts to be advected with the local fluid velocity at the injection point).
Anatomy: To investigate the impact of small anatomical structures on drug distribution, simulation was conducted with identical properties as S1 except for a geometry that did not include the NRDL. Two additional test cases were also conducted with the catheter removed from the model (no drug injected) with NRDL (test case PS1) and without NRDL (). These test cases are not reported in Table 1 because they are not directly related to IT working parameters, yet the associated results are discussed.
Governing equations
We considered that the CSF flows in the SAS domain because of time-varying pressure gradient generated by the cardiac pulsation. Moreover, since the CSF is a fluid similar to water, we assumed it to be incompressible, and we retained the viscous effects since they play a key role in a complex confined boundary like the SAS including NRDL. To obtain the CSF velocity in the SAS (below denoted by Ω), we thus adopted the following governing Eq (1) representing the mass and the momentum balance (Navier-Stokes equations) for the fluid:
| (1) |
where u = (u(x, t), v(x, t), w(x, t)) and p = p(x, t) are the unknowns of the problem and respectively denote the CSF velocity and pressure (x = (x, y, z) is the coordinate vector). Moreover, denotes a chosen time-interval, ν and ρ respectively represent the CSF kinematic viscosity and density (ν = 7 ⋅ 10−7 m2/s, ρ = 103 kg/m3 as for water at 37°), and vin represents the y-component of the CSF velocity at the inflow (Γi) cross-section, obtained from experimental measurements. Furthermore, vinj denotes the prescribed injection velocity (directly assigned within the injection volume Ωn). Finally, Γw represents the SAS walls, shown in Fig 1(d), and Γo the outflow cross-section on the cranial end of the model.
We studied drug distribution by adopting a Lagrangian particle tracking approach (see e.g. [40]). Conversely to the Eulerian continuum approach, we described the drug through p discrete particles (massless, thanks to the isobaric approximation) that do not collide with one another, and we solved the momentum equation for each particle at every time step. The vector , where (i = (1, 2, ⋯, p)) is the unknown position of the i-th particle, identified the drug distribution. We determined the particle pathline by integration of the following ordinary differential equation:
| (2) |
which represents the advective transport coupled with a specific initial condition. Moreover, with regard to particle seeding, we injected a fixed number of particles per time step () at random points inside a sphere having radius equal to the catheter inner radius and located adjacent to the injection position (the coordinates of the sphere center were obtained translating the coordinates of the injection position by a quantity equal to the sphere radius).
The numerical methods adopted in order to integrate the considered governing equations are detailed in S1 Appendix; related independence studies are detailed in S2 Appendix.
Hereafter, unless differently specified, we show the concentration c that denotes a normalized drug concentration on a fixed cross-section at a distance of Δy from the injection point. In particular, we divided the concentration in a thin volume slice (0.8 mm thick) centered at the considered cross-section by the total average concentration in the whole domain after 10 cycles.
Results
Effects of the nerve roots and denticulate ligaments
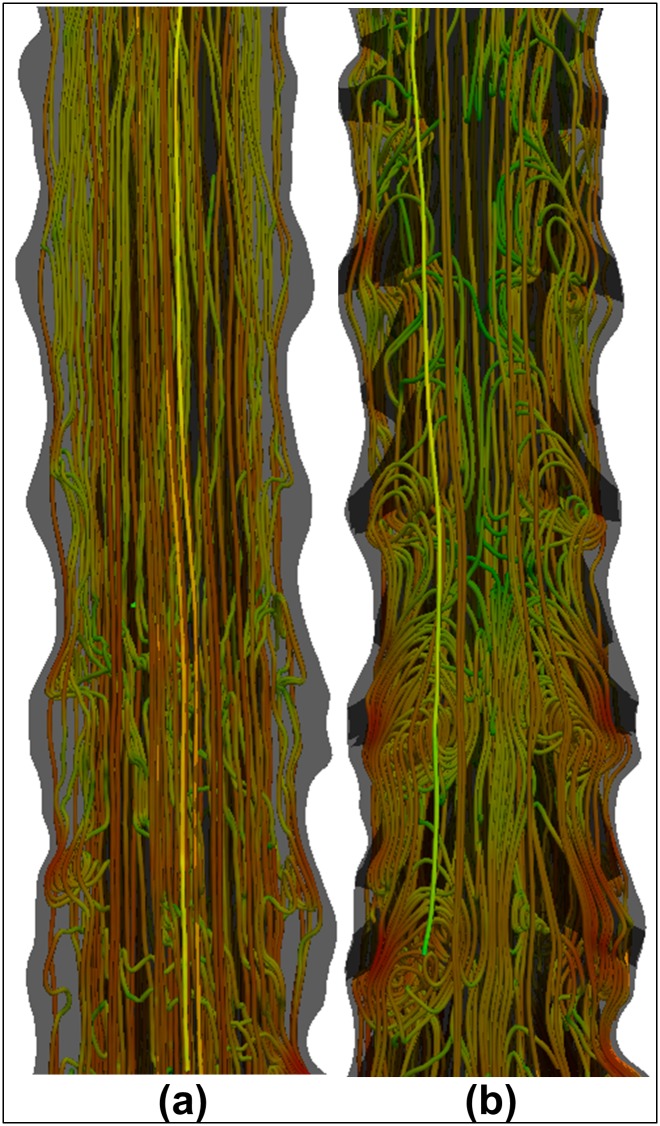
The effects of NRDL on the CSF fluid flow are shown in Figs 2–4 and Table 2. In particular, Fig 2 shows the CSF streamlines at t = 4.5 T for test cases PS1 (with NRDL) and (without NRDL). In addition, Table 2 shows the CSF peak velocity (clinically called systolic velocity, vsys) and the peak pressure drop between two consecutive spinal cross-sections (Δppeak) selected out of those reported in Fig 1(a).
Fig 2. CSF flow streamlines at t/T = 4.5.
The reported streamlines are obtained from test cases (a) (without NRDL) and (b) PS1 (with NRDL).
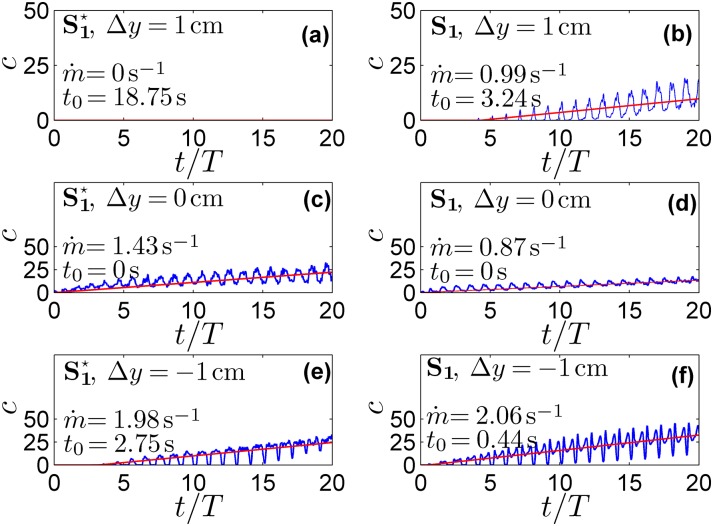
Fig 4. Time evolution of the normalized drug concentration and relative linear fitting.
The blue lines represent the time evolution of the normalized drug concentration at different cross sections from the injection point for (a) and (b) S1. The red line indicates the relative linear fitting ().
Table 2. Hydrodynamics parameters within each spinal segment resulting from test cases PS1 and .
| Level | vsys[cm/s] | Δppeak[Pa] | ||
|---|---|---|---|---|
| PS1 | PS1 | |||
| FM | 0.98 | 0.93 | - | - |
| C1 | 2.09 | 1.60 | 0.87 | 0.80 |
| C2M | 2.71 | 1.67 | 4.15 | 3.33 |
| C2P | 2.29 | 1.46 | 2.37 | 2.00 |
| C3 | 3.85 | 2.26 | 6.20 | 5.11 |
| C4 | 3.93 | 2.51 | 6.89 | 5.42 |
| C5 | 4.56 | 2.76 | 7.80 | 5.44 |
| C6 | 4.44 | 2.47 | 8.39 | 6.12 |
| C7 | 5.57 | 4.46 | 6.61 | 4.73 |
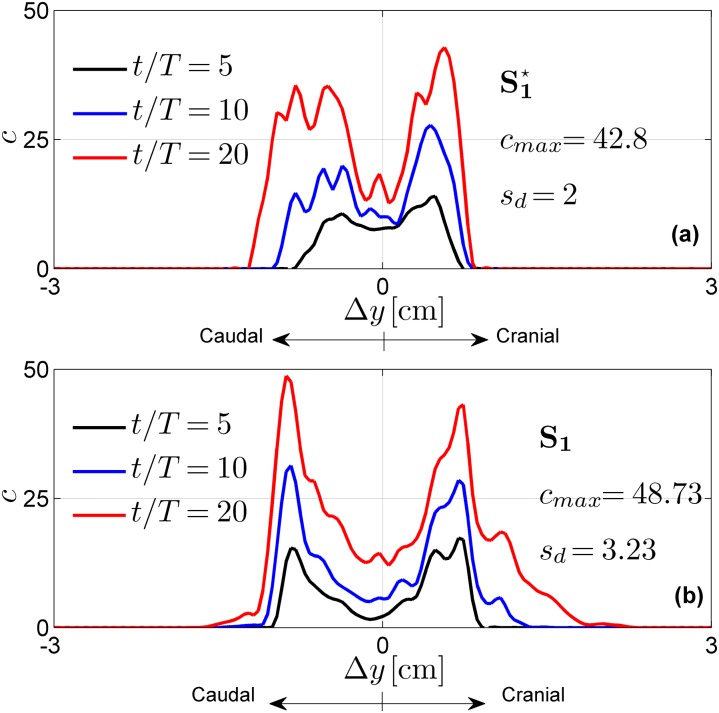
The strong differences in the CSF flow field caused by the NRDL microanatomy (i.e. microanatomy-induced CSF mixing effects) were expected to alter drug transport. This was verified by the results shown in Figs 3 and 4, where the former reports the concentration at fixed times versus Δy and the latter shows the concentration at selected Δy versus time. Moreover, from the spatial distribution at a fixed instant, we extracted the maximum drug concentration (cmax) at the selected injection time and the corresponding extent of drug spreading (sd) along the y-axis. After a linear average growth was observed in Fig 4, we introduced the following linear regression:
so as to extract the drug accumulation rate and the time t0 when drug first appears at each section.
Fig 3. Normalized drug concentration profiles as a function of the distance Δy from the injection point P1.
The reported profiles result from (a) and (b) S1.
In light of the noticeable differences brought by NRDL on the underlying CSF flow field and, consequently, on drug distribution, we analyzed the effects of the injection parameters only in relation to the mesh with NRDL, so as to obtain more realistic results.
Effects of the injection parameters
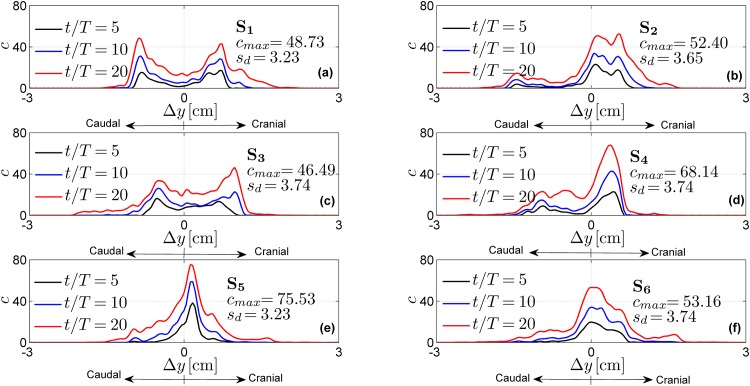
The effects of the injection parameters on the drug spatial distributions are shown in Figs 5–7 for all test cases. These figures also report maximum concentration cmax and drug spread sd at injection time t = 20 T. Tables 3–5 report the drug accumulation rate () and appearance time (t0) for selected values of Δy. In particular, Table 3 reports the effects of the injection position, Table 4 the effects of catheter angles and Table 5 the effects of injection speed. Finally, in Fig 8 we report cross-sectional views of the CSF velocity and of the dimensional drug concentration (number of particles per mm3) at t = 20 T, to qualitatively visualize how the drug spreads in the SAS annulus while moving the injection position laterally.
Fig 5. Normalized drug concentration profiles as a function of the distance Δy from the injection point for different injection positions.
The profiles are obtained with test cases S1-S6.
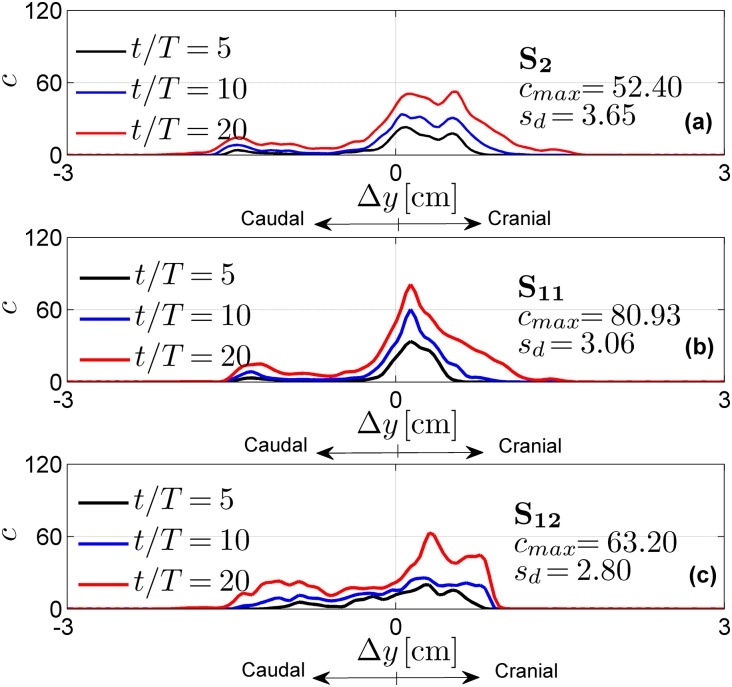
Fig 7. Normalized drug concentration profiles as a function of the distance Δy from the injection point P2 for different injection speeds.
The profiles are obtained with test cases S2, S11, S12.
Table 3. Drug accumulation rate (1/s) and appearance instant (s), as obtained by varying the catheter position.
| Δy[cm] | S1 | S2 | S3 | S4 | S5 | S6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t0 | t0 | t0 | t0 | t0 | t0 | |||||||
| 1 | 0.99 | 3.24 | 0.52 | 2.46 | 1.13 | 2.46 | 0.09 | 6.33 | 0.27 | 3.18 | 0.39 | 3.12 |
| 2/3 | 3.24 | 0.87 | 1.51 | 0.87 | 2.46 | 0.84 | 0.49 | 1.68 | 0.63 | 1.72 | 0.76 | 1.65 |
| 1/3 | 1.63 | 0.72 | 2.42 | 0.75 | 1.13 | 0.72 | 2.09 | 0.78 | 1.82 | 0.78 | 1.97 | 0.75 |
| 0 | 0.87 | 0.0 | 2.87 | 0.0 | 1.19 | 0.0 | 2.79 | 0.0 | 3.21 | 0.0 | 2.65 | 0.0 |
| -1/3 | 0.84 | 0.22 | 1.42 | 0.22 | 1.30 | 0.22 | 1.30 | 0.22 | 2.23 | 0.22 | 2.17 | 0.22 |
| -2/3 | 1.58 | 0.31 | 0.43 | 0.31 | 1.87 | 0.31 | 1.22 | 0.31 | 1.58 | 0.31 | 1.10 | 0.31 |
| -1 | 2.06 | 0.44 | 0.41 | 0.37 | 0.87 | 1.22 | 0.31 | 0.37 | 0.70 | 1.12 | 0.72 | 1.19 |
Table 5. Drug accumulation rate (1/s) and appearance instant (s), as obtained by varying the injection speed.
| Δy[cm] | S2 | S11 | S12 | |||
|---|---|---|---|---|---|---|
| t0 | t0 | t0 | ||||
| 1 | 0.52 | 2.46 | 0.42 | 4.84 | 0.24 | 4.80 |
| 2/3 | 1.51 | 0.87 | 1.39 | 1.68 | 0.91 | 3.21 |
| 1/3 | 2.42 | 0.75 | 2.15 | 0.81 | 2.47 | 0.81 |
| 0 | 2.87 | 0.0 | 3.52 | 0.0 | 2.29 | 0.0 |
| -1/3 | 1.42 | 0.22 | 1.46 | 0.25 | 0.85 | 0.25 |
| -2/3 | 0.43 | 0.31 | 0.37 | 0.31 | 1.15 | 0.37 |
| -1 | 0.41 | 0.37 | 0.41 | 0.41 | 0.74 | 1.22 |
Table 4. Drug accumulation rate (1/s) and appearance instant (s), as obtained by varying the catheter angle.
| Δy[cm] | S2 | S7 | S8 | S6 | S9 | S10 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t0 | t0 | t0 | t0 | t0 | t0 | |||||||
| 1 | 0.52 | 2.46 | 0.71 | 0.90 | 0.68 | 3.99 | 0.30 | 3.12 | 0.56 | 2.43 | 0.14 | 2.46 |
| 2/3 | 1.51 | 0.87 | 1.57 | 0.81 | 1.36 | 0.90 | 0.59 | 1.65 | 0.99 | 0.84 | 0.35 | 1.59 |
| 1/3 | 2.42 | 0.75 | 2.79 | 0.66 | 1.86 | 0.78 | 1.52 | 0.75 | 2.55 | 0.66 | 1.49 | 0.75 |
| 0 | 2.87 | 0.0 | 2.26 | 0.0 | 2.58 | 0.0 | 2.04 | 0.0 | 7.66 | 0.0 | 3.79 | 0.0 |
| -1/3 | 1.42 | 0.22 | 0.65 | 0.28 | 2.13 | 0.22 | 1.66 | 0.22 | 1.40 | 0.28 | 2.89 | 0.22 |
| -2/3 | 0.43 | 0.31 | 0.15 | 0.41 | 0.69 | 0.31 | 0.84 | 0.31 | 0.56 | 0.44 | 1.55 | 0.34 |
| -1 | 0.41 | 0.37 | 0.08 | 5.05 | 0.60 | 0.41 | 0.56 | 1.19 | 0.51 | 2.75 | 0.53 | 1.90 |
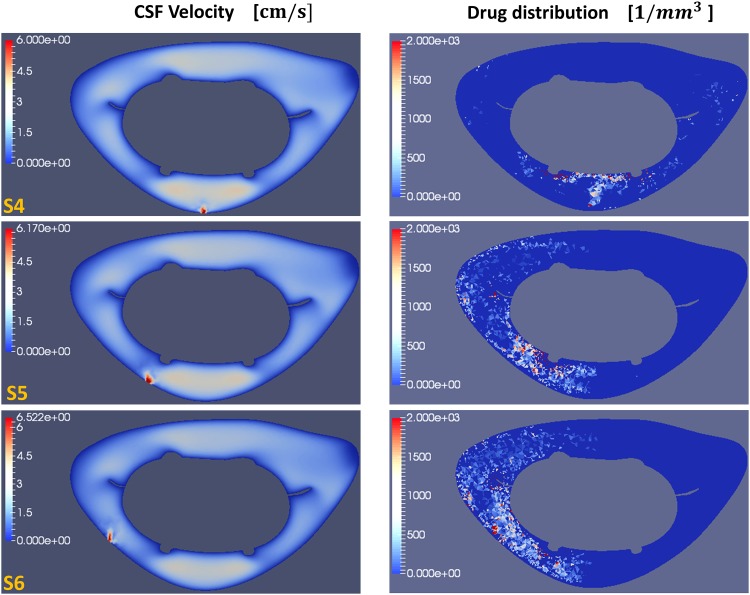
Fig 8. Cross-sectional views of the CSF velocity magnitude and dimensional drug concentration.
(left) Magnitude of the CSF velocity at t = 20 T and (right) corresponding dimensional drug concentration (number of particles per volume) at Δy = 0 cm (C5-level) for test cases S4, S5 and S6.
Discussion
This study applied computational fluid dynamics to assess IT in an anatomically detailed model of the upper cervical spine. Overall, our findings suggest that IT is sensitive to many factors and that computational modeling can offer insight into how individual factors may be tuned to produce a desired drug delivery profile. Our approach was to model the drug as massless particles within the flow field injected from a catheter located in the cervical spine and parametrically assess the impact of the following parameters on the drug spread over a short time scale (∼ 15 s) following the injection: a) influence of fine anatomical structures, b) catheter location, c) catheter angle, d) catheter flow rate. The key findings of this study were the following:
Small anatomic structures (NRDL) within the SAS increase axial drug spread by 60% in comparison to a model without these structures;
Catheter injection location can alter the axial drug distribution up to ∼90%;
Catheter angle can steer/shift the axial drug distribution up to ∼90%;
Injection flow rate modulates the peak magnitude of drug concentration up to ∼78%. Also, catheter flow rate can alter the axial distribution.
Herein, we describe the above findings in context of the results and compare the findings to previous studies focused on IT.
Spinal cord nerve roots and denticulate ligaments (NRDL) increase drug mixing
The presence of NRDL within the computational model was found to increase drug spread by 60% and alter the axial distribution of the drug along the SAS. The preliminary CFD simulations on mesh no.1 and no.2 without injection (test cases and PS1, respectively), showed that micro-anatomical structures induce vorticity (Fig 2), and NRDL generate a complex CSF flow field characterized by vortices aligned along the SAS axis that greatly enhance mixing through mechanisms similar to those observed in a turbulent flow. These results are consistent with previous studies [28, 30, 32]. Moreover, we observed that the mixing phenomenon occurs when CSF velocity shifts from the cranial to the caudal direction and vice versa, as shown in Fig 2(b) for t/T = 4.5.
Furthermore, we also noticed that microanatomy increases the CSF systolic velocity and peak pressure drop. In particular, as reported in Table 2, we observed a total average increase of 29% for velocity and 21% for pressure. Considering some deviation due to the specific spinal levels selected to observe the solution, these results are consistent with those reported in [32], where the authors ran simulations on the same geometry using ANSYS Fluent. Finally, the pressure drop between the FM and C4 is similar in magnitude with results obtained by [30] although the velocity they reported was three times lower. This elevated pressure drop is likely attributable to the presence of arachnoid trabeculae included in [30], an anatomic feature that was not included in the model used in the current study. [41, 42] completed a study of CSF flow around the brain that included arachnoid trabeculae and these structures have been shown to increase pressure gradients by a factor that varies according to their density and size. Also, the geometric and flow boundary conditions used by [30] were different from the present study. Thus, further simulations would be necessary to carry out a detailed comparison of results.
The CSF stirring effects due to NRDL impact drug transport is shown in Figs 3 and 4. In particular, Fig 3 shows that for the mesh with NRDL the drug spreads much farther, both in the cranial and caudal direction. Indeed, sd is approximately 60% higher than in the case without NRDL. This is confirmed by the parameters and t0 assessed through linear fitting shown in Fig 4. In particular, for the case with NRDL, t0 assumes lower values, especially farther from the injection point, indicating a faster drug spread. At Δy = ±1 cm, t0 is ∼6 times lower than the corresponding parameter for the case without NRDL. This aspect is further confirmed by the value of the accumulation term at the injection cross-section (Δy = 0 cm). Indeed, it is 35% lower than the case without NRDL, showing that drug accumulates less around the injection point and moves farther (e.g. in the case without NRDL drug does not reach the cross-section at Δy = 1 cm).
Catheter injection location alters axial drug distribution and spread rate
Our results showed that catheter injection location can alter the axial distribution and spread rate significantly. This IT effect is likely attributable to locally elevated CSF velocities, or jets, that may occur between NRDL and within other constricted SAS spaces. In particular, with regard to Fig 5, we observe two different trends when the catheter is inserted in the dorsal SAS (P1-P4). For an injection at P1 and P3, located in the middle of the nerve bundle, drug distributes symmetrically with two peaks in the caudal and cranial directions. For an injection at P2 and P4, located between two consecutive nerve bundles, the drug spreads with a single peak located in the cranial direction and a uniform tail distributed caudally.
These trends can be justified in light of the CSF velocity profile at these spinal levels. We observed velocity jets in P1 and P3 due to restriction of the SAS at those locations (velocity profile modulations caused by domain restrictions are also analyzed for idealized geometries, e.g. in [43]). Indeed, for an injection at P1 and P3 we do not observe concentration peaks around the injection site (where instead the drug is carried away quickly). In contrast, they appear for drug injection at P2 and P4. Thus, the different drug distributions reflect geometry-induced flow patterns. The characteristic peaks of each distribution can be also detected by the higher values of reported in Table 3. Finally, from the same table we can also observe that all the aforementioned injection positions make the drug spread faster caudally than cranially (t0 assumes lower values for Δy < 0).
For an injection performed at the dorsolateral position, namely P5 and P6, we notice that drug distribution is similar to a bell profile. The corresponding values for and t0 in Table 3, decrease and increase, respectively along both directions starting from the injection position.
Similar to our results, [26] observed that the drug spreads cranially in the ventral and dorsal SAS, while it moves caudally in the lateral region. Moreover, Fig 8 shows that shifting the injection at lateral positions, the drug starts to spread around the spinal cord, and by injecting at P5 and P6 (the two most lateral positions) it moves towards the ventral side of the SAS (Fig 8(b) and 8(c)). Finally, from Fig 5 it can be seen that although different injections positions do not produce large differences in terms of drug spreading (sd), they have significant impact on the shape of the drug distribution. All injection positions (with perpendicular catheter angle) result in a faster drug spreading in the caudal direction. However, even if the peak concentration generally occurs in the cranial direction, based on the limited number of considered test-cases it is hard to extract a general conclusion.
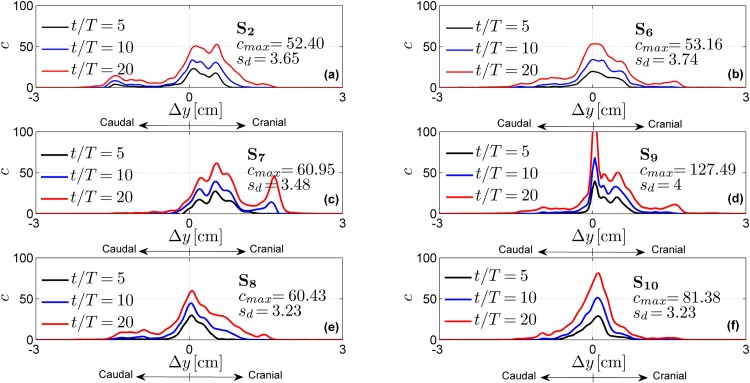
Catheter angle can tune drug spread direction
The effects of catheter angle are shown in Fig 6 respectively at a fixed dorsal (Fig 6(a), 6(c) and 6(e)) and dorsolateral (Fig 6(b), 6(d) and 6(f)) injection position. In contrast to catheter position, catheter angle was not found to broadly modify the shape of the drug concentration profile, but did shift the distribution. In particular, among the evaluated angles, the upward angle (test cases S7 and S9) moved the drug more cranially, as expected. This is confirmed by parameters listed in Table 4 where the upward injections produce the highest values of at the cranial levels and the lowest at the caudal levels compared to the results obtained with different angles in the same position. Consistently, S7 and S9 show the lowest cranial values of t0 and the highest caudal ones. Therefore, it means that the drug spreads faster in the head direction where it accumulates.
Fig 6. Normalized drug concentration profiles as a function of the distance Δy from the injection point for different catheter angles.
The profiles are obtained with a dorsal injection located at P2 (for test cases S2, S7, S8) and with a lateral injection located at P6 (for test cases S6, S9, S10).
Conversely, the right injection in the dorsal position (S8) shifted the peak concentration caudally, increasing the accumulation in the caudal direction. Indeed, between the test cases performed with dorsal injection and reported in Table 4 (i.e. S2, S7 and S8), S8 gives the highest values of t0 for Δy > 0 and of for Δy < 0. This result is consistent with that reported by [25], which shows an increment of caudal-to-cranial drug concentration ratio with a catheter angle towards the SAS wall. However, this aspect is less evident with the rightward angle at a lateral injection position (S10). Indeed, we can only notice higher values of the accumulation term for Δy < 0 compared to that of S6 and S9. However, from Fig 6 we notice that the rightward injection, in both dorsal and lateral position, reduces the drug spread sd. Finally, the effects of different catheter angles are more pronounced in terms of variations of peak concentration and drug spread by lateral injection position (e.g. S9 provides a peak concentration around 130 that is more than twice the one of S6).
Drug injection flow rate alters peak drug concentration
Drug injection flow rate altered cmax and sd (Fig 7). An higher injection speed increased drug spread and reduced the peak concentration. These results are consistent with experimental observations by [22]. Moreover, this trend is also consistent with the results in Fig 7(c) for longer injection times. Indeed, the null injection speed, S12 represents a limit case where concentration is entirely relying on the underlying CSF flow field (for which it might take time for local maxima to appear). Finally, the enhanced drug spread obtained at higher flow rate can be appreciated in Table 5 that reports for S12 values of t0 in the cranial and caudal part respectively ∼ twice and four times the ones of S2.
Limitations
Our approach included a relatively small axial section of the upper spine (18 cm axial length) within the computational domain. The limited domain extension did not allow us to take into consideration drug delivery to the brain, which represents an important goal of IT therapy, as well as drug injection within the lumbar spine (often performed in IT protocol). However, our focus was on the cervical spine as this region has not been specifically examined in the literature and is of clinical interest for certain drug delivery protocols [44–46], gene therapy [14] and for targeting drug delivery to the cord or nerve roots. In addition, the computational geometry did not include arachnoid trabeculae, structures that have been shown in the past to alter the CSF flow field [28, 30, 42]. The proposed modeling framework can be used to further investigate the impact of arachnoid trabeculae in future studies. However, we expect the key findings of the present study, using variational analysis by altering specific factors, to hold even if small anatomic structures are included. Finally, we did not lose any particles through the open domain boundaries, since none of them reached the upper/lower ends of the computational domain, yet adopting a full CSF space geometry characterized by closed boundaries would improve future CNS studies.
The complex SAS geometry requires CPU-demanding simulations since we adopted a forward-modeling approach to resolve the physics both in space and time. Thus, we chose to simulate a limited time window (15 s). Each simulation required a total of 960 CPU hours, with a total of 12700 CPU hours for all simulations performed in the study. The considered time window did not allow examination of bolus versus continuous IT over a longer time window, although our model can also describe the effects of discontinuous injection, as shown by preliminary numerical experiments (cf. S3 Appendix). In addition, the large CPU time restricted the number of the injection parameters we were able to analyze.
It should be noted that on a longer time scale, additional physical effects, such as drug diffusion and extravasation, must also be more carefully considered. It is therefore important to extend the simulation time window to improve clinical relevance of the numerical model. To reach this goal, the numerical schemes must be improved to reduce computational cost. Further model refinements include the adoption of non isobaric drug, since baricity plays an important role in IT [47], as well as reaction terms in the drug transport equation for modeling the physical interaction with porous tissue adjacent to the SAS membranes [48]. Specific drug species as well as finer interaction mechanisms/dynamics are important aspects to be included in future studies so to properly plan IT treatments on a longer time scale for a particular drug. However, it is worth highlighting that specific pharmacokinetics/dynamics parameters are not often available or easily detectable in a closed domain such as the lumbar SAS region. In addition, the breathing force affecting the CSF flow field through the mobility of the SAS walls may be important. A study by Cheng found that the effect of breathing on the CSF flow may not be important [49]. Other studies have indicated that CSF flow can be altered by respiration [50]. Future work could help understand the clinical relevance of different drug distributions by coupling in vivo MRI measurements of CSF flow, geometry and drug spread, and by improving the provided computational framework with a more extensive anatomical domain, up to including specific species transport equations to suitably describe transport mechanisms on a longer time scale.
Finally, the specific catheter geometry and drug velocity profile when exiting the catheter should be introduced to investigate possible steady streaming effects around the catheter that may enhance drug dispersion (see e.g. [23]). In general, however, experimental data related to cervical injection (in particular over a short time window) are needed in order to fully validate the numerical results.
Conclusions
We addressed the IT treatment within the cervical spine and the role of injection parameters, namely the catheter position, angle and injection flow rate on drug distribution. Within our model based on known physical laws, all investigated parameters were found to impact the IT distribution.
Catheter position was found to affect the drug distribution profile. Catheter angle shifted the concentration profile along the spine. Higher injection flow rates enhanced drug spread while reducing the peak concentration.
The computational modeling approach provides detailed insight into how the drug concentration is impacted within the CSF. The threshold at which these alterations would make a clinically significant difference is not yet known. We cannot extract general working guidelines based on these results, which however suggest to choose the injection position in view of the targeted therapeutic area. Future work could help understand the clinical relevance of different drug distributions by coupling in vivo MRI measurements of CSF flow, geometry and drug spread, by improving the provided computational framework with a more extensive anatomical domain, detailed drug properties and transport mechanisms on a longer time frame.
Supporting information
Description of the numerical approach adopted to carry out the performed simulations.
(PDF)
Convergence studies of the shown solutions.
(PDF)
Exemplary numerical results showing drug concentration evolution after injection for test case S1.
(PDF)
Data Availability
All relevant data are within the paper.
Funding Statement
This work was supported by the National Institute of General Medical Sciences, grants P20GM103408 and 4U54GM104944-04 to BM, the University of Idaho, Vandal Ideas Project to BM and by the American Syringomyelia and Chiari Alliance Project to BM. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Papisov MI, Belov VV, Gannon KS. Physiology of the intrathecal bolus: the leptomeningeal route for macromolecule and particle delivery to CNS. Mol Pharm. 2013;5(10):1522–1532. 10.1021/mp300474m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Johanson CE, Duncan JA 3rd, Klinge PM, Brinker T, Stopa EG, Silverberg GD. Multiplicity of cerebrospinal fluid functions: new challenges in health and disease. Cerebrospinal Fluid Res. 2008;5(10):441–450. 10.1186/1743-8454-5-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Heetla HW, Staal MJ, Proost JH, van Laar T. Clinical Relevance of Pharmacological and Physiological Data in Intrathecal Baclofen Therapy. Arch Phys Med Rehabil. 2014;95(11):2199–2206. 10.1016/j.apmr.2014.04.030 [DOI] [PubMed] [Google Scholar]
- 4. Bhatia G, Lau ME, Gulur P, Koury KM. Intrathecal Drug Delivery (ITDD) systems for cancer pain. F1000Res. 2013; 2(96):1–13. 10.12688/f1000research.2-96.v4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Soderquist RG, Mahoney MJ. Central nervous system delivery of large molecules: challenges and new frontiers for intrathecally administered therapeutics. Expert Opin Drug Deliv. 2010;7(3):285–293. 10.1517/17425240903540205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Dickson P, McEntee M, Vogler C, Le S, Levy B, Peinovich M, et al. Intrathecal enzyme replacement therapy: successful treatment of brain disease via the cerebrospinal fluid. Mol Genet Metab. 2007;91(1):61–68. 10.1016/j.ymgme.2006.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Belichenko PV, Dickson PI, Passage M, Jungles S, Mobley WC, Kakkis ED. Penetration, diffusion, and uptake of recombinant human α-l-iduronidase after intraventricular injection into the rat brain. Mol Genet Metab. 2005;86(1):141–149. 10.1016/j.ymgme.2005.04.013 [DOI] [PubMed] [Google Scholar]
- 8. Bottros MM, Christo PJ. Current perspectives on intrathecal drug delivery. J Pain Res. 2014;7:615–626. 10.2147/JPR.S37591 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Perruchoud C, Bovy M, Durrer A, Rutschmann B, Buchser E. Intrathecal drug delivery systems for cancer pain. Swiss Medical Weekly. 2010;140 Suppl 184.
- 10. Van Damme P, Robberecht W. Developments in treatments for amyotrophic lateral sclerosis via intracerebroventricular or intrathecal delivery. Expert Opin Investig Drugs. 2014. July;23(7):955–963. 10.1517/13543784.2014.912275 [DOI] [PubMed] [Google Scholar]
- 11. Calias P, Papisov M, Pan J, Savioli N, Belov V, Huang Y, et al. CNS Penetration of Intrathecal-Lumbar Idursulfase in the Monkey, Dog and Mouse: Implications for Neurological Outcomes of Lysosomal Storage Disorder. PLoS One. 2012;7(1):e30341 10.1371/journal.pone.0030341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Tsai SY, Markus TM, Andrews EM, Cheatwood JL, Emerick AJ, Mir AK, et al. Intrathecal treatment with anti-Nogo-A antibody improves functional recovery in adult rats after stroke. Exp brain Res. 2007. September;182(2):261–266. 10.1007/s00221-007-1067-0 [DOI] [PubMed] [Google Scholar]
- 13.Perruchoud C, Bovy M, Smit A, Rutschmann B, Durrer A, Buchser E. Intrathecal administration of Ziconotide: does single-shot injection predict efficacy?. Swiss Medical Weekly. 2010;140 Suppl 184.
- 14. Gray SJ, Kalburgi SN, McCown TJ, Samulski RJ. Global CNS gene delivery and evasion of anti-AAV-neutralizing antibodies by intrathecal AAV administration in non-human primates. Gene Ther. 2013. April;20(4):450–459. 10.1038/gt.2012.101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Schuster DJ, Belur LR, Riedl MS, Schnell SA, Podetz-Pedersen KM, Kitto KF, et al. Supraspinal gene transfer by intrathecal adeno-associated virus serotype 5. Front Neuroanat. 2014;8(66). 10.3389/fnana.2014.00066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hocking G, Wildsmith JAW. Intrathecal drug spread. Br J Anaesth. 2004. October;93(4):568–578. 10.1093/bja/aeh204 [DOI] [PubMed] [Google Scholar]
- 17. De Andres J, Perotti L, Villanueva V, Asensio SJM, Fabregat-Cid G. Role of Catheter’s Position for Final Results in Intrathecal Drug Delivery. Analysis Based on CSF Dynamics and Specific Drugs Profiles. Korean J Pain. 2013. October;26(4):336–346. 10.3344/kjp.2013.26.4.336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Narouze SN, Casanova J, Souzdalnitski D. Patients with a history of spine surgery or spinal injury may have a higher chance of intrathecal catheter granuloma formation. Pain Practice. 2014;14(1):57–63. 10.1111/papr.12024 [DOI] [PubMed] [Google Scholar]
- 19. Morrison C. $1-million price tag set for Glybera gene therapy. Nature Biotech. 2015;33(3):217–218. 10.1038/nbt0315-217 [DOI] [PubMed] [Google Scholar]
- 20. Xie H, Chung JK, Mascelli MA, McCauley TG. Pharmacokinetics and Bioavailability of a Therapeutic Enzyme (Idursulfase) in Cynomolgus Monkeys after Intrathecal and Intravenous Administration. PLoS One. 2015. April;10(4):e0122453 10.1371/journal.pone.0122453 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Perruchoud C, Eldabe S, Durrer A, Bovy M, Brookes M, Madzinga G, et al. Effects of flow rate modifications on reported analgesia and quality of life in chronic pain patients treated with continuous intrathecal drug therapy. Pain Medicine. 2011;12(4):571–576. 10.1111/j.1526-4637.2011.01088.x [DOI] [PubMed] [Google Scholar]
- 22. Robinson RA, Stewart SF, Myers MR, Lien LF, Rinaldi JR, Swisher JL, et al. In vitro modeling of spinal anesthesia. A digital video image processing technique and its application to catheter characterization. Anesthesiology. 1994. October;81(4):1053–1060. [PubMed] [Google Scholar]
- 23.Nelissen RM. Fluid mechanics of intrathecal drug delivery. Doctoral Thesis, EPFL. 2008. Available: http://infoscience.epfl.ch/record/117041
- 24. Tangen K, Narasimhan NS, Sierzega K, Preden T, Alaraj A, Linninger AA. Clearance of Subarachnoid Hemorrhage from the Cerebrospinal Fluid in Computational and In Vitro Models. Ann Biomed Eng. 2016; 6:1–17. [DOI] [PubMed] [Google Scholar]
- 25. Myers MR. A numerical investigation into factors affecting anesthetic distribution during spinal anesthesia. J Biomech. 1996;29(2):139–149. 10.1016/0021-9290(95)00043-7 [DOI] [PubMed] [Google Scholar]
- 26. Kuttler A, Dimke T, Kern S, Helmlinger G, Stanski D, Finelli LA. Understanding pharmacokinetics using realistic computational models of fluid dynamics: biosimulation of drug distribution within the CSF space for intrathecal drugs. J Pharmacokinet Pharmacodyn. 2010. December;37(6):629–644. 10.1007/s10928-010-9184-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Hsu Y, Hettiarachchi HDM, Zhu DC, Linninger AA. The frequency and magnitude of cerebrospinal fluid pulsations influence intrathecal drug distribution: key factors for interpatient variability. Anesth Analg. 2012. August;115(2):386–394. 10.1213/ANE.0b013e3182536211 [DOI] [PubMed] [Google Scholar]
- 28. Stockman HW. Effect of anatomical fine structure on the flow of cerebrospinal fluid in the spinal subarachnoid space J Biomech Eng. 2006; 128(1):106–114. 10.1115/1.2132372 [DOI] [PubMed] [Google Scholar]
- 29. Stockman HW. Effect of anatomical fine structure on the dispersion of solutes in the spinal subarachnoid space. J Biomech Eng. 2007; 129(5):666–675. 10.1115/1.2768112 [DOI] [PubMed] [Google Scholar]
- 30. Tangen KM, Hsu Y, Zhu DC, Linninger AA. CNS wide simulation of flow resistance and drug transport due to spinal microanatomy, J Biomech. 2015. July;48(10):2144–2154. 10.1016/j.jbiomech.2015.02.018 [DOI] [PubMed] [Google Scholar]
- 31. Yiallourou TI, Kröger JR, Stergiopulos N, Maintz D, Martin BA, Bunck AC. Comparison of 4D phase-contrast MRI flow measurements to computational fluid dynamics simulations of cerebrospinal fluid motion in the cervical spine. PLoS One. 2012; 7(12):e52284 10.1371/journal.pone.0052284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Heidari Pahlavian S, Yiallourou T, Tubbs RS, Bunck AC, Loth F, Goodin M, et al. The impact of spinal cord nerve roots and denticulate ligaments on cerebrospinal fluid dynamics in the cervical spine. PLoS One. 2014;9(4):e91888 10.1371/journal.pone.0091888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Clark SL, Edeson RO, Ryall RW. The relative significance of spinal and supraspinal actions in the antinociceptive effect of morphine in the dorsal horn: an evaluation of the microinjection technique. Br J Pharmacol. 1983. July;79(3):807–818. 10.1111/j.1476-5381.1983.tb10019.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. De Pinto M, Naidu RK. Peripheral and Neuraxial Chemical Neurolysis for the Management of Intractable Lower Extremity Pain in a Patient with Terminal Cancer. Pain Physician. 2015;18:E651–E656. [PubMed] [Google Scholar]
- 35. Linninger AA, Somayaji MR, Erickson T, Guo X, Penn RD. Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue. J Biomech. 2008;41(10):2176–2187. 10.1016/j.jbiomech.2008.04.025 [DOI] [PubMed] [Google Scholar]
- 36. Myers MR, Malinauskas RA. Effect of orifice-area reduction on flow characteristics during injection through spinal needles. Anaesthesia. 1998;53(2):151–156. 10.1046/j.1365-2044.1998.00286.x [DOI] [PubMed] [Google Scholar]
- 37. Stokic DS, Yablon SA, Hayes A. Comparison of clinical and neurophysiologic responses to intrathecal baclofen bolus administration in moderate-to-severe spasticity after acquired brain injury. Arch Phys Med Rehabil. 2005. September;86(9):1801–1806. 10.1016/j.apmr.2005.03.027 [DOI] [PubMed] [Google Scholar]
- 38. Pohl M, Rockstroh G, Rückriem S, Mehrholz J, Pause M, Koch R, et al. Time course of the effect of a bolus dose of intrathecal baclofen on severe cerebral spasticity. J Neurol. 2003. October;250(10):1195–1200. 10.1007/s00415-003-0178-1 [DOI] [PubMed] [Google Scholar]
- 39. Meythaler JM, Guin-Renfroe S, Brunner RC, Hadley MN. Intrathecal baclofen for spastic hypertonia from stroke. Stroke. 2001. September;32(9):2099–2109. 10.1161/hs0901.095682 [DOI] [PubMed] [Google Scholar]
- 40. Ianniello S, Di Mascio A. A self-adaptive oriented particles Level-Set method for tracking interfaces. J Comput Phys. 2010. February;229(4):1353–1380. 10.1016/j.jcp.2009.10.034 [DOI] [Google Scholar]
- 41. Gupta S, Soellinger M, Boesiger P, Poulikakos D, Kurtcuoglu V. Three-dimensional computational modeling of subject-specific cerebrospinal fluid flow in the subarachnoid space. J Biomech Eng. 2009;131(2):021010 10.1115/1.3005171 [DOI] [PubMed] [Google Scholar]
- 42. Gupta S, Soellinger M, Grzybowski DM, Boesiger P, Biddiscombe J, Poulikakos D, et al. Cerebrospinal fluid dynamics in the human cranial subarachnoid space: an overlooked mediator of cerebral disease. I. Computational model. J R Soc Interface. 2010. August;7(49):1195–1204. 10.1098/rsif.2010.0033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Berselli LC, Guerra F, Mazzolai B, Sinibaldi E. Pulsatile Viscous Flows in Elliptical Vessels and Annuli: Solution to the Inverse Problem, with Application to Blood and Cerebrospinal Fluid Flow. SIAM J Appl Math. 2014; 74(1):40–59. 10.1137/120903385 [DOI] [Google Scholar]
- 44. Farhat HI, Elhammady MS, Levi AD, Aziz-Sultan MA. Cervical subarachnoid catheter placement for continuous cerebrospinal fluid drainage: a safe and efficacious alternative to the classic lumbar cistern drain. Neurosurgery. 2011. March;68 1 Suppl Operative:52–56. [DOI] [PubMed] [Google Scholar]
- 45. Dziurzynski K, Mcleish D, Ward M, Iskandar BJ. Placement of baclofen pumps through the foramen magnum and upper cervical spine. Childs Nerv Syst. 2006. March;22(3):270–273. 10.1007/s00381-004-1129-6 [DOI] [PubMed] [Google Scholar]
- 46. McCall TD, MacDonald JD. Cervical catheter tip placement for intrathecal baclofen administration. Neurosurgery. 2006. September;59(3):634–640. 10.1227/01.NEU.0000227570.40402.77 [DOI] [PubMed] [Google Scholar]
- 47. Flack SH, Bernards CM. Cerebrospinal fluid and spinal cord distribution of hyperbaric bupivacaine and baclofen during slow intrathecal infusion in pigs. Anesthesiology. 2010. January;112(1):165–173. 10.1097/ALN.0b013e3181c38da5 [DOI] [PubMed] [Google Scholar]
- 48. Støverud KH, Alnæs M, Langtangen HP, Haughton V, Mardal KA. Poro-elastic modeling of Syringomyelia—a systematic study of the effects of pia mater, central canal, median fissure, white and gray matter on pressure wave propagation and fluid movement within the cervical spinal cord. Comput Methods Biomech Biomed Engin. 2016. May;19(6):686–698. 10.1080/10255842.2015.1058927 [DOI] [PubMed] [Google Scholar]
- 49. Cheng S, Fletcher D, Hemley S, Stoodley M, Bilston L. Effects of fluid structure interaction in a three dimensional model of the spinal subarachnoid space. J Biomech. 2014. August;47(11):2826–2830. 10.1016/j.jbiomech.2014.04.027 [DOI] [PubMed] [Google Scholar]
- 50. Dreha-Kulaczewski S, Joseph AA, Merboldt KD, Ludwig HC, Gärtner J, Frahm J. Inspiration Is the Major Regulator of Human CSF Flow. J Neuroscience. 2015;35(6):2485–2491. 10.1523/JNEUROSCI.3246-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Description of the numerical approach adopted to carry out the performed simulations.
(PDF)
Convergence studies of the shown solutions.
(PDF)
Exemplary numerical results showing drug concentration evolution after injection for test case S1.
(PDF)
Data Availability Statement
All relevant data are within the paper.